变体飞行器先进制导与控制技术专栏
基于不确定LPV系统的变体飞行器姿态控制
0 引言
变体飞行器可以在飞行过程中智能自主地改变自身形态,具有任务执行能力强、快速适应恶劣环境、飞行包线宽等优点。因此,国内外学者进行了广泛的研究[1-2],在其控制器设计领域已开发出了诸如PID[3],深度强化学习[4]等方法。由于构型的变化和极宽的飞行包线范围,变体飞行器的气动参数变化很大,这使其成为一个取决于构型和飞行条件的复杂参数变化系统[5]。目前,变体飞行器的建模与控制研究已成为航空航天领域的热点和难点。
在过去的几十年里,线性变参数(linear parameter varying,LPV)系统的分析与控制技术受到了控制界的广泛关注。文献[6]表明,在变体飞行器机翼折叠过程中,气动力和气动力矩是机翼形状变化的函数并随折翼角度近似线性变化,因此可以将机翼折叠过程看作一个LPV系统。在变体飞行器姿态控制研究中,如单刚体动力学建模和经典PID方法等,已不能满足变体飞行器实际工程要求。LPV方法有效应对了建模不精确,控制设计复杂等难题,因此得到了广泛的应用与研究。文献[7]针对后掠角可变的变体飞行器姿态跟踪系统控制问题,提出了一种平滑切换镇定控制器,保证了系统鲁棒稳定。文献[8]针对可变翼展的变体飞行器,采用鲁棒增益调度控制方法设计了LPV控制器,使系统能够顺利完成变形过渡过程。文献[9]采用参数依赖公共Lyapunov函数方法设计切换LPV控制器,保证了变体飞行器姿态系统在不同控制器间切换时的稳定性和快速性。针对切换线性变参数控制器设计中平均驻留时间的限制,文献[10]设计了一种连续平滑切换器,降低了结论的保守性。此外,研究人员还将LPV方法与其他控制方法相结合,以提高速飞行控制系统的性能。文献[11]将有限时间收敛滑模控制从线性时不变系统推广到了LPV系统,保证了飞行控制系统的L2增益性能。
在目前的大多数LPV研究中,往往需要假设调度变量是可以实时精确测量的,并且可以直接运用于控制器设计。然而控制系统中普遍存在由于传感器精度原因而导致的测量误差。此外,由于LPV系统的获取大多采用拟合的方法,因此系统的不确定性往往是广泛存在的。近年来,处理不精确调度变量和具有不确定性的LPV系统已经成为了一个重要的研究领域。文献[12]假设测量的调度参数的不确定性与实际调度参数的值成比例,设计输出反馈控制器来应对不确定性影响,但由于采用了常数李雅普诺夫函数,因此控制设计具有一定的保守性。文献[13]针对调度参数的绝对/比例不确定性,利用参数依赖线性矩阵不等式和单线搜索参数给出了H∞输出反馈控制器存在的一个充分条件。针对调度参数不确定性的建模问题,文献[14]提出了一种多重单纯形框架,使无限维线性矩阵不等式问题得到了有效解决。文献[15]将不确定调度参数的研究扩展到了切换LPV系统领域,探讨了具有不精确调度参数的LPV迟滞切换和平均驻留时间切换控制设计,保证了切换闭环系统的稳定性和L2增益性能。文献[16]研究了带有参数摄动项的不确定多面体LPV系统,采用滑模控制器保证系统在有限时间内收敛至滑模动态。然而,上述研究大多局限于系统不确定性或不精确调度参数两者之一,同时考虑模型和调度参数不确定性的研究鲜有报道。
针对变体飞行器姿态控制问题,提出了一种基于双层多面体描述的LPV多目标控制器,以便同时考虑调度参数的变化和系统不确定性的影响。第一个多面体层管理调度参数,用于获得顶点不确定系统,在此基础上设计顶点控制器;第二个多面体层建立在每个顶点系统上,以便考虑模型的不确定性并在设计步骤中增加鲁棒性。通过引入松弛变量,降低了设计保守性。较之传统的H∞控制器与H2控制器,该方法不仅可以在同时具有系统不确定性和不精确调度参数情况下保证闭环系统的稳定性,而且还使所设计的跟踪控制器具有较好的鲁棒性和动态特性。最后,仿真验证说明了控制设计的有效性。
1 LPV建模与问题描述
1.1 变体飞行器LPV建模
本文中,以Navion L-17[8]变体飞行器为研究对象进行设计,其两侧机翼可以对称伸缩,可达到的最大翼展为原翼展的两倍。变体飞行器纵向非线性动力学模型为
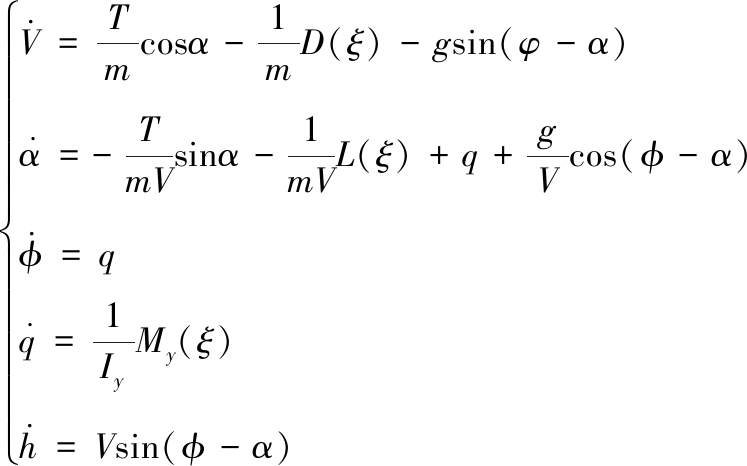
(1)
式(1)中: 定义翼展变形率为ξ=(l′-l)/l,其中l′为当前翼展,l为本体翼展,由此可知ξ∈[0,1]。V和h为飞行速度和高度; φ、q和α分别为俯仰角、俯仰角速度和攻角;m和Iy为飞行器质量和绕y轴的转动惯量;g为重力加速度。飞行器推力建模为T=Tδtδt,其中Tδt为油门推力系数,δt为油门开度;升力L,阻力D,俯仰力矩My的表达式以及其中包含的气动系数和升降舵偏角δe可参考文献[17]。
为了获取LPV模型,首先选取ξ=0, 0.1,…,1,求取共计11组平衡点,然后采用雅克比线性化方法求解平衡点处的小扰动线性化模型,对这11个模型进行差值拟合即可得到变体飞行器纵向动力学的LPV模型为
(2)
为方便研究,提取其纵向短周期模型作为研究对象,其具体表达式为[17]
(3)
1.2 问题描述
考虑如下多面体LPV系统S
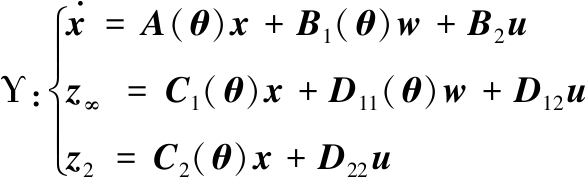
(4)
式(4)中: A(θ)、Bi(θ)、Ci(θ)、Di(θ)均为线性变参数系统Υ的相容矩阵,其中B2、D12、D22为常数矩阵;x∈Rn为状态向量,w∈Rl为干扰输入,u∈Rm为控制输入,z∞∈Rn1为H∞性能指标下的控制输出,z2∈Rn2为H2性能指标下的控制输出。LPV系统满足如下多面体结构:
Ω(θ)=(A(θ), B(θ))∈P
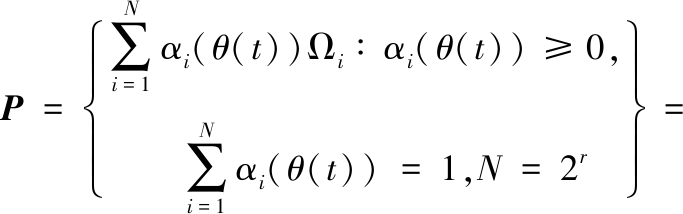
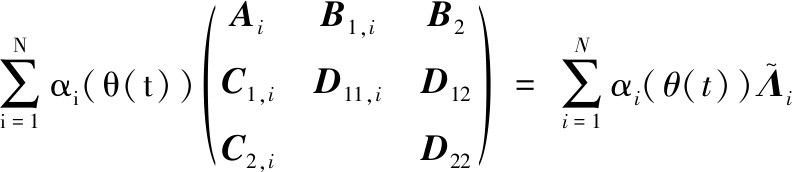
(5)
矩阵
表示多面体的第i个顶点,其中每个矩阵都包含多面体不确定性,如下所示:
(6)
针对LPV系统Υ,设计如下状态反馈控制律:
u=K(θ)x
(7)
其中,K(θ)∈Rm×n,将式(7)代入式(4)中,可以得到如下闭环LPV系统CDOF
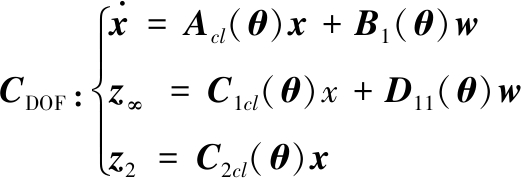
(8)
其中,系数矩阵Acl(θ),C1cl(θ)和C2cl(θ)分别为
Acl(θ)=A(θ)+B2(θ)K(θ)
(9)
C1cl(θ)=C1(θ)+D12(θ)K(θ)
(10)
C2cl(θ)=C2(θ)+D22(θ)K(θ)
(11)
注释1：文献[18]提出,LPV系统输入矩阵B2、D12、D22可以对控制输入进行滤波得到常数矩阵,因此本文中研究的LPV系统仍具有广泛代表性。
问题1：针对式(4)中的LPV系统,设计形如式(7)的LPV状态反馈控制器,使得式(8)的闭环LPV系统CDOF对所有的调度参数满足如下特性:
1) H∞性能:对于能量有界输入信号w∈L2,给定性能指标γ>0,使得由w到z∞的传递函数矩阵Tz∞w(s)的H∞范数|Tz∞w(s)|∞<γ;
2) H2性能:对于随机干扰输入信号w,给定性能指标η>0,使得由w到z2的传递函数矩阵Tz2w(s)的H2范数满足|Tz2w(s)|2<η。
2 主要结果
为了解决问题1,首先给出如下引理:
引理1[19] 考虑LTI系统
稳定且由w到z的传递函数矩阵满足|Tzw(s)|∞<γ,γ>0的充分条件为:存在对称正定矩阵X∞满足下述LMI约束:
(12)
其中,*表示由对称矩阵的对称性得到的块矩阵(以下情形类似,不再重复说明)。
引理2[19] 对于LTI系统
系统稳定且传递函数矩阵满足|Tzw(s)|2<η,η>0的充分条件为:存在对称矩阵X2和Q满足下列LMI约束:
(13)
(14)
trace(Q)<η
(15)
根据文献[20]中的思想,易将引理1-2从LTI系统推广到具有不确定性的多面体LPV系统,结合问题1,给出如下定理:
定理1：针对式(4)形式的多面体LPV系统,给定正标量γ>0和η>0,存在形如(4)中的增益调度状态反馈控制器,使得闭环系统CDOF满足问题1中3个特性的充分条件为,存在正定对称矩阵
个对称矩阵
和N个矩阵Li,满足如下LMIs约束条件:
trace(Qij)<η2
(16)
(17)
(18)
若式(16)—式(18)有解,则状态反馈调度增益K(θ)可由下式求得:
(19)
其中,Ki=LiX-1,0≤αi(θ)≤1,且
可由凸分解得到。
证明：将式(9)—式(11)中的闭环系数矩阵代入式(12)、式(13)和式(15)的左边,分别得:
trace(Q(θ))<η
(20)
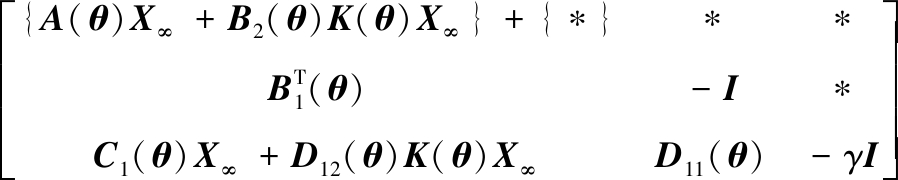
(21)
(22)
令XD=X∞=X2=X,并引入新的矩阵变量L(θ)
(23)
根据式(5)定义的LPV系统多面体特性和和式(6)定义的多面体不确定性,式(17)—式(18)可分别化为
(24)
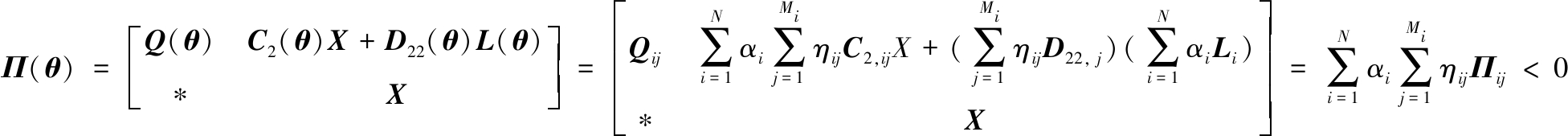
(25)
根据矩阵的基本性质:具有非负系数的正(负)定矩阵的任何和为正的线性组合都是正(负)定的。因此可得式(16)—式(18)。证毕。
注释2：由定理1的证明过程可知,此定理采用了常数李雅普诺夫函数V(x(t))=xT(t)Xx(t),并限制了XD=X∞=X2=X,即要求在所有的多面体顶点上共用一个共同的Lyapunov函数矩阵,显然,这给系统的综合带来了较大的保守性。对此,可以通过引入松弛变量的方法来降低保守性,即提出定理2如下。
定理2：针对问题1中的设计要求,其可行的充分条件为存在
个正定对称矩阵
个正定对称矩阵
个对称矩阵
个矩阵Si和矩阵H,满足如下LMIs约束条件
trace(Qij)<η
(26)
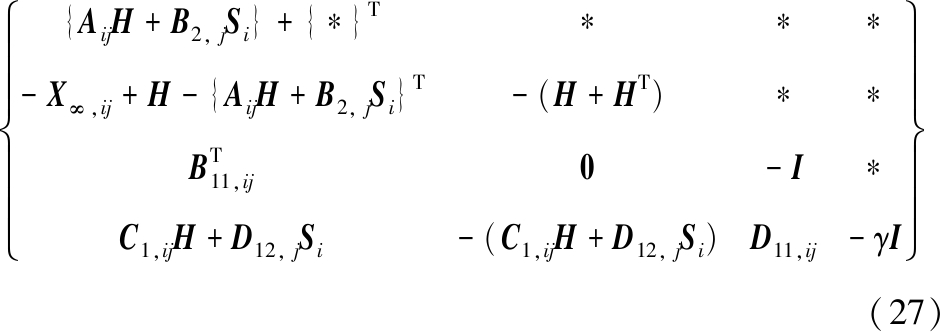
(28)
(29)
证明：首先参考如下2个线性矩阵不等式:
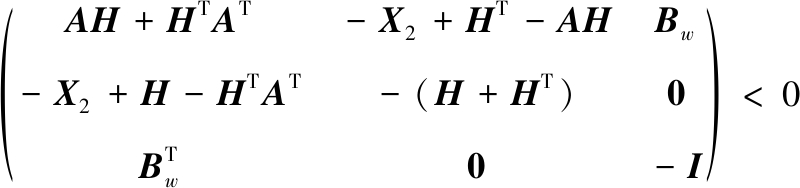
(30)
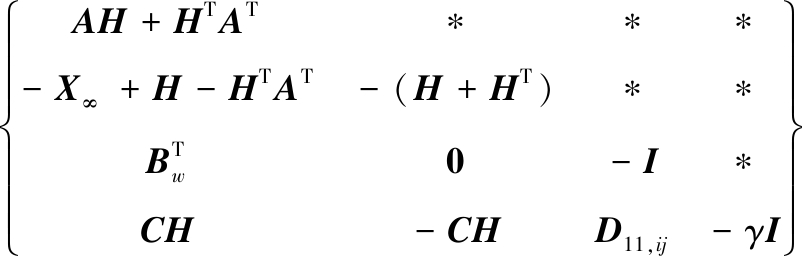
(31)
分别在式(30)左右两边分别乘以
和FT,式(30)与式(13)一致;同理,在式(31)左右两边分别乘以
和GT,式(31)与式(12)一致。
通过引入松弛变量,使Lyapunov函数矩阵与系统矩阵解耦,从而可以在不同的顶点上使用不同的Lyapunov函数矩阵。因此根据凸优化理论,式(9)—式(11)在多面模型顶点的表达式为
Acli=Aij+B2, jKi
C1cli=C1,ij+D11, jKi
C2cli=C2,ij+D22, jKi
(32)
将式(32)代入式(30)—式(31)中,并引入新的矩阵变量H1i=KiG1,H2i=KiG2,i=1,…,N,即可得到式(26)—式(29)的LMI约束条件。证毕。
注释3：注意到定理2中的LMIs是性能指标γ和η的线性约束,因此,遵循文献[21]的思想,定理2的求解条件就可转化成具有LMIs约束的线性目标函数最小化问题。然而,在实际应用中,性能指标γ与η不可能同时达到最优,必须进行加权处理,常见的加权形式如下
J=aγ+bη
(33)
其中,a,b是权值,可以根据具体的设计要求进行设定。于是,定理2的求解条件变为
(34)
3 仿真分析
通常情况下,变体飞行器的气动参数获取是基于准定常气动假设[22]。因此,变体飞行器变形过程中气动参数往往存在不确定性。此外,由于通道噪声与测量误差的影响,用于控制器调度的翼展变形率ξ也往往是不精确的。因此,考虑具有上述不确定性的变体飞行器纵向短周期LPV模型为
(35)
其中,不确定性μ1∈[0.9,1.2], μ2∈[0.8,1.2]。
根据式(5)的定义,该系统可以描述为不确定LTI系统的多面体组合,即
其中:
α1(ξ)=2-ξ
α2(ξ)=ξ-1
根据式
可用4个LTI系统以多面体的方式描述:
其中:
同理,
也可用4个LTI系统以多面体的方式描述:
其中:
考虑开环LPV系统(4),令
将上述矩阵代入式(26)—式(29)中求解LMI,最终可得H∞性能上界为γ=1.033 2,H2性能上界为η=2.149 3,LPV控制器形式为:
u(t)=K(ξ)x(t)=α1(ξ)K1x(t)+α2(ξ)K2x(t)
将控制器引入变体飞行器纵向短周期模型中,控制目标为跟踪攻角参考信号。如图1所示,在翼展变化率信号中加入幅值为0.05的正弦信号以模拟通道噪声和测量误差的影响。在非线性模型气动参数中加入如式(36)的不确定性[23]。
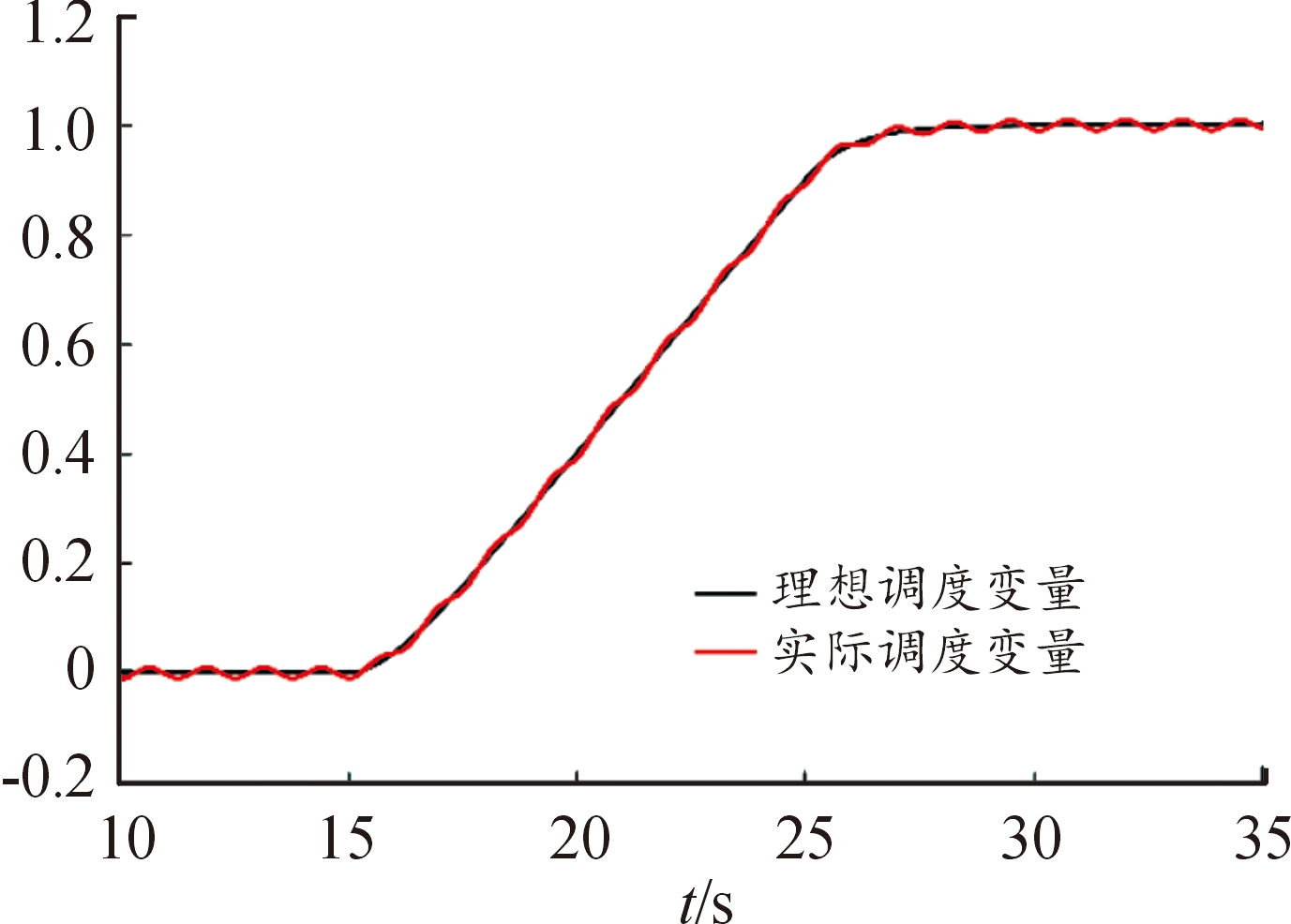
图1 翼展变形率
Fig.1 Span deformaction rate
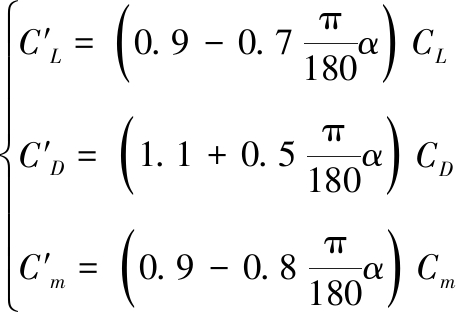
(36)
在仿真中,引入文献[8]提出的控制方法作为对比,控制效果如图2—图4所示。任务目标为在10 s和25 s时分别跟踪5°和-2°的攻角参考信号。在所提出的控制器作用下,尽管存在不精确调度参数和系统不确定性影响,系统仍然具有较好的跟踪性能,攻角能够稳定跟踪参考信号,同时俯仰角速率变化平稳,控制输入未出现饱和情况,对不确定性具有鲁棒性,有效避免了对比方法中由于未考虑鲁棒设计所导致的系统状态和控制输入震荡问题。
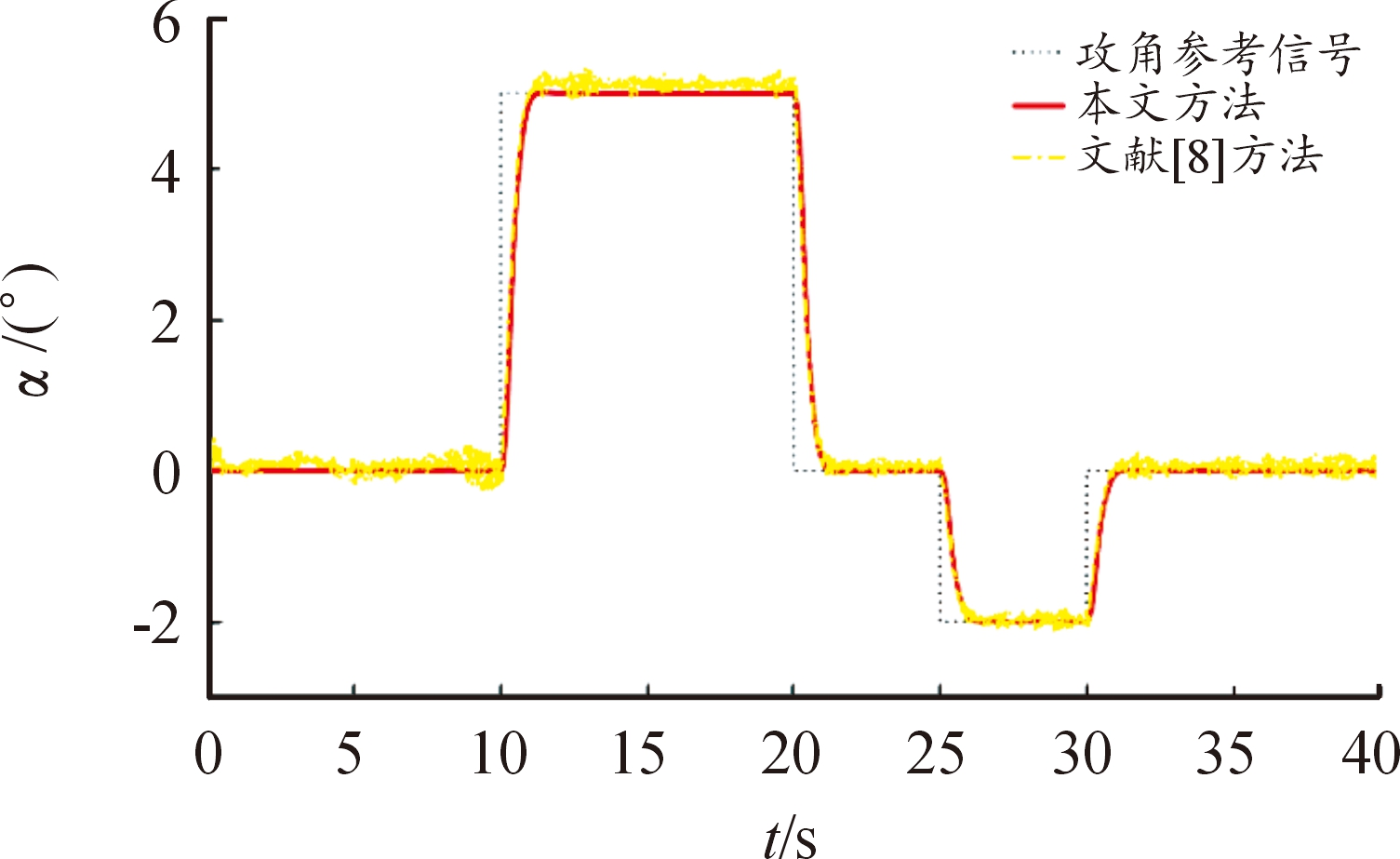
图2 攻角响应
Fig.2 Angle of attack response
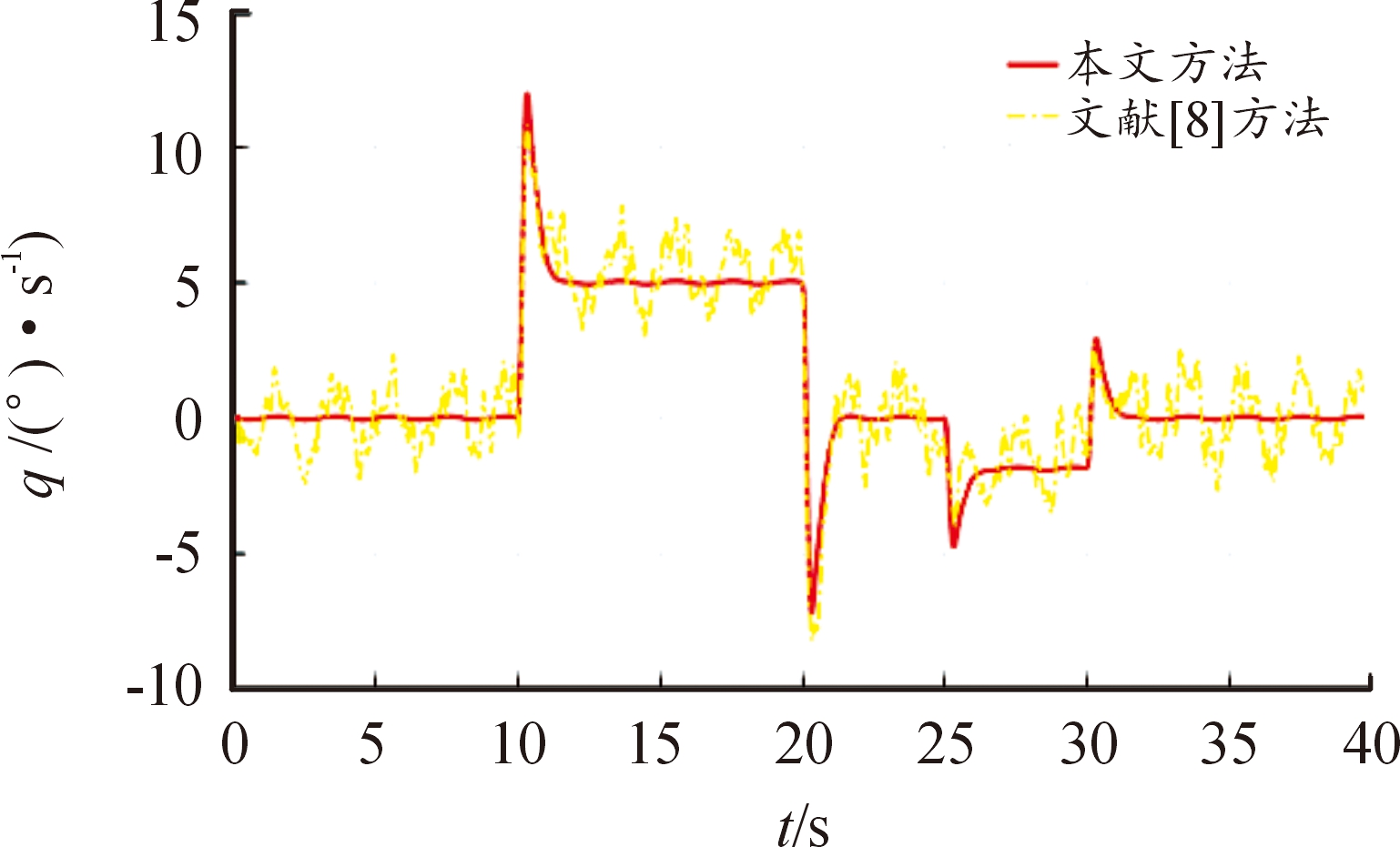
图3 俯仰角速率响应
Fig.3 Pitch rate response
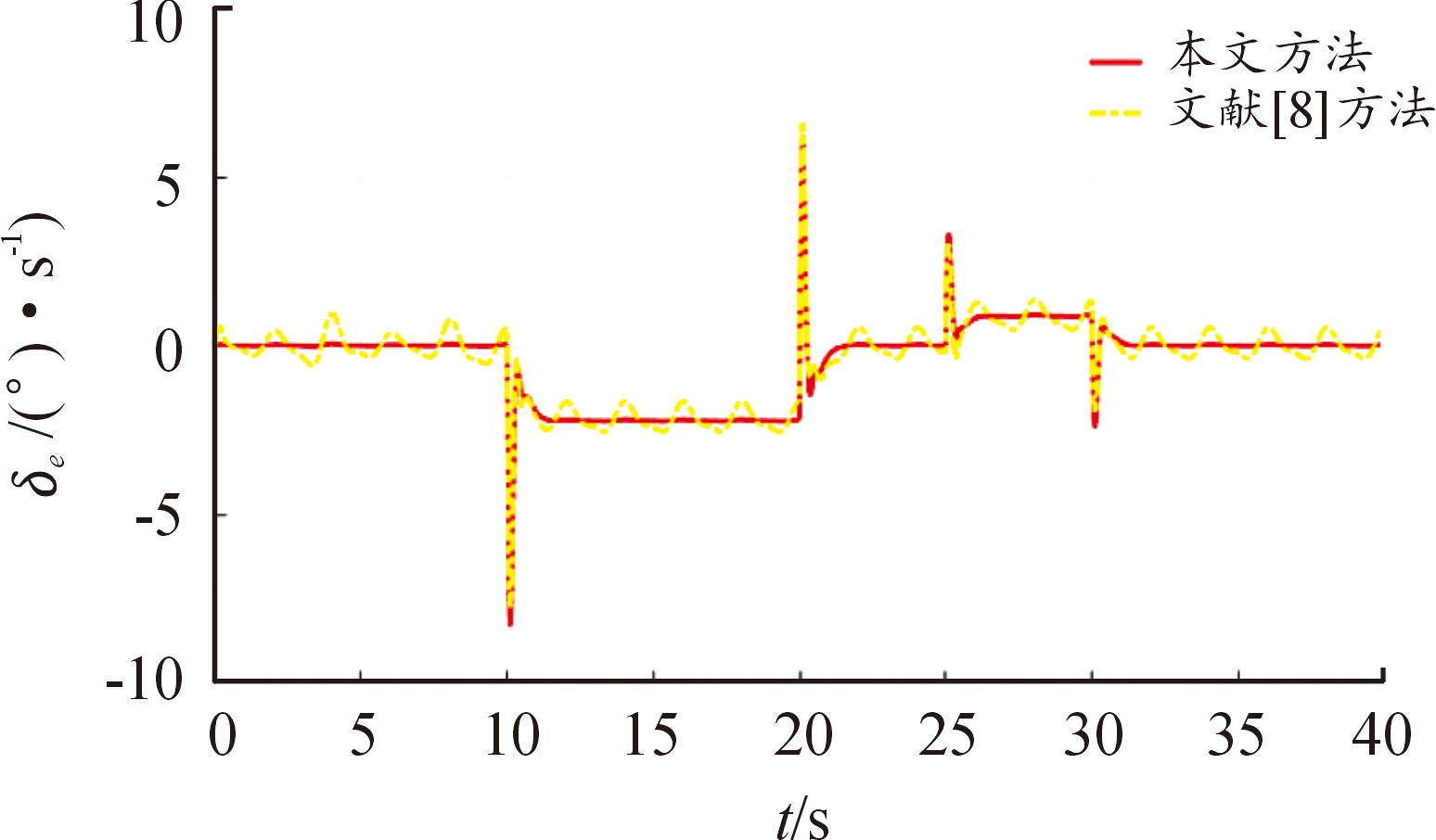
图4 舵偏角
Fig.4 Elevator deflection
4 结论
针对变体飞行器姿态控制问题,提出一种不确定LPV系统的状态反馈控制器的设计方法,在使系统稳定的同时能够保证H∞/H2性能的期望上界。通过双多面体建模,同时考虑了不精确调度参数和系统不确定性的双重影响。仿真结果表明:
1) 系统具有良好的跟踪性能,能够准确跟踪给5°和-2°的参考信号,响应时间快,无超调量产生。
2) 本文中的鲁棒设计能够有效应对不精确调度参数和系统不确定性所导致的不利影响,系统响应曲线更为平滑,有效抑制了扰动和震荡。
[1] WANG Q,GONG L,DONG C Y,et al.Morphing aircraft control based on switched nonlinear systems and adaptive dynamic programming[J].Aerospace Science and Technology,2019,93:105325.1-105325.16.
[2] WEISSHAAR T A.Morphing aircraft systems:Historical perspectives and future challenges[J].Journal of Aircraft,2013,50(2):337-353.
[3] XU D,HUI Z,LIU Y,et al.Morphing control of a new bionic morphing UAV with deep reinforcement learning[J].Aerospace Science and Technology,2019,92:232-243.
[4] YAN B B,LI Y,DAI P,et al.Aerodynamic analysis,dynamic modeling,and control of a morphing aircraft[J].Journal of Aerospace Engineering,2019,32(5):04019058.1-04019058.10.
[5] JIANG W L,WU K S,WANG Z L,et al.Gain-scheduled control for morphing aircraft via switching polytopic linear parametervarying systems[J].Aerospace Science and Technology,2020,107(2):106242.
[6] YUE T,WANG L X,AI J Q.Longitudinal linear parameter varying modeling and simulation of morphing aircraft[J].Journal of Aircraft,2013,50(6):1673-1681.
[7] 贾臻,董朝阳,王青.链式平滑切换变体飞行器LPV鲁棒跟踪控制[J].北京航空航天大学学报,2017,43(4):831-841.
JIA Zhen,DONG Chaoyang,WANG Qing.LPV robust tracking control for chain smooth switched morphing aircraft[J].Journal of Beijing University of Aeronautics and Astronautics,2017,43(4):831-841.
[8] 殷明,陆宇平,何真.变体飞行器LPV建模与鲁棒增益调度控制[J].南京航空航天大学学报,2013,45(2):202-208.
YIN Ming,LU Yuping,HE Zhen.LPV modeling and robust gain scheduling control of morphing aircraft[J].Journal of Nanjing University of Aeronautics and Astronautics,2013,45(2):202-208.
[9] 何墉,章卫国,王敏文,等.基于多目标控制的变体飞行器切换线性变参数控制器[J].控制理论与应用,2015,32(11):1518-1525.
HE Yong,ZHANG Weiguo,WANG Minwen,et al.Switching linear-parameter-varying control for morphing aircraft based on multi-objective[J].Control Theory and Application,2015,32(11):1518-1525.
[10] 江未来,董朝阳,王通,等.变体飞行器连续平滑切换LPV控制[J].系统工程与电子技术,2015,37(6):1347-1353.
JIANG Weilai,DONG Chaoyang,WANG Tong,et al.Continuous smooth switching LPV control for morphing aircraft[J].Systems Engineering and Electronics,2015,37(6):1347-1353.
[11] WEN N,LIU Z G,SUN Y,et al.Design of LPV-based sliding mode controller with finite time convergence for a morphing aircraft[J].International Journal of Aerospace Engineering,2017:1-20.
[12] DAAFOUZ J,BERNUSSOU J,GEROMEL J C.On inexact LPV control design of continuous-time polytopic systems[J].IEEE Transactions on Automatic Control,2008,53(7):1674-1678.
[13] SATO M,PEAUCELLE D.Gain-scheduled output-feedback controllers using inexact scheduling parameters for continuous-time LPV systems[J].Automatica,2013,49(4):1019-1025.
[14] ARASH S.Gain-scheduled continuous-time control using polytope-bounded inexact scheduling parameters[J].International Journal of Robust and Nonlinear Control,2018,28(17):5557-5574.
[15] ZHAO P,NAGAMUNE R.Switching LPV controller design under uncertain scheduling parameters[J].Automatica,2017,76:243-250.
[16] 刘正华,温暖,祝令谱.变体飞行器有限时间收敛LPV鲁棒控制[J].系统工程与电子技术,2018,40(6):1325-1330.
LIU Zhenghua,WEN Nuan,ZHU Lingpu.Robust LPV control for morphing aircraft with finite-time convergence[J].Systems Engineering and Electronics,2018,40(6):1325-1330.
[17] 殷明.变体飞行器变形与飞行的协调控制问题研究[D].南京:南京航空航天大学,2016.
YIN Ming.Coordinated control of deformation and flight for morphing aircraft[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2016.
[18] APKARIAN P,GAHINET P,BECKER G.Self-scheduled H∞ control of linear parameter-varying systems:a design example[J].Automatica,1995,31(9):1251-1261.
[19] 俞立.鲁棒控制:线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.
YU Li.Robust control:processing method of linear matrix inequality[M].Beijing:Tsinghua University Press,2002.
[20] LI H,GUAN C,ZHOU D,et al.Mixed H2/H∞ linear parameter varying state feedback control for bank-to-turn missile autopilot design[C]//International Conference on Computer,Mechatronics,Control and Electronic Engineering.Changchun,China,IEEE,2010:240-246.
[21] 蔡光斌,赵阳,张胜修,等.高超声速飞行器鲁棒多目标线性变参数控制[J].兵工学报,2019,40(11):2229-2240.
CAI Guangbin,ZHAO Yang,ZHANG Shengxiu,et al.Robust multi-objective linear parameter varying control for hypersonic vehicle[J].Acta Armamentarii,2019,40(11):2229-2240.
[22] 孙斌,杨凌宇,张晶.基于高阶奇异值分解的LPV鲁棒控制器设计[J].北京航空航天大学学报,2016,42(07):1536-1542.
SUN Bin,YANG Lingyu,ZHANG Jing.Robust LPV control design based on HOSVD[J].Journal of Beijing University of Aeronautics and Astronautics,2016,42(7):1536-1542.
[23] YUE T,WANG L X,AI J Q.Gain self-scheduled H∞ control for morphing aircraft inthe wing transition process based on an LPV model[J].Chinese Journal of Aeronautics,2013,26(4):909-917.