基于红外热像法的叶片受迫振动热耗散规律研究
0 引言
随着我国综合实力的提升,航空装备领域的质量可靠性愈加重要。航空发动机叶片作为发动机的核心部件,其疲劳问题受到各国学者广泛关注。在实际工况环境下,叶片受到多种复杂疲劳载荷的影响,其中叶片共振会加速部件的疲劳破坏,尤其是应力集中区域的破坏已成为导致叶片疲劳断裂或掉角的主要原因之一[1-3],因此,叶片结构共振问题需重点关注。
在振动疲劳试验中,传统研究方法采用了接触式手段,(如粘贴应力应变片、电阻应变计以及安装加速度传感器等)研究振动疲劳问题,但这种方法难以实现长时间的在线监测,并且对结构阻尼大小会产生一定的影响。因此,亟需探寻一种非接触式可在线实时监测疲劳的技术手段以解决该问题。目前,基于激光测振的位移测量方法作为主要非接触式在线监测手段,只是针对某一点(如叶尖)的振动位移进行测量,通过结构固有频率的变化,判断其是否产生损伤或断裂,但该方法难以预测叶片振动过程中的应力分布情况以及疲劳损伤位置[4-5]。Kelvin[6]最早发现材料疲劳过程与其温度变化存在一定的关联性,并提出了著名的热弹性效应理论。随着疲劳能量理论的深入研究,人们认识到疲劳过程实质上是外界对材料做功,导致材料内部微观结构发生疲劳破坏,期间伴随着能量的释放。其中,热耗散是最主要的形式,宏观表现为材料表面的温度变化;其次是储能、声发射和其他形式能量。近年来,红外热像法因具有非接触、高精度、全场监测、能够精确捕捉材料表面温度变化等特点,在无损检测和材料疲劳性能快速评估等工程领域得到了广泛应用[7-8]。
Luong等[9-10]与Risitano等[11-12]发现材料疲劳过程释放的能量与施加应力具有线性相关性,并通过红外热像法快速有效地评估了材料的疲劳极限,分别被命名为Luong法与Rasitano法。该方法与传统疲劳极限测试方法(如阶梯法、单点法等)相比,能够有效缩短时间,极大减少试验成本,可在一定程度上替代传统疲劳极限测试方法。Toubal等[13]和Meneghetti等[14]在材料疲劳损伤扩展阶段,基于热像法分别进行了损伤演化过程的预测和裂纹尖端J积分的评估。但以上研究内容仅限于传统拉压疲劳,对于航空发动机叶片,振动疲劳是其主要失效模式。振动疲劳以弹性应变为主要特征,结构表面温度变化不明显,目前基于热像法的振动疲劳研究相对较少。
Santos Silva等[15]和Talai等[16]研究发现温度场分布与结构共振响应、振动特性密切相关,结构谐振频率随温度升高而增大。因此,温度作为影响结构振动的重要参数,需要重点研究。于是,王纯等[17]采用红外热像仪监测金属元件在振动疲劳过程中的温度变化,根据温度变化特征可反映结构疲劳损伤信息。宋振等[18]发现可通过红外热图对疲劳损伤进行评估,进而预测其疲劳寿命。上述研究对材料疲劳过程能量耗散问题已取得了丰硕的成果,但航空发动机叶片在实际工况下,常受到来自气流扰动或系统振动高频激振力的影响,导致受迫振动,应力集中区域最先发生疲劳破坏。因此,关于高频激振力下受迫振动热耗散规律研究还有待进一步深入探究。
基于此,本文中通过有限元模态分析获取叶片各阶模态振型与应力云图,并确定最大振动位移和应力集中区域。根据模态分析结果,采用红外热像仪对超声激励受迫振动下的叶片进行实时监测,获取叶片表面温度场变化情况,并分析影响振动热耗散的因素以及应力集中区域温升情况。研究可为发展叶片结构振动疲劳非接触式研究方法提供新的思路。
1 疲劳热耗散理论模型
材料疲劳主要由不可逆的塑性应变累积所致,其中疲劳过程分为弹性应变和塑性应变。在卸载阶段,弹性应变是可逆的,而不可逆的塑性应变将外力做功以能量的形式储存在材料内部结构中,当能量储存到一定程度时,微观裂纹逐渐萌生和扩展,并伴随能量耗散,其中80%~90%以热能的形式释放到环境中,10%的塑性应变能以储能形式留在材料晶格内,只有极少部分能量以声发射、电、磁类形式释放[20]。若忽略声发射、电、磁类形式能量,由热力学第一定律(能量守恒)可知,式(1)中:W为外力做功输入的机械能;Q为热能;ΔU为材料内部储能。
W=Q+ΔU
(1)
对于材料不同体积单元之间的热传递和材料与环境之间的热交换,即热耗散。假设时刻t在(x,y,z)处的温度场为T(x,y,z,t),如图1疲劳加载过程中物体能量转换,物体体积为V,外表面与环境进行热耗散总能量为Q(可分为3部分热对流Scv、热传导Scd、热辐射Sra)。由传热学可得该物体的热耗散模型[21]:
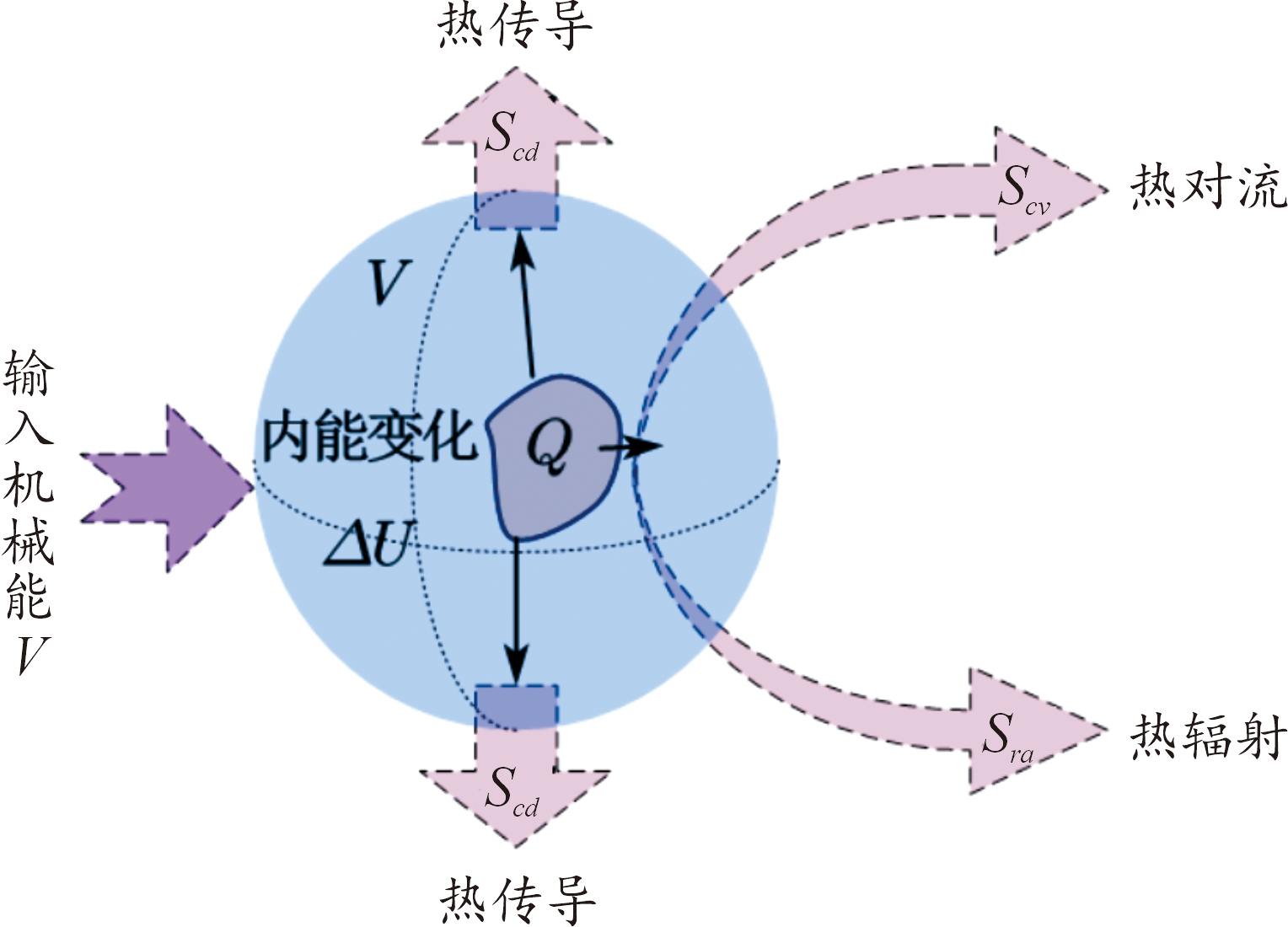
图1 疲劳加载过程中物体能量转换
Fig.1 Energy conversion of objects during fatigue loading
![]()
(2)
式(2)中:σij为应力张量;εij为应变张量; f为加载频率;k为热传导系数;![]() 为材料储能;h为对流换热系数;λ为物体表面发射率;T0为室温;ρ为密度;c为单位热量;σb为Stefan-Boltzmann常数5.67×10-8 W/(m2·K4);▽2为拉普拉斯算子,
为材料储能;h为对流换热系数;λ为物体表面发射率;T0为室温;ρ为密度;c为单位热量;σb为Stefan-Boltzmann常数5.67×10-8 W/(m2·K4);▽2为拉普拉斯算子,![]() 为某时刻沿温度增加方向上的温度变化率,即温度梯度。
为某时刻沿温度增加方向上的温度变化率,即温度梯度。
当热耗散总能量Q与热对流Scv、热传导Scd以及热辐射Sra达到热平衡时,即温度稳定阶段,表面温度T不随时间发生变化,有![]() 此时式(2)可写为
此时式(2)可写为
![]()
(3)
当裂纹开始扩展时,产生非弹性应变,并伴随大量能量产生,即温度快速升高阶段,表面温度T快速升高,因而通过表面温度T变化特征可以反映结构疲劳损伤信息。根据热力学第一及第二定律与材料的本构方程,可得到材料在疲劳过程中的热力学耦合方程[10],即:
![]()
(4)
式(4)中: ρ为材料密度;Cv为等体比热容;T为试件表面的温度;r0为热源;β为线膨胀系数矩阵;![]() 为4阶弹性张量; S为第二Piola-Kirchhoff应力张量;
为4阶弹性张量; S为第二Piola-Kirchhoff应力张量;![]() 为弹性应变张量;
为弹性应变张量;![]() 为非弹性应变张量。
为非弹性应变张量。
从式(4)中可以看出,疲劳过程中材料表面温度T主要受等式右边的四项因素的影响,分别为:由内部或外部因素引起的热噪点,即热源r0;通过热传导使得整个材料表面温度T趋于一致,即热传导因素k▽2T;材料由于发生可逆的弹性应变期间伴随可逆的热力学现象,即热弹性因素![]() 材料发生非弹性应变,所产生的大部分能量以热耗散的形式释放为不可逆过程,即固有耗散源因素
材料发生非弹性应变,所产生的大部分能量以热耗散的形式释放为不可逆过程,即固有耗散源因素![]()
2 受迫振动热耗散规律研究
2.1 模态分析建模
模态分析可确定结构的振动特性,如结构的固有频率、各阶模态振型以及应力分布,便于更准确地研究叶片应力做功生热问题,为受迫振动热耗散试验提供参考依据。
相比于平板结构,叶身为扭转型曲面具有弧度以及扭曲特性,因此叶片模态振型与应力分布更为复杂。其几何尺寸如图2所示。叶片结构选用航发压气机叶片常用材料TC11:弹性模量E=1.23×105 MPa,泊松比v=0.33,质量密度ρ=4 480 kg/m3。对其进行模态分析。由于考虑到航空发动机叶片在实际装配工况下,通过榫头固定于轮盘上,类似简支梁、悬臂梁结构,因此对叶片根部采用全固定约束。全局网格划分尺寸为1 mm,网格类型选用C3D8R单元。
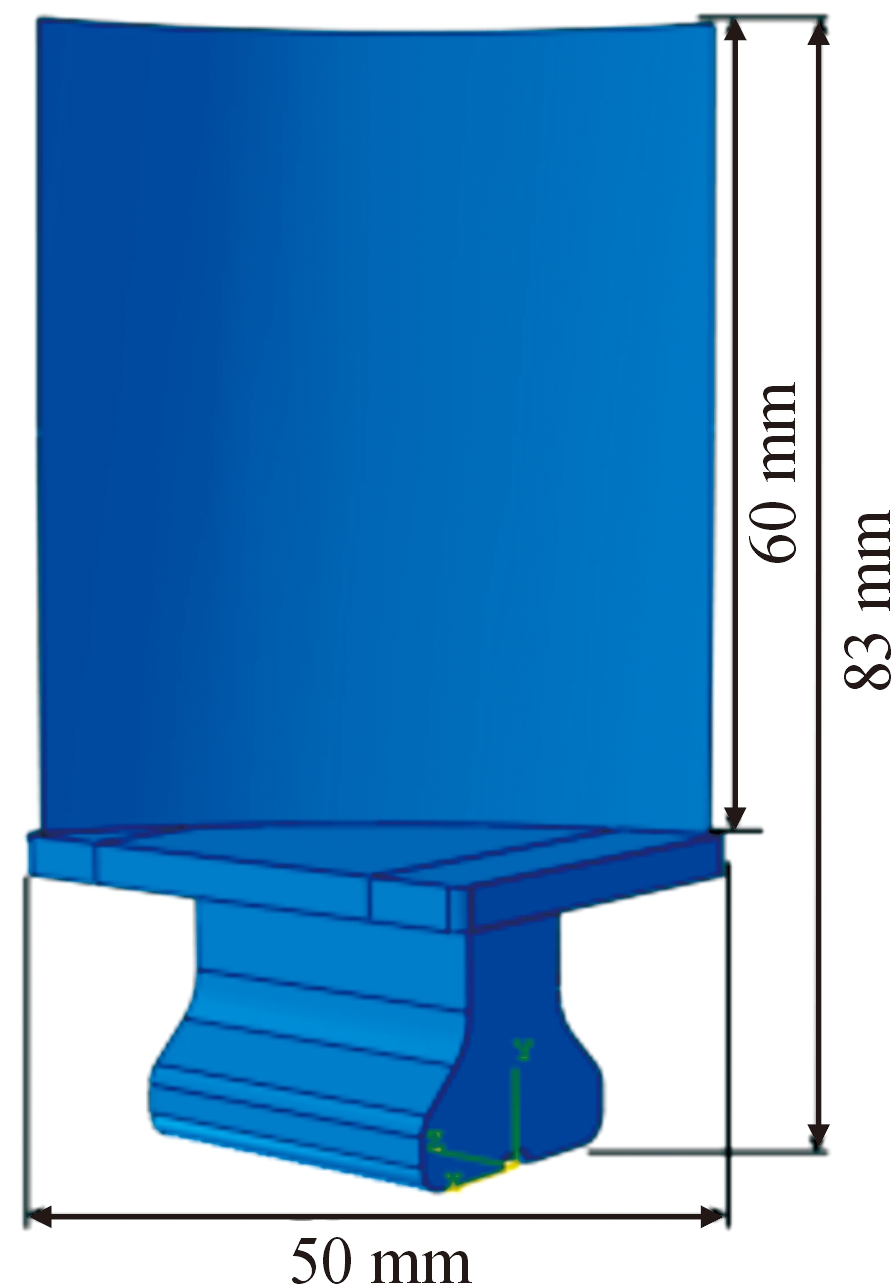
图2 叶片结构
Fig.2 Blade structure
2.2 振动模态特性分析
在模态分析中,低阶模态的等效质量较大,对结构振动响应更加明显。为更好地掌握叶片结构的振动特性,在进行加载求解后,输出叶片结构前6阶自振频率(如表1所示)和前6阶振型图与Mises等效应力云图(如图3、图4所示)。
表1 叶片结构前6阶固有模态
Table 1 First six natural modes of blade structure
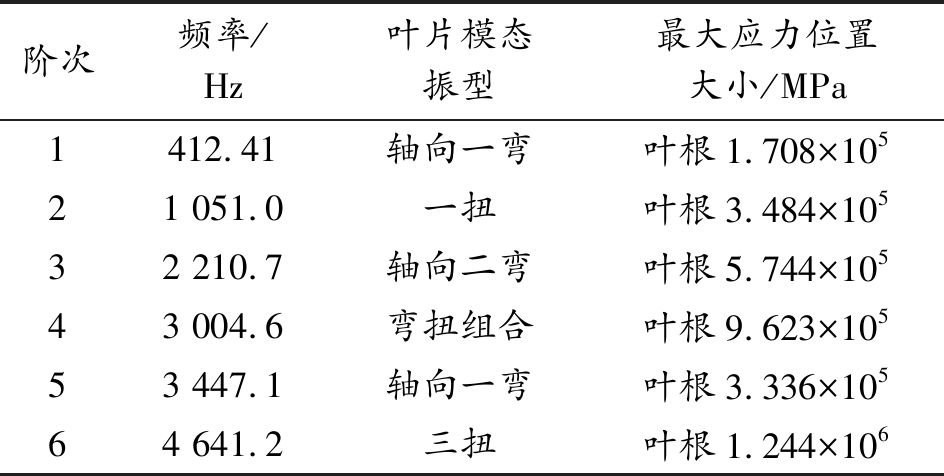
表2 红外热像仪VarioCAM hr主要参数
Table 2 Main parameters of the infrared thermal imager VarioCAM hr
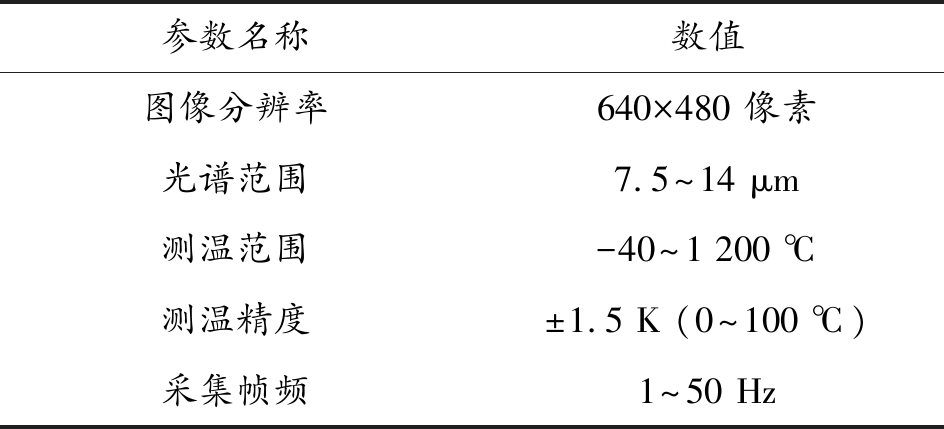
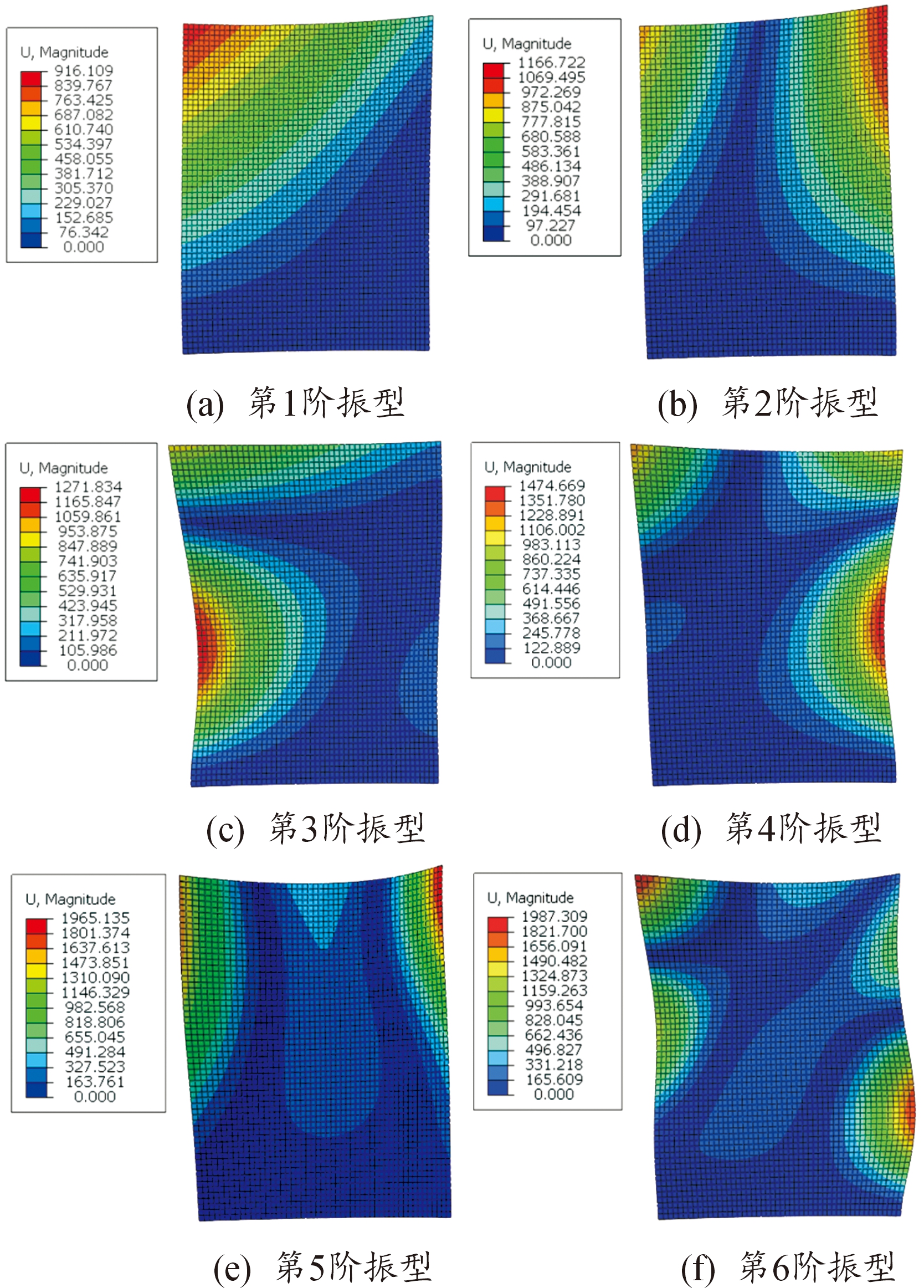
图3 叶片结构前6阶振型图
Fig.3 The first six vibration modes of blade structure
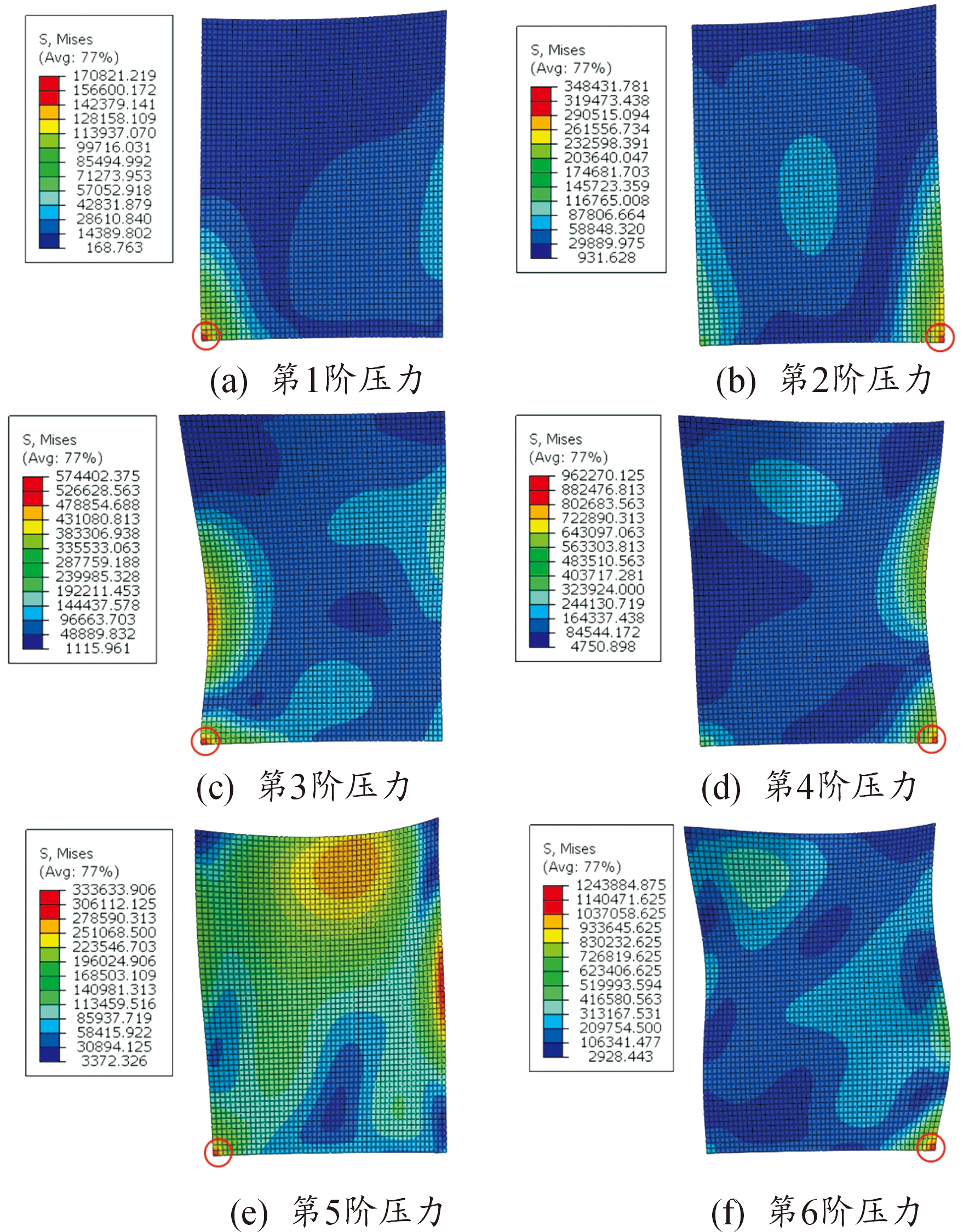
图4 叶片结构前6阶等效应力云图
Fig.4 Nephogram of the first six-orders of equivalent stress in blade structure
由图3(a)—(f)叶片结构前6阶振型图可知,叶片结构呈现出一系列不同的振动形式。其中,叶片结构第1阶振型为一阶轴向弯曲振动,变形量从上至下依次减小,最大变形量位于叶尖前缘处附近。第2阶振型为一阶扭转振动,叶片顶部发生扭转变形,叶尖前后缘振动幅值较大,其最大变形量位于叶尖后缘附近。第3阶振型为二阶轴向弯曲振动,叶身前缘、叶尖前缘发生弯曲振动,其最大变形量位于叶身前缘中部附近。第4阶振型为弯扭组合复合振动,叶尖发生扭转振动,叶身后缘发生弯曲振动,最大变形量位于叶身后缘中部附近。第5阶振型为一阶弯曲振动,与第1阶振型不同是第5阶振型叶尖前后缘均发生弯曲振动,且向同一方向发生弯曲变形,最大变形量位于叶尖后缘附近。第6阶振型为三阶扭转振动,叶尖前缘与叶身后缘振动更为剧烈,其最大变形量位于叶尖前缘附近。叶片在高阶模态下,一般是以弯曲或扭转为主的复合振型。
由图3和图4可知,其位移幅值最大位置通常位于叶尖前后缘和叶身中部,由于叶尖为自由端,可发生较大位移而不产生较大变形,而叶根作为固定端无法移动,叶尖产生的弯曲应力在叶根处通过反作用力抵消,进而导致叶根两侧附近出现应力集中。由于叶身中部发生弯曲变形使得应变较大,从而导致叶身中部产生应力集中。
然而,叶片在工况下常受到高频激振力的影响,易引发超高周疲劳断裂问题,结合现有超高周疲劳研究,超声加载激振频率一般为20 kHz[22-23]。因此,为分析叶片在高频激振力下的受迫振动特性,选取叶片结构模态第33阶模态振型,固有频率为20 191 Hz(与20 kHz相对误差0.9%可忽略),如图5所示。叶身前缘处于多阶弯曲变形状态,振动更为剧烈,最大变形量位于叶根前缘附近,应力集中区域分布在叶身前缘,最大应力点位于叶根前缘附近。
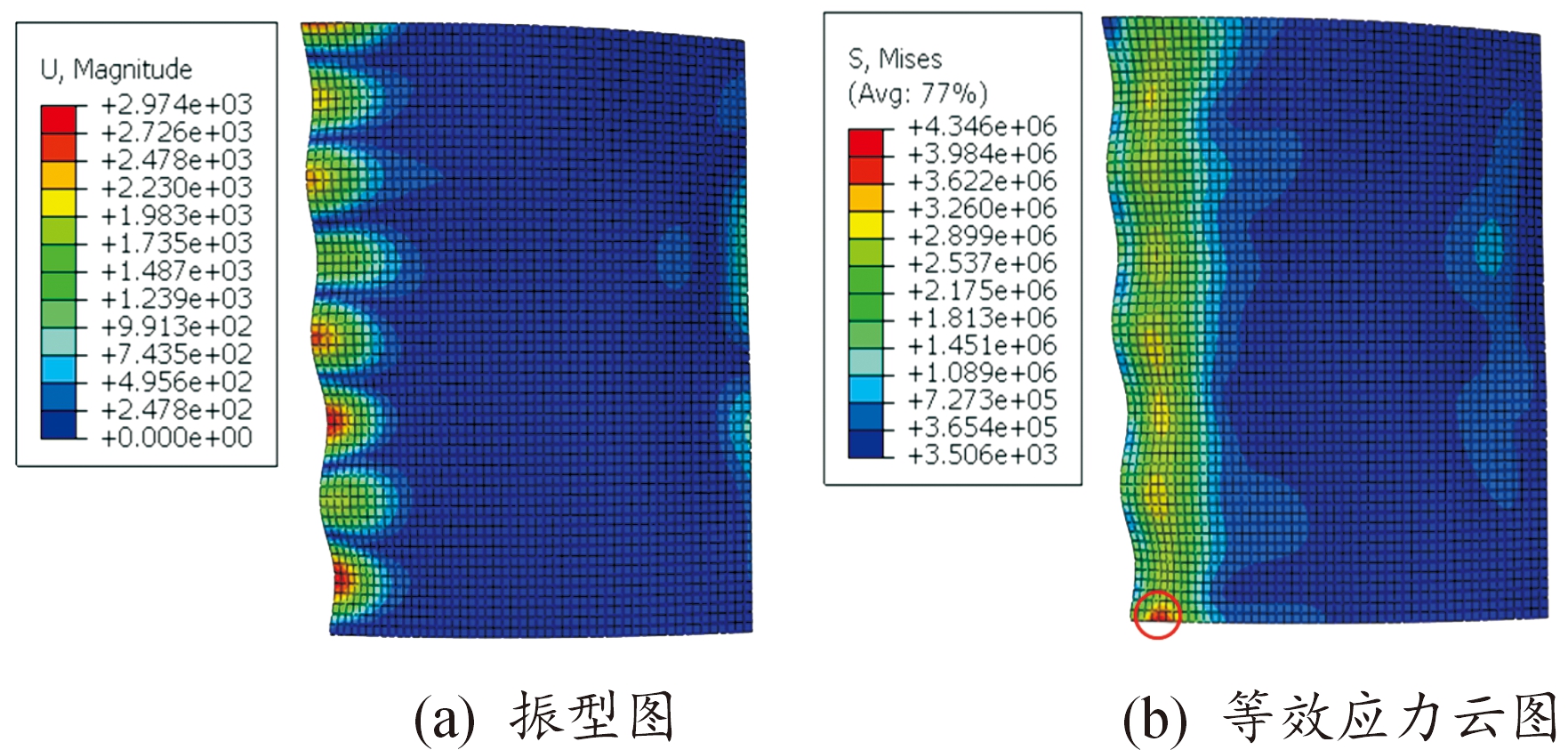
图5 叶片结构第33阶振动模态
Fig.5 The 33rd vibration mode of blade structure
因此,在叶片实际工况下,应重点关注叶片结构的危险部位——叶尖前后缘与叶根两侧位置,确保航空发动机叶片能正常运行并达到预期性能。
2.3 振动热耗散试验
通过模态分析,得到了叶片结构各阶振动特性和应力集中区域,由式(4)热力耦合方程可知,应力集中区域温度变化明显,可通过红外热像仪监测受迫振动下应力集中区域温度变化,为进一步研究叶片振动和热耗散提供参考[15-16,18]。
为研究不同材料参数和试件结构对热耗散规律的影响,试验采用3种不同试件进行对比试验研究,如图6所示,分别为1 mm厚平板、3 mm厚平板、叶片结构件,以下均简称为1 mm板、3 mm板、叶片。1 mm板、3 mm板材料均为铝合金,叶片试件材料为钛合金。由于光滑金属表面存在反射,为提高试件表面热辐射率,在其表面均匀涂抹黑色亚光漆,以更准确地获取试件表面温度场。试验系统主要包括:Infra Tec便携式红外热像仪VarioCAM hr、超声信号发生器、变幅杆和夹具等设备,如图7所示。试验中,将试件一端通过夹具夹紧固定,结合实验室前期基础,采用超声变幅杆(激振频率为20 kHz)作为高频振动激励源[16,24],激励源位置位于夹具上方,以模拟试件发生受迫振动。试件发生受迫振动时,采用Infra Tec便携式红外热像仪VarioCAM hr实时记录试件表面温度变化情况,通过系统提取热图序列,分析影响受迫振动试件表面温度变化的因素。

图6 试件实物图
Fig.6 Specimen drawing

图7 试验系统实物图
Fig.7 Test system object
2.4 试件表面温度场分析
图8为超声激励下叶片受迫振动过程中某时刻表面温度T分布。由图8可知,叶片表面存在3处温度变化明显区域,其中受激励点与叶根夹持端附近的温度明显高于环境温度T0。选取图中矩形区域作为热源分析对象,消除环境温度T0影响,可清晰地看出叶片结构轮廓。通过红外热图序列,可直观地观察叶片表面温度T的变化过程,进而研究叶片热传导规律以及应力集中区域温度变化规律。
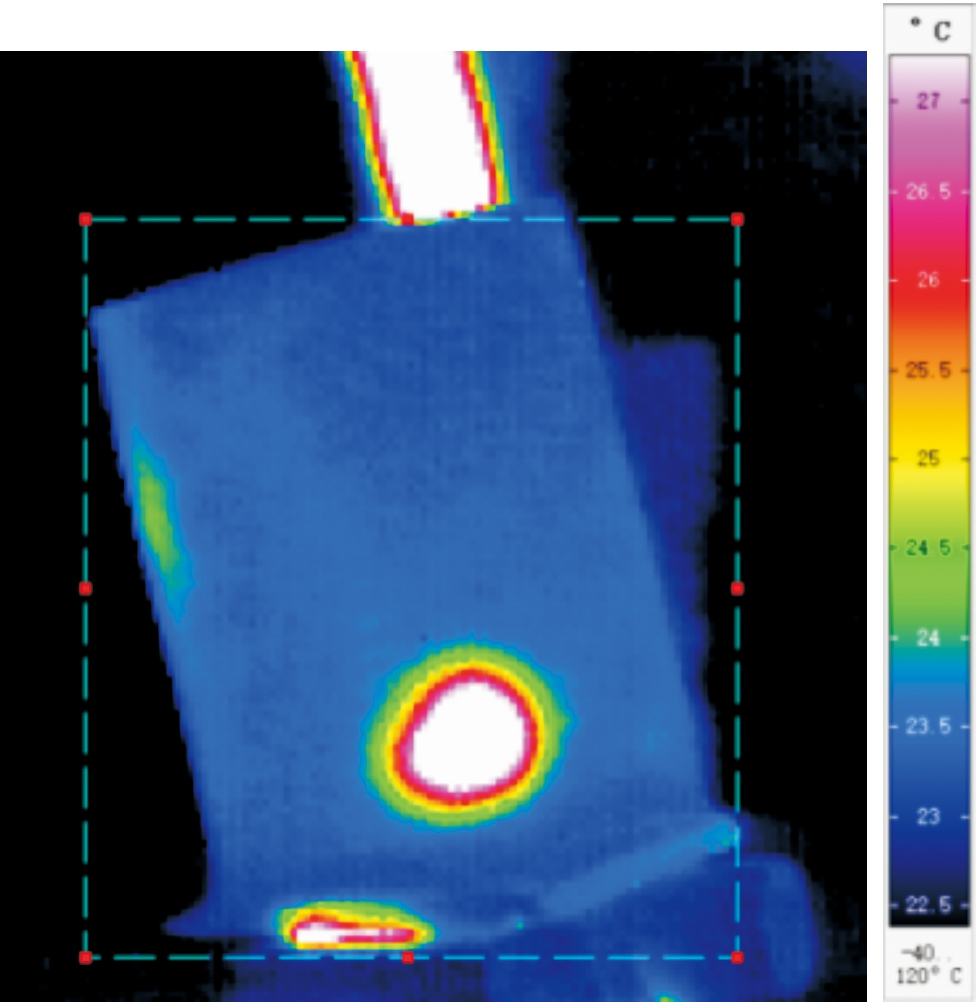
图8 受迫振动过程中叶片表面温度场
Fig.8 Temperature field of blade surface during forced vibration
图9为某时刻通过红外热像仪实时采集的热图和以受激励点为中心的直线L1上各点温度随时间变化三维图。试验中,叶片根部由夹具固定,上端为自由端。
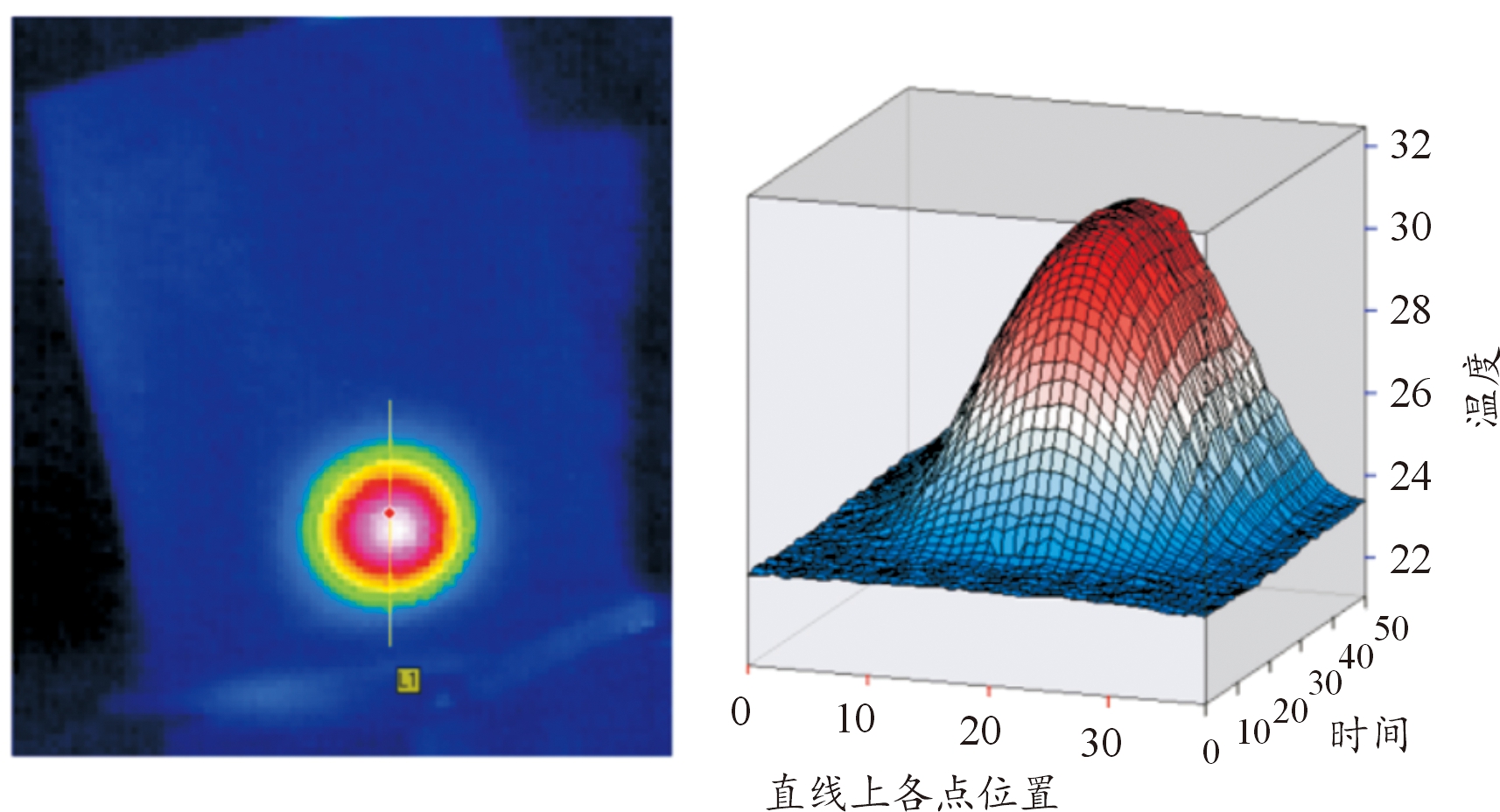
图9 叶片表面直线L1上温度分布图
Fig.9 Temperature distribution on blade surface in linear L1
由图9可知,温度分布以直线L1中点为对称中心上下对称,表明试验夹具、空气与试件之间的热传导对温度的测量影响不大,并未导致试件中心温度的偏移。此外,由于测量距离、变幅杆与试件之间接触的预紧力也会影响温度测量精度[24-25],所以后续试验将测量焦距保持一致,预紧力统一调至150 N。
2.4.1 振动热耗散规律
通过红外热像仪对叶片进行实时监测与采集,得到在超声激励下叶片受迫振动的表面温度场变化全过程。图10展示了叶片受激励点最高温度处温升变化曲线,可明显看出叶片表面温升ΔT演化的3个阶段:温度稳定阶段,快速升温阶段,缓慢降温阶段。为更直观看出叶片表面温度场变化,在温升曲线上分别取ABCDE五个不同时刻下的叶片热图序列。
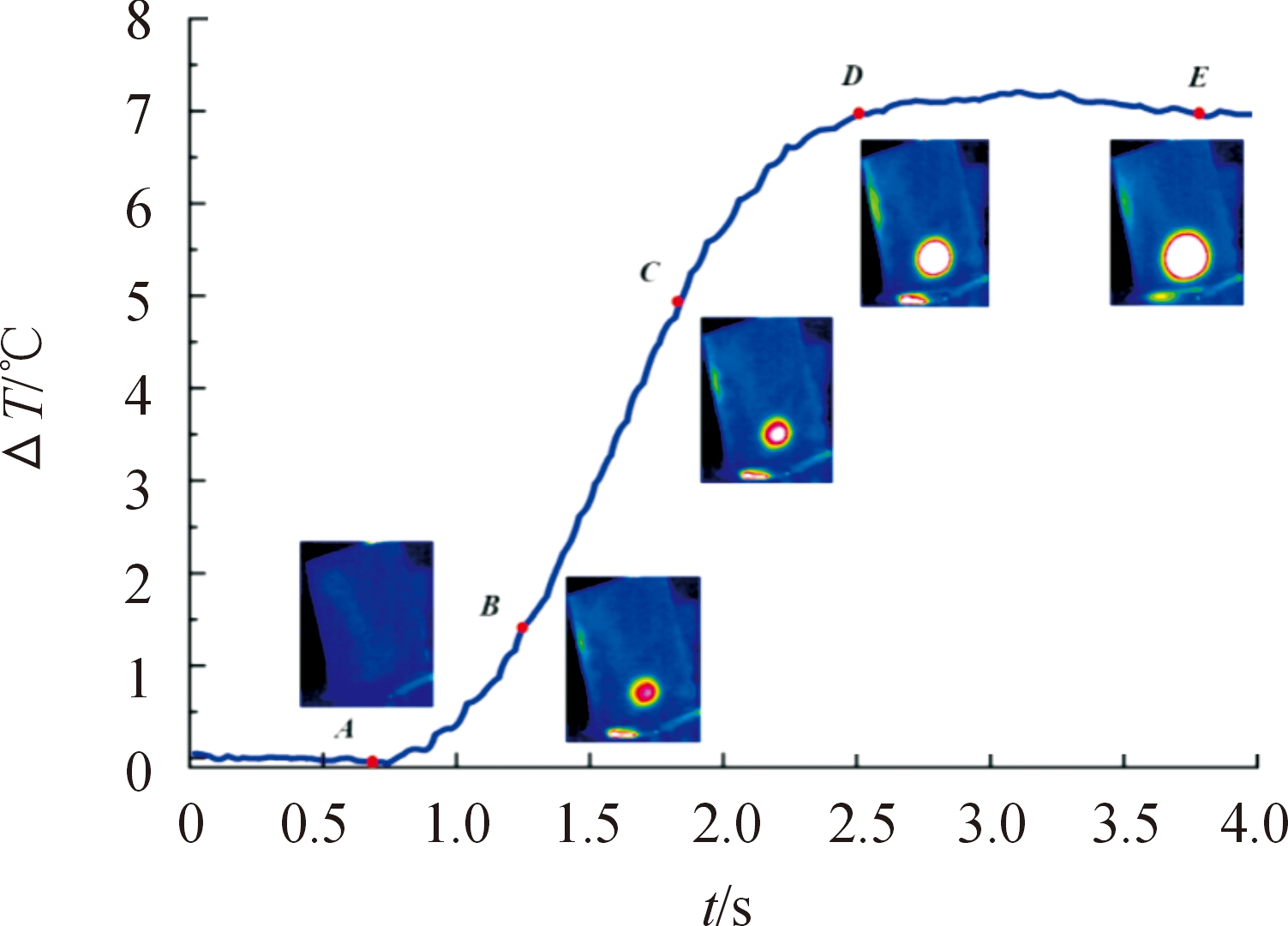
图10 叶片表面温度场变化全过程
Fig.10 The whole process of blade surface temperature field change
温度稳定阶段:起初,在A点前未激发振动,叶片并未产生应力,此时叶片与环境之间的热耗散Q处于平衡状态,叶片表面温度T与环境温度T0差别不大,因此叶片表面温升无太大变化。
快速温升阶段:随着激励开始,在B点,叶片发生受迫振动,外力做功输入的机械能W不为0,叶片受激励点处表面温度T快速上升,并高于环境温度T0,此时,叶片表面温升区域不断向环境周围进行热耗散Q。随着受迫振动的不断持续,外力做功输入的机械能W不断增加,在C点,受激励点处表面温度T不断升高,温升区域不断扩大,应力集中区域有明显升温现象。
缓慢降温阶段:激励终止,受迫振动停止,在D点,受激励点温升达到最大值,此时结构各单元间的热传导Scd与环境的热对流Scv速率最大。E点由于振动停止,外力做功W为0,受激励点温升缓慢下降,由于温升区域存在温度差,叶片结构间与环境间不断进行热耗散Q,热传递(温升)区域不断扩大,但受激励点温升总体呈下降趋势。
基于此,可进一步研究3种试件在不同振动时间下的热耗散规律。图11为试件在不同振动时间下,受激励点温升随采集时间的变化曲线。
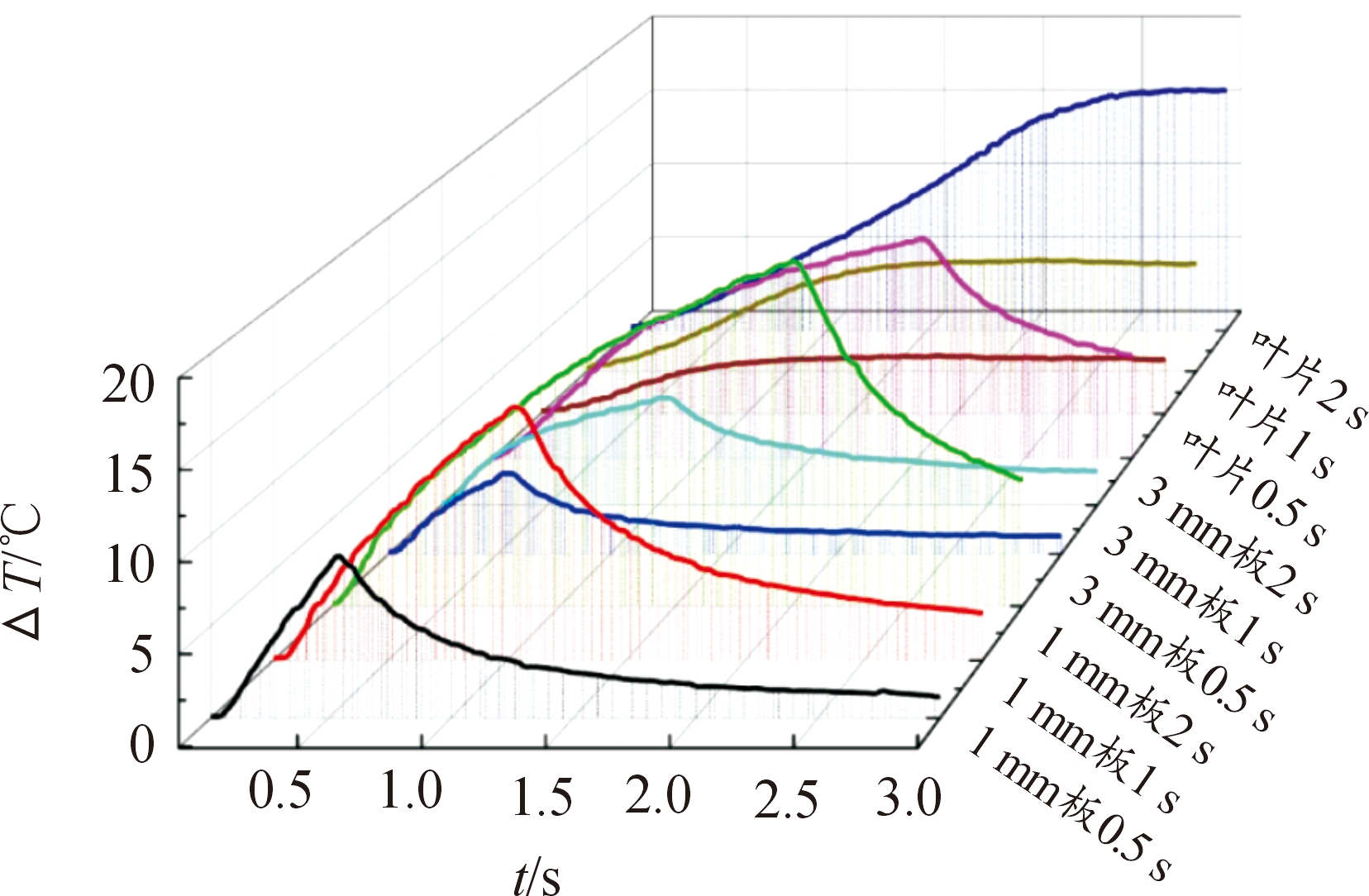
图11 试件在不同振动时间下温升变化曲线
Fig.11 Temperature curve of specimen under different excitation time
由图11可知,随振动时间的增加,受激励点最大温升值ΔT(以下简称最大温升值)也不断增加。振动开始后,试件受激励点迅速升温,且在温度上升阶段初期,同一试件温升速率大致相等;随振动的持续,受激励点温升速率有所降低,该现象在1 mm板和叶片试件振动2 s时最为明显。振动结束时,受激励点温升到达最大值,此时结构单元间以及与环境之间的温差最大,因此热耗散速率也最大。振动结束后,由于无外力做功,试件不断向结构和环境进行热耗散Q,表面温度T不断下降。由于1、3 mm板材料为铝合金,传热导热性好,而叶片材料为钛合金,相比于铝合金导热系数小,散热速度慢,因此三者温度下降速率有所差异。
将3种试件在不同振动时间下的温升曲线对比分析,如图12所示。
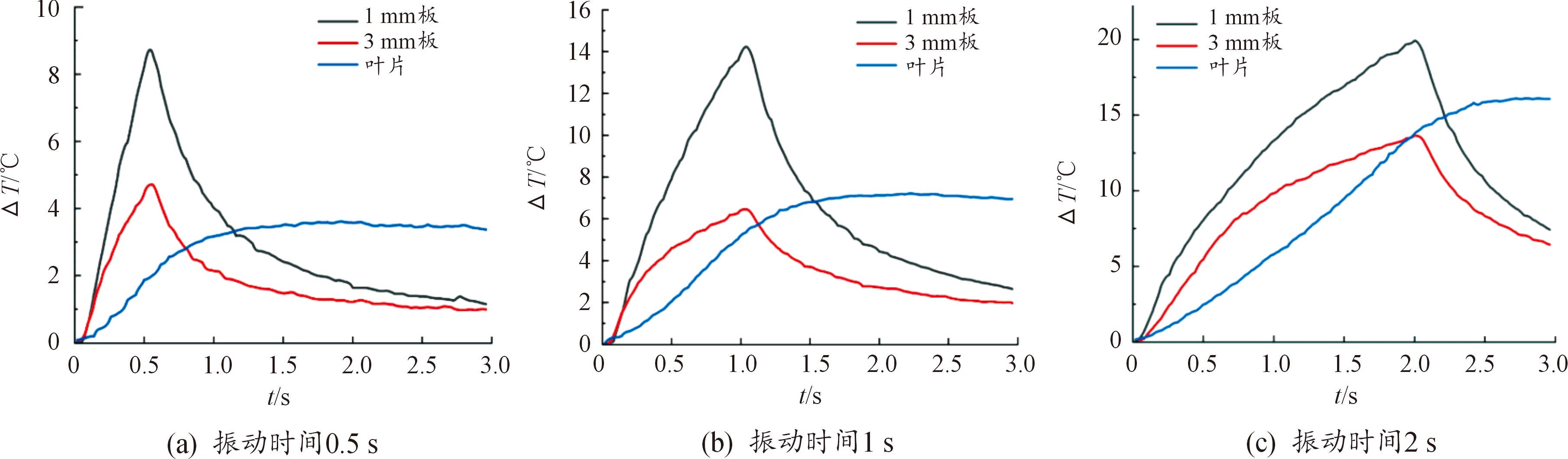
图12 三试件温升变化曲线
Fig.12 Temperature rise curve of three specimens
由图12可知,在振动过程中,1 mm板温升速率最高,3 mm板次之、叶片最慢。这是由于1 mm板质量小,受迫振动幅值更大、振动更剧烈,导致其温升速率最快,温升最大,而叶片结构强度较大,质量比1 mm板大,阻尼作用更强,相比于平板的振动幅值更小,因此温升速率相对较慢。但通过对比图12(a)(b)(c)三图可知,在(a)中叶片的最大温升值均小于1、3 mm板,在(b)(c)中叶片的最大温升值大于3 mm板,小于1 mm板。随振动时间的增加,3种试件的温升差值逐渐缩小,试件最大温升值的变化更不明显,这表明,相比于质量和阻尼作用,振动时间对温升影响更大。
由图11和图12可知,振动过程中,试件温升速率在升温后段有所下降。这是由于随着振动的不断持续,试件结构间与环境温差越来越大,热耗散率增大,所以温升速率有所下降。
2.4.2 应力集中区域温度变化规律
热耗散规律研究为应力集中区域温度变化提供了有效分析方法。从图13可明显看出,除受激励点外,在叶身前缘与叶根附近还存在较明显的温升区域。这与图4叶片应力集中区域比较相符。
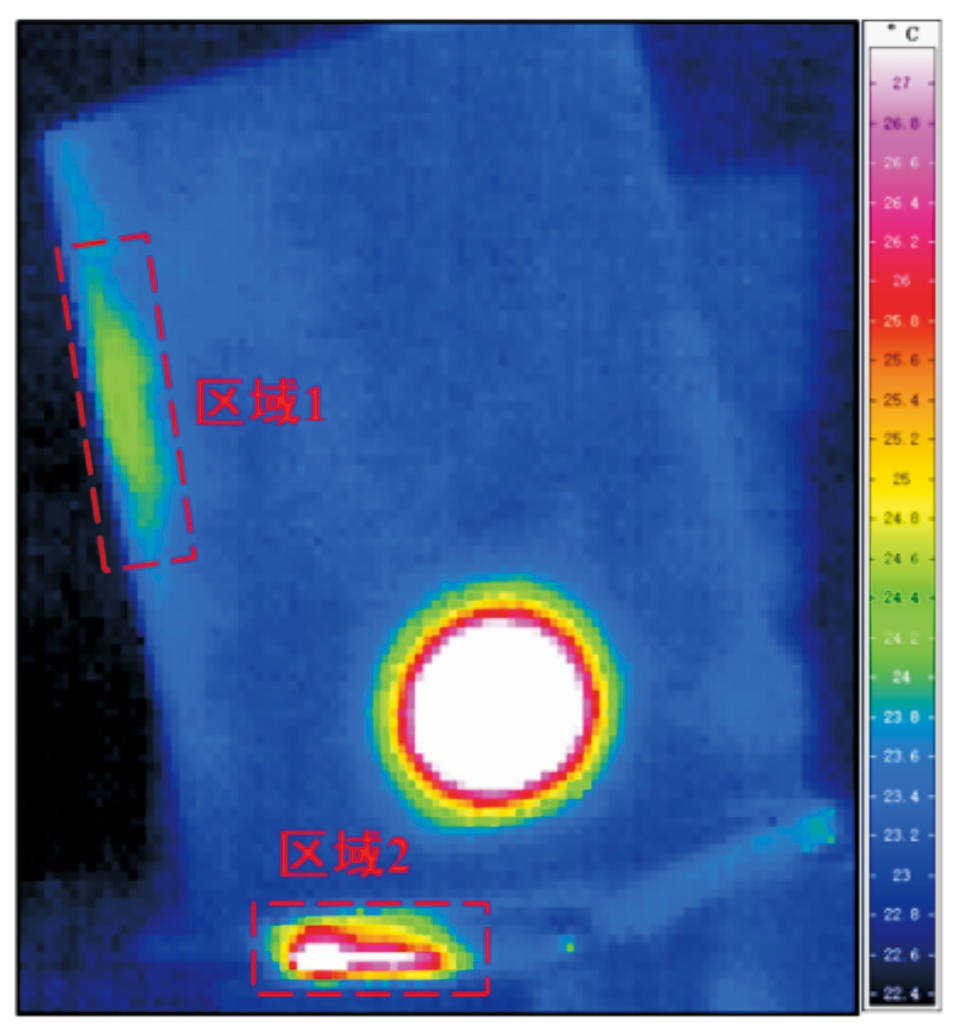
图13 某时刻叶片表面温度场
Fig.13 Temperature field of blade surface at certain time
图14和图15分别为区域1和区域2的温升变化曲线,在受迫振动开始后,应力集中区域均有不同程度温升,当振动结束后,温升逐渐下降。区域1、2在受迫振动停止后,温升初始下降趋势不同。由于区域1为集中应力做功引起温度变化,而区域2为叶根与夹具产生微动摩擦和集中应力做功共同导致温度变化,当受迫振动停止后摩擦表面产生的热量迅速耗散至空气中,当温升值下降至1.5 ℃左右时,区域2温升下降趋势与区域1一致。在图15中,振动时间2 s的温升曲线在振动过程中出现温升缓慢增长阶段,这是由于应力做功一部分热能Q与热耗散中热传导Scd、热对流Scv之和相等,所以温升趋于稳定状态。综上,可以发现,在振动过程中,应力做功输出的能量一部分转化为热能,并在应力集中区域产生热耗散Q,导致表面温度T升高。由图5(b)叶片结构第33阶等效应力云图可知,应力集中区域分布在叶身前缘,最大应力点位于叶根前缘附近,这与试验所观察到的温升区域相符合。因此,可采用红外热像法,根据结构表面温度T分布预见最危险的疲劳损伤部位(应力集中区域),对叶片结构设计、生产和强度分析提供了有效研究方法。
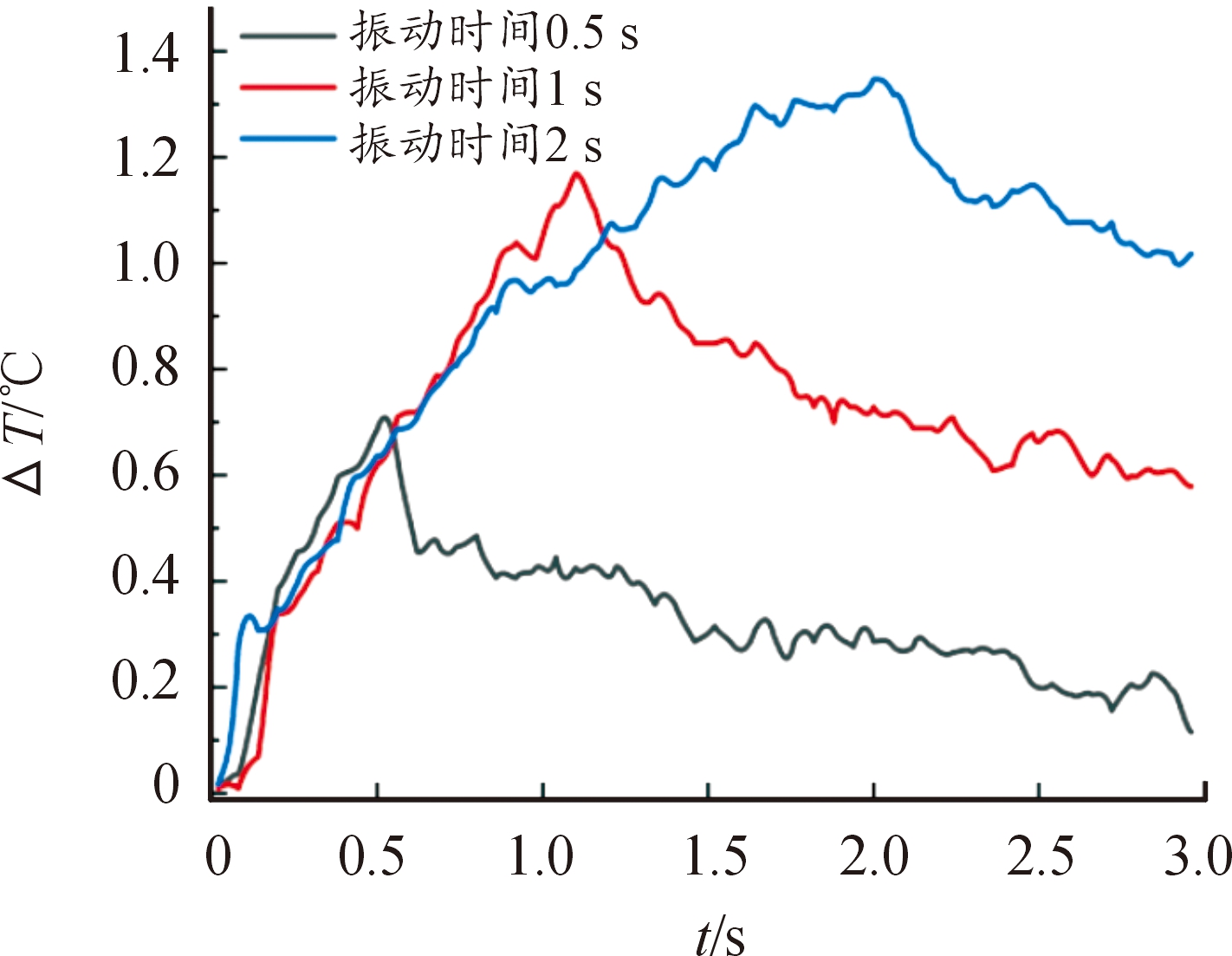
图14 区域1温升变化曲线
Fig.14 Temperature curve of zone 1
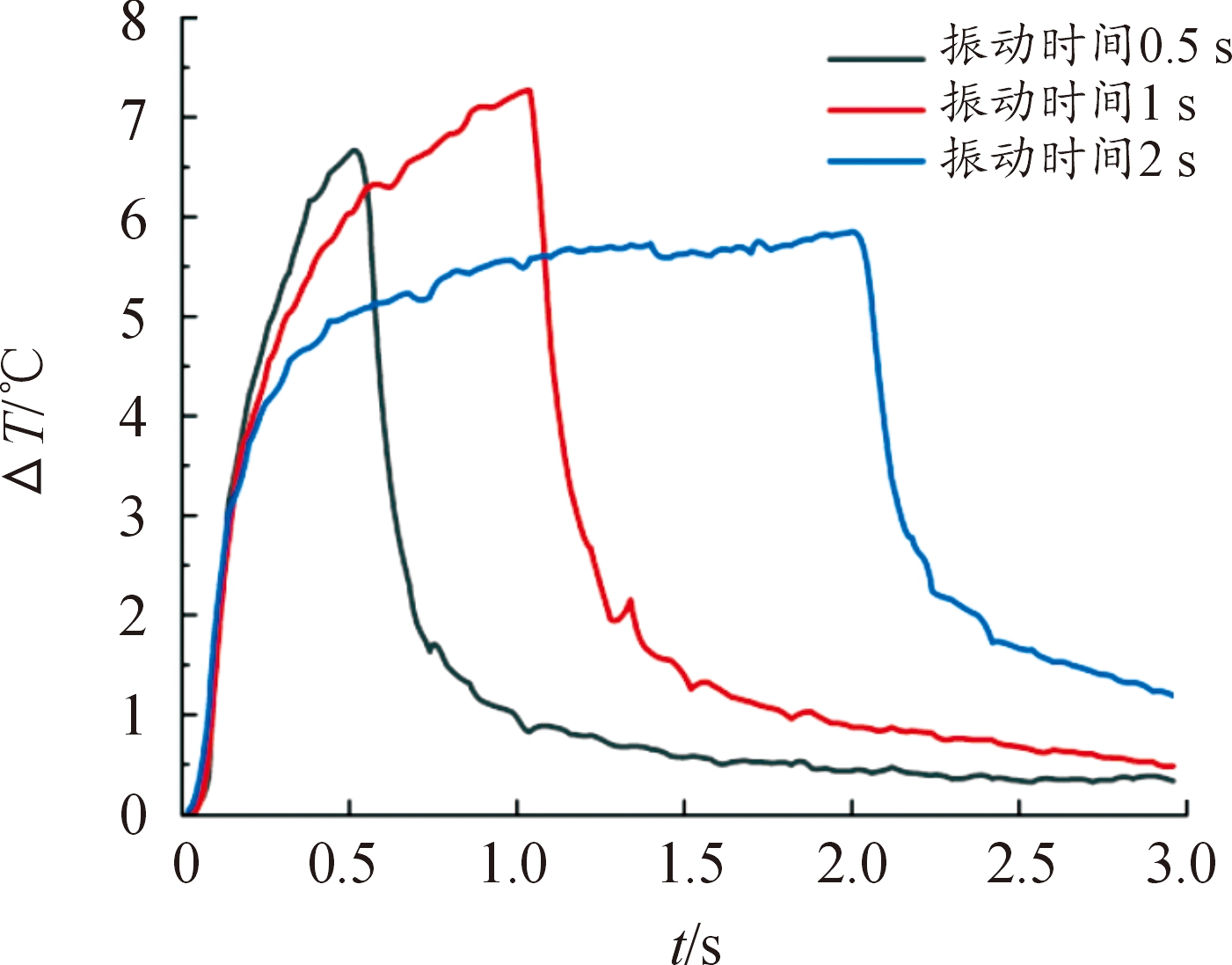
图15 区域2温升变化曲线
Fig.15 Temperature curve of zone 2
3 结论
在系统分析疲劳热耗散理论的基础上,对振动过程中叶片的各阶模态开展了研究,确定了结构振动过程中的应力集中区域。结合振动热耗散理论,提出基于红外热像法的结构受迫振动研究,采用超声变幅杆激励试件根部,通过高精度红外热像仪实时采集试件表面温度场变化。根据红外热图序列及温升变化曲线,确定影响振动热耗散的因素,获得了试件振动热耗散规律。结论如下:
1) 叶片是扭转曲面结构,高阶模态为弯曲或扭转为主的复合振动,叶尖前后缘振动幅值最大,叶根和叶身中部附近易出现应力集中现象。
2) 试验夹具、空气与试件之间的热传导对温度的测量影响不大,相比于质量、阻尼作用,振动时间对试件温升变化影响更为显著。最大温升值与振动时间并无明显的线性关系。
3) 叶片结构受迫振动下,应力集中区域有明显温升,热像法可作为结构受迫振动下应力集中区域快速检测的有效技术手段。
[1] 杨文庆,孙强,马龙,等.某型航空发动机压气机叶片振动静频与动频的关系[J].空军工程大学学报(自然科学版),2005,6(5):5-7.
YANG Wenqing,SUN Qiang,MA Long,et al.The relationship between the static frequency and the kinetic frequency for a certain aero-engine compressor blades[J].Journal of Air Force Engineering University (Natural Science Edition),2005,6(5):5-7.
[2] QIAN Z M,LI G Q,MI D,et al.Thermomechanical fatigue life prediction method of the trailing edge holes in the turbine blade for turboshaft engine[J].Journal of Physics:Conference Series,2022,2168(1):012003.
[3] YUE P,MA J,ZHOU C H,et al.Dynamic fatigue reliability analysis of turbine blades under combined high and low cycle loadings[J].International Journal of Damage Mechanics,2021,30(6):825-844.
[4] SALAWU O S.Detection of structural damage through changes in frequency:A review[J].Engineering Structures,1997,19(9):718-723.
[5] 张琦,王洪斌,姜睿,等.基于激光多普勒测振的叶片振动特性试验[J].航空发动机,2022,48(1):76-82.
ZHANG Qi,WANG Hongbin,JIANG Rui,et al.Experiment on blade vibration characteristics based on laser doppler vibration measurement[J].Aeroengine,2022,48(1):76-82.
[6] TODHUNTER I,PEARSON K.A history of the theory of elasticity and of the strength of materials[M].Cambridge:Cambridge university press,1886.291-364.
[7] BERGMAYR T,KRALOVEC C,SCHAGERL M.Vibration-based thermal health monitoring for face layer debonding detection in aerospace sandwich structures[J].Applied Sciences,2021,11(1):221.
[8] FARIA J,FONSECA L,FARIA A,et al.Determination of the fatigue behavior of mechanical components through infrared thermography[J].Engineering Failure Analysis,2022,134:106018.
[9] LUONG M P.Infrared thermography of fatigue in metals[J].Thermosense XIV,1992,1682:222-233.
[10] LUONG M P.Fatigue limit evaluation of metals using an infrared thermographic technique[J].Mechanics of Materials,1998,28:155-163.
[11] ROSA G L,RISITANO A.Thermographic methodology for rapid determination of the fatigue limit of materials and mechanical components[J].International Journal of Fatigue,2000,22(1):65-73.
[12] GERACI A L,ROSA G L,RISITANO A,et al.Determination of the fatigue limit of an austempered ductile iron using thermal infrared imagry[J].Proceedings of SPIE-The International Society for Optical Engineering,1995,2646:306-317.
[13] TOUBAL L,KARAMA M,LORRAIN B.Damage evolution and infrared thermography in woven composite laminates under fatigue loading[J].International Journal of Fatigue,2006,28(12):1867-1872.
[14] MENEGHETTI G,RICOTTA M,PITARRESI G.Infrared thermography-based evaluation of the elastic-plastic J-integral to correlate fatigue crack growth data of a stainless steel[J].International Journal of Fatigue,2019,125:149-160.
[15] SANTOS SILVA A C,SEBASTIAN C M,LAMBROS J,et al.High temperature modal analysis of a non-uniformly heated rectangular plate:Experiments and simulations[J].Journal of Sound and Vibration,2019,443(17):397-410.
[16] TALAI S M,DESAI D A,HEYNS P S.Vibration characteristics measurement of beam-like structures using infrared thermography[J].Infrared Physics &Technology,2016,79:17-24.
[17] 王纯,王建强,周苏枫.飞机典型金属结构振动疲劳损伤信息获取方法研究[J].工程与试验,2022,62(3):22-23,78.
WANG Chun,WANG Jianqiang,ZHOU Sufeng.Study on damage information acquisition method for vibration fatigue of typical aircraft metal structure[J].Engineering &Test,2022,62(3):22-23,78.
[18] 宋振,路广晨,马银行,等.基于红外热成像的CFRP板振动疲劳损伤试验研究[J].实验力学,2022,37(6):821-828.
SONG Zhen,LU Guangchen,MA Yinhang,et al.Experimental study on vibration fatigue damage behavior of CFRP plate based on infrared thermal imaging[J].Journal of Experimental Mechanics,2022,37(6):821-828.
[19] 赵卫强,鲁墨武,赵永健,等.基于UG的航空发动机涡轮叶片模态分析[J].机械设计与制造,2007(9):76-77.
ZHAO Weiqiang,LU Mowu,ZHAO Yongjian,et al.Modal analys is of aeroengine turbine blade based on UG[J].Machinery Design &Manufacture,2007(9):76-77.
[20] 吕胜利,李斌,马君峰.铝合金振动疲劳红外监测技术研究[C]//第十二届全国振动理论及应用学术会议论文集.南宁,2017,104:842-846.
LYU Shengli,LI Bin,MA Junfeng.Study on infrared monitoring technology for vibration fatigue of aluminum alloy[C]//Proceedings of the 12th National Conference on Vibration Theory and Application.Nanning,2017,104:842-846.
[21] 杨文平,郭杏林,赵延广.对流和辐射换热对金属高周疲劳能量耗散估计的影响[J].机械工程学报,2021,57(10):187-195.
YANG Wenping,GUO Xinglin,ZHAO Yanguang.Effects of convection and radiation heat transfer on energy dissipation estimation of metal in high-cycle fatigue[J].Journal of Mechanical Engineering,2021,57(10):187-195.
[22] MAYER H,Recent developments in ultrasonic fatigue[J].Fatigue &Fracture of Engineering Materials &Structures,2016,39(1):3-29.
[23] 王昭晗,燕群,陈永辉,等.航空发动机典型材料超高周疲劳试验技术研究综述[J].航空工程进展,2023,14(3):146-156.
WANG Zhaohan,YAN Qun,CEHN Yonghui,et al.A review of the research on the VHCF test technology for aero-engine typical materials[J].Advances in Aeronautical Science and Engineering,2023,14(3):146-156.
[24] 杨正伟,寇光杰,周伟,等.超声激励下不同预紧力作用的裂纹生热建模[J].红外与激光工程,2020,49(S1):90-96.
YANG Zhengwei,Kou Guangjie,Zhou Wei,et al.Theoretical model for heat generation of crack on different preload force under ultrasound excitation[J].Infrared and Laser Engineering,2020,49(S1):90-96.
[25] DONG P,ZHAO H J,MALDAGUE X,et al.Research on the influence of multiple interference factors on infrared temperature measurement[J].IEEE Sensors Journal,2021,21(9):10546-10555.
