水陆两栖车是指既能在陆地上使用车轮或履带行走,也能在水中依靠大功率螺旋桨实现航行的运载工具,集陆上和水中机动能力于一身,其在国防和民生领域均有重要应用价值[1-3]。传统的两栖车在陆地的行进方式与普通车辆一致,近年来更多的总体设计关注两栖车在水中的航行性能,如稳性、快速性和耐波性等。本文研究基于某型号水陆两栖运输车的实尺度模型,两栖车属于钝体结构物[4],流线型较差,方形系数大[5],绕流场较为复杂,因此对两栖车的阻力性能与航行姿态进行研究十分重要。此外,两栖车上配置有防浪板,其作用是使两栖车压浪航行,提高入水时的稳定性,使车体底部区域压力分布更为均匀,防止入水时出现埋首现象,减小俯仰角,使车体保持较为平稳的运动姿态[6]。大量的研究关注防浪板的设计与其对车体快速性的影响,本文则主要分析不同航速下防浪板的压浪作用及其受力特性。
两栖车的阻力性能和运动姿态测量主要依赖于基于Froude相似理论的车体模型拖曳试验,模型试验可以测量不同海况(静水、规则波和非规则波等)和不同航速下的车体水动力性能数据,可靠性高,但存在成本较高,且对流场尤其是自由液面状态的捕捉不够精确。计算流体力学方法(Computational Fluid Dynamics,CFD)能够弥补模型试验的不足,不仅能够较为准确的计算各种工况,而且能够精确的捕捉流场细节,从流体流动本质上考量影响两栖车水动力性能的各项要素,进而提出车体优化措施。徐一新[3]基于CFD计算软件Fluent研究了车体尾部形状和车轮对试验绕流场的影响,确立了车轮收放装置的的实际应用价值。余祖耀等[5]采用CFD方法和正交分析法得出了提高两栖车升阻比的最优尾滑板角度组合方案。郑翔玉等[6]同样采用数值方法验证了车轮收起后可以减小两栖车的水上行驶阻力。剧冬梅等[7]基于CFX流体计算软件,采用标准k-ε湍流模型和Level Set方法研究了车体纵倾角对阻力特性的影响,计算结果与试验结果吻合较好,结果表明纵倾角过小易引起埋首现象,过大则使车体阻力变大,随着Froude数增加,纵倾角的改变对航行阻力的影响也在变大。袁潇龙等[8]结合k-ω湍流模型和多相流模型研究了加装防浪板对水上航行阻力的影响,并研究了新型防浪板的减阻效果以及其对车体稳定性的影响。万晓伟等[9]对比了CFD数值计算与拖模试验的阻力结果,两者的误差较小,验证了k-ε湍流模型计算两栖车阻力性能的有效性。彭锟等[10]采用k-ω湍流模型和Level Set多相流模型研究了尾翼板设计的减阻效果,结果表明尾翼板减阻性能与Froude数密切相关。蔡宇峰等[11]基于可实现的k-ε湍流模型、流体体积法(Volume of Fluid,VOF)和重叠网格技术建立了两栖车三维非定常数值模型,并与试验结果进行了对比,验证了该模型的有效性。王丽丽等[12]同样采用上述数值模型研究了尾压浪板的减阻效果,表明VOF方法捕捉到的自由液面与实际情况较为相符。
综上可知,大量研究集中在采用CFD技术对两栖车进行减阻增效的优化设计,采用的数值模型大同小异。本文在上述研究的基础上,基于可实现的k-ε湍流模型和重叠网格技术建立了两栖车水中航行运动的CFD数值模型,完成了时间步无关性和网格收敛性验证,基于该模型计算两栖车在静水环境中、不同航速下运动的水动力性能,包括阻力、垂荡和纵摇性能,其中总阻力计算结果与拖曳试验结果吻合较好,验证了该数值模型的有效性。此外,本文研究了防浪板在不同航速下的受力特性,包括纵向、垂向受力以及板上不同位置的力矩。研究表明,该数值模型可以较好的实现两栖车水中运动模拟与性能预报;高航速下两栖车抬首现象严重;防浪板顶部承受力矩较大,工程设计中需对防浪板顶部连接杆件进行加强。
1 CFD模型设置
1.1 物理模型设置
本文基于CFD商业软件STAR-CCM+完成数值模拟,该软件的数值离散方式采用有限体积法(Finite Volume Method,FVM),有限体积法中每个网格节点周围通过划分网格来形成互不重叠的微小控制体,质量和动量守恒控制方程转化为每个控制体的体积分,进而得到计算域的离散方程组并求解。两栖车运动属于瞬态问题,故采用非定常求解器求解流体方程。基于文献[11-12]研究方法,两栖车在水中运动过程中存在边界层分离现象并存在车体尾部旋涡结构,因此湍流模型选择可实现的k-ε湍流模型,该模型通用性好,可以计算较为复杂的湍流问题,适用于边界层流动与分离流动问题以及外部自由流动问题的求解[13]。水面运动问题涉及自由液面的动态模拟,尤其是两栖车运动中会产生复杂的兴波,需要实现对自由液面的精确捕捉,本次研究利用VOF方法实现自由液面的模拟,设置两相流体,分别为水相和空气相,两者均为不可压缩流体且需指定相应的流体属性。计算时用与航速数值相同但方向相反的流速代替车体航速,以保证车体模型在有限区域内完成较长时间的运动模拟。
两栖车的垂荡和纵摇两自由度的运动模拟利用动态流体固体相互作用模块(Dynamic Fluid Body Interaction,DFBI)求解完成。使用该方法时需指定运动物体的相关属性,包括重量、重心位置和转动惯量,运动方式包括垂向平移(垂荡)和横向旋转(纵摇)运动两项,限制其他方向运动。此外,为提高求解精度和稳定性,设定释放时间使流体流动更加均匀,在该时间内物体不发生平移和旋转运动;设定缓冲时间来减小计算初期流体对物体的冲击效应。基于上述物理模型设置,本次研究主要计算实尺度两栖车的阻力、纵摇和垂荡数据,防浪板在纵向、垂向受力和防浪板不同位置处的横向力矩,其中力矩的监测位置包括防浪板的底部、中部、顶部三个位置,防浪板简化模型如图1。
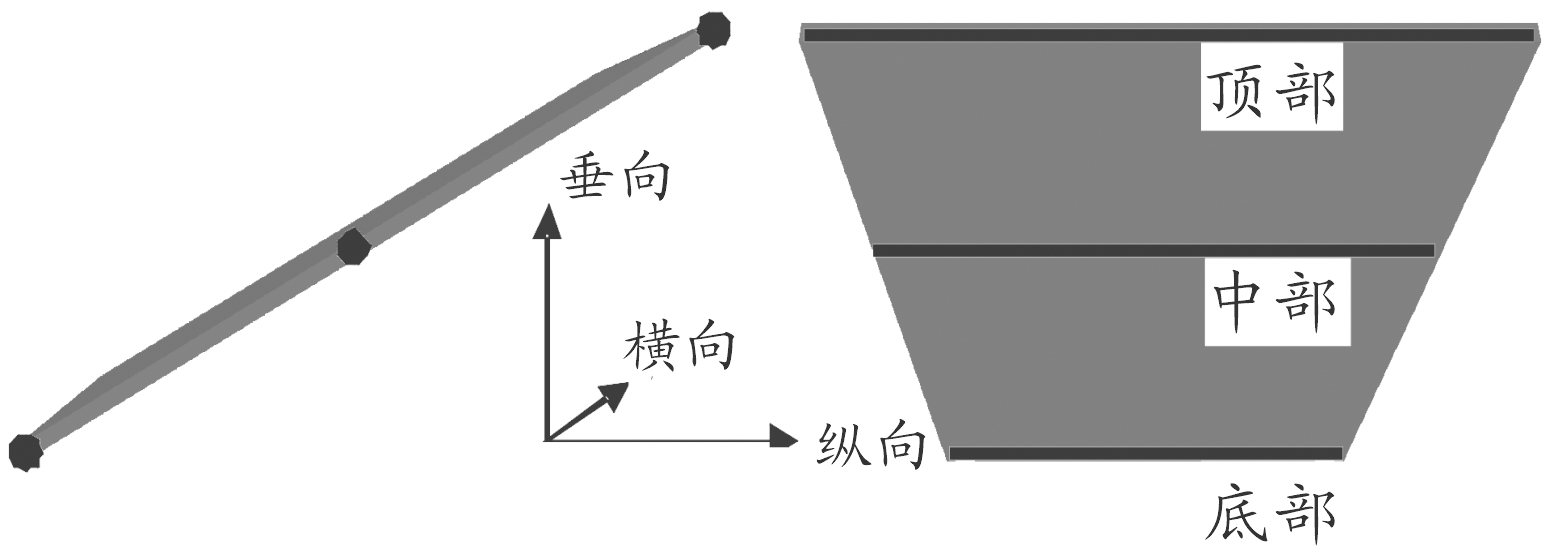
图1 防浪板受力简化模型
1.2 网格划分和边界条件设置
重叠网格技术常用来处理具有复杂外形结构物体的运动问题[14],在物体运动过程中不会发生网格的变形与挤压[15],这使得网格单元在计算过程中一直保持高质量,不仅求解精度高,而且对壁面附近粘性流场的捕捉更为精确。使用重叠网格时,计算域被分为重叠网格域和背景域两部分,重叠网格域在计算过程会随着物体的运动而移动,因此两套网格域的重叠区域一直在更新,两者之间通过重叠网格交界面进行数据交换。最终的网格划分如图2所示,图2中心偏右部位外围为粗线的大长方形框以内为重叠网格域,以外为背景网格域,网格总数333万。需要注意的是,网格划分需要对流场变化剧烈的地方进行加密。物面边界层对求解剪切力有重要的影响,本次计算取壁面y+值为50,边界层层数和增长率分别取为5和1.3;车体运动过程中,物面周围流场变化最为剧烈,因此需要对车体附近网格进行加密,本次计算主要研究防浪板上的受力特性,所以需要对防浪板前后一定范围内的区域进行加密(图2中心右部外围为黄线的小长方形框内部区域);两栖车在航行过程中会形成开尔文兴波,必须考虑自由液面的网格加密,尤其是垂向的网格尺寸(图中的水平线上下加密区域为自由液面加密区);车体物面附近网格加密,而外流域网格较为稀疏,为减小计算误差需要设置合理的网格过渡区域,因此对外流域设置了两套网格加密区。
选择合理的流域尺寸可以在保证求解精度的基础上提高计算效率。车身长度为L,车体物面为无滑移壁面边界条件;流体速度入口距离车头1L,给定流速值和方向;压力出口距离车尾3L;左右面均设置为速度入口边界条件,且各自距离车中心线1.5L;上下面同样设置为速度入口边界条件,总高度约为2L。具体的边界条件设置如图3所示。
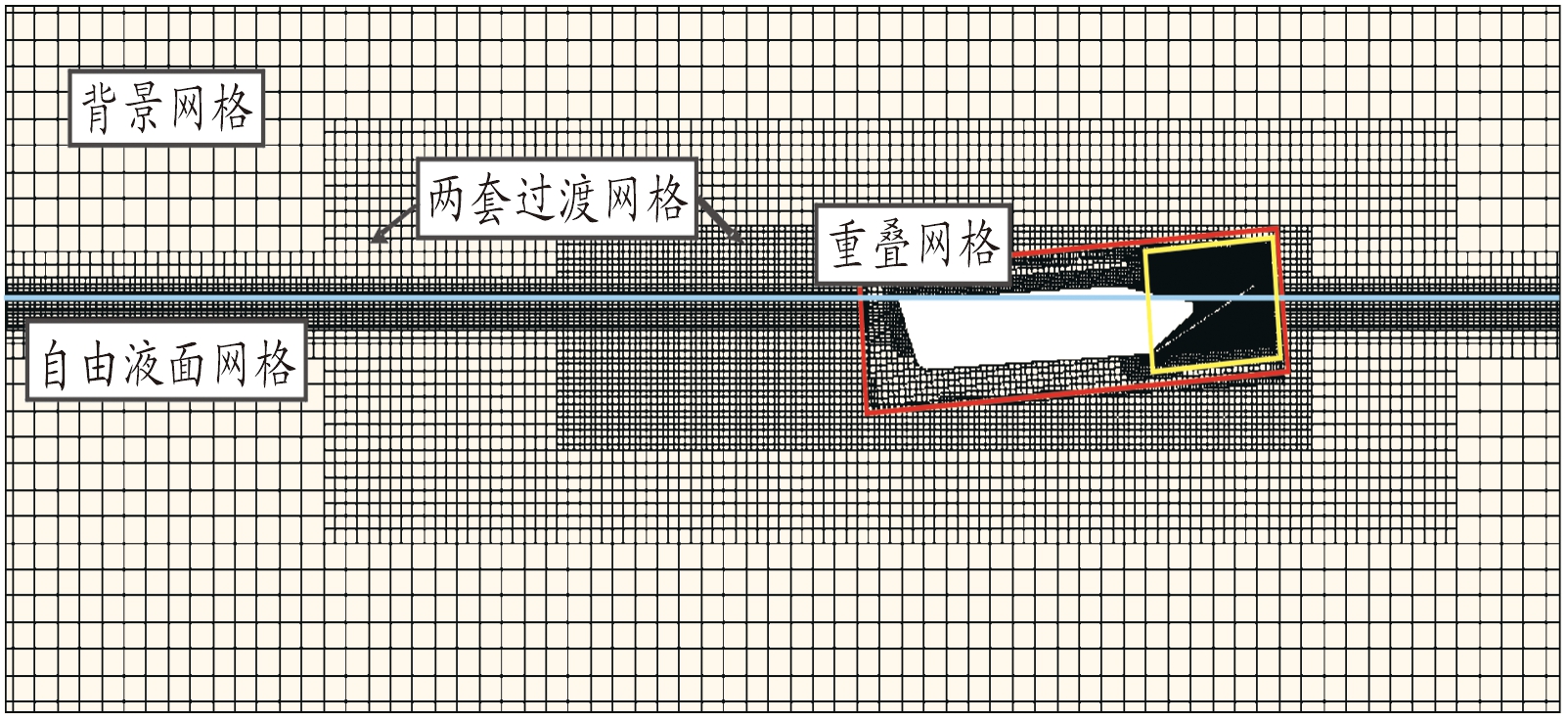
图2 网格划分
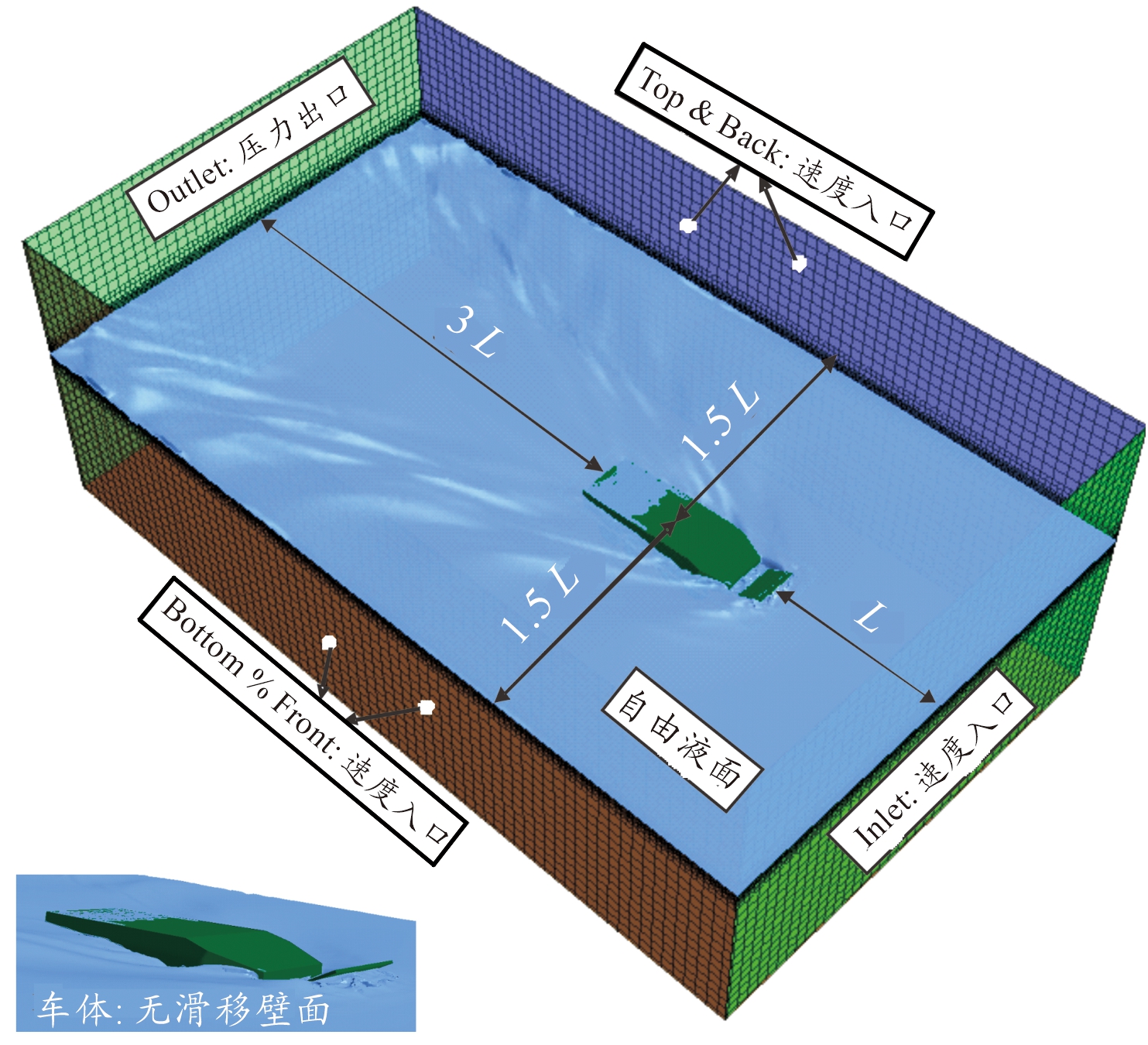
图3 边界条件设置示意图
1.3 时间步无关性验证
两栖车水动力性能数值研究属于非定常流动问题,因此需要确定时间步大小。在保证计算结果准确性的前提下,合理优化时间步长可以降低CFD模拟的计算成本。本次验证的模拟工况为航速V=12 km/h。监测了时间步长为 Δt=0.01 s,0.02 s和0.04 s三种时间步下两栖车总阻力系数时历变化,如图4所示,Δt=0.02 s与Δt=0.01 s的总阻力系数时历曲线更为接近;并且计算了10~20 s时间段内总阻力系数的平均值,以Δt=0.01 s的计算结果为标准值,Δt=0.02 s和Δt=0.04 s与标准值的相对偏差分别为-0.737 9%和-1.479 2%,如表1所示。计算结果对时间步敏感度较低,时间步为0.02 s时计算结果已趋于收敛,故本文计算采用的时间步长为Δt=0.02 s。
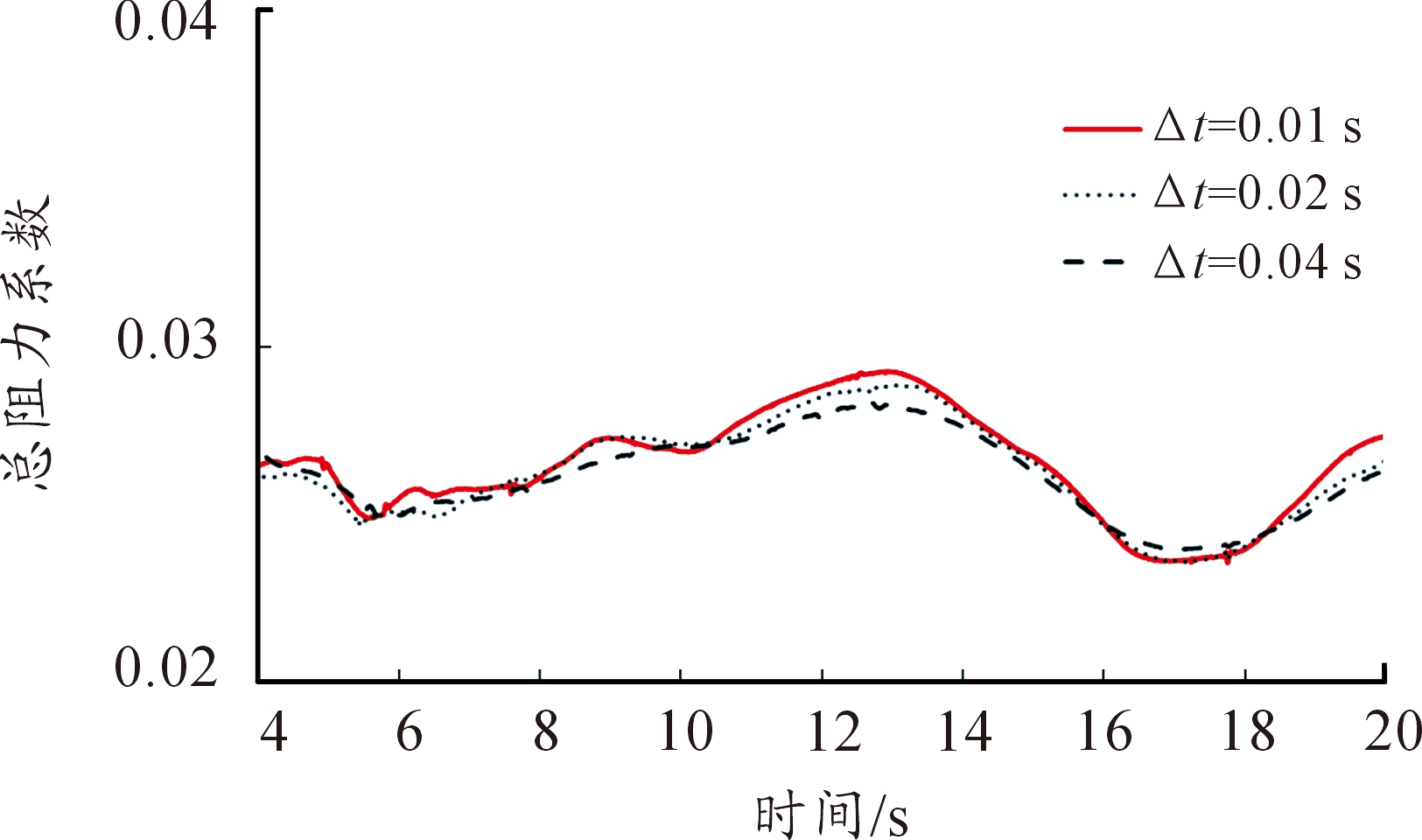
图4 两栖车总阻力系数曲线
表1 验证计算结果
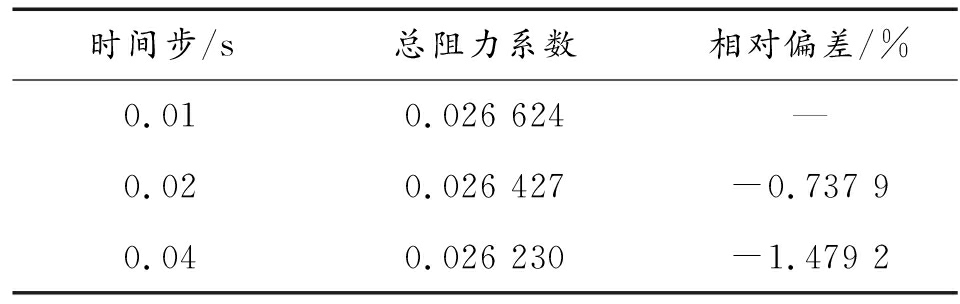
时间步/s总阻力系数相对偏差/%0.010.026 624—0.020.026 427-0.737 90.040.026 230-1.479 2
1.4 网格无关性验证
采用合适数量的网格进行计算不仅可以保证计算结果的准确性,而且可提高计算效率。本次研究在保证边界层网格不变的基础上,通过改变全局网格基础尺寸的值来调整网格数量,研究了三种不同网格数量的CFD模型的计算结果,网格数量分别为192万、333万和561万,网格具体信息如表2所示。验证选用的工况为航速V=12 km/h,时间步长0.02 s。比较了三种网格模型的总阻力系数时历数据,如图5所示。可以看出,细网格和中等网格的总阻力系数时历曲线几乎是一致的;从表2可以看出,以细网格模型的计算结果为标准,粗网格和中等网格的计算结果偏差分别为0.621 8%和3.618 0%,并且粗网格计算结果的时历曲线不光滑,网格加密程度对结果影响较大。因此,本文采用网格数量为333万的模型进行数值计算即可满足精度要求。图6是航速为12 km/h时自由液面云图,图中线条代表航行稳定段水面上各点距离水平位置的高度。
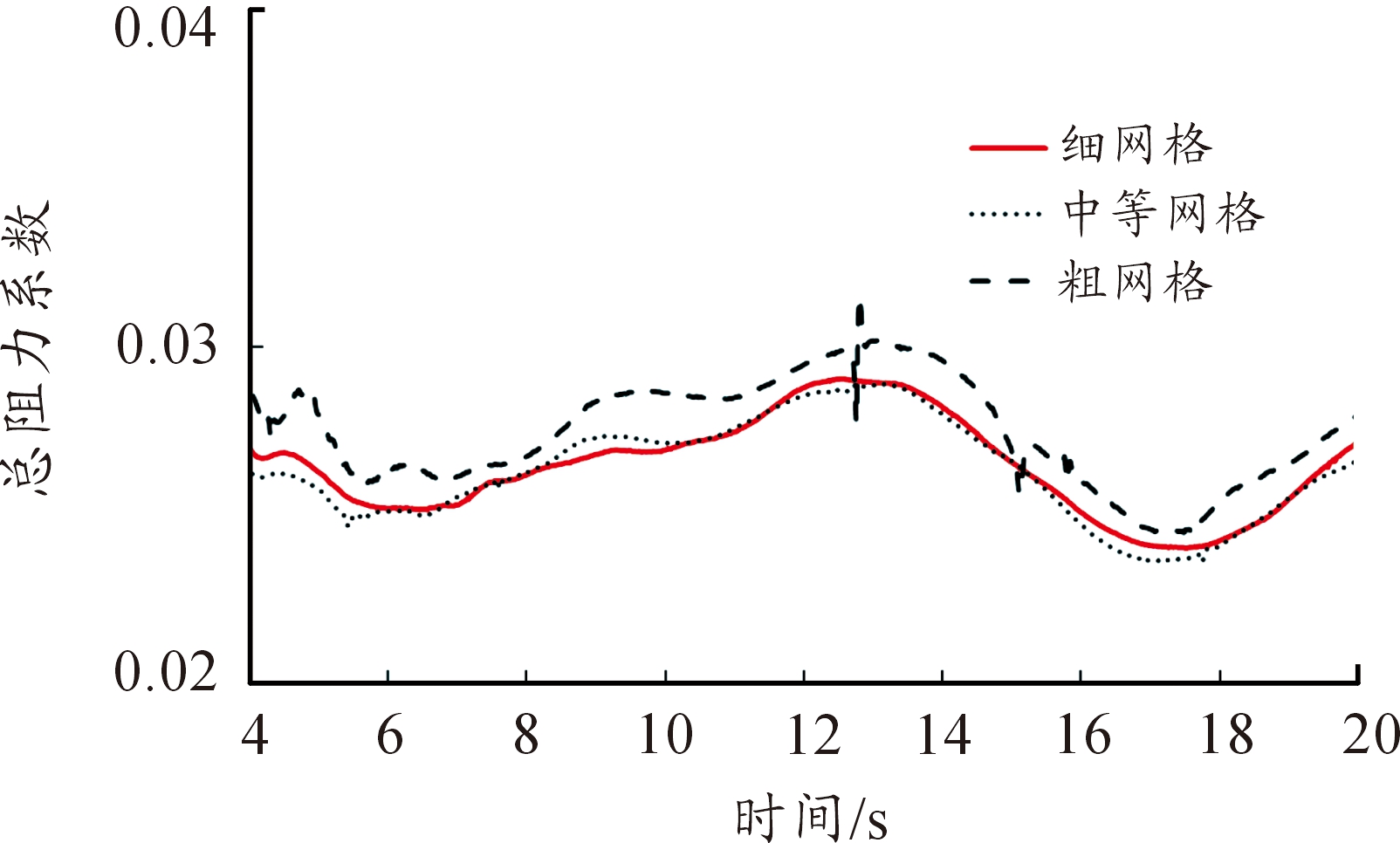
图5 两栖车总阻力系数曲线
表2 网格收敛性验证计算结果
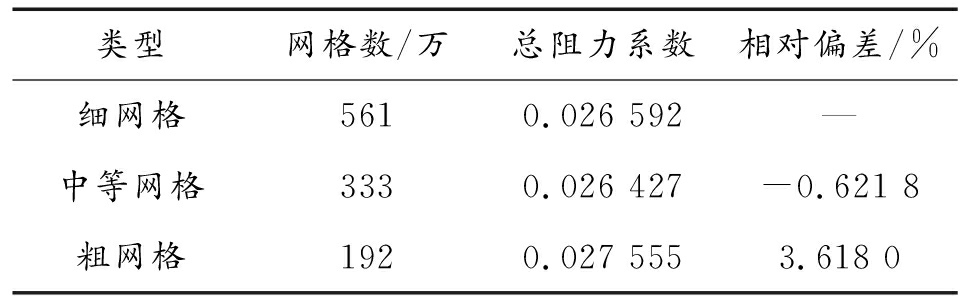
类型网格数/万总阻力系数相对偏差/%细网格5610.026 592—中等网格3330.026 427-0.621 8粗网格1920.027 5553.618 0
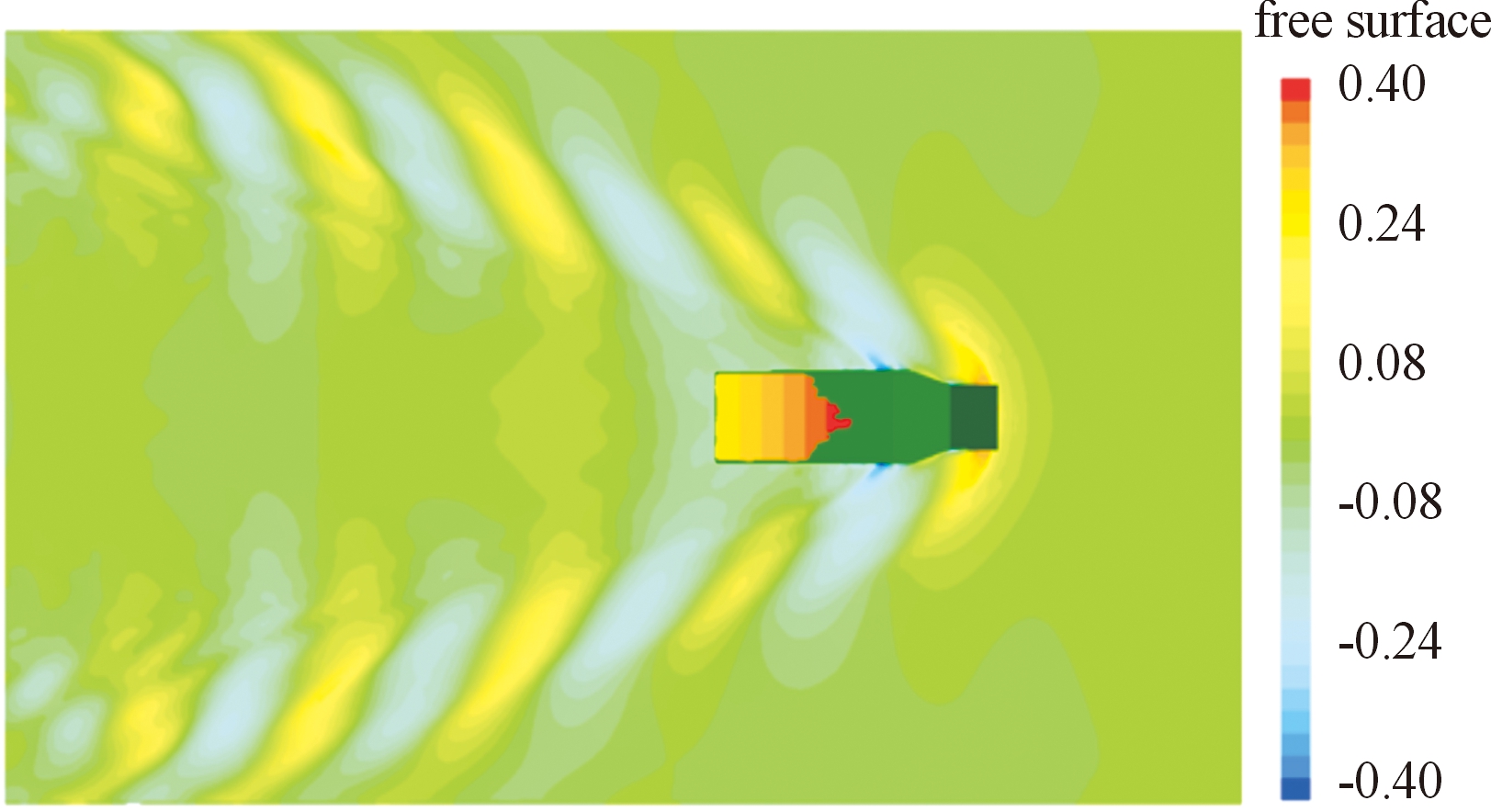
图6 12 km/h航速下自由液面流场云图
1.5 数值模型有效性验证
该型号两栖车的拖曳试验在大连理工大学船模拖曳水池完成,试验现场如图7所示。基于上述时间步和网格收敛性验证结果,本次研究计算了8、10、12、14、16、20 km/h共6种航速下的两栖车静水总阻力,结果如图8所示。图8中还包含了拖曳试验结果。可以看出,数值计算结果与试验结果吻合度较高,尤其是低航速下的数值计算更接近于试验结果。高航速状态下钝型车体航态和周围绕流场情况更为复杂,对阻力性能影响较大,因此计算误差会随航速增加而增大。基于与拖曳试验结果的对比验证了本次研究所采用的的数值模型的有效性。

图7 两栖车拖曳试验
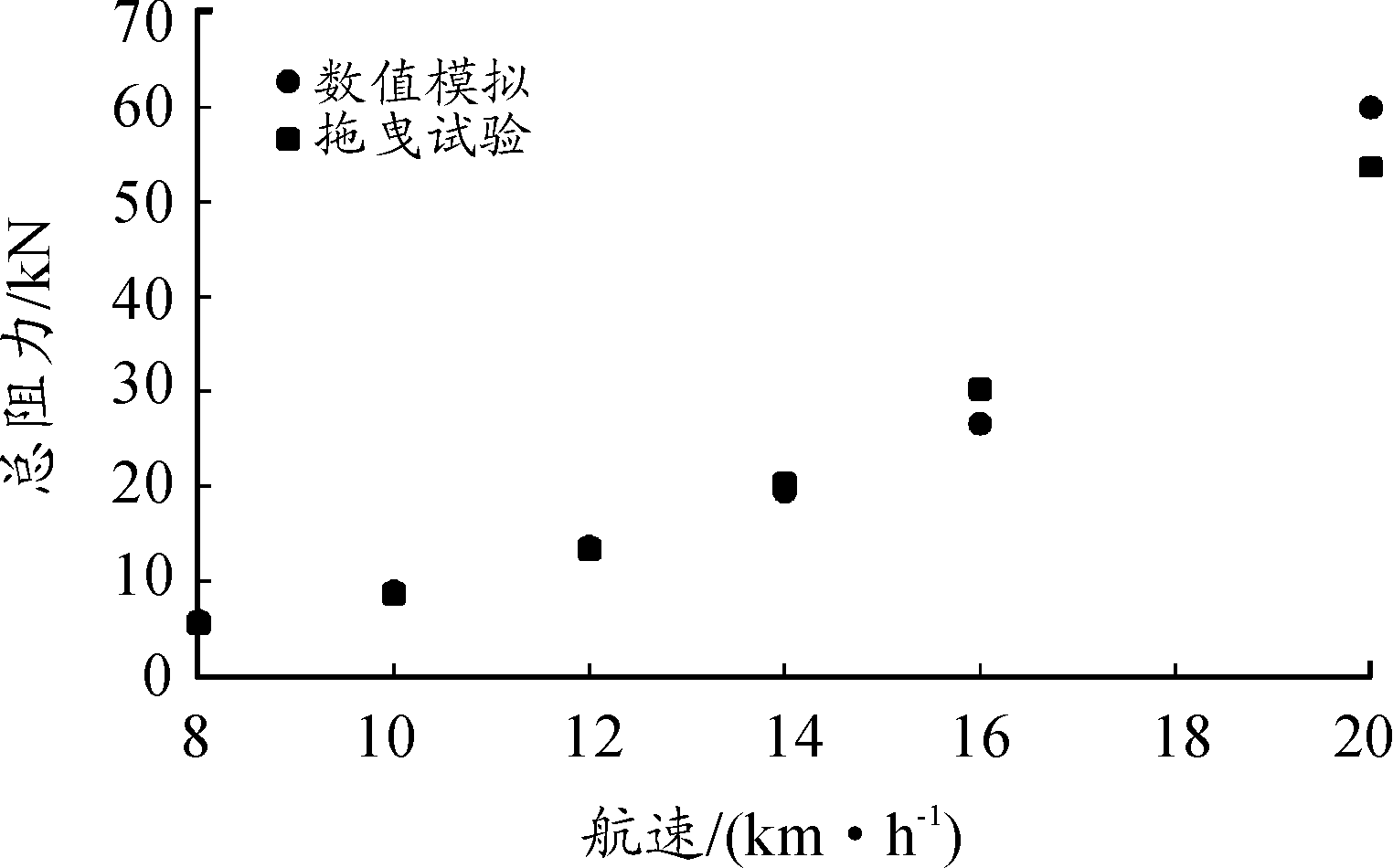
图8 总阻力计算结果与拖曳试验结果
综上,本文采用可实现的k-ε湍流模型和重叠网格技术建立了水陆两栖车的CFD数值计算模型,并对计算时间步和网格尺寸的收敛性进行了验证,与拖曳试验结果的对比验证了该模型的有效性。基于此模型,下一步对静水中不同航速下的两栖车的水动力性能和防浪板受力特性进行计算和分析。
2 两栖车水动力性能研究
本次研究计算了两栖车在静水中、不同航速下的水动力性能,包括阻力、垂荡和纵摇三项。从车体受到的应力方向来考虑,总阻力又可以分为摩擦阻力Rf(切向阻力)和压差阻力Rp两部分,计算结果以阻力系数的形式进行对比。此外,本次研究计算了防浪板在流体力作用下的受力特性,包括纵向、垂向受力和防浪板三个位置处(底部、中部和顶部)的横向力矩。
计算的航速范围为8~18 km/h,每隔2 km/h取一航速值计算,共6种工况。数值模拟采用非定常求解,特性计算值均取数值计算稳定段后10s数据的平均值进行对比研究,得到不同航速下水动力性能数据如表3所示。
表3 两栖车水动力性能数据
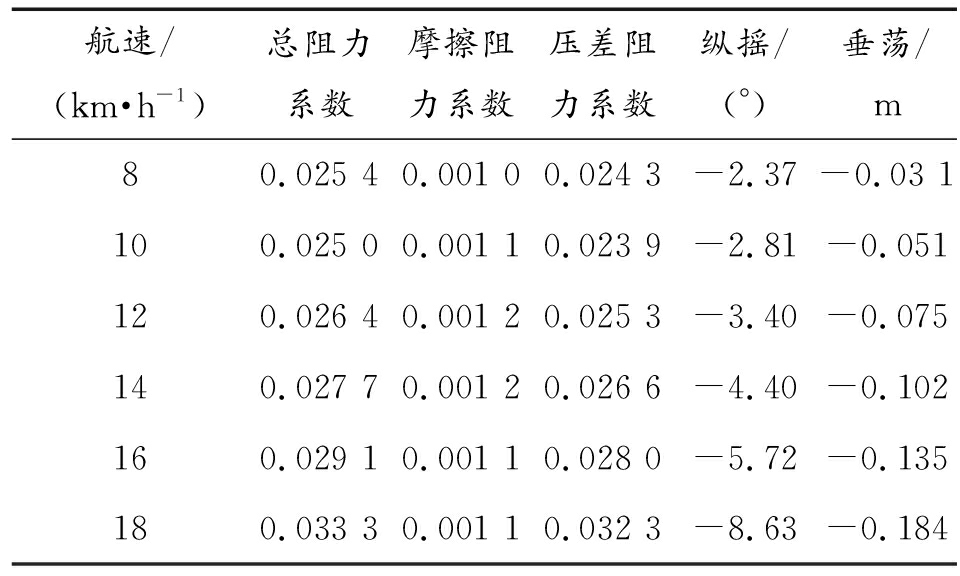
航速/(km·h-1)总阻力系数摩擦阻力系数压差阻力系数纵摇/(°)垂荡/m80.025 40.001 00.024 3-2.37-0.03 1100.025 00.001 10.023 9-2.81-0.051120.026 40.001 20.025 3-3.40-0.075140.027 70.001 20.026 6-4.40-0.102160.029 10.001 10.028 0-5.72-0.135180.033 30.001 10.032 3-8.63-0.184
防浪板受力特性计算得到的数据如表4所示。阻力、垂荡和纵摇曲线分别如图9、图10、图11所示,作用于防浪板的力和力矩曲线分别如图12和图13所示。两栖车在运动稳定段的运动状态如图14所示。
阻力系数计算公式为:
式中:Cd为阻力系数;F为阻力值;ρ为流体密度;V为航速,S为湿表面积。
表4 防浪板受力特性数据

航速/(km·h-1)纵向力/kN垂向力/kN底力矩/(kN·m)中力矩/(kN·m)顶力矩/(kN·m)83.278.11-3.0610.1723.39105.3211.33-5.5614.0433.64127.5614.62-8.0817.5943.251410.7319.10-9.9224.2658.441614.5123.91-10.9732.6776.311818.4726.89-8.5942.3293.23
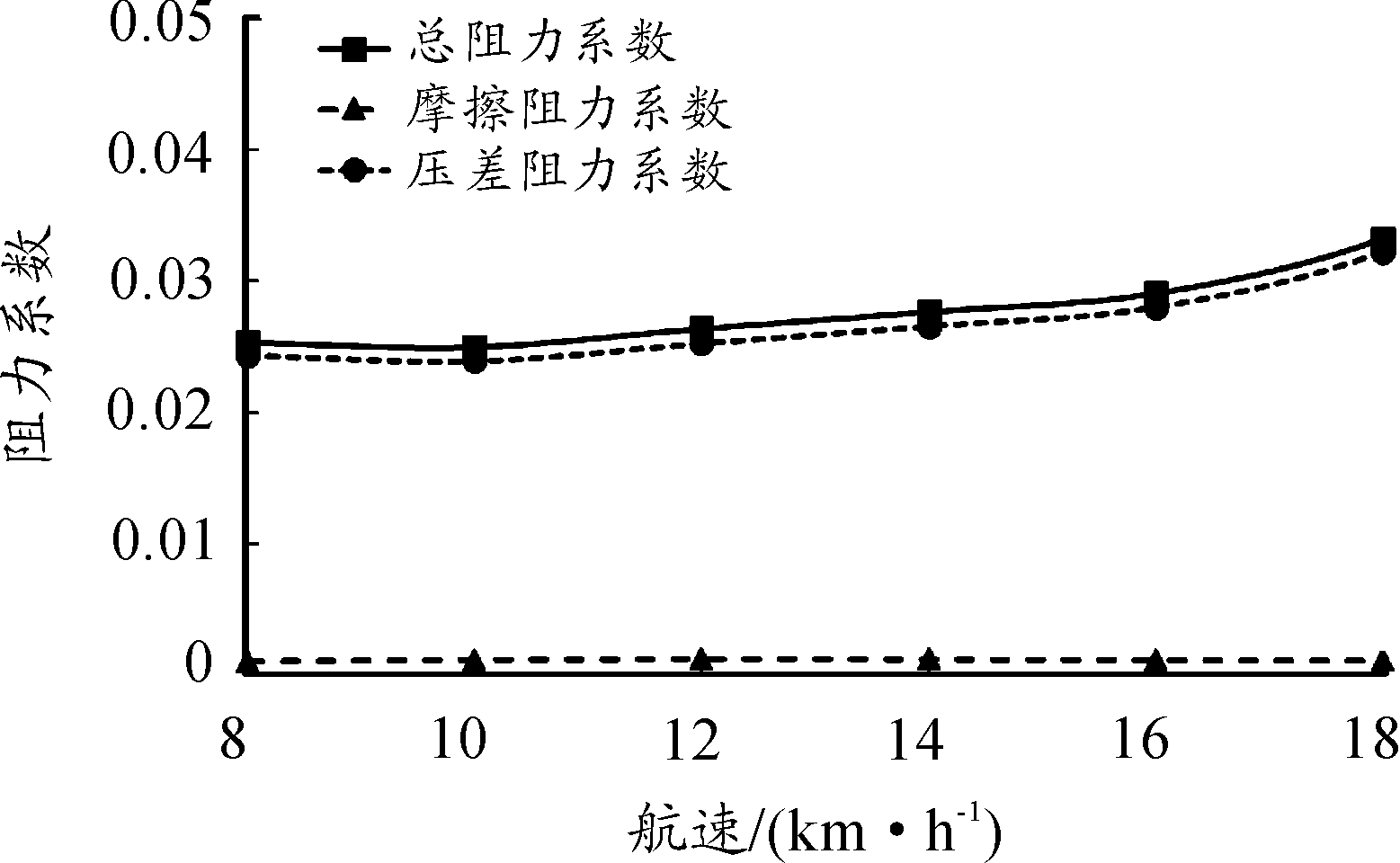
图9 阻力系数曲线
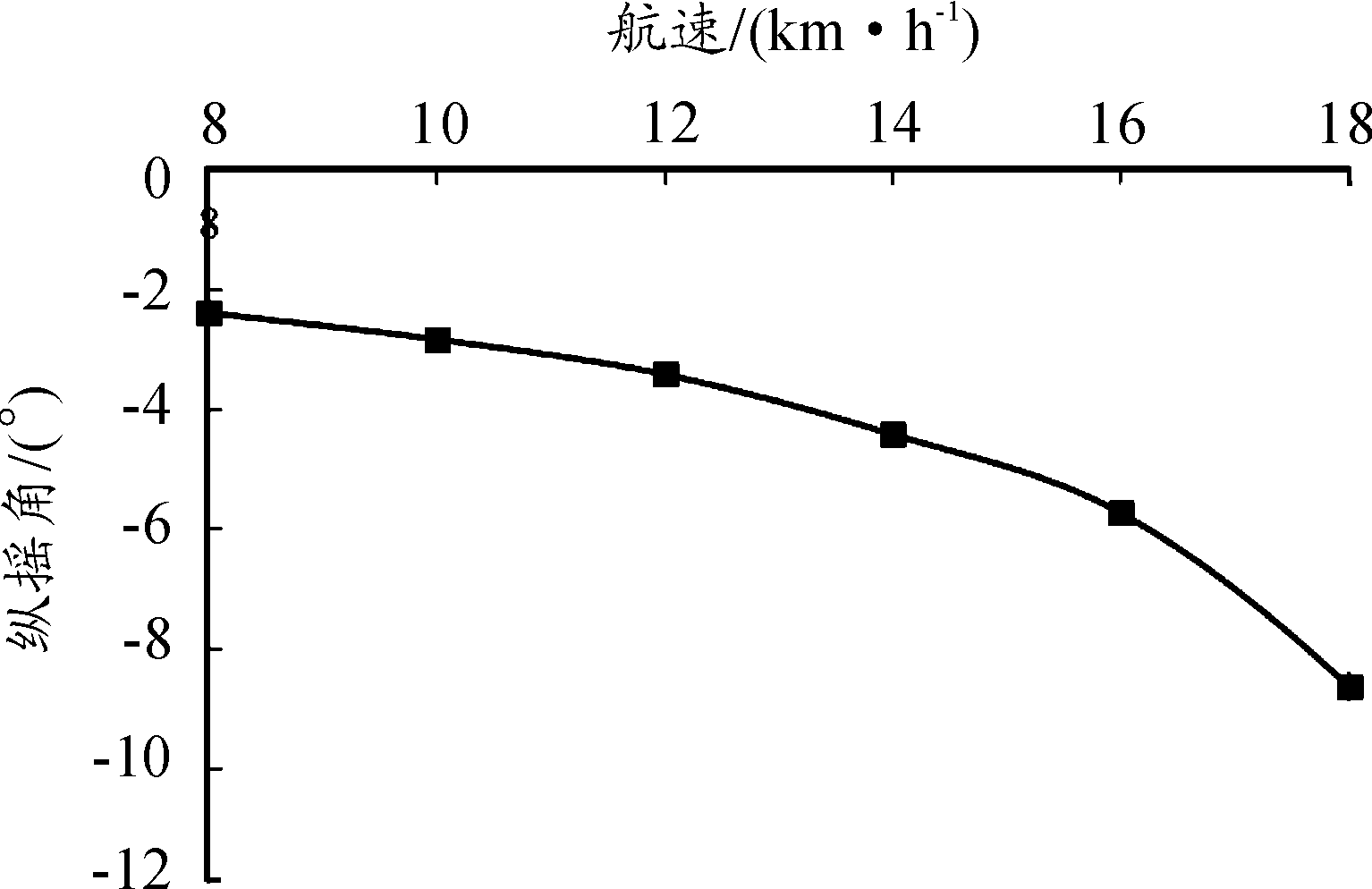
图10 纵摇运动曲线
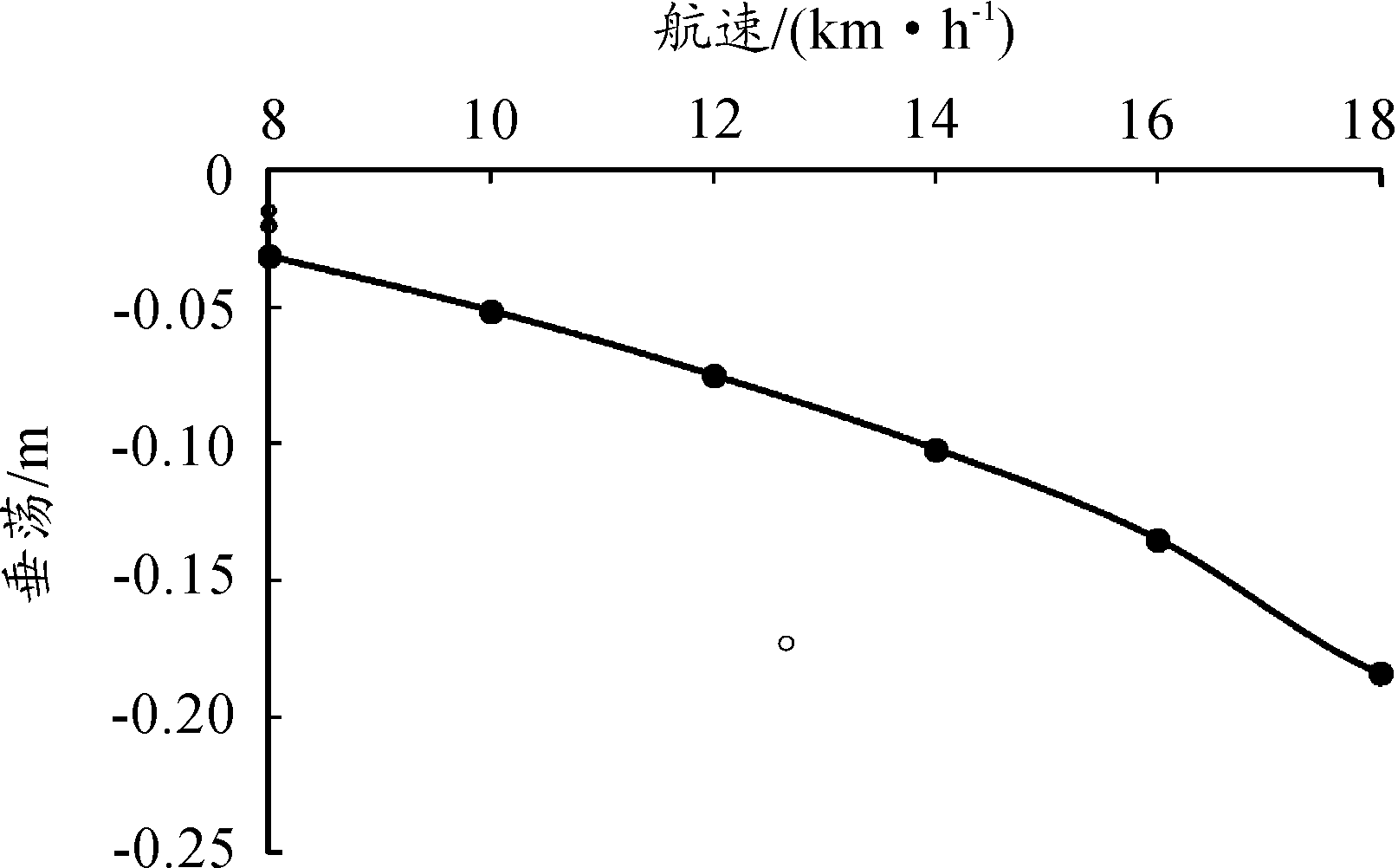
图11 垂荡运动曲线
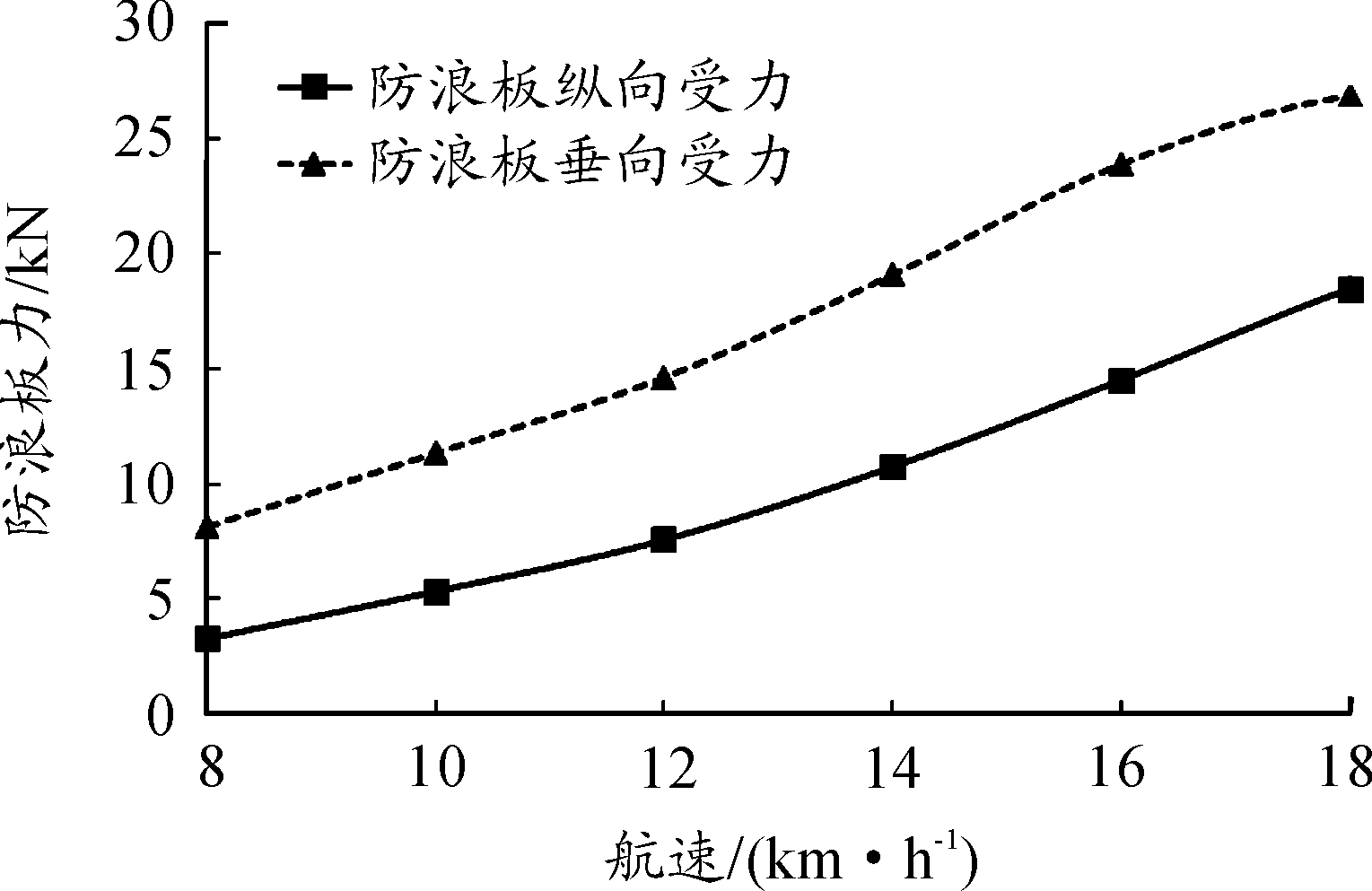
图12 防浪板受力曲线
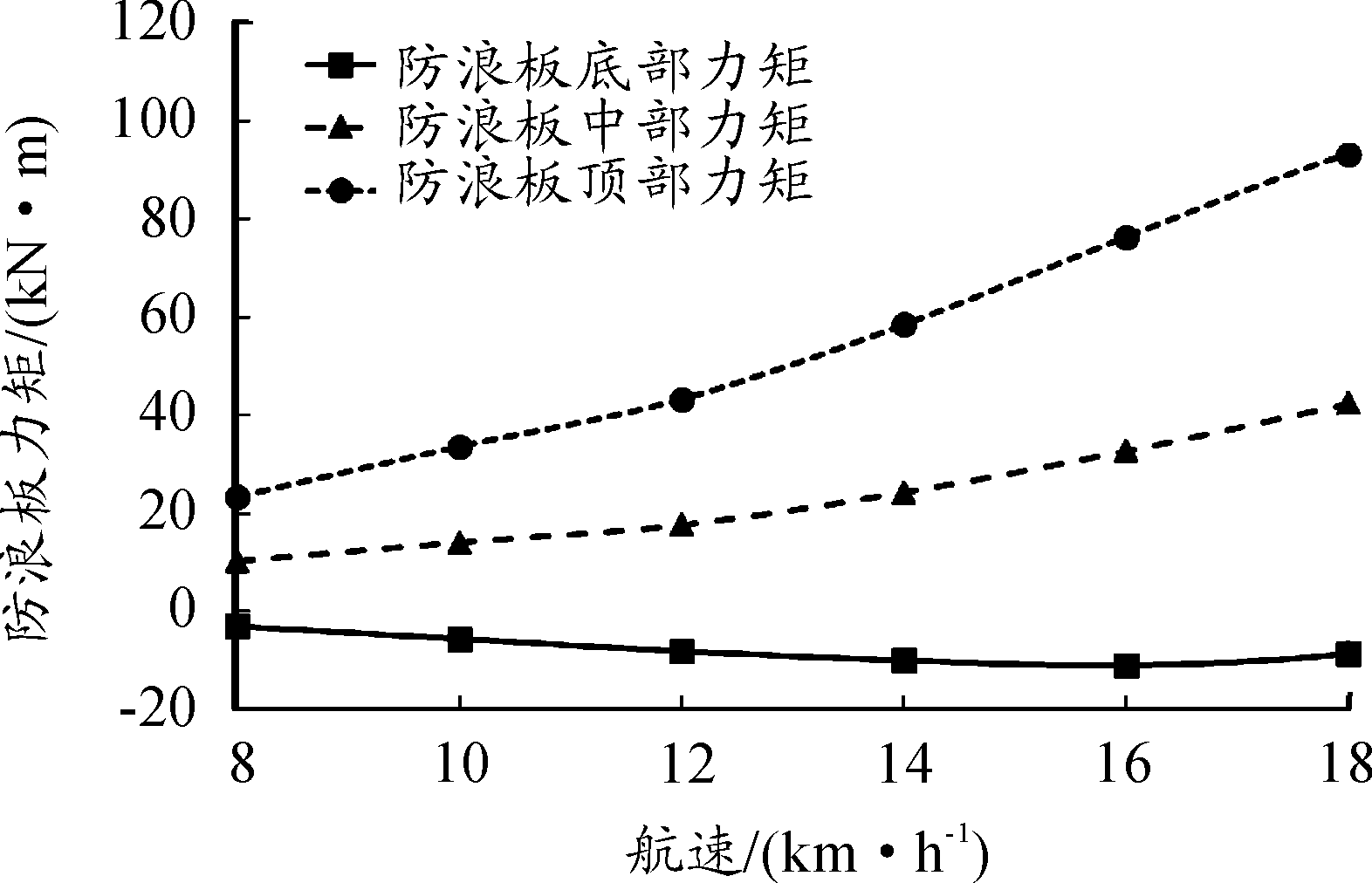
图13 防浪板横向弯矩曲线
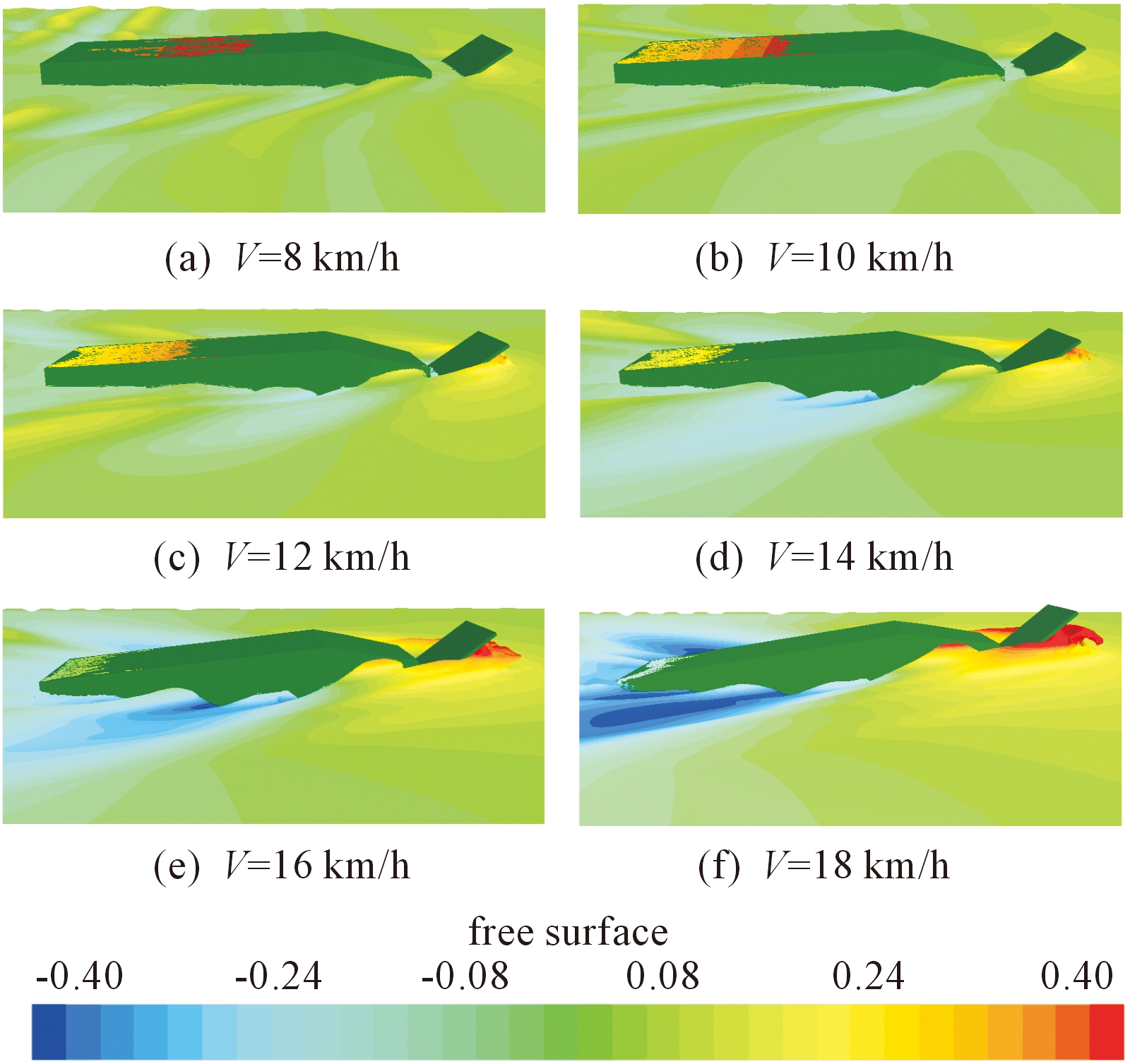
图14 不同航速下两栖车运动姿态
由表3和图9的数据可知,随着航速的增加,车体的阻力系数不断变大,且变化速率在不断增加,原因主要是因为随着航速增加,两栖车航态发生改变,其运动姿态影响周围流场变化,尤其是尾流场的变化,导致首尾压力差不断增加,进而出现压差阻力,压差阻力是两栖车水阻力的主要部分,因此总阻力也随着航速增加而增加;以车体埋首的方向为纵摇正方向,由图10可知,16 km/h航速下的车体纵摇角度超过5°,对于静水中运动的两栖车来说高航速下纵摇角度较大,这表明高航速下车体抬首现象严重,纵摇角度的变化速率也随着航速的增加而增大,工程设计中需改善高航速下车体抬首剧烈的问题;由图11可知,航速越高,车体在稳定运动状态下的下沉深度越大,车体吃水增加会进一步影响航行效率,这也是工程设计需要考虑的重要问题。
由图12可知,航速增加导致作用在防浪板上的纵向和垂向力均增加,垂向力增加相当于车首处升力增加,这导致车体纵摇角度逐渐变大,但随着航速进一步增加,车体抬首导致防浪板浸没在水中的部分减少,所以作用在防浪板上的力的变化速率在降低;由于流体(主要是水)作用力中心距离防浪板各位置的力臂不同,因此对防浪板底、中、顶部的横向力矩存在差异。由图13可知,随着航速增加防浪板底部、中部、顶部承受的力矩基本呈现上升趋势,由于压力中心在底部和中部位置之间,所以底部力矩与其他两个力矩的作用方向相反。随着航速的提高,车体纵摇角度不断增加,导致流体对防浪板的作用中心不断改变,同时作用力大小也在变化,两者的共同作用导致在一定航速内底部、中部和顶部的的横向力矩变化与航速的对应关系不同。18 km/h航速下底部力矩下降,原因可能是高航速下抬首较大,作用力中心与底部的力臂减小程度较大,导致底部力矩出现下降现象。可以看出,顶部力矩要远大于底部和中部力矩,因为压力中心位置距离顶部最远,力臂最大,因此在工程设计中需重点加强顶部连接杆件;由图14可看出,随着航速增加,自由液面尤其是车体周围流体的变化愈加剧烈,两栖车运动的周围环境逐渐恶化。
综合上述分析可知,高航速下两栖车的运动姿态和周围流场环境十分复杂,在推进装置的推力允许范围内,本次研究采用的两栖车的最高航速最好控制在14 km/h以内。
3 结论
1) 采用可实现的k-ε湍流模型、重叠网格技术建立的数值模型可以较好的预报两栖车的水动力性能,车体总阻力计算结果与拖曳试验结果的对比验证了该数值模型的有效性;
2) 随着航速的提高,总阻力系数不断提高;车体纵摇角度不断增大,抬首现象严重;车体下沉深度不断增大;作用于防浪板上的力和力矩基本呈现上升趋势;
3) 防浪板顶部承受的力矩要远大于中部和底部承受的力矩,因此工程设计中需重点对防浪板顶部连接杆件进行加强。
[1] 程龙,赵建民,李鹏.两栖工程车辆尾部形状对航态影响的分析[J].装备制造技术,2015(8):10-12.
[2] 贾小平,马俊,于魁龙,等.超高速水陆两栖车技术研究[J].机械研究与应用,2015,28(139):46-49.
[3] 徐一新.基于运动特性的两栖车辆关键技术研究[D].镇江:江苏科技大学,2013.
[4] 孙旭光,李勇,韦韬,等.基于改进叠模方法的两栖车航行阻力成分研究[J].车辆与动力技术,2019(1):54-57.
[5] 余祖耀,廖远才,李锦云,等.滑板角度组合对两栖车车辆升阻比影响的仿真研究[J].船舶工程,2015,37(3):26-29.
[6] 郑翔玉,房凌晖,王琛,等.两栖车辆水上快速性设计研究[J].四川兵工学报,2015,36(11):34-37.
[7] 剧冬梅,项昌乐,周鹏飞,等.纵倾角对轻型轮式两栖车辆的阻力特性影响研究[J].兵工学报,2015,36(1):19-26.
[8] 袁潇龙,张敏弟.防浪板对两栖车航行特性影响的研究[J].车辆与动力技术,2014(2):15-19,28.
[9] 万晓伟,姚新民,王涛.基于CFD的两栖车辆水上阻力预测[J].装甲兵工程学院学报,2013,27(3):26-30.
[10] 彭锟,刘影.尾翼板对轮式两栖车辆航行阻力特性影响的研究[J].车辆与动力技术,2014(4):15-24.
[11] 蔡宇峰,王丽丽,汪宇,等.基于计算流体动力学的两栖车辆水动力性能模拟及试验验证[J].系统仿真技术,2018,14(3):183-187.
[12] 王丽丽,张家旭,刘涛,等.压浪板对两栖车辆水动力特性影响的数值分析[J].系统仿真技术,2018,14(2):113-117.
[13] BARDINA J E,HUANG P G,COAKLCY T J.Turbulent modeling validation,testing,and development[J].NASA Technical Memorandum 110446,1997.
[14] 陶志奇,李胜忠,朱峰.基于重叠网格方法的襟翼舵水动力性能的数值模拟与分析[J].石河子大学学报(自然科学版),2016,34(2):232-237.
[15] 王建华,万德成.基于重叠网格技术数值模拟船舶纯摇首运动[J].水动力学研究与进展,2016,31(5):567-574.