防护型车辆除了应对枪弹袭击外,更大的威胁来自地雷和简易爆炸物自下而上的爆炸冲击,车辆底甲板容易发生变形、破裂等损伤,对车辆和车内乘员安全造成很大的威胁。为了减少爆炸冲击给车内乘员带来的伤害,同时减少设计成本,加快设计进程,现在多采用有限元仿真技术设计。将多物质单元算法(ALE)与流-固耦合算法[1](FSI)相结合,能提高爆炸冲击波和乘员响应的仿真精度。Kevin Genson[2]针对炸药掩埋深度以及V型靶板不同角度对爆炸条件下的结构响应进行了研究;A.Neuberger[3]针对爆炸条件下的靶板响应设计了试验台架,验证不同靶板在爆炸条件下的结构响应;韩辉等[4]从地雷的伤害原理入手,分析不同反车底雷的毁伤效应,并根据应对不同地雷的多种防护原理,列举了多种底部防雷技术和具体防护措施的发展现状。张中英等[5]对简化V型结构进行仿真研究,得出V型结构在减小地雷对车辆底部的破坏方面具有优势,并进一步研究得到了V型结构角度与车身垂直加速度衰减的关系。针对大规模仿真优化问题,国内外目前已形成了基于实验设计、响应面法的多参数优化(MO)[6]。MO具有计算精度高的优点,但是计算时间长,占用资源多,样本数量多,为缩减计算时间,工程中常通过参数筛选[7](如灵敏度、贡献度分析等),将一些在设计中不占主导作用的参数剔除,仅保留对结果起最大影响的一个或几个参数,减少实验设计的样本数量。
本文结合FSI与ALE仿真算法[8],对爆炸冲击作用下的某型车V型结构进行仿真分析与优化。通过台架爆炸实验验证台架结构仿真结果并对标。目标响应选择为降低V型结构质量、减小结构变形挠度和底板剪应力,变量选取为V型结构的底板厚度和几何形状。建立多目标优化模型,采用帕累托(Pareto)优化方法,对底部V型结构进行优化设计。
1 V型底部结构响应仿真
基于某型车底部结构建立对应V型结构台架有限元模型,根据车辆实际重量对台架结构进行配重。建立覆盖整个结构的空气流场[图1(a)中410尺寸的下尺寸界线以上的网格)和土壤(图1(a)中410尺寸的下尺寸界线以下的的网格],地雷替代物当量为6 kg TNT(STANG4569的2级防护标准[9])。地雷替代物置于试验台架正下方,浅埋地下100 mm,初始状态下V型结构最低点距离地面为410 mm。采用ALE与FSI算法相结合,应用初始体积法模拟地雷替代物,仿真模型包括空气、土壤、地雷替代物、台架模型。

图1 某型防护型车辆底部V型结构仿真分析
对V型结构台架进行爆炸实验,实验各关键参数与仿真一致,地雷替代物符合实验要求。爆炸实验结果如图1(d),底部V型结构位于炸药正上方的变形最大,试验后对底板变形进行测量,把测量结果进行拟合,得到变形后的拟合形状如图1(e)。经测量,最大变形量为230 mm,与仿真测得的底板变形量243.4 mm相差不大,仿真计算值与试验误差为5.8%。仿真过程中底板侧围发生较大变形使得横梁与底板的焊接处焊缝失效如图1(c),与试验结果的焊缝失效如图1(f)形态基本一致。综上分析,对比仿真与试验,底部结构的破坏形态近似,变形量差别不大,仿真精度满足工程需求。
2 V型防雷组件优化算法研究
2.1 多目标遗传优化算法
多目标优化特点在于存在多个优化目标,从而导致其解不确定为唯一值,而是构成一个解集,即最优解集,使用Pareto最优思想对该解集进行筛选。所谓Pareto最优就是,不可能通过优化其中部分目标而其他目标不至劣[10]。多目标遗传算法(MOGA)可以处理有约束的多目标优化问题,并提供一系列Pareto解(Pareto-optimal solution),适合本文的研究需求。
多目标优化领域中广泛采用的MOP(Multi-Objective Optimization Problem )问题的数学定义如下:
Minimizey y=f(x)={f1(x), f2(x),…, fm(x)}
Subjectto: e(x)=(e1(x), e2(x),…, em(x))≤0
Where: x=(x1, x2, xn, …,xn)∈X
y=(y1, y2,…, yn)∈Y
(1)
式中:x为n维设计变量,X为可行解集,y是目标向量, Y是目标向量y形成的目标空间,决策向量的可行取值范围由约束条件e(x)确定;m为目标响应函数的个数;n为约束条件个数。
在结构优化问题中,多目标遗传算法可计算出搜索范围足够大的Pareto最优解集,当决策者在该解集中结合实际条件选取最优解时,能最大可能覆盖最优解。
2.2 标准边界交叉法
标准边界交叉(NBI)法[11]是由Das等人提出的一种新的寻优方法,在求解高维优化问题方面效率高。NBI法的搜索域公式如下所示:
(2)
(3)
式中:Ni为第i个优化目标的Pareto解去量纲标准化结果;bu、b1为标准化边界的上下边界;Oi是第i个目标的Pareto解;Oi_max是第i个目标的Pareto解集中的最大值;m为目标函数的个数;Rp为搜索半径,在n维空间中可以选用R1、R2和R+∞。使用式(2)、式(3)可计算所需的Pareto解集的搜索半径。
2.3 台架优化数学模型
底部V型防护组件主要根据V型结构对爆炸冲击波的偏置效应和V型结构对组件刚度的加强作用,实现较强的防护能力。因此V型结构V角角度、材料厚度等因素对V型结构的实际防御能力具有极大的影响。本次优化的目标是在保证结构总重量增加不大的同时,提高V型结构在爆炸冲击下的防护能力。首先建立V型结构的台架优化数学模型,如图2所示,从而做到定量分析其抗爆炸冲击性能。在该算例中,将V型结构总质量m,内板能量吸收E,底部最大变形x,焊接区域单元剪应力σXY为目标函数。将影响V型结构抗爆轰性能最大的外底板厚度t1、内底板厚度t2、底部V型角度θ,侧壁距离l设置为设计变量,如图3所示。
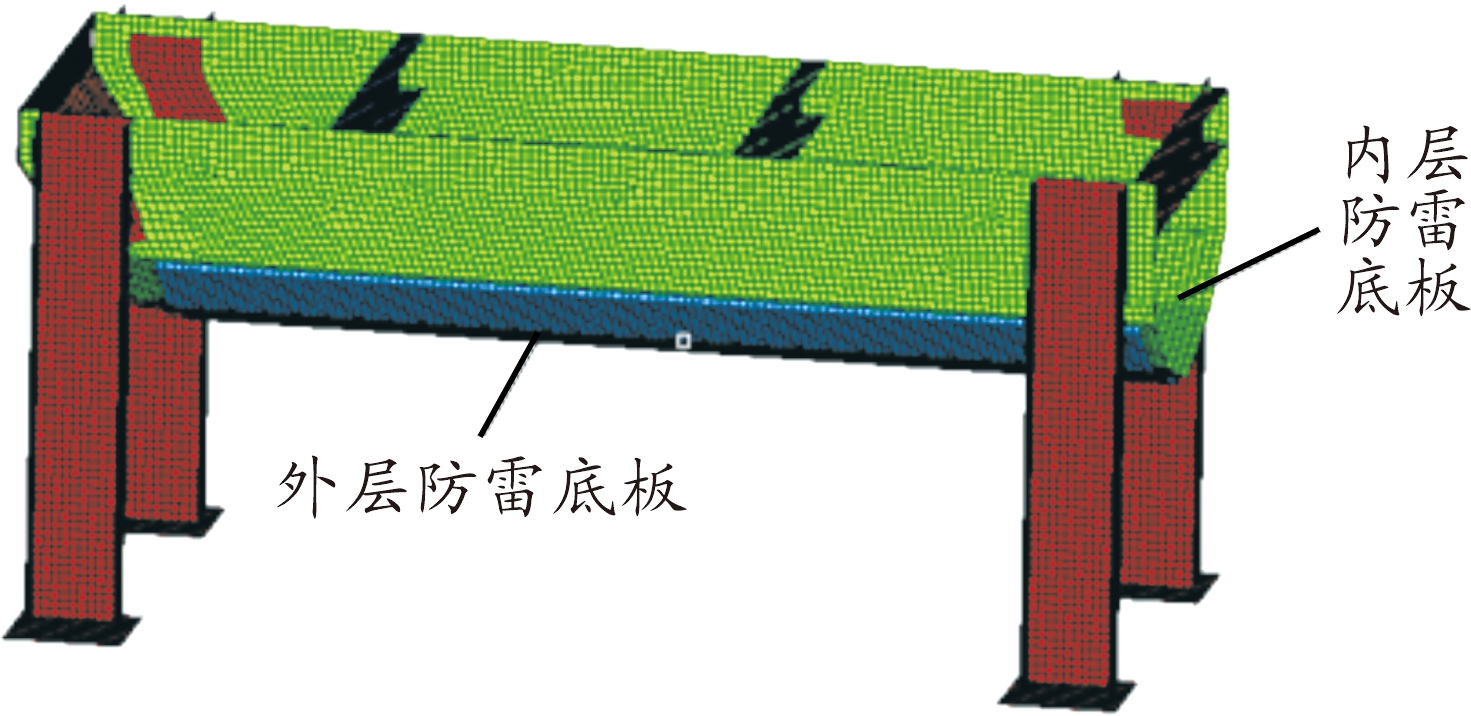
1.外层防雷底板; 2.内层防雷底板
图2 V型防护组件结构数学模型
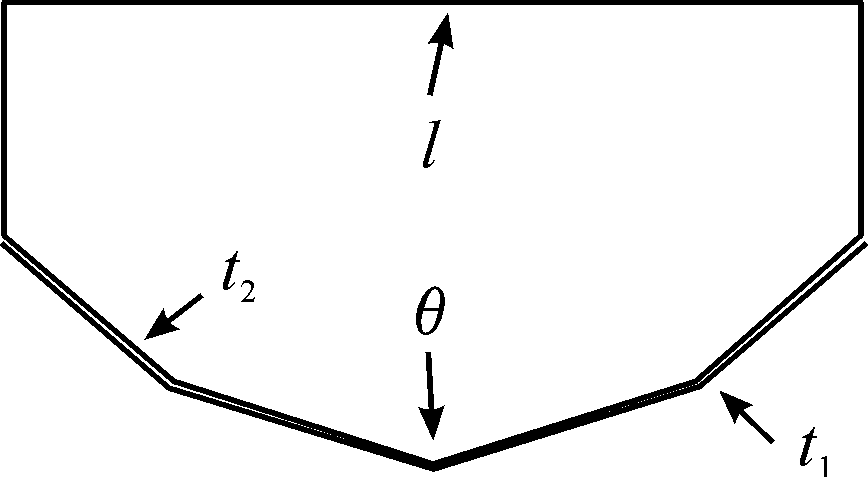
图3 设计变量分布示意图
根据结构设计状态,从工程实际来考虑,台架的优化设计变量在一定的范围内变化,具体的设计参数范围以及目标响应的仿真初值见表1和表2。
表1 底部结构设计变量

设计参数t1/mmt2/mml/mmθ/(°)初值1010650140范围4~144~11570~730100~180
表2 底部结构目标响应初值
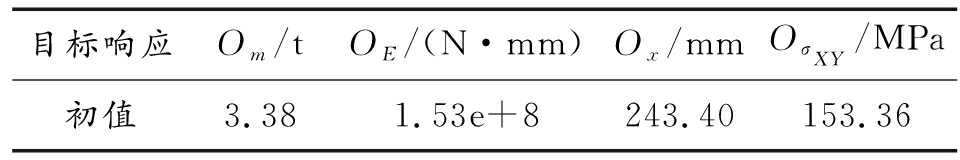
目标响应Om/tOE/(N·mm)Ox/mmOσXY/MPa初值3.381.53e+8243.40153.36
由于V型底部防雷组件底板设计中,Om、OE、Ox、OσXY都是越小越好,目标函数 f (x)在优化设计中取极小值,因此本优化问题的数学模型可以写成:
min f(x)={m, E, x, σXY}
(4)
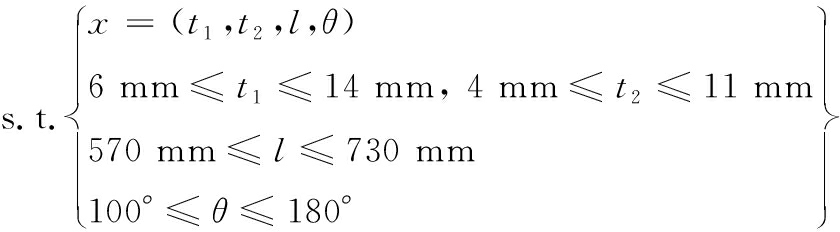
(5)
其中l变量为双向独立变化,两侧边可以向左右两侧变化,相当于2个形状变量,因此,模型可以看作存在5个设计变量。在数据采样试验时,建立因子数为5,水平数为5的拉丁超立方采样试验S21(55)。根据所得的21组仿真结果通过最小二乘法可得到相应函数的二次多项式方程组,进而得到关于4个目标函数的响应面。
3 优化结果分析
3.1 Pareto解集
对底部V型防护组件台架的优化数学模型进行求解。考虑模型可看作有5个设计变量,为了保证Pareto解集能够充分合理描述其空间曲面,在设置遗传算法参数时,将Pareto解的个数设置为 4 309个,遗传代数设置为50代,每代精英数量占样本总空间的10%,设置变异率0.1%。得到4目标函数通过遗传算法求得的Pareto解Om、OE、Ox、OσXY。使用标准边界交叉法对Pareto解进行去量纲标准化,上边界bu=0.2,下边界b1=1,使得标准化后的Pareto解落在从0.2到1的空间边界内。
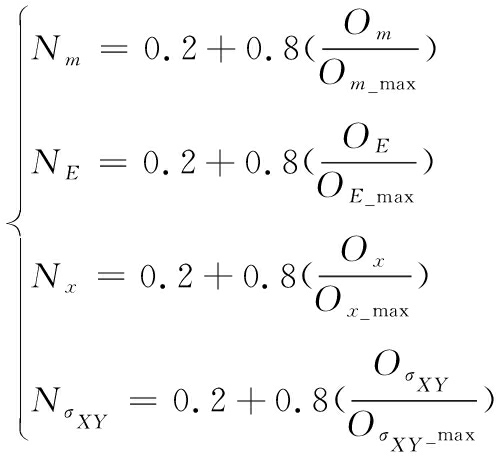
(6)
为获得最适合的优化方案,需确定合适的寻优策略。在台架优化设计中,认为最终的4个优化目标的权重相同,结合计算得出的 4 309个Pareto解,通过式(3)计算搜索半径R2。计算部分结果见表3,可以看出最小搜索半径为第1 584组解,可以认为第1 584组解是本次优化计算中,在各优化目标权重相同的情况下的最优方案(见表4)。
方案1 584在使3个目标都达到较好的结果的同时,总质量增加很小,可以认为没有牺牲任何一个优化目标的情况下,达到了优化整体设计目标的目的。
表3 部分Pareto解及对应标准化结果
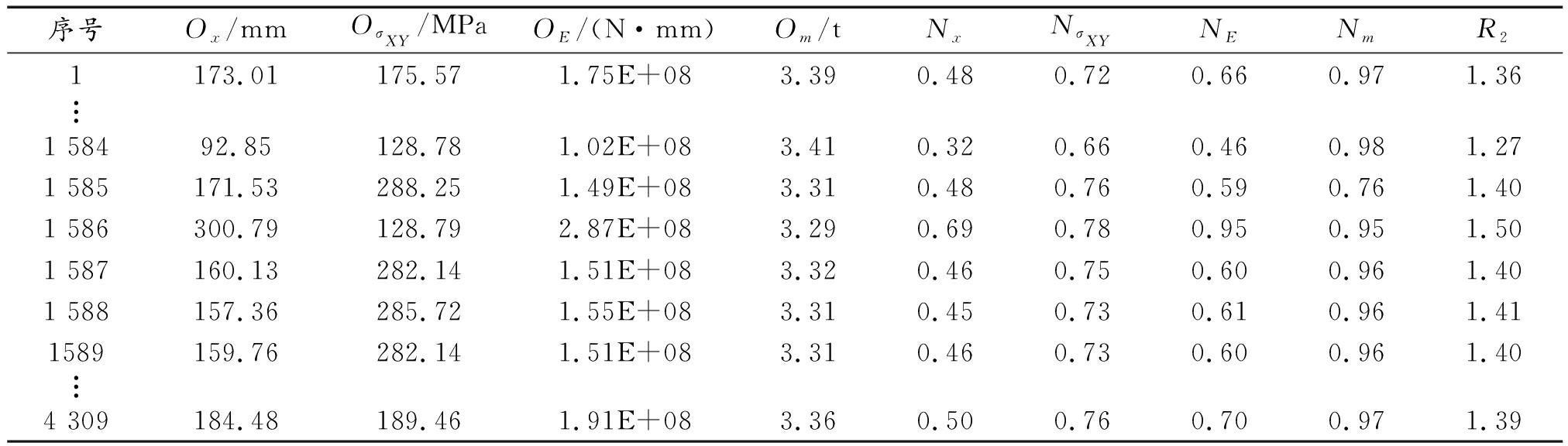
序号Ox/mmOσXY/MPaOE/(N·mm)Om/tNxNσXYNENmR21173.01175.571.75E+083.390.480.720.660.971.36︙1 58492.85128.781.02E+083.410.320.660.460.981.271 585171.53288.251.49E+083.310.480.760.590.761.401 586300.79128.792.87E+083.290.690.780.950.951.501 587160.13282.141.51E+083.320.460.750.600.961.401 588157.36285.721.55E+083.310.450.730.610.961.411589159.76282.141.51E+083.310.460.730.600.961.40︙4 309184.48189.461.91E+083.360.500.760.700.971.39
表4 部分标准化后的Pareto解集
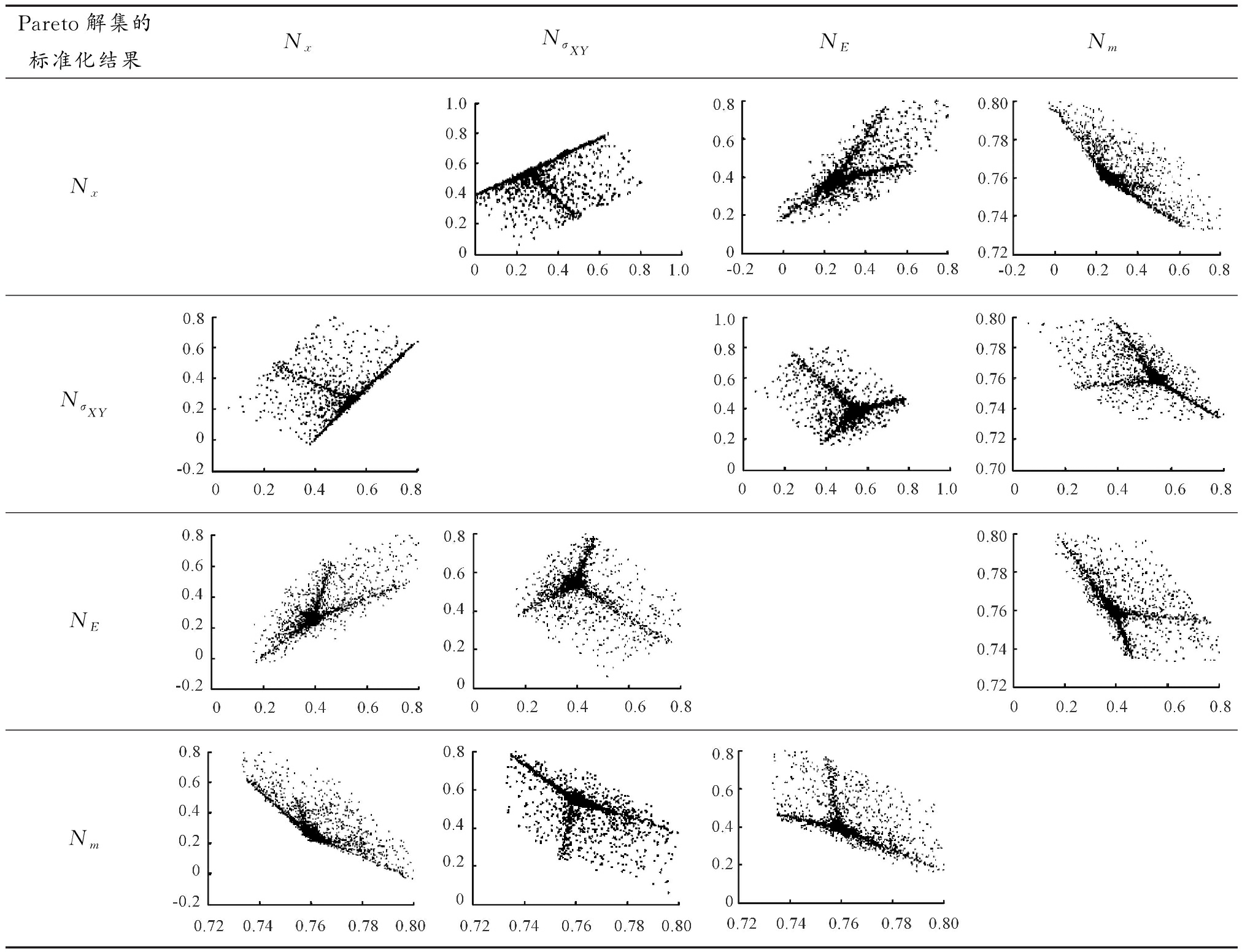
Pareto解集的标准化结果NxNσXYNENmNxNσXYNENm
3.2 Pareto结果分析与验证
由于优化结果是通过响应面模型(代理模型)计算得到的预测值,为了验证预测结果是否真实可信,须进行检验。将响应面模型的优化结果代入到前面的台架试验CAE模型中,由于台架模型已与试验实际进行对标,可以认为其提供的边界条件仍然是可信的。修改后的台架模型如图4,台架底部最低点到地面距离仍为410 mm。
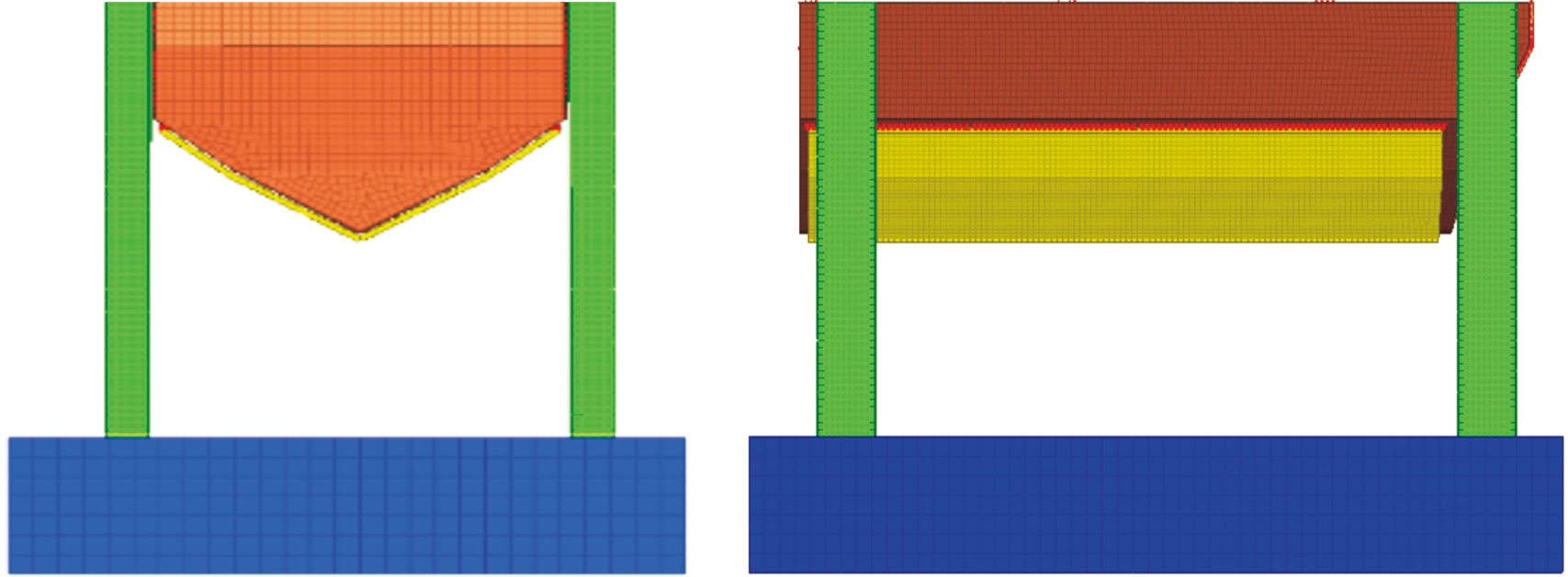
图4 优化验证CAE模型
对台架模型进行仿真计算分析,可绘制如图5所示位移云图、位移曲线和图6所示的内能曲线。由图可知,在改变底板厚度、增大夹角角度后,防护组件的底部刚度明显增大,变形最大的区域由原先集中于V型夹角中部分散到V型夹角两边。台架吸收的能量相比原先更少,证明优化后的V型结构偏置效应更明显。研究单元剪应力时,仍然选择获取初值时选定区域的单元,其中最大单元剪应力为135.02 MPa。
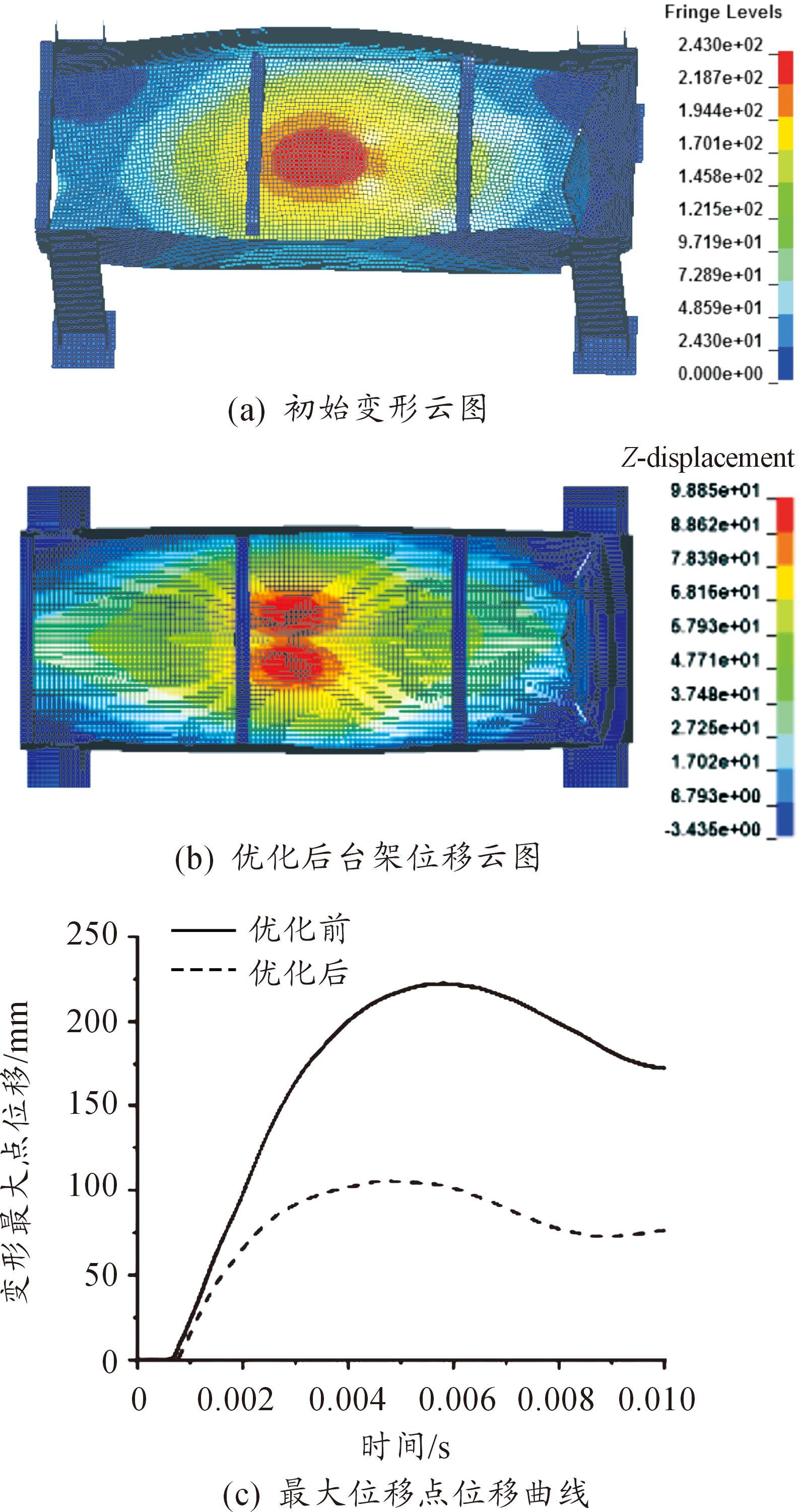
图5 台架模型位移云图和位移曲线
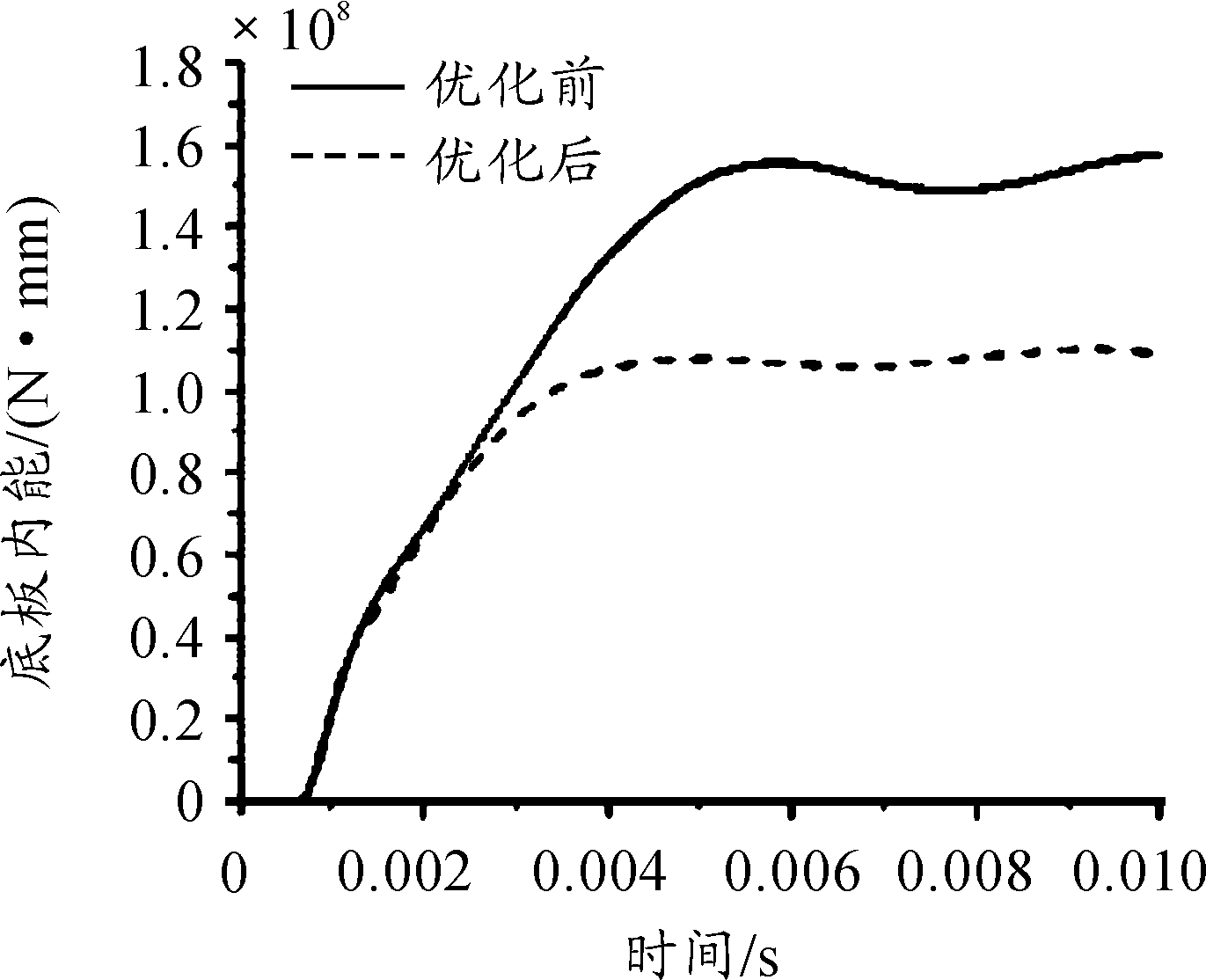
图6 台架模型内能曲线
综合以上仿真验证数据,仿真值与优化拟合的预测结果相对误差在10%之内,最终认为仿真结果与预测结果误差在工程误差范围内,预测结果可信。从上述验证数据中可以看出Om变化量很小,根据表5,在牺牲了8.8%质量的基础上,V型防雷组件在6 kg TNT爆炸条件下,变形挠度Ox减小59.39%,单元剪应力减小11.96%,内底板吸能减小27.45%。
表5 优化前后V型防雷组件爆炸冲击响应
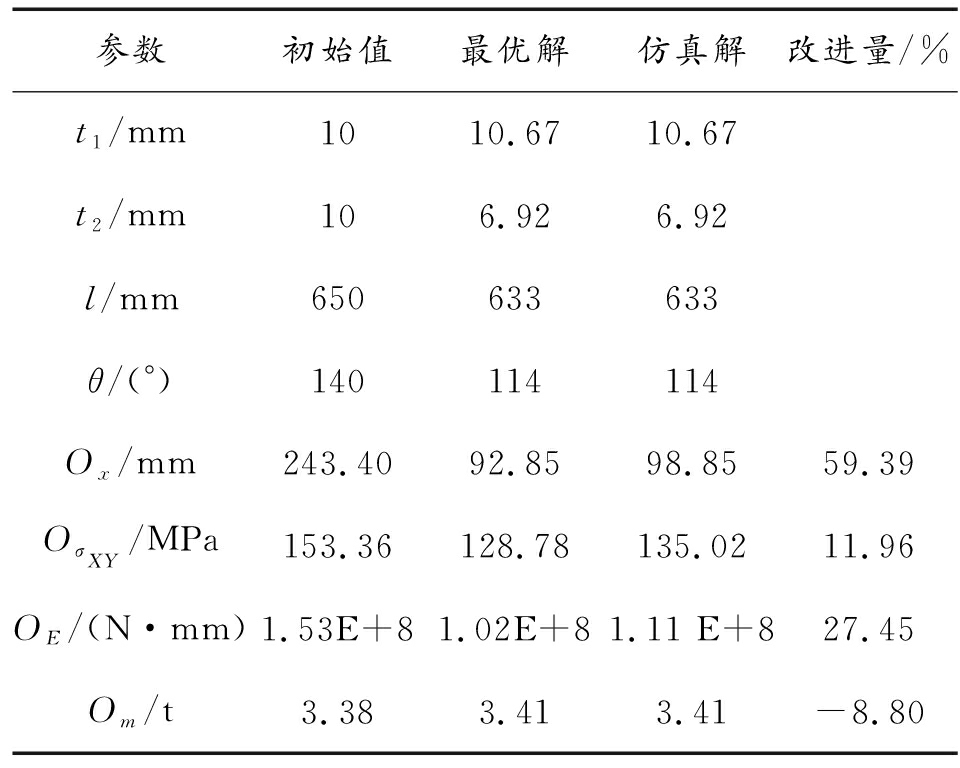
参数初始值最优解仿真解改进量/%t1/mm1010.6710.67t2/mm106.926.92l/mm650633633θ/(°)140114114Ox/mm243.4092.8598.8559.39OσXY/MPa153.36128.78135.0211.96OE/(N·mm)1.53E+81.02E+81.11 E+827.45Om/t3.383.413.41-8.80
4 结论
1) 利用ALE与FSI仿真分析,可以准确模拟在爆炸冲击作用下的台架结构响应,有效降低后期试验成本,缩短设计开发时间。
2) 通过参数设计获得的Pareto解集,验证了不用大幅增加质量,仅通过参数优化,就能够达到很好的防护效果。
3) 通过结构优化,可获得某车型最优防护性能的V型防雷组件的结构型式,最佳V型角度为114°以及最合理的内厚6.89 mm、外底板厚10.96 mm。
[1] 魏然,王显会,周云波,等.基于因子分析的车辆乘员约束系统抗爆炸冲击性能优化[C]//现代汽车设计与制造技术论坛.2015.
[2] KEVIN W G.Vehicle Shaping for Mine Blast Damage Reduction[D].The University of Maryland,2006.
[3] NEUBERGER S P, RITTEL D.Scaling the response of circular plates subjected to large and close-range spherical explosions.Part Ⅱ:Buried charges[J].International Journal of Impact Engineering 2007,34:874-882.
[4] 韩辉, 焦丽娟, 徐平.战车底部防雷技术研究[J].四川兵工学报,2007,28(3).
[5] 张中英, 何洋扬, 王乐阳, 等.车底结构对爆炸冲击波响应特性影响研究[C]//全国仿真技术学术会议论文集.中国计算机用户协会仿真应用分会,九江:2009.
[6] 魏然,王显会,周云波,等.爆炸冲击下车辆底部结构与座椅系统多参数优化研究[J].振动与冲击,2016,35(14):90-95.
[7] SHARIYAT M,DJAMSHIDI P.Minimizing the engine-induced harshness based on the DOE method and sensitivity analysis of the full vehicle NVH model [J].International Journal of Automotive Technology,2009,10(6):687-696.
[8] 杜鞠乐,李大禹,周云波,等.基于某特种车辆爆炸冲击下驾驶室内声场分析[J].科学技术与工程,2018,18(7):128-133.
[9] 王显会,佘磊,郭启涛,等.基于抗冲击波响应的新型蜂窝夹层结构多目标优化设计[J].车辆与动力技术,2014(4):25-30.
[10] PAZ J, DFAZ J, ROMERA L, et al.Crushing analysis and multi-objective crashworthiness optimization of GFRP honeycomb-filled energy absorption devices[J].Finite Elements in Analysis and Design, 2014(91):30-39.
[11] DAS I,DENNIS J E.Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multi-criteria optimization problems[J].Siam Journal on Optimization,1998,8(3):631-657.