近年来一些高超声速武器，如电磁炮[1]、电热化学炮[2]等，利用特殊的发射技术，将弹丸发射到5马赫以上，实现了高超声速和远程飞行，具有飞行高度高、飞行速度快、飞行空域广的特点，已成为当前军工领域的研究热点。但由于受发射方式和体积等诸多条件的约束，其飞行控制能力受到限制，给炮弹完成战斗技术指标带来了困难。因此，根据其发射方式、飞行特点等要求，进行气动布局设计、寻求适配的气动力工程算法并获得其气动参数，成为高超声速制导炮弹实现远程精确打击的关键一步。
目前，国内外已有众多研究机构对高超声速炮弹开展了理论和试验研究，包括其气动外形和气动特性等。国外学者Agnone和Zakkay[3]分析了尾椎对高超声速炮弹的飞行特性以及气动参数的影响，为高超声速炮弹的气动布局设计提供了借鉴思路；Stuart McIlwain等[4]对高超声速飞行下弹翼的空气动力学特性做出了研究，得出了弹翼表面阻力系数及热流畅情况，对高超声速弹翼的设计作出了理论参考。A D Dupuis和J A Edwards[5]利用飞行试验和仿真计算，研究了“锥—柱—裙”组合体气动外形的高超声速布局，并讨论了其气动特性和热流畅情况；吕水燕、张传侠等[6]通过数值模拟获得了高超声速下双椭球体经典模型的热流密度，为高超声速飞行器的热流计算提供了重要参考；孙祥程、葛畅[7]采用基于RANS的CFD数值计算方法，开展了高超声速翼型的气动特性设计与研究，并设计了两种具有更加优良的低速、跨声速气动特性的高超声速翼型。
高超声速炮弹的外形取决于诸多因素，需对其进行气动力预测。相比于数值算法，工程算法计算周期短、制作成本低，适用于高超声速的气动力工程算法包括激波-膨胀波法、切楔/切锥法、牛顿理论等等[8]。牛顿理论将流体假设为规则运动的流体微团以平行的直线轨迹流向物面，可直接计算出对应的法向和轴向力系数；其内涵简捷、工程量小，可用于快速可靠地计算高超声速制导炮弹的气动参数。
本文针对高超声速的气动布局特性，在已有高超声速炮弹理论研究的基础上，设计了一种“一”字平面鸭舵控制的尾翼式高超声速制导炮弹的气动布局，选取了适配的高超声速工程算法对其进行了气动计算，并对计算方法作出了改进；得到了相应气动参数且分析了其气动特性的变化趋势。
1 气动布局设计
1.1 头部外形和弹身弹尾设计
1) 头部尺寸及母线。炮弹的头部阻力受其弹型系数的影响，适当增加头部长度可减小空气阻力，增大头部容积，故取弹头部长度为3.5d。常见的头部母线有锥形、圆弧形、抛物形、指数形以及冯卡门形等，其各自的气动特性见文献[9]。基于它们各自的阻力特性，本文对这几种母线进行了对比，得出高超声速制导炮弹宜采用阻力较小的指数形或冯卡门形。而冯卡门形母线相对于指数形母线具有更大的头部容积和容积利用率，故冯卡门形头部母线为最适合本文设计的头部母线形状。
2) 头部钝化。高超声速下需将弹头钝化以减小气动加热，本文在鼻尖处用半径为n的半球状头部代替原有的尖头。文献[10]通过对某弹型在高超声速条件下的实验结果和理论计算得出，当头部钝度取n/R=0.03时，头部钝化后对波阻没有影响。
高超声速下弹身的阻力极大，设计弹身长细比λb时应从阻力最小的角度出发；在超声速以及高超声速的条件下，船尾对阻力的减小有轻微帮助，但尾椎的角度不宜过大，否则会因尾椎效应导致后部气流分离。综合考虑弹体结构、刚度、工艺以及设计要求等条件后，本文选取弹身长细比λb=5，尾部长细比λta=3，尾部收缩比d/D=0.8。
综上所述，本文设计的制导炮弹总长细比λ=11.5。全弹尺寸如图1所示(单位：mm)。
图1 弹体尺寸示意图
1.2 尾翼和鸭翼设计
尾翼有4片、6片和8片的布置形式，需根据稳定性要求确定翼片数量。尾翼设计时需要考虑翼平面形状、翼剖面形状、翼面面积等问题。
1) 翼平面形状。高超声速下，三角形翼的升阻比较大，压心变化范围小，是较为理想的超声速翼型。但相对于三角翼，梯形翼能够保证翼尖有足够的结构刚度，并有利于部位安排，故尾翼可选用小展弦比的梯形翼。
2) 翼剖面形状。考虑强度、刚度和气动力特性等要求，双弧形翼在高超声速下的波阻系数最小[11]，故高超声速制导炮弹的弹翼应采用双弧形剖面翼。另外，为减小气动热，翼前缘也应设计为钝头前缘。
3) 翼面面积。弹翼面积的设计主要取决于机动性和射程等要求。对于尾翼，初步设计时可按下式计算其面积S：
(1)
式(1)中：ny为需用法向过载；q为动压。为了满足静稳定要求，采用8片尾翼的布置形式。
鸭翼的设计要求与尾翼类似，高超声速下，同样用大根梢比梯形翼代替三角翼。按照控制力矩方程求舵的面积，有
(2)
式(2)中：S为参考面积；
为操纵力矩系数；
为舵的升力系数对舵偏角的导数；Kr为速度阻滞系数；l为操纵力矩系数的参考长度；xc和xr分别为导弹质心坐标和舵的压心坐标。
2 气动特性工程计算
牛顿撞击理论的示意图如图2。牛顿模型假设了所有流体微团都以平行的直线轨迹流向物面，没有任何不规则运动。而实际上作宏观运动的气体是分子的不规则运动与一种定向运动的合成，这种不规则运动由自由流的静压p∞来度量。因此，物面单位面积上的法向力应解释为与p∞的差，即
(3)
用压强系数
改写上式，得到如下形式：
Cp=2sin2θ
(4)
式(4)称为牛顿正弦平方定律，此式说明，压强系数与物面切线和自由流夹角正弦的平方呈正比。得出压强系数后，可通过积分求得相应的气动力系数。
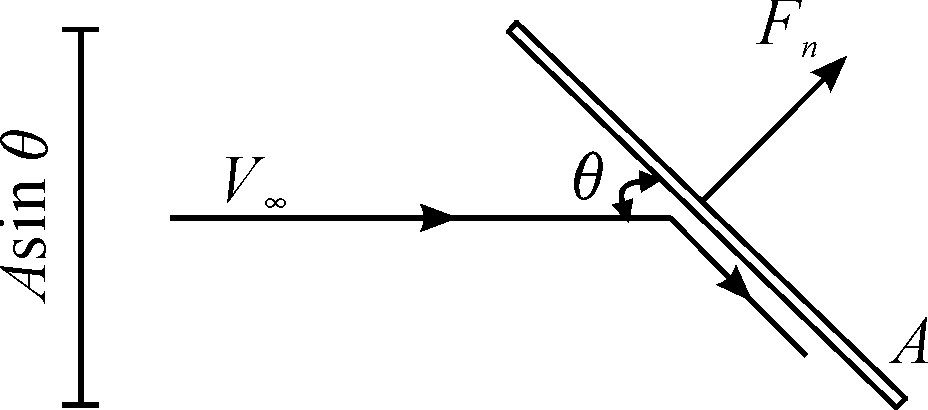
图2 牛顿撞击理论示意图
按照牛顿理论，细长尖拱形头部可用内接圆锥头部来计算[12]，当α<θc时，头部升力系数为
CL=cos2θcsin2αcosα-[2sin2θc+sin2α(1-3sin2θc)]sinα
(5)
其波阻系数为
CD=CNsinα+CAcosα
(6)
式(6)中：CN为法向力系数，CA为轴向力系数。头部压心系数表达式为
(7)
对于尖拱形头部
(8)
本文设计的制导炮弹采用了小尾椎角的船尾结构。计算全弹阻力时，应单独计算尾部的压差阻力，然后并入全弹阻力。而尾部因小尾椎角而造成的阻力影响极小，可以忽略不计，且不影响结果的准确度。
本文计算气动参数时将尾部视为圆柱，并入弹身，将整个弹体(除头部以外)视为圆柱后体，将弹身和尾部的长细比相加，视为圆柱后体长细比。这样，在计算各项气动参数时，只需要计算圆柱后体的气动参数，无需再单独计算船尾的气动参数。这一改进减少了计算量，简化了弹体气动参数的计算过程。在高超声速下，圆柱后体的升力系数可用牛顿理论加离心力修正的方法得到：
(9)
式(9)中：λC为圆柱后体的长细比。
圆柱后体的摩阻可按下式估计：
(10)
式(10)中：SC为圆柱后体表面积；SB为圆柱段弹体截面积；Re为边界层外缘处的雷诺数。
弹体底部阻力可由E.U.Fleeman提供的无动力滑行弹身底部阻力系数公式估算：
(11)
不考虑黏性干扰，由攻角产生的升力沿圆柱后体均匀分布，故圆柱后体的压心位于：
(12)
式(12)中：LN为头部长度；LC为圆柱后体长度。
3) 弹翼空气动力系数。弹翼压心位于其平均气动弦的中点，对于双弧形剖面翼，其升力系数为
(13)
式(13)中：
为相对厚度；γ为空气的比热容比。
双弧形弹翼的阻力系数为
(14)
3 仿真校验
为了验证本文所选计算方法的正确性，基于本文算法计算并分析了文献[10]中所给出的一种无翼式锥-柱型结构弹体的激波阻力系数Cdw、摩擦阻力系数Cdf和底部阻力系数Cdb。该弹型的头部长细比为3.5，圆柱后体长细比1.5，根据计算结果作出如图3所示的曲线。计算摩阻时，取空气的温度T=293 K，密度ρ=1.205 kg/m3，动力黏性系数 μ=1.82×10-5 Pa·s，声速a=343 m/s。
用本文方法计算出的各项阻力的分布及大小与原文献中给出的结果具有相当的一致性。其波阻系数几乎不随Ma变化；摩阻系数随Ma的增加而减小；底阻在低马赫时所占比例较大，且随Ma的增加而逐渐减小；波阻占总阻力的比例随Ma的增加而增加。整个计算结果与原文结果相比，误差均在可接受的范围内，与原文中实验结果吻合较好。因此，本文所用的计算方法能够可靠地获得高超声速制导炮弹的气动力特性。
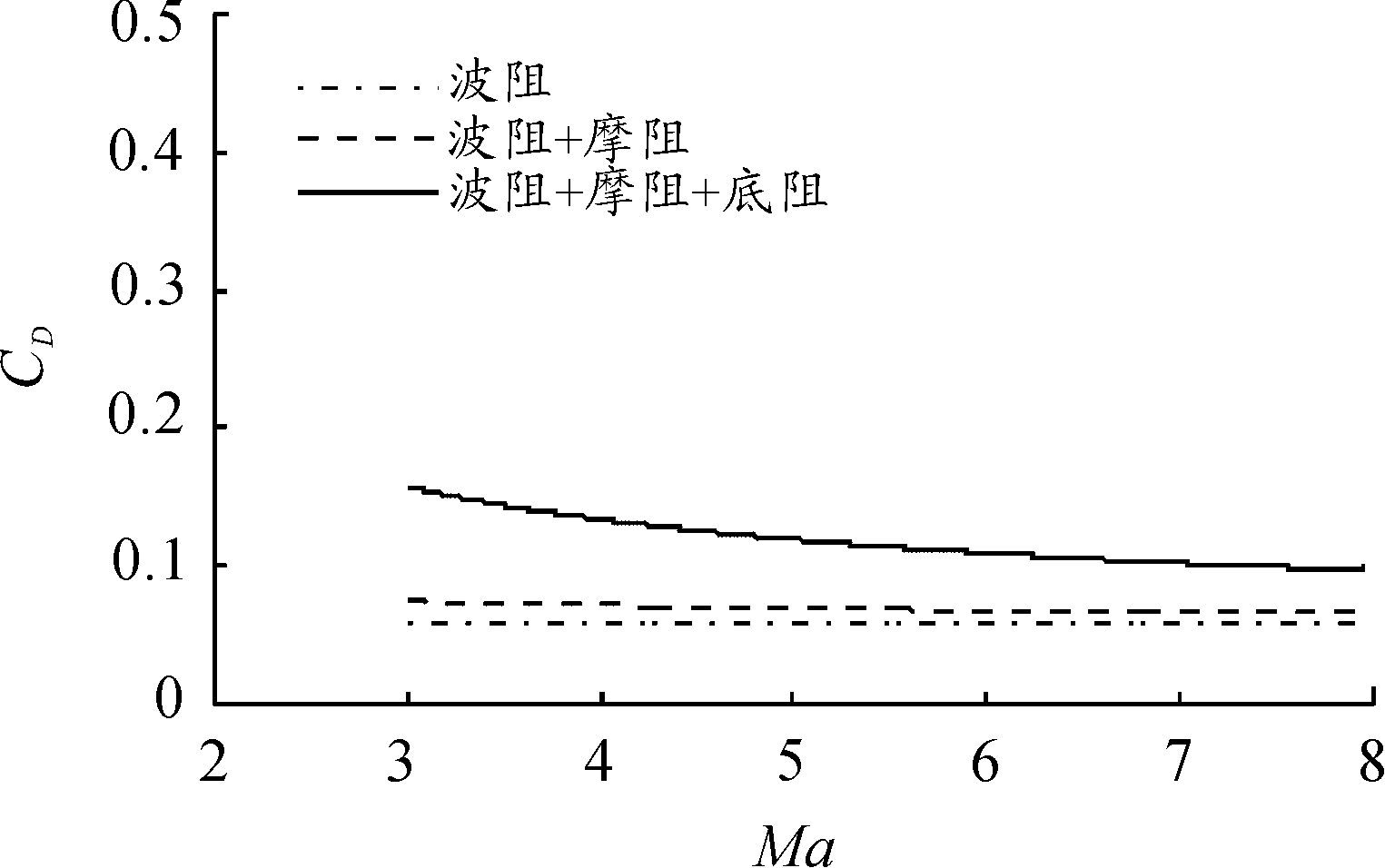
图3 计算结果曲线
3.1 气动布局设计结果
通过分析及计算，得出梯形尾翼的面积Sw=1.95SB，半展长51 mm，根弦长257 mm，梢长129 mm。本文设计的高超声速制导炮弹的气动布局如图4所示。
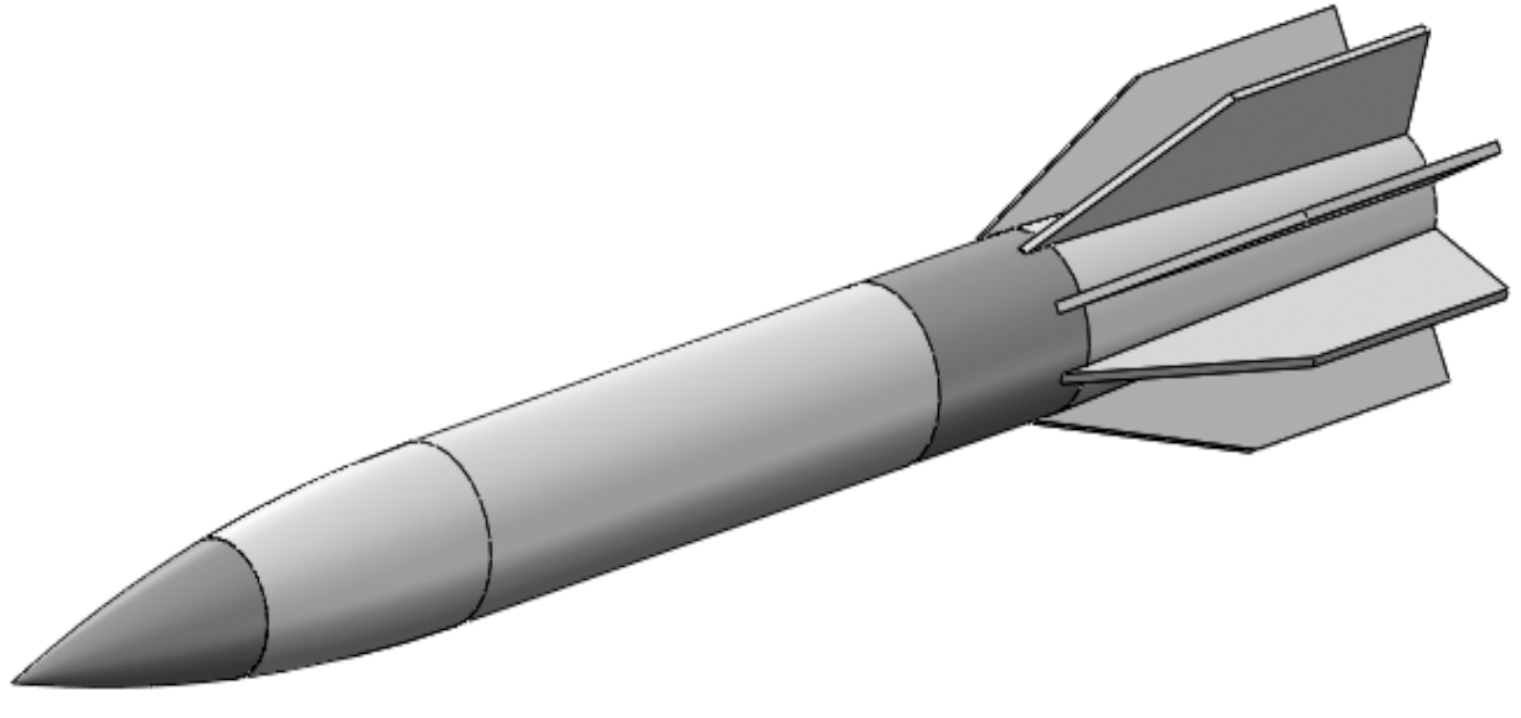
图4 八尾翼式高超声速制导炮弹气动布局
通过计算得鸭翼面积Sr=0.24SB，半展长45 mm，根弦长43.5 mm，根梢比5。压心位置距头部顶点的距离xr=140 mm。张开鸭舵后的外形如图5所示。
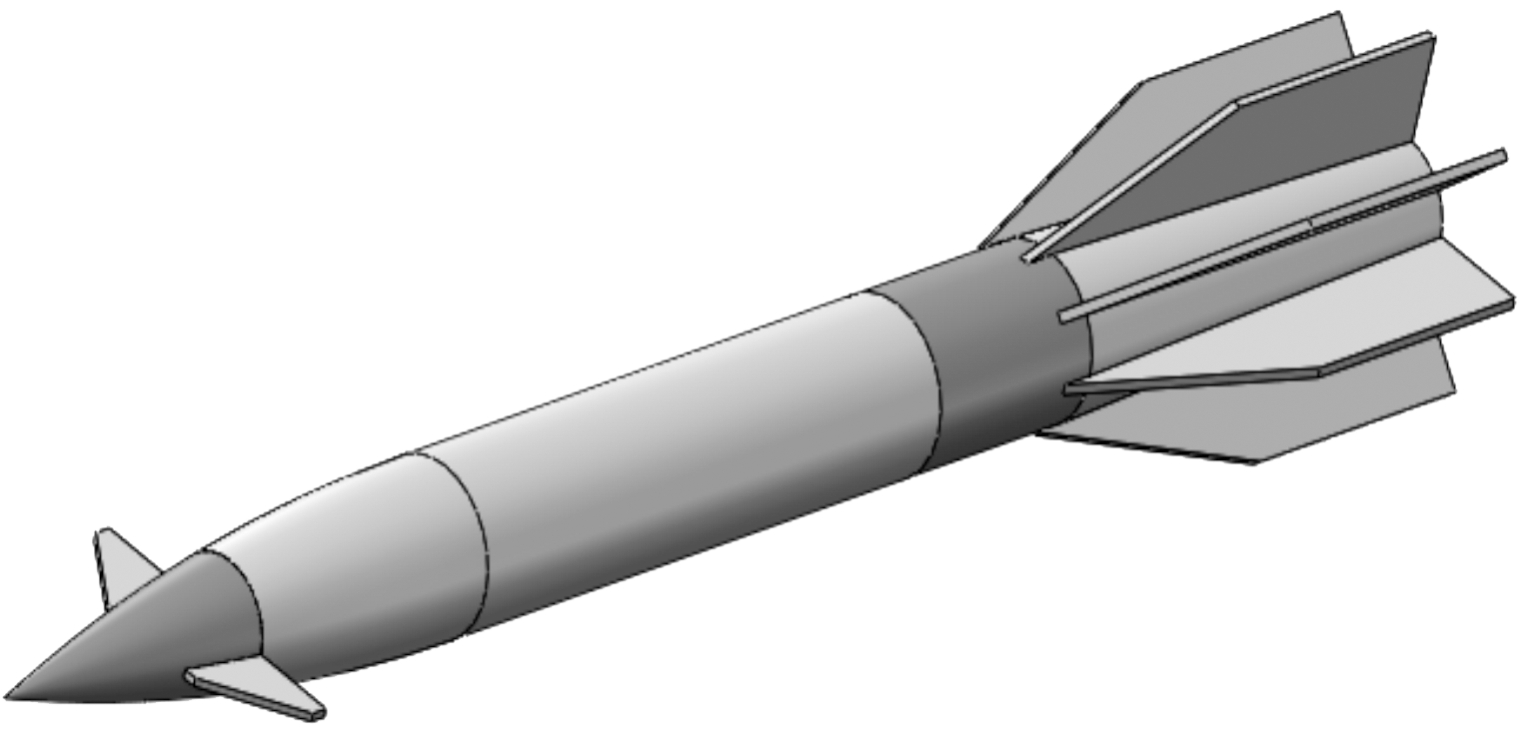
图5 鸭舵式高超声速制导炮弹气动布局
3.2 气动力计算与分析
根据牛顿理论计算出的弹体在高超声速条件下的升力系数CL与攻角α和马赫数Ma的关系曲线如图6所示。从图6可以看出：高超声速下制导炮弹的升力系数CL随攻角α的增加而增加，随马赫数Ma的增加而减小。升力随攻角和马赫数的变化均为非线性的，随着攻角的增加，升力系数的变化越来越明显，反之，马赫数的增加对升力系数的影响则越来越小。
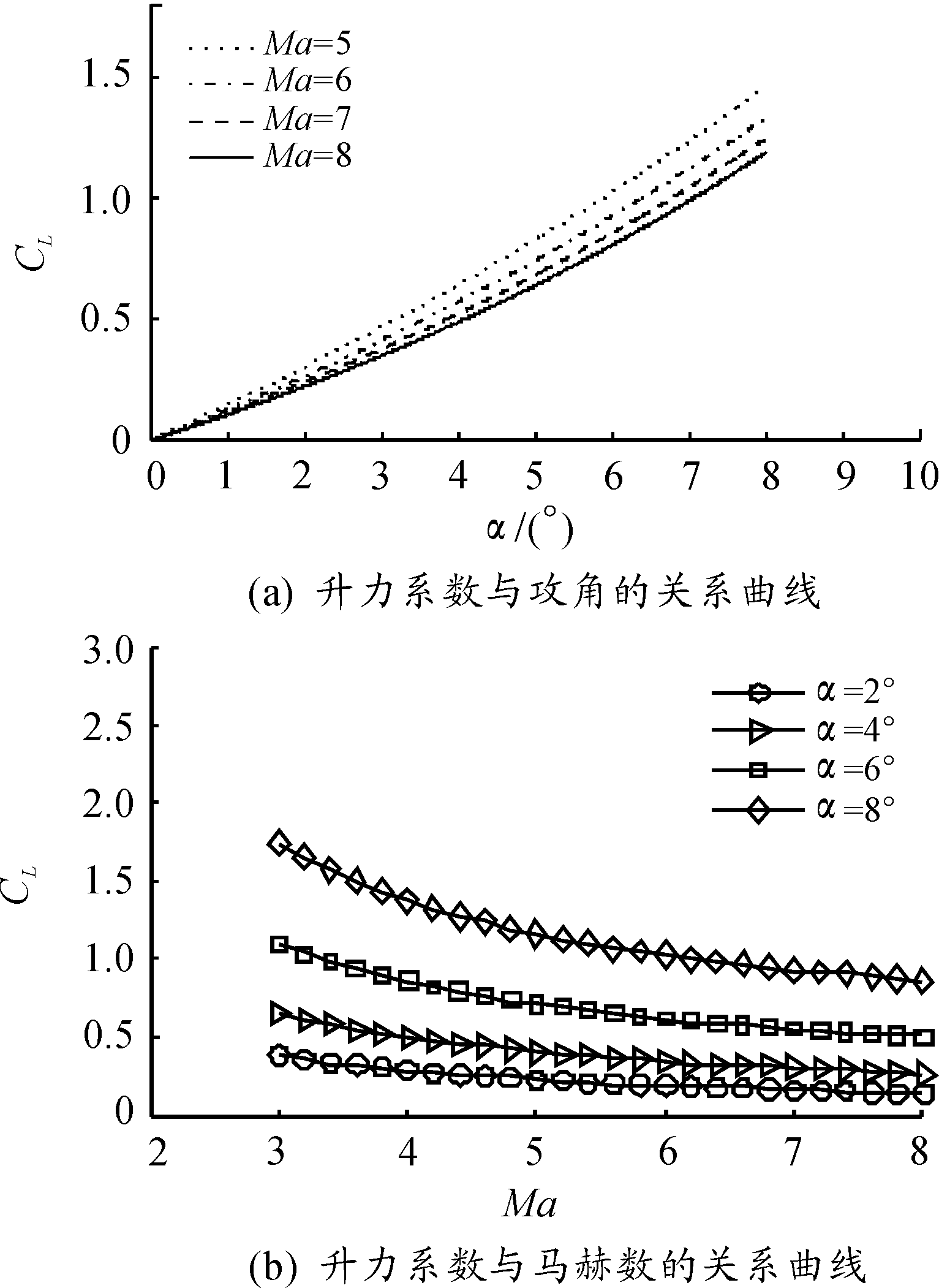
图6 升力系数与攻角和马赫数的关系曲线
图7为该制导炮弹在高超声速下的阻力系数CD与攻角α和马赫数Ma的关系曲线。阻力系数的变化规律同升力系数相同，也是随攻角α的增加而增加，随马赫数Ma的增加而减小，且变化趋势亦为非线性的，马赫数Ma越高时对阻力的影响越小。该结果与文献[10]中给出的锥-柱-船尾型布局的阻力实验结果一致。
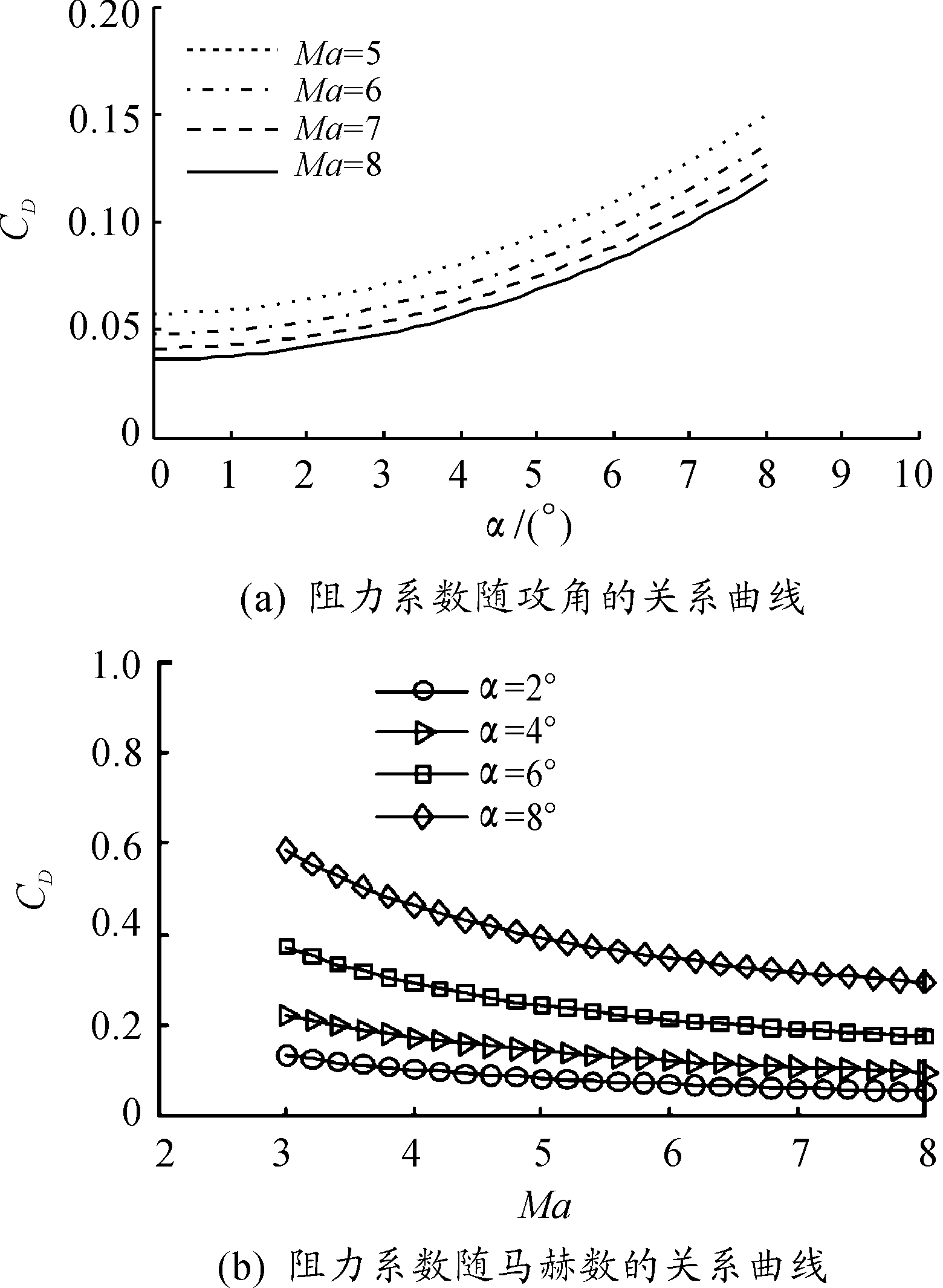
图7 阻力系数与攻角和马赫数的关系曲线
该制导炮弹的操纵力矩系数与舵偏角δ的关系曲线如图8所示。从图8可以看出：高超声速下操纵力矩系数随舵偏角的增加而增加，其随马赫数Ma的变化可分为两个区间；当舵偏角δ<6°左右时，舵面的操纵力矩系数随马赫数Ma的增加而减小；当舵偏角δ>6°时，舵面的操纵力矩系数随马赫数Ma的增加而增加，变化趋势非线性，当舵偏角δ在6°附近变化时，马赫数Ma对操纵力矩系数的影响较小。
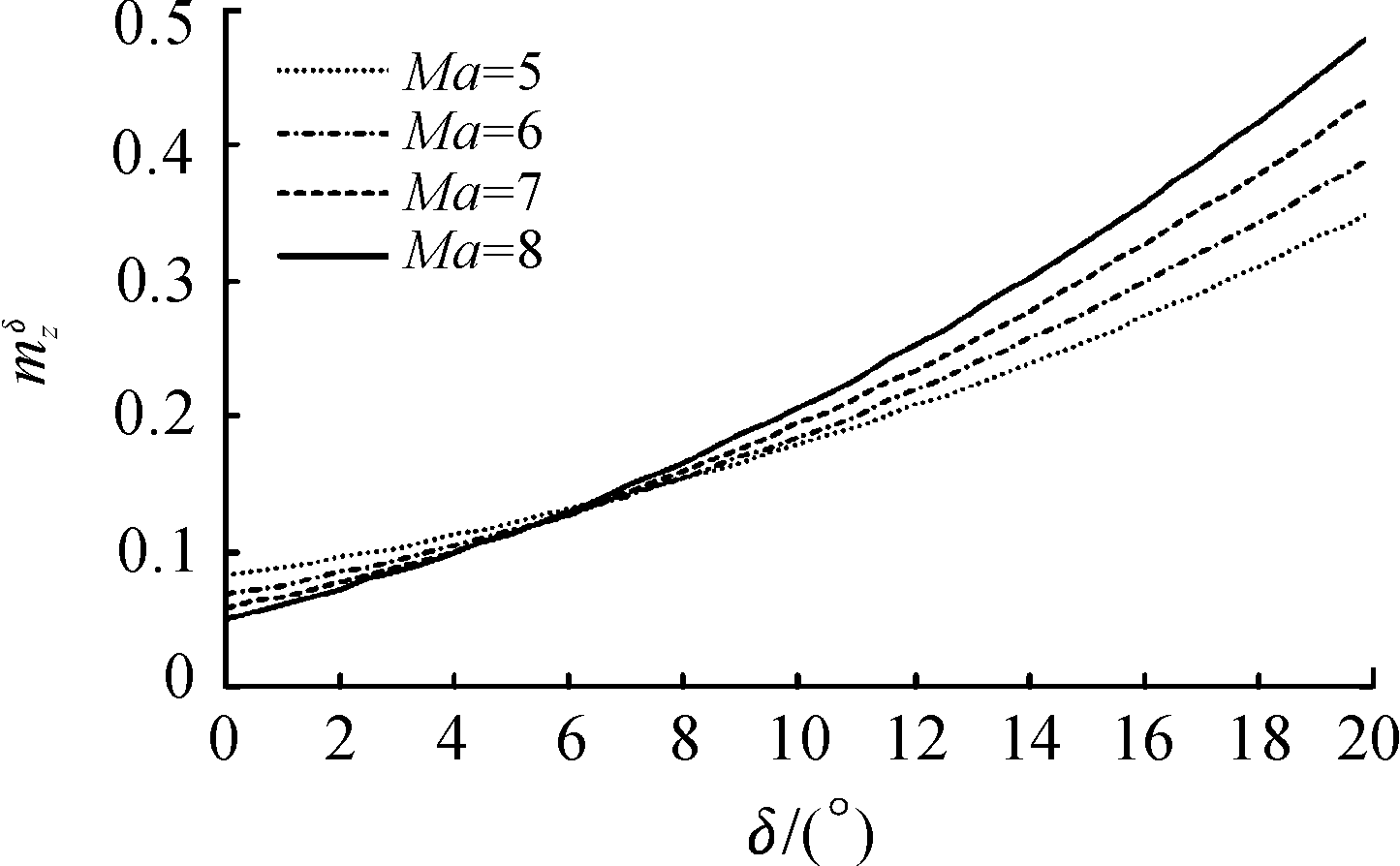
图8 操纵力矩系数与舵偏角的关系曲线
图9为该制导炮弹在攻角α=8°时，其纵向静稳定系数
与马赫数Ma的关系曲线。从计算结果可以看出：本文设计的高超声速制导炮弹能够在整个飞行过程中保持其纵向静稳定系数
满足了静稳定条件；纵向静稳定系数的绝对值随马赫数的增加而减小，说明马赫数越低时，该制导炮弹的稳定性越高。
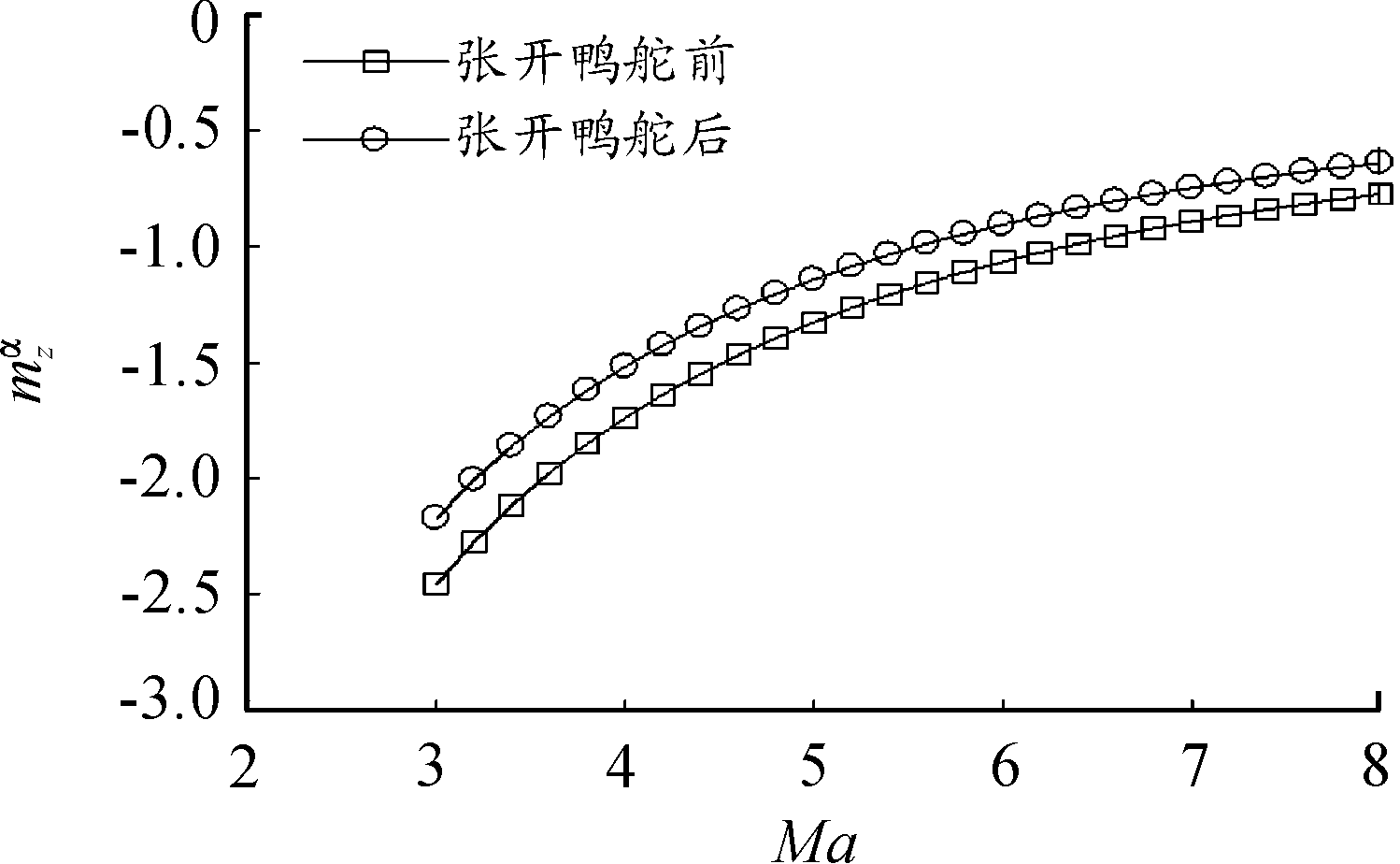
图9 纵向静稳定系数与马赫数的关系曲线
图10为张开鸭舵前全弹稳定裕度η曲线，图11为该弹张开鸭舵后与张开鸭舵前稳定裕度比值η2/η1的曲线。
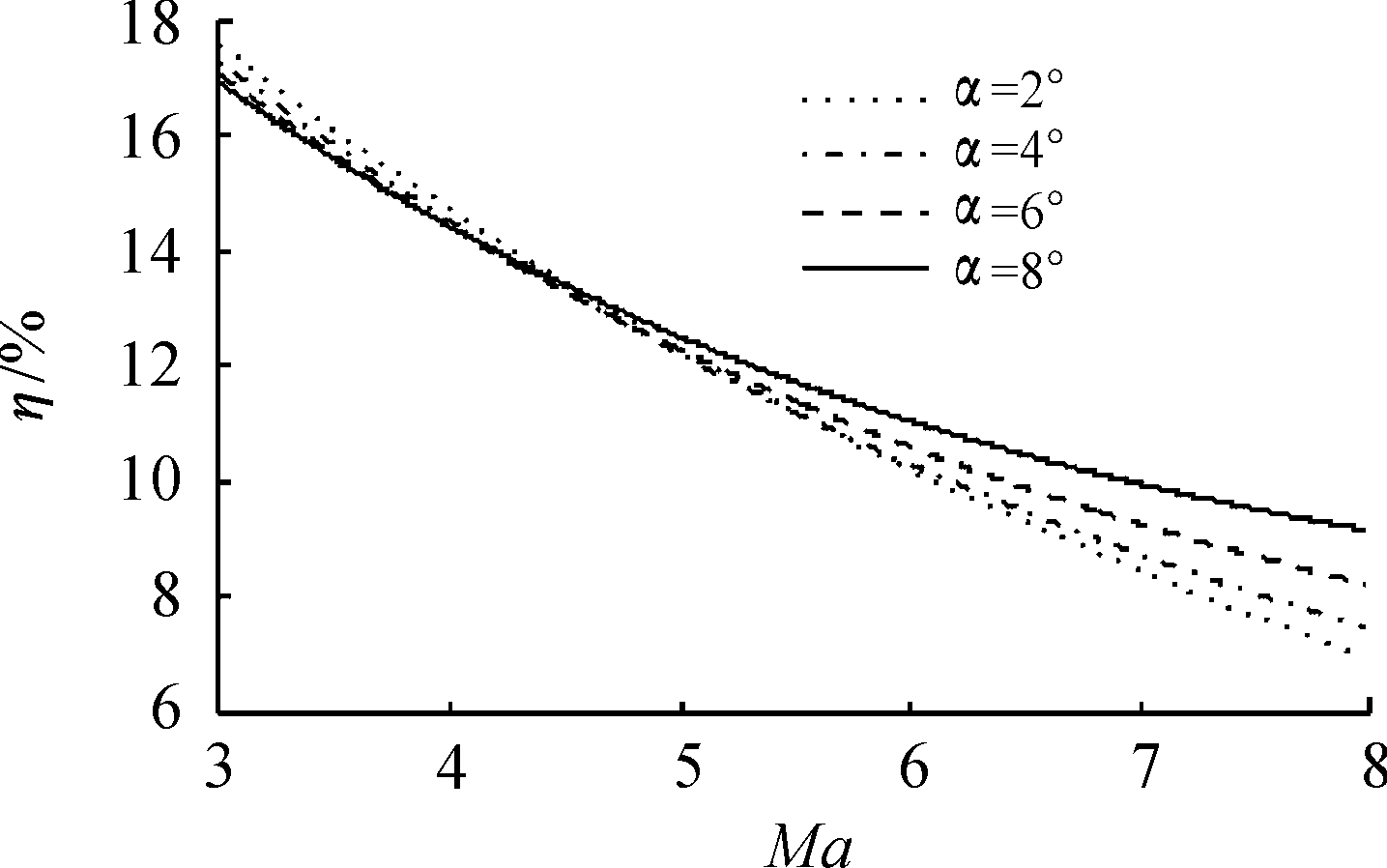
图10 张开鸭舵前的稳定裕度曲线
图11 张开鸭舵后与张开鸭舵前稳定裕度之比曲线
结果表明：本文设计的高超声速制导炮弹在Ma=7.3，α=8°时的稳定裕度为9.7%。在Ma>5的高超声速条件下，该制导炮弹的稳定裕度η随攻角α的增加而增加，随马赫数Ma的增加而减小。张开鸭舵会使稳定裕度减小，在α=8°、Ma=5时张开鸭舵会使稳定裕度下降17%；鸭舵张开后与张开前稳定裕度的比值随攻角α的增加而增加，随马赫数Ma的增加而减小。稳定裕度η的大小可以通过改变弹体外形的方式来调整，在同一马赫数下，η随尾翼面积、圆柱后体长度的增加而增加，随弹头部长度、鸭舵面积的增加而减小。
4 结论
本文采用了改进的气动力计算方法：将弹身、弹尾视作圆柱后体，一并计算气动参数，缩小了计算量，并计算了全弹的升力系数、阻力系数、操纵力矩系数、静稳定系数和稳定裕度。升力、阻力系数均随攻角的增加而增加，随马赫数的增加而减小；操纵力矩系数随舵偏角的增加而增加；静稳定系数小于零，该弹为静稳定弹；高超声速下稳定裕度随马赫数的增加，随攻角的增加而减小。计算结果表明：本文设计的高超声速制导炮弹可控性良好，满足设计要求。
[1] 伍尚慧.国外电磁轨道炮的发展现状与作战效能分析[J].军事文摘,2018,429(21):36-40.
[2] 倪琰杰，程年恺，金涌，等.30 mm电热化学炮膛内压力波数值模拟研究[J].兵工学报,2016,37(9):1578-1584.
[3] AGNONE A,ZAKKAY V,STUREK W.Effects of Boattail Geometry on the Aerodynamics of Hypersonic Projectiles[C]//20th Aerospace Sciences Meeting,2013.
[4] MCILWAIN S,CHEN S,KHALID M.CFD Investigation of Fin Aeroheating on a Hypersonic Projectile[J].Journal of the Physical Society of Japan,2013,16(2):343.
[5] DUPUIS A,EDWARDS J.Flight Tests and Computational Analysis of Two Hypersonic Research Projectiles[C]//33rd Aerospace Sciences Meeting and Exhibit,2013.
[6] 吕水燕，张传侠，叶坤，等.高超声速气动热数值模拟的网格模式相关性研究[J].兵器装备工程学报,2019,40(3):82-86.
[7] 孙祥程，葛畅.高超声速翼型气动特性设计与研究[J].现代机械,2018(5):49-53.
[8] 黄玉才.高超音速炮弹气动分析及弹道研究[D].南京:南京理工大学,2017.
[9] 唐伟，江定武，桂业伟，等.旋成体导弹头部母线线型的选择问题研究[J].空气动力学学报,2010,28(2):218-221.
[10] DANIEL D,MILTON J.A Drag and Stability Analysis of Hypersonic Spin Stabilized Projectiles[C]//Atmospheric Flight Mechanics Conference,2013:271-279.
[11] 于剑桥，文仲辉，梅跃松，等.战术导弹总体设计[M].北京：北京航空航天大学出版社,2010:69-70.
[12] 雷娟棉，吴甲生.制导兵器气动特性工程计算方法[M].北京：北京理工大学出版社,2015:232-267.