导弹装填装置可以克服传统装填手段的不足,有利于提高导弹装填的工作效率,减少人员工作量,充分发挥人员工作效能,但如何实现装填时导弹与装填位置的精确对准是目前亟待解决的问题。
并联机构由于具有控制精度高、工作空间小、负载能力强等特点[1],作为微动机器人在精密工程领域中得到了广泛应用,因此用并联机构作为导弹装填平台实现导弹姿态的精确调整具有一定优势。
较其他传感器相比,视觉传感器因其信息量大、适用范围广、非接触性等特点已成为最重要的传感器之一,因此视觉伺服与基于传统传感器的控制相比也具有更高的灵活性,更高的精度等优势[2]。而视觉伺服中基于无标定的图像视觉伺服技术由于不需要对摄像机进行标定和目标模型的位姿进行检测,使其较其他视觉伺服方法拥有了更高的鲁棒性,目前已成为无标定视觉伺服控制中的主流技术[3,4]。
本文提出了基于视觉伺服的导弹装填平台自动对准方法,结合图像视觉伺服技术和并联平台在控制精度上的优势,在装填平台运动学模型的基础上利用视觉伺服控制实现六自由度并联机构的姿态调整和自动对准。
1 装填平台及坐标系介绍
整个装填装置由提升机构、并联装填平台以及推弹机构组成,摄像机与推弹机构固连,其结构如图1所示。其中装填平台为六自由度的并联机构,由动平台A1A2A3A4A5A6和静平台B1B2B3B4B5B6组成,采用半正六边形的形状,上下平台通过液压缸和虎克铰相连接,该平台主要通过视觉伺服技导弹空间六自由度位姿进行调整以实现与发射装置装填位置的对准功能。
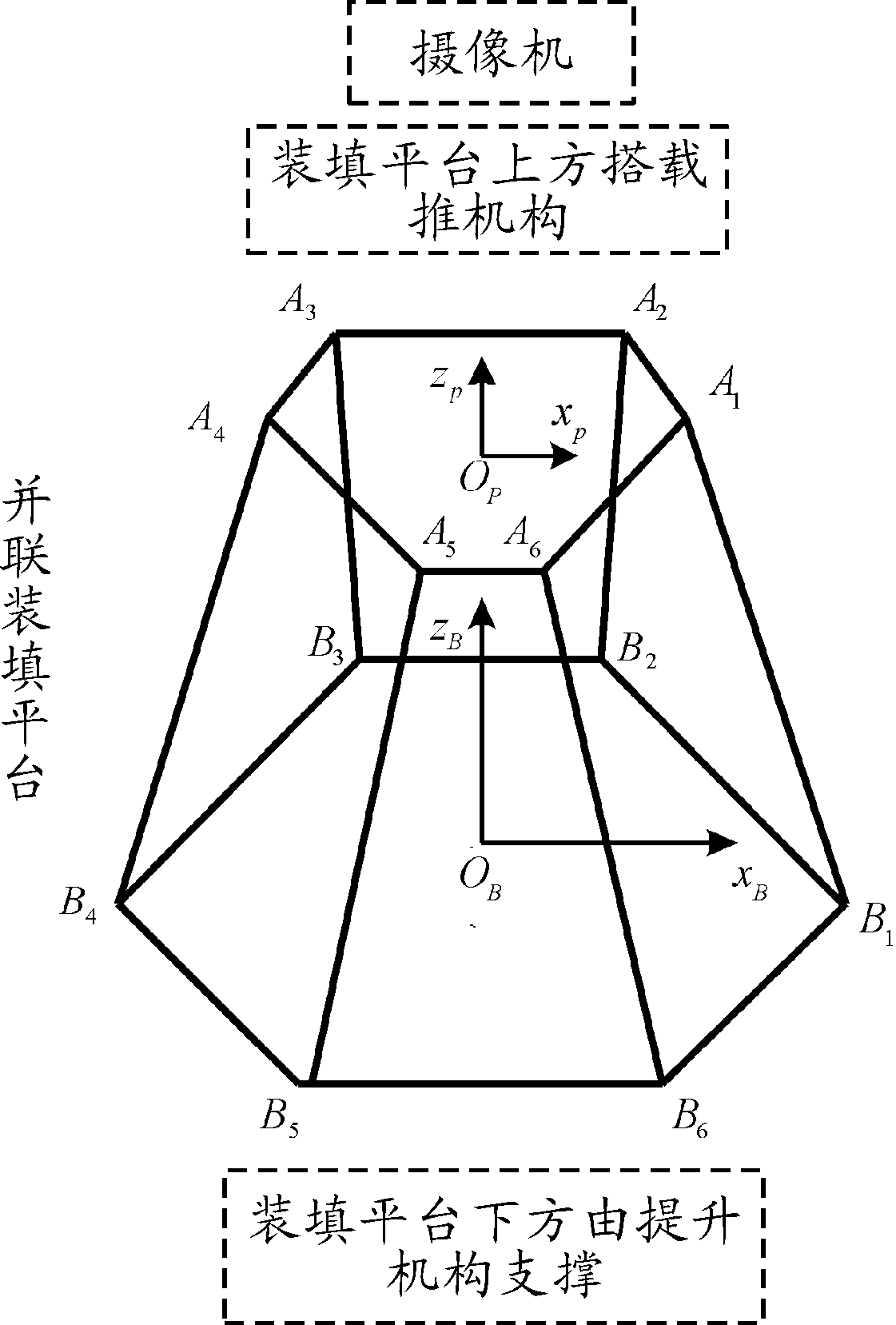
图1 装填装置结构示意图
为了满足自动对准的需要,装填平台和视觉伺服系统共使用了六种坐标系,分别为世界坐标系OWxWyWzW,动平台坐标系OPxPyPzP,静平台坐标系OBxByBzB,相机坐标系OCxCyCzC,图像平面坐标系Ocxyz以及像素坐标系Ouv。
动平台坐标系和静平台坐标系建立在上下平台中心,见图1,符合右手坐标系规则。世界坐标系与静平台坐标系重合,相机坐标系建立在摄像机中心,如图2所示,其x轴正向与动平台y轴负方向相同,z轴正向与动平台x轴正向相同。图像平面坐标系与像素坐标系建立在摄像机内部,用于相机的小孔成像模型。设空间中一点P在相机坐标系中的坐标为(XC,YC,ZC),则空间中一点的坐标由相机坐标系到像素坐标的转换关系为[5]
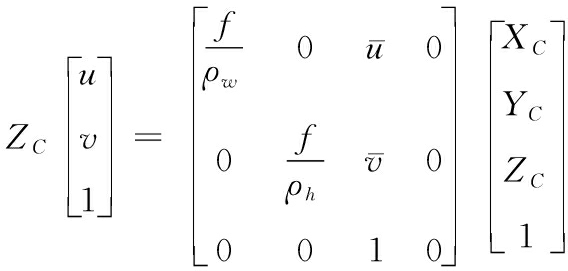
(1)
其中,内在参数描述了相机的固有特征,包括焦距f,像素的宽和高ρw、 ρh,以及相对于主点的像素坐标![]()
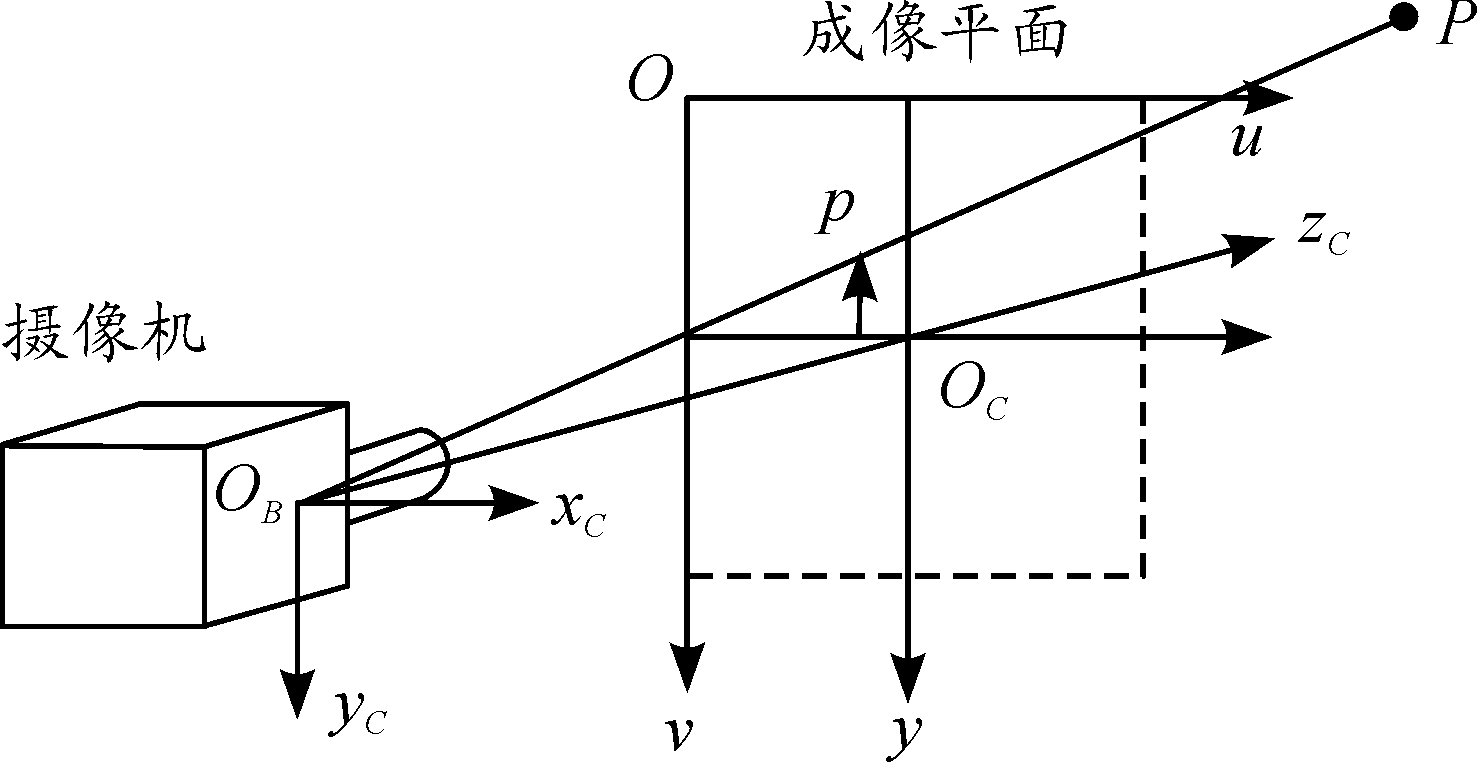
图2 相机坐标系示意图
2 装填平台运动学模型建立
2.1 运动学逆解
运动学逆解即通过动平台位姿求得六个液压支腿的长度[6]。动平台相对静平台的位置用向量t=[x,y,z]T表示,即OP在静平台中的坐标。动平台相对静平台的姿态通常使用Roll-Pitch-Yaw旋转表示,假定偏航角为α,俯仰角为β,横滚角为γ,则动平台相对静平台的姿态为
BRP=R(z,γ)R(y,β)R(z,α)=
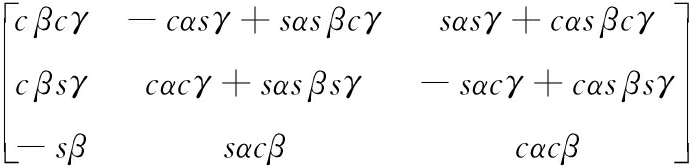
(2)
其中,s(·)=sin(·),c(·)=cos(·)。则动平台相对静平台的位姿可以表示为
p=[x,y,z,α,β,γ]T
(3)
动、静平台上的铰点坐标分别用ai和bi表示,因此液压支腿的空间向量可描述为
li=t+BRPai-bi
(4)
故液压支腿的长度为
(5)
进一步令![]() 并将其两边对时间求导可得到上铰点速度在静坐标系的速度为
并将其两边对时间求导可得到上铰点速度在静坐标系的速度为
(6)
为了得到液压缸速度,将上式得到的上铰点速度向液压缸矢量方向投影,即
(7)
整理可得到装填平台空间度到液压支腿伸缩速度的雅克比矩阵及其传递关系
(8)
式中,![]() 为各液压支腿伸缩速度构成的矩阵,L为液压支腿单位矢量构成的矩阵,A为动坐标系下上铰点坐标构成的矩阵。
为各液压支腿伸缩速度构成的矩阵,L为液压支腿单位矢量构成的矩阵,A为动坐标系下上铰点坐标构成的矩阵。
2.2 运动学正解
运动学正解即通过六个液压支腿的长度求得动平台位姿。目前关于六自由度并联机构的运动学正向求解方法主要分为解析解法和数值解法两大类,解析法主要致力于获得全部解,而数值解致力于提高求解效率,更适用于实际应用[7]。数值解法中Newton-Raphson方法是一种传统且被广泛使用的迭代求解方法,有较好的实时性和通用性[8]。Newton法的迭代式为
pk+1=pk-(F′(pk))-1F(pk)
(9)
从迭代式可以看出Newton法的关键是构造动平台位姿的函数F(pk),文献[9]提出了一种F(pk)的构造方法,在此基础上定义了改进的Jacobian矩阵[9],并给出了解析表达式。文献[7]经过仿真计算表明了改进的Jacobian矩阵方法较其他数值解法具有更好的计算效率。由于视觉伺服系统每个采样周期均需要正向运动学的解算,对算法的实时性要求较高,因此在装填平台的正向运动学中应用改进的Jacobian矩阵方法,结合式(9),该算法的流程框图如图3所示。
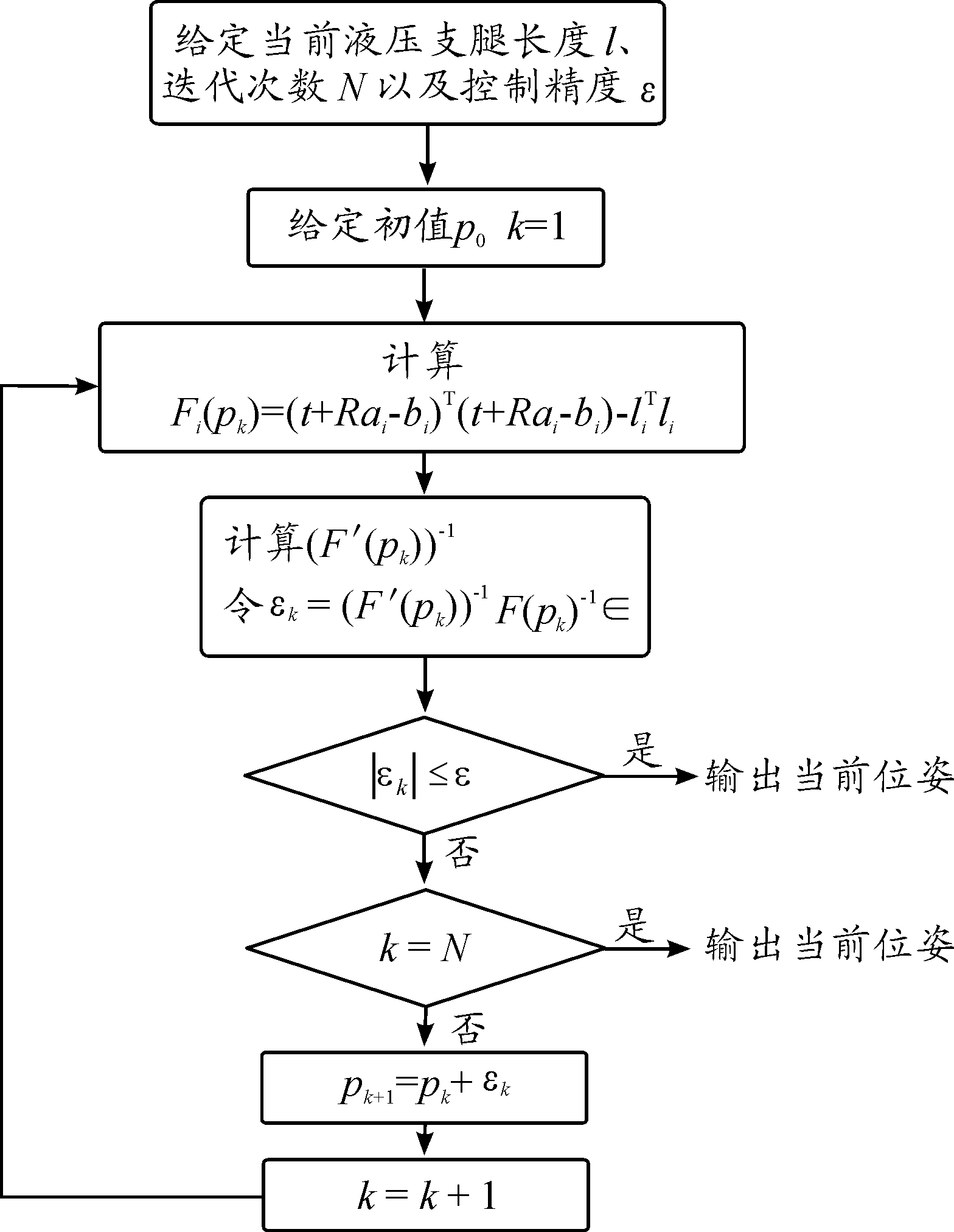
图3 Newton法求解运动学正解流程框图
3 基于图像视觉伺服的自动对准方法
3.1 基于图像的视觉伺服
基于图像的视觉伺服有两个关键问题需要解决,一是图像特征的选取,通常分为局部特征和全局特征。考虑到实际情况中相机视场的限制,同时点特征作为局部特征容易提取,其图像雅克比矩阵也易于获得[2],因此可以选取发射装置上的点特征为图像特征。
第二个关键问题是图像雅克比矩阵的求取。图像雅克比矩阵描述了执行机构的空间速度到图像空间速度的映射关系,即
(10)
其中vC=[vx,vy,vz,ωx,ωy,ωz]T,表示了摄像机在自身坐标系中的空间速度。一个点特征的图像雅克比矩阵为[10]
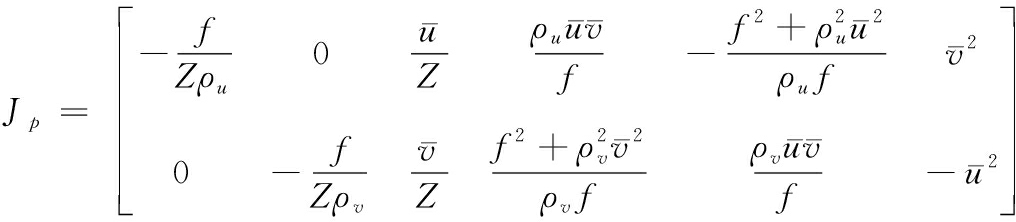
(11)
3.2 自动对准流程
装填装置在执行装填任务时主要分为3个阶段,其中前两个阶段实现导弹的自动对准过程:
1) 由于装填时装填装置和发射装置的位置相对固定,因此先由提升机构搭载装填平台使装填平台上的推弹机构运动至装填位置下方附近;
2) 考虑到发射装置复位误差、舰面不平等因素,装填平台应用图像视觉伺服技术实现推弹机构的位姿调整以使导弹与装填位置位姿一致。基于装填平台的运动学原理,该阶段的自动对准流程如图4所示。首先,摄像机在当前位姿下通过图像处理过程获得图像特征的像素坐标f,然后与期望的像素坐标值fd相比对形成负反馈控制产生控制误差e。视觉控制器可采用比例控制产生摄像机所需速度,即
(12)
控制误差经过视觉控制器并结合图像雅克比矩阵形成摄像机的控制速度,该速度可进一步转换为装填平台的控制速度。最后,装填平台的动平台根据控制速度进行运动并使摄像机到达新的位姿,至此完成了摄像机一个采样周期内装填平台位姿的调整过程。当图像特征的像素坐标达到期望的坐标值或误差满足精度要求时,装填平台搭载导弹运动到指定位置并完成了与装填位置的对准。

图4 装填平台自动对准流程框图
3) 在完成前两个阶段的对准过程后,推弹机构将导弹送入装填位置,至此完成了一次装填。
需要指出的是,发射装置上有多个装填位置,每次装填时都要先执行上述第一阶段的过程,使导弹与装填位置粗略对准,再进一步由装填平台实现导弹位姿的精确调整。
3.2 装填平台对准过程中的速度转换关系
在装填平台的对准流程中,存在图像特征的运动速度,摄像机的运动速度,动平台的运动速度、液压支腿的伸缩速度以及速度之间的雅克比矩阵,但不同的速度是在不同的坐标系中表示的,为了实现对装填平台的控制,应使上述速度之间形成闭环的转换关系。
记相机坐标系与动平台坐标系之间的转换关系为PRC,则相机坐标系与静平台坐标系即世界坐标系之间的转换关系为
![]()
(13)
通过视觉伺服得到的相机控制速度是在相机坐标系中表示的,由于动平台与推弹机构、摄像机固连,因此相机的控制速度即是动平台的控制速度,将其转换到世界坐标系中
(14)
在装填平台的运动学分析中,动平台的转动速度是用Roll-Pitch-Yaw表示的,所以应进一步将式(14)得到的速度中的转动速度分量转换成角速度分量,转换关系为
(15)
其中[11]
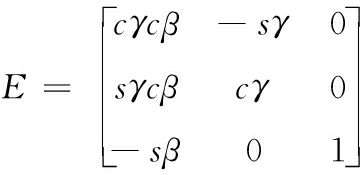
(16)
至此综合式(8)、式(12)、式(14)、式(15)可以得到由图像特征速度和液压支腿伸缩速度的转换关系
(17)
4 仿真计算
根据自动对准流程以及装填平台的运动学模型,建立了装填平台对准流程的数学模型,如图5所示。
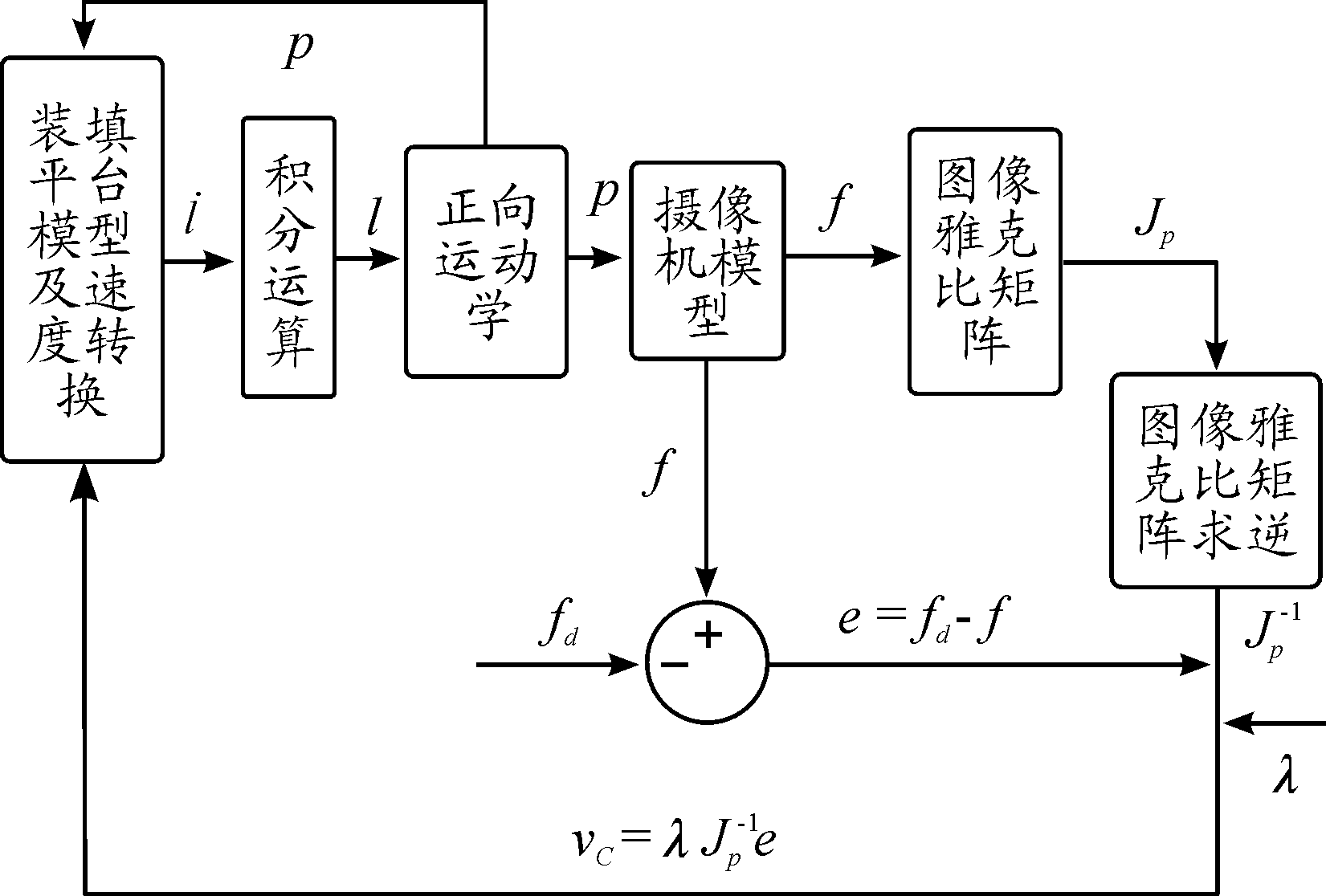
图5 对准流程仿真计算模型简图
仿真计算时假设推弹机构已运动至某一装填位置附近,以静坐标系为世界坐标系,液压支腿的初始长度均为0.65 m,其最大长度为1 m,并给定上、下铰点在各自平台坐标系中的坐标以及摄像机相对动平台的坐标位置。在发射装置上选取4个特征点作为图像特征且特征点在一个平面内,模拟给出了实际情况下相机的初始位姿和图像特征的空间位置,如图6所示。在初始姿态下,可以得到当前图像特征的像素坐标为
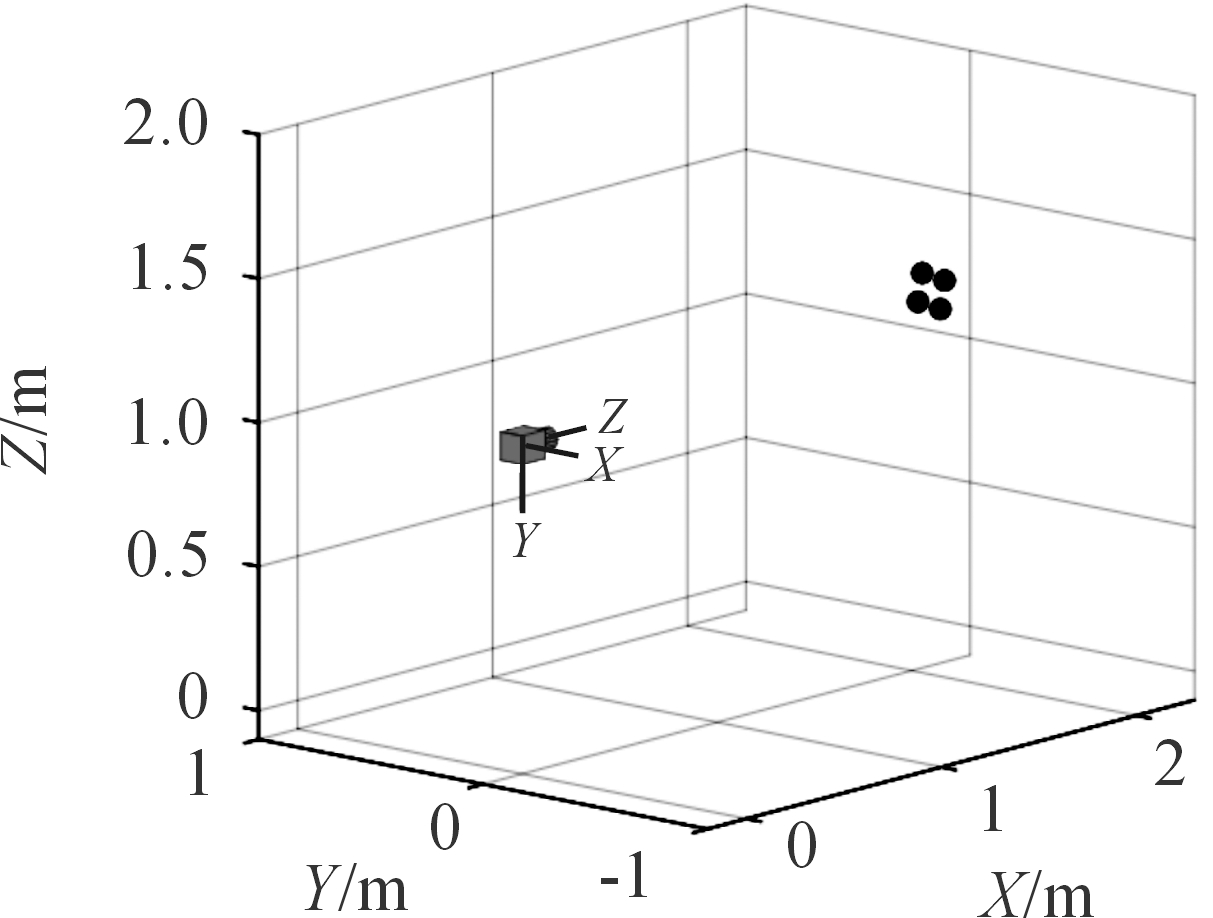
图6 摄像机及特征点初始位姿
当装填平台完成对准时,摄像机获取的期望的图像特征像素坐标为
令λ=3,经仿真计算可以得到6个液压支腿的运动的速度如图7所示,支腿长度变化如图8所示。图9给出了摄像机成像平面下点特征的运动轨迹,其中圆形表示特征点初始位置,五角形表示特征点期望位置。
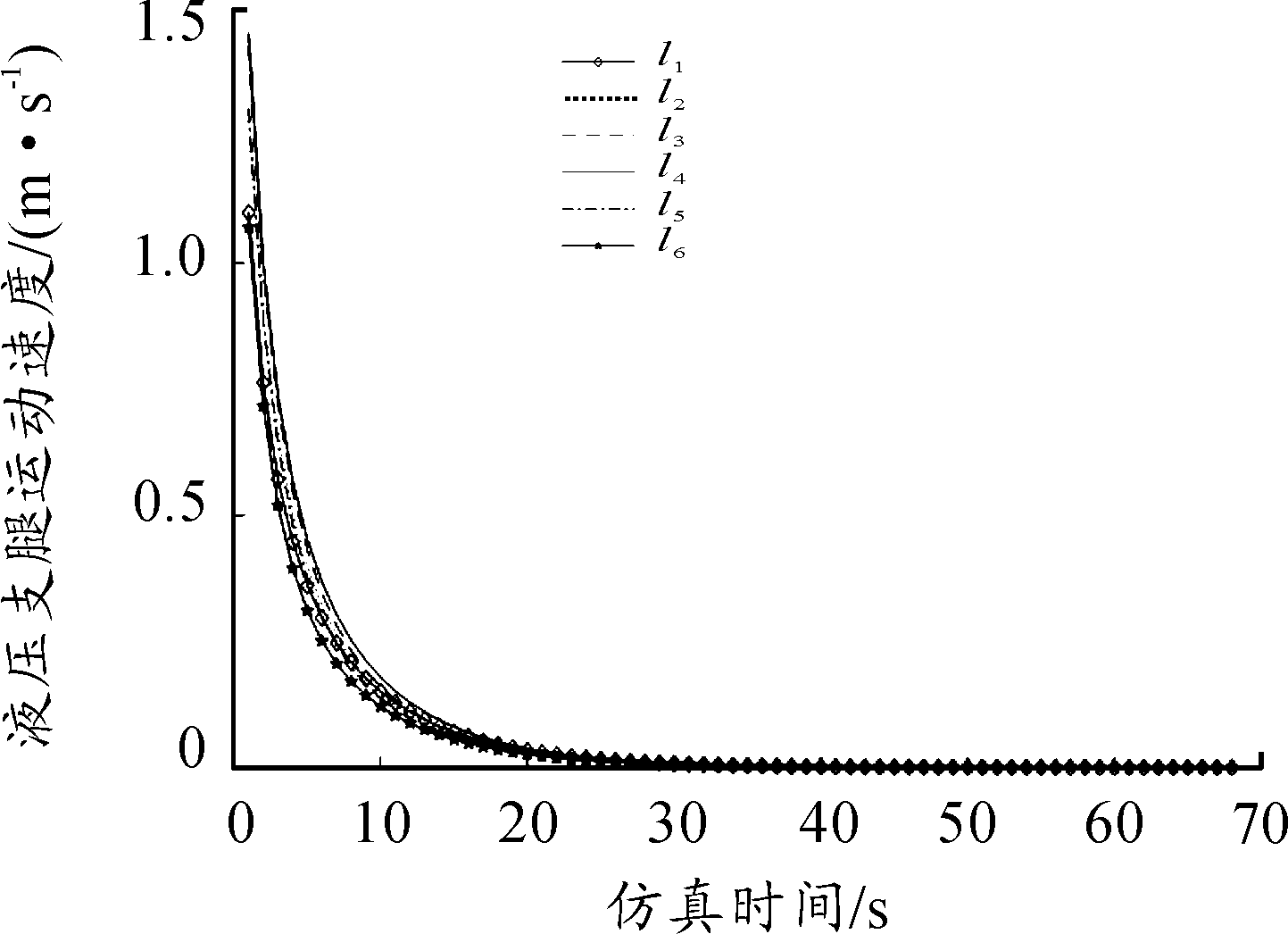
图7 液压支腿速度变化曲线
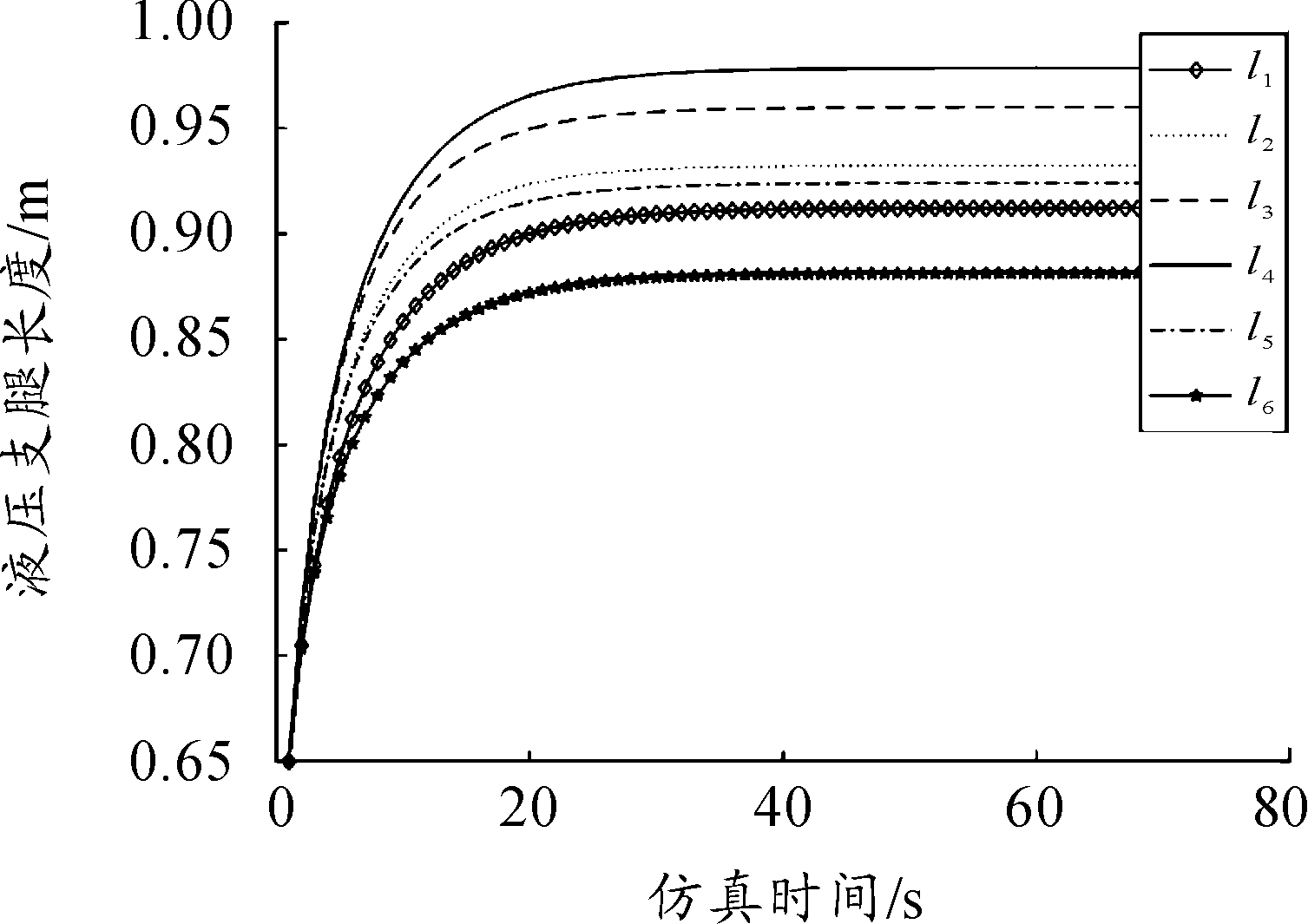
图8 液压支腿长度变化曲线
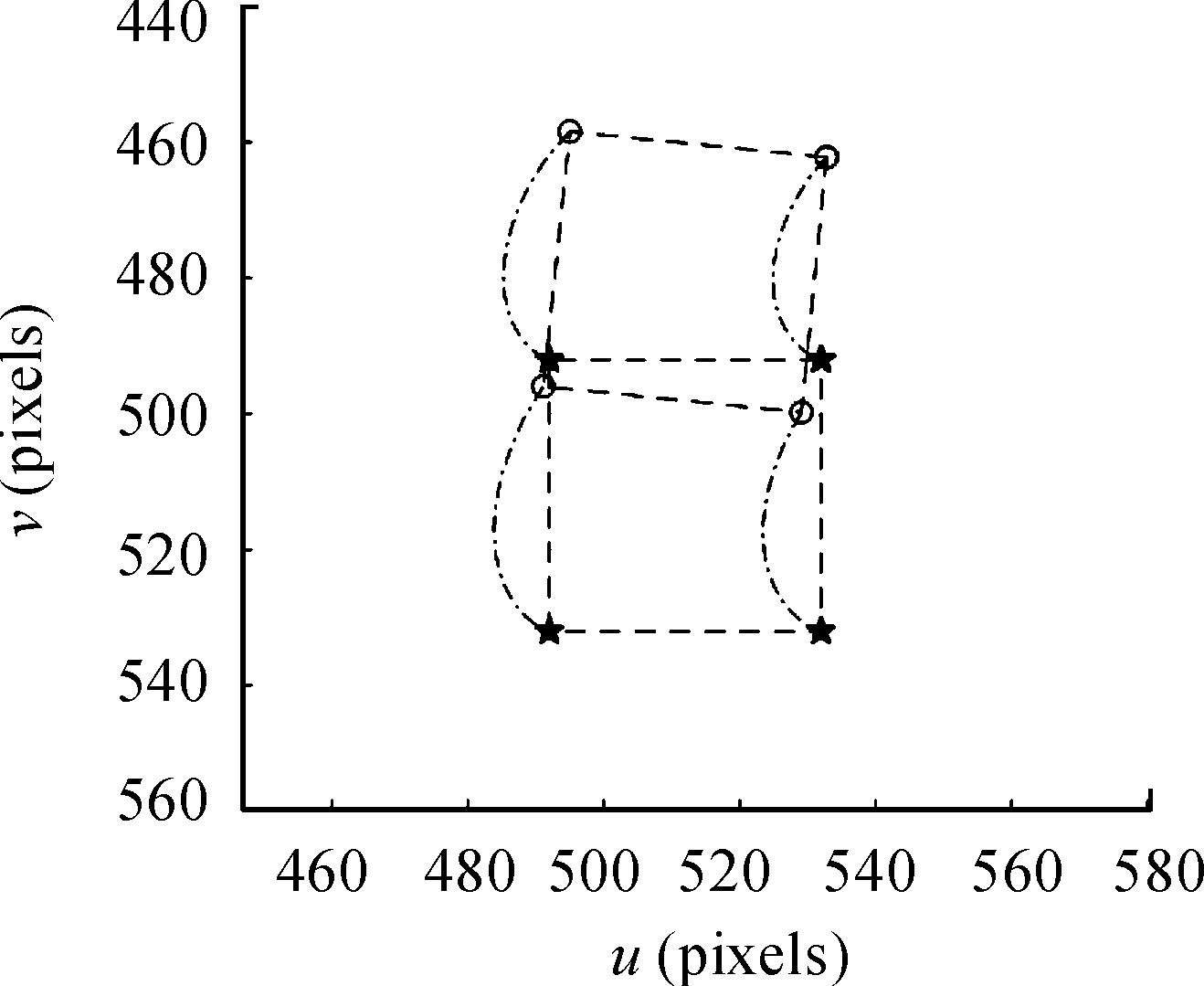
图9 特征点运动轨迹
仿真结果分析:
1) 液压支腿运动速度随仿真时间逐渐趋于零,表明装填平台可以按照设定好的比例控制规律运动。
2) 从摄像机成像平面可以看出特征点在向期望的位置运动,表明装填平台可以实现对准过程。
3) 理想装填情况下,特征点所在平面应与相机坐标系的Z轴垂直,但实际情况中存在发射装置复位误差以及舰面不平等因素,因此仿真时使发射装置上特征点所在的平面位置与理想位置具有大于实际的位姿差异,这从初始姿态下图像特征的像素坐标可以看出。仿真结果表明在此时的装填位置下液压支腿的长度变化符合预期,且没有超过其最大长度,结合自动对准流程可以认为在其他装填位置也可以实现对准过程。
5 结论
将无标定的图像视觉伺服技术应用于六自由度并联结构形式的导弹装填平台上,结合装填平台的运动学模型,根据图像特征偏差建立了伺服控制方法,仿真计算表明,该方法能够实现装填平台的姿态调整和自动对准过程。
[1] 蒋丙栋,王茂森,戴劲松.基于双目视觉技术的供补弹机构对接方法[J].兵器装备工程学报,2019,40 (1) :184 -187.
[2] 李牧.机器人无标定视觉伺服关键技术的研究[D].哈尔滨:哈尔滨工业大学,2008.
[3] 贾丙西,刘山,张凯祥,等.机器人视觉伺服研究进展:视觉系统与控制策略[J].自动化学报,2015,41(5):861-873.
[4] 徐德.单目视觉伺服研究综述[J].自动化学报,2018,44(10):1729-1746.
[5] CORKE P.Robotics,vision and control:fundamental algorithms In MATLAB second,completely revised[M].Springer,2017.
[6] TAGHIRAD H D.Parallel robots:mechanics and control[M].CRC press,2013.
[7] 张辉,王启明,叶佩青,等.通用 Stewart 平台运动学正向数值求解方法及应用[J].机械工程学报,2002,38(增刊):108-112.
[8] 耿明超,赵铁石,王唱,等.基于拟 Newton 法的并联机构位置正解[J].机械工程学报,2015,51(9):28-36.
[9] NGUYEN C C,ZHOU Z L,ANTRAZI S S,et al.Efficient computation of forward kinematics and Jacobian matrix of a Stewart platform-based manipulator[C]//IEEE Proceedings of the Southestcon’91.IEEE,1991:869-874.
[10] ESPIAU B,CHAUMETTE F,RIVES P.A new approach to visual servoing in robotics[J].ieee Transactions on Robotics and Automation,1992,8(3):313-326.
[11] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2014.