弹道修正弹药相对于常规弹药具有更高的打击精度、更低的成本和更小的后勤保障负担等优点。用弹道修正引信替换原有弹药引信是实现弹道修正的最佳方式[1],可以在不对弹丸进行改动的情况下实现对外弹道的修正、提高打击精度和减少弹药损耗[2],特别适合对库存无控弹药的精确化改造。
仅对炮弹射程进行修正的一维弹道修正引信技术已经足够成熟,能够同时修正射程和横向偏差的二维弹道修正引信目前已成为热点研究领域[3-7]。美国ATK公司的MGK是典型的迫击炮弹二维弹道修正组件技术,提供用来替换120 mm迫击炮弹制式引信的弹道修正组件,加装该种MGK引信的炮弹精度提高明显,CEP可达10 m以内。但是,应用MGK技术需要对迫击炮弹尾翼进行改动设计。国内在迫击炮弹上实现二维弹道修正功能主要采用固定舵方案,需要对弹身、尾翼等进行改动以保证稳定性和弹身连续旋转。在弹身增设“一”字形可变弹翼,通过控制弹翼前缘后掠角改变弹翼面积,可调控射程,实现制导[8]。一种迫击炮弹弹道修正组件引信气动外形,采用固定舵方案,可对尾翼进行气动优化设计[9]。不同翼形几何参数对某弹道修正迫弹流场特性和气动特性的影响[10],如采用可动舵方案,也需要重新设计弹丸结构和外形实现二维修正功能,无法仅通过引信自身不改变弹丸结构和气动外形就能实现二维弹道修正功能。
在不改变弹丸气动外形的基础上进行引信的改装,将舵片“×”型放置,利用鸭舵与弹身的气流影响可解决静稳定性问题。调整舵滚转角和舵偏角修正,两对舵片均可提供操纵力,也可以成为差动舵。基于该种双旋弹的结构特性,进行几种不同引信气动布局的气动特性分析,获得一种相对较为合理的气动布局方案,通过6D弹道仿真计算得弹丸的修正能力[11]。
1 气动仿真模型的建立与求解
以某制式120迫弹为基础进行制导引信的改装,根据迫弹静稳定性对引信气动外形改变较为敏感的特点,预先设计了两种引信气动布局方案。方案Ⅰ为长引信小舵片(翼型为NACA0012);方案Ⅱ为短引信大舵片(翼型为NACA0014),方案Ⅱ引信外露长度较短,静稳定性会有所提升,为了保证修正能力,因此将舵片加大加厚;方案Ⅲ是以前两种方案为基础进行优化后的引信气动外形。弹道修正引信外形如图1所示。
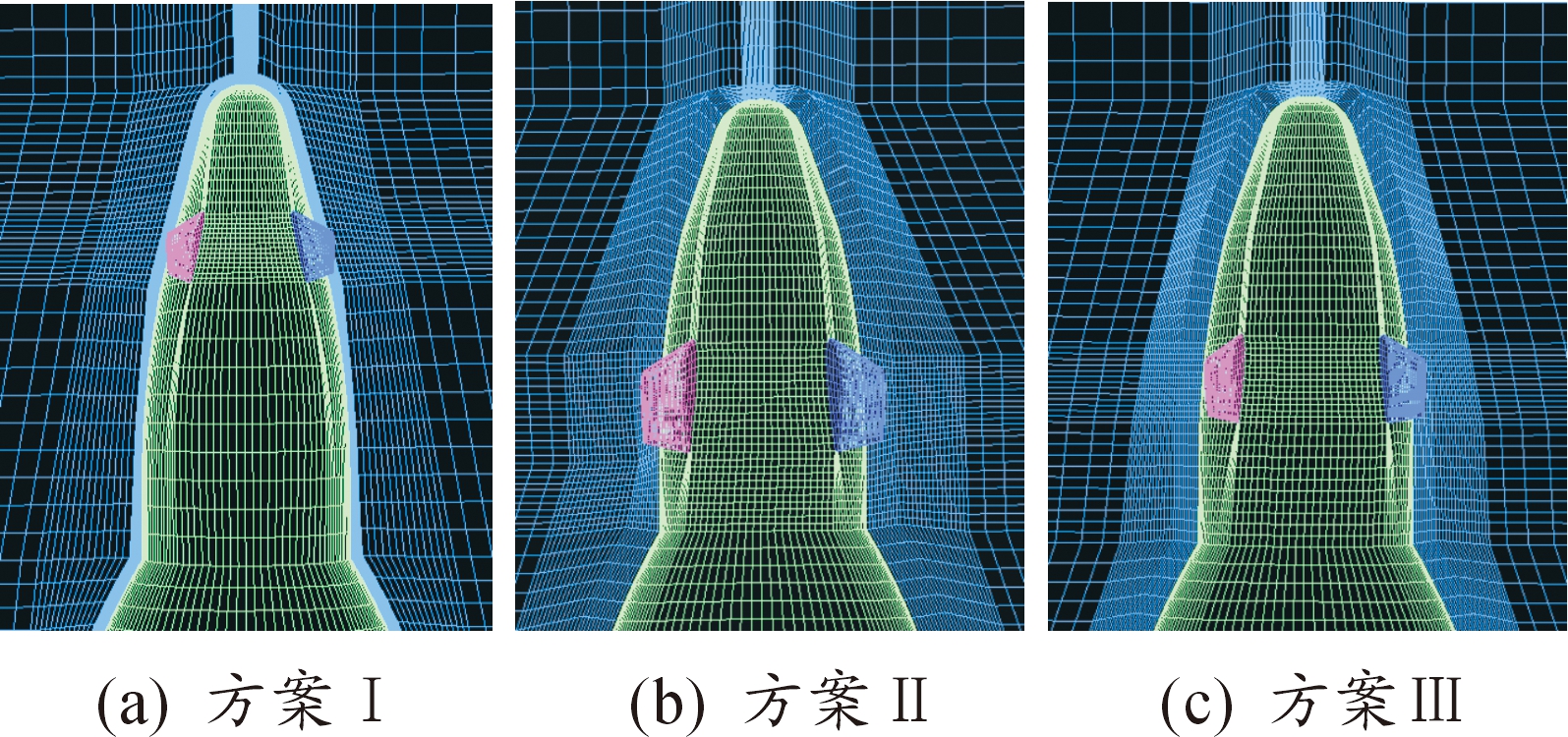
图1 弹道修正引信气动外形示意图
气动外形的设计的思路为:
1)为验证气动计算的准确性,先仿真计算原制式弹丸的气动系数,进行6D弹道仿真对气动计算结果进行验证。
2)分别对两种修正引信弹丸进行气动计算。
3)在气动计算的基础上进行稳定性、操纵性分析,进而优化弹丸气动外形结构。
1.1 原弹气动计算
将原制式弹三维模型导入ICEM CFD中建立空间计算域4 500 mm×3 600 mm×4 000 mm,进行网格划分,采用全结构网格,在前处理中采用四阶Shear Stress Transport湍流模型,该模型综合了BSL k-ω模型在近壁区计算的优点和标准k-ε模型在远场计算的优点,将k-ω模型和k-ε模型都乘以一个混合函数后再相加就得到这个模型。在近壁区,混合函数的值等于1,因此在近壁区等价于k-ε模型,在远离壁面的区域混合函数等于0,因此自动转换为标准k-ε模型,SST模型适用于翼型计算和跨音速激波计算等,求解器中采用高阶求解格式,时间尺度为0.1,控制方程包含连续性方程、能量方程、动量方程、湍流涡频率方程和湍流动能方程。利用弹丸轴对称的特性,可将结构网格数减少一半从而降低计算量[12],最终网格总数约为59万。网格划分示意图如图2。

图2 原制式弹网格划分示意图
原制式弹丸外形如图2所示,计算工况马赫数范围为0.5~1.2Ma,攻角范围为0°~15°。计算结果如图3所示。
由气动计算结果可知弹丸在高马赫数时阻力增大明显。弹丸的升力系数且在小攻角下线性度较好。静力矩系数在小攻角时线性度较好。原弹静稳定储备量在1.2Ma、15°攻角时达到最低,为6.9%;在0.5Ma、15°攻角时达到最高,为19.51%。利用原弹气动参数,在45°射角下对弹丸进行6D弹道仿真,与射表结果射程的相对误差为0.14%,最大弹道高的相对误差为0.82%,因此气动计算结果基本符合实际。
1.2 弹道修正引信气动计算
对方案Ⅰ和方案Ⅱ进行气动仿真。方案Ⅰ的计算结果如图4。方案Ⅰ弹丸在1.2Ma下静稳定储备量低至1.68%,为探究其原因,针对方案Ⅰ不带舵片的情况进行仿真,1.2Ma、10°攻角时弹丸的静稳定储备量低至3.29%,因此方案Ⅰ的引信外露长度过长是导致弹丸静稳定性差的主要原因。
方案Ⅱ的计算结果如图5(a)和图5(c)所示。由图5(a)、图5(b)和图5(c)可知,在高马赫数下由于舵片接近弹身,涡流特征明显,而在低马赫数下则没有涡流的作用。方案Ⅱ的静稳定储备量如图5(d)所示,其静稳定性随着马赫数的变化规律与方案Ⅰ不同,在高马赫数时静稳定性较方案Ⅰ要高,原因在于舵片较为靠近弹身部分,当气流流过有攻角的舵片后,舵片附近气流的流动方向发生变化,由于弹身与弹道修正引信间不是流线型结合,气流运动由于弹丸气动外形的局部骤变而产生涡流,压力云图如图5(b)所示。在速度坐标系Y轴上,涡流对舵片产生了力![]() 的方向与攻角产生的升力方向相反,在高马赫数下
的方向与攻角产生的升力方向相反,在高马赫数下![]() 大于舵片攻角产生的升力,提高了弹丸的静稳定性,而随着马赫数的降低,涡流的作用逐渐削弱,低马赫数下
大于舵片攻角产生的升力,提高了弹丸的静稳定性,而随着马赫数的降低,涡流的作用逐渐削弱,低马赫数下![]() 小于舵片产生的升力。
小于舵片产生的升力。
方案Ⅱ中舵片在高马赫数下提升了静稳定性,但是由于舵片距离弹身太近,在亚声速时,受涡流的影响升力不足,故修改舵片位置,使舵片能够兼顾稳定性和修正能力。
2 气动优化仿真
在方案Ⅱ的基础上将舵片往弹头方向移动,在多次仿真计算和优化之后,最终得到方案Ⅲ的结构。方案Ⅲ采用短引信小舵片结构(翼型为NACA0014)。引信长度与方案Ⅱ相同,舵片位置距离引信和弹丸连接处38 mm,舵片面积为方案Ⅱ的0.7倍。方案Ⅲ的引信气动外形如图1(c)所示。
方案Ⅲ计算工况的马赫数范围为0.3~1.2Ma,攻角范围为0°至8°。静稳定储备量曲线如图6(a)所示,弹丸的升力系数曲线、静力矩系数曲线和单片舵的升力曲线如图6所示。
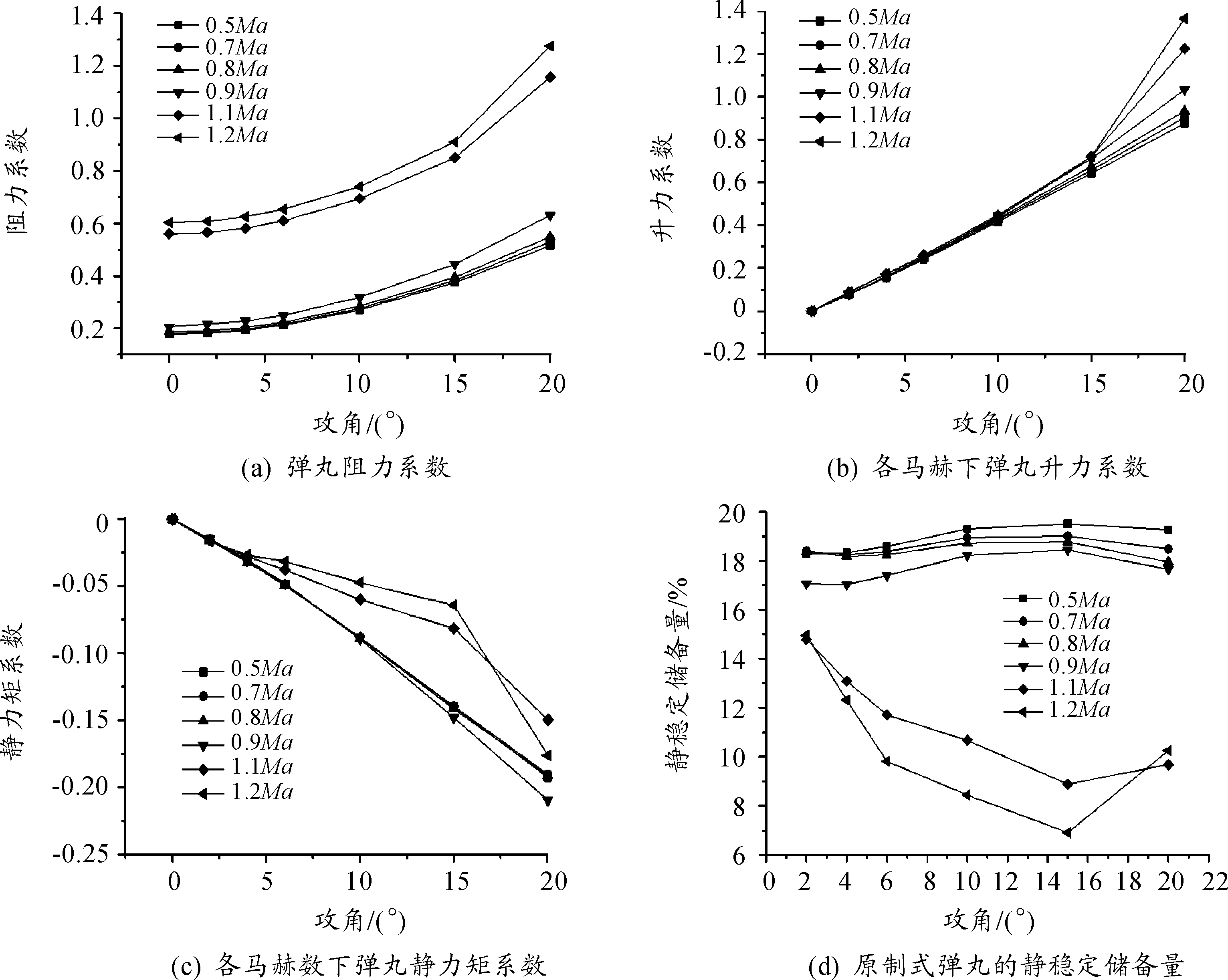
图3 原制式弹丸气动参数曲线和静稳定储备量曲线
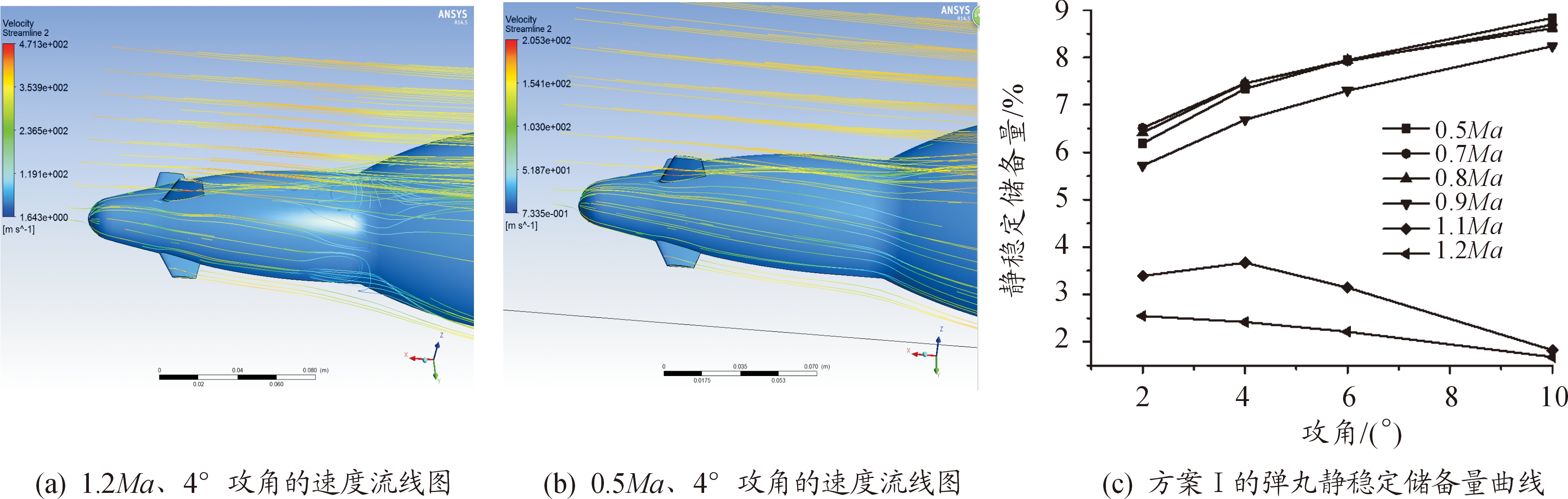
图4 方案Ⅰ的气动仿真结果和静稳定储备量曲线
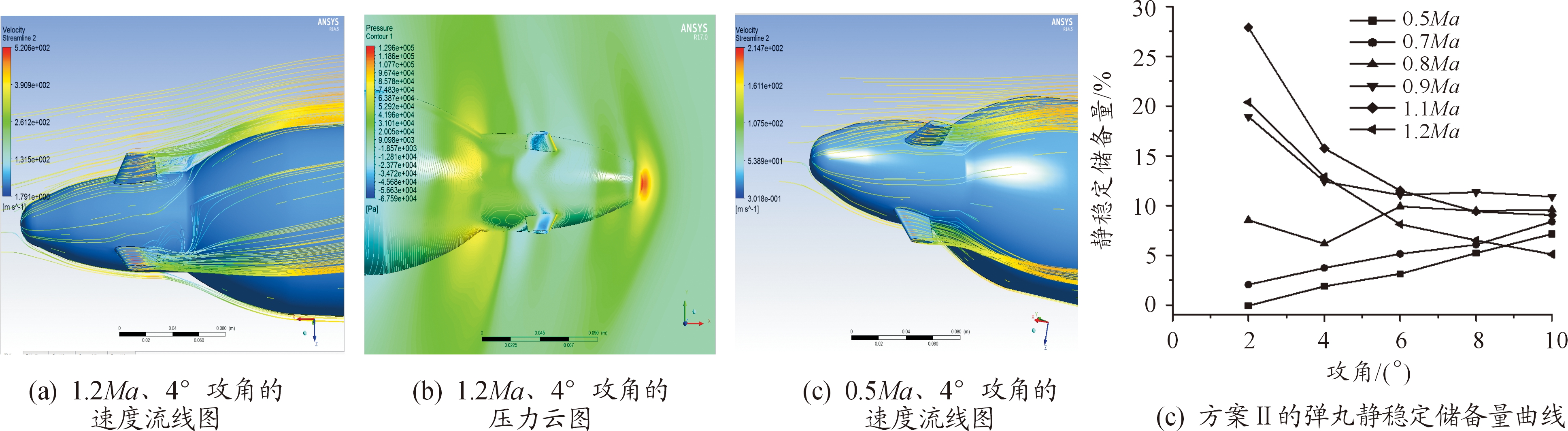
图5 方案Ⅱ的气动仿真结果和静稳定储备量曲线
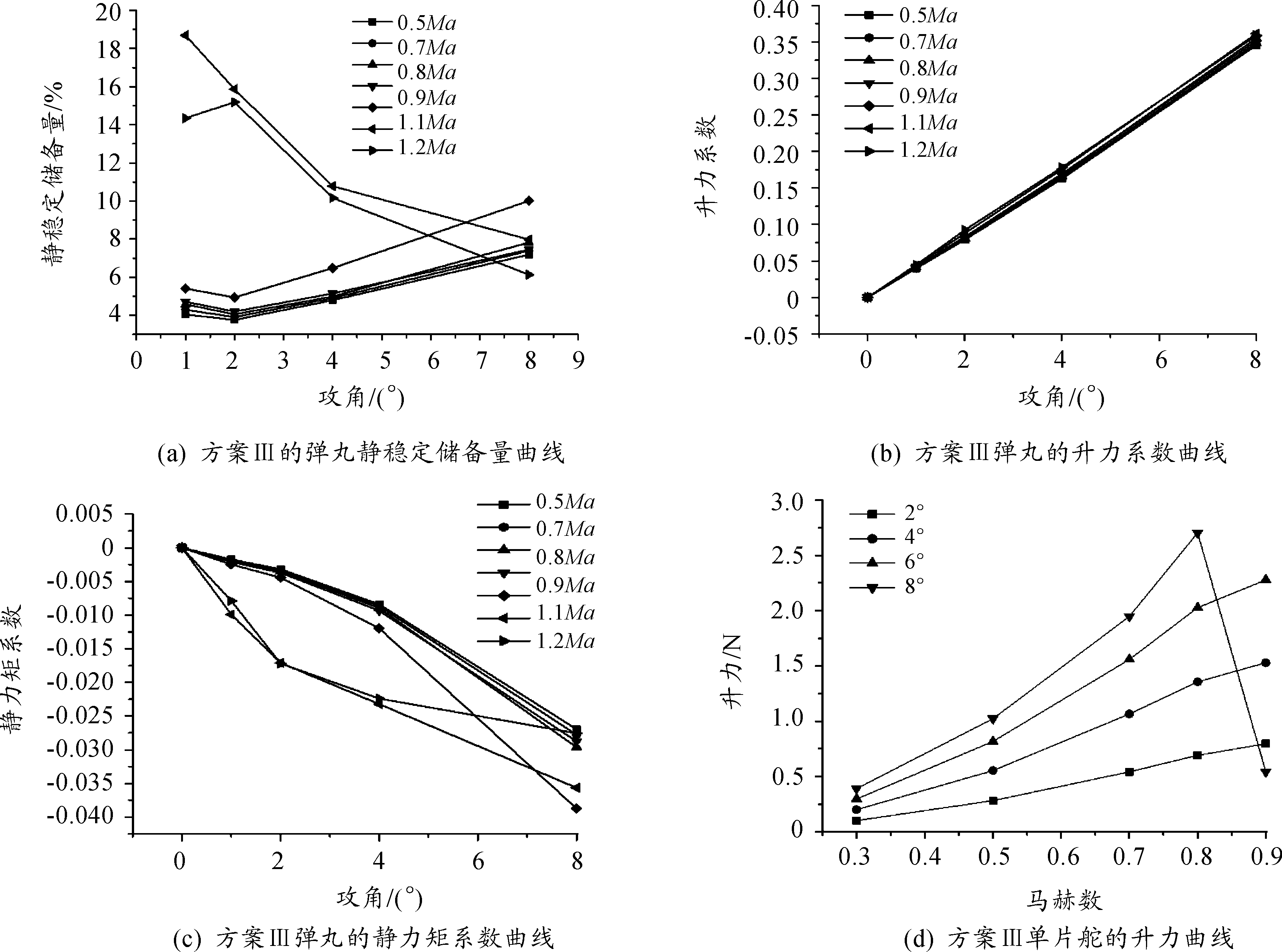
图6 方案Ⅲ弹丸的气动参数曲线和静稳定储备量曲线
对比前两种弹道修正引信气动布局,方案Ⅲ在亚声速时舵片的气动特性较符合规律,舵片能够在0.8Ma以下提供升力,且升力与舵偏角和马赫数变化基本成正比。0.9Ma、8°舵偏角时舵片出现了失速情况。在各马赫数下静稳定性都满足要求,静稳定性在0.3Ma达到最低,约为4%,高马赫数时静稳定性较好。
表1列出了3种方案0°攻角下单个舵片在不同马赫数和舵偏角的操纵力,即为垂直于0°舵偏角下的舵片纵向对称面的操纵力的数值,可以看出方案Ⅱ和方案Ⅲ中高马赫数下舵片由于涡流的影响产生了负的操纵力。
3 带可动鸭舵的弹道仿真结果
基于上一节得到的方案Ⅲ的引信气动布局方案,设舵偏角为0°,采用6-D弹道模型仿真求得45°射角下的无控弹道仿真结果值,见表2。
根据表2可以看出0°舵偏角的弹道修正引信对射程会造成一定损失,约为15 m,相比于全弹道射程,损失不大。
表1 各方案下单片舵产生的操纵力值 N
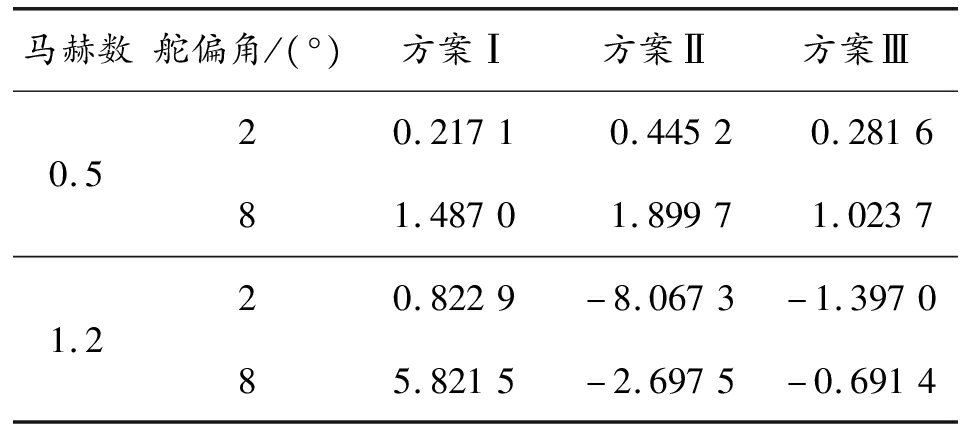
马赫数舵偏角/(°)方案Ⅰ方案Ⅱ方案Ⅲ0.520.21710.44520.281681.48701.89971.02371.220.8229-8.0673-1.397085.8215-2.6975-0.6914
表2 45°射角下改装引信后弹与原弹的重要参数仿真结果值
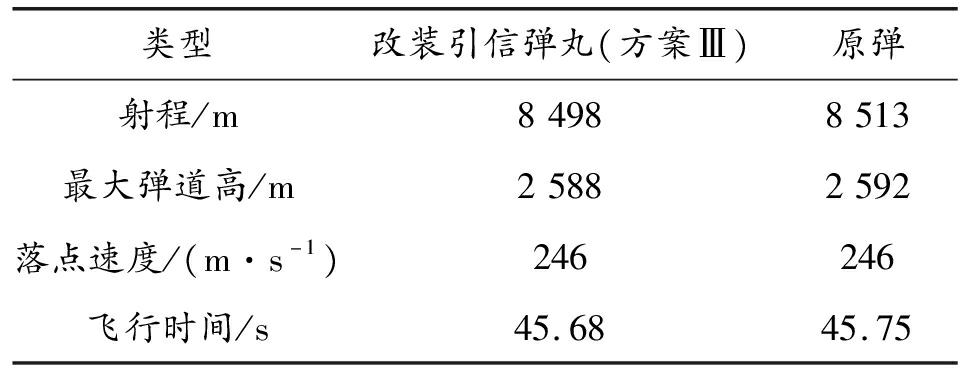
类型改装引信弹丸(方案Ⅲ)原弹射程/m84988513最大弹道高/m25882592落点速度/(m·s-1)246246飞行时间/s45.6845.75
图7为不同马赫数、不同舵偏角下弹丸的平衡攻角(此时每个舵片偏转相同的舵偏角以保证产生最大的升力合力)曲线。
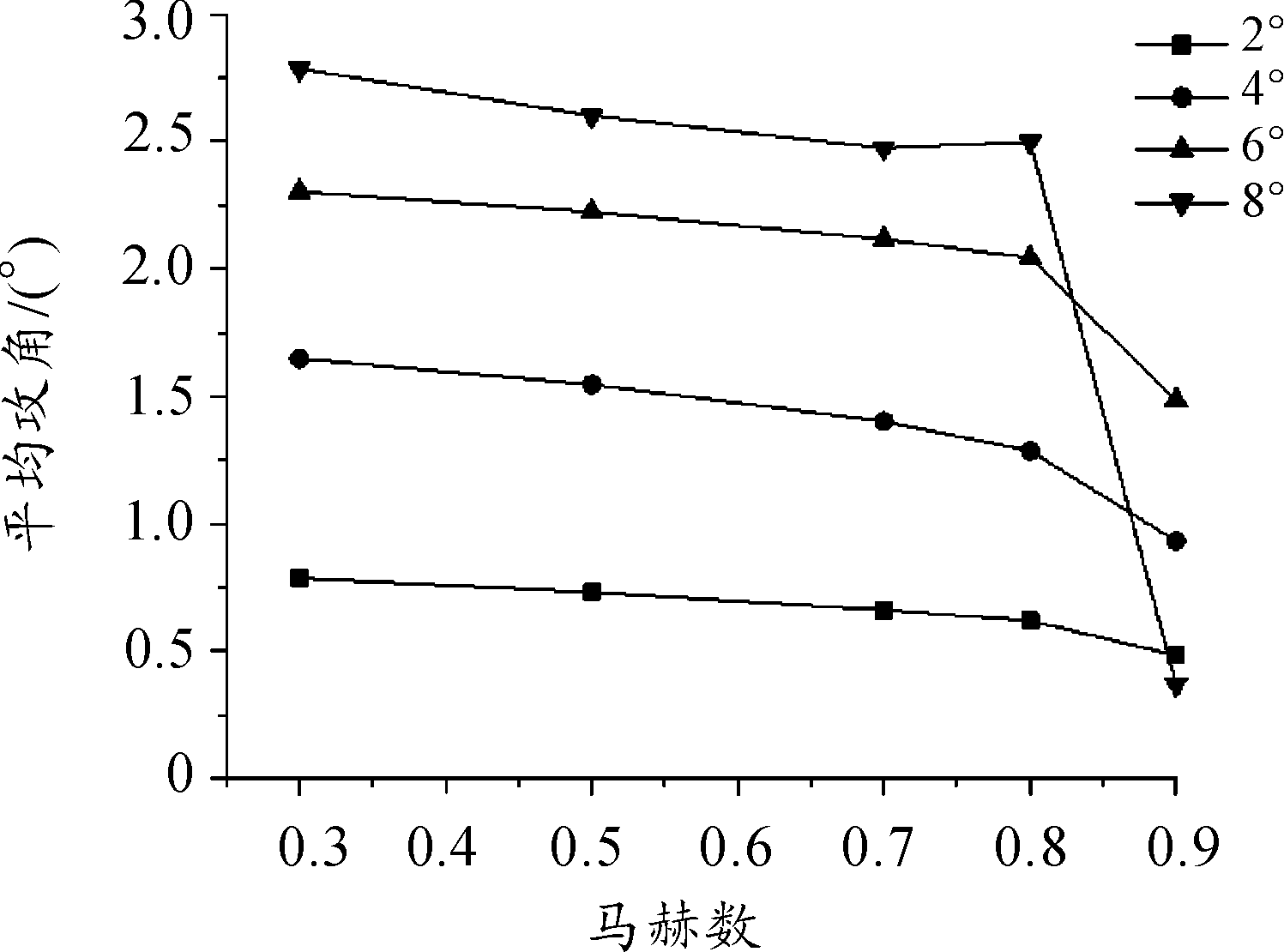
图7 不同马赫数不同舵偏角下的平衡攻角曲线
由图7可知,弹丸平衡攻角随马赫数的增加而减小。平衡攻角最大为2.8°左右。不同舵偏角和平衡攻角基本成比例。舵偏角为8°时在高马赫数下出现失速情况。
针对方案Ⅲ,采用6D弹道模型对不同舵偏角和不同修正方向的修正能力进行开环弹道仿真,在不同修正方向上的弹道修正量示意图如图8。
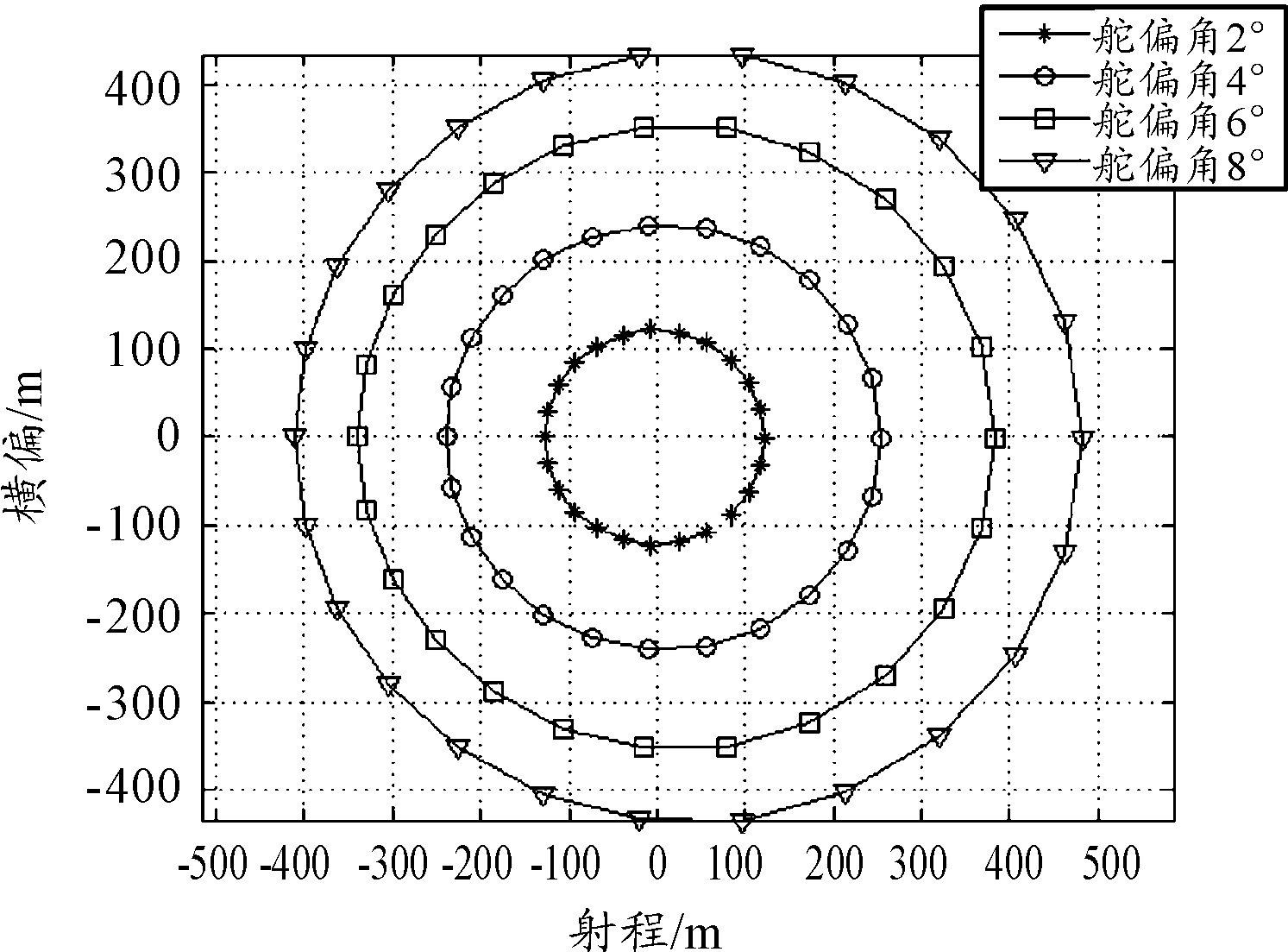
图8 方案Ⅲ不同修正方向下的开环修正量示意图
4 结论
针对120 mm迫击炮弹,设计了可动舵引信气动布局,在不改变弹丸气动外形的基础上可以同时兼顾迫击炮弹稳定性和修正能力。气动计算表明在高马赫数飞行时舵片与弹身之间的气流扰动能够改善弹丸在高马赫数飞行时的稳定性,飞行马赫数为1.2Ma、攻角为8°时弹丸的静稳定储备量为6.13%。通过6D弹道仿真求得该弹道修正引信的修正能力,最大修正量可达到400 m。本文的研究结果将为后续深入开展迫击炮弹二维弹道修正引信提供参考。
[1] 赵金强,龙飞,孙航.弹道修正弹综述[J].制导与引信,2005(4):1-2.
[2] 刘旭东.旋转稳定弹二维弹道修正技术[D].北京:北京理工大学,2016.
[3] 陈杰春,丁振良,袁峰,等.MEMS惯性测量组合初始标定方法研究[J].南京理工大学学报(自然科学版),2008(3):1-2.
[4] CHANG Sijiang,WANG Zhongyuan,LIU Tiezheng.Analysis of Spin-Rate Property for Dual-Spin-Stabilized Projectiles with Canards[J].Journal of Spacecraft and Rockets,2014,51(3).
[5] JUBARAJ S,KAREN R.Heavey,Richard Buretta.Numerical Computations of Transonic Flow Over a Course Corrected Spinning Projectile[C]//26th AIAA Applied Aerodynamics Conference.Hawaii: American Institute of Aeronautics and Astronautics,2008(6740):18-21.
[6] JAMES D.Effects of Base Shape on Spin-Stabilized Projectile Aerodynamics[C]//26th AIAA Applied Aerodynamics Conference.Hawaii: American Institute of Aeronautics and Astronautics,2008(6738):18-21.
[7] JAMES D,KAREN R.Heavey,CFD Computation of Magnus Moment and Roll Damping Moment of a Spinning Projectile[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Rhode Island:American Institute of Aeronautics and Astronautics,2004:1-3.
[8] 任波,杨博.基于可变弹翼迫击炮弹的制导方法研究[J].成组技术与生产现代化,2014(4):1-6.
[9] 许立松,闻泉,王雨时,等.迫击炮弹引信精确制导组件气动外形优化[J].探测与控制学报,2019(3):2-8.
[10] 沈皓敏,杨新民.翼型参数对某弹道修正迫弹气动特性的影响[J].弹道学报,2017,29(3):1-6.
[11] 韩子鹏.弹箭外弹道学[M],北京:北京理工大学出版社,2008:127-143.
[12] 丁源,吴继华.ANSYS CFX14.0从入门到精通[M].北京:清华大学出版社,2013:189-201.