弹药作为一次性消耗产品,其可靠性试验是破坏性的,每次试验只能抽取少量的样品进行小样本试验。因此在对弹药系统进行故障分析及可靠性评估时,往往因为缺少足够的试验数据,使得分析具有较大的不确定性,对故障发生概率估计不足,分析决策结果缺乏较高的可信性。
故障树作为常用的弹药系统可靠性、安全性分析模型,其优点在于能够简洁直观地对弹药系统内故障进行定位,但由于其自身对事件状态假设为二态性以及故障逻辑关系的不确定性,故障树分析法对弹药系统的不确定性分析能力存在不足[1]。而贝叶斯网络模型有着充分的概率论基础,并且具有双向推断的能力,相较于其他分析方法,贝叶斯网络在信息的多元性表达和不确定性问题的处理方面具有诸多优势。近年来,贝叶斯网络在故障分析领域中的应用不断深入,其模型可集故障检测、推理和决策于一体[2]。
通过比较分析可以得出,经典故障树分析与贝叶斯网络具有先天的相似性,能够实现优势互补,采用贝叶斯网络方法来描述系统的故障模式与故障原因之间的关系,能够更加深刻地揭示系统发生故障的前因后果[3]。本文以弹药故障树分析为基础,根据故障树与贝叶斯网络结构上存在相似的内在关系,从图形结构与数值概率两方面将故障树向贝叶斯网络进行转化,得到故障贝叶斯网络模型。并在缺乏足够先验试验数据的情况下,利用专家经验和模糊评判推理方法进行故障检测,很好地弥补了传统可靠性分析方法的不足,大大提高了方法的准确性。
1 故障树分析法
故障树分析法(Fault Tree Analysis,FTA)就是在系统设计过程中,通过对可能造成系统故障的各种因素(包括硬件、软件、环境、人为因素等)进行分析,画出逻辑框图,从而确定系统故障原因的各种可能组合及其发生概率,以便采取相应的纠正措施,提高系统可靠性的一种设计分析方法[4]。
故障树的建造是FTA法的关键,故障树建造的完善程度将直接影响定性分析和定量计算结果的准确性。在建立故障树时,一般将人们最不希望发生的显著影响系统技术性能、经济性、可靠性和安全性的故障事件作为顶事件,置于故障树的顶端。然后在充分熟悉分析对象及其资料的基础上,对有可能导致该故障顶事件发生的各种可能的其他故障事件以树状分支的形式进行不断细分并体现其逻辑关系,做到既不遗漏又分清主次地将全部重大故障事件一一列举,将最后不能再细分的故障事件作为底事件,底事件与顶事件之间的所有故障事件均称作中间事件。
2 故障树向贝叶斯网络的转化
2.1 贝叶斯网络概述
贝叶斯网络(Bayesian Network,BN)是概率论与图论结合的产物,是可以计算的概率模型,表现形式是一种由节点和有向边组成的有向无环图(Directed Acyclic Graph,DAG)。其中,随机变量用节点表示,变量之间的因果关系通过有向边反映。通过贝叶斯网络,可以利用各种来源的数据,用概率来表示各种形式变量的不确定性,对这些数据进行综合的推理,同时也可以根据概率规则来实现网络的推理和学习。设V={V1,…,Vn}为离散变量的有限集合,其贝叶斯网络由以下两部分组成[5]:
1)用G(V,E)表示该有向无环图,其节点集V={V1,…,Vn}中的元素表示节点变量,变量可以是对任何对象的抽象,如部件状态、环境因素等。E表示节点间的有向边(Vi,Vj),Vj称为Vi的父节点,Vi称为Vj的子节点,描述了变量之间的因果关系;
2)P为V中变量的联合概率分布,在贝叶斯网络中表示与每个节点相关的条件概率分布表(Conditional Probability Table,CPT)。由贝叶斯网络的条件独立性假设可知,节点条件概率分布可以用P(Vi|pa(Vi))来表述。
对于已有历史数据的节点,采取依据历史数据的方法,根据历史数据中近些年来根节点发生故障的次数,计算其故障发生频率,即为根节点发生故障概率;对于历史数据残缺或没有历史数据的根节点,采取专家经验的方法,主要根据专家经验给出,将专家的语言变量进行模糊化处理,得到精确概率[6]。通过上述方法获得模型的先验概率。而对于条件概率的得到,则是由节点的逻辑关系,如事故树的逻辑门一样,由概率表的形式给出,对于具体的系统应该具体分析。
2.2 故障树向贝叶斯网络转化
故障树转化法是通过对故障树分析将其各事件环节的故障树转换为贝叶斯网络,并组合成最终所确定的贝叶斯网络拓扑结构图的一种方法,具有更好的逻辑性和直观性。从贝叶斯网络的构造原理可以看出,贝叶斯网络的两大组成要素分别为节点与有向边,可分别对应故障树中的故障事件和逻辑门。
根据建立BN的一般步骤,可以得出建立故障贝叶斯网络(Fault Bayesian Network,FBN)模型的过程如下[7]:
1)将弹药故障树中的事件对应表达为贝叶斯网络中的节点,底事件对应贝叶斯网络的父节点,中间事件及顶事件对应贝叶斯网络的子节点,若在弹药故障树中出现多次相同的底事件,则在贝叶斯网络中可将其合并为一个父节点。各节点状态对应事件状态,采用多态变量进行描述。
2)将弹药故障树中各基本事件的先验概率值作为贝叶斯网络中对应根节点的先验概率进行赋值。
3)将弹药故障树中的逻辑门对应表达为贝叶斯网络中的有向边概率分布,根据逻辑门表达的逻辑关系列出相应的CPT,对于中间事件及顶事件的条件概率进行赋值。
4)依照弹药故障树中各事件之间的逻辑关系对贝叶斯网络中的各个节点进行连接。
2.3 结合模糊评判的贝叶斯网络判别方法
模糊综合评判法是根据模糊数学和最大隶属度原则,将某些非随机不确定性的因素进行综合分析的一种评估方法。结合模糊评判的故障贝叶斯网络检测方法是利用故障贝叶斯网络对研究对象进行检测得到后验概率的检测结果后,再结合专家对各个故障发生后果的影响程度进行综合评判而建立的判别方法。该方法不仅具有贝叶斯网络处理不确定性问题的优势,而且结合了多因素影响的综合评判,使得利用贝叶斯网络进行故障检测更具科学性、合理性。
将经过贝叶斯网络对系统的检测后得到各元部件发生故障的后验概率的精确值记为qi,并结合各因素进行模糊综合评判。评判的一般步骤为[8]:1)确定因素集U={U1,U2,…,Un};2)建立评判集V={V1,V2,…,Vm};3)确定权重向量W={W1,W2,…,Wn};4)构造模糊评价矩阵R=(rij)n×m;5)依据模糊运算B=W·R,并根据最大隶属度原则进行综合评判。最终得到检测效果的综合值,从而可以得到结合概率的模糊综合故障重要度,利用贝叶斯网络还可以通过重要度分析可以得出影响弹药系统可靠性的薄弱环节;根据故障重要度的大小,可以为确定维修顺序、优化维修模型、优化试验项目模型提供依据。结合概率的故障重要度评判值Di,表达式为[9]:
(1)
式(1)中:di为第i个部件的模糊综合评判权重值;qi为通过贝叶斯网络检测得到的第i个部件的后验概率;n为危害度等级,![]() 为第i个部件第n等级的模糊评判。
为第i个部件第n等级的模糊评判。
3 弹药系统失效检测与分析
下面以某型防暴闪光弹为例,处于贮存状态的闪光弹弹药虽不工作,但要受到环境应力的作用,使弹药的各种元件发生腐蚀、老化、分解等变质现象,致使弹药的性能退化,可靠度降低,以致弹药不能完成其规定的功能而失效,轻则影响战斗任务的完成,重则引起安全事故,甚至造成人员伤亡,故应引起高度重视。
3.1 建立故障树模型
本文研究的闪光弹可视为由战斗部和药筒两个结构、功能相对独立的子系统,战斗部主要包括上下弹壳、爆震药柱、扩爆药柱、调整垫、套管、延期雷管等组成,药筒部件结构由高压室(药筒)、低压室(药筒)、药盂、底火等零部件组成,发射药盛装在高压室里[10]。
其作用原理为:发射时,当枪的击针击发底火后,底火喷出的火焰点燃发射药,产生高温高压的火焰气体瞬间冲破药盂,并从高压室六个排气孔泄出后进入低压室。进入低压室的火焰气体推动弹丸前,同时点燃延期雷管合件,飞行达到规定的延期时间,雷管作用,起爆扩爆药,然后主装药被起爆,该弹正常作用。
通过对本产品结构特点及作用原理的分析,根据其寿命剖面,主要收集该产品在贮存、使用以及进行可靠性试验的过程中曾出现的失效现象和同类产品发生过的质量问题,同时借鉴和参考相关技术资料,总结出该型防暴闪光弹的失效模式为:
{近弹、膛炸、留膛、早炸、半爆、战斗部解体、瞎火、75 m立靶密集度不合格、配套性差、储存性差}。
根据以上确定的顶事件,对每个顶事件进行详细的原因分析。以“留膛”这一失效模式为例,画出顶事件A为“留膛”的故障树如图1所示。底火失效、发射药受潮失效、发射药药量少、药室制作工艺缺陷为四个失效底事件,分别记作X1、X2、X3、X4。任意一个失效模式的发生均有可能导致留膛的发生。
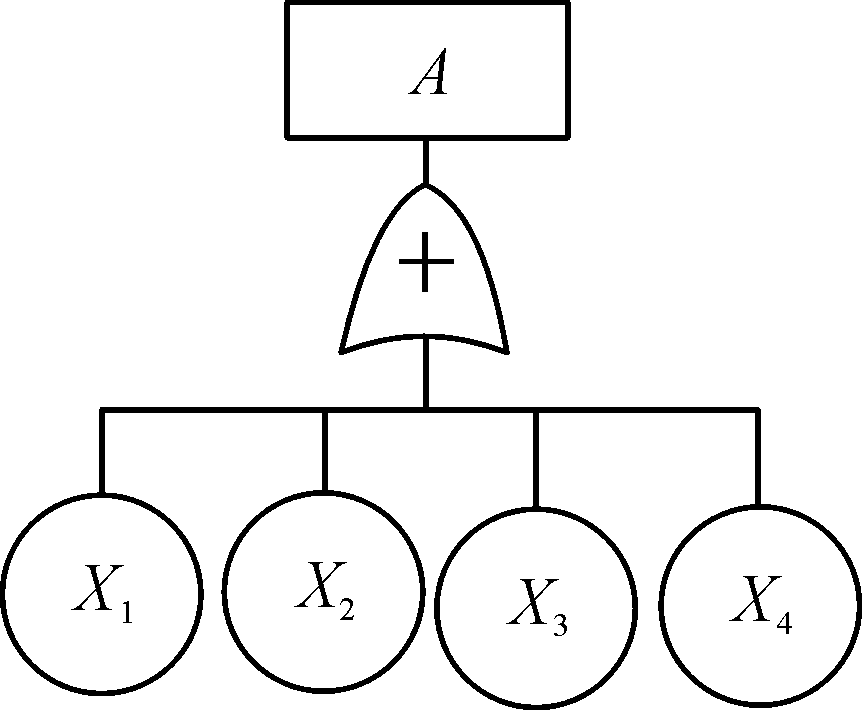
图1 “留膛”顶事件的故障树
3.2 由故障树向贝叶斯网络转换
根据2.2节中的转化步骤将故障树转换为贝叶斯网络,得到贝叶斯网络结构如图2所示,并进行可靠性分析。
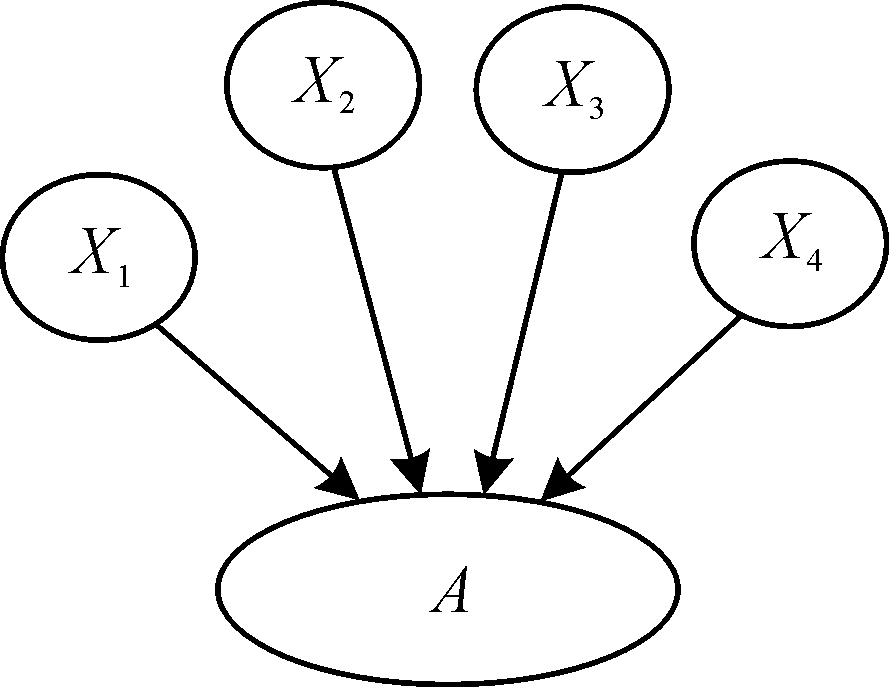
图2 “留膛”顶事件的贝叶斯网络表示
基于历史数据与专家经验得到贝叶斯网络根节点先验概率如表1所示。
表1 根节点先验概率

节点X1X2X3X4先验概率0.250.400.420.12
当任一根节点发生失效时,即发生“留膛”这一失效模式,因此条件概率表不再赘述列出表格。利用贝叶斯网络进行诊断,当发生留膛失效模式时,得到各根节点的后验发生概率值如表2所示。
表2 根节点后验概率

节点X1X2X3X4后验概率0.320.510.590.15
通过贝叶斯网络的检测结果可以得到:当发生留膛这一故障模式时,可能引起该故障发生的各故障底事件发生概率大小顺序为:
X3>X2>X1>X4
3.3 结合贝叶斯网络的模糊综合评判
依据重要因素筛选原则,建立基本因素集U={U1,U2,…,U4},分别对应4个失效模式底事件:其中U1为底火失效,U2为发射药受潮失效,U3为发射药药量少,U4为药室制作工艺缺陷。建立评判集V={V1,V2,…,V4},其中V1为影响极小,V2为影响较小,V3为影响较大,V4为影响极大。为准确反映各因素影响程度,我们请四位弹药方面的专家组成了专家组,依据其知识和经验对因素集中的各因素进行了打分,经处理,对应评判集结果如表3所示。
表3 专家评判结果

U1U2U3U4专家1V1V3V3V1专家2V2V3V3V1专家3V1V4V2V1专家4V2V4V3V1
隶属度矩阵为:

依据“德尔菲法”的基本原理,继续让四位专家以独立填表选取权数的形式给出权重集,将专家各自选取的权数进行整理和统计分析,最后确定出各因素、各指标的权数。集合了各方面专家的智慧和意见,并运用数理统计的方法进行检验和修正。得到专家给出的权重集为:
以X1为例,其模糊综合评判为:![]() 通过贝叶斯网络得出X1的后验概率q1=0.32,模糊评判结果为:根据式(1),得到X1结合贝叶斯网络的综合评判
通过贝叶斯网络得出X1的后验概率q1=0.32,模糊评判结果为:根据式(1),得到X1结合贝叶斯网络的综合评判![]() 同理可得,D2=1.239,D3=0.982,D4=0.323。
同理可得,D2=1.239,D3=0.982,D4=0.323。
经过比较可以得出,在结合专家经验评判的情况下,故障模式的故障重要度大小顺序为:
X2>X3>X1>X4
因此,即使在上一节贝叶斯网络检测的结果表明发射药药量少X3的发生概率高于其他底事件,需要最先进行检查与解决。但在此基础上结合模糊综合评判,并结合了专家经验评价后,通过比较可以发现,发射药受潮失效X2的故障重要度更高,X2才是弹药发生留膛这一失效模式的最主要原因。而在实际情况中,导致弹药失效最主要的因素正是在贮存或使用过程中,弹药受湿度这一环境应力影响,发射药受潮吸湿,经吸附、凝露和渗透等作用使得发射药内部化学成分质量逐渐变坏,导致发射药受潮,弹药发生失效。
通过两种方法对比,模糊综合评判的贝叶斯网络分析方法能够对弹药进行全面的分析,更符合实际过程中对于可靠性分析的要求,使分析更有效、更具实用性与经济性。
4 结论
利用故障树与贝叶斯网络结构上存在相似的内在关系且能够优势互补的因素,从图形结构与数值概率两方面将故障树向贝叶斯网络转化,建立了一种优化的弹药系统可靠性分析模型,利用专家经验和模糊评判推理方法进行故障检测,解决了不确定信息的干扰问题,改变了弹药系统故障状态概率值可信性较低的局限性,提高了方法的准确性。以通过该方法分析出系统中节点结合概率的模糊综合故障重要度,确定维修顺序、优化维修模型、优化试验项目模型。
[1] 刘芳,王宏伟,宫华,等.基于改进ACO-BP算法的弹药贮存可靠性评估[J].兵器装备工程学报,2019(4):177-181.
[2] 刘文博,梁敏,张欧亚,等.基于贝叶斯网络的侦察威胁等级评估研究[J].火力与指挥控制,2019,44(3):72-76.
[3] 刘江,姚安东,王攀,等.新型弹药可靠性评估方法[J].兵工自动化,2014,33(5):1-3.
[4] 甘茂治,康建设,高崎.军用装备维修工程学[M].2版.北京;国防工业出版社,2005.
[5] LIU Z,LIU Y,SHAN H,et al.A Fault Diagnosis Methodology for Gear Pump Based on EEMD and Bayesian Network[J].Plos One,2015,10(5):e0125703.
[6] 邱玮,张增磊,田文祥,等.基于层次分析法和模糊综合评判的装备保障人员能力评估[J].兵器装备工程学报,2018,39(4):108-113.
[7] 赵晶晶.基于模糊贝叶斯网络的故障诊断方法研究及其在列控系统中的应用[D].北京:北京交通大学,2013.
[8] 吴景泰,王莲莲.基于FMECA模糊贝叶斯网络的无人机起落架可靠性分析[J].沈阳航空航天大学学报,2018,35(6):90-96.
[9] 马德仲,任锁,刘凯辛,等.贝叶斯网络和模糊评判结合的滚动轴承故障诊断[J].哈尔滨理工大学学报,2018,23(5):113-118.
[10] 李明伦,李东阳,郑波.弹药储存可靠性[M].北京:国防工业出版社,1997.