目前无人机技术已经得到了极大的发展，并在军事、民用等多个领域得到了广泛的应用，发挥着不可替代的作用[1-2]。然而，随着军事对抗程度越来越激烈，民用领域的多样化需求不断提高，单架无人机越来越难以满足实际的需求。在2017年6月19日的巴黎航展上，美国克瑞托斯公司展出XQ-222“女武神”和UTAP-22“灰鲭鲨”两款无人机[3-4]，标志着美国空军2015年提出“忠诚僚机”研制项目进入新的阶段[5-8]。在美国之后，欧盟、日本也提出了相似的发展规划[9-10]。随着美国新一代隐身战机F-35的服役，以F-35为核心的网络中心战作战体系构造完成，有人机/无人机协同编队执行侦察、打击和空战的时代已经来临[11-12]。随着无人机编队飞行的价值被普遍认同，中国、美国[13]、英国[14]、法国[15]等相继推出了无人机编队飞行验证、演示项目，以及无人机编队协同作战方面的研究。近年来，在无人机编队的基础上，更是发展出了“蜂群作战”理论[16-17]。该作战理论的出现对传统作战形式提出了极大的挑战。
与单架无人机相比，多架无人机编队飞行进行协同侦察、协同作战等任务的成功率大为提高。综合来看，无人机编队飞行具有以下优势：扩大视野，增加搜索和侦察范围，提高情报的可靠性和实效性；提高定位精度，多角度成像，为任务功能扩展提供可能；发挥协同优势，提高整体效率；提高高风险任务的成功率和可靠性。
无人机编队飞行面临着复杂的任务环境、编队间的非线性和耦合特性等。这种复杂的对象系统，单一性能指标最优并不能满足带来满意的控制效果。例如，响应特性最优控制器往往稳定性和鲁棒性较差；鲁棒性最优的控制器操作性能和动态特性往往不能令人满意。因此，编队飞行更加需要一种各项指标都能满足需求的控制器。
为了解决该问题，本文在深入分析无人机编队控制需求的基础上，提出了一种满足多种性能指标约束的控制器设计方法。
1 无人机编队飞行运动模型及控制需求分析
1.1 无人机二阶自动驾驶仪模型
为了精确反映编队飞行无人机的飞行品质，考虑到控制延迟带来的影响，本文采用二阶无人机自动驾驶仪模型：
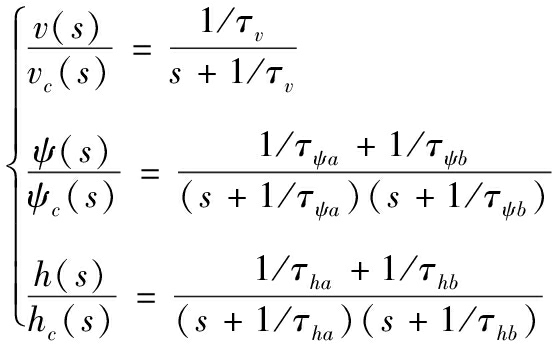
(1)
式中：v、ψ、h分别为无人机速度、航向和高度；τv、τψa、τψb、τha、τhb分别为3个通道上的时间常数。
该二阶自动驾驶仪模型相较于一阶自动驾驶仪模型不仅使得航向和高度相应明显得到改善，而且比在用大时间常数的一阶自动驾驶仪模型的响应更精确。在实际应用中，假定编队中的长机和僚机具有相同的飞行品质，即可采用相同的二阶自动驾驶仪模型。为了设计方便，该模型可表示成以下微分形式：
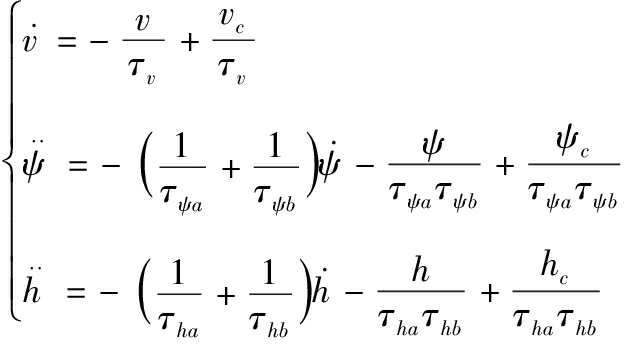
(2)
1.2 无人机编队运动模型
由式(2)可知，长机的自动驾驶仪模型课表示为
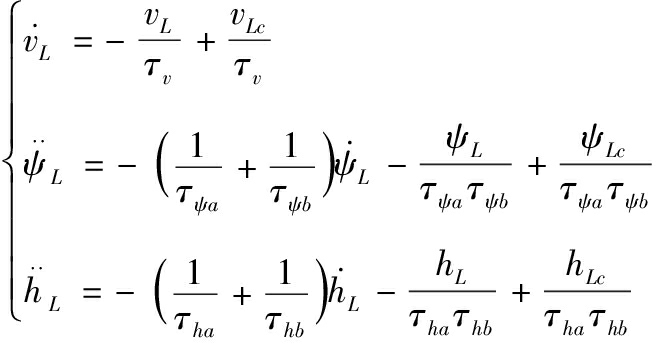
(3)
在无人机松散编队飞行时，编队间的气动藕合效应可以忽略不计。然而，随着各国防空体系日渐完善、任务环境越来越复杂，松散编队飞行已经很难满足任务需求。因此，紧密编队成为研究的热点。在进行紧密编队研究时，长机尾流对僚机的耦合影响就不得不考虑。
长机尾流对僚机的耦合主要表现为对僚机的上洗流引起的上洗力。该上洗力会引起僚机迎角的变化，进而导致升力、阻力向量的旋转和大小改变。根据耦合因素产生的根源，其影响课表示为僚机升力L、阻力D、侧力Y的改变。
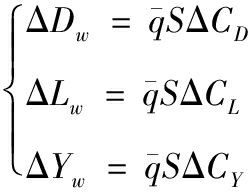
(4)
式中：
为东压；S为机翼面积。
另外，长机和僚机间的相对距离也是决定着编队间耦合效应影响的关键因素之一。因此，在考虑耦合因素影响下，对僚机的自动驾驶仪模型做如下修正：
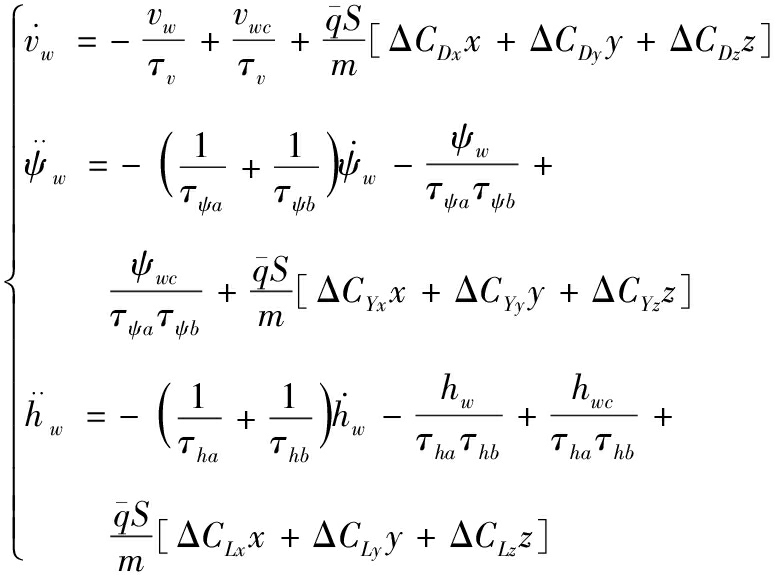
(5)
式中：x,y,z是编队间隔相对额定间隔x0,y0,z0的扰动量。
另外，长机和僚机间的相对运动学方程可表示为
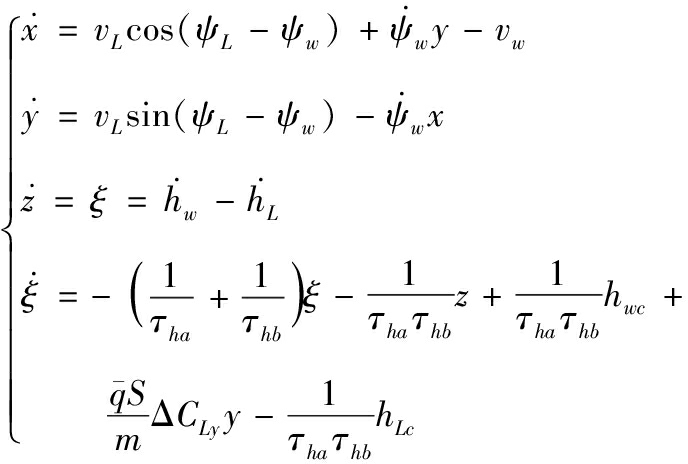
(6)
对于式(3)、式(5)、式(6),可得如下线性化方程：
(7)
式中：
U=[vwc ψwc hwc vL ψL hLc]T
w为随机扰动，代表编队所受到的外界扰动以及编队线性化带来的影响项。
1.3 控制需求分析
从上面的建模过程可知，无人机紧密编队飞行的运动模型主要长机的自动驾驶仪模型(式3)、僚机的自动驾驶模型(式5)和长机和僚机间的相对运动学模型(式6)组成。从式(5)、式(6)可知：长机的下洗流会对僚机以及整个编队的保持产生重大的影响。因此，在编队控制过程中，如何有效消除编队间气动耦合带来的影响至关重要。另外，为了更好的适应任务需求，编队整体应具有一定的机动能力。这就要求编队整体具有一定的稳定性、快速响应、航路精确跟踪的能力。然而，由于受到编队个体无人机机动能力的限制，编队整体的机动能力不可能超过个体无人机的机动能力。同时，编队飞行过程中，各种扰动和外界干扰也会对无人机编队飞行产生影响，从而影响编队飞行稳定和航迹跟踪精度。所以，对控制器的鲁棒性也有较高的要求。
因此，对于无人机编队控制来说，对控制器的要求包括稳定性、快速响应、稳态误差小，以及较强的鲁棒性。这些指标之间同时满足并不容易，甚至各个指标间的要求是相互矛盾的。对于这种情况，追求单一性能指标最优并没有意义。因此，本文在设计编队控制器时，并不强调这些中某一性能指标的最优，而是强调所有性能指标都能满足编队飞行性能需求。
2 多性能控制器设计方法
2.1 性能指标的数学表达
对于线性系统模型可表示成如下形式：
(8)
在满足各种指标需求的控制理论思想指导下，对于带有控制器的闭环系统，建立满足各种系统性能指标需求的约束条件。以系统(8)为例，其带有状态反馈的闭环系统为
(9)
式中：K为状态反馈控制器参数。
该闭环控制系统各项指标以及数学约束如下：
1)极点指标
该指标主要体现系统的稳定性要求和快速响应要求。该指标约束要求闭环系统的极点位于左半复平面区域Ω={s∈C∶Re(s)≤-α}(α>0)。该指标约束可用方程表示为[10]
(A+BK+αI)TP0+P0(A+BK+αI)<0
P0>0
(10)
2)方差指标
方差指标是系统无稳态误差需求的体现。在数学上，该指标为闭环系统的稳态协方差矩阵E满足diag(E)≤σ2。该指标约束可用方程表示为：
(A+BK)TP1+P1(A+BK)+DWDT<0
P1=diag(σ2)
(11)
3)H∞指标
H∞指标是系统鲁棒性的要求。在数学上，该指标是指对于给定的正数γ，闭环系统的传递函数矩阵H(s)满足‖H(s)‖≤γ。该指标约束可用方程表示为
(A+BK)TP2+P2(A+BK)+γ-2P2CTCP2+DDT<0
P2>0
(12)
设计满足各种需求的控制器，就是求解有式(10)～(12)所确定的线性不等式方程组。
2.2 基于增广系统的控制器设计
2.2.1 控制器设计
由式(8)可知，无人机编队飞行线性连续时不变系统可表示为
(13)
式中：ω为随机扰动，是均值为零的高斯白噪声，其强度为W>0；A、B、C、D为适维矩阵。
对于式(13)所确定的系统，在控制输入点之前引入积分环节构建增广系统可得：
(14)
式中：
设增广系统的状态反馈为
uz=Kz
(15)
令
(16)
则可得原系统(8)的PI形式的控制器：
uPI=K3x+K4
x(τ)dτ
(17)
式中：K3=K2(BTB)-1BT, K4=K1-K2(BTB)-1BTA
通过式(14)所建立的增广系统，和上节所确立的性能约束条件，通过求解多维线性矩阵不等式组，则可以得到系统(13)类似传统PI控制器的满足多性能要求的控制器[18]。
2.2.2 控制器存在性条件
从上节的设计过程可知，多性能控制器设计最后归结为求解三个线性矩阵不等式。但是，这里面临着一个问题：是否存在这样的反馈控制参数K，使得闭环系统满足这些线性矩阵不等式的约束？
为了回答该问题，本文做如下证明。令X=A+BK为要求解的矩阵，对以上指标约束方程在形式上做简单变形，都可以表示成以下统一的形式：
XG+GTXT+Q<0
(18)
下面以确定该线性矩阵不等式方程的可解性条件，从而判断两种控制器可解空间的大小。为了给出线性矩阵不等式(18)式具有可行解的条件，先给出下面的投影定理。
投影定理：给定矩阵
线性矩阵不等式：
(19)
可行的充分必要条件是
是矩阵E的直交互补空间。
对式(13)中的矩阵E和F进行满秩分解，可表示为E=ELER，F=FLFR。令Y=ERXFL，则Y满足
对式(19)左乘
右乘
其中，
为EL的Moore-Penrose逆。则式(19)等价于：
(20)
由Schur补引理，式(20)等价于：
(21a)
(21b)
其中：
当式(21a)成立时，有W≥0。当且仅当
时，W=0；当W=0时，式(21b)退化为式(18)XG+GTXT+Q<0。
由投影定理可知，式(18)具有可行解的条件是：
GT⊥QGT⊥T>0
(22)
因此，可以得到如下结论：
定理1： 线性矩阵不等式XG+GTXT+Q<0可行的充分必要条件为：
GT⊥QGT⊥T>0 XG+GTXT+Q<0
(23)
3 无人机编队飞行控制器设计
3.1 无人机编队控制策略分析
对于无人机编队飞行来说，长机的飞行完全独立于僚机，而且长机的自动驾驶仪发出整个编队的飞行指令，同时，单架僚机的控制指令来源于编队控制器根据长机飞行指令所计算得到的飞行指令。因此，无人机编队飞行控制器的整体结构如图1所示。
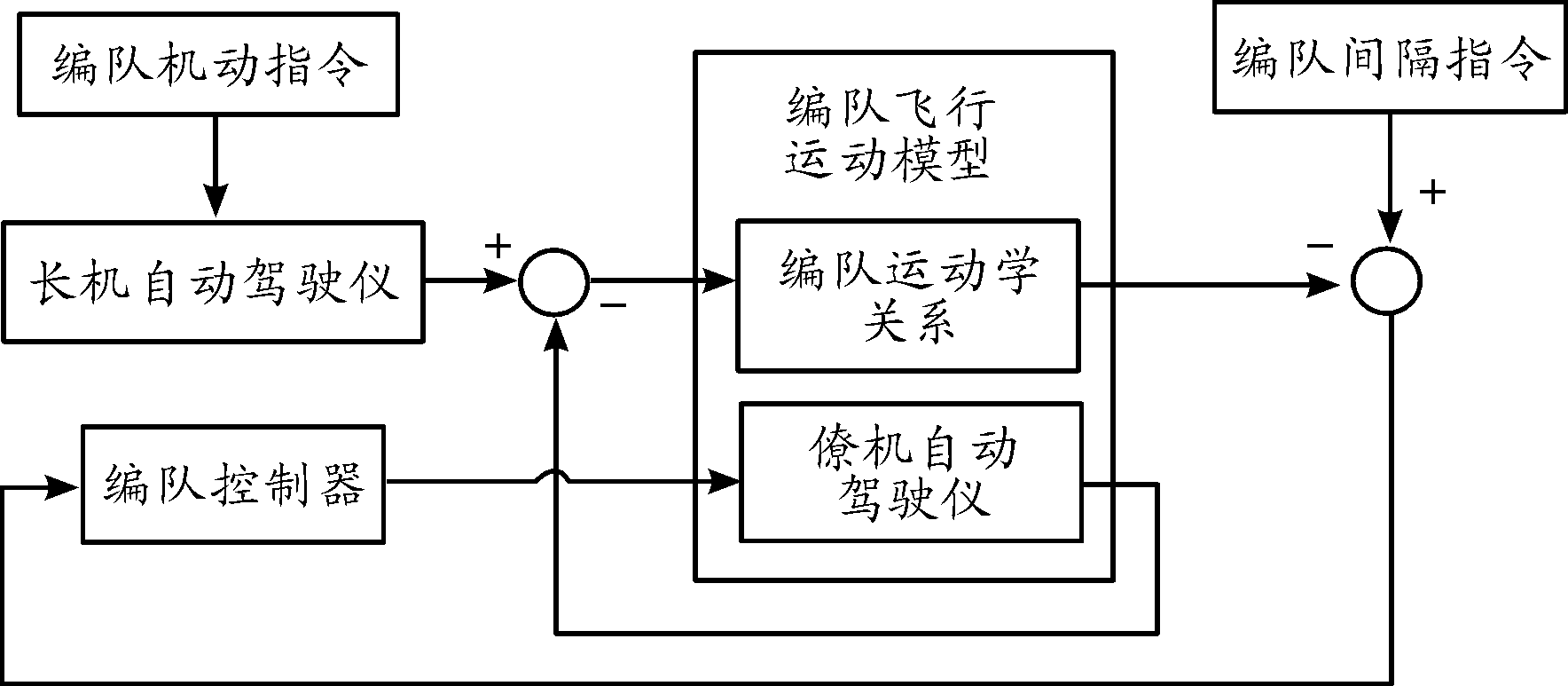
图1 无人机编队飞行控制结构
从前面建立的无人机编队飞行运动模型式(7)可知，该模型为7阶的运动模型。对于该7阶的运动模型，采用上节所介绍的多性能控制器设计方法不仅很难满足控制器存在的条件。这就大大降低了该方法的普适性。而且即使满足了该存在性条件，控制器设计过程中的计算量也是惊人的。因此，有必要对该运动模型做进一步的处理。
3.2 无人机编队模型解耦处理
从无人机编队飞行运动模型式(3)、式(5)、式(6)以及基于该运动模型所得到的线性化模型式(7)可知，编队运动的高度Z通道和纵向X通道间是不存在耦合影响，既是完全解耦的。而且侧向Y通道与纵向X通道间的耦合也不严重，进近发生在纵向X通道的航向角速率之间。这种运动模型自然的解耦关系，就为控制器设计的简化提供了基础。
根据无人机编队运动自然的结构关系，可以把无人机的运动按照如下方式划分为三组：
(24)
根据该解耦关系，无人机编队飞行侧向Y通道的运动模型可表示为
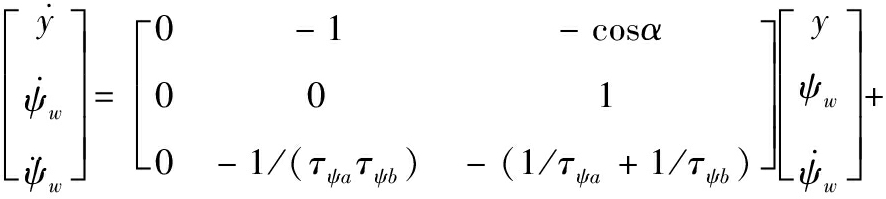
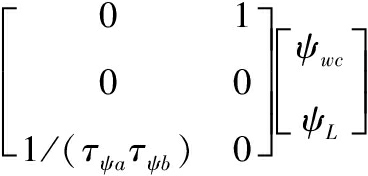
(25)
对于侧向Y通道的控制，其目的主要是使系统能精确的跟踪长机发出的航向角指令，并按照编队间距要求保持僚机参考系中y方向间距不变。
由于高度Z通道完全解耦，则解耦的度Z通道运动模型可表示为：
(26)
对于高度Z通道的控制，其目的主要是按照编队高度间距要求保持僚机参考系中z方向间距不变。
纵向X通道相对比较麻烦，其存在两个干扰项：长机速度vL和由于航向改变Y通道和X通道间的耦合项
对于该情况，结合前面章节建立的运动方程，纵向X通道运动模型可表示为
(27)
对于纵向X通道的控制，其目的主要是使系统能精确的跟踪长机发出的速度指令，并按照编队间距要求保持在僚机参考系中x方向间距不变。
根据该解耦方法，可以应用前面章节所介绍的多性能控制器设计方法，首先对侧向Y通道和高度Z通道进行控制器设计。然后根据设计结果，将控制器加入到编队系统之后再对纵向X通道进行设计。这样既可以考证控制器的存在性，又可以降低控制器设计过程中的难度。
4 仿真验证
无人机编队飞行，僚机主要跟踪长机的航向、速度和高度指令，从而实现跟随长机进行机动的编队飞行目标，并在机动过程中保持编队间隔不变。根据图1所示的控制结构，以及上文所介绍的编队控制器设计方法，对无人机编队飞行控制效果进行仿真验证。编队初始飞行条件为：航向角ψ0=0°，飞行高度h0=900 m，编队速度v0=135 m/s；编队间隔分别为x0=18 m，y0=7 m，z0=0 m。在该初始编队飞行条件下，编队采取航向角ψc=20°机动指令，采用本文设计方法得到的控制器控制效果如图2、图3所示。
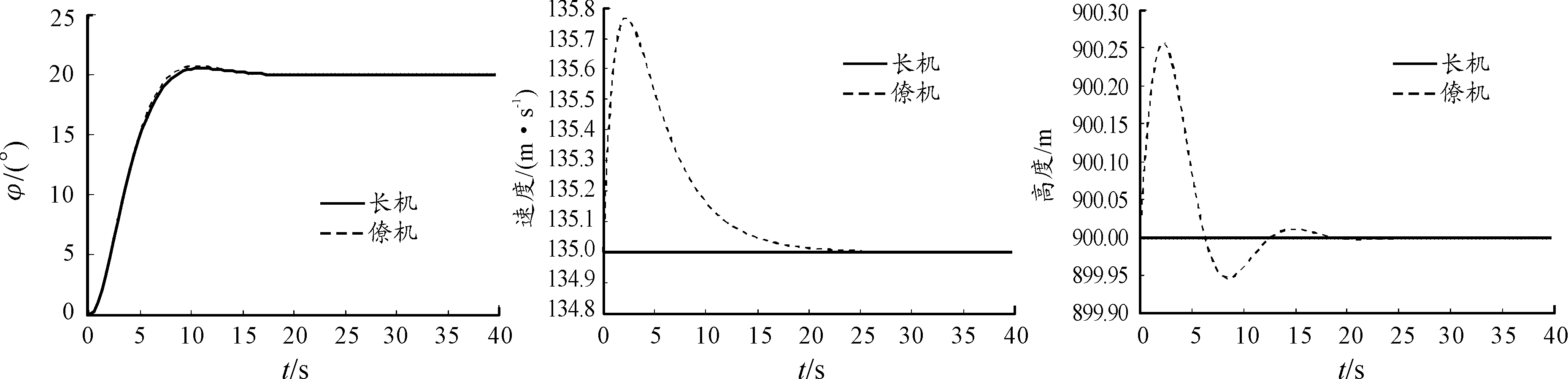
图2 机动时编队姿态响应
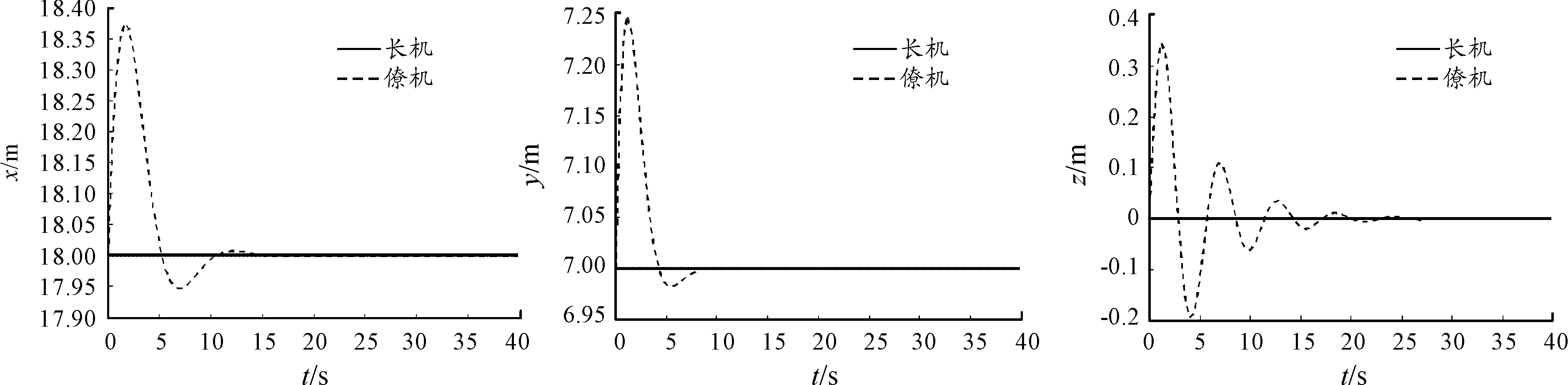
图3 机动飞行时编队间隔变化
从仿真结果可知：编队僚机迅速跟上了长机的航向角机动指令，并且无误差。在航向角机动过程中，编队中僚机的速度偏差仅为0.77 m/s,高度偏差仅为0.26 m。在机动过程中，编队的间隔保持良好，最大航向距离偏差为0.37 m，最大侧向偏差为0.25 m。僚机的高度误差出现轻微震荡，但最终得到了消除。高度间隔的震荡主要是由编队间非线性耦合所引起的。从仿真可知，本文所提方法设计得到的无人机编队控制器具有较好的效果。
5 结论
建立了无人机编队飞行动力学模型；针对编队飞行多性能指标约束的实际需求，提出一种满足多性能需求的控制器设计方法，并证明了该设计方法控制器存在的条件；针对无人机编队飞行控制器设计控制器参数存在性问题和设计过程复杂等问题，提出了编队运动方程解耦方法并提出了单通道设计的思路。对无人机编队航向机动非线性仿真表明，该控制方法是有效的。
[1] 周健,龚春林,谷良贤.非匹配不确定性条件下的编队分布式协同控制[J].系统工程与电子技术,2019,41(3):636-642.
[2] 岳源,屈高敏.分布式多无人机协同侦察目标分配研究[J].兵器装备工程学报,2018,39(3):57-62.
[3] 惠凯.巴黎航展:无人机阵容异军突起[R].中国航天报,2017-07-01.
[4] 张乃千.出击吧!我的“无人僚机”[N].解放军报,2017-06-23.
[5] 王宇.美空军提出无人机“忠诚僚机”概念[J].防务视点,2015，10(6)：6-10.
[6] 郑大壮.“忠诚僚机”概念将大幅提升有人/无人机协同作战能力[J].防务视点,2016(6):63-63.
[7] 温杰.忠诚僚机——美国空军验证有人/无人编队技术[J].航空世界,2017(7):9.
[8] 温杰.“战隼”变“飞镖” 美国空军“忠诚的僚机”作战概念[J].兵器知识,2016,9(7):36-39.
[9] 李洪兴.日本的无人僚机计划[J].现代军事,2016,11(4):16-17.
[10] 张珂.日本启动无人僚机发展计划[J].防务视点,2016,12(6):58-59.
[11] 刘飞.F-35的无人机僚机编队[J].现代军事,2017,9(5):8-10.
[12] 袁政英.F-35战斗机或将采用人工智能控制无人僚机作战[J].防务视点,2017,8(5):60-61.
[13] 徐秉君.未来空战主角——X-47B隐形无人战机[J].科技创新与品牌,2013,6(7):64-67.
[14] 周军,车易.英国雷神无人机将进行第三阶段飞行试验[J].飞航导弹,2015,12(9):1-2.
[15] 张翼麟,王一琳.达索航空公司完成神经元无人机与有人机编队飞行[J].飞航导弹,2014,6(5):11-15.
[16] 燕清锋,肖宇波,杨建明.美军无人机蜂群作战探析[J].飞航导弹,2017,12(10):49-53.
[17] 陈方舟,黄靖皓,赵阳辉.美军无人“蜂群”作战技术发展分析[J].装备学院学报,2016,27(2):34-37.
[18] 张艳红,杨启贵.具有唯一平衡点的四维超混沌Lü like系统的研究[J].重庆工商大学学报(自然科学版),2017,34(3):49-55.