在岛岸强杂波背景下,打击岛岸附近目标过程中,反舰导弹末制导雷达对岛岸附近弱小目标准确的检测和跟踪显得尤为重要。与远海作战不同,反舰导弹对近岸目标检测和跟踪的难度更大,主要有以下两点:一是岛岸复杂背景下目标信噪比低;二是岛岸附近目标杂糅。
检测前跟踪(track-before-detect,TBD)是一种在低信噪比下检测跟踪小目标的方法,能够有助于解决对岛岸附近弱小目标检测跟踪的问题。它利用多帧扫描将每次扫描的能量点沿着可能的航迹进行累计,最后同时宣布检测结果和目标航迹[1]。DP-TBD算法最早由BarnivY.提出,后由Kramer和Wallance应用在雷达对弱小目标的检测和跟踪上[2-4]。传统的DP-TBD算法,在进行多帧累计时,能量扩散严重,易造成“团聚效应”,不适用于信噪比过低的情况,且检测门限值的设置复杂困难,计算量巨大,伪迹数量过多,实时性不强[5-7]。针对以上问题,现有可查阅的文献主要从改进动态规划算法,以及设计门限值等方面来解决传统算法的不足。文献[8]中提出了一种既适用于常规机动目标又适用于弱机动目标的动态规划检测前跟踪算法,提高了目标的状态搜索效率,但积累值函数难以确定。文献[9]中采用双门限检测,设置高低门限来提取目标航迹,但对低信噪比目标性能较差,伪航迹多,对末级判决门限值的设定要求较高。文献[10]中用多级检验判决方法代替常用的两极门限检测[11-12],设计一个惩罚项来改进值函数,能够有效消除伪轨迹,减小计算量,但对低信噪比目标不能有效检测和跟踪[13]。针对岛岸附近目标机动特性,本研究在文献[10]中所提出的多级门限DP-TBD算法基础上,对算法进行改进,提出了方向加权多级门限DP-TBD算法,通过仿真进行了验证,算法性能提升明显。
1 双门限及多级门限DP-TBD算法分析
反舰导弹末制导雷达在对目标区域扫描时会产生多帧距离-多普勒图,记在第k时刻记录的一帧图像数据为D×M矩阵单元(i,j)(其中D为距离单元数,M为多普勒单元数)的测量值为zij(k),表达式为:
![]()
(1)
其中:A(k)为目标幅度,nij(k)为服从正态分布的背景噪声。
1.1 DP-TBD算法流程图
双门限TBD算法最早由意大利科学家Grossi提出,通过设立一个较低滤波门限值以及一个合适的末级判决门限值实现对弱目标的检测和跟踪,算法流程框图如图1。
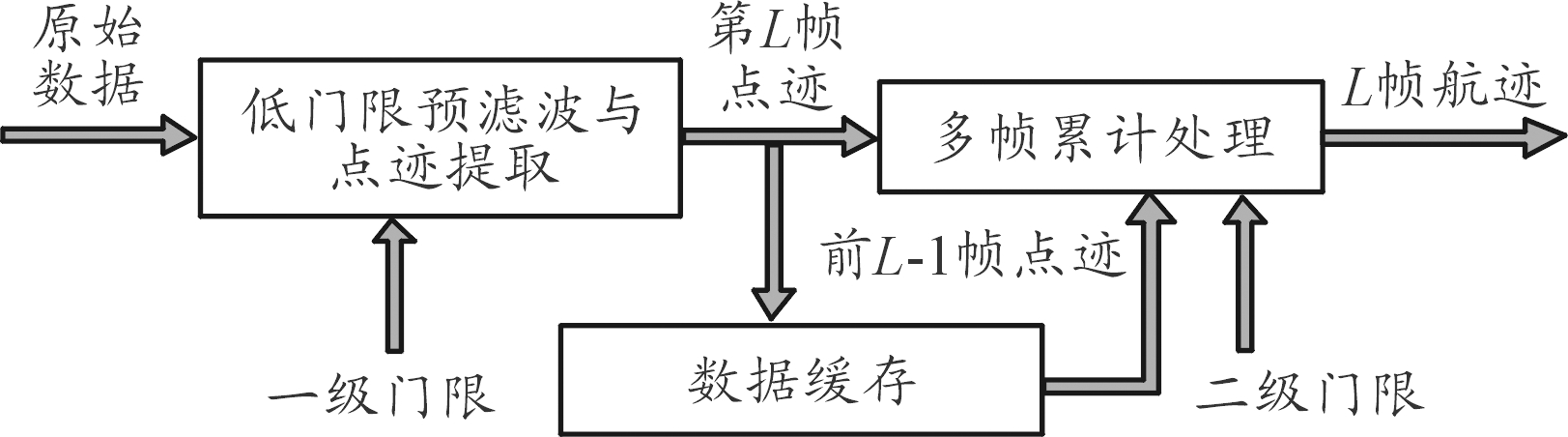
图1 Grossi双门限TBD算法框架
双门限TBD算法流程如图1,在进行多帧累计之前首先对单帧雷达回波原始数据进行一次低门限滤波,除去能量值低的点迹,减少无效累计,然后利用动态规划的方法根据点迹之间的关联对点迹进行多帧联合处理,获得累计函数值,通过末级判决门限筛选出最优航迹。双门限DP-TBD算法在检测和跟踪弱小目标时,较传统TBD算法相比,对初始数据进行了处理,减少了一定的计算量,但是仍存在滤波门限设置难、航迹累计时伪航迹较多、末级判决门限设置较难等缺点,对目标航迹不能有效筛选。
针对双门限DP-TBD算法存在的伪航迹较多,运算累计量较大的缺点,文献[10]中提出了多级门限DP-TBD算法,有效减少了伪航迹的数量,减少了计算量。多门限TBD算法流程如图2所示,对单帧雷达回波数据先进行低门限滤波处理,然后进行数据累计,当累计帧数达到最低轨迹判决长度J时,设立高、低两个门限,与每条航迹积累的能量值进行比较,超过高门限Vht的被认为是目标候选门限,低于低门限Vlt被认为是伪航迹剔除,介于高低门限之间的继续延伸。下一级重复以上判决,直至最后一帧雷达回波数据时,采用末级判决,确定最为可靠的目标轨迹,并终止积累过程。
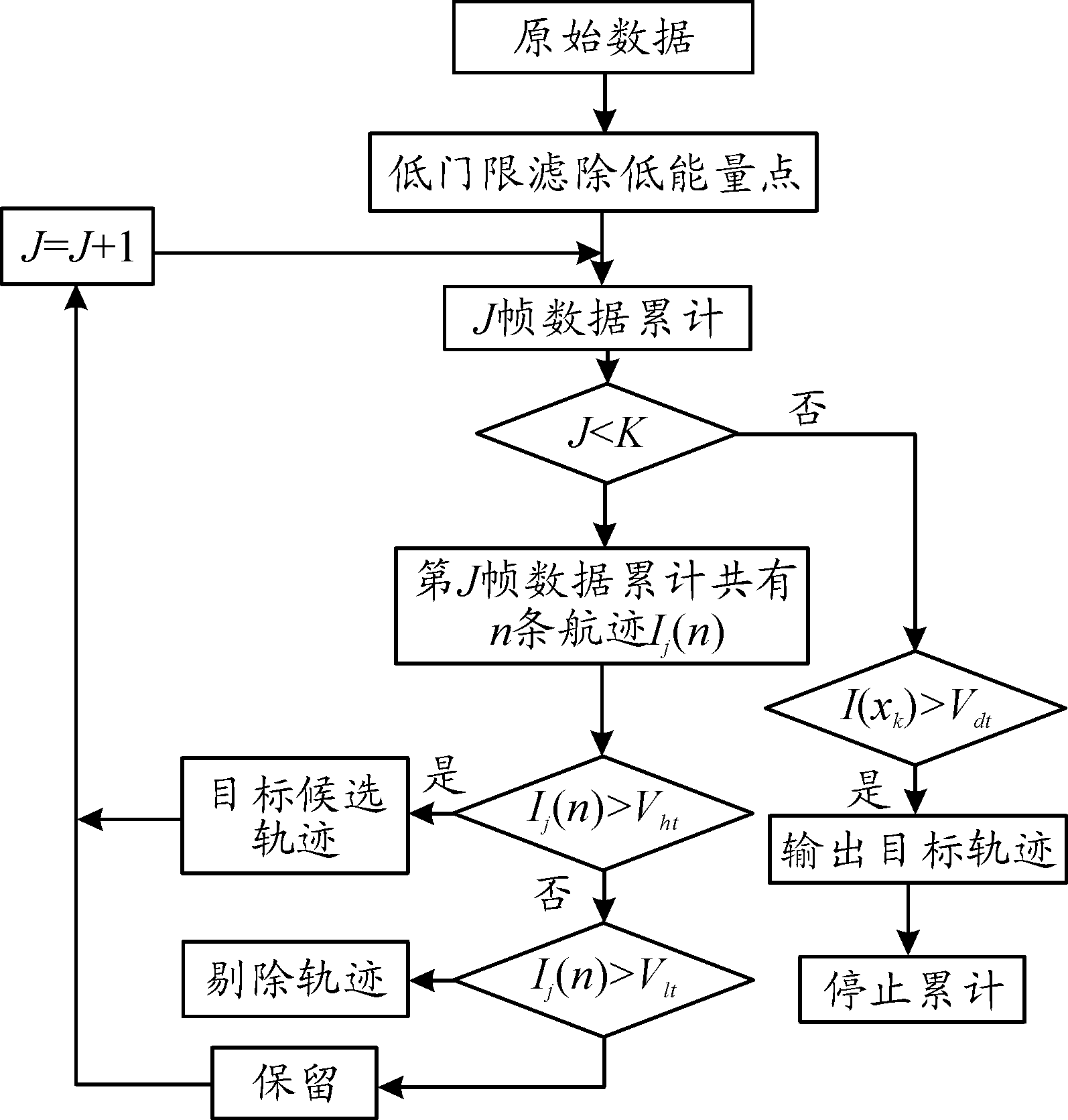
图2 多级门限TBD算法流程图
多级门限TBD算法与双门限TBD算法相比,多级门限TBD算法增加了判决次数,减少了累计过程中的计算量,在最终末级判断时,需要筛选的目标轨迹数少,末级门限设置相对简单。设待处理的雷达回波数据共K帧,在J帧判断前,采样单元数据累计计算量为W,共有N条轨迹延伸。多级门限判决每一次能够筛选掉Xi(i=1,2,…,k-j)条轨迹,且单条轨迹筛选计算复杂度与目标累计计算复杂度相同。则双门限TBD算法计算的复杂度Dd可由式(2)表示。
Dd=W+2×8k-jN
(2)
多门限TBD算法的复杂度可由式(3)估算得到。
(3)
1.2 多级门限DP-TBD算法步骤
基于动态规划的多级门限TBD算法步骤如下:
1)预处理。在动态规划前对每帧图像进行低门限预处理,滤除测量中的低能量数据。
对所有的1≤k≤K有:
![]()
(4)
式中:Vmt为初始门限值,对雷达回波原始数据处理时,对采样单元中回波能量值高于初始门限的点迹进行保留,而对于低于门限值的点迹归零去除。
2)初始化。对第一帧雷达回波数,定义值函数I(xi)的初始函数为该状态的测量值,并将函数Ψxi初始值设为0。
I(x1)=z11(x1), Ψx1(1)=0
(5)
3)轨迹积累。对1≤k≤K帧所有的xk构建累计函数:
(6)
(7)
式中:![]() 为惩罚函数根据欧式距离计算得到。
为惩罚函数根据欧式距离计算得到。
4)对J帧积累后存在的n条候选轨迹进行多级假设检验,摒弃累计能量值低的轨迹:

(8)
式中:Vlt为累计轨迹判决的低门限值; Vht为累计轨迹判决的高门限值,门限值的大小随累计帧数的变化而变化。
5)末级检测判决。K帧累计后,如果对门限Vdt,I(xk)>Vdt,则判断为目标迹。
6)轨迹回溯。对所有的![]() 对
对![]() 则可得到航迹序列的估计值
则可得到航迹序列的估计值![]()
多级门限DP-TBD算法是在双门限DP-TBD算法上进行的改进,在能量值累计过程中加入了判决高低门限,对目标累计轨迹进行了分类,使得目标轨迹的可能性更加明确,但与此同时增加了算法复杂度,实时性有待加强。在一定程度上减少了计算量和伪轨迹数量,但是每一帧的累计都需要重新设置高低门限检测值。在对弱小目标的检测和跟踪时,每一级门限值的设定更加困难,对目标航迹不能有效筛选,同时门限值过高很有可能导致直接漏掉目标信息,目标轨迹不能得到有效累计,甚至得到错误的目标轨迹。
2 方向加权多级门限DP-TBD算法分析
为提高算法的实时性,准确筛选出目标轨迹的同时不遗漏掉弱小目标点迹,尽可能多地剔除噪声点,减少伪航迹的数量,本文在多级门限DP-TBD算法的基础上进行了改进,提出了方向加权多级门限DP-TBD算法。
2.1 方向加权多级门限DP-TBD算法流程图
加权多级门限DP-TBD算法流程如图3所示。如图3所示为方向加权多级门限DP-TBD算法流程图,在进行多帧累计处理前,对每帧数据进行低门限滤波,去掉低能量点,减少无效累计。当累计到第J帧时,对目标轨迹进行筛选,累计值I(k)>Vt(k),被选为候选轨迹,并对下一帧参与累计的点赋予权值qk(j≤k≤l-j, k∈Z)。累计值I(k)<Vt(k),被作为伪轨迹删除。当累计到第L帧时,通过末级判决门限值Vdt,确定目标轨迹,并终止累计过程。
不同于广阔的海洋,岛岸附近目标多,同时带来了“交通拥堵”的问题,因此船舶目标机动受限,且航向在短时间内不会发生大的改变。据此,通过对已经累计过的点迹线性回归拟合,计算下一帧雷达回波数据中动态规划速度窗口内点迹与线性回归方程的偏离度进行权值设定。设雷达回波数据经J帧累计后,得到n条候选轨迹,轨迹集合记做{Ψi|0≤i≤n,且n∈Z}。以轨迹集合中一条候选轨迹Ψi为例,将轨迹Ψi前J帧累计的点迹对应的距离-多普勒坐标转换到直角坐标系中,得到的新的一组坐标{(xi,yi)|0≤i≤j,i∈Z},取第J+1帧累计时速度滑窗中一点迹,坐标为(xj+1,yj+1)。则动态规划时轨迹的权值可由式(9)~(16)计算得到。
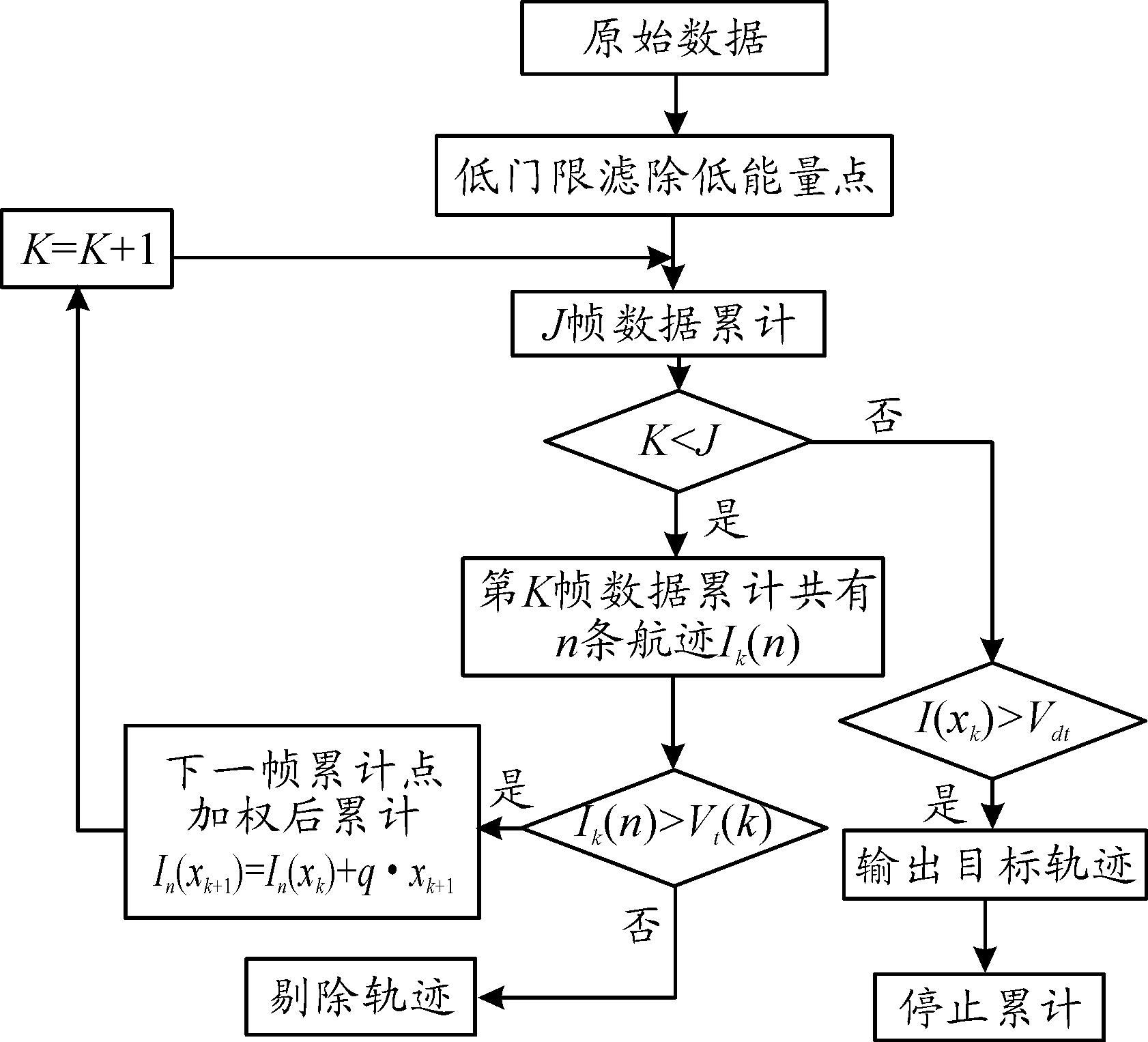
图3 加权多级门限DP-TBD算法流程图
设一元线性回归方程为:![]() 则线性系数由式(9)~(10)计算得到。
则线性系数由式(9)~(10)计算得到。
(9)
(10)
采样单元观测值偏离度用σ表示,di表示采样点到线性回归方程的距离,![]() 为采样的距离均值,Si表示前i个轨迹上的点迹的距离标准差,δi+1为第i+1点的距离误差。
为采样的距离均值,Si表示前i个轨迹上的点迹的距离标准差,δi+1为第i+1点的距离误差。
(11)
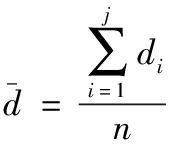
(12)
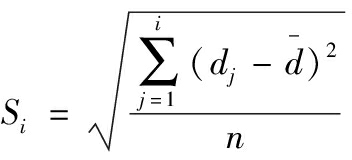
(13)
(14)
轨迹偏离度ω计算:
(15)
其中:![]()
则轨迹累计值赋予的权值q1可由式(16)确定。
(16)
2.2 方向加权多级门限DP-TBD算法步骤
基于动态规划的方向加权多级门限TBD算法步骤如下:
1)预处理。在动态规划前对每帧图像进行低门限预处理,滤除测量中低能量数据。对所有的1≤k≤L有:
(17)
式中:Vmt为初始门限值,对雷达回波原始数据处理时,对采样单元中回波能量值高于初始门限的点迹进行保留,而对于低于门限值的点迹归零去除。
2)初始化。对每帧数据,定义值函数I(xi)的初始函数为该状态的测量值,并将函数Ψxi初始值设为0。
I(x1)=z11(x1), Ψx1(1)=0
(18)
3)轨迹积累。对1≤k≤L帧所有的xk构建累计函数:
(19)
(20)
4)对K帧积累后存在的n条候选轨迹进行门限判决,摒弃能量累计值低的轨迹,并根据下一个参与能量累计点迹的状态对该条轨迹进行加权赋值:
(21)
5)末级检测判决。L帧累计后,如果对门限Vdt,I(xl)>Vdt,则判断为目标轨迹。
6)轨迹回溯。对所有的![]() 对
对![]() 则可得到航迹序列的估计值
则可得到航迹序列的估计值![]()
方向加权多级门限DP-TBD算法是在多级门限DP-TBD算法的基础上进行的改进,在轨迹累计过程中减少了轨迹筛选分类,仅通过一个门限对累计轨迹值进行筛选,对速度滑窗中点迹状态进行评估,根据评估值对滑窗内点迹进行加权,减小了无效轨迹的累计,降低了轨迹筛选难度,提高了目标检测跟踪的准确性和稳定性。但加大了累计过程中轨迹点迹处理的计算量。
3 算法性能仿真
根据岛岸附近目标运动特性,以单目标船只运动轨迹检测与跟踪为例,在不同性噪比环境、不同累计帧数下用Matlab对3种TBD算法进行性能仿真及对比。
背景噪声为功率1 dB的高斯白噪声,目标信噪比为5 dB,单帧雷达回波信号仿真图如图4。
图4可以看出,当目标信噪比为5 dB时,目标信号已经淹没在背景噪声中。下面将对3种动态规划的TBD算法,在不同信噪比及不同累计帧数的条件下,进行目标进行检测与跟踪性能仿真。
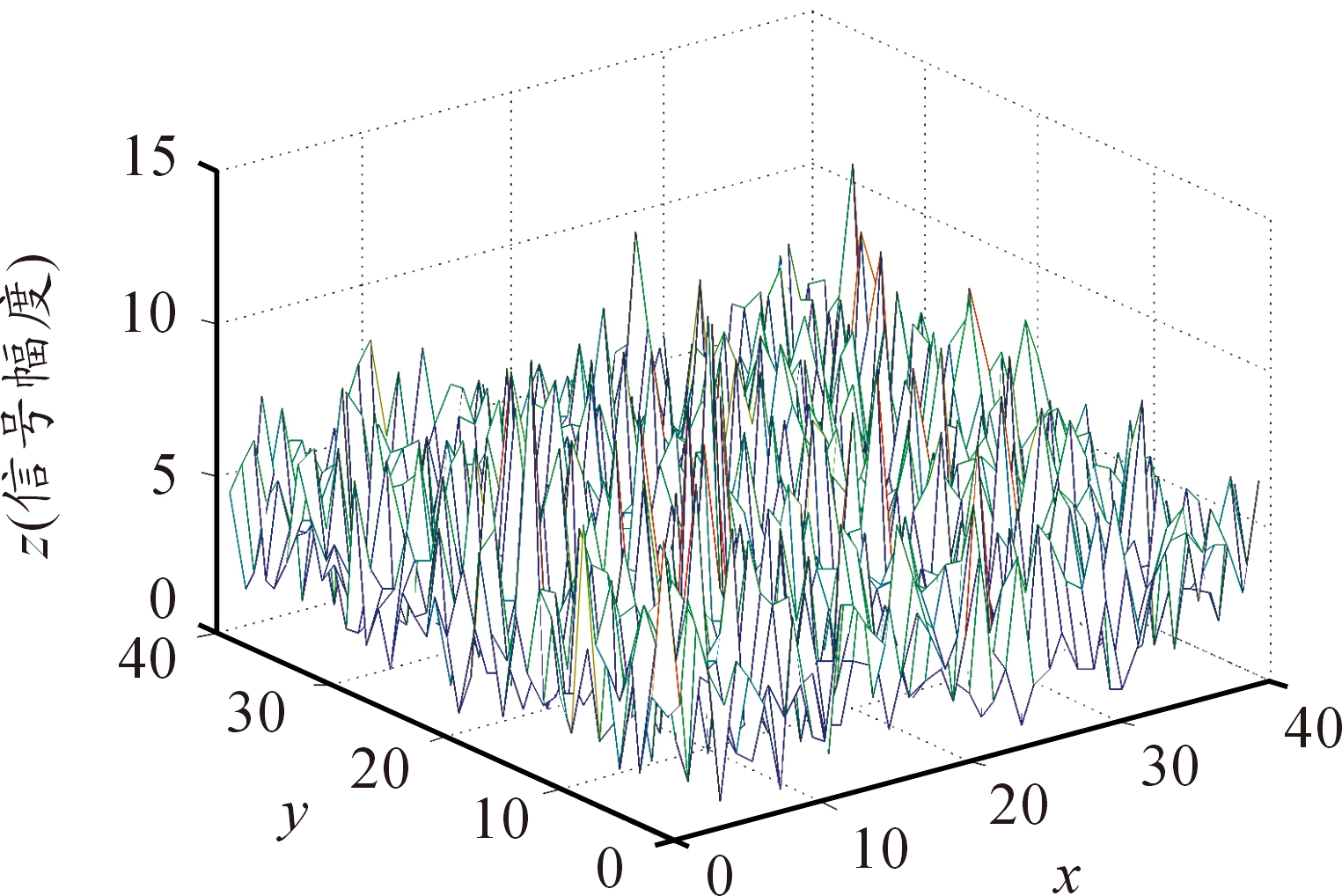
图4 单帧雷达回波信号图
仿真条件:背景噪声为功率1 dB的高斯白噪声,目标性噪比5 dB,采样时间1 s。目标运动模型为CV模型,目标运动横向速度为1个检测单元格/秒,纵向速度为1个检测单元格/秒,速度状态转移量q=2。检测单元大小40×40,累计帧数10。
图5、图6、图7为3种TBD算法在目标信噪比为5 dB时,通过检测与跟踪得到的目标轨迹。在低信噪比情况下,相同末级检测门限,双门限与多级门限都存在丢失目标点迹的情况,而方向加权多级门限能够跟踪到目标轨迹且伪轨迹也相比较少。
增加累计帧数,当累计帧数为20帧时,3种TBD检测算法仿真结果如图8~图10所示。
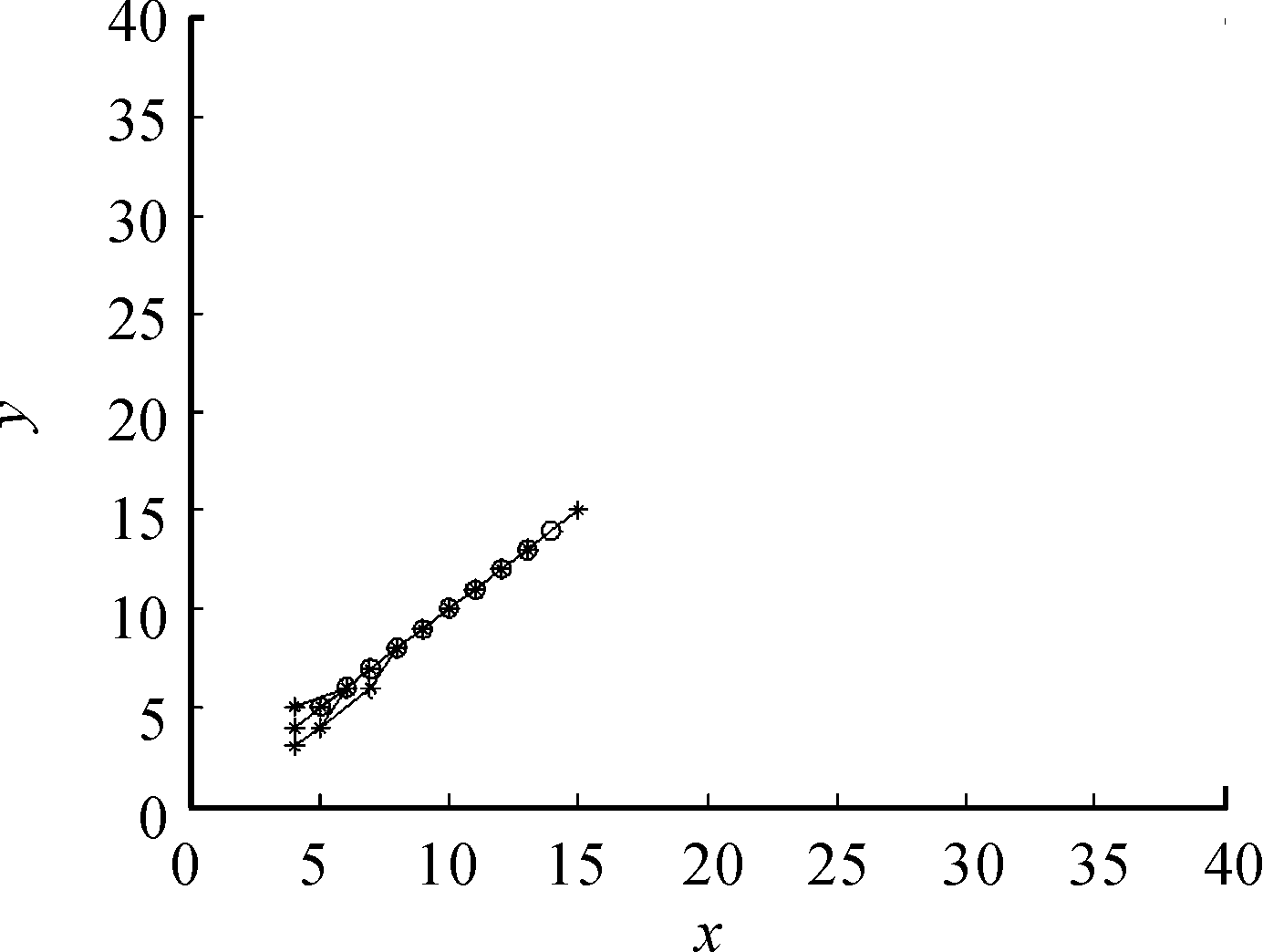
图5 双门限检测跟踪目标轨迹
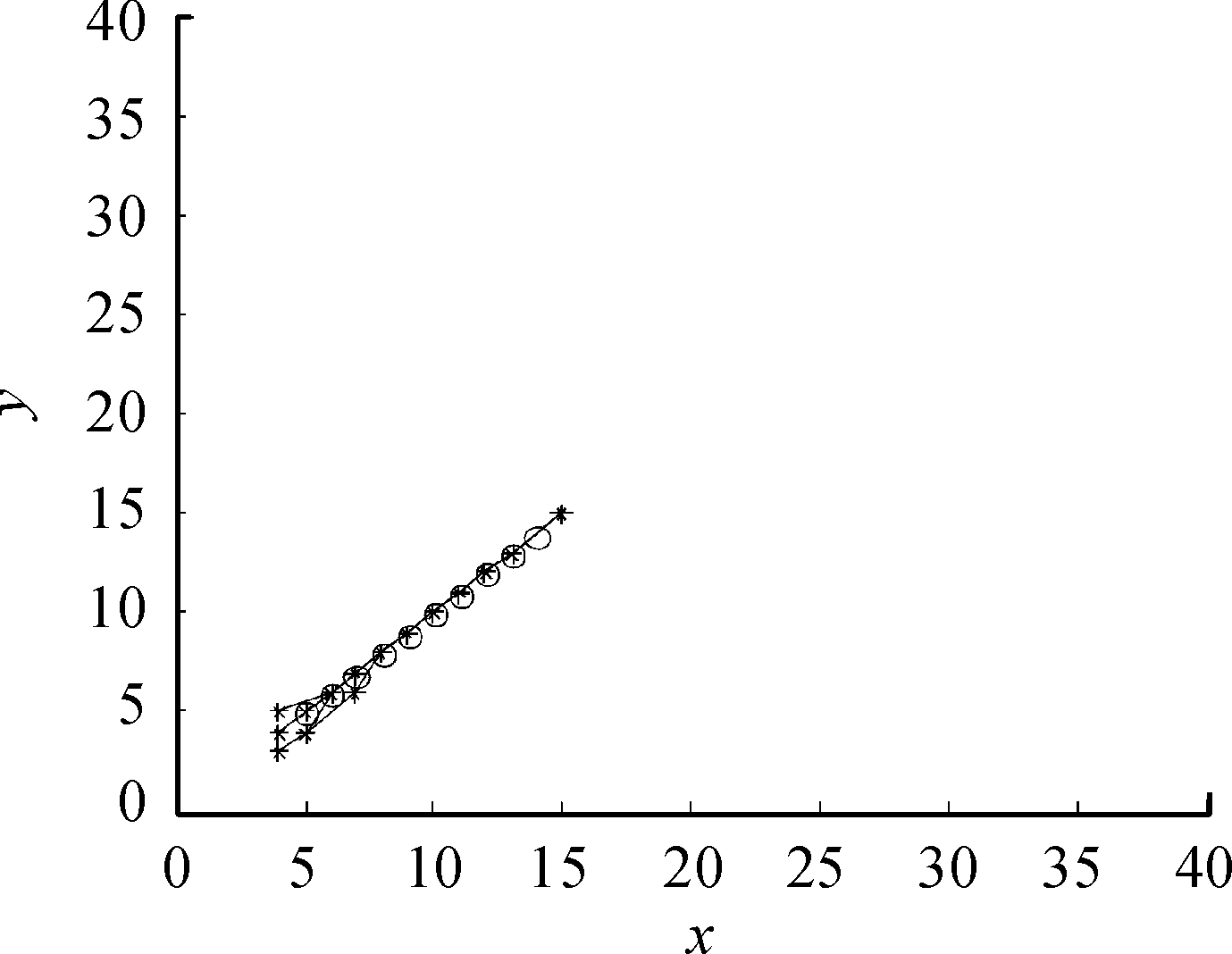
图6 多级门限检测跟踪目标轨迹
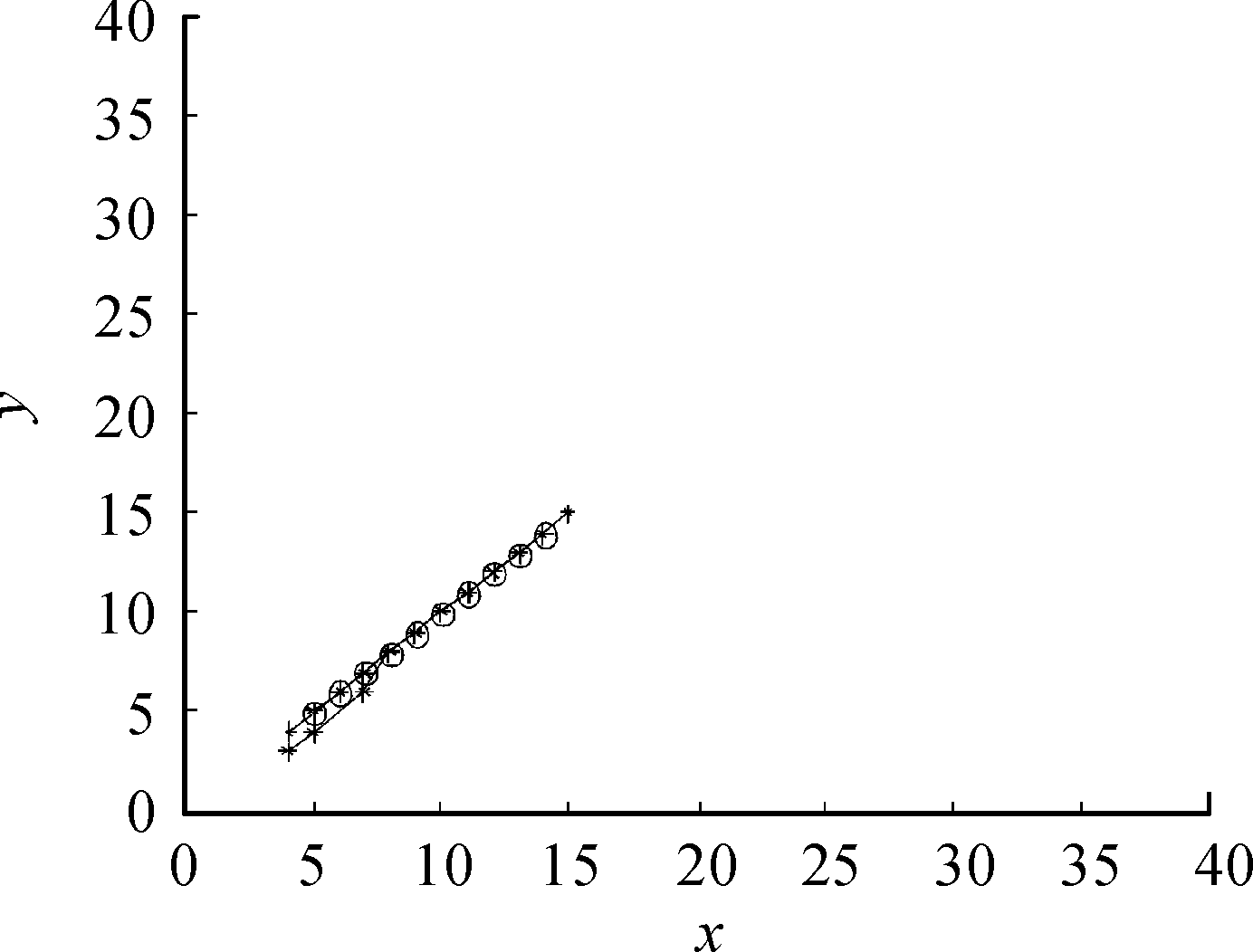
图7 方向加权多级门限检测跟踪目标轨迹
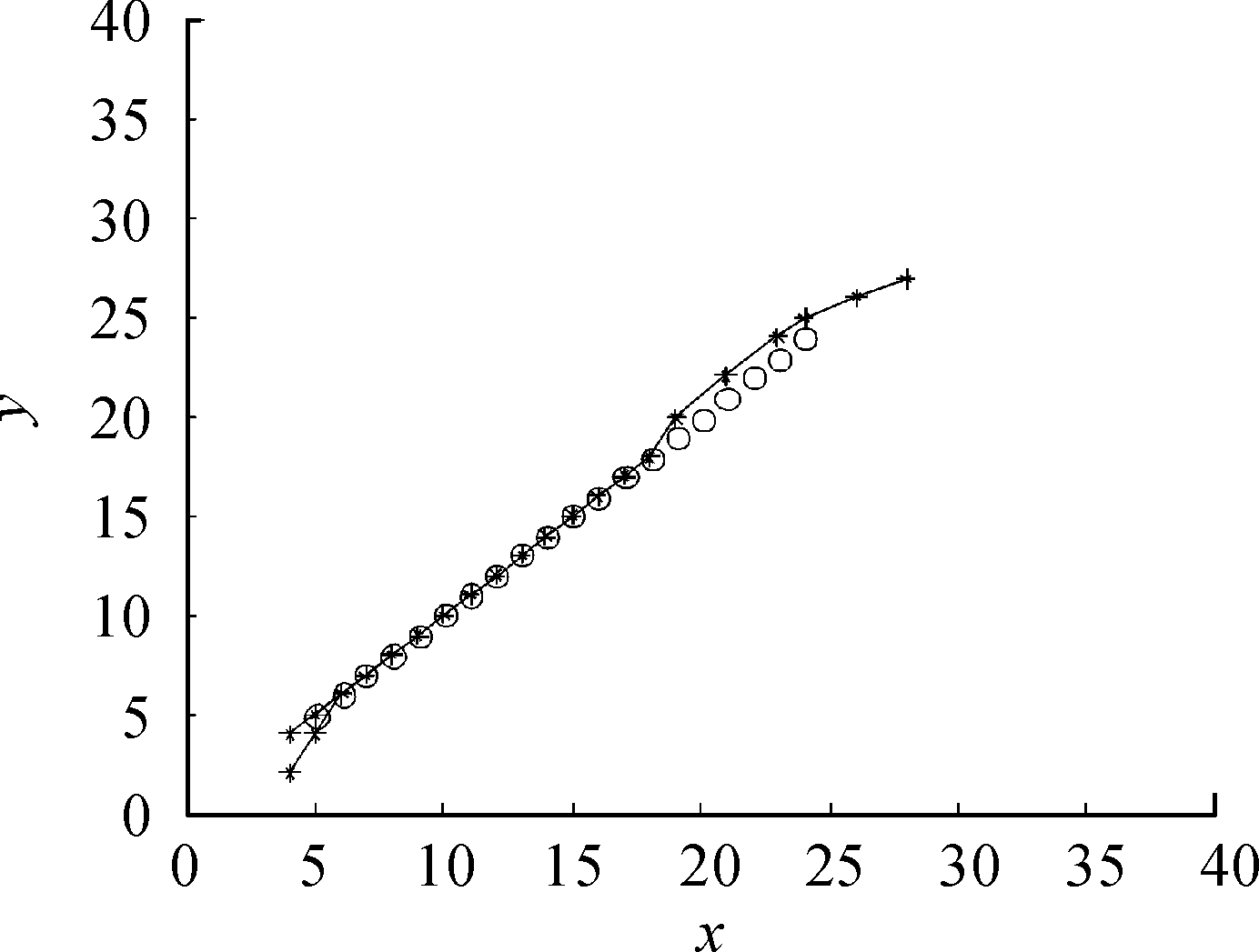
图8 双门限检测跟踪目标轨迹
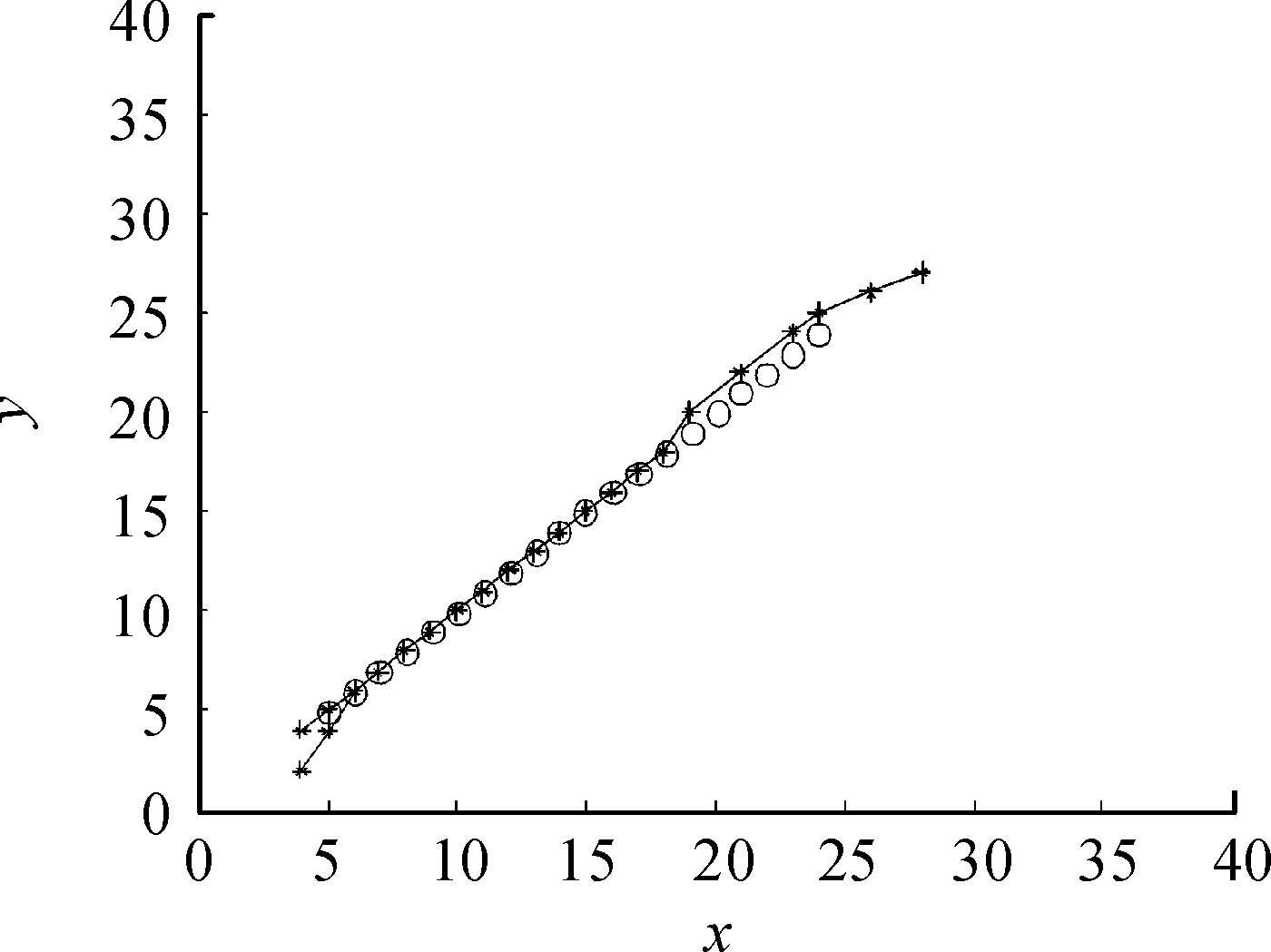
图9 多级门限检测跟踪目标轨迹
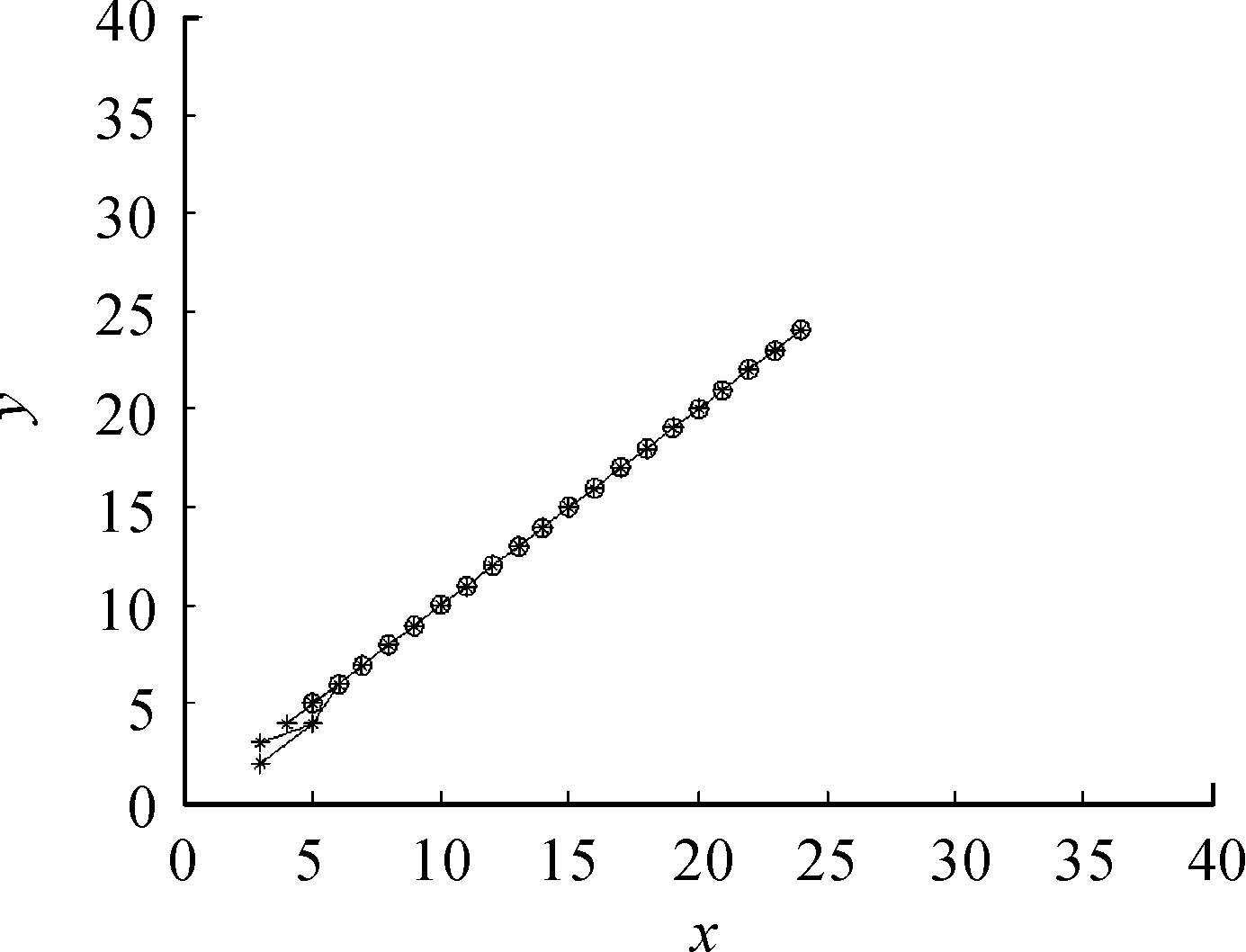
图10 方向加权多级门限检测跟踪目标轨迹
图8、图9、图10为3种TBD算法在目标信噪比为5 dB时,通过检测与跟踪得到的目标轨迹。在低信噪比情况下,相同末级检测门限,随着累计帧数的增加,双门限与多级门限丢失目标点迹的情况愈加明显,而方向加权多级门限TBD算法能够很好跟踪到点迹,起始航迹点的确定需要进一步地改善。
对比仿真实验可以得出,在低信噪比下,当累计帧数较少时,双门限TBD算法及多级门限TBD算法不能准确检测和跟踪目标,会出现漏跟的情况且起始航迹点较多,随着累计帧数的增加,伪轨迹的数量减少,但是漏跟的情况愈加严重。相比其他两种TBD算法,方向加权多级门限算法虽然牺牲了实时性性能,但能够准确跟踪目标轨迹。
4 结论
在低信噪比目标检测与跟踪时,加权多级门限DP-TBD算法能够准确地恢复目标轨迹,而其他两种算法存在漏跟、错跟的情况且随着累计帧数的增加愈加严重。但加权多级门限DP-TBD算法仍存在起始航迹点无法确定的问题,后文将对加权多级门限DP-TBD算法起始航迹点的确定进行进一步的研究。
[1] DAVEY S J,RUTTEN M G,CHEUNG B.A comparison of detection performance for several track-before-detect algorithms[J].Eurasip Journal on Advances in Signal Processing,2007,2008(1):1-10.
[2] BANIV Y.Dynamic Programming Solution for Detec-ting Dim Moving Targets[J].IEEE Trans.onAero-space and Electronic Systems,1985,21(1):144-156.
[3] HADZAGIC M,MICHALSKA H,LEFEBVRE E.Track-before-detect methods in tracking low-observable targets:A survey[J].Sensors&Transducers,2005,54(1):374-380.
[4] REID W S.Track-Before-Detect Pro-cessingfor an Airborne Type Radar[C]//IEEE Interna-tional Conference on Radar,Arlington,VA,USA,1990:422-427.
[5] WALLANCE W R.The Use of Track-Before-Detect inPulse-Doppler Radar[C]//Radar 2002,Edinburgh,Scotland,2002:315-319.
[6] 李涛,吴嗣亮.基于动态规划的雷达检测跟踪新算法[J].电子学报,2008,39(9):1824-1828.
[7] 陈铭.基于动态规划的弱小目标检测前跟踪(DP-TBD)算法研究[D].成都:电子科技大学,2014.
[8] 陈帅霖,罗丰.采用动态规划的机动目标检测前跟踪算法[J].西安电子科技大学学报,2017,44(5):39-44.
[9] 谢春思,吴帅,李军玲,等.末制导雷达双门限DP-TBD算法的工程实现研究[J].弹箭与制导学报,2019,39(2):79-82.
[10] 曹晓英,张智军.基于改进动态规划的雷达弱小目标检测与跟踪[J].现代防御技术,2013,44(4):141-146.
[11] ALEXIS P,DANA H.Detecting Small Moving Objects Using Temporal Hypothesis Testing[J].IEEE Trans.on AES,2002,38(2):570-586.
[12] 刘向阳.弱小目标检测前跟踪算法研究[D].杭州:杭州电子科技大学,2010.
[13] 陶海印.基于一种新的惩罚函数的动态规划算法的检测前跟踪[J].舰船电子对抗,2010,33(1):109-111.