近年来随着仿真技术的发展,仿鸟和仿昆虫的扑翼飞行器成为各国研究的焦点之一,由于扑翼飞行存在明显的非线性特征[1-2],且飞行机理复杂,扑翼飞行器相关问题也成为了研究难点。
仿鸟扑翼飞行器的尾翼在飞行器飞行过程中具有重要的作用,如德国Festo公司研发的SmartBird[3-4]模仿了海鸥的外形,设计了一种聚氨酯泡沫材料的倒V型可动尾翼,尾翼具有一定柔性,在飞行过程中起到了稳定作用,同时利用巧妙的机械结构,使得尾翼面能进行小角度的俯仰和偏航运动,一定程度上实现了飞行的控制。国内,南京航空航天大学的样机[5-7]采用V型固定尾翼,也能起到稳定飞行的作用,而西北工业大学的ASN·211[8-9]采用倒T型尾翼,与传统的固定翼类似,其中两片对称的水平尾翼控制俯仰和滚转运动,一片垂直尾翼控制偏航运动。
目前关于尾翼的研究,大多以刚性化作为基础开展,对于柔性尾翼的作用和影响研究较少,难以适应仿生鸟类飞行器的研究。本文主要针对鸟类扑翼飞行器的尾翼气动特性,考虑不同尾翼材料的变形效果,引入柔性变形度,建立了尾翼的动力学模型,分析尾翼的形状、张开角度和柔性对机体所受力和力矩的影响,为扑翼飞行器的设计提供一种新的方法。
1 尾翼的力学模型
1.1 尾翼坐标系的建立
尾翼构想图如图1。对鸟类实际飞行运动模型进行简化分析,飞行过程中尾翼存在两种运动情况,分别是沿机身轴线x1的滚转运动和以zw轴为旋转中心的扑动,这两种运动是沿轴线的旋转运动,还有一种比较特别,是尾翼面角度θw变化的收展运动,在此视为翼面形状变化的运动。
Z计算尾翼面在某一状态下所受力和力矩,定义机体坐标系Ox1y1z1、速度坐标系Ox3y3z3和尾翼坐标系 Oxwywzw,用尾翼扑动角αw和尾翼滚转角γw表示尾翼状态,其中αw为x1轴和xw的夹角,γw为z1轴和zw轴的夹角,于是可推导得三个坐标系的转换关系:
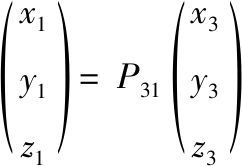
(1)
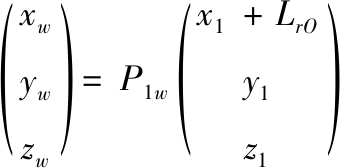
(2)
式中: P31和P1w分别是对应的坐标转换矩阵;LrO为尾翼扑动旋转中心到质心的距离。通过以上关系,可求得在某一瞬时速度矢量的作用下尾翼受力情况。
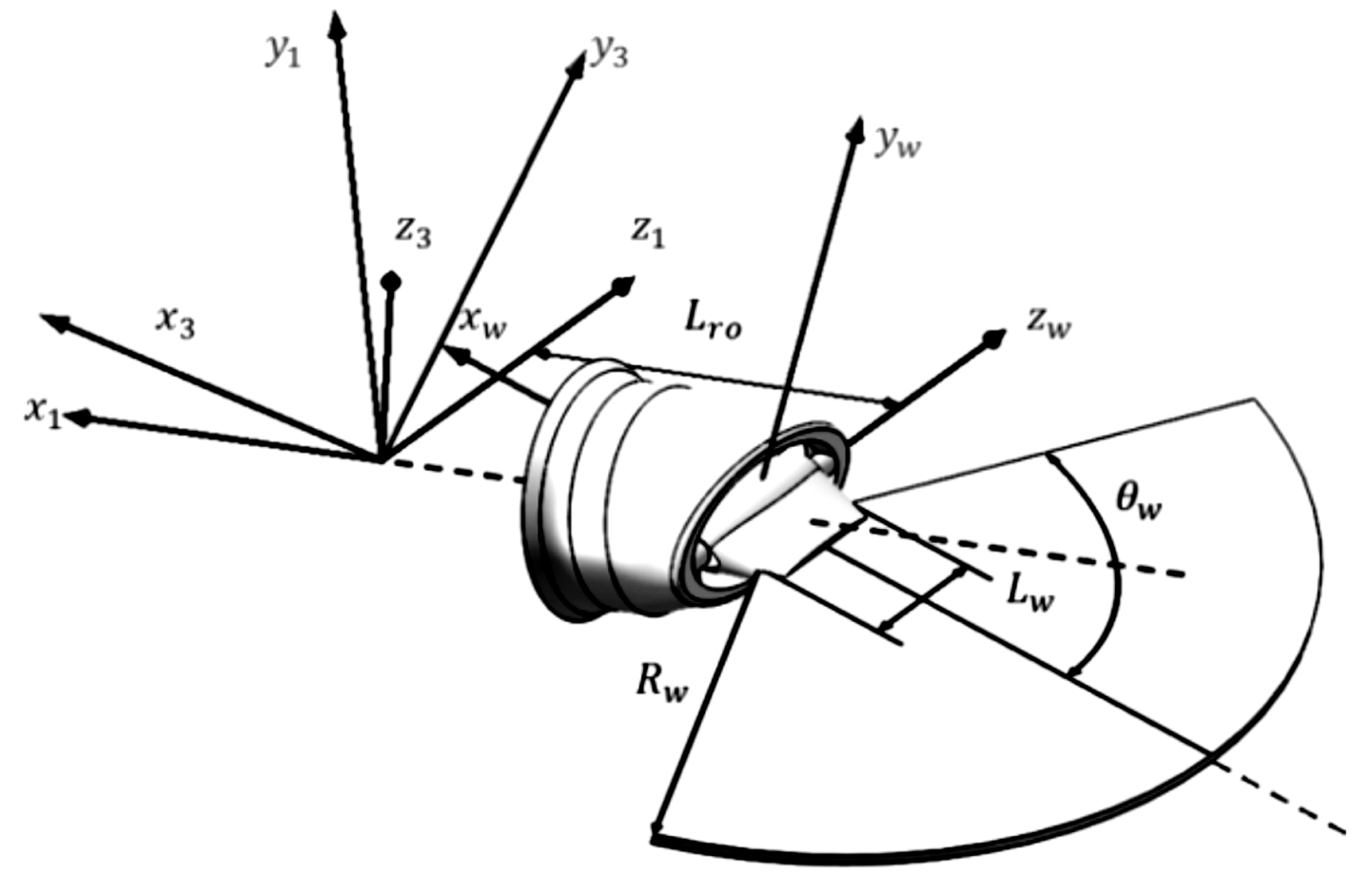
图1 尾翼构想图
1.2 尾翼模型的建立与假设
为推导尾翼动力学模型,应对其进行适当假设,以简化次要的影响因素。下面总共提出了四点假设:
1) 模型的推导只考虑尾翼在某一时刻受到来流的作用而产生了相应的力和力矩,并不考虑来流对机体的作用以及机体和尾翼的相互作用;
2) 翼面只受到来流对其特征面积的作用,不考虑空气粘滞阻力以及其他因素对作用效果的影响;
3) 不考虑尾翼厚度的影响,来流下尾翼将产生柔性变形,固定边只有前端,变形为小变形且满足理想上的抛物线方程[10];
4) 尾翼只存在扑动和滚转两种运动,而尾翼无论处于何种状态,机身轴线始终在其对称面上,使尾翼两边受到的力对称,于是尾翼不产生作用于机身轴线的滚转力矩Mx1,即Mx1≡0。
尾翼的柔性变形如图2所示。当飞行器某一瞬时速度为v时,尾翼面将受到来流v作用并产生迎面阻力、升力和侧向力,三者的大小与方向均与来流和尾翼特征面积有关。于是阻力FD、升力FL和侧向力FS的表达式为:
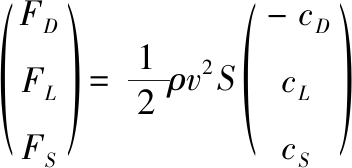
(3)
其中: ρ为空气密度;S为尾翼特征面积; cD、cL和cS分别为尾翼无量纲的阻力系数、升力系数和侧向力系数,3个系数的大小与来流和尾翼面法线的夹角αvS以及尾翼相对来流的偏转角βvS有关[11],有:
cD=2cos2αvS
(4)
cL=sin2αvS
(5)
cS=sin2βvS
(6)
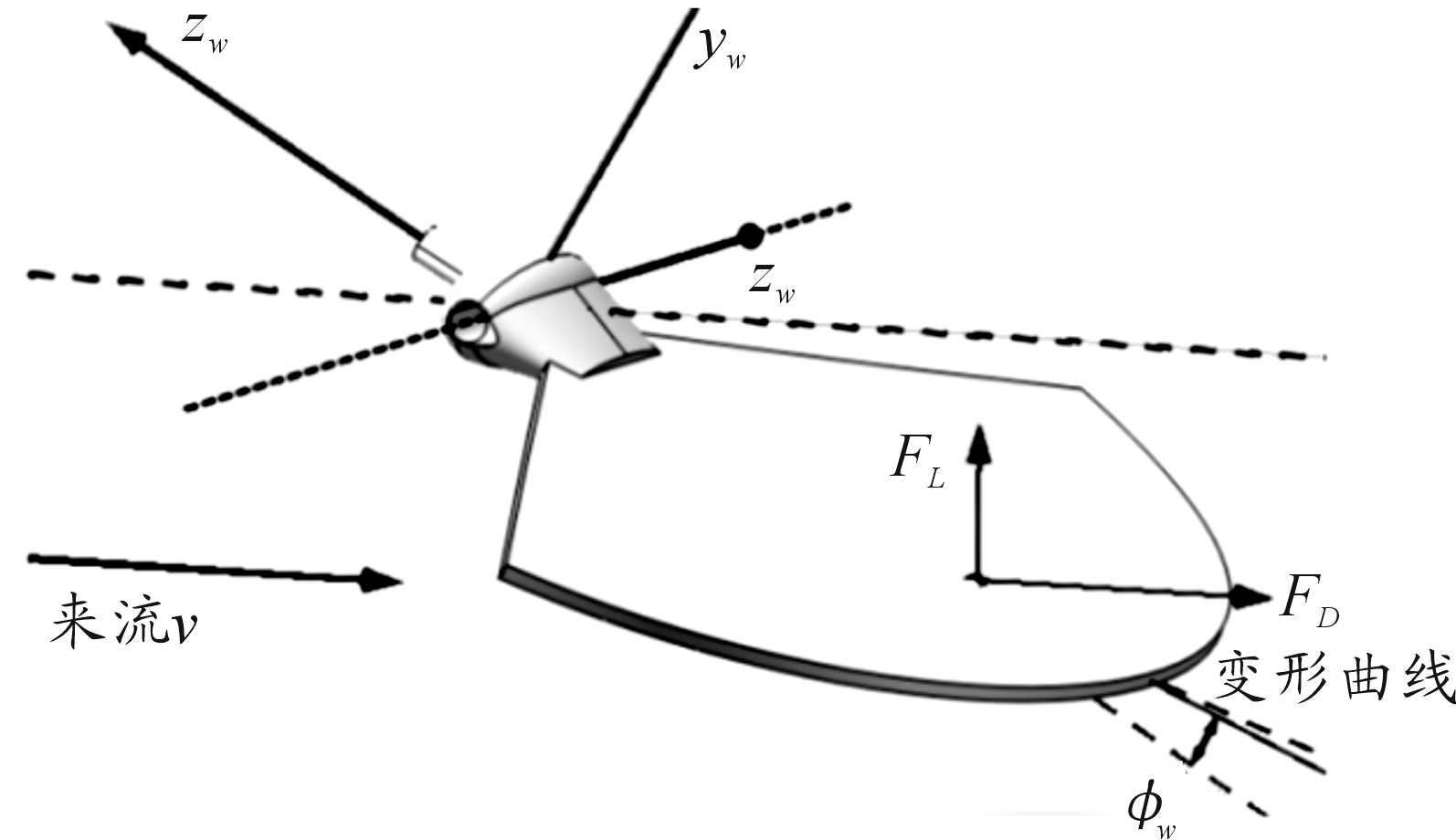
图2 尾翼柔性变形
实际的扑翼飞行过程中,总是存在尾翼的柔性变形,变形量主要受翼面迎面来流的影响。为了衡量尾翼受到来流v时的变形程度,定义变形方程为:
yw=μw![]()
(7)
其中μw是与材料和来流速度有关的系数,表征在不同材料和来流速度下尾翼的变形程度,μw越大柔性变形越大,当μw=0时表示无变形。变形后的尾翼如图2所示,尾翼将沿变形曲线变化到相应位置,其中φw为变形后某点切线与xw轴的夹角。
尾翼变形后,原本应作用于点(xw,0)的力变成了作用于点(xw1,yw1)。由于尾翼面只受来流的作用,于是面上与zw距离相同的位置受到的力和力矩关于尾翼面轴线对称且柔性变形量相同,可将尾翼面划分成xw值不同的微元并将力和力矩集中于对称轴上,方便对整个尾翼面变形后的状态进行求解。这里利用矢量表示力的作用点和大小方向,尾翼面来流速度在尾翼变形后,利用坐标系变化矩阵可求得新的矢量为:
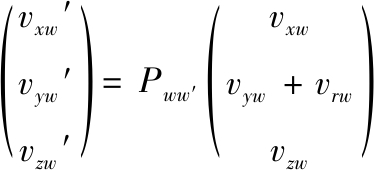
(8)
式中: Pww′为变形前后的转换矩阵;vrw为尾翼某点旋转的速度,当尾翼处于某一静止状态时vrw=0。于是αvS和βvS两个角度变为:
(9)
(10)
其中: αvS1是柔性变形后来流与微元面法线的夹角,βvS1是变形后尾翼相对来流的偏转角。由空气动力学方程可得到翼面上微元的受力为:
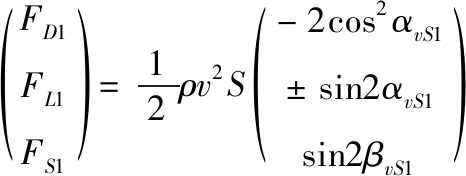
(11)
其中: Sw为微元面积,变化规律由形状决定;FD1、FL1和FS1为变形后微元面所受的阻力、升力和侧向力,FL1的符号代表升力的作用方向,应与vyw′的符号一致。应注意,当尾翼变形量与来流方向的夹角为零时,剩下的尾翼部分实际上不再变形,且无受力,是否达到变形最大点的判断依据为:
(12)
为将所求得的作用在与来流相关的方向的力转换到尾翼坐标系下,重新确定αvS1的大小与符号,有:
![]()
(13)
αvS1的符号同样应与vyw′的符号相同,利用转换关系可得:
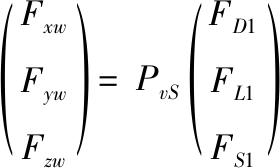
(14)
其中PvS为相关的转换矩阵。于是利用坐标转换的逆过程求得:

(15)
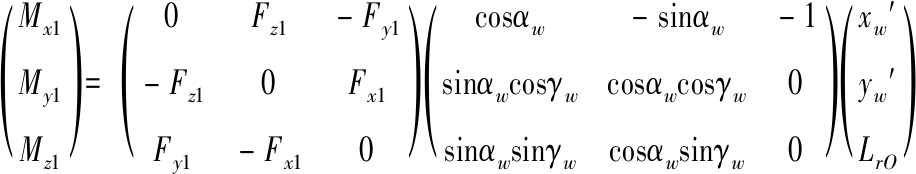
(16)
通过以上推导方法可求得一定尾翼姿态角和来流速度下尾翼微元部分力和力矩的大小,对整个尾翼面进行求解,就可获得尾翼对机体质心的作用影响。以上六个参数,是转换到机体坐标系下的结果,其中Fx1表示飞行时的前进阻力,影响机体飞行速度;Fy1表示升力,影响机体的飞行高度与载重;Fz1表示飞行时的侧向力,影响飞行轨迹;My1和Mz1表示偏航力矩和俯仰力矩,影响飞行器的姿态角。
2 影响因素
响尾翼飞行特性的因素有形状、角度和柔性变形度,下面简要分析每个因素对尾翼作用效果的影响。
鸟类尾翼形状常见的有扇形和燕尾形两种,如扇形尾翼有鸽子、麻雀等,具体来说应为椭圆扇形,而燕尾形最常见为燕子,这里通过从扇形到燕尾形的形状变化确定力和力矩的变化规律,如图3所示。根据空气动力学理论公式,随着迎风面积增大空气阻力也将增大,相同迎风面积时的阻力与形状无关,但会影响力矩,因此为研究不同形状的变化规律,所取形状的面积都相同,用尾翼面边长Rw表示不同的形状。
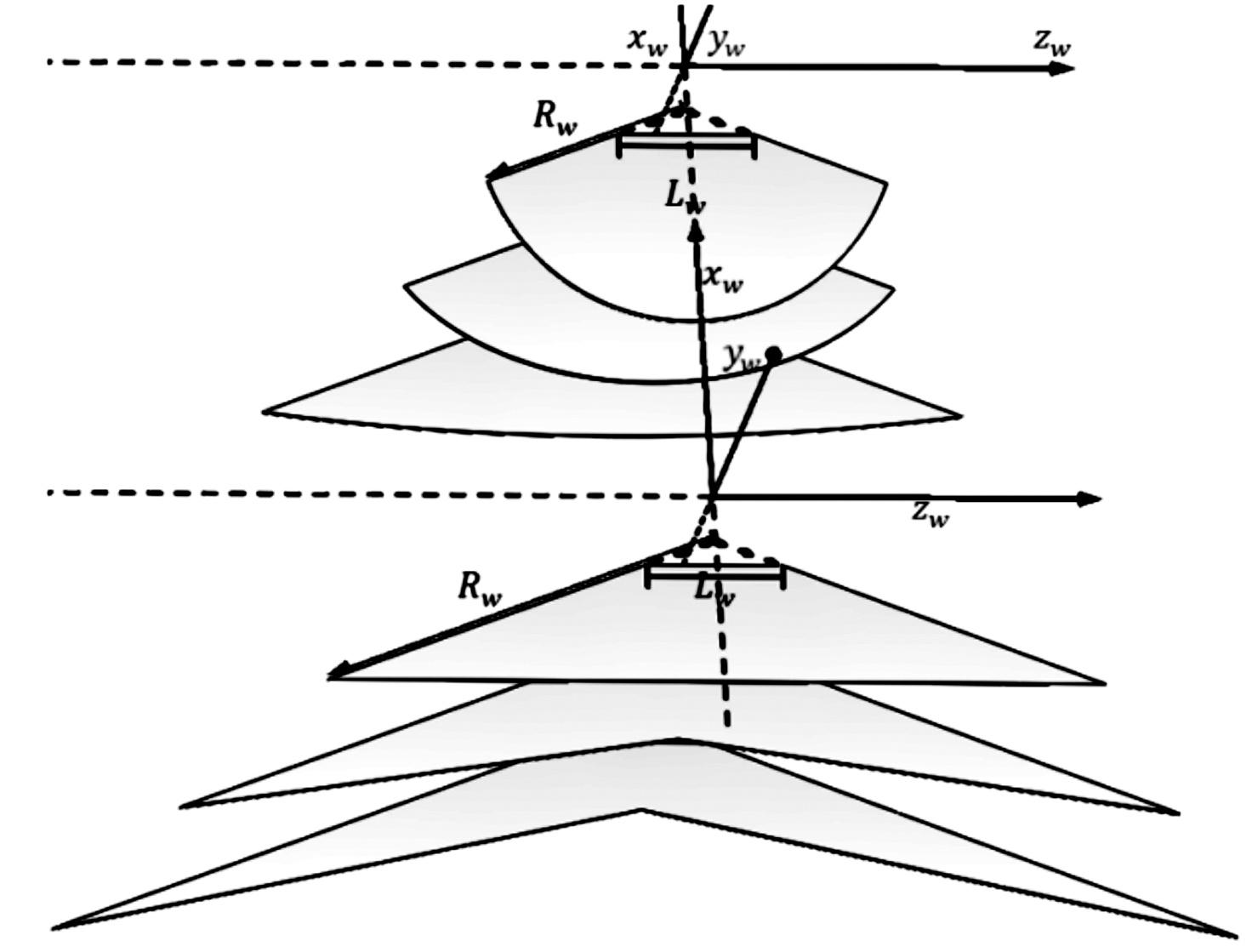
图3 不同形状尾翼示意图
翼面张开角度是一个比较特殊的形状参数,鸟类尾翼形状和长度是不变的,通过改变张开角度控制尾翼面变化,如图4所示。由于实际飞行时尾翼面并不是一直处于完全张开状态,此时折叠的尾翼形状不规则且厚度的影响无法忽略,这里只研究完全张开时的角度的不同对力和力矩变化的影响。
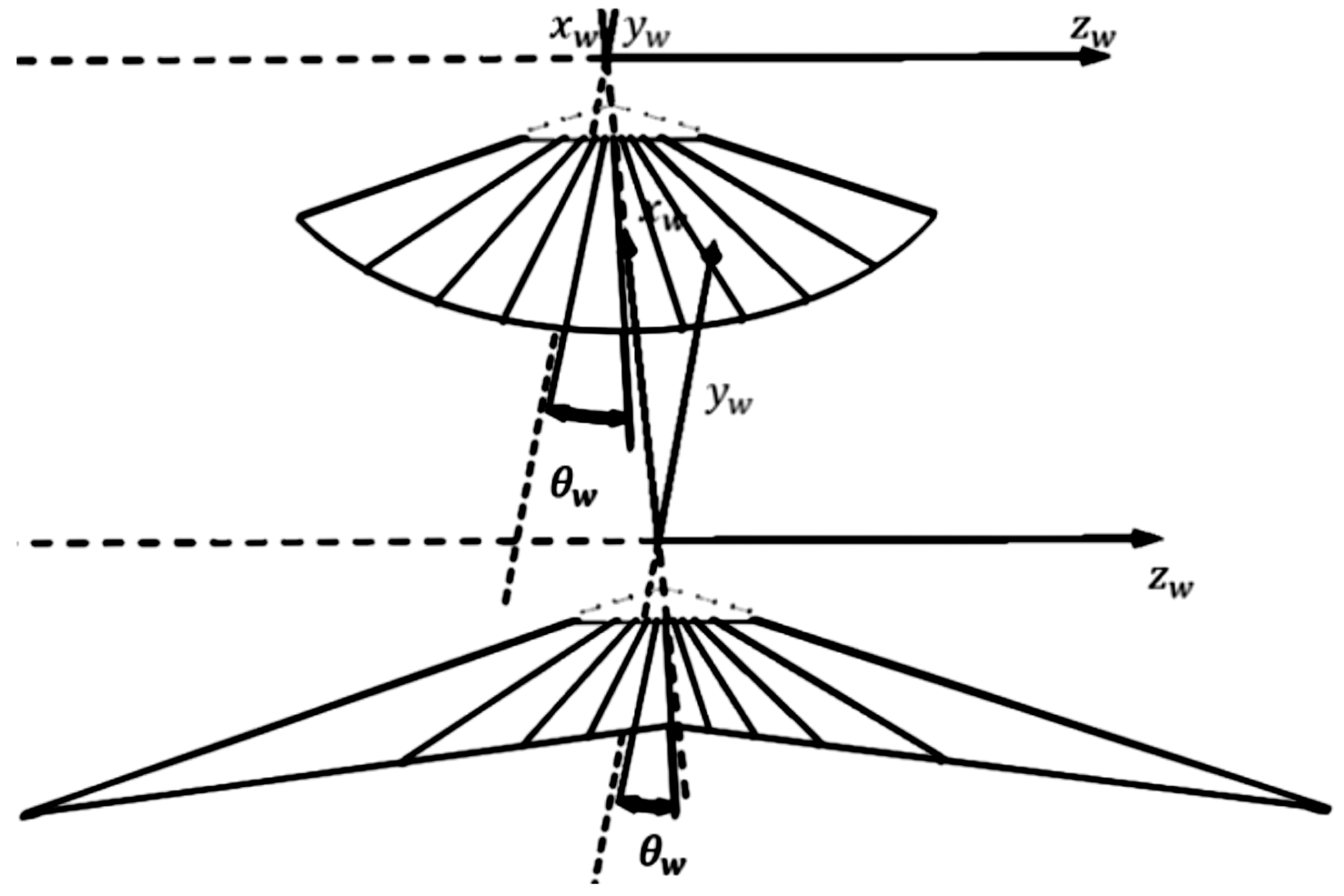
图4 不同角度尾翼示意图
翼的变形对飞行效率有较大的影响,尾翼材料在不同的速度、尺寸和环境下的变形结果不同,需要通过大量的试验获得柔性变形规律。这里用式(7)中的μw的值表示不同材料在不同条件下的变形情况,通过μw获得不同柔性变形对变化规律的影响。
3 计算结果
3.1 理论模型计算方法
用前文推导的方法计算不同状态下的力和力矩,利用C++软件对每个过程进行编程计算。给定计算需要的初始值,保持单一变量,对于不同的形状采用对应的方程,先计算每一个微元的结果,再进行叠加以获得整个尾翼面的结果。算例的初始参数如表1所示。
表1 初始参数设置

参数参数值空气密度ρ/(kg·m-3)1.225重力加速度g/(N·kg-1)9.807旋转中心到质心距离LrO/m0.075尾翼前部到质心距离LwO/m0.090
3.2 形状变化规律
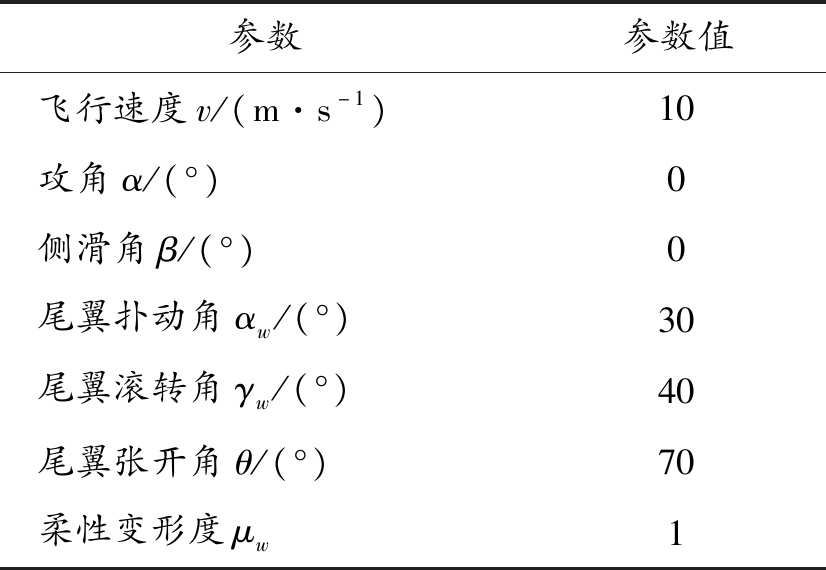
选取一组形状变化规律,将其他飞行参数设定为不变值,如表2所示。
表2 飞行参数设置
参数参数值飞行速度v/(m·s-1)10攻角α/(°)0侧滑角β/(°)0尾翼扑动角αw/(°)30尾翼滚转角γw/(°)40尾翼张开角θ/(°)70柔性变形度μw1
此时尾翼面积为Sw=2 521.39 mm2,尾翼前沿宽度为Lw=0.03 m,利用编程好的计算过程获得曲线如图5所示,横坐标为Rw,即尾翼边长,单位为mm,纵坐标依次为Fy1、Fz1、Fx1、My1和Mz1,力和力矩的单位分别为mN和mN·m。
如图5所示,随着Rw的增大,当形状从扇形到燕尾形的变化过程中,机体升力Fy1和侧向力Fz1先增大后减小,但同时阻力Fx1也是先增大后减小,而俯仰力矩Mz1和偏航力矩My1则是先减小后增大。分析原因,从扇形到三角形的过程中,重心与尾翼旋转中心的距离减小,因此总体的变形量减小,使得来流和尾翼面法线夹角相对增大;而从三角形到燕尾形的形状变化相反,总体变形量越来越大,夹角相对减小。尾翼面的微元与来流的夹角决定着cD和cL的大小,从而影响各个力和力矩的变化。综合来说,相同尾翼面积和尾翼角度下,椭圆扇形尾翼和较长的燕尾形尾翼能获得更大的升力和侧向力,但也会使阻力更大,且两个力矩较小;而对于形状介于扇形和燕尾形的三角形尾翼,虽然升力和侧向力较小,但阻力也较小,且俯仰力矩和偏航力矩更大。
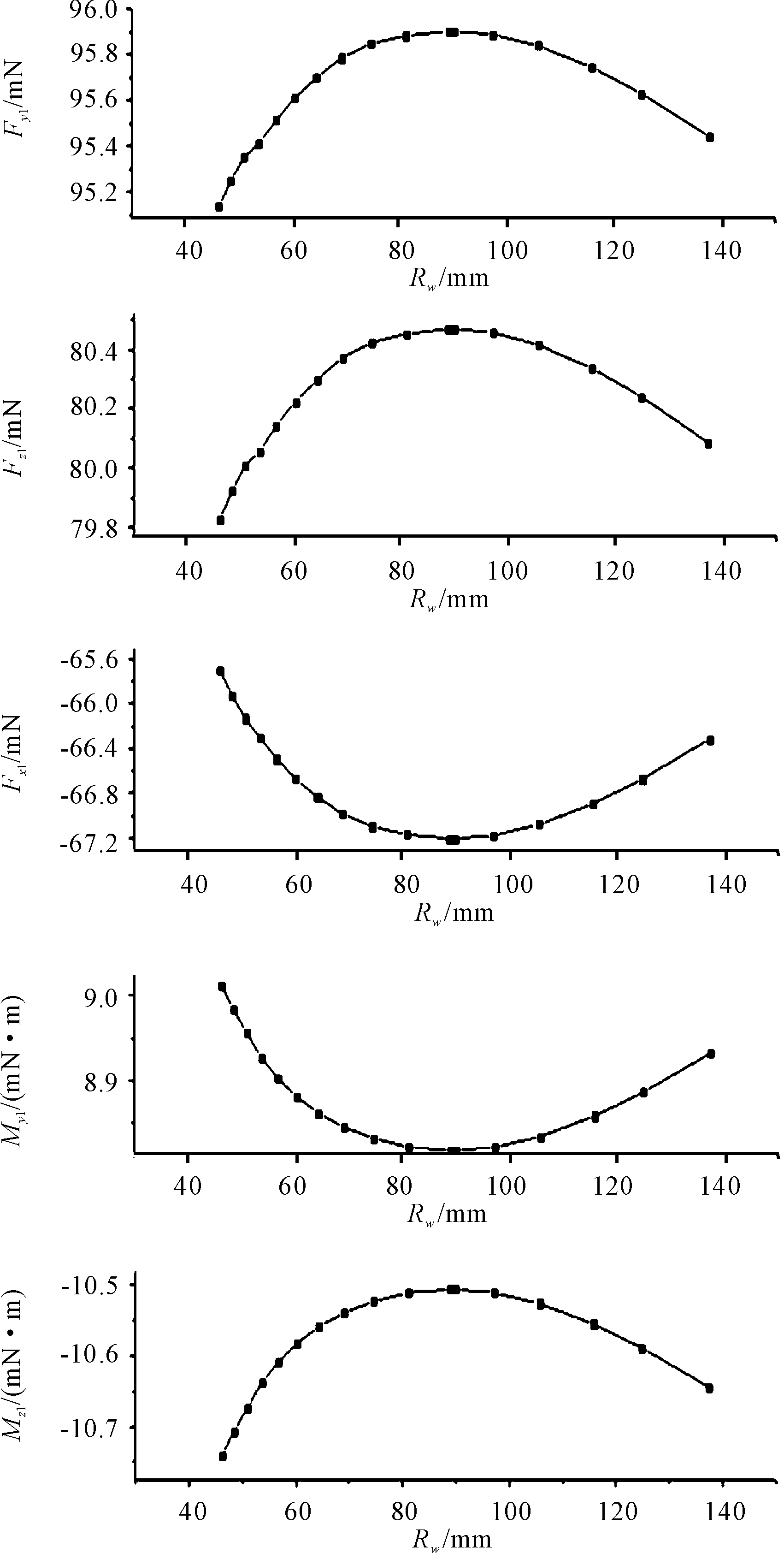
图5 不同形状的曲线
3.3 张开角度变化规律
为研究尾翼张开过程中各个力和力矩的变化规律,选取完全张开时面积相同的椭圆扇形和燕尾形尾翼各一组,张开过程如图4所示。各种飞行状态参数与3.2节中的表2相同,但尾翼张开角θ设定为从20°开始,以2°的变化率逐渐增大,最大角度为70°,而Lw大小随张开角大小变化,计算后得到图6所示的曲线。
图6给出的是Fx1和My1的变化规律,阻力Fx1由于方向与来流方向相反因此为负值,数值随角度增大而增大,同样偏航力矩Fy1也随角度增大而增大,变化过程中椭圆形尾翼的数值较大,燕尾形较小,在70°时由于尾翼面积相同,两种形状的力和力矩大小区别不明显。随着θw从20°开始增大,椭圆形尾翼的变化曲线接近于线性,斜率随着角度变化有较少的增大,和椭圆形尾翼的长轴与短轴之比有关,比值越大斜率变化越明显;而燕尾形尾翼的曲线斜率随角度增大而增大,接近70°时变化最大,这是由燕尾形的形状所决定。Fy1和Fz1随角度增大而增大且数值为正,变化规律与Fx1近似,而Mz1也是随角度增大而增大且数值为负,变化规律与My1近似。综合来说,尾翼张开角度对椭圆形尾翼的力和力矩变化的影响较为均匀,而对于燕尾形尾翼的影响较为显著。
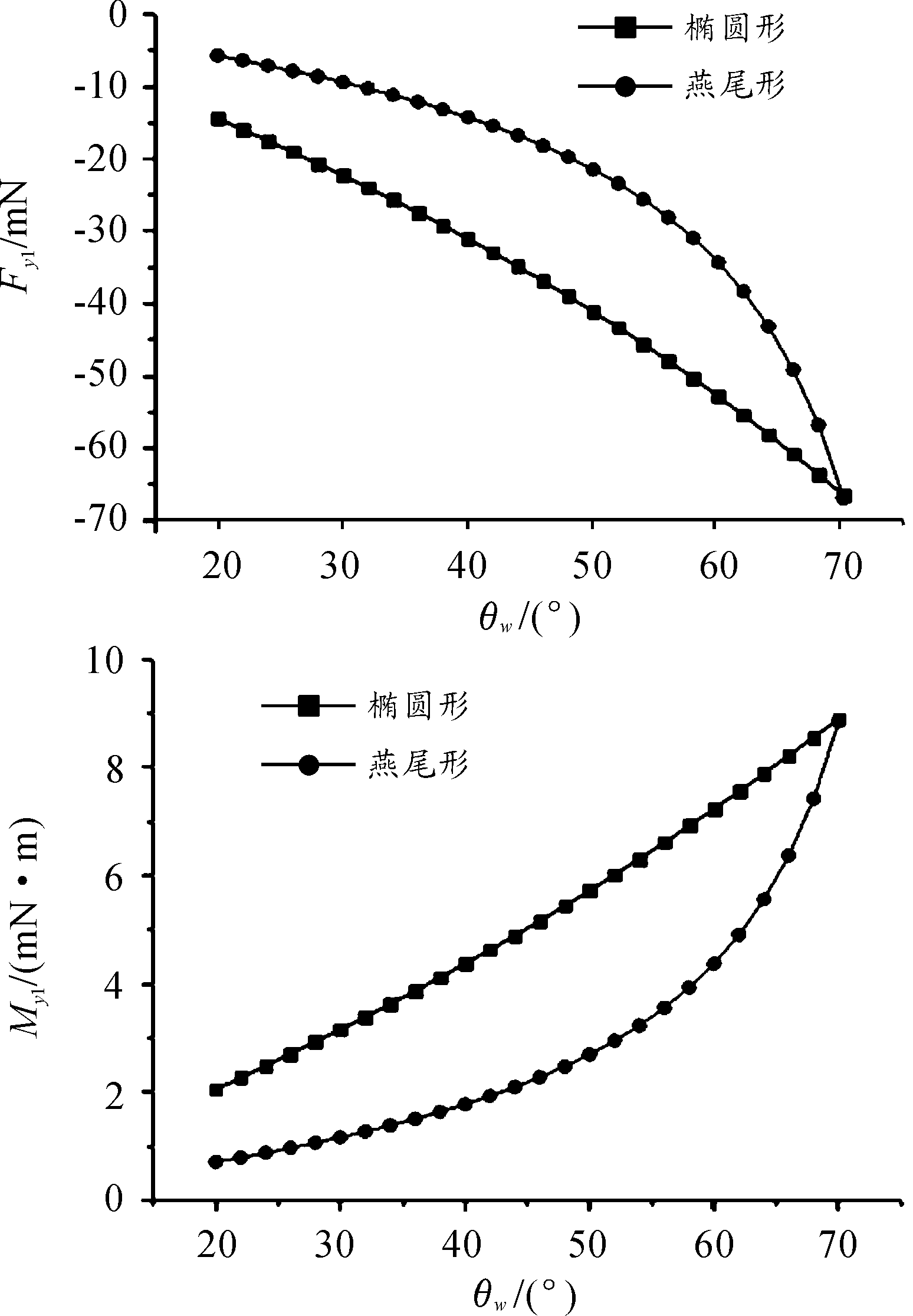
图6 尾翼张开时的曲线
3.4 不同柔性变形度变化规律
尾翼变形量除了受材料和来流的影响,也和沿变形方向的尾翼长度有关,为研究不同柔性变形度的影响,选取椭圆形和燕尾形尾翼各一组,尾翼张开角度为70°,其他参数和3.1节相同,使变形度μw从0开始以0.2为步长增加到5,于是得到如图7所示变化规律。
观察图7变化规律,随着μw增大,Fx1不断减小而My1也逐渐减小,由于选取的两种形状面积相同,当μw=0时Fx1相同,但随着变形增大,椭圆形尾翼Fx1的值大于燕尾形Fx1的值,这是由于相同面积下燕尾形尾翼的长度大于椭圆形尾翼,变形量更大;而当μw=0时,燕尾形尾翼My1的值略大于椭圆形尾翼,在μw的值增大到2.2左右时两者My1的值相等,最后在μw=5时,椭圆形My1的值大于燕尾形My1的值。Fy1、Fz1和Mz1的变化规律与Fx1和My1类似,变化规律与上图类似,综合来说,尾翼的柔性变形能减小阻力但也使其他几个数值减小,而柔性的变化对于燕尾形尾翼的影响更为显著。

图7 不同柔性变形度的曲线
3.5 模型计算与仿真结果对比
利用XFlow流体力学仿真软件进行仿真,XFlow是基于粒子和完整拉格朗日函数的无网格方法,具有自适应踪迹改良功能,有更好的应对复杂模型的能力。
选取3.2节算例进行分析,计算模型采用单相外部绝热流动,为保证风洞的阻塞干扰足够小,选取0.3 m×0.4 m×0.4 m的风洞尺寸,计算得到的阻塞比均小于1%,满足不需要修正干扰的要求;其他参数与理论计算时选取的参数一致,仿真计算结果如图8所示。
仿真获取了5个参数的变化规律,其中3个力先增大后减小,2个力矩先减小后增大,理论模型计算结果与XFlow仿真的变化规律一致。对于Fy1和Fz1,XFlow仿真结果和理论模型计算结果的相对误差在9.48%~27.41%,平均相对误差为16.87%,当Rw=105.64 mm时误差最小;对于Fx1,两种计算结果相对误差在0%~29.28%,平均相对误差为14.90%,当Rw=48.39 mm即形状为扇形时误差最小,而越接近燕尾形尾翼,计算结果的相对误差越大;而对于My1和Mz1,两种计算结果相对误差在8.82%~26.04%,平均相对误差为19.62%,当Rw=137.51 mm即形状为燕尾形时误差最小,越接近扇形误差越大。这些相对误差除了包含模型及仿真条件的误差外,也体现了理论模型的不足之处,即尾翼尺寸的变化对翼面产生的力和力矩的大小变化的作用效果不显著,具体的原因在结果中讨论。总体上看,理论模型的计算结果与仿真结果的变化规律一致,模型可以反映尾翼在来流作用下的真实受力情况,证明理论模型是有效的。另外,由于本文主要是研究对尾翼简化模型的建立,因此没有进行相关风洞或水洞的实验验证,相关的试验会在其他文章中进行。
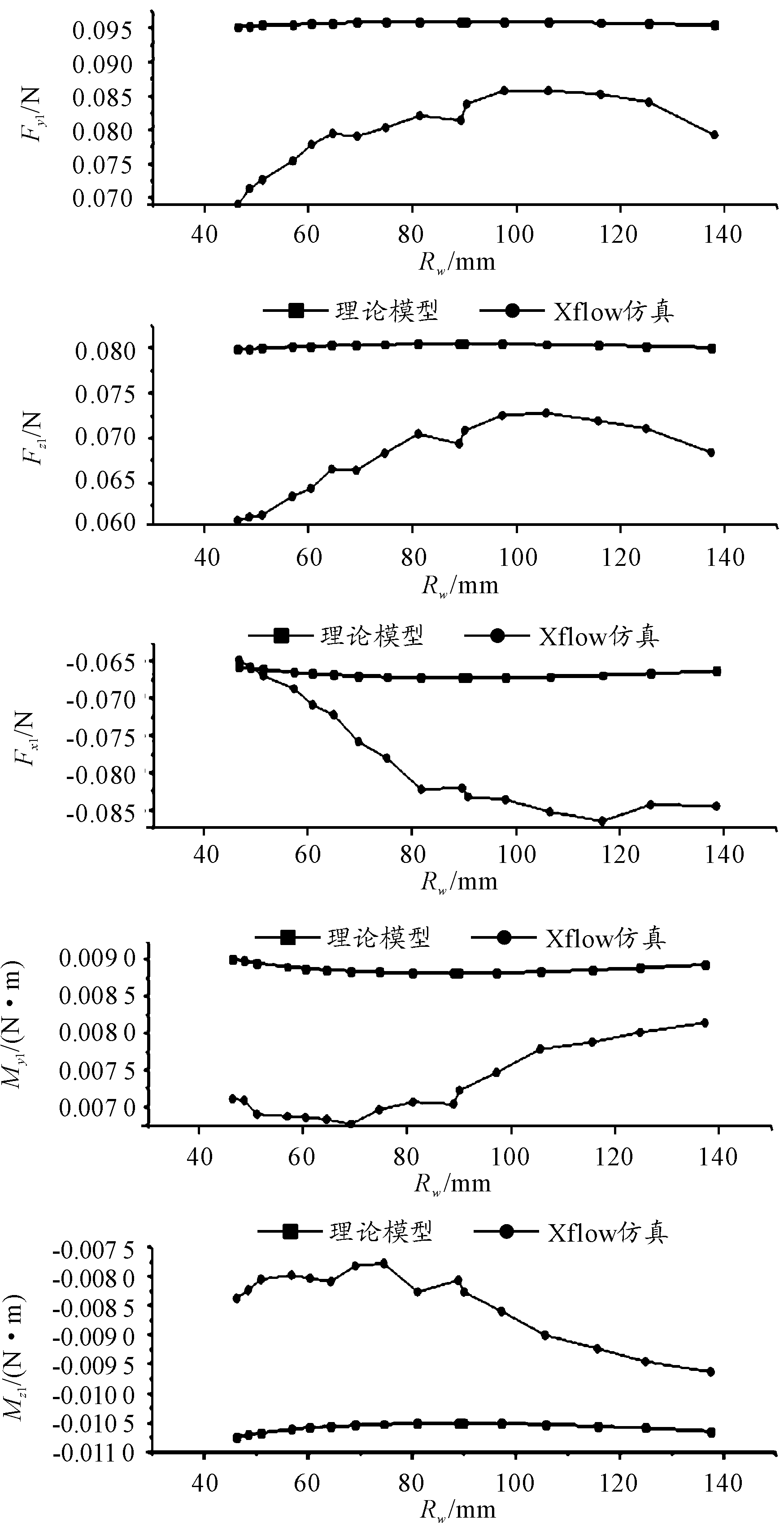
图8 不同形状的XFlow仿真计算曲线
4 结论
1) 建立了包含2个自由度的尾翼动力学简化模型,单独分析了尾翼受力对机体的影响,为扑翼飞行器尾翼气动问题的研究提供了新的建模方法与途径。
2) 对尾翼的形状、张开角度及材料柔性3个因素进行计算分析,获得了相应的变化规律。其中,椭圆形和燕尾形尾翼具有更大的力矩,而形状越接近三角形,3个方向上的受力越大;张开角度越大,两种形状尾翼的力和力矩都会越大,但椭圆形尾翼随角度变化较为均匀,而燕尾形尾翼在小角度时变化不明显,大角度时变化快;随着柔性变形度变大,各个力和力矩均减小,且柔性的不同对燕尾形尾翼的影响大于对椭圆形尾翼的影响。
3) XFlow仿真软件计算与建立的理论模型计算结果的变化规律一致。其中Fy1和Fz1的XFlow仿真结果和理论模型计算结果的平均相对误差在形状接近三角形时最小;Fx1的两种计算结果的平均相对误差在形状为扇形时最小;My1和Mz1的两种计算结果的平均相对误差在形状为燕尾形时最小。理论模型计算结果的变化幅度远小于仿真结果的变化幅度,可能是柔性变形后,翼面不再只是受到迎面来流的作用,在无变形下的空气粘滞阻力和翼面两侧绕流等次要因素变化较大,对尾翼的受力有一定影响,力和力矩变化较大。
[1] JACKOWSHI J,BOOTHE K,Albertani Retal.Modeling the flight dynamics of a micro air vehicle[C]//American Control Conference.USA,2004.
[2] WASZAK M R,DAVIDSON J B.Simulation and flight control of an aero-elastic fixed wing micro aerial vehicle[R].USA:AIAA,2002.
[3] WONG B.New robot designs are for the birds[J].Electronic Design,2011,59(6):14.
[4] MACKENZIE D.A flapping of wings[J].Science,2012,335(6075):1430-1433.
[5] 曾锐.仿鸟微型扑翼飞行器的气动特性研究[D].南京:南京航空航天大学,2004.
[6] 黄鸣阳,肖天航,昂海松.多段柔性变体扑翼飞行器设计[J].航空动力学报,2016,31(8):1838-1844.
[7] 段文博,昂海松,肖天航.可差动扭转扑翼飞行器的设计和风洞试验研究[J].实验流体力学,2013,27(3):35-40.
[8] 张亚锋,宋笔锋,袁昌盛.微型扑翼飞行器推力特性试验[J].航空动力学报,2007,22(12):2078-2082.
[9] 张明伟.基于仿生学的微扑翼飞行器控制技术研究[D].西安:西北工业大学,2007.
[10] 昂海松.柔性扑翼微型飞行器升力和推力机理的风洞试验和飞行试验[J].航空动力学报,2007,22(11):1838-1845.
[11] 段洪君.微型飞行器飞行姿态控制方法研究[D].哈尔滨:哈尔滨工业大学,2007.