RLV再入过程一般可分为再入段、末端能量管理段和自动着陆段。RLV再入段制导精度、鲁棒性和可靠性直接影响再入过程是否能够顺利完成;再入段高度跨度大,环境复杂,由于大气扰动、飞行器气动模型和再入段初值的偏差,严重影响了RLV的制导精度 [1]。自SpaceX公司2015年12月22日成功实现可重复使用运载火箭的垂直回收,火箭回收以其低成本的优势掀起了国内的研究热潮,RLV再入段的弹道优化和制导也成为研究热点。
弹道优化是指在各种约束条件下,求解满足预设性能指标最小的弹道。弹道优化本质上是最优控制问题,其数值求解方法有间接法和直接法。间接法需要推导最优控制问题的一阶必要条件,得到关于最优控制的Hamiltonian边值问题(HBVP),再用数值方法参数化HBVP,间接法求解精度高,但是必须提供解析形式的最优必要条件和精确的初值,对多约束问题求解比较困难 [2]。RLV再入段弹道优化包含过程约束、终端约束和控制量约束等,工程上存在初值不稳定的问题,不适宜用间接法求解;直接法避免了推导一阶必要条件,求解易收敛[3]。伪谱法属于直接法的一种,已经广泛应用于飞行器轨迹优化[4],文献[5]用Gauss伪谱法求解月球定点着陆优化问题;文献[6]用Gauss伪谱法求解火星大气进入的轨迹优化问题; 文献[7]将Radau伪谱法用于解决航天飞机再入段弹道优化问题;文献[8]将hp自适应伪谱法应用于再入轨迹优化;文献[9]将hp自适应伪谱法用于飞行器多阶段的轨迹优化。本文采用hp自适应伪谱法进行RLV再入段弹道优化,将RLV再入段连续最优控制问题的求解转化为求解非线性规划(NLP)问题[10]。hp自适应伪谱法结合Radau伪谱法和hp有限元法,与Radau伪谱法相比,能够自动减少配点数目,从而降低NLP问题求解规模并提高计算效率,对初值的敏感程度较Gauss伪谱法要低。
飞行器制导分为标准弹道制导和预测校正制导。标准弹道制导包括弹道生成和在线弹道跟踪,在初始偏差较小时可以实现较高精度的制导[11];文献[12]研究了运载器大气层内的制导问题,利用线性二次型调节器(LQR)方法对规划弹道进行跟踪,LQR方法多用于多输入多输出系统[13],存在状态和初值偏差时仍能取得较好的制导效果;文献[14]提出了轨迹线性化的制导方案,该方案对参考弹道依赖性小、制导精度较高。但是标准弹道制导精度很容易受到环境干扰和初值偏差的影响[15],鲁棒性能较弱。预测校正制导无需储存标准弹道,根据预测的终端状态与目标参数之差实时产生制导指令。基于伪谱法的预测制导方法能够根据当前飞行器的状态实时产生制导指令,有效地消除环境和气动干扰,属于最优闭环制导。文献[16]研究了基于伪谱法的再入飞行器最优闭环制导问题,该方法可以有效应对各类干扰;文献[17]研究了伪谱法在巡航导弹的应用,该方法对初值扰动和阵风干扰不敏感,有效减小了导弹的脱靶量。但是伪谱法计算量大,求解耗时较长,且在大的初值估计误差和干扰下很可能造成无法收敛的情况,因此很难在工程上得到应用。文献[18]基于BP神经网络研究了滑翔飞行器的制导问题,制导周期较短,但采用了多个神经网络控制器,结构复杂,且只对单个变量进行拉偏仿真验证,未体现控制器抗组合干扰性能。
基于精确模型设计的制导方案难以克服组合干扰,无法同时满足飞行器对过程约束、控制变量约束、终端位置、终端速度和落点姿态的要求。hp自适应伪谱法能够在初值偏差和任意干扰条件下规划出满足性能指标和约束条件的最优弹道,本文充分发挥hp自适应伪谱法求解精度高的优势,解决了预测制导周期长的问题,利用BP神经网络强大的学习和快速预测的能力,设计了用于RLV再入段制导的神经网络制导控制器,实现方法简便。在飞行过程中,RLV受到外界环境干扰和初始偏差的影响,实际飞行路线偏离优化弹道,基于实时获取的捷联导航信息,所设计的神经网络制导控制器可在0.01 s内产生制导指令引导RLV飞向目标点。
1 伪谱法弹道优化和神经网络原理
1.1 RLV再入段弹道优化模型
对RLV再入段的空间弹道方程作一些简化假设:1) 将地球视为均质圆球;2) 忽略地球扁率和地球自转的影响。
RLV再入段只受气动力作用,发射系下的数学模型为
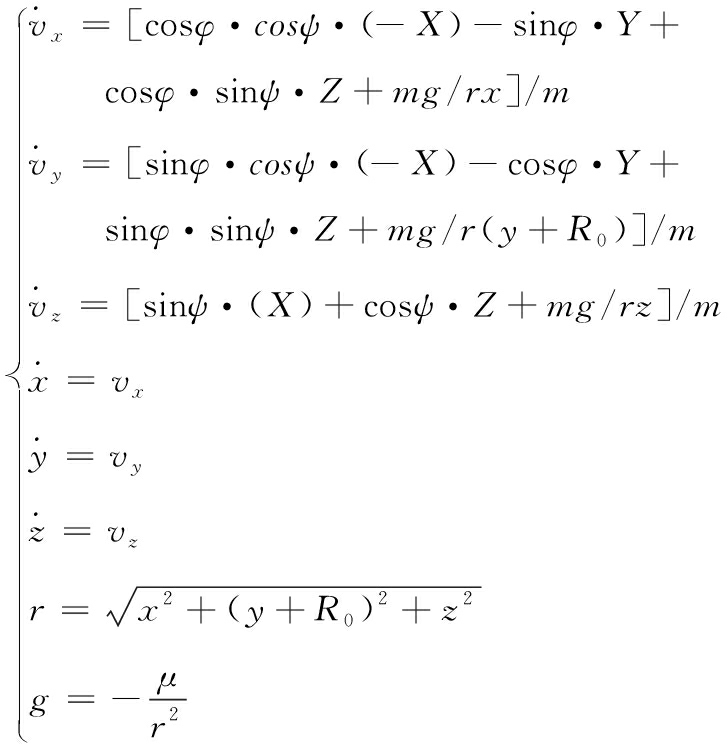
(1)
其中,φ、ψ为俯仰角和偏航角;X、Y、Z为气动力;R0为地球半径;m为RLV质量;x、y、z、vx、vy、vz为RLV的位置和速度;r为地心矢径; μ为地球引力常数;g为地球引力。
RLV运动时满足下列约束条件:
1) 边界约束

(2)
2) 路径(控制)约束:
![]()
(3)
3) 过程约束包括热流密度约束、动压约束和总过载约束,分别为

(4)
其中: kQ是与RLV结构相关的常数;![]() 和nmax分别为热流密度上限、动压上限和过载上限。
和nmax分别为热流密度上限、动压上限和过载上限。
4) 目标函数。针对上述非线性系统,hp自适应伪谱法优化的原理是:满足边界条件、控制约束和动力学模型的同时找到控制量攻角α和侧滑角β,满足:
J=min(ka·α2+kb·β2)
(5)
J最小化控制量的加权平方和,其中ka和kb是权重,当α、β约束范围不同时,可以通过调整ka和kb改变α、β的权重。
上述RLV再入段的最优控制问题,可以通过GPOPS Version5.0软件求解。
1.2 hp自适应伪谱法原理
关于RLV再入段弹道优化的最优控制问题可表述为:在满足边界和路径约束的条件下,寻找控制变量u=[α, β]T,使以下积分性能指标最小:
J=Φ(x(t0),t0,x(tf),tf)+![]() g(x(t),u(t),t)dt
g(x(t),u(t),t)dt
(6)
其中,t∈[t0,tf],x=[x,y,z,vx,vy,vz]T, Φ和g分别为终端和积分指标函数。
求解最优控制问题需满足下列约束:
1) 运动模型
(7)
2) 边界约束
E(x(t0),t0,x(tf),tf)=0
(8)
3) 路径(控制)约束
Cmin≤C(x(t),u(t),t)≤Cmax
(9)
hp自适应伪谱法将控制量和状态量在一系列离散点上离散化,构造离散点处的拉格朗日多项式逼近控制量和状态量,状态量的导数可通过对全局插值多项式求导获得。
将时间t分为K个子区间对应RLV再入段的k个阶段,有∀t∈[tk-1,tk], t0=t1<…<tK=tf,由式(10)可将t∈[t0,tf]转换到τ∈[-1,1],
(10)
其中,k=1,2,…,K。构造离散点处的拉格朗日多项式逼近状态量x和控制量u:
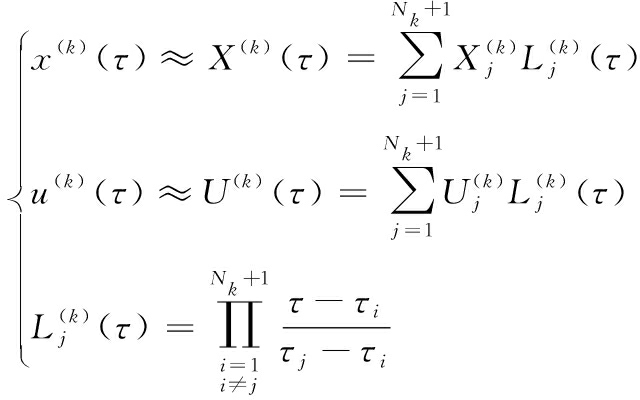
(11)
其中,Nk是阶段k的配点数目,X(k)(τ)和U(k)(τ)分别是阶段k的状态量和控制量的近似值,![]() 分别为τj处的状态值、控制量值和Lagrange多项式,τj是阶段k的节点。
分别为τj处的状态值、控制量值和Lagrange多项式,τj是阶段k的节点。
将式(11)代入式(7)运动方程,将状态量x和控制量u在Legendre-Gauss-Radau(LGR)点离散化:
(12)
其中,![]() 是阶段k的Nk×(Nk+1)阶状态微分矩阵。
是阶段k的Nk×(Nk+1)阶状态微分矩阵。
式(13)、式(14)是对RLV再入段约束条件的离散化。
边界约束:
(13)
路径(控制)约束:
(14)
式(6)所述性能指标函数在LGR点离散化后,近似为
(15)
1.3 BP神经网络原理
如图1所示,前向神经网络是一种3层网络结构,包括输入层、输出层和隐含层,BP神经网络(Back Propagation Neuron Network)是一种误差反向传播的前向神经网络,因其能逼近任意非线性函数和良好的学习能力而应用广泛[19]。
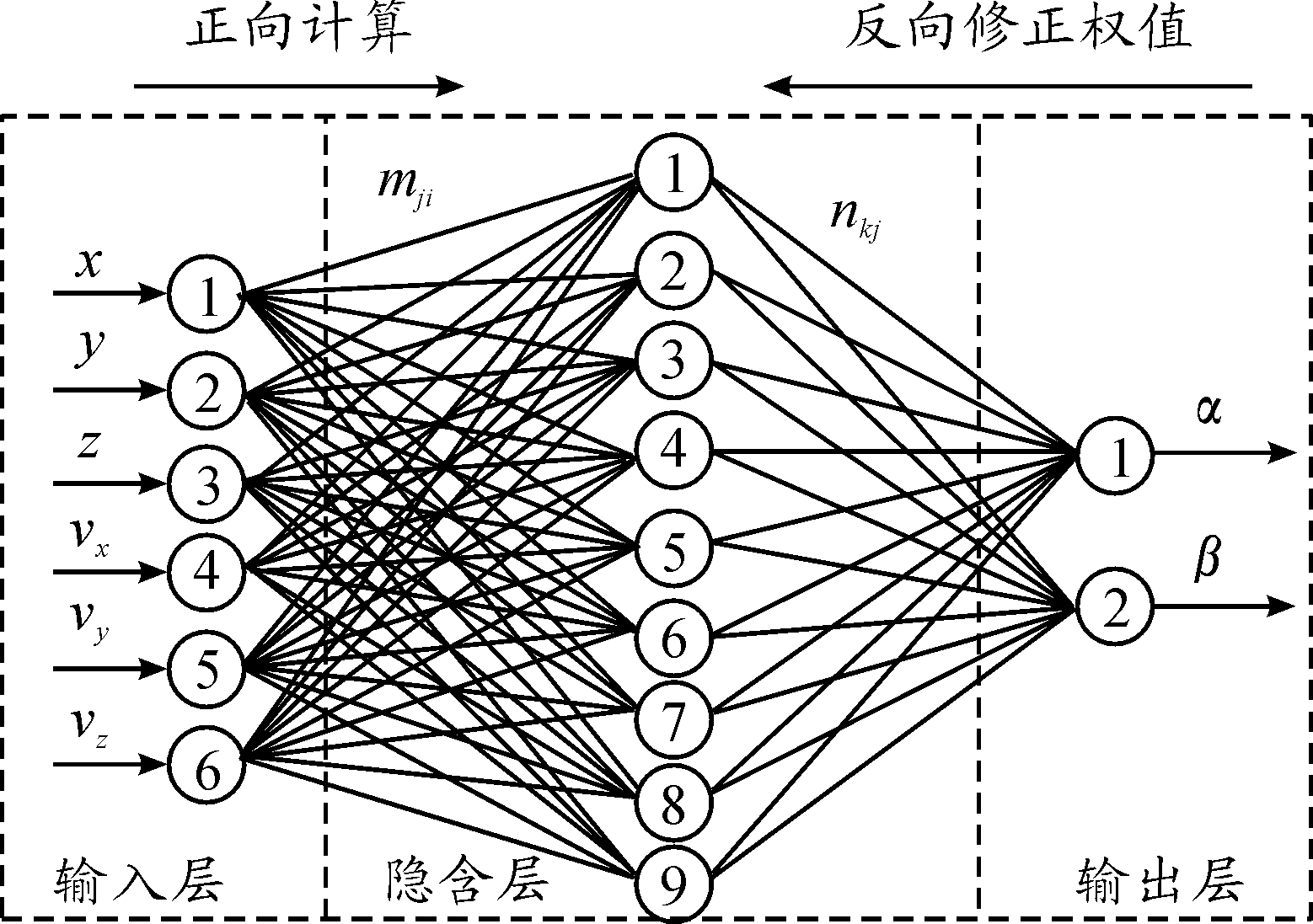
图1 BP神经网络模型
假设BP神经网络的输入层、隐含层和输出层神经元分别用变量i、j、k表示,其中,i=1,2,…,P、 j=1,2,…,Q、k=1,2,…,R神经网络的输入数据用X=[x1,x2,…,xP]表示,神经网络的输出数据用Y=[y1,y2,…,yR]表示。隐含层任意神经元的输入为netj,输出为yj:
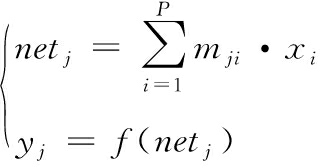
(16)
其中,mji是输入层和隐含层任意两神经元之间的权值,netj经过激活函数y= f(·)输出yj,常用的激活函数有线性函数、斜坡函数、阈值函数、S型函数和双极S型函数,可根据研究对象选择合适的激活函数。
输出层任意神经元的输入为netk,输出为yk:
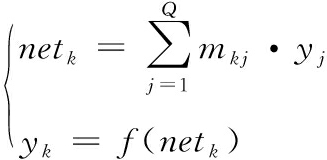
(17)
其中,mkj是输出层和隐含层任意两神经元之间的权值。当BP神经网络正向传播输出与期望值的误差未达到期望精度,就会反向传播修正权值,直到BP神经网络的输出达到期望精度。
2 神经网络制导控制器设计
设计神经网络制导控制器,关键在于通过伪谱法产生大量关于RLV状态量x、y、z、vx、vy、vz和控制量α、β的数据对构成样本库,样本库反映了RLV再入段状态量和控制量之间的非线性模型, BP神经网络通过学习样本库逼近非线性模型。对任意状态量x、y、z、vx、vy、vz,神经网络控制器都可以预测出控制量α、β。图2给出了设计神经网络制导控制器的方法和将其用于在线指导的总体方案。
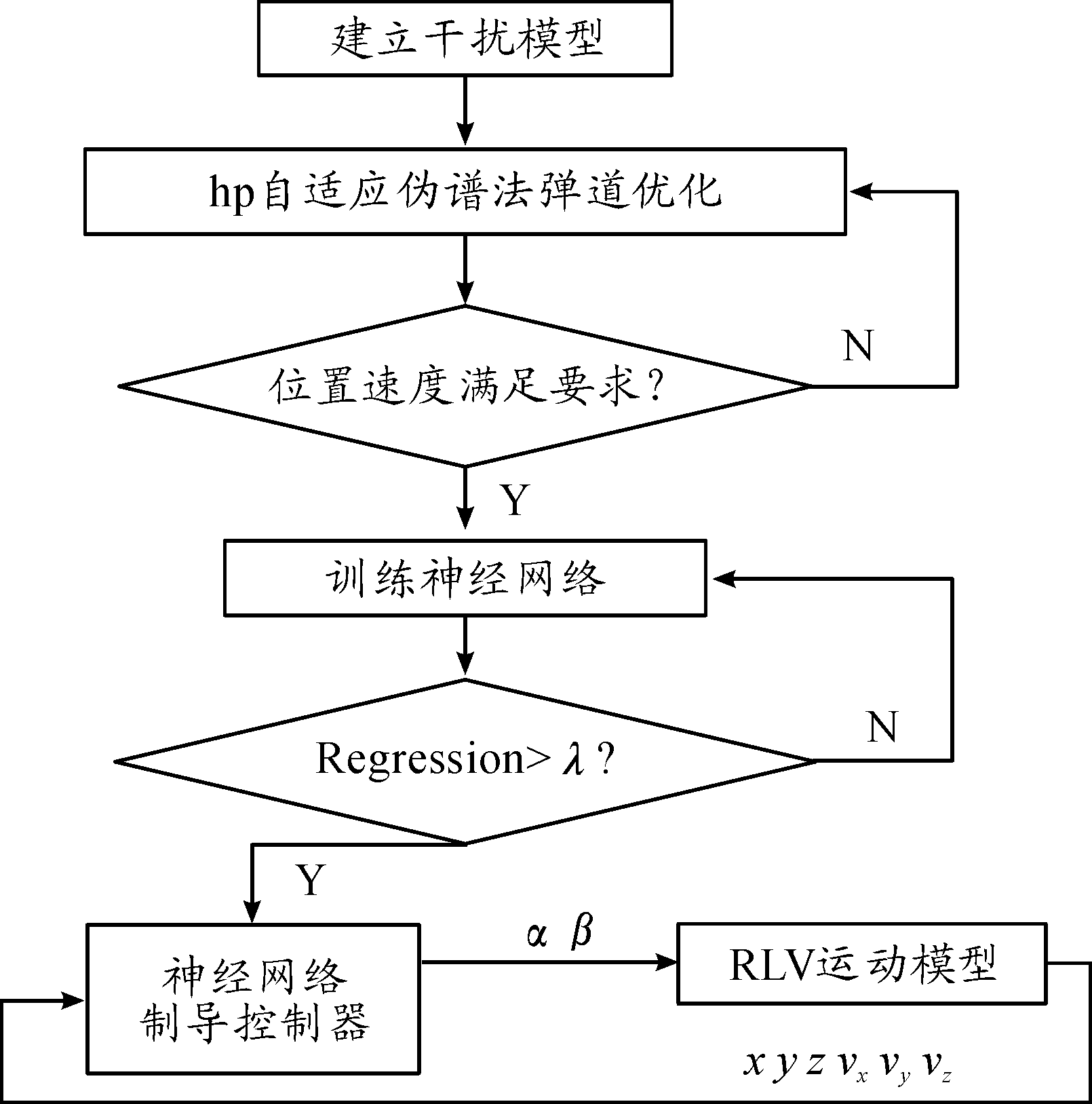
图2 神经网络制导控制器制导总体方案框图
制导总体方案实现步骤:
1) 对RLV的质量、气动系数、初始位置和偏差同时进行拉偏,产生多组干扰数据,构成干扰库;
2) 基于干扰库数据,多次利用hp自适应伪谱法优化弹道获得关于状态量和控制量的数据对,构成样本库;
3) BP神经网络训练样本库获得神经网络制导控制器,用神经网络控制器去逼近状态量和控制量之间的复杂非线性模型,其中步骤1)~3)都是离线完成;
4) 将神经网络制导控制器与RLV再入段运动模型构成闭环,飞行状态下RLV的运动状态量x、y、z、vx、vy、vz反馈到神经网络制导控制器,神经网络制导控制器再根据当前飞行状态实时产生制导指令α、β;
5) RLV将状态量x、y、z、vx、vy、vz反馈给神经网络制导控制器后,神经网络制控制器需要对状态量进行归一化、预测控制量、对控制量反归一化得到控制指令α、β。定义神经网络制导控制器从获取RLV反馈状态量到产生控制量α、β经历的时间T为制导周期,利用神经网络制导控制器进行飞行弹道积分仿真验证,评估其制导周期和鲁棒性。
2.1 建立干扰库
对RLV质量m、气动系数CA、CN、CZ、初始位置和初始速度x0、y0、z0、vx0、vy0、vz0施加组合干扰,10个干扰项的极值见表1。
表1 干扰项

Δx0/mΔy0/mΔz0/mΔCA/%ΔCN/%1001001001010-100-100-100-10-10Δvx0/(m·s-1)Δvy0/(m·s-1)Δvz0/(m·s-1)ΔCZ/%m/kg1010101010-10-10-10-10-10
在干扰项极值内产生100组随机组合干扰,为了在伪谱法优化阶段产生状态量x、y、z、vx、vy、vz的最大值和最小值,以防止神经网络制导控制器制导开始时对RLV反馈的状态量归一化时超出区间(0,1),需要对10个干扰项施加极限干扰得到20组极限单项干扰,上述问题得到解决,干扰库由这120组干扰数据构成。
2.2 基于伪谱法生成样本库
生成样本库框图如图3。RLV飞行任务是以目标速度(vxf,vyf,vzf)到达目标位置(xf,yf,zf),基于GPOPS软件建立伪谱法优化程序;将120组干扰施加到伪谱法优化模型,利用伪谱法产生120条优化弹道,由于hp自适应伪谱法得到的数据点比较少,不能较好的覆盖飞行全过程,无法精确反映出任意弹道状态点上的非线性模型,所以需要对伪谱法产生的状态量和控制量进行插值,或者以步长0.01对伪谱法产生的控制量进行四阶龙格库塔积分计算,得到大约85.5万个关于状态量x、y、z、vx、vy、vz和控制量α、β的样本对,构成样本库。
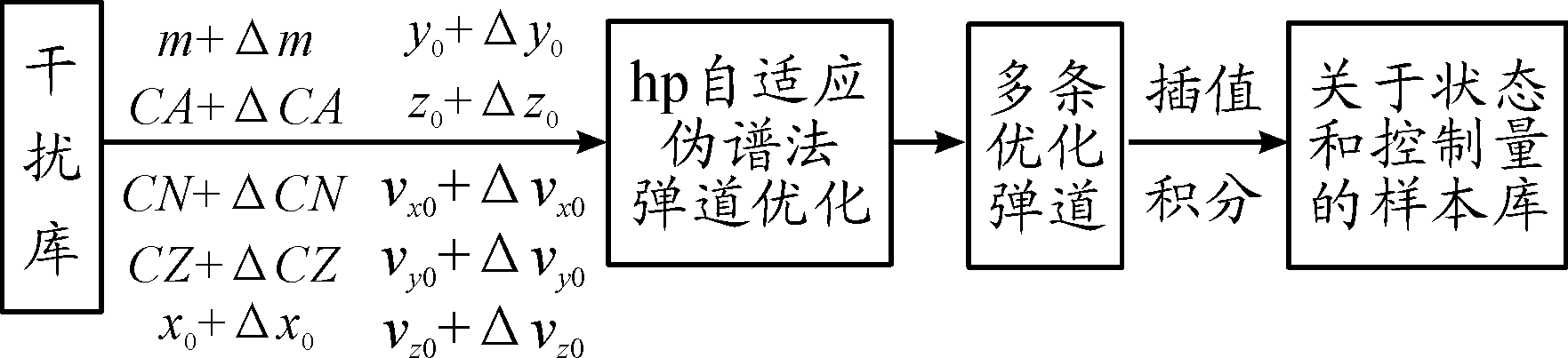
图3 伪谱法产生样本库框图
2.3 BP神经网络学习样本库
BP神经网络学习样本库的算法流程如图4所示。对样本库进行数据归一化处理,目的在于:样本数据范围大小在模式分类中的作用程度差别较大,会降低神经网络收敛速度,使训练时间变长,要避免输入神经网络的数据范围过大;初始化神经网络隐藏层神经元个数、权值、阈值、迭代次数、学习率和目标误差ξ;神经网络正向传播计算隐含层和输出层的输出,当神经网络预测值和真实值的差小于目标误差ξ则输出保存权值,否则误差开始反向传播修正权值矩阵,再次进行训练,学习完所有样本后输出神经网络结构和权值矩阵;当样本库训练BP神经网络的拟合度(Regression)>λ,再用检测样本对神经网络模型进行检验,剔除过拟合和欠拟合的神经网络模型,最终得到神经网络制导控制器。
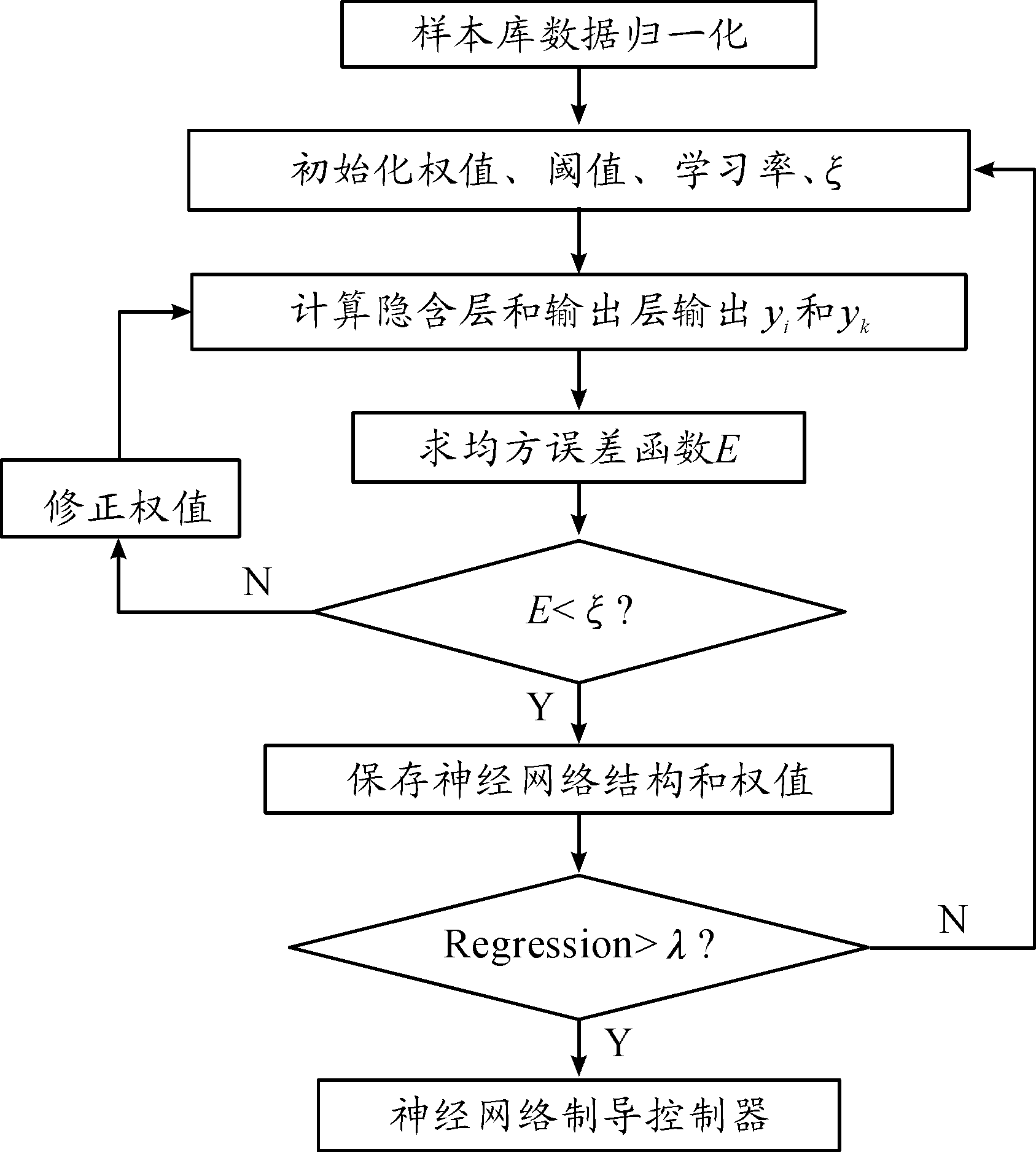
图4 BP神经网络学习算法流程框图
3 仿真验证
3.1 伪谱法计算
用伪谱法的弹道优化计算软件环境:Win10 64 bit操作系统、MATLAB R2019a;仿真计算硬件环境Intel Corei7-7700处理器、16.0 GB RAM。RLV弹道优化约束条件如表2所示。
表2 约束条件

[x y z]/mv/(m·s-1)α/(°)[x0 y0 z0] =[508 347 17 298 15 889]v0=1 677αmax=3[xf yf zf] =[538 925 -17 937 17 175]vf=185αmin=-3β/(°)q/kPan/gβmax=2qmax=60nmax=7βmin=-2qmin=0nmin=0
图5~图10表示了标准条件下hp自适应伪谱法所得优化弹道参数,图5~图10同时给出了基于伪谱法产生的控制指令进行弹道积分计算得到的结果,图11给出了过载和动压曲线。
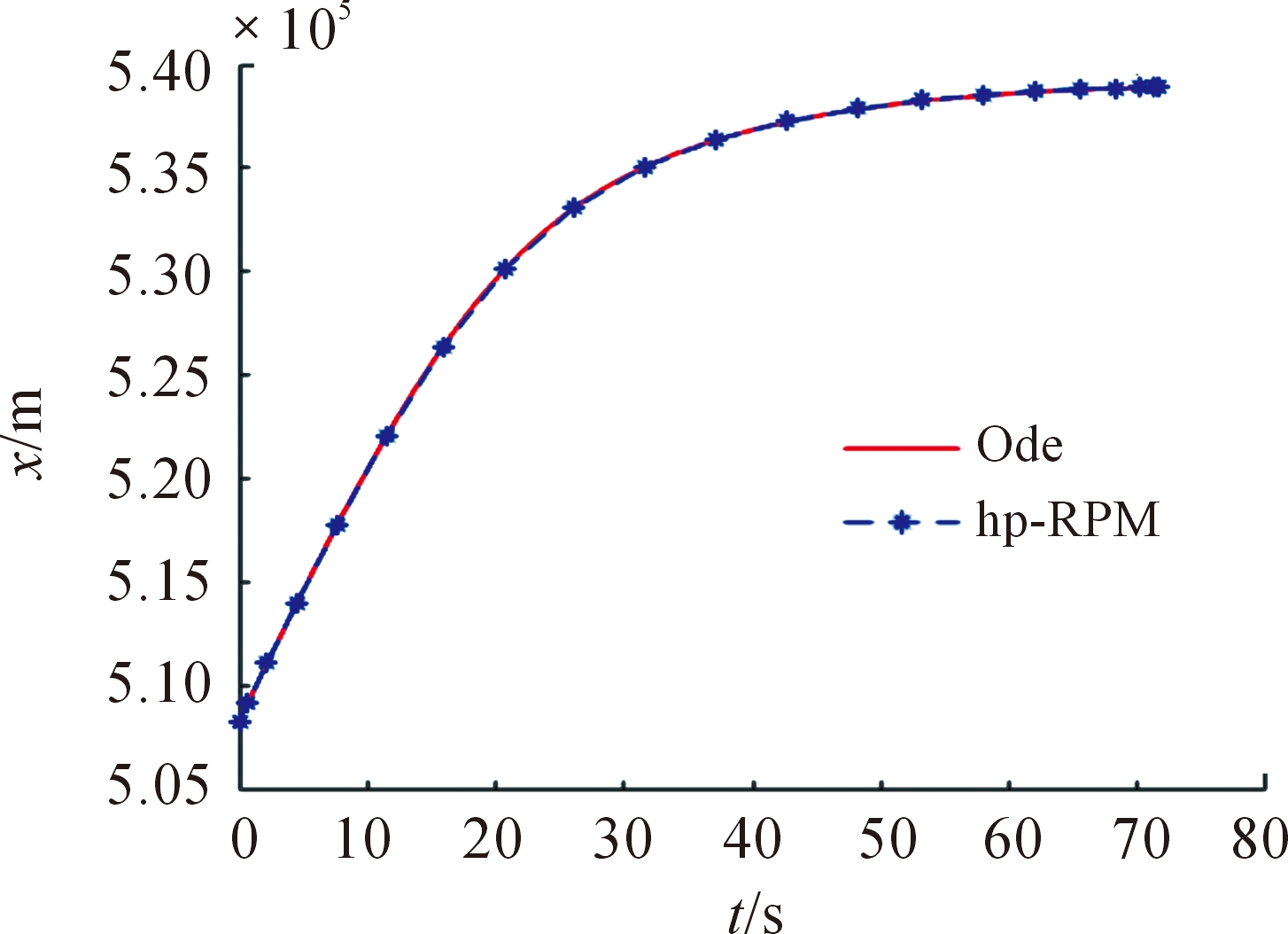
图5 位置x曲线
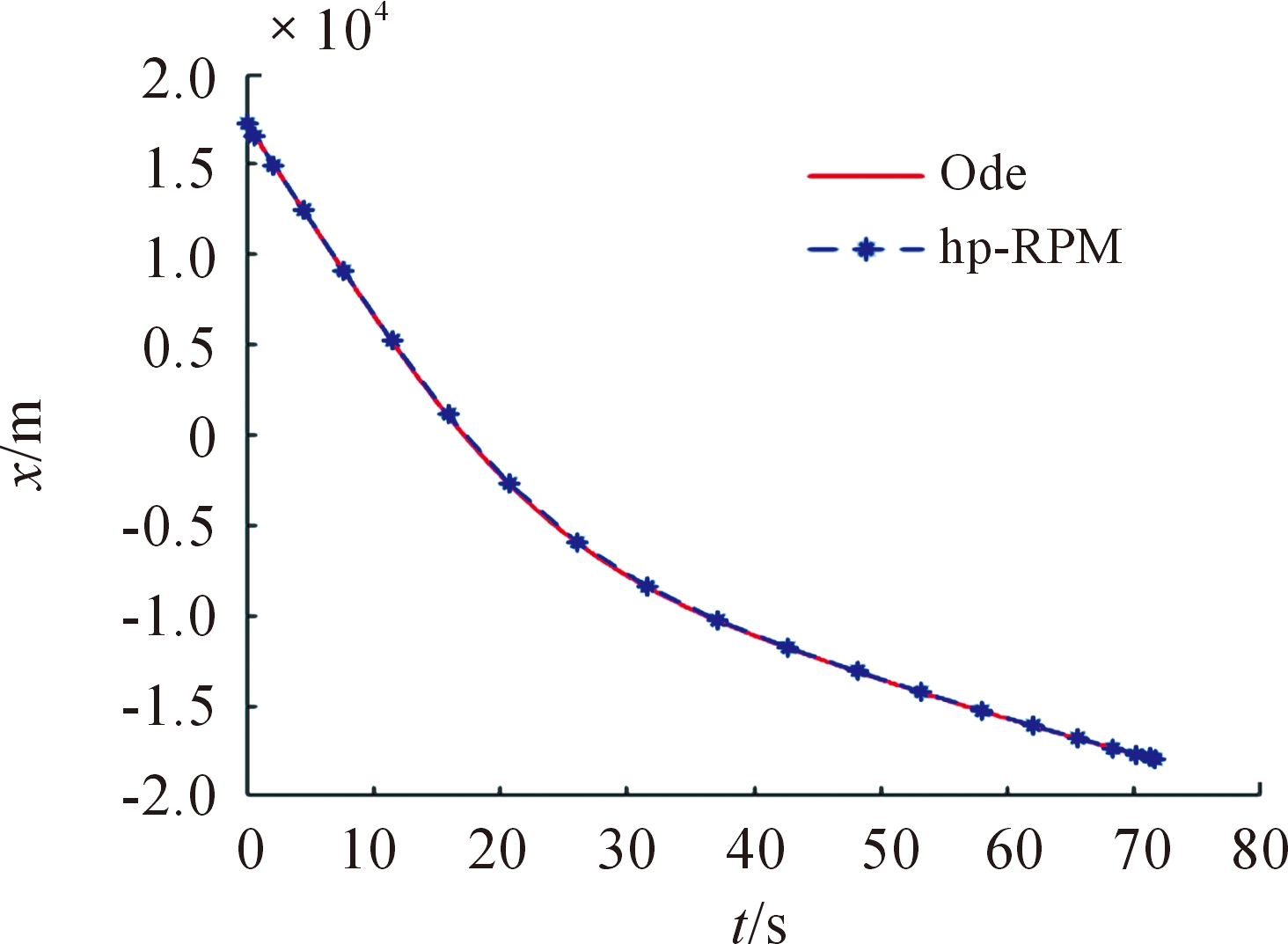
图6 位置y曲线
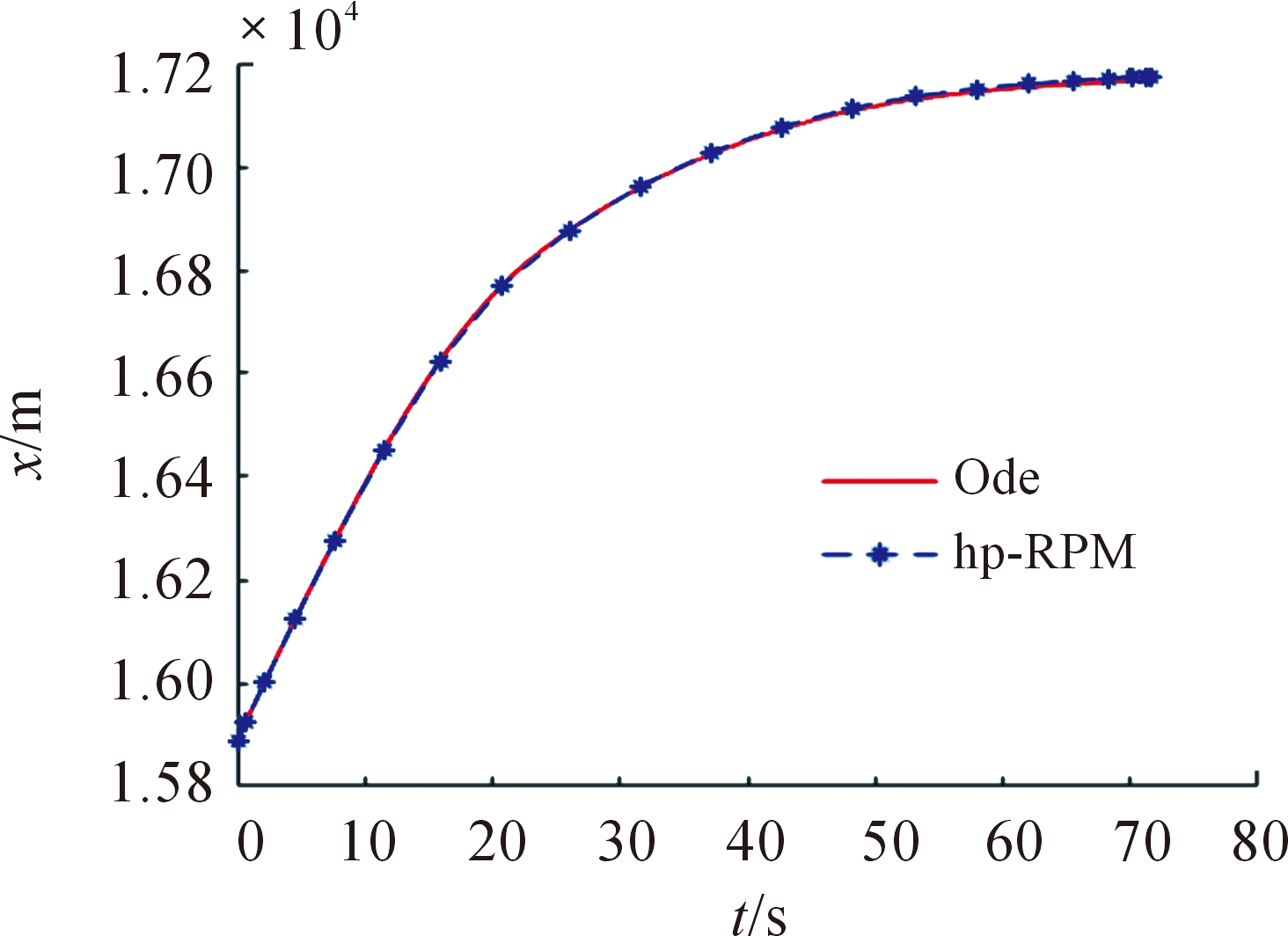
图7 位置z曲线
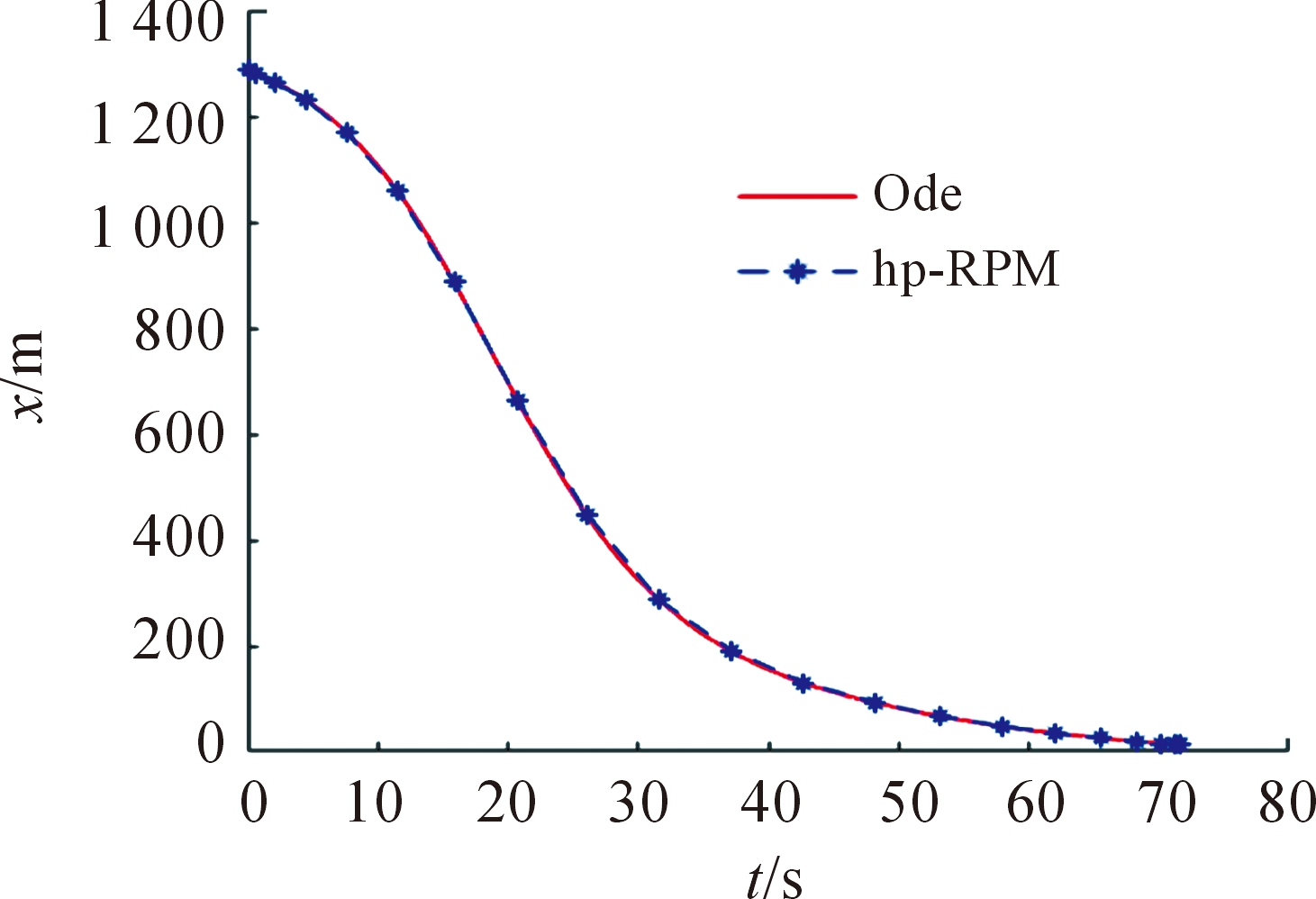
图8 速度vx曲线
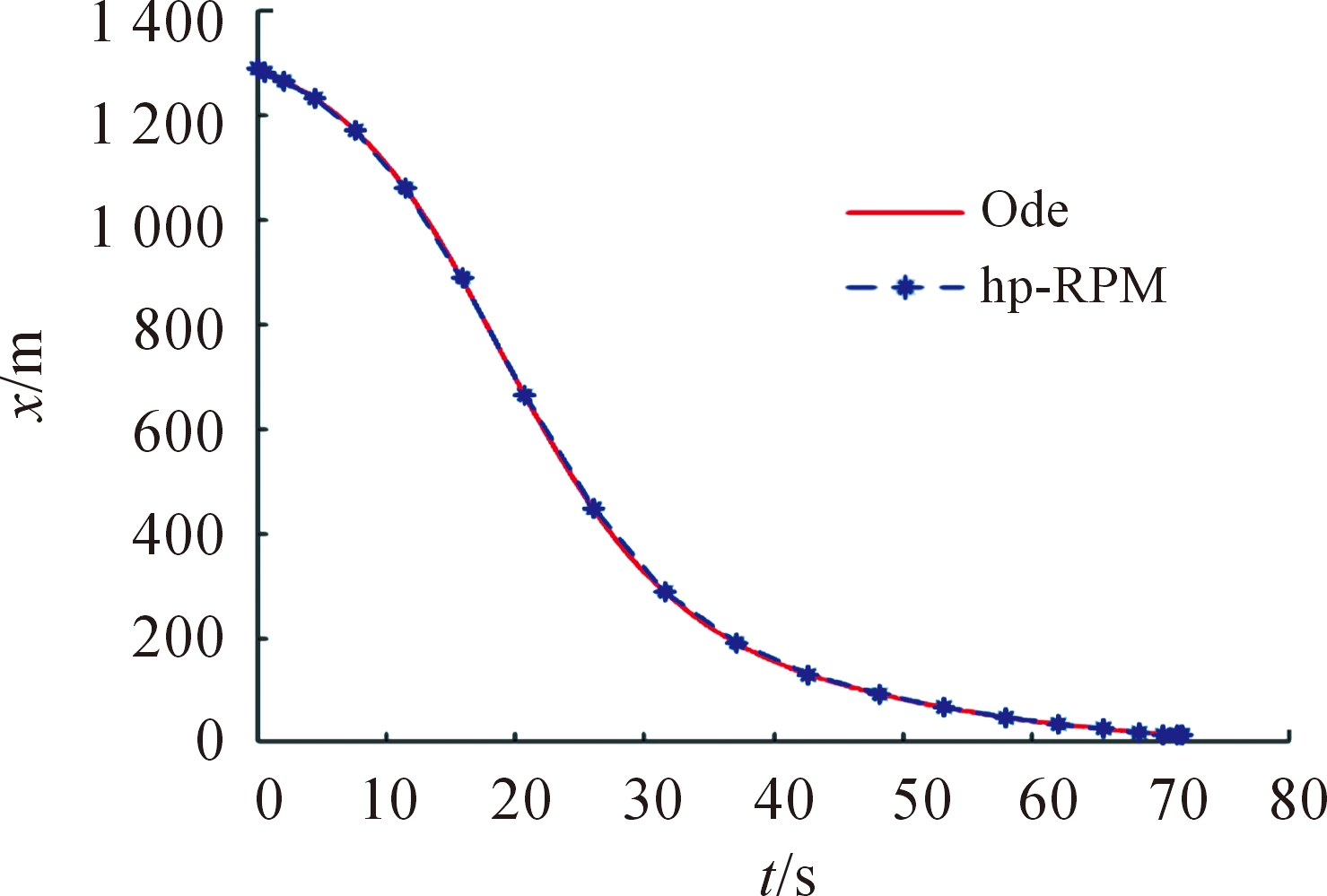
图9 速度vy曲线
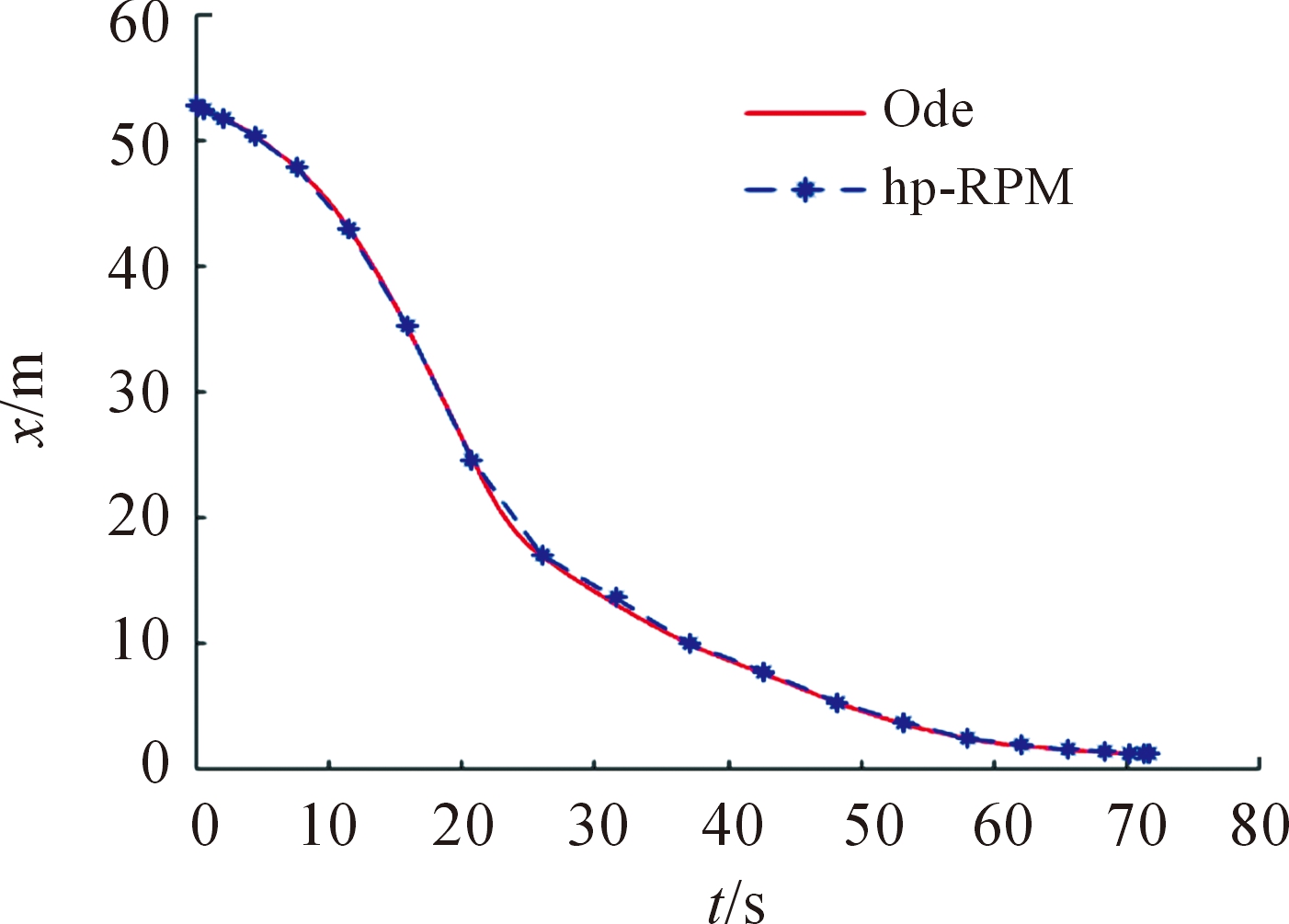
图10 速度vz曲线
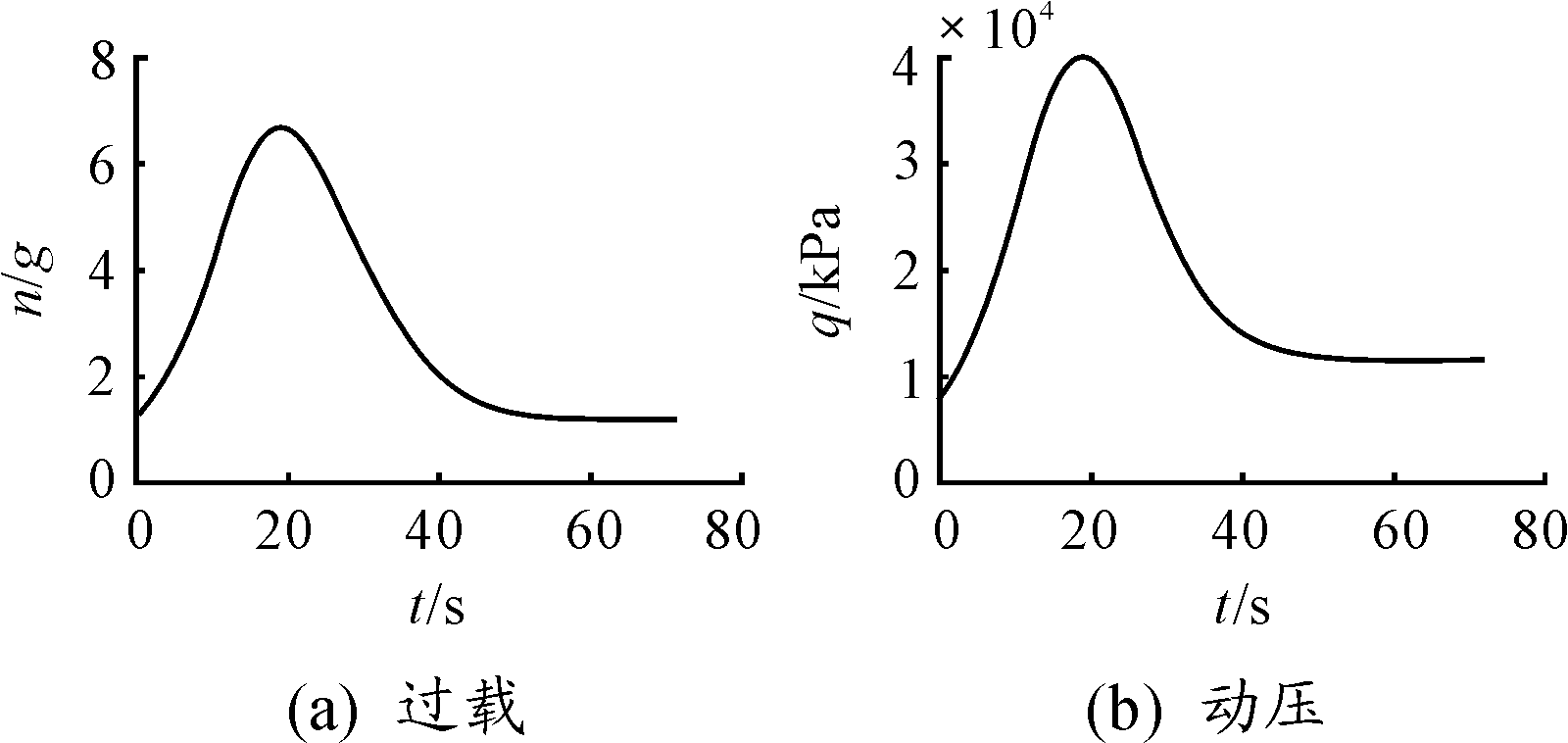
图11 过载和动压变化曲线
表3给出了标准条件下弹道积分和伪谱法优化所得状态终端值satea、sateb的相对偏差ERR,ERR定义为式(18)。
ERR=|satea-sateb|/satea
(18)
表3 终端值相对偏差

x/%y/%z/%vx/%vy/%vz/%0.006 860.1330.044 10.187 60.040 30.049 3
可以看出,伪谱法和弹道积分计算结果一致,终端值最大相对偏差小于0.2%,由图11可知过载和动压小于上限值,表明通过伪谱法可以得到有效满足终端状态的控制指令。
图12给出了120组干扰数据的伪谱法弹道优化的结果。
可以看出RLV飞行时间为68~76 s,位置和速度准确收敛到终端值。对伪谱法产生的状态量和控制量插值得到样本库,用样本库训练BP神经网络得到神经网络制导控制器。

图12 伪谱法弹道优化曲线
3.2 神经网络制导控制器制导仿真
随机产生200组组合干扰验证神经网络制导控制器的制导效果,xi、yi、zi、vxi、vyi、vzi表示每组数据的终端位置和速度,仿真终止条件为|yi-yf|≤2,总位置偏差L和总速度偏差V定义为式(19)和式(20):
(19)
(20)
可以看出,不同组合干扰条件下RLV终端位置和终端速度能够收敛到同一区域。由于组合干扰包含初值偏差,RLV的起始位置和速度成分散状态,图13表明:RLV位置从起点(图右下方)逐渐向终端位置(图左上方)收敛,图14表明RLV速度从起点(图14左上方)向终端速度收敛(图14右下方)。图15给出了200次仿真的终端位置偏差。
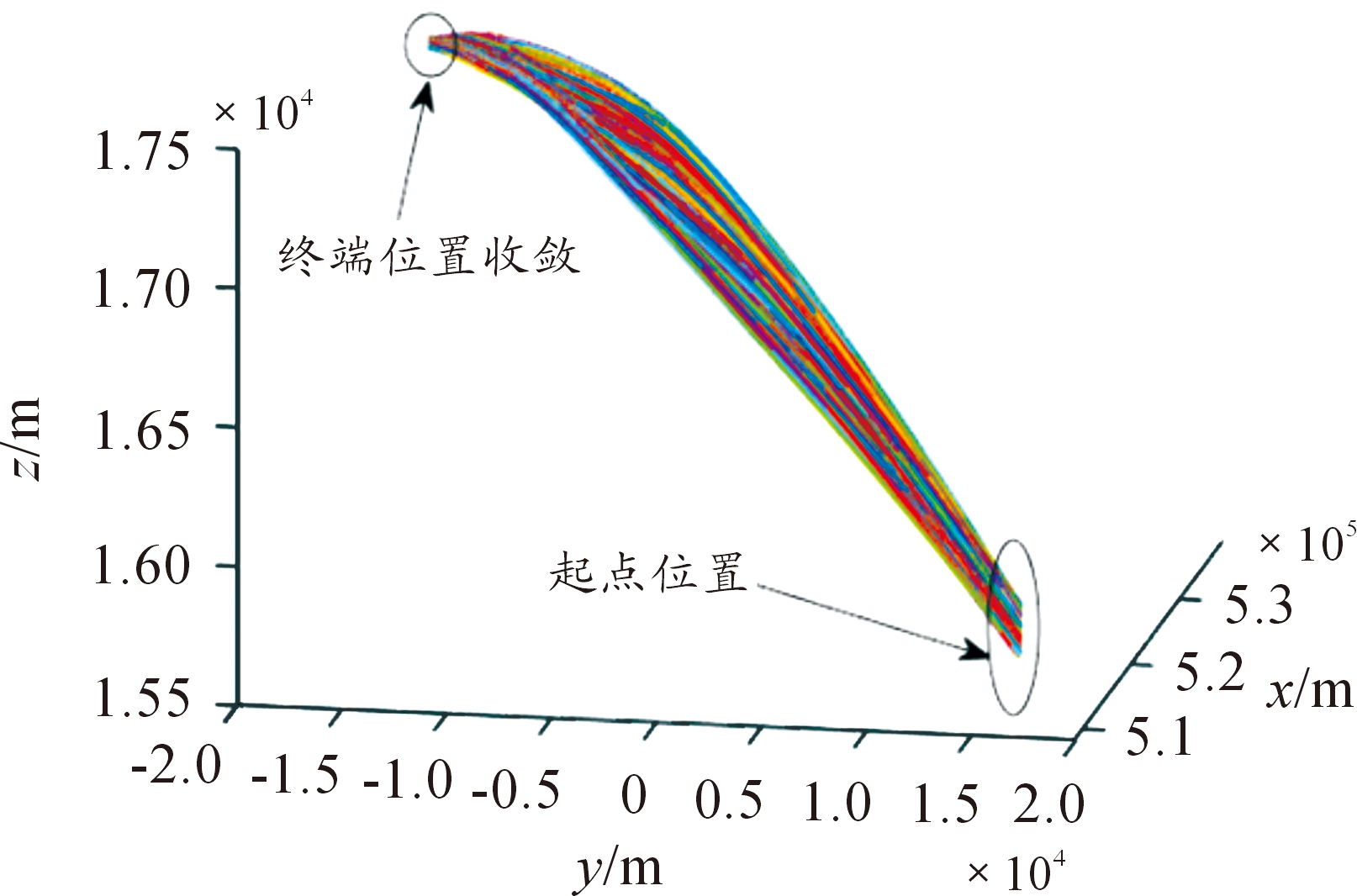
图13 RLV空间运动曲线
200次仿真的平均总速度偏差为5.42 m/s,平均总位置偏差为13.48 m,最大总位置偏差为45 m,说明RLV终端位置分布在以目标点(538 925, -17 937, 17 175)为圆心,半径为45 m的圆球区域内。
假设RLV飞行过程中还存大气环境干扰,同时对大气压强和密度施加幅值为理论值50%的正弦干扰进行仿真,结果见表4。

图14 RLV速度曲线

图15 位置偏差曲线
表4 终端值绝对偏差

x/my/mz/mvx/(m·s)vy/(m·s)vz/(m·s)0.280.660.590.650.580.43
可以看出,存在大气环境等其他干扰时,神经网络制导控制器能够保持比较稳定的制导效果。无论是初值偏差、气动系数偏差和还是环境干扰,最终都将导致RLV的飞行状态发生变化产生控制量,这些扰动对于神经网络制导控制器来说相当于黑箱,所以能够有效克服不同类型的组合干扰。
4 结论
本文提出基于伪谱法的神经网络制导控制器,充分利用hp自适应伪谱法和BP神经网络的优势,具有强鲁棒性能和求解速度快的特点。所提出的制导方案能够有效适应各类干扰影响,终端位置和速度误差较小,具有较强的鲁棒性能;制导周期小于0.01 s,可满足工程应用需求。
[1] 张鹏.可重复使用运载器再入预测校正制导与控制系统设计[D].南京:南京航空航天大学,2018.
[2] 黄长强,国海峰,丁达理.高超声速滑翔飞行器轨迹优化与制导综述[J].宇航学报,2014(4):369-379.
[3] MA L,SHAO Z J,CHEN W F,et al.Three-Dimensional Trajectory Optimization for Lunar Ascent Using Gauss Pseudospectral Method[R].AIAA-2016-1372.
[4] 雍恩米,陈磊,唐国金.飞行器轨迹优化数值方法综述[J].宇航学报,2008,29(2):397-406.
[5] 彭祺擘,李海阳,沈红新,等.基于Gauss伪谱法和直接打靶法结合的月球定点着陆轨道优化[J].国防科技大学学报,2012,34(2):119-124.
[6] XIU Y L.Study on Mars Atmospheric Entry Trajectory Optimization and Guidance[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2014.
[7] HERMANT A.Optimal control of the atmospheric reentry of a space shuttle by an homotopy method[J].Optimal Control Applications and Methods,2011,32(6):627-646.
[8] 王海涛. 基于hp自适应Radau 伪谱法的再入飞行器轨迹优化[J].科学技术与工程,2015(02):165-171.
[9] 邱文杰,孟秀云.基于hp自适应伪谱法的飞行器多阶段轨迹优化[J].北京理工大学学报,2017(04):412-417.
[10] TOHIDI E,LOTFI N S.An efficient legendre pseudospectral method for solving nonlinear quasi bang-bang optimal control problems[J].Journal of Applied Mathematics,Statistics and Informatics,2012,8(2):73-85.
[11] 韦常柱,琚啸哲,徐大富,等.垂直起降重复使用运载器返回制导与控制[J].航空学报,2019,40(7):322782.
[12] 崔乃刚,郑殿双,李源,等.运载器大气层内轨迹在线规划与闭环制导[J].战术导弹技术,2017(04):11-17.
[13] DUKEMAN G A. Profile-following entry guidance using linear quadratic regulator theory[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit. Reston:AIAA Inc.,2002:1-10.
[14] 沈作军,朱国栋.基于轨迹线性化控制的再入轨迹跟踪制导[J].北京航空航天大学学报,2015(11):1975-1982.
[15] 赵汉元.航天器再入制导方法综述[J].航天控制,1994(1):26-33.
[16] TIAN B,ZONG Q.Optimal guidance for reentry vehicles based on indirect Legendre pseudospectral method[J].Acta Astronautica (S0094-5765),2011,68(7/8):1176-1184.
[17] 廖瑛,季海雨,薛高雄.基于伪谱法的巡航导弹最优闭环制导方法[J].系统仿真学报,2018(9):3464-3471.
[18] 曾庆华,董荣华,皮术武.基于最优制导模板的神经网络预测制导方法[J].国防科技大学学报,2014,36(01):137-141.
[19] 黄丽.BP神经网络算法改进及应用研究[D].重庆:重庆师范大学,2008:8-15.