电磁继电器是信号控制的基础电子元器件，具有信号传递、执行控制、系统配电等功能[1]，在航天器控制系统、测量系统等核心设备中应用广泛。航天器在全寿命周期过程中会经历复杂多样的冲击环境，在冲击载荷作用下，电磁继电器容易发生触点的误动作，甚至造成内部结构的变形与破坏，导致输出控制信号异常，严重影响航天器可靠性[2,3]。电磁继电器冲击失效边界是指一系列导致电磁继电器发生临界失效的冲击环境的包络，当冲击环境达到失效边界时，即认为该冲击环境将导致电磁继电器发生失效。目前电磁继电器冲击失效边界的研究还不够系统全面，从而导致两个问题：首先，传统的航天电子设备研制方法依然采用“试错”式流程，即设计生产完成后，需要开展一系列冲击环境试验，若试验未通过则需要重新更改设计，极大地影响了研制效率与研制成本；其次，某些关键航天电子设备中的电磁继电器处于临界失效冲击环境附近，地面试验并不能完全包络天地差异以及冲击环境散差，导致实际飞行过程中电磁继电器存在发生失效的风险，进而可能引发航天电子设备故障，甚至造成飞行事故。因此，为了提高航天电子设备研制效率，降低研制成本，确保航天器的可靠性与环境适应性，亟需针对电磁继电器冲击失效边界开展研究。
电磁继电器利用输入电流或电压，在电磁铁铁芯与衔铁间产生的吸引力作用而工作[4]。针对电磁继电器的振动特性，翟国富等[5-6]通过分析电磁继电器簧片系统结构，建立了簧片系统振动特性数学模型，给出了求解簧片系统振动响应的解析表达式以及检验电磁继电器触簧系统抗振性的判据，并分析了影响电磁继电器触簧系统振动加速度的相关因素，包括材料特性参数、尺寸参数、触点初压力、触点质量等。任曾勋[7]通过建立继电器的数学模型，研究了继电器在冲击载荷作用下的动力响应特性，针对几种典型的冲击载荷给出了响应的解析解和首次断开的时间间隔，并讨论了继电器的断开条件。陈英华等[8]通过有限元仿真和振动台试验对电磁继电器冲击特性进行了研究，分析了在不同幅值、方向冲击载荷下继电器接触系统的触头间力响应时间历程和“抖断”现象，归纳了尺寸参数与继电器冲击特性间的影响关系，给出了提高电磁继电器耐冲击性能的方法。综上所述，现有研究主要集中在振动冲击环境对于继电器性能的影响，而对于电磁继电器冲击失效边界的系统性研究较少。
本研究首先结合电磁继电器的结构形式与工作原理，建立简化的力学模型，对电磁继电器冲击动力学响应与失效模式进行分析，得到不同失效模式的控制参数与失效边界；设计并开展电磁继电器临界失效冲击试验，通过不同冲击环境的逐级加载，得到电磁继电器的冲击失效边界，验证理论分析的结果，为航天电子设备冲击环境适应性设计提供参考。
1 电磁继电器冲击动力学响应与失效模式分析
电磁继电器作为一种常用的电子元器件[9]，主要由线圈、衔铁、触簧等部件组成(如图1所示)，其中触簧系统是电磁继电器的重要组成部分，也是完成输出功能的执行机构。触簧系统主要包括基座、动簧片、静簧片、动触头、静触头等(如图2所示)，在电磁驱动力作用下，动触头与静触头保持接触或断开，实现信号控制等功能[9-10]。
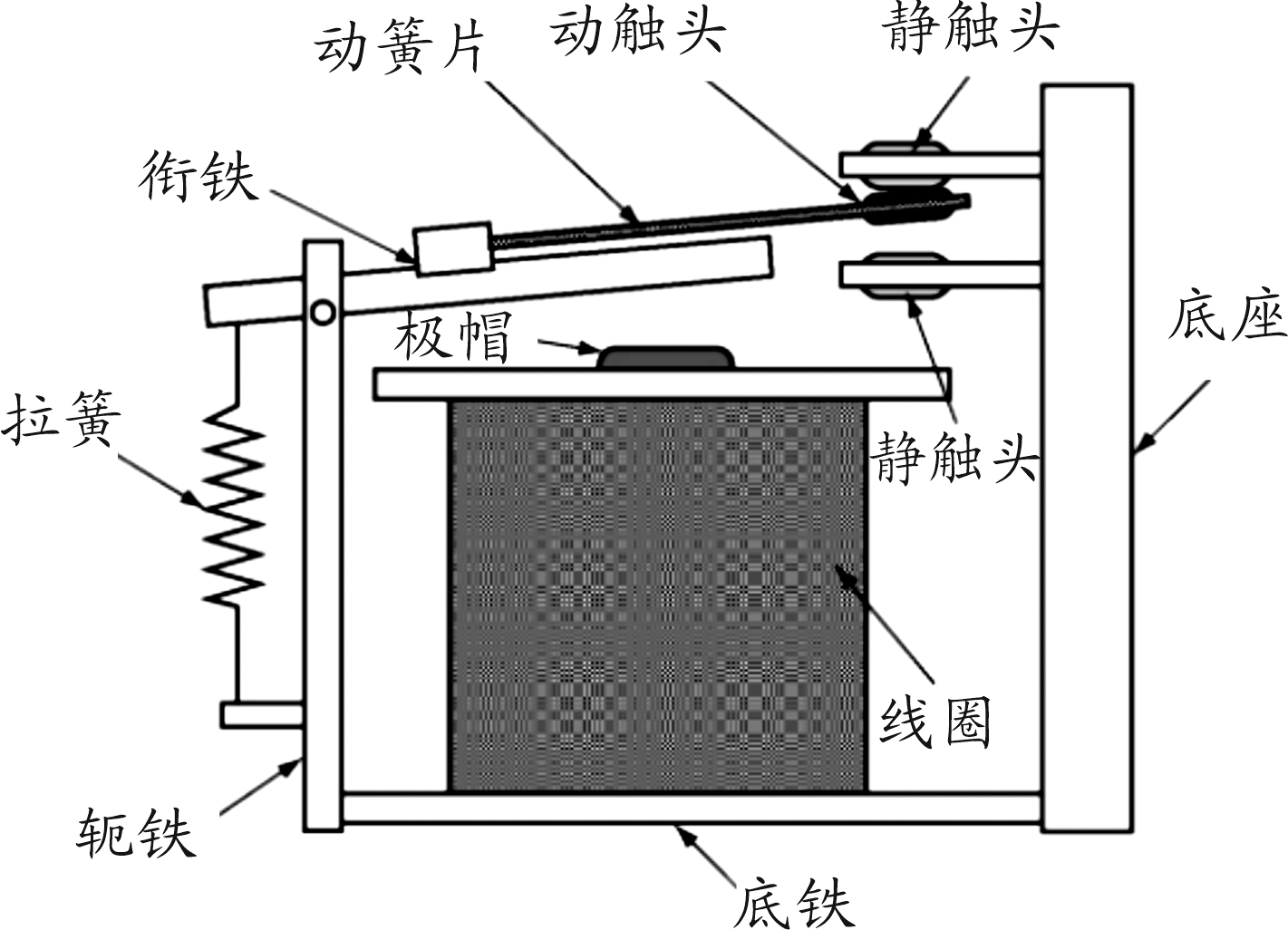
图1 电磁继电器结构示意图
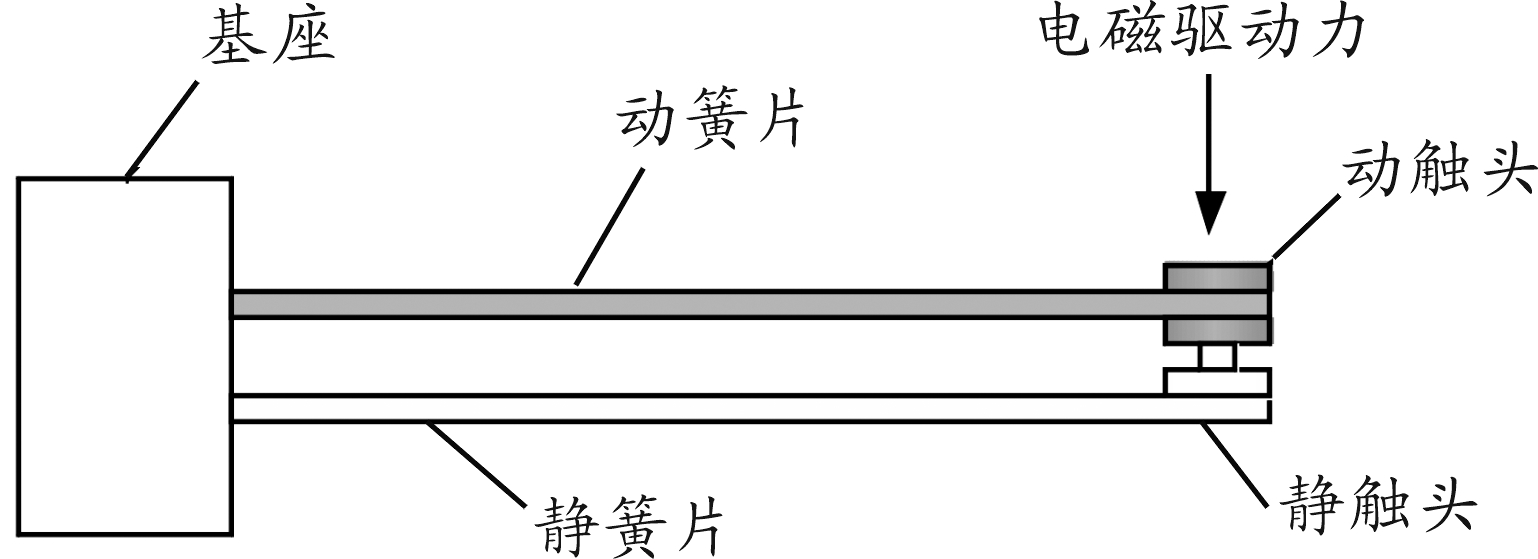
图2 触簧系统结构示意图
根据触簧系统特性，可以将其简化为一端固支、一端活动铰支的等截面梁，梁上质量均匀分布，动触头可以简化为与梁固连的集中质量，如图3所示。
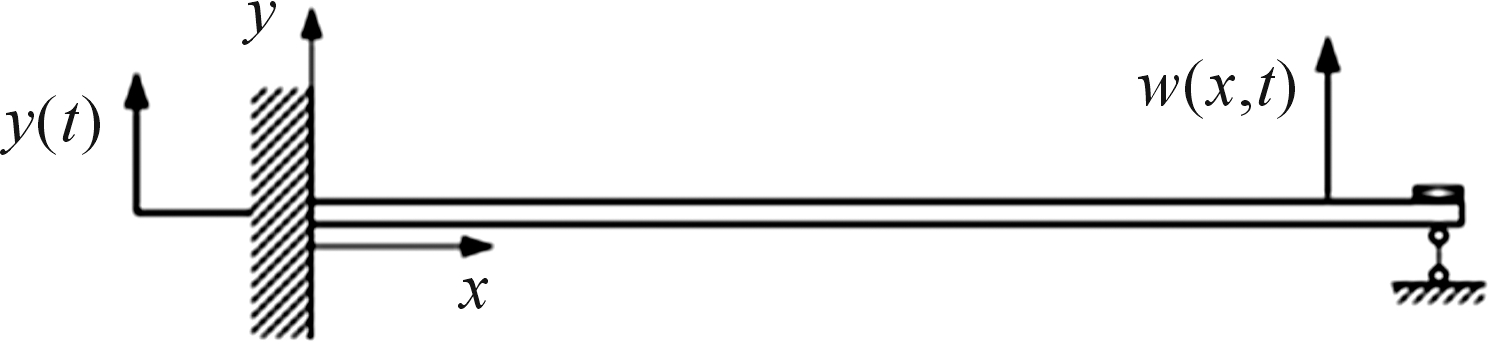
图3 触簧系统简化力学模型
冲击载荷的作用可以等效为基础激励y(t)，触梁的绝对位移响应为w(x,t)，触梁结构的相对位移为z(x,t)=w(x,t)-y(x,t)，忽略阻尼效应，梁的运动平衡方程为
(1)
其中： A为梁的截面积； ρ为材料密度；EI为抗弯刚度。
利用振型叠加法，假设方程解的形式为
(2)
其中：Zi(x)为第i阶主振型；Ti(t)为第i阶广义位移。梁结构边界条件为
z(0,t)=z′(0,t)=0
z(l,t)=z″(l,t)=0
(3)
假设满足边界条件的主振型函数为
Zi (x) = Ci (sin(ki x)-sh(ki x)) +
Di (cos(ki x)-ch(ki x))
(4)
其中：
为各阶固有频率，可以根据主振型函数与边界条件求得；系数Ci、Di由初始条件确定。Ti(t)可由广义自由度运动方程求得
(5)
其中： Fi(t)=
q(x,t)Zi(x)dx为广义力；
为等效外部激励；
为广义质量；
为广义刚度。
梁上各点处剪力为
(6)
触点处的支反力Fy为
Fy=Q(l,t)
(7)
记静止状态下触点处的电磁驱动力为F0，则动触点与静触点保持接触的条件为
(8)
其中：mB为动触点质量；
为触点处加速度响应；g为重力加速度。由式(8)可以看出，若触点处某一时刻的加速度响应过大，则可能导致电磁驱动力不足以提供足够的支反力与惯性力，造成触点的瞬间抖动。冲击过程结束后，梁结构响应趋近于零，触点恢复闭合状态，因此 “触点抖动”是一种短时失效模式，且该失效模式由结构加速度响应导致。
在冲击载荷作用下，梁上各截面处最大正应力为
(9)
其中:
为梁上各点处的弯矩；h为梁截面的高度。当梁内部应力达到材料极限应力时，触梁结构将会发生永久变形甚至断裂破坏，即
σ(x,t)≥σc
(10)
其中，σc为材料极限应力，一般为材料的屈服强度或抗拉强度。触簧系统发生高应力失效破坏后，将导致继电器发生“常闭触点断开/常开触点闭合”的失效模式，且冲击结束后无法恢复，因此“常闭触点断开/常开触点闭合”是一种不可逆的失效模式，且该失效模式由结构内部应力导致。
2 基于冲击响应谱的失效边界
冲击环境主要特性包括幅值、持续时间、波形等，由于复杂冲击环境时间历程具有较大的随机性，因此一般采用冲击响应谱(Shock Response Spectrum,SRS)对冲击环境进行表征。冲击响应谱是指将冲击激励施加到一系列线性单自由度弹簧质量系统(如图4所示)，将各单自由度系统(SDOF)的最大响应值作为对应于系统固有频率的函数绘制而成的响应曲线[11]。
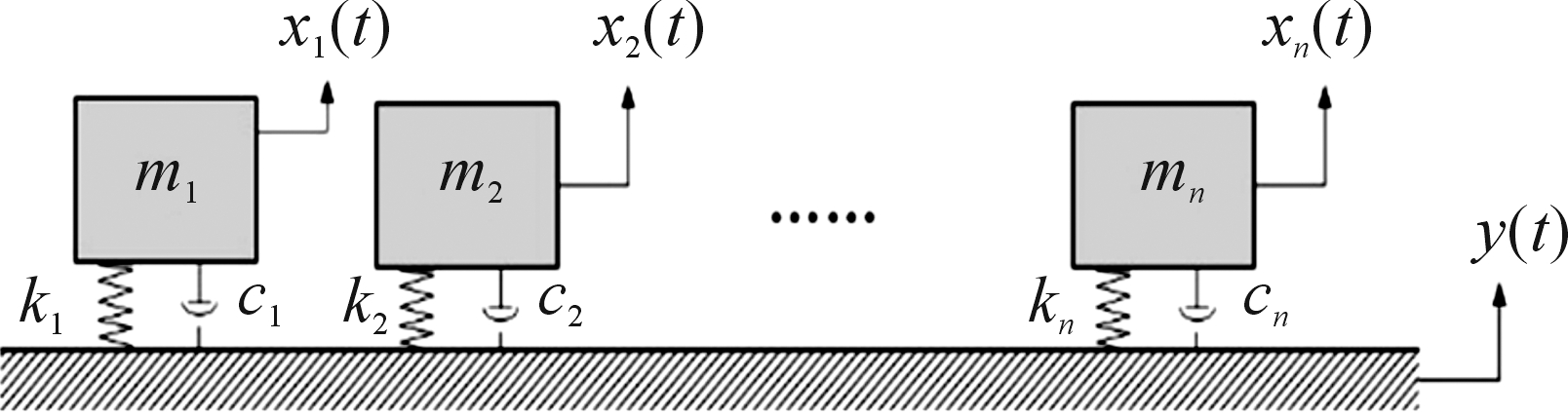
图4 受到基础激励的一系列单自由度系统示意图
将各单自由度系统的相对位移响应、伪速度响应、绝对加速度响应在时域的最大值绘制成谱即可得到相对位移冲击响应谱、伪速度冲击响应谱、加速度冲击响应谱，三者之间存在如下关系[12-14]
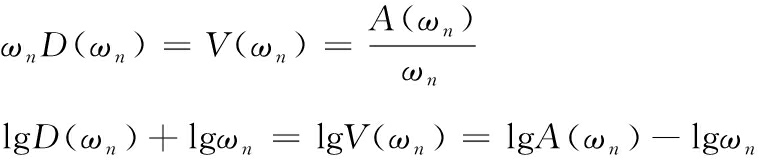
(11)
其中，D、V、A分别为相对位移冲击响应谱、伪速度冲击响应谱、加速度冲击响应谱的谱值
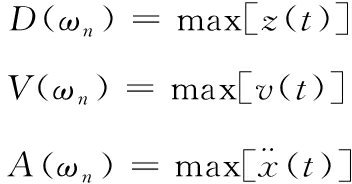
(12)
其中，
分别为固有频率为ωn的单自由度系统在时域最大的相对位移响应、伪速度响应、绝对加速度响应。
任何一个结构系统的动力学响应都可以视为一系列单自由度系统响应的叠加，因此利用冲击响应谱可以表征结构在冲击载荷作用下的响应水平[15,16]。对于高加速度响应引发的电磁继电器触簧系统触点“触点抖动”的失效形式，其失效边界由结构加速度响应控制。因此，可以采用加速度冲击响应谱表征“触点抖动”的失效边界。当冲击环境加速度响应谱未达到损伤边界时，继电器不发生“触点抖动”失效；当冲击环境下加速度响应谱最大值达到或超过损伤边界时，继电器将发生“触点抖动”失效
(13)
其中：Amax 为加速度冲击响应谱最大值；Ac 为加速度冲击响应谱损伤边界。
对于高应力造成的电磁继电器“常闭触点断开/常开触点闭合”失效模式，其失效边界由结构内部应力水平控制。结构应力水平与冲击环境最大伪速度响应相关[13-14,17-18]，
σmax=κρcVmax/λ
(14)
其中：κ为结构形状系数；ρ为结构材料密度；
为结构中应力波传播速度；Vmax为冲击环境最大伪速度响应；λ 为载荷因子。对于受到横向激励的梁结构，结构形状系数κ为，
(15)
其中：h为梁表面与中性轴的距离；
为截面惯性矩；S为截面面积。因此，可以采用冲击环境伪速度冲击响应谱表征“常闭触点断开/常开触点闭合”的失效边界。当冲击环境伪速度响应谱未达到损伤边界时，继电器不发生“常闭触点断开/常开触点闭合”失效；当冲击环境下伪速度响应谱最大值达到损伤边界时，继电器将发生“常闭触点断开/常开触点闭合”失效，如式(16)所示
(16)
其中： Vmax为伪速度冲击响应谱最大值；Vc 为伪速度冲击响应谱损伤边界。
3 电磁继电器临界失效冲击试验方案
为了进一步探究电磁继电器冲击失效环境特性，验证理论分析的结果，设计并开展了电磁继电器临界失效冲击试验。选取同批次1JT10-1型电磁继电器，质量等级为“七专级”，参试电磁继电器安装在专用电路板上，每块电路板上均安装4只状态相同的电磁继电器，如图5所示。
图5 参试电路板
将冲击试验条件分为冲击响应谱拐点频率700 Hz与2 000 Hz两组，分别对应1号与2号参试电路板。每组加载量级由低到高逐级加载，直至电磁继电器发生失效。采用空气炮冲击试验台(如图6所示)模拟元器件所处的冲击环境，并实现规定试验条件的逐级加载。
利用分布于板上的5个测点对PCB板上冲击环境进行测量，其中1～4号测点为加速度传感器测点，5号测点为激光测点(如图5所示)。针对被测电磁继电器，通过测试设备采集电磁继电器输出的电压值信号，电磁继电器正常工作输出电压为：常开触点0±0.15 V，常闭触点5±0.15 V，若输出电压超过此范围，则认为继电器发生失效。
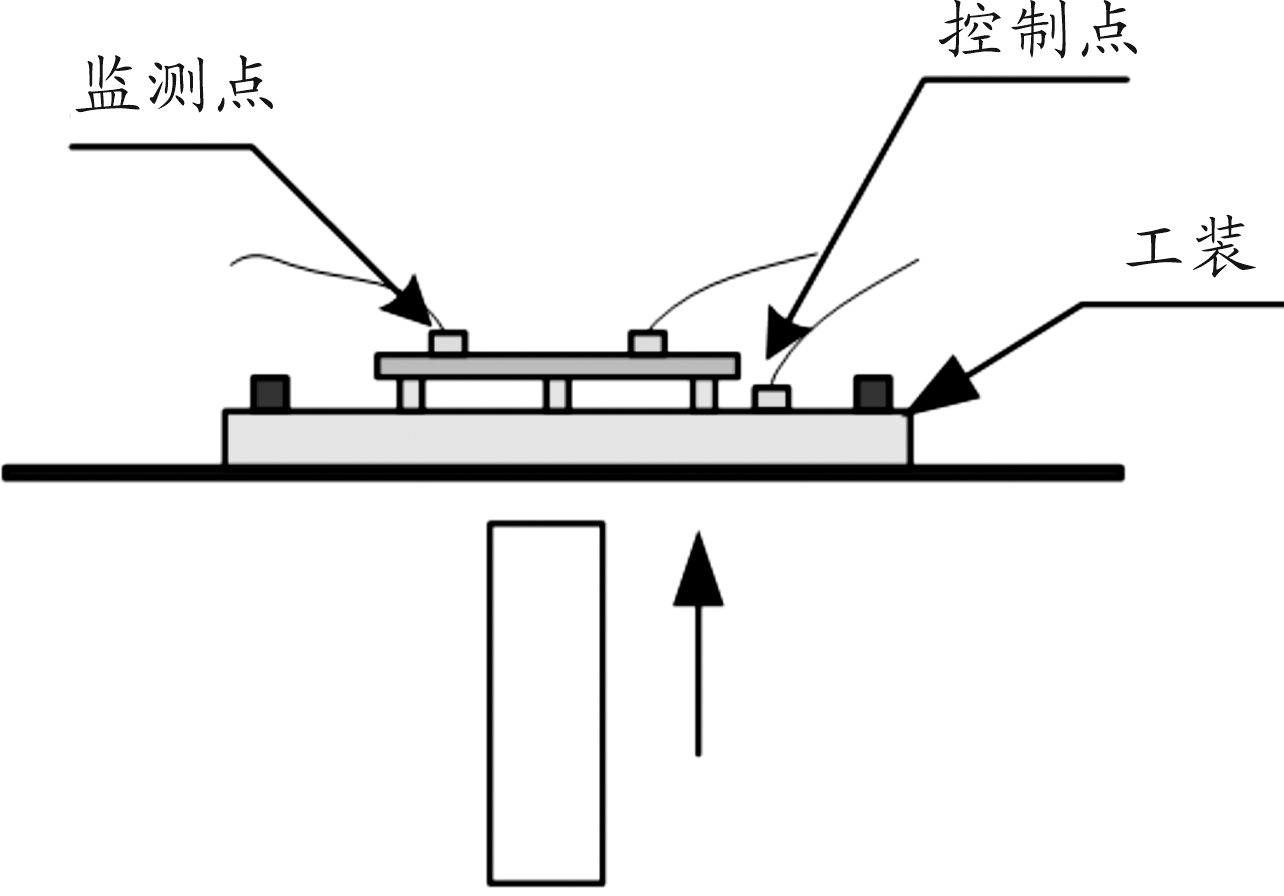
图6 空气炮冲击试验台示意图
4 试验结果与讨论
在700 Hz与2 000 Hz冲击响应谱拐点频率冲击环境逐级加载过程中，两组参试电磁继电器试验板先后发生“触点抖动”与“常闭触点断开/常开触点闭合”的失效模式。
4.1 “触点抖动”失效模式
随着载荷量级的逐步提高，电磁继电器首次发生“触点抖动”的失效模式时，两组参试电路板的电性能测试数据如图7所示，其中横坐标为采集时间，纵坐标为电压，实线为常开触点输出电压，虚线为常闭触点输出电压。可以看出，1号参试电路板1号、2号继电器的常闭触点与常开触点以及2号参试电路板1号继电器的常闭触点与常开触点，输出电压发生抖动且超过阈值。冲击结束后自检测，发生触点抖动的继电器输出电压均恢复正常。因此，可以认为电磁继电器“触点抖动”是冲击瞬间的短时失效模式。
首次发生“触点抖动”失效时，各测点测得的700 Hz与2 000 Hz拐点频率临界失效冲击环境的加速度冲击响应谱如图8所示，伪速度冲击响应谱如图9所示，其中横坐标为单自由度系统频率，纵轴为单自由度系统在冲击环境下的最大加速度/伪速度响应。可以看出，该失效模式发生时，不同频率临界失效冲击环境的加速度冲击响应谱水平相当，其中1号试验板为769～1 057 g，2号试验板为991～1 875 g；伪速度冲击响应谱则存在较大差异，其中1号试验板为2.12～2.71 m/s，2号试验板为0.78～1.52 m/s。
第1节与第2节理论分析得到，电磁继电器“触点抖动”失效由触簧系统加速度响应过大造成，加速度冲击响应谱可以表征冲击环境下结构系统加速度响应水平。冲击试验结果也表明，引发该失效模式的不同冲击环境的加速度冲击响应谱水平相当。因此，对于电磁继电器“触点抖动”的失效模式，冲击环境的加速度冲击响应谱可以表征冲击冲击环境严酷度，该失效模式下电磁继电器失效边界为临界加速度冲击响应。
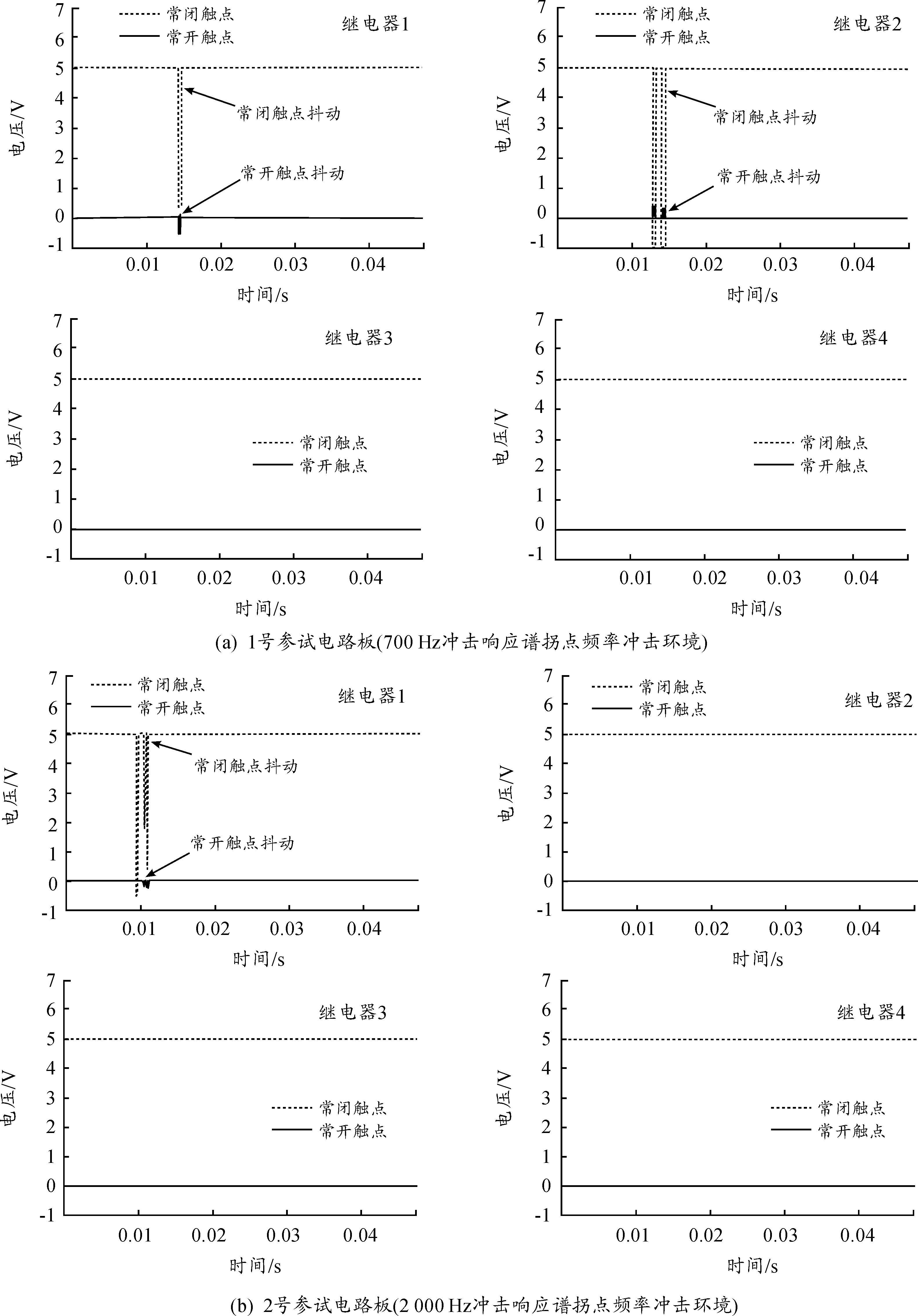
图7 参试电路板电性能测试数据图(“触点抖动”失效模式)
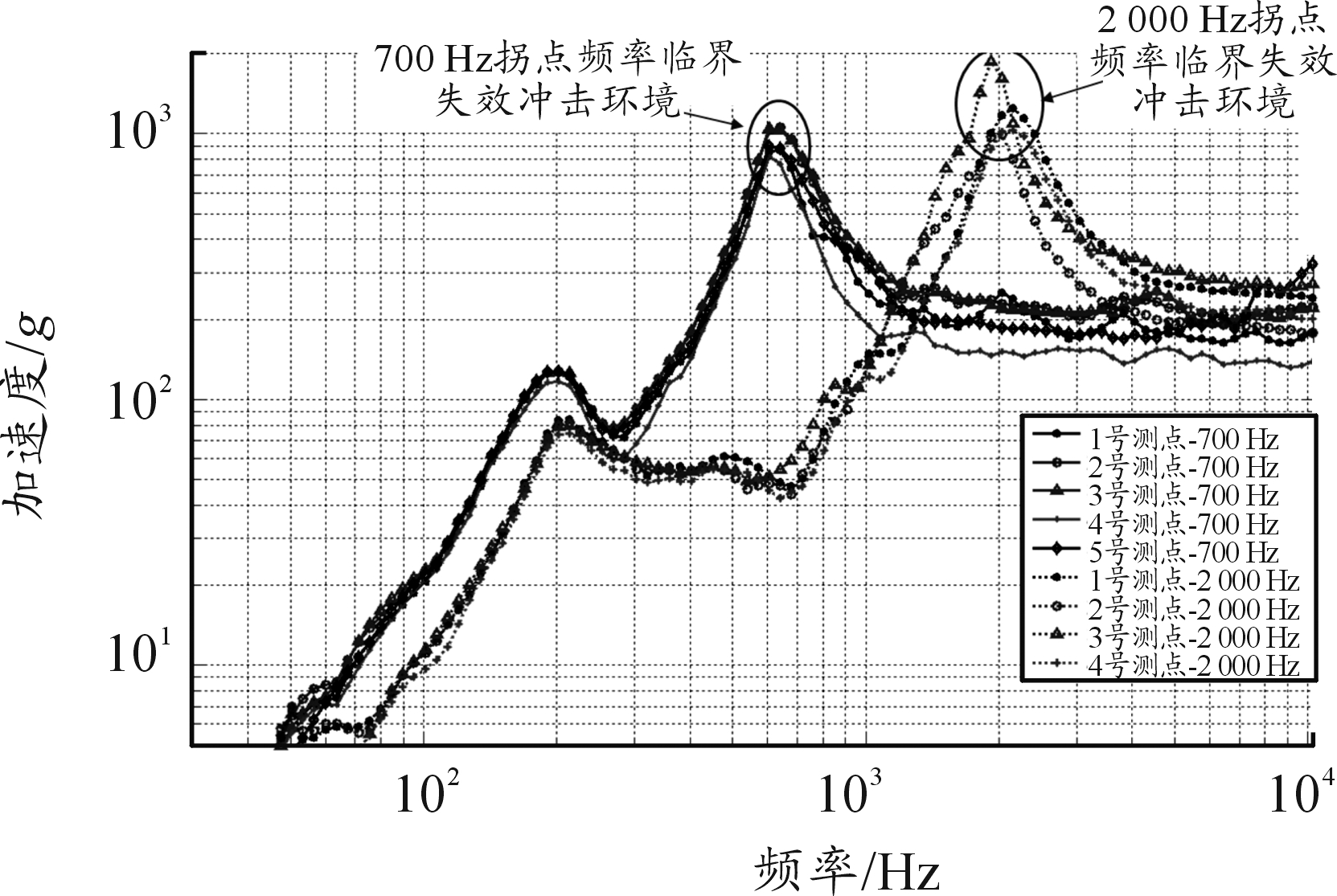
图8 临界失效冲击环境加速度冲击响应谱
(“触点抖动”失效模式)
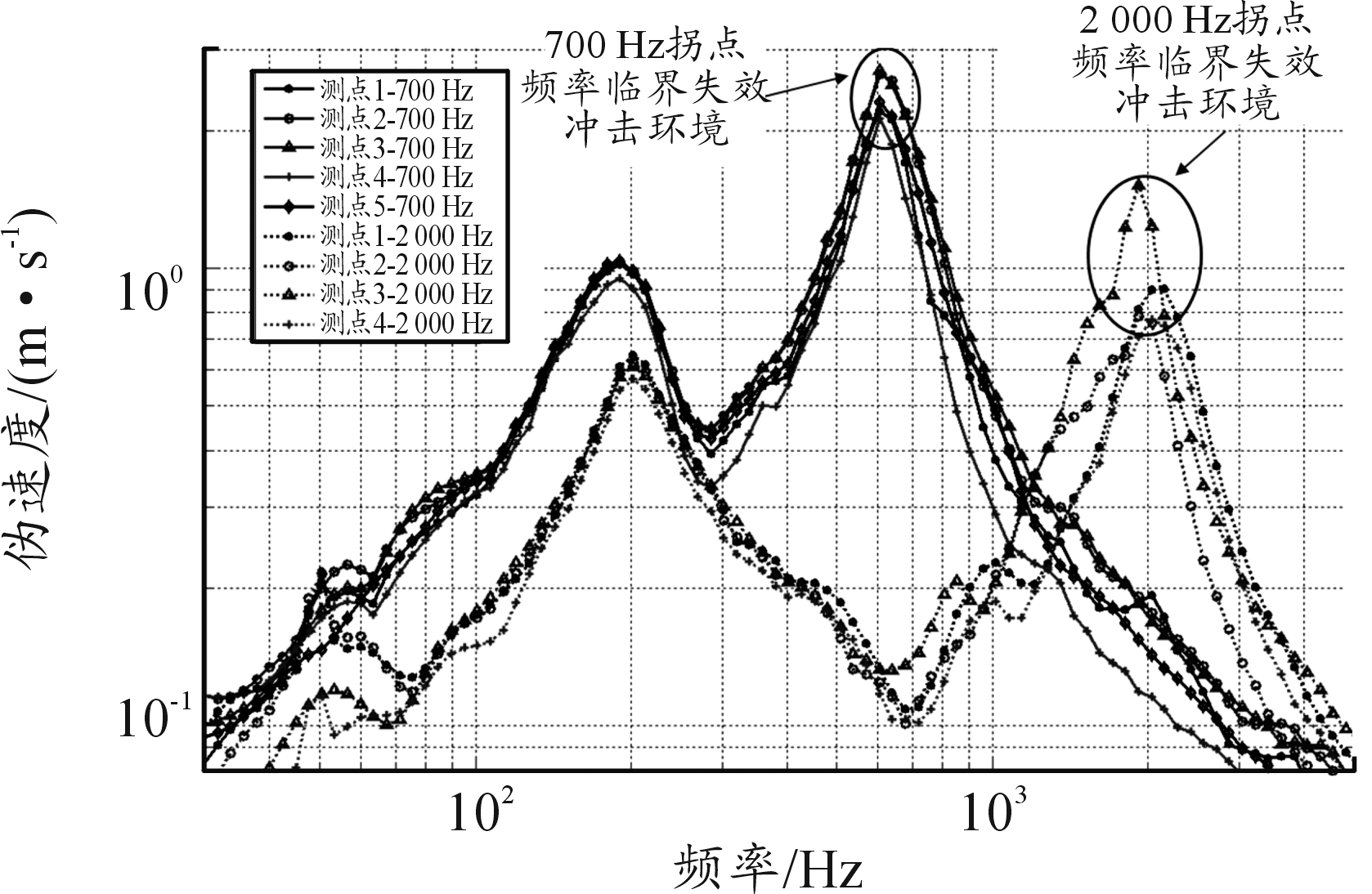
图9 临界失效冲击环境伪速度冲击响应谱
(“触点抖动”失效模式)
4.2 “常闭触点断开/常开触点闭合”失效模式
随着载荷量级的进一步提高，电磁继电器首次发生“常闭触点断开/常开触点闭合”的失效模式时，冲击结束后自检测数据如图10所示。可以看出，冲击结束后1号参试电路板1号继电器常闭触点断开、常开触点闭合，3号继电器常闭触点断开；2号参试电路板1号继电器常闭触点断开，3号继电器常闭触点断开、常开触点闭合，4号继电器常开触点闭合。因此，可以认为电磁继电器 “常闭触点断开/常开触点闭合”是一种高量级冲击载荷造成的不可恢复的失效模式。
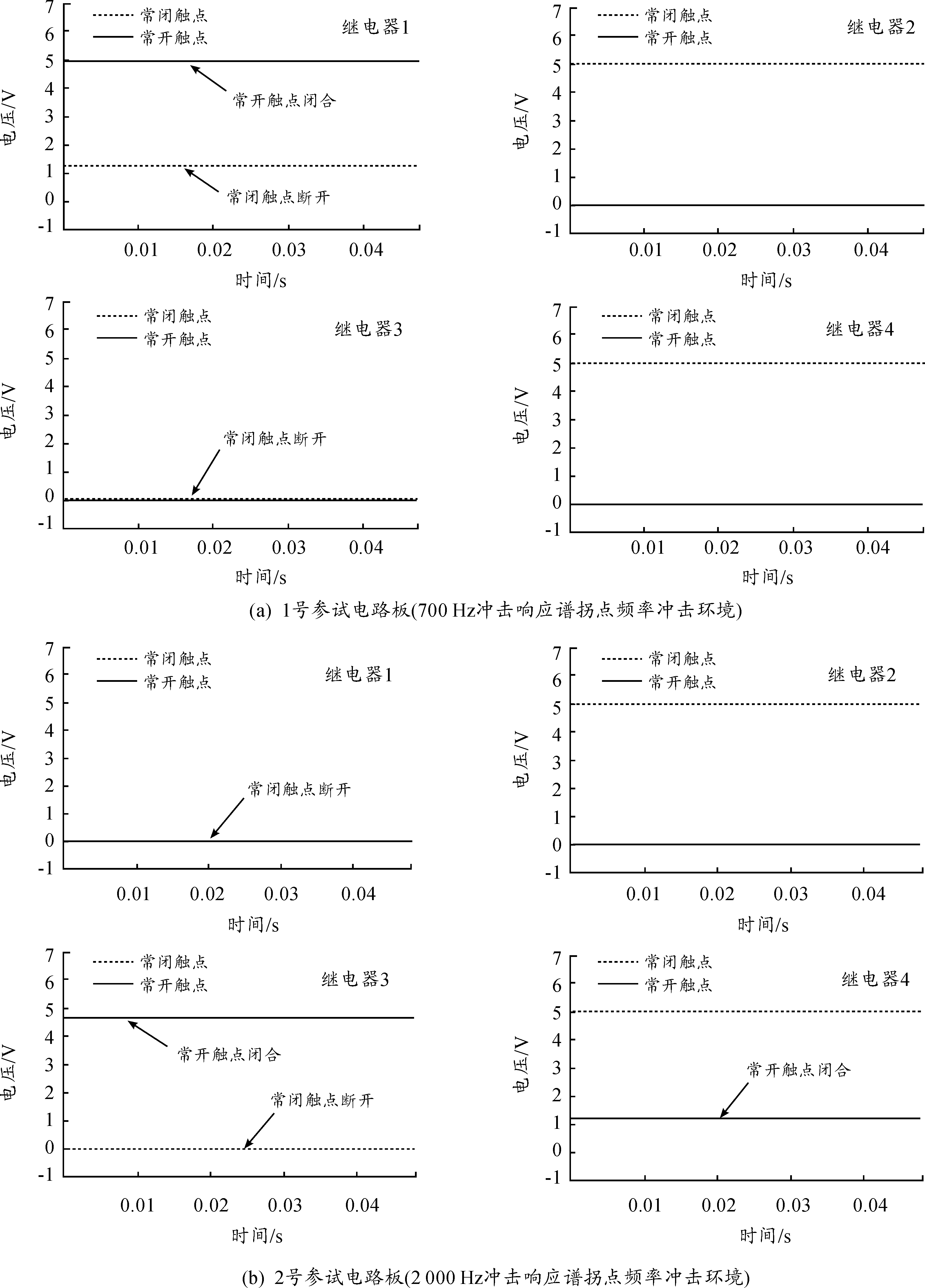
图10 参试电路板自检测数据图(“常闭触点断开/常开触点闭合”失效模式)
首次发生“常闭触点断开/常开触点闭合”失效时，各测点测得的700 Hz与2 000 Hz拐点频率临界失效冲击环境的加速度冲击响应谱如图11所示，伪速度冲击响应谱如图12所示。可以看出，该失效模式发生时，不同频率冲击环境的伪速度冲击响应谱水平相当，其中1号试验板为21.20～26.56 m/s，2号试验板为19.57～28.76 m/s；加速度冲击响应谱则存在较大差异,其中1号试验板为7 892～10 290 g，2号试验板为22 840～30 100 g。
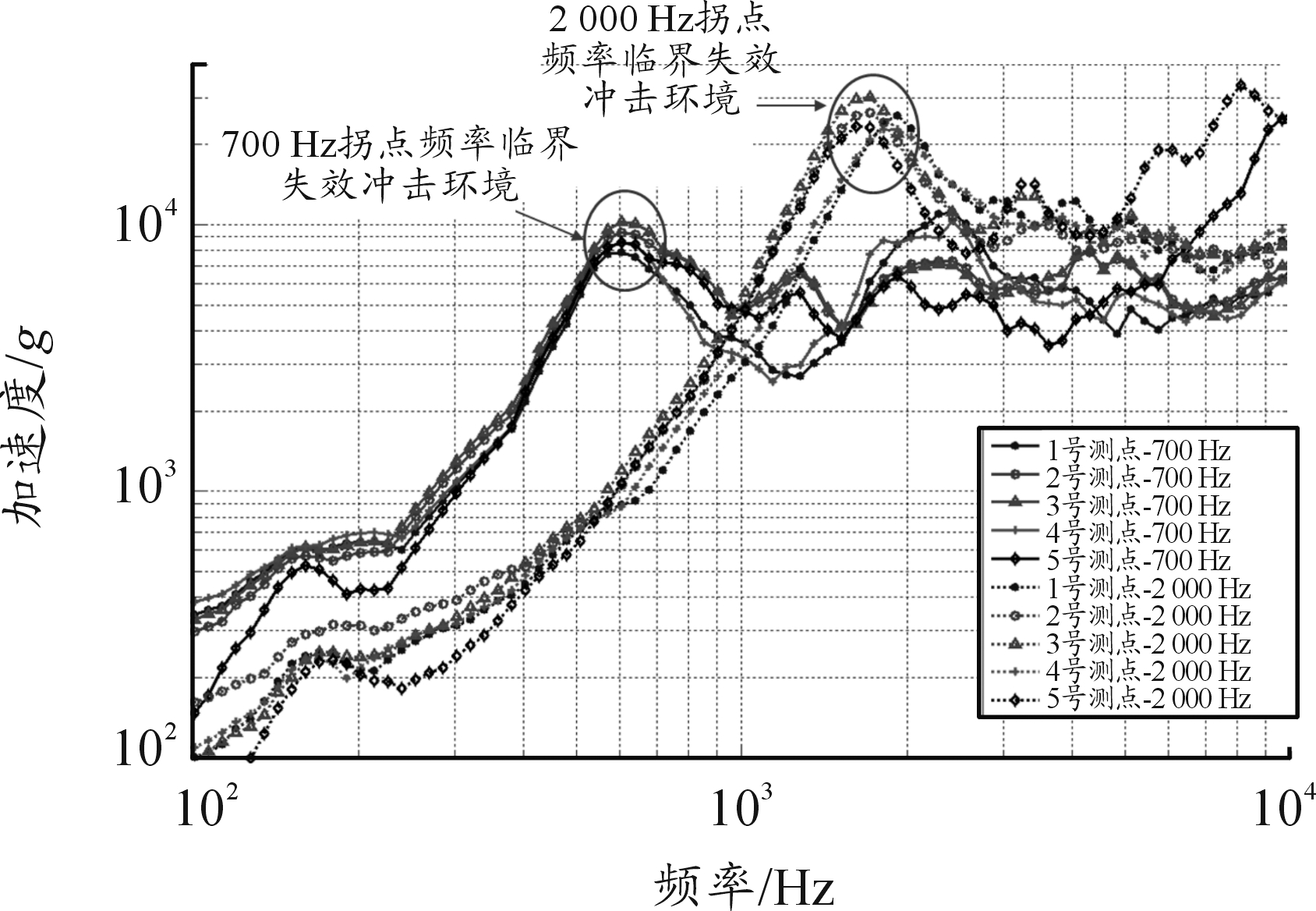
图11 临界失效冲击环境加速度冲击响应谱
(“常闭触点断开/常开触点闭合”失效模式)
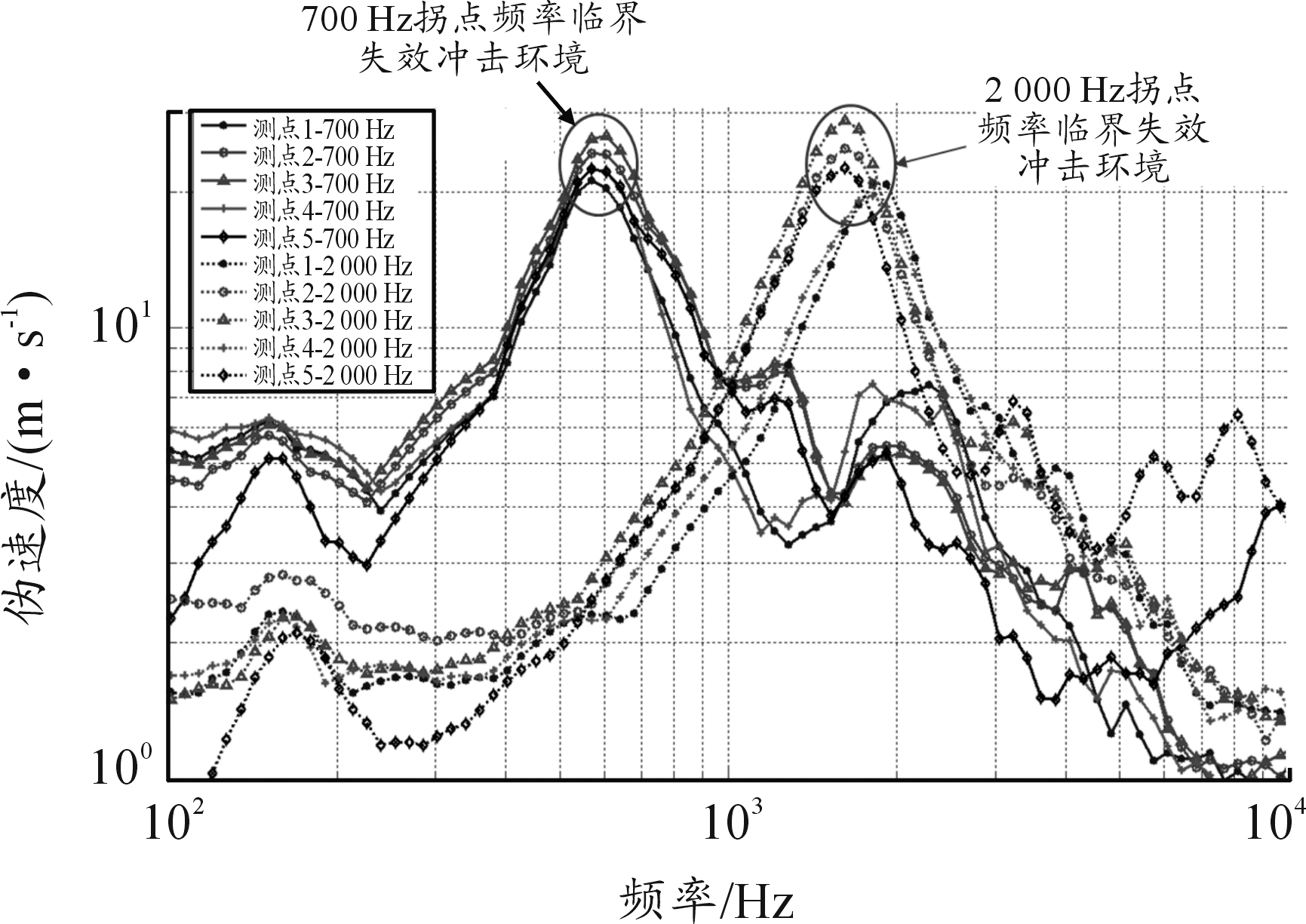
图12 临界失效冲击环境伪速度冲击响应谱
(“常闭触点断开/常开触点闭合”失效模式)
第1节与第2节理论分析得到，电磁继电器“常闭触点断开/常开触点闭合”失效是由于触簧系统应力过大造成永久变形甚至断裂破坏，伪速度冲击响应谱可以表征冲击环境下结构应力水平。冲击试验结果也表明，引发该失效模式的不同冲击环境的伪速度冲击响应谱水平相当。因此，对于电磁继电器“常闭触点断开/常开触点闭合”的失效模式，冲击环境的伪速度冲击响应谱可以表征冲击冲击环境严酷度，该失效模式下电磁继电器失效边界为临界伪速度冲击响应。
5 结论
1) 冲击载荷作用下，电磁继电器会发生“触点抖动”与“常闭触点断开/常开触点闭合”两种不同的失效模式，对应的失效控制参数分别为结构加速度响应与结构内部应力；
2) 对于“触点抖动”失效模式，冲击环境的加速度冲击响应谱可以表征冲击冲击环境严酷度，该失效模式下电磁继电器失效边界为临界加速度冲击响应；
3) 对于“常闭触点断开/常开触点闭合”失效模式，冲击环境的伪速度冲击响应谱可以表征冲击环境严酷度，该失效模式下电磁继电器失效边界为临界伪速度冲击响应；
4) 通过电磁继电器临界失效冲击试验，得到电磁继电器不同失效模式对应的临界冲击环境，验证了冲击失效边界有效性。
后续将进一步开展电磁继电器的失效分析，利用无损检测、开封检测等手段，求得内部结构形式、尺寸、材料特性等详细信息，探究其内部微结构与材料层面的冲击失效机理，建立有效的冲击损伤/失效评估方法，提高航天电子设备研制效率，为航天器冲击环境适应性设计提供参考。
[1] 翟国富,崔行磊,杨文英.电磁继电器产品及研究技术发展综述[J].电器与能效管理技术,2016(2).
[2] 马跃.航天继电器失效机理与寿命预测方法的研究[D].哈尔滨：哈尔滨工业大学,2013.
[3] 余琼.航天继电器可靠性评价及寿命试验方法的研究[D].哈尔滨：哈尔滨工业大学,2011.
[4] 张仲满,臧照祥,赵雯娴.宇航电子产品电磁继电器应用研究[J].电子技术与软件工程,2016(13):117-119.
[5] 翟国富,任万滨,刘茂恺,等.电磁继电器簧片系统振动特性分析方法的探讨[J].机电元件,2002,(03):3-7.
[6] 翟国富,任万滨,许峰,等.电磁继电器触簧系统振动加速度的分析方法[J].振动工程学报,2004,(01):67-71.
[7] 任曾勋.继电器在冲击载荷作用下的断开响应分析[J].振动与冲击,1985(2):42-55.
[8] 陈英华,翟国富,任万滨,等.冲击环境下拍合式继电器的接触失效分析方法[C]//第三届电工产品可靠性与电接触国际会议论文集.中国电工技术学会电工产品可靠性研究会，温州,2009.
[9] 焦玉斌,郑浩野,任万滨,等.振动环境对电磁继电器特性参数影响的试验研究[J].电器与能效管理技术,2011(3):8-11.
[10] 曹云东,孙宏杰,王贝贝,等.铁路信号继电器触簧系统冲击特性应用研究[J].机电元件,2014,34(5):16-20.
[11] BIOT MAURICE A.Transient oscillations in elastic systems.General theorems.Vibrations of buildings during earthquake.Critical torsional vibrations of accelerated rotating shafts[D].California Institute of Technology,1932.
[12] LALANNE CHRISTIAN.Mechanical Shock:Mechanical Vibration and Shock Analysis,Volume 2,Second Edition[M].[S.l.]:[s.n.],2010.
[13] GABERSON H.A.Pseudo velocity shock spectrum rules for analysis of mechanical shock[C]//IMAC XXV.[S.l.]:[s.n.],2007.
[14] LI B W,LI Q M.Damage boundary of structural components under shock environment[J].International Journal of Impact Engineering,2018,118:67-77.
[15] 向树红.航天器力学环境试验技术[M].北京:中国科学技术出版社,2010.
[16] 都军民,戴宗妙.冲击响应谱在冲击试验中的应用研究[J].舰船科学技术,2007,29(a01):19-21.
[17] IRVINE TOM.Shock and vibration stress as a function of velocity[J].Revision A,Vibrationdata,2010.
[18] LI Bingwei,LI Qingming,LIU Bo,et al.Critical Shock Response Spectrum of A Beam Under Shock Loading[C]//ASME 2016 35th International Conference on Ocean,Offshore and Arctic Engineering.[S.l.]:[s.n.],2016.