装药是影响弹药产品杀伤能力和爆破能力的关键因素[1],为提高弹药的装药密度和质量,在装药过程往往会对弹药频繁施加压力、剪切力、热载荷等外界作用,而弹药主体通常是对外界刺激有一定敏感性的含能材料,存在意外爆炸的风险。因此,在装药工艺过程中合理的进行保护措施是保护企业生命财产安全的关键[2]。设置防爆间是最简单有效的保护措施之一。防爆间结构设计和材料选择与其抗爆性能息息相关,仿真模拟手段可以验证不同结构和材料组成的防爆间的抗爆性能,对防爆间的设计与改善有着重要的指导意义。吴义田等[3]利用LS-DYNA有限元软件对某抗爆门的结构防护性能进行了仿真模拟,为其结构优化设计提供了依据。赵凯[4]采用AUTODYN有限元软件研究了防爆挡墙对爆炸冲击波的防护效应。Jones等[5]对某柱状炸药进行了数值模拟和试验,对比了6 mm和12 mm钢壳对爆炸冲击波的影响。廖黎莹等[6]采用ABAQUS有限元软件对金属防护外壳的防爆性能进行了仿真分析,提出了一种含有中间柔性材料缓冲层的复合防护结构。
在弹药工程领域,结构钢是防爆板主要使用的材料,其防爆性能与板材厚度有着直接的关系,然而目前缺少防爆板厚度与防爆性能间的定量关系研究。本文选用某装药线的压药防爆间为分析对象,选择Q235钢为防爆板的构成材料,对其厚度与防爆性能的关系进行了仿真模拟研究,给出了不同厚度下防爆板的极限工作药量,得到了二者间的定量关系,为防爆板的设计选型提供了指导作用。
1 计算模型及参数
1.1 几何尺寸
本文重点关注对象为防爆板,对装药间其余部分不予考虑,因此为提高计算效率,将装药间简化为如图1所示,其主体部分长×宽×高分别为2 000 mm×2 000 mm×2 500 mm,防爆板初始厚度为14 mm,装药间下方设有200 mm厚的地面,上方为完全开放结构,作为泄爆口。TNT中心放置于离地面1 000 mm,距后防爆板100 mm,距两侧防爆板1 000 mm处。TNT的几何尺寸设置为长方形,其底面长×宽设为40 mm×40 mm,其高度由TNT的当量控制。
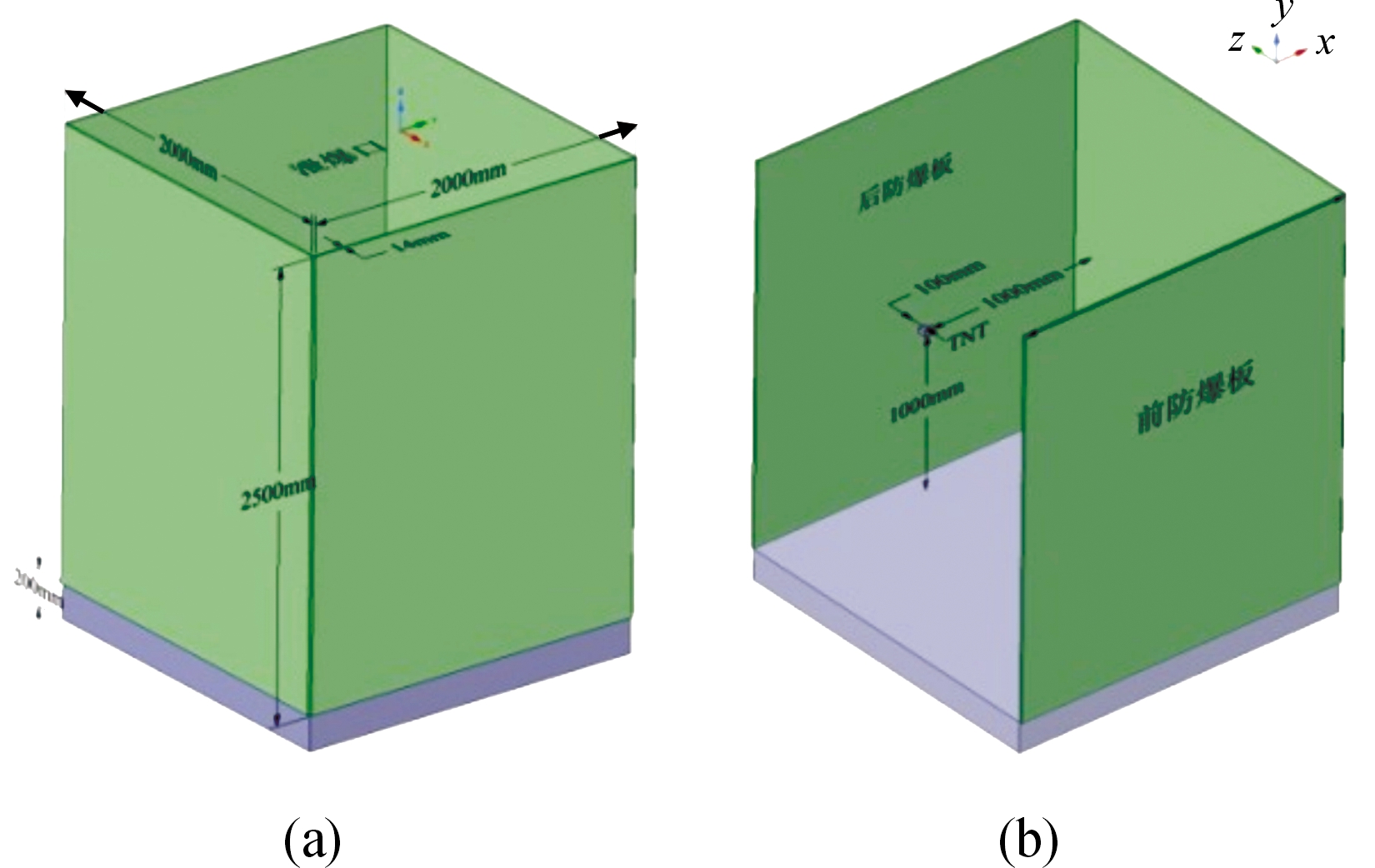
图1 装药间(a)及TNT放置位点(b)示意图
1.2 有限元网格尺寸选择
优质的网格质量对有限元计算结果的精度极其重要,网格单元质量计算公式是评估网格质量的有效方法,其计算公式如下:
(1)
(2)
其中,Qs为二维网格质量;Qv为三维网格质量;S为网格总面积;V为总体积;di为单元格边长;C为常数,其值[7]如表1所示。
表1 常数C的取值
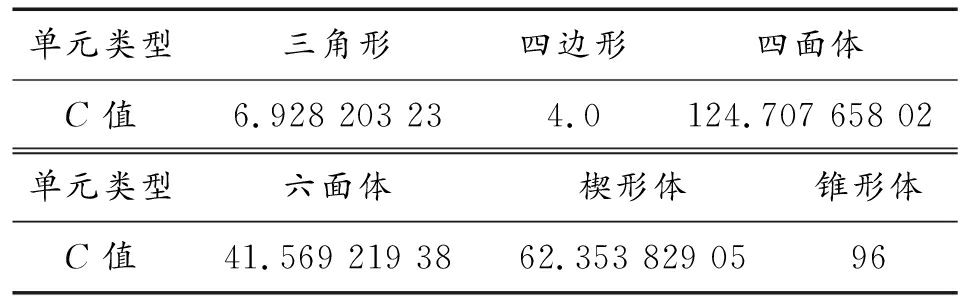
单元类型三角形四边形四面体C值6.928 203 234.0124.707 658 02单元类型六面体楔形体锥形体C值41.569 219 3862.353 829 0596
表2给出了30 mm防爆板,在385 g TNT爆炸冲击作用下,不同网格大小计算得出的最大等效应力。网格大小包括30 mm、15 mm、10 mm、7.5 mm、6 mm对应的厚度方向的网层数分别为1、2、3、4、5层。5种网格尺寸网格质量Qv值均接近1,但计算所得的防爆板的最大等效应力值差别很大,如表2所示。图2给出了最大等效应力随网格尺寸变化曲线,可看出随着网格尺寸的不断减小,应力值并未趋近一精确值,而是不断增大,并且增加幅度不断上升,这是一种典型的应力奇异现象,这是由于网格位移函数在应力最大处的导数不连续造成的。根据曲线的变化趋势,取斜率变化最明显的区域为最佳尺寸范围,即10~15 mm之间。
表2 防爆板不同网格尺寸下的最大等效应力
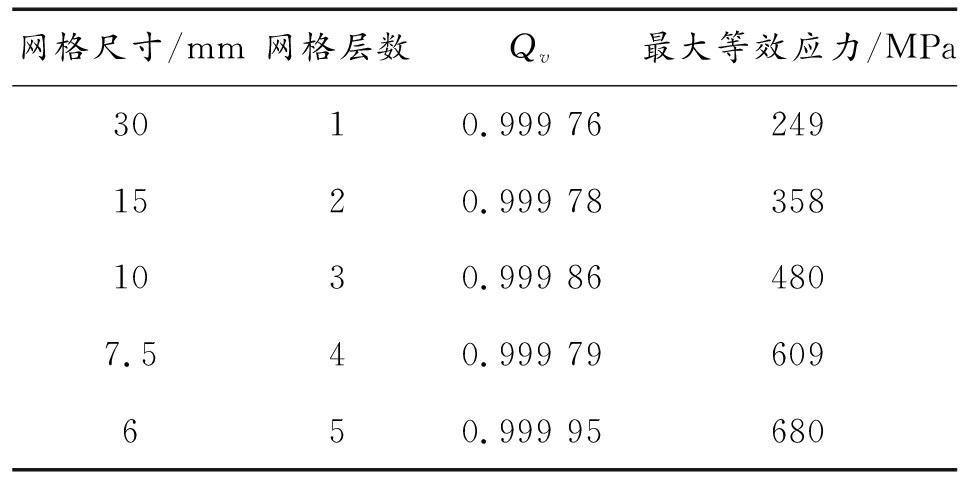
网格尺寸/mm网格层数Qv最大等效应力/MPa3010.999 762491520.999 783581030.999 864807.540.999 79609650.999 95680
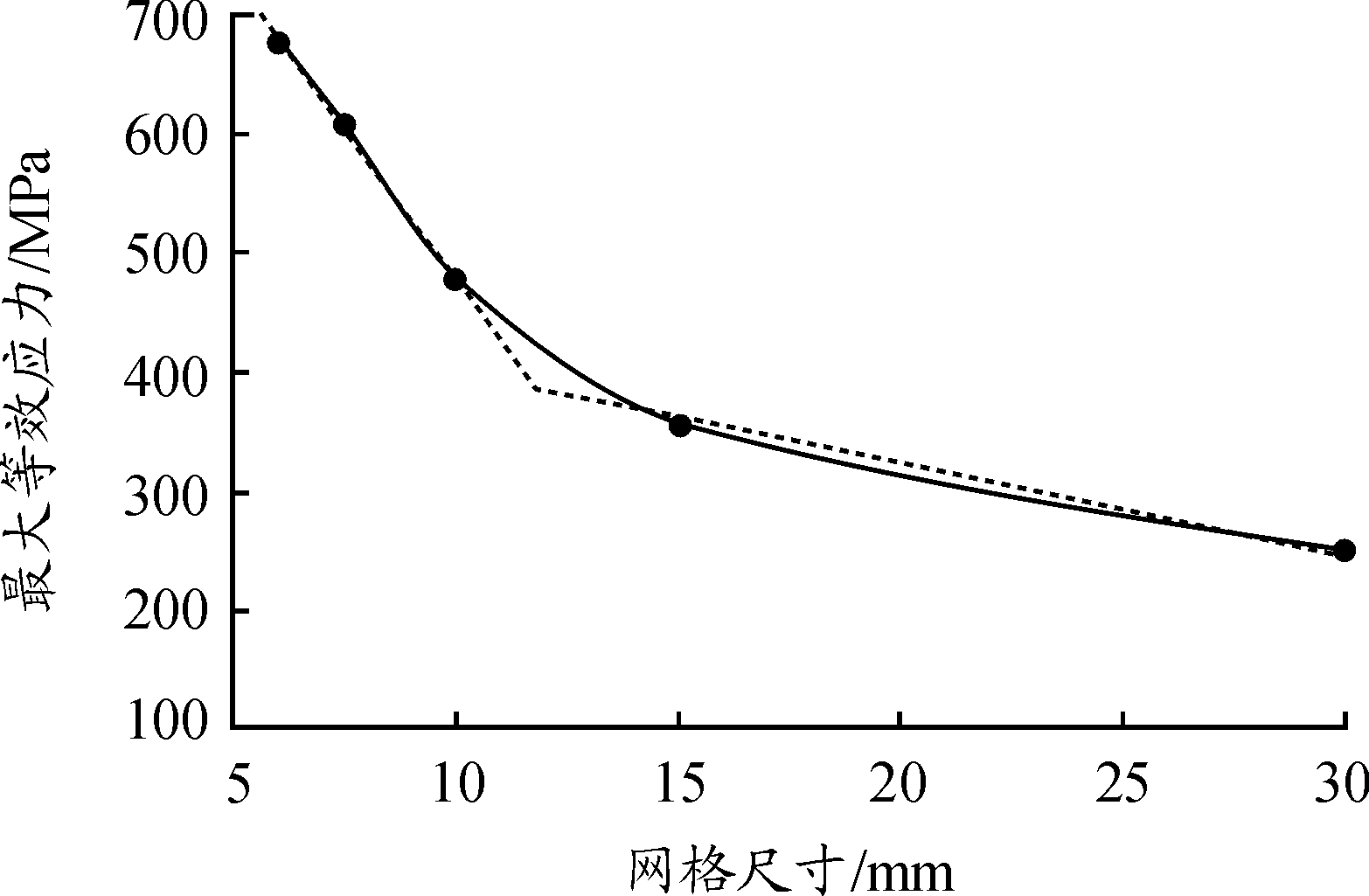
图2 最大等效应力随网格尺寸变化曲线
1.3 有限元模型及参数
整个装药间有限元模型包括炸药、空气、地面和防爆板4种材料。炸药网格尺寸为10 mm,空气网格尺寸为40 mm,地面的网格尺寸为100 mm, 防爆板的网格尺寸根据其厚度不同在10~15 mm间调整。图3给出了防爆板厚度为14 mm的整个防爆间的网格离散结构,所有部分均采用六面体单元,共计245 910个单元,网格单元质量为0.985 9,网格质量优异。
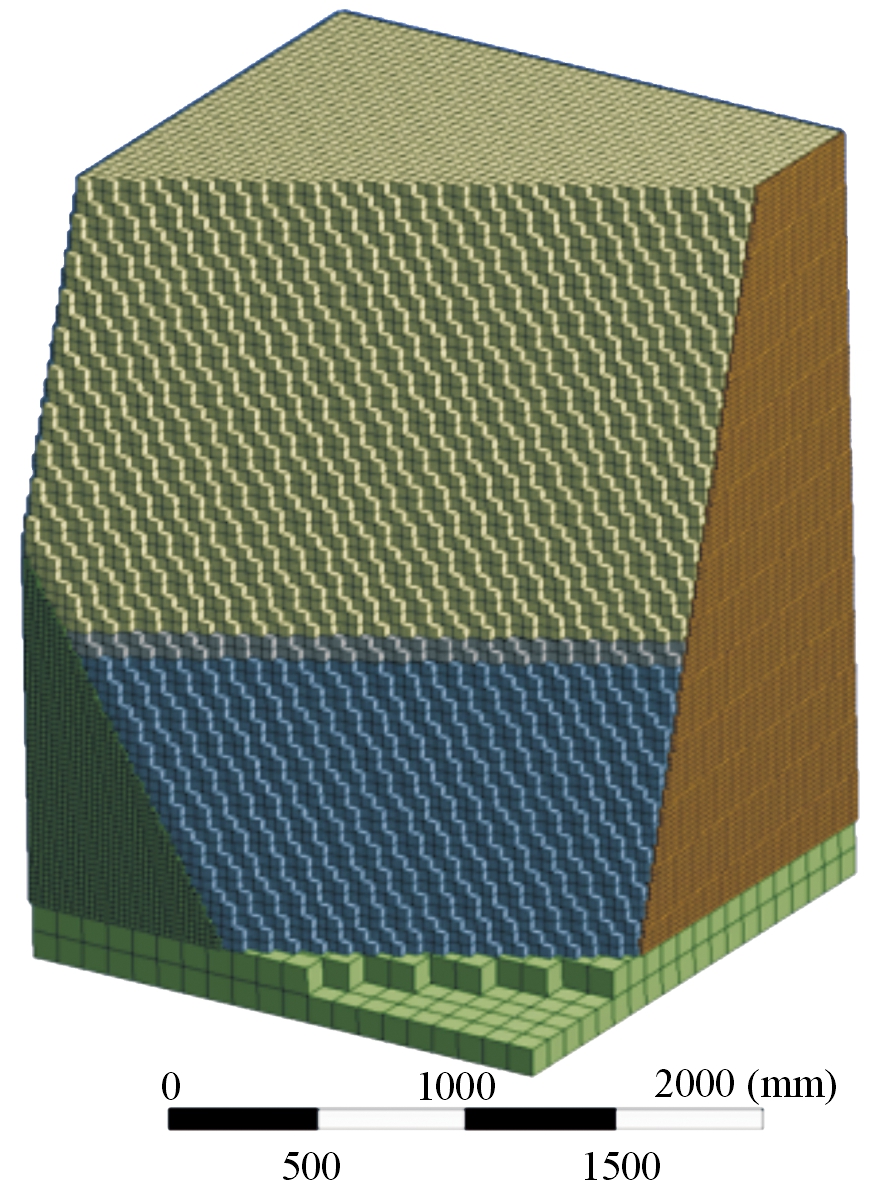
图3 防爆间三维有限元模型剖面图
防爆板材料采用Q235钢,其材料参数[8]如表3所示。炸药材料为TNT,其爆轰状态采用JWL状态方程描述,其相关参数如表4所示。空气采用标准大气,密度为1.225 kg/m3,比热为717.6 J/(kg·K),比内能为200 kJ/kg,所有材料参数均来自ANSYS Workbench 材料数据库中。
表3 Q235钢材料参数
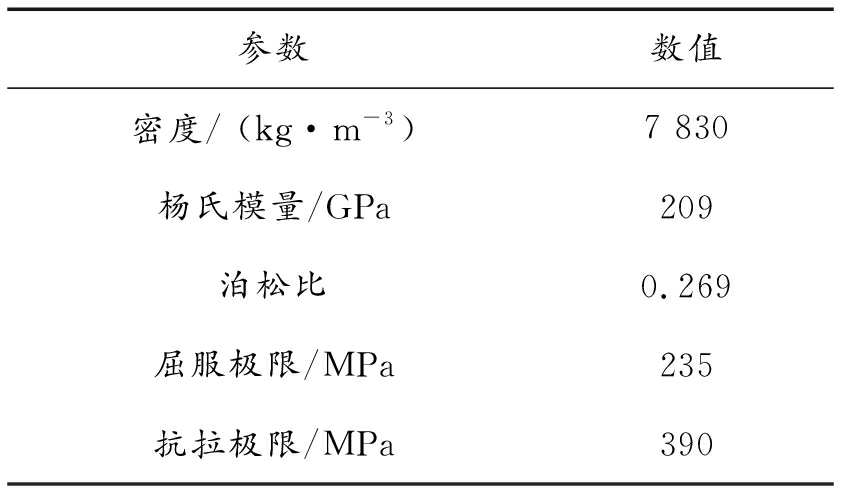
参数数值密度/ (kg·m-3)7 830杨氏模量/GPa209泊松比0.269屈服极限/MPa235抗拉极限/MPa390
表4 TNT材料参数

参数数值密度/(kg·m-3)1 630爆速/(m·s-1)6 930能量密度/(kJ·m-3)6×106爆压/GPa21
模型中空气与炸药的接触关系设置为无摩擦,除空气外其余部分相互之间接触关系均设置为绑定。炸药和空气均采用欧拉坐标系描述,其余部分采用拉格朗日坐标系描述,地面设置为固定面,起爆点设置在炸药上表面中心处。
采用Ansys workbench中显示动力学模块进行建模分析,使用Autodyn求解器进行有限元求解。计算时间设置为2 ms,初始时间步与最小时间步均设置为程序自身控制。计算结果输出50个采集点,并均匀设置10个重启节点。
2 结果分析与讨论
2.1 防爆间爆轰过程分析
图4给出了14 mm厚防爆板组成的防爆间在170 g TNT炸药起爆情况下6个不同时刻的等效应力分布云图。从图4可以看出,由于起爆点到后防爆板的距离很小,仅100 mm,TNT起爆后产生的冲击波会迅速对后防爆板产生明显的应力作用,虽然刚开始防爆板受到应力作用范围不大,如图4(b)所示,但其最大等效应力值σmax很高,在t=0.08 ms时就达到了232.94 MPa。当t=0.2 ms时,冲击波对后防爆板产生最大等效应力σmax=393.4 MPa,随后冲击波不断从泄爆口泄出,防爆板受到的最大等效应力值不断减小,当时间达到2 ms时,整个防爆板的最大等效应力为143.6 MPa,大部分面积应力小于80 MPa,应力作用逐渐消失。整个过程中爆轰冲击波对防爆间的作用几乎全部作用于后防爆板上,这是由于起爆点的位置距离后防爆板太近,整个防爆间的空间相对较大,再加上防爆间上部有大面积的泄爆口造成的,所以后防爆板是整个防爆间的主要防爆部位,其厚度直接决定了此防爆间的抗爆性能。
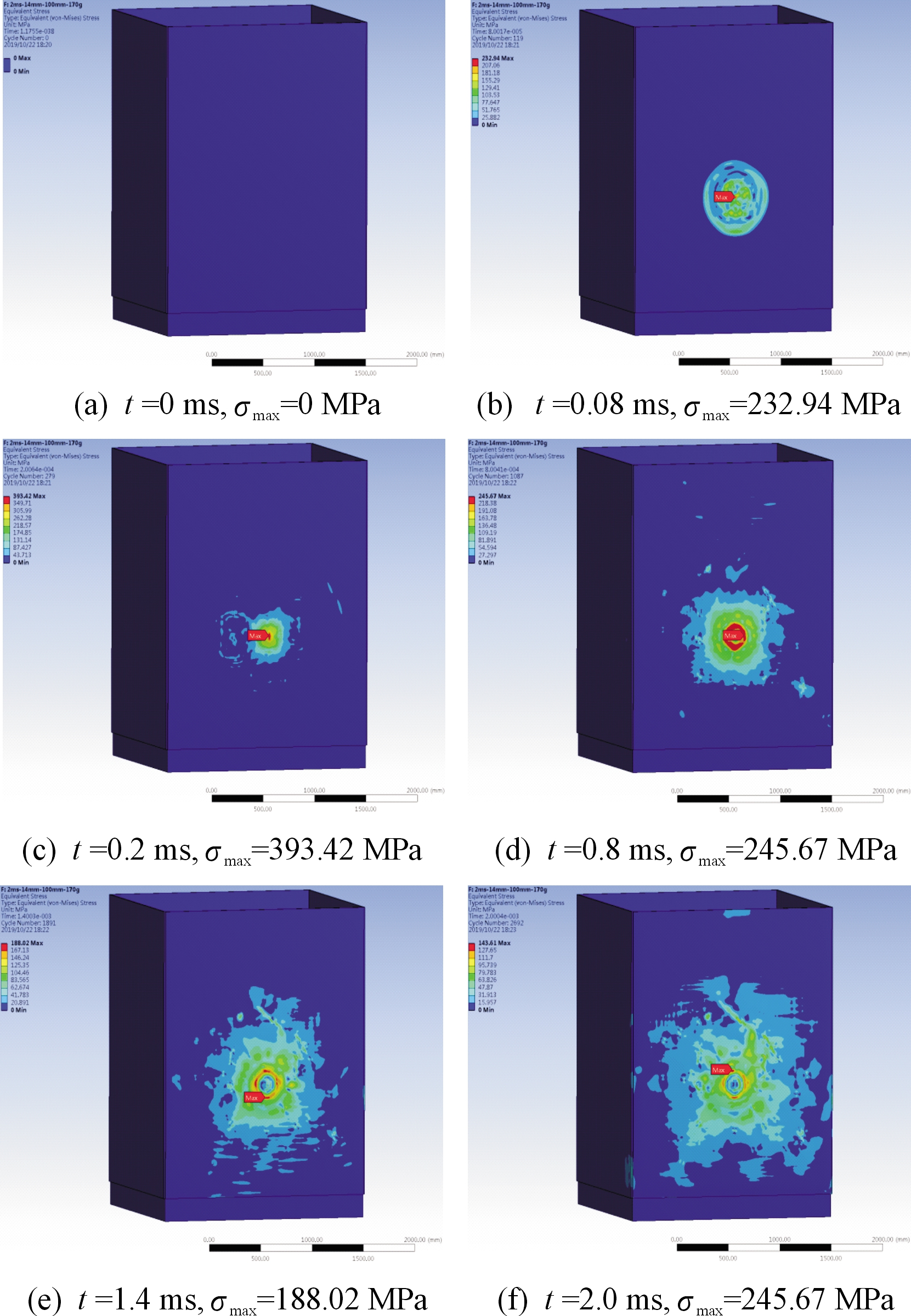
图4 不同时刻下防爆间的等效应力分布云图
图5(b)给出了后防爆板的最大等效应力时程曲线,由曲线可知,炸药被起爆后最大等效应力σmax迅速上升,当时间达到0.2 ms时σmax达到最大值,随后曲线缓慢下降,应力逐渐减小。整个过程防爆板的最大位移为15.3 mm(见图5(c)和图5(d)),发生形变的位置集中在防爆板中间离最大形变点200 mm左右半径内,为重点防爆部位。
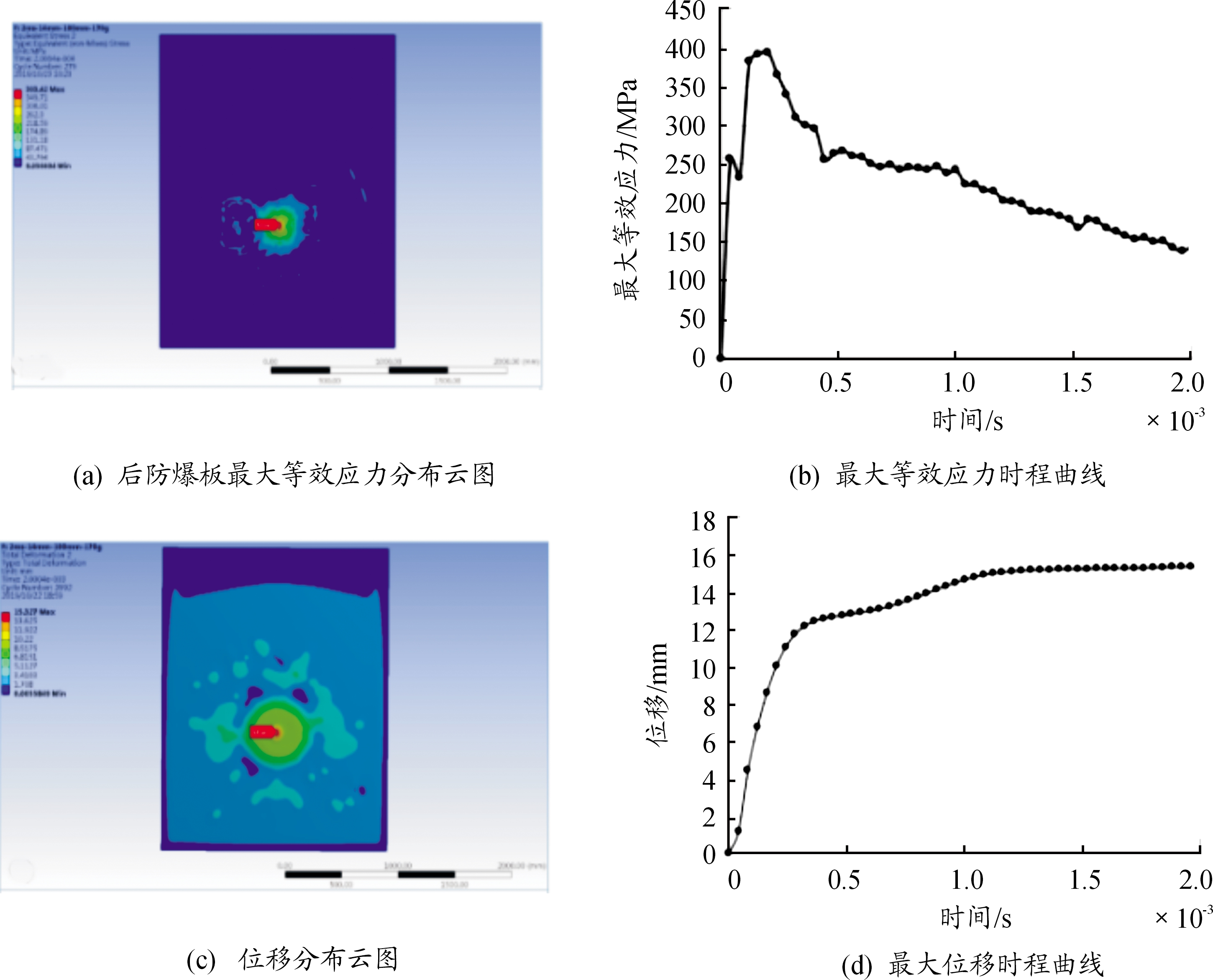
图5 后防爆板应力、位移分布云图及曲线图
由于整个过程中后防爆板的最大等效应力σmax=393.4 MPa,与Q235钢材的拉伸极限390 MPa十分接近,可将170 g TNT视为14 mm厚度下防爆板的极限工作药量,即小于此TNT当量下的工况可满足防爆要求。
2.2 防爆板厚度与极限工作药量关系
由于防爆板的厚度d直接影响防爆间的极限工作药量w,进一步选择了除d=14 mm外,另4种常见厚度(d=10 mm、20 mm、25 mm和30 mm)的防爆板进行了爆轰过程仿真分析,其网格尺寸和网格质量如表5所示。为确定不同d值下的w值,采取以每5 g TNT为增量的方法,在不同d值情况下进行多次仿真模拟,找出最大等效应力最接近Q235钢材拉伸极限的工作药量,定为该厚度下的极限工作药量w,具体数值见表5。
表5 不同厚度下防爆板的极限工作药量
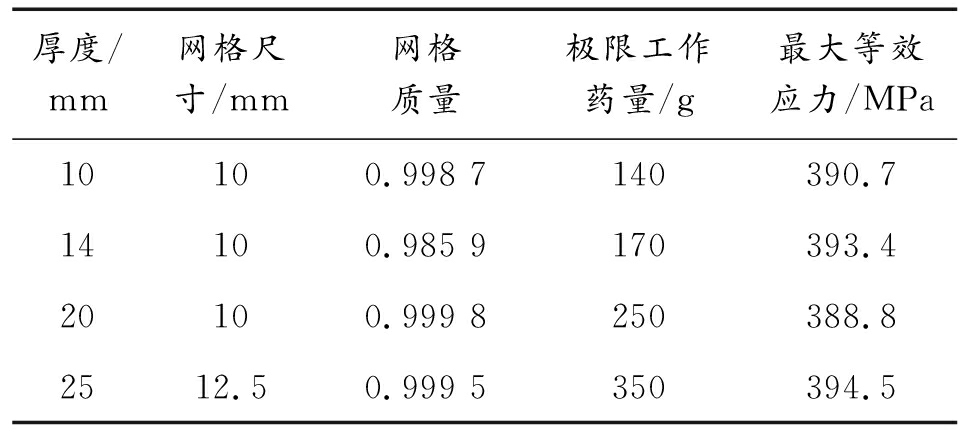
厚度/mm网格尺寸/mm网格质量极限工作药量/g最大等效应力/MPa10100.998 7140390.714100.985 9170393.420100.999 8250388.82512.50.999 5350394.5
由表5可知:厚度d为10 mm防爆板的极限工作药量w为140 g,而厚度d为30 mm防爆板的极限工作药量w为475 g,随着防爆板厚度的增加,极限工作药量增加的幅度加大,表明增加防爆板厚度可以明显改善防爆板受到冲击波的应力作用。不同厚度防爆板在极限工作药量下的最大等效应力分布如图6所示,可以看出不同厚度下的防爆板出现最大等效应力时刻均在0.2 ms左右,应力集中区域也与先前分析的14 mm的防爆板相似,设计人员应对此部分区域进行重点保护。
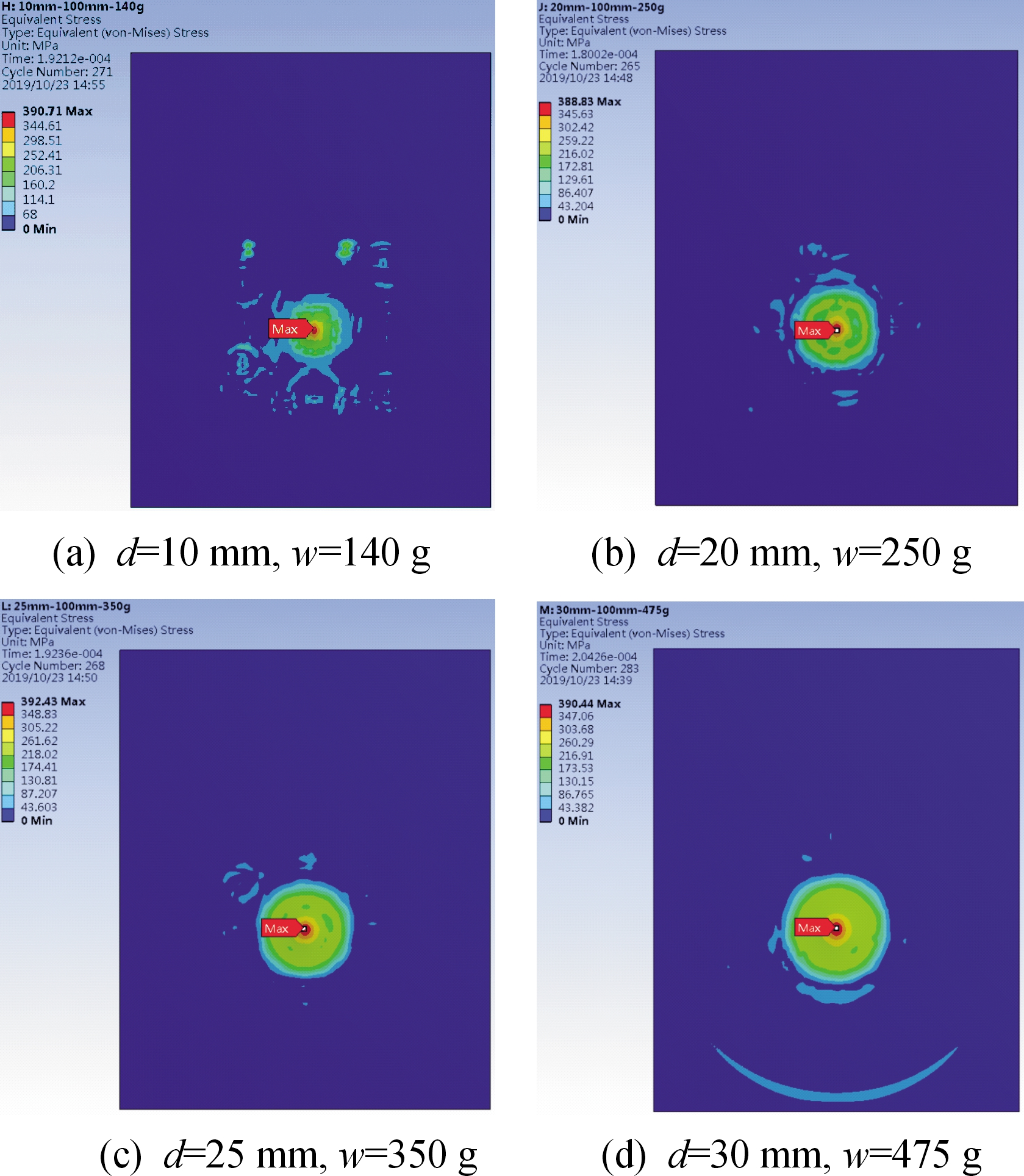
图6 不同厚度(d)的防爆板在极限工作药量(w)下的最大等效应力分布云图
为进一步确定其他厚度防爆板的极限工作药量,将上述5种防爆板厚度d与极限工作药量w进行了多项式拟合,结果表明d值与w值成二次函数关系,拟合曲线如图7所示,对应的计算公式为
w=0.596 4d2-5.986 4d+142.59(10<d<30)
(3)
可以简单推测不同厚度防爆板的极限工作药量,亦可根据所需的工作药量选择满足防爆要求的防爆板,但值得注意的是此拟合公式是在固定起爆点位置和防爆板材质的前提下得到的,其他防爆间借鉴时应根据自身具体的工况,如起爆点离防爆板的距离,防爆板的材质,泄爆口等进一步加以校正。
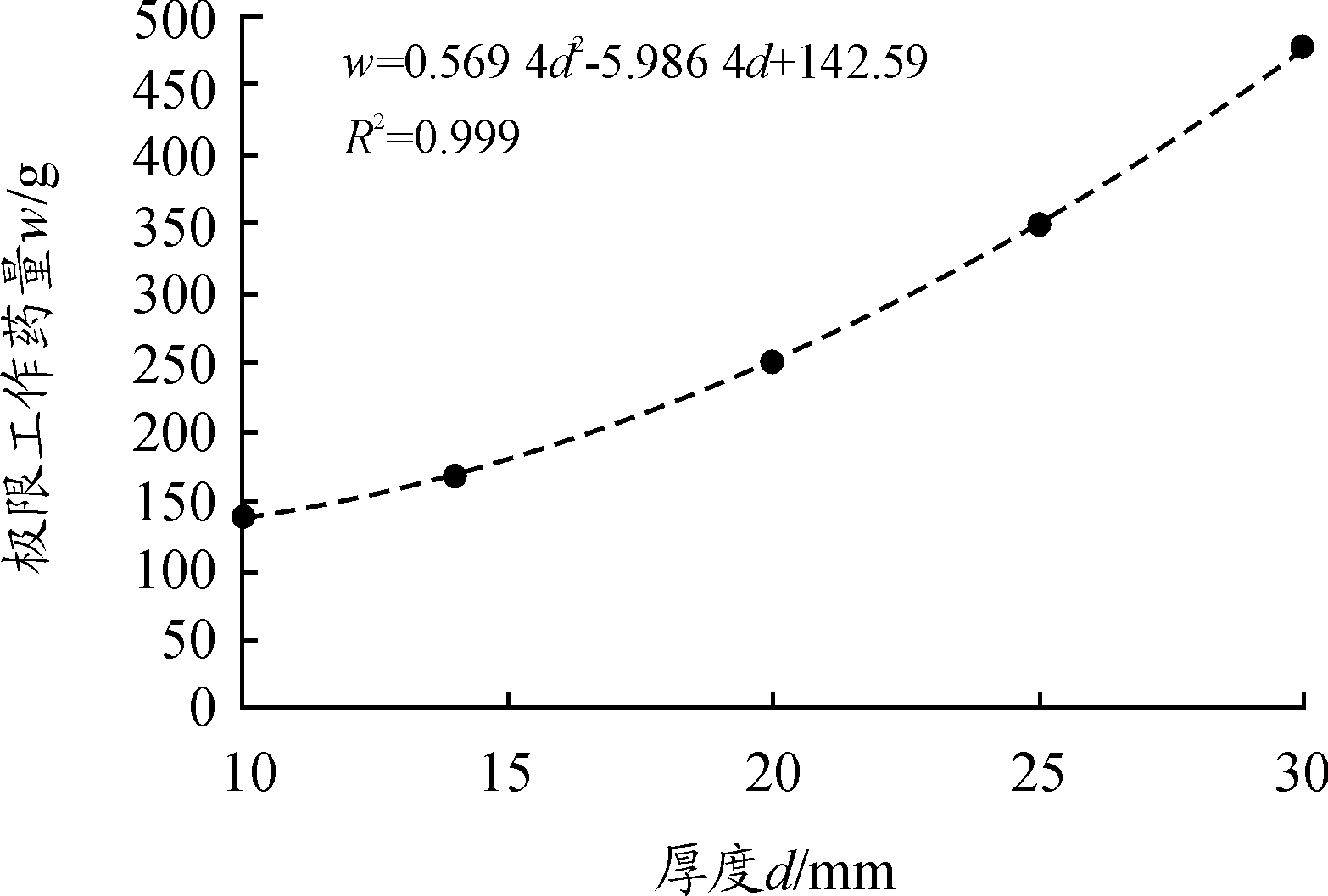
图7 极限工作药量随防爆板厚度变化曲线
3 结论与展望
采用Ansys Workbench软件中显示动力学模块及AUTODYN求解器,对某压药防爆间的抗爆性能进行了分析和预测,给出了防爆板厚度与其极限工作药量的定量关系。后防爆板是整个防爆间最危险的部分,爆炸冲击波会对其产生很强的应力作用,其应力作用集中在以最大应力点为中心的200 mm左右半径范围内,此区域为设计时应重点加强的区域。厚度为14 mm的Q235钢防爆板的极限工作药量为170 g,30 mm防爆板的极限工作药量为475 g,多项式拟合结果显示Q235钢防爆板的厚度d与极限工作药量w成二次函数关系。
本文为某防爆间的防爆板的设计选型和防爆性能验证提供了一种简单的经验计算方法,其他类型防爆间根据其自身工况亦可进行参考。本文仅在固定起爆点位置的情况下,对Q235钢的防爆板进行了抗爆性能分析,进一步的研究可考虑不同起爆距离和防爆板材质对其抗爆性能的影响。
[1] 王泽山.火药装药设计原理[M].北京:兵器工业出版社,1995.
[2] 李亮亮,沈飞,屈可朋,等.炸药装药在不同应变率响应条件下的安全性研究进展[J].火炸药学报,2016,185(01):22-30.
[3] 吴义田,张庆明,付跃华.某抗爆门结构防护性能的有限元分析[J].弹箭与制导学报,2007,27(02):245-247.
[4] 赵凯.防爆挡墙对爆炸空气冲击波防护效应的数值模拟研究[J].中小企业管理与科技(上旬刊),2011(09):324-325.
[5] JONES D A,NORTHEAST E D.Effects of Case Thickness on the Performance of Underwater Mines[R].Defence Science and Technology Organization Canberra,DSTO-TR-0120,1995.
[6] 廖黎莹,王国清,王志武.冲击载荷作用下金属防护外壳的防爆仿真分析[J].计算机仿真,2019,26(01):320-326.
[7] FREY P J,GEORGE P L.Mesh Generation:Application to Finite Elements[M].ISTE,2007.
[8] 方昆凡.机械工程材料实用手册[M].沈阳:东北大学出版社,1995.