车辆悬挂包括弹性元件、减振元件及导向机构三部分构成[1-4]。人们对乘坐舒适度和操作稳定性等性能要求越来越高,悬挂形式逐渐由基本的被动悬挂向性能可调的悬挂发展。目前悬挂系统分为被动悬挂、半主动悬挂和主动悬挂三大类[5]。被动悬挂结构简单,价格低廉,不需要额外消耗能量,在民用领域广泛使用,但在不同路面下不能自主调节,因此无法获得最好的乘坐和驾驶体验。主动悬挂利用作动器代替阻尼器,根据实时路况,通过闭环控制产生主动力,抑制车身振动。但是,由于主动悬挂系统的有源性,需要消耗较多外界能量,且成本很高,因此普通车辆很难普及主动悬挂技术[6];半主动悬挂可以依据车身的振动程度对弹簧刚度或阻尼系数进行实时调节,相对前述2种悬挂,性价比较高。但目前半主动悬挂大多集中在对阻尼系数调节模式[7-8],其中阻尼连续可调的称为连续型半主动悬挂,阻尼分级可调的称为有级半主动悬挂。
按悬挂结构实现形式,半主动悬挂可分为电磁式、液力式、磁流式、空气式等;控制方法上,1974年Karnopp等[9]提出了天棚控制;2003年Sammier等[10]将天棚控制进一步改进,提出了一种连续可变阻尼的天棚控制;2005年Savaresi等[11]又提出了加速度驱动的阻尼控制;2006年Giorgetti等[12]提出了混合模型最优控制。实际目前各种单一控制策略各有优点和局限性,将控制策略进行合理的结合,成为半主动悬挂控制策略发展的一个方向。
1 机电悬挂系统
机电悬挂也称为电磁悬挂,是一种用电机替代传统的减速器的悬挂形式。机电悬挂的结构还包括导向机构、负载电路和弹性元件。由于电机力一般不能直接作用在车身上,因此在电机一端要增加变速机构。按电机的类型,机电悬挂可分为旋转式和直线式两种;按导向机构形式可分为滚珠丝杠式、齿轮齿条式等等;按负载类型可分为,超级电容式、电池式和电阻式;机电悬挂通常的弹性元件为螺旋弹簧。半主动模式下,车辆受到路面激励时,车轮跳动并带动悬挂导向机构压缩拉伸,推动直线电机压缩拉伸或旋转电机转子转动。负载电路与电机构成通路时,在电路中产生电流并经过电机中的绕组线圈,进而产生阻碍电机转动的电磁阻尼力。经过变速机构放大,作用在车身上抑制振动。
本研究基于一种用于履带车辆的扭杆弹簧机电悬挂系统,如图1所示。该悬挂的电机采用直流无刷电机,与行星变速机集成为机电执行器;弹性元件采用履带车辆上常见的扭杆弹簧;导向机构为连杆总成,包括平衡肘、连杆和摇臂。机电执行器与扭杆弹簧的一端分别通过螺栓、花键与车体固定,并通过连杆总成与车轮连接。连杆机构将车轮与车身之间的垂向相对运动通过摇臂转化为机电执行器的旋转运动,经过行星变速器增速,带动无刷直流电机转动。图1中的限位器起到限制车轮最高位置的作用。后文中的机电悬挂均指本研究对象。
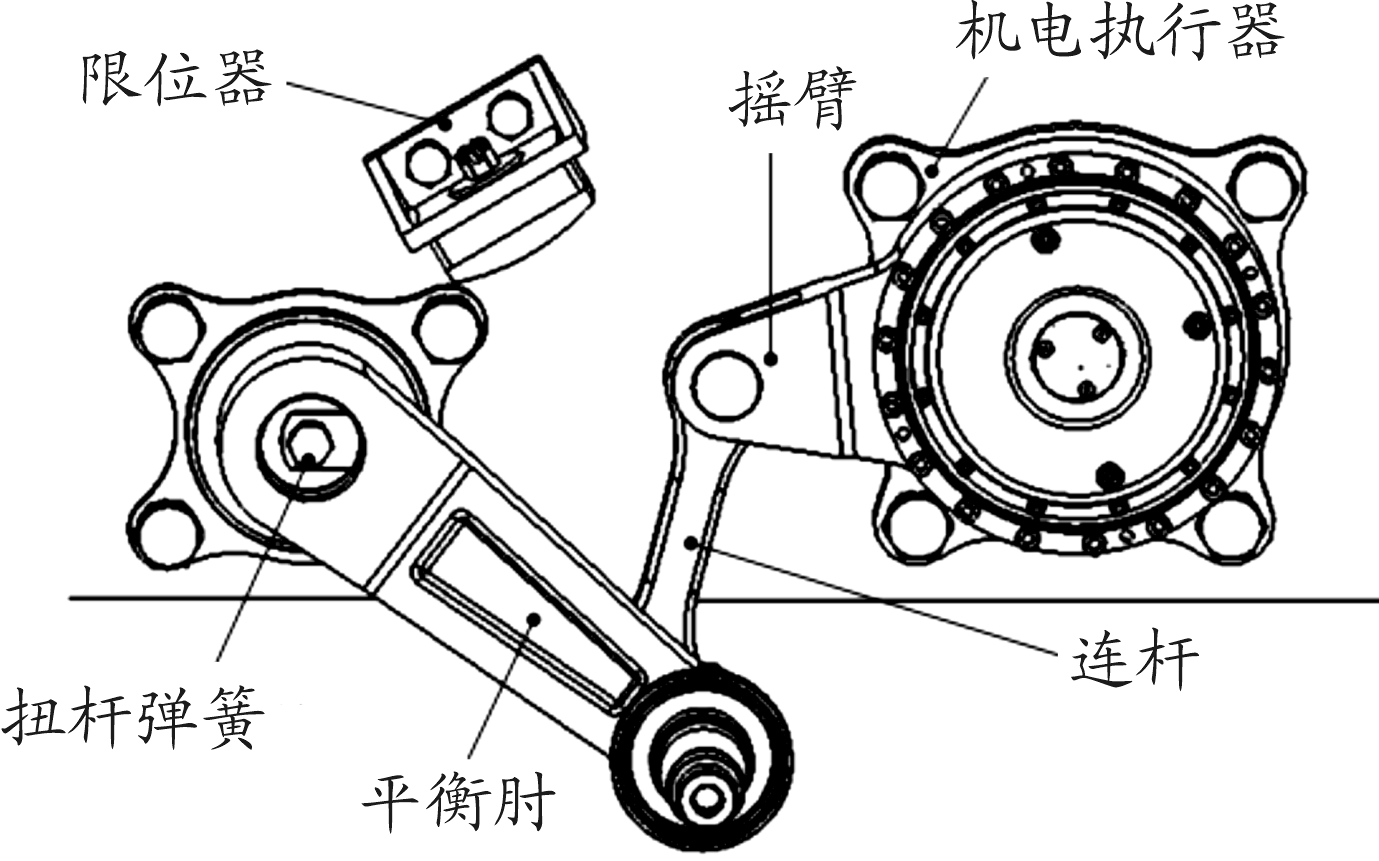
图1 机电悬挂示意图
当车辆受到路面激励时,车轮与车体之间发生相对运动,引起悬挂系统往复振动。同时通过变速器带动直流无刷电机高速往复旋转,产生电动势。此时,直流无刷电机工作在发电状态。如图2所示,当负载电阻接入负载电路并形成通路时,电流经过电机线圈电感L、电机内阻Rin及负载电阻Rout。此时,通电线圈在磁场中转动,产生电磁阻力矩,并经过变速机构放大,传递到车身和车轮上形成机电悬挂的半主动模式下的阻尼力。由于机电执行器的电感较小,因此在电路中忽略它的影响;通常线圈内阻很小,负载电阻大于电机内阻。
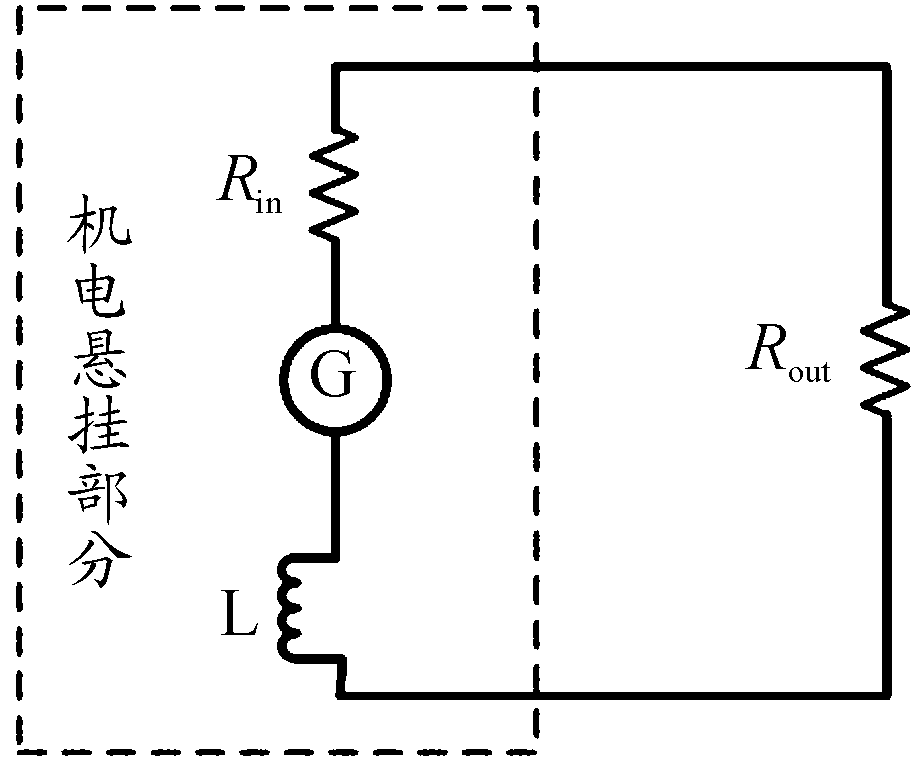
图2 负载电路图
在机电悬挂系统中,连杆之间的摩擦力及齿轮啮合阻力较小,在建模可以忽略。在一定的路面激励下,机电执行器的输入是一定的,调节负载电路中电阻值大小,可以改变电路中电流大小,电流大小的改变直接引起输入端的转矩大小改变。因此,调节机电执行器负载电路上的电阻值就可以对系统的输出力进行控制。
2 数学模型
本研究的对象为单轮机电悬挂系统,将该系统简化为如图3所示二自由度振动模型,它包含悬挂系统的主要运动特征。

图3 二自由度悬挂模型示意图
根据建立的车辆悬挂模型,得到如式的动力学微分方程:
![]()
(1)
式中:ms为簧载质量(kg);mu为非簧载质量(kg);ks为簧载质量刚度(N·m-1);ku为非簧质量刚度(N·m-1);cem为机电悬挂垂向阻尼系数(Ns·m-1);xs为簧载质量位移;xu为非簧载质量位移;xr为路面高程。
扭杆弹簧在负重轮上的垂直载荷Ff随着悬挂行程不同变化,根据扭杆扭转刚度和扭转角求得扭杆得扭矩,再利用平衡肘长度和倾角可以根据式(2)直接求得Ff。实际上由于扭杆的存在,簧载质量刚度是(xs-xu)函数,这里不作推导。
(2)
(3)
θ=α-α0
(4)
(5)
式中:G为扭杆材料的剪切弹性模量(Pa);J为扭杆弹簧的极惯性矩(m4);l和d分别为扭杆弹簧的工作长度和工作直径(m);L为平衡肘的长度(m);α0为平衡肘安装角(rad);θ为扭杆弹簧的扭转角,按式(4)计算;α为平衡肘倾角,按式(5)计算。
车轮履带模型包括履带和车轮两部分,由于两者的阻尼系数非常大,因此只考虑两者刚度。两部分相当于串联,总刚度可以表示为
ku=klkf/(kl+kf)
(6)
式中:kl为履带刚度(N·m-1);kf为车轮刚度(N·m-1);ku为簧下质量刚度(N·m-1)。
机电悬挂系统的阻尼力由机电执行器的电机产生,并经过行星轮系放大作用在簧载质量与非簧载质量上。悬挂垂向阻尼力大小为
(7)
式中:Fem为悬挂系统垂向阻尼力;Fac为机电执行器等效到摇臂外侧的电磁力;γ为摇臂与水平方向的夹角。其中Fac为
(8)
根据式(7)、式(8),机电悬挂垂向阻尼系数可表示为
(9)
式中:i为行星轮系减速比;Ke为反电动势常数(Vs·m-1);Kt为转矩常数(N·A-1);Rin为电机内阻(Ω);Rout为负载电阻(Ω);λ1、λ2分别为电机效率和行星减速器效率(%)。仿真主要参数见表1所示。
3 控制策略设计
3.1 经典天棚阻尼系数控制算法
天棚控制的原理是将天空和车身通过一个阻尼连接起来,减少簧载质量和非簧载质量的垂向振动。实际中这个阻尼器是一个虚拟的,无法实现理想的控制力,因此,将阻尼器置于簧载质量和非簧载质量之间。经典的天棚控制是通过一个开关控制,在高阻尼和低阻尼之间切换来提高车辆的乘坐舒适性,其控制规则可以表示为:
![]()
(10)
式中:cmin为机电执行器设定的输出的最小阻尼系数;cmax为机电执行器设定的输出的最大阻尼系数。
半主动机电悬挂可以输出的最大阻尼系数可以认为是负载电阻为0 Ω时输出的阻尼系数,并且,随着机电执行器内阻越小,输出的最大阻尼系数越大,但是实际上,内阻大小由无刷电机的结构决定的,不能实时改变。而且,电路中的负载电阻不能一直减小,电流过大会导致发热严重,影响系统性能。式(9)可以推出,输出阻尼的大小与负载电阻大小负相关,推出负载电阻满足式(11)。利用式(10)、式(11),经典天棚控制算法在机电悬挂上表示为
(11)
![]()
(12)
式中:Rmax、Rmin分别为大负载电阻和小负载电阻,分别对应选定的小阻尼系数和大阻尼系数。
天棚控制算法的优势在于简单,在实际的应用中,需要两个传感器来采集簧载质量和非簧载质量的状态。
3.2 天棚-加速度混合算法
传统天棚阻尼算法以簧载质量速度和悬挂变形速度为控制参数。对于简化的二自由度机电悬挂模型,簧载质量速度与悬挂变形速度之间的传递函数可以表示为
(13)
式中:![]() 为悬挂变形速度,等于簧载质量速度与非簧载质量速度的差值。
为悬挂变形速度,等于簧载质量速度与非簧载质量速度的差值。
对G1(s)进行频域分析,获得相频曲线如图4所示。从图4中可以看出,在低频时,簧载质量的速度与悬挂变形速度在低频范围内的相位差较小,高频时,两者相位角较大。根据图像可以认为,路面输入为低频时,经典的天棚控制算法可以抑制车辆的振动,但路面输入为高频时,控制能力差。
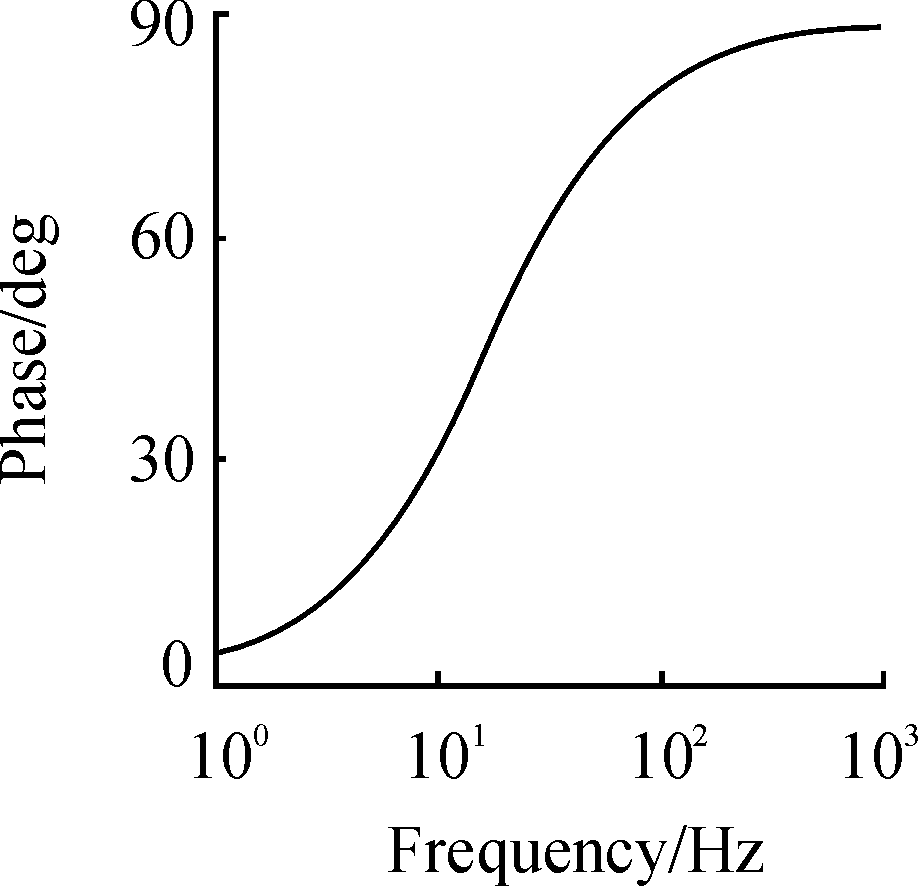
图4 G1(s)的相频曲线
类似于天棚控制算法的加速度驱动阻尼算法,由簧载质量加速度和悬挂变形速度为输入量。对两个输入参数求传递函数获得式(14)。
(14)
对G2(s)进行频域分析,获得相频曲线如图5所示。
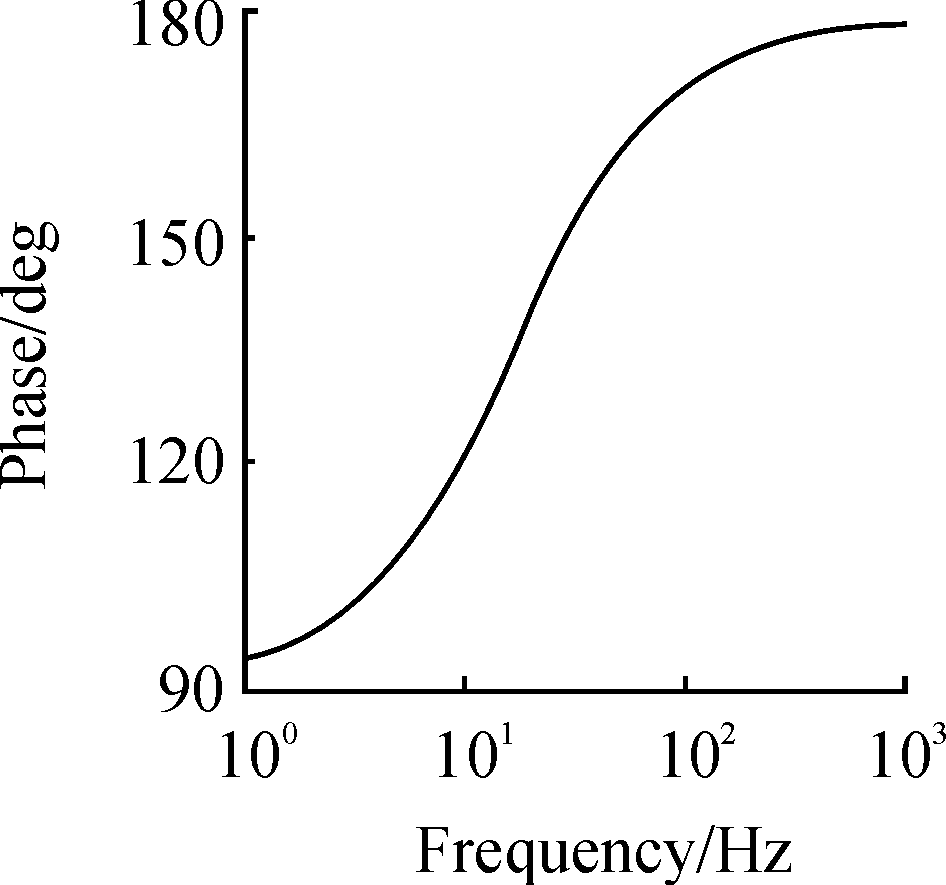
图5 G2(s)的相频特性曲线
从图5中可以看出在低频时,簧载质量加速度与悬挂变形速度在低频范围内的相位差较大,高频时,两者相位角较小。根据图像可以认为,路面输入为高频时,加速度驱动的阻尼控制算法可以很好得抑制车辆的振动,但路面输入为低频时,控制能力很差。它的控制特点与传统的天棚控制算法恰好相反。
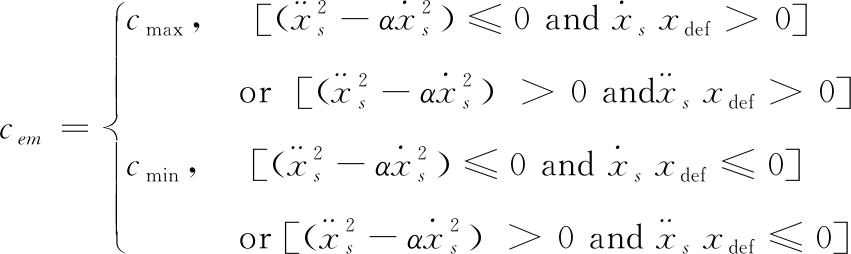
(15)
因此,考虑到两者在高低频分别具有显著的优点和缺点,可以利用一种天棚-加速度算法,兼备二者优点。它的规则如式(15)。式中因子α为高频与低频的分界点。根据式![]() 起到一个频段选择器得作用。SAVARESI于2010年证明了这个频段选择器的合理性[13]。
起到一个频段选择器得作用。SAVARESI于2010年证明了这个频段选择器的合理性[13]。
4 建立仿真模型及仿真分析
4.1 路面模型
利用时域路面模型作为半主动机电悬挂系统的输入,本文采用滤波白噪声法生成路面时域模型。路面不平度密度为
(16)
式中:Gq(n0)为不平度系数;n0为标准空间频率,n0=0.1 m-1;u为行驶速度。
当ω→0时,Gq(ω)→∞,考虑下截止角频率ω0后,使用功率谱密度可以表示为:
(17)
根据随机振动理论,式(17)可以变换为:
Gq(ω)=![]() Sω
Sω
(18)
式中:H(ω)为频率响应函数;Sω为白噪声。
因此,白噪声激励下的路面频响函数为:
(19)
将频响函数转化为微分方程的形式,可得白噪声输入的路面时域模型为:
(20)
式中:n00为路面下截止空间频率(0.01 m-1);w(t)为均0功率谱密度为1的白噪声。在MATLAB/Simulink中搭建路面模型,如图6。
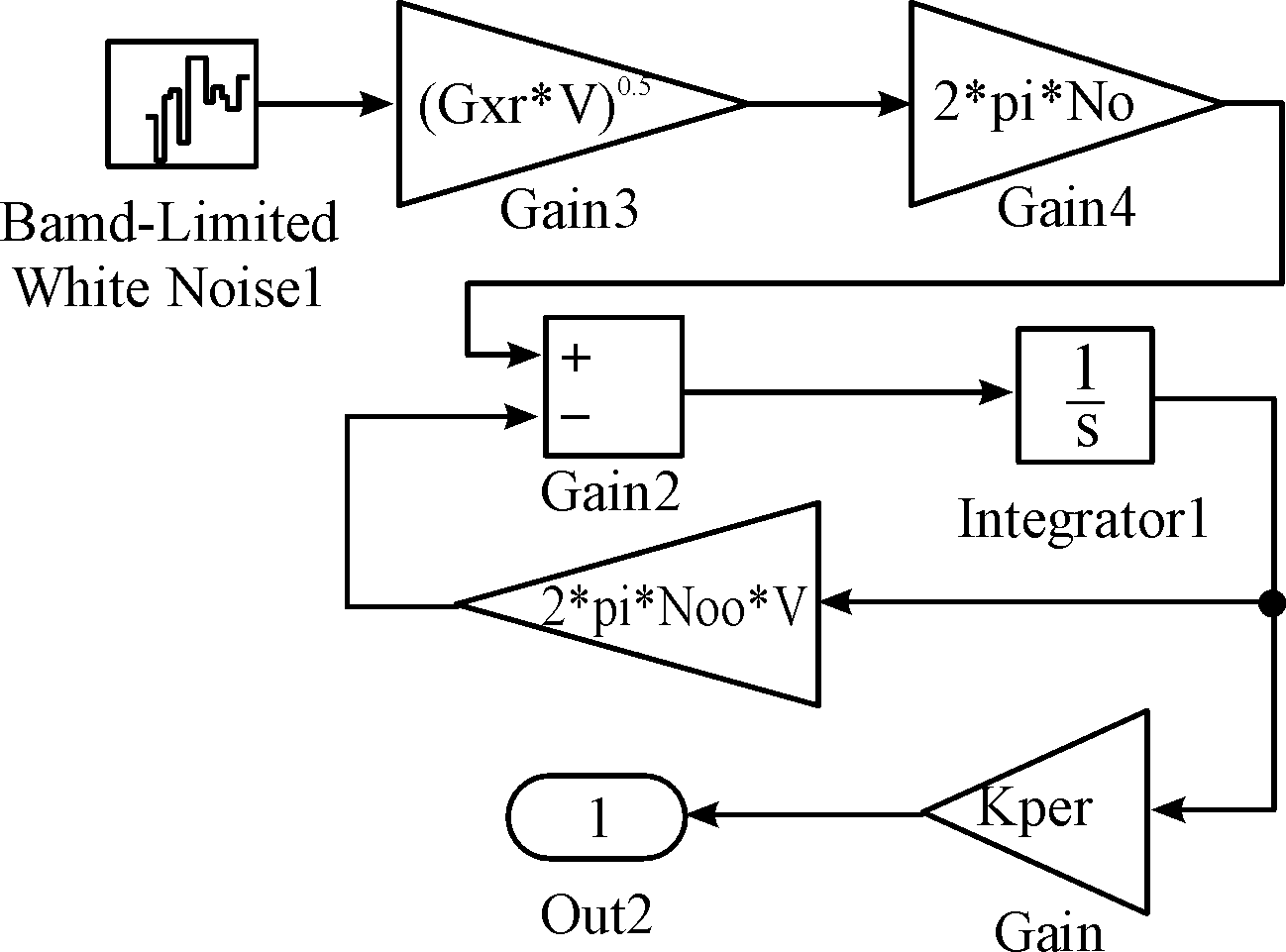
图6 随机路面时域模型框图
4.2 机电悬挂仿真模型
根据机电悬挂的基本原理,在MATLAB/Simulink中,分别按照各部分的关系建立连杆机构及弹簧模型、车轮履带模型、簧上质量模型及机电执行器模型,各模块分别独立建模有利于后期修改优化模型。完整的仿真模型如图7所示。机电悬挂模型的输入为上一节建立的路面高程。
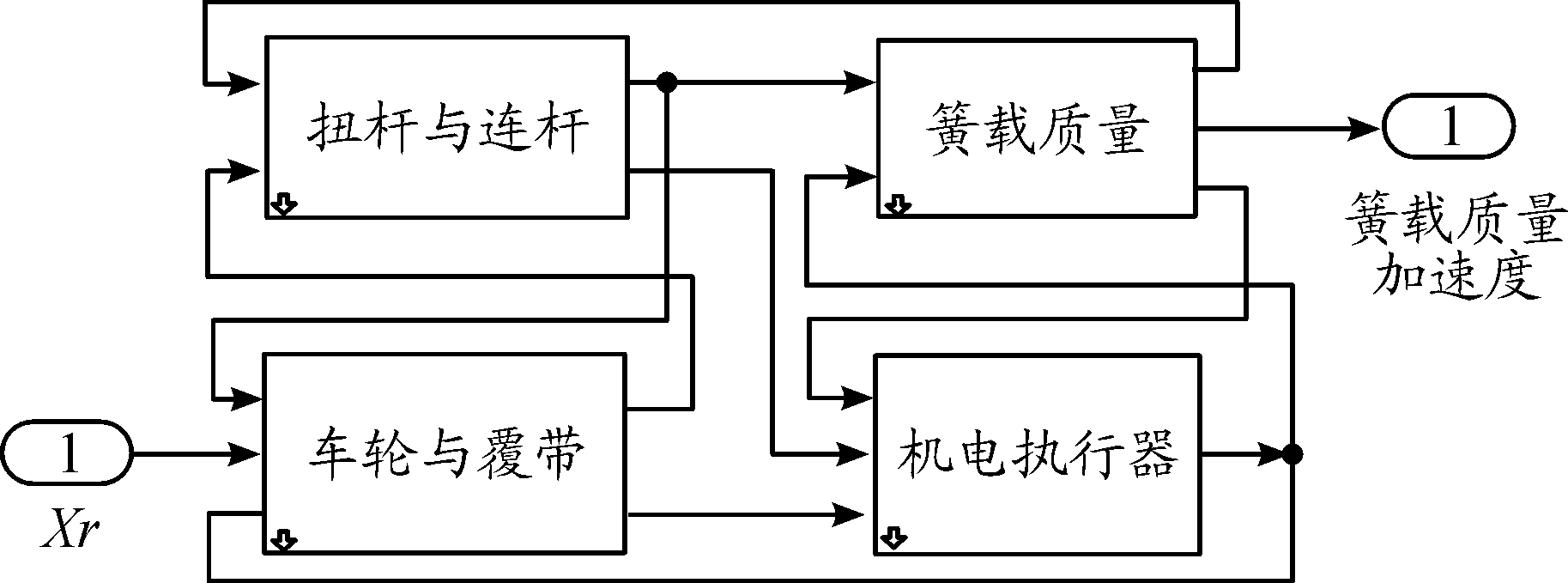
图7 半主动机电悬挂仿真模型框图
其中,根据上文建立的混合控制及经典天棚控制的数学模型,分别搭建基于两种控制策略的机电执行器的仿真模型如图8所示。天棚控制下,将用于切换的不同的负载电阻的阻值设为相同值,实现机电执行器的定阻尼系数的状态,从而模拟其被动模式。实际上,机电悬挂的被动模式就是通过固定负载电阻阻值实现的。机电执行器模块的输入为簧载质量速度与非簧载质量速度。
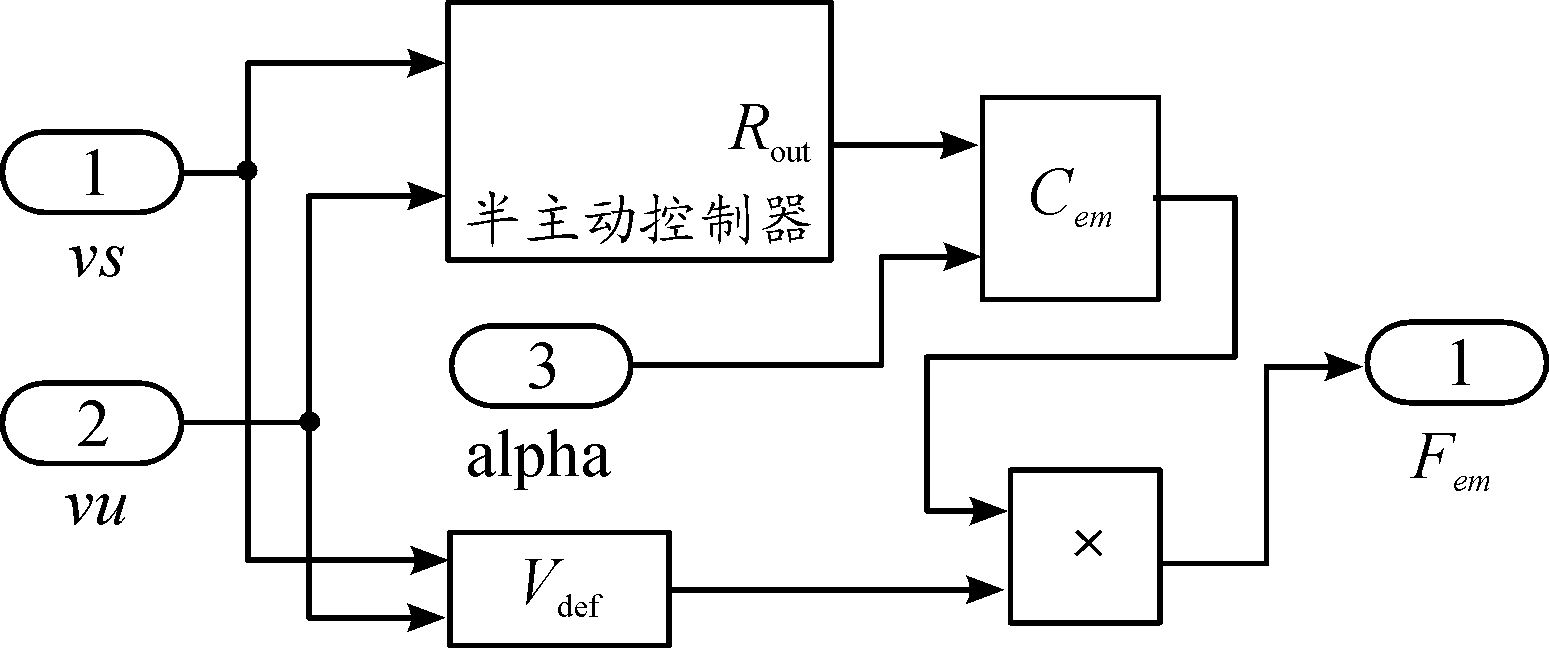
图8 机电执行器仿真模型框图
4.3 时域分析
机电悬挂系统的基本参数如表1所示。不平路面激励是车辆行驶的主要激励,利用上文中路面时域模型,产生一段车速20 km/h的F级路面作为半主动机电悬挂的输入信号,对系统进行仿真。对被动、经典天棚阻尼控制和天棚-加速度混合控制的簧载质量加速度的时域响应进行对比,设置运行时间为30 s。
表1 半主动机电悬挂部分系统参数

参数/单位数值参数/单位数值ms/kg2 200kl/(N·m-1)40 000 000mu/kg240kf/(N·m-1)2 500 000G/GPa78.3Rin/Ω3.02L/m0.359i50.4l/m1.94λ1/%85d/m0.048λ2/%94
由图9可知,相比于被动模式,采用半主动控制的簧载质量加速度更小;与经典天棚阻尼控制相比,混合控制对簧载质量加速度的衰减能力更强。但是在某些时刻,混合控制产生的簧载质量加速度会发生激增。表2为三种控制条件下的簧载质量加速度计算结果。
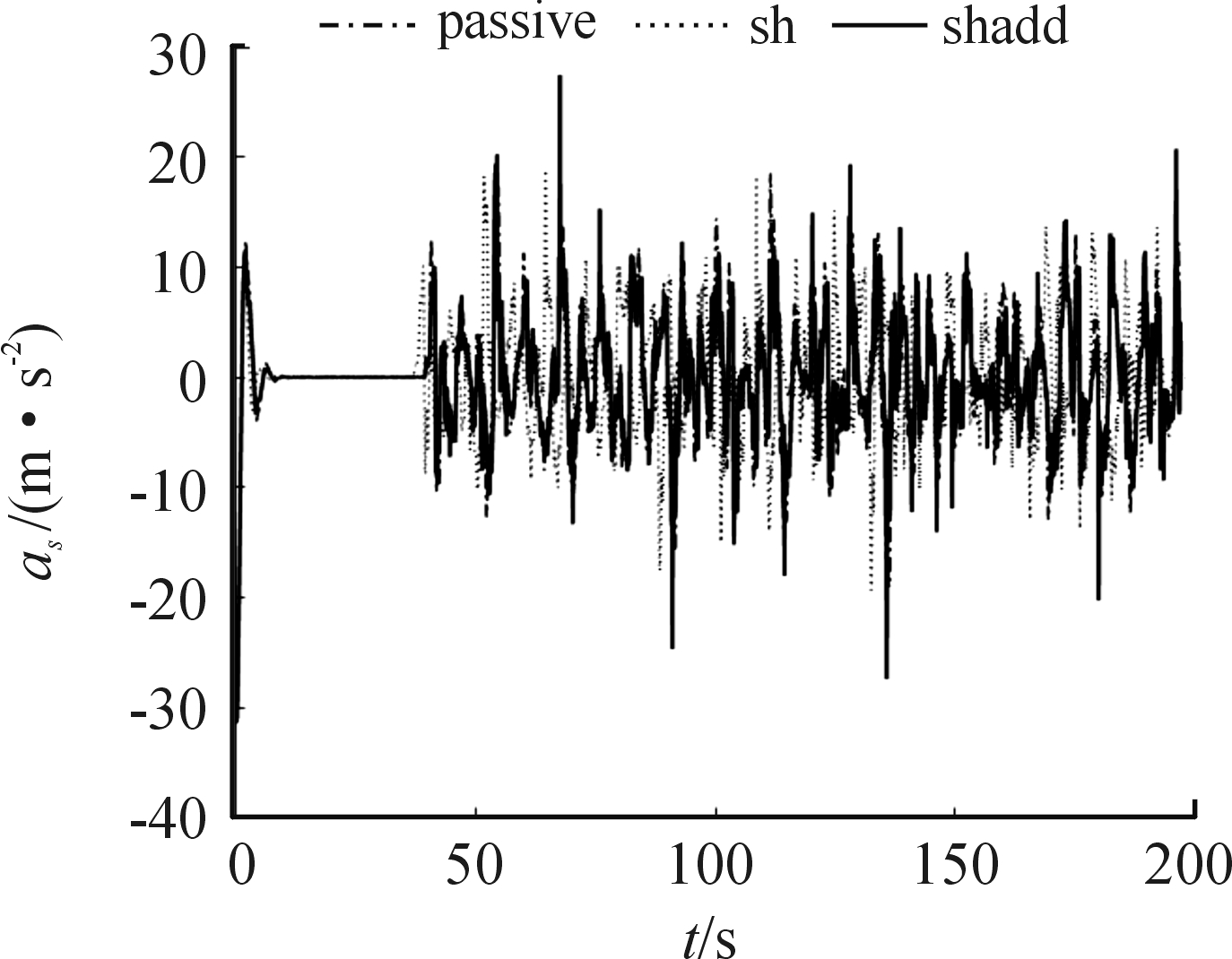
图9 三种控制条件下的车身加速度仿真结果
表2 三种控制条件下的簧载质量加速度计算结果
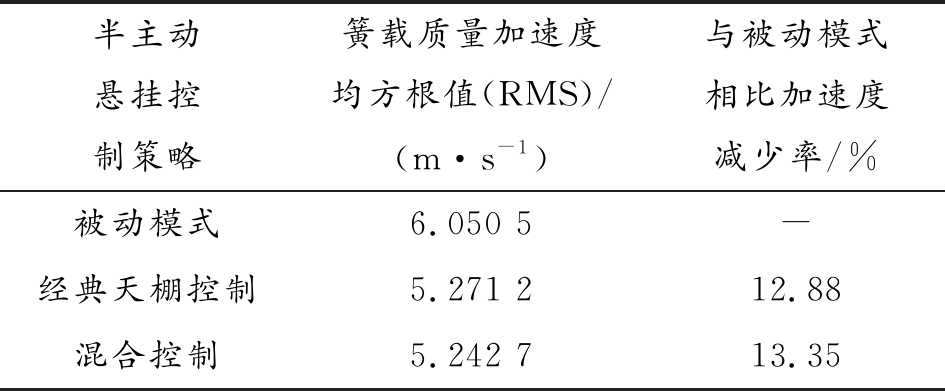
半主动悬挂控制策略簧载质量加速度均方根值(RMS)/(m·s-1)与被动模式相比加速度减少率/%被动模式6.050 5-经典天棚控制5.271 212.88混合控制5.242 713.35
4.4 频域分析
在路面位移激励下,悬挂频域响应图像出现两个共振峰,分别对应机电悬挂簧载质量的共振峰与非簧载质量的共振峰。从图10中可以看出,在第一个共振点处,混合控制与经典天棚控制下加速度频域响应的峰值接近,混合控制略低于经典天棚控制下的值,两者均小于被动模式下的响应;在第二个共振点处,结合放大的峰值部分图像,可以看出混合控制的峰值低于经典天棚控制下和被动模式下的峰值,后两者接近。所以,该混合控制策略在两个共振峰处,对峰值加速度响应均具有有效控制能力。
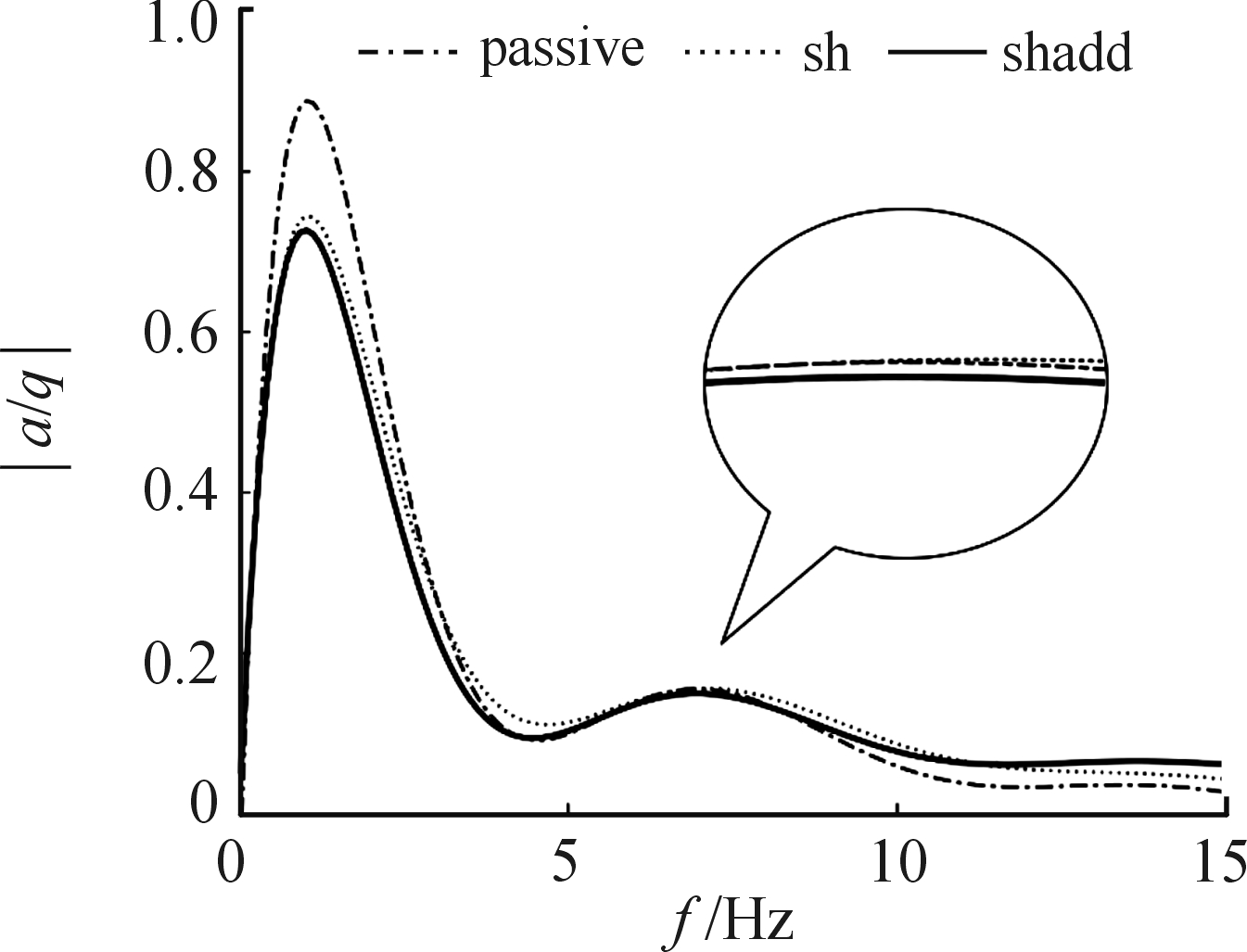
图10 随机路面输入下三种控制条件下的频域响应曲线
5 对比试验及验证
以簧载质量垂向加速度为指标,设定车辆运动速度为20 km/h,匀速行驶在F级路面上,进行连续不平路面输入的试验,分别采用被动模式,经典天棚阻尼控制及天棚-加速度控制,用于验证天棚-加速度控制的有效性。
试验台如图11所示,机电悬挂系统固定在可以上下浮动的质量块上,控制器接在机电悬挂上,将控制策略写入控制器中。被动模式下,电路接入一个定值电阻,阻尼系数大小不变;两种半主动模式下,控制器根据控制策略,令两个固定阻值的电阻按要求接入负载电路。
实验对比曲线如图12所示。

图11 机电悬挂样机试验台
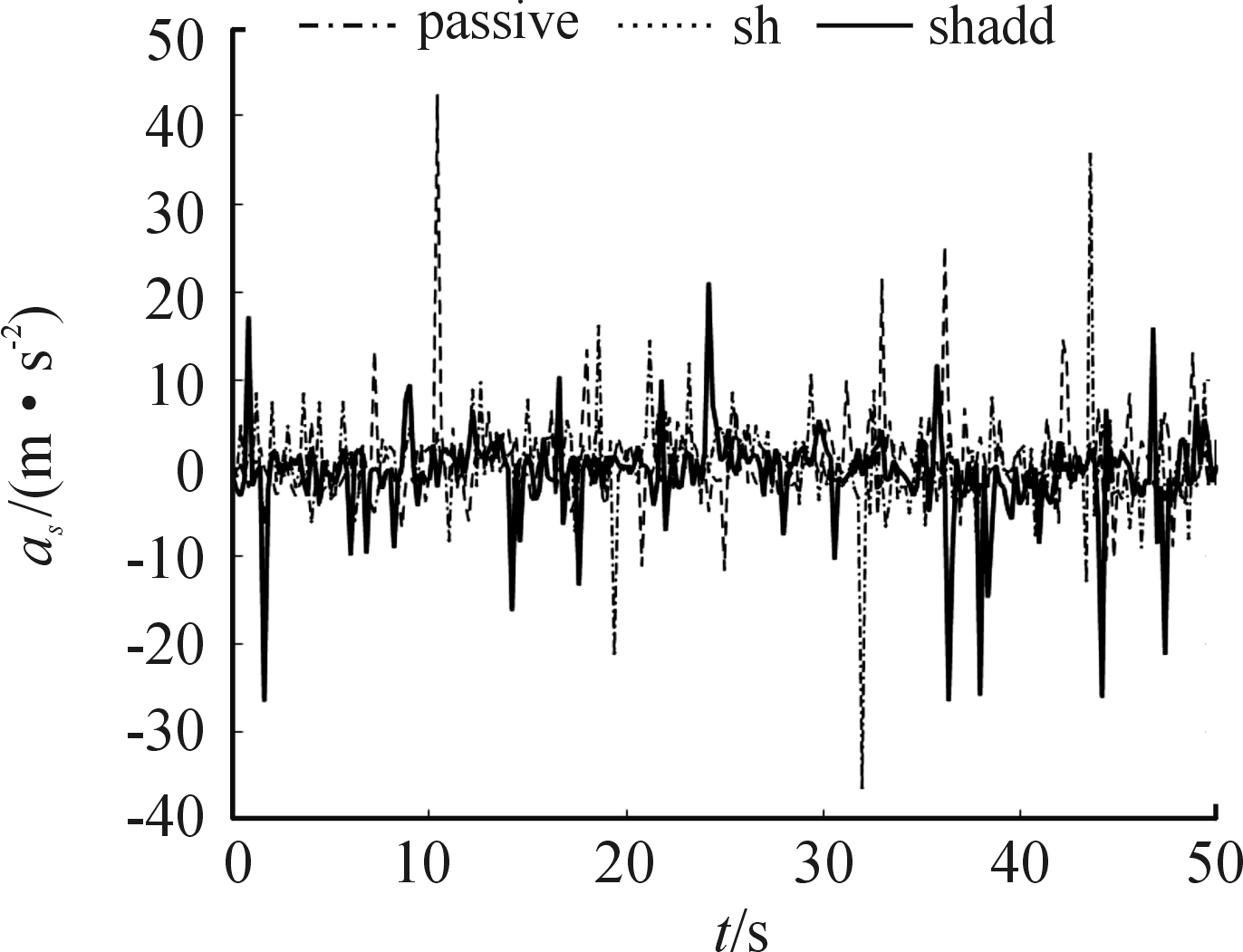
图12 三种控制策略下的车身加速度试验结果曲线
从图12中可以看到,试验中采用经典天棚控制和混合控制的半主动机电悬挂在大部分时间,对簧载质量的垂向加速度控制效果好于被动悬挂;无论经典天棚阻尼控制还是混合控制都会偶尔出现尖峰,但是出现尖峰的次数少于机电悬挂的被动模式。结合表3,相比于天棚阻尼控制策略,混合控制下,簧上质量加速度均方根值更小,并且出现的尖峰的次数更少。上述结果说明,基于天棚-加速度控制的半主动机电悬挂具有良好的隔振能力。
表3 三种控制策略下的簧载质量加速度试验结果
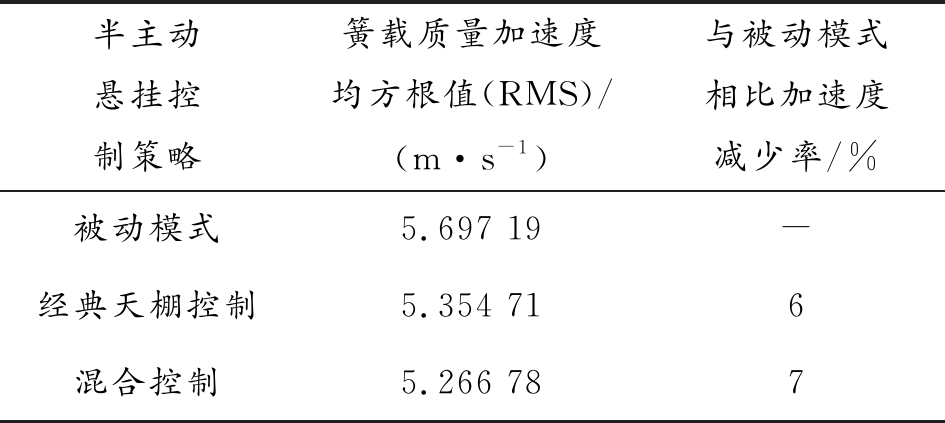
半主动悬挂控制策略簧载质量加速度均方根值(RMS)/(m·s-1)与被动模式相比加速度减少率/%被动模式5.697 19-经典天棚控制5.354 716混合控制5.266 787
6 结论
1) 在时域中,两种半主动悬挂对簧载质量加速度的控制效果均强于被动悬挂,可以有效改善平顺性指标,证明了混合控制策略的有效性。
2) 在时域中,混合控制策略相较于经典的天棚控制算法,簧载质量加速度均方根值更小,控制效果更显著。
3) 在频域中,混合控制策略下的机电悬挂可以有效得对两个共振频率下的加速度响应进行控制。
但是实际效果与仿真结果还有一定差别。无论是天棚-加速度控制还是经典天棚控制下的半主动机电系统,在某些时刻,系统仍然会输出短暂但数值较大的加速度值,这对车辆的平顺性造成了很大伤害。削减簧载质量加速度的尖峰的方法仍然需要继续研究。当频率超过较大共振频率之后,半主动控制下的加速度响应大于被动模式,优化半主动控制策略也需要进一步研究。
[1] 赵雷雷,周长城,于曰伟.半主动悬架系统的最佳阻尼比控制策略研究[J].汽车工程,2018,40(01):41-47.
[2] MATA G T,KUMAR H,MAHALINGAM A.Performance analysis of a semi-active suspension system using coupled CFD-FEA based non-parametric modeling of low capacity shear mode monotube MR damper[J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2018(2):589-595.
[3] CONCILIO A,SIMONE M C D,RIVERA Z B,et al.A new semi-active suspension system for racingvehicles[J].Fme Transactions,2017,45(4):578-584.
[4] QIN Y,LANGARI R,WANG Z,et al.Road excitation classification for semi-active suspension system with deep neural networks[J].Journal of Intelligent & Fuzzy Systems,2017,33(1/2).
[5] 李芳.悬架结构参数优化及基于卡尔曼滤波的主动悬架控制研究[D].长春:吉林大学,2017.
[6] ALDAIR DAA.Neurofuzzy Controller Based Full Vehicle Nonlinear Active Suspension Systems[J].University of Sussex,2012.
[7] 任勇生,周建鹏.汽车半主动悬架技术研究综述[J].振动与冲击,2006,25(3):162-165.
[8] 郑玲,刘巧斌,犹佐龙,等.汽车发动机半主动悬置技术研究现状与展望[J].汽车技术,2017(4):29-35.
[9] KARNOPP C M,HARWOOD R.Vibration control using semi-active force generators[J].Journal of Engineering for Industry,1974 96(2):619-626.
[10] ALASKA A,SAMMIER D,SENAME O,et al.Skyhook and H control of active vehicle suspensions:some practical aspects[J].Vehicle System Dynamics,2003,39(4):279-308.
[11] SAVARESI S,SICILIANI E,BITTANTI S.Acceleration driven damper (ADD):an optimal control algorithm for comfort oriented semi-active suspensions[J].ASME Transactions:Journal of Dynamic Systems,Measurements and Control,2005,127(2):218-229.
[12] GIORGETTI N,BEMPORAD A.TSENG H,et al.Hybrid model predictive control application toward optimal semi-active suspension[J].International Journal of Control,2006,79(5):521-533.
[13] SAVARESI S,POUSSOT-VASSAL C,SPELTA C,et al.Semi-active suspension control design for vehicles[M].Oxford:Elsevier,2010.