起圈织物是一种新型的机织物,相对于平面机织物,起圈织物具有特殊的三维结构,其织物表面含有一定高度的Z方向的毛圈。起圈织物作为增强材料,其预制体的毛圈能很好地嵌入如树脂层、泡沫等相关结构中,使结构的抗分层能力、冲击性能、剪切性能及层间韧性等得到有效提高。
起圈织物织造工艺的主要步骤包括经纱预处理、整经、穿综、机织、下机和整形等[1]。一般是通过杆织造法,将不带圈的地经和带圈的绒经储存在两个经轴上,并与纬轴上的纬纱交织形成[2]。毛圈的Z向高度由绒经轴的送经量所控制,纱线之间的间距通过设计经纱密度和纬纱密度来控制。
目前,对于起圈织物增强复合材料力学性能的研究处于初步阶段。燕得利等[3]从起圈织物增强复合材料层合板的细观结构出发,建立了起圈织物的细观几何模型,并对其拉伸、层间剪切、压缩、纵横剪切性能进行了初步的理论研究、有限元模拟分析和试验研究,研究表明,起圈织物增强复合材料相比平面机织复合材料,其层间剪切强度提高了约20%。Chen等[4-5]研究了起圈织物增强泡沫夹芯结构在平拉、双面剪切下的力学性能,并且进行了平拉和双面剪切有限元仿真模拟,研究表明U-cor有着优异的平拉性能,相对于2D织物的泡沫夹芯复合材料,能够成倍增加界面的强度。陈海立等[6]基于渐进损伤模型分析了起圈织物增强泡沫夹芯结构的平拉性能。赵亚娣[1]从试验角度,对起圈织物预制体的压缩率和压缩性能进行了分析,并重点研究了起圈织物复合材料的断裂韧性与增韧机制,实验结果表明,起圈织物复合材料相比于未增韧的二维织物复合材料,其断裂韧性值增加了72.58%。
综上所述,起圈织物增强复合材料具有优异的力学性能和广泛的应用前景。建立完善的起圈织物复合材料力学性能分析方法具有重要理论意义和工程价值。
此外,囊体材料作为浮空器的主体结构材料,一般由多层高分子功能材料组成,包括承重层、阻氦层、耐候层、粘结层等。其中承重层根据囊体材料具体性能要求由不同的织物(可采用起圈织物)构成,起圈织物复合材料能够成倍提升承重层的层间剪切强度,对整体材料的力学性能起到决定性作用。因此,起圈织物增强复合材料的研究可为其应用于囊体材料提供一定的依据和支持。
本研究以起圈织物增强复合材料层合板为研究对象,根据机织工艺,确定了经纬纱的排列方式与空间走向,建立了起圈织物增强复合材料层合板的单胞模型。通过引入周期性边界条件,建立了起圈织物复合材料层合板的等效弹性性能数值预测模型。选取合适的强度准则和刚度折减方式,分别对其在拉伸载荷和层间剪切载荷下的刚度、强度和损伤演化过程进行了预测,并与试验结果进行了对比。
1 单胞模型
为建立合理的单胞模型,采用了三维数字显微镜分别对起圈织物复合材料层合板的经向切片和纬向切片进行了观察,显微镜观测图像(放大倍数为10)如图1所示。可以看出,经纱始终沿着机织方向上下穿梭,而纬纱基本保持伸直。

图1 起圈织物复合材料层合板的显微镜观测图像
起圈织物复合材料层合板的实体模型需考虑更多较为复杂的因素,因此有必要在建立单胞模型的过程中,做一些重要的基本假设。本研究不考虑纤维和基体中的裂纹、空隙和缺陷等影响,在单胞的内部空间结构中具有连续性和变形协调性[4]。忽略纱线因挤压等变形导致的在不同截面位置中截面面积的变化。对于纱线截面形状,纬纱截面采用八边形假设,地经和绒经截面采用矩形假设。
在上述假设的基础上,根据起圈织物材料的织造参数,在三维建模软件CATIA中建立了双面起圈织物层合板的单胞模型,如图2所示,图中经纱(红色)方向为X轴方向,纬纱(蓝色)方向为Y轴方向,厚度方向为Z轴方向。
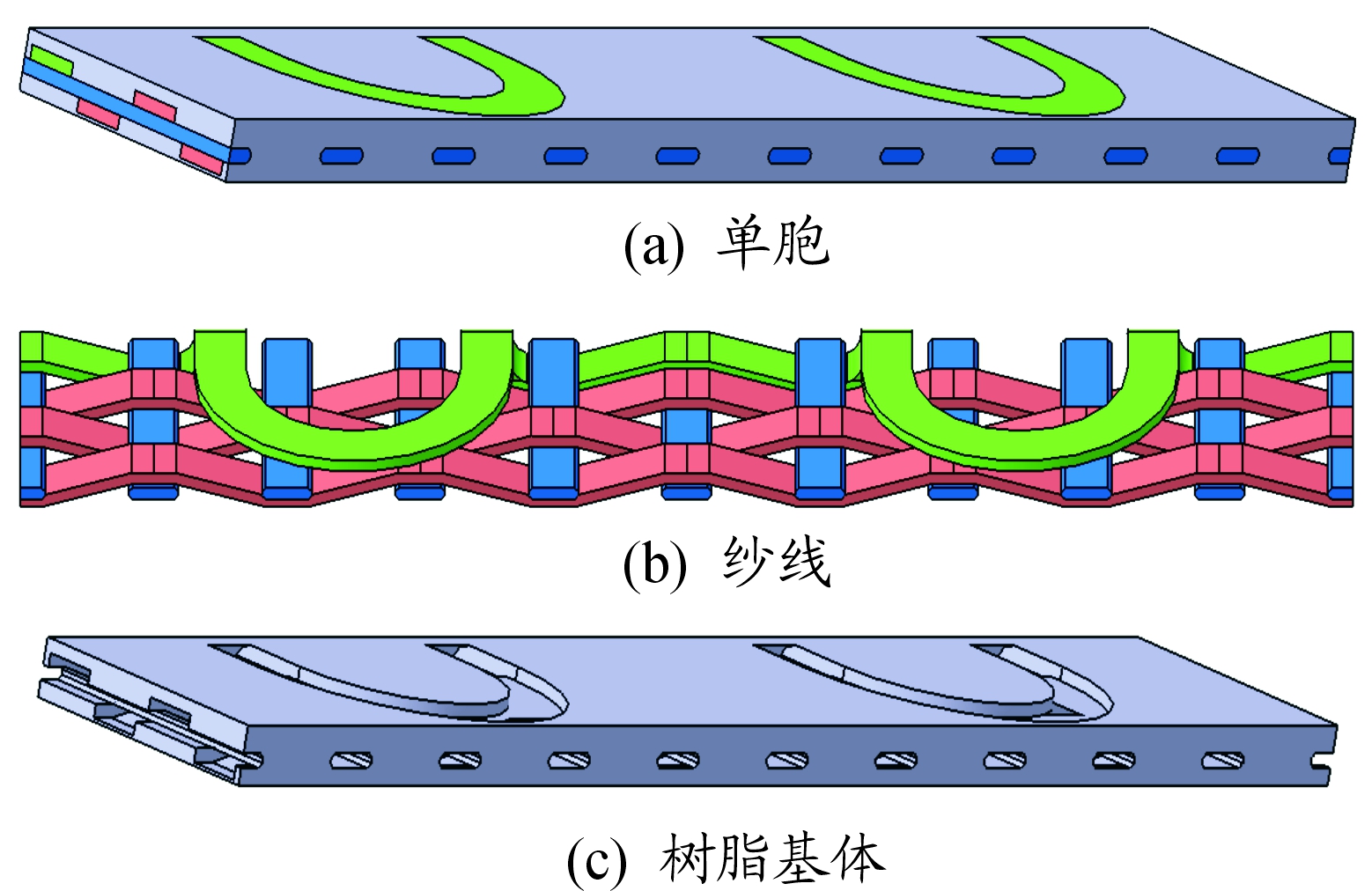
图2 起圈复合材料层合板单胞模型示意图
2 有限元分析
2.1 材料属性
起圈织物复合材料是由经纱、纬纱和基体3种组分材料组成的,起圈织物复合材料的经向和纬向纤维束中均含有一定量的纤维单丝和树脂基体,纤维束视为横观各向同性,本文所使用的纤维为无碱玻璃纤维,基体使用的是环氧树脂基体。根据NASA经验公式和Chamis公式[7]分别预测无碱玻璃纤维束(基体为环氧树脂)的工程弹性常数和强度,具体结果见表1所示。
表1 纤维束力学性能参数
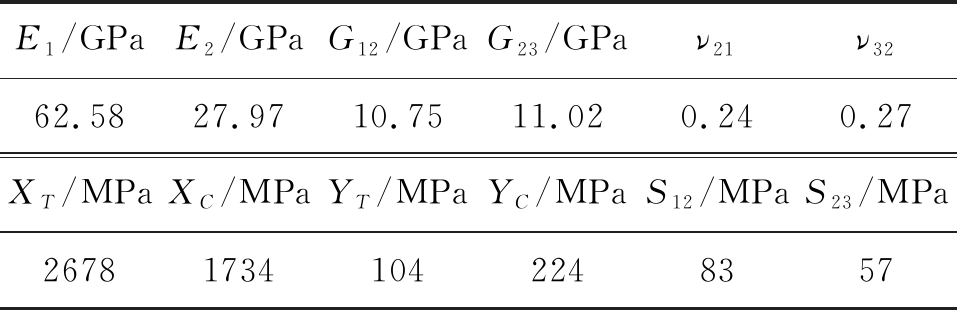
E1/GPaE2/GPaG12/GPaG23/GPaν21ν3262.5827.9710.7511.020.240.27XT/MPaXC/MPaYT/MPaYC/MPaS12/MPaS23/MPa267817341042248357
2.2 周期性边界条件
起圈织物层合板的单胞模型具有周期性,在用单胞代替材料进行等效力学性能分析时,需要对其施加周期性边界条件,以保证相邻单胞之间满足位移连续性条件和应力连续性条件[8],即材料的每个单胞都具有相同的变形模式。在相邻边界处应同时满足位移连续和应力连续要求。
对于六面体单胞模型,Xia等[9]提出的在其中任一边界面上周期性位移场表达式为:
![]()
(1)
式中:![]() 为单胞的平均应变;上标j+和j-分别表示沿xj轴的正方向和负方向;
为单胞的平均应变;上标j+和j-分别表示沿xj轴的正方向和负方向;![]() 为单元体任意点坐标的线性位移;
为单元体任意点坐标的线性位移;![]() 为在全局坐标系下的周期性位移分量,由于在周期性单元体的平行相对面上位移
为在全局坐标系下的周期性位移分量,由于在周期性单元体的平行相对面上位移![]() 相同,两式相减得:
相同,两式相减得:
(2)
对于六面体单胞而言,在![]() 给定的情况下,
给定的情况下,![]() 为常数,即:
为常数,即:
(3)
2.3 强度准则和刚度折减方案
本文采用三维Hashin准则对起圈织复合材料中的纤维束进行失效判断,该准则可以区分纱线中的4种失效形式。三维Hashin准则表达式如下所示:
纤维束拉伸失效(σ11≥0)
![]()
(4)
纤维束压缩失效(σ11<0):
(5)
基体拉伸失效(σ22+σ33≥0)
(6)
基体压缩失效(σ22+σ33<0)
![]()
(7)
式中:σii和τij(i, j=1,2,3)分别为材料6个方向上的应力;XT和XC分别为轴向拉伸和压缩强度;YT和YC分别为横向拉伸和压缩强度;S12、S13和S23为剪切强度。
树脂区的基体属于各向同性材料,可采用Von-Mises失效理论作为其失效判据。相比于最大应力准则,Von-Mises准则不需要求解最大主应力特征值,且形式较为简单。Von-Mises准则表达式为
(8)
式中:σi和τij(i, j=x,y,z)分别为材料六个方向上的应力;Xm为树脂屈服强度。
当单元应力满足失效判据时,单元将发生损伤,而单元并没有完全失去承载能力,而是通过相应的损伤模式修改损伤后刚度值,更新单元损伤后的刚度矩阵进行迭代运算,从而实现渐进损伤分析。本研究采用Camanho[10]提出的刚度折减方式作为材料刚度退化准则,见表2所示。相关的强度准则、损伤退化及刚度折减方案的有效性已得到了众多学者的研究和验证[11-13]。
表2 材料性能退化方案
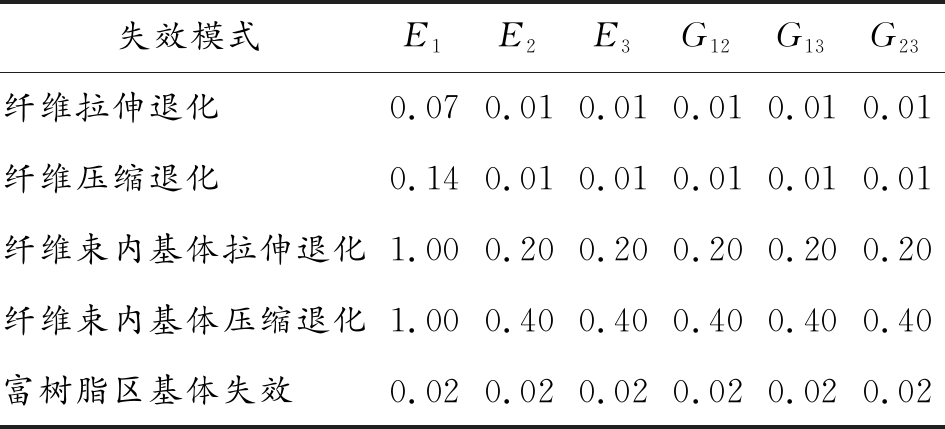
失效模式E1E2E3G12G13G23纤维拉伸退化0.070.010.010.010.010.01纤维压缩退化0.140.010.010.010.010.01纤维束内基体拉伸退化1.000.200.200.200.200.20纤维束内基体压缩退化1.000.400.400.400.400.40富树脂区基体失效0.020.020.020.020.020.02
3 有限元结果分析
3.1 力学响应
图3是起圈单胞在拉伸作用下的变形图,为便于观察单胞的变形情况,将变形缩放系数调整至1 000。图3从左至右分别是起圈单胞拉伸方向正向部分和负向部分的变形图以及对厚度边界面上投影的变形图。由图3可见,在拉伸载荷下,单胞表面发生了翘曲,不再是一个平面。但六面体单胞平行相对面的变形完全一致,单胞侧面一面向内凹,同时另一边向外凸,此现象验证了周期性边界条件的变形协调条件。

图3 满足周期性边界条件的单胞变形示意图
由图4和图5分别给出了起圈单胞在拉伸和层间剪切载荷工况下的Mises应力云图。单胞在变形过程中不仅保持了位移的连续性,同时单胞平行相对面上的应力传递也具有连续性,即验证了周期性边界条件中的应力连续条件。在经向拉伸工况下经纱是结构的主要承力部件,且在经纱的转角部位具有一定程度的应力集中。在层间剪切工况下,单胞结构的上下表面之间出现了明显的层间错动的变形趋势,结构表面也出现一定程度的翘曲变形。进一步观察可知,绒经的毛圈根部具有明显的应力集中现象。
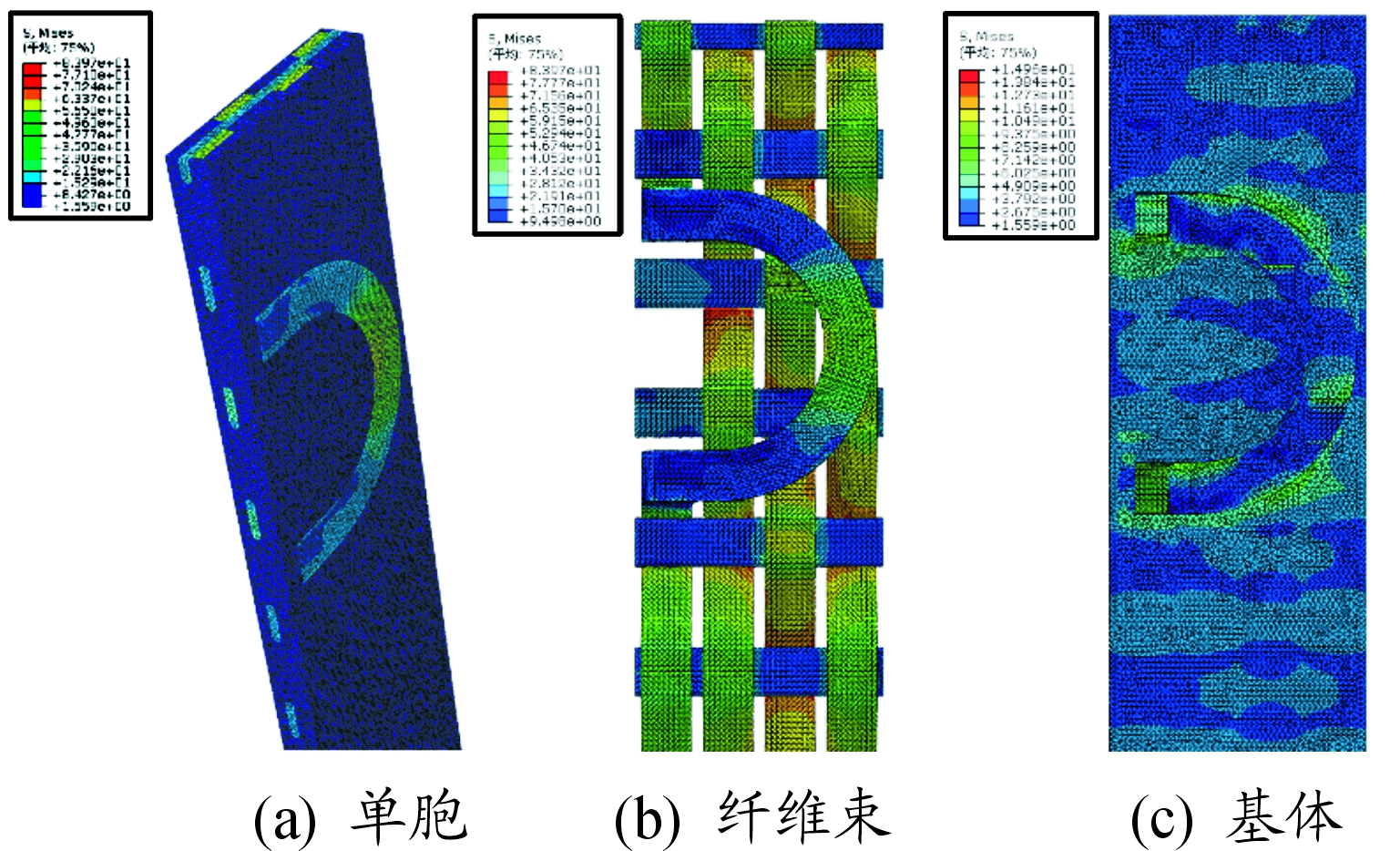
图4 起圈单胞经向拉伸Mises应力云图
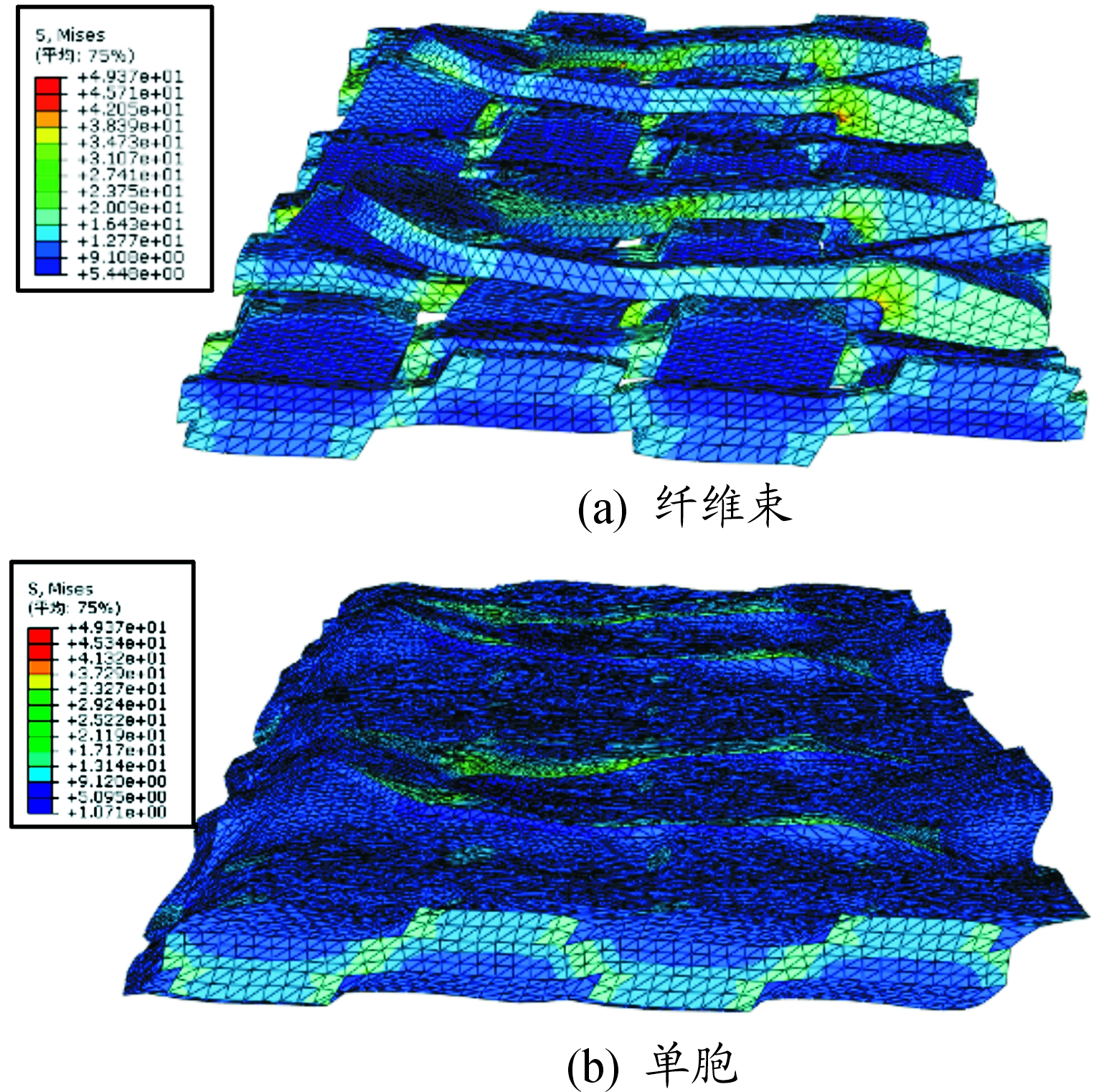
图5 起圈单胞纬向层间剪切Mises应力云图
3.2 损伤过程
图6展示了起圈复合材料在经向拉伸作用下的损伤过程。当ε1=0.95%时,基体首先出现少量损伤,ε1=1.07%时,经纱方向的部分纤维出现了拉伸失效。随着位移载荷的不断增加,其纤维束损伤和基体损伤也不断扩展。最终,在ε1=1.55%时,材料各部位损伤单元迅速延展,此时复合材料因纤维拉伸断裂和基体失效而失去承载能力。从图6(c)可以看出,纤维束内的基体也发生了一定程度的拉伸失效损伤,损伤主要集中在纤维束和基体的交界处,这主要是交界处的应力集中导致的。
图7展示了起圈复合材料在经向层间剪切作用下的损伤过程。当剪切应变达到1.2%左右时,基体单元首先达到损伤失效判据,出现了少量损伤。当层间剪切载荷不断增加时,基体逐渐出现大范围失效,从而承载能力逐渐降低。基体与起圈织物中含毛圈的绒经所接触的位置有应力集中现象,基体损伤开始均发生在与绒经接触的交界面上,并沿着交界面逐步扩展,最终整体结构失效。

图6 起圈单胞经向拉伸损伤扩展云图

图7 起圈单胞层间剪切损伤扩展云图
3.3 结果对比
为验证有限元模型的可靠性,对起圈复合材料层合板进行了准静态拉伸试验和梁剪切试验。拉伸性能试验根据国标GB/T 1447—2005进行,短梁剪切试验根据国标GB/T 30969—2014进行。在本研究中制备成型的起圈层合板的纤维体积含量为28.6%。
图8为试验件破坏后的照片。拉伸试验件的拉断截面断口较为整齐,树脂和玻璃纤维均被拉断。部分试验件出现在加强片附近断裂的现象,这是由试验件形状和试验机夹头端部效应造成的。在小跨距的短梁剪切载荷下,试验件表现的失效形式是中部分层破坏,说明其失效是剪切应力所导致。

图8 试验件破坏后的照片
表3给出了有限元分析结果和试验结果。从表中数据可以看出,有限元仿真结果与试验结果吻合较好,最大相对误差为12.7%,在可接受的范围内,说明仿真结果具有一定的准确性。仿真误差来源主要有以下几点:① 有限元计算过程中对几何模型和强度失效模型作了理想的假设,材料参数也并不能完全表征试验中的实际性能;② 在有限元仿真模型中,纤维束与基体通过共节点的方式合并成了一个整体,则忽略了纤维束和树脂间的滑移,且两种材料的刚度不同,在整体变形过程中交界面上容易出现应力集中,从而影响有限元分析;③ 试验件在制备过程中,不可避免会出现气泡,纤维缺陷等,对试验结果造成影响。
表3 有限元分析结果与试验结果
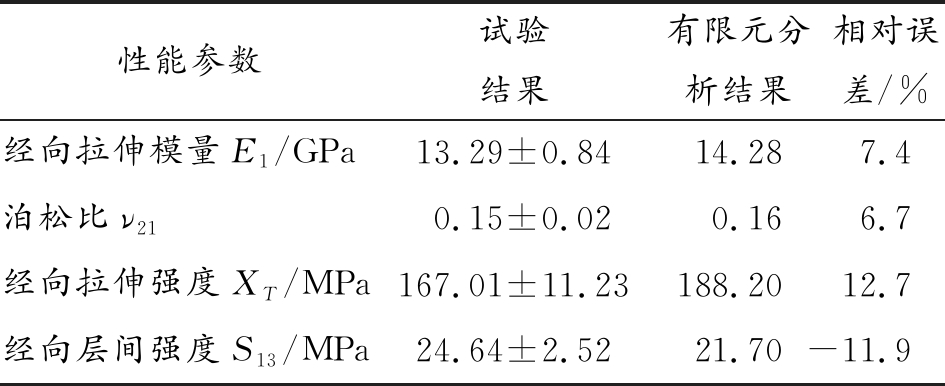
性能参数试验结果有限元分析结果相对误差/%经向拉伸模量E1/GPa13.29±0.8414.287.4泊松比ν210.15±0.020.166.7经向拉伸强度XT/MPa167.01±11.23188.2012.7经向层间强度S13/MPa24.64±2.5221.70-11.9
4 结论
本研究建立了起圈织物的单胞模型,通过引入周期性边界条件对单胞模型的等效弹性性能进行了有限元分析。分别以Von-Mises准则和三维Hashin准则作为起圈织物复合材料中基体与纤维束的失效准则,并考虑了材料在满足失效判据时的刚度折减,对起圈织物复合材料进行了强度和失效行为分析,并与试验数据进行了对比,结果吻合较好。
通过显微镜观察起圈织物复合材料的经纬向切片截面形状,建立了起圈织物复合材料的单胞模型,引入周期性边界条件和相应的基体与纤维束失效准则,对起圈织物复合材料单胞进行了有限元模拟,通过结果对比发现,两者最大误差为12.7%,在可接受范围以内,验证了所建立的单胞模型的可靠性。
在经向拉伸下起圈织物中的经纱是结构的主要承力部位。在层间剪切下,复合材料结构表面出现了一定程度的翘曲变形,且绒经的毛圈根部具有明显的应力集中现象。由于纱线和基体的交界处的应力较为集中,基体损伤均开始发生于此。经向拉伸时,起圈织物失去承载能力的主要原因是纤维拉伸断裂。层间剪切时,起圈织物失去承载能力的主要原因是基体的破坏。
[1] 赵亚娣.基于结构化增韧的新型织物织造及复合材料力学性能研究[D].天津:天津工业大学,2017.
[2] 燕德利.起圈织物增强复合材料的细观结构和力学性能研究[D].南京:南京航空航天大学,2012.
[3] 燕德利,周光明,王佳佳.起圈织物增强层合板层间力学性能有限元分析与实验研究[J].材料导报,2012,26(12):137-140.
[4] DAI B,ZHOU G,SUN J,et al.Experimental study on the mechanical properties of looped fabric reinforced foam core sandwich composite[J].Journal of Composite Materials,2016,50(20):2807-2821.
[5] CHEN M,ZHOU G,WANG J.On mechanical behavior of looped fabric reinforced foam sandwich[J].Composite Structures,2014,118:159-169.
[6] 陈海立,周倩,胡唐,等.基于渐进损伤模型的U-cor增强泡沫夹层结构平拉性能仿真[J].材料科学与工程学报,2016 (3):491-496.
[7] CHAMIS C C.Mechanics of composite materials-Past,present and future[J].Journal of Composites Technology & Research,1989,11(1):3-14.
[8] 孙琎.三维面芯编织复合材料力学性能及渐进损伤研究[D].南京:南京航空航天大学,2016.
[9] XIA Z,ZHANG Y,ELLYIN F.A unified periodical boundary conditions for representative volume elements of composites and applications[J].International Journal of Solids and Structures,2003,40(8):1907-1921.
[10] CAMANHO P P,MATTHEWS F L.A progressive damage model for mechanically fastened joints in composite laminates[J].Journal of composite materials,1999,33(24):2248-2280.
[11] 王力立,陈宏,林国伟,等.复合材料帽型单筋板弯曲破坏数值分析[J].兵器装备工程学报,2019,40(04):208-214.
[12] 雷良超,周光明,陆方舟,等.复合材料缠绕接头拉伸失效性能有限元分析[J].兵器装备工程学报,2018,39(04):180-184.
[13] 吴龙兴,周光明,邓健,等.含斜坡复合材料夹芯壁板剪切稳定性研究[J].兵器装备工程学报,2019,40(05):220-225,242.