命中精度直接影响导弹的精确打击能力,是装备试验鉴定过程中需重点检验的指标之一。导弹武器系统要求高命中精度,但由于地域、经济等因素的制约,使得装备试验次数有限,且每次试验环境、条件不尽相同,导致现场试验信息不足,造成精度分析和评估的困难。因此运用科学的方法对导弹武器系统的命中精度作出准确的分析和评估是研制、试验、军队等各方始终关注的问题之一。导弹武器命中精度评估属于典型的小子样问题,结合小子样问题的特点,如何进行误差源分析和误差处理、如何有效的挖掘和利用验前信息、如何实现异质多源信息融合、采取怎样的评定方法等都是非常值得深入研究的课题。本文针对命中精度评估这一军事需求,对上述问题进行了全面综述。
1 评估指标及研究体系
1.1 评估指标
导弹武器命中精度评估就是指根据各类仿真试验及特殊弹道飞行试验的结果进行统计分析,以此来评估导弹命中精度是否满足要求,在评估同时确定影响命中精度的误差因素,为实现误差补偿、提高导弹精确打击能力提供理论依据。导弹命中精度评估的特点在于试验次数有限且试验数据异质多源。评判命中精度最为常用的指标是圆概率偏差,由下式给出:
其中落点坐标(x,z)为独立随机变量且服从正态分布,![]() 即为所求圆概率偏差。
即为所求圆概率偏差。
对于三维精度问题,文献[1]提出采用球概率误差(Sphercial Error Probable,SEP)作为三维精度问题的评估指标。其定义为以目标点为中心,以R为半径作一球体,导弹落入该球体内的概率为50%,此R即为SEP,由下式给出:
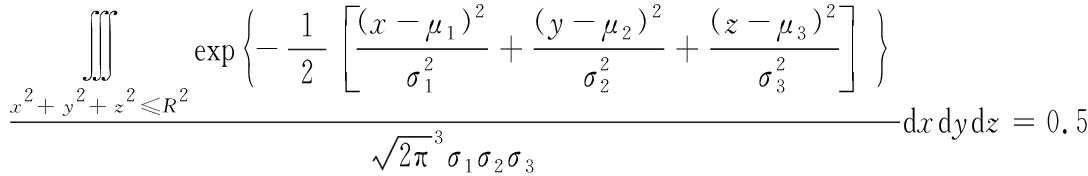
其中落点坐标(x,y,z)为独立随机变量且服从正态分布,![]()
1.2 研究内容体系框架
命中精度评估隶属于导弹武器试验鉴定研究领域,它贯穿于导弹武器的全寿命周期中。主要研究内容包含误差源分析、误差系数分离、弹道精度折合、多源试验信息融合和命中精度评定方法。内容体系如图1所示。
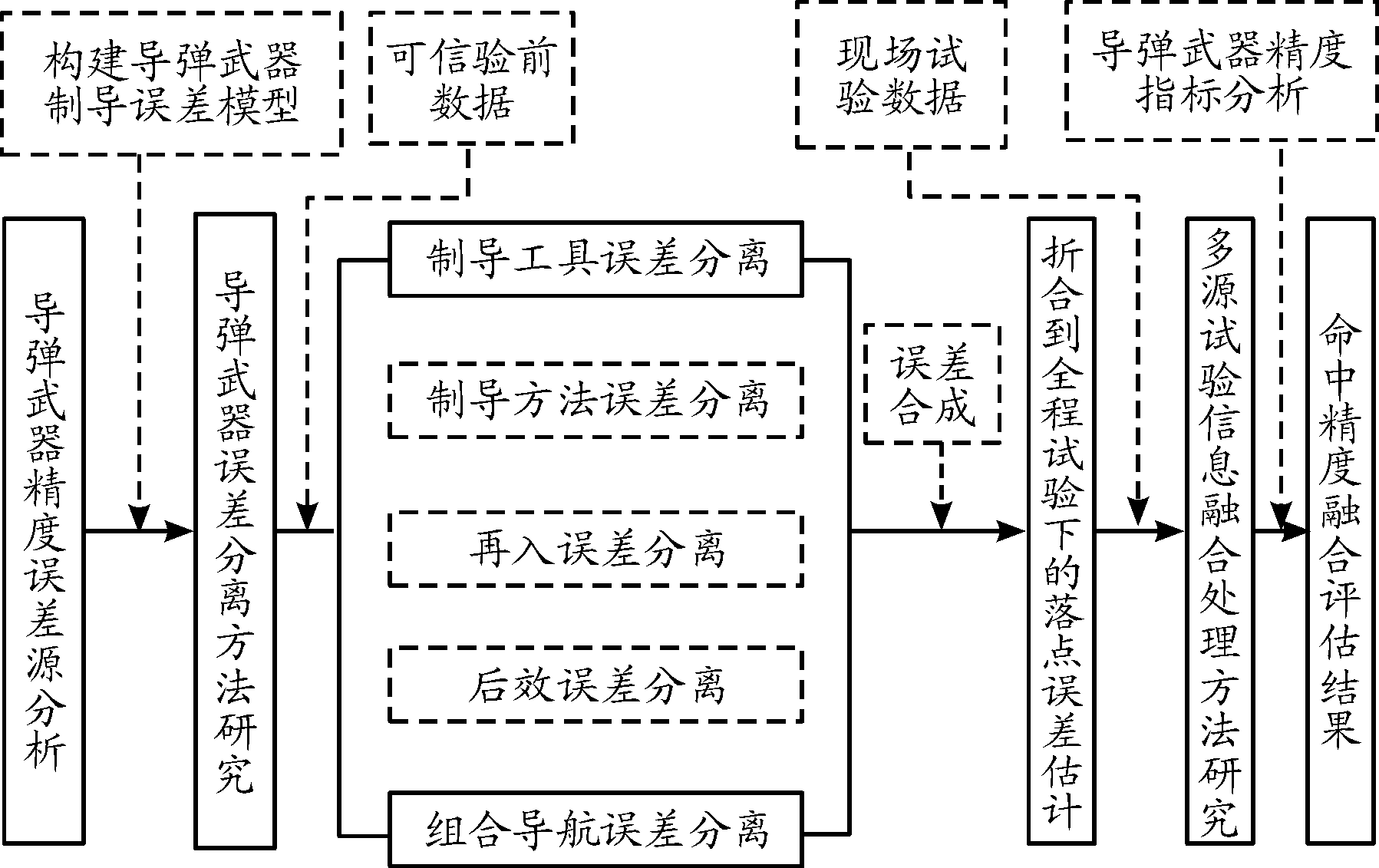
图1 命中精度评估主要研究内容体系框图
2 导弹武器命中精度评估研究内容
美、俄等国家对导弹武器命中精度的评估工作较为重视,从公开资料来看,主要通过以下几种手段增强精度鉴定及评估能力:
1) 加强统计理论的研究与应用,实现理论计算与试验检验相结合。如苏联曾提出:进行精度鉴定,应当利用序贯分析等方法检验、确定系统的可靠性[2];
2) 加强靶场建设,提高靶场装备的测量精度以获取更小误差,保证试验数据的可靠;
3) 模仿实战环境下进行大量地面试验以及特殊弹道飞行试验,并采用先进的半实物仿真技术进行精度测量和仿真[3],获得大量可靠的验前试验信息;
4) 提高导弹武器系统全寿命周期信息的利用率,增强导弹型号之间的技术继承性,缩短研制和试验周期。如俄罗斯的“白杨-M”洲际弹道导弹,其工程研制时间较短,列装前仅进行了4次飞行试验,皆是得益于其“白杨”导弹的研制基础和大量的历史试验信息。
由上述可见国外关于命中精度的评估手段及方法经过了型号的验证甚至实战的检验,具有较为深厚的技术积累。我国在命中精度方面的研究,大多是基于制导回路的建设,利用统计学方法对制导精度指标进行分析[4]。一批专家学者如张金槐、唐雪梅等开展了大量理论与应用研究,并出版了一系列专著,论述了小子样情况下各种评估方法在武器装备试验中的应用,以及武器装备性能指标分析与评估的基本方法。结合国内外学者研究情况和1.2节研究框架,本文着重对导弹武器命中精度评估涉及的5个方面问题进行综述。
2.1 误差源分析
影响导弹武器命中精度的误差因素有很多,按飞行过程可分主动段误差源、自由段误差源及再入段误差源;按制导过程可分为制导误差源和非制导误差源。制导误差包括工具误差和方法误差,其中制导工具误差约占整个命中精度的60%~80%[5];非制导误差主要是指非制导因素及外界影响产生的误差。具体分类如图2所示。
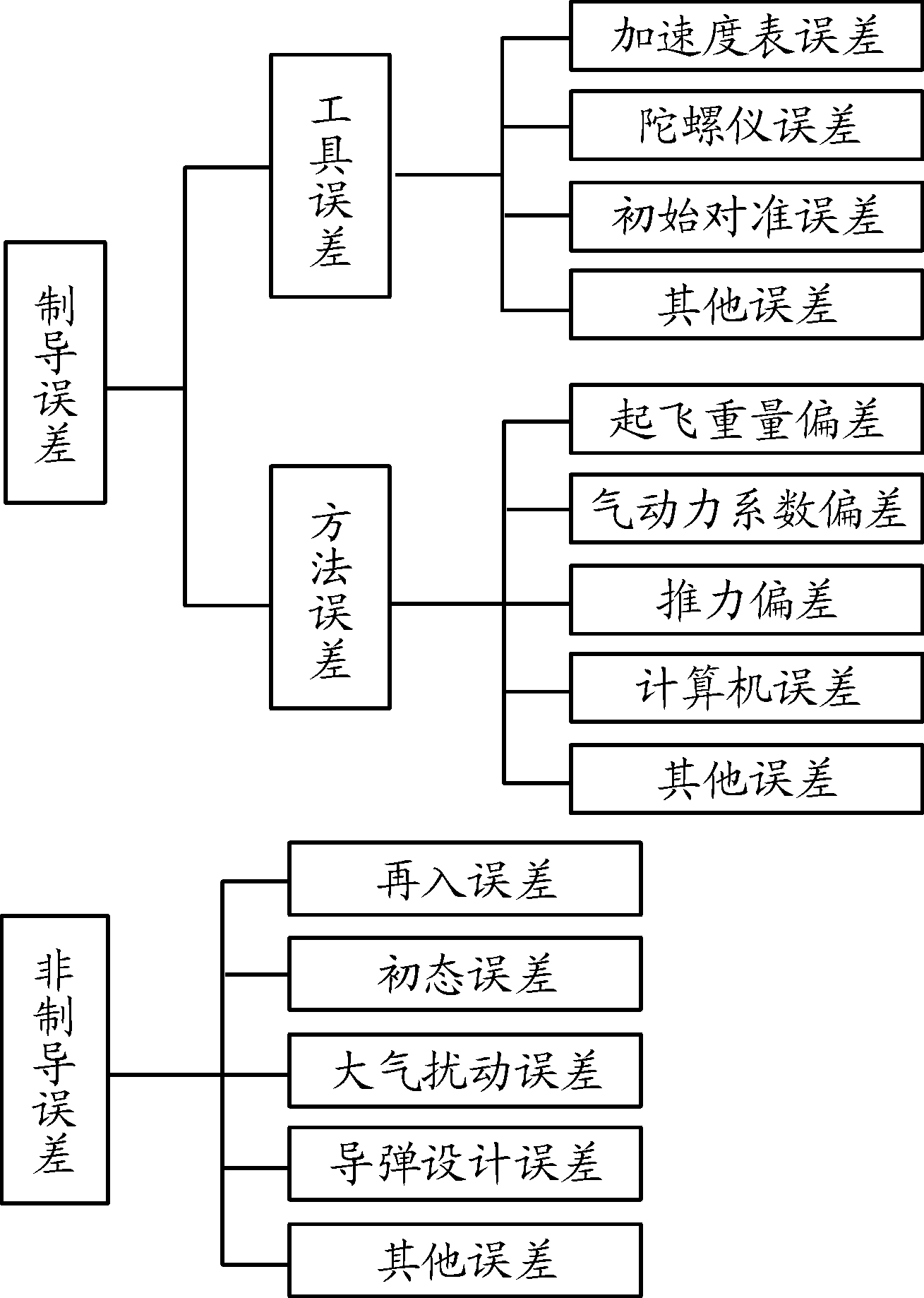
图2 误差源分类框图
误差源分析是命中精度评估工作的重要内容,精准的误差分析是误差分离及精度折合的基础。一方面由于公开资料有限,另一方面惯导工具性能已经接近设计的极限,因此目前关于导弹命中精度误差因素的分析研究主要集中在非制导误差。
其中关于初态误差的研究较多,但是由于其概念在导航、制导领域界定模糊,部分文献对初态误差的认识理解不尽相同,如文献[6]将发射点垂线偏差和大地测量误差归为初态误差范畴;而文献[7]将初态误差分为初始定位误差、定向误差、速度误差和重力误差,并分析了它们在扰动重力场中的形成机理,利用动力学方程确定了它们对位置偏差的影响情况,但是研究只是对单个误差源进行了仿真,并未综合各误差源进行整体分析。文献[8-9]针对初始误差和工具误差分别提出了基于线性模型和基于非线性模型的两种误差估计方法,结合动基座飞行器的精度分析进行了验证,但是两种方法均强烈依赖于先验信息,否则无法给出准确的误差估计;垂线偏差是影响导弹命中精度的重要因素[10],文献[11]分析了垂线偏差产生的原因及其对导弹命中精度的影响机理,给出垂线偏差对初始姿态角的影响关系;文献[12]研究了垂线偏差对弹道参数的影响情况,定量计算出了垂线偏差引起的落点偏差,上述两篇文献深入分析了垂线偏差产生的原因及垂线偏差对命中精度影响机理,但是缺少补偿技术的研究,未能提出提高落点精度的补偿方法。
除此之外,文献[13]研究了一种复合制导条件下再入机动弹头的再入误差分析方法;文献[14]研究了后效冲量误差对导弹命中精度的影响,并提出一种消除后效冲量误差的方法,文献[15]利用六自由度弹道仿真系统模拟打靶,并根据仿真结果对空地微型导弹的误差源进行分析。
需要指出的是,误差源与导弹的设计方案及设计要求有关,因此在具体分析导弹误差因素时,应当充分结合导弹武器系统的制导方式、相关的导航算法特性以及导弹武器的工作环境特点,这样才能得到准确的误差分析。特别是目前列装和在研的弹道导弹多采用复合制导方案,在导弹不同飞行段,组合制导方式不同,飞行环境也不尽相同,因此应结合具体情况进行分析。
2.2 制导工具误差分离方法
为获取更多试验信息,通常需对特殊试验弹道进行工具误差系数分离,而后将误差系数折合至全程弹道作为验前信息。制导工具误差分离主要利用环境函数和观测数据对误差系数向量进行估计[16]。常用分离方法如图3所示。
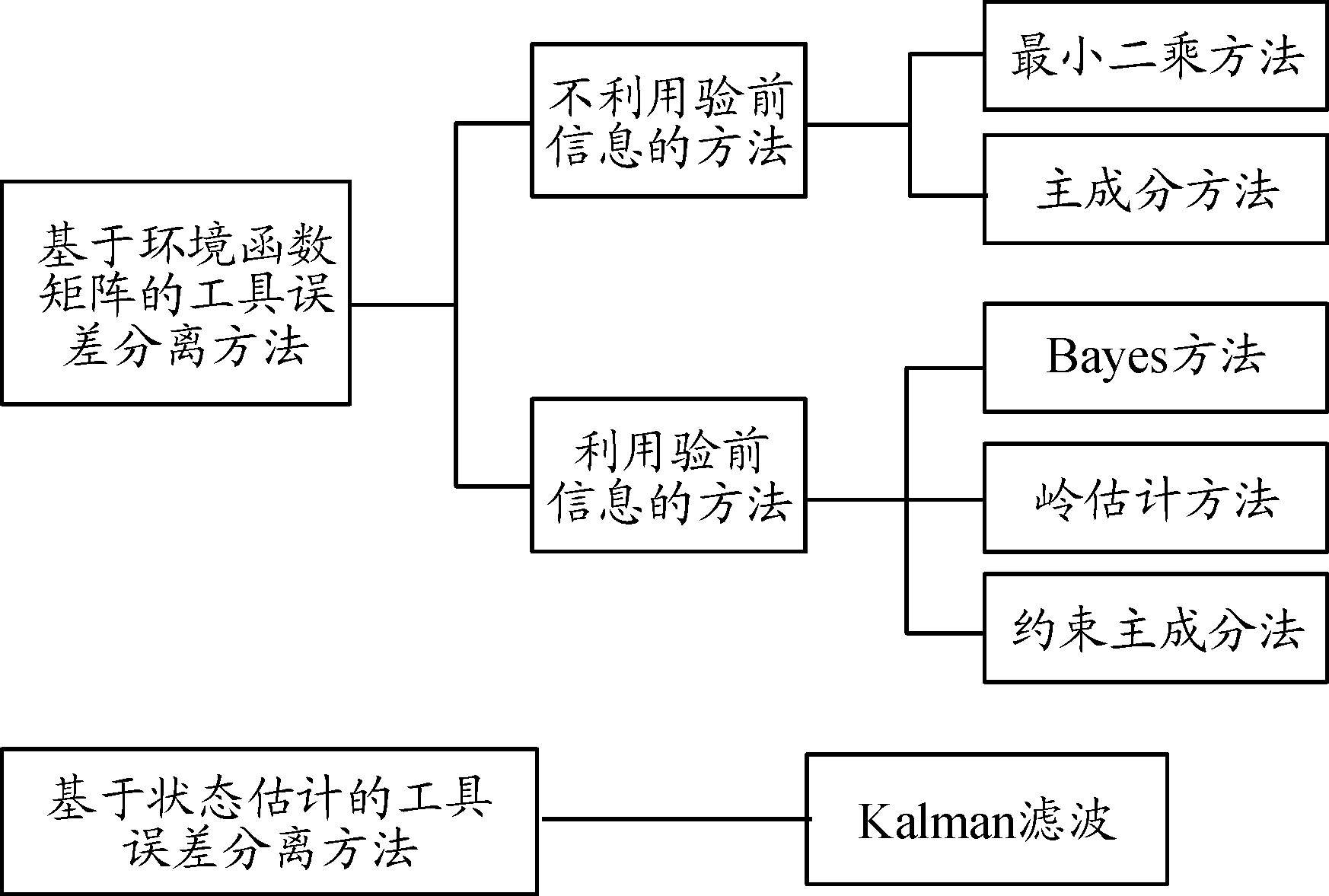
图3 制导工具误差分离方法框图
制导工具误差分离是一个高维复共线性估计问题,在很多情况下由于环境函数严重相关,导致传统的最小二乘法、主成分法等方法难以获得精确解。目前关于上述问题主要有两种解决途径:一是设计能够激励各种误差源的飞行试验弹道,增强观测条件,减弱环境函数矩阵的病态,如美国曾研制制导鉴定弹和制导误差飞行器等;二是利用参数估计方法实现误差分离,文献[17]较早提出制导工具误差分析的一般思想。
目前应用较多的方法为主成分法和约束主成分法,但是其原理仍然是建立在最小二乘基础之上的,结果可信度不高,无法有效解决环境函数矩阵的复共线性问题。随着计算机技术和仿真技术的发展,一些新方法得到应用,本节重点对以下工具误差分离新方法进行综述。
1) 基于支持向量机方法
支持向量机方法结合了统计学、机器学习等多种智能方法,最早应用于手写字符识别问题[18]。由于制导工具误差分离这一回归问题可看作优化问题,基于此文献[19]提出利用支持向量机方法获得工具误差系数的思想,并证明方法的有效性;但是当问题样本量较大时,标准支持向量机方法求解实时性差、效率低,针对此问题文献[20]提出最小二乘法与支持向量机方法结合用于制导工具误差分离,有效的提升了训练速度。
2) 基于进化策略方法
进化策略方法是一种智能算法,通过模拟生物遗传和进化过程来解决优化问题。文献[21]提出一种基于进化策略的误差分离方法,能够在全局范围内寻优,避免了环境函数矩阵的复共线性问题;文献[22]引入了一种协方差矩阵自适应进化策略,通过自适应策略调节参数实现优化,文献[23]和文献[24]分别讨论了该方法在不同环境不同条件下的应用,文献[25]则利用该方法对制导工具误差系数进行了求解,并讨论了白噪声与求解精度的关系。基于进化策略的方法能够有效避免环境函数的复共线性问题,但该方法通常存在收敛慢、易“早熟”等问题,同时传统进化策略算法中精英个体在交叉、变异过程中有被破坏的风险,上述文献并未就算法本身的缺陷进行相应探讨研究。
3) 基于主成分改进方法
基于主成分方法求解工具误差系数存在一些问题,一是主成分方法的本质仍是基于最小二乘法,是有偏估计;二是确定主成分筛选准则过程中主观因素较大;三是主成分会根据不同的计算单位而发生变化。就上述问题有学者提出一些改进方法。文献[26]提出一种将岭估计和主成分估计结合起来的岭型主成分估计方法,文献[27]将该方法应用于制导工具系统误差的分离,利用岭型主成分的优良性质提高了估计结果;针对主成分子集选择上存在的问题,文献[28]提出利用遗传算法确定最佳主成分子集的方法,显著增强了算法的分离能力。基于主成分改进的方法较传统主成分方法能够利用验前信息,但是此类方法仅在一定程度上克服了环境函数矩阵病态的影响,因此对估值改善的程度有限。
除上述方法之外,文献[29]结合海基导弹误差分离的特点,分析比较了Bayes估计、主成分和正则化3种改进方法;文献[30]针对环境函数矩阵严重病态性的特点,提出将误差系数求解问题转化为动力系统的数值求解问题,基于该项研究成果,文献[31]提出一种将病态代数方程组的求解转化为相应的刚性动力系统求解的算法;文献[32]基于捷联惯导平台,提出交叉验证的误差分离方法,并建立了精度检验指标。这些方法为求解制导工具误差系数提供了新的思路,在一定程度上降低了病态环境函数对求解的影响。
2.3 弹道精度折合
分析导弹武器命中精度的评定结果,应当基于大量全程飞行试验落点偏差量的统计,但是一方面由于全程飞行试验组织复杂、成本高昂,另一方面受地域、政治等因素的制约,难以进行大量的全程飞行试验,因此需要对特殊试验弹道的落点偏差向全程弹道推算,即弹道精度折合。
弹道精度折合的主要研究对象包括各类特殊试验弹道及误差项,如小射程试验弹道、高弹道以及后效误差和再入误差的折合等。主要折合方法目前包括两大类[33]:一是利用制导工具误差分离方法,获得特殊试验弹道的误差系数估计值,而后代入全程飞行弹道,推算出全程试验弹道下制导工具误差引起的落点偏差;二是利用特殊试验弹道的测量信息直接推算全程飞行弹道所产生的偏差。方法一利用误差分离技术确定落点偏差,虽然制导工具误差系数分离困难,传统方法难以得到高精度解,但是该方法可以增强研究人员对惯性器件各项误差的了解,有助于改进设计及采取相应误差补偿手段;方法二虽能避免分离误差系数,但是只能估计出误差项对落点的综合影响,且估计精度不高,另外这种方法不利于认识器件及改进设计。
文献[34]分析了求取折合误差系数时外测误差精度、采样点数和弹道特性等3个因素对折合精度的影响程度,但是文献只给出了定性分析,未能提出有效的折合方法;文献[28]和文献[35]针对传统主成分法主要成分选择困难的问题,提出利用遗传算法确定最佳主成分子集,并证明该方法折合精度更高。除此之外,文献[36]针对惯性/星光复合制导导弹,介绍了误差辨识和折合系数两种弹道折合方法;针对潜射远程弹道导弹,文献[37]首先构建初始误差、工具误差等误差折合模型,而后利用弹道仿真的方法实现了弹道折合,折合结果与理论值一致。
2.4 多源验前信息融合
由于导弹武器造价高昂,且试验条件约束限制多,导致现场飞行试验次数及观测数据有限,因此开展导弹命中精度评估需要充分利用各种验前信息进行决策分析,如各分系统的地面试验信息、不同试验阶段的验证性试验信息、相关型号的历史信息等[38]。利用验前信息与现场试验信息进行融合评估可提高评估的可信性和有效性,目前常用的融合方法有Bayes统计方法、Fiducial统计方法等,其中Bayes方法在工程中应用较为广泛。运用Bayes方法的关键就是如何将各类验前数据及参数以分布形式表示出来。
针对验前信息融合问题,国外较早就进行了研究,其中文献[39]引入无信息验前计算方法,极大减轻了主观因素对验前可信度的影响;文献[40]通过建立允许专家之间存在依赖关系的共识模型,首创利用Bayes方法确定验前信息;文献[41]首次将最大熵方法用于验前信息融合。国内方面,针对信息融合过程中引入大量先验信息时,现场试验信息可能会被“淹没”的问题,文献[42]提出应当在试验数据相容性检验基础上进行融合,并结合可信度改进了贝叶斯算法,以避免“淹没”现象发生;文献[43]充分利用仿真信息作为验前信息,结合多层先验信息融合方法实现反舰导弹的综合评估;针对多源信息融合中信息权重确定的问题,文献[44]提出一种基于Dirichlet验前分布的整体推断模型用于确定权重系数;文献[45]提出一种基于第二类极大似然估计确定验前融合分布方法;文献[46]基于ML-Ⅱ信息融合方法得到了k/n(G)系统可靠性指标的Bayes估计,提高了异质多源信息融合的稳定性和可靠性;文献[47]利用参数和非参数检验方法,对不同验前信息进行相容性检验。上述文献均是基于数据分布差异来判定验前信息的可信度,但是目前很多验前信息的物理来源是已知的,因此仅从数据层面考虑可信度显然不够全面,针对这一问题文献[48]和文献[49]利用了基于数据物理来源的验前信息可信度评判方法完成融合评估。
文献[50]提出根据验前信息与现场试验信息的相容性水平判定验前信息的可信度;文献[51]对比了Bayes方法和经典方法,证明同总体的情况下经典方法要优于Bayes方法。上述两篇文献均是基于验前信息与现场试验信息服从同一分布的情况,然而事实上验前数据与现场数据不完全服从同一总体分布,因此有学者对多源异总体的信息融合方法展开研究:文献[52]通过建立基于专家之间存在依赖关系的共识模型,在利用Bayes方法确定验前信息方面取得了开创性成就;文献[53]利用组合方法收集可靠验前数据,并综合考虑了不同环境条件下验前信息的差异性;文献[54]利用验前信息确定验前分布,并提出一种验前分布选择准则,提高了多源信息融合的确定性。上述文献针对多源异总体情况下的验前信息融合问题进行了探索,在Bayes分析方法的基础之上,结合改进措施提供了有效可行的思路。
2.5 导弹武器命中精度评定方法
命中精度评定的本质是根据试验对象的验前信息及现场试验信息进行融合推断。经典的命中精度评定方法在解决小子样问题时存在一些弊端,如试验子样量与评定结果置信度的矛盾,以及无法综合利用导弹研制的各类试验信息等。针对上述问题,学者们研究提出了针对小子样精度评定的方法,包括自助评定法、Bayes方法、序贯Bayes方法和仿真方法等。
2.5.1 命中精度的自助评定方法
自助评定法是一种利用再抽样技术来扩大样本容量的方法。文献[55]最早提出自助再生抽样方法;文献[56]分析了自助法中样本的获取方式及样本量等问题,针对导弹命中精度评定这一小子样问题,利用改进非参数自助评定法法对试验样本数据进行扩充;文献[57]利用自助评定法法和非参数核密度估计方法实现武器系统精度评估;文献[58]对运用自助法和随机加权法确定Bayes估计的验前分布进行了分析,基于其数学原理讨论了对飞行试验样本进行精度评估的方法,并给出工程实际应用中两种方法的选用原则;文献[59]提出一种改进自助方法,能够利用验前信息弥补现场试验信息存在的一些不足。但是,由于自助方法是大子样条件下渐进收敛特性的方法,目前对自助方法在小子样问题中的作用还有一些质疑,如文献[60]提出自助方法并不能提升密集度估计的精度,而且在小子样下应用存在较大风险,要“慎重使用”。因此,在小子样甚至特小子样条件下应用自助法进行命中精度评定还有待进一步研究。
2.5.2 命中精度评定的Bayes方法
在导弹精度评定中,研制方风险和使用方风险是相互矛盾的,Bayes统计方法为了均衡双方风险需要获取较大的信息量,适用于小子样条件下的精度评定,其详细方法参考文献[61]。文献[62]综合考虑使用方和研制方的风险,利用序贯检验方法确定了最小试验样本数,并讨论了自助法和Bayes法在密集度估计中的应用;文献[63]提出将自助法与Bayes方法结合运用,充分利用验前信息与现场信息进行命中精度评定。传统的Bayes方法在小子样精度评定中可能会出现验前信息“淹没”现场试验信息等问题,上述文献并没有提出相应的解决方案。文献[64]提出利用打靶的仿真信息和现场数据,结合Bayes方法进行命中精度的综合鉴定,并给出先验样本量确定方法;文献[65]基于Bayes估计考虑仿真信息的验前分布及数据权值,并证明考虑验前信息可信度的Bayes方法对导弹落点散布估计更准确;文献[66]证明在评估导弹落点精度方面,贝叶斯估计法要优于传统的区间估计法。上述方法能够从如何利用验前信息以及如何提高验前信息可信度两方面出发,提出Bayes改进方法,一定程度上避免“淹没”现象。另外在进行Bayes统计决策分析时,通常会采用大量的仿真信息作为验前信息,与之带来的问题是提高仿真模型的精度以及如何确定仿真信息样本容量,相关问题有待进一步研究。
2.5.3 基于序贯分析的命中精度评定方法
统计学家Wald[67]于1947年首次提出了序贯概率比检验(sequential probability ratio test,SPRT),为序贯分析方法的研究奠定了基础。这种“试试看看,看看试试”的试验方法能够降低试验所需样本容量,在武器装备试验鉴定领域得到深入的研究和应用。针对小子样序贯分析问题的研究,目前主要集中以下2个方面:一是改进传统序贯分析方法以提高试验结果的可靠性和准确性,如改进判定准则、截尾准则等,文献[68]结合蒙特卡洛仿真分析,指出运用序贯截尾检验方法能够减少导弹精度评定的试验次数;文献[69]提出了基于序贯分析的一次抽样试验方案,但该方法不能充分利用验前信息,因此仍需相当大的样本量。另一个研究方向是将序贯分析法与Bayes方法相结合,这样既能充分利用验前信息,又能降低样本容量,如文献[70]在利用验前信息的基础上,较早的提出一种序贯验后加权检验方法;文献[71]对Bayes序贯试验方法中存在的不足进行了进一步的研究,阐述了序贯试验方法在工程应用的风险和决策问题;文献[72]提出将Bayes小子样方法与序贯网图检验法相结合,并采用截尾策略,确定试验所需最大样本数。基于序贯Bayes分析的命中精度评定方法能够利用验前信息,显著减少试验样本,但能否在抽样试验前确定假设检验问题所需样本容量、针对特小子样评定时序贯方法的有效性等问题依然有待研究。
3 研究展望
导弹武器命中精度的评估涉及到导弹误差建模分析、误差分离方法、弹道精度折合、多源信息融合方法等多方面的研究,其研究内容复杂,是一项综合性较强的系统工程。通过分析导弹武器命中精度评估的研究现状,结合当前部队武器装备试验鉴定的开展情况,下一步需要重点解决的问题主要包括以下3个方面。
1) 建立健全全寿命周期的导弹武器命中精度评估研究体系
从武器装备试验鉴定角度出发,命中精度的评估应当贯穿于导弹武器的全寿命过程中,既要充分利用各类验前信息,更要对列装后的各类飞行数据和测试数据进行采集、处理和应用。然而就目前搜集的文献资料来看,研究成果主要集中于导弹武器装备列装使用之前。因此应当加强装备列装部队后产生的实战条件下导弹武器的试验数据的研究,如数据的采集处理方法、融合方法等。建立、建全命中精度评估研究体系,为导弹升级、改造以及后续型号的设计研发提供数据支撑,同时为实现全寿命周期导弹武器命中精度评估提供基础。
2) 加强复合制导条件下导弹武器制导误差建模分析研究
随着装备技术的发展以及战场攻防对抗的增强,纯惯性制导武器越来越不能满足现代战场需求。目前很多在研、列装的导弹武器都采用了两种甚至两种以上的制导方式进行复合制导,不同的制导方式会引入不同的制导误差,对于复合制导条件下导弹武器的误差源分析、误差建模以及组合导航误差折合都有待进一步研究。
3) 关注新形势下验前信息的获取及多源信息融合方法的改进
导弹武器命中精度评估是典型的小子样问题,实现多源异总体信息的获取、融合是小子样研究需要解决的根本问题。前文已介绍过先验信息的种类及样本扩容的方法,新形势下,导弹武器从设计定型到研制生产再到试验飞行,期间的数据信息种类更多、数据量更大,如何开发更多的可用的先验信息、如何有效的扩充样本容量等问题亟待解决;同时,先验信息的可信性及相容性分析还有进一步研究的空间。
4 结论
本文综合国内外相关研究成果,叙述了导弹武器命中精度评估研究内容和研究框架,对命中精度评估过程中相关内容进行了综述,分析了研究现状及存在问题,最后对导弹武器命中精度评定研究的未来发展方向进行了展望。由于该项研究涉及技术范围广,研究方向多,同时与导弹制导技术发展紧密相关,因此新形势下开展该项研究需统筹兼顾,全局规划,整合部队、试验单位及研制部门各方力量,以保证评估的可靠性、有效性。
[1] 曹渊.导弹末端导引精度小子样试验评估方法研究[D].长沙:国防科学技术大学,2008.
[2] 唐雪梅.精度鉴定与试验决策系统[J].国防科技大学学报,1994(1):101-107.
[3] 高远,姜涛.导弹武器系统作战效能评估方法研究[J].国防制造技术,2017(2):56-57.
[4] 李斌.主动式雷达制导系统制导精度统计分析[D].哈尔滨:哈尔滨工程大学,2013.
[5] 张金槐.远程火箭精度分析与评估[M].长沙:国防科技大学出版社,1995.
[6] 马宝林,张洪波,吴杰.初态误差对显式制导弹道导弹命中精度的影响特性[J].弹道学报,2016,28(3):23-29.
[7] ZHENG X,YANG Y D,GAO H,et al.On formation mechanism and influence characteristic of initial state error in disturbing gravity field[C]//2016 35th Chinese Control Conference (CCC).IEEE,2016.
[8] 李冬,魏超,周萱影.初始误差和制导工具误差估计的非线性方法[J].国防科技大学学报,2018,40(06):64-70.
[9] 李冬,龚磊.初始误差和制导工具误差的线性估计方法[J].兵器装备工程学报,2018,39(7):112-116.
[10] 常晓华,蒋鲁佳,杨锐,等.垂线偏差对弹道落点精度的影响分析[J].国防科技大学学报,2017(4):1-5.
[11] RUI C,YANMENG C.An assistant method for correcting the deviation of vertical line in strapdown inertial guidance[J].Aerospace Electronic Warfare,2007,23(05):21-23.
[12] 李伟明,申景诗,孙瑞胜,等.地球模型偏差对远程弹箭弹道仿真的影响及修正[J].火力与指挥控制,2015(3):11-15.
[13] 王刚,段晓君,谢美华,等.复合制导再入机动弹头再入误差分析[J].弹道学报,2009,21(4):1-5.
[14] 王明海,杨颖,李邦杰.后效冲量引起导弹弹道误差的一种计算方法[J].飞行力学,2008(2):48-50.
[15] 普承恩,王良明,傅健.基于EKF落点预测的二维弹道修正弹制导方法[J].兵器装备工程学报,2018,39(06):52-57.
[16] 周萱影,王正明,李冬,等.线性模型的海基制导系统误差分离方法性能分析[J].国防科技大学学报,2019(3):179-186.
[17] 张最良.关于惯性制导工具误差分析的一个注记[J].国防科技大学学报,1981(4):87-92.
[18] CORTES C,VAPNIK V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.
[19] 杨华波,张士峰,蔡洪,等.惯导工具误差分离与折合的支持向量机方法[J].系统仿真学报,2007,19(10):2177-2179.
[20] YANG H B,ZHANG S F,CAI H.Separation andconversion for guidance instrumentation error using optimal least squares support vector machines[J].SystemsEngineering & Electronics,2008(7)1308-1311.
[21] 徐德坤,刘伟,孟云鹤,等.基于进化策略的误差分离方法[J].宇航学报,2008,29(1):352-356.
[22] HANSEN N.The CMA Evolution Strategy:A Comparing Review[M]//Towards a new evolutionary computation.Advances on estimation of distribution algorithms.2007.
[23] BENHAMOU E,ATIF J,LARAKI R,et al.A Discrete Version of CMA-ES[J].SSRN Electronic Journal,2018(1):212-223.
[24] MAKI A,SAKAMOTO N,AKIMOTO Y,et al.Application of optimal control theory based on the evolution strategy (CMA-ES) to automatic berthing[J].Journal of Marine Science and Technology,2019,25(11):221-233.
[25] 韩成柱,梁红,张志国.一种基于CMA-ES的制导工具误差分离方法研究[J].航天控制,2017(04):49-51,72.
[26] 李兵,朱宁,等.基于岭型主成分估计的最优与经典预测的最优性判别[J].济南大学学报(自然科学版),2007,21(3):261-263.
[27] 谢玉珍.岭型主成分估计分离制导工具系统误差方法研究[J].弹箭与制导学报,2013,33(3):189-191.
[28] 夏青,杨华波,张士峰,等.基于遗传算法的工具误差分离与弹道折合[J].系统仿真学报,2007,19(18):4130-4133.
[29] 周萱影,王正明,李冬,等.线性模型的海基制导系统误差分离方法性能分析[J].国防科技大学学报,2019,41(3):179-186.
[30] WU X,SHAO R,ZHU Y.New iterative improvement ofa solution for an Ill-conditioned system of linear equations based on a linear dynamic system[J].Computers & Mathematics with Applications,2002,44(8/9):1109-1116.
[31] Zhao H,Huang J,Liang X,et al.New Algorithm for Guidance Instrument Error Separation[J].Journal of Spacecraft Tt & C Technology,2017:453-463.
[32] 段秀云,黄瑜.基于交叉验证的捷联惯导制导工具误差分离方法[J].航天控制,2014,32(6):8-11.
[33] 陈璇.复合制导武器系统战技指标的融合评估方法研究[D].长沙:国防科学技术大学,2011.
[34] 宋维军.制导工具误差折合精度影响因素分析[J].航天控制,2008,26(4):13-15.
[35] 徐德坤,杨华波,张士峰,等.制导工具误差折合的遗传主成分方法[J].航天控制,2007,25(6):22-26.
[36] 高春伟.惯性/星光复合制导误差辨识与弹道折合方法研究[D].长沙:国防科学技术大学,2014.
[37] 佟力永,王浩宇,肖凡.潜射远程弹道导弹弹道折合方法研究[J].弹箭与制导学报,2015,35(4):133-136.
[38] 唐雪梅,张金槐,邵凤昌等.武器装备小子样试验分析与评估[M].北京:国防工业出版社.2004.
[39] JEFFREYS H.Theory of Probability[M].Oxford University Press,1961.
[40] WINKLER R L.Combining Probability Distributions from Dependent Information Sources[J].Management Science,1981,27(4):479-488.
[41] LEVY W B,DELI? H.Maximum entropy aggregation of individual opinions[J].IEEE Transactions on SystemsMan & Cybernetics,1994,24(4):606-613.
[42] 张志辉,蒯伟.小子样试验数据融合算法研究[J].航天电子对抗,2014,30(2):40-42.
[43] SUN J,LI G L,XU C.Synthetical evaluation method of anti-ship missile in range trial in condition of small sample based on simulation information[J].Systems Engineering-Theory & Practice,2014,34(4):1077-1088.
[44] 曹渊,胡正东,郭才发,等.基于整体推断的Bayes方法及其在精度评定中的应用[J].宇航学报,2009,30(6):2354-2359.
[45] 冯静,周经伦,孙权.Bayes分析中多源验前信息融合的ML-Ⅱ方法[J].数学的实践与认识,2006,36(6):142-145.
[46] 胡俊梅,师义民.多源验前信息下k/N(G)系统可靠性指标的Bayes估计[J].科技通报,2013(1):13-16.
[47] 戴家君,郑锦.验前信息在武器装备试验中的应用研究[J].舰船电子工程,2019,39(06):142-145.
[48] 黄寒砚,段晓君,王正明.考虑先验信息可信度的后验加权Bayes估计[J].航空学报,2008,29(5):1245-1251.
[49] 邢国强,曲兆宇,冯殿震.考虑可信度的平均寿命验后分布Bayes融合评估方法[J].科学技术与工程,2012(09):199-202.
[50] JAMES O BERGER.Statistical decision theoy and Bayesian analysis[M].New York,1995.
[51] 张士峰,蔡洪.Bayes分析中的多源信息融合问题[J].系统仿真学报,2000,12(1):54-57.
[52] WINKLER R L.Combining Probability Distributions from Dependent Information Sources[J].Management Science,1981,27(4):479-488.
[53] MYHRE J,JESKE D R,LI J,et al.Combining binomial test data via two-stage solutions[J].Applied Stochastic Models in Business and Industry,2018,34(1):20-30.
[54] ZOU T J.DANG W,ZHANG G,et al.Prior distribution selection criterion in accelerated degradation testing Bayesian optimization design based on Bayes factors[C]//Proc.of the International Conference on Sensing,Diagnostics,Prognostics,and Control,2017:694-698.
[55] EFRON B.Bootstrap Methods:Another Look at the Jackknife[J].The Annals ofStatistics,1979,7(1):1-26.
[56] 宋贵宝,刘泽坤,罗亚民,等.基于验前信息的改进Bootstrap导弹命中精度评定方法[J].舰船电子工程,2017,37(12):105-110.
[57] YU H,HAN D,MA L,et al.The accuracy evaluation method of weapon system based on median distribution density[J].Acta Armamentarii,2010,31(1):54-57.
[58] 刘新爱,张磊.基于自助法和随机加权法的导弹精度评定的探讨[J].弹箭与制导学报,2006,26(1):195-197.
[59] 胡正东,曹渊,张士峰,等.特小子样试验下导弹精度评定的Bootstrap方法[J].系统工程与电子技术,2008,30(8):1493-1497.
[60] 郑小兵,董景新,孟令晶,等.Bootstrap方法在导弹落点密集度评估中的误用[J].中国惯性技术学报,2012,20(2):239-243.
[61] 张金槐,唐雪梅.Bayes方法(修订版)[M].长沙:国防科技大学出版社,1993.
[62] 郑小兵,董景新,张志国,等.弹道导弹落点密集度综合评定方法[J].中国惯性技术学报,2011(04):125-130.
[63] DONG G,HE C,DAI Z,et al.Bayesian Sample Size Optimization Method for Integrated Test Design of Missile Hit Accuracy[C]//Proceedings of the 5thInternational Conference on Simulation and Modeling Methodologies,Technologies and Applications.SCITEPRESS-Science and Technology Publications,Lda,2015.
[64] 董光玲,姚郁,贺风华.制导精度一体化试验的Bayesian样本量计算方法[J].航空学报,2014,36(2):575-584.
[65] 马金龙,马立元,方丹.导弹制导精度估计方法研究及其应用[J].舰船电子工程,2019(6):56-60.
[66] JIAN-BO L.A Method of Bayes Estimation for Missile Accuracy of the Fall Points[J].Journal of Applied Statistics and Management,2010,29(2):227-231.
[67] WALD A.Sequential analysis[M].New York Wiley,1947.
[68] 马康.基于序贯截尾检验的一维修正弹精度评估方法[J].兵器装备工程学报,2017,38(3):31-34.
[67] 李阿楠,廖学军.基于序贯分析的制导弹药命中精度试验一次抽样方案[J].探测与控制学报,2018,40(1):111-114.
[70] 张金槐.利用验前信息的一种序贯检验方法:序贯验后加权检验方法.[J].国防科技大学学报,1991(2):1-13.
[71] 刘琦,冯文哲,王囡,等.Bayes序贯试验方法中风险的选择与计算[J].系统工程与电子技术,2013,35(1):223-229.
[72] 王康,史贤俊,秦亮,等.基于Bayes小子样理论和序贯网图检验的武器装备测试性验证试验方案设计[J].兵工学报,2019,40(11):2319-2328.