爆炸活塞式分离器采用火炸药爆炸的方式产生驱动力,推动活塞来产生推力。有着体积小,做功能力强等优点,在国内外的研究中,主要应用于开断器[1]、爆炸螺栓[2-3]等。在相关领域的研究中,陈搏等人通过理论计算,得到了爆炸活塞中药量及爆炸产生的压力[4]。杨锋等[5]还推导了爆炸活塞式开断器可靠分断时爆炸活塞所需药量的计算公式。许多学者通过内弹道的数值仿真对爆炸活塞部分进行研究。冯福全[6]采用经典内弹道描述药室内火药燃烧情况和活塞运动过程。结合有限元的发展,该领域有了进一步的发展。对于爆炸活塞式分离的应用,孙巍等人基于ANSYS11.0建立了直流爆炸活塞式限流器的三维热电耦合仿真模型,仿真结果和试验也基本一致[7]。李枫等[8]以LS-DYNA为仿真平台建立了非线性动力学模型,对炸药腔室的结构进行了研究,分析了炸药与活塞距离、活塞半径、药腔半径对开断性能的影响,结果表明炸药腔室结构参数存在最优值。杜龙飞等[9]利用ANSYS/LS-DYNA对不同爆速和爆压下,爆炸活塞式结构的分离过程进行了数值模拟,得到了分离速度的变化规律。Hwang D等[10]采用一种活塞式分离装置,建立了数学模型研究其内部的燃烧、变形以及摩擦,并通过实验进行了验证。Li Y H[11-12]使用AUTODYN模拟了活塞式爆炸螺栓的分离过程,并分析了装药量对分离时间,分离速度和分离冲击的影响。结果表明:活塞式爆炸螺栓遵循拉伸断裂机理,分离的临界装药量为354~398 mgPETN。Lee J等[13-14]利用AUTODYN进行数值模拟,研究了爆炸活塞式的爆炸螺栓分离可靠性,还对爆炸活塞的振动进行了数值分析,并使用LDV进行实验测试,验证了数值方案。但针对爆炸活塞内部压力变化的研究较少,本文设计了一种爆炸活塞式分离器,同时采用不同装药量进行推力实验,通过经典内弹道的理论计算,得到活塞作用压力随时间的变化,并与有限元数值模拟相结合。将仿真结果与试验结果进行对比分析,得到分离器的做功能力以及响应时间。
1 推力实验
1.1 爆炸活塞式分离器的设计
爆炸活塞式分离器总体结构主要由外壳和活塞组成,为了保证使用强度,各部分的连接采用螺纹连接。图1为爆炸活塞式分离器的结构简图。所标注的尺寸单位为mm。
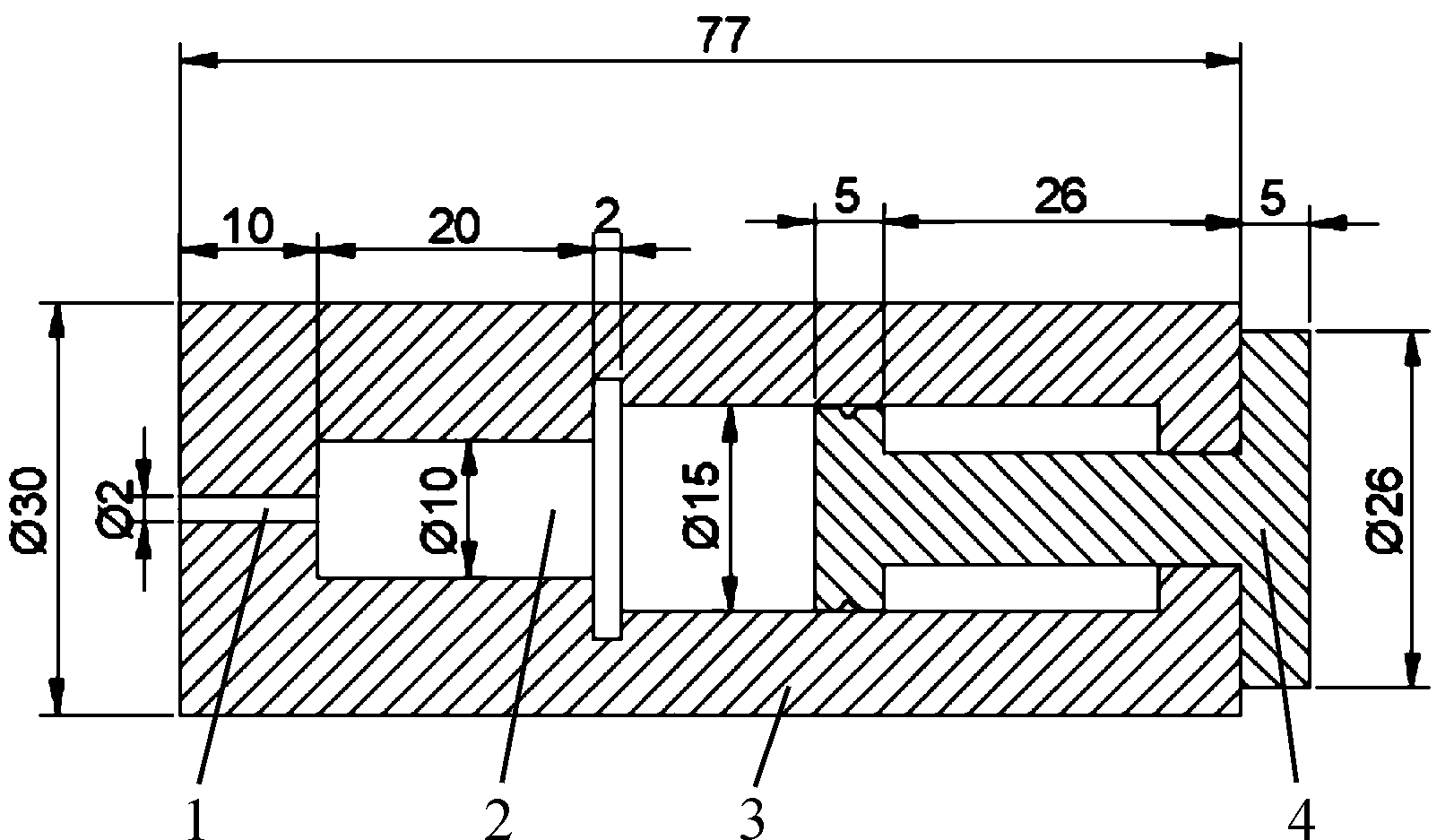
图1 爆炸活塞式分离器的结构简图
图中1为点火孔,2为药室,3为外壳,4为活塞。通过点火孔点燃药室中的火药,火药快速燃烧生成具有做功能力的高压气体,压力作用于活塞内挡板形成推力,推力做功从而实现分离的功能。
1.2 试验方法
试验装置如图2所示。试验在工装上进行,分离器固定在工装上,高度为1 m,活塞的外推板前放置一枚3.0 kg重的钢球,为了测量钢球开始运动后的移动距离,在钢球后侧安装钢尺,伸出距离为200 mm。同时,试验时用高速录像记录活塞作用和钢球飞行过程,并通过这方法,估算钢球初始阶段飞行的距离。试验使用的装药量为2种,分别是0.5 g和1 g。

图2 试验装置
为了提高分离器的响应时间,采用多-45火药。这是一种多气孔火药,燃烧时间一般在0.001 s以内[15],它的特点是药粒中含有大量细小均匀的微孔,孔径大小、数量多少和分布均匀状况与制备过程有关,因而密度较小,其燃速与气孔的数量有关,而与燃烧层厚度无关。气孔愈多,燃烧速度愈快。火药的性能参数是描述火药燃烧过程的关键,多-45的主要参数如表1所示[16]。
表1 多-45的主要特征参数
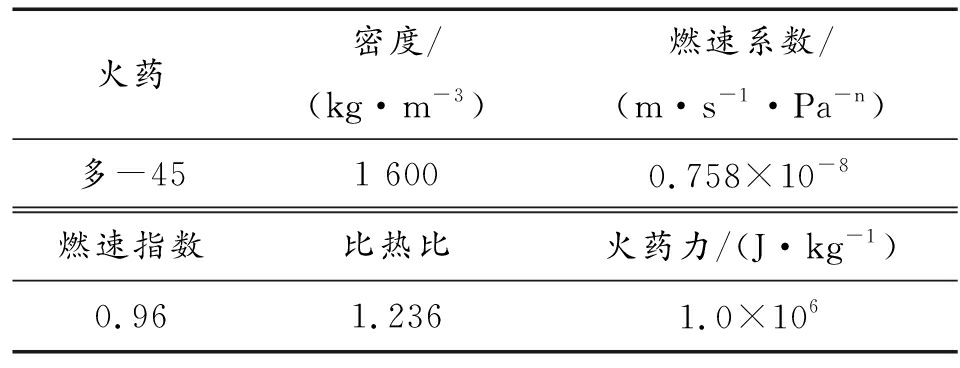
火药密度/(kg·m-3)燃速系数/(m·s-1·Pa-n)多-451 6000.758×10-8燃速指数比热比火药力/(J·kg-1)0.961.2361.0×106
1.3 试验结果及分析
试验后,测量钢球的实际落点以及通过录像测得的落地时间分别计算钢球的初速,试验结果如表2所示。
表2 试验结果
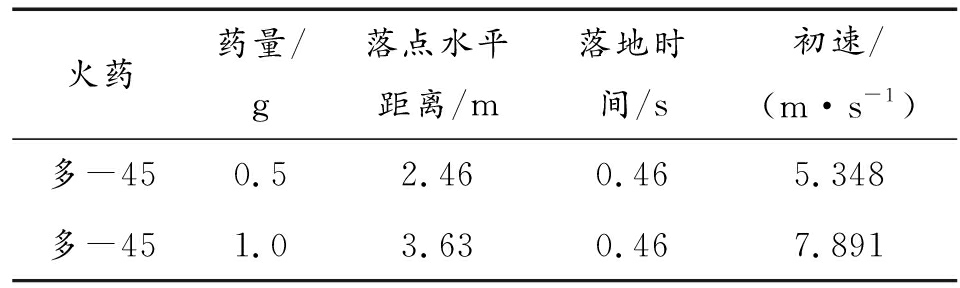
火药药量/g落点水平距离/m落地时间/s初速/(m·s-1)多-450.52.460.465.348多-451.03.630.467.891
通过后处理,可得到爆炸活塞式分离器做功以及钢球初始阶段运动的过程,图3为1 g药量时的过程图,0.5 g药量时过程类似。

图3 1 g药量时钢球运动过程
根据图3的结果同样可以计算钢球初速,如表3所示。
表3 录像试验结果
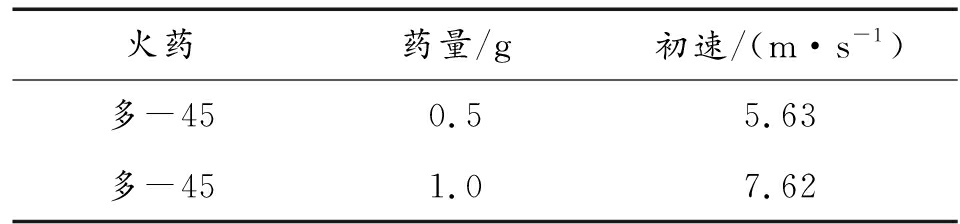
火药药量/g初速/(m·s-1)多-450.55.63多-451.07.62
通过对比可知,对不同药量的情况下,两者计算出的初速大致相同,误差分别为1.6%和2.5%。取平均值后,可以计算出0.5 g药量时分离器的做功能力为42.2 J,1 g药量时做功能力为91.1 J。
从试验结果可以看出,钢球飞出过程几乎沿水平方向。将活塞达到行程时的时间作为分离器的响应时间。两种药量下响应时间都在3~5 ms之间。另外,由于有点火孔,在火药燃烧过程中,有部分火药气体会从点火孔流失,这也会造成一定的压力损失。
2 分离器的内弹道计算
在高装填密度下,火药的装药结构容易产生压力波,甚至发生燃烧转爆轰(DDT),这也将导致所产生的压力急剧增大[17]。通常用理论最大密度(TMD)来描述装药的疏密程度,表达式如下:
![]()
(1)
式中:Δ为装填密度;ρP为火药颗粒的物质密度。研究表明,对多-45火药,TMD为41.6%~75.6%时将发生燃烧转爆轰现象。对于所设计的爆炸活塞式分离器,通过计算可知药量分别为0.5 g和1 g时,TMD分别为7.73%和15.45%,由此可知,多-45在药室中仅发生燃烧。因此可以采用经典内弹道理论模型对其进行理论计算。
为了建立经典内弹道理论模型,假设:忽略点火孔对火药气体做功过程的影响;次要功系数仅考虑活塞的摩擦功和气体的运动功;火药按多孔火药计算形状特征量等参数;其他假设与经典内弹道假设相同。
根据假设可以得到内弹道基本方程:
火药燃速方程
(2)
活塞运动方程
(3)
内弹道基本方程
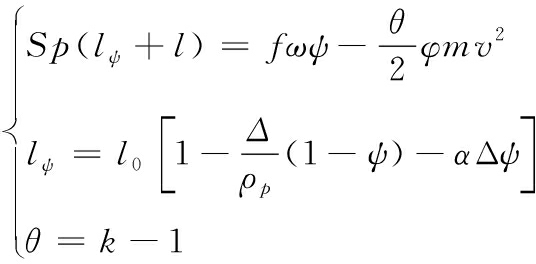
(4)
活塞速度与行程关系
(5)
其中:Z为火药已燃相对厚度;u1为燃速系数;e1为起始厚度;n为燃速指数,取0.96;p为压力;φ为次要功系数;m为活塞质量,推物体时为物体和活塞质量之和;S为外壳内壁的截面积;V为速度。lψ为药室自由容积缩径长;l为活塞行程;f为火药的火药力;α为火药余容;ω为装药质量;ψ为火药已燃百分数;k为比热比,取1.236。采用MATLAB语言编写内弹道计算程序,使用四阶精度的龙格库塔法进行计算,对应的在MATLAB中使用ode45函数。将爆炸活塞以及火药的各项参数代入程序中,活塞质量取为钢球质量后,分别计算了装药量为0.5 g和1.0 g时的内弹道过程,得到两种药量下,活塞内挡板表面的压力随时间的变化曲线,如图4所示。
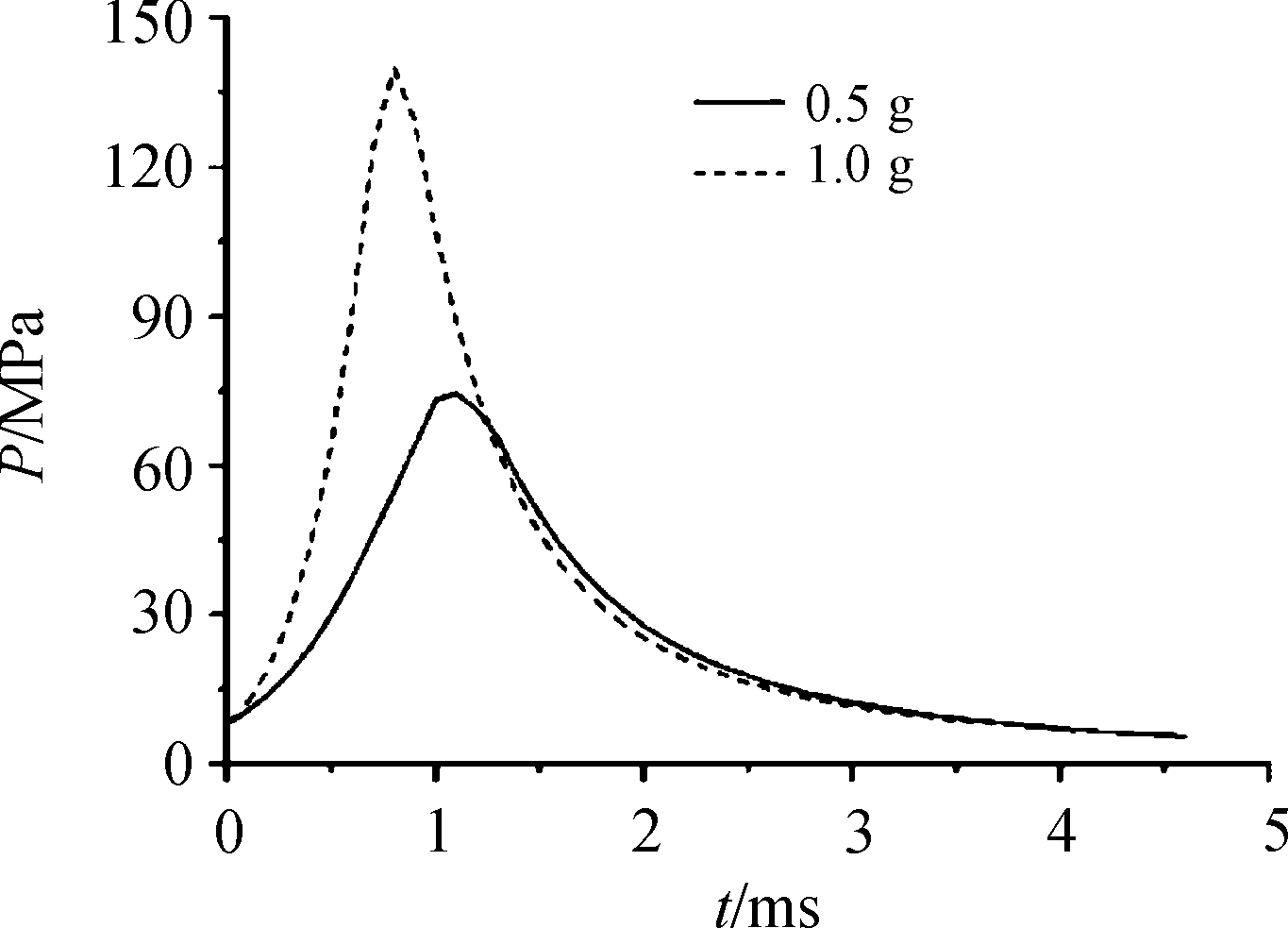
图4 活塞内挡板压力时间曲线
3 有限元分析及结果
3.1 有限元模型
利用LS-DYNA建立有限元模型进行仿真时,对结构进行了简化,省略了点火孔结构,外壳和活塞是由不同部件通过螺纹连接形成的,这里简化为一个整体式的结构。并根据模型的对称性,建立1/4的三维模型,其由外壳、活塞以及钢球组成,模型如图5所示,初始时刻钢球与活塞的外挡板接触,建模时保证钢球运动方向沿x轴方向。整个模型均采用六面体映射网格划分,每部分网格质量如图6所示。
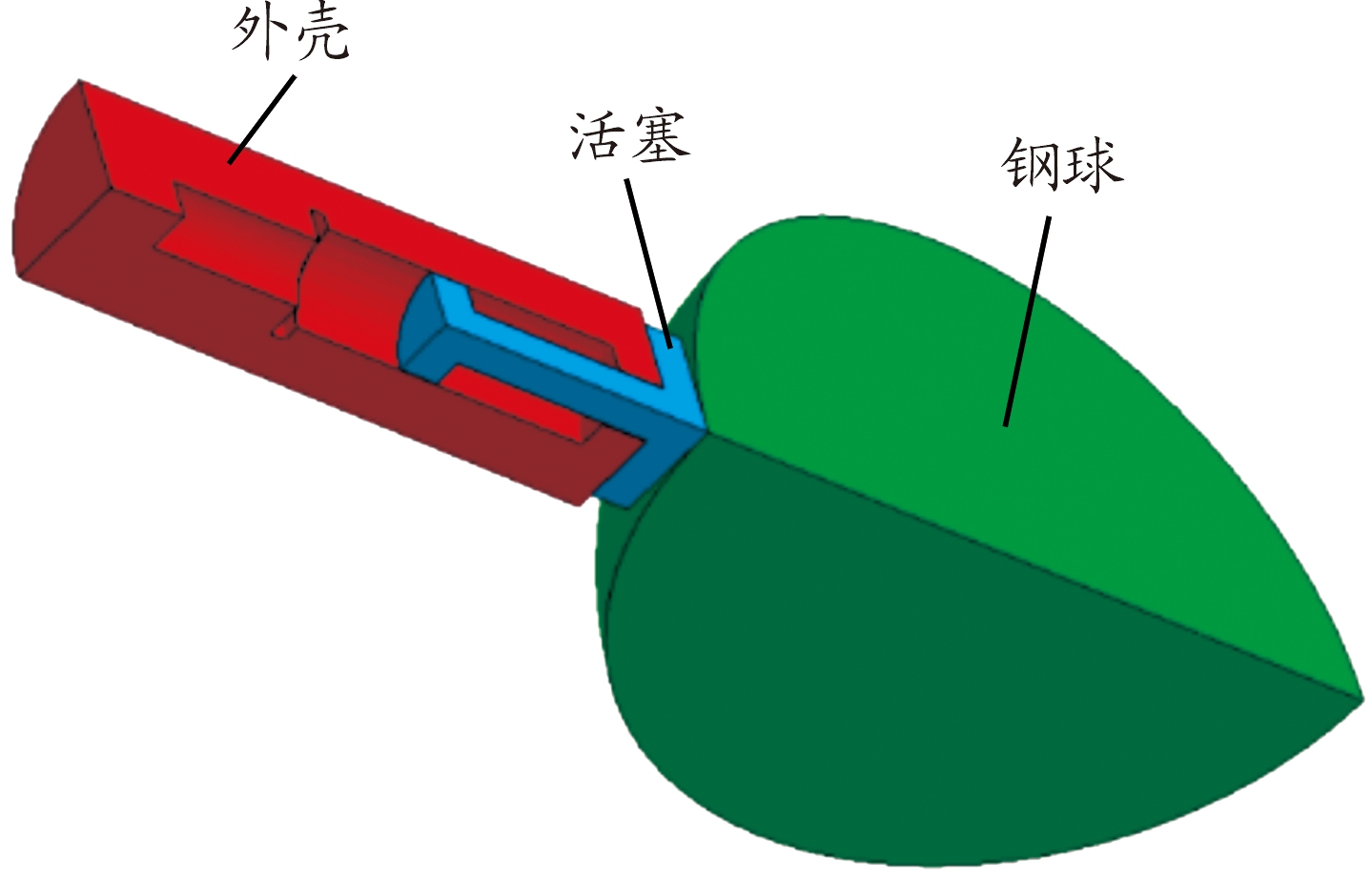
图5 1/4有限元模型示意图
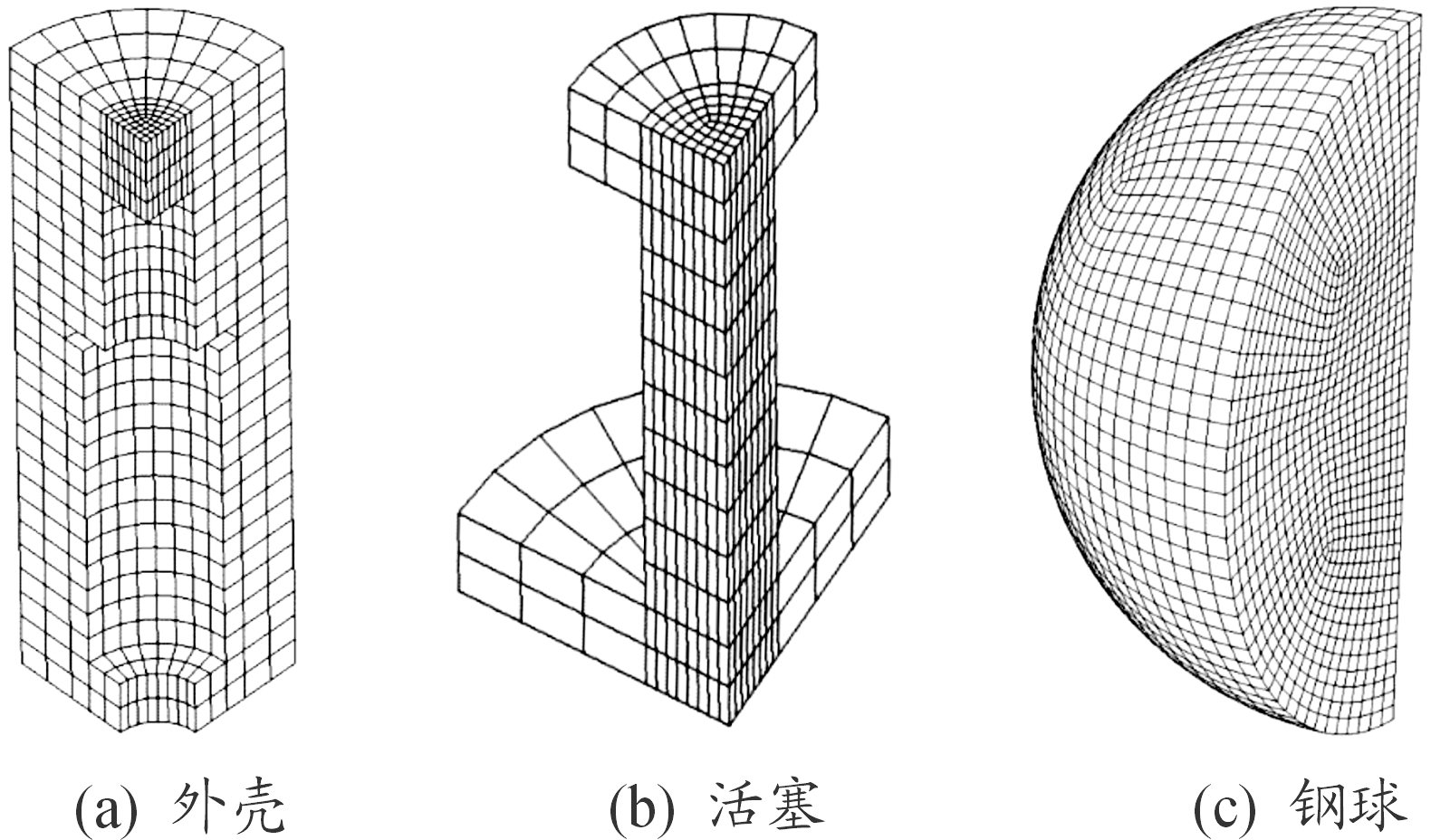
图6 网格质量示意图
在模型的对称面上施加对称约束,分离器外壳施加全自由度约束。同时采用自动面面接触定义外壳、活塞以及钢球之间的相互接触。利用关键字*LOAD_SEGMENT_SET进行载荷的施加,将内弹道计算的压力曲线施加到活塞的内挡板表面进行仿真计算。
3.2 材料模型
每部分均为钢材料,除了材料编号不同,其他参数相同。选用JOHNSON-COOK材料模型进行描述,关键字及部分参数如表4所示。
表4 材料关键字及部分参数
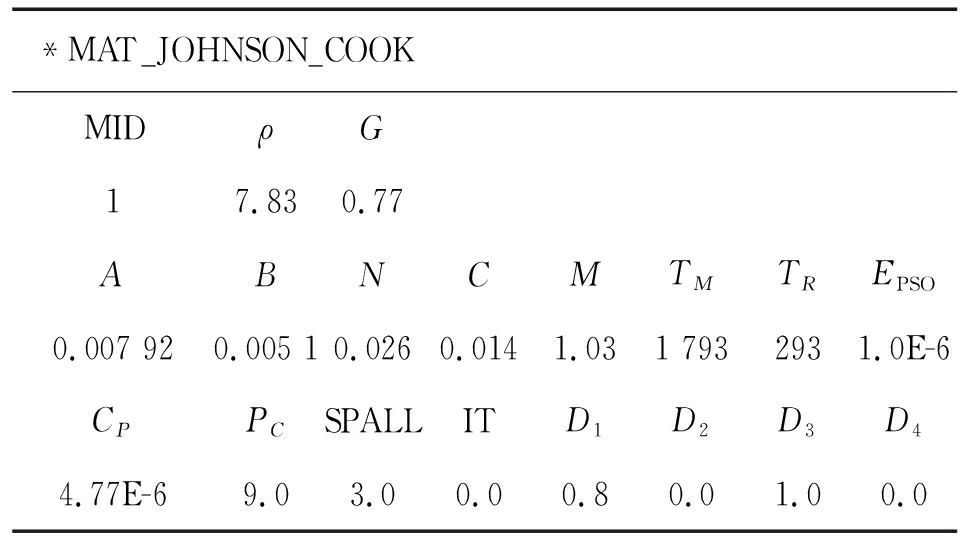
*MAT_JOHNSON_COOKMIDρG17.830.77ABNCMTMTREPSO0.007 920.005 10.0260.0141.031 7932931.0E-6CPPCSPALLITD1D2D3D44.77E-69.03.00.00.80.01.00.0
其中MID为材料编号;ρ为材料密度(g·cm-3);G为剪切模量(g/(μs2·cm));TM为熔体温度(K);TR为室温(K);EPSO为准静态阈值应变率(μs-1);CP为比热;PC为拉伸失效应力(g/(μs2·cm));SPALL为层裂类型;D1~D5为失效参数;C2/P为可选应变率参数;EROD为侵蚀设置,值为0时允许单元侵蚀;EFMIN为计算断裂应变的下限;A、B、N、C、M为应力计算表达式中的常数:
(6)
(7)
式(6)中:![]() 为等效塑性应变;
为等效塑性应变;![]() 为应变率。
为应变率。
对应的状态方程关键字*EOS_GRUNEISEN,参数如表5所示。
表5 状态方程关键字及参数
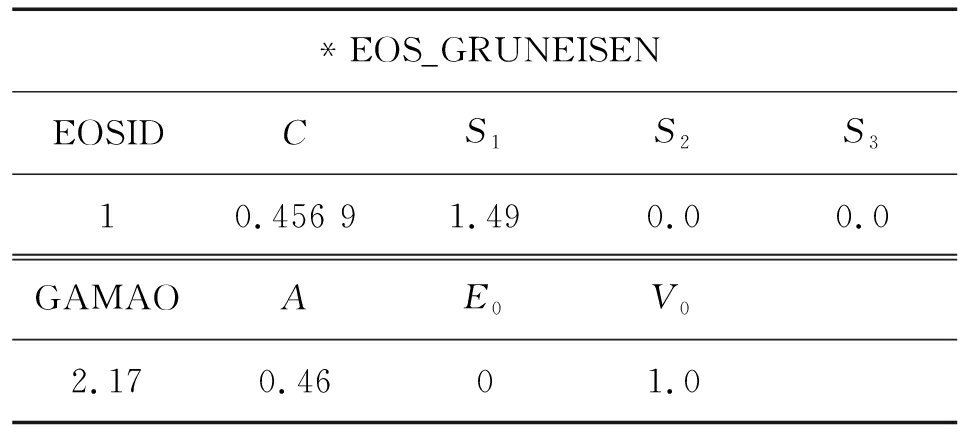
*EOS_GRUNEISENEOSIDCS1S2S310.456 91.490.00.0GAMAOAE0V02.170.4601.0
EOSID为状态方程编号,E0为初始内能(g·cm2/μs2),V0为初始相对体积,S1、S2、S3、GAMAO、A均为常数。
3.3 仿真结果及分析
分别对装药量为0.5 g和1.0 g的工况进行了仿真计算,在LS-PREPOST中进行对称处理,观察整体模型的计算结果,1.0 g装药量下不同时刻的结果如图7所示。
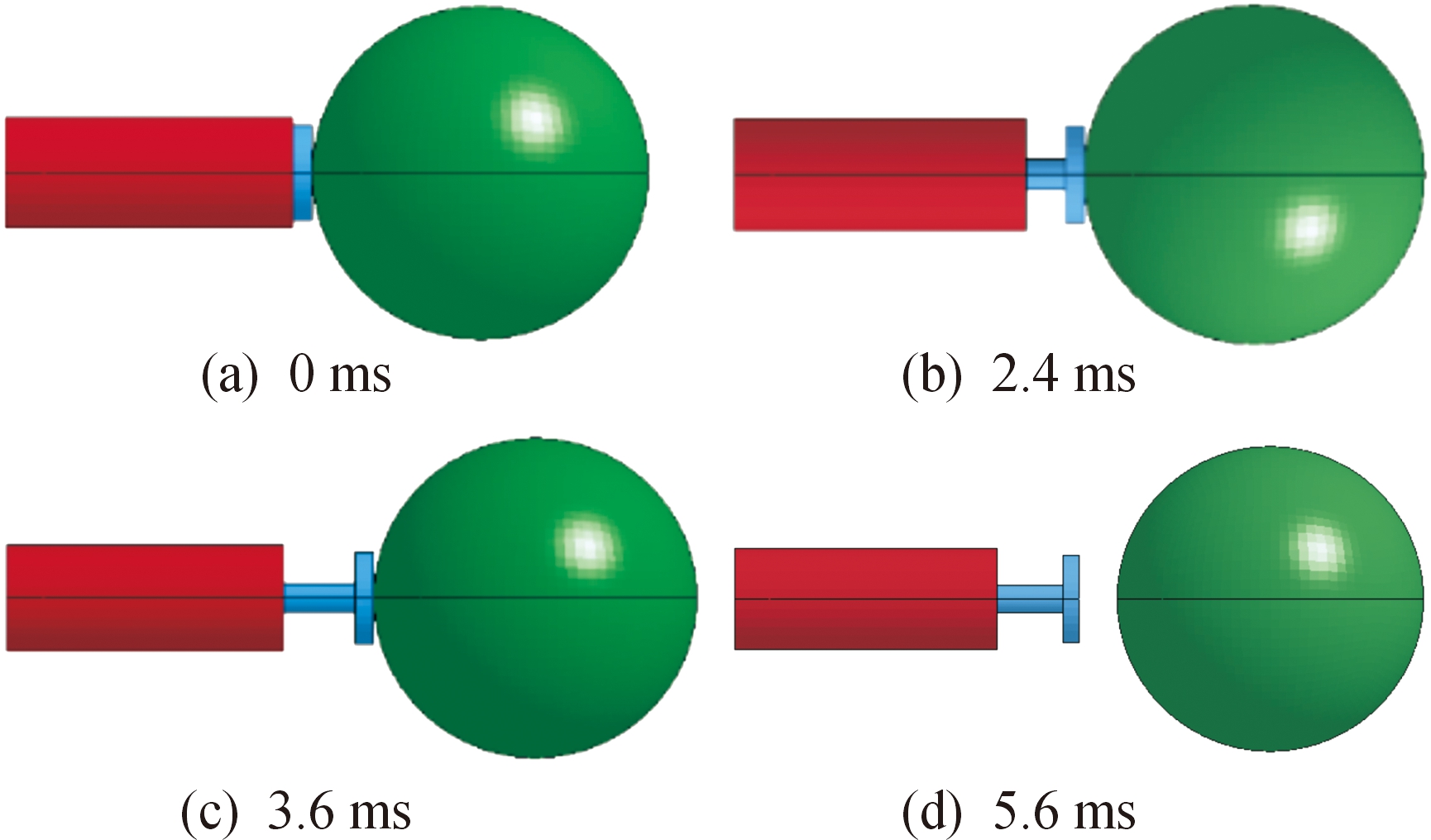
图7 1.0 g药量计算结果
从仿真结果可以看出,药量为0.5 g时,分离器响应时间为4.57 ms;药量为1.0 g时,响应时间为3.61 ms。通过后处理,得到钢球从开始运动到分离后的位移、速度以及加速度随时间的变化曲线。
图8显示,药量为1.0 g时分离器比0.5 g响应更快。从图9可以看出:速度增加到分离时刻后保持不变。分离器达到响应时间时,两种工况下钢球的速度分别为6.73 m/s和8.45 m/s,因此可得分离器对应不同药量下做功能力分别为45.3 J和107.1 J,相比较试验结果误差为6.8%。对比分析可知,误差产生的是由于仿真进行了简化,实际上在点火孔,活塞与外壳间隙都存在压力损失,整个过程还存在热散失,这些因素都会导致能量的损失。
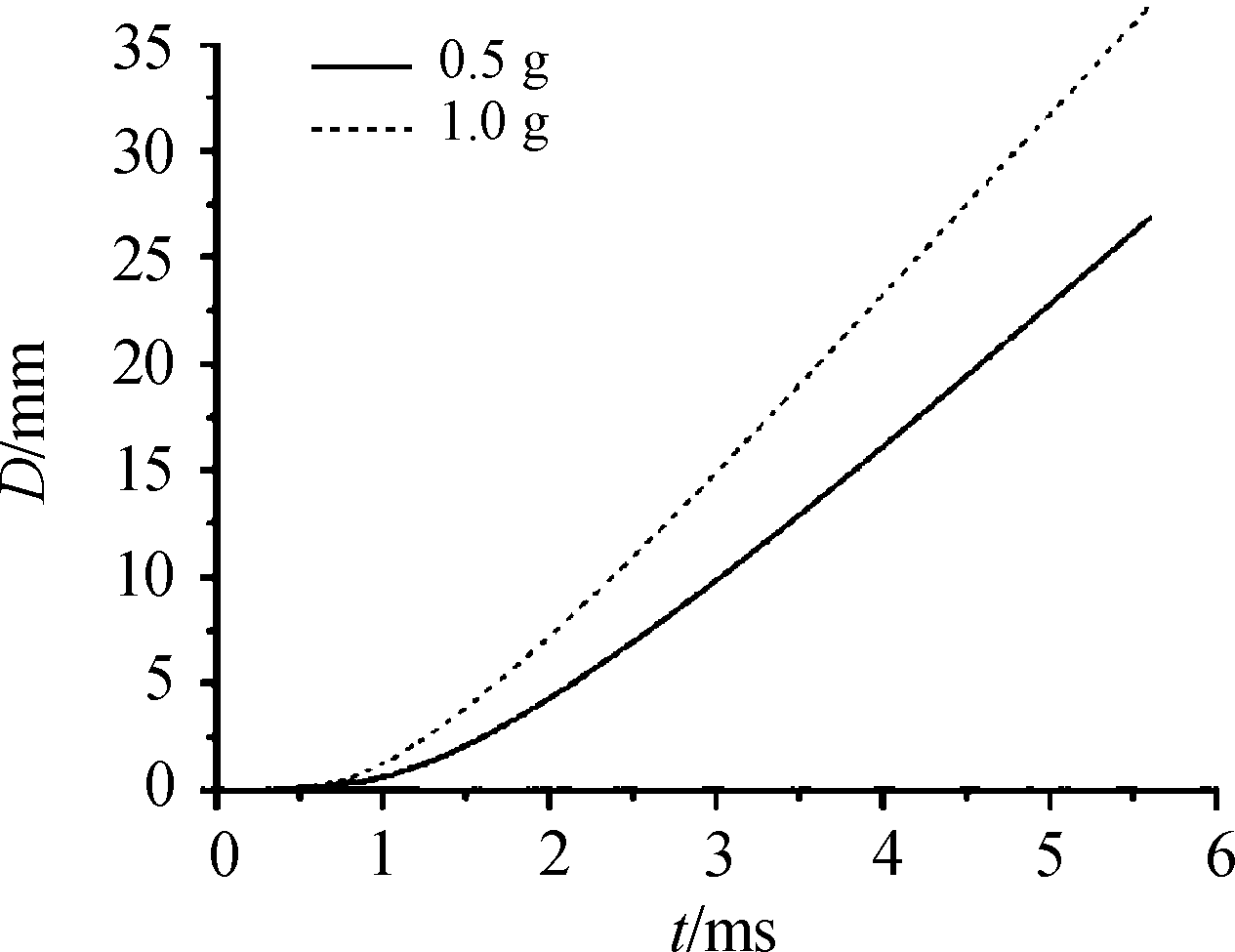
图8 不同药量下钢球的位移曲线
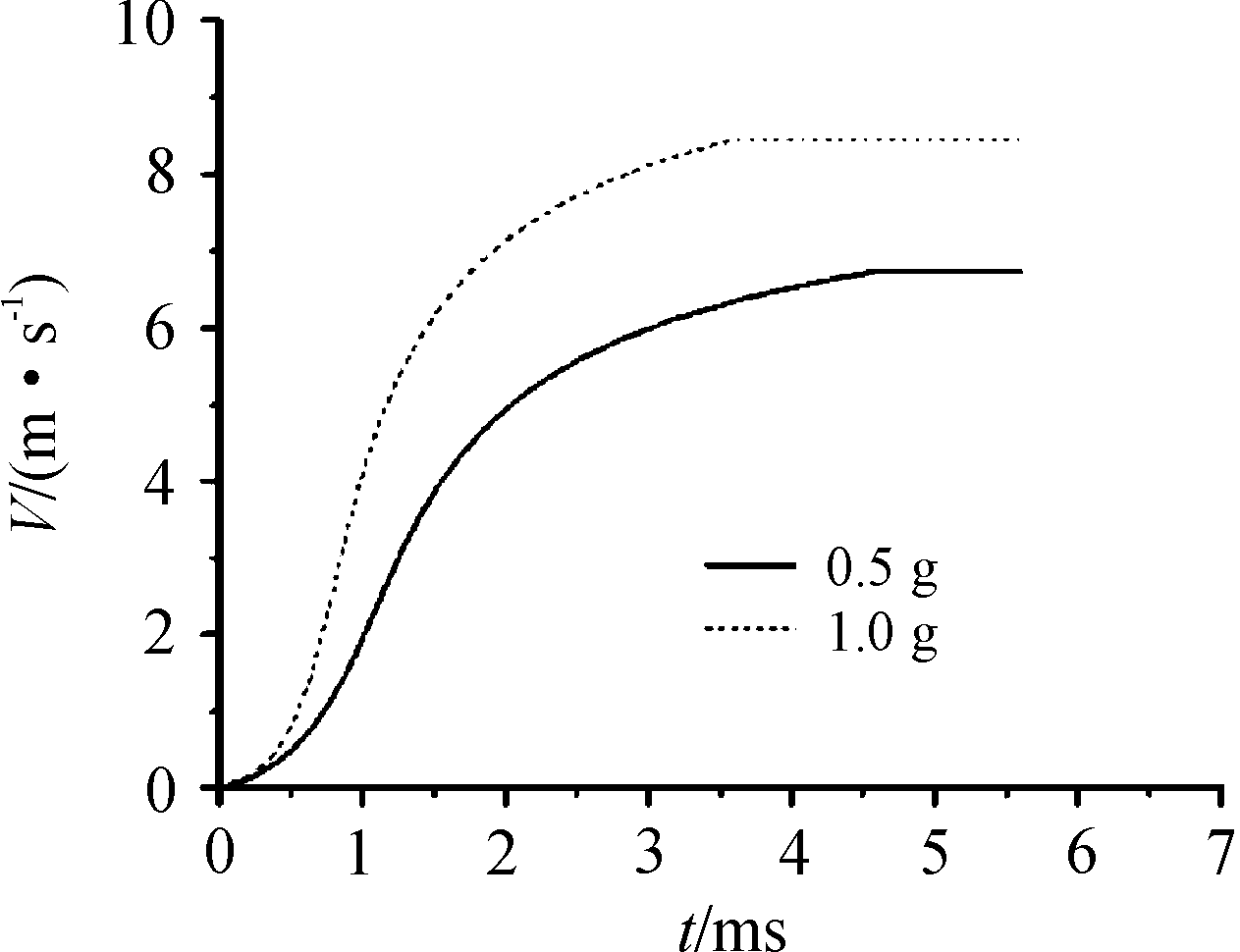
图9 不同药量下钢球的速度曲线
4 结论
本文设计了一种爆炸活塞式分离器,针对0.5 g和1.0 g装药量,进行了钢球的推力试验,同时结合经典内弹道理论,建立了内弹道模型,并与LS-DYNA进行联合仿真,得出以下结论:对应药量分别为0.5 g和1.0 g时,爆炸活塞式分离器的做功能力分别为42.2J和 91.1J;爆炸活塞式分离器的响应时间在3~5 ms。
[1] 戴超,庄劲武,杨锋,等.大容量爆炸活塞式高速开断器分析与优化设计[J].高电压技术,2011,37(01):221-226.
[2] 杨浩.基于有限元的爆炸螺栓断裂特性研究[D].哈尔滨:哈尔滨工业大学,2017.
[3] 杜龙飞,马玉环,陈慧能,等.爆炸螺栓作用过程的仿真研究[J].火工品,2015(03):29-32.
[4] 陈搏,庄劲武,杨锋.爆炸活塞式高速开关的分析与设计[J].武汉理工大学学报(交通科学与工程版),2010,34(03):468-471.
[5] 杨锋,张晓锋,戴超,等.爆炸活塞式大电流高速限流开断装置的设计与分析[J].电力自动化设备,2010,30(04):109-111.
[6] 冯福全.二级轻气炮内弹道仿真研究[D].南京:南京理工大学,2008.
[7] 孙巍,王晨,徐国顺,等.爆炸活塞式限流器的温升仿真分析与试验[J].船电技术,2012,32(05):62-64.
[8] 李枫,庄劲武,江壮贤,等.混合型限流熔断器爆炸活塞式高速开断装置炸药腔室结构分析及优化[J].高电压技术,2017,43(07):2417-2424.
[9] 杜龙飞,马玉环,陈慧能,等.爆炸螺栓作用过程的仿真研究[J].火工品,2015(03):29-32.
[10] HWANG D H,HAN J H,LEE J,et al.A mathematical model for the separation behavior of a split type low-shock separation bolt[J].Acta Astronautica,2019,164:393-406.
[11] LI Y,WANG J,XIONG S,et al.Numerical study of separation characteristics of piston-type explosive bolt[J].Shock and Vibration,2019(2):1-18.
[12] LI Y,WANG J,CHENG L,et al.Numerical simulation of separation shock characteristics of a piston type explosive bolt[J].Vibroengineering PROCEDIA,2018(21):214-219.
[13] LEE J,HAN J H,LEE Y J,et al.Separation characteristics study of ridge-cut explosive bolts[J].Aerospace Science and Technology,2014,39(07):153-168.
[14] LEE J,HWANG D,JANG J K,et al.Pyroshock prediction of ridge-cut explosive bolts using hydrocodes[J].Shock and Vibration,2016,2016(6):1-14.
[15] 刘继华.火药物理化学性能[M].北京:北京理工大学出版社,1997.
[16] 金志明,翁春生.高等内弹道学[M].北京:高等教育出版社,2003.
[17] BANG B,AHN C,KIM Y,et al.Deflagration-to-detonation transition in pipes:The analytical theory[J].Applied Mathematical Modelling,2019,66(FEB):332-343.