爆炸产生的冲击波是战斗部威力考核的重要依据,特别是近年来精确制导武器的高速发展,使得炸点与目标之间的距离越来越近,从而使冲击波的毁伤作用越来越突出。研究空气冲击波的传播特性一方面可以提高武器毁伤效率,另一方面通过对冲击波的测量可以反推爆源的爆炸当量,重现爆炸现场,评判爆源反应类型[1-4]。
衡量爆炸冲击波的参数主要包括峰值超压、正压作用时间和比冲量[5-7]。一般认为冲击波峰值超压是比例距离的函数,在此基础上国内外学者进行了大量的试验研究,并总结出了多种经验公式。比较典型的自由场冲击波经验公式有Henrych超压公式[8]、Садовский球面冲击波经验关系式[9]和Baker超压公式[10]。实际上,真正意义上的自由场爆炸场景较少,更多的是近地爆炸。近地爆炸时,地面反射部分冲击波能量使得相同距离处峰值超压有所增大,同时也因地面受到冲击产生变形和破坏而消耗部分能量,从而近地爆炸冲击波超压计算经验公式误差较大。在弹药热烤试验中,对冲击波超压的测量是评定弹药反应类型的主要方法之一。为准确预测观测点冲击波峰值超压,采用数值模拟的方法不仅可以节约试验成本、缩短试验周期,还能直观地分析冲击波的传播过程,避免经验公式带来的误差。
本文借助显示动力分析程序AUTODYN,分别建立自由场和近地球形TNT爆炸的二维模型,采用EULER方法,模拟得到了空中爆炸冲击波的传播过程。通过提取压力、位置、时间等参数,并与经验公式进行对比,验证了数值模拟的准确性。研究修正了近地爆炸时经验公式的适用范围,得到了特定工况下冲击波超压的空间分布特性,为试验时传感器的布置和数据分析奠定基础。
1 自由场空气冲击波数值模拟
1.1 相似理论与经验公式
由爆炸相似率[11]可知:
(1)
式中: Δp为峰值超压;C为装药质量;r为观测点与爆心之间的距离。函数f的具体形式一般由实验确定。经典的空气中自由场冲击波经验公式有Henrych超压公式、Садовский球面冲击波经验关系式、Baker超压公式。Henrych超压公式的具体形式如下:
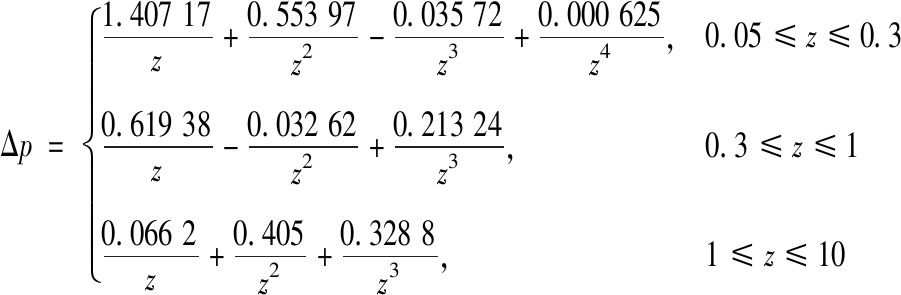
(2)
Садовский球面冲击波经验关系式为:
(3)
Baker超压公式具体形式为;

(4)
式中: Δp为冲击波峰值超压(MPa);z为比例距离,![]()
1.2 数值计算模型
3.3 kg球形TNT在自由场中爆炸可以简化为二维轴对称模型,如图1。模型由TNT炸药和空气两部分组成,建模区域为4 000 mm×8 000 mm。采用EULER网格,为保证计算得到的峰值超压不失真,在炸药附近将网格边长细化为1 mm左右,共计划分425 000个矩形网格。网格中首先填充空气材料,然后将TNT材料填充在区域底部中心位置。为避免边界对冲击波的反射作用,除对称边界外,其余边界均设置物质流出条件,所模拟的三维场景如图2所示。

图1 自由场爆炸二维模型图示意图
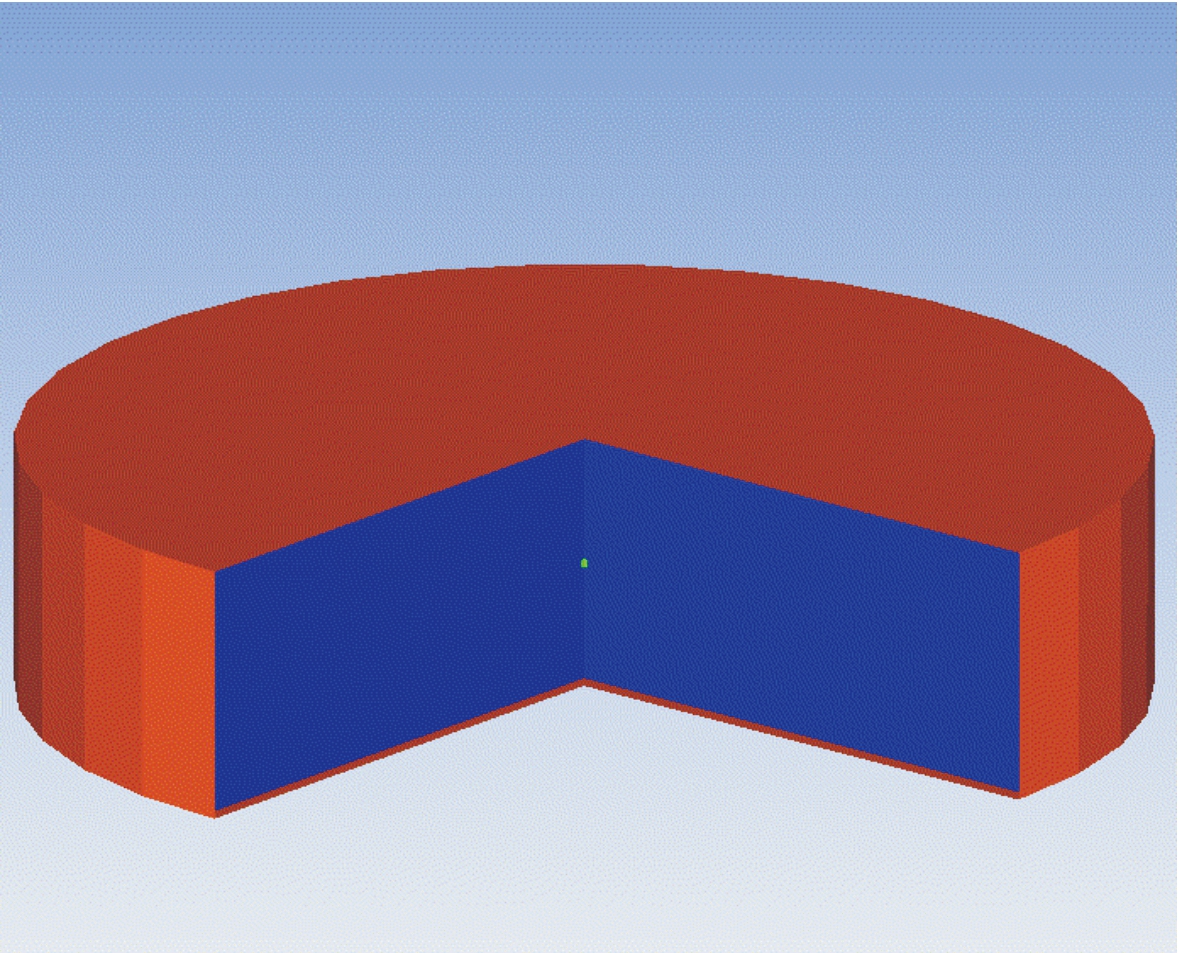
图2 自由场爆炸模型三维示意图
TNT 爆轰产物压力P与单位体积内能e及相对体积V的关系用JWL状态方程来描述[12]:
(5)
式中A、B、R1、R2、ω为常数。具体参数值见表1。
表1 TNT炸药参数值

A/kPaB/kPaR1R2ω3.7383.7474.150.900.35ρ/(kg·m-3)D/(m·s-1)e/(J·m-3)PCJ/kPa163069306×1092.1×107
空气采用MAT-NULL材料模型和理想气体状态方程[13]:
(6)
式中:e为比内能; γ为绝热指数(取1.4); ρ0为空气初始密度(取 1.225 kg·m-3); ρ为当前密度。
1.3 自由场爆炸空气冲击波分布
自由场中冲击波传播过程如图3所示,炸药起爆以后,瞬间反应成为高温高压爆轰产物,并对周围空气进行压缩,在空气中形成规则球面波,同时向爆轰产物内部传入稀疏波,使得产物压力迅速下降。距爆心每隔0.5 m设置一个观测点,典型冲击波时程曲线如图4所示。冲击波到达观测点之前,观测点压力保持大气压力P0,冲击波经过该观测点后,压力瞬间跃升至最大值,压力最大值与P0的差值即为峰值超压。随后压力迅速下降,经过正压作用时间ta后压力重新恢复P0。此时由于空气的膨胀惯性,压力将进一步下降至负压区,从图4中可看出不同距离处空气压力的变化规律一致。
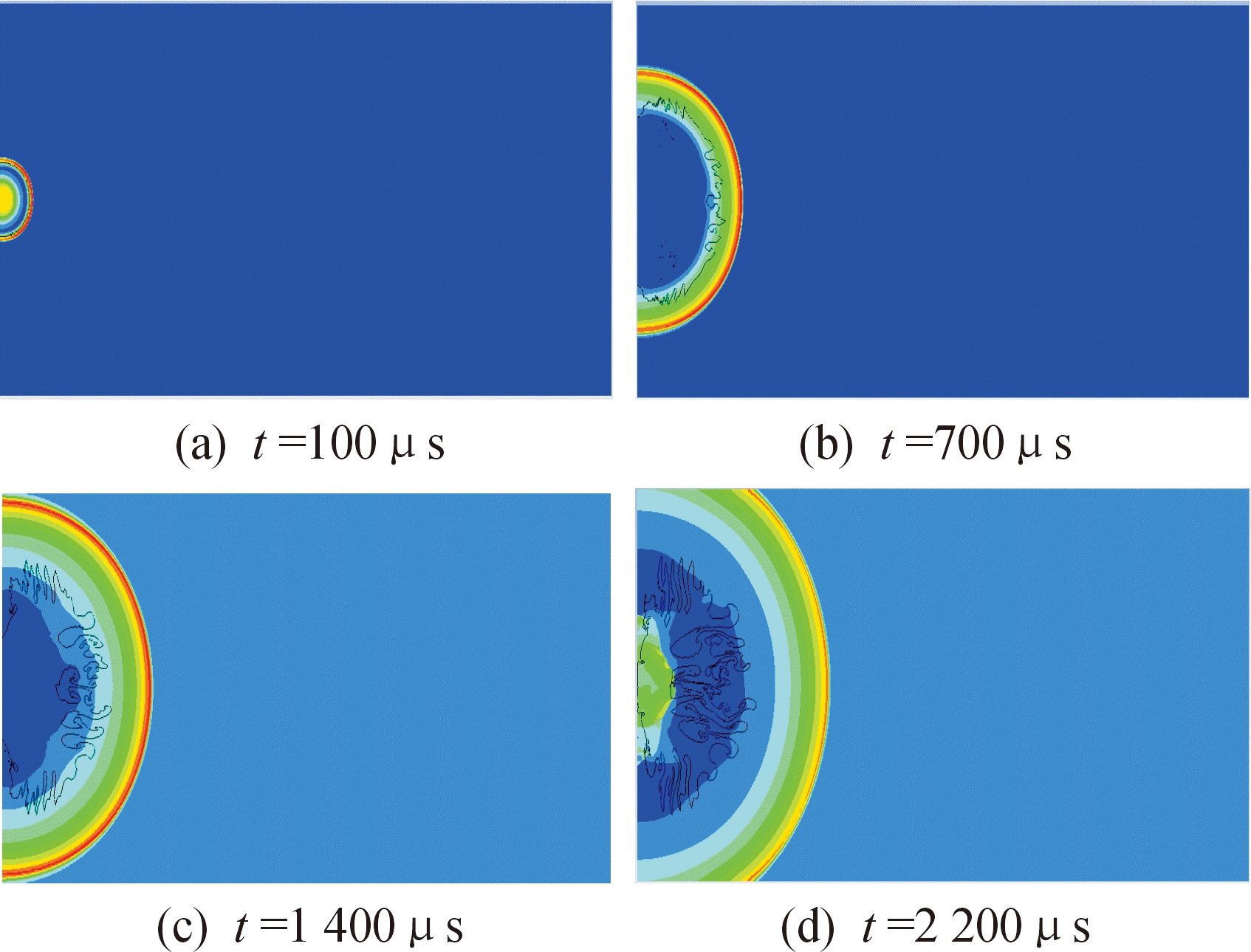
图3 自由场冲击波压力云图
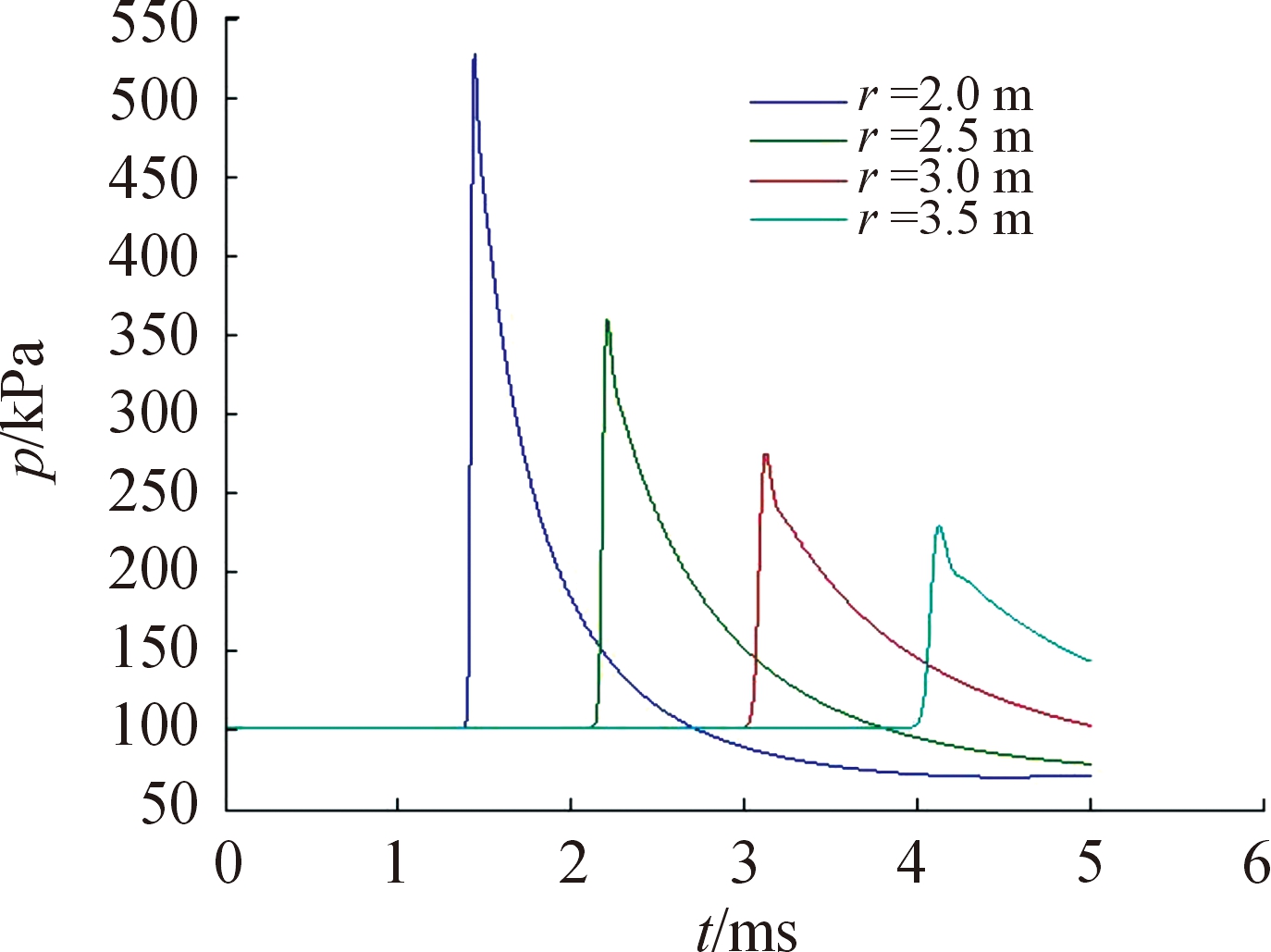
图4 不同距离典型冲击波压力时程曲线
将各观测点峰值超压与由经验公式计算所得到的数据作曲线,如图5,发现距爆心越近经验公式之间的误差越大,随着距离的增加,各经验公式计算结果也越来越接近。数值模拟结果介于各经验公式中间,更加接近Henrych超压公式,爆心距离大于1.5 m时相对误差在5%以内,说明了数值模拟的准确性。
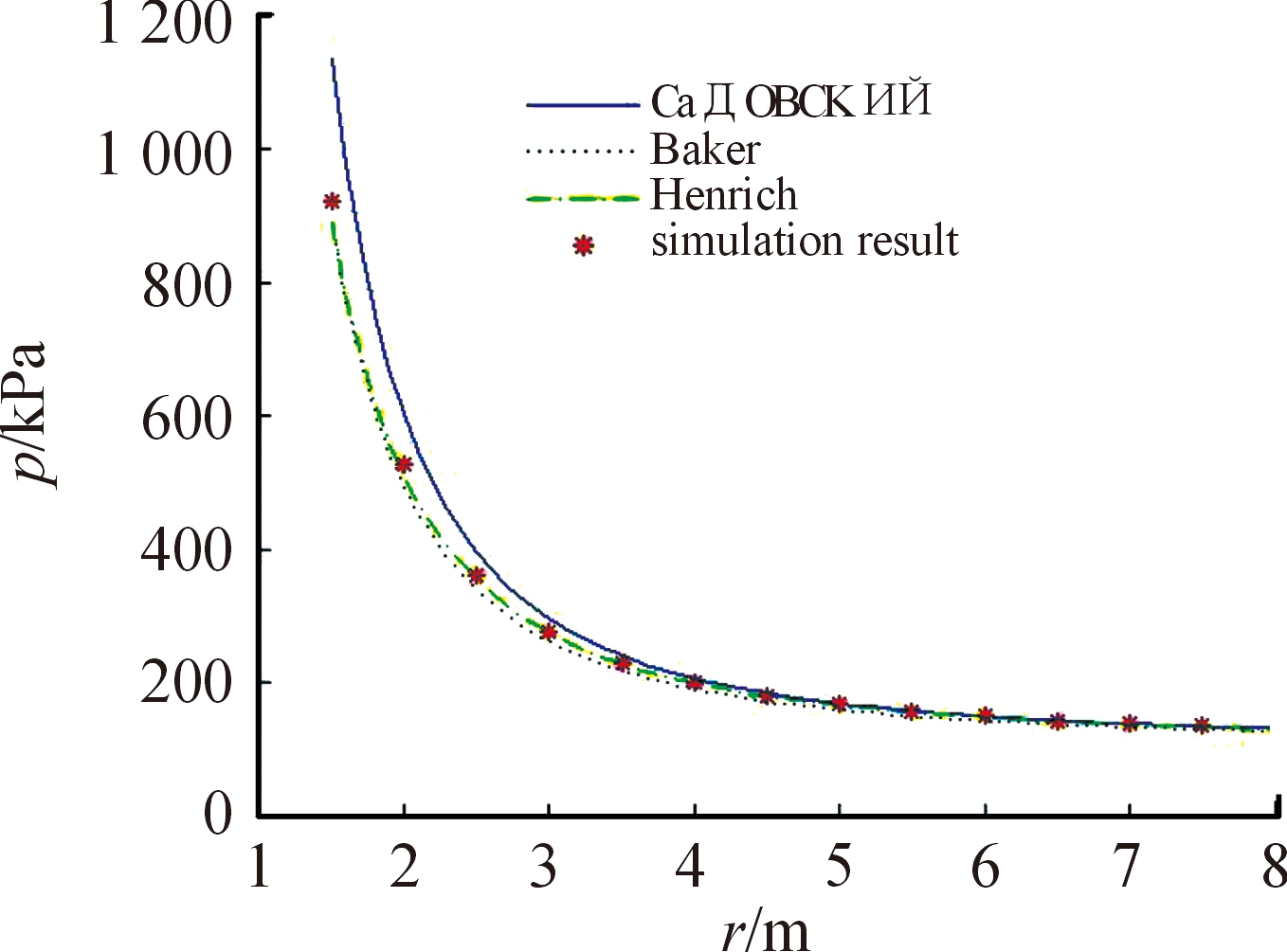
图5 峰值超压与经验公式数值曲线
2 近地爆炸空气冲击波数值模拟
3.3 kg球形TNT在爆心距离地面0.925 m处爆炸时,假设地面为刚性平面,则模型可以简化为二维轴对称模型,建模区域:1 850 mm×8 000 mm,网格划分及算法与自由场空气冲击波超压模拟相同。将建模区域下表面设置为刚性界面,允许冲击波发生发射。
近地爆炸时,冲击波的传播过程较为复杂。一般来说分为四种类型[14],即自由场冲击波传播、冲击波正反射、冲击波规则斜反射和马赫反射。自由场冲击波传播发生在炸药起爆以后但冲击波接触地面之前,认为这段过程爆炸产生的球面冲击波未收到干扰,为理想的自由场冲击波传播过程,冲击波超压可以借助自由场超压公式计算。冲击波的正反射发生在爆心正下方地面处,这也是地面最先受到冲击的地方,冲击波作用下运动的质点遇到地面后速度被制止为零,并不断累积形成高压区,从而产生冲击波反射现象。冲击波在刚性壁面发生正反射时,反射超压可按下式计算:
(7)
式中: Δp1为入射冲击波超压;Δp2为反射冲击波超压;p0为大气压力;K 为空气的比热,一般情况下 K=1.4。
除爆心正下方地面处,其余各点地面将发生斜反射,随着入射角度不同,各点处反射情况不同。存在一个临界角ψ0,入射角度小于ψ0时,发生规则斜反射,入射角度大于ψ0时,发生规则马赫反射。正规斜反射和马赫反射冲击波压力计算过程非常复杂,当入射波压力小于300 kPa时,反射波的压力与入射角无关,仍可用式(7)计算,当入射波压力大于300 kPa时可用下式计算:
(8)
马赫反射的理论尚不很完善,计算比较复杂,实际使用时常采用经验公式:
Δpm=Δpmgr(1+cosφ0)
(9)
式中: Δpm为峰值超压; Δpmgr为地面爆炸时空气冲击波的峰值超压。
![]()
(10)
图6所示为近地爆炸时冲击波传播过程,图7为给出了爆心同高,距爆心2.5 m处观测点压力时程曲线与自由场2.5 m处压力时程曲线。在反射波到来之前,该观测点先受到入射冲击波的压缩,其压缩过程与自由场中冲击波压缩过程完全一致,峰值压力为360 kPa。此后随着压力的下降,t=2.835 ms时该观测点再次受到冲击压缩,出现第二波峰,峰值压力为290 kPa,从图6观察到这是反射波二次冲击的结果。通过观察不同距离处观测点压力时程曲线(图8)发现,各观测点的压力变化规律差异较大。r=1.5 m、r=2 m、r=2.5 m、r=3 m处,均存在2个波峰,r=3.5 m处仅一个波峰,对比冲击波传播过程可知,先后到达的波峰分别是入射冲击波和规则反射冲击波。r=1.5 m、r=2 m、r=2.5 m处第一波峰均大于第二波峰,而r=3 m处第二波峰大于第一波峰。以上可知,近地爆炸时冲击波的分布比较复杂,利用现有经验公式进行计算时可能存在较大误差或出现双波峰时无法进行数据分析,而通过数值模拟可以清晰地判断观测点处到达的冲击波类型和预测压力变化情况。

图6 近地爆炸冲击波压力云图
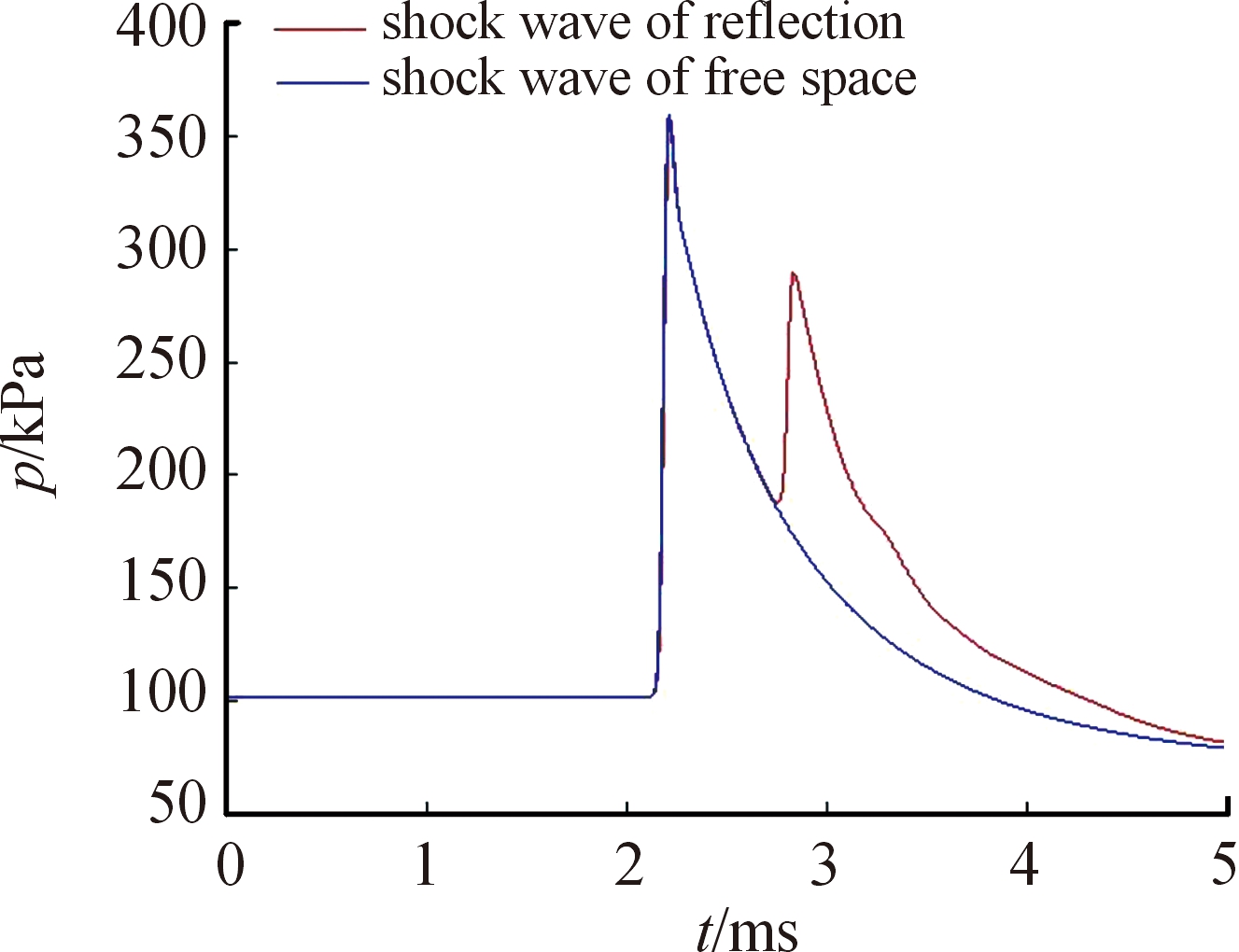
图7 2.5 m处不同工况下的时程曲线
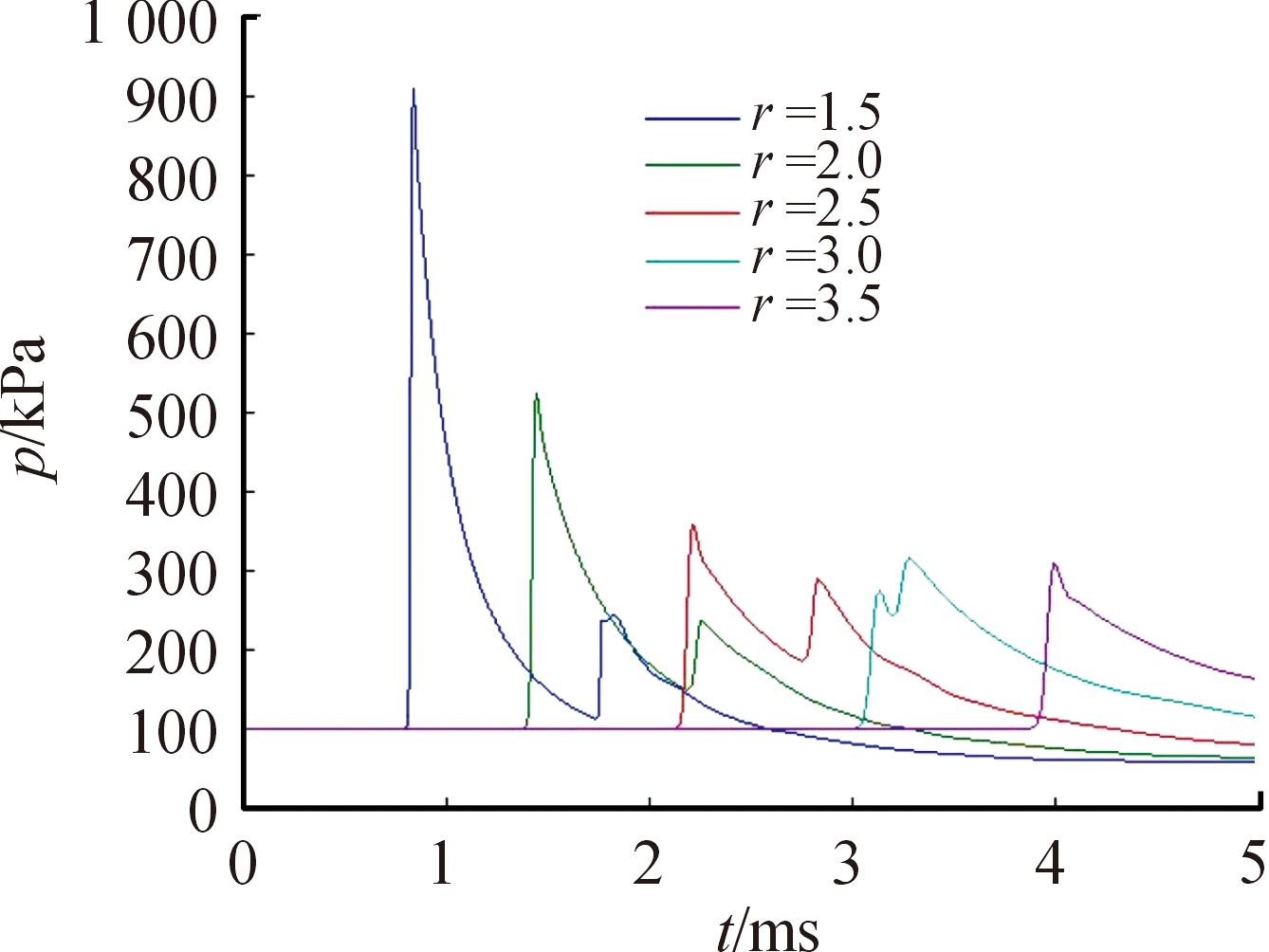
图8 近地爆炸时压力时程曲线
从图6中可以看出,马赫波与地面相交的地方始终垂直于地面,马赫杆始终是弯曲的。入射波、规则反射波与马赫波的交点被称为三波点,观测点相对于三波点的位置是区分观测点冲击波类型的关键,因此,本文提取了马赫杆形成后三波点的移动路径,根据其结果绘制如图9所示的三波点移动路径曲线。从图9中可以看出,三波点的高度随着距爆心距离的增加而不断增加,并且最终超过爆高。当测量点处于三波点运动轨迹以下时,将受到马赫反射波的冲击;当测量点处于三波点运动之上时,将首先受到入射波冲击,再受到反射波冲击。随着三波点高度的增加,与炸点等高的所有观测点都将只受到马赫波的单次冲击,这也是图8中不同观测点压力峰值情况不同的原因。
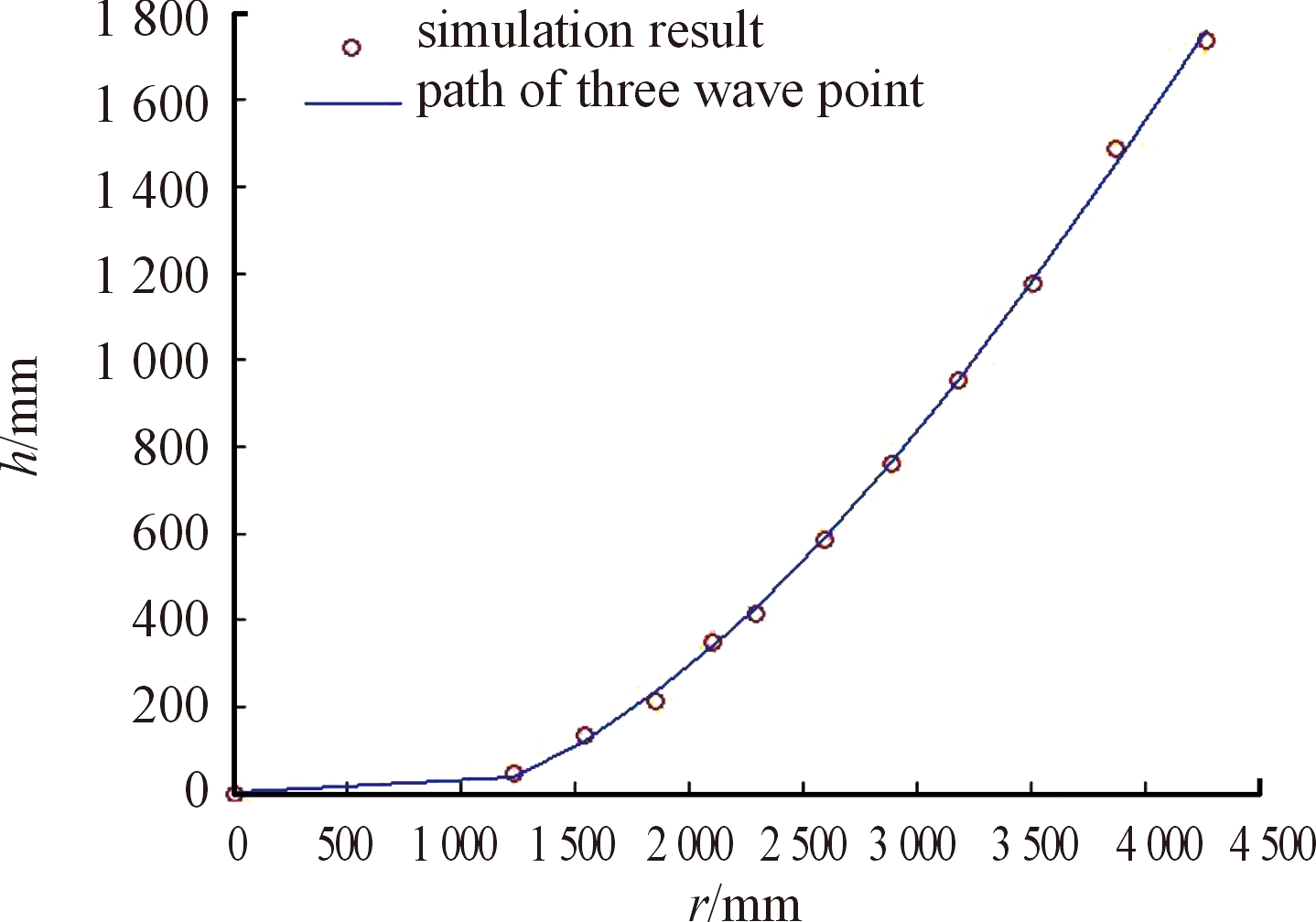
图9 三波点移动路径曲线
3 冲击波传播特性数值模拟应用研究
3.1 冲击波超压经验公式适用范围与传感器的布设问题
经验公式是在相似理论的基础上,通过大量实验数据的分析拟合得到的[15]。因为计算的简便快捷,在工程实践中得到了广泛应用,但是在使用过程中往往容易忽视经验公式的使用条件,增加了计算的误差,尤其在弹药热烤试验中,冲击波峰值超压的预测结果精度直接影响弹药响应等级评定。通过数值模拟研究发现,对于本研究工况中,在与爆心等高的不同测点中,适用的经验公式不同,所得到的值如图10所示。r<2.5 m时,测点冲击波超压服从Henrych超压公式(2),r>3.5 m时测点冲波超压服从近地反射超压经验公式(10),2.5 m <r<3.5 m时,冲击波超压介于两者之间。
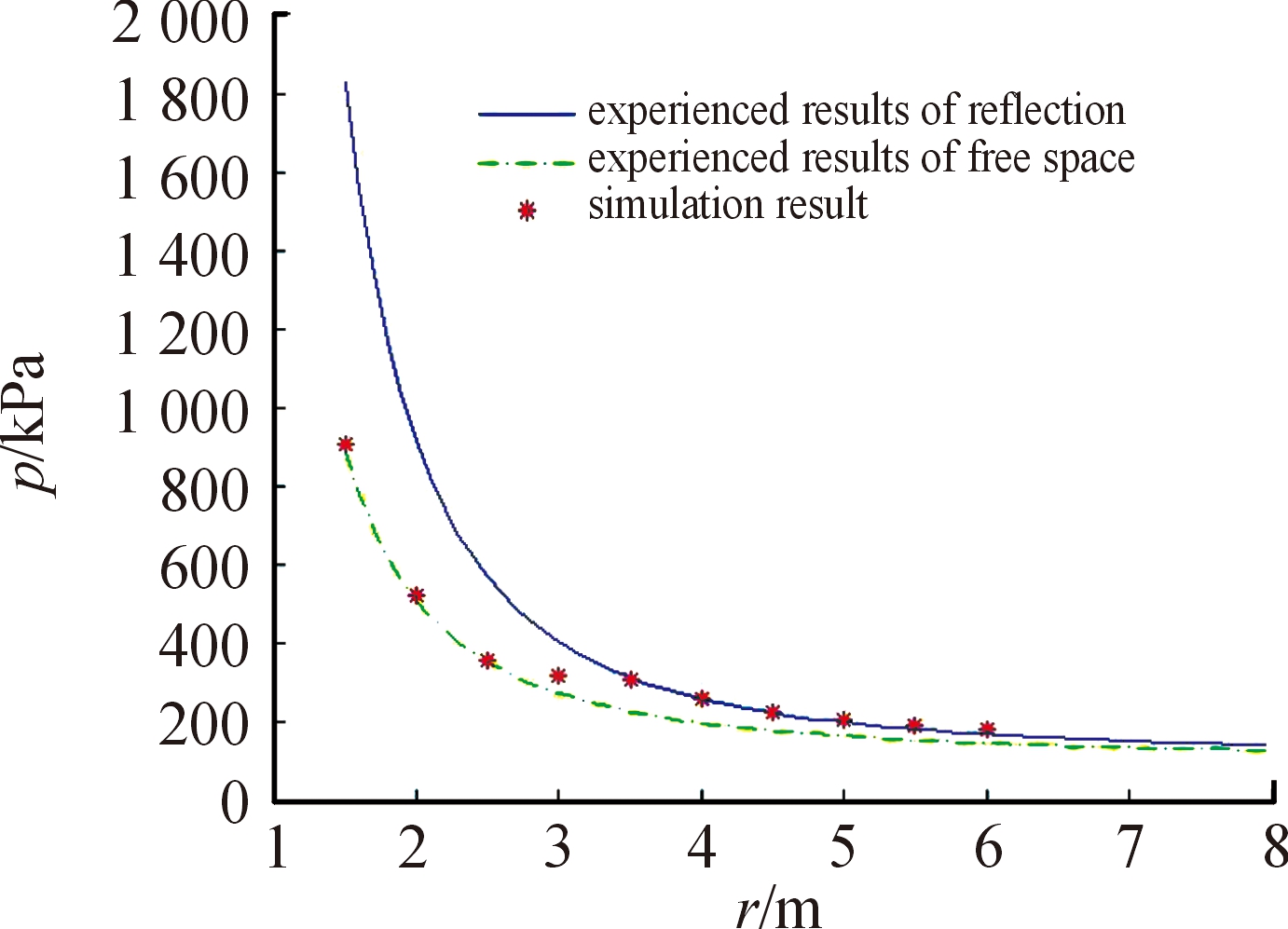
图10 近地爆炸数值模拟与经验公式计算数据曲线
冲击波超压测试中往往需要预估观测点的超压值,以选定匹配的超压传感器量程。或是已知测试的压力范围,预估测点位置。为了评定弹药热烤试验过程中含能材料的反应类型,北约STANAG4382推荐的冲击波超压测试范围为 3.5~70 kPa,对比试验中传感器布置位置,所测得的冲击波超压分布(图11),发现本试验中传感器布设在距爆心6.0 m之外的地点。
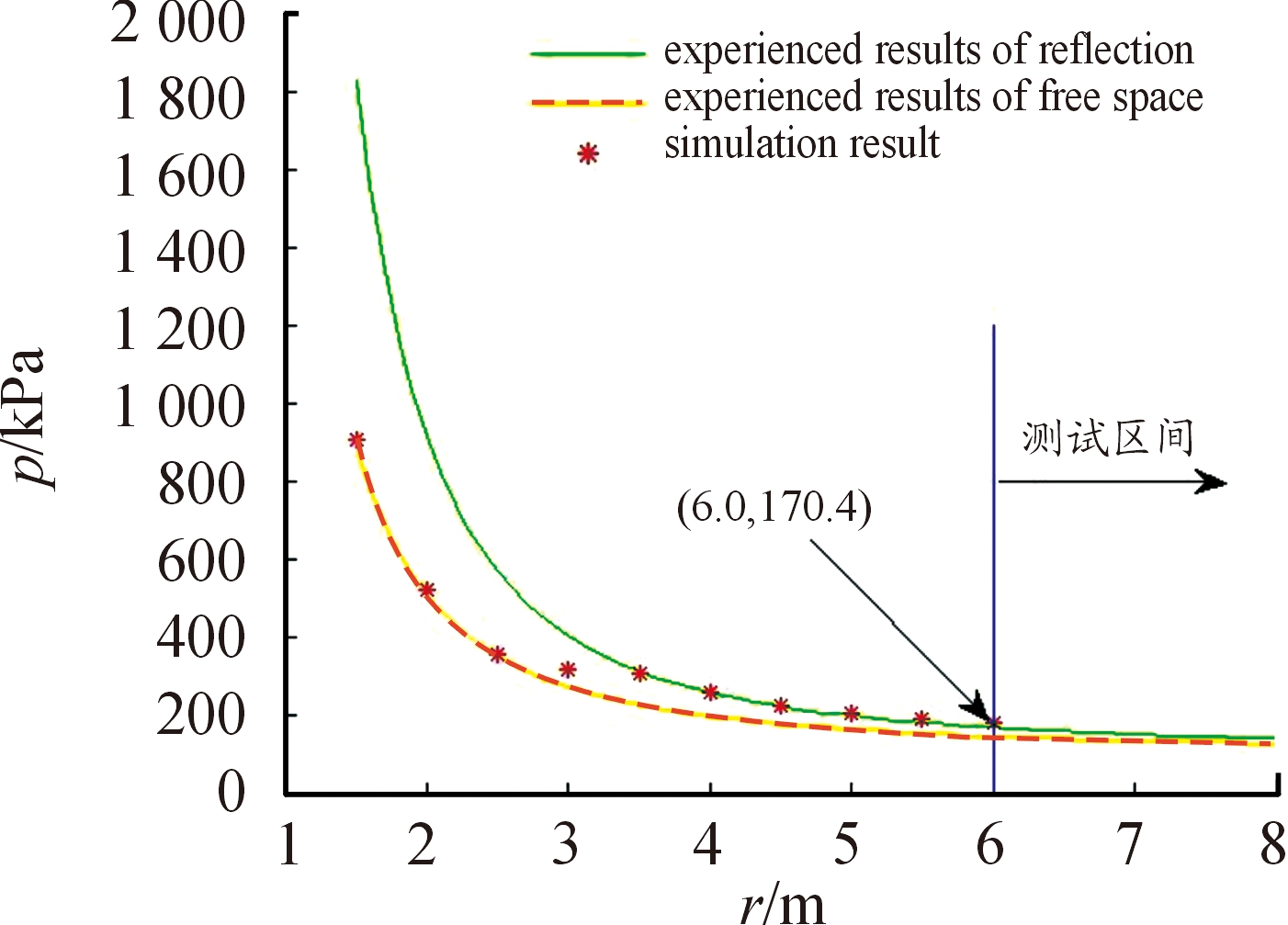
图11 试验中传感器布置位置与冲击波超压分布的关系
3.2 冲击波损伤的防护问题
装药在空气中爆炸产生的冲击波对不同距离处的人员、装备和设施具有不同的杀伤作用。仅从安全防护的角度考虑,冲击波对人员的杀伤作用主要包括引起血管破裂、导致皮下或内脏出血。在试验过程中应注重人员、装备的防护,使其处于安全距离之外。根据冲击波对人员的杀伤作用(表2)和近地爆炸时冲击波超压分布,得到试验中球形TNT爆炸时人员危险区域如图12所示,对于冲击波的防护,试验中人员距离爆心最近不能跨越5区。
表2 空气冲击波对人员的杀伤作用
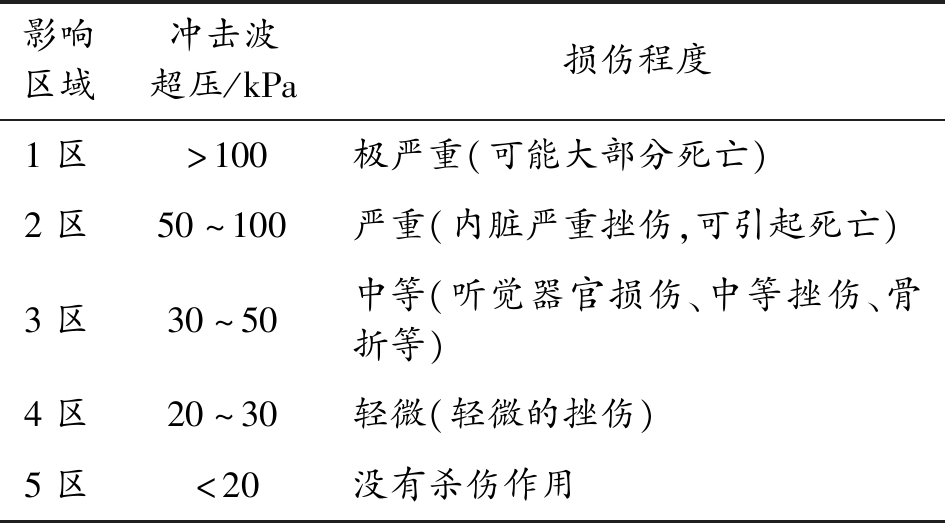
影响区域冲击波超压/kPa损伤程度1区>100极严重(可能大部分死亡)2区50~100严重(内脏严重挫伤,可引起死亡)3区30~50中等(听觉器官损伤、中等挫伤、骨折等)4区20~30轻微(轻微的挫伤)5区<20没有杀伤作用
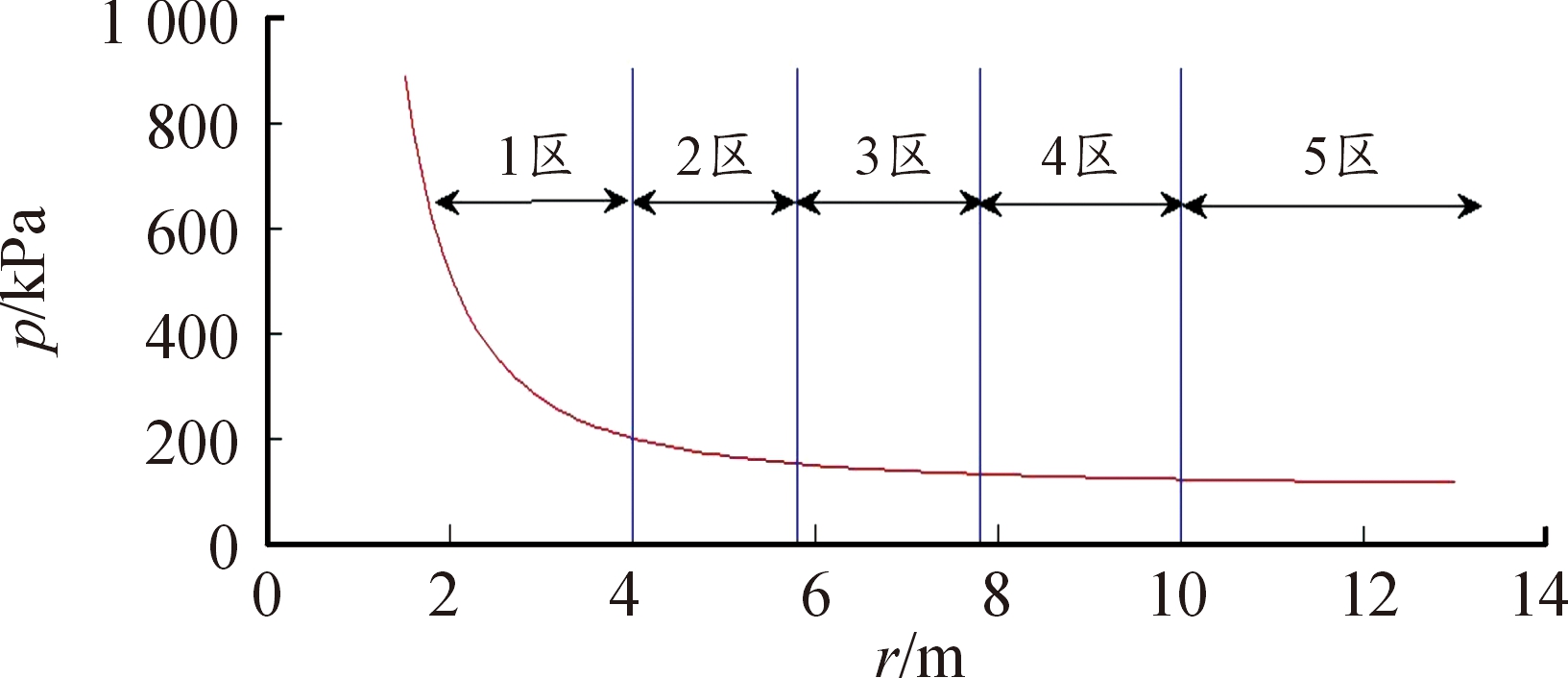
图12 不同距离冲击波对人员的杀伤作用示意图
4 结论
1) 利用现有经验公式计算近地爆炸冲击波,当测量点处于三波点运动轨迹以下时,将受到马赫反射波的单次冲击;当测量点处于三波点运动轨迹之上时,将首先受到入射波冲击,再受到规则反射波冲击。
2) 对于特定工况下球状TNT近地爆炸,在与爆心等高的不同测点中,r<2.5 m时,测点冲击波超压服从自由场冲击波超压经验公式,r>3.5 m时测点冲波超压服从近地反射超压经验公式,2.5 m<r<3.5 m时,冲击波超压介于两者之间。
3) 热烤试验过程中冲击波传感器建议布设在距爆心 6.0 m 之外的地点,试验过程中人员最近不能越过5区。
[1] 郭炜,俞统昌,金朋刚.三波点的测量与实验技术研究[J].火炸药学报,2007,30(4):55-61.
[2] JAMES H R.Predicting the response of explosives to attack by high-density shaped-charge jets[J].Journal of Energetic Materials,1989,7(4/5):243-264.
[3] 王新颖,王树山,卢熹,等.空中爆炸冲击波对生物目标的超压—冲量准则[J].爆炸与冲击,2018,38(1):106-111.
[4] ZUKAS J A,ZHANG Zhiyun,DING Shiyong,et al.Impact Dynamics Translated[M].Beijing:Publishing Company of Weapons Industry,1989:264-265.
[5] 姚成宝,王宏亮,浦锡锋,等.空中强爆炸冲击波地面反射规律数值模拟研究[J].爆炸与冲击,2019,39(11):24-31.
[6] 赵海涛,王成.空中爆炸问题的高精度数值模拟研究[J].兵工学报,2013,34(12):1536-1546.
[7] 蒋海燕,李芝绒,张玉磊,等.运动装药空中爆炸冲击波特性研究[J].高压物理学报,2017,31(03):286-294.
[8] 张社荣,李宏璧,王高辉,等.空中和水下爆炸冲击波数值模拟的网格尺寸效应对比分析[J].水利学报,2015,46(3):298-306.
[9] 奥尔连科.爆炸物理学[M].3版.北京:科学出版社,2011.
[10] 张宇.爆炸荷载作用下高强H型钢柱的动力响应及稳定性研究[D].沈阳:东北林业大学,2014.
[11] 华雨,于纪言,张庆,等.静爆冲击波在空气中的传播规律[J].兵器装备工程学报,2016,37(07):168-172.
[12] 辛春亮,王俊林,余道建,等.TNT 空中爆炸冲击波的工程和数值计算[J].导弹与航天运载技术,2018(3):98-102.
[13] 张社荣,孔源,王高辉.等.水下和空中爆炸冲击波传播特性对比分析[J].振动与冲击,2014,33(13):148-153.
[14] 杜红棉,曹学友,何志文,等.近地爆炸空中和地面冲击波特性分析和验证[J].弹箭与制导学报,2014,34(4):65-68.
[15] 李科斌,李晓杰,闫鸿浩,等.不同真空度下空中爆炸近场特性的数值模拟研究[J].振动与冲击,2018,37(17):270-276.