自然界中的鸟类经过亿万年的飞行进化,形成了出色的飞行能力,飞行效率、机动性都远远超过了目前所有的人造飞行器。鸟类飞行过程中翅膀的运动由上下扑动、弦向扭转、展向折弯和前后挥摆等几种运动复合而成[1-3]。鸟类飞行时翅膀通过周期性的复合运动产生飞行所需的上升升力和前向推力,实现爬升、俯冲、盘旋、悬停等动作,从而具备高超的机动性能。而扑翼飞行器根据鸟类翅膀扑动而设计的一种仿生飞行器,具有体积小、质量轻、能耗低、噪音低,机动性能优越、隐蔽性强等特点。因此,小型的扑翼飞行器是未来无人飞行器发展的一个重要方向[4,6]。
目前,国内外对扑翼飞行器的研究主要集中在2个方面:一方面是仿生扑翼飞行器的结构设计与运动学分析,通过观察鸟类翅膀的运动规律,建立扑翼运动学与动力学模型,设计高效驱动机构,结合新型柔性致动材料,多种形式的仿生扑翼飞行器应运而生[5]。如加利福尼亚工学院MicroBat、Aero Vironment公司研制的“蜂鸟”、哈佛大学研制的RoboBee X-Wing、荷兰Delft大学研制的BatBot(B2)的仿蝙蝠扑翼飞行器等。另一方面对扑翼飞行机翼非定常气动力特性开展研究,通过理论分析、数值模拟和实验测试相结合的方式展开。Tuncer等[16]对扑翼拍动过程中的升阻力变化进行了分析。Delaurier等[7-12,14]采用改进的条带理论建立了对称扑翼在飞行过程中翅翼运动的空气动力学模型。国内的研究人员对扑翼的非定常理论也展开了深入研究,昂海松等采用非定常涡格方法对扑翼复合运动的气动力特性展开研究。孙茂[13]通过Navier-Stokes equations(N-S)方程与涡动力学分析昆虫翅翼的非定常运动气动力特性。
目前对扑翼非定常运动的空气动力特性的研究有很多,且形成了一定的理论基础。但在气动分析时,机翼大多为上下对称扑动。而通过观察鸟类翅膀的运动规律,飞行过程中翅膀下拍和上拍的时间占比不同,下拍时间较短速度较快,而上扑占整个扑动周期的时间较长速度较慢。本文针对扑翼非对称拍动的运动特定,建立扑翼非对称运动控制方程,构建三维扑翼气动分析模型,研究采用动态混合网格技术,并结合布西涅斯克假设,求解N-S方程,分析扑翼在运动非对称时对扑翼气动力特性、气动效率以及机翼附近流场变化的影响。
1 非定常气动理论
扑翼飞行速度较低,飞行过程中空气的粘性力体现较为明显,属于低雷诺数范畴。扑翼非对称拍动产生飞行所需的升力和前进推力,扑翼拍动过程中流场时刻发生变化,此时流场为非定常流动。本文研究扑翼非定常气动力特性时采用有限体积法离散三维不可压缩流动Navier-Stokes(N-S)方程,此时流场控制方程的数学表达式可用连续性方程与动量方程描述[15]:
(1)
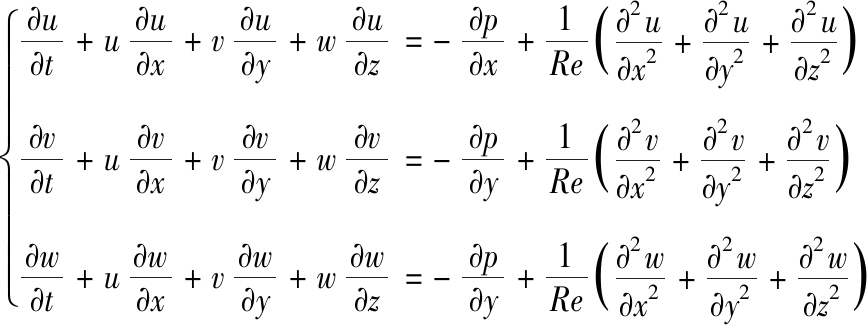
(2)
方程(1)为连续性方程,(2)为动量方程,u、v、w分别为速度在x、y、z方向上的分量;p为流场压力; ρ为流体密度;Re为雷诺数。
雷诺数可以表示为:
(3)
其中:U为一个运动周期扑翼拍动的平均速度;c为弦长;μt为流体运动黏度。
为使得流体控制方程组封闭,引入布西涅斯克假设(Boussinesq):
(4)
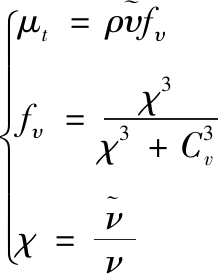
(5)
其中:κ表示湍流动能; μt表示流体运动黏度系数; fυ为黏滞阻尼系数。
2 扑翼几何模型
2.1 三维扑翼气动分析模型
气动分析时建立的三维扑翼气动模型如图1所示。整个模型分为3个部分:左右机翼和机身部分,分析时两侧机翼绕机身按照预定运动规律上下拍动。以机身质心为坐标原点建立坐标系O-XYZ,X轴与机身轴线重合,由头部指向尾部为正方向,Z轴垂直于X轴指向左侧机翼,Y轴根据右手坐标系确定,U∞表示来流风速的方向。机翼拍动过程,机翼位于OXZ面上方,拍动幅值角度α为正,反之为负。机身与水平方向呈8°的攻角。机翼的翼型选用NASA翼型库中的BE6356,如图2(b)所示。分析时,由于两侧机翼的运动规律相同,为节约计算资源,数值计算时只分析单侧机翼拍动时的气动力特性。
计算采用的扑翼气动模型尺寸参数如图2(a)和表1所示。
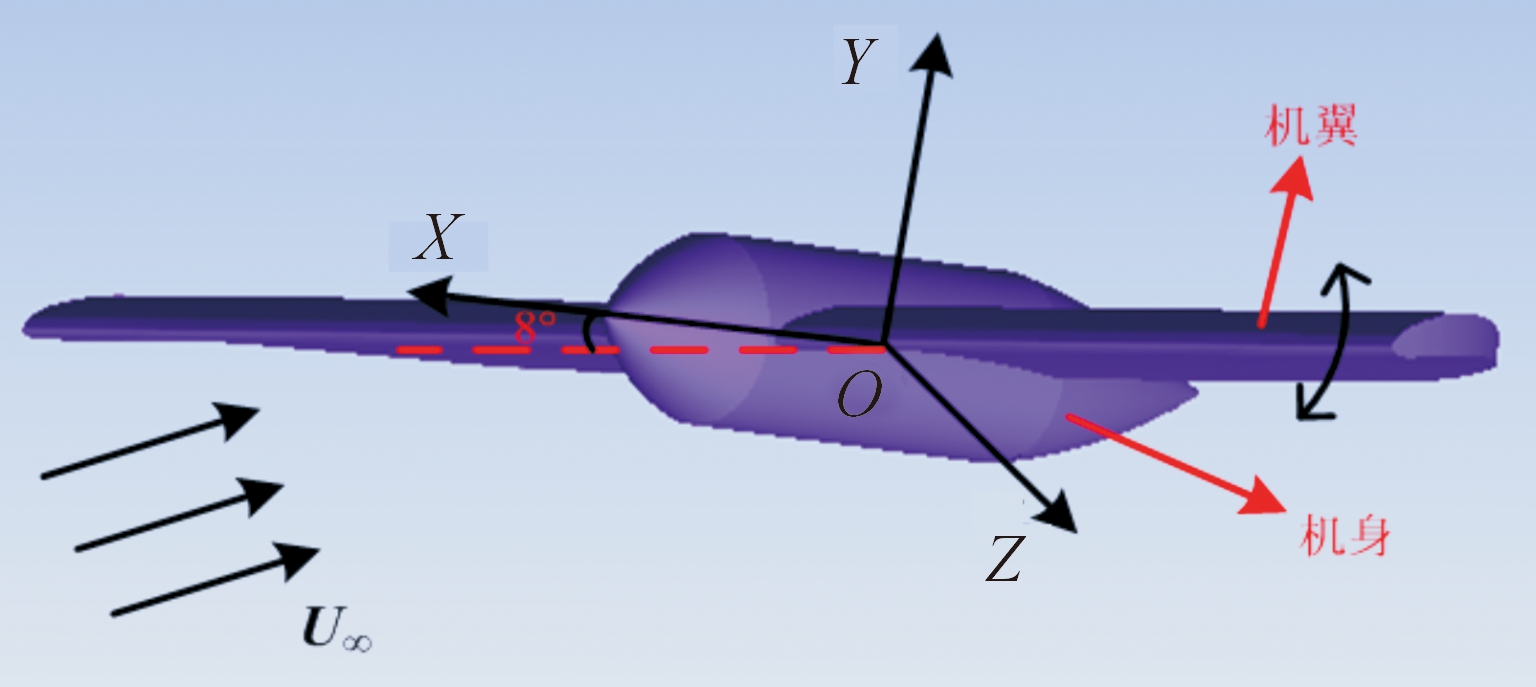
图1 三维扑翼气动分析模型
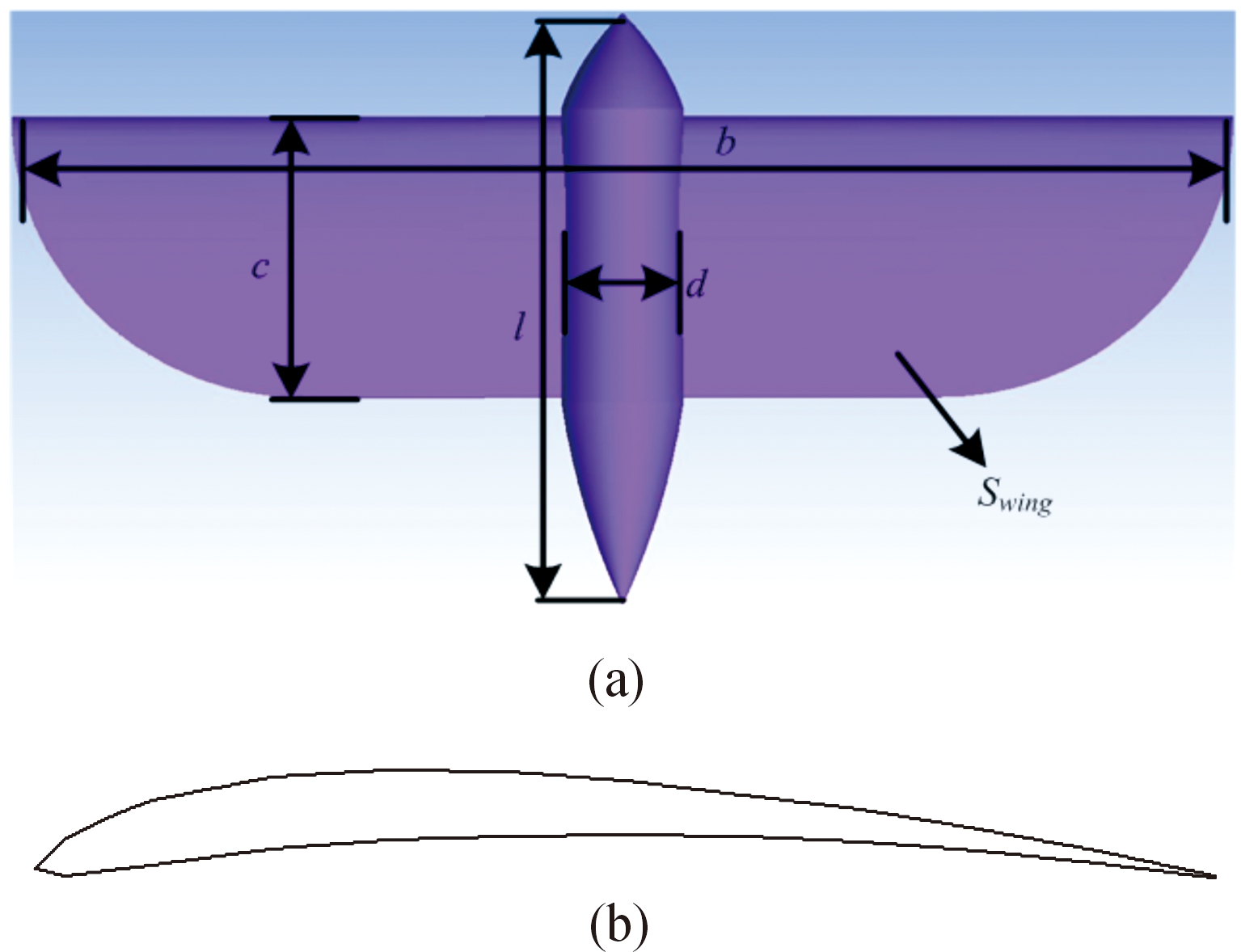
图2 BE6356翼型和扑翼气动模型几何参数示意图
表1 三维扑翼模型尺寸参数

参数数值翼展R/mm1000翼面面积Swing/m20.2机身长度L/mm500弦长b/mm230机身直径d/mm10
机翼通过拍动提供飞行所需的动力,拍动过程可以分为上拍和下拍过程中。扑翼拍动过程的数学形式如式(6)所示
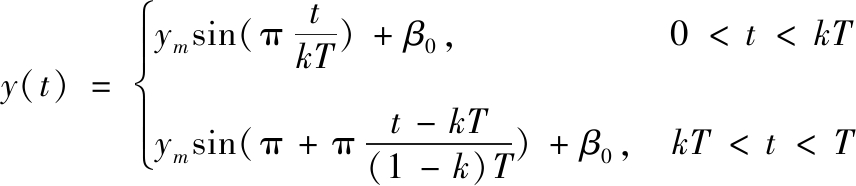
(6)
式中:ym为拍动幅值; β0为拍动初始相位;k为拍动时间周期占比; T为拍动周期。
分析时通过调整k的值,调整机翼上拍和下拍在一个拍动周期内的时间占比,从而实现扑翼快扑慢回动作,达到提供扑翼飞行过程中飞行升力。
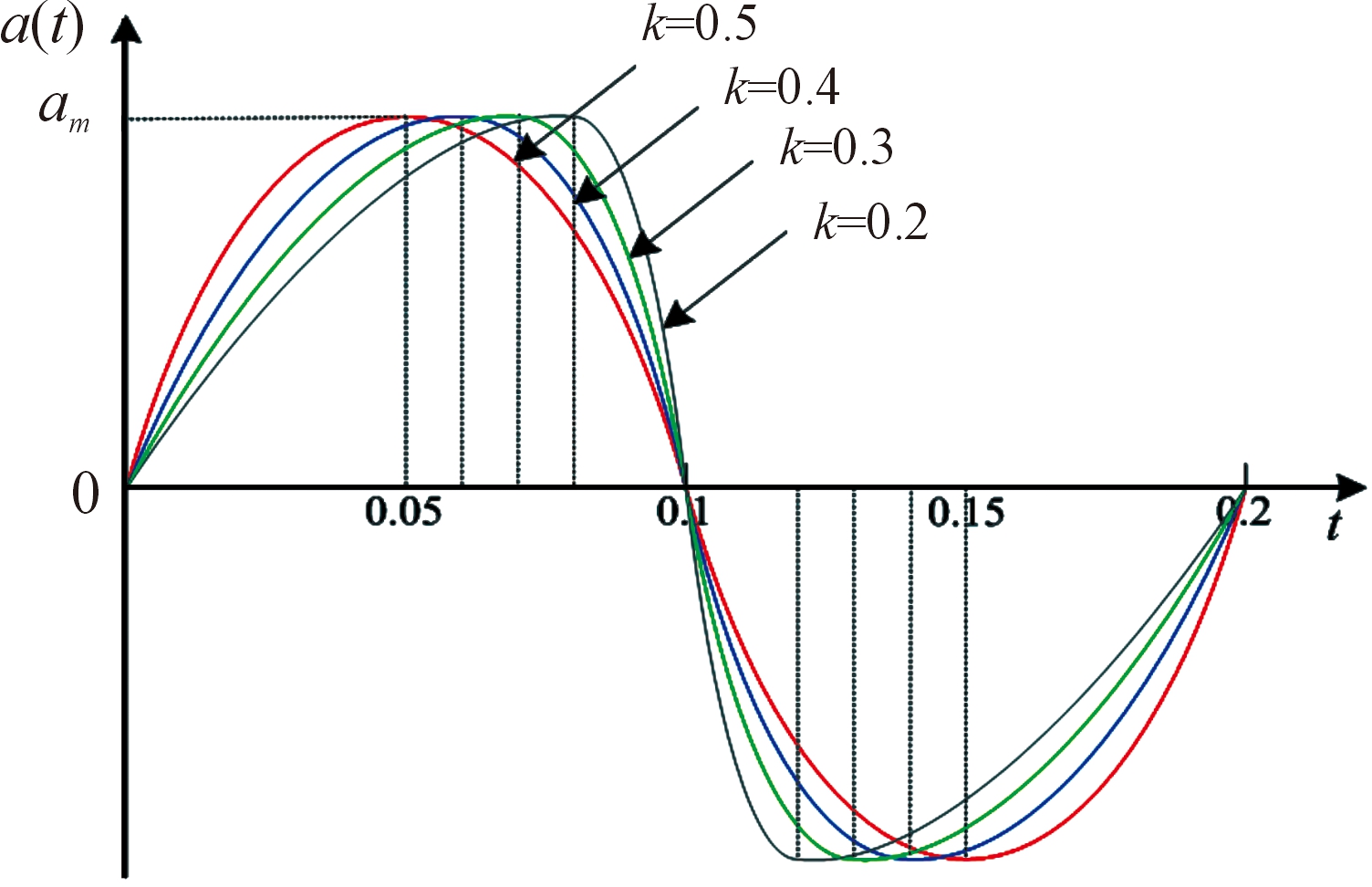
图3 不同k时扑翼拍动规律曲线
2.2 流场域构建及网格划分
为了避免边界回流对扑翼拍动时气动力的影响,构建分析流场域时采用翼展长度的15~20倍构建,采用四面体网格对整个流场域进行网格划分,构建的流场域及网格划分如图4所示,总的网格数量为 1 194 220,最小网格尺度0.04 mm。仿真分析时,为更好地获取机翼的气动力及机翼附近的流场变化情况,因此在处理机翼附近处的网格时,对机翼前后缘和机身头部、尾部的网格进行了加密。对流场域网格及扑翼模型网格进行优化,得到较高的网格质量,以获得更好地计算精度。选用网格的长宽比(Aspect Ratio)作为网格质量的评价标准对构建的流场域进行优化,优化后整体的网格质量能够达到0.53以上,如图5所示。而对于采用动网格方法进行仿真时,网格质量达到0.2以上就可以使用,越高的网格质量数值计算时收敛精度越高,收敛速度越快。
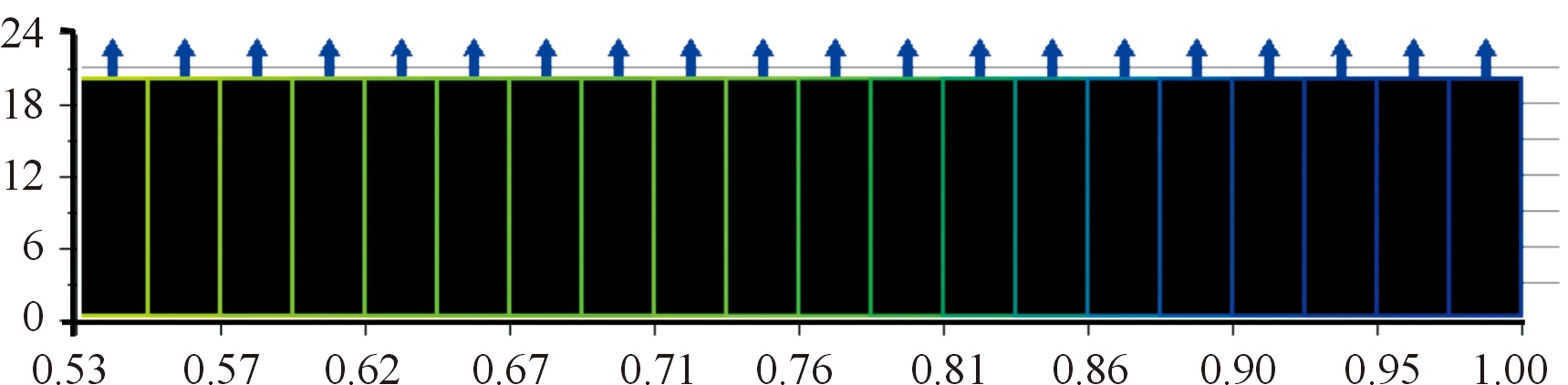
图4 流场域网格划分
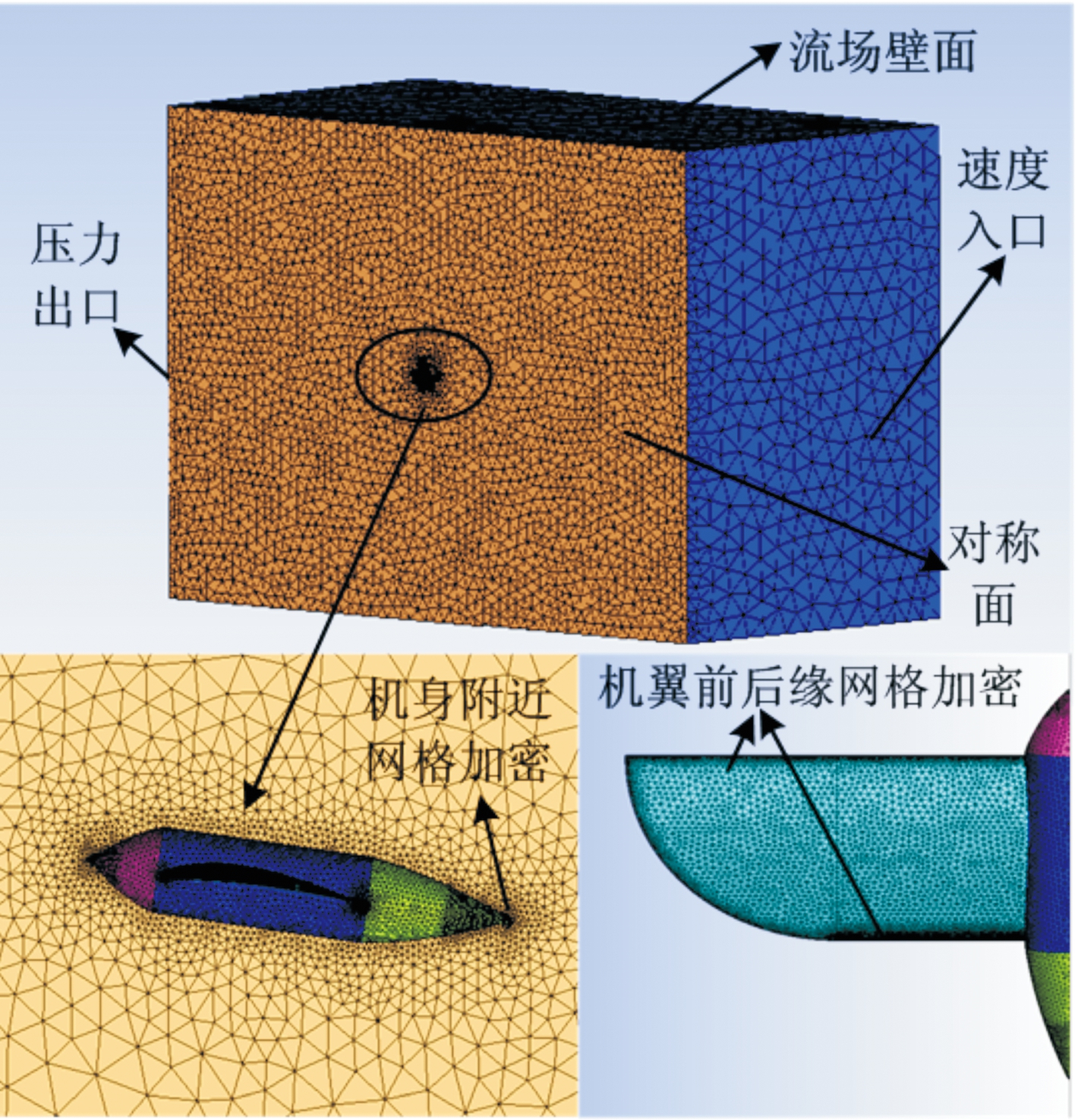
图5 流场域构建及模型网格划分
3 扑翼气动力计算方法
气动升力的计算,将翅翼分为若干微元,如图6所示。假设扑翼飞行过程中,气动力方向一直垂直于机翼翼面。扑动过程中,微元的瞬时速度为ωr,该微元产生的瞬时气动升力为:
(7)
Γ=1/2ρair(ωr)2
(8)
其中: Γ为该微元在流体内动压; ρair为空气密度; CL(α)为微元攻角下的气动力系数;c(r)为扑翼展向位置处的弦长。通过对扑翼该微元进行展向积分,即可计算得到整个扑翼的瞬时气动力为:
(9)
其中:![]() 分别为机翼的翼面面积、翼展长及平均弦长。
分别为机翼的翼面面积、翼展长及平均弦长。
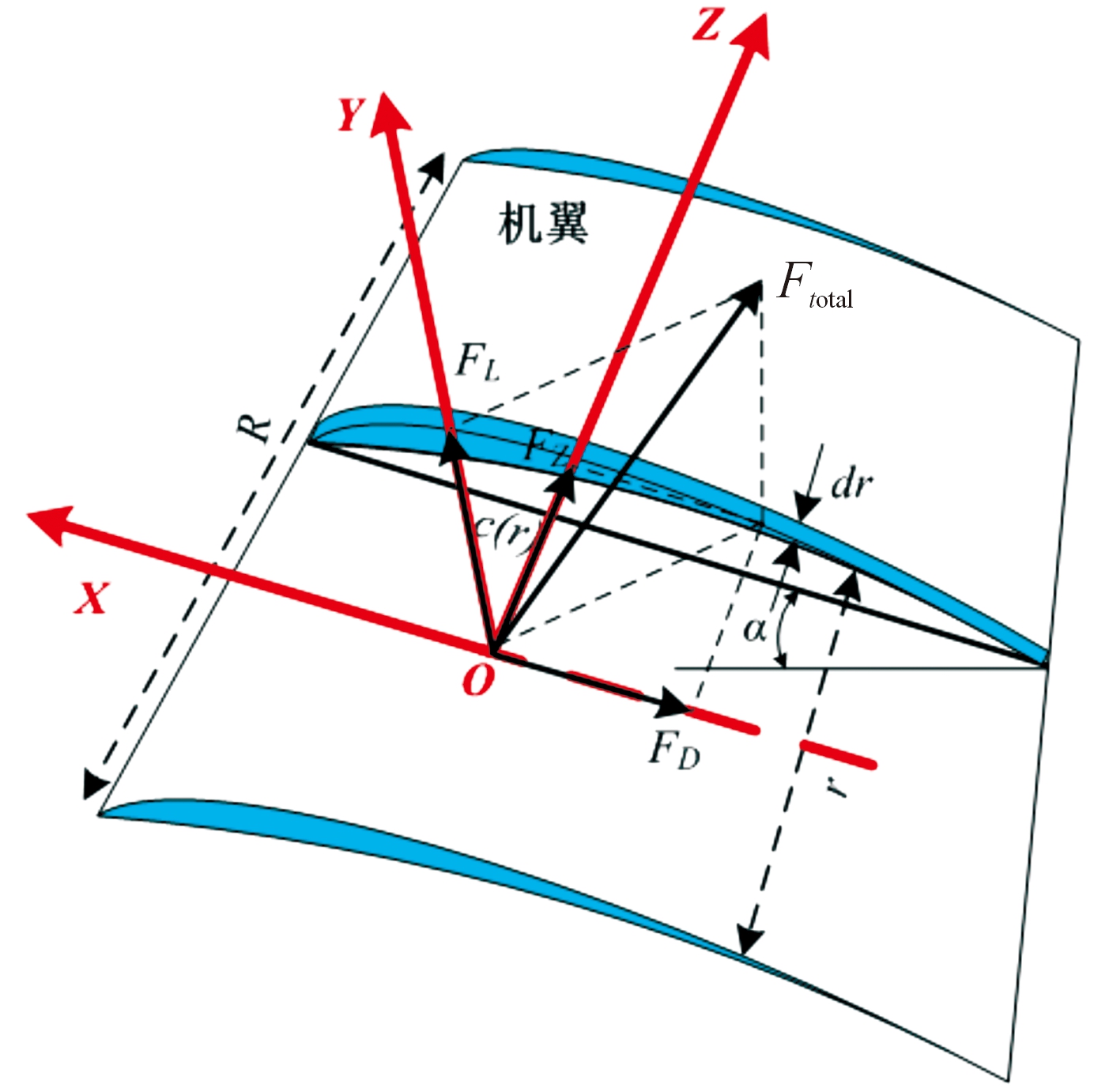
图6 扑翼气动力计算模型
同理可以得到扑翼扑动过程中的气动阻力FD、推力FT、功率PW、推进效率η等参量为:
(10)
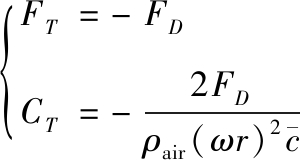
(11)
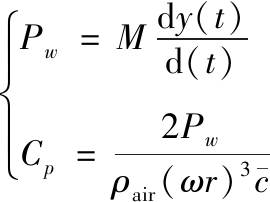
(12)
(13)
4 仿真结果和分析
4.1 扑翼气动力特性分析
数值仿真分析时,为提高求解计算精度,采用采用双时间步隐式迭代方法。计算采用压力速度耦合求解,由于扑翼运动时会由于翅翼扑动会产生推力作用的湍流,因此本文数值计算过程采用湍流模型中的切应力传输(SST k-ω)模型。
扑翼的气动力特性受多种因素的影响,拍动幅值、拍动频率、来流速度等参数均能够使得扑翼的气动性能产生改变。而本文在分析扑翼的气动力特性时主要考虑扑翼的非对称拍动对气动力产生的影响。因此,在数值仿真时,拍动幅值、拍动频率、空气来流速度、雷诺数均保持不变,分别设置为:ym=π/4,f=1/T=5 Hz,v=5 m/s,Re=2 500。
数值仿真残差曲线收敛后,不同拍动时间占比k=0.2、0.3、0.4、0.5时的瞬时升力、瞬时阻力与瞬时力矩随时间变化的曲线如图7所示。
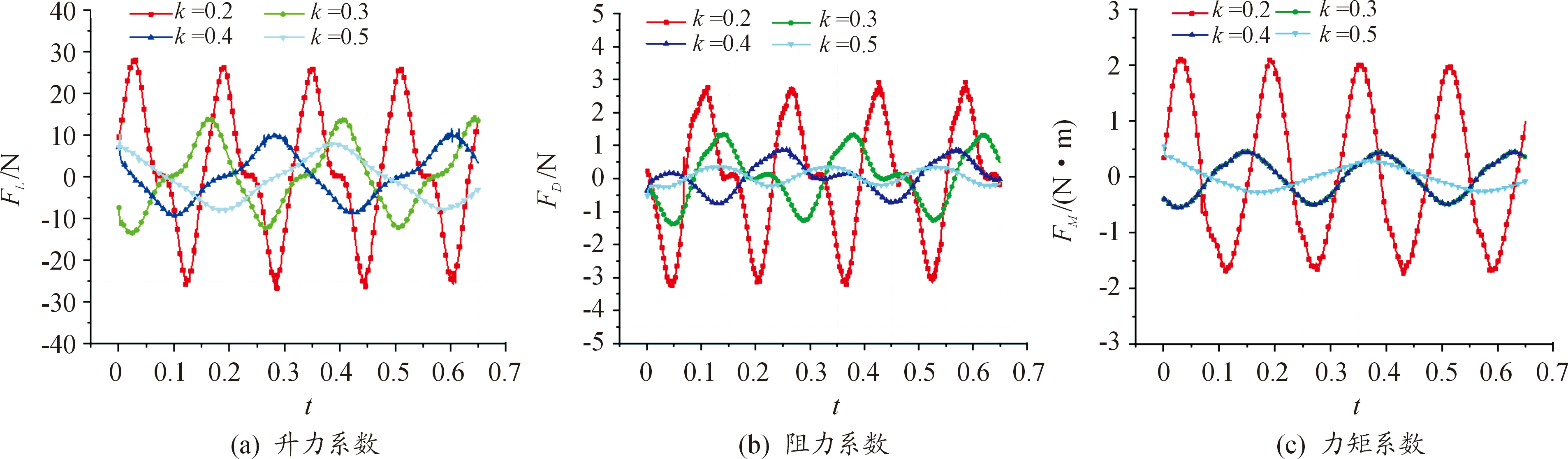
图7 不同k值时扑翼瞬时气动力特性
分析不同时间占比时扑翼的瞬时气动力变化曲线得知,随着机翼随着下扑速度的增快,机翼产生的升力越大。当k分别为0.2、0.3、0.4、0.5时,扑翼上下拍动产生的最大升力分别为28.15 N、14.67 N、11.64 N和10.07 N。下扑运动占整个扑动周期时间的20%,上扑占80%时,扑翼产生的升力较对称拍动时产生的升力增加了18.08 N。由此可以看出,通过提高扑翼的下拍速度,可以有效提高扑翼飞行过程中产生的瞬时升力。而分析阻力变化曲线可知,扑翼拍动过程中的阻力随着下扑速度的加快逐渐增大。当k=0.2、0.3、0.4、0.5时,扑翼拍动过程产生的瞬时阻力最大值分别达到了2.92 N、1.36 N、0.93 N和0.34 N。下拍速度的增大,使得扑翼拍动时产生的阻力也明显增大。k=0.2时(下拍速度最大)的最大阻力较k=0.5(对称拍动)时增大了2.58 N。因此,在设计扑翼上下拍动时间占比时,要充分考虑拍动时间占比所引起的升力与阻力的变化情况。
观察分析图6(c)中扑翼瞬时力矩变化曲线可知,当k=0.3和0.4时,扑翼产生的瞬时力矩基本相同,k=0.5时,扑翼产生的力矩与k=0.3和0.4时的力矩相差不大。而当机翼以较快的下拍速度时(k=0.2),机翼产生的力矩明显增大。由于机翼拍动时产生的力矩为绕机身轴线的力矩。过大的力矩会对扑翼飞行过程中的姿态稳定产生影响。因此,图6所示为扑翼拍动时产生是瞬时升力变化曲线,其代表的是扑翼在拍动过程中某时刻机翼瞬时气动力特性,为更加全面地分析扑翼在整个拍动运动周期的升阻变化情况,图8所示给出了扑翼不同k值时的平均升阻力及气动效率的变化曲线。
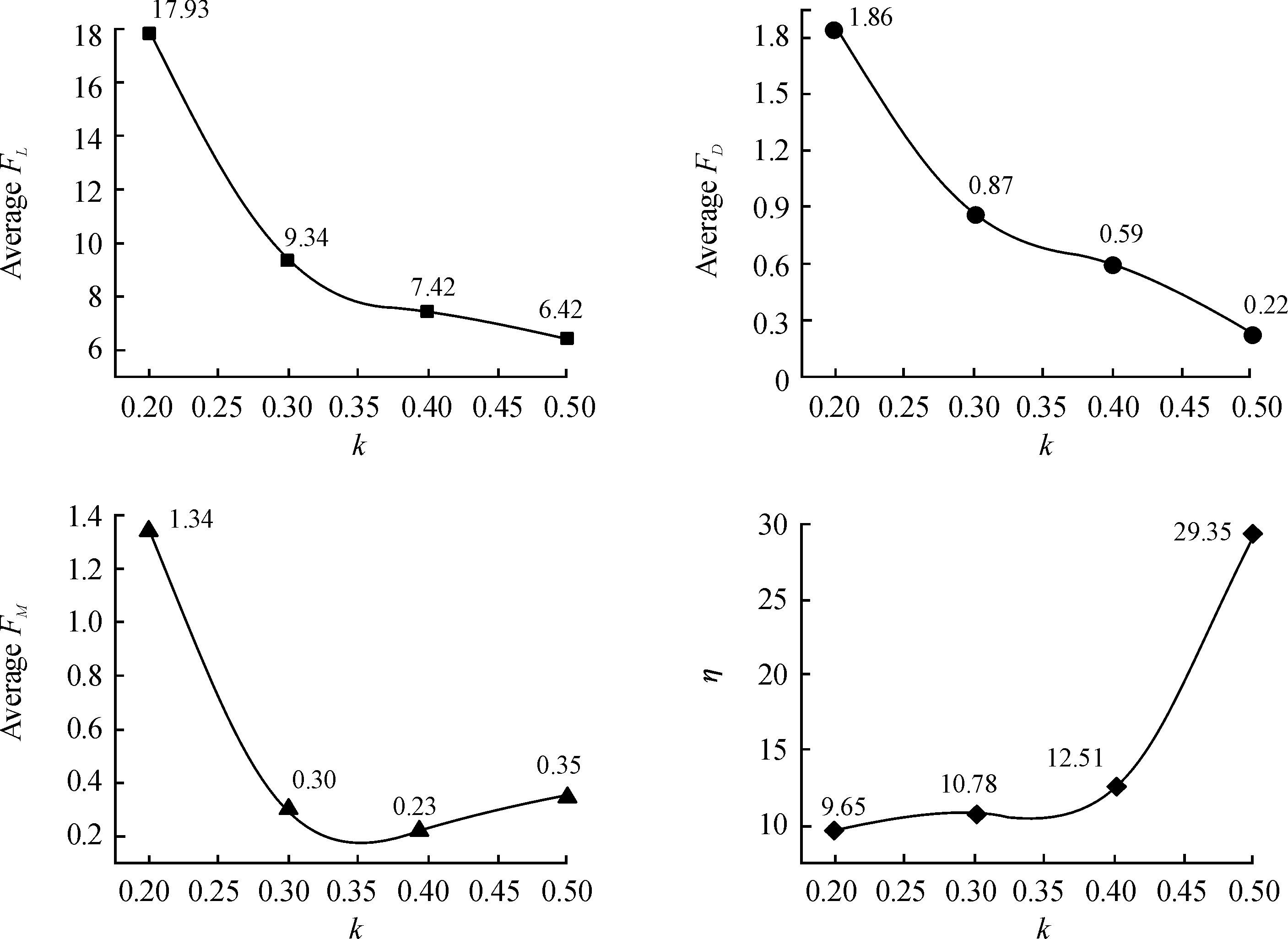
图8 不同k时扑翼平均气动力及气动效率变化曲线
由图8所示不同k时扑翼的平均升力变化曲线可以得知,扑翼拍动产生的平均升力与平均阻力随着k值的增大而逐渐减小。平均升力与平均阻力的变化与瞬时升力峰值的变化趋势相一致。而平均力矩随着k值的增大先减小后增大,当k=0.4时,扑翼产生的力矩最小。而分析不同k值时扑翼的气动效率变化曲线可知,扑翼的气动效率随着k值的增大而逐渐增大。当k=0.5时,扑翼的气动效率达到最大值,为29.35,这是由于当上下对称扑动时,扑翼拍动过程中的阻力减小,使得扑翼在整个拍动过程中的气动效率增大。k=0.2时扑翼产生的升力最大,但由于下扑速度过快,上拍速度较慢,导致上拍过程中的阻力增大很多,从而使得整体的气动效率下降。因此在设计扑翼飞行器是,要确定合理的上拍与下拍的时间占比,从而获得较大升力的同时保证具备较高的扑翼气动效率。
4.2 扑翼运动流场分析
根据上述分析,通过调整上下拍动的周期时间占比k值能够改变扑翼拍动过程中扑翼产生的升力及阻力特性,而在扑翼的非对拍动时,机翼附近的流场也时刻发生变化。如图9所示为不同时刻扑翼上拍与下拍过程中上下翼面的压力变化云图。
分析图9(a)所示的扑翼下拍过程翼面的压力变化。随着扑翼向下拍动,扑翼下方的压力逐渐增大,当扑翼拍动到中间位置时刻时,此时扑翼下拍的速度达到最大值,上下翼面的压差达到最大,气动力出现峰值。随着扑翼继续向下拍动,拍动速度逐渐减小,上下翼面的压差开始减小,当拍动到最低位置时刻时,上下翼面的压差最小。从下拍过程中上下翼面的压力变化中可以看出,下拍开始,齿根处开始出现前缘涡,随着扑翼不断向下拍动,前缘涡不断向翼尖处发展并不断变大,当拍动到最低位置时,涡旋从翼尖处脱落,从而产生向前的推力,从而推动扑翼向前飞行。图9(b)所示为扑翼上拍过程的压力变化与上拍过程中翼面的变化相反。上拍过程中上翼面的压力较大,下翼面出现负压力。上拍阶段产生的为负升力,上拍时间过长会导致上拍过程中的阻力增加较多。因此在调整扑翼上下拍动的时间占比时,要平衡快扑慢回动作时的升阻力变化,从而达到较高的气动效率。
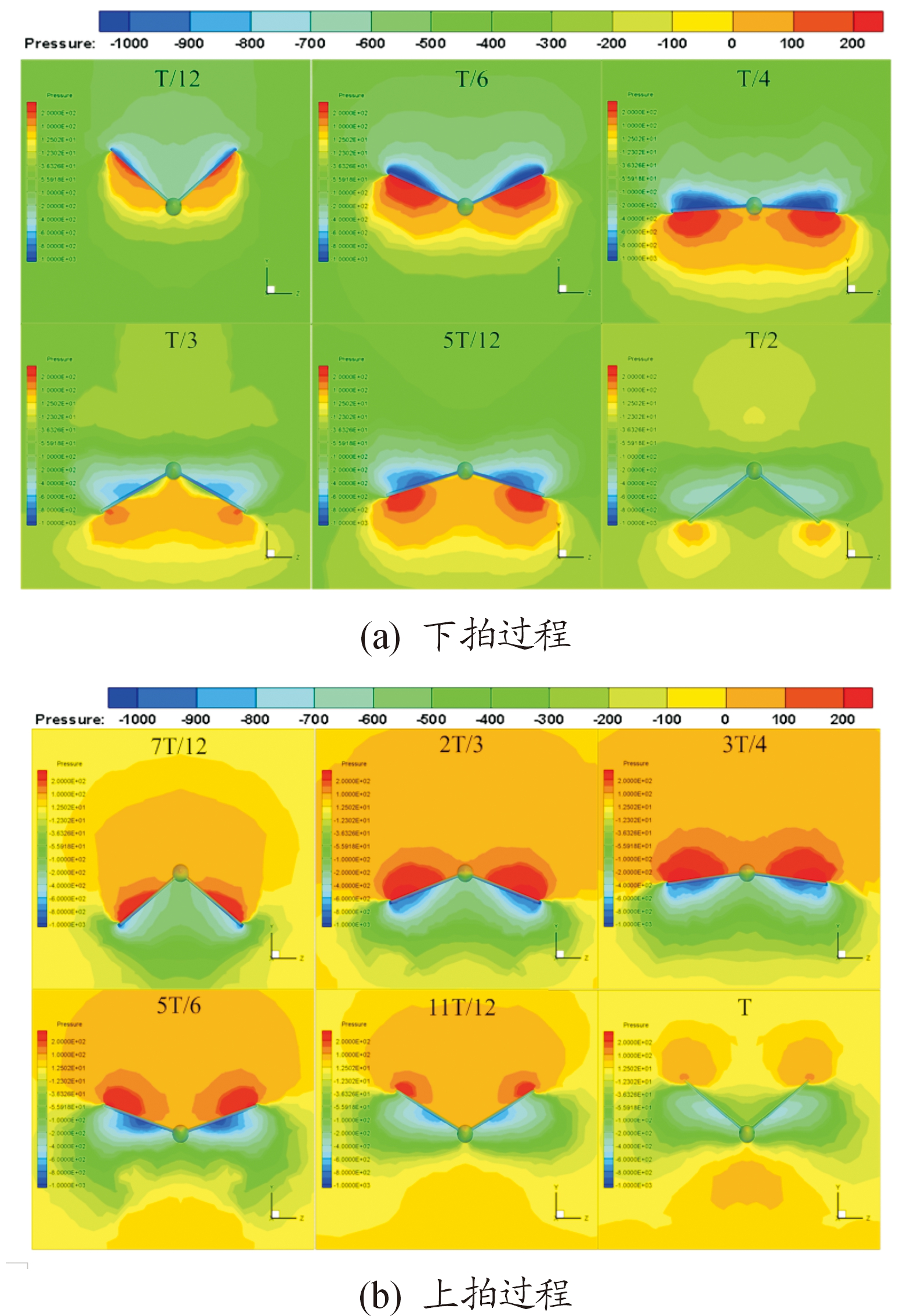
图9 一个拍动周期扑翼上下翼面压力变化过程
5 结论
本文根据鸟类翅膀的快扑慢回的运动规律,建立不同时间周期占比的扑翼拍动运动模型,采用动态混合网格技术,数值求解N-S方程,同时结合布西涅斯克假设,分析不同拍动时间周期占比时扑翼的气动特性的变化。通过数值仿真结果表明:扑翼下拍速度越快,扑翼拍动产生的升力越大,然然而下拍速度过快会使得拍动过程中产生的阻力也会随着增大,导致扑翼整体的气动效率下降。因此,在设计扑翼上拍与下拍的时间周期占比时,要充分考虑拍动周期占比对扑翼升阻力的影响,设计合理的时间周期占比,保证扑翼具备较大升力的同时,使得产生的阻力较小,从而使得扑翼飞行过程中具备较佳的气动效率。本文的数值仿真结果,能够为仿鸟型扑翼飞行器驱动机构设计提供理论参考。
[1] 朱建阳,蒋林,雷斌.三维仿生悬停扑翼的时间非对称扑动气动特性[J].航空动力学报,2017,32(4):858-864.
[2] 谢鹏,姜洪利,周超英.一种仿生扑翼飞行器的设计及动力学分析[J].航空动力学报,2018,33(3):703-710.
[3] 赵红燕,张鹏飞,宁建国.扑翼模型的气动力研究[J].北京理工大学学报,2014,34(增刊1):172-175.
[4] ZHU J Y,ZHOU C Y.Aerodynamic performance of a two-dimensional flapping wing in asymmetric stroke[J].Journal of Aerospace Engineering,2014,288(2):1-12.
[5] 杨文青,宋笔锋,宋文萍.高效确定重叠网格对应关系的距离减缩法及其应用[J].航空学报,2009,30(2):205-212.
[6] MURPHY J R,HU H.An experimental study of a bio-inspiredcorrugated airfoil for micro air vehicle applications[J].Experiments in Fluids,2010,49(2):531-546.
[7] TAKIZAWA K,HENICKE B,A Puntel,et al.Computer modeling techniques for flapping-wing aerodynamicsof a locust[J].Computers & Fluids,2013,85:125-134.
[8] 昂海松,曾锐,段文博,等.柔性扑翼微型飞行器升力和推力机理的风洞实验和飞行实验[J].航空动力学报,2007,22(11):1838-1845.
[9] ZHU L L,WU C J.Numerical simulation and control of the angle of pitch of self-propelled flying bird with flapping wings[J].SCIENTIA SINICA Physica,Mechanica & Astronomica,2016,46(6):1-13.
[10] 杨淑利,宋文萍,宋笔锋,等.微型扑翼飞行器机翼气动特性研究[J].西北工业大学学报,2006,24(6):768-773.
[11] 龚凯.有限翼展扑动翼的欧拉方程数值模拟[D].西安:西北工业大学,2003.
[12] SHYY W,AONO H,CHIMAKURTHI S K,et al.Recent progress in flapping wing aerodynamics and aeroelasticity[J].Progress in Aerospace Sciences,2010,46:284-327.
[13] 孙茂,刘彦鹏,王济康.昆虫悬停飞行的动稳定性:理论分析与数值模拟[J].空气动力学报,2008,26(21):6-13.
[14] 侯宇,方宗德,刘岚,等.仿生微扑翼飞行器机构动态分析与工程设计方法[J].航空学报,2005,26(2):173-178.
[15] WEIS-FOGH T.Quick Estimates of Flight Fitness in Hovering Animals,Including Novel Mechanisms for Lift Production[J].The Journal of experimental biology,1973,59(1):169-230.
[16] TUNCER I H,PLATZER M F.Computational study of flapping airfoil aerodynamics[J].Journal of Aircraft,2000,37(3):514-520.