随着新型推力矢量涡扇发动机、先进气动设计、双向数据链和隐身技术的应用,第四代战斗机和无人作战飞机等新一代航空武器相继出现,使得在未来战争中空空导弹将面临机动能力更强、逃逸方式更复杂、可探测性更差的攻击目标[1-2]。另一方面,随着技术发展,空空导弹的弹间组网技术逐渐具备了应用可能。近年来,多导弹协同攻击[3]以其特有的优势正在受到越来越多的关注。在进攻方面,多弹协同制导可以通过弹群协同,将多枚导弹融合成一个信息共享、功能互补、战术协同的作战群体,利用群体优势对敌防御体系和目标进行多层次、全方位的打击,实现攻击效能的整体提升[4-5]。
本文利用多导弹协同攻击体系,根据双弹协同角度定位结果,构造距离伪量测信息,将测量方程进行扩维,以改善纯角度跟踪系统中目标估计精度,最终实现减小脱靶量的目的。
1 多弹协同体系中被动跟踪系统设计
被动雷达在跟踪机制上属于纯方位跟踪,仅对目标的方位进行测量,不能测距,目标运动状态方程和观测方程不可能都是线性的,使得传统的线性滤波方法不适用于被动雷达目标跟踪问题[6-8]。其次,被动雷达目标跟踪是从含有观测噪声的角度测量序列中估计目标的运动状态参数(包括位置、速度和加速度等),经研究证明,仅利用测角信息对目标进行无源被动定位,有效估计出目标的运动状态参数,这有较为苛刻的可观测性条件限制,在单观测平台对运动目标定位时,要求观测平台做特殊的机动运动,并且机动运动的航路直接影响着目标运动要素的收敛速度和精度。这一苛刻的可观测性条件同样限制了被动雷达目标跟踪的工程化应用。
多弹协同体系中可充分发挥多枚被动导弹的多角度观测优势,利用角度信息进行协同定位,得到目标状态信息[9]。测向定位法的基本原理是利用多部接收雷达测得的方位信息或一个运动的接收雷达在不同时间测得的多条方位信息交叉对目标定位[10-11]。二维平面空间的测向定位法,如图1 所示。两部雷达对回波信号进行检测与信号处理,可分别得到目标相对于测量点的方位角。雷达测得方位角后,可知目标的实际位置在以本雷达为起点,以方位角为方向角的射线上。两部雷达同时测量时,目标的位置处于两条射线的交点上,由此即完成对目标定位[12-17]。
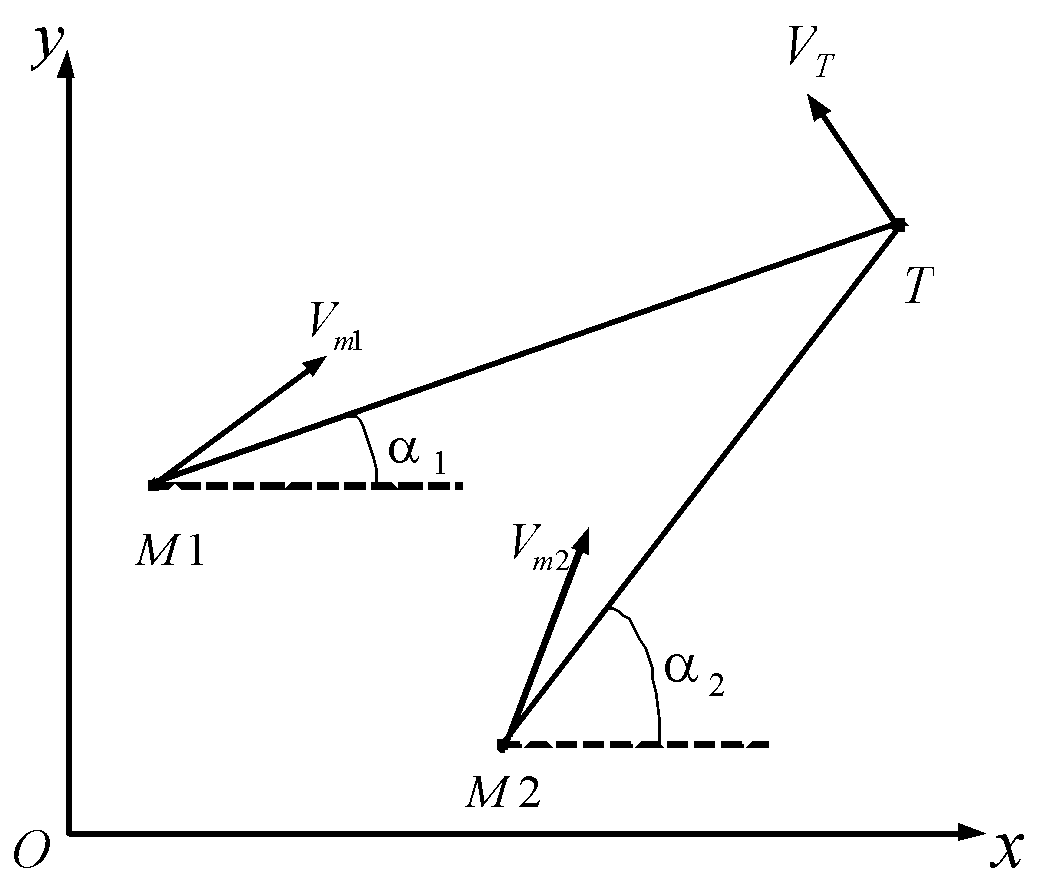
图1 测向定位法原理示意图
通常被动跟踪中,观测量为方位角、俯仰角,根据协同测向定位得到弹目相对距离后,可将此作为伪观测量引入测量方程。测量方程扩维后再进行滤波处理,得到可供制导使用的目标信息。系统原理如图2所示。
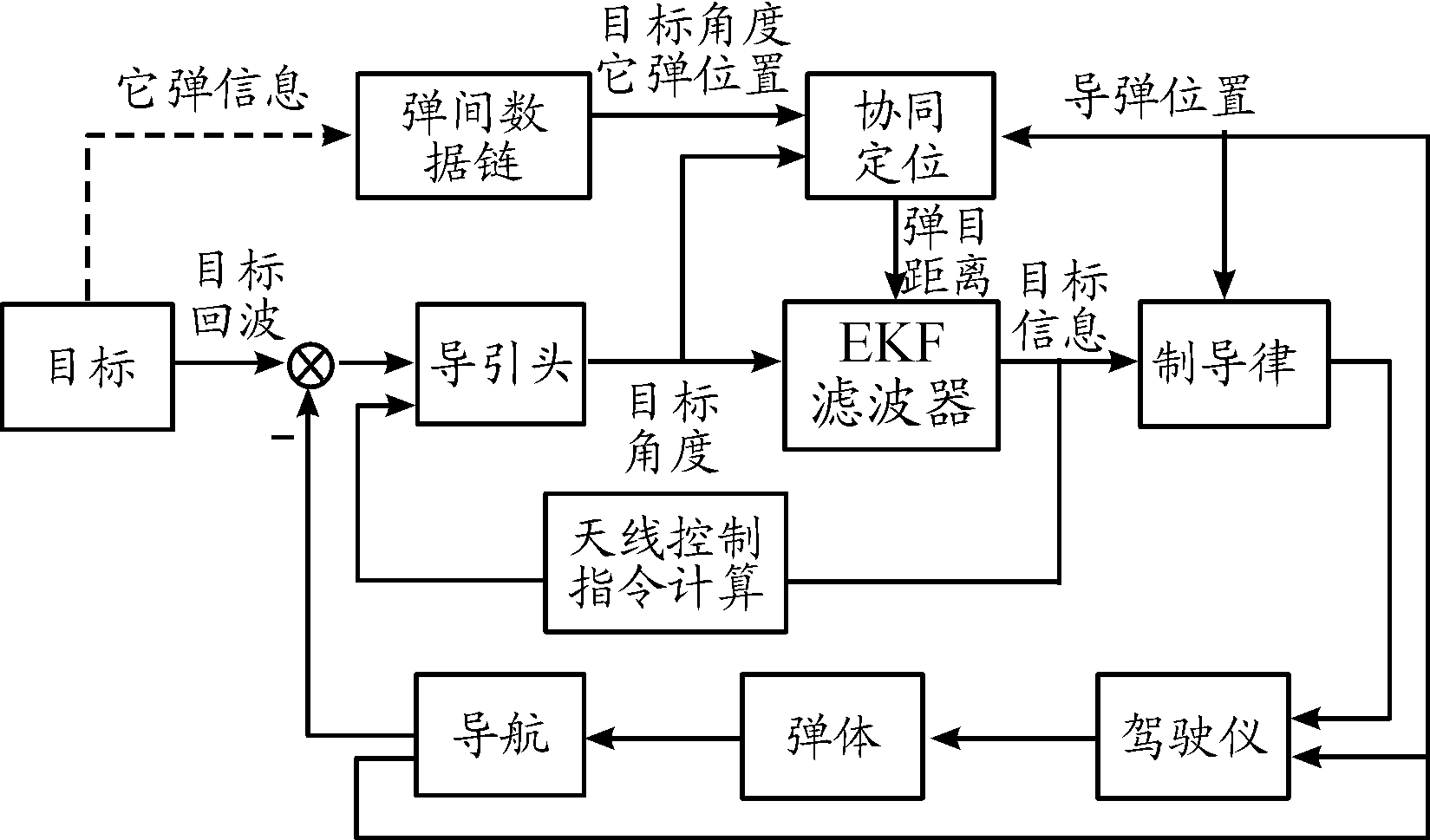
图2 基于协同定位的被动跟踪系统原理框图
2 基于多弹协同定位的目标估计算法
2.1 协同定位算法
两枚导弹进行协同定位时,不考虑各种误差的理想情况下,目标位于两条视线交点处。然而,由于导航误差、测量误差等影响,实际系统中两条视线不会相交。那么在该情况下,认为目标点是相距两条方位线最近的点,因此本文设计的协同定位算法思想为:实际目标点到两条方位线二阶距的和最小。
设空间两条视线(方位线)的方程为A和B,其形式分别表示为:
式(1)、(2)中:[xM1 yM1zM1]T和[xM2 yM2zM2]T是惯性空间中两枚导弹的位置:分别记为XA和XB,[α1β1γ1]T和[α2β2γ2]T是两枚导弹测量的视线方向余弦。
目标点是同时对方程A和B二阶距之和最小的点,即:
(3)
由于点到直线的二阶距即为点到直线距离的模的平方,因此交叉定位算法又可以描述为:确定目标点X=[xTyTzT]T,使式(4)最小,即:
(5)
式(4)中,d1和d2是空间中某点到A、B两条直线的距离。即:
min[f(x,y,z)]|(xT ,yT ,zT )
(5)
根据点到直线的距离公式,有:
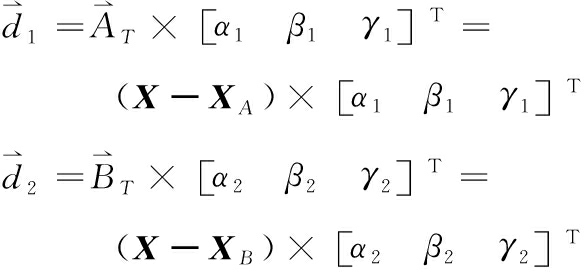
(6)
将式(6)写成反对称阵的形式,有:
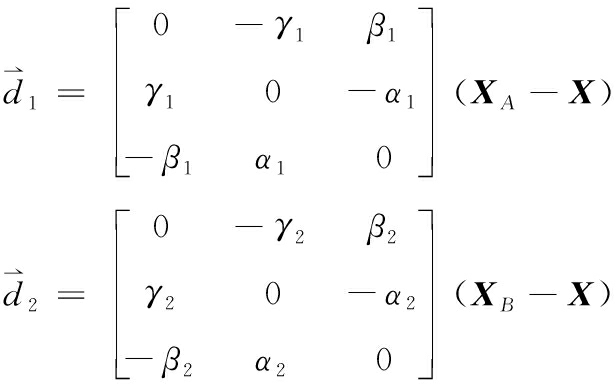
(7)
记:
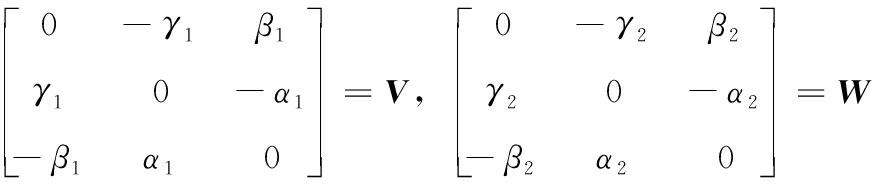
有:
f(X)=![]()
(8)
求使 f (X) 极小的点,解方程![]() 可求得:
可求得:
X=(VTV+WTW)-1VTVXA+
(VTV+WTW)-1WTWXB
(9)
式(9)即为协同定位算法确定的目标点坐标。有了协同定位的目标点坐标,即可得到每一枚导弹的弹目距离信息估值,将此信息作为伪量测信息进行目标状态估计。
2.2 目标估计算法
2.2.1 目标运动模型
机动目标模型是通过数学描述目标真实运动,是目标跟踪的重要要素之一,目标运动描述越准确反应目标的实际运动,对目标状态估计效果越好。描述目标运动常用的模型有CV模型,CA模型,Singer模型,机动目标“当前”统计模型等。
机动目标“当前”统计模型是一种采用零均值和修正瑞利分布表征机动加速度特性的时间相关模型,在具体的场景下,该模型仅需考虑目标在当前条件下的机动可能性,即机动加速度的当前概率密度,这样机动加速度的取值范围大大减小。大量实验表明,该算法在跟踪机动目标时具有良好的跟踪结果[18]。
可以描述如下:
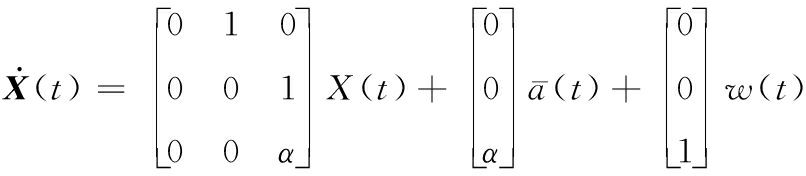
(10)
对应的离散时间形式为:
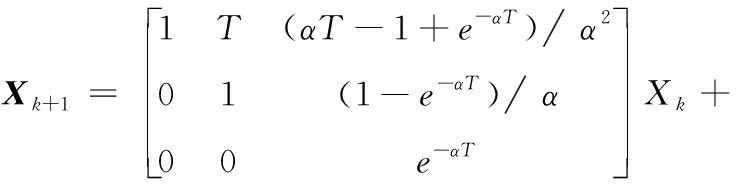
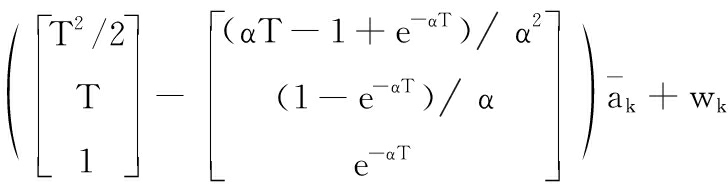
(11)
2.2.2 混合量测模型
导引头一般在球坐标系下测量目标信息,而状态方程一般在直角坐标系下建立。因此卡尔曼滤波的状态方程和量测方程势必存在一定的耦合,需要对量测方程进行线性化,得到线性卡尔曼滤波器,便于工程应用。根据导引头测量的失调角、框架角和导弹姿态,求取导引头测量视线相对于惯性空间的高低角和方位角。并根据多弹协同定位结果得到弹目距离信息估值作为伪量测信息,建立混合量测方程。
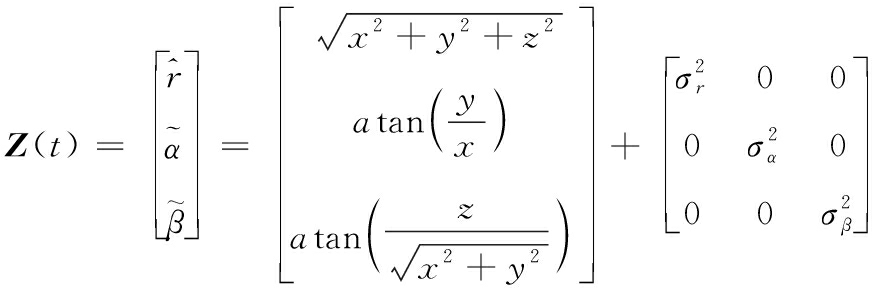
(12)
式(12)中:![]() 和
和![]() 为方位角和高低角量测噪声,为零均值白噪声;
为方位角和高低角量测噪声,为零均值白噪声;![]() 为伪距离量测噪声。
为伪距离量测噪声。
协同定位获得的目标位置误差受两部分误差影响,一是导引头测量的角噪声,另一部分是导航系统产生的位置误差。当这两种误差满足正态分布并相互独立,则测量方差满足叠加关系。根据数据融合理论,伪距离量测噪声可写为:
![]()
(13)
式(13)中:![]() 和
和![]() 是两枚导弹的导引头测量方差,为零均值白噪声;
是两枚导弹的导引头测量方差,为零均值白噪声;![]() 和
和![]() 是两枚导弹弹目距离估值。
是两枚导弹弹目距离估值。
所建立的卡尔曼量测方程为非线性方程,对量测方程在k时刻进行线性化,得到:
Zk=![]() ·ΔXk
·ΔXk
(14)
展开得:
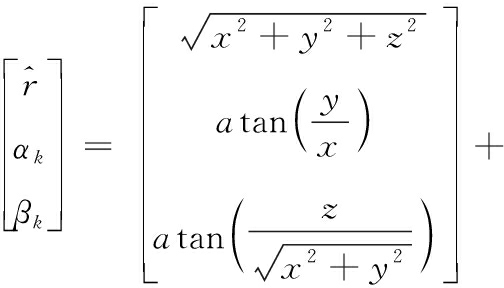
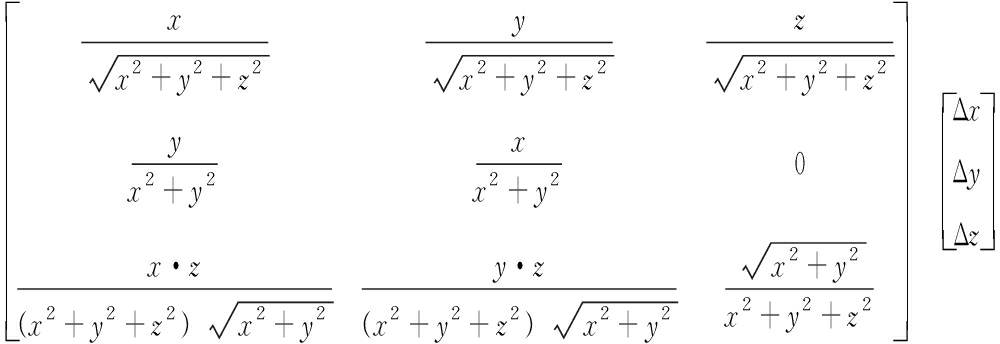
(15)
2.2.3 滤波算法
系统的状态方程是线性的,不存在线性误差。但是测量方程是非线性的,因此采用扩展卡尔曼滤波进行目标状态估计。基本卡尔曼滤波实现原理如图3所示。
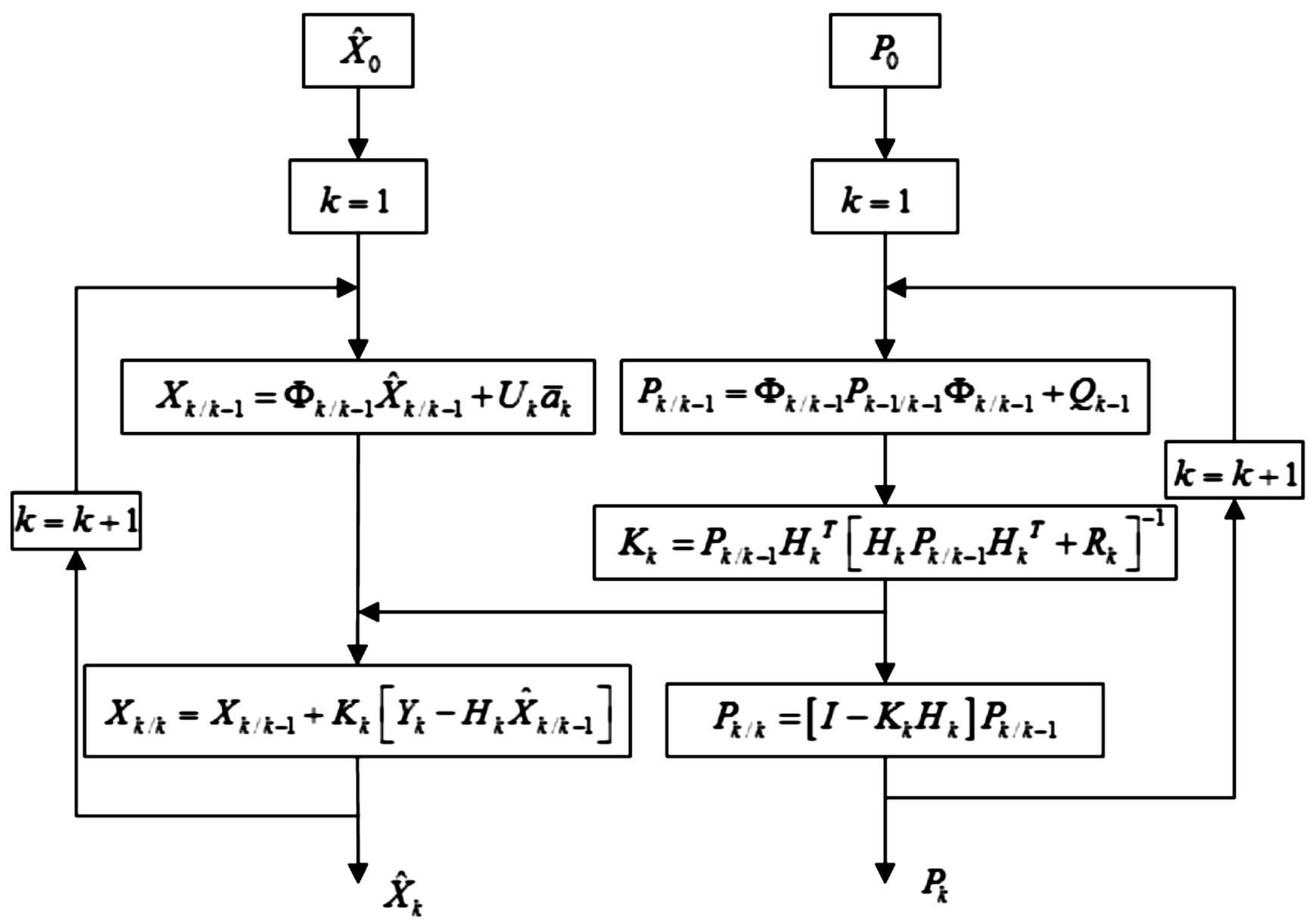
图3 卡尔曼滤波实现原理框图
3 仿真分析
在Matlab中建立跟踪系统模型,对该算法进行仿真分析。导引头测量特性设置为:方位角和高低角观测噪声均方误差分别为σα=0.2°和σβ=0.2°。
仿真基本条件如下:导弹M1与目标距离15 km,目标迎头进入速度300 m/s,10 s时开始以3g水平过载做S机动;导弹M2视线在空间保持与导弹M1视线夹角30°,并将其观测信息实时传送至导弹M1。导弹M1的状态估计误差如图4~图7所示。
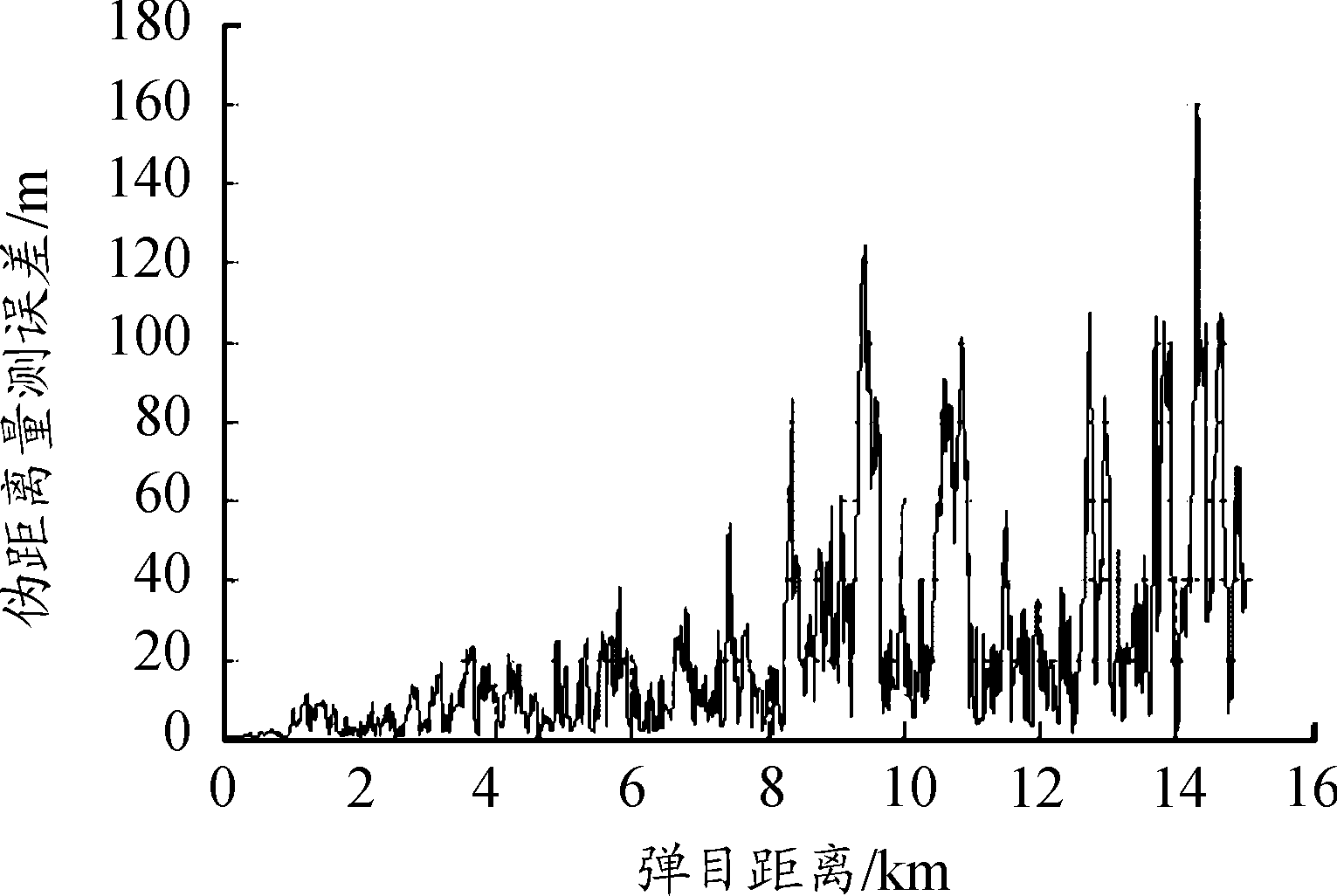
图4 伪量测量弹目距离估计误差曲线
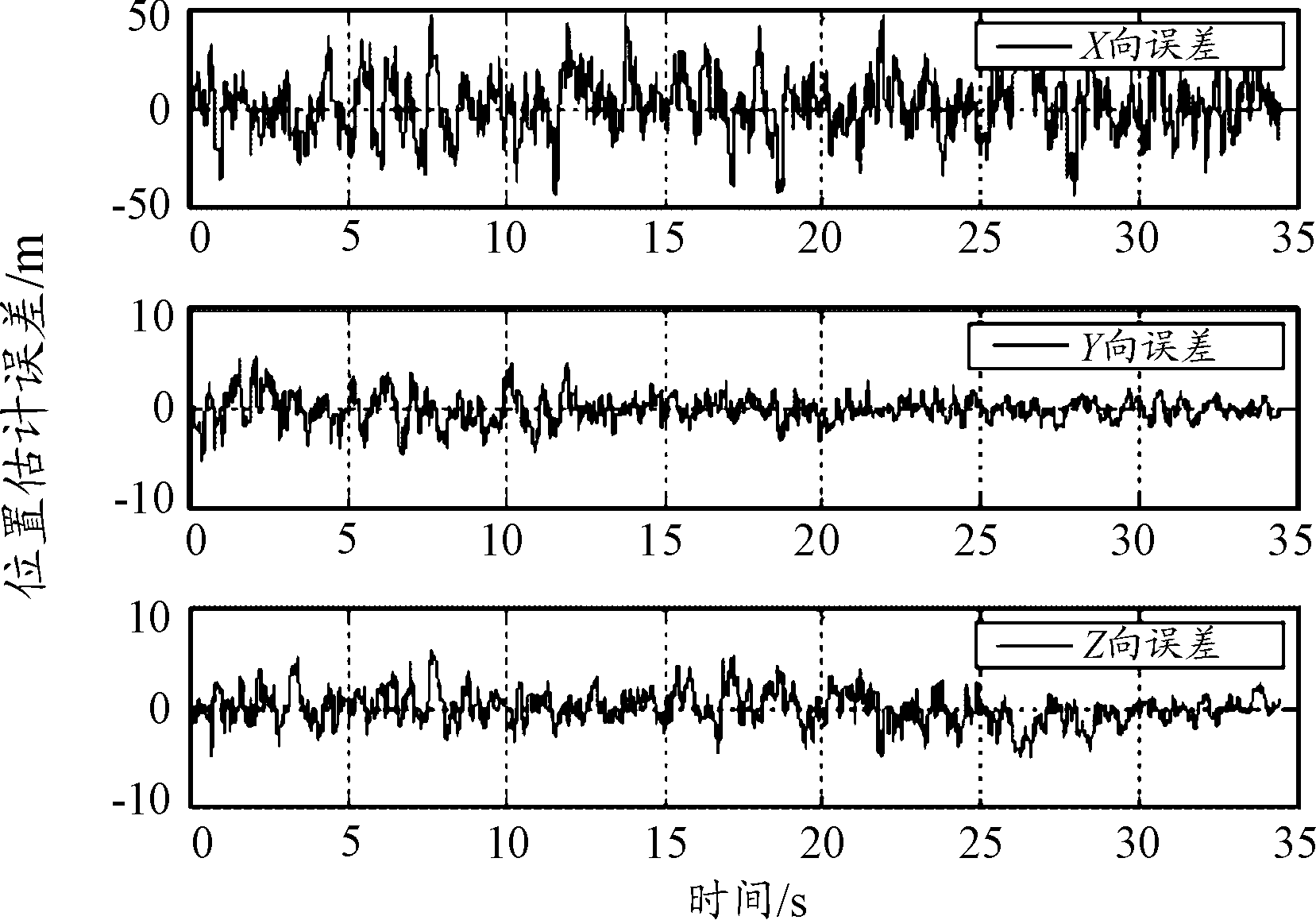
图5 目标位置估计误差曲线
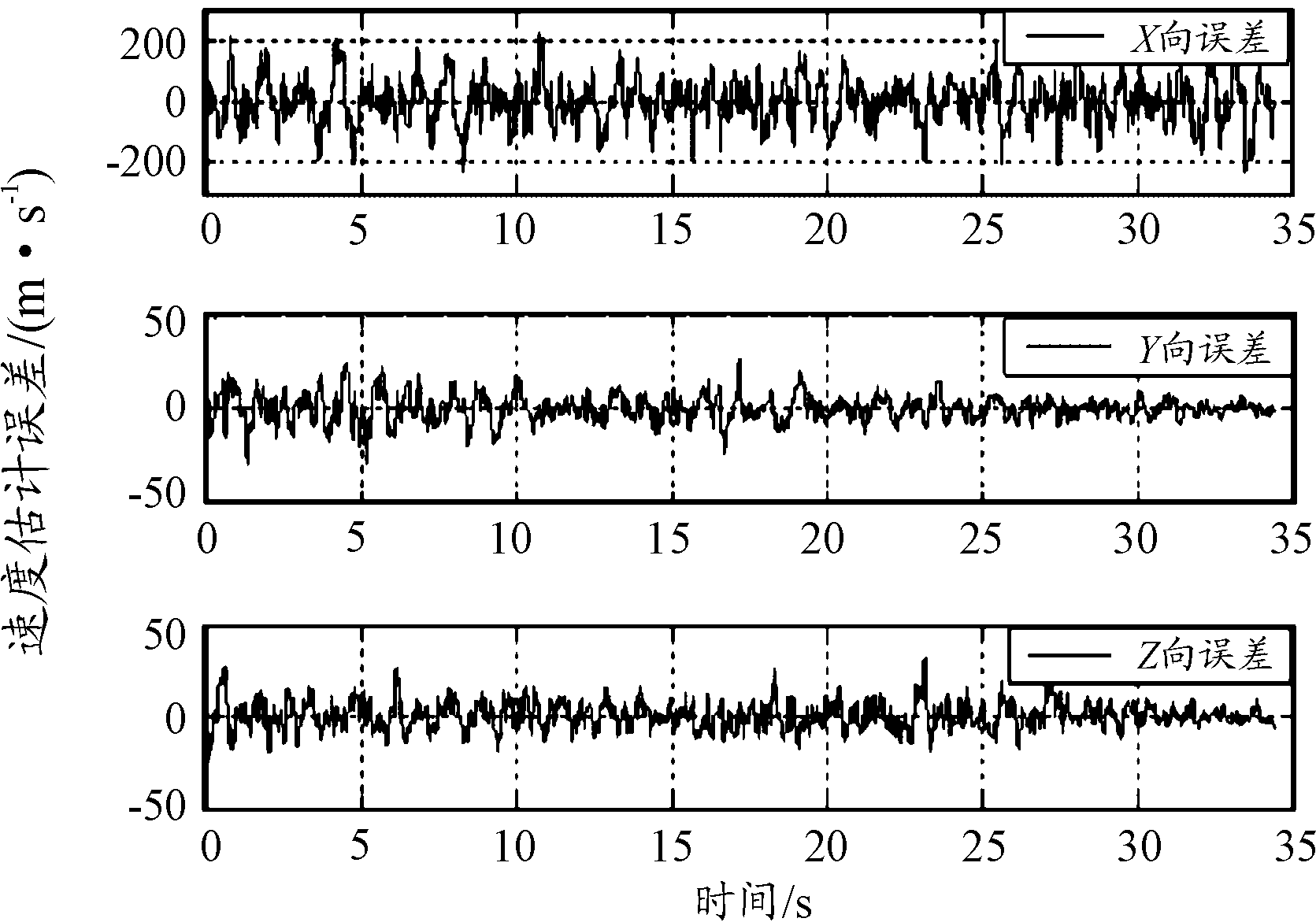
图6 目标速度估计误差曲线
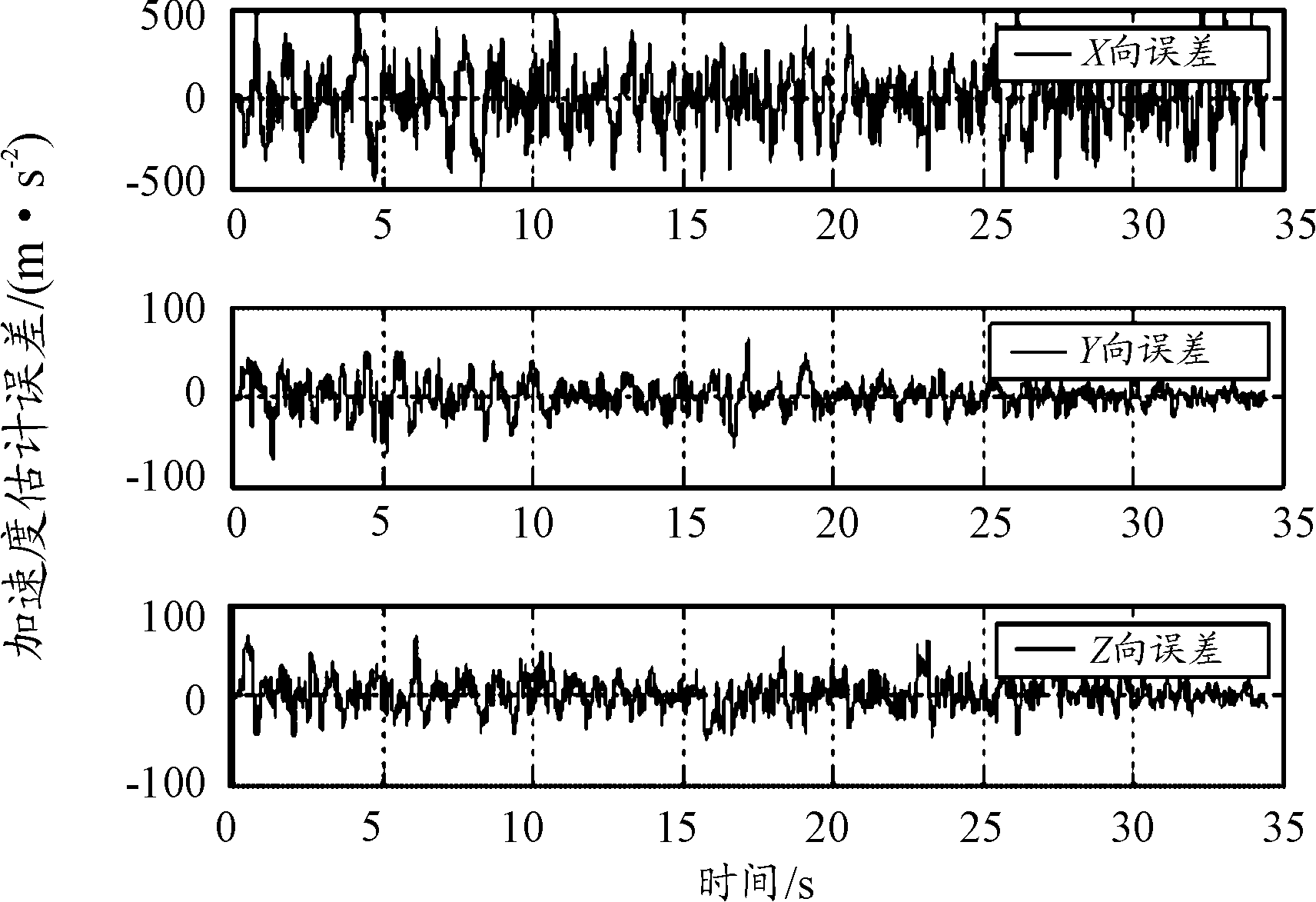
图7 目标加速度估计误差曲线
通过仿真结果可见,双弹目标定位误差随弹目距离接近不断减小,8 km内距离误差已收敛至50 m以内。将双弹协同定位的结果作为伪量测信息得到的目标状态估计结果精度较高。X方向为目标接近方向,目标状态估值误差主要反映了伪量测信息的误差。
4 结论
本文考虑了分布式协同体系中信息资源优势,利用多弹协同对目标进行定位,并作为伪量测信息引入目标跟踪滤波器中。通过理论分析与数字仿真验证,证明了该方法的有效性。本文提出的技术方法可应用于多红外或被动雷达导引头协同探测系统中,也可应用于雷达型导弹距离测量受干扰时的制导信息估计算法。后续将进一步考虑协同体系中影响协同定位的因素以及不同伪量测信息精度下滤波器设计问题。
[1] 候冰,张金鹏,曹有亮,等.抗目标大机动的制导指令校正算法研究[J].航空兵器,2018(02):29-33.
[2] 樊会涛.第五代空空导弹的特点及关键技术[J].航空科学技术,2011(03):1-5.
[3] 樊会涛,闫俊.自主化——机载导弹重要的发展方向[J].航空兵器,2019,26(01):1-10.
[4] 赵建博,杨树兴.多导弹协同制导研究综述[J].航空学报,2017,38(01):17-29.
[5] 王芳,涂震飚,魏佳宁.战术导弹协同突防关键技术研究[J].战术导弹技术,2013(03):13-17.
[6] ZHAO Y B,SHUI P L,LIU H W.Computationally Efficient DOA Estimation for MIMO Radar[C]//Proc.of the 2009 2nd International Congress on Image and Signal Processing.IEEE,2009:1-3.
[7] 王艳苹,张志斌,陈娟,等.MIMO雷达DOA估计方法分析[J].电子科技,2010,23(03):76-80.
[8] GAO X,ZHANG X F,FENG G P,et al.On the MUSIC-derived approaches of angle estimation for bistatic MIMO radar[C]//Proc.of the Wireless Networks and Information Systems,2009.WNIS’09.International Conference on.IEEE,2009:343-346.
[9] 李兴民,李国君,李健,等.双站交叉定位雷达布站方法研究[J].雷达科学与技术,2011,9(05):405-408.
[10] 曲付勇,孟祥伟.基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J].电子与信息学报,2014,36(05):1075-1081.
[11] 钟建林,刘方,石章松,等.基于测向交叉定位的空舰导弹协同攻击方法[J].航空兵器,2019,26(04):47-53.
[12] 邱硕丰,刘军.无源双站交叉定位误差分析[J].舰船电子对抗,2018,41(05):22-26.
[13] 田晗.多站测向交叉定位中的非线性改进最小二乘法[J].科技通报,2018,34(05):112-116.
[14] 黄雪梅.基于分段线性KF的测向交叉定位算法[J].现代防御技术,2017,45(01):113-118.
[15] 盛丹,王国宏,孙殿星.存在系统误差下交叉定位系统最优交会角研究[J].系统工程与电子技术,2016,38(07):1516-1523.
[16] 程翔,单忠伟.基于运动单站的多观测点交叉角无源定位技术[J].现代电子技术,2015,38(18):13-15,18.
[17] 沈晓峰,徐保根,邹继锋,等.基于正性约束的测向交叉定位方法[J].电子科技大学学报,2014 (06):834-837.
[18] 马慧敏,何金刚,胡士强.一种用于仅有位置观测信息的机动目标跟踪滤波算法[J].弹箭与制导学报,2011(03):63-66.