靶弹飞行性能的好坏直接影响防空导弹的校验。靶弹可用来模拟超音速导弹类、飞机类目标,其本身还要成本低、操作使用简单、性能可靠,且能够模拟俯冲、平飞等超音速目标的飞行弹道[1-3]。靶弹可通过专门研制、导弹改造和火箭弹改装等3种途径获得[4-5]。专门研制和利用导弹改装的研制周期长、成本高,不利于大量部署;利用技术成熟的无控大射程尾翼稳定式火箭弹改装成超音速靶弹省时省力[6]。由于无控火箭弹的弹道为抛物线,无法模拟滞空时间长、平飞类目标的运动特性。因此,在无控大射程火箭弹的基础上加装控制机构和执行机构,使其成为有控火箭靶弹,延长滞空时间。修正执行机构主要有微型脉冲发动机、空气动力舵和燃气射流控制发动机三种形式,前一种执行机构脉冲矢量大小有限,无法连续修正,喷流推力会产生偏心问题,不能实现靶弹的准平飞弹道;利用空气动力舵可进行连续控制,在滑翔增程弹箭中已大量应用。本文采用空气动力舵这种修正执行机构对无控火箭靶弹进行改装。
有控火箭靶弹通过不同的舵面控制方式,使舵面偏转产生控制升力和控制力矩,以抵消重力的影响,改善飞行弹道特性,实现滑翔飞行,在一段时间内提供近似水平的飞行弹道,甚至是平飞弹道[7-9]。
1 供靶弹道[10-12]
有控火箭靶弹采用不同的舵面控制方式,可得到平飞、准平飞和滑翔飞行等3种形式的弹道曲线(如图1所示),以满足超音速目标的供靶需求。
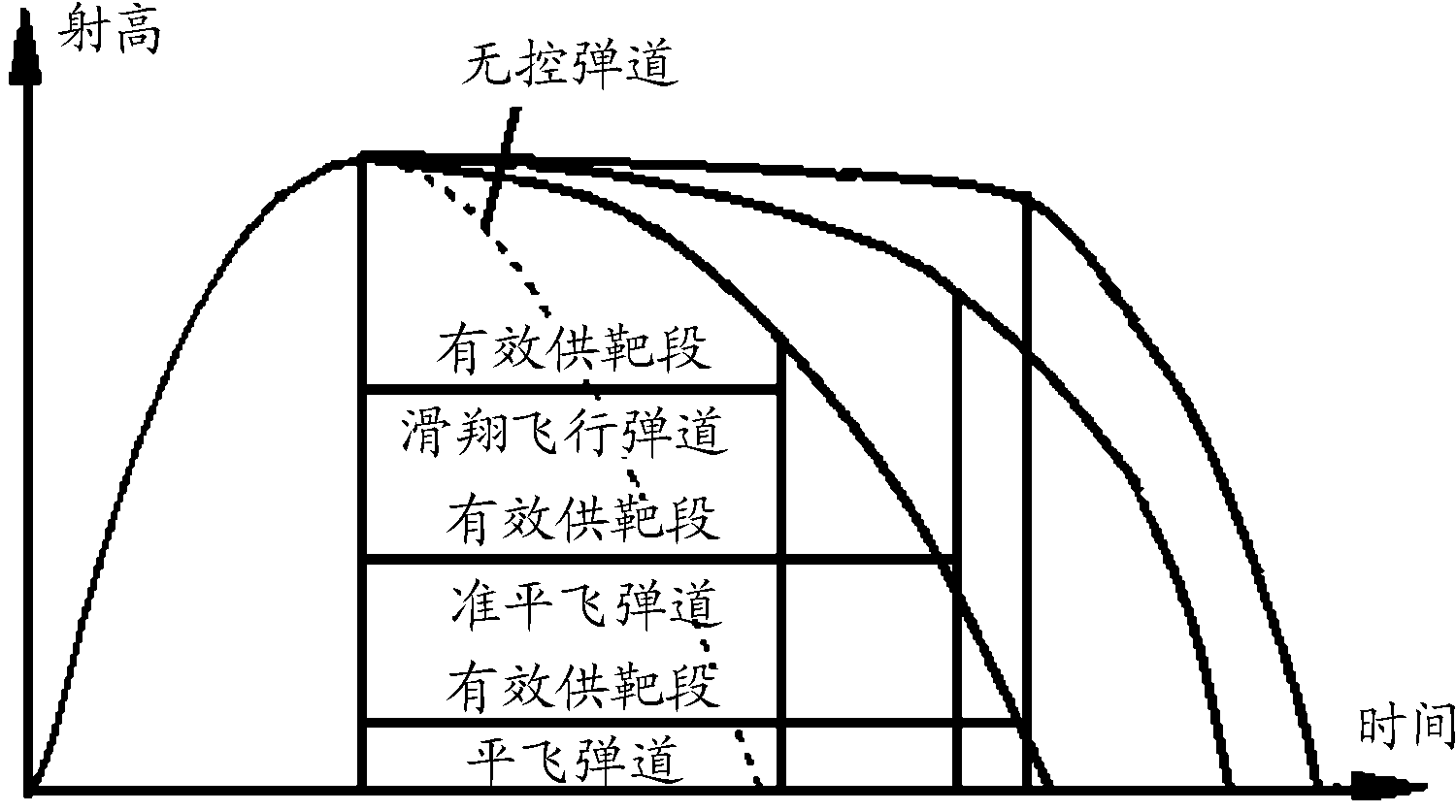
图1 供靶弹道曲线
控制机构的作用过程可分为4个阶段:发射前准备、起飞无控段、上升稳定控制段和滑翔飞行段。
2 舵面控制方式
有控火箭靶弹基于无控尾翼式火箭弹进行改装,增加差动×型控制舵和姿态控制系统,控制舵实现靶弹的俯仰、滚转和偏航姿态稳定控制,姿态控制系统通过惯性测量组件——3个方向的速率陀螺和加速度计,测量弹体姿态,形成姿态控制信号,并控制舵面偏转,产生控制力和控制力矩,控制弹体姿态,使靶弹沿预定弹道稳定飞行。
要得到不同的供靶飞行弹道,可采用以下几种舵面偏转控制方式[13-14]:固定舵偏角控制、变舵偏角控制和直线滑翔飞行控制。
1) 固定舵偏角控制
固定舵偏角控制方式是最简单的,在弹箭飞行过程中的某时刻,舵面偏转为固定角度,从滑翔飞行一直到弹道终点将不再进行变化。若设计固定舵偏角合理,能够基本实现预期滑翔飞行目的。
2) 变舵偏角控制
采用固定舵偏角控制方式时,火箭靶弹在高空中飞行(海拔高度10 km以上时),空气密度小,鸭舵为提供足够的平衡升力(舵面产生的升力随空气密度的减小而减小),舵偏角相对较大,但到了低空飞行时,空气密度骤然增加,导致升力增加的同时火箭靶弹所受的阻力也急剧增大,使火箭靶弹的速度衰减加快、高度降低也变快,甚至会出现火箭靶弹被拉起的情况,这些都不利于火箭靶弹供靶弹道的实现[15][16]。设计时可考虑舵偏角在整个飞行过程中进行有限次的舵面偏转控制,将升力变化控制在一定范围之内,以适应不同环境的要求。
3) 直线滑翔飞行控制
若使滑翔飞行段的法向加速度为0,即dθ/dt=0,则弹道倾角θ将保持不变,火箭靶弹沿直线轨迹飞行,即直线滑翔飞行。在直线滑翔飞行弹道中,升力由攻角产生的升力和舵偏角产生的升力两部分组成,与攻角和舵偏角有关,同时与空气密度及飞行速度也有关。舵面产生的升力对靶弹重心形成的力矩
直线滑翔下的平衡攻角α和舵偏角δ的表达式如式(1)、式(2)所示。
(1)
![]()
(2)
式中:m为质量; g为重力加速度; ρ为空气密度; Sm为火箭靶弹最大横截面积;![]() 为控制舵升力系数导数;
为控制舵升力系数导数;![]() 为火箭靶弹升力系数导数; Lδ为控制舵压心到全弹质心的距离; Lα为全弹压心到质心的距离。
为火箭靶弹升力系数导数; Lδ为控制舵压心到全弹质心的距离; Lα为全弹压心到质心的距离。
4) 控制方式对比
固定舵偏角方式结构简单、易于实现,但在低空飞行时的阻力较大,速度和高度衰减较快,不利于供靶弹道的实现;变舵偏角控制方式是在固定舵偏角方式基础上的改进,在高空时俯仰舵偏角较大,低空时较小,这既保证高空时能够提供足够的升力,又能使弹丸在低空时速度衰减相对较慢,从而提高舵控效率,这种控制方案的成本相对也比较低。直线滑翔飞行控制方式能够得到平飞效果很好的平飞弹道,但需要实时调整舵偏角,以使火箭靶弹的升力与重力分量在竖直平面内平衡,这对火箭靶弹的弹载探测系统、实时弹道解算系统和控制执行系统的精度、灵敏性要求高,整个系统复杂且成本高。
针对变舵偏角控制方式和直线滑翔飞行控制方式进行外弹道仿真计算,可实现满足目标运动特性指标的供靶弹道。
3 弹道仿真分析
3.1 变舵偏角控制弹道仿真
射角不同,弹道高度和到达弹道顶点的时间也不同,所以火箭靶弹舵面偏转时间点也就不同。以30°射角为例,仿真起始舵偏角分别为0°、4°、8°和12°时的弹道,舵面偏转起控时间在弹道顶点处。射高曲线和速度曲线的仿真结果如图2、图3所示。
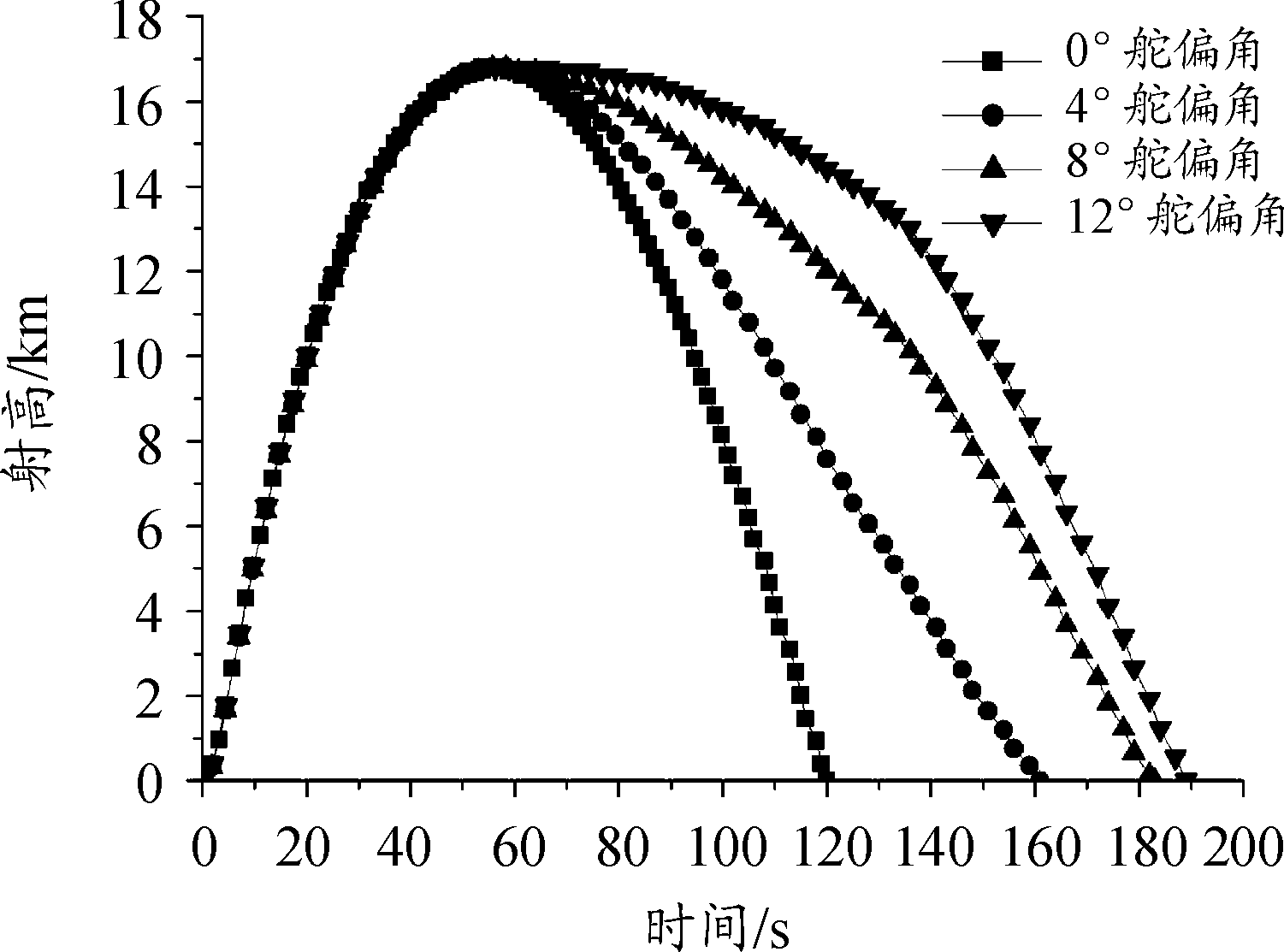
图2 射高曲线
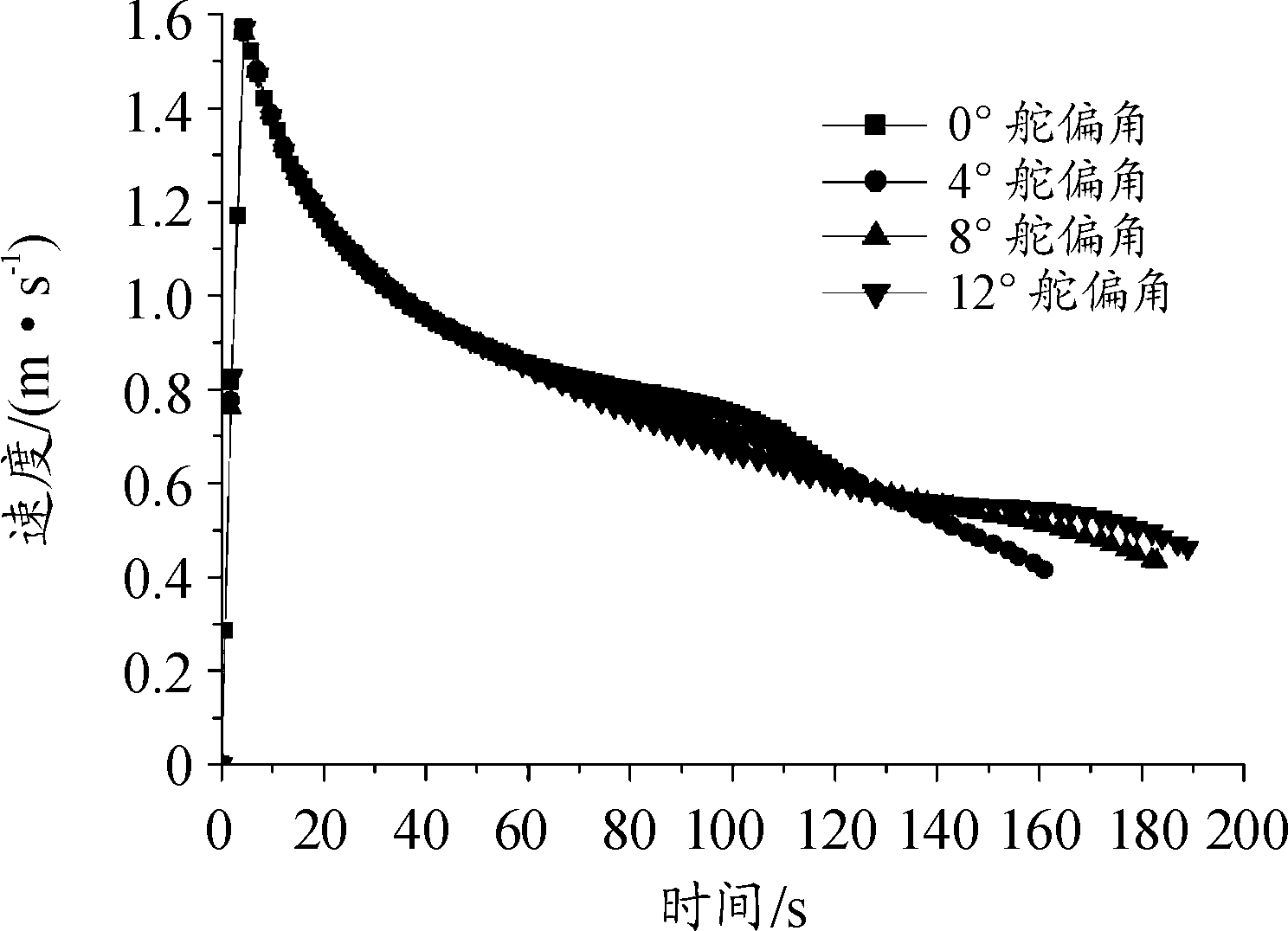
图3 速度曲线
由弹道曲线可知:相比于无舵偏角火箭靶弹的抛物线弹道,变舵偏角控制方式通过有限次调整舵偏角大小和控制时间,可以得到滑翔飞行弹道。
火箭靶弹的射程和飞行时间随舵偏角的增大而增大,滑翔飞行效果越明显。因此,只对12°舵偏角时的弹道进行分析,其供靶方案曲线如图4所示。
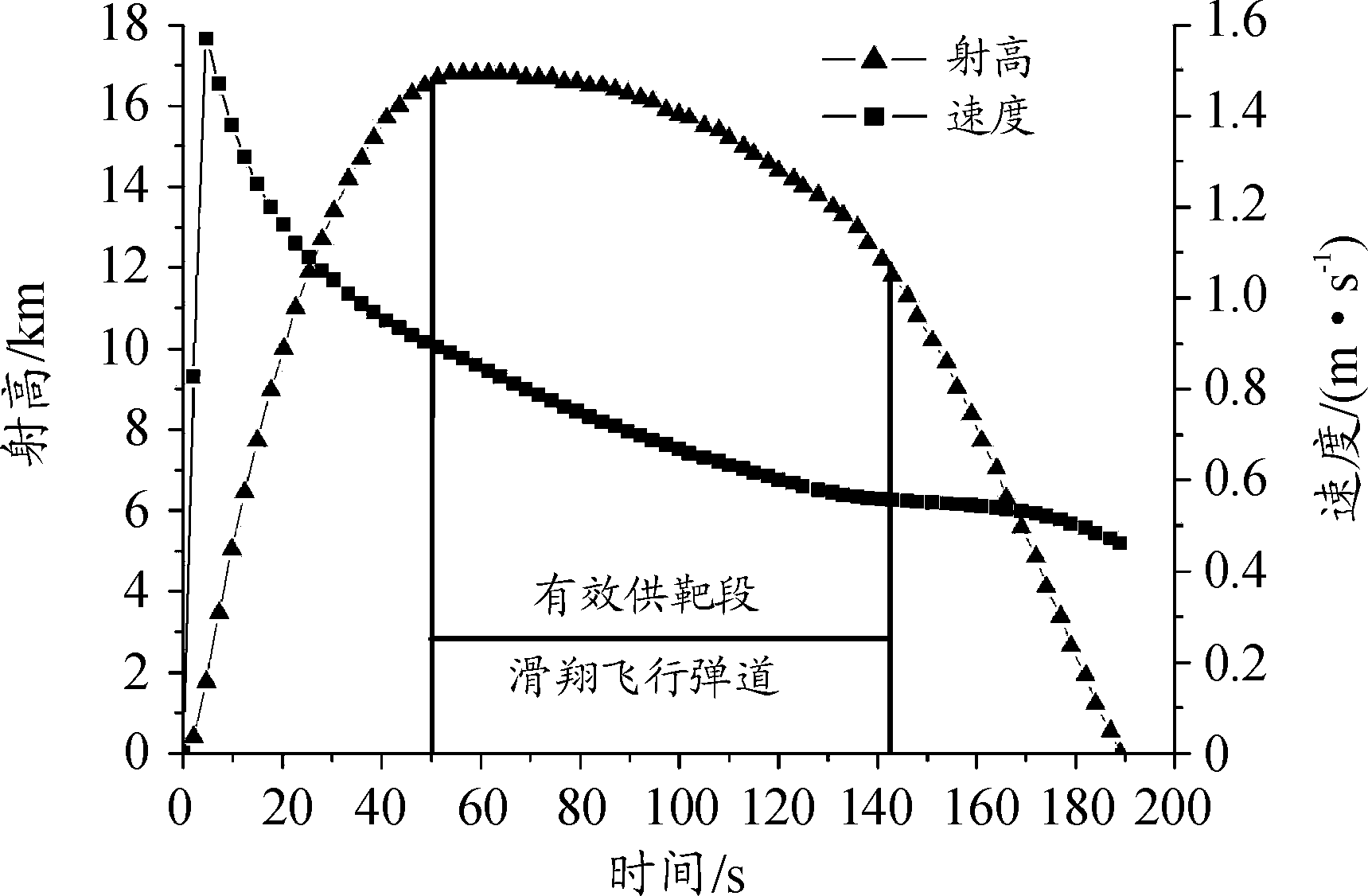
图4 12°舵偏角下供靶方案曲线
3.2 直线滑翔飞行控制弹道仿真
直线滑翔飞行控制的弹道仿真的初始条件和气动参数与变舵偏角控制方式一致。不同射击角度下的弹道参数曲线如图5、图6所示。
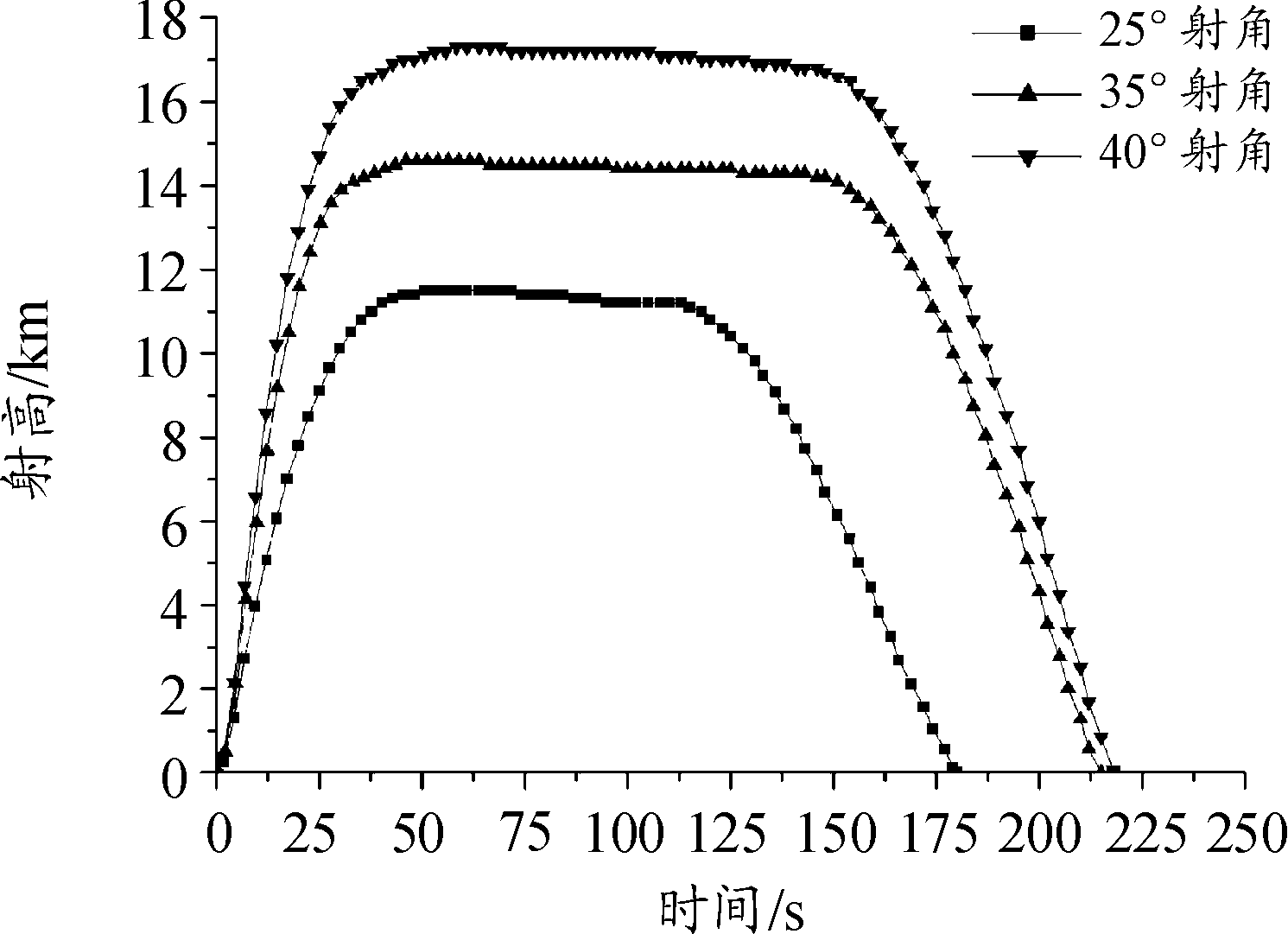
图5 不同射角下射高-时间曲线
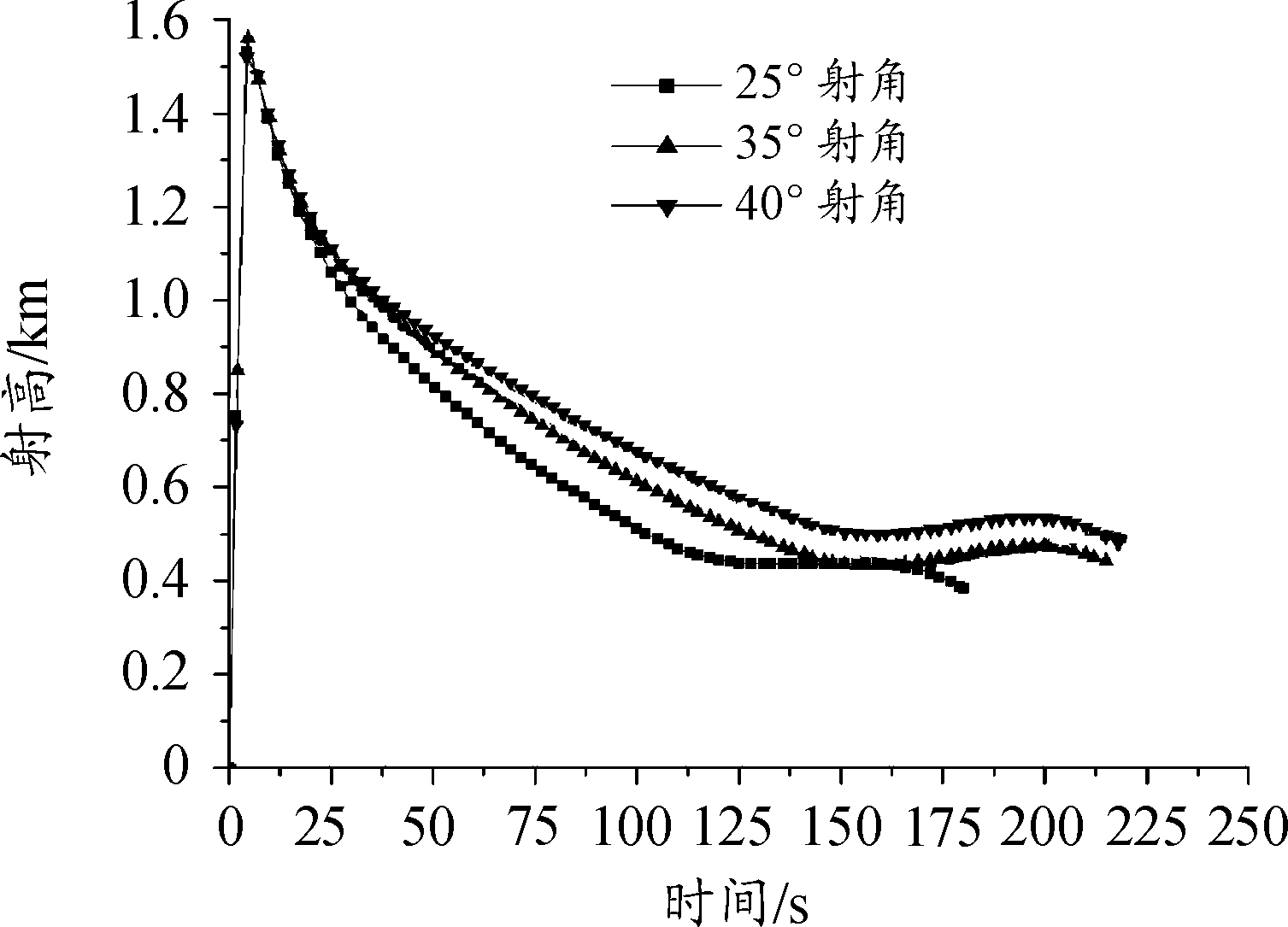
图6 不同射角下速度-时间曲线
由弹道曲线知:不同射角下,火箭靶弹的飞行弹道都出现一段平飞弹道,形成平飞段的高度和时间范围有所不同。仿真参数中,各射角下平飞段,其弹道倾角θ的值都在零附近变化(弹道倾角变化范围基本为-7.7°~3.63°。没有严格水平飞行,主要考虑火箭靶弹在较大的舵偏角下的稳定性)。
对比供靶指标,不同射角下,直线滑翔飞行控制的弹道均满足供靶要求。因此,只对35°射角的弹道进行分析,其供靶方案曲线如图7所示。
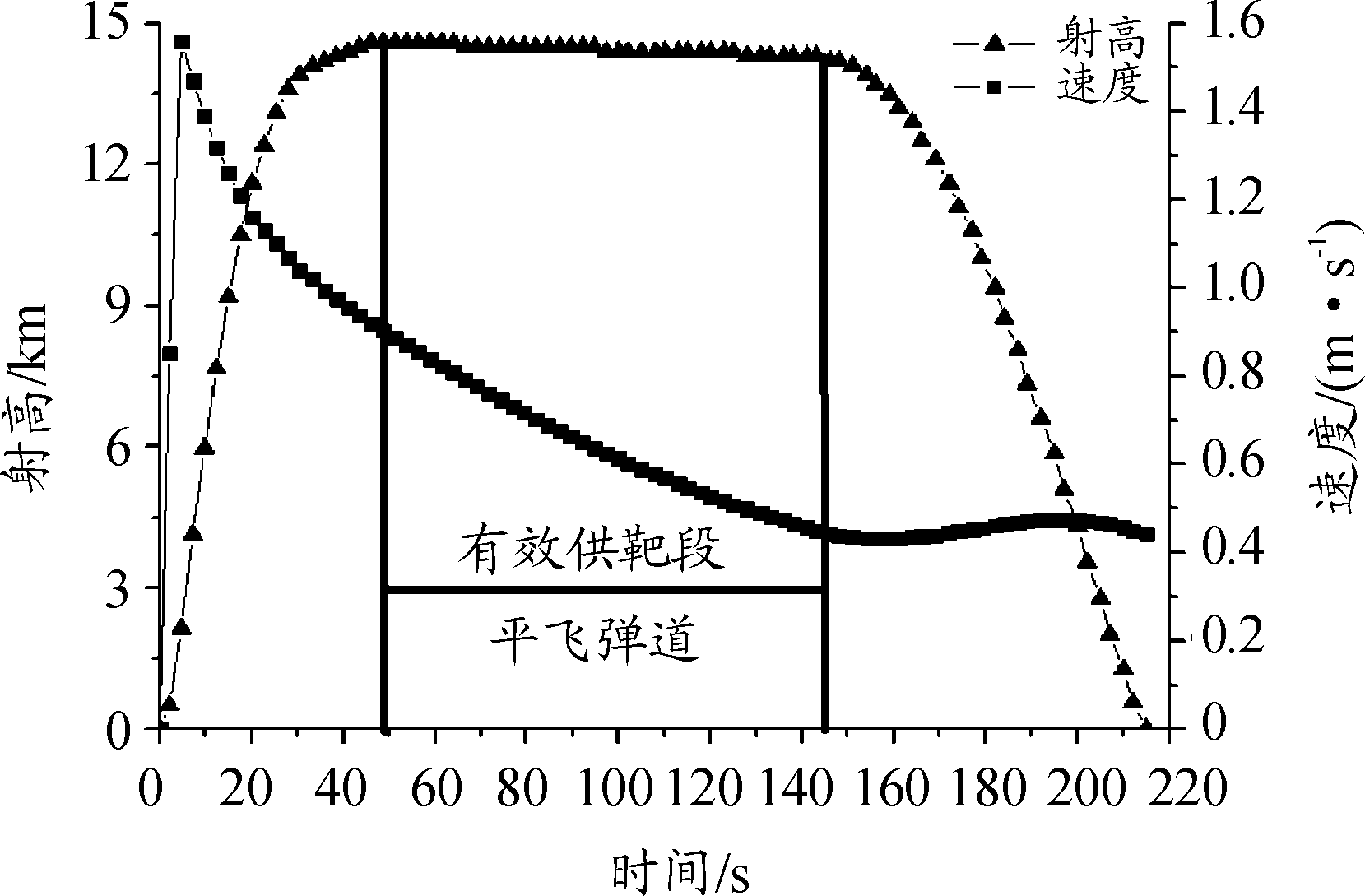
图7 35°射角下供靶方案曲线
4 结论
1) 变舵偏角和直线滑翔飞行两种舵面控制方式,均可改善无控飞行弹道。变舵偏角控制方式通过调整舵偏角大小、舵面控制时间,可以得到滑翔飞行弹道;在一定范围内,随着舵偏角的增大,火箭靶弹的滑翔效果越显著,越能满足供靶要求。直线滑翔飞行控制方式可实现平飞弹道,射角不同,平飞段的高度不同,可模拟不同的飞行目标。
2) 变舵偏角和直线滑翔飞行两种舵面控制方式得到的滑翔飞行弹道和平飞弹道,均可满足供靶条件。变舵偏角控制方式控制结构较简单、易于实现,但控制精度较差;直线滑翔飞行控制方式控制精度较高,但控制系统复杂、成本高。
[1] 郑旭,杨锁昌.靶弹系统技术现状及发展趋势分析[J].飞航导弹,2018:1-6.
[2] 史震,赵万生,张惠平.超低空靶弹弹道设计[J].战术导弹控制技术,2003(3):6-8.
[3] MENTAS M.U.S.Aerial Target Programs[C]//46th annual targets,uavs & range Operations Symposium.san antonio,Texas.2008:51-55.
[4] 李晓斌,王英杰,孙晓峰.简易控制火箭靶弹总体设计[J].弹道学报,2010,22(1):41-44.
[5] 王朋飞,周前进,江多琨.中高空超音速有控火箭靶弹的弹道设计[J].兵器装备工程学报,2019,40(05):52-55.
[6] 沈冠军,冯顺山,曹红松.一种超音速火箭靶弹程序角优化方法研究[J].兵工学报,2015,36(4):644-647.
[7] YAN X D,LYU S,TANG S.Analysis of optimal initialglide conditions for hypersonic glide vehicles[J].Chinese Journal of Aeronautics,2014,27(2):217-225.
[8] 王刚,张驰,吴建业.靶弹平飞高度拓展的设计与实现[J].船舶电子工程,2017,2:38-39.
[9] 李晓斌,董敬文.火箭靶弹零升阻力系数辨识[J].固体火箭技术,2010,33(1):5-8.
[10] 罗会甫.鸭舵式二维弹道修正引信修正控制原理研究机修正执行机构设计[D].北京:北京理工大学,2007.
[11] Pat Buckley.U.S.Navy Aerial Target Systems[C]//49th Annual NDIA Symposium & Exhibition.Monterey CA,10 October 2011.
[12] 张艳,单时卓.基于有控方案的超音速火箭靶弹平飞弹道设计[J].战术导弹技术,2014,1:37-41.
[13] ROGERS J,COSTELLO M.Design of a Roll-Stabilized Mortar Projectile with Reciprocating Canards[J].Journal of Guidance,Control,and Dynamics.2010,33(4):356-359.
[14] 史金光,王中原,曹小兵,等.滑翔增程弹滑翔弹道设计[J].南京理工大学学报,2006,31(2):147-151.
[15] 杜韩东.单组舵控火箭弹气动布局与控制策略研究[D].太原:中北大学,2011.
[16] 郭飞帅,张高瑜,刘冬.助推滑翔导弹滑翔段优化研究[J].四川兵工学报,2011,32(8):27-30.