在深水环境中工作承受高静水压力的脆性薄壁中空结构物,当受到水流晃动等外部载荷时,容易被压溃,使外部高压水流向结构物压溃中心汇聚,发生相撞,形成内爆(Implosion)[1-2],产生内爆冲击波,会对周围结构造成冲击损伤。潜艇的水下外部携带设备、水下照明灯、水下管道等均具有发生内爆的风险。
国内外对水下内爆进行了诸多研究。Orr M、Schoenberg M等[3]在实验室进行了中空玻璃球水下内爆试验,测得了内爆冲击波,得出球形内爆冲击波压力时域曲线具有首先产生负压,然后是尖锐峰值的特点。Stephen E T等[4]开展了中空玻璃球内爆试验和数值模拟研究,发现玻璃球结构的失效时间对内爆冲击波特性有显著影响。杜志鹏等[5]将水下爆炸气泡动力学与水下内爆相结合,基于能量守恒关系,推导出不可压缩流体中球形容器内爆理论模型,分析了容器尺寸、静水压力等参数对内爆冲击波压力、气泡溃灭时间周期的影响规律。Gupta S等[6]进行了一系列薄壁铝合金管的水下内爆试验,得出内爆后的铝合金管呈现为平坦的双瓣压溃塌陷状态。Gish L、Vignati F等[7-9]在大型压力罐中进行了金属圆柱壳的内爆试验和仿真研究,探究了圆柱壳长度、直径和厚度对内爆冲击波的影响。Pinto M等[10]通过水下内爆试验研究了不同结构形式下的碳纤维增强环氧树脂复合材料管内爆冲击波压力特征,评估其破坏潜力。除此之外,在中微子探测领域,内部真空、形如白炽灯泡的光电倍增管在深水环境中工作容易发生内爆,Milind D等[11]在压力罐中对光电倍增管进行了2次水下内爆试验,并利用任意拉格朗日欧拉(ALE)计算方法对光电倍增管内爆进行了仿真,得到的仿真结果与试验结果吻合较好。
上述研究主要针对球形、圆柱形及特定结构的内爆特性进行了理论、试验及仿真研究,但是对于椭球形内爆特性的研究并未开展。本文基于有限元软件Abaqus中的欧拉-拉格朗日耦合(CEL)计算方法,建立了扁椭球内爆仿真计算模型,分析了扁椭球内爆发生过程,探究了扁椭球内爆水中压力分布及内爆冲击波传播特性,并得到了扁椭球体的椭圆旋转截面长、短径比对扁椭球内爆冲击波的影响规律。该研究对中空物体水下内爆的设计具有参考意义。
1 扁椭球内爆仿真模型
1.1 内爆仿真工况的拟定
在直角坐标系下,扁椭球体是由椭圆截面以其短轴为旋转轴旋转一周而成。图1为扁椭球结构示意图,图1(a)为旋转截面,a为椭圆截面长半径,c为短半径,以c轴为旋转轴旋转一周得到如图1(b)所示的扁椭球。为了探究扁椭球形状对内爆特性的影响,定义无量纲扁椭球体的椭圆旋转截面长、短径之比k表达扁椭球的形状。
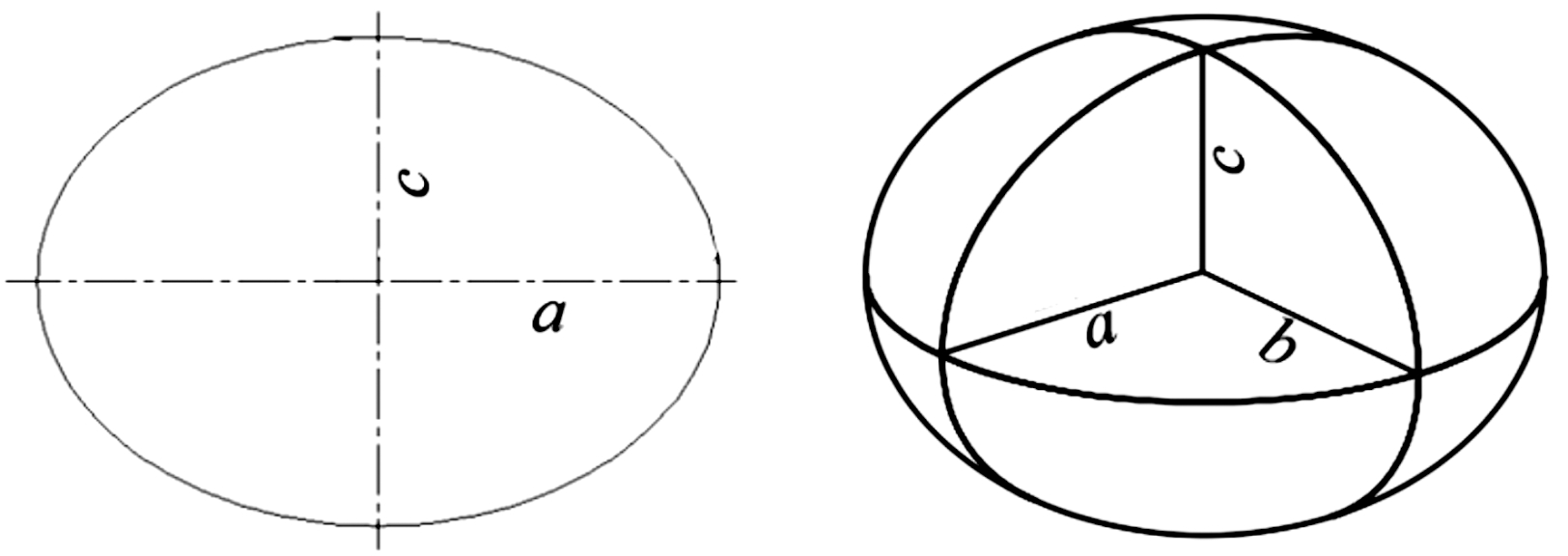
图1 扁椭球结构示意图
选取体积为0.05 m3的扁椭球体在50 m深水环境中发生内爆进行研究。不同的k值下,扁椭球的各半径长可按式(1)进行计算:
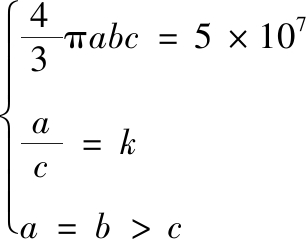
(1)
式(1)中:a、b为扁椭球椭圆旋转截面的长半径;c为椭圆旋转截面的短半径。
本文选取5种工况对扁椭球形内爆进行研究,当k取不同比值时,根据式(1)分别求得各工况下扁椭球的各半径长,如表1所示。
表1 各工况下扁椭球半径长
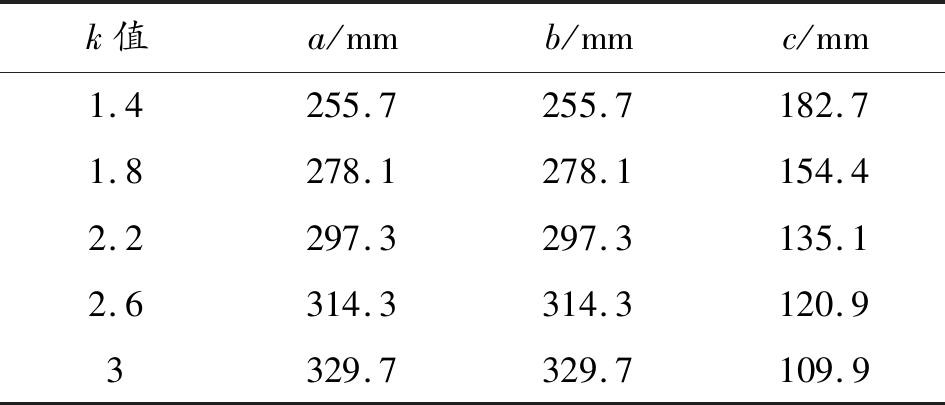
k值a/mmb/mmc/mm1.4255.7255.7182.71.8278.1278.1154.42.2297.3297.3135.12.6314.3314.3120.93329.7329.7109.9
1.2 内爆有限元模型的建立
Abaqus/Explicit显式动态求解算法是为了求解碰撞、冲击、爆炸等非线性瞬态动力学问题发展而来,应用其中的欧拉-拉格朗日耦合(CEL)算法可对扁椭球内爆进行数值模拟[12]。以扁椭球的椭圆旋转截面长、短径比k=1.8工况为例对扁椭球内爆有限元模型进行介绍,图2为扁椭球内爆计算模型的中部剖视图,整个球体欧拉域直径为3 m,采用三维实体欧拉网格,单元类型为EC3D8R,水域中部网格密度大,外部网格密度小,共计 973 600 个单元,以保证内爆计算精度。球体欧拉域外部灰色部分欧拉网格赋予水材料属性,采用线性Us-UpHugoniot形式的Gruneisen状态方程进行描述,其状态参数为:密度ρ=1.0×103 kg/m3,c0=1 450 m/s,s=0,黏度μ=1.0×103 Pa·s。内部红色部分欧拉网格赋予真空材料属性。外部水域中利用初始应力场的方式施加0.5 MPa的初始静压力模拟50 m深水环境,且在欧拉域外边界设置冲击波无反射、流体自由流入和流出的边界条件,以模拟无限水域。有限元模型建立完成后,为了分析扁椭球内爆的冲击波强度和传播规律,分别在水域中X方向、Y方向、斜向45°方向,距扁椭球中心0.25~1.45 m沿直线均匀设置25个压力测点;在距离扁椭球中心0.25 m的周向位置均匀设置6个压力测点。
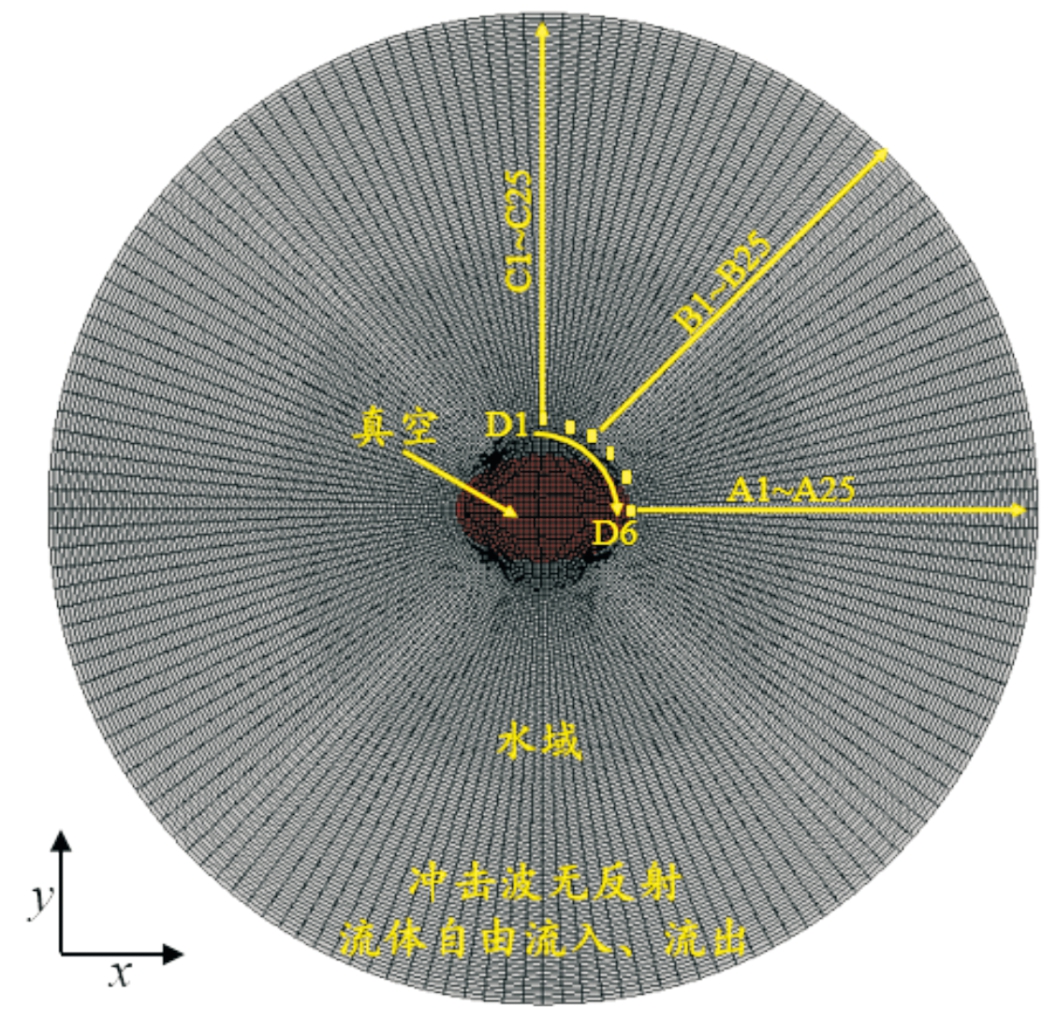
图2 扁椭球内爆有限元计算模型剖视图
2 扁椭球形内爆特性分析
根据1.1节所设计的扁椭球内爆工况,修改真空域尺寸,建立各工况下扁椭球内爆仿真模型,初始静压力、边界条件、测点位置均保持不变,对各工况的仿真模型进行数值模拟,分析扁椭球内爆发生过程及其内爆冲击波特性。
2.1 扁椭球内爆发生过程分析
图3为扁椭球的椭圆旋转截面长、短径比k=1.8的情况下,仿真计算中扁椭球内爆发生过程:图3(a)为扁椭球初始状态;图3(b)、图3(c)为扁椭球在外部0.5 MPa静水压力下收缩的过程,短半轴侧水流运动较慢,长半轴侧水流运动较快使扁椭球体积迅速减小;图3(d)为内涌水流发生碰撞产生内爆冲击波的瞬间,可看出扁椭球内爆冲击波主要是由于扁椭球长半轴侧水流高速碰撞产生的。从扁椭球内爆发生过程可看出:扁椭球内爆整个发生过程共经历了9.3 ms,其中,内爆初期水流运动速度较慢,随着时间的增加,水流运动速度快速增加,最终长半轴侧水流发生碰撞产生扁椭球内爆冲击波。
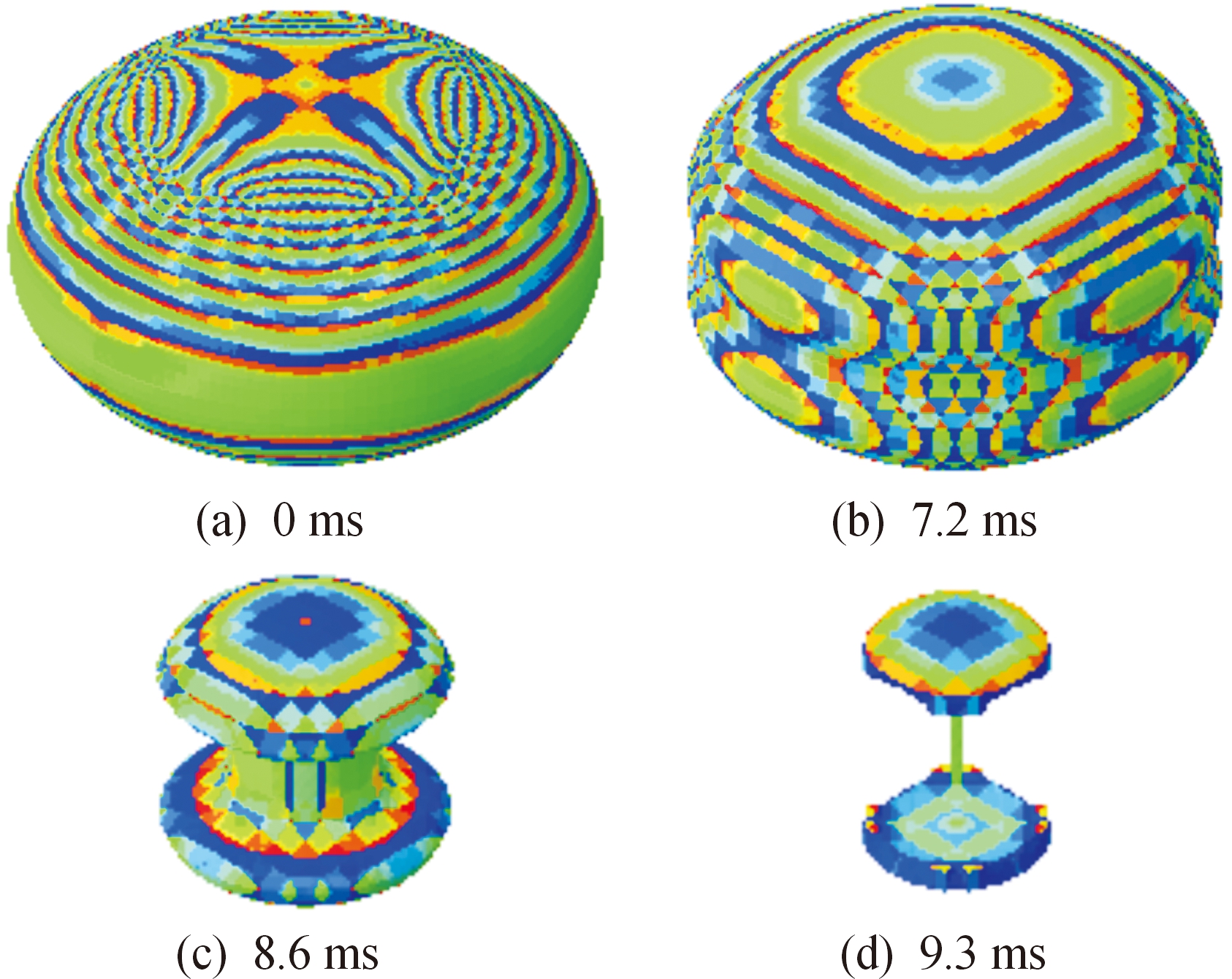
图3 扁椭球内爆发生过程示意图
2.2 扁椭球内爆冲击波特性分析
基于已建立的扁椭球内爆仿真模型,研究内爆中心附近的压力场分布特征、内爆冲击波的比冲量变化规律、各方向内爆冲击波的传播规律和不同k值下的扁椭球内爆冲击波特点等问题对于深水环境下扁椭球的抗爆设计和危害分析具有应用价值。
图4为数值模拟中扁椭球内爆发生时刻内爆中心附近的压力场分布情况,可看出扁椭球发生内爆后,在内爆中心附近,水域中压力呈轴对称分布,X、Y轴方向上的欧拉单元呈现深红色,水中压力较高;斜向45°方向上,水中压力较低;随着时间的增加,扁椭球内爆冲击波压力以此种分布方式向外传播。
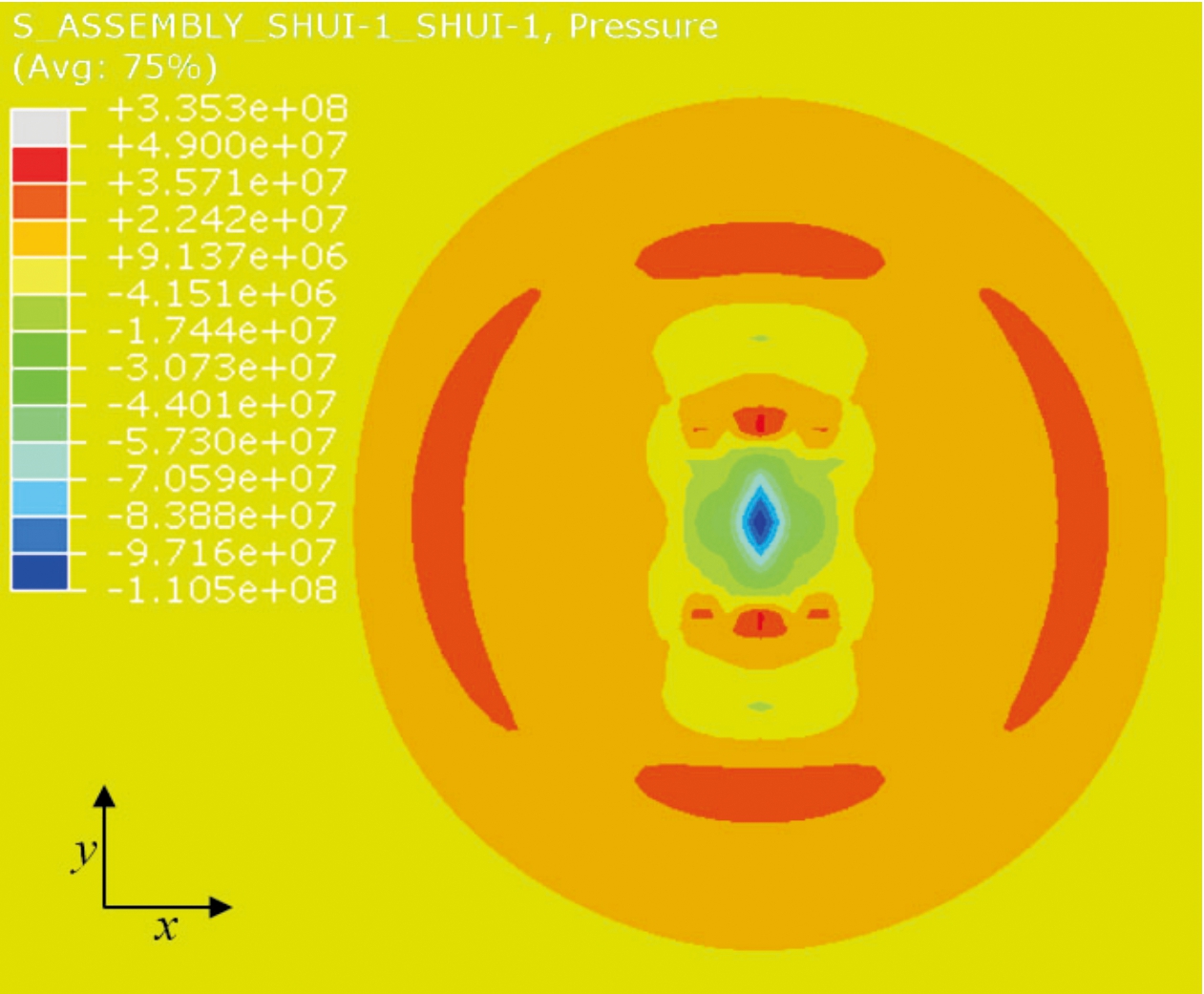
图4 扁椭球内爆压力场变化图
进一步对仿真模型中圆周方向测点的内爆冲击波压力进行研究。图5(a)为圆周方向(D1~D6)测点的扁椭球内爆冲击波时域曲线,可看出各测点在同一时刻测得了内爆冲击波峰值,与水下炸药爆炸冲击波相比脉宽小、峰值高,这种冲击波对脆性材料破坏明显;压力峰值过后,冲击波曲线出现震荡式衰减趋势,最终快速恢复到平衡位置。为了清晰显示圆周方向测点的扁椭球内爆冲击波峰值信息,选取内爆冲击波峰值段进行分析,如图5(a)中详细图所示,统计各测点的内爆冲击波峰值,绘制扁椭球内爆冲击波峰值随周向测点编号变化曲线如图5(b)所示,可看出D1~D6测点的内爆冲击波峰值先减小后增大,这与图4中扁椭球内爆发生时水域中压力分布相同。
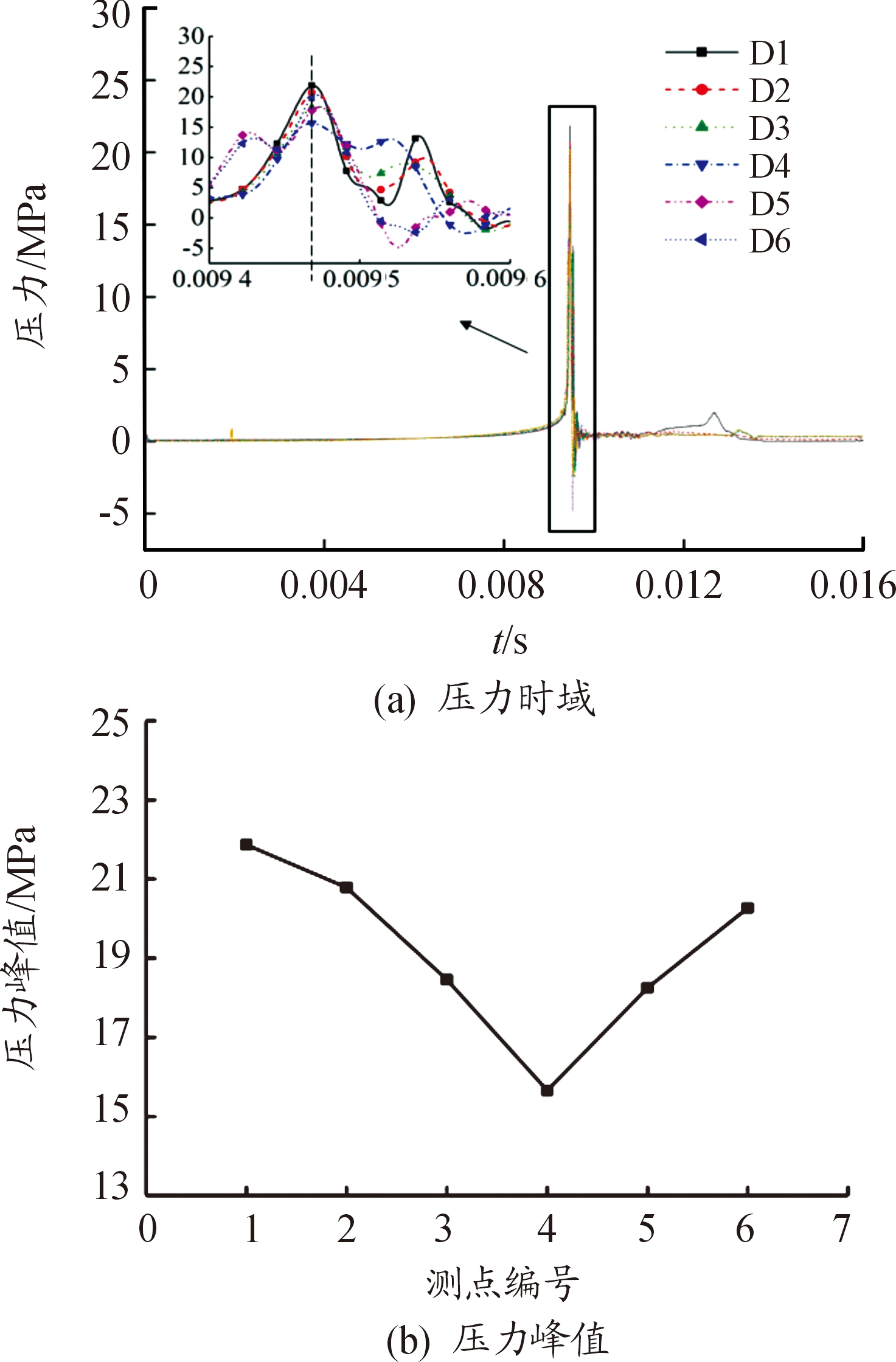
图5 扁椭球周向测点内爆冲击波时域及峰值变化曲线
将扁椭球周向各测点的内爆冲击波数据统一减小0.5 MPa,去除静水压力对内爆冲击波比冲量的影响,并进行积分得到扁椭球内爆冲击波的比冲量曲线如图6(a)所示,取各曲线的最大值与最小值差值作为扁椭球内爆冲击波比冲量峰值,以比冲量峰值为纵坐标,周向测点编号为横坐标绘制曲线如图6(b),可得出扁椭球发生内爆,其比冲量峰值沿周向近似线性增加;这是由于扁椭球内爆发生时长半轴侧水流首先发生碰撞,产生X方向的水射流使得该方向的冲击波能量偏大导致的。
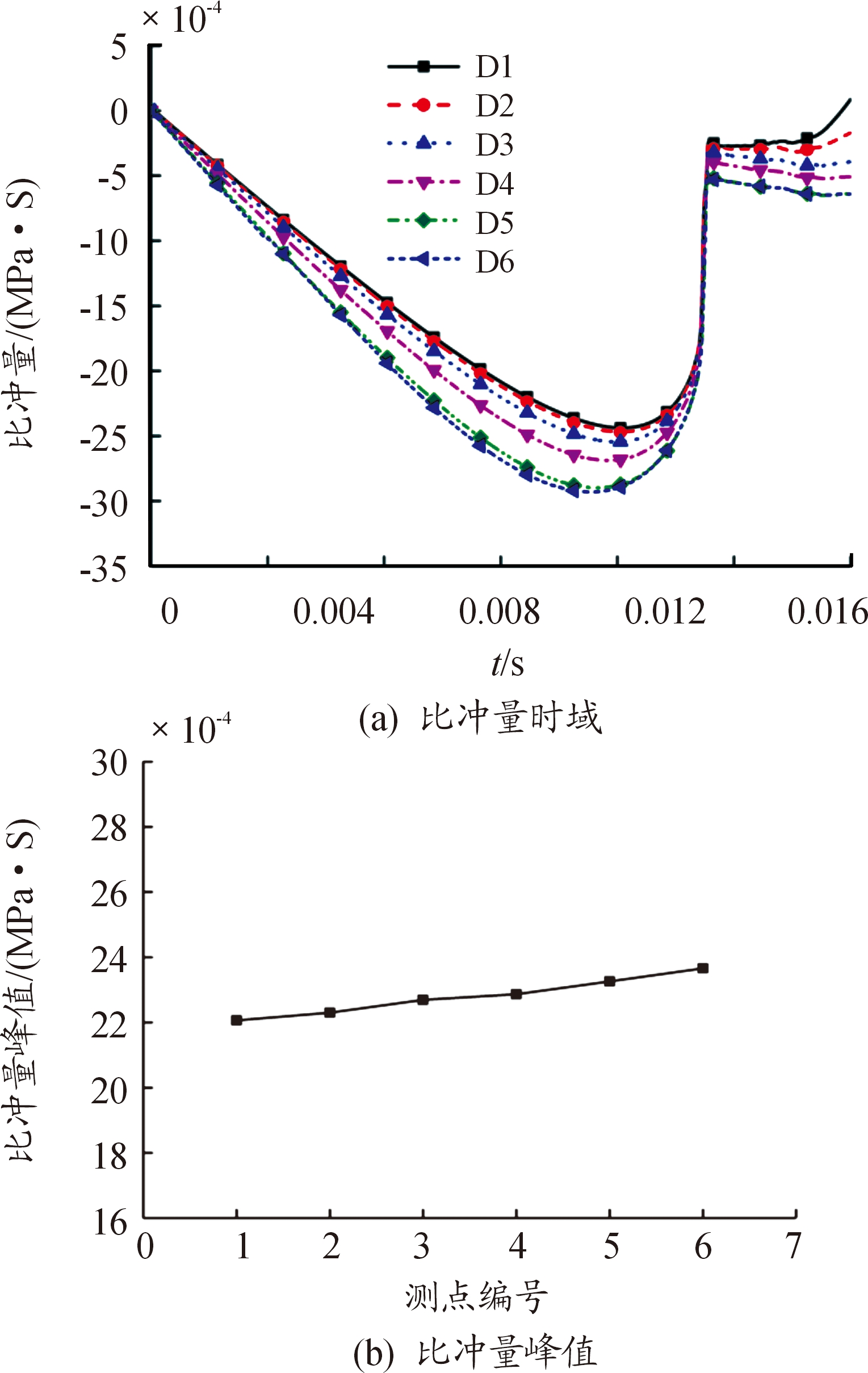
图6 扁椭球周向测点内爆冲击波比冲量时域及峰值变化曲线
下一步对扁椭球各方向内爆冲击波的传播规律进行研究。图7(a)为扁椭球内爆发生时,X轴方向上典型距离测点在0.009~0.012 s时间段的冲击波压力时域曲线,可看出扁椭球内爆冲击波峰值随着距离的增加呈下降趋势,脉宽基本未发生变化,波形震荡形式大致相同。同样,分别取3个方向各测点内爆冲击波压力峰值进行分析,如图7(b)所示,以测点距离为横坐标,各测点冲击波压力峰值为纵坐标,进行描点绘图,并进行函数拟合。由拟合效果可知,指数函数吻合度较好,故对其进行y=axb函数拟合。冲击波峰值拟合系数a的范围为3.69~4.60,衰减系数b的范围为1.04~1.19,其中X方向的衰减系数b数值最大,内爆冲击波峰值衰减最快,斜向45°方向衰减最慢。
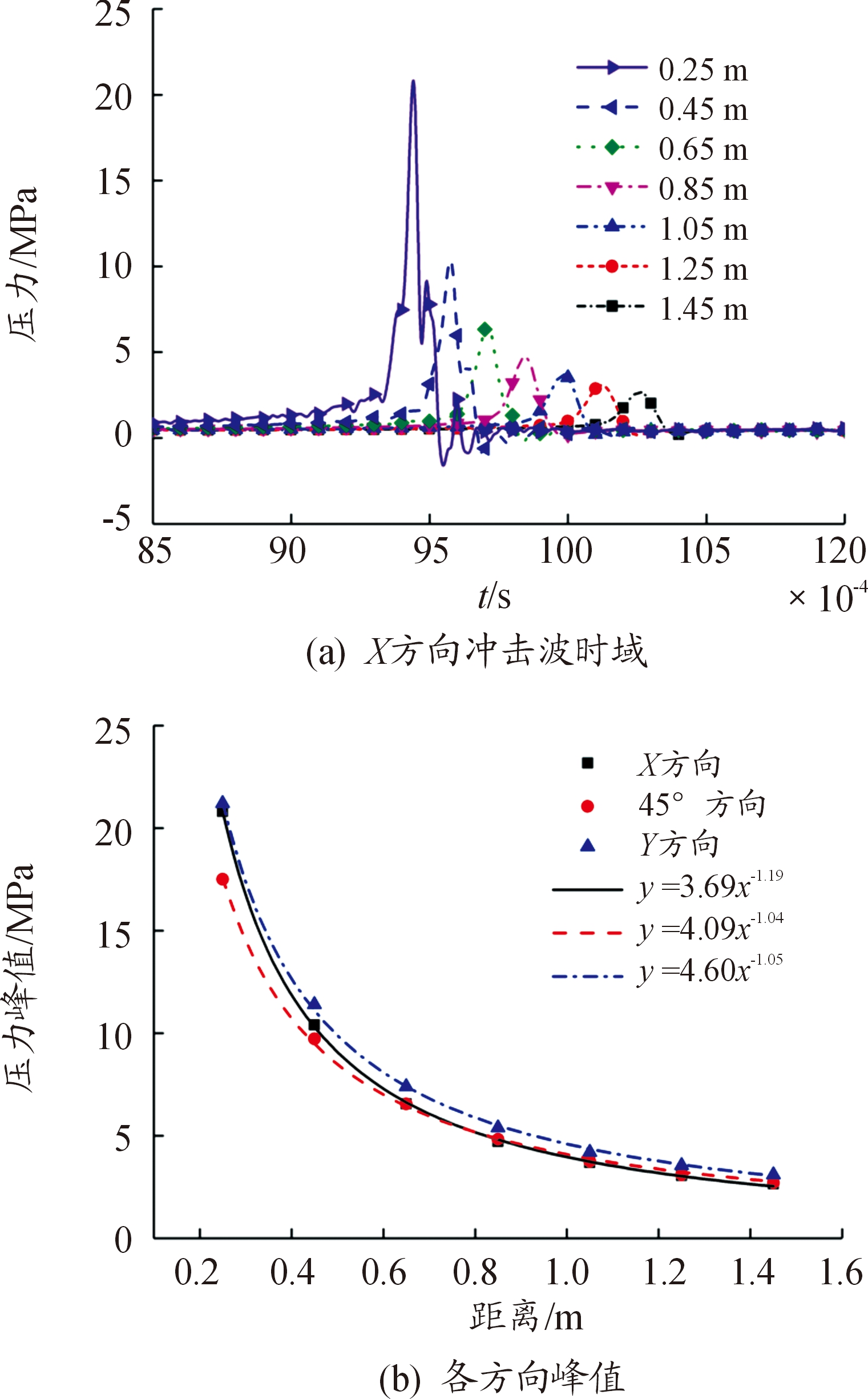
图7 扁椭球内爆冲击波随距离变化曲线
下面探究不同k值下的扁椭球内爆冲击波特性。首先,选取B1测点在不同k值下的扁椭球内爆冲击波压力数据进行分析,为了清晰显示内爆冲击波压力的特征,选取0.008 8~0.010 2 s时间段进行绘图,如图8(a)所示。可以看出:随着k值的增加,扁椭球发生内爆的时间明显减小,冲击波脉宽基本不变;同时,内爆冲击波压力峰值随着k值的增加逐渐降低。
进一步对扁椭球内爆冲击波峰值进行分析,提取A1、B1、C1测点内爆冲击波峰值,以峰值为纵坐标,k值为横坐标进行描点绘图,如图8(b)所示,可以看出各方向上的扁椭球内爆冲击波峰值随k值的增加均呈逐渐减小的趋势,且X、Y方向的扁椭球内爆冲击波峰值明显大于斜向45°方向,说明扁椭球内爆在半轴方向的内爆冲击波峰值较大。通过分析发现扁椭球内爆冲击波压力峰值随k值的变化规律可利用线性函数y=c·k+d进行拟合,拟合结果如图8(b)中虚线所示,可看出X、Y方向上的拟合直线斜率较大,因而得到:当扁椭球体积一定时,内爆冲击波峰值在半轴方向上随k值的增加衰减较快;斜向45°方向衰减较慢。
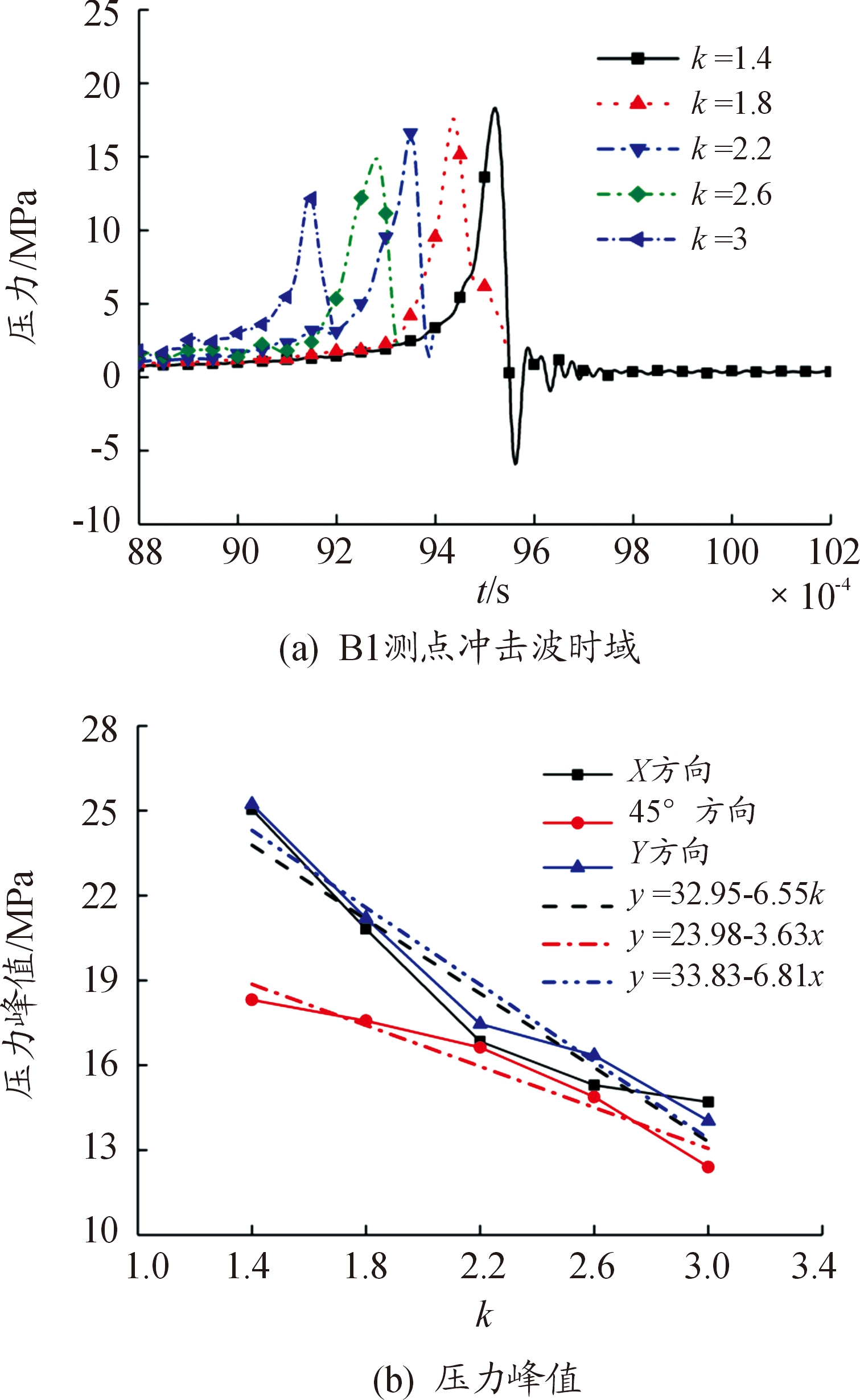
图8 扁椭球各方向内爆冲击波随k值变化曲线
3 结论
扁椭球内爆发生过程中,内爆初期水流运动速度较慢,随着时间的增加,水流运动速度快速增加,且长半轴侧水流运动速度大于短半轴,最终长半轴侧水流发生碰撞产生内爆冲击波。
在扁椭球内爆中心附近,水域中压力呈轴对称分布,在半轴方向上压力较高,且冲击波峰值随传播距离衰减较快;在斜向45°方向上压力较低,且冲击波峰值随传播距离衰减较慢。圆周方向测点的扁椭球内爆冲击波峰值随测点编号的增加先减小后增大。
当扁椭球体积一定时,随着扁椭球的椭圆旋转截面长、短径比k值的增加,扁椭球内爆发生时间明显减小,各方向上的内爆冲击波峰值线性减小,且在X、Y方向衰减较快,斜向45°方向衰减较慢。
[1] HARBEN P E,BORO C.Implosion Source Development and Diego Garcia Reflections[C]//23rd Seismic Research Review Worldwide Monitoring of Nuclear Explosions,2001:21-23.
[2] TACEY R K.Implosion Research[J].Sea Frame,2008,4(01):13-15.
[3] ORR M,SCHOENBERG M.Acoustic Signatures from Deep Water Implosions of Spherical Cavities[J].The Journal of the Acoustical Society of America,1976,59(05):1155-1159.
[4] STEPHEN E T.Underwater Implosion of Glass Spheres[J].The Journal of the Acoustical Society of America,2007,121(12):844-852.
[5] 杜志鹏,杜俭业,李营.不可压缩流体中球型容器内爆理论模型[J].兵工学报,2015,36(S1):92-96.
[6] GUPTA S,BLANC L,JAMES M.Implosion of Longitudinally Off-centered Cylindrical Volumes in a Confining Environment[J].Journal of Applied Mechanics,2015,82(05):43-48.
[7] GISH L,WIERZBICKI T.Estimation of the Underwater Implosion Pulse from Cylindrical Metal Shells[J].International Journal of Impact Engineering,2015,77(04):166-175.
[8] VIGNATI F,GUARDONE A.Multi-Domain Simulations of Shock Wave Interaction with Aerodynamic Obstacles in Cylindrical Implosions[J].Journal of Computational and Applied Mathematics,2015,283(01):218-227.
[9] GNING P B,TARFAOUI M,COLLOMBET F,et al.Damage Development in Thick Composite Tubes under Impact Loading and Influence on Implosion Pressure:Experimental Observations[J].Composites B Engineering,2005,36(04):306-318.
[10] PINTO M,GUPTA S,SHUKLA A.Study of Implosion of Carbon/Epoxy Composite Hollow Cylinders using 3-D Digital Image Correlation[J].Composite Structures,2015,779(09):272-286.
[11] MILIND D,DOLPH J,LING J J,et al.Underwater Implosions of Large Format Photo-Multiplier Tubes[J].Nuclear Instruments and Methods in Physics Research,2012,37(07):61-67.
[12] 孟令存,闫明,杜志鹏,等.基于面积折减等效模型的光电倍增管水下内爆机理研究[J/OL].爆炸与冲击,2020(06):1-10[2020-06-18].http://kns.cnki.net/kcms/detail/51.1148.O3.20200401.1726.022.html.