海面舰艇作为海军的主要装备,其具有目标尺寸大,防护能力较弱,机动性能差,造价昂贵等特点,因此其生存能力一直是各国专家着力解决的问题。舰艇受到最大的空中威胁是具有精确打击能力的反舰导弹,现代反舰导弹在攻击样式多样、末端攻击速度、制导方式等有了很大的提高,要想防御反舰导弹多批次、多方位的饱和攻击,应采用软、硬防御相结合的方式[1]。本文主要研究软武器系统的干扰作用,目前国外反舰导弹制导方式多采用主动雷达制导,还有红外成像制导,并向雷达/红外复合制导的方向发展。反舰导弹末端制导系统工作时离舰船已经非常近,此时是舰艇防御的最后时机,因此设计一种装备在舰艇上的低空复合干扰弹。当探测到敌方反舰导弹末端制导开机以后,在合适的时机将复合干扰剂抛洒到舰艇周围,形成烟幕墙,对雷达、红外成像以及复合制导的反舰导弹进行干扰,舰艇趁机回转机动。
初步设计一种亚音速飞行的火箭弹,射程在0.5~1 km,最大射高300~500 m,在200~500 m高度范围开仓抛洒干扰剂。装有烟幕子弹和箔条束的子母战斗部抛洒后,形成宽度:30~40 m,高度:40~50 m的烟幕墙,从而达到干扰目的。干扰弹外形结构是总体设计中很重要的一个环节,通过仿真优化确定干扰弹的外形结构。
1 干扰弹的外形方案
干扰弹的头部体积相对整体来说比较小,头部形状应采取较大的容量的结构方案,而且干扰弹的飞行速度区间在低亚音速范围内,参考低亚音速范围内的空气动力特性,以及加工工艺方面的因素,综合考虑头部形状略钝的曲线母线形、半球形、球头截锥形头部这3种方案比较适合[2],图1为不同头部形状结构图。

图1 不同头部形状
为了装备尽量多的干扰剂,战斗部体积相对来说较大一些,在弹径一定的情况下,弹体长细比应大一些,但是长细比越大稳定性越差[3],选择长细比分别为λ=8、8.5、9的3种结构方案进行分析。
干扰弹飞行区间是低空亚音速范围,选用尾翼稳定的方式,尾翼采用升阻比相对较大的无后掠角的矩形翼,为了充分利用弹体空间、安装方便设计成刀型,图2为刀型翼示意图。同时考虑飞行稳定性,翼片数在4~8片的范围选择。

图2 翼片的结构简图
2 气动特性仿真分析方法
2.1 网格模型的建立
首先建立干扰弹的几何模型,然后划分计算域,本次仿真计算时的计算域是由长度为10倍弹长,半径为干扰弹直径加尾翼展长的20倍的圆柱体与干扰弹外表面所组成的区域。采用的网格形式为一种混合网格,即用分块对接的方式将计算域分成若干区域,再根据各个子块的结构特征选取不同的网格划分策略,共划分约70万体单元,弹体表面网格如图3所示。

图3 弹体表面网格划分
2.2 边界处理
边界条件:弹体表面使用无滑移绝热壁面边界的固体壁面(wall),用于限定流体和固体区域;计算区域用压力远场边界条件(pressure-far-field),用于模拟无穷远处的自由可压流动,选用此边界条件时气体的密度通过理想气体来定义[4]。
来流条件:自由来流条件为标准大气条件,压 强 p0=101 325 Pa,温度 T0=298 K。
计算条件:来流马赫数Ma=0.1、0.2、0.3、0.4、0.5、0.6;攻角α=0°、1°、2°、3°、4°
2.3 数值计算方法
在流体仿真计算时要遵守三大守恒定律:质量守恒定律、动量守恒定律和能量守恒定律[5]。当流动处于湍流状态时,还要考虑湍流方程的约束问题。
采用S-A(Spalart-Allmaras)湍流模型,S-A模型是一个相对简单的单方程模型,只求解一个有关涡粘性的输运方程,比较适用于具有壁面限制流动的流动问题,计算量相对较小[6]。
离散格式:采用二阶迎风格式,利用2个上游单元的物理量来确定控制体积单元的物理量,这种格式精度较高。
2.4 仿真计算及结果分析
经计算流体力学仿真分析,图4为不同头部形状下阻力系数随马赫数变化的曲线,图5为升阻比随马赫数变化的曲线。从阻力系数和升力系数变化曲线看出,球头截锥形和曲线母线形头部两种方案相对较好。
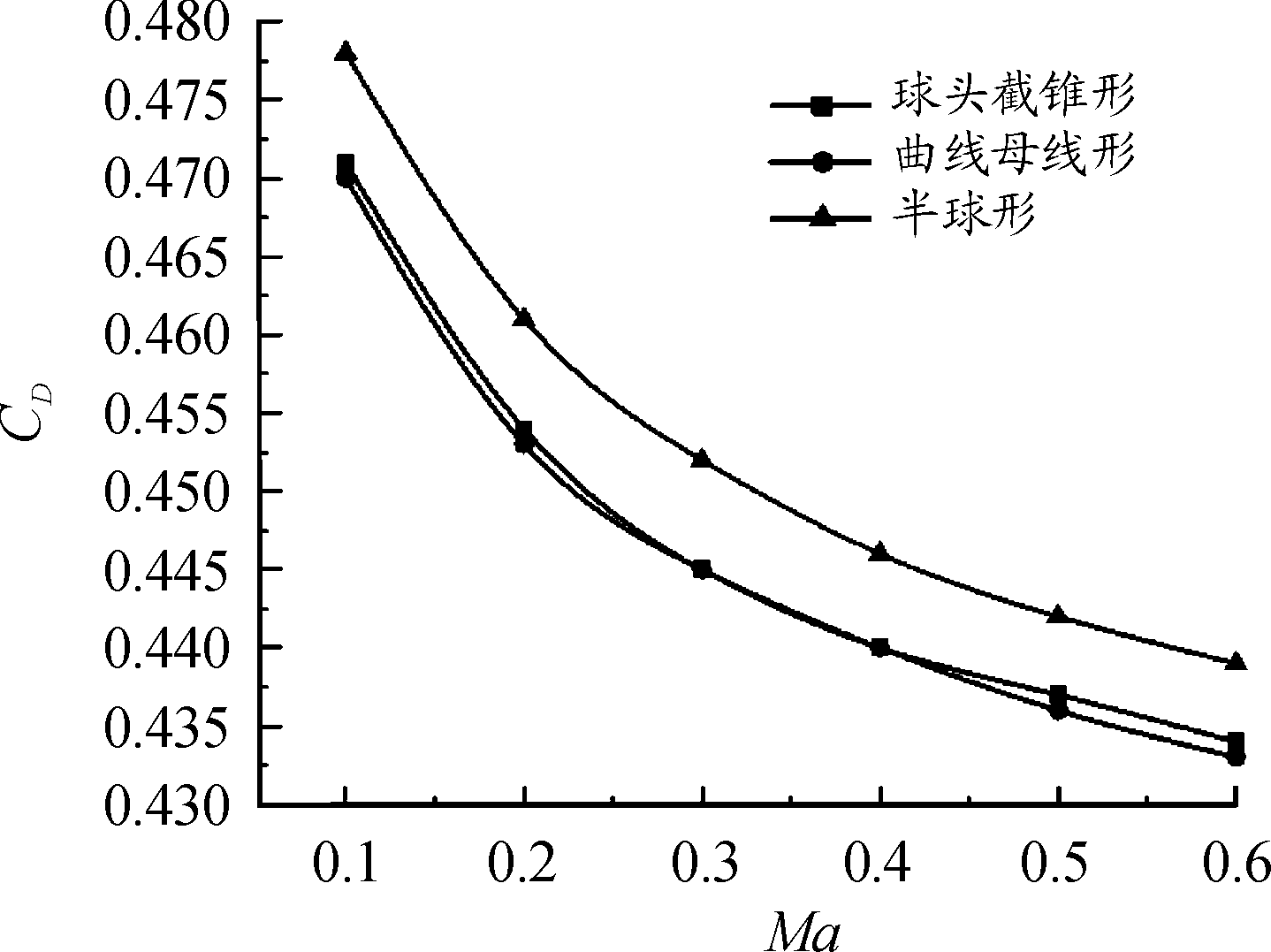
图4 阻力系数随马赫数变化的曲线
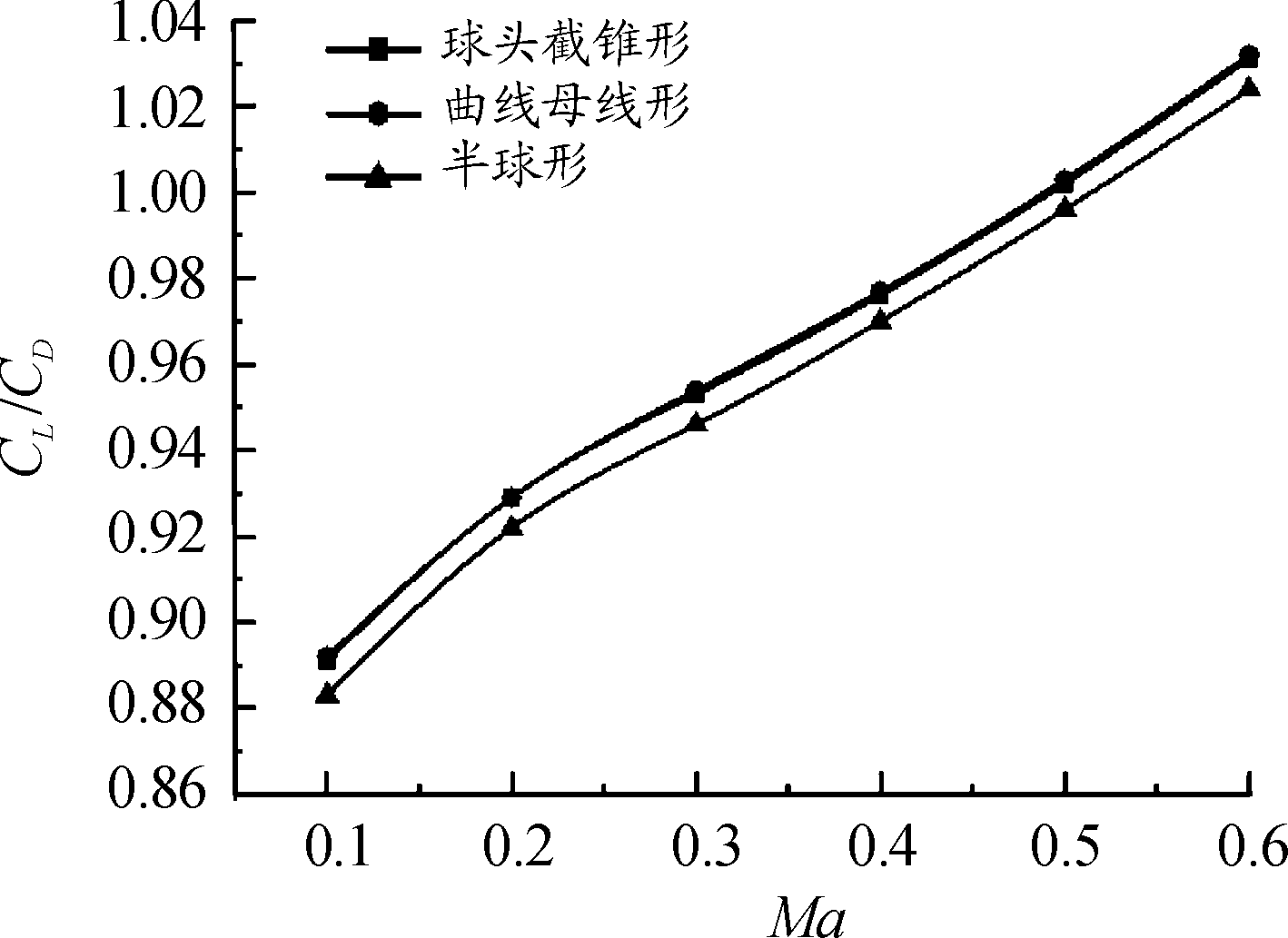
图5 升阻比随马赫数变化的曲线
仿真分析后得到长细比λ=8、8.5、9三种条件下,升阻比随马赫数的变化曲线如图6所示,稳定储备随马赫变化曲线如图7所示。升阻比变化的3条曲线非常接近,可见在亚音速范围内长细比对升力的影响不大,长细比对干扰弹的静稳定性影响比较大,但3种结构稳定储备量在15%~23%,具有良好的尾翼稳定性,因此3种长细比的干扰弹都满足稳定要求。
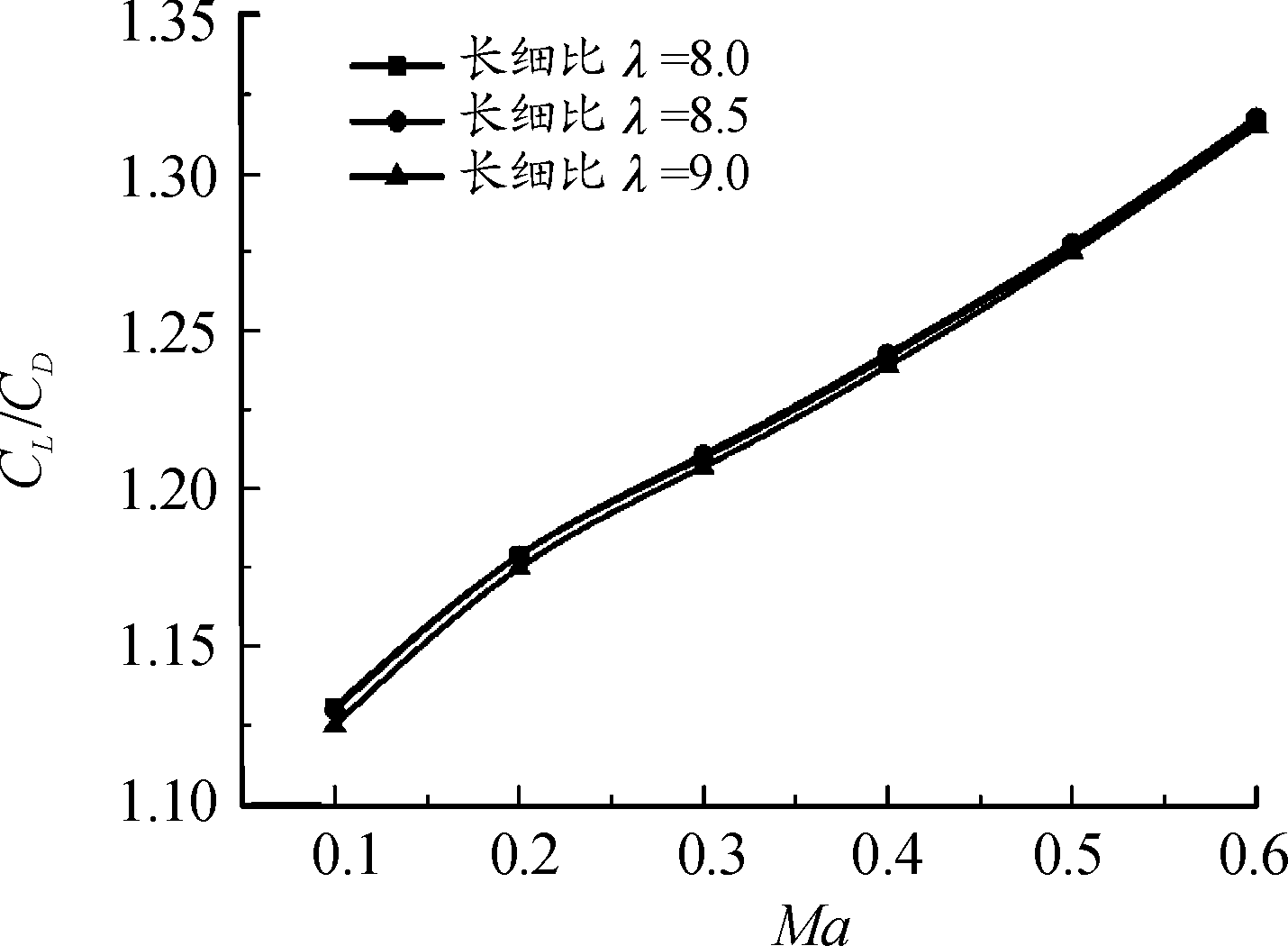
图6 升阻比(CL/CD)的变化曲线
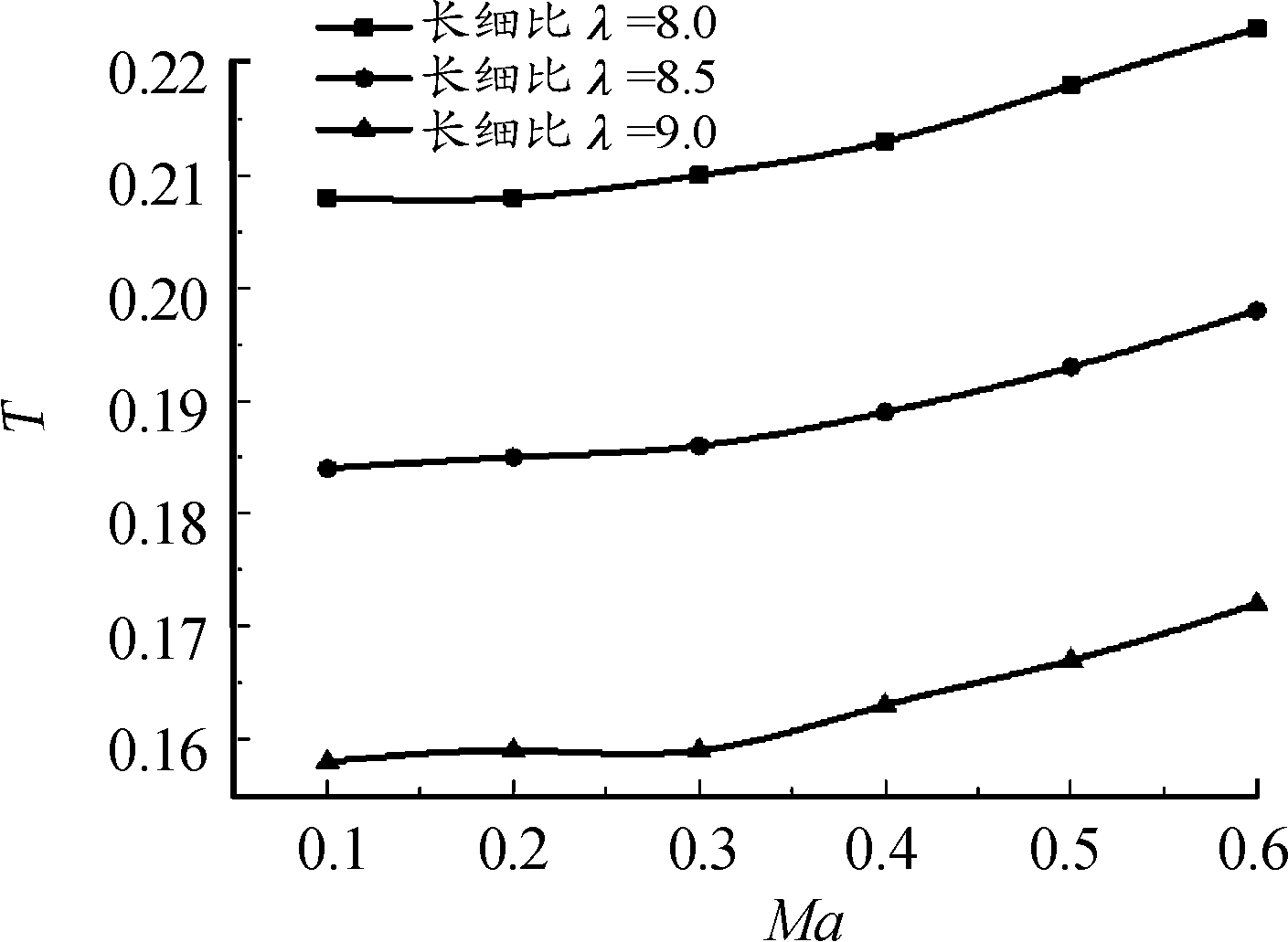
图7 稳定储备量(T)的变化曲线
由仿真得到具有2对、3对、4对翼片的干扰弹结构,升阻比随马赫数的变化曲线如图8所示,稳定储备量随马赫数的变化如图9所示。由图可以看出随着翼片的增加升阻比增加,四对翼片的结构升阻比最大。随着翼片对数的增加干扰弹稳定储备量增加,稳定储备量在15.6%~24.0%,满足稳定性要求。
由以上仿真分析可知,单从一方面考虑,球头截锥形和曲线母线形头部2种方案、长细比λ=8的结构方案、尾翼选择4对尾翼片的结构较优。弹体结构最终选择并不单单是几种方案的简单堆砌,受多种因素影响的,需进行多种验证选择出最优结构。
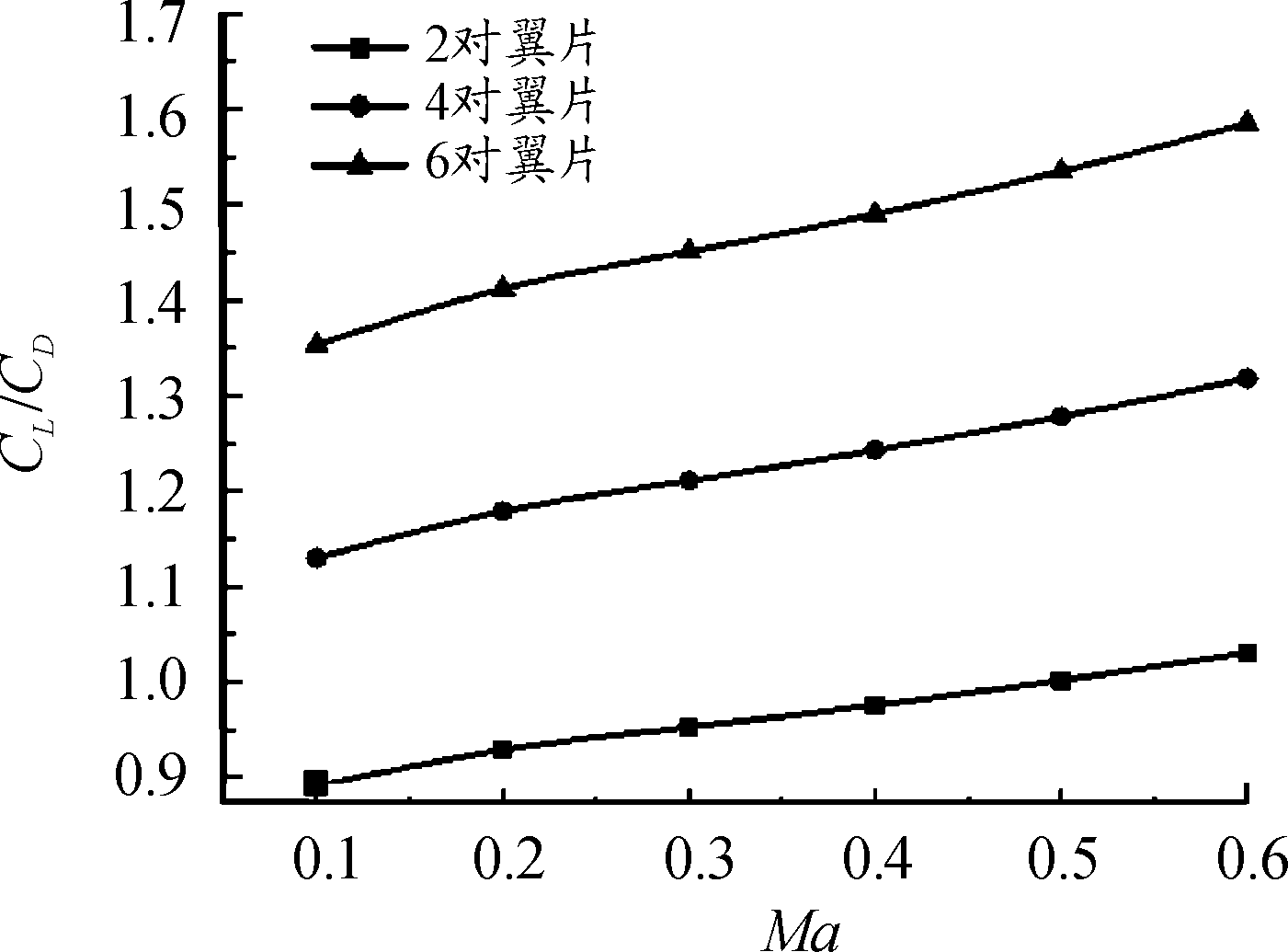
图8 升阻比(CL/CD)的变化曲线
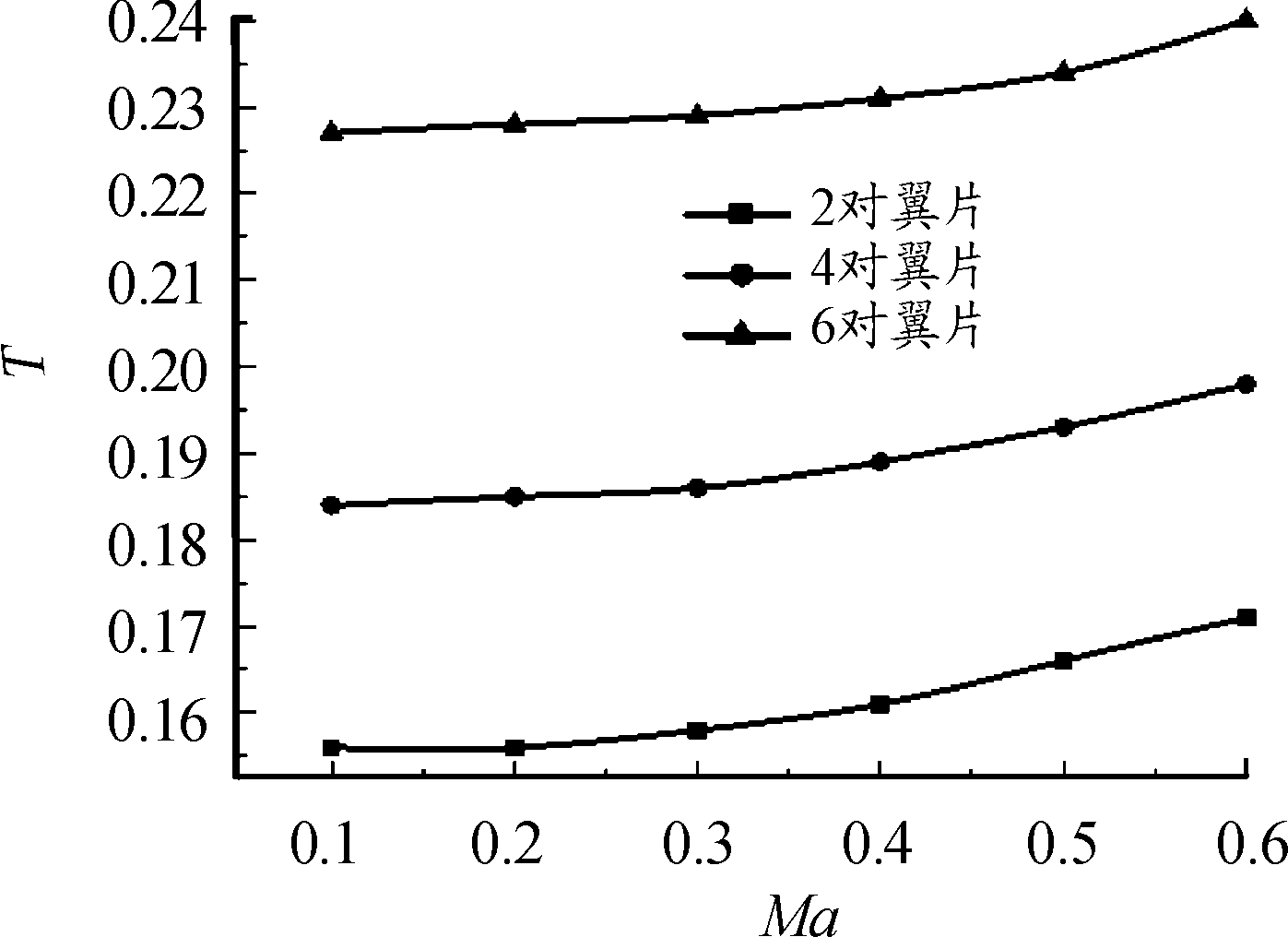
图9 稳定储备量(T)的变化曲线
3 气动外形参数优化
正交试验法是一种比较科学的试验方法,它利用一套规格化正交表来设计计算方案和分析试验结果,在比较多的试验中,选出少数几个代表性强的试验条件,并通过这几种试验的数据,找到最优的方案[7]。本节采用3因素三水平试验,以一个立方体表示3个因素的选优区,任一因素均为3个水平,则将立方体划分为了27个格点,在图上表示为27个“.”均为立方体内的点,如图10所示。选择图10中标记的9个点可使选优区内的基本情况得到非常全面的展现[8]。
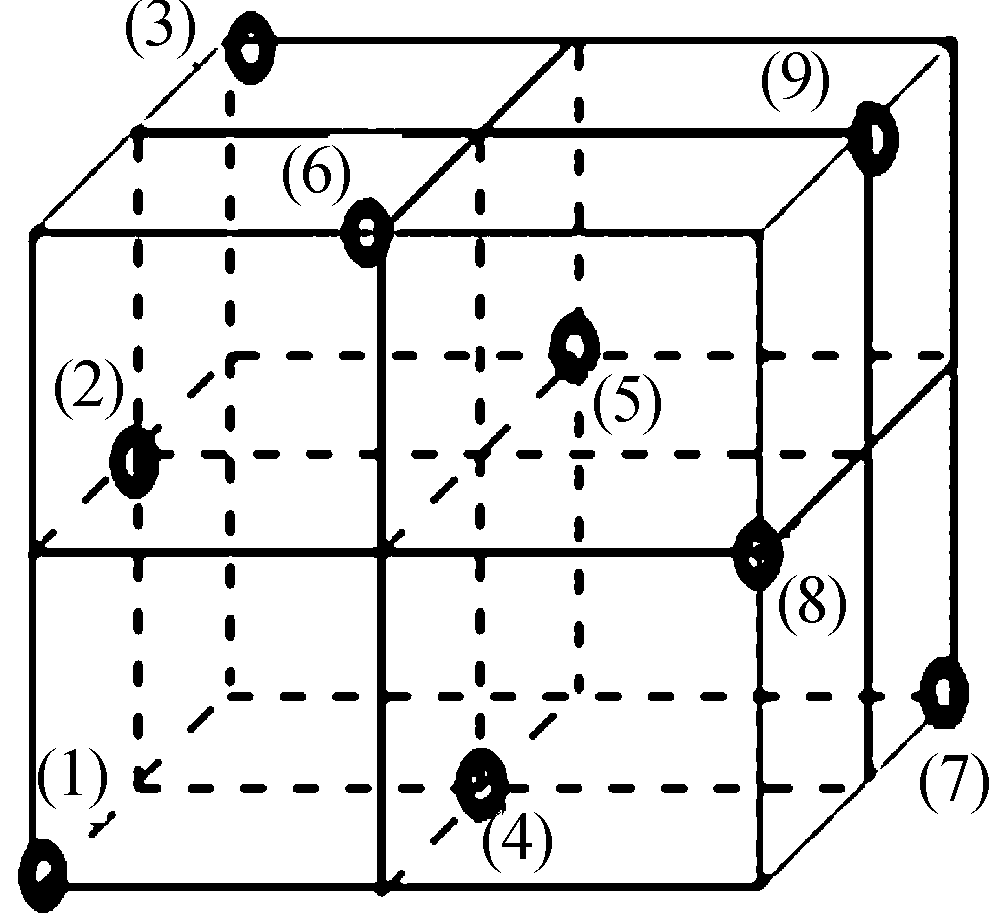
图10 3因素3水平试验的均衡分散立体图
对于头部形状半球形、球头截锥形、曲线母线形分别记为A1、A2、A3,3种不同的长细比λ=8、8.5、9分别记为B1、B2、B3,不同的尾翼对数:2对、3对、4对分别记为C1、C2、C3。则采用正交试验法的9个试验点分别为:方案(1)A1B1C1、方案(2)A2B1C2、方案(3)A3B1C3、方案(4)A1B2C2、方案(5)A2B2C3、方案(6)A3B2C1、方案(7)A1B3C3、方案(8)A2B3C1、方案(9)A3B3C2
通过对以上9组情况进行仿真计算,分析9种组合对升阻比CL/CD和稳定性影响,从而获得最佳的组合。在攻角α=4°时,图11稳定储备量随马赫数的变化曲线,图12为不同的试验方案下火箭弹的升阻比对比曲线。
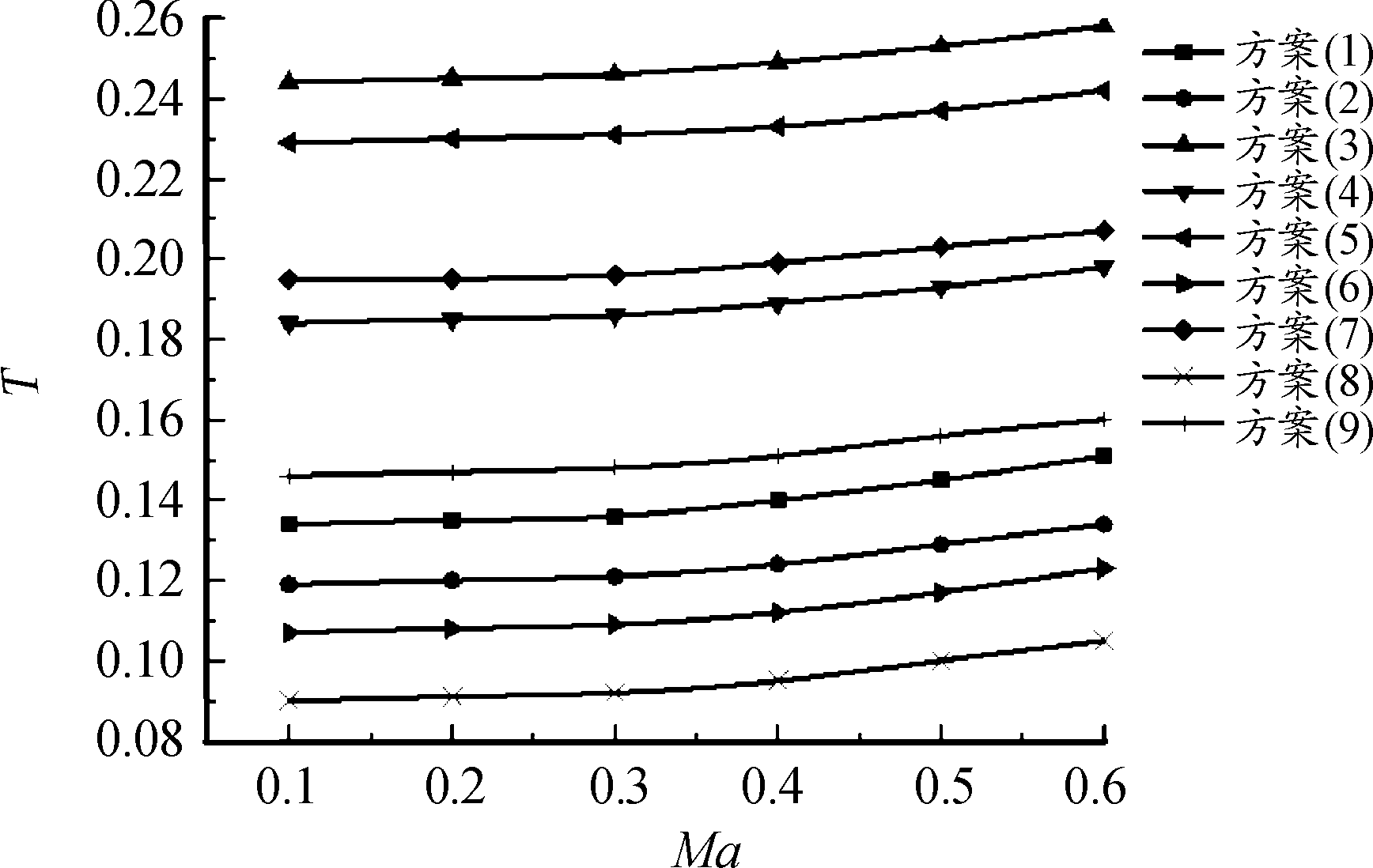
图11 稳定储备量(T)的变化曲线
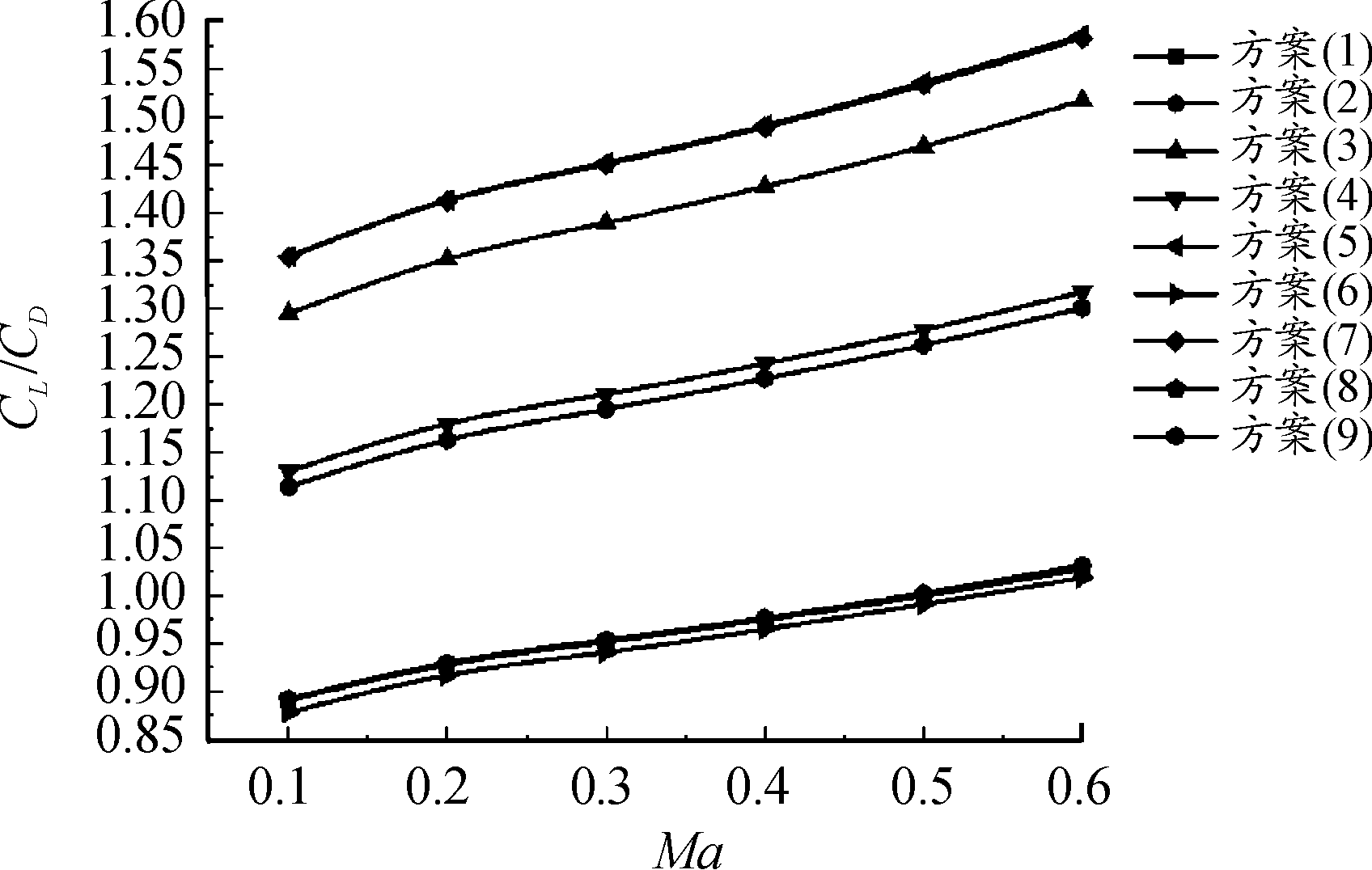
图12 升阻比变化曲线
分析可知方案(3)、方案(5)、方案(7)稳定储备量最高,且均是具有四对尾翼片的方案,可以看出长细比λ=8.5的方案稳定储备量相对比较高一些,头部形状对稳定储备量的影响较小,球头截锥形和曲线母线形两种方案较好一些。方案(5)、方案(7)的升阻比最大,方案(3)次之,从升阻比方面来看最优组合的选择和稳定性选择的一样,采用具有4对尾翼片、长细比λ=8.5、头部形状为球头截锥形或曲线母线形的方案。由于曲线母线形的头部较长一些,所以选择球头截锥形。采用正交试验法最终选择的方案是头部采用球头截锥形、长细比λ=8.5、4对尾翼片的结构。
对优选出的干扰弹的结构进行仿真计算,计算来流条件为:马赫数Ma=0.1、0.2、0.3、0.4、0.5、0.6;攻角α=0°、1°、2°、3°、4°。由仿真计算的出不同攻角下,阻力系数随马赫数的变化如图13所示,升阻力随马赫数的变化如图14所示,稳定储备量如表1所示。

图13 阻力系数(CD)随马赫数的变化曲线

图14 升阻比(CL/CD)随马赫数的变化曲线
表1 不同马赫数、攻角α下的稳定储备量
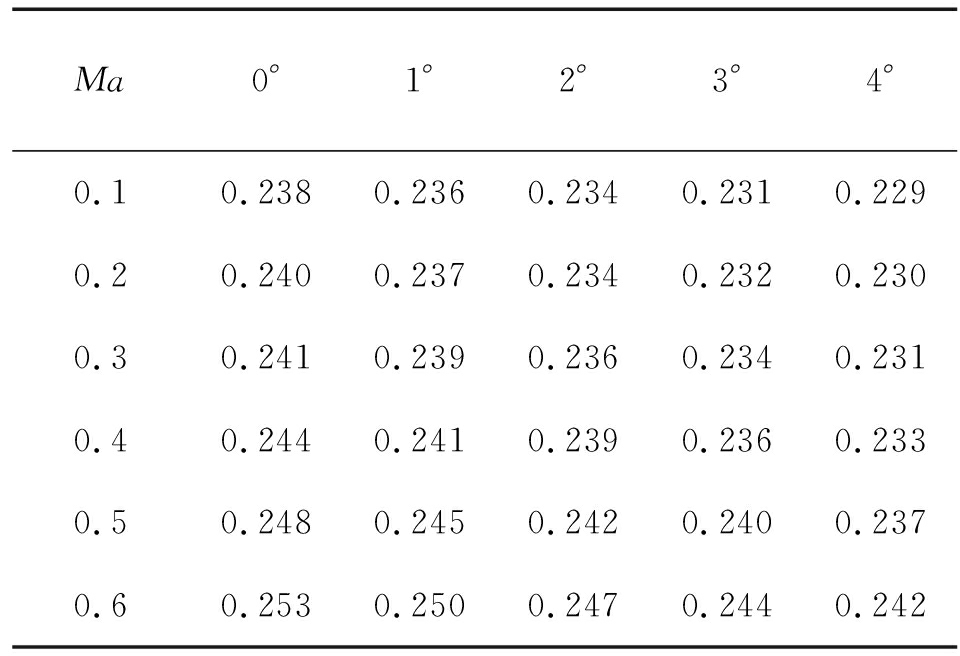
Ma0°1°2°3°4°0.10.2380.2360.2340.2310.2290.20.2400.2370.2340.2320.2300.30.2410.2390.2360.2340.2310.40.2440.2410.2390.2360.2330.50.2480.2450.2420.2400.2370.60.2530.2500.2470.2440.242
由图13、图14可看出随马赫数的增加,阻力系数的和升阻比的变化符合一般变化规律,均能满足要求;干扰弹的稳定储备量(T)在22.9%~25.3%,满足干扰弹的静稳定性要求。
4 弹道分析验证
采用质点弹道计算方法,仿真验证在不同射角下干扰弹的弹道特性,验证能否满足开仓抛洒干扰剂的指标。
射角:50°~85°仿真条件:标准气象条件。
通过仿真得到在不同射角下的速度-时间曲线和不同射角下的射程-射高曲线分别为图15和图16所示。
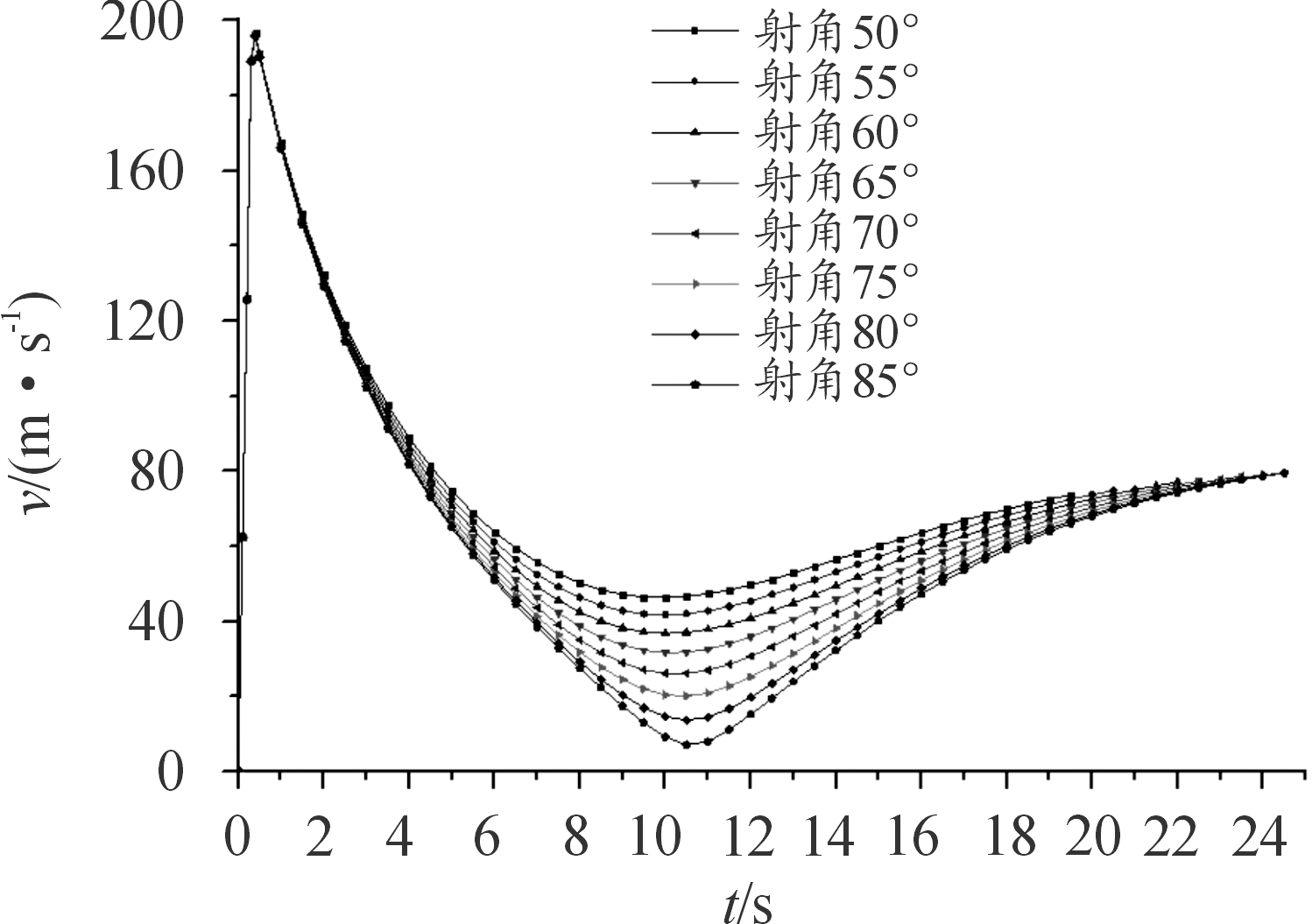
图15 不同射角下的速度-时间曲线
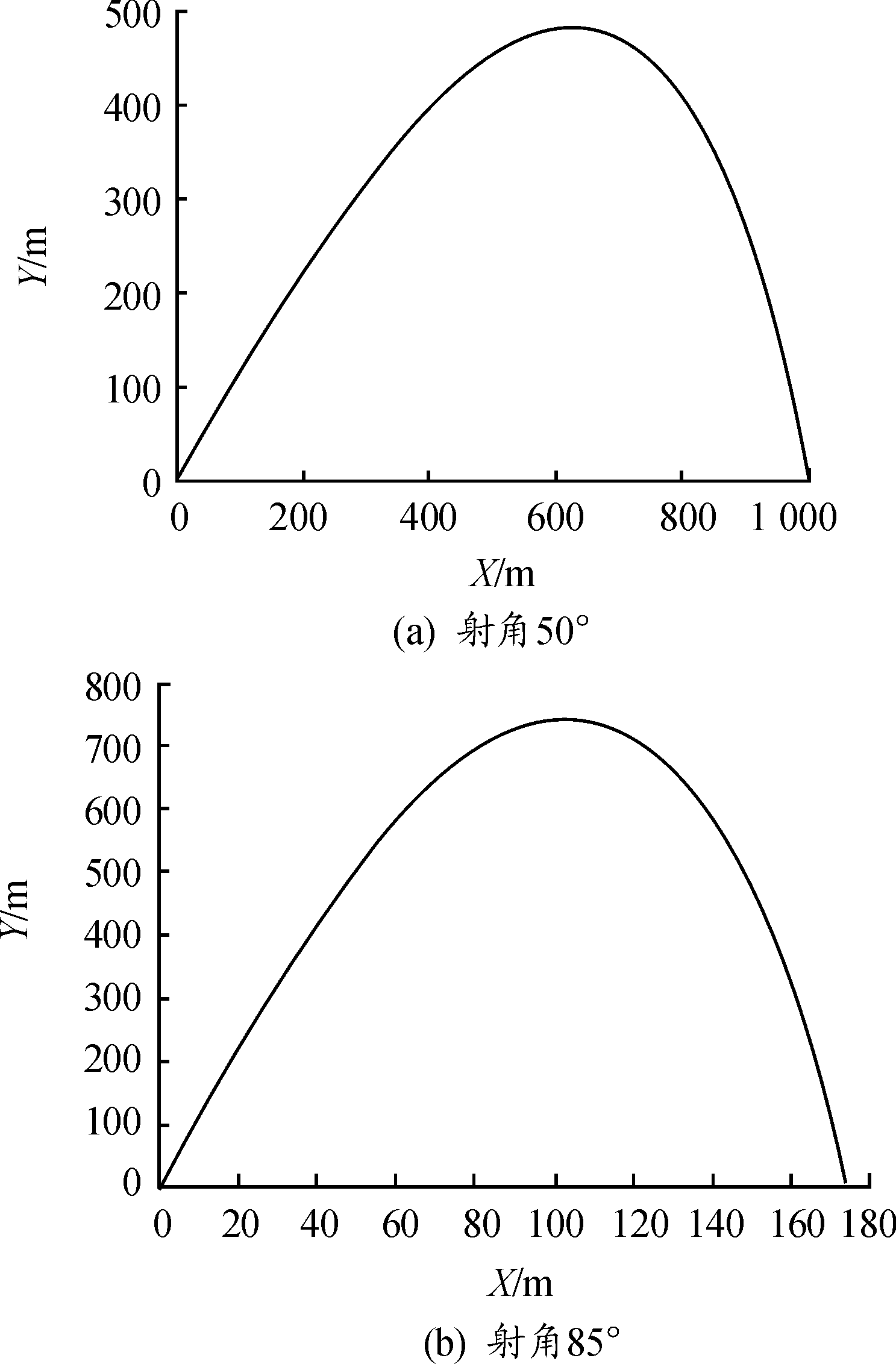
图16 不同射角下的弹道射程-射高曲线
干扰弹不同射角下速度随时间的变化曲线,可以看出0.32 s时发动机推进剂燃烧完全,此时速度达到最大值 200 m/s,然后速度先减小后增大,在射高最大处速度最小;在同一时间下,速度随着射角的增大而减小,符合一般的弹道速度变化规律。由图16看出不同的射角下,随着射角的增大射程减小,最大射高增大。在射角50°时最大射高最小482 m,射角85°时最大射高744.9 m。在射角50°时射程最大1 055.9 m,在射角85°时射程最小174.3 m。可将将开仓点设置上升段的200~500 m高度范围能满足一般舰艇的要求,仿真分析验证满足抛洒干扰剂的指标要求。
5 结论
根据反舰导弹的制导方式,设计一种低空干扰火箭弹。首先根据战技指标设计干扰弹的外形结构,然后进行流体力学仿真得到所选方案各有优缺点,通过正交试验法确定球头截锥形、长细比λ=8.5、四对尾翼片的结构方案最优,最后验证所选结构满足战技指标要求。
[1] 秦剑冬,邢昌风,吴玲.舰载软硬武器协同反导兼容性问题研究[J].舰船科学技术,2012(7):114-117.
[2] 谷良贤,温炳恒.导弹总体设计原理[M].西安:西北工业大学,2004.
[3] 郑健,鞠玉涛,陈雄.火箭弹设计理论[M].北京:北京理工大学出版社,2014.
[4] 温正.FLUENT流体计算应用教程[M].北京:清华大学出版社,2007.
[5] 陆飞龙.双鸭舵近距耦合效应及其对全弹气动特性影响的研究[D].南京:南京理工大学,2012.
[6] 于勇,张俊明.fluent入门与进阶教[M].北京: 北京理工大学出版,2008:86-107.
[7] 刘瑞江,张业旺.正交试验设计和分析方法研究[J].试验技术与管理,2010,27(9):52-55.
[8] 沈丽琴,桂涛.注塑工艺参数优化的正交法应用实例[J].电子机械工程,2010,26(4):39-42.