运动体入水问题的研究至今已有较长的历史,最初,学者Von Karman[1]引入了附加质量这个概念,获得了求解入水冲击载荷的理论方法。Herbert Wagner[2]考虑了楔形体入水过程形成的水面凸起及喷溅厚度,引入了楔底倾角修正因子,并采用伯努利方程,求解了楔形体沾湿表面的压力分布。Shiffman和Spencer[3-5]进行了大量的球体和锥体垂直入水理论研究。
Romain等[6]引入FCB概念,使用 ABAQUS /Explicit 软件对非对称体垂直入水进行数值模拟研究。Bao等[7]开展了低速非对称体楔形体垂直、倾斜和旋转角度进入水数值仿真研究。Korobkin把入水过程流体运动分为五个阶段[8-10]并建立了模型进行了具体的研究。
叶取源[11-12]建立了圆锥体垂直入水的三维数值模型,得到了入水空泡从形成、发展到闭合的变化规律。张岳青等[13]对于鱼雷入水的忽扑现象进行了研究,针对鱼雷入水复杂的过程, 利用实验和数值仿真结合的方法,对造成忽扑的低压力进行了分析。王瑞琦等[14]进行了平头弹丸低速入水实验与数值仿真,通过获得不同时刻的实验图像和数值仿真图像,对表面闭合空泡和深闭合空泡进行了分析,获得了射弹冲击水面时产生的射流对射弹运动的影响。熊天红等[15]在实验室的水靶道中进行了 4 种不同结构参数的射弹实验,并使用 FLUENT 软件针对实验做了一系列数值仿真,对影响射弹阻力特性的弹体长径比、空化器直径、空化数等因素进行了分析。
以开展高速射弹入水转向弹道特性研究为背景,本文拟运用数值仿真方法对不同角度、不同入水速度的射弹高速入水转向问题进行研究,分析系列入水参数下,弹塑性射弹入水过程受力情况,揭示射弹入水转向规律,具有一定的参考价值。
1 计算模型
1.1 有限元模型
本文采用AUTODYN 软件进行数值仿真。
对于高速射弹入水问题,本文采用一种切削15°的射弹结构,如图1所示。其网格使用Workbench软件进行划分,因为形状比较复杂,采用六面体网格效果不好,因此采用的四面体自由网格划分,弹身长78.5 mm,直径 12.7 mm,网格尺寸大小选取1.5 mm,典型网格示意图见图2。

图1 射弹示意图

图2 典型网格示意图
为减小计算量采用二分之一模型进行计算。水域尺寸设置为射弹各尺寸的10倍,水域尺寸为800 mm、800 mm、60 mm,网格尺寸大小为1 mm,网格总数为38 400 000 个。射弹入水处设为距离右边界四分之一处,选定标准之后的局部网格划分如图3。

图3 计算模型局部网格图
针对8种情况做了数值仿真计算,具体编号如表1所示。
表1 各种入水条件编号
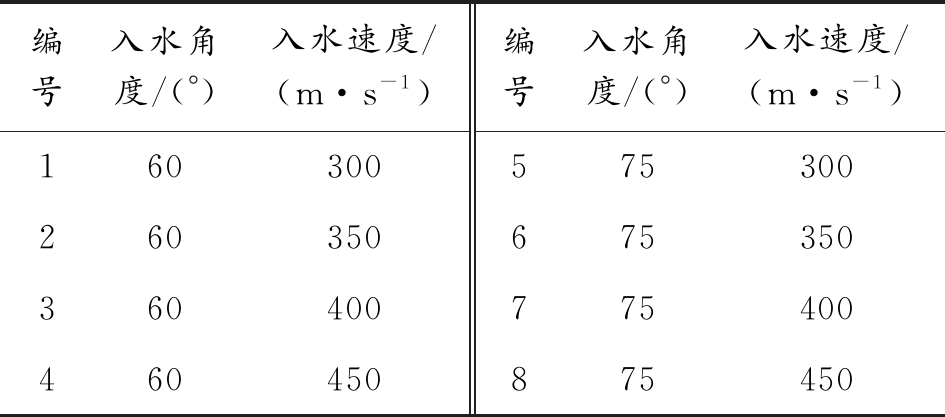
编号入水角度/(°)入水速度/(m·s-1)编号入水角度/(°)入水速度/(m·s-1)160300575300260350675350360400775400460450875450
1.2 材料模型和参数
射弹的材料模型选取STEEL S-7 高强度钢材料,状态方程则选取Shock状态方程,强度模型则选取JC强度模型,该种材料模型的状态方程参数如表2所示。
表2 STEEL S-7材料参数
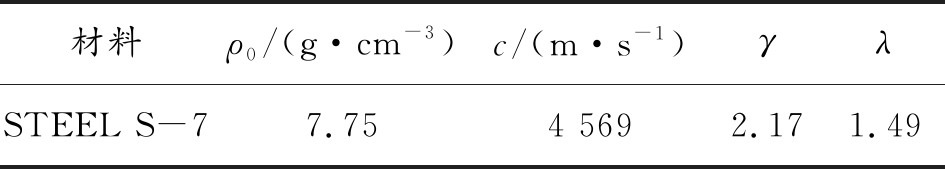
材料ρ0/(g·cm-3)c/(m·s-1)γλSTEEL S-77.754 5692.171.49
在1983年,Johnson GR和Cook W.H提出了Johnson-Cook(JC)模型,该模型对温度以及应变较敏感,且其参数通过实验数据拟合相对比较容易获得,能够较好地描述金属材料的应变和由于温升出现的软化效应,这种材料本构在冲击、爆炸等领域均有通用性较强等优点。对于本文射弹高速入水转向引起的大变形、高应变率等问题,采用该强度模型可以提供还原度较高的模拟,该模型屈服应力定义为:
其中
式中:σy 为材料屈服强度;εp 为等效塑性应变;![]() 其中
其中![]() 为等效应变率,
为等效应变率,![]() 为参考应变率。T为材料瞬时温度。A为材料在准静态下的屈服强度;B为硬化常数;n为硬化指数;C为应变速率常数,m为温度软化系数Tr 为参考温度,Tm为材料熔点。STEEL S-7的Johnson-Cook强度模型如表3所示。
为参考应变率。T为材料瞬时温度。A为材料在准静态下的屈服强度;B为硬化常数;n为硬化指数;C为应变速率常数,m为温度软化系数Tr 为参考温度,Tm为材料熔点。STEEL S-7的Johnson-Cook强度模型如表3所示。
表3 STEEL S-7的Johnson-Cook强度模型参数

材料剪切模量/GPa屈服强度/GPa硬化常数/GPa硬化指数应变速率常数STEEL S-781.81.530.4770.180.012
水的多项式状态方程根据压缩状态的不同具有不同的形式。
当水压缩时(μ>0 时),状态方程为:
P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e
当水膨胀时(μ<0时),状态方程为:
P=T1μ+T2μ2+B0ρ0e
当水既不压缩也不膨胀时(μ=0时),可以简化为同一形式:
P=B0ρ0e
式中: P为水中压力;μ为压缩比,μ=ρ/ρ0-1 ; e为水的内能; ρ0 为水密度。
水的SHOCK状态方程为:
P=PH+Γρ(e-eH)
式中,PH和eH分别为材料冲击Hugoniot态的压力和比动能; Γρ为Gruneisen系数。
这里假设Γρ=Γ0ρ0=常数,且
式中: ρ0 和e0 分别为材料初始密度和声速; μ为材料的压缩比; λ为冲击Hugoniot参数; λ 和e0为常数,由以下冲击波实验关系式确定:
D=λu+e0
式中:D为冲击波速度; u为波后质点速度。
2 射弹入水应力分析
为了便于进行分析,对弹体进行上、侧、下部的定义,弹头切削平面与弹体轴线为15°角(参见图1),在弹体入水运动过程中,弹头的切削平面朝向水域,因而与弹体切削平面同一侧的弹体部位定义为弹体下部,与之相反,在弹体切削平面另一侧的弹体部位定义为弹体上部。选用工况3的射弹对其入水航行初期、航行中期及航行末期进行受力分析,所得压力云图如图4~图6所示。

图4 0.5 ms时刻射弹上、侧、下部压力云图
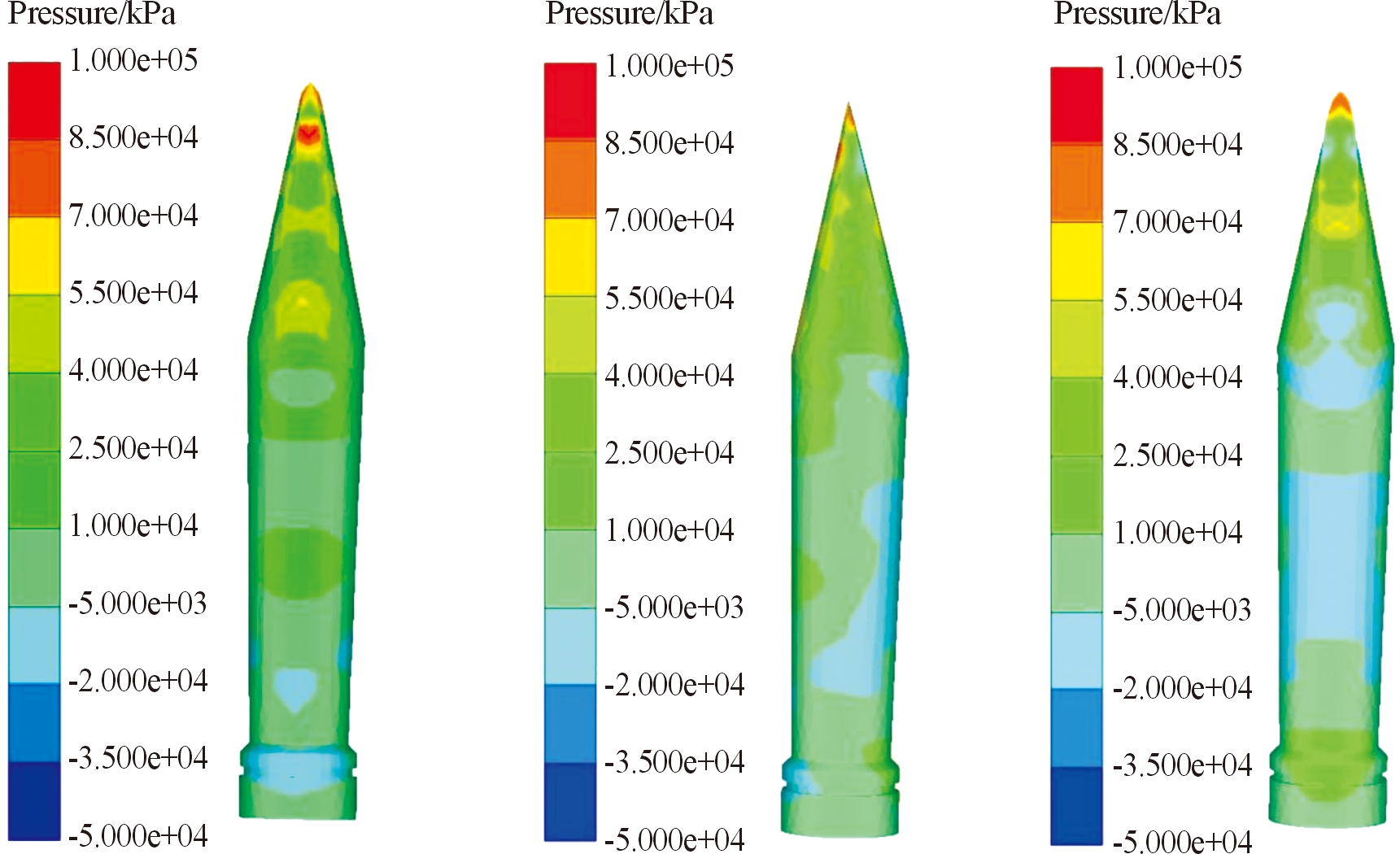
图5 1.5 ms时刻射弹上、侧、下部压力云图
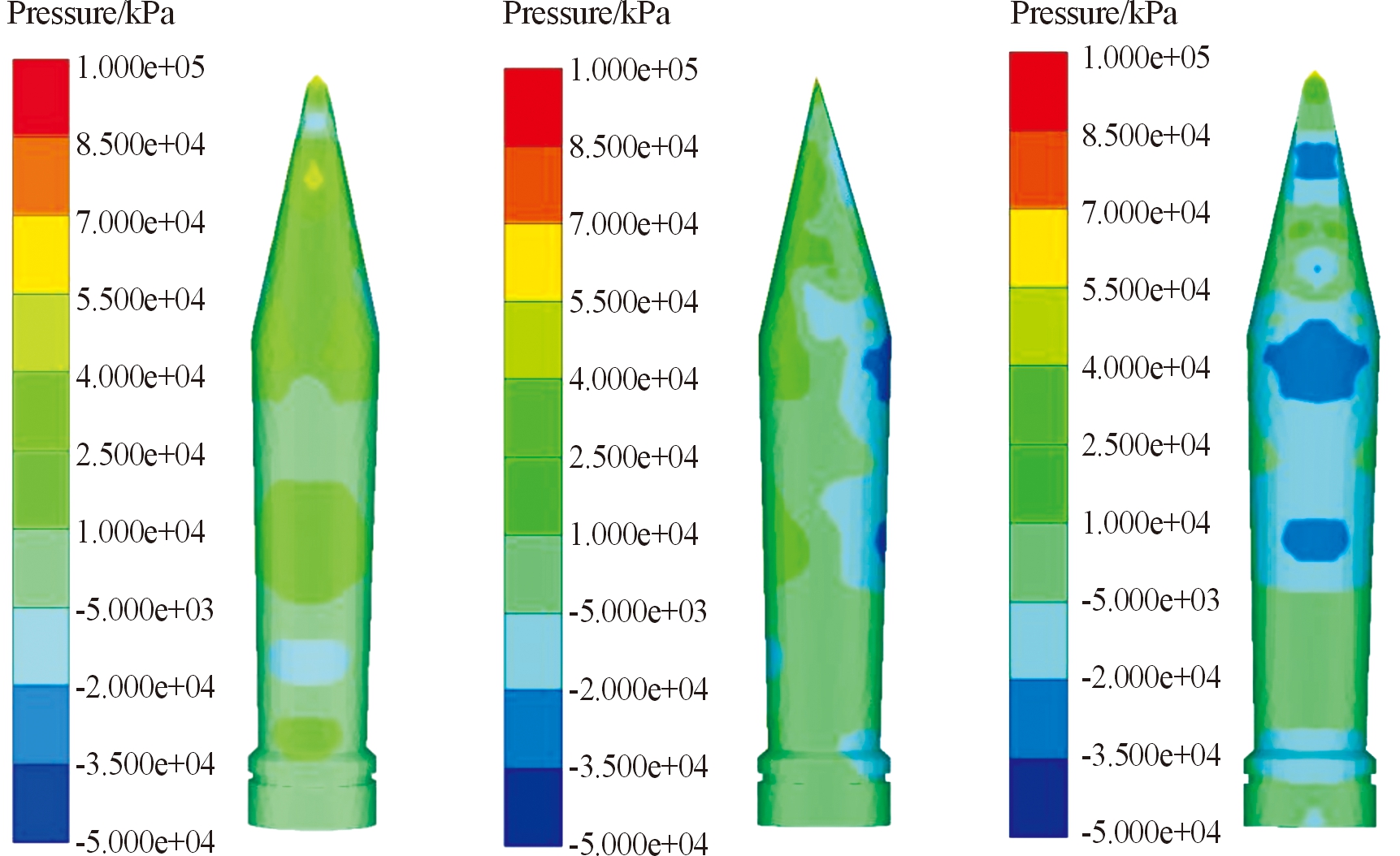
图6 2.5 ms时刻射弹上、侧、下部压力云图
由云图可以看出,航行初期(0.5 ms)射弹压力主要集中在头部,而射弹中部至尾部受力非常小,此时由运动轨迹(图7)可以看出,射弹刚入水时形成超空泡,射弹后部几乎没有碰到水域,头部是主要的受力部分。在航行中期(1.5 ms)压力则主要集中在射弹下部,此时射弹下部基本全部与水域接触,而射弹上部进一步远离水域,导致头部受力略微增大。在航行后期(2.5 ms),射弹上部受力持续减小,射弹下部压力受力位置有向弹尾移动的趋势,原因是随着入水时间的推移,空泡有闭合的趋势,这个时刻与 1.5 ms时刻相比弹尾与水域接触的更彻底,且射弹偏转角度更大,射弹前部受力更小,因此呈现出受力位置向弹尾移动的趋势。同时射弹上部仍不接触水域,主要受力与弹体前部的受力及弹头的应力有关,因此射弹上部受力也更小。
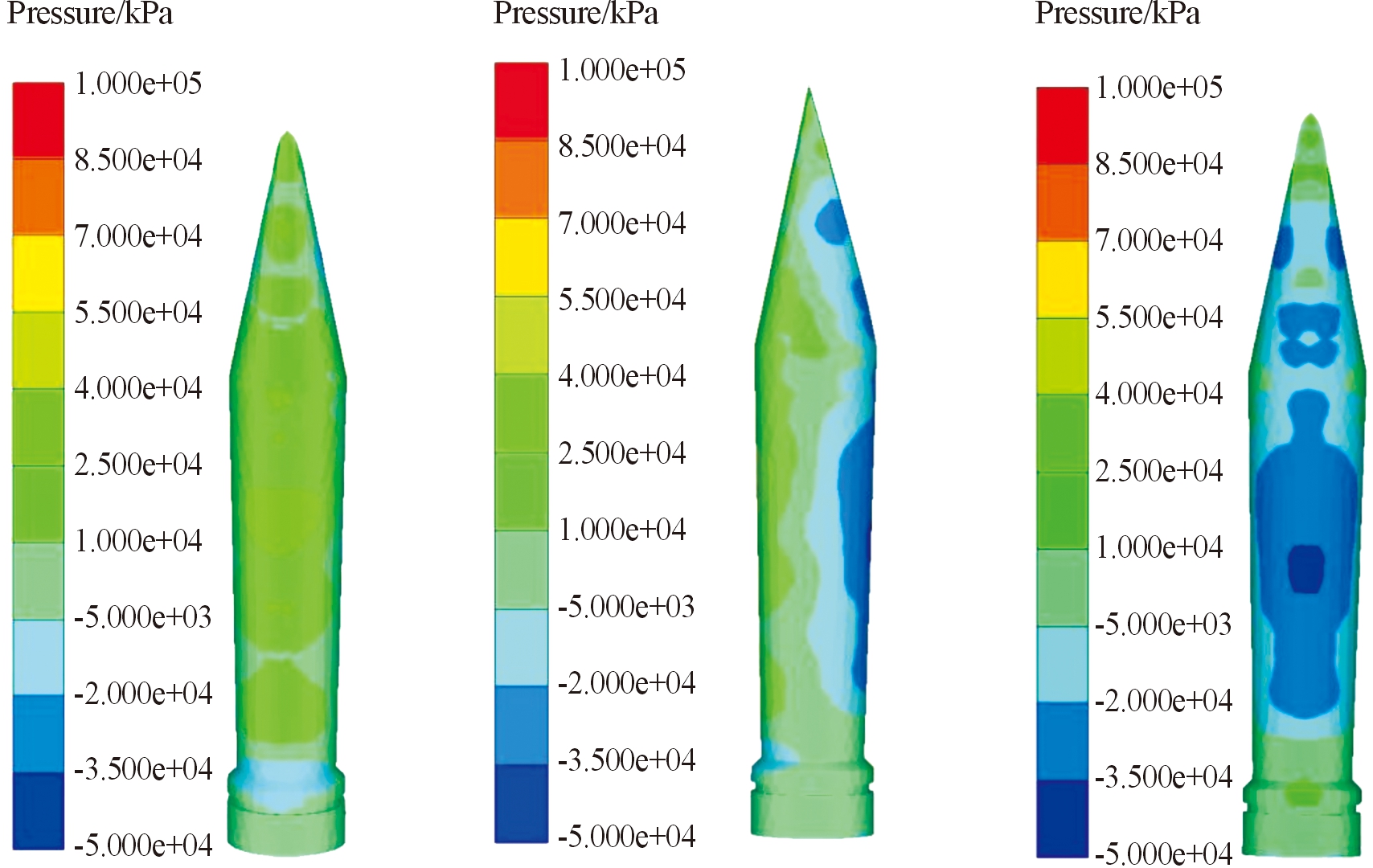
图7 各时刻射弹入水轨迹图
3 入水角度影响分析
由于射弹垂直入水时,射弹会出现弹道失稳的情况。由此,本文采取斜入水的方式进行仿真,为了方便建模与分析,采用 60°和 75°两种入水角度。通过仿真得出的数据绘制出相同入水速度下不同入水角度的俯仰角变化曲线,进行入水角度对射弹入水转向影响的分析,仍规定俯角初始为正,仰角初始为负,如图8。
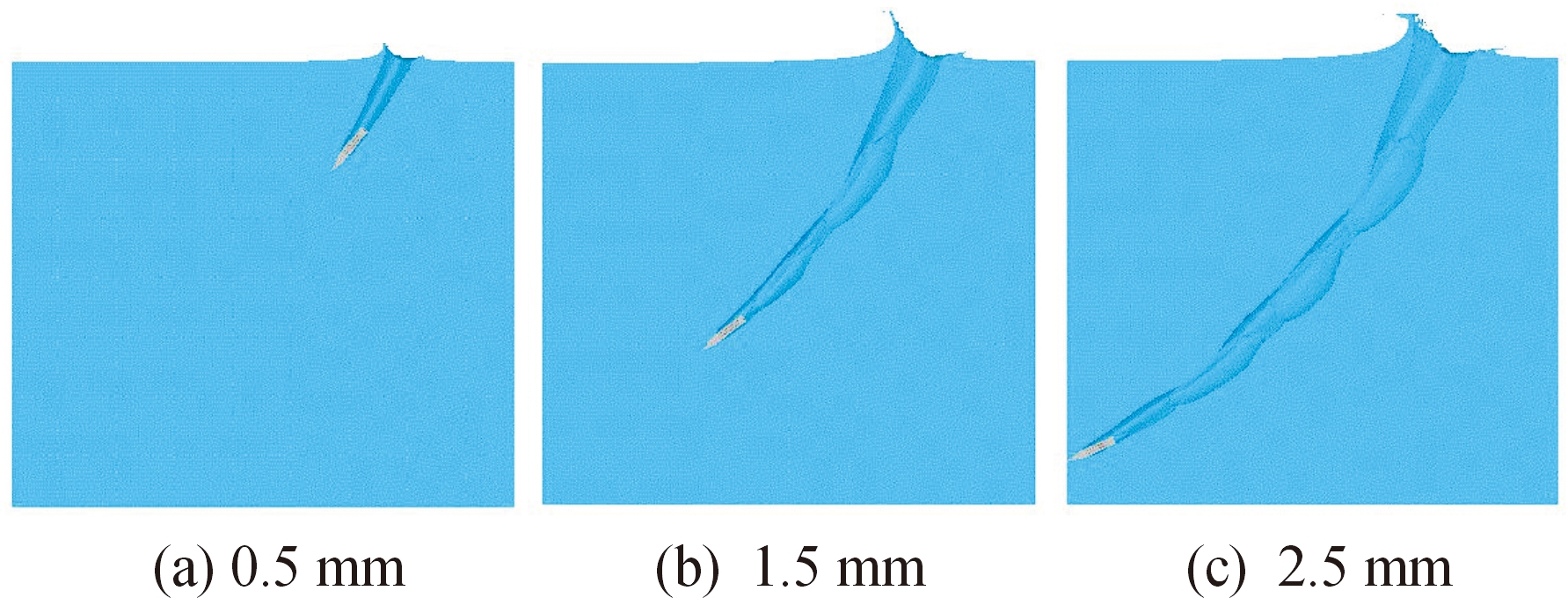
图8 各速度下俯仰角曲线
由图8可以看出,俯仰角曲线中,前0.5 ms由于射弹只有头部受力,弹身与水域不接触,俯仰角变化与入水角度关系不大,两种角度下的俯仰角减小的速率相当。
当0.5 ms之后射弹俯仰角在 0.5~1 ms之间由于发生了第一次忽扑,俯仰角快速减小,而60°的射弹俯仰角下降速率更大,说明在从忽扑中恢复之后,入水角度为60°的射弹转向更大。1 ms之后,两种入水角度的俯仰角下降速度都开始变缓,初始角度为60°的射弹在之后的阶段角度变化速率稍快。说明入射角度为60°的射弹转向效率较高。
规定水平方向速度为Vx竖直方向速度为Vy,其曲线如图9、图10所示。
水平方向速度上,入水角度为75°的射弹水平速度在波动的同时有明显提升,而通过具体数据分析,速度提升至少 50%以上,而入水角度为60°的射弹水平速度提升不显著,提升不超过 20%,从这一点上来看,入水角度 75°比入水角度60°对射弹转向的影响更好一些。从速度曲线的波动程度来看,入水角度60°射弹的水平方向速度波动程度更小一些,而入水角度 75°的射弹水平方向速度波动程度更大一些,同时入水角度为60°的射弹忽扑开始都要略早于入水角度为75°的射弹,忽扑结束也早于入水角度为75°的射弹,且每个忽扑周期入水角度为 60°的射弹都比入水角度为75°的射弹短,其在2.5 ms之前共发生4次忽扑,而入水角度为75°的射弹在 2.5 ms之前共发生3次忽扑,说明射弹在发生忽扑之后,入水角度为60°的射弹比入水角度为75°的射弹可以更快地恢复弹道稳定,主要是由于在相同时间下,入水角度为60°的射弹弹身下部接触水域面积比入水角度为75°的射弹大,受力更均匀,因此弹道更容易恢复稳定,于是在相同时间内忽扑的次数更多,且在不断地忽扑过程中,射弹逐渐转向。综上所述,入水角60°对射弹转向更为稳定更有利。
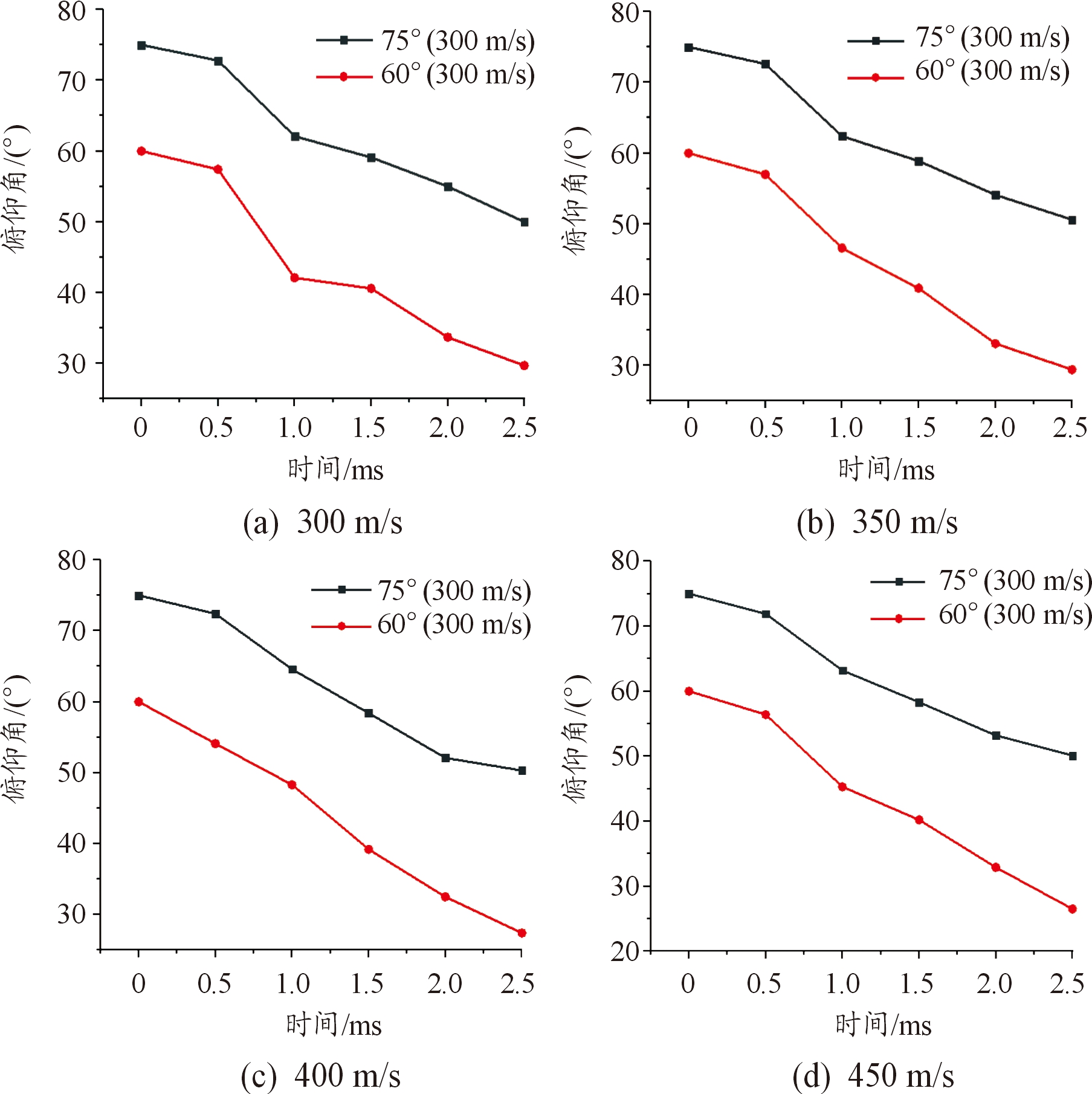
图9 各初速下不同入射角度水平方向速度曲线
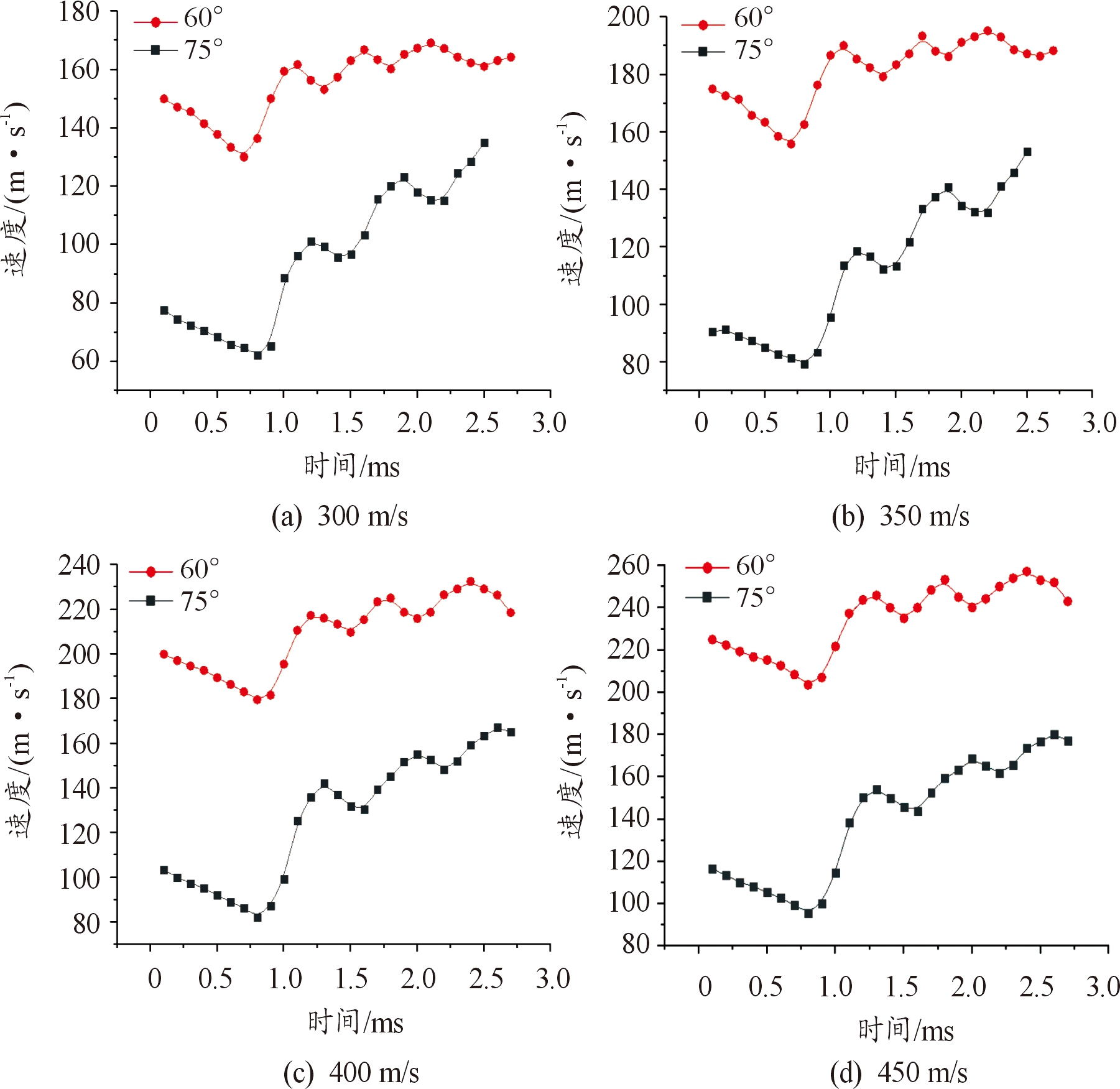
图10 各初速下不同入射角度竖直方向速度曲线
4 入水速度影响分析
由于在各种速度条件下环境存在差距,可能会对射弹入水产生影响,因此绘制出相同入水角度下不同入水速度的俯仰角变化曲线,进行入水速度对射弹入水转向影响的分析,仍规定俯角初始为正,仰角初始为负,如图11所示。
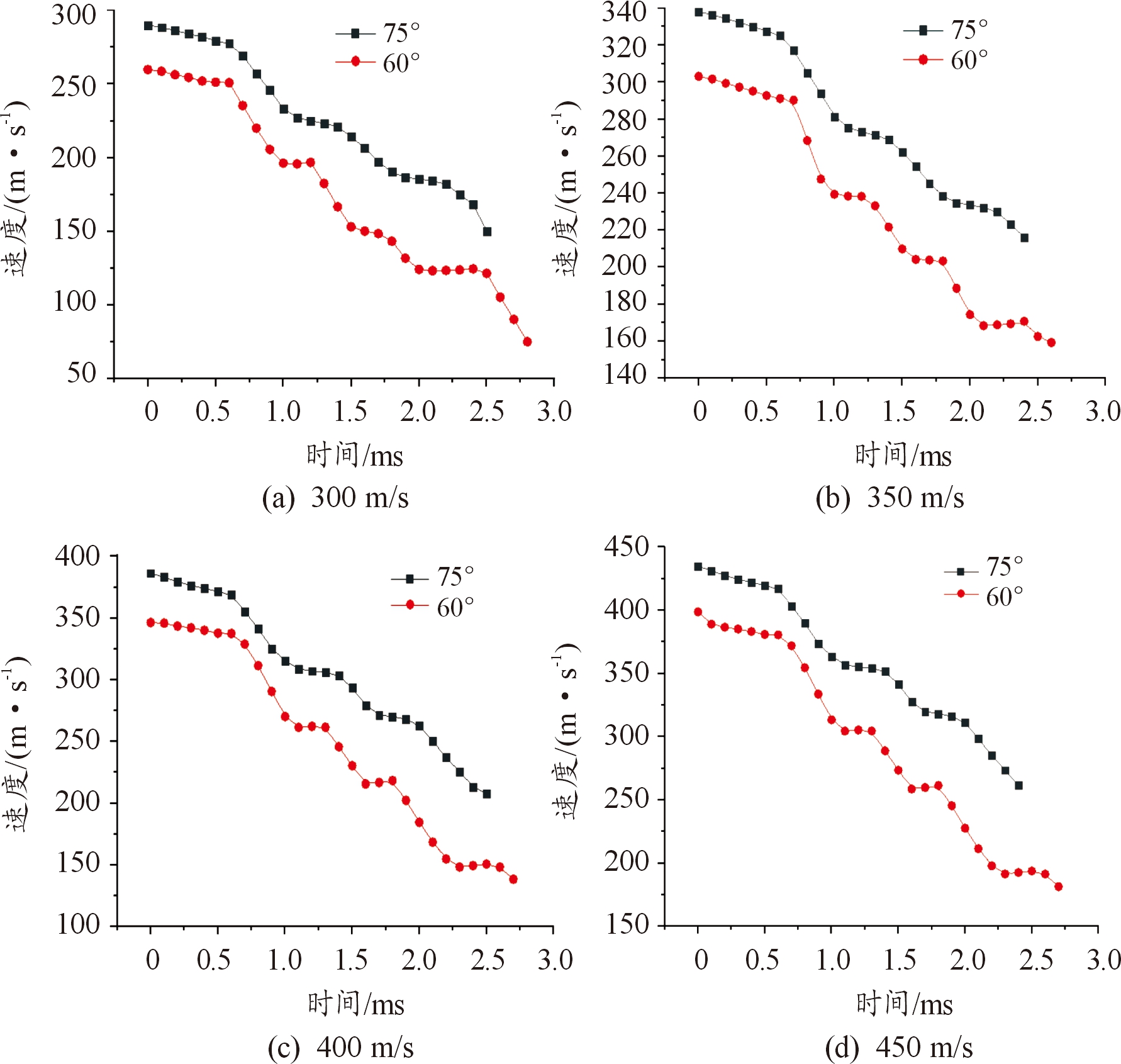
图11 入射角度为60°、75°下俯仰角曲线
由俯仰角曲线图中可以看出,0.5 ms之前,射弹刚入水,4种速度下俯仰角变化幅度都很小,但可以明显看出入水速度较低的射弹俯仰角变化更为剧烈,根据数据分析,0.5 ms时刻入水速度为400 m/s的射弹俯仰角要比其他速度的射弹要低3°~4°,可以看出在0.5~1 ms之间,射弹俯仰角变化较大,上文中也进行了分析,由于正好处于第一次波动最大的忽扑状态,因此俯仰角变化较大,1 ms之后,射弹俯仰角变化趋于平缓,这时速度最小的射弹,俯仰角变化最为平缓,在这之后四种速度的弹体俯仰角变化趋于一致,速度较小的弹体变化相比于速度较高的弹体变化略为平缓,差别很小可以忽略不计。从稳定性和转向效率来说,在后期稳定性相差不大的情况下,转向效率更好的入水速度明显对射弹入水转向有着更好的影响,在本文的速度范围内,入水速度更高的射弹有着更好的稳定性和转向效率。
由速度曲线可以讨论期间发生的各种变化,例如各种射弹经历的忽扑,以及在亚音速和超音速条件下对射弹的各种影响,也是讨论入水速度对射弹的转向能力影响的重要因素。规定水平方向速度为Vx竖直方向速度为Vy,以及合速度Va,有关曲线如图12~图14。
由图可知,初入水时,由于只有头部受到阻力,因此弹体水平方向速度下降率差距不大,而速度更低的弹体到达忽扑点的时间更早,而速度更高的弹体忽扑时间点随速度的增大而略微滞后,到达忽扑点后,水平与竖直方向上的速度变化都十分剧烈,在之后时间里,射弹在经历了第一次忽扑之后速度都随着之后的忽扑呈现波动上升的状态,可以看出,在第1次上升与第2次上升时,入水速度更高的射弹速度上升幅度要大于入水速度低的射弹,其后上升幅度逐渐接近,说明入水速度更高的射弹在将速度转换为水平方向速度上更有优势。
竖直方向速度上,初入水时速度下降仍然不快,射弹竖直方向速度随着每一次的忽扑呈波动下降状态,入水速度高的射弹竖直方向速度下降地要比入水速度为低的射弹快,且入水速度高的的射弹竖直方向速度逐渐靠近入水速度低的射弹,原因之一是射弹速度快则弹体受力更大,减速更快,其二是从之前的分析中可以得出,由于射弹进行了更大的转向,因此竖直方向速度有一部分转换为水平方向速度。总的来看入水速度越高的射弹,转向能力与稳定性更好,同时能量损失相比于低速射弹并没有太大。
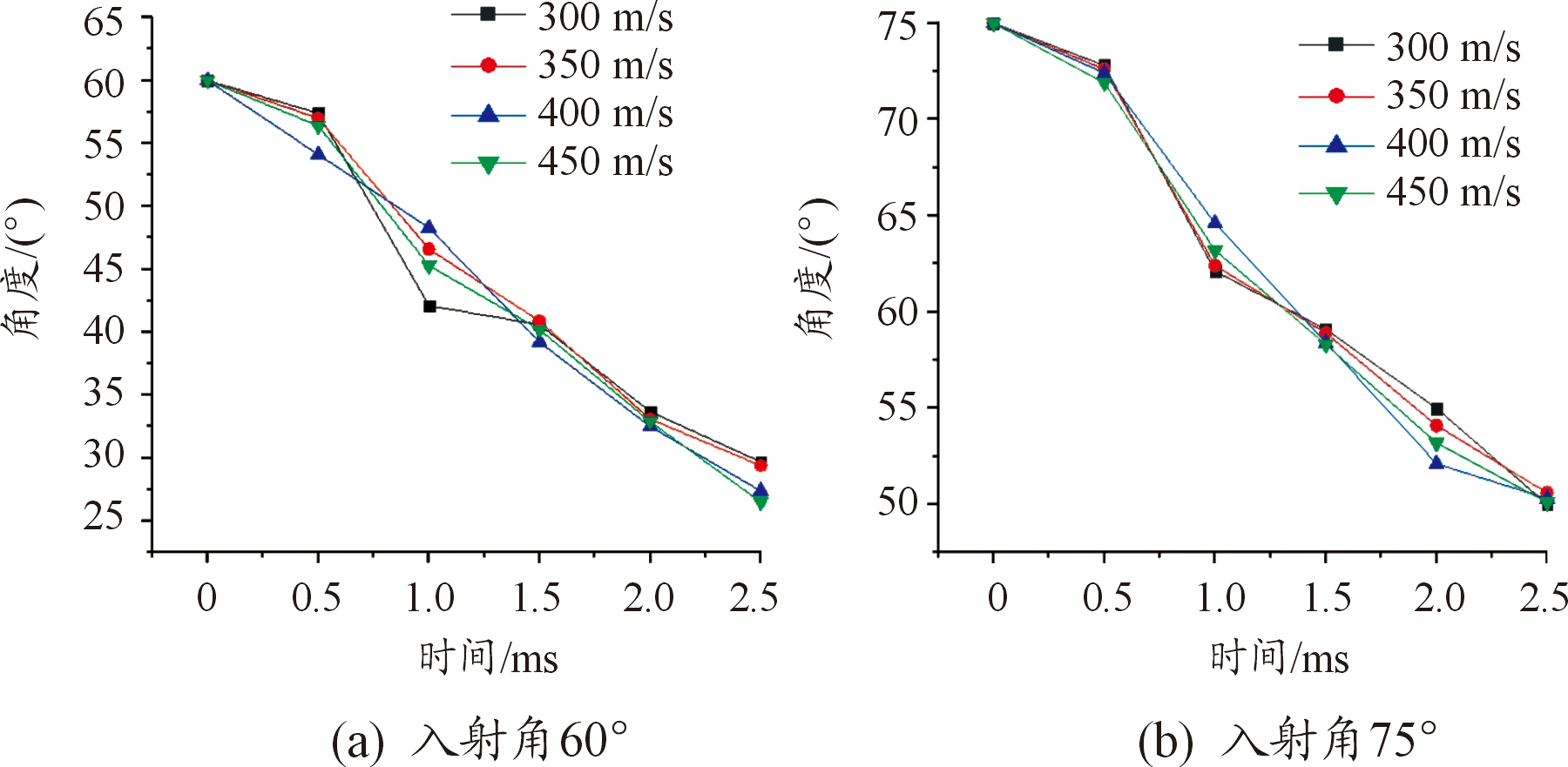
图12 入射角为60°与75°条件下各初速水平方向速度曲线
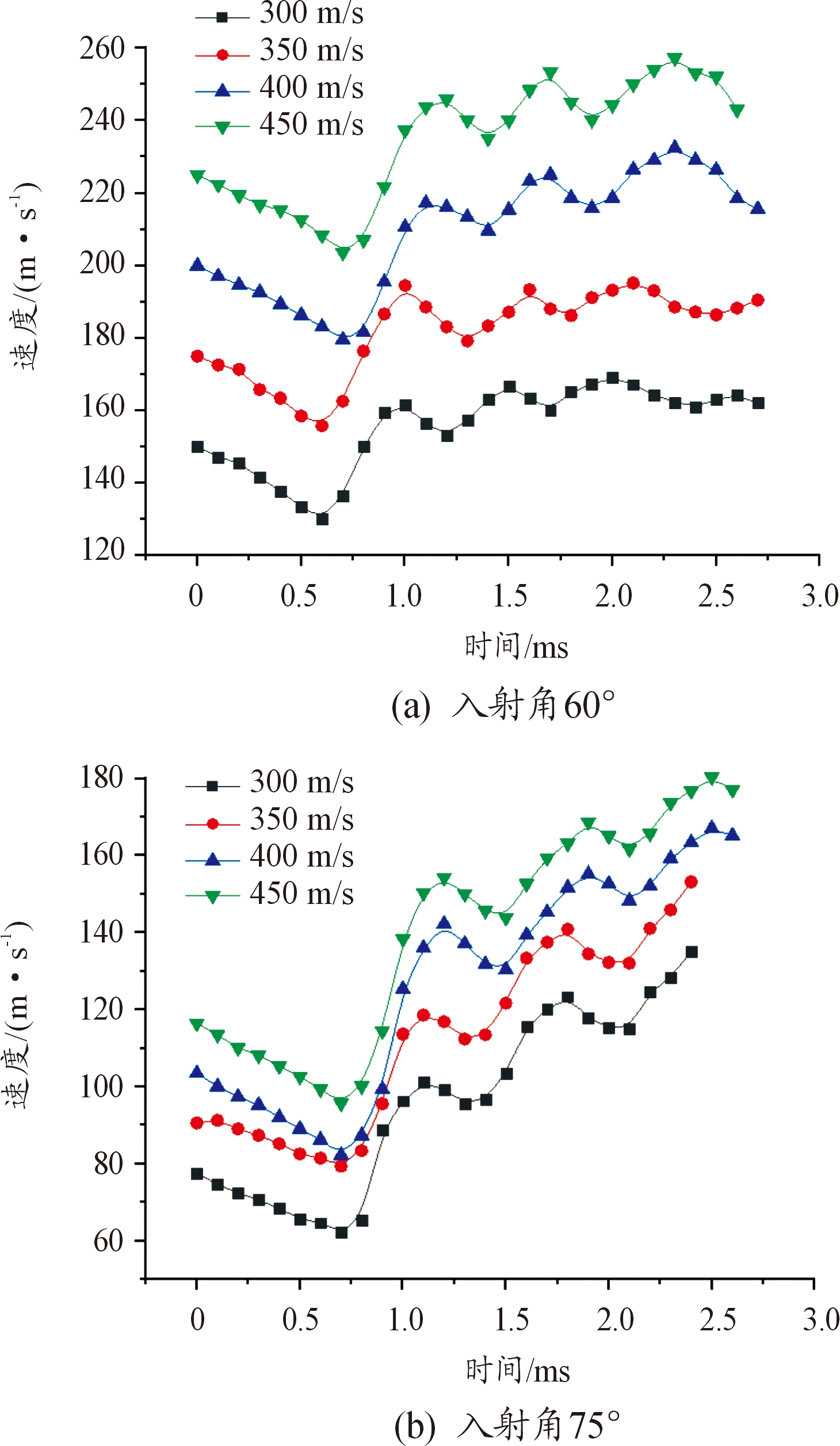
图13 入射角为60°与75°条件下各初速竖直方向速度曲线
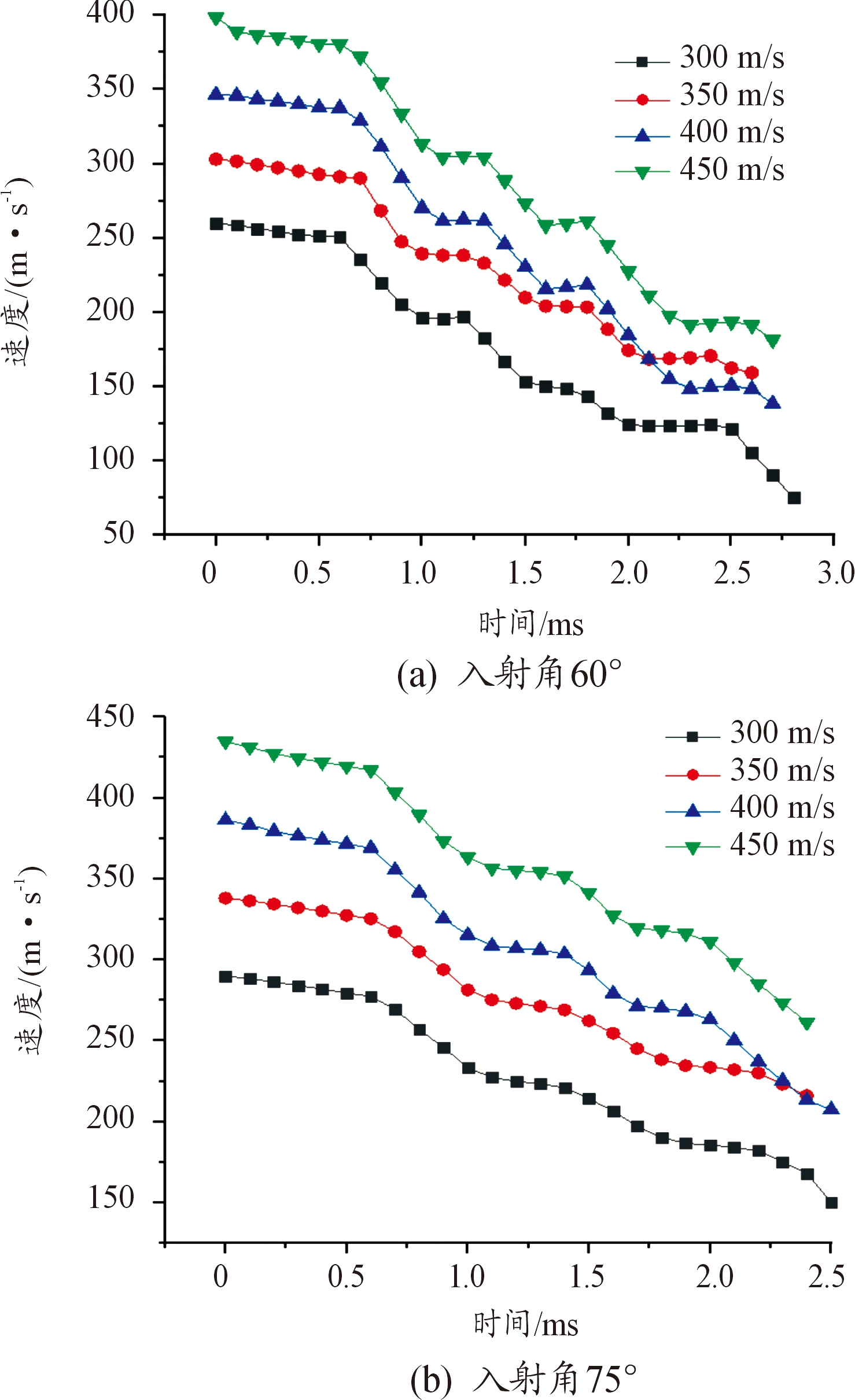
图14 入射角为60°与75°条件下各初速射弹合速度曲线
5 结论
1) 弹塑性钢制射弹入水初期应力应变主要集中在射弹的头部,应力在入水初期增加极快,随着入水时间的增加,射弹下部受力变大,而射弹上部逐渐远离水域,射弹逐渐完成转向。
2) 带有15°切削角的异形弹塑性射弹在入射角度分别为60°和75°的跨介质入水过程中都展现了良好的转向性能,其中入射角为60°的射弹的稳定性及转向性能更为优良。
3) 在相同入射角的情况下,在300 m/s到450 m/s的速度范围,随着射弹速度的提高射弹入水后的弹道稳定性提升,且转向性能提高,但能量损失增大,在入水速度为450 m/s情况下0~2.5 ms间弹体的动能损失是入水速度为300 m/s情况下动能损失的2倍以上。速度更高的射弹具有更好的转向性能与稳定性,但弹体能量损失也更大。
[1] VON KARMAN T.The impact on seaplane floats during landing[J].1929.
[2] TRANS W H.Phenomena associated with impacts and sliding on liquid surfaces[J].Journal of Applied Mathematics and Mechanics,1932,12(4):193-215.
[3] SHIFFMAN M,SPENCER D C.The force of impact on a sphere striking a water surface (approximation by the flow about a lens)[R].AMP Report 42.1R AMG-NYU no.15,Applied Mathematics Panel,February 1945.
[4] SHIFFMAN M,SPENCER D C.The force of impact on a sphere striking a water surface (second approximation)[R].Report 42.2R AMG-NYU no.133,Applied Mathematics Panel,July 1945.
[5] SHIFFMAN M,SPENCER D C.The force of impact on a cone striking a water surface(vertical entry)[J].Communications on Pure and Applied Mathematics,1951(4): 379-417.
[6] HASCOЁT R,JACQUES N,SCOLAN Y M,et al.Applied OceanResearch[J].2019,92:101878.
[7] BAO C M,WU G X,XU G.Water entry of a finite width wedge near a floating body[J].Applied Ocean Research,2019,84:12-31.
[8] KOROBKIN A.Blunt-body impact on a compressible liquid surface[J].Journal of Fluid Mechanics,2006,244(01):437-453.
[9] KOROBKIN A A.Blunt-body impact on the free surface of a compressible liquid[J].Journal of Fluid Mechanics,1994,263(01):319-342.
[10] KOROBKIN A A.Acoustic effects on water impact[C]//Proc.10th Int.Workshop on Water Waves and Floating Bodies,Oxford.1995.
[11] 叶取源.锥头物体垂直入水空泡的发展和闭合[J].水动力学研究与进展:A辑,1989(02):33-41.
[12] 叶取源.用E-L方法计算圆平头物体垂直入水空泡的表面闭合和深闭合[J].应用力学学报.1990,7(4):17~25.
[13] 张岳青,蔡卫军,李建辰,等.鱼雷斜入水忽扑现象数值仿真[J].水下无人系统学报,2018,26(2):146-151.
[14] 王瑞琦,黄振贵,朱世权,等.平头弹丸入水空泡闭合实验研究及数值模拟[J].兵器装备工程学报,2017,38(12):36-39.
[15] 熊天红,易文俊.高速射弹超空泡减阻试验研究与数值模拟分析[J].工程力学,2009,26(08):174-178.