1 引言
在飞机的模拟仿真过程中,飞机气动参数辨识是飞行控制律参数调整、飞行仿真等工作的前提和基础[1]。快速访问记录器(quick access recorder,QAR)数据忠实记录了飞机运行中大量原始数据[2],包含与飞机空气动力学特性相关的变量,因此QAR数据可以用于辨识飞机气动参数。并且相对于飞行测试数据,QAR数据获取相对容易,利用QAR数据辨识飞机气动参数也是一种可行的技术途径。
王青等[3]结合QAR数据和神经网络Delta法估计高原环境下的飞机气动参数,证实QAR辨识飞机气动参数的可行性,但是神经网络不能完全反应真实的飞行系统,并且Delta法对飞行数据的质量、数量要求较高[4]。玉杉杉等[5]采用极大似然法估计无人机的空气动力学参数,模型参数工程实用性良好,但是该方法对初值特别敏感。因此本文利用QAR数据,结合极大似然法和ISPBO(improved student psychology based optimization)启发式优化算法对飞机气动参数进行辨识。
SPBO算法是由BikashDas等[6]提出的一种基于学生心理的启发式优化算法,该算法显著特点是给定待辨识气动参数的大致范围,即可随机赋予待辨识参数初值,对初值敏感较小,目前粒子群[7](partical swarm optimization,PSO)、鸽群优化[8](pigeon inspired optimization,PIO)等启发式算法已广泛应用到气动参数辨识中。ISPBO在SPBO的基础上,采用Logistic映射[9]对学生群体初始化,增强初值分布的随机性和均匀性;根据优化过程中迭代次数和适应度值的变化情况,动态调整最佳学生的迭代步长,提高算法后期的搜索精度,降低对初值选取范围要求。最后,将ISPBO算法辨识得到的气动参数代入到飞机模型中,通过对比模型输出与QAR原始数据,验证该算法在工程上的可行性。
2 气动参数辨识
2.1 运动模型
根据动力学原理,结合飞机地速VE、空速V和风速W三角关系,VE=V+W,建立机体系下含扰动风参数的六自由度运动方程组,即:
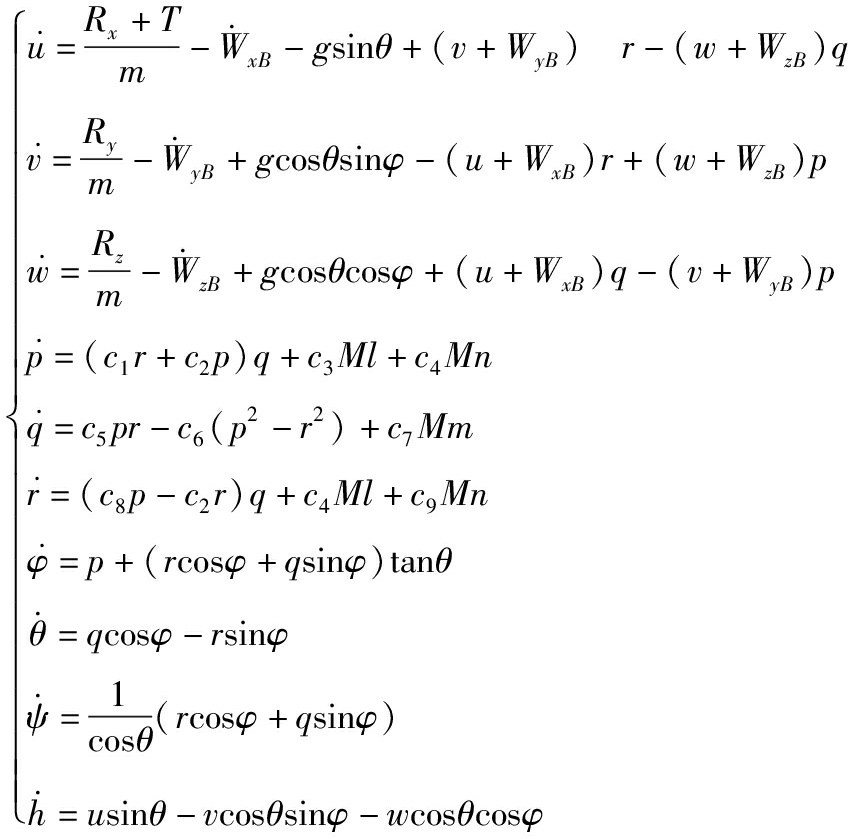
(1)
式(1)中:u、v、w分别为飞行速度三轴分量;p、q、r分别为滚转角速度、俯仰角速度、偏航角速度;Φ、θ、Ψ分别为滚转角、俯仰角、偏航角;Rx、Ry、Rz分别为空气动力三轴分量;WxB、WyB、WzB分别为风速矢量在机体坐标系下三轴分量;Ml、Mm、Mn分别为滚转力矩、俯仰力矩、偏航力矩;ci(i=1,…,9)由转动惯量和惯性积得到。
2.2 气动模型
采用多项式模型作为气动数学模型,根据对应物理意义选择相应状态参数[10],最终确定模型结构为:
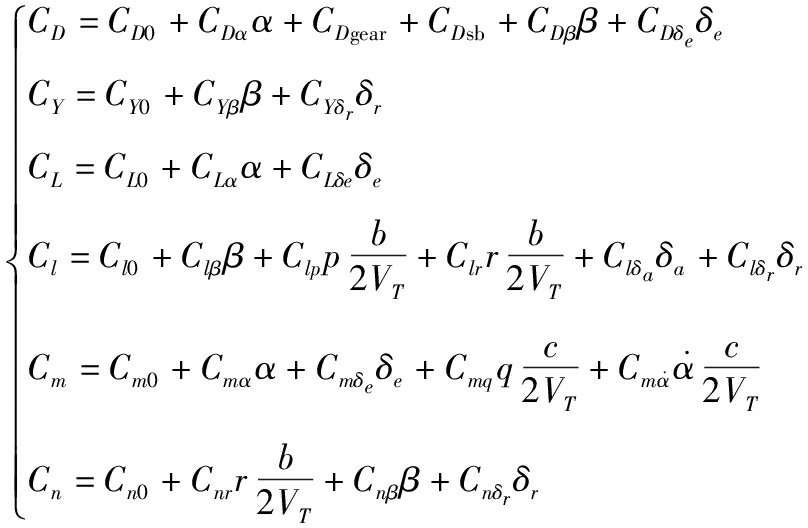
(2)
式(2)中:C*δα、C*δe、C*δr分别为力和力矩相对于副翼、升降舵、方向舵的控制导数;C*α、C*β分别为力和力矩相对于迎角、侧滑角的稳定性导数[1];C*p、C*q、C*r分别为滚转角速度、俯仰角速度、偏航角速度气动导数;CDgear和CDsb分别为阻力相对于起落架和减速板的气动导数;C*0为力和力矩基本系数。
2.3 目标函数
将气动参数矢量代入到飞机模型中,得到模型输出矢量为:
y(i)=[φ,θ,ψ,α,β,V,h]T
(3)
其次根据式(1)建立QAR数据观测矢量ym(i),依据极大似然判据,可得目标函数为:
(4)
式(3)中:N为数据段中数据点数;e(i)=y(i)-ym(i);R为为观测噪声的协方差矩阵。气动参数辨识问题转化为极值寻优问题[11],即寻求最优待辨识气动参数,使目标值J达到最小值。
3 参数辨识算法
3.1 ISPBO算法
SPBO算法[6] 是基于班级中学生心理而制定的启发式优化算法,该算法分为最佳学生、好学生、普通学生和尝试随机改善的学生4种迭代方式,学生对一门学科所做的努力取决于对该学科获得的兴趣,这取决于学生心理,并且可能因学生和学科的不同而有所差异,基于这种心理,在提出的SPBO算法中,除最佳学生外,其余3类学生主题选择被认为是随机过程。
将SPBO算法应用到飞机气动参数辨识中,并对该算法初始化以及最佳学生迭代步长进行改进,得到改进学生心理学(ISPBO)优化算法。ISPBO算法工作对象为班级学生群体,总学生数为SN,每个学生由不同变量组成Xi=(Xi,1,Xi,2,…,Xi,M),这些变量即为待辨识气动参数,也表示为学生每门科目,总科目为M,该算法以学生获得分数为气动模型寻优目标,根据学生对科目努力程度,划分不同迭代阶段,通过目标函数求得目标值J,目标值最小者学生表现最佳。
3.2 Logistic映射初始化
SPBO算法中班级学生群体初始化通常是随机产生,而初值分布是否均匀,将影响算法寻优过程中收敛速度和寻优效率,Logistic映射是一种无规则混沌运动,其特点是具有很好随机性和遍历性,采用Logistic映射初始化学生成绩,用于替代SPBO算法中随机策略,可以提高初值分布均匀性,使得改进后得到的ISPBO算法在初值规定范围内包含更全面的初值变量,增强ISPBO算法前期的全局搜索能力,即使存在一些不合理初值,也不影响整体辨识效果,对初值准确度依赖较小,Logistic映射初始化由以下步骤完成:
Step 1:对M个待辨识参数生成随机数,作为每维空间中第一个学生成绩;
rand_old=rand(1,M),rand_old∈[-1,1]
(5)
Step 2:将rand_old中每一维的学生利用式(6)进行SN-1次迭代,生成混沌变量rand_new;
rand_old(n+1)=4rand_old(n)×(1-rand_old(n)
(6)
Step 3:按照式(7)对待辨识参数进行初始化;
θi.,m=θi,ml+rand_new*(θi,mu-θi,ml)
(7)
其中SN表示学生的数量,即种群大小,m表示待辨识参数位置,m∈(1,2,3,…,M),θi,ml和θi,mu分别表示第m个待辨识参数在整个种群里面最小和最大数值,根据理论计算、风洞试验等数据得到,rand是0到1之间的随机数。
随机法和Logistic法如图1所示。
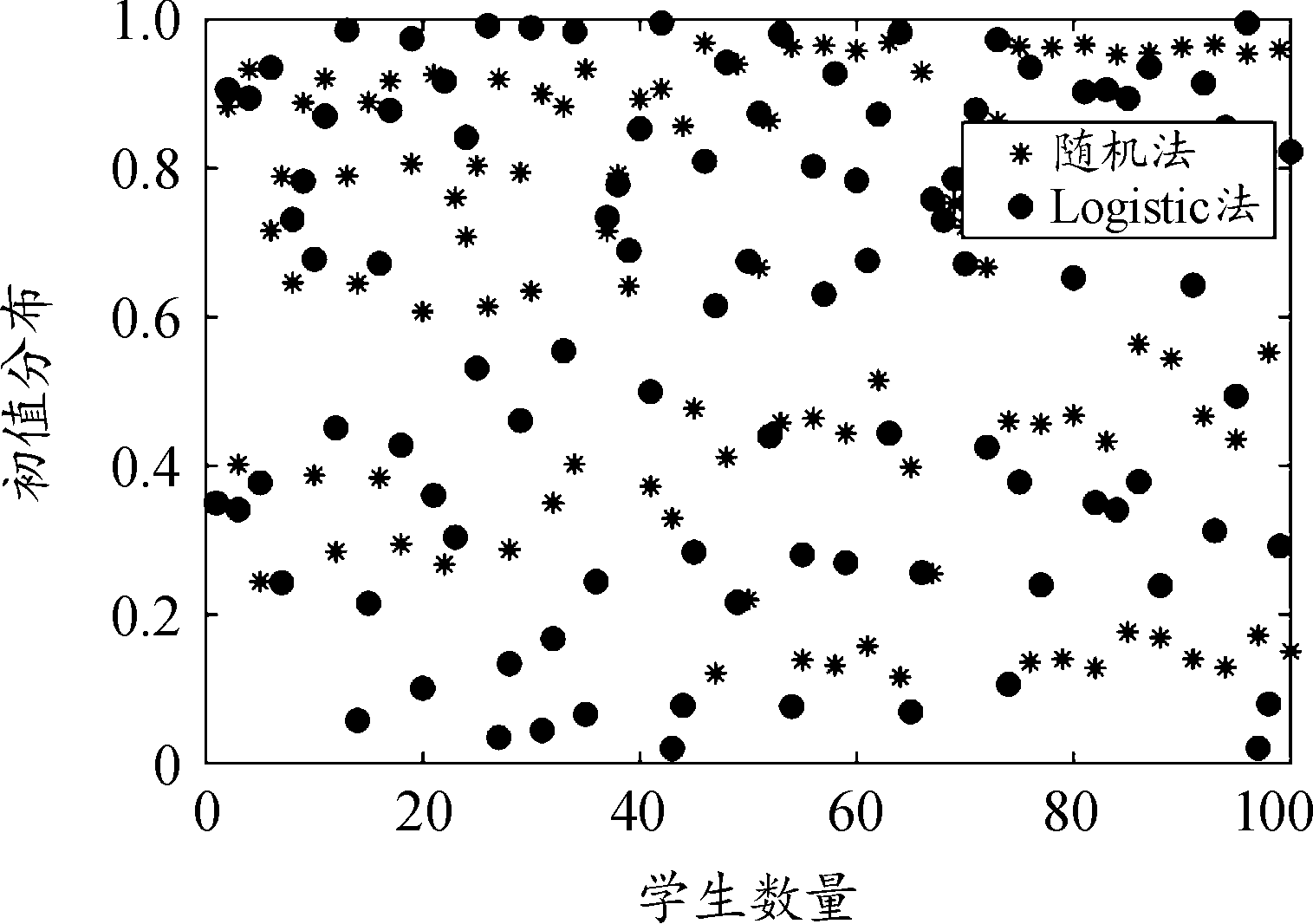
图1 随机法和Logistic法表示的初值分布与学生数量的关系示意图
Fig.1 Comparison of random and Logistic methods
3.3 迭代过程
ISPBO算法是在整个数据段上寻优,每次迭代方向和方式均为随机选取,使其迭代过程呈现全局性,并且相比较SPBO算法,ISPBO算法对最佳学生阶段增添迭代步长控制因子HF,使迭代步长范围随着迭代次数和适应度值变化而动态调整,增强算法后期的搜索精度,即使初值选取范围较大,也有着较高的搜索效率,降低对初值选取范围要求,ISPBO算法由以下4个迭代阶段组成。
1)最佳学生对达到最佳解决方案的贡献比较多,往往需要付出比任何随机选择学生更刻苦的努力,SPBO算法表示为:
θbest new,m=θbest,m+(-1)k×rand×(θbest,m-θj,m)
(8)
式(8)中:θbest,m和 θj,m分别为最佳学生和第j个随机选择学生的待辨识气动参数;rand为0到1之间随机数;k为随机选择的一个参数(1或2)。
ISPBO算法的最佳学生迭代表示为:
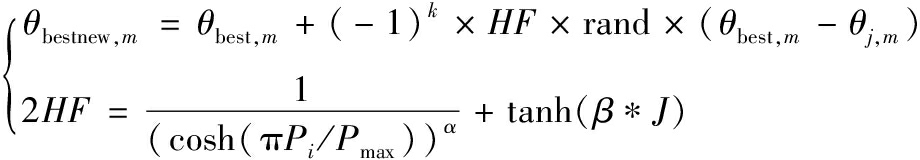
(9)
式(9)中:Pi为当代迭代次数;Pmax为最大迭代次数;J为适应度值;α、β为调节因子,α越大,HF下降的越快,β越大,HF后期范围越大,取α=2,β=9为最佳。HF随着迭代次数增加和适应度值减小而变小,HF变小使得迭代步长范围减小,增强算法后期快速收敛和精细搜索能力。
2)好学生对任何科目感兴趣,将尽力为该科目付出更刻苦的努力,以便提高整体表现。一些学生会尝试做出与最佳学生相同或更刻苦的努力,由式(10)表示;一些学生尝试在学习中付出比班上普通学生更刻苦的努力,并且试图去模仿最佳学生,由式(11)表示。
θnewi,m=θbest,m+rand×(θbest,m-θi,m)
(10)
θnewi,m=θi,m+rand×[(θbest,m-θi,m)+(θi,m-θmean,m)]
(11)
式(10)~(11)中:θi,m为第i个学生的待辨识气动参数;θmean,m是第m个待辨识气动参数班级平均值。
3)普通学生为班级平均水平学生,以班级平均水平学习该学科的同时,学生将尝试在其他学科上付出更多的努力。
θnewi,m=θi,m+rand×(θmean,m-θi,m)
(12)
4)尝试随机改善学生会随机地对科目进行学习,以提高考试的整体表现。
θnewi,m=θmin,m+rand×(θmax,m-θmin,m)
(13)
式(13)中,θmin,m和θmax,m分别是第m个待辨识气动参数在整个班级里面最小和最大数值。
ISPBO算法受到试图获得考试最高分数的学生心理学启发,最优秀学生对达到最佳解决方案的贡献最多。但也可以观察到,所有阶段都有其作用,如果任何一个阶段不起作用或被淘汰,则该算法可能无法产生理想最优解,或者需要更多迭代次数达到收敛。ISPBO参数辨识算法如图2所示。
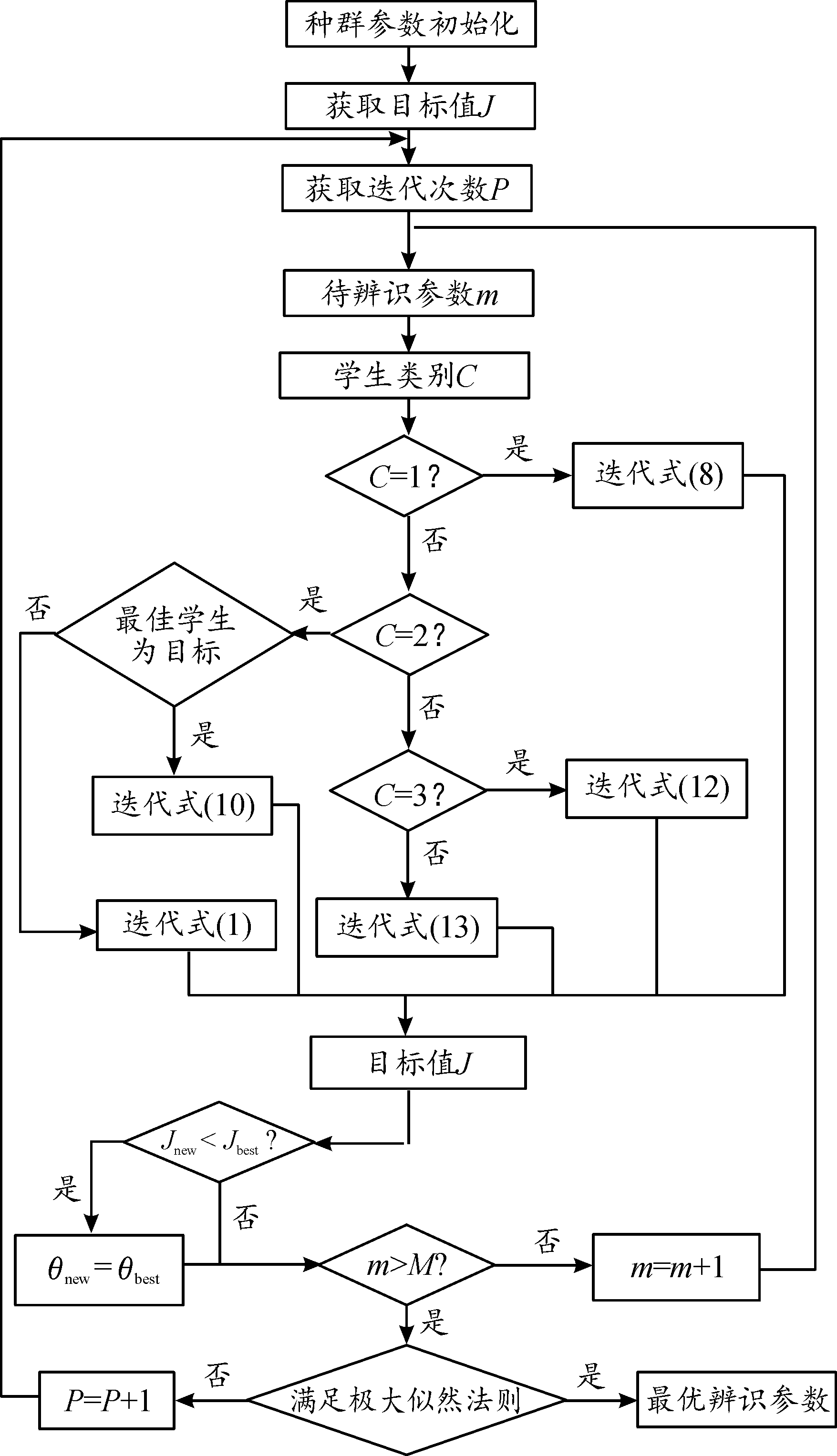
图2 ISPBO参数辨识算法流程框图
Fig.2 ISPBO parameter identification algorithm
4 仿真实验
考虑飞机气动参数与迎角和侧滑角相关性较大,因此采用多重分区[12]思想,即在原迎角分区基础上,进一步根据侧滑角大小划分区间,通过小区间常数法将飞行数据划分为若干小区间,在各区间内忽略迎角-侧滑角变化对气动特性影响,认为各区间内气动参数是常数。
4.1 辨识结果
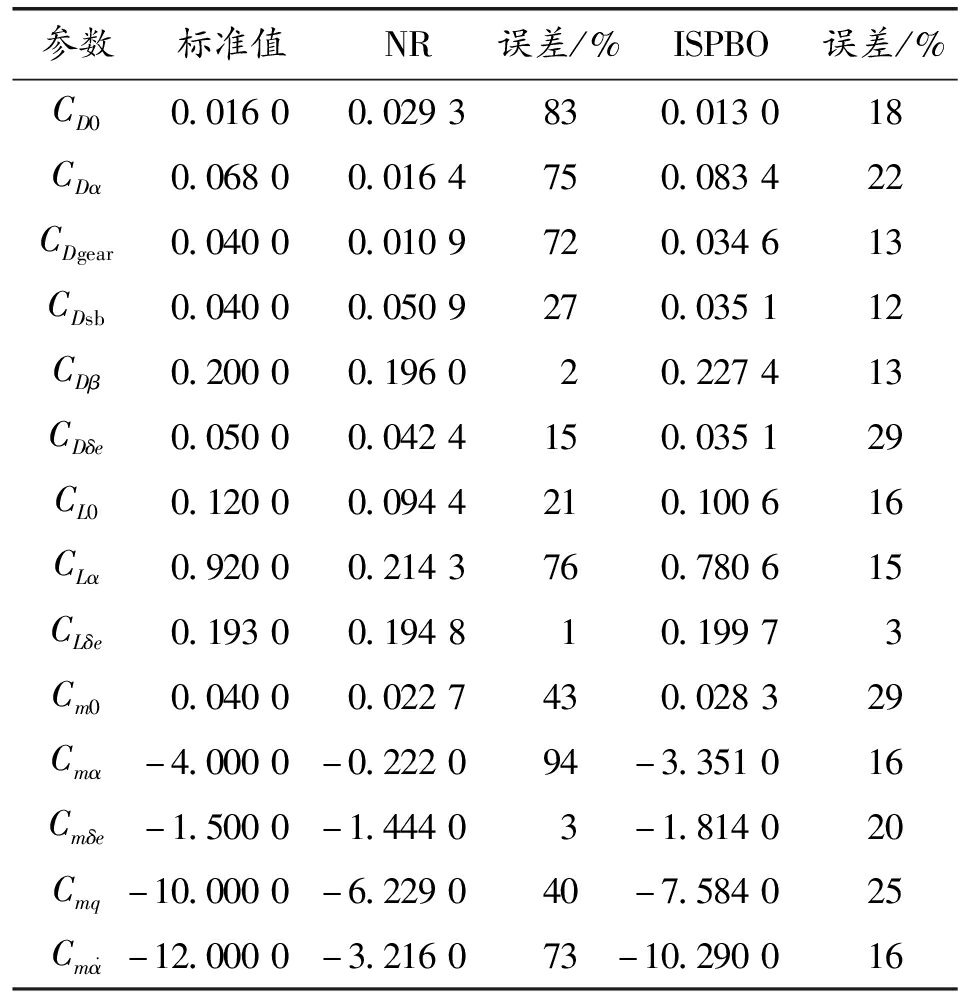
NR、ISPBO算法所有待辩气动参数初值均为随机获取,选取一组QAR数据,其中迎角范围在7°~8°、侧滑角范围在0.25°~0.50°,数据大小为40,进行气动参数辨识,以纵向气动参数为例,辨识结果如表1所示。
根据表1可知,NR算法辨识得到的气动参数差异较大,与标准值的相对误差处于1%~90%范围内,ISPBO算法辨识得到气动参数与标准值相对误差均处于10%~30%左右,初步分析为待辨识参数初值为随机选取,NR算法初值为个体类型,初值选取不同会影响辨识结果,特别当初值选取不准确时,NR算法容易陷入初值附近的局部最优解,导致辨识结果不合理,ISPBO考虑初值范围区间内所有初值,并采用Logistic映射初始化,增加初值分布均匀性,即使存在一些不合理初值,也不影响整体辨识效果。因此ISPBO降低了对初值选取要求。
表1 纵向气动参数辨识结果
Table 1 Identification of longitudinal aerodynamic parameters
参数标准值NR误差/%ISPBO误差/%CD00.01600.0293830.013018CDα0.06800.0164750.083422CDgear0.04000.0109720.034613CDsb0.04000.0509270.035112CDβ0.20000.196020.227413CDδe0.05000.0424150.035129CL00.12000.0944210.100616CLα0.92000.2143760.780615CLδe0.19300.194810.19973Cm00.04000.0227430.028329Cmα-4.0000-0.222094-3.351016Cmδe-1.5000-1.44403-1.814020Cmq-10.0000-6.229040-7.584025C α-12.0000-3.216073-10.290016
4.2 收敛性分析
为了验证ISPBO算法解决初值敏感的有效性,分别进行3次对比实验,进一步验证初值对NR、SPBO以及ISPBO算法收敛性的影响,其中NR算法待辩气动参数初值分为3组,依次在标准值基础上增加0.5倍、1倍、2倍,SPBO以及ISPBO算法初值为群体类型,因此按照初值选取范围划分3组,选取方式为在标准值基础上增加0.5倍、1倍、2倍,目标值J随迭代次数变化曲线如图3所示。
根据图3可知:① NR算法初值选取不同,将导致辨识过程中收敛速度、收敛精度趋于不同,其中当初值接近标准值时,收敛精度达到10-2量级,收敛速度为10次迭代接近收敛;当初值与标准值相差较大时,NR算法收敛速度和收敛精度大大降低,目标值最终收敛到0.2,且收敛速度需要60次迭代,可以看出NR算法对初值要求较高,否则难以得到较好辨识结果。② ISPBO初值为群体类型,选取方式为在一定范围内随机选取,即使当初值选取范围增大,导致辨识过程出现不合理初值,ISPBO算法辨识收敛精度也均达到10-8量级,收敛速度均处于10次左右,可以看出ISPBO算法对初值敏感较小。③ SPBO算法与ISPBO算法有所差异,ISPBO算法在20次迭代达到满意的收敛精度,SPBO算法经过50次迭代才达到较好收敛精度,初步分析为ISPBO采用 Logistic映射初始化,增加初值分布均匀性,提高算法前期全局搜索能力,为后续迭代提供很好的基础,从初始目标值也可以看出,SPBO初始目标值为2,ISPBO初始目标值为0.5,其次当初值选取范围增大时,ISPBO算法收敛精度始终处于10-8量级,而SPBO算法收敛精度从10-3降低到10-2,主要由于ISPBO算法经过持续动态调整迭代步长,大大增加算法后期搜索效率,提高算法收敛精度,降低对初值选取范围要求。
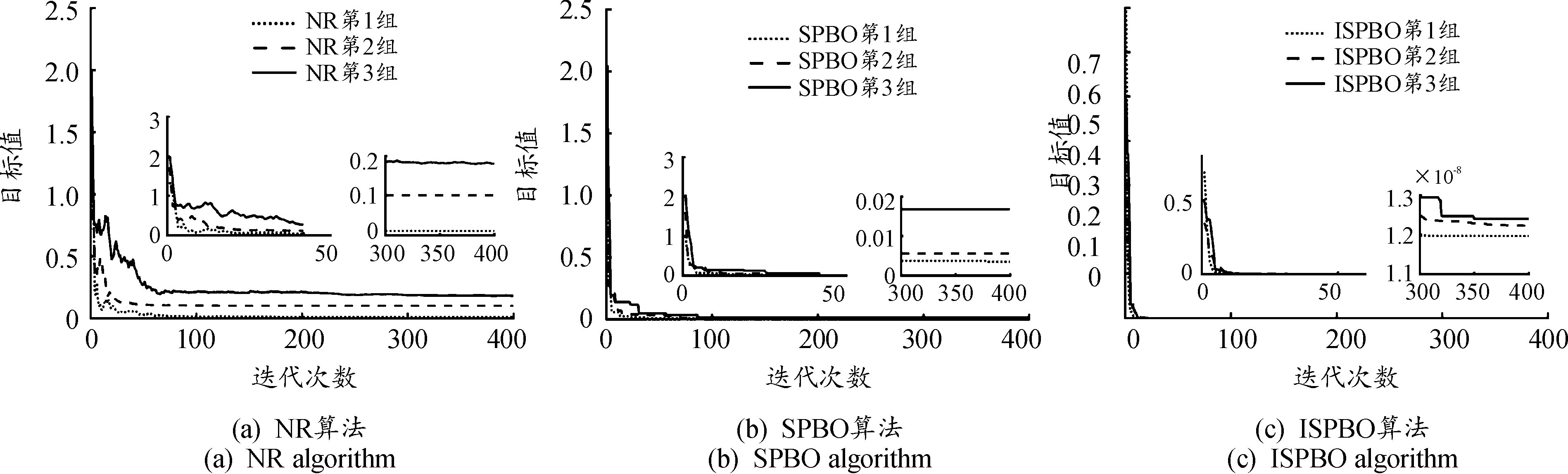
图3 目标值J变化曲线
Fig.3 Change curve J target value
4.3 算法收敛对比
为了分析ISPBO算法的优势,分别采用PSO、PIO、NR和ISPBO等4种参数辨识算法对飞机气动参数进行辨识,其中初值均为随机选取,3种启发式算法种群数量均取50,迭代次数均取400次,PSO算法中学习因子C1、C2=2,惯性权重wmax=0.9,wmin=0.4,PIO算法中地磁因子R=0.3,ISPBO算法没有影响其性能的可调参数。几种目标值J的适应度值曲线如图4所示。
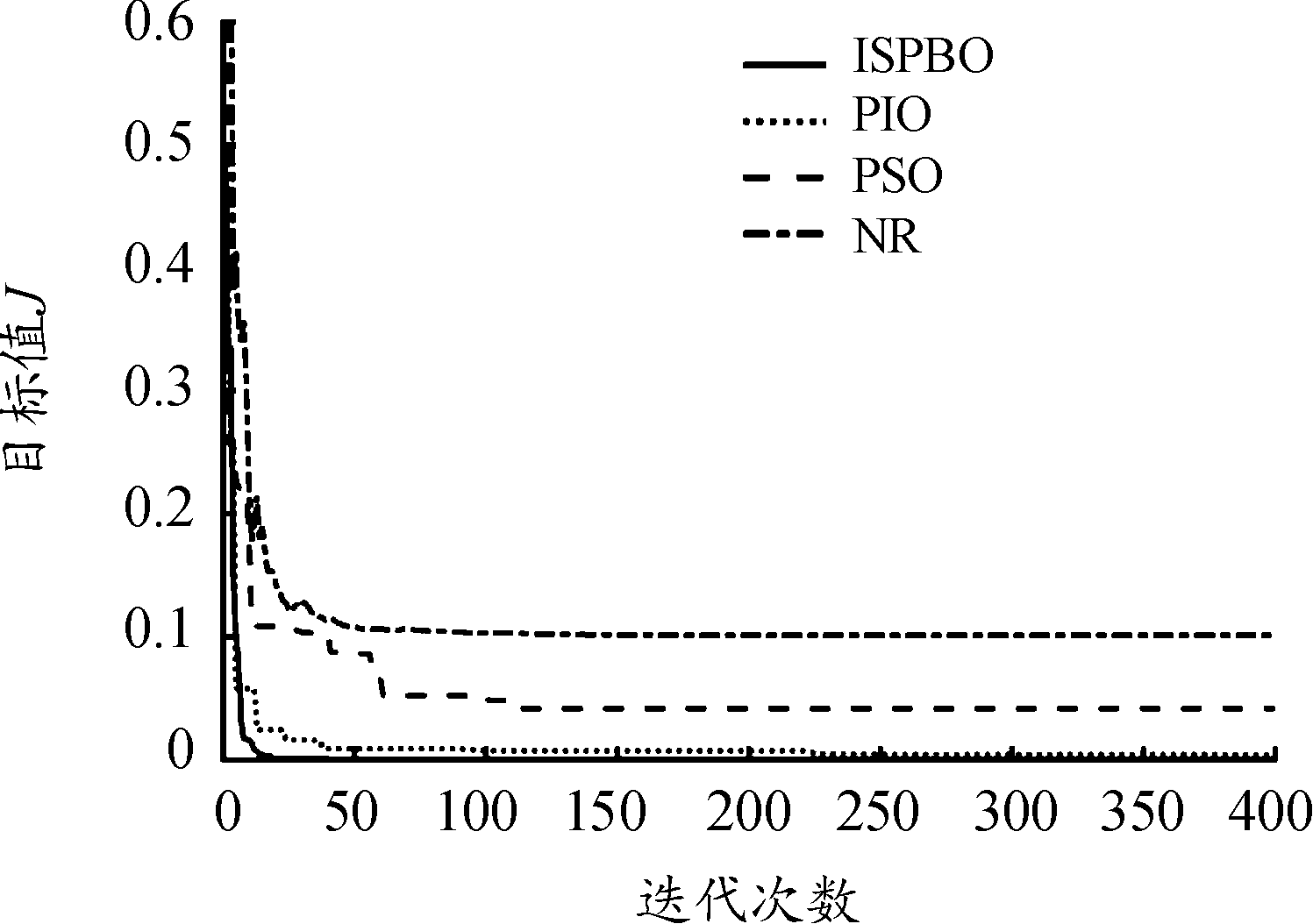
图4 目标值J对比曲线
Fig.4 Comparison J target value
由图4可知,ISPBO算法经过30次迭代适应度值J就可以达到收敛,收敛精度最高,NR算法需要60次迭代达到收敛,但是NR算法收敛精度最低,PSO算法相对提高了收敛精度,但是后期收敛速度急剧下降,PIO算法需要200次迭代才能接近收敛,且收敛精度低于ISPBO算法。相比较其他算法,ISPBO参数辨识算法前期采用Logistic映射初始化,提高算法前期全局搜索能力,使得目标值快速收敛,其次ISPBO算法采用4种迭代方式,增加算法搜索多样性,并且后期经过持续动态调整迭代步长,大大增加算法后期搜索效率,进而提高收敛精度,同时ISPBO算法没有影响其性能的可调参数,降低人为因素影响,因此,综合分析,ISPBO算法提高了收敛精度和收敛速度。
4.4 仿真结果验证
将辨识得到的气动参数代入到气动模型中,仿真验证结果如图5所示,其中虚线为QAR原始数据,实线为模型仿真数据。
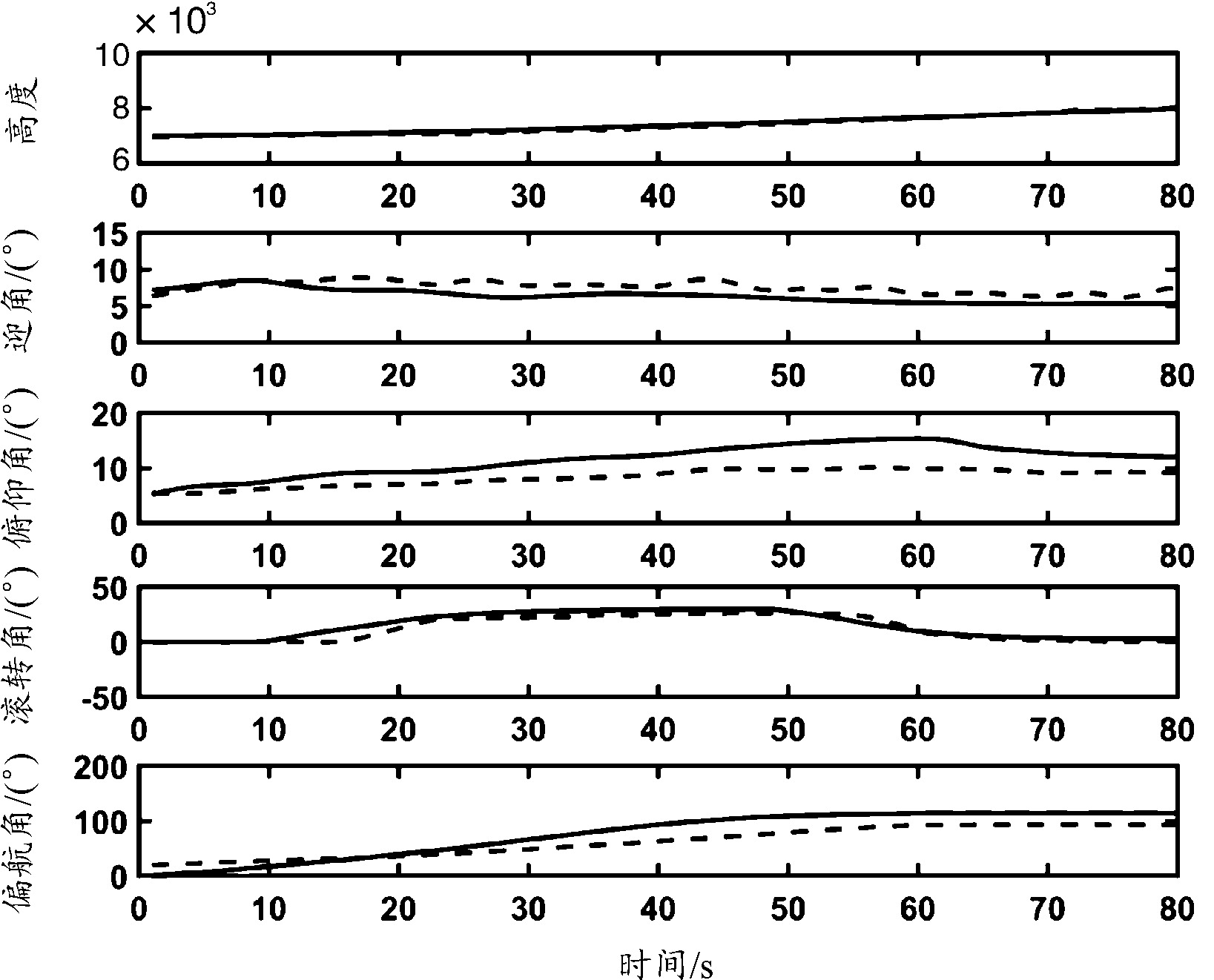
图5 QAR原始数据及模型输出值曲线
Fig.5 QAR raw data and model output contrast curves
根据图5可知,QAR原始数据及模型输出值曲线中高度曲线平均百分比误差处于1%左右,吻合较好,迎角曲线、俯仰角曲线、偏航角曲线、滚转角曲线平均百分比误差处于20%左右,但是曲线后期误差较大,主要由于模型采用数值积分,经过持续累积误差,积分趋势会趋于不同。目前,CCAR-60中模拟机客观测试标准规定高度容差为90ft,姿态角容差为20%,国军标GJB 1690-93对于工程中姿态约束性能指标规定最大偏差为20%,ISPBO算法辨识得到的模型输出与QAR原始数据具有相同的时变趋势,虽然曲线存在一定差异,但是曲线误差均处于20%范围内,满足工程要求,证实了利用QAR数据辨识飞机气动参数在工程上的可行性。
5 结论
1)在仿真精度要求不高的工程应用中,利用QAR数据辨识飞机气动参数是一种可行的解决方案。
2)ISPBO算法解决了传统极大似然法对初值选取敏感问题,使得气动参数辨识初值选取只需确定大致范围即可,降低了初值选取要求。
3)ISPBO算法在SPBO算法基础上,进行Logistic映射初始化以及动态调整最佳学生迭代步长的改进,相比较其他启发式算法,提高了收敛精度和收敛速度。
[1] Kumar A,Ghosh A K.ANFIS-Delta method foraerodynamic parameter estimation using flight data[J].Proceedings of the Institution of Mechanical Engineers,2019,233(08):3016-3032.
[2] Huang R S,Sun H B,Wu C.Estimating Eddy Dissipation Rate with QAR Flight Big Data[J].Applied Sciences,2019,9(23):5192.
[3] Wang Q,Wu K Y,Zhang T J.Aerodynamic modeling and parameter estimation from QAR data of an airplane approaching a high-altitude airport[J].Chinese Journal of Aeronautics,2012,25(03):361-371.
[4] Kumar A,Ghosh A K.ANFIS-Delta method foraerodynamic parameter estimation using flight data[J].Proceedings of the Institution of Mechanical Engineers,2019,233(08):3016-3032.
[5] Yu S S,Wang Z J,Gottlicher C.System identification for an unmanned aerial vehicle using the maximum likelihood method[C]//Proc.of the 2017 9th International Conference on Modelling,Identification and Control,BEIJING SECTION:IEEE,2017:664-669.
[6] Das B,Mukherjee V,Das D.Student psychology based optimization algorithm:A new population based optimization algorithm for solving optimization problems[J].Advances in Engineering Software,2020,146:102804.
[7] 史继刚,易文俊,管军.基于粒子群-牛顿算法的弹丸阻力系数辨识[J].兵器装备工程学报,2017(02):23-26,29.
Shi J G,Yi W J,Guan J.Identification of marvel resistance coefficient based on particle swarm-newton algorithm[J].Journal of Ordnance Equipment Engineering,2017(02):23-26,29.
[8] Zhang D F.Identification for a reentry vehicle via levy flight-based pigeon-inspired optimization[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2018,232(04):626-637.
[9] Han C Y.An image encryption algorithm based on modified logistic chaotic map[J].Optik-International Journal for Light and Electron Optics,2019,181:779-785.
[10] Verma H O.Parameter estimation of aircraft using extreme learning machine and Gauss-Newton algorithm[J].The Aeronautical Journal,2019,124(1272):271-295.
[11] Wang C F,Liu K, Shen P P.A novel genetic algorithm for global optimization[J].Acta MathematicaeApplicatae Sinica,2020,36(02):482-491.
[12] 胡爽,朱纪洪.基于飞行数据多重分区的高机动飞机气动建模及参数辨识[J].控制理论与应用,2016,33(10):1289-1295.
Hu S,Zhu J H.Multiple partioning of flight data for mamnoeuvrable aircraft aerodynamic modeling and parameter estimation[J].Control Theory and Applicatons,2016,33(10):1289-1295.