1 引言
膛压是各类武器系统的重要技术指标之一,是各类兵器在生产、设计、校验等环节中必测的一项重要参数。由于膛压作用时间短、压力量程大,且同时伴随着高温和振动,所以在测试方法上有一定的特殊性[1]。铜柱测压法和电子测压法是常用的枪械膛压测量方法,需要在枪械身管开孔,安装特制的测压器进行测量[2],这2种测压方法无法用于不宜开孔的枪械。
内弹道雷达是根据多普勒原理设计的一种膛内弹丸速度测量仪器,工作时,由雷达发射天线向枪膛内部发射出连续电磁波,同时接收弹丸反射回来的电磁波信号,通过提取多普勒频移,由速度与频移之间关系解算出弹丸速度[3-4]。本文基于内弹道雷达测量的弹丸速度信息,根据内弹道基本理论,建立弹丸运动数学模型,间接计算得到膛内火药燃气压力的大小,模型中主要参数通过实际测量的方法获取,提高计算精度,实现非接触式的膛压测量。
2 内弹道雷达测量原理
内弹道雷达一般采用高频连续波进行测量,作用距离较短,适用于膛内弹丸的运动速度测量。测量原理如图1所示,基于多普勒原理,雷达发射的电磁波经运动的弹丸反射后,电磁波频率会发生改变,通过测量频率的变化大小得到弹丸的径向运动速度。

图1 内弹道雷达测量原理示意图
Fig.1 Schematic diagram of interior ballistic radar measurement principle
假设雷达发射天线发射的电磁波频率为f0,遇到弹丸返回时,接收天线接收到的弹丸反射的电磁波频率为f1,则二者有如下关系:
(1)
其中:vr是弹丸相对雷达天线的径向速度,c为自由空间电磁波传播速度3×108m/s。
则多普勒频移fd为:
(2)
那么可以得到弹丸运动的径向速度vr与多普勒频移fd之间关系如下所示:
(3)
其中:λ0为发射电磁波的波长。
在枪械膛内,入射的电磁波相当于在圆波导中传输[5],此时的电磁波波长如下所示:
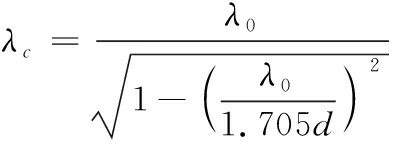
(4)
其中:λc为射入枪械膛内电磁波的波长,d为枪管口径。
那么在枪械膛内的弹丸径向速度vr的表达式如下所示:
(5)
因此,根据式(5),采用内弹道雷达测量多普勒频移即可得到枪械膛内弹丸的径向速度。
3 膛内压力计算数学模型
3.1 膛内压力变化规律
膛内火药燃气压力的变化曲线如图2,图中:P0为挤进压力,Pm为最大压力,Ph为后效期开始时膛内压力。根据膛压曲线的变化规律,可将火药燃气作用的全过程分为静力燃烧时期、内弹道时期和后效期[6]。
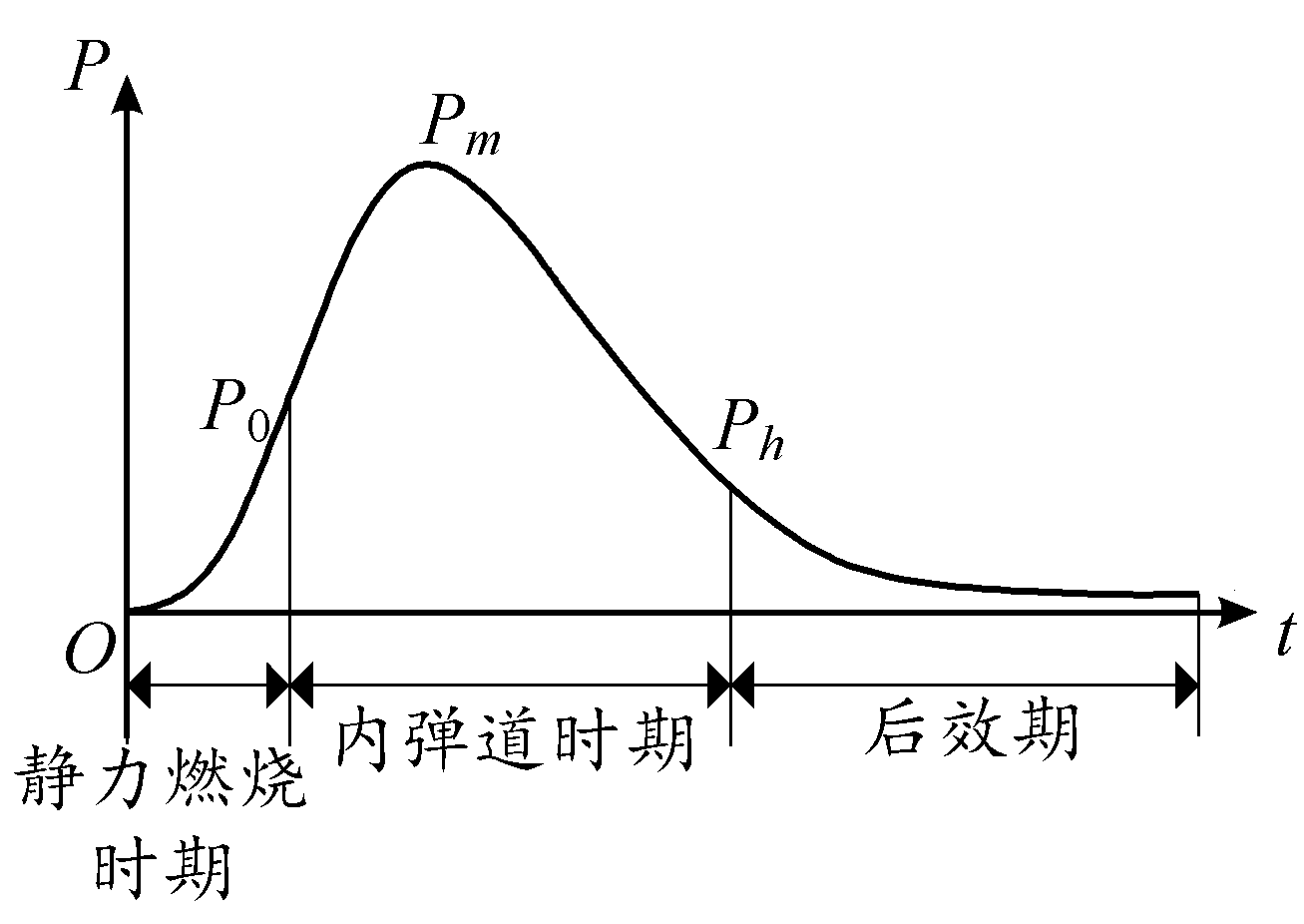
图2 膛压曲线
Fig.2 Pressure variation curve in chamber
静力燃烧时期指的是从击发底火开始到弹头完全嵌入膛线之前的一段时间,弹头全部嵌入膛线受到最大阻力时所对应的膛内火药燃,气压力即挤进压力[7]。由于该时期的时间比较短,可认为在该时间段内,膛内压力近似呈指数规律增大。
内弹道时期指的是从弹头起动到弹头出膛口为止的一段时间。在该时期中,由于弹头的运动,弹后空间的火药燃气也跟着一起运动,因此在膛内形成了燃气流。弹头和燃气都存在运动,并形成复杂的气流运动。在该时期中,复杂的运动使得内弹道的解算需经过解内弹道方程组来得到相应的膛压变化规律,并且通过内弹道学计算方法得到的膛压是每瞬时弹后空间火药燃气压力的平均值。
后效期指的是弹头飞出膛口以后的一段时间,弹头在火药燃气射流以及激波的相互作用下继续运动[8]。在此时间段内,膛内火药燃气压力也近似呈指数规律衰减。
3.2 膛内弹丸运动模型
在经典的内弹道学理论中,假设:火药气体密度和未燃烧的装药密度处处相等;从膛底到弹底膛内每一截面的装药运动速度是按线性规律增加的;枪管都是圆柱形,即药室没有扩大。此时膛内弹丸运动速度弹丸速度v与弹底压力Pd(t)之间存在以下关系[9]:
(6)
其中:m为弹丸质量,φ为次要功系数,S为枪管横截面积。
弹底压力Pd(t)和膛底压力Pt(t)存在以下关系:
(7)
其中:ω为火药质量。
由于膛内弹丸运动速度与径向速度十分接近,即v≈vr,根据式(6)和式(7),可以实现内弹道雷达所测量的速度值和膛底压力值之间的转换。
使用该模型计算压力时,其中各参数值的确定是根据弹药的标称值和固定的经验值,如次要功系数φ对于枪械取值范围为(1.06~1.10)[10],而实际上,受火药燃烧、弹丸运动以及枪管本身特性等影响,这些参数并非常数,那么采用此种方法计算压力值将造成较大的计算误差。
根据式(6)和式(7),得到下式:
(8)
根据式(8),定义系数M的表达式如下所示:
(9)
其中:M含次要功系数、火药质量、弹丸质量、枪管横截面积等参数。
此时式(8)可表示为:
(10)
其中:![]()
式(10)即为通过膛内弹丸的速度计算膛内压力的数学模型,该模型通过系数M建立了内弹道雷达测量的速度和膛内压力之间的转换关系,只要准确获得M的值,就可以准确计算膛内压力。
3.3 模型参数测试方法
获取膛内压力需要准确计算得出弹丸运动数学模型中的系数M,因此可采用带测压孔的枪械,应用内弹道雷达和电子测压设备共同测量,同时获取膛内压力数据和弹丸运动速度数据,测量方案如图3所示。
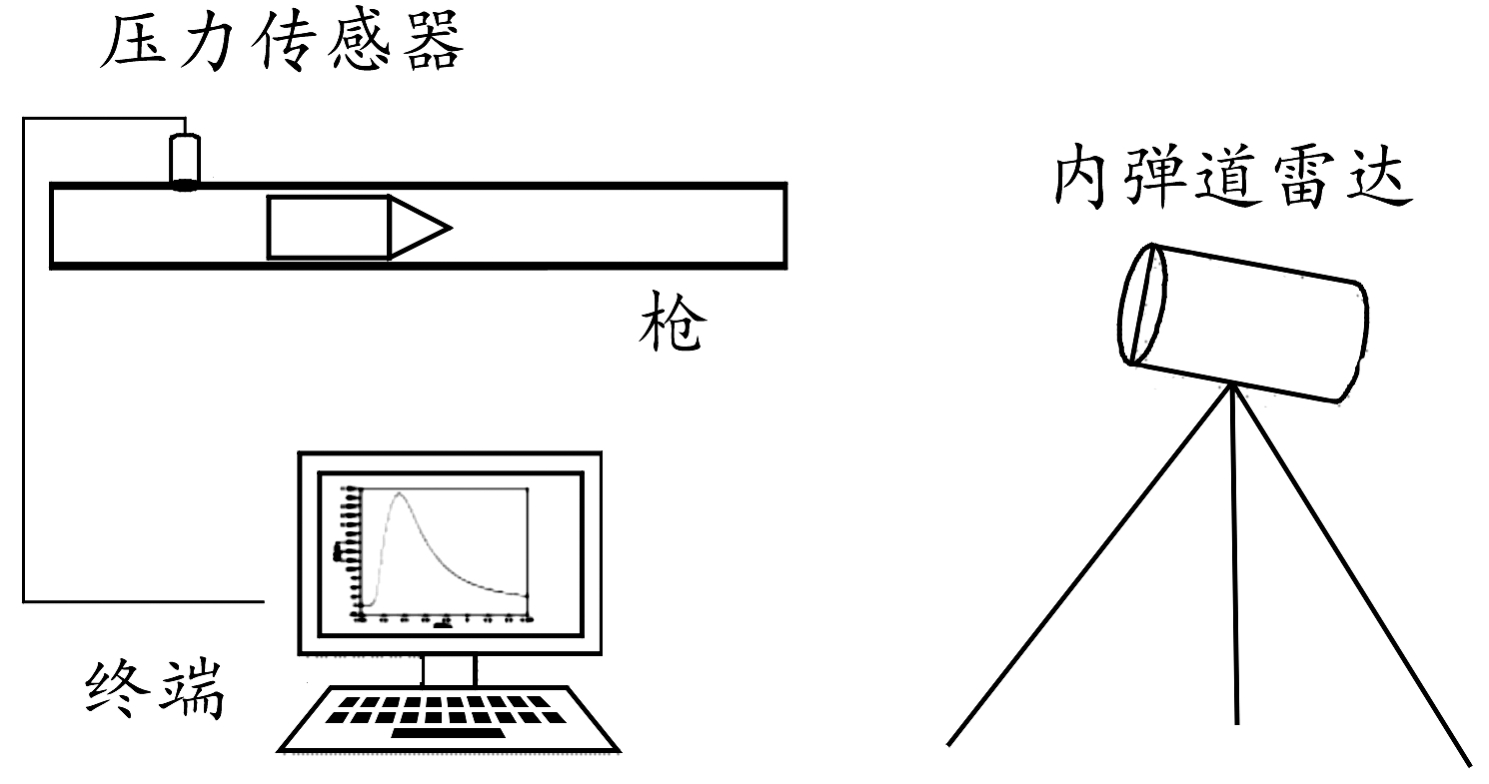
图3 测量方案示意图
Fig.3 Simple schematic diagram of measurement scheme
图3中,电子测压设备由高精度的压电式压力传感器、电荷放大器和数据采集终端组成,能够实时测量得到压力-时间曲线,且测量的精度很高,一般可以认为测量结果为标准量[11]。电子测压传感器的安装位置一般位于坡膛位置,其测量结果可近似为膛底压力Pt(t)。内弹道雷达测量结果为速度-时间曲线,计算其一阶时间导数得到Pv(t)。
为了选取同时含有电子测压数据和内弹道雷达测速数据的时间区间,应确保该区间处于内弹道时期。由于弹丸挤进压力的大小一般可占到最大压力的60%左右,而枪口压力一般可占到最大压力的20%左右,因此选取的时间区间(t1,t2)可按如下方法计算:
P(t1)≥Pm·70%, t1<tm
P(t2)≤Pm·30%, t2>tm
(11)
则根据式(10)可得:
(12)
在理想情况下,对于同一种弹药,式(12)求得的M应为常数,但实际上,随着火药的燃烧、弹丸的运动,M将产生一定的变化,在变化趋势上,M中的次要功系数将随速度的增大而逐渐减小,因此可将M表示为时间t的函数M(t)。此时通过一元回归分析,基于最小二乘法确定M(t)的近似表达式M′(t),如下所示:
M′(t)=a0+a1t+a2t2+…+antn, t1<t<t2
(13)
其中:n为多项式的阶数。
拟合误差采用近似表达式拟合曲线的N点数值相对误差的均方根计算,表达式如下所示:
(14)
根据式(13)和式(14)确定满足需求的误差范围内的最佳拟合多项式阶数。
需要注意的是,模型参数测试可根据需要测试一次或者多次,在已获取该型枪械模型参数时可不必进行再次测试,即无需再使用电子测压方法。
3.4 膛内压力计算方法
根据得到的最佳拟合多项式M′(t),对于膛内结构(口径、膛线数量、膛线形状、坡膛结构等)基本相同的无测压孔枪械,即可采用M′(t)作为膛内压力计算数学模型中的系数M,此时式(10)可表示为:
Pt(t)=M′(t)·Pv(t)
(15)
根据式(15)即可实现对于无法安装测压器的枪械,应用内弹道雷达进行非接触式膛压测量,测量方案参照图3中所示(不含电子测压设备),内弹道雷达的布站位置一般尽可能与模型参数测试中位置相同。
此时,通过内弹道雷达测量的速度-时间曲线和计算得到的膛内压力-时间曲线,可进一步计算膛内压力-弹丸行程曲线,获得膛内压力在枪管内部随弹丸运动的变化情况和分布情况,进行更全面的膛压分析。
这种方法既突破了必须应用带测压孔的枪械进行膛压测量的限制,又通过准确测量模型参数保证测试的精度,在实际应用中,更加便于结合其他试验项目同时进行,监测枪械膛压,为枪械、弹药性能鉴定提供更多可供分析的测量数据。
4 实验
结合某型弹药的膛压测试试验,对本文提出的测压方法进行实弹射击实验。首先进行膛内压力计算数学模型的参数测试,按照图3所示的测试方案,使用带测压孔的枪械,应用电子测压设备和内弹道雷达进行共同测量,得到实测数据如图4所示,图中内弹道雷达测量的数据经已转换为加速度曲线。

图4 某型弹药实测的加速度和膛压曲线
Fig.4 Measured acceleration and chamber pressure curve of a certain ammunition
对测量得到的数据进行必要的处理,按照膛内压力的峰值时刻相同统一2种测量数据,并根据式(11)选取合理的时间区间,得到处理后的数据如图5所示。

图5 初步处理后的加速度和膛压曲线
Fig.5 Acceleration and chamber pressure curve after preliminary processing
根据式(12)计算M的值,如图6所示。
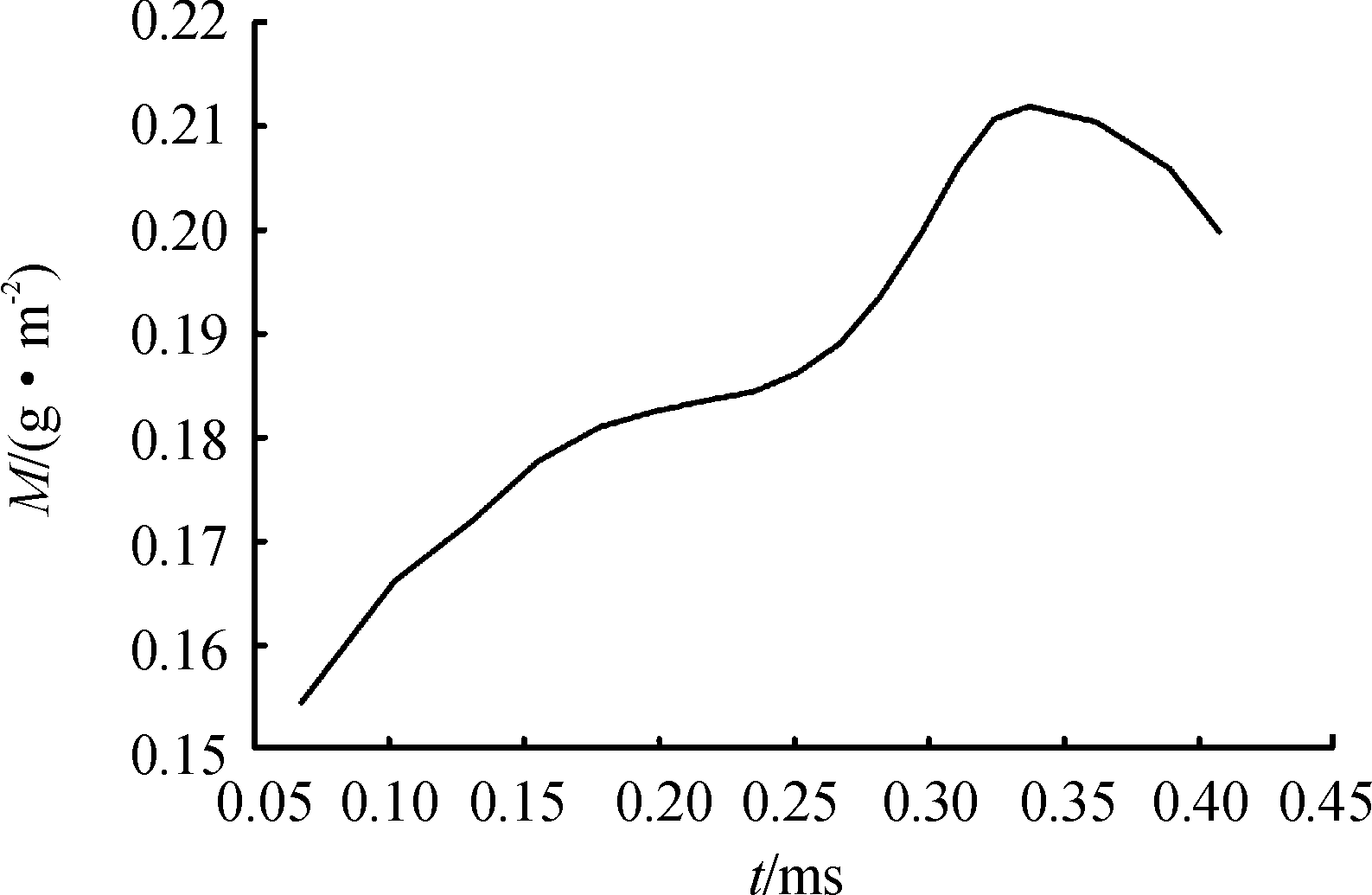
图6 计算的M值曲线
Fig.6 Variation curve of calculated M value with time
由图6可知,M并非恒定不变的常系数,随时间将产生一定的变化。对M的值进行一元回归分析,应用最小二乘法得出拟合多项式的参数,计算拟合误差。得到不同阶数的拟合多项式和拟合误差如表1所示,枪械膛压测试一般要求相对误差低于2%,因此,根据表1中数据,可采用4阶的拟合多项式。
表1 不同阶数的拟合函数表达式和拟合误差
Table 1 Fitting polynomials and errors of different orders
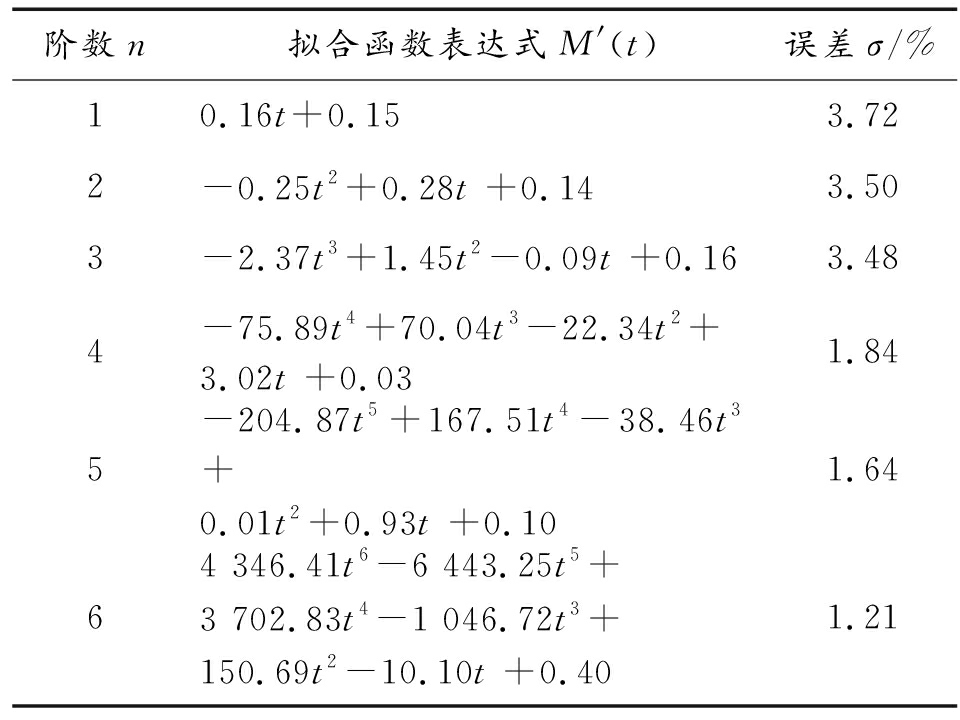
阶数n拟合函数表达式M'(t)误差σ/%10.16t+0.153.722-0.25t2+0.28t +0.143.503-2.37t3+1.45t2-0.09t +0.163.484-75.89t4+70.04t3-22.34t2+3.02t +0.031.845-204.87t5+167.51t4-38.46t3+0.01t2+0.93t +0.101.6464 346.41t6-6 443.25t5+3 702.83t4-1 046.72t3+150.69t2-10.10t +0.401.21
根据式(15),将计算的膛底压力,对比采用以往方法[式(6)]直接计算得到的弹底压力,如图7所示。

图7 计算的膛底压力和弹底压力曲线
Fig.7 Comparison of calculated chamber bottom pressure and projectile bottom pressure
由图7可见,在膛压曲线的上升沿部分,计算得到的弹底压力要大于膛底压力,而在内弹道理论中,由于弹丸的运动,弹底压力一般会小于膛底压力。进一步将应用本文提出方法计算得到的膛底压力数据对比电子测压数据,如图8所示,可见二者基本相符。因此,综合图7和图8可以看出,本文提出的压力计算方法的准确度高于以往方法,设计的测试方案是基本合理的。
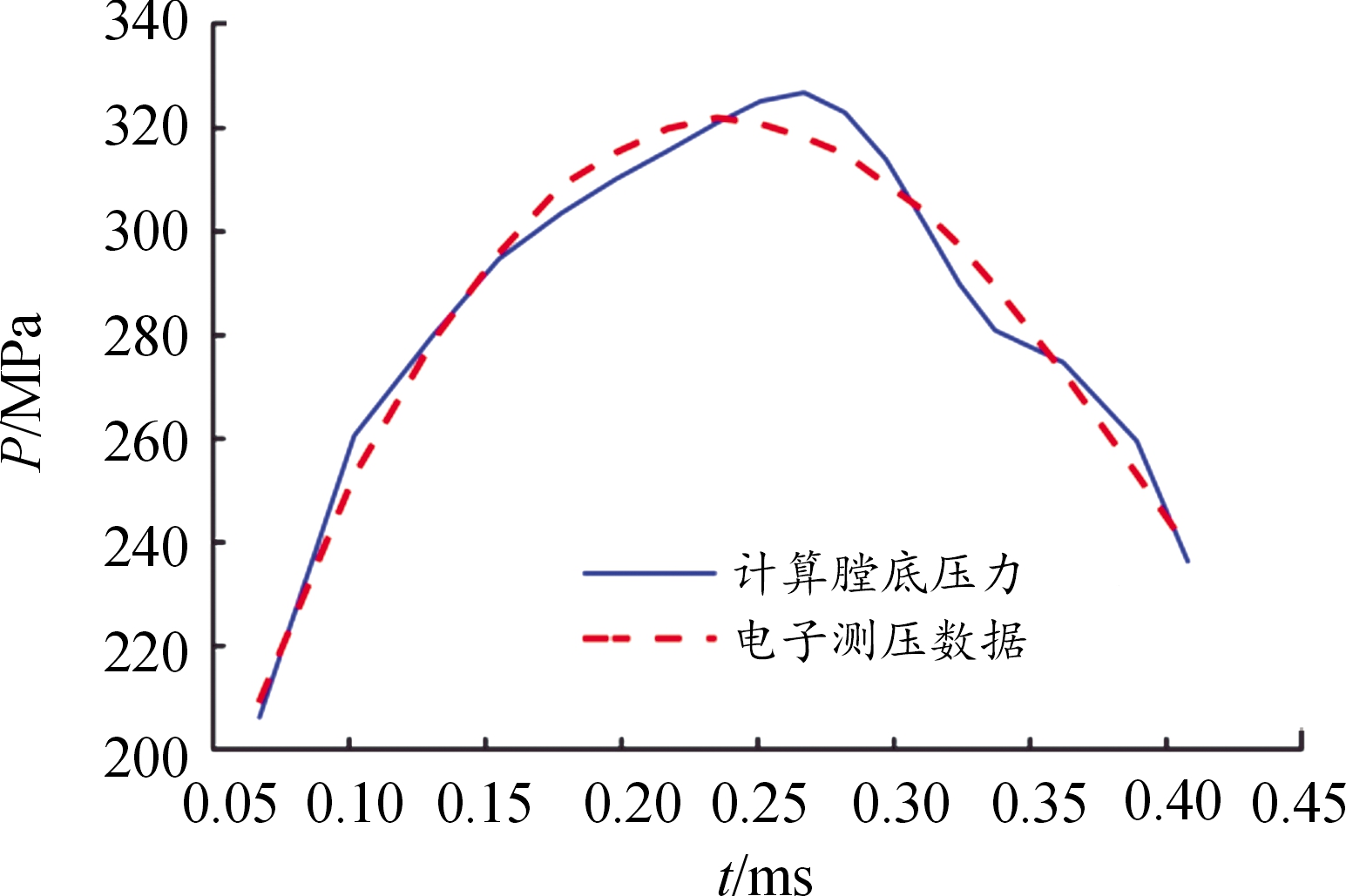
图8 计算的膛底压力和电子测压曲线
Fig.8 Comparison of calculated bore bottom pressure and electronic pressure measurement data
由图8可见,计算的膛底压力在部分位置偏差较大,计算其相对误差如图9所示。
图9中,最大相对误差为3.0%,要大于膛压测试的2%指标要求。分析其原因是由于膛内弹丸的运动速度快,运行时间短,回波信号的频率变化大,造成弹丸速度测量精度不高,一般约为3%左右,远差于外弹道的0.1%测速精度。因此,膛内弹丸运动速度测量误差是膛内压力计算的主要误差来源。另外,模型中参数M的拟合误差、内弹道雷达布站位置等均是影响膛内压力计算精度的主要因素。
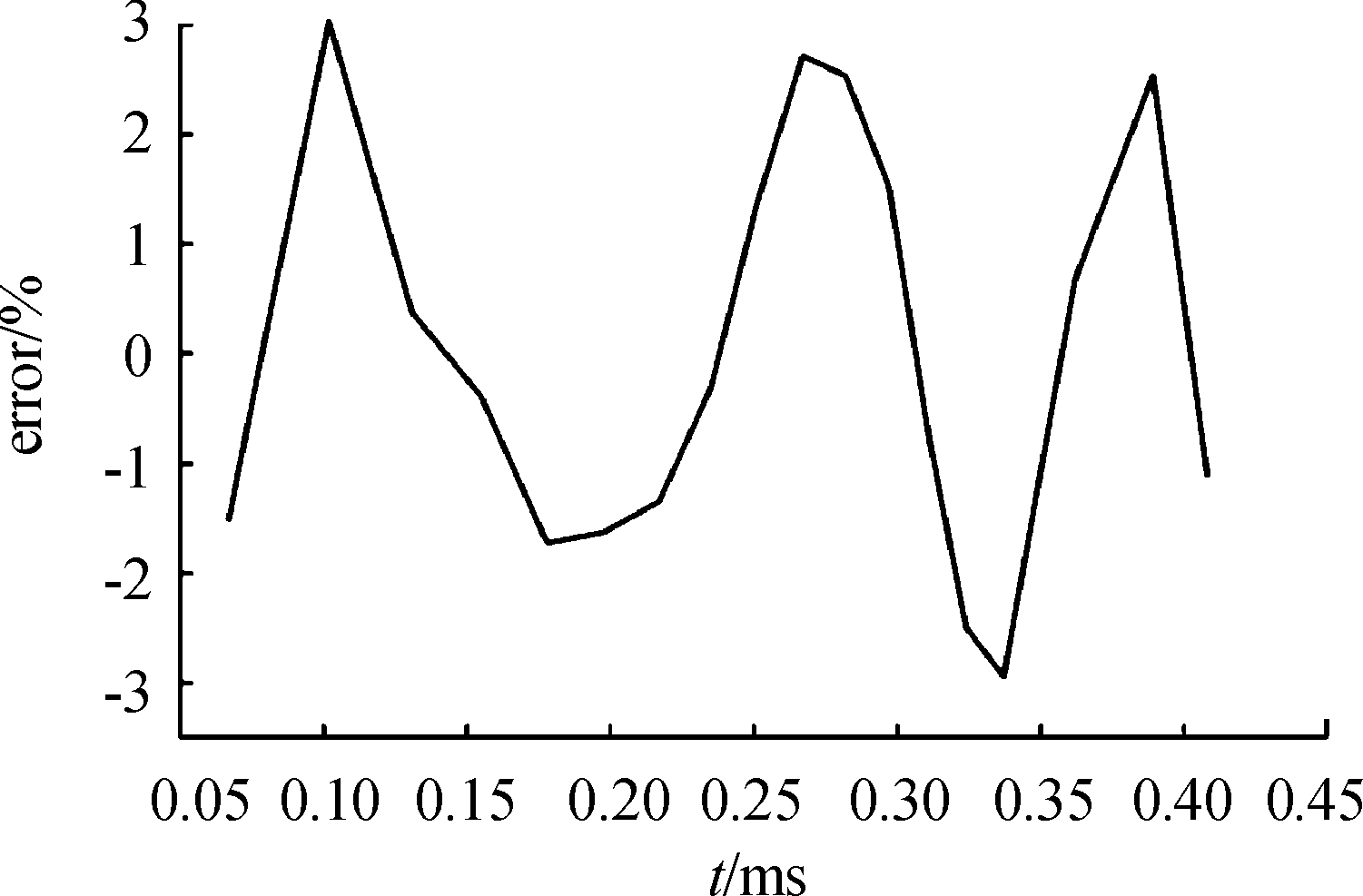
图9 计算的膛底压力相对误差曲线
Fig.9 Relative error of calculated chamber bottom pressure
获取膛压计算数学模型中的参数后,即可针对无测压孔的枪械,应用内弹道雷达进行测量,将测量的数据与已得到的拟合多项式M′(t)按公式(15)进行计算,得到膛内压力数据如图10所示。
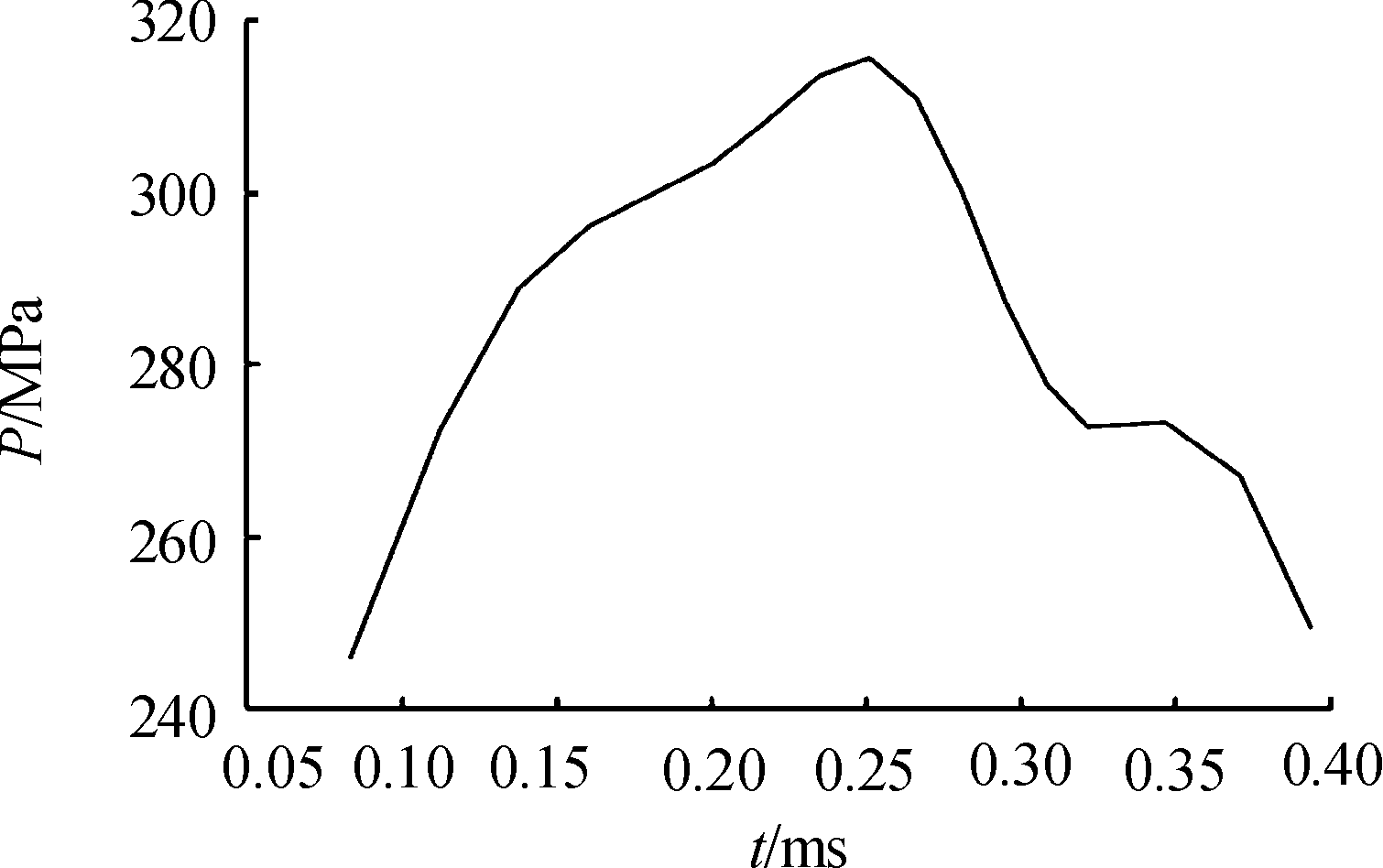
图10 无测压孔枪械膛压计算曲线
Fig.10 Calculation results of chamber pressure for firearms without pressure holes
由图10所示,膛压变化曲线基本符合膛压变化规律,能够较好的反映枪械膛内火药燃气压力的变化过程,通过提取最大压力Pm、挤进压力P0、枪口压力Ph等参数实现武器内弹道性能的评估。此时,膛内压力的计算误差来源还包括枪械间膛内结构差异。
根据得到的数据作进一步计算,得到膛内压力-弹丸行程曲线如图11,为分析火药燃气压力在膛内的分布情况提供更多参数。
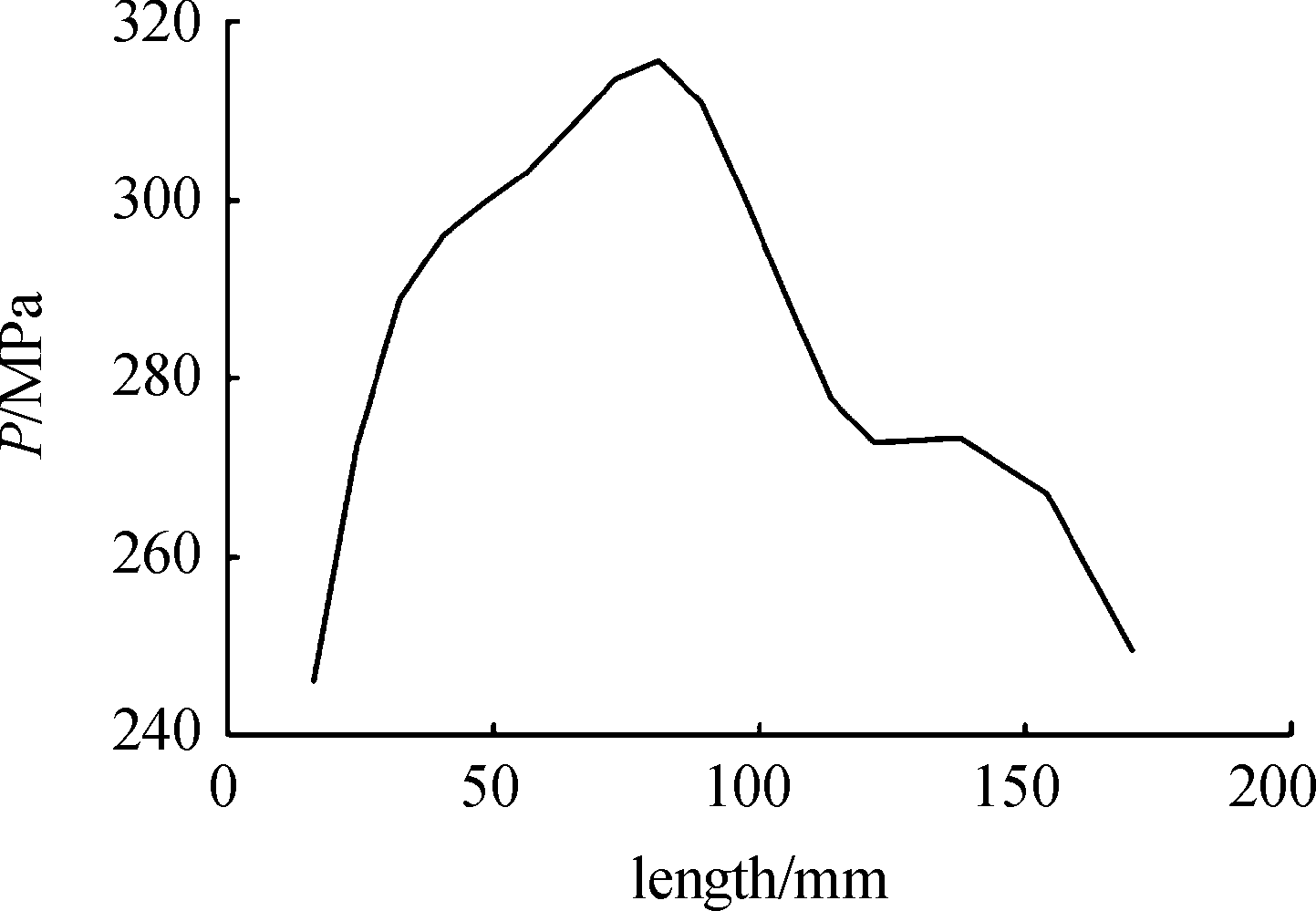
图11 膛内压力-弹丸行程曲线
Fig.11 Variation curve of chamber pressure with length of projectile
综上,应用内弹道雷达间接测量得到的膛压与电子测压数据是基本相符的,通过计算得到膛压-时间曲线和膛压-弹丸行程曲线有利于分析膛内火药燃气压力的变化过程、分布情况,使得武器的内弹道分析不必依赖于专用的带测压孔枪械,丰富武器的性能考核参数和依据。
5 结论
1) 通过共同应用电子测压设备和内弹道雷达同时测量膛内压力和弹丸运动速度,根据内弹道理论选取内弹道时期的数据进行计算,确定膛压计算数学模型中的主要参数,按此方法计算得到的膛内压力较按经验参数值计算方法更加准确;
2) 由膛内弹丸运动速度转换得到的膛内压力精度较高,实测数据最大相对误差为3%,其主要来源是膛内弹丸运动速度测量误差;
3) 基于内弹道雷达测量的速度转换为膛内压力,实现枪械膛压的非接触式测量,能够避免枪管开孔对枪械完整性的破坏以及对弹丸挤进过程的不利影响;
4) 本文提出的基于内弹道雷达的枪械非接触式膛压测量方法,有利于通用枪械和弹药的内弹道性能分析,是武器性能评估的有力支撑。在后续的工作中,需要继续研究提高非接触式膛压测量方法的准确度。
[1] 孔德仁.塑形测压器材准动态校准技术及实验研究[D].南京:南京理工大学,2003.
Kong D R.Researches on quasi-dynamic calibration technique and experiment with plastic pressure-measuring elements[D].Nanjing:Nanjing University of Science and Technology,2003.
[2] 余尚江,杨吉祥,陈显.动高压测试技术研究综述[J].防护工程,2011,33(04):65-72.
Yu S J,Yang J X,Chen X.A review on measurement techniques of high dynamic pressure[J].Protective Engineering,2011,33(04):65-72.
[3] 张建宏,武锦辉,王高,等.多普勒雷达弹丸测速信号的速度重建方法[J].中国测试,2020,46(04):31-35.
Zhang J H,Wu J H,Wang G,et al.Method for velocity reconstruction of doppler radar projectile velocity signal[J].China Measurement & Test,2020,46(04):31-35.
[4] 刘丹.毫米波干涉仪膛内信号处理方法研究[D].太原:中北大学,2016.
Liu D.Millimeter wave interferometer signal research within the bore[D].Taiyuan:North University of China,2016.
[5] 李毅伟.一种新型Ku/Ka双频段动中通天线馈源网络设计[D].成都:电子科技大学,2020.
Li Y W.A new design of ku/ka dual-band feed network of sotm antenna[D].Chengdu:University of Electronic Science and Technology of China,2020.
[6] 王力,杨臻,邓大建,等.基于ISIGHT的人枪系统多参数动态优化设计[J].兵器装备工程学报,2020,41(11):55-60.
Wang L,Yang Z,Deng D J,et al.Multi parameter dynamic optimization design of man-gun system based on ISIGHT[J].Journal of Ordnance Equipment Engineering,2020,41(11):55-60.
[7] 陆野,周克栋,赫雷,等.坡膛结构参数对枪械内弹道挤进时期的影响研究[J].兵工学报,2015,36(07):1365-1369.
Lu Y,Zhou K D,He L,et al.Influence of structure parameters of forcing cone on small arms interior ballistics during engraving[J].Acta Armamentarii,2015,36(07):1365-1369.
[8] 陈川琳,黄陈磊,许辉,等.小口径步枪弹头后效期运动特性试验与数值研究[J].兵工学报,2019,40(02):265-275.
Chen C L,Huang C L,Xu H,et al.Experimental and numerical research on motion characteristics of a small caliber bullet in muzzle flows[J].Acta Armamentarii,2019,40(02):265-275.
[9] 沈静华,裴东兴,张瑜.基于弹底压力的炮口速度解算方法[J].探测与控制学报,2017,39(05):81-83,90.
Shen J H,Pei D X,Zhang Y.Muzzle velocity resolving method based on projectile bottom pressure[J].Journal of Detection & Control,2017,39(05):81-83,90.
[10]程林,霸书红,蒋大千,等.大口径火炮内弹道参数的计算及仿真[J].兵器装备工程学报,2017,38(11):69-72.
Cheng L,Ba S H,Jiang D Q,et al.Interior ballistic parameters calculation and simulation of large caliber gun[J].Journal of Ordnance Equipment Engineering,2017,38(11):69-72.
[11]尤文斌,马铁华,丁永红,等.铜柱测压器膛压测试产生误差的机理研究[J].仪器仪表学报,2015,36(10):2290-2296.
You W B,Ma T H,Ding Y H,et al.Research on the deviation mechanism in artillery chamber pressure test with copper cylinder pressure gage[J].Chinese Journal of Scientific Instrument.2015,36(10):2290-2296.