1 引言
电涡流阻尼器已应用于楼盖减振控制系统、桥梁风振、汽车悬挂与制动系统等领域中,并且取得了较好的效果[1~6]。在火炮上,电涡流阻尼器与制退机工作原理相似,都在物体的运动过程中提供阻力,起到减缓物体运动的作用,所以电涡流阻尼器式制退机能够在火炮上被使用。除此之外,电涡流阻尼器式制退机结构简单,不存在传统液体气压式制退机难以解决的漏液等问题,且在工作过程中不与机械部件发生直接接触与摩擦,具有线性粘滞阻尼、不产生附加刚度等优点[7-8]。相比于液体气压式制退机,电涡流阻尼器式制退机可靠性高、维护简单,因此,将电涡流阻尼器运用到火炮上对火炮反后坐装置技术领域的发展具有重要的意义。
王楠楠等[9]基于电磁场有限元理论研究了圆筒型电涡流阻尼器在冲击载荷下的动力学特性,并通过冲击加载试验数据对结论进行验证;李启坤等[10]提出一种Hallbach阵列的电涡流阻尼器结构并对它的磁场分布特性进行了研究,通过引入火炮后坐运动方程验证了电涡流阻尼器可以满足火炮后坐运动特性;李子轩等[11]研究了电涡流阻尼器在强冲击载荷下产生的去磁效应,通过对阻尼器结构进行优化,有效减弱了去磁效应。上述学者都对电涡流阻尼器的不同方面进行了研究,但是,电涡流阻尼器的结构原理可以使制退机相对于身管同心式布置,而传统的液压式复进机却很难做到,并且这种电涡流阻尼器制退机同心式布置方案的研究还很少,本文以射击后火炮的炮口振动为研究对象,通过建立火炮的非线性有限元模型,对不同电涡流阻尼器制退机布置方式对炮口振动的影响进行研究。
2 火炮同心式电涡流阻尼器结构原理
2.1 同心式电涡流阻尼器布置方案
电涡流阻尼器在火炮发射过程中起到制退机的作用。同心式电涡流阻尼器包括动子和定子等2个部分,动子由永磁体和磁靴组成,依托身管安装,随身管运动,定子由导体筒和导磁筒组成,是筒形摇架的组成部分,如图1所示。火炮发射后,炮身在后坐过程中,身管带动永磁组高速后坐,与摇架导体筒发生相对运动,身管受到与运动方向相反的电涡流阻尼力,控制火炮的后坐运动。由于电涡流阻尼力作用线与身管同心,避免了传统制退机偏置布置方案对炮身产生的偏置力矩。偏置式电涡流阻尼器与同心式阻尼器的结构原理相同,在总体布局上以取代液压式制退机[12-13]。
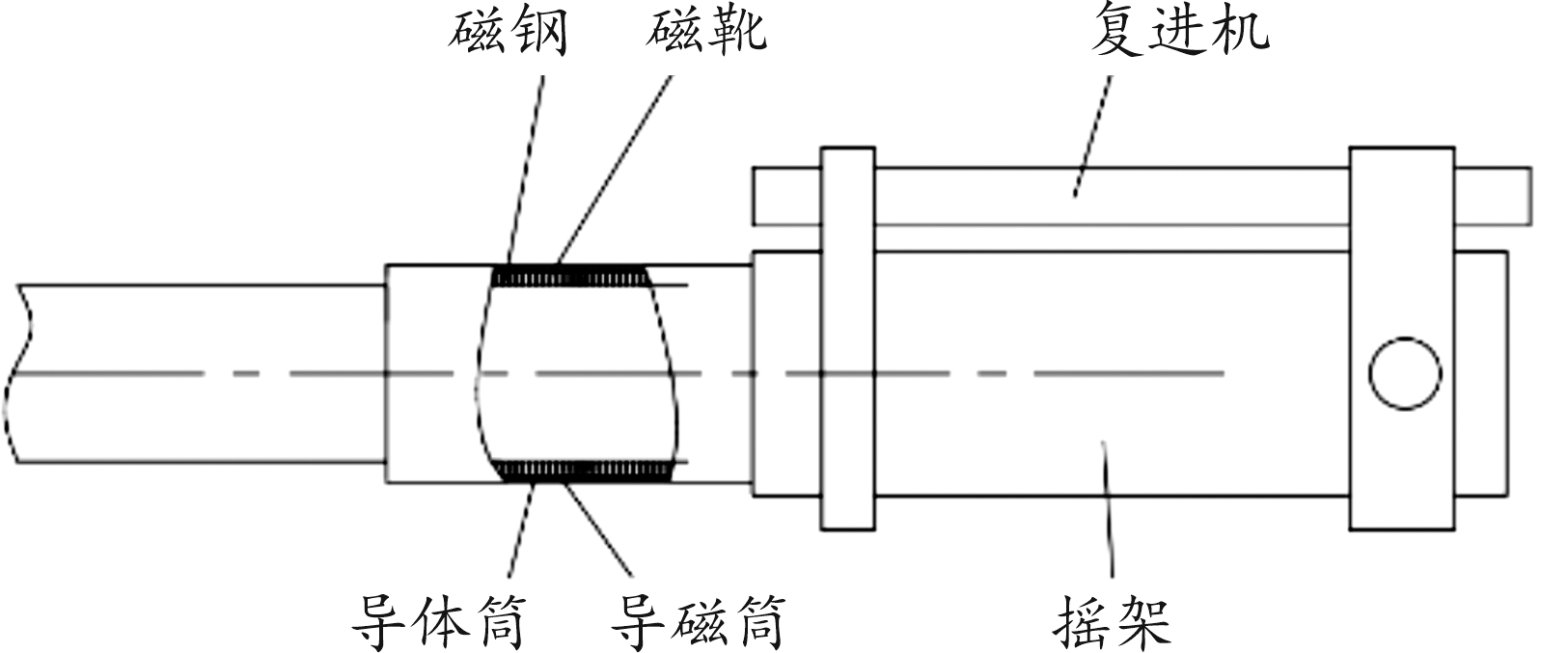
图1 电涡流阻尼器同心式布置示意图
Fig.1 Concentric layout of eddy current damper
2.2 电涡流阻尼力模型
电涡流阻尼器的磁路单元结构如图2所示,2个永磁体之间采用同极相对的安装方式,以提高阻尼性能,若干磁路单元组成电涡流阻尼器的永磁组。在制退机同心式和偏置式2种布置方案当中,永磁组分别与身管、后坐部分连接的芯杆连接。
图2中,τm为永磁体厚度,H为磁组与导体筒的间隙,τ为极距,ri为导体筒内径,rm为导体筒外径,ro为导磁筒外径,Ri为永磁体内径,Ro为永磁体外径,Rc为磁靴半径。
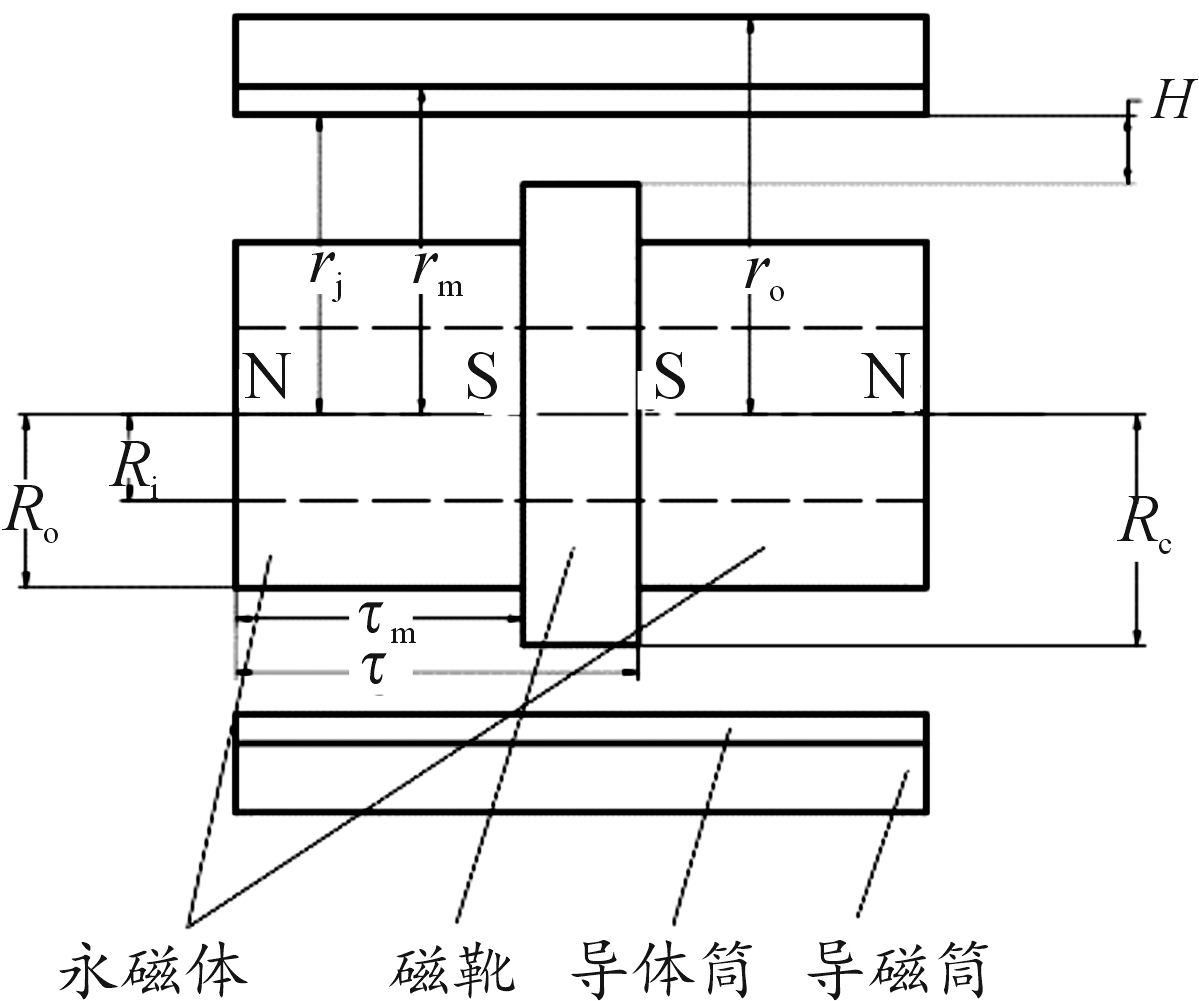
图2 磁路单元示意图
Fig.2 Schematic diagram of magnetic circuit unit
电涡流阻尼器结构参数中,间隙越小,磁路的有效磁通就越大,能够显著提升阻尼器的制动性能,因此,在满足磁组运动精度的情况下,应尽量减小间隙,使得阻尼器获得更优越的性能[14-15]。此外,阻尼器的阻尼系数也会随着磁靴厚度的增加而增加,最后趋于饱和[9-11]。而导体筒厚度、导磁筒厚度也会对阻尼器的性能产生一定的影响[16]。
电涡流阻尼力通过麦克斯韦方程组计算得出,麦克斯韦方程组由安培环路定律、法拉第电磁感应定律、高斯定律和高斯磁通定律组成,该方程组的积分形式为:
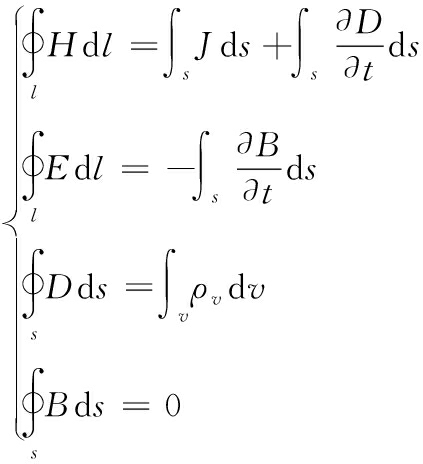
(1)
式(1)中:H为磁场强度;J为传导电流密度;D为电场的电通量密度;E为电场强度;B为磁感应强度;ρv为电荷体密度。
对于各向同性、均匀、线性的介质,有如下关系:
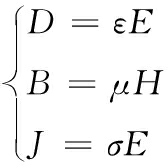
(2)
式(2)中:ε为介质的介电常数;μ为介质的磁导率;σ为介质的电导率。
3 火炮发射动力学建模
3.1 有限元建模
火炮各部件间的连接关系非常复杂,具有高度非线性。本文以座圈以上部分为研究对象,其中,身管与炮口制退器、炮尾部分相对固定,沿着摇架衬瓦的轴向运动。摇架通过耳轴能够绕着上架的耳轴孔旋转,摇架的前卡箍两侧结构与上架的平衡机座共同安装平衡机,此外,摇架上的高低机齿弧与上架的高低机齿轮轴通过齿轮啮合,控制身管的高低方向。偏置式电涡流阻尼器方案中制退机和复进机的静止部分与摇架前后卡箍固定连接,移动部分与炮尾上的安装孔固定,随后坐部分运动;同心式电涡流阻尼器方案中制退机永磁体安装在身管上,随身管运动,复合筒与摇架结合,不参与后坐运动,复进机安装方式保持不变。活动座圈与上架固定连接,固定座圈与台架固定,滚珠位于活动座圈与固定座圈之间并与两者相接触。
身管-电涡流阻尼器同心布置的全炮有限元模型如图3所示,对身管、摇架、上架、高低机齿轮齿弧等主要部件使用六面体网格进行划分,而对于炮尾、闩体等非主要部件,由于这些部件结构上存在一定的复杂性并且相对而言计算精度要求不是很高,采用适应性强的大尺寸四面体网格来替代较小尺寸六面体网格,以减小网格划分难度和网格数量,提高模型计算速度。平衡机用非线性弹簧进行模拟,弹簧端点置于平衡机支点处,且在弹簧两端点处添加质点来以模拟平衡机的质量特征。
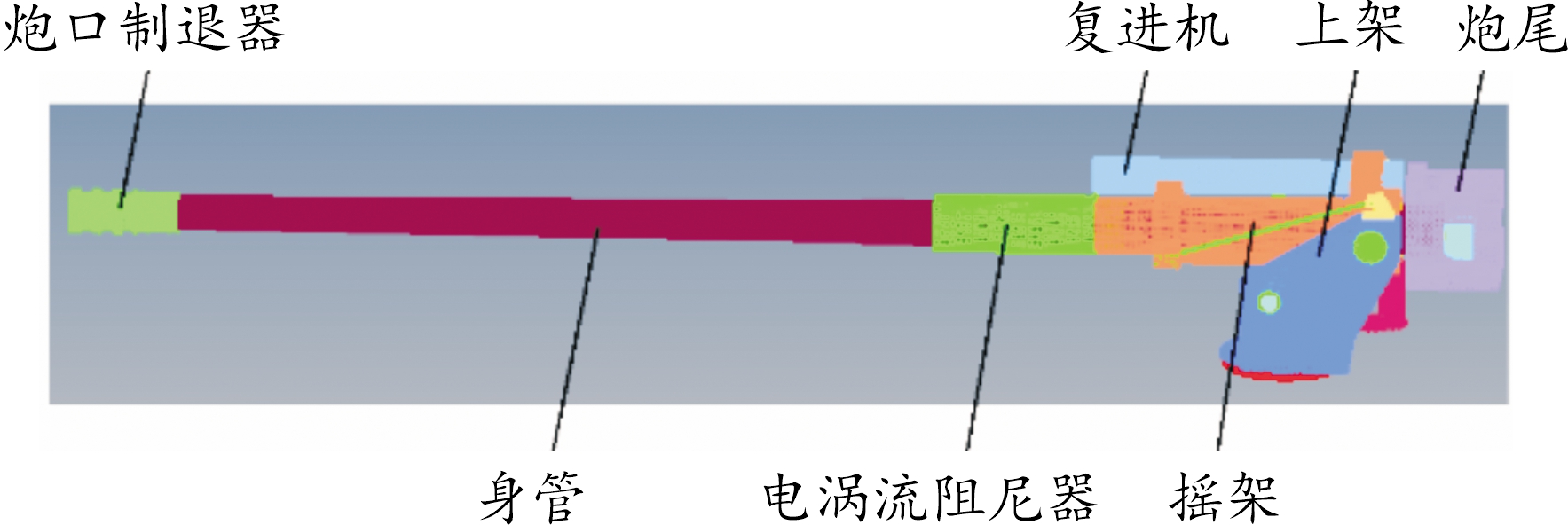
图3 身管-电涡流阻尼器同心布置网格模型示意图
Fig.3 Grid model of concentric eddy current damper
火炮部件间存在多个接触行为,如身管与摇架衬瓦的接触,高低机大齿弧和齿轮轴的接触等,对于这类接触关系,通过对两者可能发生接触的表面区域定义面对面的接触对来模拟。
考虑到传统火炮制退机采用偏置式布置方案,为了对比制退机不同布置方式对火炮发射过程的影响,本文同时建立了电涡流阻尼器偏置布置的发射模型,如图4所示。
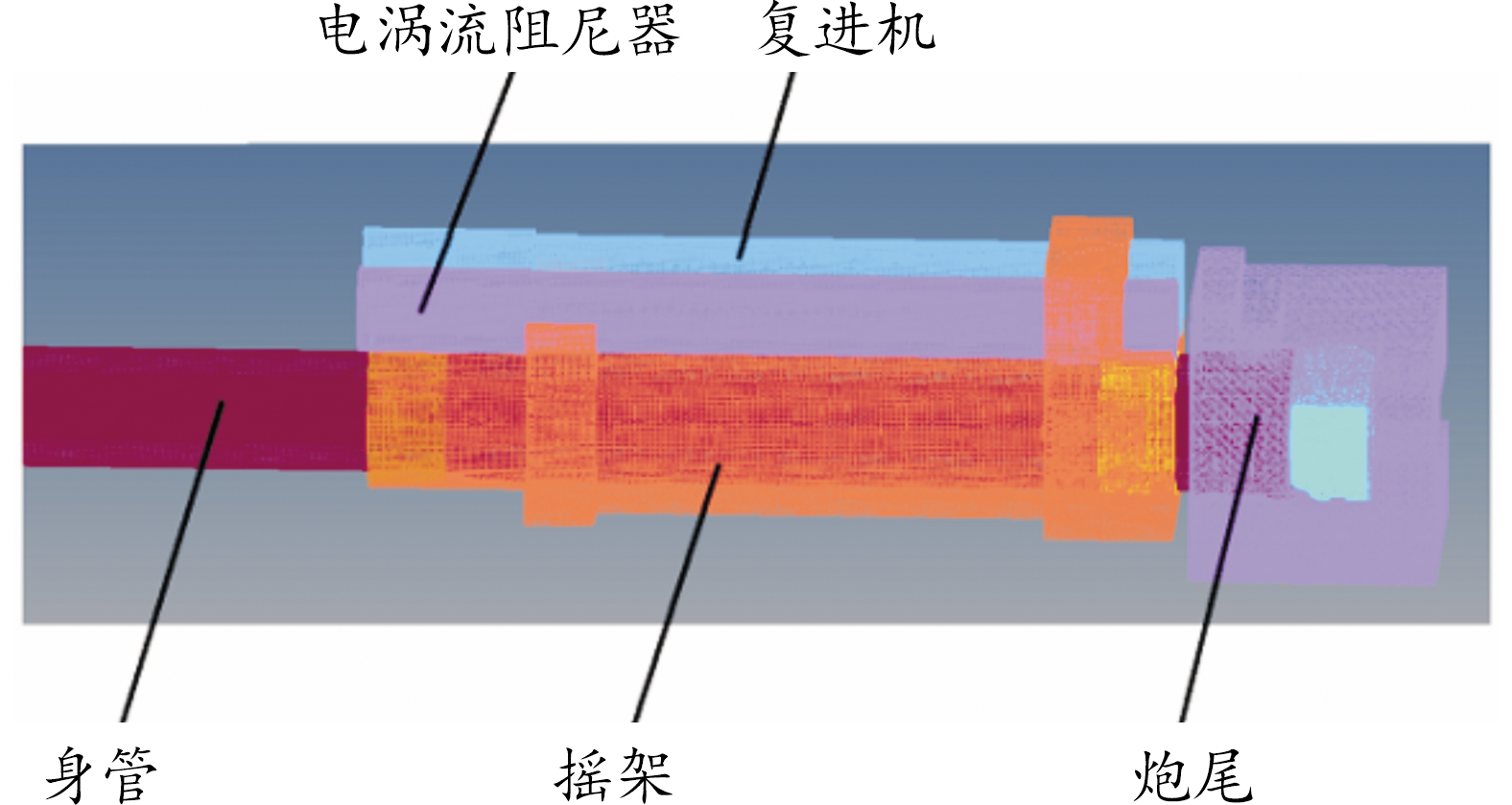
图4 身管-电涡流阻尼器偏置布置网格模型示意图
Fig.4 Grid model of offset eddy current damper
3.2 发射载荷
火炮发射时,后坐部分主要受到重力G、炮膛合力Fpt、制退机力Fz、复进机力Ff及平衡机力的共同作用。在施加载荷时,重力作为不随时间变化的常力直接作用在整个模型上,炮膛合力由火炮的内弹道过程决定,加载随时间变化的压力在闩体承压面上,炮膛合力F pt -t曲线如图5。平衡机力则通过上文中的非线性弹簧进行模拟。
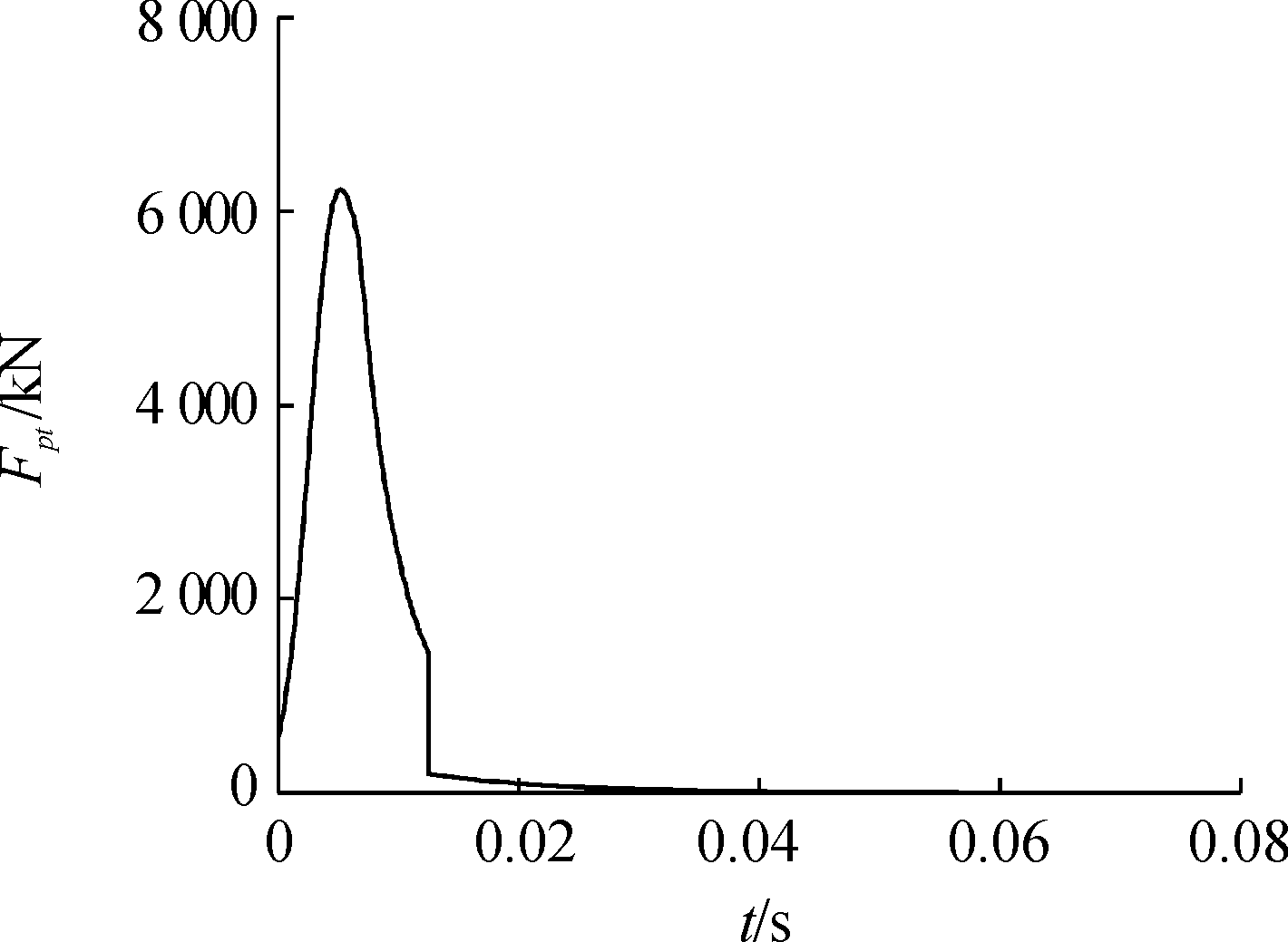
图5 炮膛合力曲线
Fig.5 Action curve of gun bore resultant force
对电涡流阻尼器的结构参数进行调整,能够使2种电涡流阻尼器布置方案模型中的电涡流阻尼力大小相近。制退机偏置式布置模型中电涡流阻尼器采用现有样机模型,结构参数如表1所示,通过有限元仿真软件Maxwell进行仿真,得到电涡流阻尼力规律,如图6所示。
表1 电涡流阻尼器结构参数(mm)
Table1 Structural parameters of eddy current damper
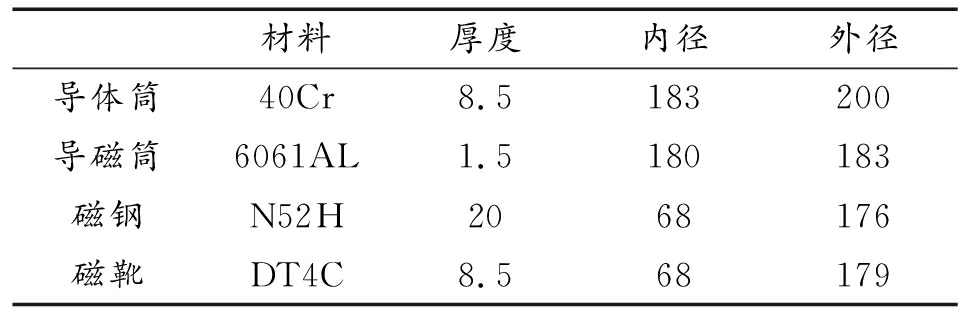
材料厚度内径外径导体筒40Cr8.5183200导磁筒6061AL1.5180183磁钢N52H2068176磁靴DT4C8.568179
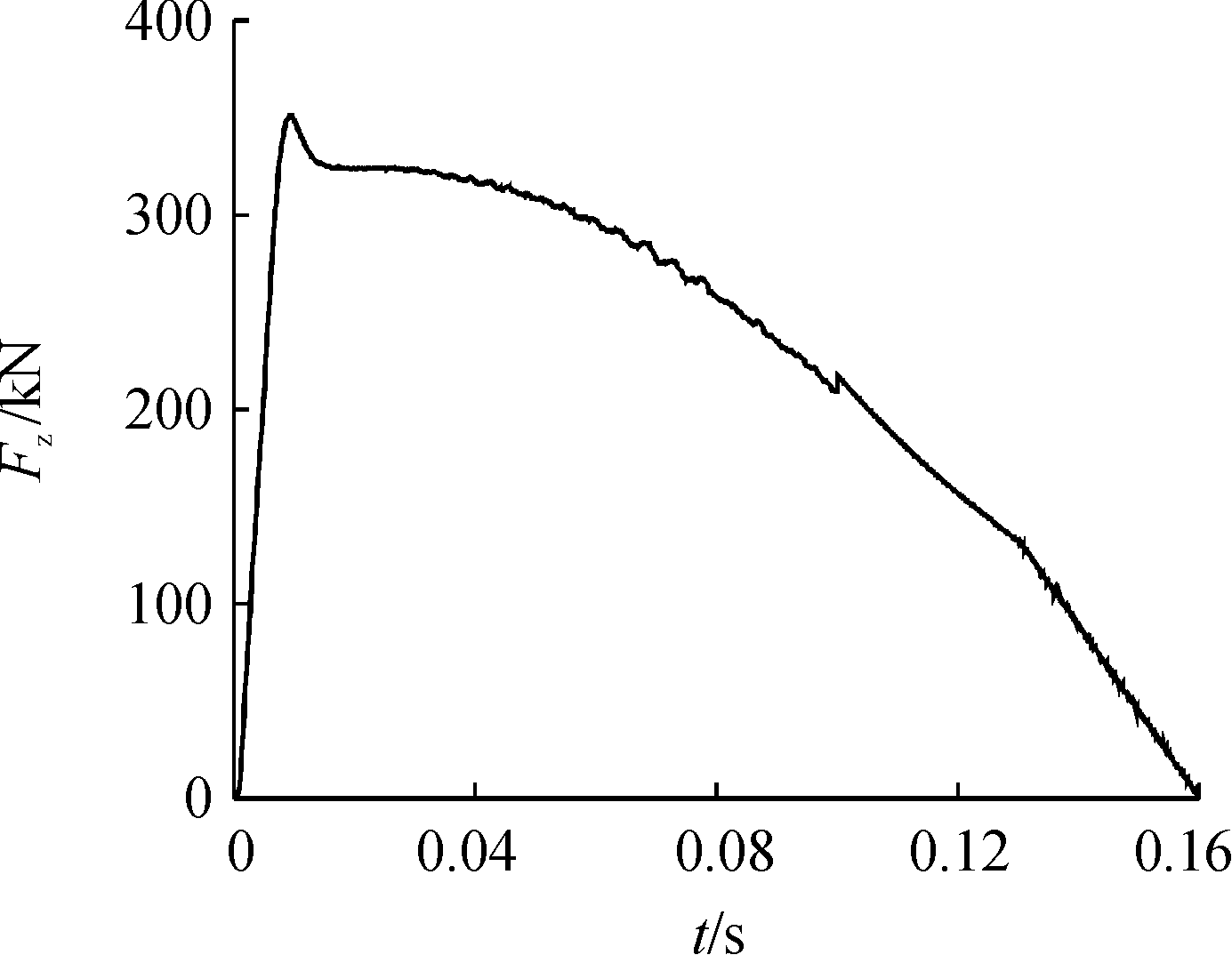
图6 电涡流阻尼力作用曲线
Fig.6 Action curve of eddy current damper force
复进机为传统液体气压式复进机,复进机力作用曲线如图7,通过使用UAMP子程序将电涡流阻尼力和复进机力导入至火炮发射动力学仿真模型。
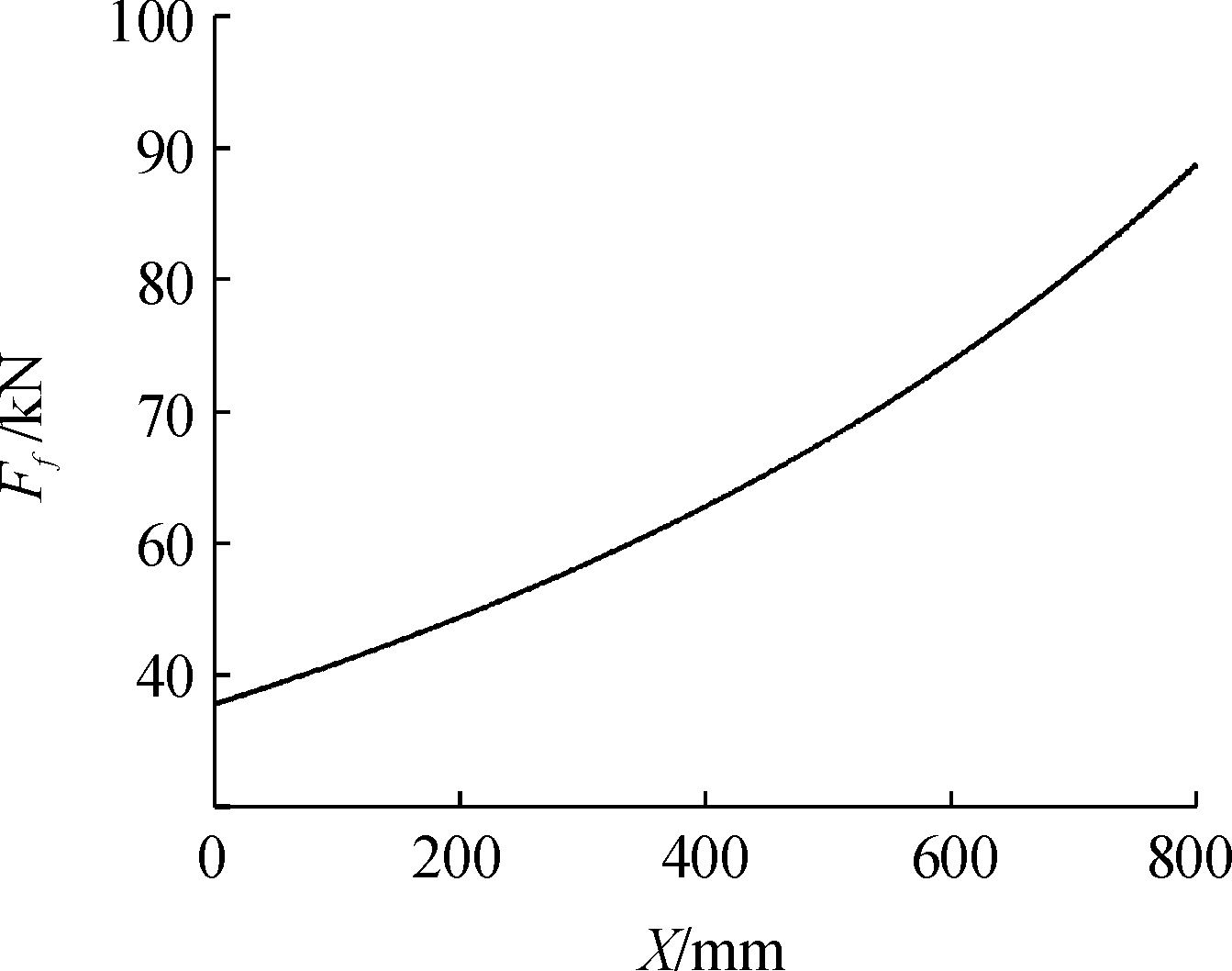
图7 复进机力曲线
Fig.7 Action curve of counter-recoil mechanism force
4 数值计算结果分析
对建立的2种电涡流阻尼器布置方案有限元模型进行数值仿真,分析比较在后坐过程中2种电涡流阻尼器布置方案炮口位置的水平角位移及角速度、高低角位移及角速度、高低机齿轮齿弧接触力、前衬瓦和后衬瓦接触力。
数值仿真得到2种电涡流阻尼器布置方案模型的后坐速度和后坐位移曲线,如图8所示,2种电涡流阻尼器布置方案的后坐速度和后坐位移曲线基本重合,表明采用制退机同心式布置不改变原制退机偏置式布置模型的后坐运动规律。
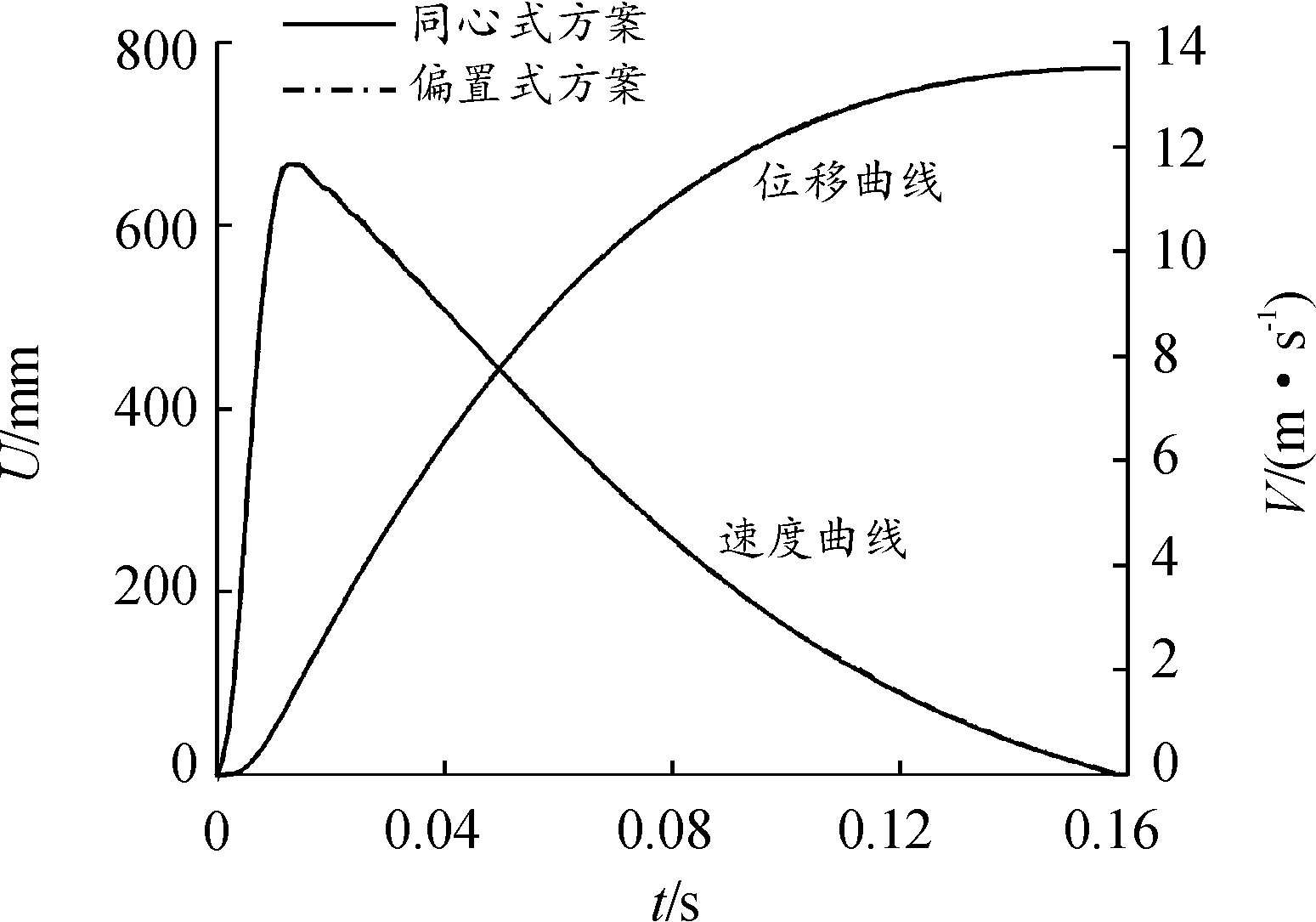
图8 后坐速度与后坐位移曲线
Fig.8 Recoil speed and recoil displacement comparison curve
对模型进行静平衡求解后,得到静平衡状态的2种电涡流阻尼器布置方案炮口角位移初始值分别为:偏置式方案的炮口水平初始角位移为1.4 μrad,高低初始角位移为4.35 μrad;同心式方案炮口水平初始角位移为1.95 μrad,高低初始角位移为4.31 μrad。
在后坐运动中,后坐部分受到炮膛合力、制退机力、复进机力和重力的共同作用。其中,炮膛合力作用时间很短,制退机力、复进机力除了对后座部分沿后坐方向的运动起作用外,还因力作用线与身管轴线有一定的空间距离而产生偏置力矩,此外,还有因后坐部分质心沿着后坐方向运动而产生的后坐部分对摇架与身管配合段的倾覆力矩。制退机力和复进机力引起的偏置力矩对炮口位置的高低角位移和水平角位移都会产生影响,重力引起的倾覆力矩主要对炮口位置的高低角位移产生影响。
水平方向上,在0~0.02 s,2种电涡流阻尼器布置方案的炮口高低角位移值和水平角位移值都对炮膛合力作出响应,当炮膛合力作用结束后,由制退机力和复进机力控制后坐部分的运动。在偏置式方案中,对于炮口位置水平角位移,制退机力和复进机力产生的偏置力矩作用效果相反,但制退机力的作用效果更强,结合炮口水平角位移曲线(见图9),表现为在0.02~0.13 s炮口水平角位移开始增大直至最大值2.24 μrad。而对于炮口高低角位移,重力产生的倾覆力矩与制退机力和复进机力产生的偏置力矩作用效果相反,但偏置力矩的作用效果更强,结合炮口高低角位移曲线(见图10),表现为在0.02~0.13 s高低角位移也开始增大直至最大值11.2 μrad。
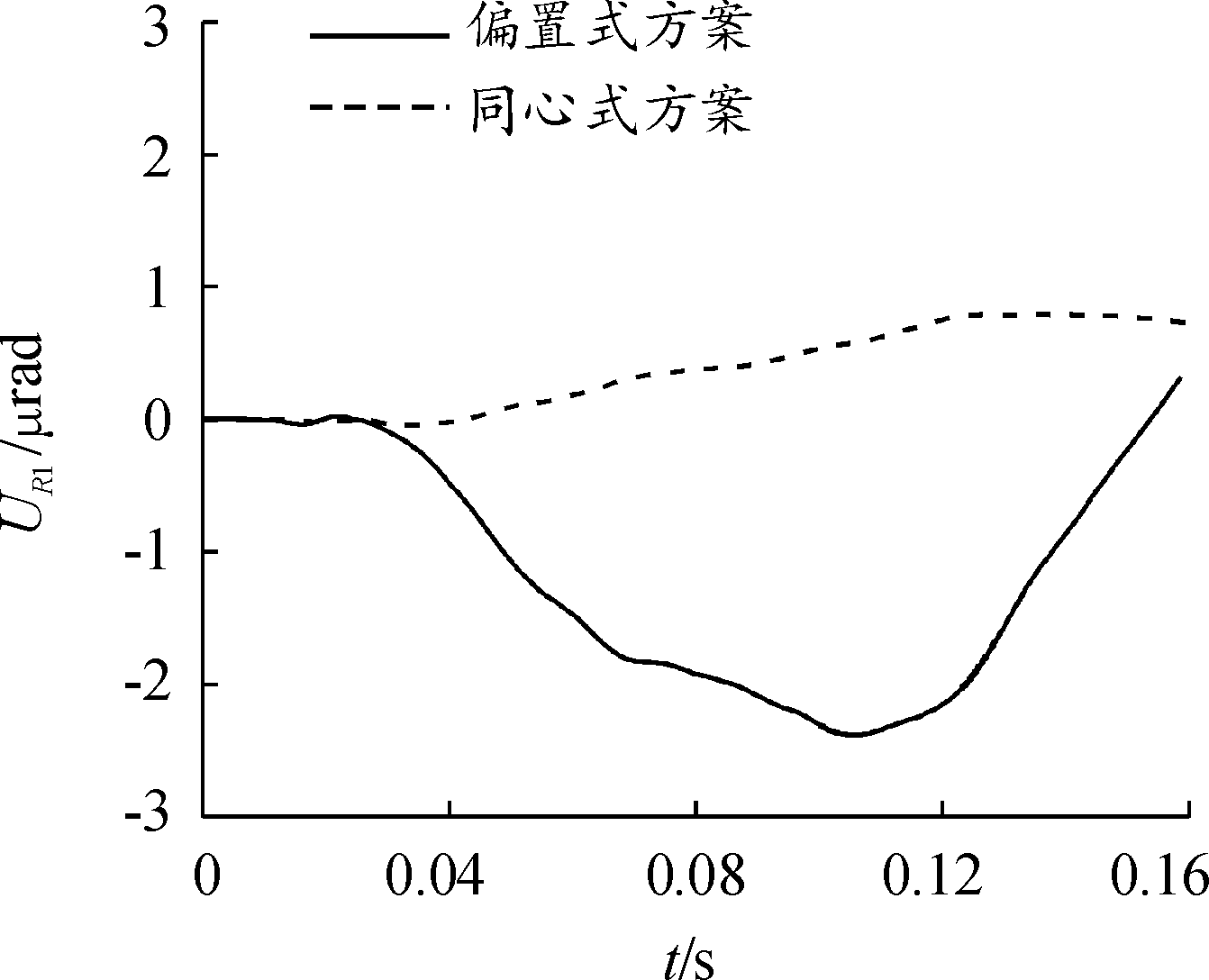
图9 炮口水平角位移对比曲线
Fig.9 Comparison curve of muzzle horizontal angular displacement
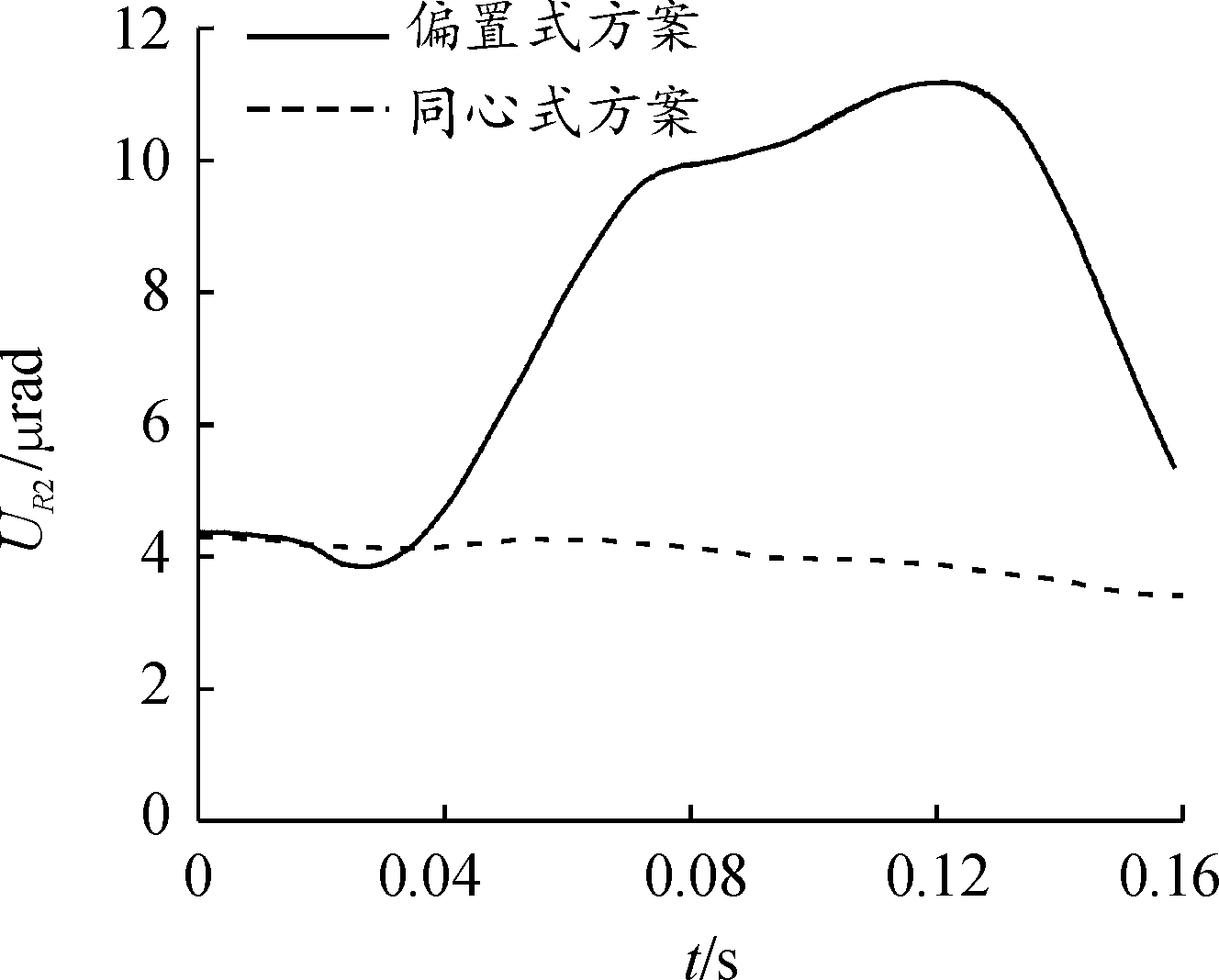
图10 炮口高低角位移对比曲线
Fig.10 Comparison curve of high-low angular displacement of muzzle
而对于同心式方案,由于避免了制退机力偏置力矩的影响,仅受复进机力产生的偏置力矩和重力产生的倾覆力矩的作用,且复进机力产生的偏置力矩和重力产生的倾覆力矩作用效果较弱,因此炮口水平角位移最大值0.97 μrad和炮口高低角位移最大值4.3 μrad,仅为偏置式方案的43%和38%。在0.13~0.16 s,偏置式方案中制退机力产生的偏置力矩效果减弱,结合图9和图10,表现为炮口水平角位移和高低角位移开始减小,而同心式方案仍与上一时间段的变化趋势相同。
炮口水平角速度、高低角速度曲线如图11和图12所示,由图11和图12可知,同心式方案模型的炮口水平角速度和高低角速度数值都明显低于偏置式方案模型的炮口角速度,且数值波动更稳定。数据表明,采用制退机同心式布置的火炮在射击过程中,炮口振动幅值远小于传统偏置布置方案,对提高火炮的射击精度具有积极的作用。
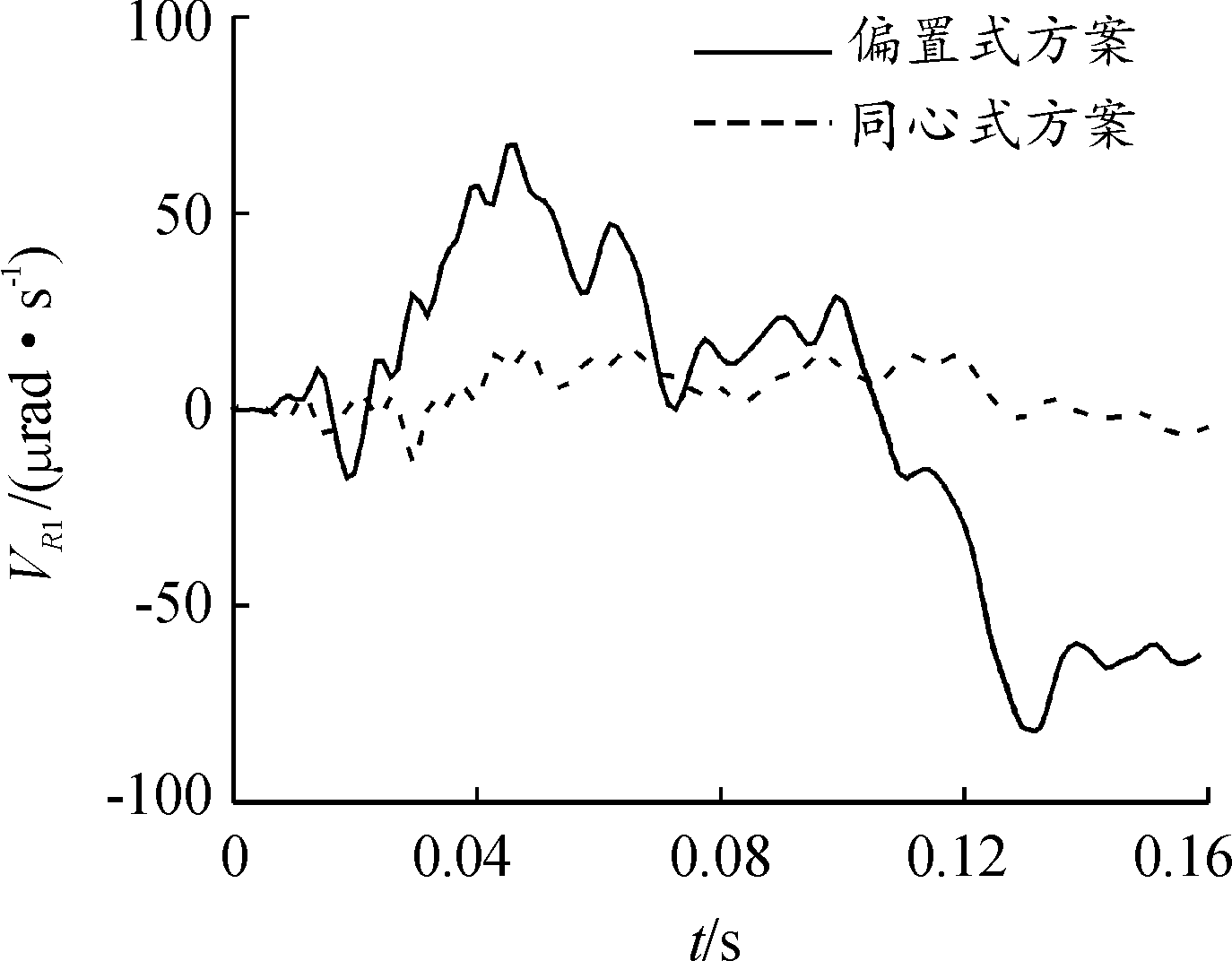
图11 炮口水平角速度曲线
Fig.11 Comparison curve of muzzle horizontal angular speed
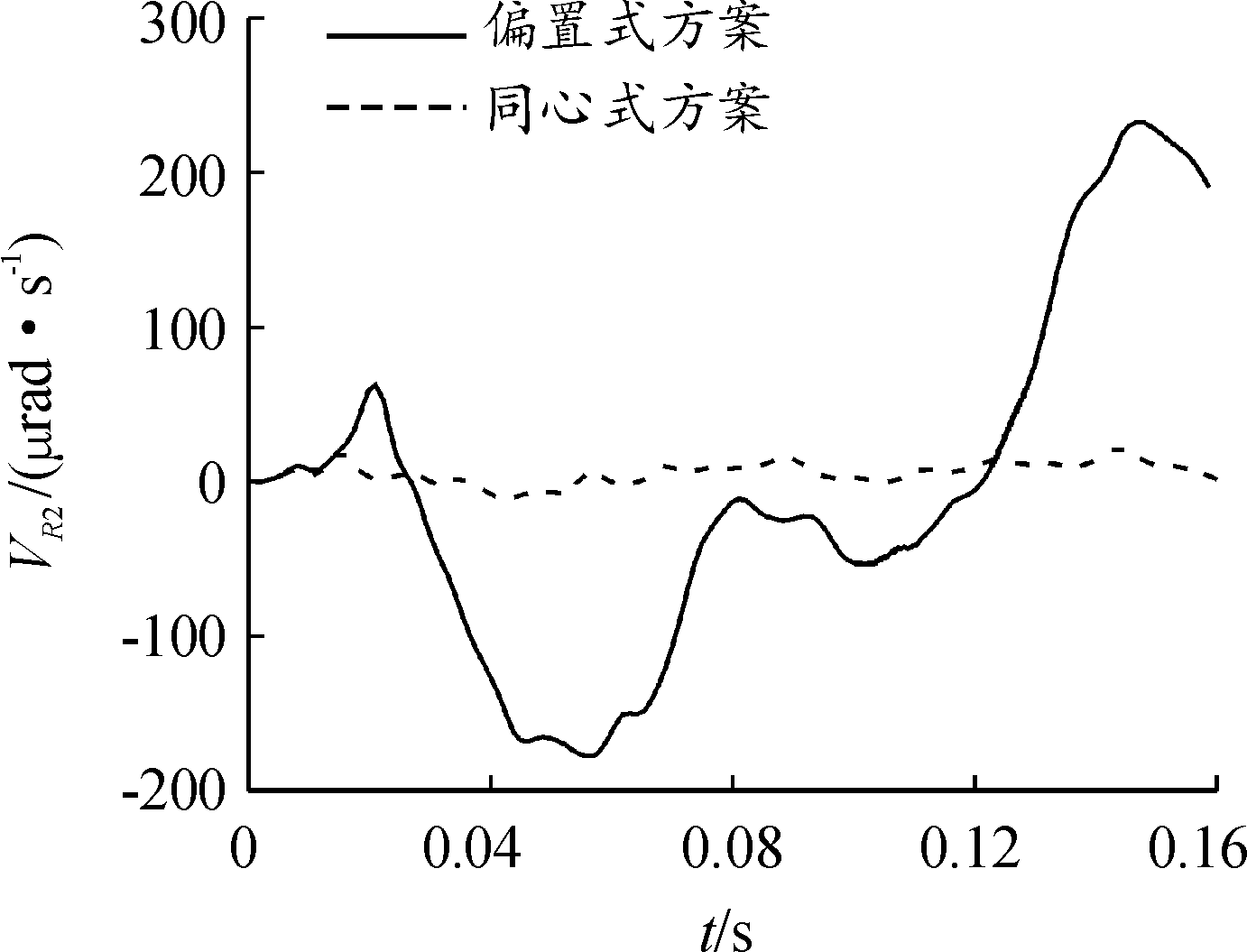
图12 炮口高低角速度对比曲线
Fig.12 Comparison curve of high and low angular speed of muzzle
根据图13、图14和图15可知,在0~0.02 s,2种电涡流阻尼器布置方案的齿轮齿弧、前衬瓦和后衬瓦接触力差距都很小,而这段时间后坐部分的受力主要受炮膛合力的控制,在0.02 s之后,炮膛合力迅速衰减消失,制退机力和复进机力开始控制火炮后坐部分运动。之后,偏置式方案模型的齿轮齿弧、前衬瓦和后衬瓦所受接触力在0.1 s达到了最大,分别为344 kN、127 kN和120 kN;而同心式方案模型的齿轮齿弧、前衬瓦和后衬瓦所受接触力的数值变化不大,齿轮齿弧所受接触力最大不超过100 kN,前衬瓦所受接触力最大在30 kN左右,后衬瓦所受最大接触力为20 kN,分别是偏置式方案齿轮齿弧、前衬瓦和后衬瓦所受接触力的29%、24%和17%。
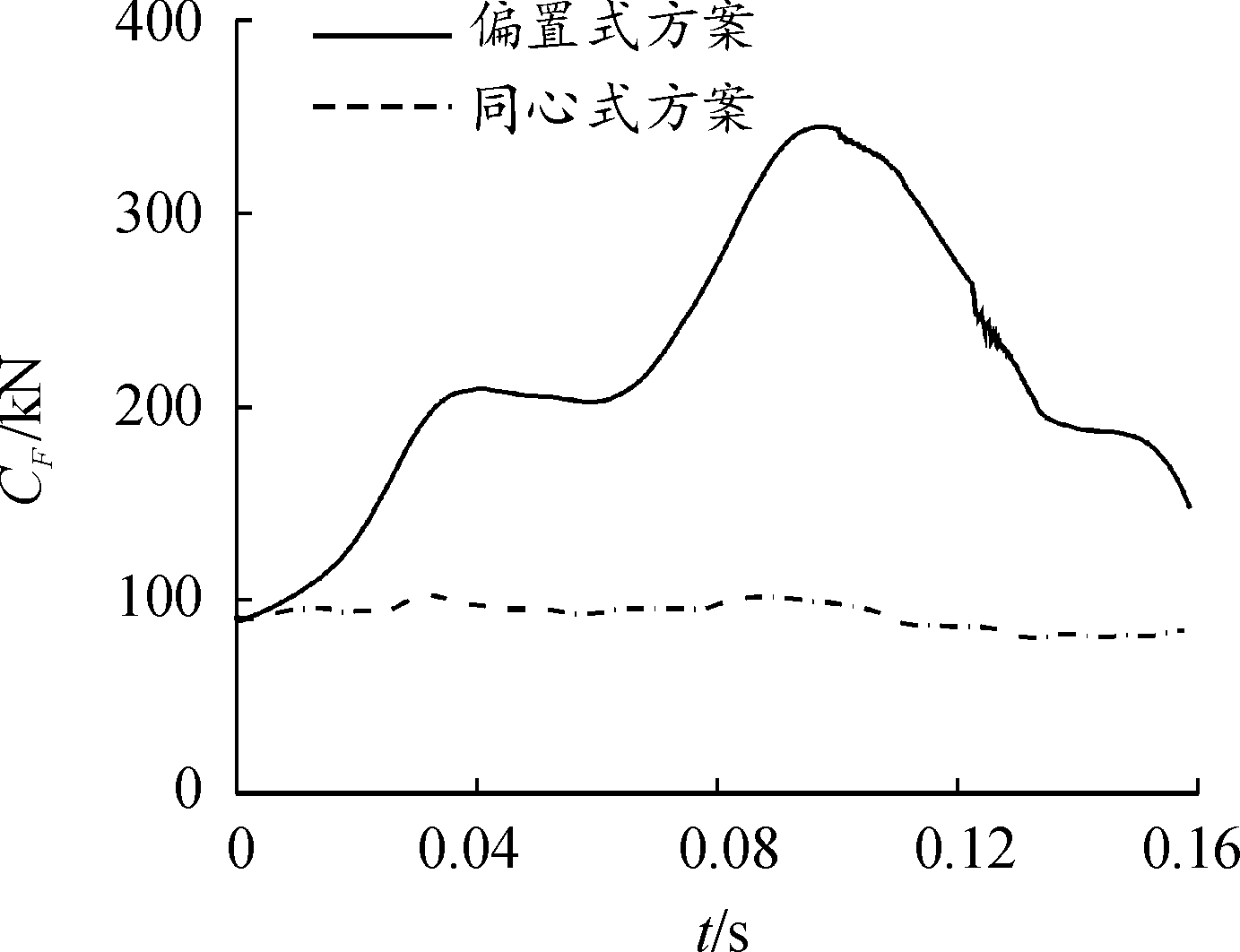
图13 高低机齿轮齿弧接触力曲线
Fig.13 Comparison of arc gear contact force of high and low gear
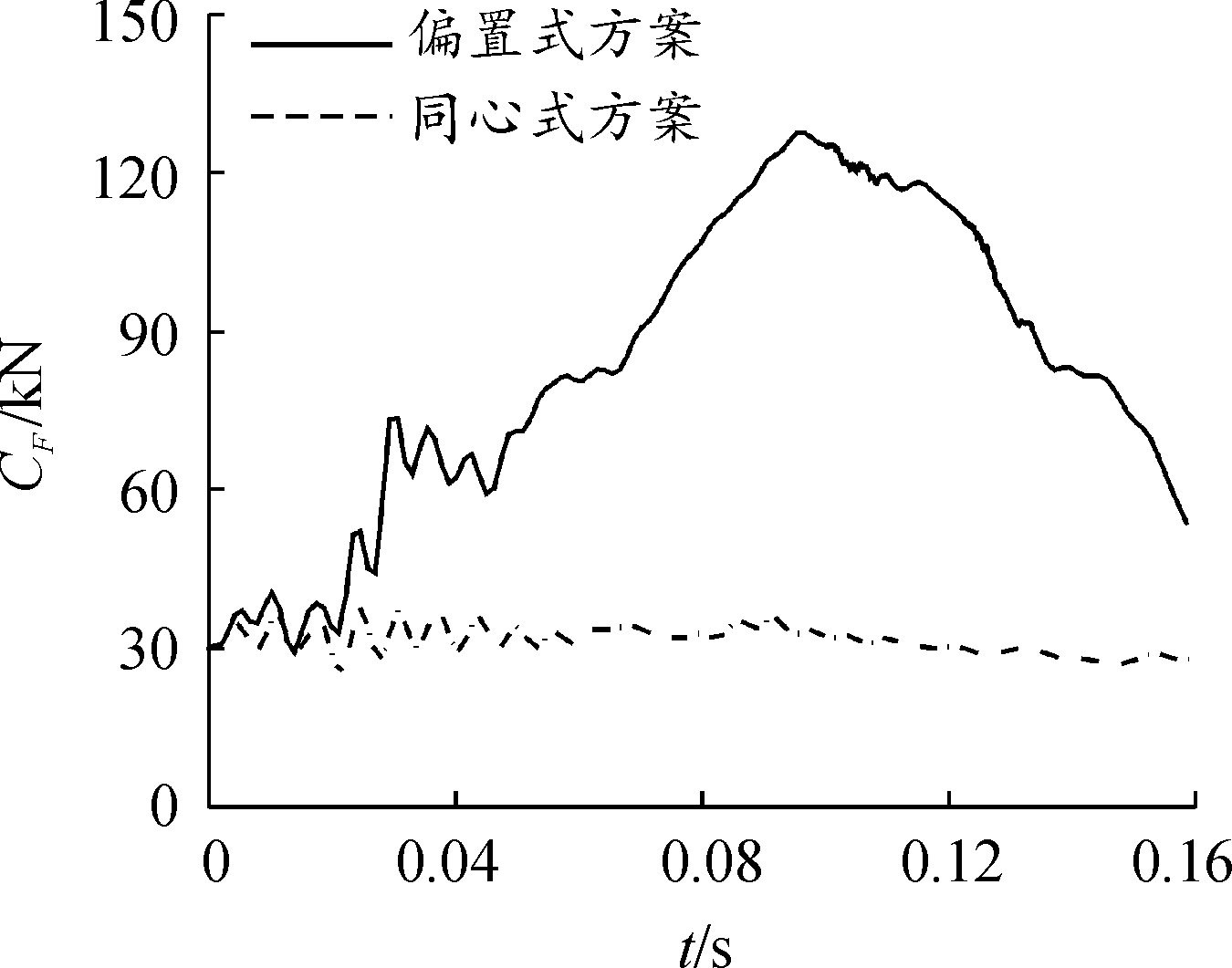
图14 前衬瓦接触力曲线
Fig.14 Comparison of contact force of front liners

图15 后衬瓦接触力曲线
Fig.15 Comparison of contact force of rear liners
由于偏置式方案中制退机力产生偏置力矩的影响,使得图13、图14和图15中部件所受接触力大小差异悬殊,而同心式方案中避免了制退机偏置力矩的影响,高低机齿轮齿弧和摇架衬瓦受力曲线平缓。结果表明,采用制退机同心式布置,火炮在射击过程中会改善全炮的受力条件。
5 结论
1) 电涡流阻尼器制退机同心式方案布置比偏置式方案布置对减小炮口振动具有显著的作用。
2) 采用同心式电涡流阻尼器制退机能够改善全炮受力条件。
[1] 潘毅,包韵雷,国巍,等.摆式电涡流TMD-钢框架结构的耦合计算方法与减震分析[J].土木与环境工程学报,2020,42(04):84-93.
Pan Y,Bao Y L,Guo W,et al.Coupling calculation method and seismic analysis of pendulum eddy current TMD-steel frame structures[J].Journal of Civil and Environmental Engineering,2020,42(04):84-93.
[2] Stein G J,Tobolka P,Chmúrny R.Ferromagnetic eddy current damper of beam transversal vibrations[J].Journal of Vibration and Control,2018,24(05):892-903.
[3] Zhang H Y,Chen Z Q,Hua X G,et al.Design and dynamic characterization of a large-scale eddy current damper with enhanced performance for vibration control[J].Mech Syst Signal Process,2020,145(03):106879.
[4] Sodano H A,Bae J S,Lnman D J,et al.Concept and model of eddy current damper for vibration suppression of a beam[J].Sound and Vibration,2005,288(04/05):1177-1196.
[5] Sodano H A,Bae J S,Eddy current damping in structures[J].The Shock and Vibration Digest,2004,36(06):469-478.
[6] Bae J S,Hwang J H,Park J S,et al.Modeling and experiments on eddy current damping caused by a permanent magnet in a conductive tube[J].Mechanical Science and Technology,2009,23(11):3024-3035.
[7] 陈政清,张弘毅,黄智文.板式电涡流阻尼器有限元仿真与参数优化[J].振动与冲击,2016,35(18):123-127.
Chen Z Q,Zhang H Y,Huang Z W.FEM simulation and parameter optimization of a planar eddy current damper[J].The Shock and Vibration Digest,2016,35(18):123-127.
[8] 杨玉栋,张培林,傅建平,等.考虑液体空化的火炮制退机性能分析[J].振动与冲击,2012,31(20):94-98.
Yang Y D,Zhang P L,FU P J,et al.Performance of a gun recoil mechanism considering liquid cavitation[J].Journal of Vibration and Shock,2012,31(20):94-98.
[9] 王楠楠,刘宁,沈艳萍,等.冲击载荷下圆筒型电涡流阻尼器动力特性研究[J].振动与冲击,2021,40(11):65-69,93.
Wang N N,Liu N,Shen Y P,et al.Research on the dynamic characteristics of the cylindrical eddy current damper under impact load[J].The Shock and Vibration Digest,2021,40(11):65-69,93.
[10]李启坤,葛建立,李加浩,等.强冲击载荷作用下Halbach阵列电涡流阻尼器动力学特性仿真分析[J].弹道学报,2021,33(01):23-28.
Li Q K,Ge J L,Li J H,et al.Simulation analysis of dynamic characteristics of Hallbach array eddy current damper under strong impact load[J].Journal of Ballistics,2021,33(01):23-28.
[11]李子轩,杨国来,孙全兆,等.强冲击载荷下永磁式电涡流阻尼器阻力特性及优化研究[J].兵工学报,2018,39(04):664-671.
Li Z X,Yang G L,Sun Q Z,et al.Optimization and resistance characteristics of permanent magnet eddy current damper under intensive impact load[J].Acta Armamentarii,2018,39(04):664-671.
[12]黄通,郭保全,毛虎平.一种新型电磁制退机性能分析[J].火炮发射与控制学报,2018,39(02):12-16.
Huang T,Guo B Q,Mao H P.An analysis of the performance of a novel electromagnetic recoil[J].Journal of Gun Launch & Control,2018,39(02):12-16.
[13]寇宝泉,金银锡,张赫,等.电磁阻尼器的发展现状及应用前景[J].中国电机工程学报,2015(12):3132-3143.
Kou B Q,Jin Y X,Zhang H,et al.Development and application prospects of the electromagnetic damper[J].Proceedings of the CSEE,2015(12):3132-3143.
[14]刘洋,高跃飞,王登.板式电涡流阻尼器的阻尼特性分析[J].中北大学学报(自然科学版),2020,41(03):209-213.
Liu Y,Gao Y F,Wang D.Analysis of damping characteristics of a planar eddy current damper[J].Journal of North University of China(Natural Science Edition),2020,41(03):209-213.
[15]汪志昊,李国豪,周佳贞,等.竖向TMD用板式电涡流阻尼器磁路对比分析[J].振动与冲击,2019,38(07):233-239.
Wang Z H,Li G H,Zhou J Z,et al.Contrastive analysis for magnetic circuit of a planar eddy current damper used in a vertical TMD[J].The Shock and Vibration Digest,2019,38(07):233-239.
[16]Ahn H J,Hwang K J,Nguyen D C.Eddy current damper type reaction force compensation mechanism for linear motor motion stage[J].International Journal of Precision Engineering and Manufacturing Green Technology,2017,231(05):67-74.