1 引言
便携式无坐力炮主要编配于步兵班组和地面作战小分队[1-2],遂行摧毁敌装甲车辆、火力点、有生力量、轻型土木工事等任务,是步兵班组主要火力打击武器。典型代表产品为瑞典“卡尔·古斯塔夫”无坐力炮,配用反装甲、反人员、反工事等多类弹药[3],主用弹种[4]包括多用途弹、杀伤弹、云爆弹、破甲弹等,装备美、英、德、日、印等50多个国家,曾在1982年的马岛战争、1999年的印巴卡吉尔冲突[5]、2001—2014年的阿富汗战争、2003—2010年的伊拉克战争、2011年的利比亚内战、2011年至今的叙利亚内战、2022年俄乌冲突等局部战争中大量使用。
为了综合评定便携式无坐力炮在典型作战场景下的作战效能,将根据步兵分队作战使用流程,编制便携式无坐力炮基本作战想定,制定作战任务剖面;根据作战任务剖面、任务强度和武器基本战术技术性能参数,构建作战效能评定模型;针对装甲车辆、火力点、有生力量三类典型目标,选用多用途弹、杀伤弹两型弹药,进行作战效能计算分析,最终确定便携式无坐力炮兵组完成典型作战任务的最佳携弹量、毁伤目标数、生存概率等作战使用数据。
2 兵组作战任务剖面
以步兵连进攻战斗为例,便携式无坐力炮兵组在步兵连、排火力支援下遂行战斗任务,兵组由2人组成,携带4~6发弹药[6-8],在集结地域(距敌防御前沿约30 km)受领战斗任务,乘车开进至待机地域(距敌防御前沿约10 km),进行短暂停顿和调整,而后向冲击出发阵地接近;到达冲击出发阵地后,兵组下车,按协同时间发起冲击,冲击过程中,接受步兵分队指挥员的命令,对威胁步兵冲击的当面目标实施射击。典型任务剖面如图1所示,典型作战任务期间所经历的全部事件及有关数据见表1所示[5]。
表1 轻型无坐力武器典型任务剖面事件及有关数据
Table1 Typical mission profile events and related data of light recoilless weapon
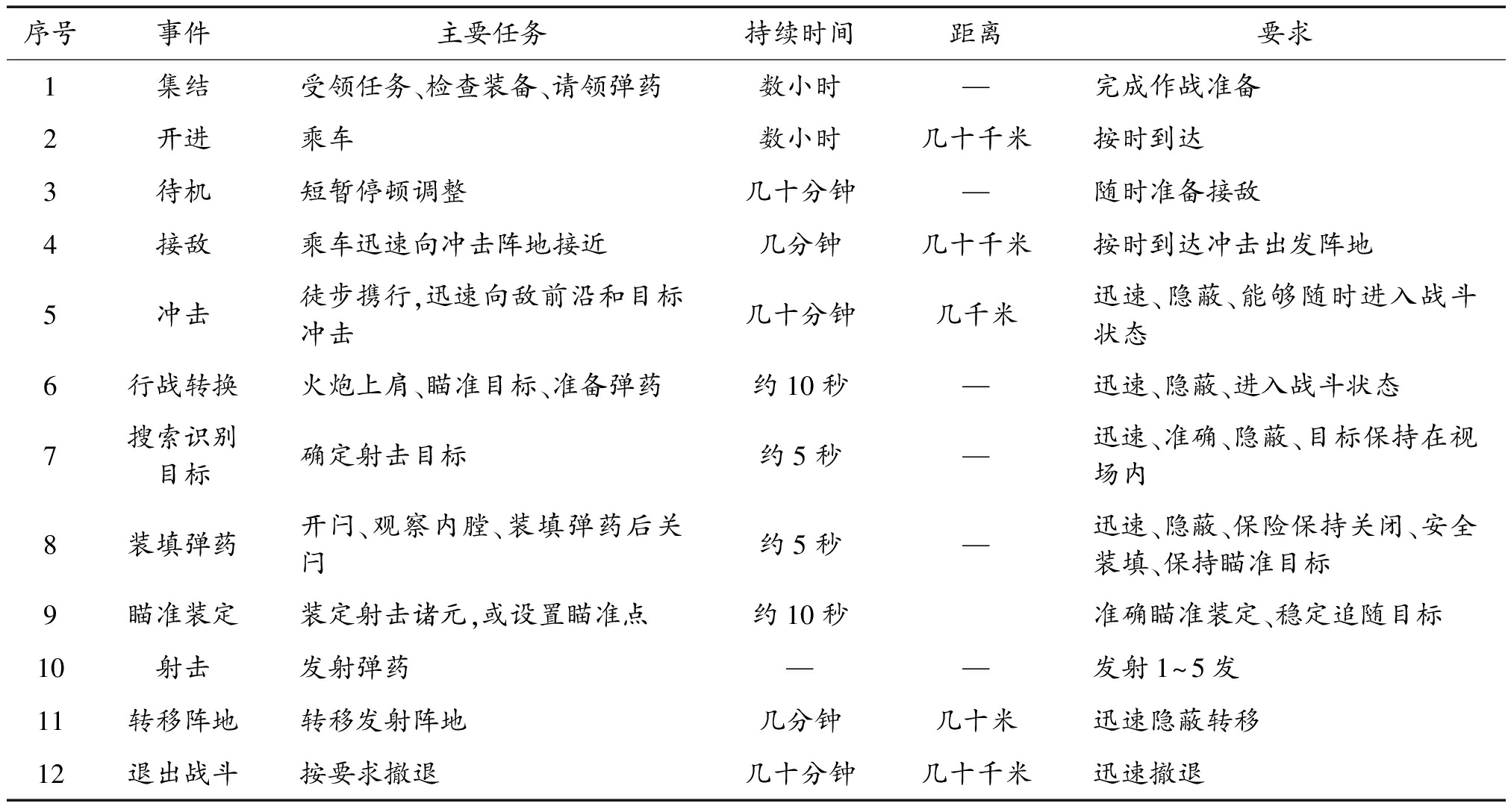
序号事件主要任务持续时间距离要求1集结受领任务、检查装备、请领弹药数小时—完成作战准备2开进乘车数小时几十千米按时到达3待机短暂停顿调整几十分钟—随时准备接敌4接敌乘车迅速向冲击阵地接近几分钟几十千米按时到达冲击出发阵地5冲击徒步携行,迅速向敌前沿和目标冲击几十分钟几千米迅速、隐蔽、能够随时进入战斗状态6行战转换火炮上肩、瞄准目标、准备弹药约10秒—迅速、隐蔽、进入战斗状态7搜索识别目标确定射击目标约5秒—迅速、准确、隐蔽、目标保持在视场内8装填弹药开闩、观察内膛、装填弹药后关闩约5秒—迅速、隐蔽、保险保持关闭、安全装填、保持瞄准目标9瞄准装定装定射击诸元,或设置瞄准点约10秒准确瞄准装定、稳定追随目标10射击发射弹药——发射1~5发11转移阵地转移发射阵地几分钟几十米迅速隐蔽转移12退出战斗按要求撤退几十分钟几十千米迅速撤退
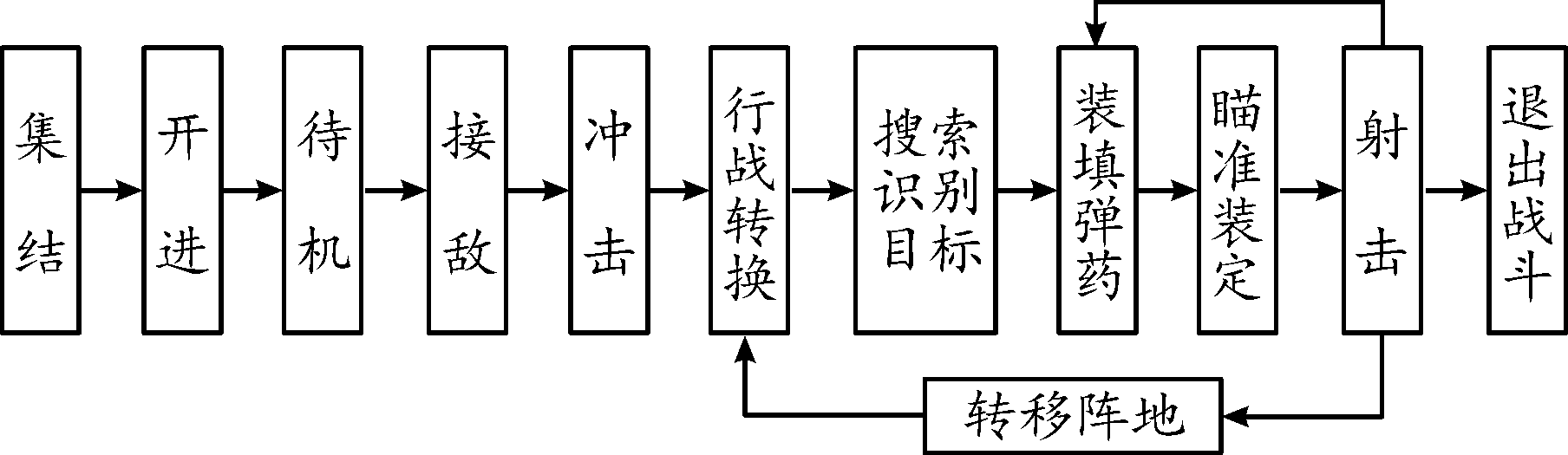
图1 便携式无坐力炮典型任务剖面
Fig.1 Typical mission profile of portable recoilless gun
对敌方机步排进攻时,机步排防御正面300~400 m,装备4辆步兵战车,每辆步兵战车防御正面为75~100 m;在班组进攻正面范围内可能出现1~2辆步兵战车。
对敌方战车排进攻时,战车排防御正面300~600 m,装备4辆战车,每辆战车防御正面为75~150 m;在班组进攻正面范围内可能出现1辆战车。
考虑敌军各种轻武器的有效射程,在阵地防御作战时,在100~150 m防御正面设置2个~3个火力点。
一般情况下,在火力准备阶段能够对敌目标造成的30%伤害[9],当班组发起冲击时,进攻正面出现的目标为1个~2个,典型目标包括步兵战车、火力点、有生力量等[6]。
用于便携式无坐力炮作战效能评定的典型作战任务剖面规定为:2人兵组自冲击阵地下车,按协同时间向敌前沿和目标发起冲击,冲击距离1 000~2 000 m;在冲击过程中对当面目标实施射击,目标数量1~2个;对单个目标连续射击1~4次,期间根据需要转移阵地1次,转移距离50~200 m,至全部消灭遭遇目标或携带弹药发射完毕,为完成一次战斗任务[5]。
3 作战效能评定模型
3.1 作战效能量度
用兵组完成规定作战任务的概率P作为作战效能量度,计算公式为:
(1)
式中:Ne为兵组完成一次作战任务中实际毁伤目标数量,与任务时间内命中并毁伤目标的概率有关,由射击距离、射速、命中精度、毁伤率、系统可靠性等因素决定;Ne0完成作战任务需要毁伤的目标总数。
完成规定作战任务概率P定义如下:
P<0.5时,不能完成作战任务;
0.5≤P<0.65时,基本完成作战任务;
0.65≤P<0.8时,较好完成作战任务;
P≥0.8时,圆满完成作战任务。
3.2 命中并毁伤目标的概率模型
便携式无坐力炮配用不同的弹种打击不同目标,多用途弹用于毁伤敌步兵战车、装甲车辆、火力点等目标,杀伤暴露的有生力量;杀伤弹用于杀伤敌暴露、半遮蔽掩体和堑壕内有生力量,压制敌火力点。
1)多用途弹命中并毁伤目标的概率模型
已知射击精度σy、σz时,多用途弹命中并毁伤装甲车辆、火力点等目标的概率F(N)计算公式见式(2)、式(3):
(2)
(3)
式(2)中,N为连续发射的弹药数量,一般情况下对每个目标至少连续发射2发。
R为武器系统可靠性,国内外同类便携式武器的可靠性可达0.95以上,此处可取值为0.95。
H为毁伤率,对于步兵战车目标,多用途弹使用破甲射流进行毁伤,步兵战车装甲厚度一般不超过50 mm,多用途弹对其毁伤率可到达0.95以上,此处取值为0.95;对于沙袋掩体构筑的机枪火力点目标,多用途弹使用射流和破片综合效能进行毁伤,根据经验值毁伤率可取值为0.7。
M为命中精度,与武器系统误差和立靶精度相关,在直射距离(250 m)内的命中目标概率达95%以上。便携式无坐力炮配用高精度光电火控,具备激光测距、环境参数采集、射表自动查询与射击诸元装订等功能,可将系统误差修正至忽略不计,因此其射击精度取决于立靶密集度,射击精度σy、σz的表达式为:
σy=Ey/0.674 5
σz=Ez/0.674 5
(4)
式中:Ey、Ez为立靶密集度的高低和方向中间误差,设多用途弹400 m立靶密集度Ey×Ez=0.35 m×0.35 m,则在600 m 距离上对步兵战车的命中概率为70%。
S为目标易损面积范围,典型步兵战车和沙袋掩体火力点易损面积范围均取值为y=±1.15 m、z=±1.15 m。
2)杀伤弹命中并毁伤目标的概率模型
杀伤弹命中并毁伤有生力量目标的概率计算公式与多用途弹相同,见式(2)、式(3)。根据目标距离的不同,连续发射弹药数量N取值1~4发。命中精度M直接取值为杀伤弹地面密集度,纵向中间误差取值为射击距离的1/150,横向中间误差取值为射击距离的1/500。毁伤率H取决于杀伤弹引信空炸精度和破片威力范围,在命中有生力量易损面积范围内,毁伤率平均为0.95。有生力量目标易损面积范围S取值为x=±12.5 m、z=±12.5 m。
3.3 毁伤目标数量模型
毁伤目标数量为兵组毁伤每个目标的概率之和,其表达式为:
(5)
3.4 兵组在任务时间内的生存概率模型
兵组在任务时间内可能被敌方发现并毁伤,生存概率与敌方侦察效率、火力毁伤效能和任务时间有关,生存概率表达式为:
Q=1-(1-e-t/θ)pf
(6)
式中:(1-e-t/θ)为敌方发现概率;pf为敌方发现情况下,兵组被毁伤的概率;θ为敌方侦察设备发现目标的平均搜索时间,受能见度、目标可视度、地形、天气及战场条件的影响,一般情况下,平均搜索时间θ约为20 min。
t为兵组任务时间,由机动时间、展开时间、射击时间和阵地转移时间组成,可表示为:
t=tj+tz+ts+ty
(7)
式中,tj为兵组徒步机动时间,与平均冲击距离、冲击速度有关,冲击距离1 000~2 000 m时,冲击时间为10~20 min;tz为阵地展开时间,便携式筒式武器一般取值为15 s;ts为阵地射击时间,与目标搜索时间、射击弹药数目有关,便携式无坐力炮配备昼夜观瞄装置,目标平均搜索时间约10 s,平均射速为5发/min;ty为阵地转移时间,与兵组阵地转移速度相关,便携式筒式武器阵地转移200 m用时约2 min。
根据敌方武器弹药性能,一般情况下在兵组周围25 m×25 m范围内遭受敌炮弹袭击时,认为便携式无坐力炮兵组被毁,则兵组被毁概率可表示为:
pf=1-(1-Δs1/Δs2)Nf
(8)
式中,Nf=n×t为在t时间内、兵组周围每平方千米范围内落入的敌炮弹总数(敌方一旦发现步兵分队活动范围,则在1~2 min内进行反击,按敌方压制纵深600 m计算,在步兵分队突破地段4 000~8 000 m内平均每千米正面每秒落下炮弹0.4~0.6发),n为在突破地段内平均每千米正面每秒落下炮弹发数;Δs1为单发炮弹有效杀伤面积;Δs2为炮弹每千米压制区域面积。
4 作战效能计算与分析
4.1 多用途弹作战效能计算与分析
4.1.1 多用途弹对单个目标作战效能分析
以步兵战车和火力点为典型目标,对单个目标连续发射2发或3发弹药,在不同射击距离上对不同目标的作战效能和生存概率计算结果见表2所示。
表2 多用途弹对单个目标作战效能计算结果
Table 2 Calculation results of combat effectiveness of multi-purpose missile against single target
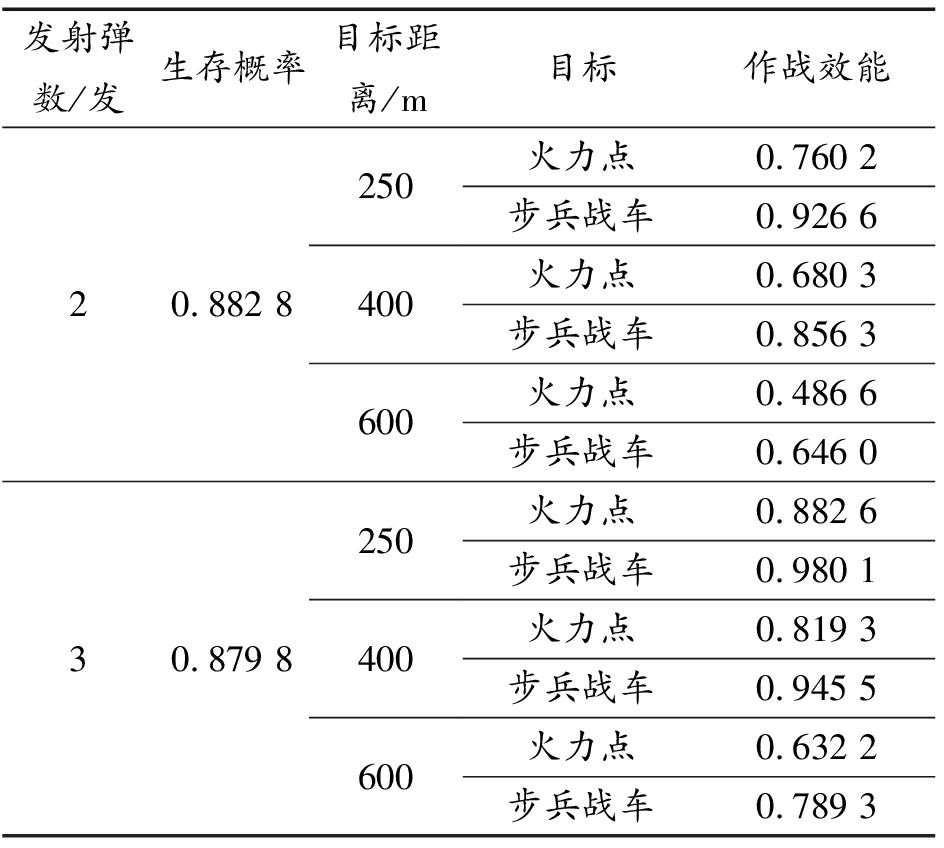
发射弹数/发生存概率目标距离/m目标作战效能20.882 8250400600火力点0.760 2步兵战车0.926 6火力点0.680 3步兵战车0.856 3火力点0.486 6步兵战车0.646 030.879 8250400600火力点0.882 6步兵战车0.980 1火力点0.819 3步兵战车0.945 5火力点0.632 2步兵战车0.789 3
可以看出:
1)随着射击距离的增大,便携式无坐力炮作战效能明显下降。发射2发弹药时,对火力点目标的作战效能由0.76(250 m)下降到0.49(600 m),对步兵战车的作战效能由0.93(250 m)下降到0.64(600 m)。
2)对400 m范围内的火力点目标,发射2发多用途弹即可较好地完成作战任务;对600 m距离的火力点目标,至少需要发射3发多用途弹才能基本完成作战任务。
3)对600 m范围内的步兵战车目标,发射2发多用途弹可基本完成作战任务,发射3发可较好完成作战任务。
4)由于便携式无坐力炮反应快、射速高,兵组生存概率较高,在同一阵地发射3发弹药的生存概率可达0.88。
5)为了发挥最大作战效能,便携式无坐力炮兵组在第一阵地上针对一个目标应尽量连续发射3发弹药。
4.1.2 多用途弹对2个目标作战效能分析
以步兵战车和火力点为典型目标,选择3种典型任务场景发射5发多用途弹打击2个目标,进行作战效能计算和分析。3种任务场景的目标距离和目标类型分别为(400 m步兵战车,250 m火力点)、(600 m火力点,400 m步兵战车)、(250 m火力点,600 m步兵战车),每种场景选择2个射击阵地,第一阵地发射3发弹药,第二阵地发射2发弹药,仿真计算结果见表3。
表3 多用途弹对2个目标作战效能计算结果
Table 3 Calculation results of operational effectiveness of multi-purpose missile against two targets
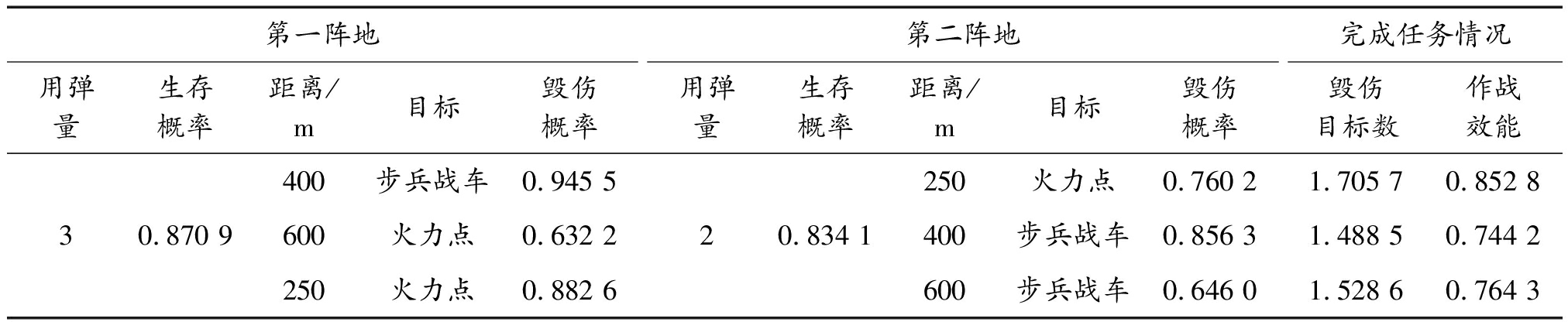
第一阵地用弹量生存概率距离/m目标毁伤概率第二阵地用弹量生存概率距离/m目标毁伤概率完成任务情况毁伤目标数作战效能30.870 9400步兵战车0.945 5600火力点0.632 2250火力点0.882 620.834 1250火力点0.760 21.705 70.852 8400步兵战车0.856 31.488 50.744 2600步兵战车0.646 01.528 60.764 3
可以看出:
1)对3种典型场景的作战效能均达到0.74以上,综合作战效能达到0.79,能够较好完成作战任务。
2)对400 m范围内的目标具有较好的毁伤概率,如果2个目标距离均在400 m以内,作战效能可达0.85以上,能够圆满完成作战任务。
3)兵组生存概率较高,在转移一次阵地的情况下,生存概率达到0.83。
4)兵组携带5发多用途弹,能够较好地完成典型作战任务,无需携带更多弹药。
4.2 杀伤弹作战效能计算与分析
4.2.1 杀伤弹对单个目标作战效能分析
以有生力量为典型目标,对不同距离上的单个目标连续发射1~5发弹药,毁伤概率随目标距离、发射弹药数量之间的关系曲线如图2所示。
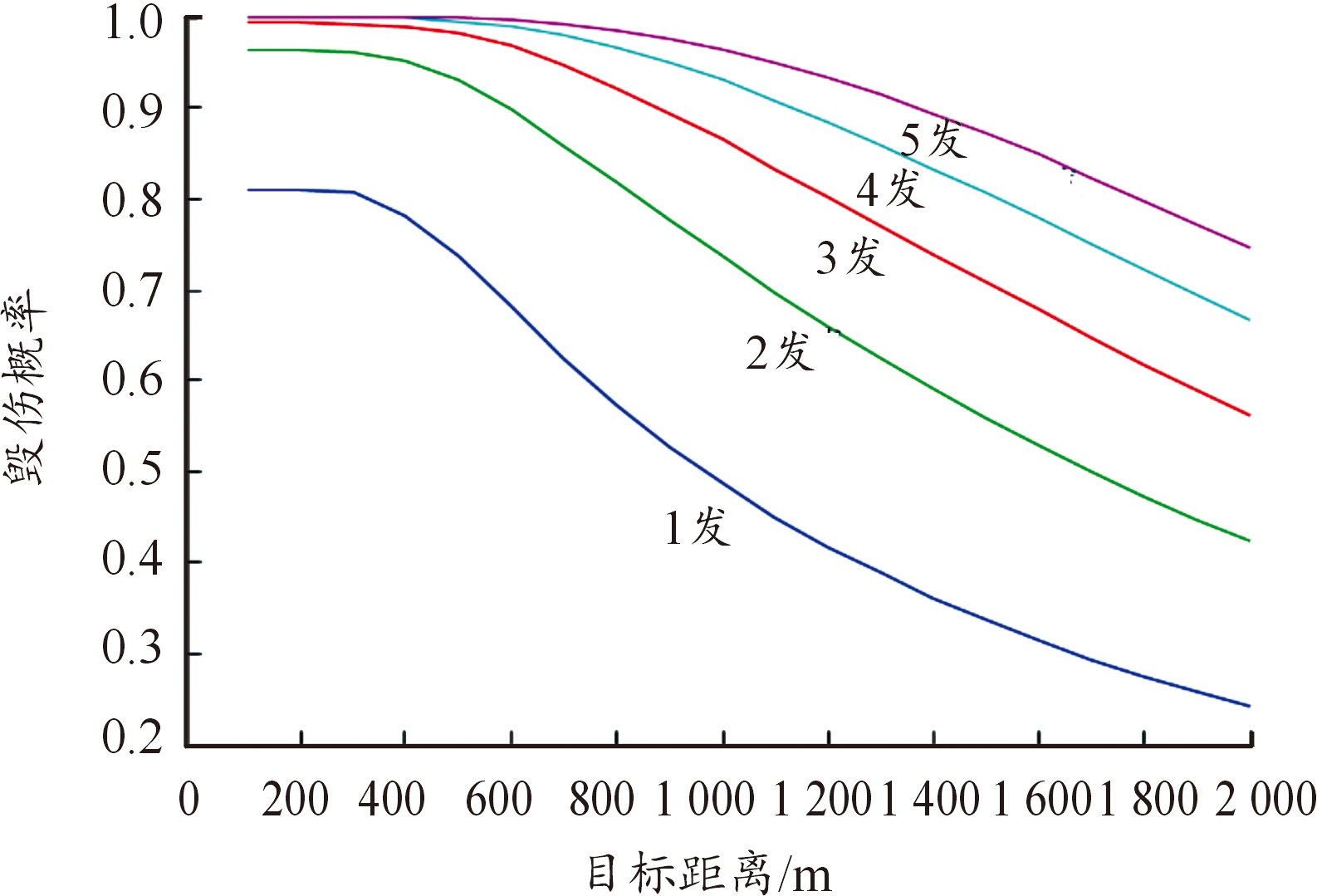
图2 杀伤弹对单个有生力量目标的毁伤概率曲线
Fig.2 Damage probability curve of a kill bomb to asingle effective force target
可以看出:
1)随着目标距离增大,毁伤概率明显下降,目标距离超过900 m时,发射1发杀伤弹难以完成作战任务。
2)对600 m范围内的单个有生力量目标,发射1发杀伤弹,毁伤概率达到0.69以上,才能够较好完成作战任务。
3)对中远距离600~1 100 m范围内的单个有生力量目标,至少需要连续发射2发杀伤弹,毁伤概率可达到0.7以上,才能够较好或圆满完成作战任务。
4)对远距离1 500 m以远的单个有生力量目标,至少需连续发射3发杀伤弹,毁伤概率可达到0.7以上,才能够较好或圆满完成作战任务。
4.2.2 杀伤弹对2个目标作战效能分析
针对不同目标距离,选择5种典型任务场景发射5发杀伤弹打击2个有生力量目标,进行作战效能计算和分析。5种任务场景的2个目标距离分别为(400 m,400 m)、(400 m,1 000 m)、(400 m,1 500 m)、(1 000 m,1 500 m)、(1 500 m,1 500 m),每种场景选择2个射击阵地,第一阵地发射1发或2发弹药,第二阵地发射3发或4发弹药,仿真计算结果见表4。
表4 杀伤弹对2个有生力量目标作战效能计算结果
Table 4 Calculation results of the operational effectiveness of the antipersonnel bomb against two effective force targets
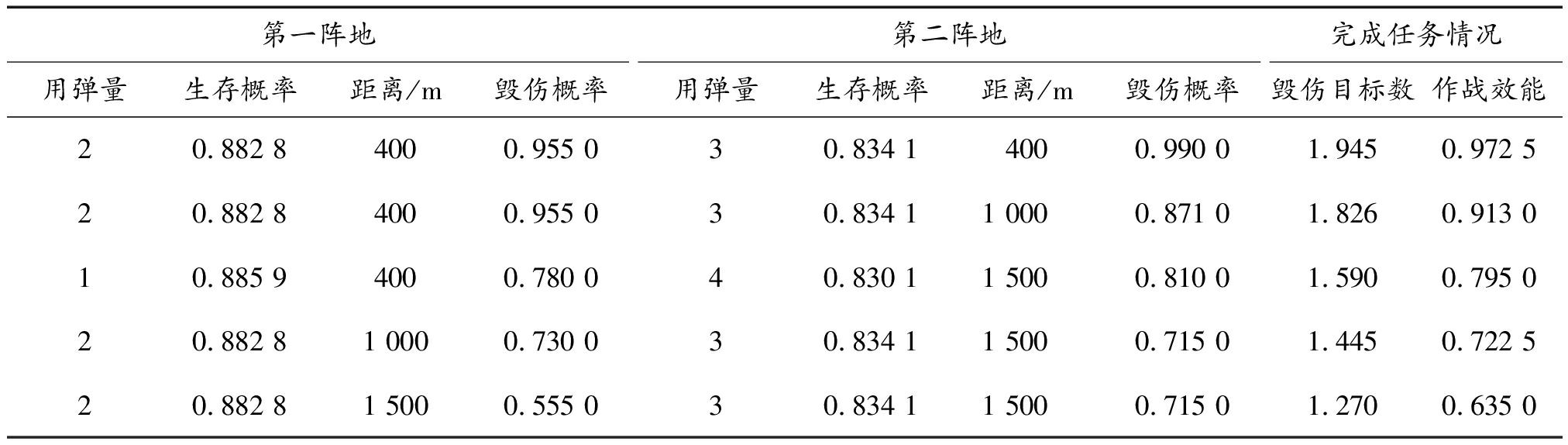
第一阵地用弹量生存概率距离/m毁伤概率第二阵地用弹量生存概率距离/m毁伤概率完成任务情况毁伤目标数作战效能20.882 84000.955 030.834 14000.990 01.9450.972 520.882 84000.955 030.834 11 0000.871 01.8260.913 010.885 94000.780 040.830 11 5000.810 01.5900.795 020.882 81 0000.730 030.834 11 5000.715 01.4450.722 520.882 81 5000.555 030.834 11 5000.715 01.2700.635 0
可以看出:
1)对5种典型场景的作战效能最低值为0.64,综合作战效能达到0.80,能够圆满完成作战任务。
2)2个目标距离均在1 000 m以内时,作战效能可达0.80以上,能够圆满完成作战任务。
3)2个目标距离均在1 000~1 500 m时,作战效能在0.72以上,能够较好完成作战任务。
4)兵组携带5发杀伤弹,能够有效毁伤1 500 m范围内2个有生力量目标,无需携带更多弹药。
4.3 2种弹药作战效能计算与分析
针对战场可能出现的三类目标,兵组通常需要同时携带多用途弹和杀伤弹,以兵组携带3发多用途弹和2发杀伤弹毁伤步兵战车、火力点和有生力量目标为例,选择5中典型作战任务场景,作战效能仿真计算结果见表5。
表5 2种弹药对2个目标作战效能计算结果
Table 5 Calculation results of operational effectiveness of two kinds of ammunition against two targets
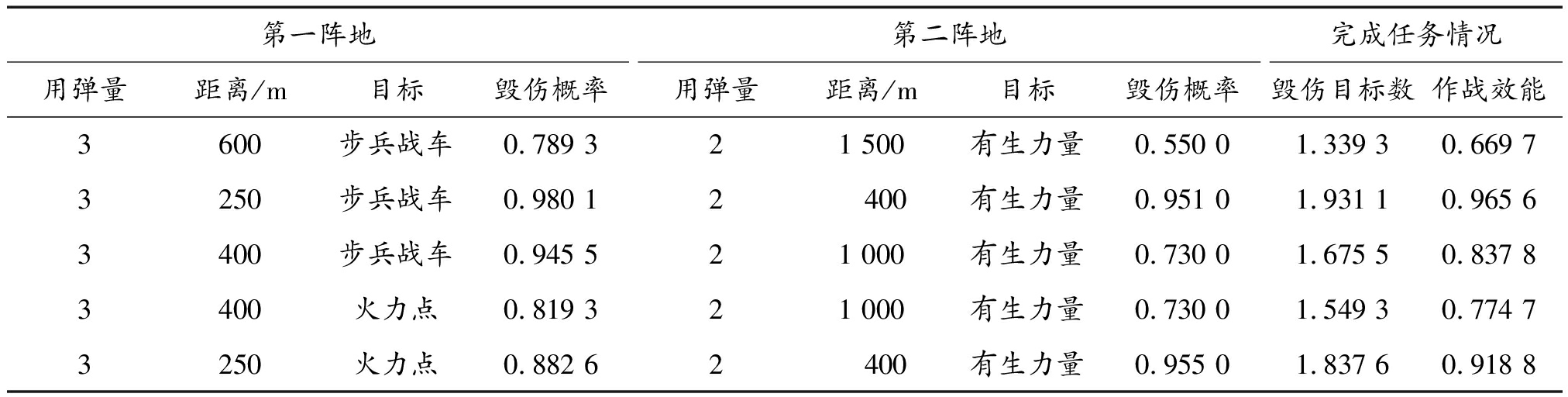
第一阵地用弹量距离/m目标毁伤概率第二阵地用弹量距离/m目标毁伤概率完成任务情况毁伤目标数作战效能3600步兵战车0.789 321 500有生力量0.550 01.339 30.669 73250步兵战车0.980 12 400有生力量0.951 01.931 10.965 63400步兵战车0.945 521 000有生力量0.730 01.675 50.837 83400火力点0.819 321 000有生力量0.730 01.549 30.774 73250火力点0.882 62 400有生力量0.955 01.837 60.918 8
可以看出,兵组携带5发弹药(3发多用途弹、2发杀伤弹)对典型作战任务的平均作战效能达到0.83以上,能够圆满完成作战任务。
5 结论
综上分析,按规定的典型作战任务剖面,兼顾携行质量和作战效能,便携式无坐力炮2人兵组最佳携弹量为5发,根据战场目标的现实需要,调整携行的弹种比例,其在任务时间内的综合作战效能达到0.74以上,生存概率达到0.807 6以上,能够较好地规定的作战任务。为了发挥最大作战效能,针对步兵战车或火力点目标,兵组在第一阵地上应尽量连续发射3发多用途弹;针对有生力量目标,根据目标距离兵组在第一阵地上可视情连续发射1~3发杀伤弹。
本文的作战效能模型和生存概率模型是基于规定的典型作战任务剖面建立的,对于其他作战想定和作战任务剖面下的作战效能,可基于该模型进行修正和拓展,进行综合评定,为便携式无坐力炮和同类武器作战效能综合评定奠定了基础。
[1] 中国人民解放军总参谋部兵种部.炮兵射击理论研究与应用[M].北京:解放军出版社,1995.
Arms Department of the General Staff of the Chinese People’s Liberation Army.Research and application of artillery firing theory[M].Beijing:Liberation Army Press,1995.
[2] 宋宝贵.武器系统工程[M].北京:国防工业出版社,2009.
Song B G.Weapon system engineering[M].Beijing:National Defense Industry Press,2009.
[3] 张东妍.无后坐力炮设计手册[M].北京:国防工业出版社,1978.
Zhang D Y.Design manual of recoilless gun[M].Beijing:National Defense Industry Press,1978.
[4] 李春雷,王雨时,张志彪,等.瑞典84毫米口径古斯塔夫无后坐力炮弹药技术综述[J].兵器装备工程学报,2018,39(04):72-80.
Li C L,Wang Y S,Zhang Z B,et al.Review of the characteristics of ammunition of gustav 84 mm calibre recoilless of Sweden[J].Journal of Ordnance Equipment Engineering,2018,39(04):72-80.
[5] 罗兴柏.陆军武器系统作战效能分析[M].北京:国防工业出版社,2007.
Luo X B.Operational effectiveness analysis of army weapon system[M].Beijing:National Defense Industry Press,2007.
[6] 李智宇,陶钢,李召.反坦克部队与坦克部队在丘陵地区的作战效能分析[J].兵器装备工程学报,2019,40(12):45-49.
Li Z Y,Tao G,Li Z.Operational effectiveness analysis of anti-tank company against tank forces in hilly areas[J].Journal of Ordnance Equipment Engineering,2019,40(12):45-49.
[7] 王庆国,李天宇,朱宇飞.火力对抗条件下的反坦克导弹作战效能评估[J].舰船电子工程,2021,41(08):119-124.
Wang Q G,Li T Y,Zhu Y F.Evaluation of combat effectiveness of anti-tank missiles under the condition of firepower cut[J].Ship Electronic Engineering,2021,41(08):119-124.
[8] 黄文香,江永政,路继海.反坦克导弹分队作战效能分析[J].装备指挥技术学院学报,2002,13(03):4-51.
Huang W X,Jiang Y Z,Lu J H.Analysis on combat efficiency of anti-tank missile detachment[J].Journal of Equipment Academy,2002,13(03):4-51.
[9] 吴晓颖,吴东亚,张万君.反坦克弹药对装甲毁伤能力的比较分析[J].科技导报,2009,27(13):60-63.
Wu X Y,Wu D Y,Zhang W J.Comparative analysis of the destroy effectiveness to tank Armor caused by anti-tank ammunition[J].Science and Technology Review,2009,27(13):60-63.
[10] 刘玉文,侯明,薛晓中,等.一种改进的炮兵作战兰彻斯特方程[J].弹道学报,2010,22(02):107-110.
Liu Y W,HOU M,XUE X Z,et al.An improved lanchester equation of artillery countermeasure[J].Journal of Ballistics,2010,22(02):107-110.