1 引言
目前,部分中小型的军用装备在布设时主要采取由直升机和降落伞协同抛撒的方法,在到达指定地点后,需要一个高精度,能快速达到水平且抗冲击的平台作为基座,以保证后续设备的正常使用[1]。但是大部分调平装备的设计是专为某些大中型设备进行服务的[2-5],对于小型设备的研究则还不够。由于载荷较小,且需要实现调节速度快,精确、抗冲击等的特性,本文中设计了一种抛投式调平装置,结合新建的旋转调平策略[6-7],整体采用机电式驱动[8-9]。调平装置抛投后经降落伞牵引跌落过程中会受到较大的冲击[10-11],所受冲击的大小决定了调平装置的可靠性。最初研究调平装置抗冲击性能的方法就是通过碰撞试验来确定机械结构跌落到地面上的破损情况,这种试验对于跌落姿态的控制较低,能测得的物理量也少,试验成本较高[12],现在传统跌落试验已逐步由有限元仿真来完成[13-15]。本文旨在调平装置的正确设计基础上,建立合理的分析模型,对其跌落过程进行有限元分析,为今后进一步优化设计,提高抗冲击性能提供参考依据。
2 调平装置的结构设计
2.1 支撑与驱动
目前而言,调平装置的支撑结构形式有3点、4点和多点支撑等。3点支撑即使用3个调平支撑腿,优点是调节方便,缺点是稳定性较差;4点支撑的支撑点数量增加,支撑强度明显提高,但弊端是其中一个支撑腿不受力或悬空,会出现“虚腿”现象,造成平台侧翻;多点支撑的抗倾覆能力更加突出,缺点是几何问题和控制算法为了达到要求会很复杂。以上支撑方法受到冲击后,若发生塑形变形,会使机构卡死,不能正常作业。通过对比各支撑方式的优缺点,设计调平装置采用平板旋转和3支点结合方式进行调平。
调平装置的驱动方式主要分为液压式和机电式2种。液压传动的承载能力很强,但结构复杂、体积较大、控制成本高、维修困难。机电传动就是电动机通过传动机构带动执行机构工作的方式。相较而言,结构简单、布置灵活、控制成本低、环境适应能力强、反应速度快、调节精度高,这里选用机电式传动。
2.2 调平策略
从运动学的角度看,调平装置是以电机和丝杆作为执行机构,由旋转副和移动副组合成的运动刚体。目前,描述该问题的方法有多种,如矩阵齐次变换法(D-H矩阵法)、旋量理论及空间4元数[16-19]等,由于D-H矩阵法能够将空间运动、坐标变换及映射等问题以4阶矩阵运算的形式统一起来,故将以该方法为主进行调平策略的研究。
角度控制调平,即通过电机直接改变平台的倾斜角使其达到水平状态。该方式的支撑机构包含方位旋转和俯仰旋转2个部分,依靠啮合齿轮和丝杆螺母2种传动装置,分别提供绕2个相互垂直轴线的转动自由度,即一个以垂直于底盘的方向为旋转轴,另一个方向则平行于底盘,仅通过旋转调整实现支撑平台的调平。
角度控制调平数学模型如图1所示,依据以上数学模型的建立,首先,以水平面为x、y轴所在平面建立绝对坐标系,并以垂直于底座的旋转轴方向为z′轴,建立固连于支撑机构的坐标系{Ax′y′z′}。

图1 角度控制调平数学模型
Fig.1 Angle control leveling mathematical model
调平操作的第1步通过平台绕轴2旋转,将轴1调整至与水平面平行,在坐标系中{Axyz}中取一向量L=(Lx,Ly,0),向量L绕坐标轴x旋转α角(传感器测量角),再绕y轴旋转β角后得到向量L′,并且向量L′与旋转轴1所在方向一致。根据旋转变换矩阵可得:
L′=Rot(Y,β)Rot(X,α)L=
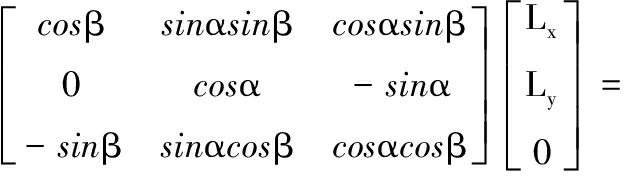
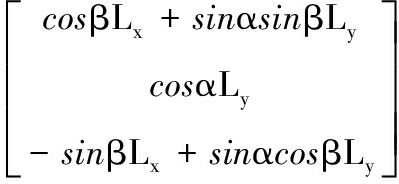
(1)
同理可以求得旋转轴2的方向向量为:
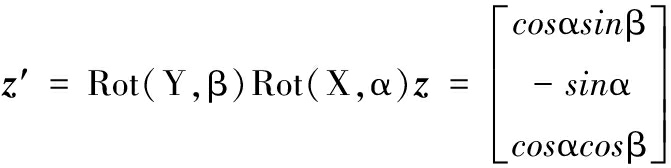
(2)
将向量L′绕向量z′旋转θ角得到向量L″,则由任意旋转变换公式,有:
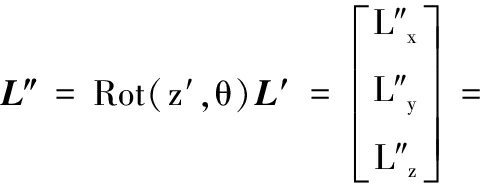
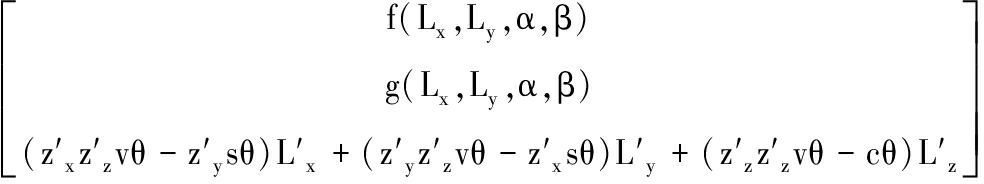
(3)
若轴1绕轴2旋转θ角后可以调整至水平,则![]() 若在试验操作中,将倾角传感器的x轴固定在与旋转轴1平行的位置,则Ly=0,最后求得的θ角形式将会极大简化,最终得到:
若在试验操作中,将倾角传感器的x轴固定在与旋转轴1平行的位置,则Ly=0,最后求得的θ角形式将会极大简化,最终得到:
(4)
式(4)中: θ>0表示顺时针旋转; θ<0表示逆时针旋转。
当旋转轴1位于水平位置时,平台所在平面的姿态角倾角β=0,即此时倾角传感器度数为α=Φ和β=0,只需再将平台围绕轴1旋转Φ角,即可完成调平。事实上通过坐标变换也可直接通过初始测量值求得Φ角,其过程不再赘述。
Φ=arccos(cosαcosβ)
(5)
这种方法以传感器的测量值为依据,直接通过旋转运动改变平台的倾角,使其达到允许误差以内的水平状态,更为简单直观,而且在试验中也更容易通过控制执行机构运动来实现。
2.3 结构设计
结合调平策略,设计了一种通过2套步进电机和3个支撑杆配合传动的二自由度调平装置,如图2所示。为了更好地展示内部结构,将外壳进行了隐藏,整体采用3层圆盘的结构,自上而下由承载盘、传感器、丝杆电机、步进电机、2个配套驱动器、3个支撑杆、单片机、方位盘、圆锥滚子轴承、大小啮合齿轮、底盘和外壳组成。
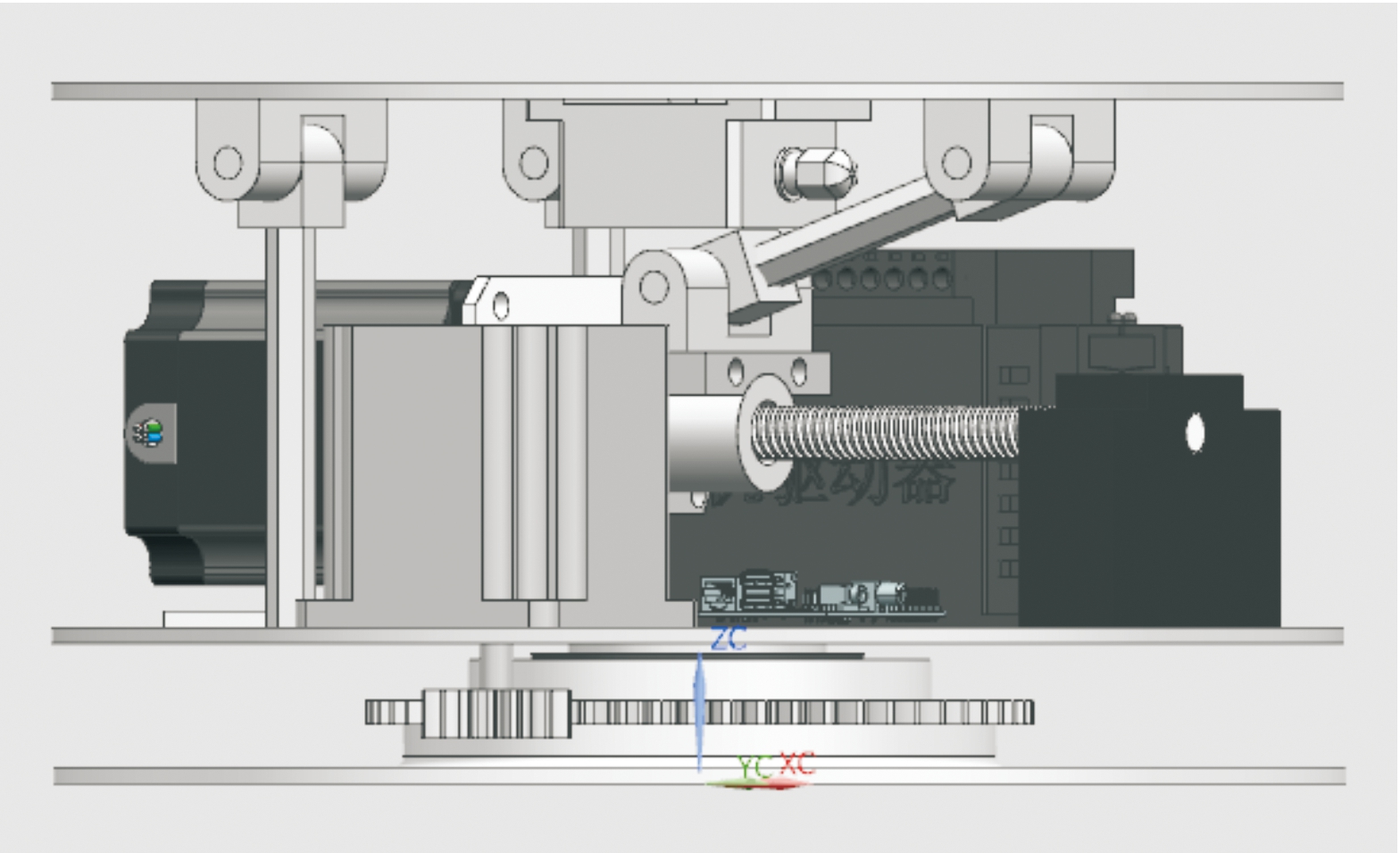
图2 调平装置模型
Fig.2 Modulation device model
根据调节装置三维模型建立ADAMS动力学仿真模型,然后根据实际情况给各个构件施加约束、载荷和动力(MOTION)等,可得到调平装置能够按照确定驱动完成调平动作。
3 有限元模型建立
3.1 调平装置有限元模型的简化
由于调平装置的结构复杂和实际应用条件恶劣,为了更准确得到装置受到跌落冲击时的响应特性,在有限元模型的建立过程中做出以下假设[20-21]和简化:
1)整体结构在受到冲击载荷作用时只产生弹性变形,只有在载荷受力点位置可能发生塑性变形;
2)结构满足连续性和均匀性基本假设;
3)把不是承受结构且轻质的stm32单片机和传感器进行了删除;
4)将不直接承受冲击的部件作为配重质点处理。
3.2 调平装置有限元模型的建立
调平装置跌落到地面的过程,是调平装置的自由落体与地面相碰撞的过程,因此,在进行调平装置跌落分析时,需要在调平装置模型的下面增加一地面。调平装置跌落系统(下文统称为跌落组件)由底盘、方位盘、承载盘、轴承、俯仰电机、方位电机、连杆、支撑杆、电源、驱动器以及地面组成。为便于进行后续处理,直接在ANSYS中建立跌落组件模型。仍将模型的外壳进行了隐藏,其有限元模型如图3所示(下文同样用隐藏外壳后的模型进行展示)。各部件的材料属性见表1。
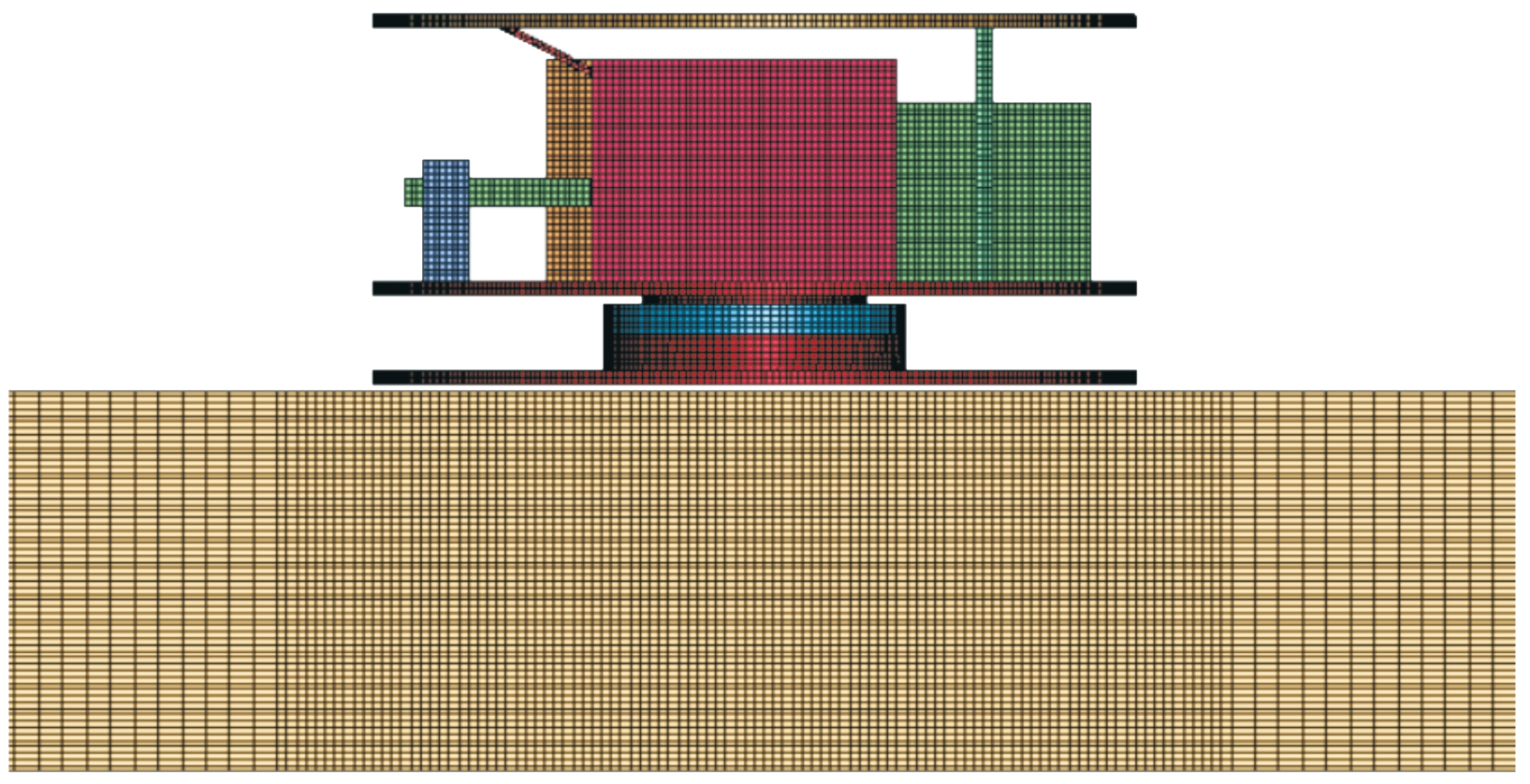
图3 调平装置有限元模型
Fig.3 Finite element model of the leveling device
表1 各部件材料参数
Table 1 Material parameters of each component
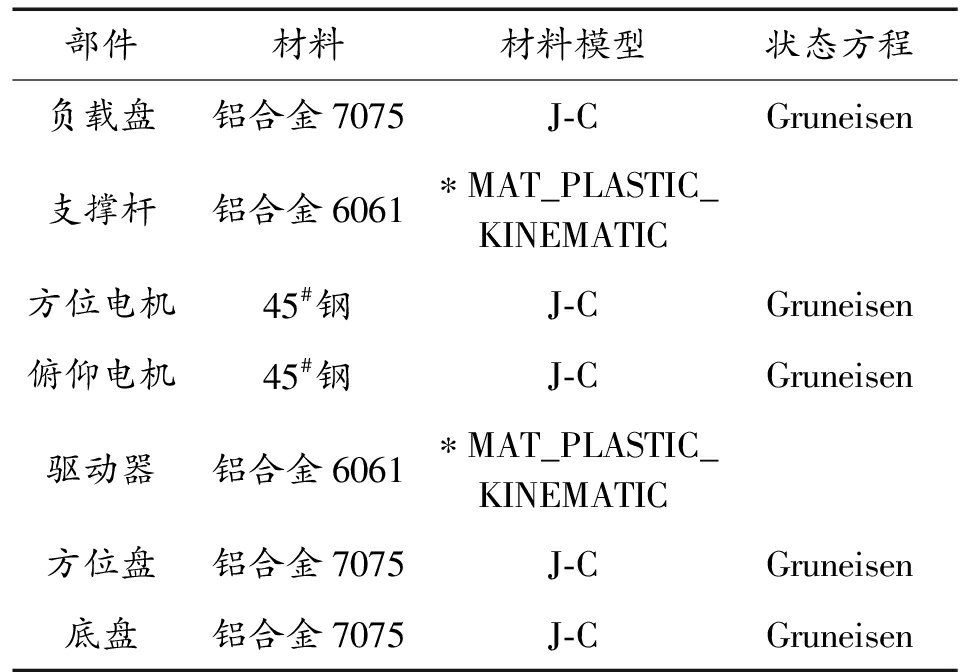
部件材料材料模型状态方程负载盘铝合金7075J-CGruneisen支撑杆铝合金6061∗MAT_PLASTIC_KINEMATIC方位电机45#钢J-CGruneisen俯仰电机45#钢J-CGruneisen驱动器铝合金6061∗MAT_PLASTIC_KINEMATIC方位盘铝合金7075J-CGruneisen底盘铝合金7075J-CGruneisen
3.3 跌落工况的设置
跌落组件在降落伞的牵引下不断减速至平稳下落,最终以一定速度着陆,跌落冲击造成的变形和破坏主要发生在撞击地面后,而在跌落过程中受力和变形几乎不会发生变化。根据能量守恒定律有:
![]() 即
即![]()
(6)
式(6)中:v为冲击速度;m为物体的质量;g为重力加速度(取9.806 7 m/s2)。
因此为了提高求解效率,减少计算时间,可将实际跌落工况进行等效处理,研究调平装置以一定初速度与地面碰撞,具体设置如下:
1)为了减少计算时间,将调平装置距地面的初始距离设置为2 mm,求解时间设置为20 ms,结果数据输出步数设置为800。
2)跌落速度设置为4 m/s,7 m/s,10 m/s。
3)跌落角度优先设置为0°、10°、20°和30°。
4)由于军品装备所处的战场环境大多数为丘陵地区,地面一般为土地或者石子地,因此设置跌落地面材料为硬土地。
5)调平装置与地面为侵蚀接触。
6)由于仿真过程从调平装置临接触地面的一刻开始,因此可设调平装置只受重力载荷。
4 跌落分析及优化方案
根据调平装置结构特点,提出以下关注点:① 方位旋转输出轴受力情况;② 俯仰旋转输出轴即丝杆的受力情况。根据关注点在模型上选择不同节点对其不同跌落工况进行分析。
4.1 跌落速度对冲击特性的影响
对于方位旋转输出轴,关注应力较大的轴肩下端,选取了节点269357。如图4所示,装置倾斜跌落至地面时,先接触地面的一侧产生应力,此时应力都比较小。当另一侧也跌落至地面时,由于此时装置全接触地面,全部重量都会对节点269357有作用,因此可以看到7 ms附近,应力陡然增大至最大值。后续由于装置全接触时刻的冲击力,应力随时间的变化呈现振荡的趋势。且从数值上来看,节点269357在装置全接触地面的前期和后期,3种速度下产生的应力均小于材料的许用应力。10 m/s时,在全接触时刻应力增大至最大值278 MPa,接近许用应力。
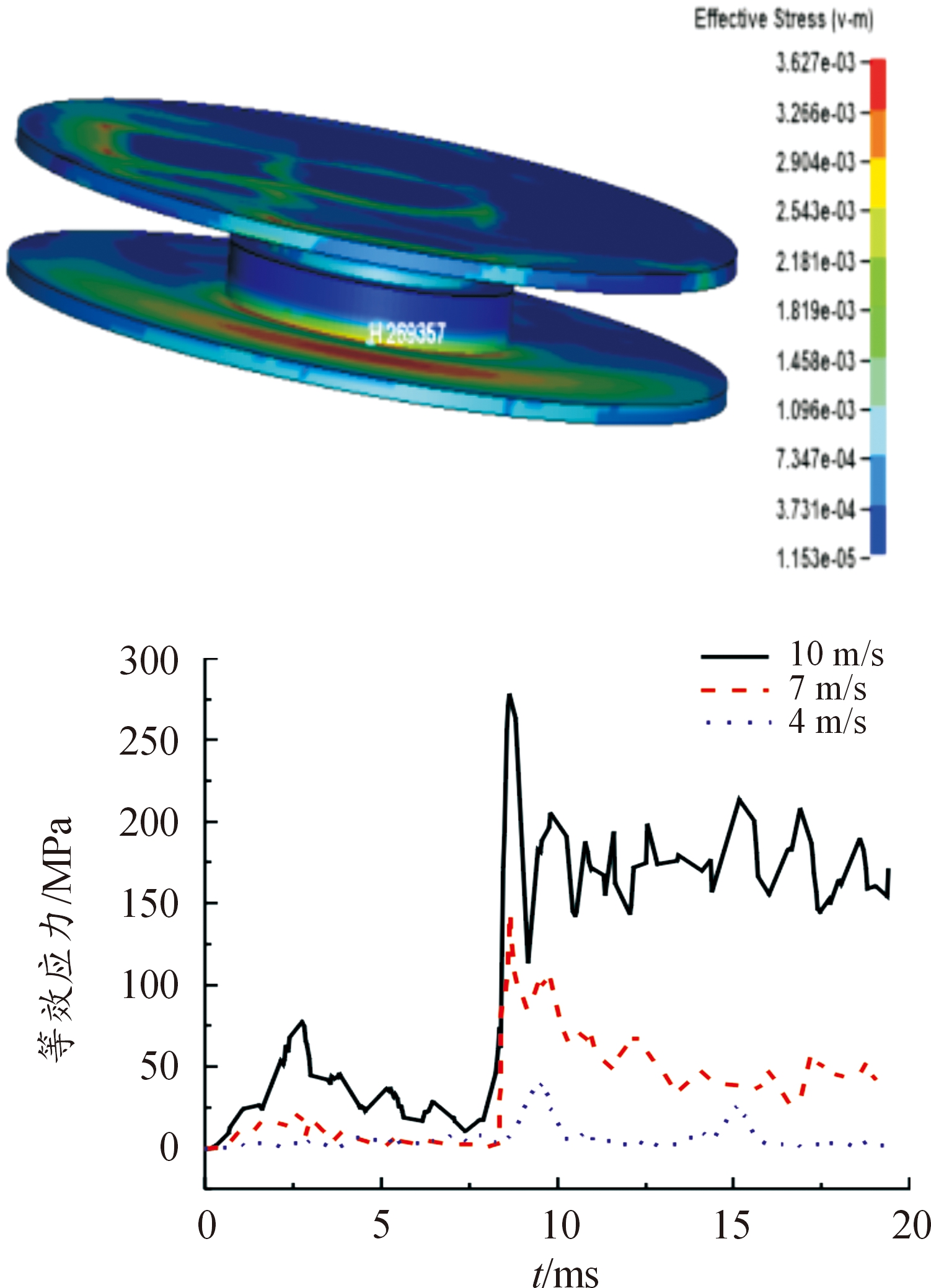
图4 方位旋转输出轴应力云图和变化规律
Fig.4 Cloud map and shift pattern of azimuthal rotation output axis
对于俯仰旋转输出轴即丝杆,同样关注存在应力集中的根部。如图5所示,选取根部一节点63446,在装置一侧接触到地面后,节点63446开始小幅度的产生应力。装置全接触地面后,产生的应力陡然增大至最大值,在10 m/s下的最大值为458 MPa,超过了许用应力,而且后续变动幅度依然很大,这种现象产生的原因是丝杆在装置中的位置相当于横梁,在受到冲击力后,会大幅振荡。
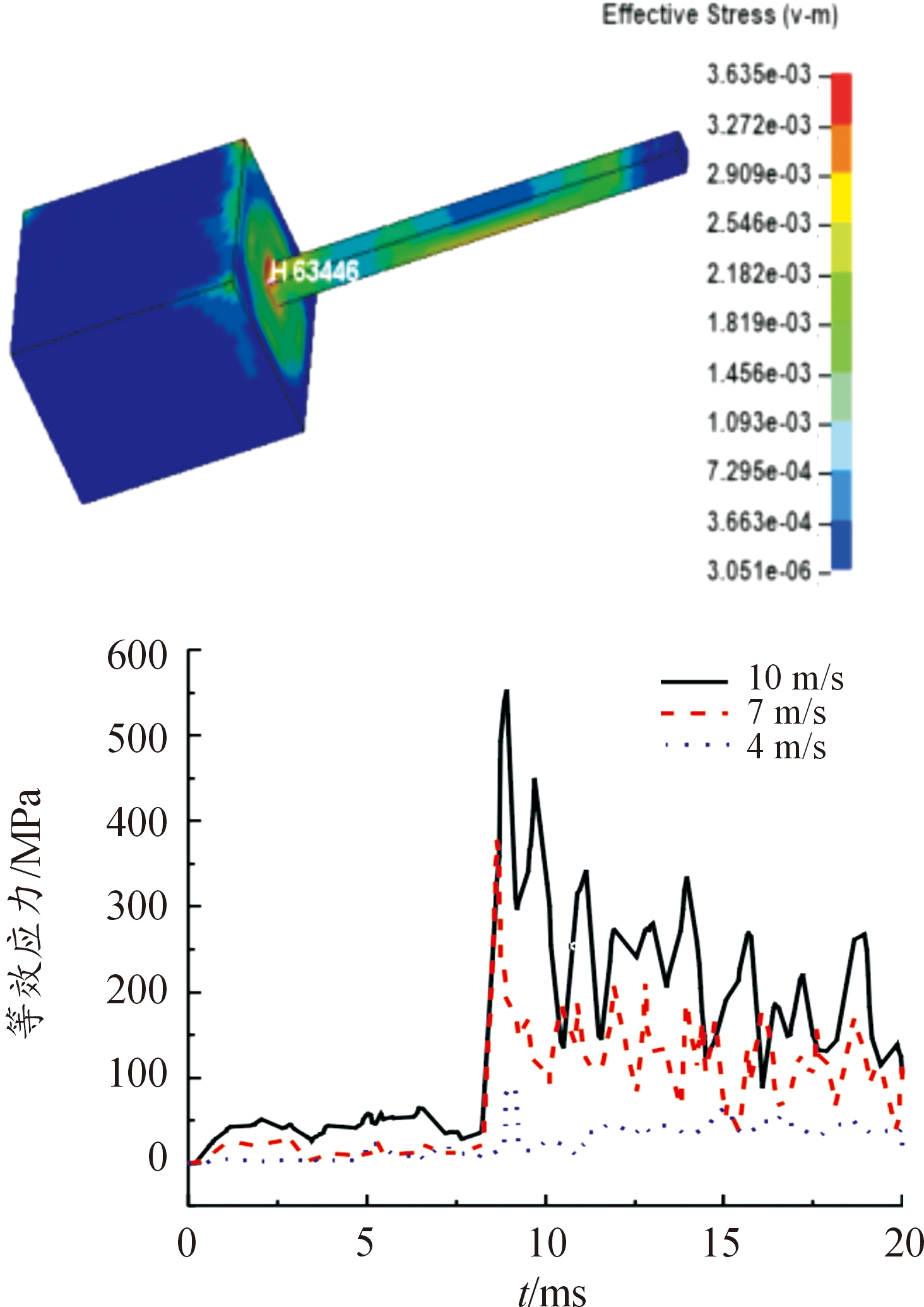
图5 丝杆根部应力云图和变化规律
Fig.5 Stress cloud map and change pattern of silk rod root
因此,跌落速度越大,冲击振荡越激烈。从数值上可以看到,在10 m/s的速度下,调平装置中某些组件产生的应力会超过其许用应力,但都小于强度极限,即发生永久变形但不会破裂。所以在调平装置的跌落过程中,10 m/s及以上是危险速度。
4.2 跌落角度对冲击特性的影响
跌落组件以垂直于地面的姿态着陆是一种比较理想的工况,实际上跌落组件着陆时,由于质量分布不太均匀或者降落伞受风力改变姿态等原因,在接触到地面时可能会呈现一定的角度。为了探究跌落组件接触地面时的损坏状态随角度的变化规律,设置跌落最终速度为10 m/s,以跌落组件底盘平面与水平方向夹角为0°、10°、20°、30°,做了不同角度下跌落组件的跌落仿真分析。
图6为跌落组件以20°角跌落时的整个过程的应力云图。跌落组件近地端首先与地面发生碰撞,在重力作用下,另一侧也随之落地,此时跌落组件处于与地面全接触的状态,此时产生的应力最大。由于硬土地密度较大,地质较硬,土地变形量极小,因此会使得跌落组件反弹,后续仍在重力作用下跌落至地面,发生2次碰撞。
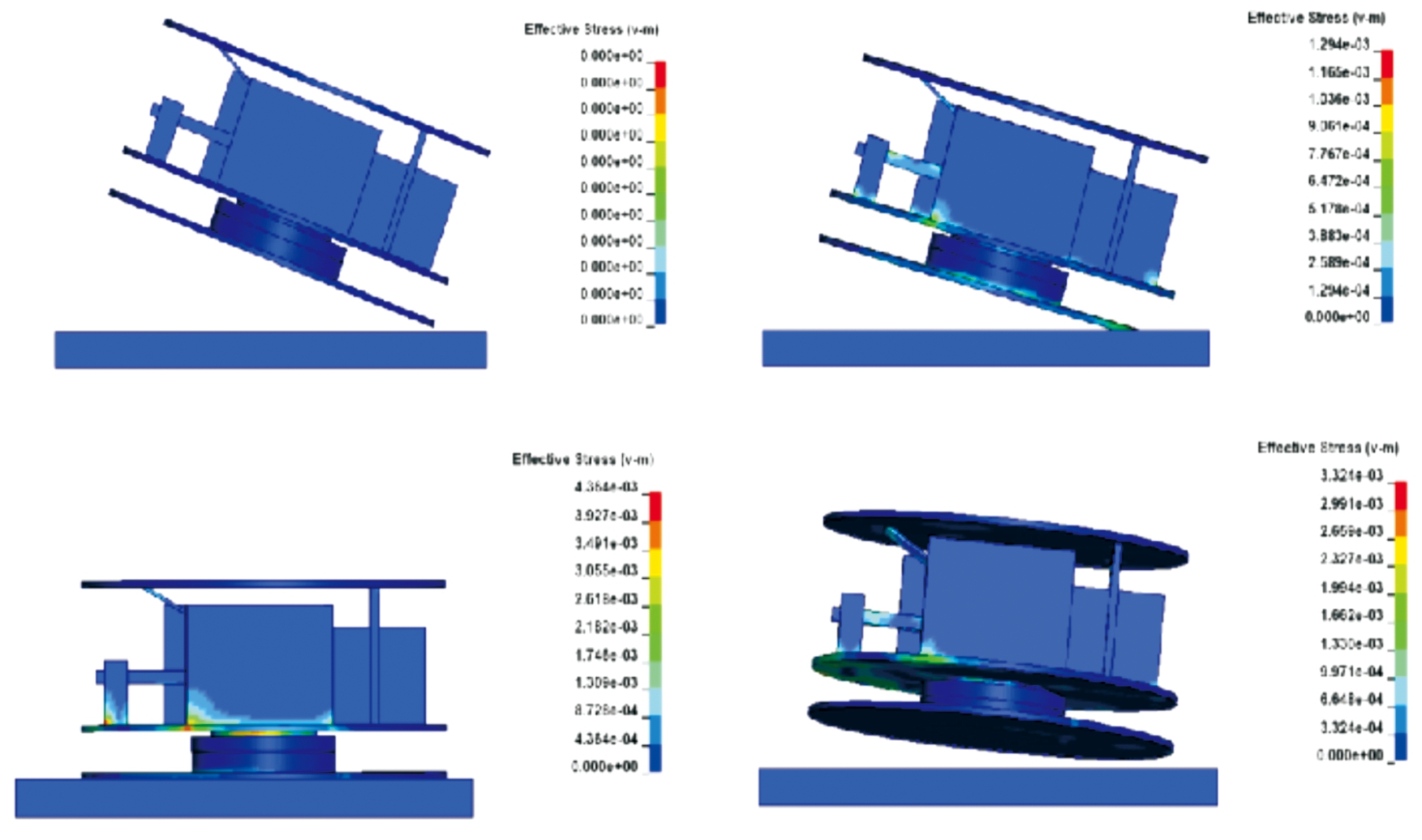
图6 倾斜跌落应力云图
Fig.6 Stress cloud diagram of tilt fall
为进一步分析倾斜跌落时对装置的损坏作用,仍选取节点269357和节点63446对不同倾角发生跌落时产生的等效应力进行研究。
方位旋转输出轴应力变化曲线如图7所示,节点269357在不同倾角下发生跌落时,应力变化的趋势一致。随着倾角增大,跌落组件全接触地面的时刻变大,产生最大等效应力的时刻随之变大,最大等效应力减小。从数值上来看,除了最大等效应力时刻会接近许用应力外,其余时刻均远小于许用应力。
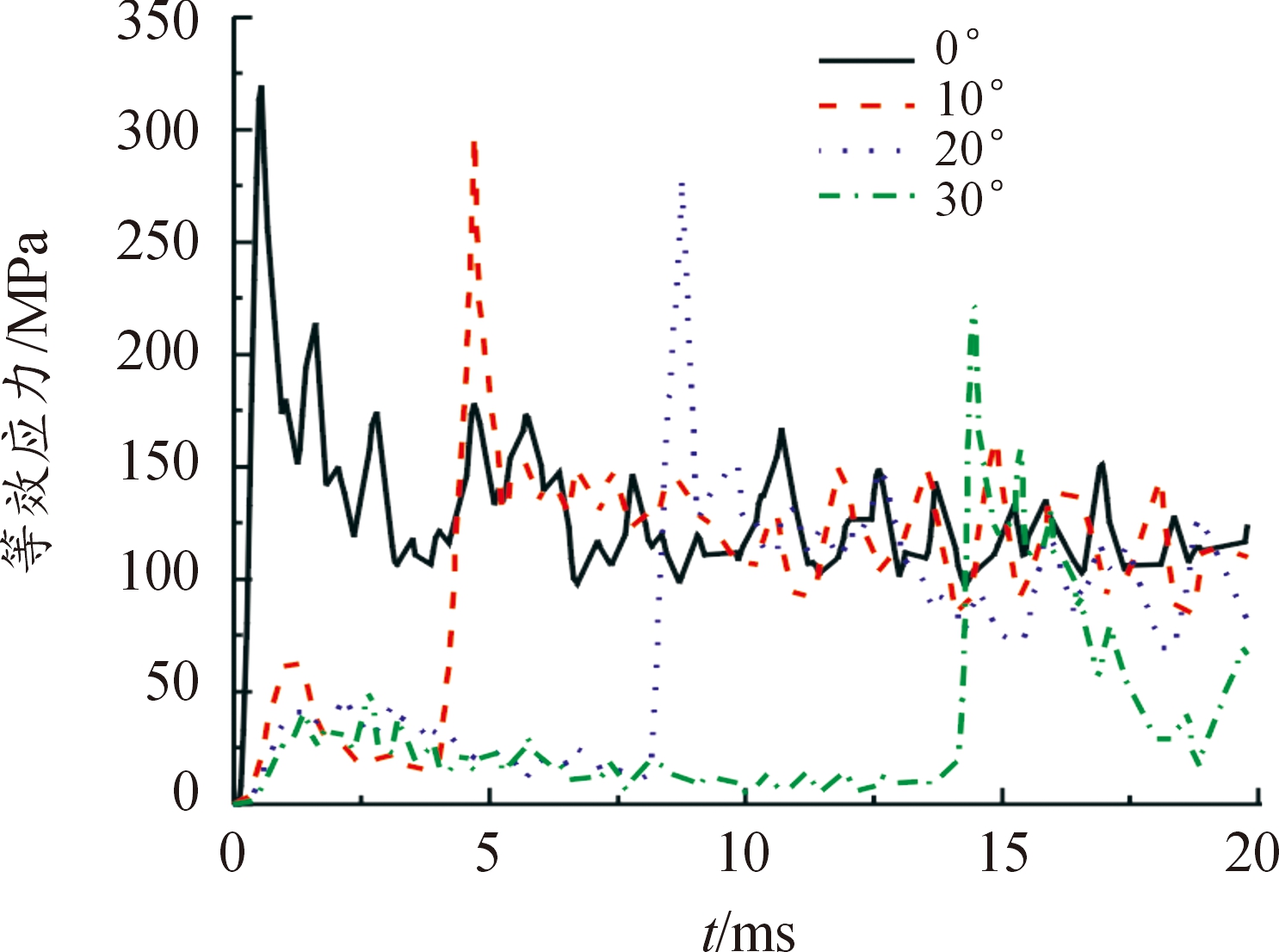
图7 方位旋转输出轴应力变化曲线
Fig.7 Stchange curve of azimuth rotation output axis
丝杆根部应力变化曲线如图8所示,丝杆根部的节点63446在不同倾角下发生跌落时产生的应力趋势,与节点269357一样,随着倾角增大,产生最大等效应力的时刻也随之变大,但是最大等效应力随着角度的增大,变化不大,而且在跌落过程中节点63446的应力振幅在各个角度的表现都比较大,这是由于丝杆在跌落组件中支撑点比较少,在跌落组件全接触地面后产生大幅振荡造成的。在数值上节点63446产生的应力值部分超过许用应力,是后续优化的重点结构。
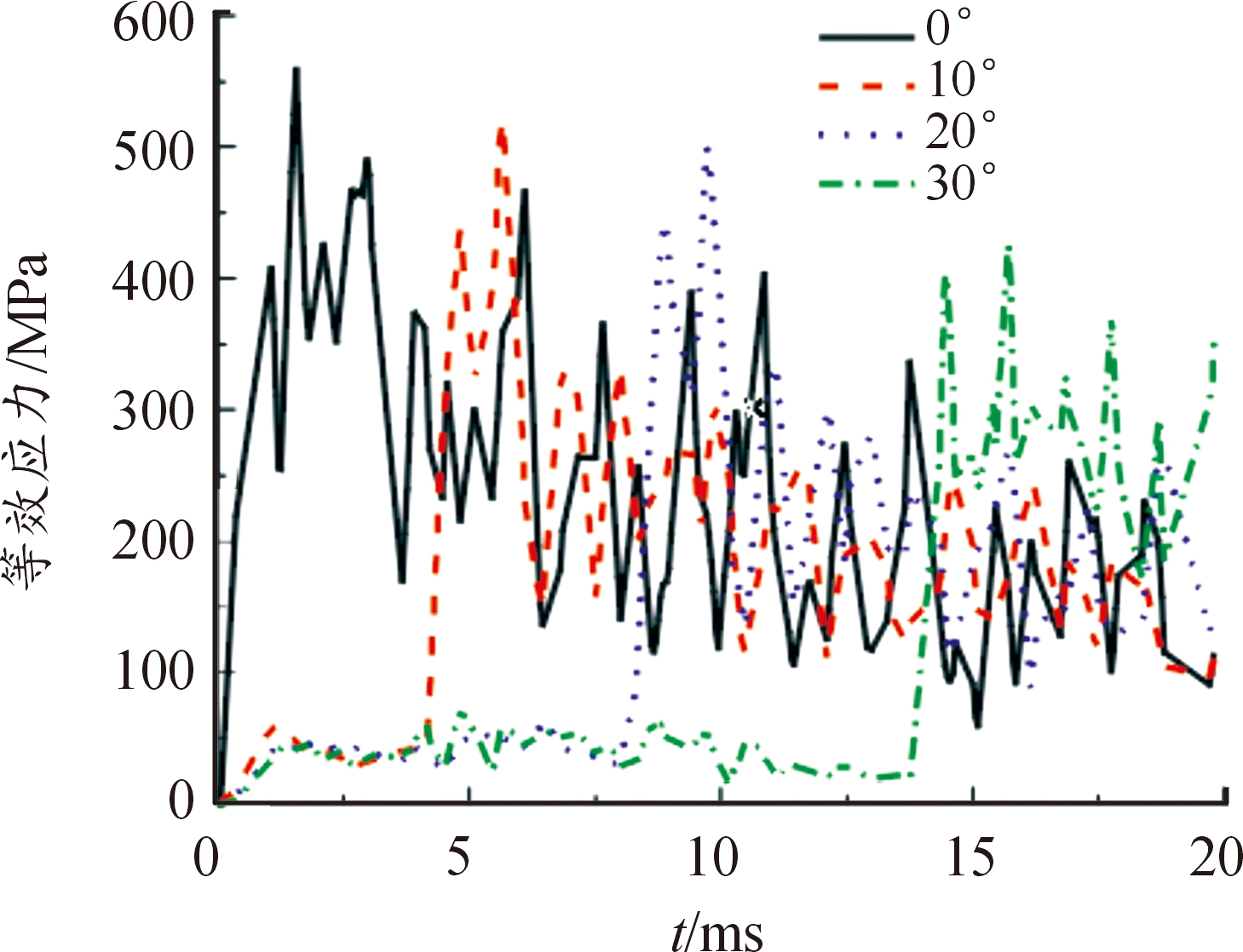
图8 丝杆根部应力变化曲线
Fig.8 Stress change curve of silk rod root
从图8中还可以看出,地面对于跌落组件的第1次碰撞时的冲击作用时间很短,在大约3 ms时间内,而且不同角度下的冲击作用时间变化不大。
4.3 关键部件的优化方案
俯仰电机的丝杆和方位旋转的输出轴是最易受损的,仅能承受有限的弯矩和较小的轴向力,如果不采取一定的轴向和径向缓冲措施,冲击力会从方位旋转的输出轴传递至俯仰电机的丝杆,一旦发生损坏,则意味着调平装置无法正常工作。为了避免上述情况发生,需要对丝杆和方位旋转的输出轴设计有轴向和径向的减振措施,从而保证调平装置能够承受来自任意方向的落地冲击。改善结构抗冲击失效的方案主要采用以下2种:
1)由于方位旋转输出轴的撞击面属于外观面,无法增加缓冲材料来减少冲击应力,只能从增加结构本身刚度出发改善结构抗冲击能力。采用增加根部的圆角的方案,减少应力集中现象;
2)对于丝杆,与方位旋转的输出轴不同的是,有一部分处于俯仰电机内部,属于内部结构范畴,只能增加缓冲材料来减少冲击应力,采用在俯仰电机与方位盘之间加装橡胶缓冲垫和在丝杆下方增加弹簧支撑件的方案,以达到吸收部分冲击力能量的目的。
5 结论
本文中结合3点支撑方式和平板旋转,采用机电式传动,设计了一种二自由度的抛投式调平装置,并用ADAMS在实际约束、载荷和驱动下进行动力学仿真,调平装置能够按照确定驱动完成调平动作。在此基础上通过LS-DYNA软件对调平装置进行了不同工况下的跌落仿真,得到了跌落冲击过程中调平装置的应力数据,结果表明:
1)跌落速度越大,所受冲击越大,调平装置越容易失效。且10 m/s是其发生变形的危险速度,也可为降落伞的设计提供依据。
2)调平装置以小角度倾斜跌落至地面不会降低其可靠性。
3)提出了处于外表面旋转输出轴根部倒圆角和加装橡胶缓冲垫及弹簧支撑件的方法,以此降低调平装置受到的冲击应力,提高了调平装置的抗跌落性能。
[1] 李翰朋,宣兆龙.智能雷发展现状及关键技术[J].现代防御技术,2018,46(02):6-11.
Li H M,Xuan Z L.The development status and keytechnologies of intelligent thunder[J].Modern Defense Technology,2018,46(02):6-11.
[2] 王武,付小强,卢青山,等.某型火箭炮运弹车自动调平控制系统的设计与实现[J].兵工学报,2022(03):1-7.
Wang W,Fu X Q,Lu Q S,et al.Design and implement of the automatic leveling control system of a certain rocket launcher[J].Journal of Military Engineering,2022(03):1-7.
[3] Wei X H,Huang S C.Intelligent laser leveling control system for cement concrete based on MCU control[J].Journal of Physics:Conference Series,2021,1885:042041.
[4] Papadopoulos E,Mu B,FrenetteR.Modeling and identification of an electrohydraulic articulated forestry machine[C]//Proceedings of International Conference on Robotics and Automation.IEEE,1997.
[5] 常飞翔.浅海移动式平台自动调平系统的研究[D].秦皇岛:燕山大学,2019.
Chang F X,Research on automatic ping system of shhai mobile platform[D].University On The Mountain Of Swallows,2019.
[6] 韩峰,孙堃博,陈放.无人值守智能雷的调平算法研究[C]//第十六届全国战斗部与毁伤技术学术交流会.2019:1117-1120.
Han F,Sun K B,Chen F.Research on the leveling algorithm of unattended intelligent mine[C]//The 16th National Combat Department and Destruction Technology Academic Exchange Meeting.2019,08:1117-1120.
[7] Feng H,Sun K B,Chen F.A motor-driven self-leveling device for unmanned weapon systems[C]//Proceedings of the 2019 IEEE International Conference on Unmanned Systems,2019:148-151.
[8] Zhang J,Huang D,Lu C.Research on dynamic modeland control strategy of auto-leveling system for vehicle-borne platform[C]//International Conference on Mechanical and Automation.IEEE,2007:973-977.
[9] 戴壮,肖峻,潘运平,等.一种车载平台自动调平方法与控制技术研究[J].数字制造科学,2021,19(02):107-111.
Dai Z,Xiao J,Pan Y P,et al,Research on an automatic leveling method and control technology[J].Digital Manufacturing Science,2021,19(02):107-111.
[10] 田静敏,黄秀玲.包装件跌落冲击研究现状[J].包装工程,2016(11):199-203.
Tian J M,Huang X L.Research status of packaging parts falling impact[J].Packaging Engineering,2016(11):199-203.
[11] Ali Arab,QianmeiFeng.Reliability research on micro-and nano-electromechanical systems:A review[J].The International Journal of Advanced Manufacturing Technology,2014,74(9/12):1679-1690.
[12] 王叶奔儒,潘孝斌,周鑫,等.榴弹包装箱跌落实验装置的设计与分析[J].机床与液压,2018,46(11):145—148.
Wang Y B R,Pan X B,Zhou X,et al.Design and analysis of gripping device for grenade crates dropping experiment[J].Machine Tool and Hydraulics,2018,46(11):145—148.
[13] 袁惠群,陶文斌,龙哲,等.某新型导弹包装箱动力学特性分析[J].包装工程,2019,40(05):124—130.
Yuan H Q,Tao W B,Long Z,et al.Dynamic characteristic of a new structure missile packing case[J].Packaging Engineering,2019,40(05):124—130.
[14] Frano R L,Sanfiorenzo A.Demonstration of Structural Performance of IP-2 Package by Simulationand Full-scale Horizontal Free Drop Test[J].Progressin Nuclear Energy,2016,86(01):40-49.
[15] 张帆,王匀,赵燕,等.圆形电连接器跌落冲击分析及改进设计[J].机械设计与制造工程,2018,47(03):108-111.
Zhang F,Wang J,Zhao Y,et al,Analysis and improved design of circular electrical connector[J].Mechanical Design and Manufacturing Engineering,2018,47(03):108-111.
[16] 杨优,孙先松.机器人齐次变换矩阵的研究[J].机械工程师,2016(03):61-64.
Yang Y,Sun X S.Research of robot homogeneous transformation matrices[J].Mechanical Engineer,2016(03):61-64.
[17] Ghosh N N.Theory of analytical spinorsI[J].Proceedings of the Indian National Science Academy,2015,31(5A):477-484.
[18] Ghosh N N.Theory of analytic spinorsII[J].Proceedings of Indian National Science Academy,2015,35(2A):477.
[19] 彭航.6-DOF串联机器人运动学算法研究及其控制系统实现[D].合肥:合肥工业大学,2016.
Peng H.6-DOF Series robot kinematics algorithm research and Its control system Implementation[D].Hefei University of Technology,2016.
[20] Costa C,Gaewsky J P,Stitzel J D,et al.Development and implementation of a time-and computationally-efficient methodology for reconstructing real-world crashes using finite element modeling to improve crash injury research investigations[J].Computer methods in biomechanics and biomedical engineering,2021,25(12):1332-1349.
[21] Huang Y,Vasan A S S,Doraiswami R,et a1.MEMS reliability review[J].IEEE Thnscationon Device and MaterialReliability,2012,12(02):482-493.