1 引言
威胁评估是建立在目标状态、属性估计与态势估计基础上的高级信息融合技术[1]。实际战场中,编队指挥员依据来袭目标的指标信息对目标威胁度进行评估,为我方编队的火力分配和战术决策提供依据,快速、准确地评估空中目标威胁度对战场态势发展具有重要意义。
威胁评估涉及众多不确定性,属于信息不全面、不确定下的战术评估问题。传统空中来袭目标威胁评估的常用方法有:专家经验、模糊理论、多属性决策理论、神经网络和静态贝叶斯网络[2-7]。专家经验方法依据专家打分获得来袭目标威胁程度,方法主观性较强。模糊理论威胁评估方法具有较强的模糊表达能力,但该方法不具备对目标威胁程度的动态推理能力。多属性决策方法具有操作简单的优点,但该方法完全依赖样本数据,不能处理不确定性数据。神经网络威胁评估方法能够实现威胁度的智能计算,但需要大量数据进行参数训练,不适合军事小样本数据,而且威胁评估结果具有波动性。静态贝叶斯威胁评估方法采用条件概率表达目标指标与威胁度间的关系强度,能够从不完全、不确定的战场知识或信息中获取目标威胁度,是静态目标威胁度评估的主要方法。传统的空中来袭目标威胁度评估方法为战场目标威胁程度的评估提供了多种策略与方案,促进了战场态势评估的快速发展。但传统空中威胁评估方法均不具备战场动态环境的表达能力,不能满足现在战场整体、动态的目标威胁评估需求。
动态贝叶斯网络将静态贝叶斯网络在时间上进行扩展,其具有的动态性、自适应学习能力、不确定性处理能力,使其在医疗诊断、图像处理、网络安全等领域被广泛应用[8-10]。近几年,军事研究学者也尝试将动态贝叶斯网络应用于空中目标动态威胁评估领域。高晓光[11]在静态贝叶斯网络基础上加入时间变量,设计动态贝叶斯网络评估方法。Wang[12]针对指标数据缺失问题,建立基于期望最大化的缺失数据处理动态贝叶斯网络评估模型。Di[13]利用单调性约束进行动态贝叶斯网络条件参数学习,建立小样本威胁评估模型。尽管动态贝叶斯网络提升了目标威胁评估的整体性和动态性,但将其应用于战场目标威胁度评估问题中仍存在两大挑战:一是数据类型处理挑战,贝叶斯网络的输入数据为概率,只能处理离散型数据,对连续型数据不能有效处理;二是推理结果是目标威胁等级概率向量形式,不能直接对多个目标进行排序。
综上所述,本文综合考虑威胁目标特性及动态贝叶斯网络缺陷,提出一种模糊动态贝叶斯网络和TOPSIS法的融合威胁评估模型。结合战场实际情况,基于目标运动特性与自身属性建立空中威胁评估指标体系,采用模糊方法对连续型指标数据划分模糊集,确定隶属度;对离散型指标进行等级划分。以威胁等级、威胁意图作为父节点,根据指标间的依赖关系建立双层贝叶斯网络指标体系。基于动态贝叶斯网络对导弹、轰炸机、无人机等多个同时来袭空中目标进行威胁评估推理。采用构造理想解的TOPSIS 方法对模糊动态贝叶斯推理出的威胁等级概率向量进行量化处理,获得目标威胁度数值,对多个目标的威胁度进行排序。实验结果显示:DBN-TOPSIS融合威胁评估方法合理、稳定。
2 空中目标威胁评估流程
对空中来袭目标进行威胁评估,是一个具有多属性指标、涉及不确定性决策下的动态综合评估问题。首先,依靠战场各传感器采集各指标数据,所获得的数据需要进一步处理。其次,利用动态贝叶斯网络进行各目标威胁等级概率推理,解决来袭目标具有的不确定性问题。最后,对目标各威胁等级概率进行综合评估判断,获得目标准确威胁排序。评估流程如图1所示。
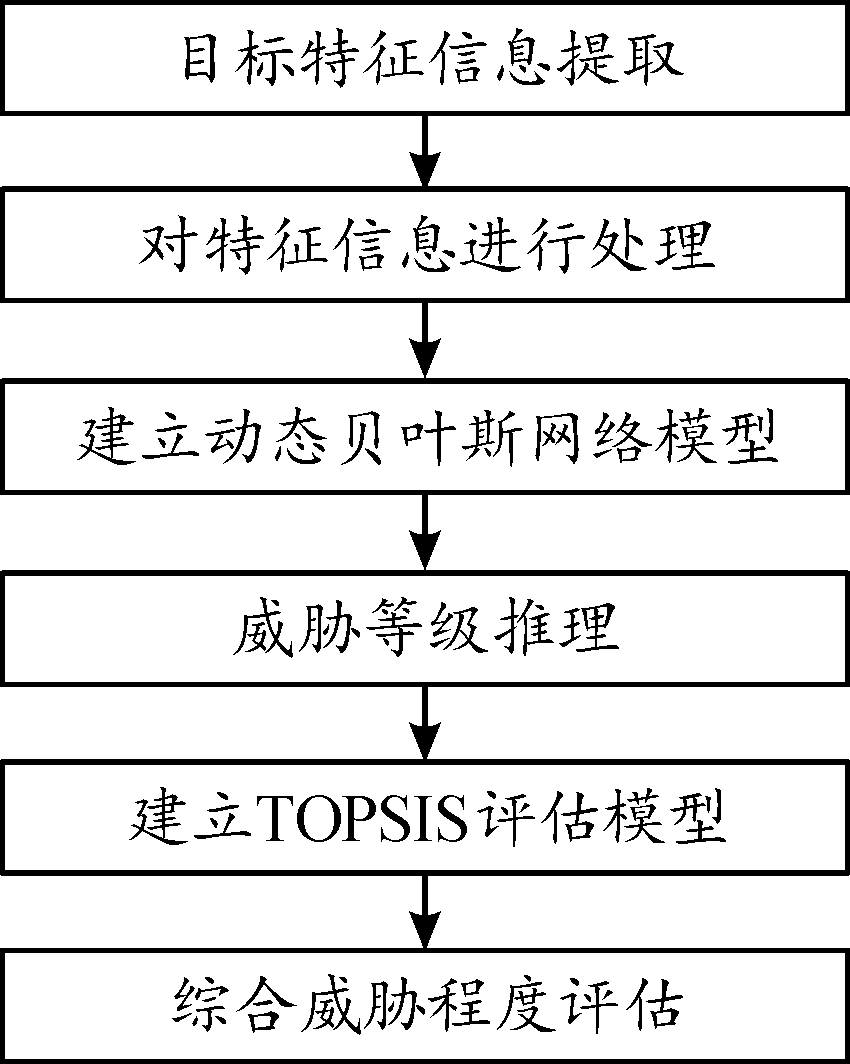
图1 威胁评估流程
Fig.1 Threat assessment process
3 威胁评估指标体系
空中目标威胁评估指标主要有目标运动特性指标与自身属性指标两类指标,指标选取过少会导致评估结果不精确,过多会出现数据难以获取,推理速度慢的情况。
3.1 指标选取
分析已有威胁评估模型指标,本文选取8个指标建立威胁评估模型。其中,速度、高度、距离、航路捷径、航向角,威胁意图等6个指标体现目标运动特性,能够全方位、较准确地判断出目标的位置、方向、速度、目的。目标类型、电子干扰能力2个指标体现目标自身属性,能够衡量目标硬攻击与软攻击能力。在以上指标中,威胁意图为隐节点,其余指标为可观测节点。指标示意图如图2所示。
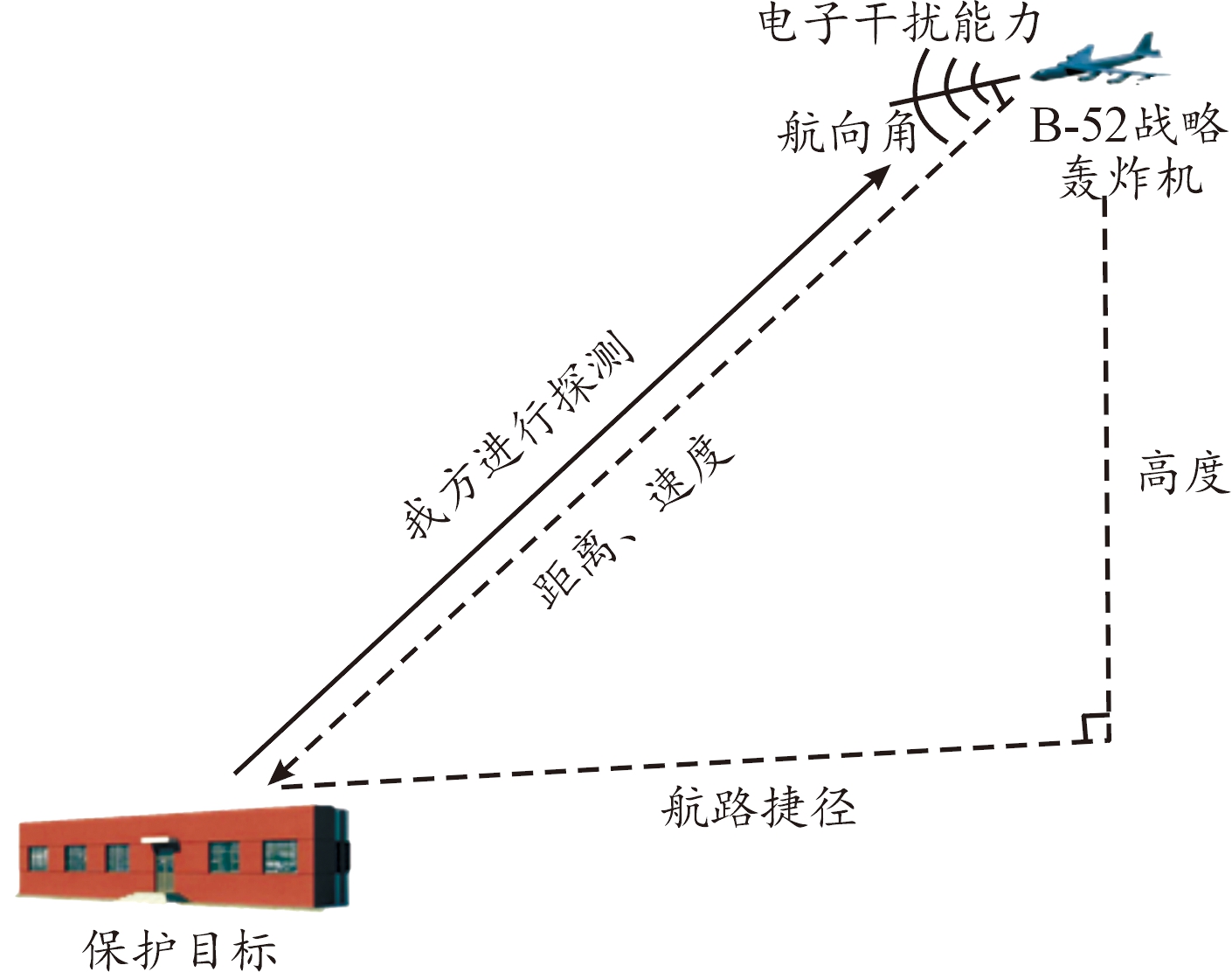
图2 指标示意图
Fig.2 Schematic diagram of indicators
图3为空中目标双层指标体系。图3中第1层各指标中,目标速度是目标与防御基地的相对速度;目标距离是目标与防御基地的直线距离;威胁意图为目标攻击意图,是衡量威胁程度的重要依据;目标类型将不同种类目标进行划分,不同种类目标威胁度不同;目标航路捷径为目标与防御基地内防御目标航路任意点切线的垂直距离。目标速度、目标距离、目标威胁意图、目标类型和目标航路捷径对目标威胁程度的影响如表1所示。
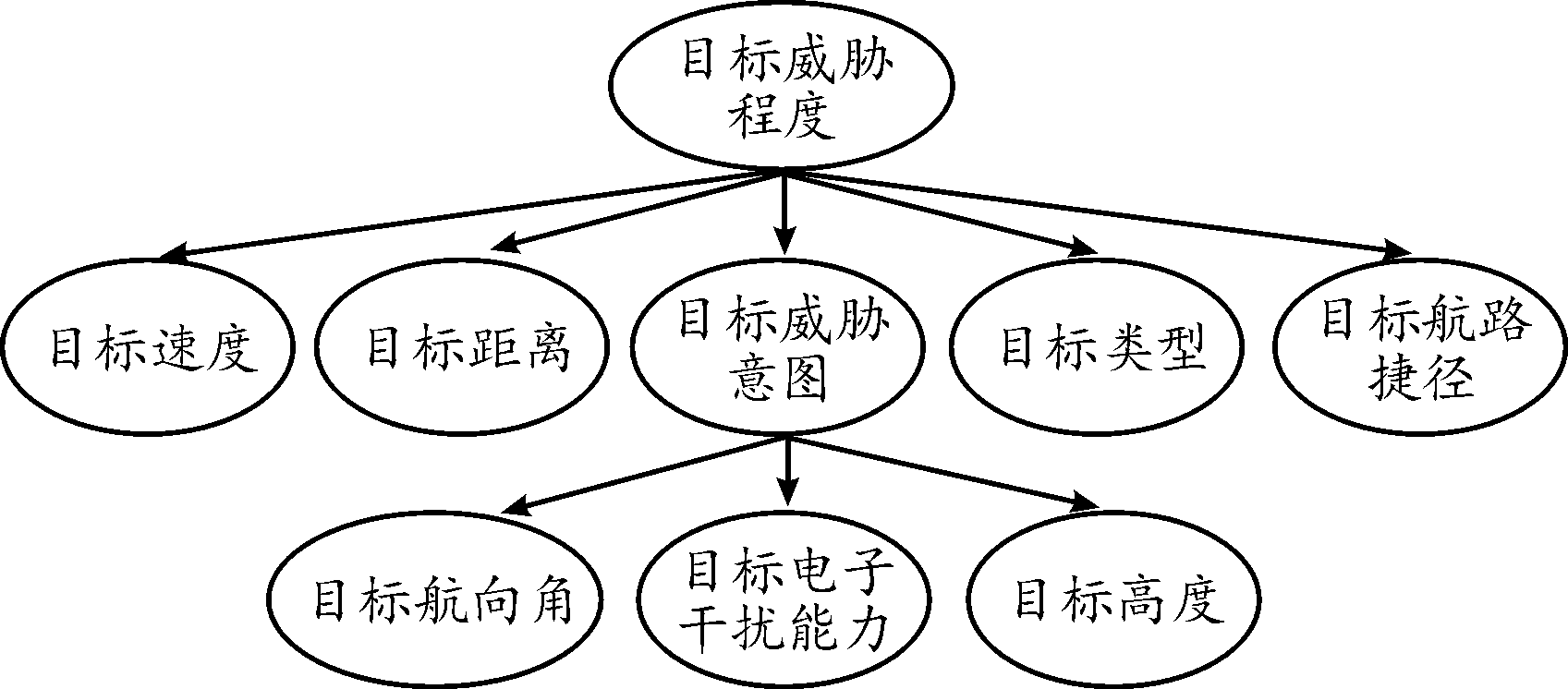
图3 指标依赖关系
Fig.3 Schematic diagram of indicator dependence
表1 节点变化对威胁程度影响
Table 1 Influence of index change on threat degree
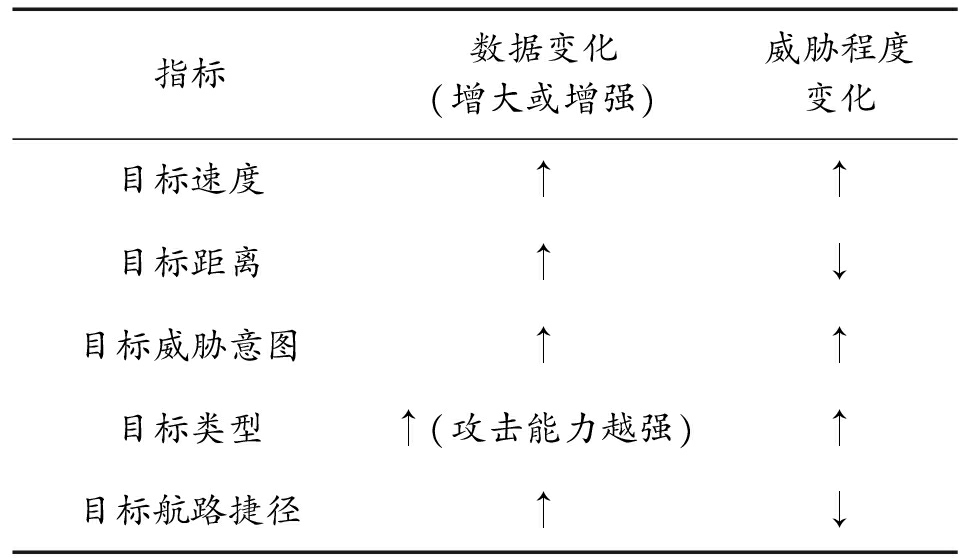
指标数据变化(增大或增强)威胁程度变化目标速度↑↑目标距离↑↓目标威胁意图↑↑目标类型↑(攻击能力越强)↑目标航路捷径↑↓
图3中威胁意图对应的第2层各指标中,目标航向角是目标飞行方向与目标和防御基地连线的夹角;目标电子干扰能力是使敌方电子设备和系统丧失或降低效能所采取的电波扰乱措施;目标高度是威胁目标与防御基地的垂直距离。以威胁意图作为父节点,目标航向角、目标电子干扰能力、目标高度作为子节点,子节点对目标威胁意图的影响如表2所示。
表2 节点变化对威胁意图影响
Table 2 Influence of index change on threat intention
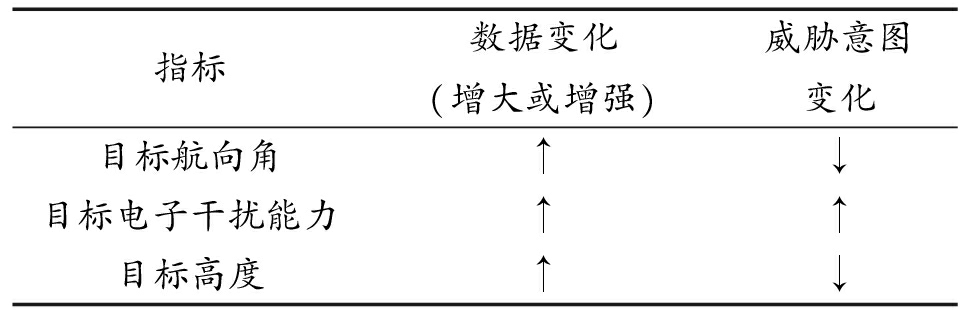
指标数据变化(增大或增强)威胁意图变化目标航向角↑↓目标电子干扰能力↑↑目标高度↑↓
威胁等级是最终需要确定的结论,是其他所有指标的父节点,包括同为隐节点的威胁意图。
3.2 连续型指标模糊化处理
贝叶斯网络为概率图模型,其输入和输出都为概率。当输入数据为离散型变量时,样本数据中该指标属于某一类,该类型取1,该指标的其他类型取0。当输入数据为连续型变量时,如速度、高度、距离等,监测仪器所采集数据为连续型数据,而不是属于某一个集合的概率。传统贝叶斯网络只能评估目标属性指标对威胁度的影响,而对目标动态性指标(如速度、高度、距离、航路捷径等)不能有效处理。
定义:对论域U上的模糊集合A,指定一个从U到[0,1]的映射:
μA:U→[0,1]
u→μA(u∈[0,1])
当μA(u)=1时,u∈A;当μA(u)=0时,u∉A。当μA(u)仅取0、1值时,隶属度函数μA退化为普通集合的特征函数、A退化为普通集合。图4为包含3个模糊集的三角形隶属度函数。
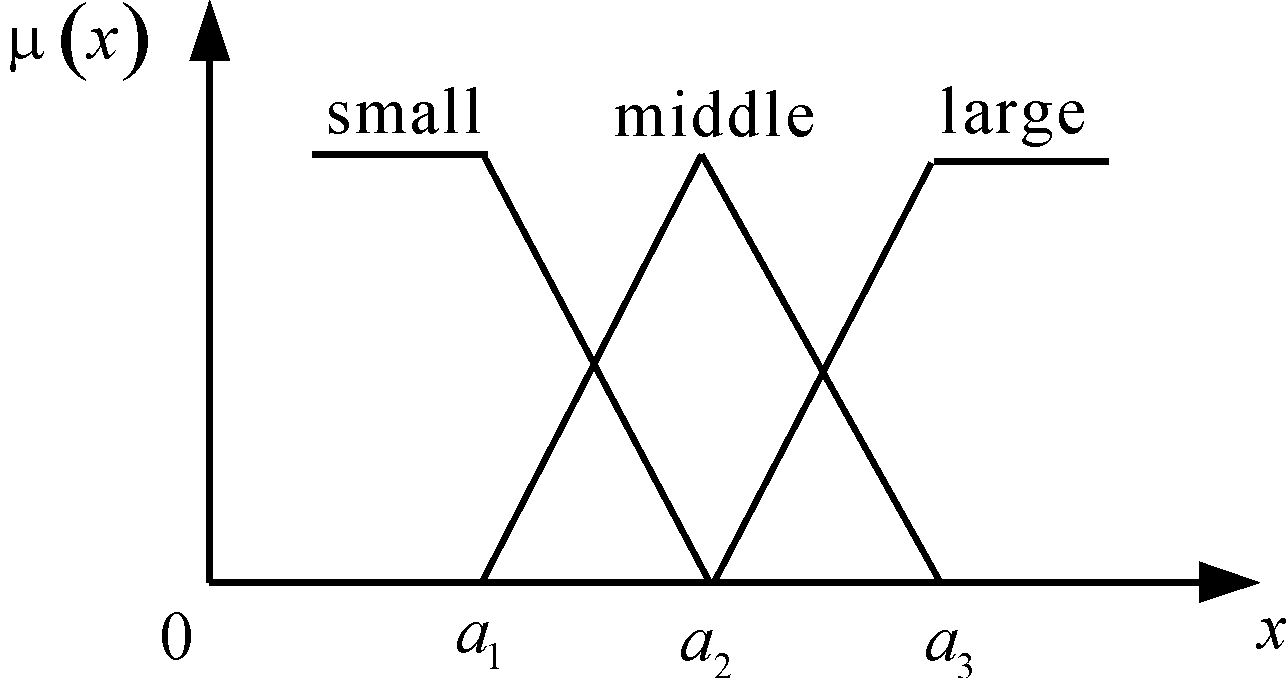
图4 三角形隶属度函数
Fig.4 Triangular membership function
三角形隶属度函数表达式为:
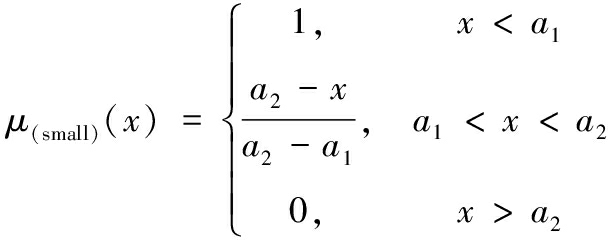
(1)
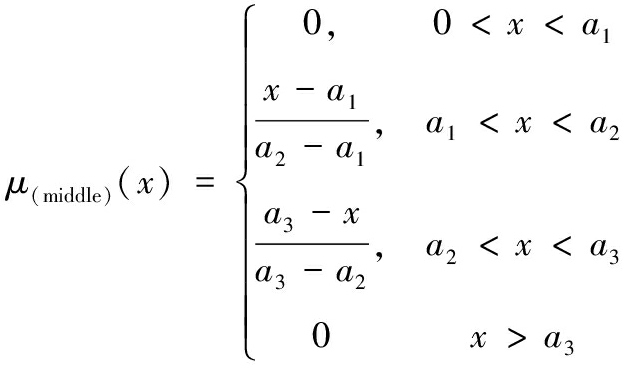
(2)
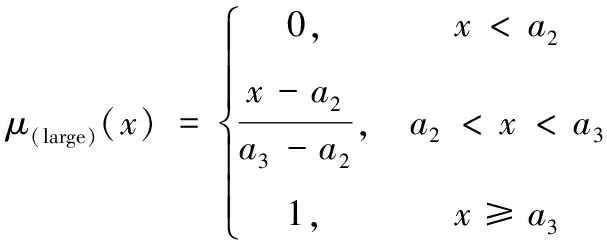
(3)
式(1)~(3)中,a1、a2、a3为隶属度函数的参数,需要根据连续型变量取值的论域和模糊集范围以及实际情况来确定。假设高度指标论域为0~12 km,取a1=3 km、a2=5 km、a3=7 km。则高度为6.5 km的模糊证据为μH=(0/small, 0.25/middle, 0.75/large)。对于离散型指标则需要进行分类、分段等处理。
4 DBN-TOPSIS融合评估模型
采用模糊函数将威胁评估体系中的连续型指标进行离散化处理,基于战场时间序列,利用模糊动态贝叶斯定性评估各目标的威胁度,建立多目标动态贝叶斯网络评估结果与TOPSIS法评估矩阵之间的关系,设计 TOPSIS法和DBN算法的威胁评估融合模型,对多目标威胁度进行综合排序。
4.1 模糊动态贝叶斯网络
静态贝叶斯网络表达为:BN=(G,θ),其中G是贝叶斯网络结构,表示一个有向无循环图。θ是网络中节点之间依赖关系的条件参数。DBN网络是向BN中引入状态转移参数,是BN在时间轴上的扩展。贝叶斯网络推理过程,实质是求网络节点的联合概率。应用模糊隶属度对条件参数进行加权,获得节点多状态下的综合概率值,模糊动态贝叶斯网络的推理计算如式(4)所示。
p(x11,x12,…,xT1,…,xTn|y11,y12,…,yT1,…,yTm)=
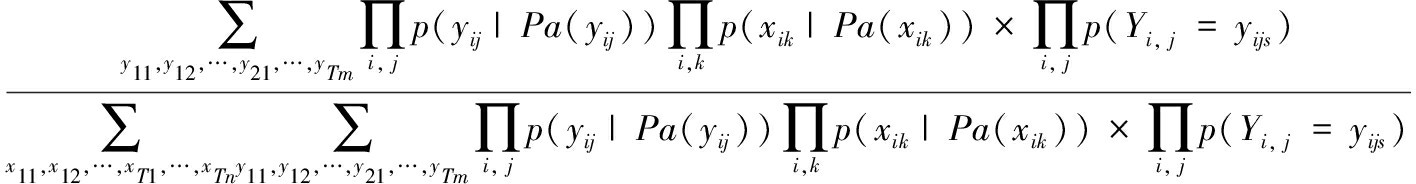
(4)
式(4)中:T代表时间片个数;m代表BN观测节点个数;n代表BN中隐藏节点的个数;i=1,2,…,T;j=1,…,m;k=1,…,n;xTn代表隐藏节点XTn的取值;yTm代表观测节点。YTm的取值;yijs表示第i个时间片内第j个观测变量的模糊状态s的取值;p(Yij=yijs)表示Yij处于相应s状态的概率。
4.2 TOPSIS法与动态贝叶斯融合推理
动态贝叶斯网络的推理结果为多个目标各自属于威胁程度高、中、低的隶属度,无法直接观测出各目标威胁程度大小,常用方法有按“高”排序法[14-15],或对3个隶属度进行加权求和[16],前者忽略了“中”、“低”威胁度结果,后者难以确定准确权重。采用构造理想解的TOPSIS方法,可以全面地考虑动态贝叶斯网络的推理结果,且不需要确定指标权重。
动态贝叶斯威胁评估结果矩阵为:
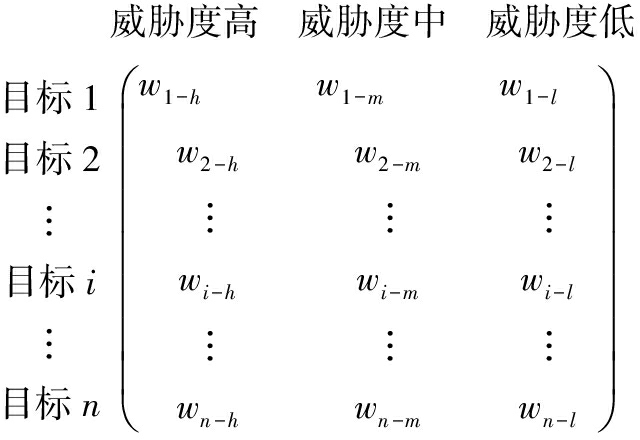
其中,wi-h、wi-m、wi-l分别表示第i个目标属于威胁度高、中、低模糊集的概率。将动态贝叶斯推理结果矩阵作为TOPSIS法的评估矩阵。
由于指标表示威胁度概率,构造最优理想解为(1,0,0),即目标威胁度完全属于高;最劣理想解为(0,0,1),即目标威胁度完全属于低。传统TOPSIS方法中对指标加权,从加权评估矩阵中获得的最优、最劣理想解,得到目标中的相对最优、最劣理想解。而理想解的构造是得到绝对最优、最劣理想解,避免了指标权重的确定,且相较传统TOPSIS计算方法,更符合问题需求。融合威胁评估方法计算过程如图5所示。
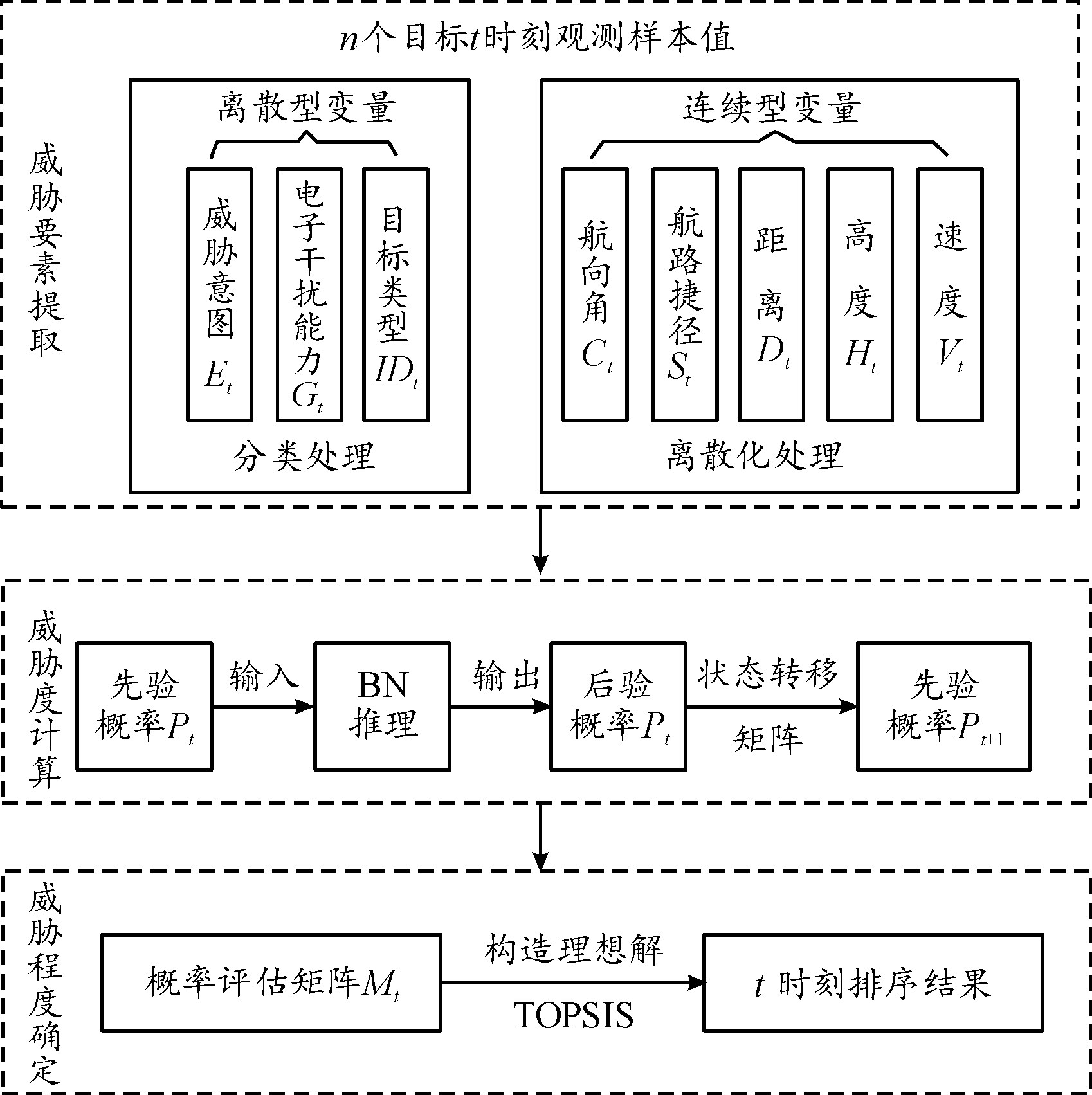
图5 融合威胁评估方法计算过程
Fig.5 Calculation process of fusion threat assessment method
DBN-TOPSIS融合威胁评估方法计算步骤如下:
Step 1 对当前时间片n个目标样本数据进行离散化、分段等处理。
Step 2 使用联合概率公式对第i个目标进行静态贝叶斯推理,并与先验概率相乘,得到该目标后验概率。
(5)
Step 3 汇总多目标推理结果,构造TOPSIS评估矩阵。
Step 4 计算各目标概率向量值到最优理想解(1,0,0)、最劣理想解(0,0,1)的欧式距离,记为![]() 和
和![]() 则第i个目标的综合评分为:
则第i个目标的综合评分为:
(6)
Ci越接近1,第i个目标排名越靠前,威胁度越大。
Step 5 将Ci进行归一化处理,得到当前时刻各目标融合威胁评估方法威胁度。
Step 6 将当前时刻各目标后验概率与状态转移概率矩阵相乘,计算各目标下一时刻先验概率。
Step 7 重复步骤Step 1-Step 6。
在Step2中,L代表当前节点父节点的威胁等级;p(Li)代表第i个目标总威胁度为高、中、低值;X代表各个指标节点(目标类型、高度、航向角、电子干扰能力、速度、距离、航路捷径);k代表每个指标节点划分等级个数,j=1,…,k;ppX(j)为指标X模糊分类后第j个等级的模糊隶属度;![]() 为条件概率,表示节点X父节点在L等级下,节点j等级时,依赖关系大小。
为条件概率,表示节点X父节点在L等级下,节点j等级时,依赖关系大小。
5 仿真实验
为了验证融合威胁评估方法有效性,根据战场实际情况,选取实验数据,对评估方法进行排序合理性实验、稳定性实验。实验环境为windows 10操作系统、PyCharm Community Edition 2020.3 x64编译器、python 3.7语言。
5.1 实验数据
选择7个来袭目标、8个时间片,每个时间片间隔75 s,贝叶斯网络结构如图2所示,初始时刻先验概率取(0.3,0.4,0.3)。目标观测数据如表3、表4所示,节点状态集合如表5所示,网络部分参数如表6、表7所示。
表3 75 s来袭目标名称及各指标信息
Table 3 75 s incoming target name and index information

编号目标名称类型电子干扰能力高度速度距离航向角航路捷径75 s时间片1BGM-109C“战斧”式巡航导弹导弹中0.1120.6135701272AGM-86B空地导弹导弹强0.1130.61148701393AH-64A“阿帕奇”武装直升机直升机中1.570.27250752354F-16C战斗机战斗机中81.3367853325F-22隐形战斗机战斗机强9.431.8450754356B-52H战略轰炸机轰炸机强8.1830.65300652727MQ-9“死神”无人机无人机强12.90.1520070188
表4 600 s来袭目标名称及各指标信息
Table 4 600 s incoming target name and index information

编号目标名称类型电子干扰能力高度速度距离航向角航路捷径600 s时间片1BGM-109C“战斧”式巡航导弹导弹中0.0740.69201232AGM-86B空地导弹导弹强0.070.69301553AH-64A“阿帕奇”武装直升机直升机中1.130.2820015174F-16C战斗机战斗机中7.041.531461265F-22隐形战斗机战斗机强7.451.921201496B-52H战略轰炸机轰炸机强6.170.6918012147MQ-9“死神”无人机无人机强10.60.261621213
表5 节点状态集合
Table 5 Node state collection

节点节点状态航向角C/(°)C={小(c<45),大(45
节点节点状态类型IDID={无人机(id1),武装直升机(id2),轰炸机(id3),战斗机(id4),导弹(id5)}航路捷径S/kmS={短(s1),中(s2),(s3)}威胁意图EE={侦察(e1),干扰(e2),攻击(e3)}威胁程度LL={低(l1),中(l2),高(l3)}
表6 P(目标高度|目标威胁意图)条件概率表
Table 6 P(target height|target threat intention)conditional probability table
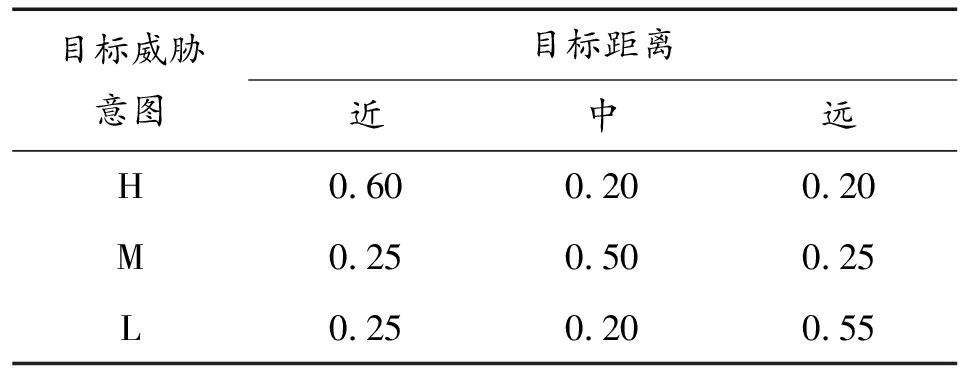
目标威胁意图目标距离近中远H0.600.200.20M0.250.500.25L0.250.200.55
表7 状态转移概率表
Table 7 State transition probability table
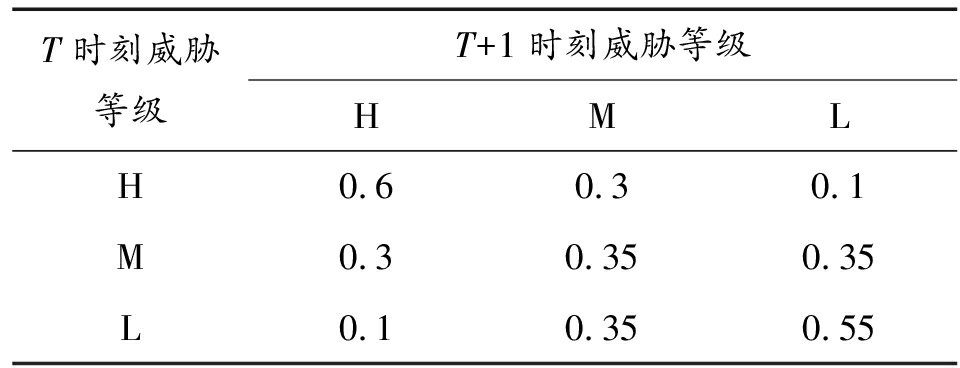
T时刻威胁等级T+1时刻威胁等级HMLH0.60.30.1M0.30.350.35L0.10.350.55
5.2 DBN-TOPSIS融合威胁评估实验结果
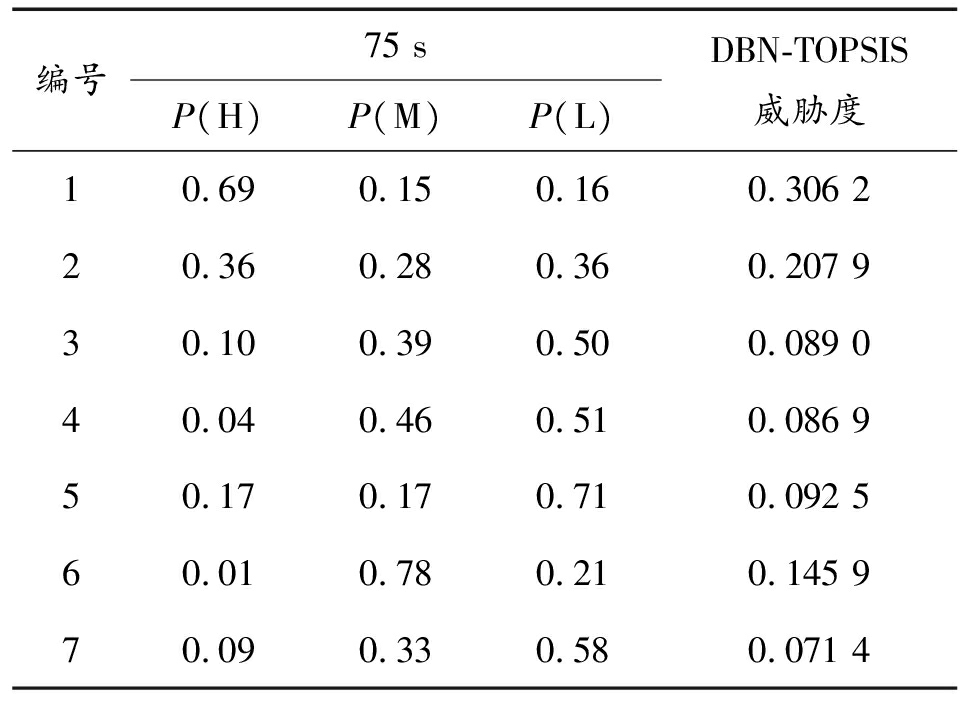
表8、表9分别为75 s初始时间片、600 s结束时间片时,7个目标的评估结果。P(H)、P(M)、P(L)表示动态贝叶斯推理出目标属于威胁度高、中、低的概率。综合威胁度表示融合威胁评估结果,体现目标之间相对威胁度,威胁度数值越大,威胁度越高。75 s时目标1、目标2威胁度较高,随着战场态势发展,各目标指标数值威胁性逐渐增大,目标间相对威胁度差值逐渐缩小。
表8 75 s时DBN-TOPSIS融合评估方法目标威胁度
Table 8 Target threat degree of DBN-TOPSIS fusion evaluation method in 75 s
编号75 sP(H)P(M)P(L)DBN-TOPSIS威胁度10.690.150.160.306 220.360.280.360.207 930.100.390.500.089 040.040.460.510.086 950.170.170.710.092 560.010.780.210.145 970.090.330.580.071 4
表9 600 s时DBN-TOPSIS融合评估方法目标威胁度
Table 9 Target threat degree of DBN-TOPSIS fusion evaluation method at 600 s
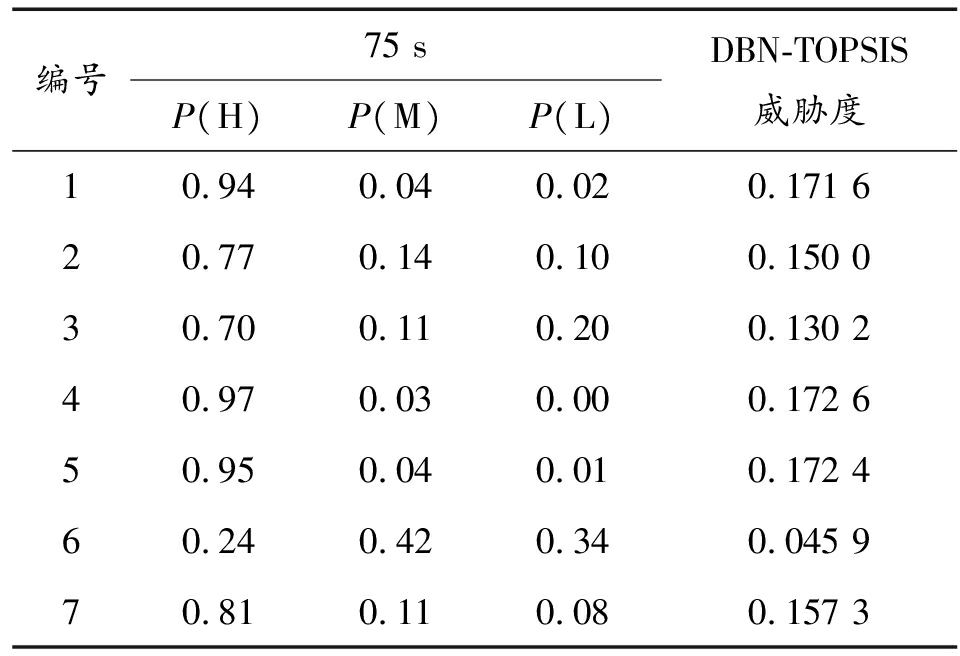
编号75 sP(H)P(M)P(L)DBN-TOPSIS威胁度10.940.040.020.171 620.770.140.100.150 030.700.110.200.130 240.970.030.000.172 650.950.040.010.172 460.240.420.340.045 970.810.110.080.157 3
5.3 实验对比
将按“高”动态贝叶斯方法、TOPSIS威胁评估方法与融合威胁评估算法对比,验证融合威胁评估方法的排序合理性和稳定性。
5.3.1 排序合理性
评估结果的合理性是评估模型的核心。为了验证融合评估模型评估的合理性,本文将DBN-TOPSIS评估方法和传统的按“高”动态贝叶斯评估方法进行对比,对比结果如表10所示。
表10 融合评估与按“高”动态贝叶斯评估对比
Table 10 Comparison results between fusion evaluation and dynamic Bayesian evaluation by “high”
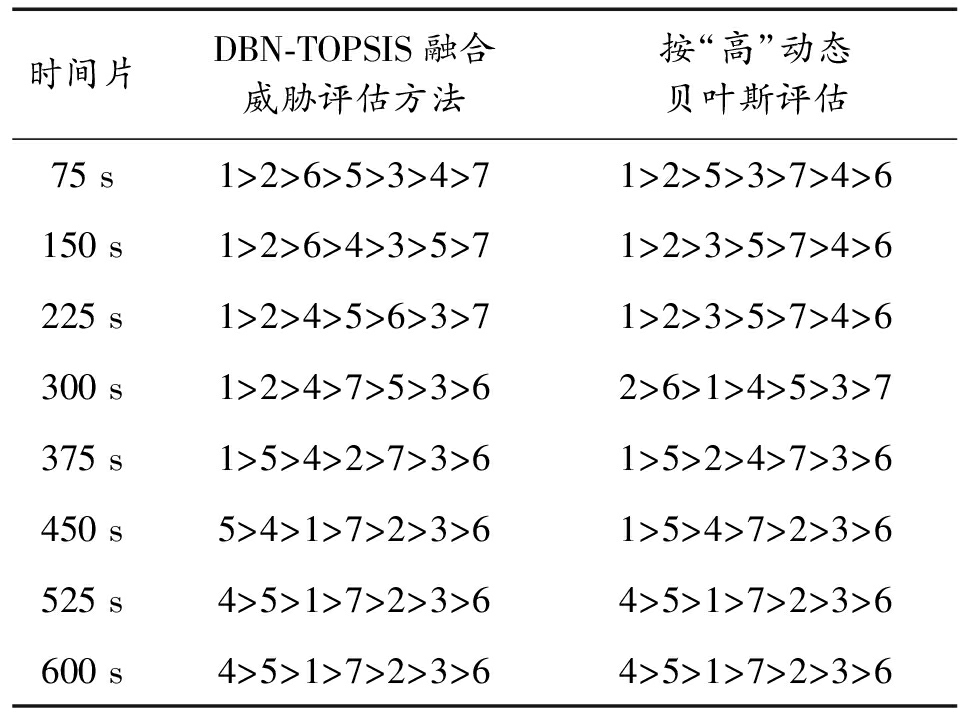
时间片DBN-TOPSIS融合威胁评估方法按“高”动态贝叶斯评估75 s1>2>6>5>3>4>71>2>5>3>7>4>6150 s1>2>6>4>3>5>71>2>3>5>7>4>6225 s1>2>4>5>6>3>71>2>3>5>7>4>6300 s1>2>4>7>5>3>62>6>1>4>5>3>7375 s1>5>4>2>7>3>61>5>2>4>7>3>6450 s5>4>1>7>2>3>61>5>4>7>2>3>6525 s4>5>1>7>2>3>64>5>1>7>2>3>6600 s4>5>1>7>2>3>64>5>1>7>2>3>6
2种排序方法的结果相似度为57%,当目标指标数据威胁度较大或较小,易于区分时,2种方法排序结果相同。如初始时刻,75~225 s时间片的前2个目标威胁度较大,525 s与600 s时间片,各目标威胁度都变大,排序结果相同。由于按“高”动态贝叶斯评估完全忽略了威胁度“中”和“低”的影响,使之在威胁度数值最大概率属于“中”或“低”模糊集时,结果不合理。例如150 s时,融合威胁评估法将目标3排在第5位,排序法将目标3排在第3位,目标3属于高中低的隶属度分别为(0.10,0.25,0.65),其隶属度最大的是威胁等级为低的模糊集,而按“高”动态贝叶斯评估方法将其对结果的影响完全忽略,会造成动态贝叶斯网络推理结果的失真。融合威胁评估法能够对3个模糊集隶属度进行综合考量。综上所述,DBN-TOPSIS融合威胁评估方法排序结果具有合理性,且优于按“高”动态贝叶斯评估。
5.3.2 稳定性对比
战场仪器所监测数据,由于天气环境等原因会出现异常情况,评估模型的稳定性是模型有效性的重要指标。通过对目标数据进行灵敏度分析,进而评价2种评估方法的稳定性。在600 s时间片下,随机选取AGM-86B速度指标、F-16C距离指标数据进行实验。
对AGM-86B速度指标做扰动分析:原有速度为0.69 Ma,取其15%做步长。在其他指标数据不变的情况下,分别计算速度在-30%(0.483Ma)、-15%(0.586 5Ma)、0(0.69Ma)、15%(0.795Ma)、30%(0.897 Ma)幅度变化时,DBN-TOPSIS融合威胁评估方法和TOPSIS方法的威胁度值。计算结果如表11所示。AGM-86B速度变化对其他目标威胁度的影响如表12所示。
表11 AGM-86B在不同速度下的威胁度评估结果(600 s)
Table 11 Threat assessment results of AGM-86B at different speeds(600 s)
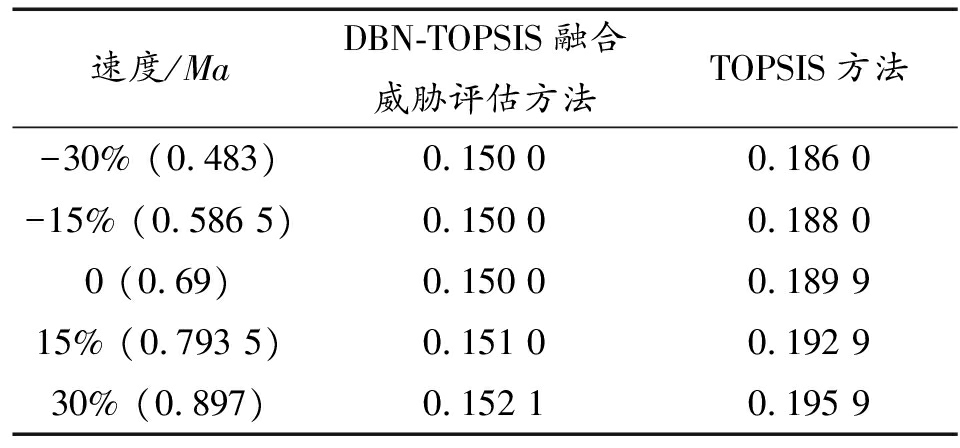
速度/MaDBN-TOPSIS融合威胁评估方法TOPSIS方法-30% (0.483)0.150 00.186 0-15% (0.586 5)0.150 00.188 00 (0.69)0.150 00.189 915% (0.793 5)0.151 00.192 930% (0.897)0.152 10.195 9
表12 AGM-86B速度变化时其他目标威胁度评估结果(600 s)
Table 12 Assessment results of threat degree of other targets when AGM-86B speed changes(600 s)
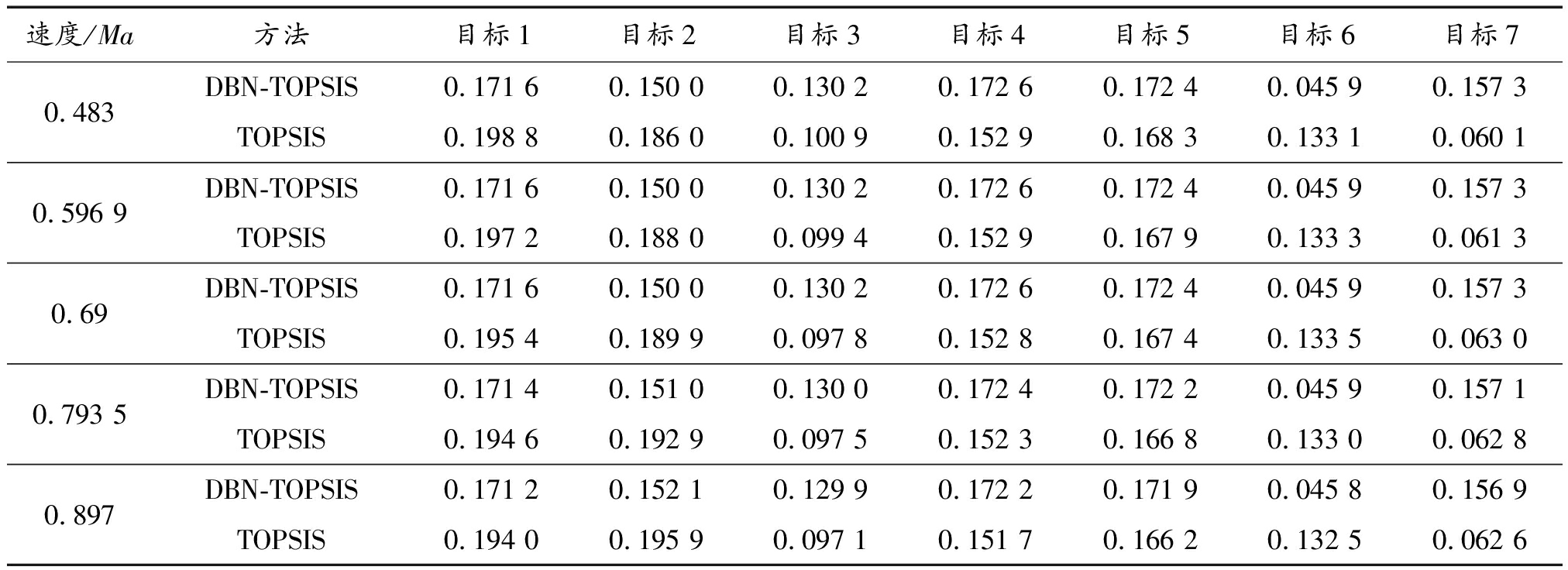
速度/Ma方法目标1目标2目标3目标4目标5目标6目标70.483DBN-TOPSIS0.171 60.150 00.130 20.172 60.172 40.045 90.157 3TOPSIS0.198 80.186 00.100 90.152 90.168 30.133 10.060 10.596 9DBN-TOPSIS0.171 60.150 00.130 20.172 60.172 40.045 90.157 3TOPSIS0.197 20.188 00.099 40.152 90.167 90.133 30.061 30.69DBN-TOPSIS0.171 60.150 00.130 20.172 60.172 40.045 90.157 3TOPSIS0.195 40.189 90.097 80.152 80.167 40.133 50.063 00.793 5DBN-TOPSIS0.171 40.151 00.130 00.172 40.172 20.045 90.157 1TOPSIS0.194 60.192 90.097 50.152 30.166 80.133 00.062 80.897DBN-TOPSIS0.171 20.152 10.129 90.172 20.171 90.045 80.156 9TOPSIS0.194 00.195 90.097 10.151 70.166 20.132 50.062 6
根据表11所示,速度变化幅度在0~30%内,融合评估方法威胁度评估结果变化幅度小。TOPSIS方法威胁度评估结果随速度值的增大而增大。图6为表12的折线表示,纵坐标是威胁度差值,代表各目标在AGM-86B速度变化幅度为-30%和30%时威胁度差的绝对值。
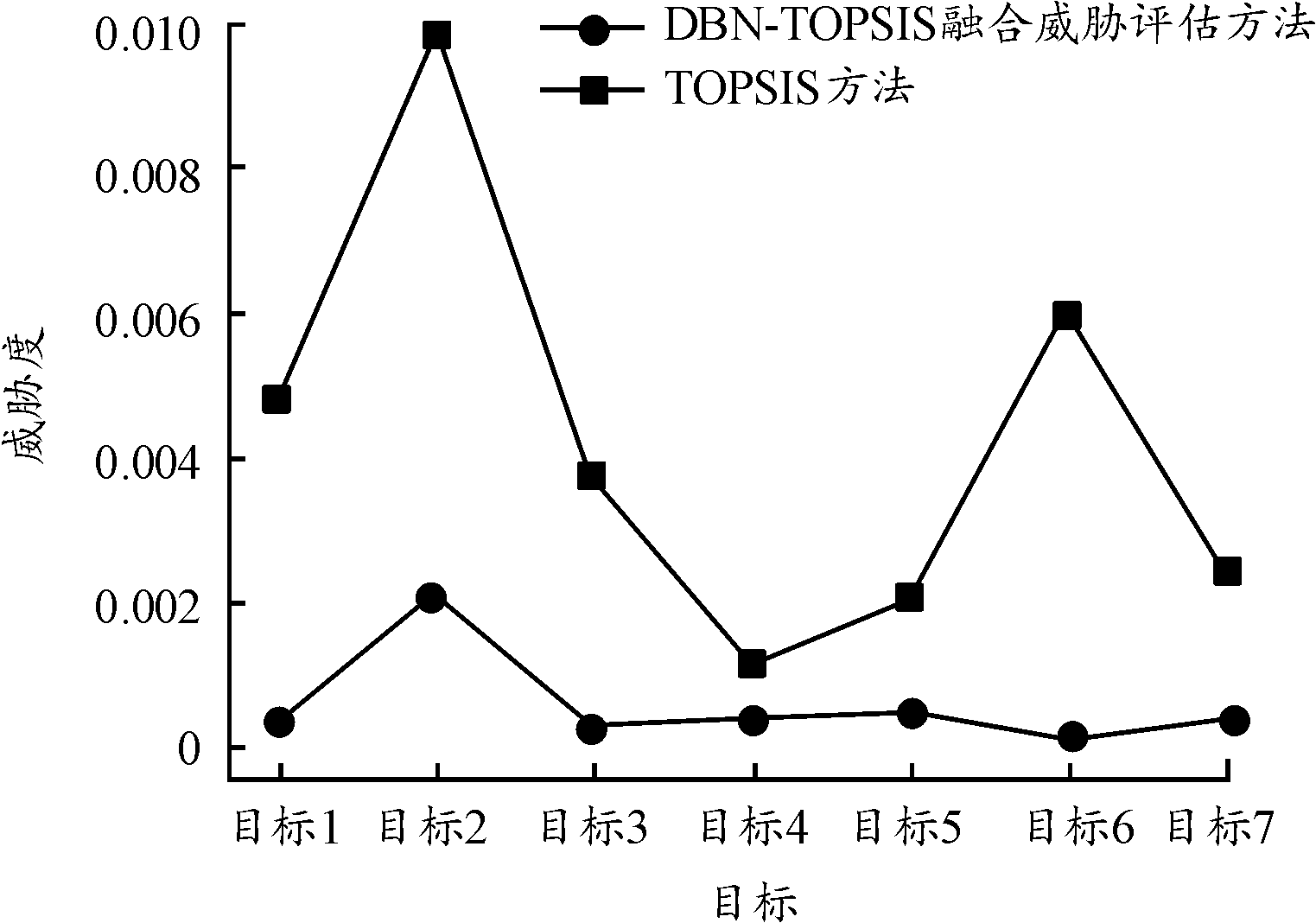
图6 AGM-86B速度变化时其他目标威胁度评估结果(600 s)
Fig.6 Assessment results of threat degree of other targets when AGM-86B speed changes(600 s)
由图6所示,对目标1到目标7,DBN-TOPSIS威胁评估方法与TOPSIS威胁评估方法的波动误差比值分别为7.7%、17.5%、7.3%、2.5%、19.2%、14.3%和13.8%,DBN-TOPSIS评估方法曲线波动程度显著小于TOPSIS威胁评估曲线波动程度。有异常发生时,不论是对目标自身威胁度的影响,还是对其他目标威胁度的影响,融合威胁评估方法稳定性都优于传统TOPSIS法。
6 结论
本文基于融合方法研究了空中目标威胁评估问题。通过选取能够体现目标运动特性和自身属性的指标,综合考虑目标指标特性、目标动态性及结果合理性,建立基于模糊动态贝叶斯与构造理想解的DBN-TOPSIS融合威胁评估模型,解决空中目标威胁度定量排序问题。实验表明:融合威胁评估方法充分利用了贝叶斯网络概率推理能力,解决了不确定性战场目标的动态威胁评估问题,相对于传统的按“高”动态贝叶斯威胁评估方法和TOPSIS威胁评估方法,具有更好的合理性与稳定性。
[1] 梁洪泉.动态贝叶斯网络在战场目标态势威胁评估中的应用[D].北京:北京邮电大学,2007.
Liang H Q.Application of dynamic Bayesian network in battlefield target situation threat assessment[D].Beijing:Beijing University of Posts and Telecommunications,2007.
[2] 许黎黎,刘治国,潘成胜.基于灰色层次评价的指挥自动化系统效能评估[J].沈阳理工大学学报,2007,26(03):5-8,16.
Xu LL,Liu Z G,Pan C S.Effectiveness evaluation of command automation system based on grey hierarchy evaluation[J].Journal of shenyangligong university,2007,26(03):5-8,16.
[3] 张峰,胥文,吴东岩,等.作战仿真中基于BP-Adaboost目标威胁估计研究[J].系统仿真技术,2019,15(03):180-183.
Zhang F,Xu W,Wu D Y,et al.Research on target threat estimation based on BP-Adaboost in combat simulation[J].System Simulation Technology,2019,15(03):180-183.
[4] 陈德江,王君.基于直觉模糊集的防空作战目标威胁评估[J].探测与控制学报,2019,41(04):46-51.
Chen D J,Wang J.Threat assessment of air defense targets based on intuitionistic fuzzy sets[J].Journal of Detection and Control,2019,41(04):46-51.
[5] Sahni M,Das S K.A method of risk analysis and threat management using analytic hierarchy process:An application to air defence[J].Journal of Battlefield Technology,2015,18(03):27-30.
[6] 刘文博,梁敏,张欧亚,等.基于贝叶斯网络的侦察威胁等级评估研究[J].火力与指挥控制,2019,44(03):72-76.
Liu W B,Liang M,Zhang OY,et al Dai Haifeng.Research on evaluation of reconnaissance threat level based on Bayesian network[J].Firepower and Command and Control,2019,44(03):72-76.
[7] 丁达理,罗建军,王铀,等.基于模糊贝叶斯网的威胁等级评估研究[J].电光与控制,2014,21(09):7-15.
Ding D L,Luo JJ,WangU,et al.Research on threat level assessment based on fuzzy Bayesian network[J].Electro-optic and Control,2014,21(09):7-15.
[8] Tamada Y,Imoto S,Araki H,et al.Estimating genome-wide gene networks using nonparametric bayesian network models on massively parallel computers[J].IEEE/ACM Transactions on Computational Biology & Bioinformatics,2011,8(03):683-697.
[9] Gonzales C,Romdhane R,Dubuisson S.Video event detection based non-stationary Bayesian networks[C]//Proc.of the International Conference on Advanced Concepts for Intelligent Vision Systems,Auckland,New Zealand:Springer Cham,2016:419-430.
[10] Dshire S,Tshir F,JiaoY,et al.Bayesian network inference for probabilistic strength estimation of aging pipeline systems[J].International Journal of Pressure Vessels and Piping,2018,162(03):30-39.
[11] 高晓光,杨宇.基于贝叶斯网的舰艇防空威胁评估[J].战术导弹技术,2020(04):47-57,70.
Gao X G,Yang Y.Assessment of naval air defense threat based on Bayesian network[J].Tactical Missile Technology,2020(04):47-57,70.
[12] Wang Y,Sun Y,Li J Y,et al.Air defense threat assessment based on dynamic bayesian network[C]//Proc of the 2012 International Conference on Systems and Informatics,YanTai:IEEE,2012:721-724.
[13] Di R H,Gao X G,Guo Z G,et al.A threat assessment method for unmanned aerial vehicle based on bayesiannetworks under the condition of small data sets[J].Mathematical Problems in Engineering,2018,2018:1-17.
[14] 张银燕,李弼程,崔家玮.基于云贝叶斯网络的目标威胁评估方法[J].计算机科学,2013,40(10):127-131.
Zhang YY,Li B C,Cui J W.Target threat assessment method based on cloud Bayesian network[J].Computer Science,2013,40(10):127-131.
[15] 孟光磊,龚光红.基于混合贝叶斯网的空域目标威胁评估方法[J].系统工程与电子技术,2010,32(11):2398-2401.
Meng G L,Gong G H.Airspace target threat assessment method based on mixed Bayesian network[J].systems engineering and electronics,2010,32(11):2398-2401.
[16] 孙海文,谢晓方,孙涛,等.小样本数据缺失状态下DBN舰艇编队防空目标威胁评估方法[J].系统工程与电子技术,2019,41(06):1300.
Sun H W,Xie X F,Sun T,et al.Threat assessment method of air defense targets of DBN naval fleet in the absence of small sample data[J].systems engineering and electronics,2019,41(06):1300