1 引言
火箭橇是一种利用固体或液体火箭发动机进行动力推动,沿地面固定轨道高速滑行,以模拟被试品高速飞行状态的大型地面动态试验设备[1-3]。火箭橇试验是最逼近真实环境和置信度最高的一种现代武器试验手段,具有试验速度范围宽、灵活性大、可重复性强、精确试验数据获取难度低和代价小等优点,被广泛应用于飞机、导弹、航空救生和航天发射武器等在研制阶段的综合动态性能试验[4-5]。
火箭橇体约束在滑轨上高速运行时,由于轨道不平顺、滑靴与轨道间隙、火箭燃烧产生的脉动推力和高速气流的脉动压力等因素耦合作用,导致橇车振动环境恶劣,远远大于飞机、导弹和火箭等武器系统在空中飞行时的真实冲击振动环境[6]。因此,为确保试验结果的“天地一致性”,被试品在火箭橇上的安装平台必须具有相当的减振/隔振功能。
控制滑靴-轨道间隙、提高轨道平顺度和优化火箭橇体自身结构等减振措施提升空间小、适应性较差,无法满足不同被试品试验考核的需求。为改善火箭橇体的冲击振动环境,董治华等[7]对双层浮筏火箭橇减振系统进行了分析,并通过某型引信火箭橇台架试验验证了有效性,但该双层浮筏隔振系统会放大火箭橇的振动位移,影响侧向和横向运动稳定性。丁春全等[8]对传统被动动力吸振火箭橇减振平台进行了研究。利用被动动力吸振器进行振动能量转移可有效降低被试品的振动而无须改动火箭橇的基础结构,其结构简单、使用成本低,但在激励频带内具有多个共振峰的宽频带振动吸振的效果不够理想[9]。主动/半主动动力吸振器能够通过实时调节附加结构的刚度或者阻尼实现宽频段振动的抑制[10-12]。半主动动力吸振器的性能与主动动力吸振器接近,但相比实现简单,成本更低。Koo等[10]和郎君等[9]分别比较分析了基于速度与位移的开关和连续型地棚控制动力吸振器的性能,仿真结果都表明半主动控制动力吸振器的性能均显著优于被动动力吸振器。磁流变阻尼器是由在磁场作用下可在毫秒级时间内由牛顿流体变为Bingham半固体,屈服强度连续可逆可调的磁流变液制作而成的半主动控制器件,具有响应快速、动态范围宽、功耗低和结构简单等优点,在土木、建筑和车辆悬架等半主动控制领域得到了广泛的应用[13-15]。为此,本研究提出一种基于磁流变阻尼器的火箭橇半主动动力吸振器,在不改变现有火箭橇基础结构的前提下抑制大强度、宽频带恶劣振动。
2 火箭橇动力吸振器力学模型
2.1 火箭橇动力吸振器模型
图1为火箭橇动力吸振器动力学模型,其动力学方程为:
![]()
(1)
式中:ma为动力吸振器质量;m为火箭橇主系统质量;ka为动力吸振器刚度;k和c分别为火箭橇主系统的刚度和阻尼;FMR为磁流变阻尼力;x为动力吸振器的振动位移;xa为火箭橇主系统的振动位移。

图1 火箭橇动力吸振器力学模型
Fig.1 Mechanical model of the rocket sled with the DVA
2.2 磁流变阻尼器力学模型
磁流变阻尼器的力学模型根据控制器需求可分为正向模型和逆向动力学模型两类。正向模型用于描述磁流变阻尼器的力学特性;逆向动力学模型用于根据期望阻尼力预测控制的电压。对于开关控制策略仿真,可只需正向模型,磁流变阻尼器的力学模型用于根据位移、速度和控制电压预测实际的阻尼力。本研究采用经典的Bouc-Wen模型[13]:
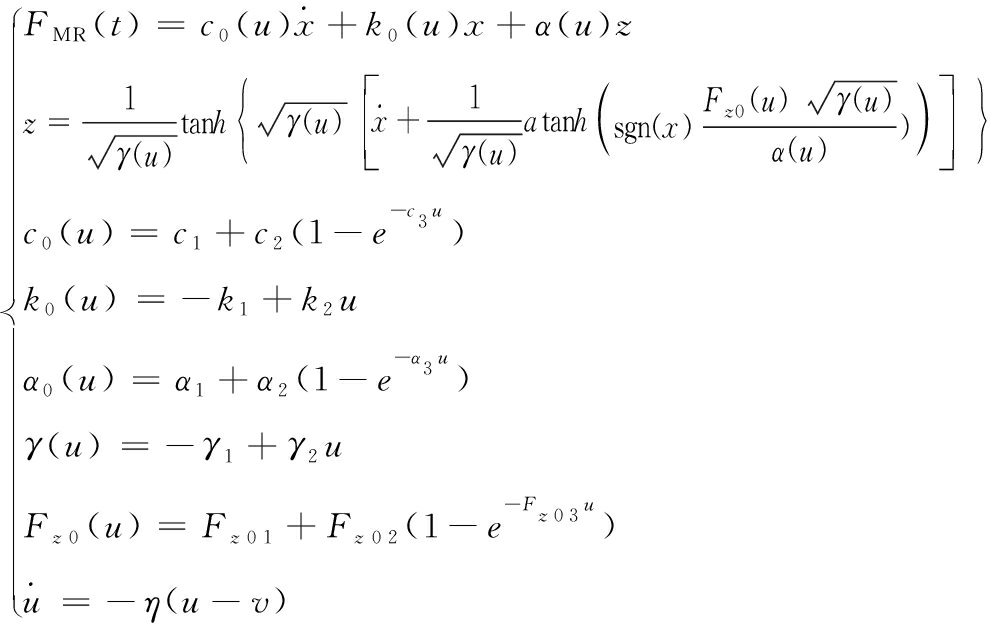
(2)
式中: 13个常数c1,c2,c3,k1,k2,α1,α2,α3,γ1,γ2,Fz01,Fz02和Fz03为Bouc-Wen模型参数; η为表示磁流变阻尼器响应时间的常数;x和![]() 分别为磁流变阻尼器活塞与缸体的相对位移和速度;u为施加到磁流变阻尼器的励磁电流;v为控制电压。磁流变阻尼器力学模型的参数如表1所示。
分别为磁流变阻尼器活塞与缸体的相对位移和速度;u为施加到磁流变阻尼器的励磁电流;v为控制电压。磁流变阻尼器力学模型的参数如表1所示。
表1 磁流变阻尼器模型参数 Table1 Model parameters of MR damper
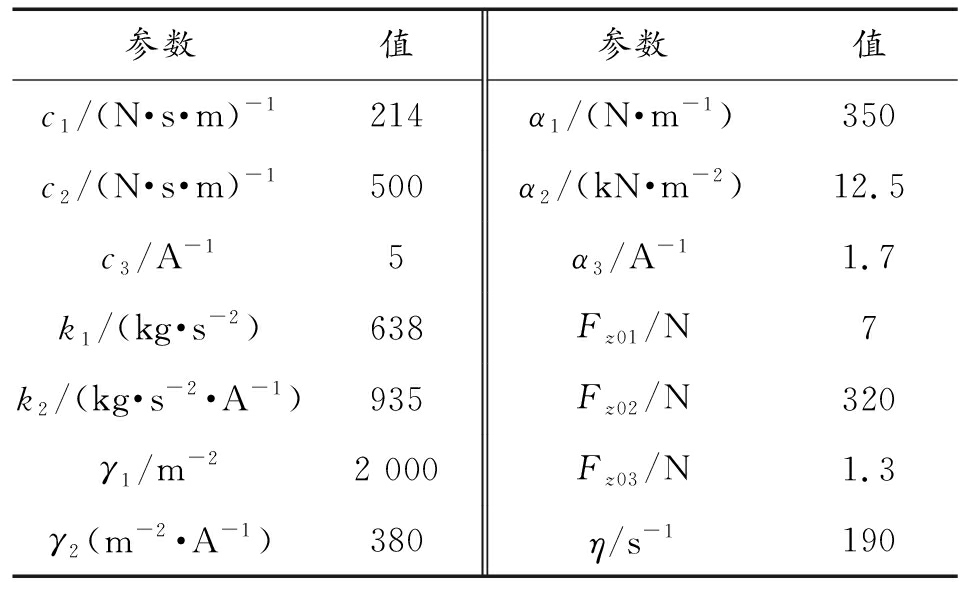
参数值参数值c1/(N·s·m)-1214α1/(N·m-1)350c2/(N·s·m)-1500α2/(kN·m-2)12.5c3/A-15α3/A-11.7k1/(kg·s-2)638Fz01/N7k2/(kg·s-2·A-1)935Fz02/N320γ1/m-22 000Fz03/N1.3γ2(m-2·A-1)380η/s-1190
3 火箭橇动力吸振器控制策略
火箭橇服役环境恶劣复杂,火箭橇试验时以50~400 Hz 高频振动为主,振动强度大、振动能量频率范围宽,对控制系统带宽要求高。半主动开关控制策略以最大化耗散系统的振动能量为目标,通常利用最优控制理论或动力学原理得到阻尼力或阻尼系数的切换规则,进而通过系统状态切换所需的控制模态。开关控制由于只有开(最大阻尼力/阻尼系数)和关(最小阻尼力/阻尼系数)2种控制模态,不需要建立减振器复杂的力学模型,因此控制系统的实时性强,工程实现容易。
本研究以火箭橇体振动加速度为控制目标,选择开关地棚(ground hook,GH)控制和开关混合控制(mixed control,MC)进行控制仿真。
3.1 开关地棚控制
地棚控制是在天棚控制的基础上发展起来的,假想将减振器设置在主系统与惯性坐标(地棚)之间,根据主系统的垂直振动绝对速度和主系统与吸振器相对速度方向来调节减振器,使之阻尼系数为最小或最大。当主系统绝对速度与主系统对吸振器的相对速度同向时,地棚阻尼器产生作用;反之,地棚阻尼器则关断。地棚控制的表达式为:
(3)
式中:ca为磁流变阻尼器的等效阻尼系数;camax和camin分别为阻尼器最大和最小阻尼系数。在每一采样时刻,有:
(4)
虽然磁流变阻尼器是连续半主动作动器,每一采样时刻都可以根据控制律求解磁流变阻尼器逆向动力学模型得到控制电流,但对控制系统实时性要求较高,因此本研究采用开关控制策略,阻尼器最大和最小阻尼系数分别对应最大和最小控制电压,即
![]()
(5)
式中,vmax和vmin分别为磁流变阻尼器容许的最大和最小控制电压。
3.2 开关混合控制
在每一采样时刻阻尼系数可当为常数,因此动力吸振器与主系统振动绝对速度的传递函数为:
(6)
式中,s为拉普拉斯变量。
图2为传递函数的幅频响应。由图2可以看出吸振器与主系统之间关于阻尼系数ca在全频域范围内存在折衷:为了抑制吸振器的振动,在低频段需要大阻尼,在高频段需要小阻尼;反之,对于主系统,在低频段则需要小阻尼,在高频段则需要大阻尼。
考虑到在低频段,![]() 在高频段,
在高频段,![]() 开关混合控制律可写为:
开关混合控制律可写为:
(7)

图2 幅频响应
Fig.2 The frequency response of the magnitude
4 仿真分析
某型火箭橇主系统参数为m=100 kg,k=2 500 kN/m,c=2 500 Ns/m。动力吸振器质量比取为0.1,即ma=10 kg,并以火箭橇主系统振动加速度和位移峰值最小为目标,利用遗传算法得到优化的动力吸振器刚度ka=250 kN/m,阻尼系数ca=1 000 Ns/m。
火箭橇振动控制的主要目标是降低振动加速度和位移峰值,以保护被试样品和仪器不被损坏。利用频率范围为[1,200]Hz固定振幅的正弦信号对火箭橇动力吸振器激励,得到每个频率激励下主系统振动的归一化加速度和位移:
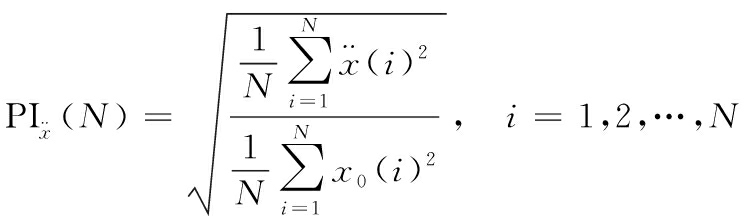
(8)
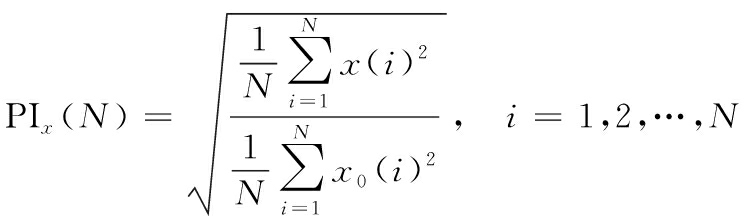
(9)
无吸振器单自由度Kelvin模型火箭橇主系统,0、2.5 A、开关地棚控制(GH)和开关混合控制(MC)下火箭橇主系统的加速度和位移的非线性频域响应如图3所示,其中开关地棚控制和开关混合控制的最大和最小电流分别设置为2.5 A和0 A。从图3可以看出,相比单自由度Kelvin模型,动力吸振器能够更显著地降低火箭橇主系统的加速度与位移响应峰值和共振响应。0、2.5 A、开关地棚控制和开关混合控制下的火箭橇主系统相比Kelvin模型,归一化加速度响应峰值分别降低了4、6.2、6.6和7.1 dB,归一化位移响应峰值分别降低了2.4、4.4、4.5和4.4 dB。
图4为扫频信号(振幅为1.5 mm,频率为0.1~200 Hz)激励下火箭橇动力吸振器主系统加速度和位移响应。与非线性频域响应分析结果相同,在扫频信号激励下动力吸振器比Kelvin模型也具有更好的减振效果,0、2.5 A、开关地棚控制和开关混合控制下的动力吸振火箭橇主系统相比Kelvin模型,加速度响应峰值分别降低了40.1%、46.2%、51.7%和58.2%,位移响应峰值分别降低了24.5%、36.4%、41.0%和42.3%。
同时从图3和图4中也能看出,混合控制相比地棚控制具有更优的“软”、“硬”阻尼协调性能。虽然二者具有基本相同的位移控制效果,但开关混合控制能够更加显著地降低火箭橇主系统的振动加速度。
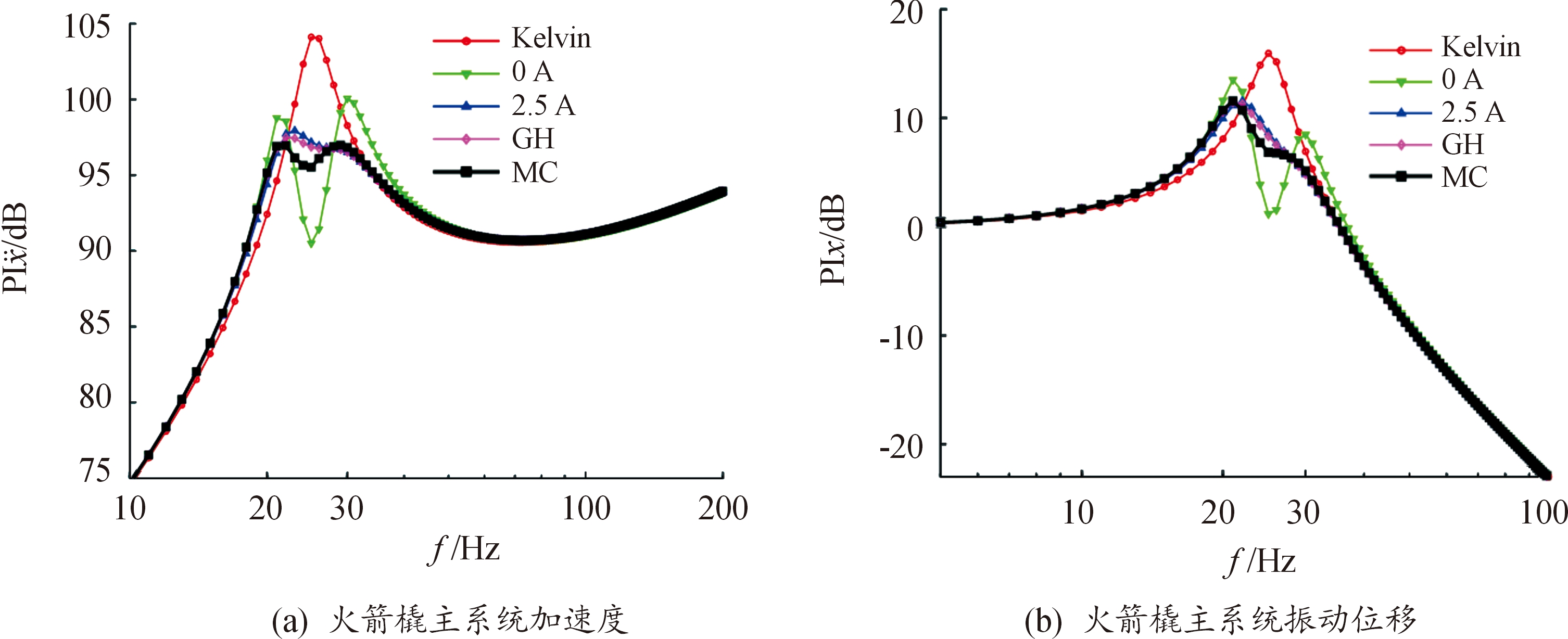
图3 非线性频域响应
Fig.3 The nonlinear frequency response
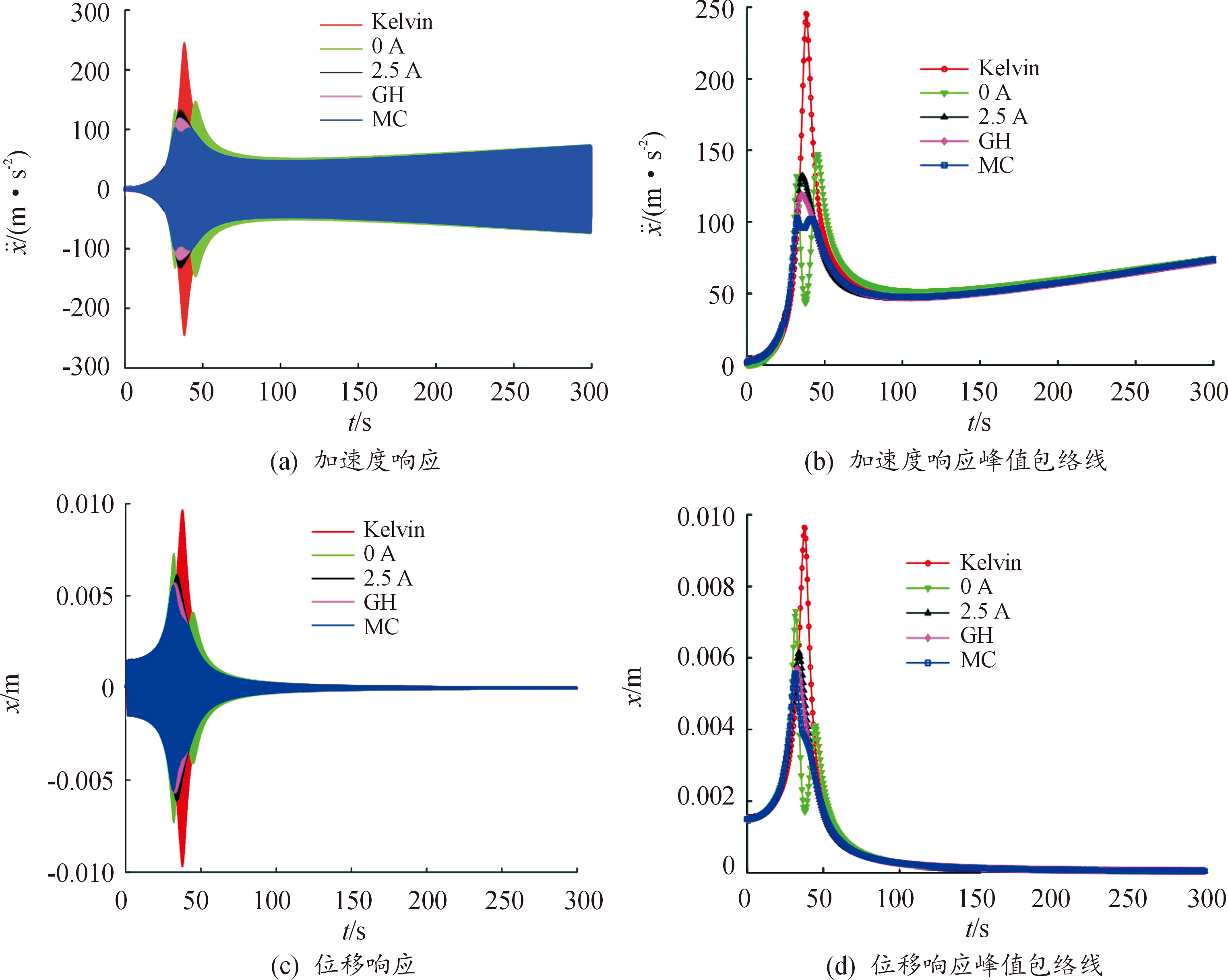
图4 扫频激励下火箭橇的时域响应
Fig.4 Time history of the rocket sled under the sweep signal excitation
5 结论
针对超声速火箭橇动态试验时大强度、宽频带恶劣振动环境,提出了一种火箭橇磁流变半主动动力吸振器,通过仿真比较分析验证了可行性。
1) 与无吸振器单自由度Kelvin模型火箭橇减振系统相比,动力吸振器对火箭橇系统的加速度峰值在非线性频域和扫频激励下分别可降低7.1 dB和58.2%,位移峰值可分别降低4.4 dB和42.3%。
2) 与开关地棚控制相比,开关混合控制在全频域内具有更优的“软”、“硬”阻尼协调性能。虽然振动位移控制效果基本相同,但能够更显著地降低火箭橇主系统的加速度。
[1] 周学文,赵项伟,杨珍,范坤.单轨火箭橇在轨动力特性数值分析[J/OL].航空动力学报:1-9[2022-05-15].DOI:10.13224/j.cnki.jasp.20210254.
Zhou X W,Zhao X W,Yang Z,et al.Numerical analysis of dynamic characteristics of monorail rocket sled on rail[J/OL].Journal of Aerospace Power,1-9[2022-05-15].DOI:10.13224/j.cnki.jasp.20210254.
[2] 顾凯旋,龚明生,王磊,等.双轨火箭橇全时程动力学仿真分析研究[J].航空工程进展,2020,11(02):245-250.
Gu K X,Gong M S,Wang L,et al.Study on full time dynamics simulation of two-track rocket sled[J].Advances in Aeronautical Science and Engineering,2020,11(02):245-250.
[3] 董龙雷,张静静,赵建平.基于冲击响应谱的高速火箭橇滑轨路谱分析[J].西南交通大学学报,2015,50(06):1170-1174.
Dong L L,Zhang J J,Zhao J P.Road spectrum analysis of highfull time dynamics simulation of two-track rocket sledspeed rocket sled rail based on shock response spectrum[J].Journal of Southwest JiaoTong university,2015,50(06):1170-1174.
[4] 郑奎涛,龚明生,蒋大鹏,等.基于火箭橇的无人机碰撞民用飞机试验技术研究[J].航空工程进展,2020,11(05):724-729.
Zheng K T,Gong M S,Jiang D P,et al.Research on the test technology of civil aircraft impacted by UAV based on rocket sled[J].Advances in Aeronautical Science and Engineering,2020,11(05):724-729.
[5] 张雨诗,余元元,赵良玉.火箭橇轨道系统有限元建模及振动特性研究[J].兵器装备工程学报,2018,39(07):56-60.
Zhang Y S,Yu Y Y,Zhao L Y.Finite element modeling and vibration characteristics of rocket sled system[J].Journal of Ordnance Equipment Engineering,2018,39(07):56-60.
[6] 余元元,叶俊杰,张雨诗,等.火箭橇轨道系统瞬态动力学特性研究[J].兵器装备工程学报,2019,40(12):205-209.
Yu Y Y,Ye J J,Zhang Y S,et al.Transient dynamics analysis of rocket sliding track system[J].Journal of Ordnance Equipment Engineering,2019,40(12):205-209.
[7] 董治华,肖军,张林锐,等.火箭橇减振系统设计[J].兵器装备工程学报,2018,39(08):15-20.
Dong Z H,Xiao J,Zhang L R,et al.Vibration damping system design for rocket sled[J].Journal of Ordnance Equipment Engineering,2018,39(08):15-20.
[8] 丁春全,周昊,冯志杰,等.火箭橇试验减振系统力学仿真研究[J].舰船电子工程,2012,32(08):87-89,112.
Ding C Q,Zhou H,Feng Z J,et al.Studies on mechanics simulation of a rocket pulley reduce-oscillation system[J].Ship Electronic Engineering,2012,32(08):87-89,112.
[9] 郎君,申永军,杨绍普.一种半主动动力吸振器参数优化及性能比较[J].振动与冲击,2019,38(17):172-177.
Lang J,Shen Y J,Yang S P.Parametric optimization and performance comparison for 2 semi-active Voigt DVAs[J].Journal of Vibration and Shock,2019,38(17):172-177.
[10] Koo J H,Ahmadian M,Setareh M,et al.In search of suitable control methods for semi-active tuned vibration absorbers[J].Journal of Vibration & Control,2004,10(2):163-174.
[11] Shi A,Shen Y,Wang J.Parameter optimization of a grounded dynamic vibration absorber with lever and inerter[J].Journal of Low Frequency Noise,Vibration and Active Control,2022,41(2):784-798.
[12] Etedali S,Zamani A A.Semi-active control of nonlinear smart base-isolated structures using MR damper:sensitivity and reliability analyses[J].Smart Materials and Structures,2022,31(6):065021.
[13] Dominguez A,Sedaghati R,Stiharu I.Modelling the hysteresis phenomenon of magnetorheological dampers[J].Smart Materials and Structures,2004,13(6):1351.
[14] Wang X L.Semi-active adaptive optimal control of vehicle suspension with a magnetorheological damper based on policy iteration[J].Journal of Intelligent Material Systems and Structures,2018,29(2):255-264.
[15] Liu Y,Zuo L.Mixed skyhook and power-driven-damper:A new low-jerk semi-active suspension control based on power flow analysis[J].Journal of Dynamic Systems,Measurement,and Control,2016,138(8):1-10.