0 引言
薄壁球壳结构具有质轻、跨度大、承载力高等多种优点。故被广泛应用于航天、航空、航海等交通运输工具以及机械、化工、建筑等工程领域中。薄壁球壳能够同时承载薄膜力和弯矩,具有优异的力学性能。早在20世纪60年代,研究者们就开始了对薄壁球壳结构在载荷作用下的动力响应及变形特性进行研究。最初的研究始于固支球壳结构受刚性板压缩的准静态分析,如Lekie F A[1]进行了薄壁半球壳的大变形研究,即典型的后屈曲问题。Updike[2-3]用2个刚性版挤压半球壳,讨论了半球壳出现的大变形问题。Gupta[4-7]对准静态压缩和动态冲击下的动态响应进行了实验和数值模拟研究,实验中测量了滚动塑性铰的半径然后根据能量吸收理论得到了理论模型,分析了球壳在各种加载形式下的变形形式、压溃机理、吸能能力和径厚比对变形模态的影响。Gupta指出,在落锤加载条件下,薄壁半球壳存在局部压平、内凹形成和内凹多边形的出现3种变形模态,产生不同变形模态的原因是径厚比。杨桂通、宁建国等[8-9]研究了球形薄壳在冲击荷载作用下的超临界变形及其动态响应。他们注意到,壳体的大变形是载荷作用点周围形成近似于等距变形的凹陷,并在凹陷的边缘处薄壁壳开始突然弯曲,出现隆起。并给出了扁球壳中心最大凹陷半径关于冲击荷载的近似表达式。然而以上研究主要集中在准静态加载或是动态加载条件下单个薄壁半球壳的塌陷行为,对于复合半球壳的动态加载行为,相关研究却并不多见。
近年来结构耐撞性被学术界广泛关注并得到了迅速发展,对薄壳的抗冲击和吸能能力要求也随之增加。结构的轻量化设计需求促生了比吸能大、强度高的材料的出现,泡沫铝作为一种新型多功能吸能材料,具有低密度、高比强、高阻尼、吸声吸能等特性,在工程界中被广泛用于结构填充材料,可有效提高结构的承载能力和吸能特性[10-13]。桂良进等[14]对轴向压缩以及轴向冲击下泡沫铝填充圆管的吸能特性进行了研究,系统地分析了结构的几何尺寸、材料参数、加载速率对吸能的影响,并对结构进行了优化设计。Hou[15-16]通过数值模拟的方法对泡沫铝填充方管进行了轴向冲击的耐撞性研究,并以方管厚度和填充泡沫铝的相对密度为参数进行了多目标优化。Santosa[17-18]通过实验和数值模拟的方法对轴向压缩下的泡沫铝填充方管的力学响应进行了研究,在模拟中用动态显式分析法模拟准静态实验,所预测出的变形模式以及压溃力,与实验得到的结果吻合较好。
泡沫金属材料与传统的致密金属组成的复合结构具有优异的力学、热学和声学性能,常见的泡沫金属复合结构以平板型或圆弧形为主,而在空间飞行器、客机、船舶等装备的端部区域(见图1),为在有限质量条件下提高端部区域的防护性能,采用泡沫铝填充半球壳结构能够在保证结构轻量化的同时,提高局部区域的承载能力、抗变形能力和冲击吸能等综合性能。

图1 泡沫铝填充半球壳应用场景
Fig.1 Foam filled thin-walled hemisphere application
然而,上述关于泡沫铝填充结构的研究大多集中在方管或圆管等管类结构,对于填充泡沫铝的薄壁半球壳在动态加载条件下变形行为却研究的很少。
本文中在前人对薄壁半球壳和泡沫填充结构分别研究的基础上,提出一种泡沫填充半球壳结构,采用数值模拟方法研究了该结构在落锤冲击作用下的变冲击动力学行为,系统分析了径厚比等参量对结构耐撞性和吸能特性的影响,研究了该填充结构的变形模态,为填充半球类结构的应用和进一步探究提供参考。
1 有限元模型及验证
本文中采用有限元软件LS-DYNA来模拟泡沫填充薄壁半球壳结构在落锤冲击作用下的变形模态和吸能特征。半球壳采用各向同性强化的弹塑性不锈钢材料。泡沫铝选用LS-DYNA材料库中材料64#MAT_CRUSHABLE_FOAM材料模型,该模型认为材料各项同性,弹性模量在计算过程中与给定的应力/应变曲线在弹性阶段的斜率一致,沿单一方向压缩时泊松比为0,拉伸时强化行为与弹性-理想塑性材料相似。材料模型的相关参数取值如表1[23-25]所示。相对密度是泡沫铝的重要参数,是指泡沫铝密度与铝基材密度之比,本文中采用3种相对密度(10%,15%和20%)的泡沫铝准静态应力-应变曲线作为DIFINE_CURVE,如图2所示[23]。落锤选用刚体单元,采用集中质量法赋予刚体质量55 kg。半球壳半径90 mm,采用四边形shell163单元来模拟,薄壁壳边界条件为下端固定。泡沫选用四面体solid164单元建模,边界条件为下端固定。落锤与半球壳间采用surface_to_surface面面接触,泡沫铝与半球壳间采用surface_to_surface面面接触以避免冲击过程中的相互渗透,薄壁半球壳和泡沫铝均采用single_surface单面接触。图3为有限元网格模型图。
表1 CURSHABLE_FOAM材料参数
Table 1 Parameters of CURSHABLE_FOAM
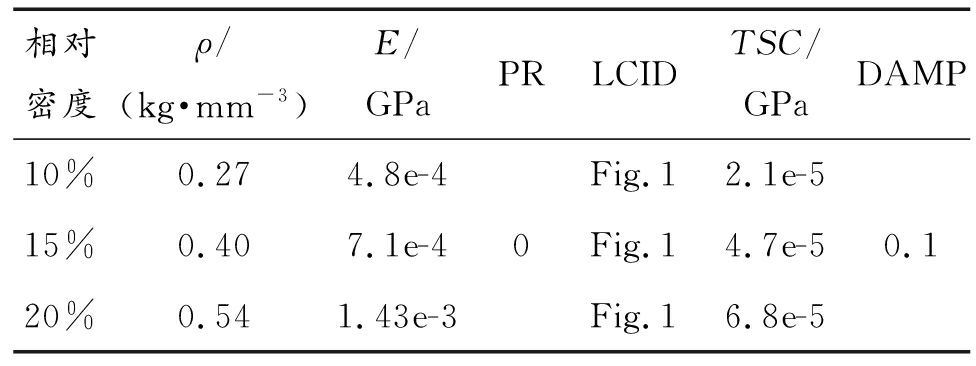
相对密度ρ/(kg·mm-3)E/GPaPRLCIDTSC/GPaDAMP10%0.274.8e-415%0.407.1e-420%0.541.43e-30Fig.12.1e-5Fig.14.7e-5Fig.16.8e-50.1

图2 泡沫铝压缩应力-应变曲线
Fig.2 Stress-strain curves of aluminum foam under compression

图3 有限元模型网格模型
Fig.3 Finite element mesh model
首先验证有限元模型的有效性。受限于球型泡沫铝试样的加工精度,采用圆柱形试样进行实验,落锤试验采用Instron9450型落锤实验机(见图4),试样尺寸与实验参数如表2所示。其中试样1和试样2为内空圆柱壳体,试样4为泡沫铝填充圆柱壳体。圆柱形壳体直径76 mm,长度90 mm,壳体材质为304级不锈钢,其密度7 930 kg/m3,屈服强度220 MPa,弹性模量192 GPa,泊松比0.3。试样底端用专用夹具与实验机固定,落锤锤头为直径10 mm的圆柱形,锤头高度30 mm,材质为高强度钢,锤头形状如图4所示。实验所用泡沫铝型号为RPML-C1D0.5,为熔体铸造闭口泡沫铝,发泡原材料为1系纯铝,发泡后泡沫铝密度0.53~0.54 g/cm3,泡沫铝孔径3~5 mm,泡沫铝试样形状与开孔尺寸如图4所示。
表2 落锤实验参数
Table 2 Experiment parameters of drop weight test

式样编号壳体直径/mm壳体长度/mm壳体厚度/mm泡沫铝密度/(kg·m-3)落锤质量/kg落锤初速度/(m·s-1)176901-7.522 53276901-9.522 53.54769015309.522 53.5

图4 落锤冲击实验装置及试样
Fig.4 Drop weight impact testing machine and specimens
内空圆柱壳体(试样1和试样2)侧向冲击的试验与数值模拟接触力对比如图5(a)所示。泡沫铝填充壳体(试样4)接触力对比如图5(b)所示。数值模拟与试验曲线趋势相同,峰值力基本一致,吻合良好。图6—图8分别为试样1、试样2和试样4实验与数值模拟变形情况对比。对于内空壳体,不锈钢壳体中心向内凹陷,形成与锤头大小一致的冲击痕迹,圆柱壳体竖直方向向内凹陷,形成沿长度方向的凹痕,凹痕左右凸起,壳体变形沿竖直方向左右对称。泡沫铝填充壳体顶部中心区域受落锤冲击向内凹陷,塑性变形向周围辐射扩散,壳体变形量明显小于非填充试样,未形成沿长度方向的塑性变形。
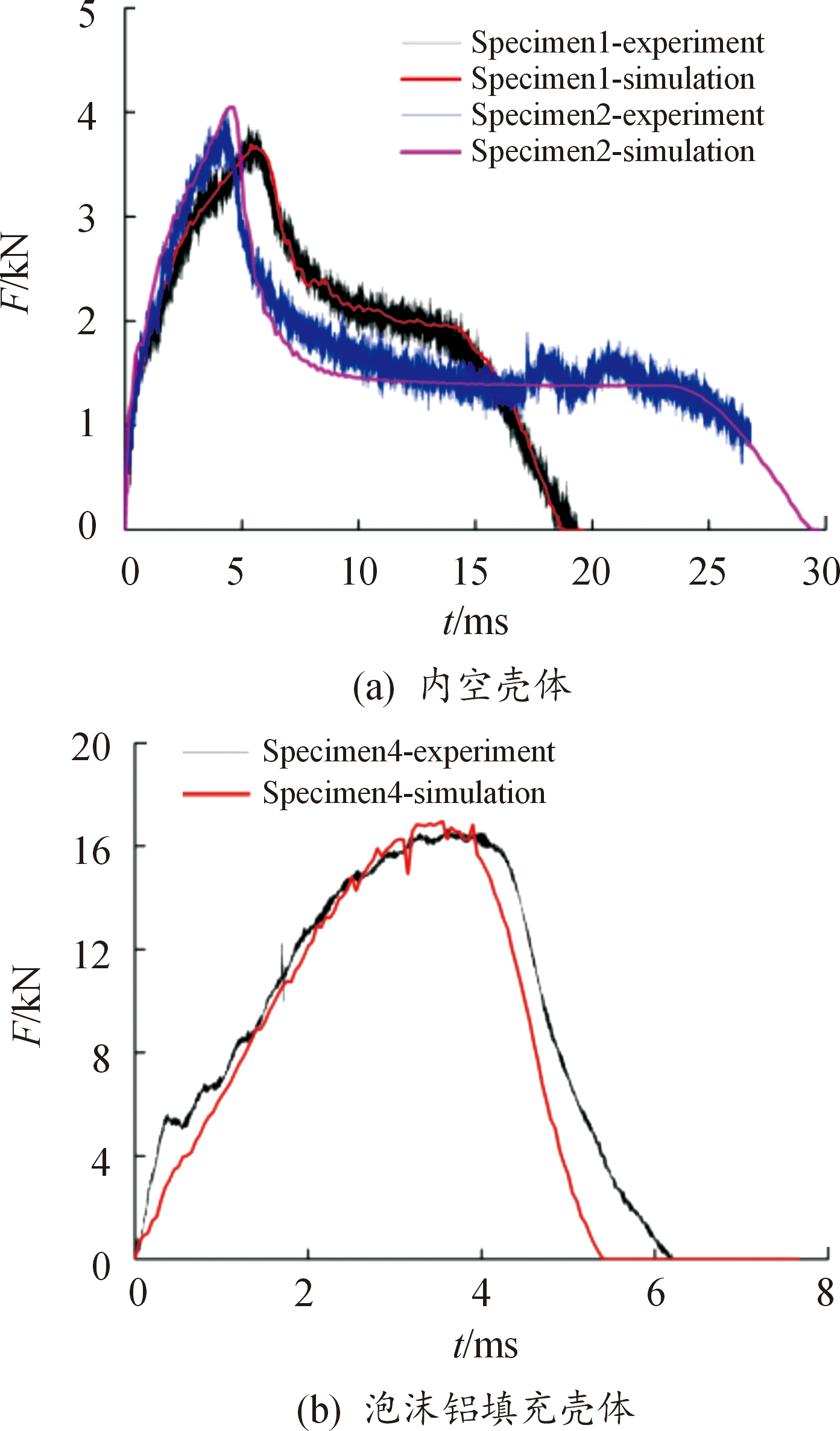
图5 圆柱壳侧向冲击仿真与实验接触力时程曲线
Fig.5 Impact force comparison of test and simulation results
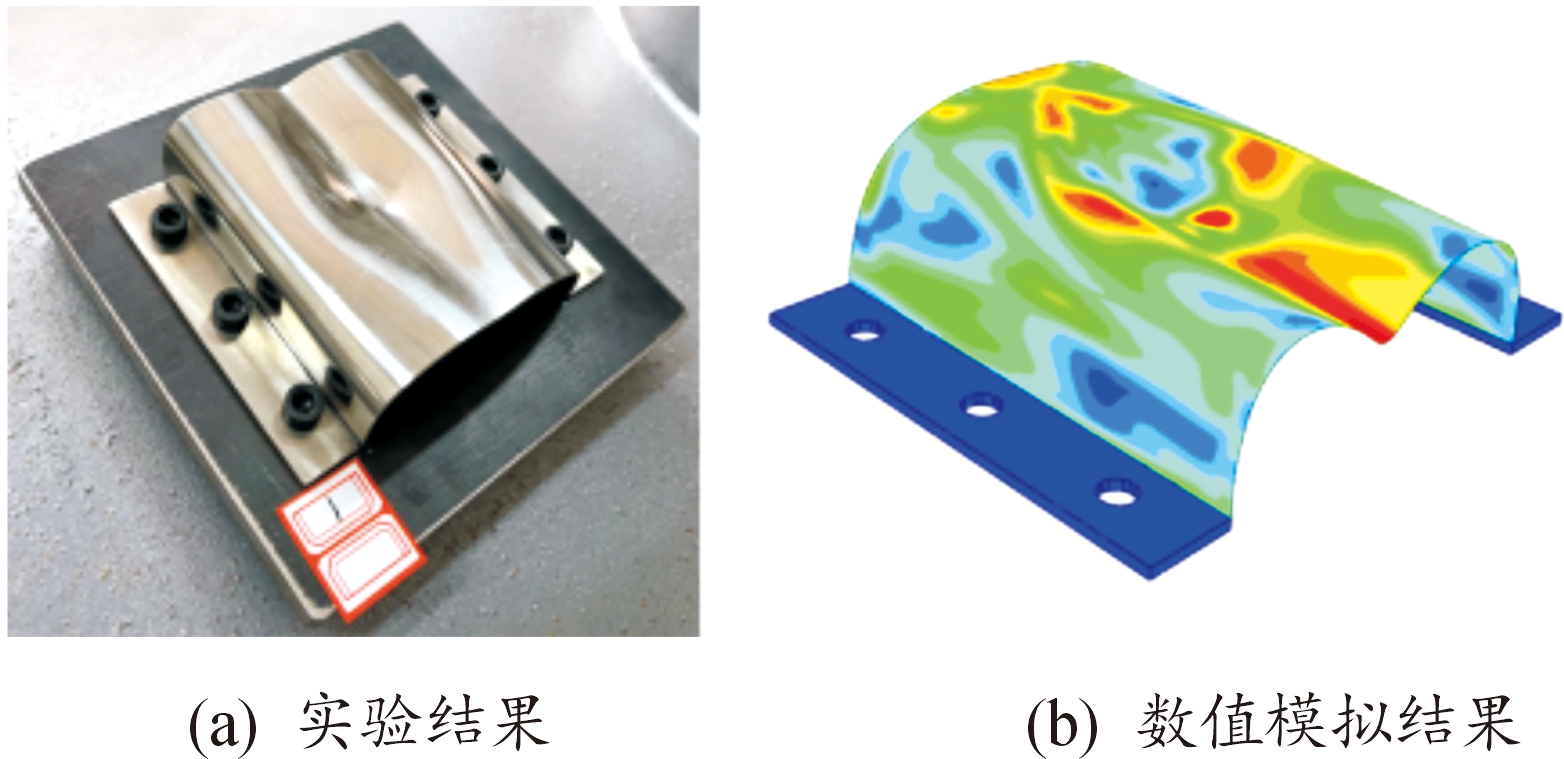
图6 试样1变形模式
Fig.6 Deformation mode of specimen 1
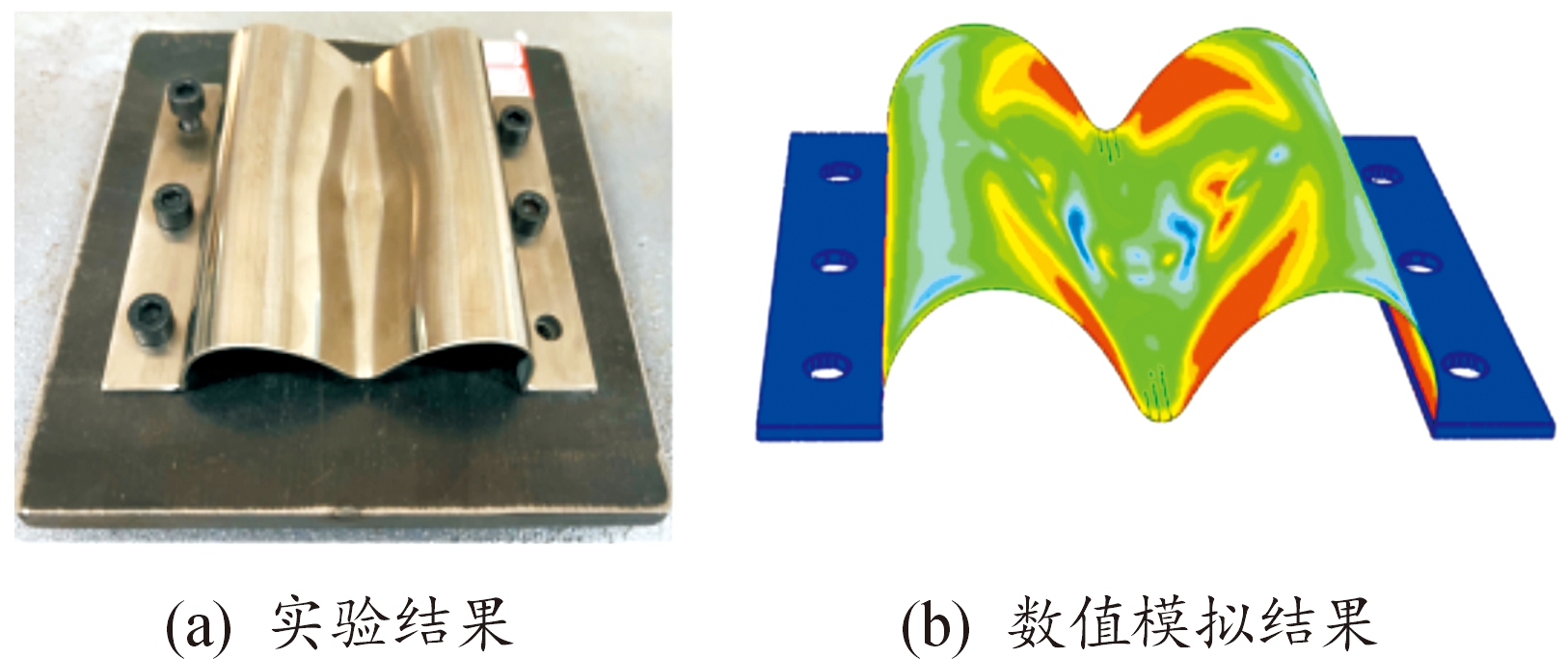
图7 试样2变形模式
Fig.7 Deformation mode of specimen 2
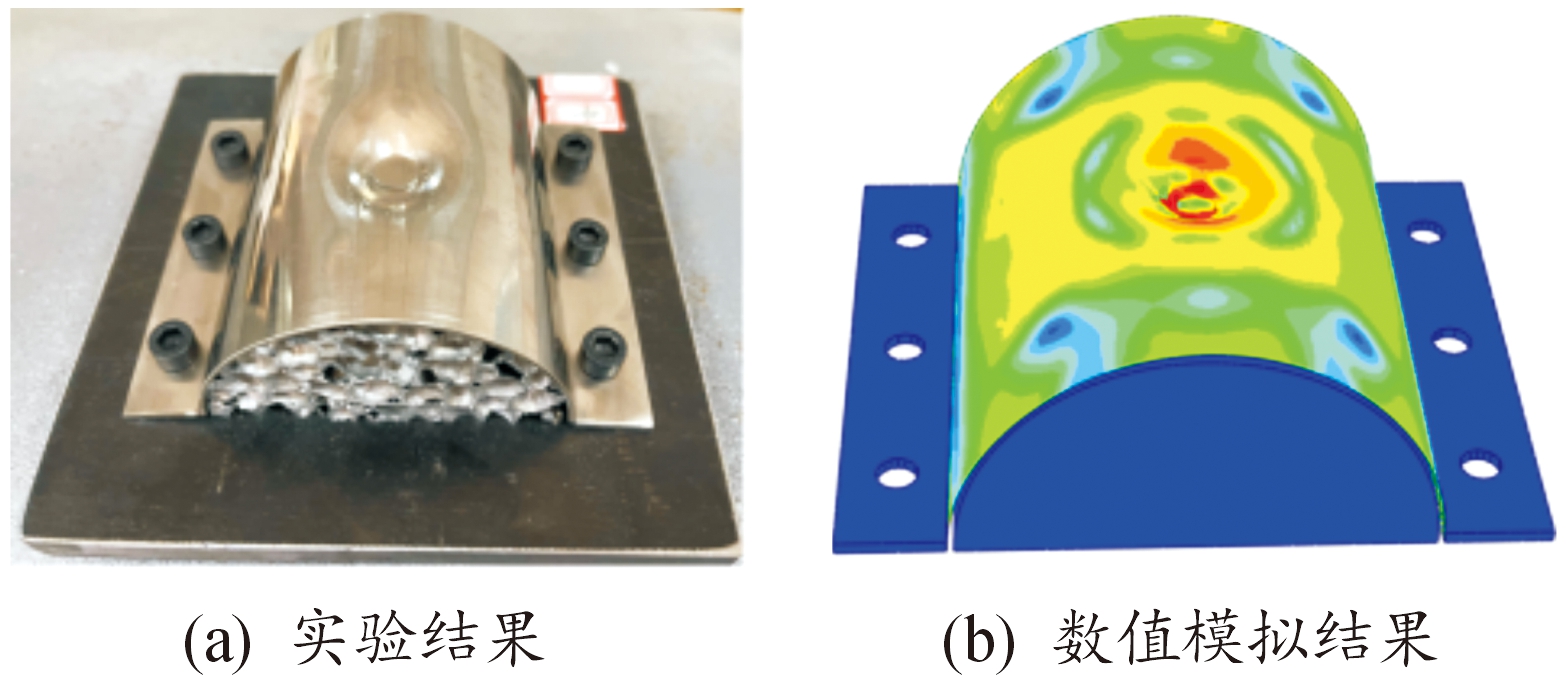
图8 试样4变形模式
Fig.8 Deformation mode of specimen 4
填充泡沫铝顶部中心区域受冲击作用向内压缩产生凹坑,变形区域与变形形貌与外壳体基本一致,如图9所示。落锤冲击区域四周由于壳体变形对泡沫铝形成挤压,压缩量由边缘向冲击点渐变增大,如图10所示。仿真计算泡沫铝变形区域最大压缩量7.9 mm,卸载后剩余压缩量为6.4 mm,实验测得泡沫铝压缩量为6.0 mm,填充泡沫铝在落锤冲击下的仿真计算结果与实验结果基本吻合。
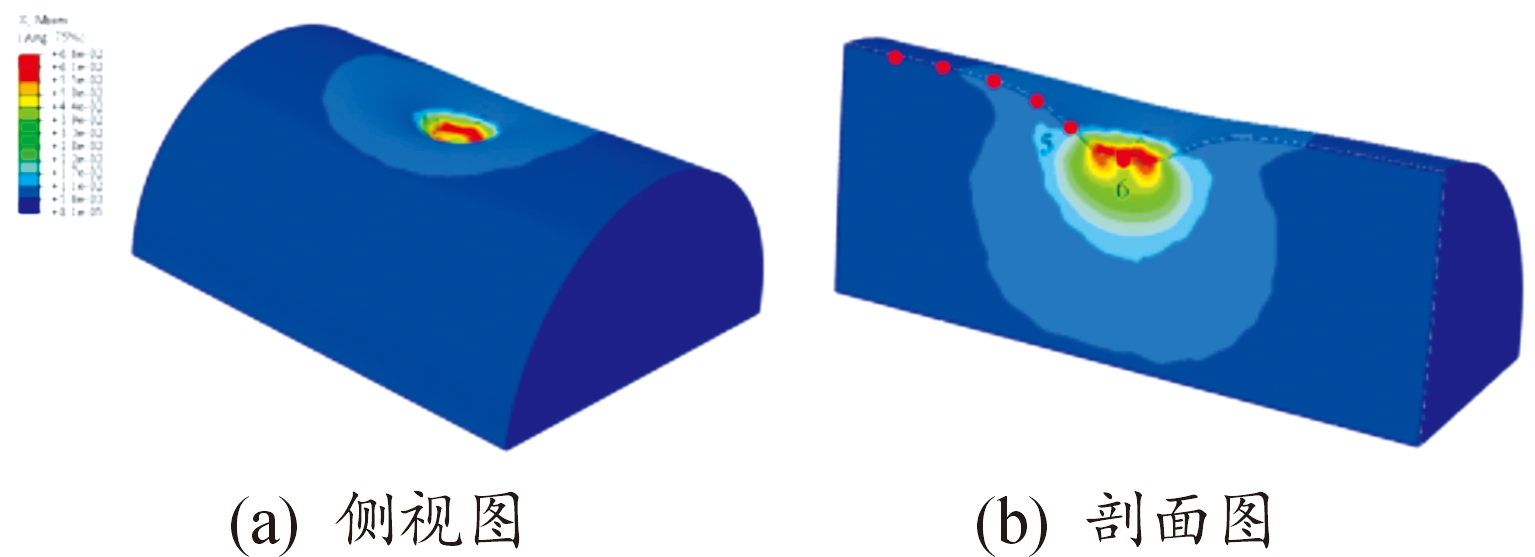
图9 填充泡沫铝变形结果
Fig.9 The deformation of foam aluminum
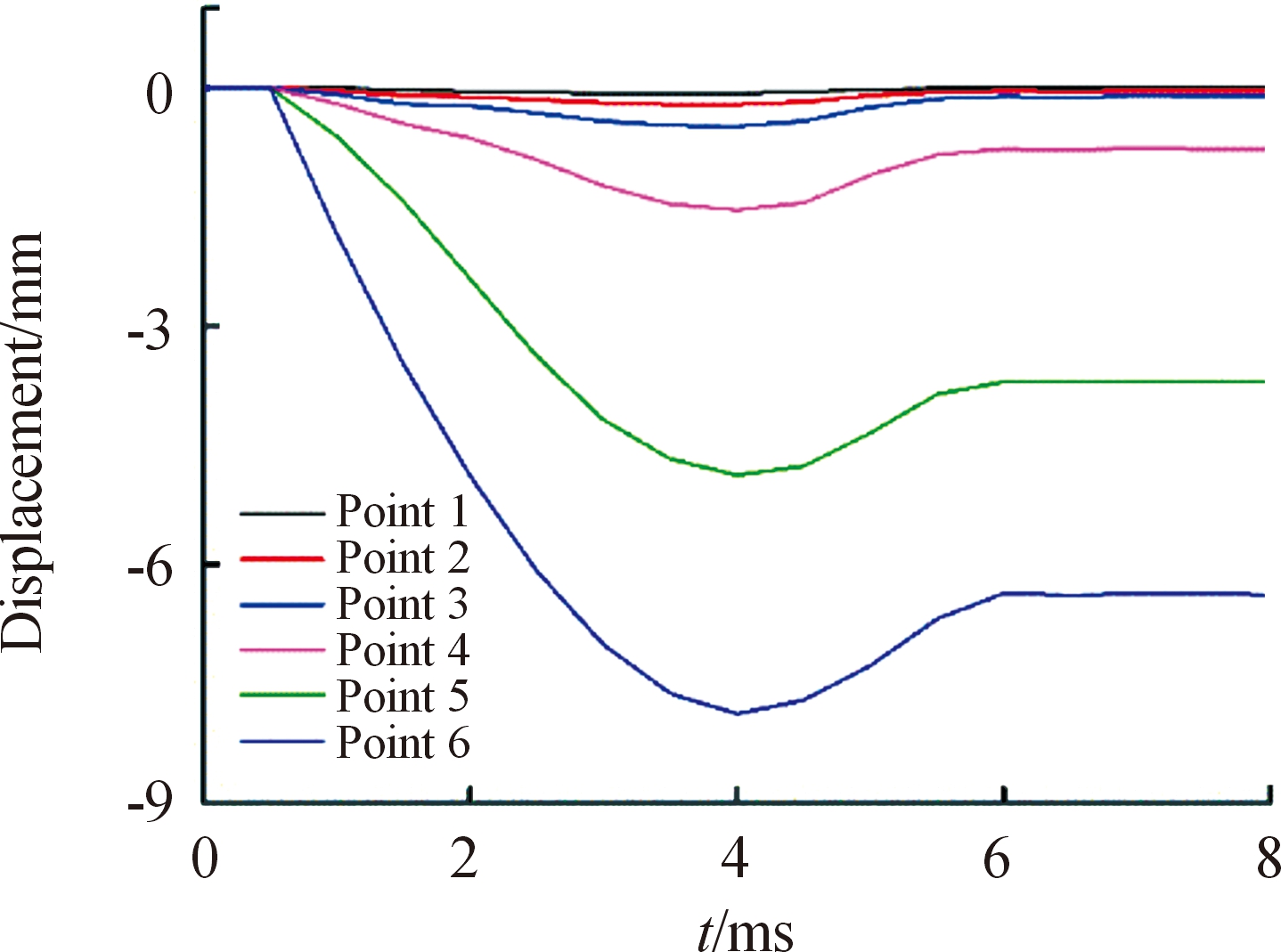
图10 填充泡沫铝变形时程曲线
Fig.10 The time history curves of foam aluminum displacement
有限元模型与实验结果在接触力时程曲线、变形模式以及变形量等方面具有良好的一致性,以此验证当前有限元模型的有效性,在接触算法、约束条件、材料本构不改变的条件下,可用于半球形结构的数值模拟分析。
2 对比分析
首先对泡沫填充半球在落锤冲击作用下的的变形模态进行数值模拟,其中,落锤质量55 kg,半球壳壁厚1 mm,泡沫铝相对密度20%。同时对内空薄壁半球壳的变形模态进行模拟作为对比,其中内空半球的半径、壁厚以及加载条件与泡沫填充半球相同。
图11为内空半球壳与泡沫填充半球壳分别在落锤下落高度4 m,半球壳厚度为1 mm的参数条件下,利用数值模拟得到的变形图。同一初速度和落锤质量下,内空半球响应时长为25 ms,泡沫铝填充半球响应时长为11.6 ms。
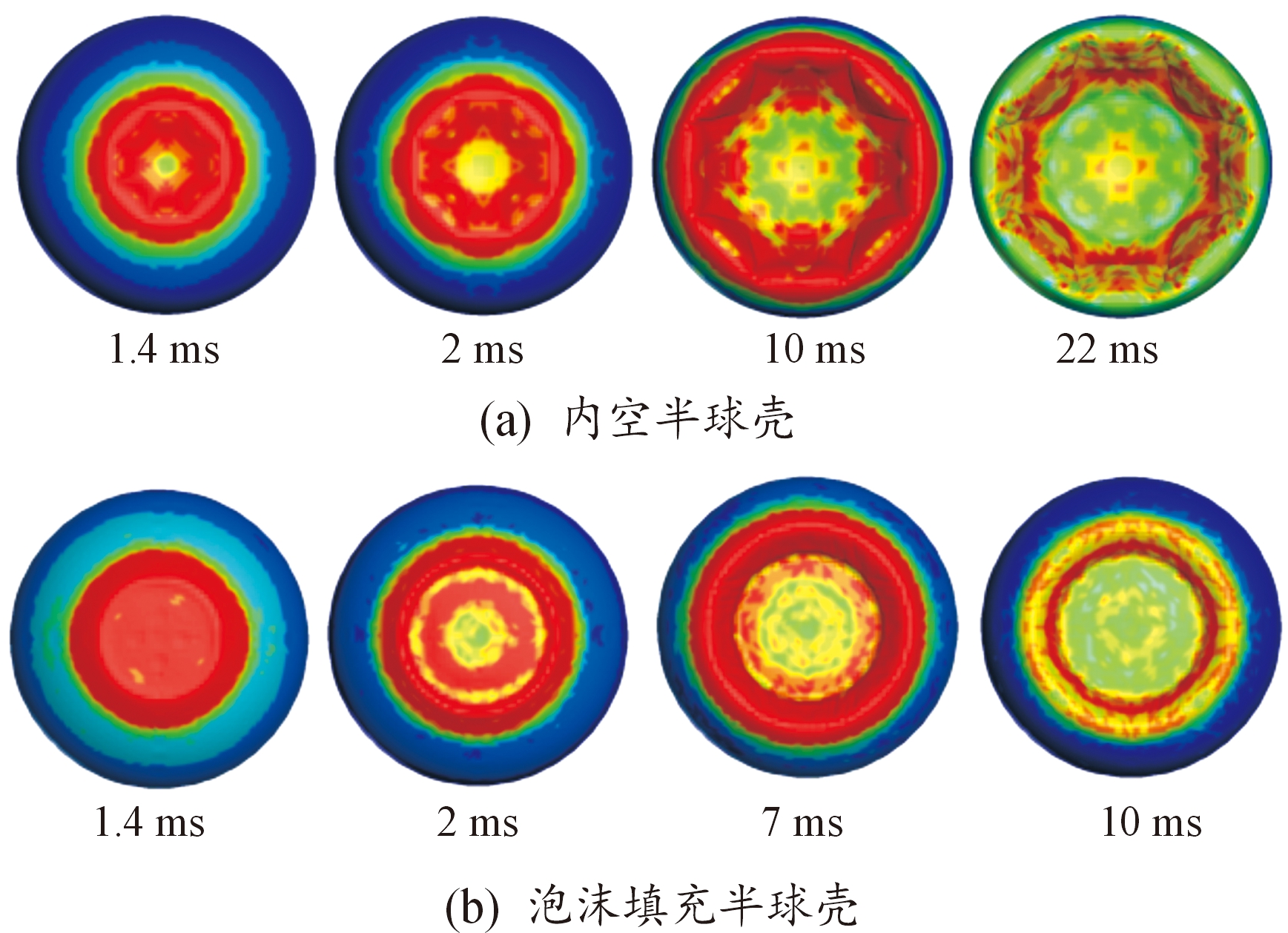
图11 内空半球壳与泡沫半球壳相同载荷条件下变形模态对比
Fig.11 Comparison of deformation diagrams in the same load condition between foam-filled hemisphere and hollow hemisphere
其中,图11(a)为内空半球变形图,由图可知内空半球在落锤冲击作用下经过如下几个阶段:局部压平,向内凹陷,凹陷边缘出现隆起并形成塑性铰,内凹扩大,最后形成多边形。从应力角度分析,应力仅开始阶段分布于整个受压区域,随后塑性铰形成的受压边缘应力逐渐增大,最后在多边形形成的区域出现较大的应力集中,由此可知,内空半球在加载过程中应力分布明显不均匀,结构利用不充分,有明显的应力集中发生,并且结构的变形程度较大,不利于承受较大荷载。图11(b)为泡沫填充半球壳变形图,其变形阶段可分为:局部压平,冲击边缘隆起形成塑性铰,塑性铰增大,冲击区域压实。从应力角度分析,冲击初始阶段应力分布于整个受压区域,随后在塑性铰的产生、发展至成型过程中,应力在塑性铰处均匀分布。与内空半球壳相比,泡沫填充半球向内凹陷幅度小,与落锤的冲击接触区域受力更加均匀,能够充分利用外壳材质的塑性变形能力,形成和发展塑性铰,降低变形量。
图12给出了泡沫填充半球壳与内空半球壳的接触力、动能以及顶点位移时程曲线。其中图12(a)为碰撞力-时间曲线图,由图可知,泡沫填充半球壳产生的接触力明显大于内空半球壳,时间历程短于内空半球壳,冲击能量很快被吸收。泡沫填充半球的接触力曲线出现2个极值点。锤头接触球壳后,球壳与锤头接触范围内压平,随后出现塑性铰,塑性铰区域刚度降低,故接触力先增大后减小;塑性铰发展至一定阶段后,球壳整体被压缩,填充区域压实,接触力上升至锤头速度为0。图12(b)给出了2种结构壳体内能的吸收曲线,对于内空半球结构,壳体的塑性变形吸收了绝大部分的冲击能量,约占总冲击能量的98.6%;泡沫填充半球结构的冲击能量,一部分由壳体塑性变形吸收,约占总冲击能量的40.07%,另一部分由填充材料的塑性变形吸收,约占总冲击能量的56.68%。图12(c)对比了2种结构在冲击过程中半球壳最高点的顶点位移。内空半球壳形成塑性铰后发生内凹,顶点位移大并且长时程,卸载后位移几乎无恢复;泡沫填充半球结构顶点位移约为内空半球的1/3,卸载后顶点位移有约2 mm的恢复。说明泡沫填充结构在控制结构变形方面效果十分明显。
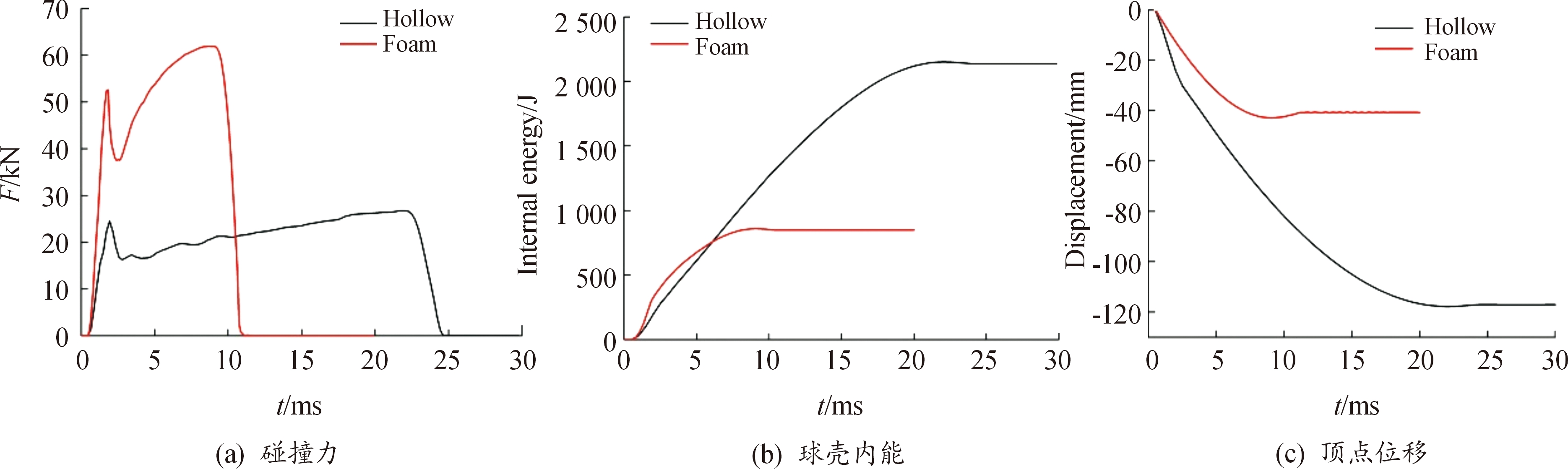
图12 泡沫填充半球壳与内空半球壳吸能特性曲线
Fig.12 Comparison of crashworthiness performance between foam-filled hemisphere and hollow hemisphere
3 讨论
3.1 径厚比的影响
给出径厚比公式R=D/T,其中:R为径厚比;D为半球壳直径;T为半球壳厚度。为了研究径厚比对泡沫填充半球壳吸能性能的影响,分别取薄壁壳厚度为0.8、1.4、2.0、2.6 mm,泡沫铝相对密度为20%,在相同落锤质量55 kg,下落高度5 m的条件下进行数值模拟。得到每种厚度下碰撞力、泡沫铝内能和顶点位移的时间历程曲线如图13所示。
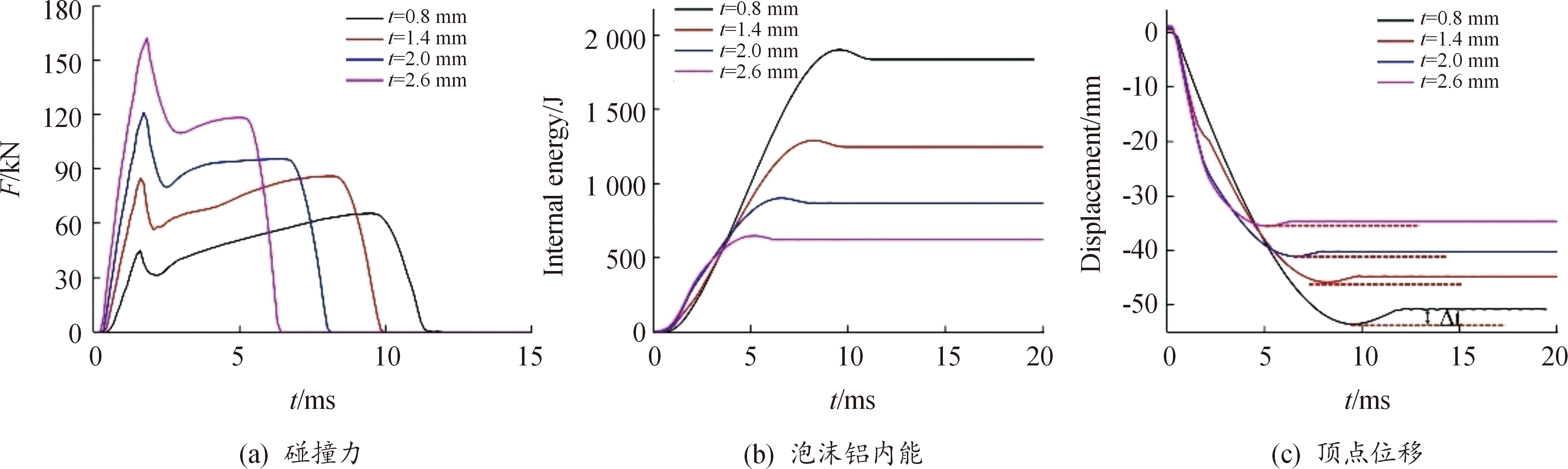
图13 不同径厚比泡沫填充半球壳吸能特性曲线
Fig.13 Comparison of crashworthiness performance with different diameters to wall thickness ratios
图13(a)给出了不同半球壳厚度下碰撞力-时间曲线图。4种厚度的时程曲线均有2个极值点,壳体越厚,承载能力越强,首个极值点越高,而极值点对应的时刻基本一致,表明在此阶段主要抵抗冲击的部分为金属壳体。图13(b)为填充泡沫铝内能随时间变化的能量吸收曲线。填充泡沫铝的能量吸收经历了线性上升和弹性恢复阶段,最后保持定值。由于4种厚度填充半球的加载条件一致,故总能量相同,泡沫铝吸能随壳体厚度的增加而减少。外壳体壁厚为0.8 mm时,泡沫铝内能为1 840 J,占冲击总能量的71.07%,壁厚为2.6 mm时,泡沫铝内能为622 J,占冲击总能量的24.09%。图13(c)为5种厚度下的顶点位移曲线,壳体厚度越大,顶点位移越小,时间历程也越短,在能量一定的情况下,承载能力也越强。随着壳体厚度的减小,其顶点恢复位移越大,位移恢复能力呈现随厚度增加呈现递减的趋势。图中Δt的值分别为2.74、1.06 、0.826和0.802 mm。
3.2 泡沫相对密度的影响
铝的密度取2 700 kg/m3,取相对密度分别为10%、15%和20%,从而泡沫铝密度分别为270 、405 和540 kg/m3。在相同落锤质量55 kg,落锤下落距离4 m,半球壳壁厚1 mm的条件下进行数值模拟,得到的结果如图14所示。
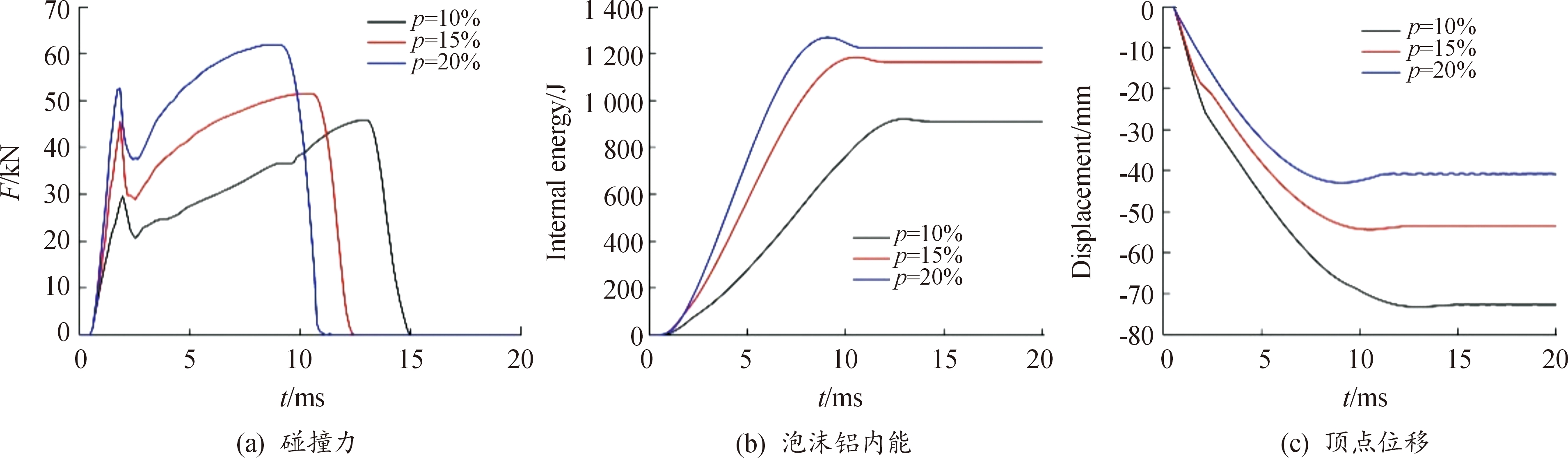
图14 不同泡沫相对密度填充半球壳吸能特性曲线
Fig.14 Comparison of crashworthiness performance with different relative densities of aluminum foam
图14(a)为不同泡沫铝相对密度的碰撞力-时间曲线,从中可以看出,提高泡沫铝的密度可以提高结构的承载力峰值,减少冲击时程。图14(b)为填充泡沫铝的能量吸收曲线。能量吸收能力总体随泡沫铝相对密度增大而增大。但在总能量一定的前提下,相对密度由10%~15%的能量吸收差值明显大于15%~20%。10%、15%和20%的泡沫铝相对密度最终内能分别为910、1 163和1 225 J,差值分别为253 J和63 J。计算得到10%~20%相对密度的泡沫铝吸收内能占总能量的比例分别为44.2%,56%和59.1%。表明泡沫铝能量吸收能力可能存在上限值。图14(c)为不同泡沫铝相对密度下的顶点位移时程曲线,顶点位移体现结构的抗变形能力,填充泡沫铝相对密度越高,承载能力提高,相应顶点位移降低,球壳向内凹陷程度越小。
3.3 不同加载初速度的影响
为了探讨不同冲击速度产生的吸能影响,选取5种落锤下落高度,分别为1、2、3、4和5 m,对应冲击初速度分别为:4.43、6.26、7.67、8.85和9.90 m/s。在落锤质量55 kg,半球壳壁厚1 mm,填充泡沫铝相对密度15%的条件下进行数值模拟,结果如图15所示。
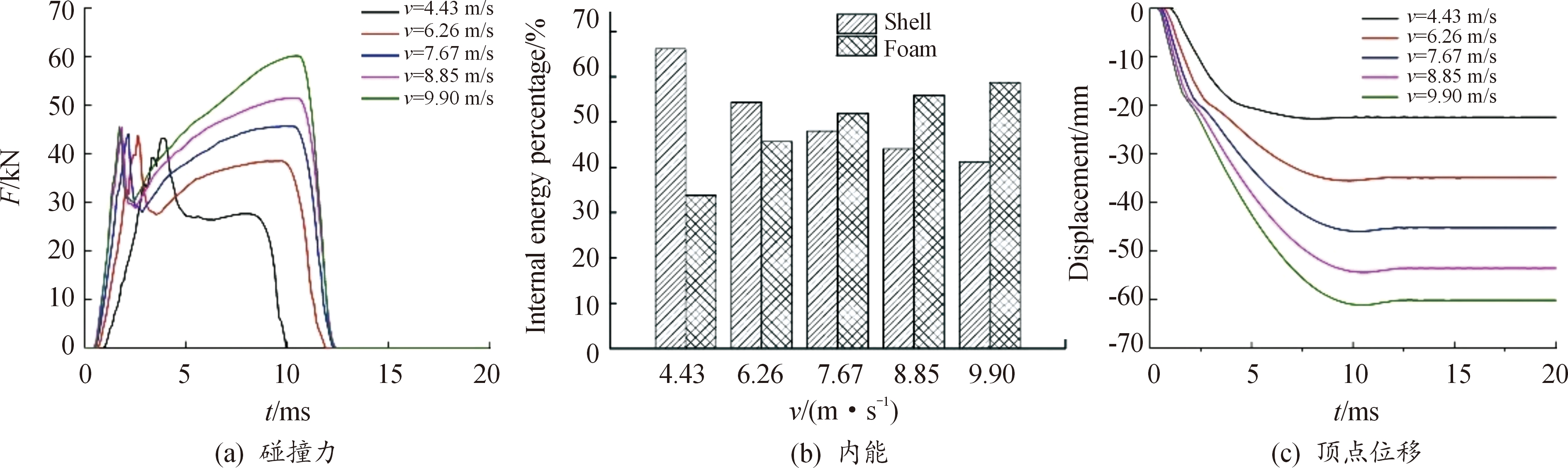
图15 不同加载初速度下填充半球壳吸能特性曲线
Fig.15 Comparison of crashworthiness performance with different initial velocities
图15(a)所示的是不同加载初速度下接触力时程曲线,不同落锤下落高度对于抗冲击结构而言意味着不同冲击能量。图15(a)中接触力曲线第一个极值点基本一致,表明第一个极值点是在形成塑性铰阶段,与结构整体刚度和塑性变形能力有关,与冲击能量无关。接触时程曲线第二个极值主要与填充材料的抵抗变形能力,载荷越大,泡沫铝压缩量增大,越容易压实,相应接触力随泡沫铝压实程度增加而提高。图15(b)为壳体和泡沫铝吸能占比柱状图,落锤冲击能量较低时,壳体吸能比重高于填充泡沫铝,随着冲击载荷增加,壳体吸能比重降低,填充泡沫铝比重上升,落锤下落速度为7.67 m/s后,填充材料吸能比重高于壳体。图15(c)所示不同落锤下落高度下顶点位移随时间的变化曲线。可以看出,初速度越大,冲击载荷能量越高,结构需要更长的时间以及更大的变形抵消冲击能量,顶点位移也就越大。
图16给出了落锤下落高度1 m(冲击初速度4.43 m/s)时3种填充泡沫铝相对密度的变形模态。相对密度为10%时,不锈钢壳体向外隆起形成塑性铰,塑性铰直径与落锤直径一致,落锤区域向内凹陷,且在凹陷区域内由塑性铰内边缘向球壳中心汇集形成4条对称凹痕,凹痕周围外凸,并在凹痕与塑性铰交界处产生应力集中。在冲击能量不变的条件下,提高泡沫铝相对密度,凹陷深度逐渐减小,凹陷区域内4条凹痕逐渐变浅,但交界处仍存在应力集中。泡沫铝相对密度20%时,塑性铰仍存在,但塑性铰内区域趋于平坦,无凹痕与应力集中产生。
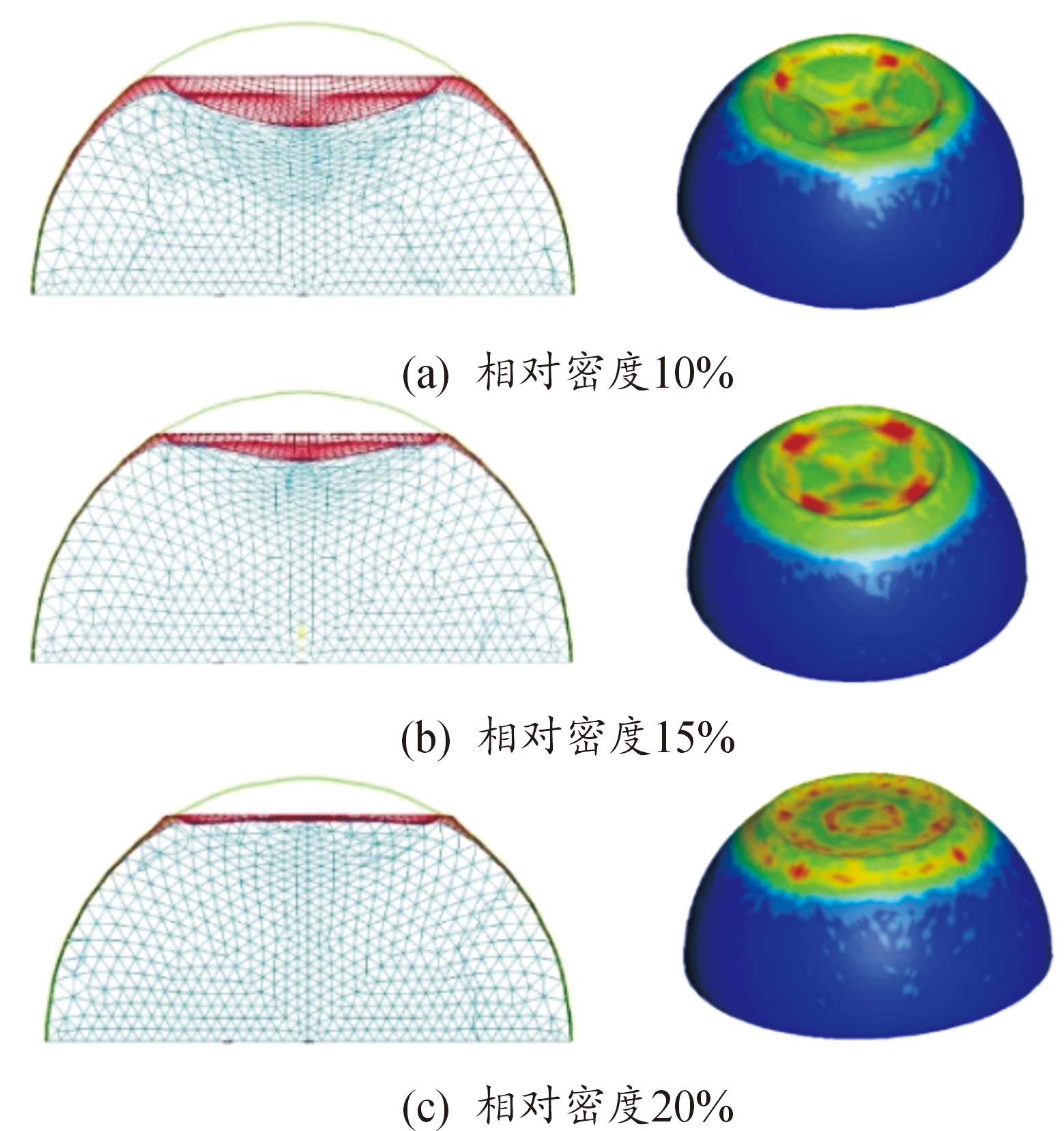
图16 冲击速度4.43 m/s时不同泡沫铝相对密度下半球结构变形模态图
Fig.16 Comparison of deformation modes with different relative densities
图17给出了落锤下落高度5 m(冲击初速度9.90 m/s)时3种填充泡沫铝相对密度的变形模态。相对密度为10%时,壳体向内凹陷形成塑性铰,并出现与锤头直径等长的凹坑,凹坑内变形模式与图16(a)一致,存在4条对称凹痕。凹坑与塑性铰的连接区域形成与图11(a)中形状相近的八边形凹痕,但由于内部泡沫铝的能量吸收和填充作用,八边形凹痕浅而平滑。随着泡沫铝相对密度的增加,八边形凹痕消失,塑性铰逐渐趋于平滑,凹陷区域趋于平坦,内部无凹痕与应力集中。
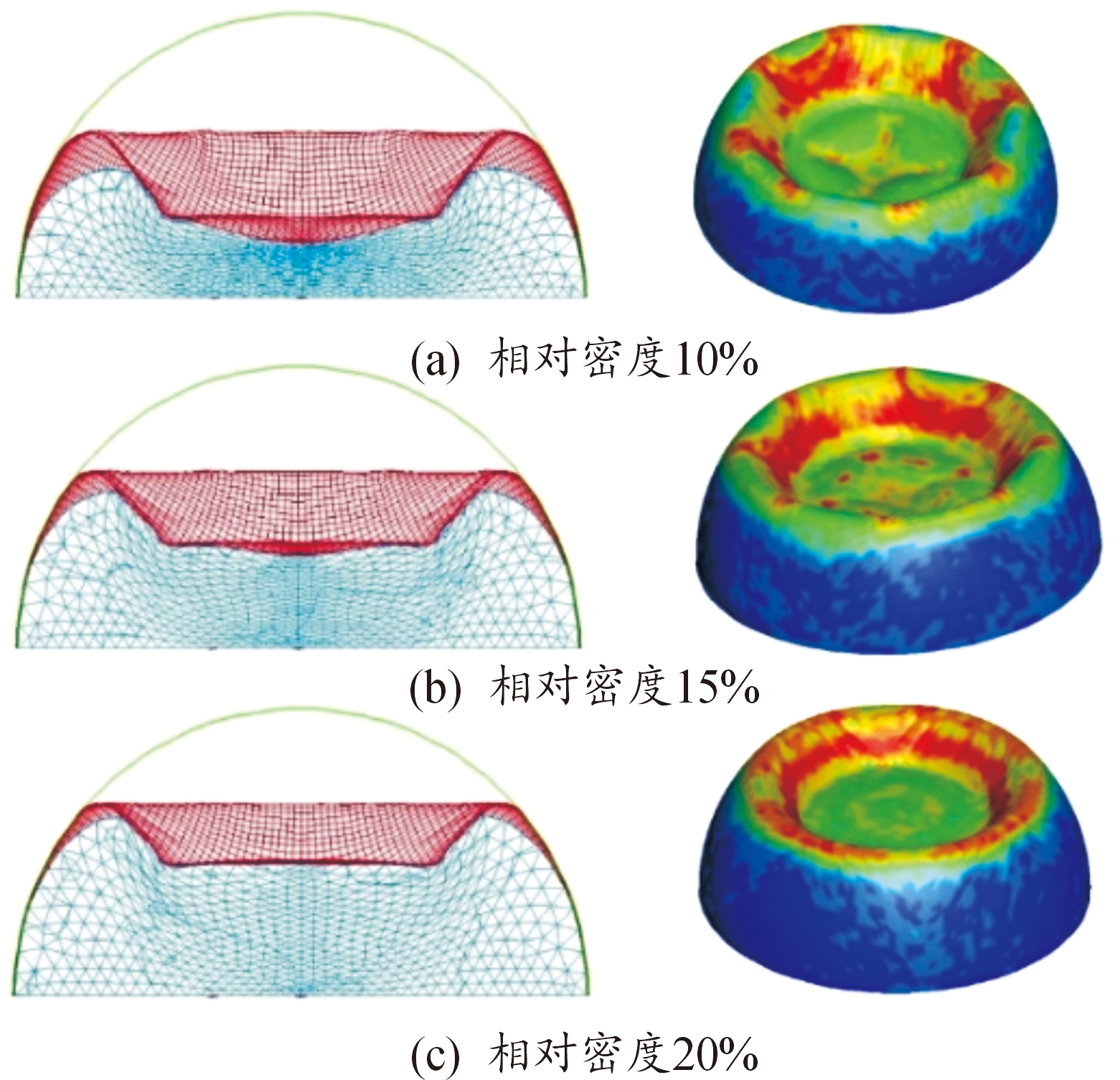
图17 冲击速度9.90 m/s时不同泡沫铝相对密度下半球结构变形模态图
Fig.17 Comparison of deformation modes with different relative densities
综合分析前述不同径厚比、泡沫铝相对密度以及加载初速度等不同参数条件下的变形模式,将泡沫铝填充半球在平头落锤冲击载荷下的变形模式总结归纳为4种。模式一,壳体边缘隆起,冲击区域产生4条对称分布的凹痕,如图18(a)所示;模式二,壳体边缘隆起,冲击区域压平,与落锤锤头形状一致,如图18(b)所示。模式三,壳体向内凹陷形成八边形塑性铰,与内空半球塑性铰形状一致,冲击区域产生四条对称分布的凹痕,如图18(c)所示。模式四,壳体向内凹陷形成平整塑性铰,冲击区域压平,与落锤锤头形状一致,如图18(d)所示。
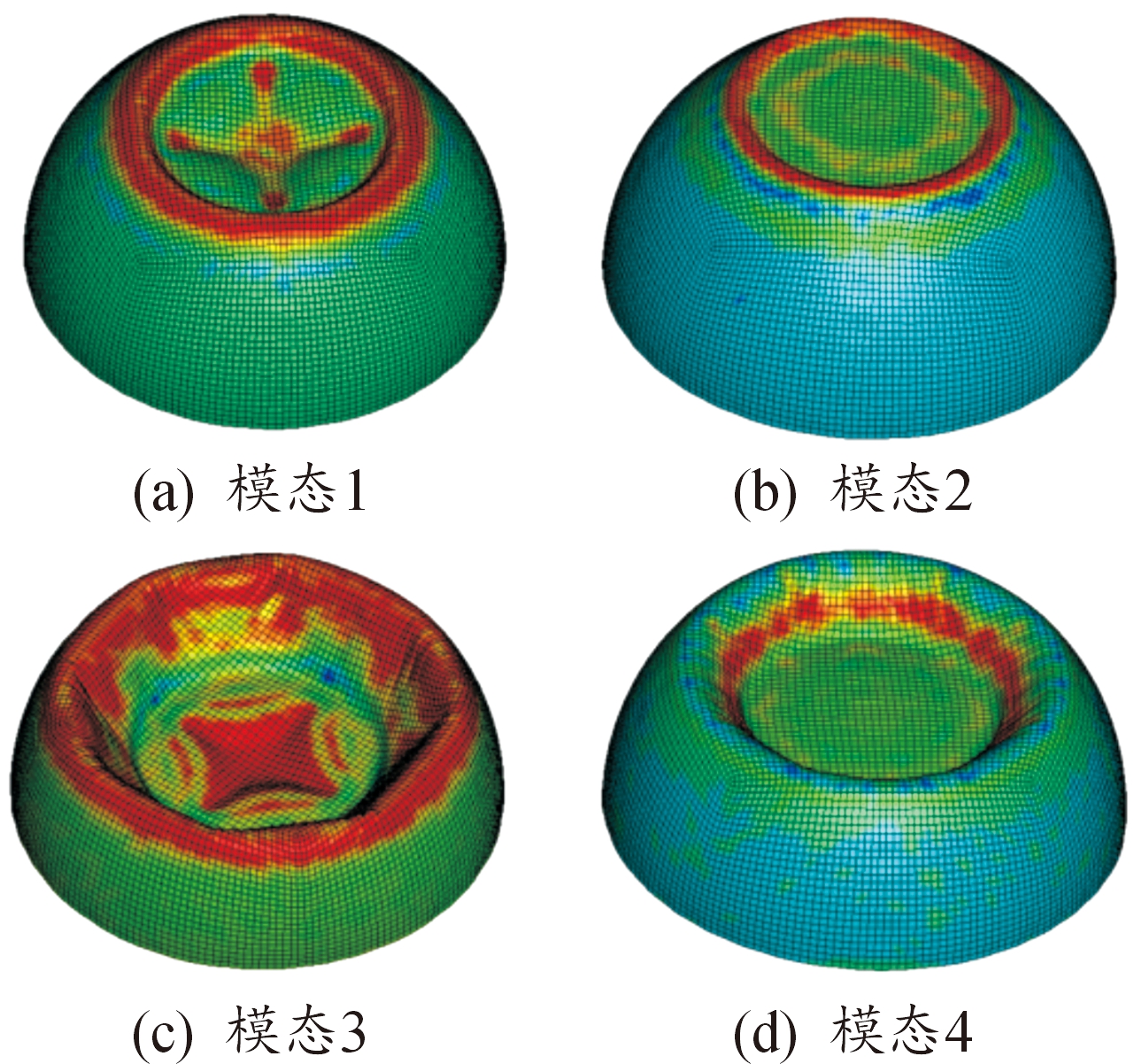
图18 平头落锤冲击载荷下泡沫铝填充半球4种典型变形模态
Fig.18 Four deformation modes of foam filled thin-walled hemisphere
4 结论
本文对泡沫铝填充薄壁半球壳结构在落锤冲击作用下的力学行为进行了研究,得到该结构的变形模态和吸能特性,同时分析了径厚比、泡沫密度以及加载初速度对该结构吸能特性的影响,得到了以下结论:
1) 相同加载条件下,泡沫铝填充半球壳比内空半球壳抵抗变形能力强,受力更加均匀,能够充分利用外壳材质的塑性变形能力,形成和发展塑性铰,降低变形量。泡沫填充半球壳具有良好的吸能性能,能够在更短时间内可以吸收较内空半球相同的能量。
2) 冲击载荷下泡沫铝填充半球结构的接触力时程曲线存在2个极值点,首个极值点出现在壳体塑性铰形成阶段,极值点大小与结构刚度有关。第二个极值点出现在内凹阶段,极值点大小与填充材料的抗压缩能力有关。
3) 冲击载荷下泡沫铝填充半球结构的主要变形模式与冲击能量和填充泡沫铝密度有关,主要有4种变形模态:模式一,壳体边缘隆起,冲击区域产生四条对称分布的凹痕;模式二,壳体边缘隆起,冲击区域压平,模式三,壳体向内凹陷形成八边形塑性铰,冲击区域产生4条对称分布的凹痕,模式四,壳体向内凹陷形成平整塑性铰,冲击区域压平。
泡沫填充半球结构结合了球形结构和泡沫材料的优点,是一种具有很大潜力的防护结构。本文从接触力、能量吸收以及变形模态等方面研究了泡沫铝填充半球结构在落锤冲击载荷作用下的抗冲击性能,为今后球形填充结构的优化设计、强动载荷下的试验和数值模拟研究提供参考。
[1] LECKIEF A,PENNYP K.Plastic instability of a spherical shell[M].Engineering Plasticity,1968:401-411.
[2] UPDIKED P.On the large deformation of a rigid-plastic spherical shell compressed by a rigidplate[J].Journal of Engineering for Industry,1972,94(3):949-955.
[3] UPDIKED P,KALNINS A.Axisymmetric behavior of an elastic spherical shell compressed between rigid plates[J].Journal of Applied Mechanics,1970,37(3):635-640.
[4] GUPTA N K,PRASADG E,GUPTA S.Axial compression of metallic spherical shells between rigid plates[J].Thin-walled Structures,1999,34(1):21-41.
[5] GUPTAN K.Experimental and numerical studies of dynamic axial compression of thin walled spherical shells[J].International Journal of Impact Engineering,2004,30(8):1225-1240.
[6] GUPTAN K,SHERIFFN M,VELMURUGAN R.Experimental and theoretical studies on buckling of thin spherical shells under axial loads[J].International Journal of Mechanical Sciences,2008,50(3):422-432.
[7] GUPTA N K,SHERIFF N M,VELMURUGAN R.Experimental and numerical investigations into collapse behaviour of thin spherical shells under drop hammer impact[J].International Journal of Solids and Structures,2007.44(10):3136-3155.
[8] 宁建国,杨桂通.球形壳在撞击载荷作用下的超临界动态响应[J].太原理工大学学报,1994(1).
NING Jianguo,YANG Guitong.Supercritical dynamic response of spherical shells impacted by a missile[J].Journal of Taiyuan University of Technology,1994(1).
[9] 宁建国,杨桂通.球形扁壳在冲击载荷作用下的超临界变形[J].爆炸与冲击,1992,12(3):206-212.
NING Jingguo,YANG Guitong.Supercritical deformation of shallow spherical shells under impact[J].Explosion and Shock Waves,1992,12(3):206-212.
[10]周志伟,王志华,赵隆茂,等.复合应力下泡沫铝屈服行为实验研究[J].高压物理学报,2011,26(2):171-176.
ZHOU Zhiwei,WANG Zhihua,ZHAO Longmao,et al.Experimental investigation on the yield behavior of aluminum foams under combined stress states[J].Chinese Journal of High PressurePhysics,2011,26(2) 171-176.
[11]WANG Y H,ZHAI X M,YAN J C,et al.Experimental,numerical and analytical studies on the aluminum foam filled energy absorption connectors under impact loading[J].Thin-Walled Structures,2018,131:566-576.
[12]习会峰.泡沫铝夹芯板高温下冲击力学性能的研究[D].广州:华南理工大学,2014.
XI Huifeng.Research on impact mechanical properties of aluminum foam sandwich plate at elevated temperatures[D].Guangzhou:South China University of Technology,2014.
[13]朱长锋.复杂应力状态/动态压缩下的泡沫金属本构模型[D].合肥:中国科学技术大学,2019.
ZHU Changfeng.Constitutive model of metal foam under complex stress/dynamic compression[D].Hefei:University of Science and Technology of China,2019.
[14]桂良进,范子杰,王青春.泡沫填充圆管的轴向压缩能量吸收特性[J].清华大学学报( 自然科学版),2003.43(11):1526-1529.
GUI Liangjin,FAN Zijie,WANG Qingchun.Energy-absorption properties of foam-filled circular tubes subjected to axial crushing[J].J Tsinghua Uni(Sci&Tech),2003,43(11):1526-1529.
[15]HOU S J,LI Q,LONG S Y,et al.Crashworthiness design for foam filled thin-wall structures[J].Materials &Design,2009,30(6):2024-2032.
[16]ZHANG Z Y,SUN W,ZHAO Y S,et al.Crashworthiness of different composite tubes by experiments and simulations[J].Composites Part B-Engineering,2018.143:86-95.
[17]SANTOSA S P,WIERZBICKI T,HANSSEN A G,et al.Experimental and numerical studies of foam-filled sections[J].International Journal of Impact Engineering,2000.24(5):509-534.
[18]NASRULLAH A I H,SANTOSA S P,DIRGANTARA T.Design and optimization of crashworthy components based on lattice structure configuration[J].Structures,2020.26:969-981.
[19]王永滨,武士轻,牟金岗,等.可重复使用新型着陆缓冲装置设计[J].航天返回与遥感,2021.42(4):1-9.
WANG Yongbin,WU Shiqing,MOU Jinggang,et al.Research on new reusable landing buffer[J].Spacecraft Recovery and Remote Sensing,2021,42(4):1-9.
[20]张威.薄壁球壳结构的动力学行为与优化设计[D].太原:太原理工大学,2015.
ZHANG Wei,Dynamic Behavior and optimization for thin-walled spherical shell structures[D].Taiyuan:Taiyuan University of Technology,2015.
[21]李正洲.某型客机增升装置的气动/机构优化设计[D].南京:南京航天航空大学,2013.
LI Zhengzhou.Aero-mechanical optimization design of a civil aircraft’s high-lift system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2013.
[22]陈俊.球鼻艏结构在船桥碰撞下的压溃载荷研究[D].武汉:武汉理工大学,2020.
CHEN Jun.Study on the crushing load of bulbous bow structure under ship-bridge collision[D].Wuhan:Wuhan University of Technology,2020.
[23]敬霖.强动载荷作用下泡沫金属夹芯壳结构的动力学行为及其失效机理研究[D].太原:太原理工大学,2012.
JIN Lin.The dynamic mechanical behavior and failure mechanism of sandwich shells with metallic foam cores under intensive loading[D].Taiyuan:Taiyuan University of Technology,2012.
[24]李世强.分层梯度多孔金属夹芯结构的冲击力学行为[D].太原:太原理工大学,2015.
LI Shiqiang.The dynamic behavior of sandwich structure with layered graded porous metallic cores[D].Taiyuan:Taiyuan University of Technology,2012.
[25]向宇,程涛.梯度泡沫铝的撞击动力学分析[J].轻金属,2012.49(10):51-57.
XIANG Yu,CHENG Tao.Impact dynamics analysis of functionally graded foamed aluminum[J].Light metal,2012,49(10):51-57.