0 引言
地面智能封控弹药是一种集组网、通信、探测、跟踪和攻击于一体的分布式智能探测控制网络化区域封锁弹药,周向敏感子弹药是其实现目标毁伤的子系统,可以通过打击机场准备起降的飞机和通过战略要道的轻型装甲车辆并完成对机场或道路的封锁。周向敏感子弹药系统的外弹道作用流程和运动特性直接关系到能否顺利探测、捕获、打击并毁伤目标。
伞-弹药系统是一种复杂的动力学系统,通常采用高塔试验或空投飞行试验等方法研究其动力学特性,但由于试验方法对测试设备精度以及试验条件要求较高,理论建模和数值仿真相结合方法成为研究该类问题的重要手段,国内外学者提出许多理论建模方法。Ericksen等[1]考虑了伞绳和吊带的弹性,建立了物-伞系统的平面6自由度动力学模型。Wolf等[2]建立了物-伞系统刚性伞和回收物的5自由度动力学模型。Doherr等[3]建立了伞-弹系统9自由度动力学模型,引入了四元数的思想。Dobrokhodov等[4]针对可控圆形伞-物系统进行了动力学建模,并开发了相应的控制硬件。Guglieri等[5]建立了伞-回收物系统动力学模型,并通过飞行试验验证了动力学模型的有效性。Neuhaus等[6]编译了伞-弹系统动力学求解软件并分析了伞-弹系统建模过程中伞绳模型、伞的空气动力和表观质量等问题。She等[7]从火星进入制导中的一种新的跟踪律ADRC入手建立了降落伞与飞行器系统的六自由度非线性数学模型。Tang等[8]讨论了稳定下降阶段降落伞-有效载荷系统在不同风剖面下的精准着陆问题。Cao等[9]建立了大型盘式间隙带降落伞-有效载荷系统6自由度刚体飞行动力学模型,并预测了该系统的飞行轨迹和落点分布。Zhu等[10]建立了伞式战斗部系统(PWS)的充气模型和末端降落动力学模型,有效预测了该系统的落点范围。舒敬荣等[11]建立了伞-弹系统三体运动学模型。唐乾刚等[12]建立了伞-弹系统9自由度动力学模型,分析了伞-弹系统下落过程的动力学特性。朱勇等[13]基于拉格朗日第二类方程,推导伞弹系统动力学方程。何民等[14]应用凯恩方法建立了9自由度箭伞系统动力学模型。师娇等[15]采用离散时间传递矩阵法建立了铅垂平面内伞-弹系统减速稳定段的动力学模型,回避了传统多体动力学研究在伞-弹系统建模中存在的问题。马晓冬等[16]基于第一类拉格朗日方程建立了旋转伞-弹系统动力学模型,模拟了末敏弹稳态扫描弹道特性。马宗成[17]基于拉格朗日力学方法建立了伞弹系统的七自由度模型,并分析了系统稳态扫描阶段的弹道特性。杨永亮等[18]推导了超大攻角条件下子弹的空间6自由度弹道方程,并分析了子弹的稳态扫描运动特性。张俊等[19]建立了涡环伞降末敏子弹五刚体动力学模型,并进行了稳态扫描弹道计算和可视化仿真。岳明凯等[20]采用第二类拉格朗日力学方法建立了伞-伞盘-弹体系统三刚体动力学模型,得到系统稳态扫描阶段的运动特性。
周向敏感子弹药因其独特的工作原理和扫描方式必定具有与传统末敏弹不同的运动特性,设计有效可行的子弹药外弹道方案,建立合适的周向敏感子弹药动力学模型,开展其运动规律的分析非常关键。本文分析了周向敏感子弹药的系统组成、工作原理以及具体作用流程;其次,基于经典牛顿力学方法和拉郎日方法分别建立上抛段和自由下落段的质点弹道方程以及减速-导旋段及稳态扫描段的导旋伞-子弹药系统12自由度的四刚体动力学模型;考虑了实际装配误差、开伞延时误差以及风等扰动因素的情况下,对比分析了理想条件与实际扰动存在下的周向敏感弹药系统的外弹道特性。本文建立的周向敏感子弹药全外弹道模型以及获得的弹道特性参数对弹道方案的优化、系统的捕获目标概率的计算提供了参考。
1 子弹药工作原理及弹道方案设计
1.1 子弹药结构及工作原理
周向敏感子弹药系统主要由导旋伞、伞盘、摩擦盘、周向敏感子弹药、敏感器等构成,如图1所示。
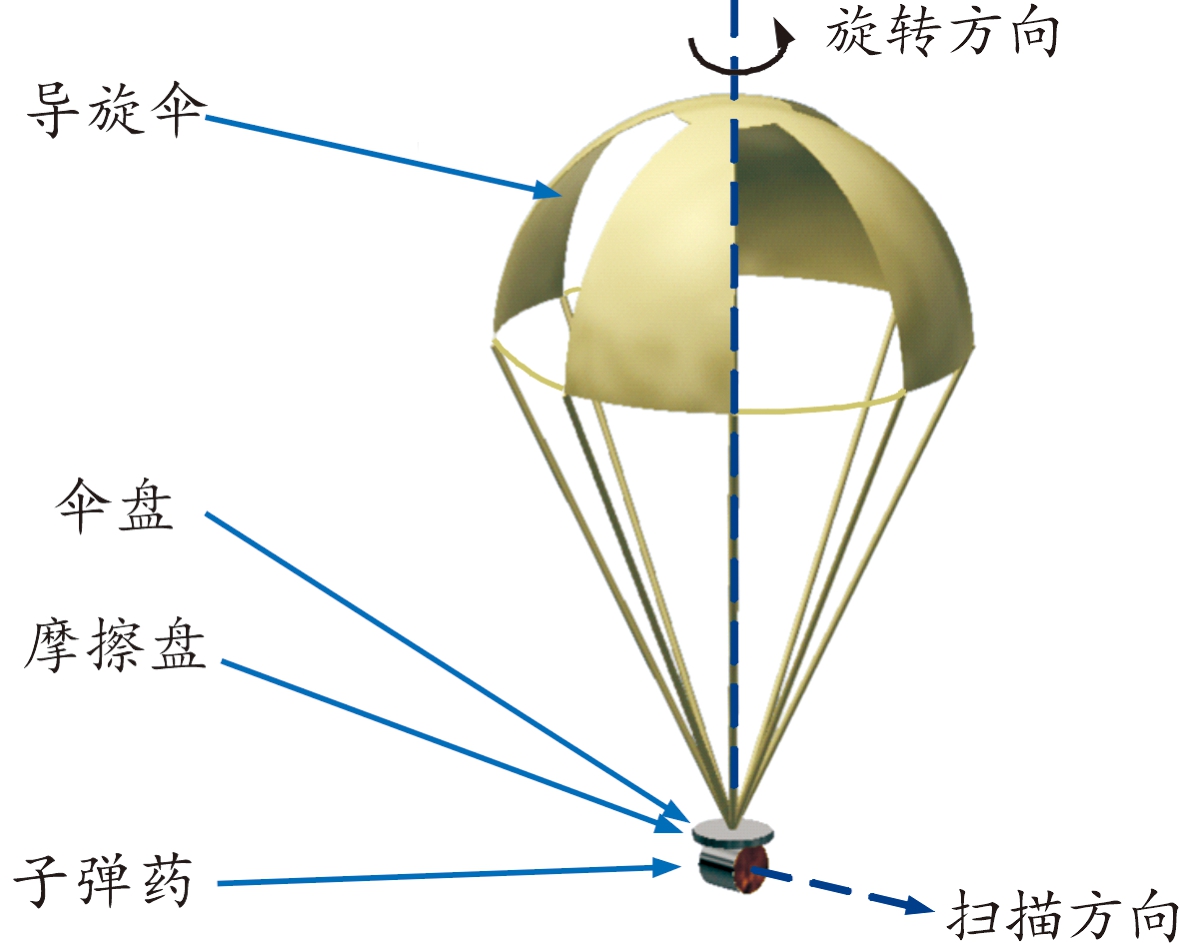
图1 开伞后周向敏感子弹药系统结构简图
Fig.1 Schematic diagram of trajectory scheme of the transverse sensitive submunition
周向敏感子弹及伞舱经母弹身管(以下简称发射筒)内发射装药的作用下竖直上抛,子弹出炮口具有一定的速度,通过调节发射药量,将上抛速度调节在合适的范围内。当过了上抛弹道的最高点后,周向敏感子弹药开始自由下落,并在下落过程中打开导旋伞,导旋伞在空气动力作用下产生导旋力矩带动其下方伞盘同步转动,伞盘通过摩擦力矩带动摩擦盘逐渐旋转,子弹药与摩擦盘连接,摩擦盘带动悬挂的周向布置的敏感子弹药旋转,并逐渐与导旋伞同步转动,落速和转速逐渐趋于平衡,进入稳态扫描段,子弹在导旋伞的作用下,稳定旋转下落,并在此过程中扫描识别目标,若发现目标则立即发射EFP弹丸进行打击。
1.2 子弹药弹道方案设计
周向敏感子弹药在发射药作用下从发射筒抛出(内弹道段),随后子弹药系统进入外弹道段,其飞行外弹道过程大致分为4个阶段,即上抛段、自由下落段、减速-导旋段、稳态扫描段,如图2所示。在周向敏感子弹药的弹道流程中,上抛段及自由下落段所涉及到的对象为子弹与伞舱整体,减速-导旋段和稳态扫描段涉及到的对象有子弹药、摩擦盘、伞盘和旋转伞。
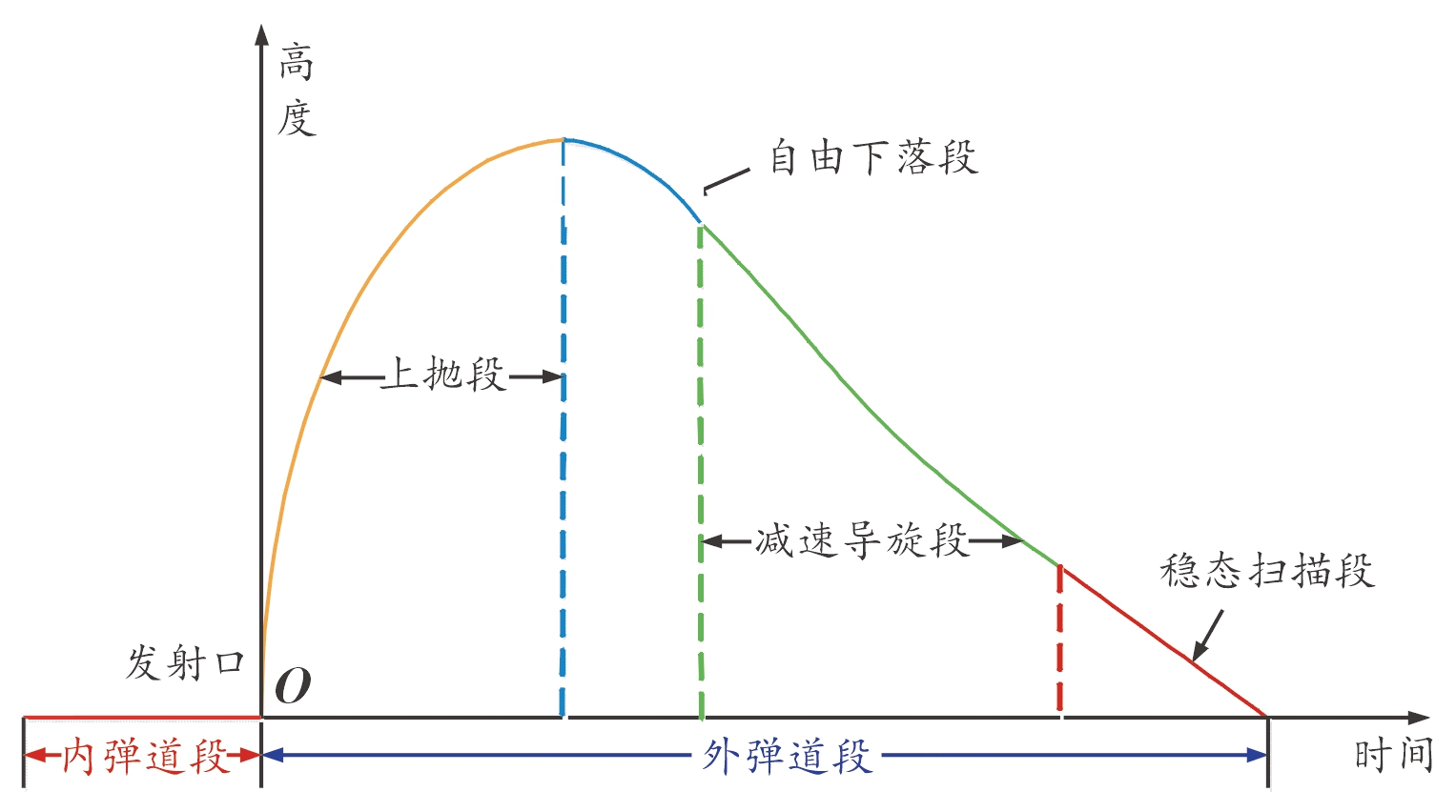
图2 周向敏感子弹药弹道流程示意图
Fig.2 Schematic diagram of trajectory scheme of the transverse sensitive submunition
2 子弹药外弹道模型
2.1 上抛段和自由落体段模型
上抛段和自由落体段属于无控弹道,主要受重力和空气动力的影响。此过程中导旋伞还没有开伞,把伞舱和子弹药看成一个整体作为研究对象。由于其运动过程受风的影响较小,因此这2个阶段内暂不考虑风干扰影响,将其简化为质点模型[21],受力分析如图3所示。
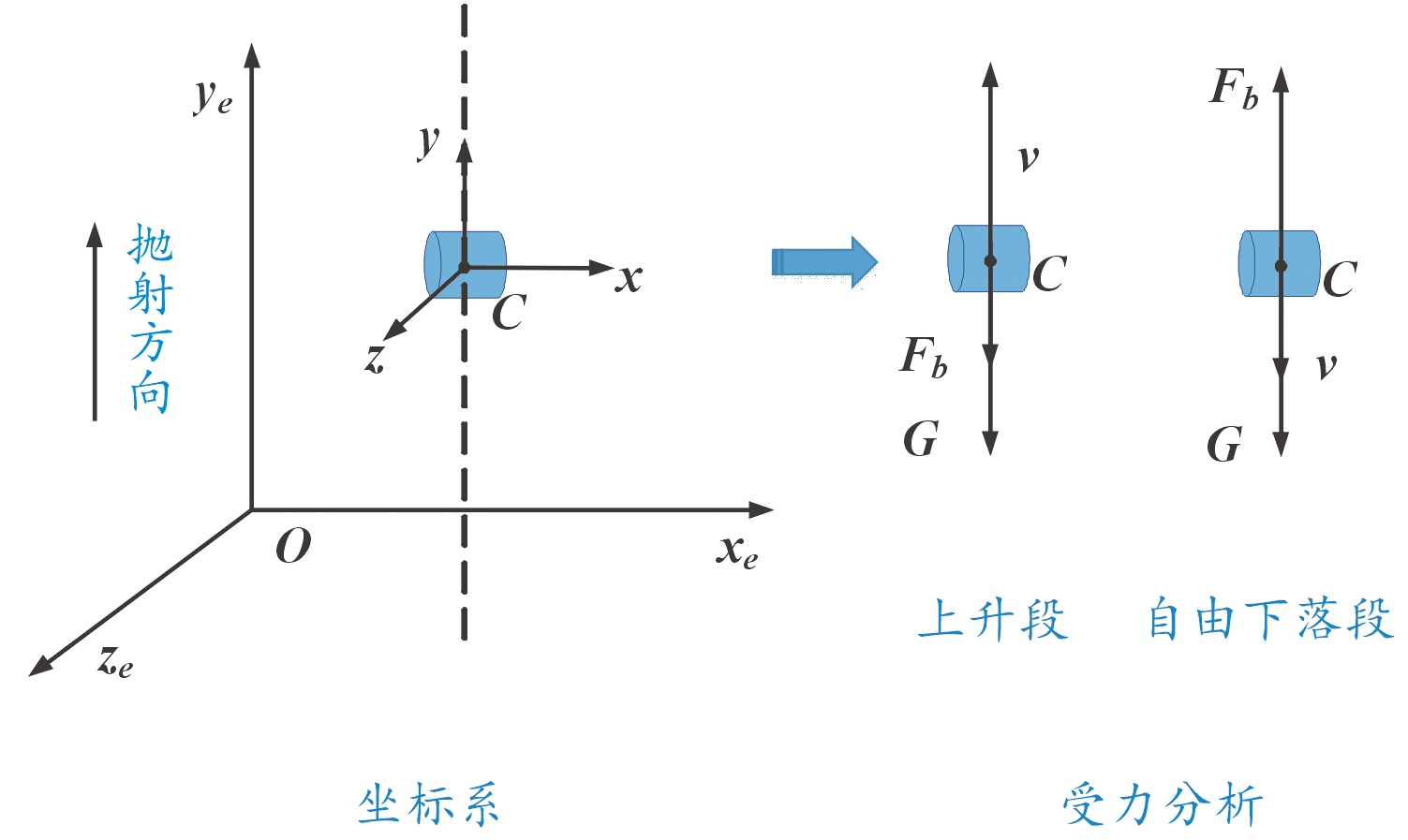
图3 上升段及自由落体段的坐标系及受力示意图
Fig.3 Coordinate system and force diagram of ascending stage and free falling stage
将弹体所受的力在地面坐标系上投影,得到有风情况下周向敏感子弹药上升段和自由下落段的空间三维弹道方程为:
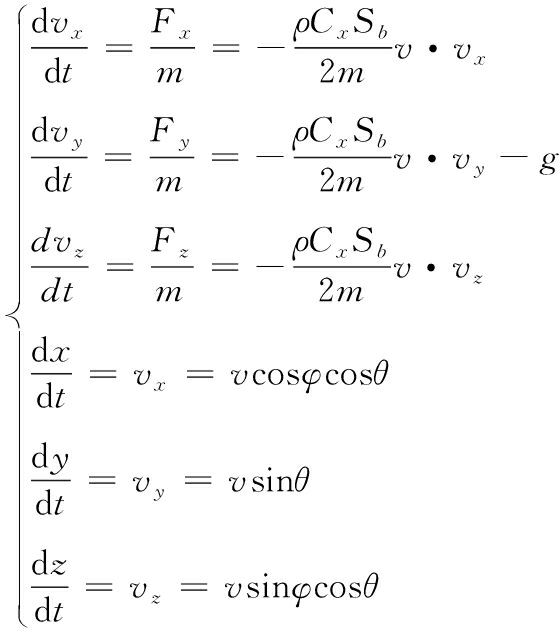
(1)
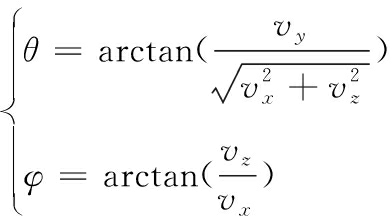
(2)
式(1)和式(2)中:m为周向敏感子弹药的总质量;g=9.8 m/s2为重力加速度;ρ=1.206 kg/m3为空气密度;v是合速度;vx、vy、vz分别为水平方向分速度、竖直方向分速度、侧向分速度;G为重力;Fb为弹体所受的空气阻力;Cx为弹体阻力系数;Sb为弹体特征阻力面积;θ为弹道倾角;φ为弹道偏角。
2.2 减速导旋段及稳态扫描段模型
导旋伞-子弹药系统属于多刚体力学系统,鉴于分析力学在处理复杂刚体力学系统问题上远远优于经典牛顿力学,本文将采用基于虚功原理和达朗贝尔原理的第一类拉格朗日力学方程建立导旋伞-子弹药系统动力学模型。在建立导旋伞-周向敏感子弹系统动力学模型之前,做出如下假设:
1) 认为导旋伞瞬间开伞,导旋伞衣幅完全充满,忽略导旋伞的形状变化。
2) 不考虑导旋伞的透气性,将其视为轴对称刚体,伞绳视为弹簧。
3) 忽略导旋伞产生的附加质量和附加力矩。
4) 忽略子弹弹体、摩擦盘、伞盘等尾流对伞的影响。
5) 忽略伞盘、摩擦盘产生的空气动力。
6) 认为导旋伞及子弹体的气动参数为常数。
7) 地球重力加速度g为常数,忽略地球科氏加速度和曲率的影响。
8) 气象环境中空气密度为常数,风力等级≤4级。
2.2.1 坐标系及坐标变换
由周向敏感子弹药结构可将其分为导旋伞(a)、伞盘(b)、摩擦盘(c)、子弹药(d)组成的四刚体模型,分别建立各个部件的基准坐标系Ci-xyz(i=a,b,c)以及固连坐标系Ci-xiyizi(i=a,b,c)。以导旋伞为例,如图4所示,第1次将导旋伞基准坐标系(Ca-xyz)绕Cay轴旋转ψa角,转到位置Ca-x′yz′;第2次再绕Caz′轴旋转θa角,转到新的位置
第3次绕Caya轴旋转φa角度,即得到导旋伞固连坐标系Ca-xayaza。以此类推,可得到其他刚体的坐标变换。
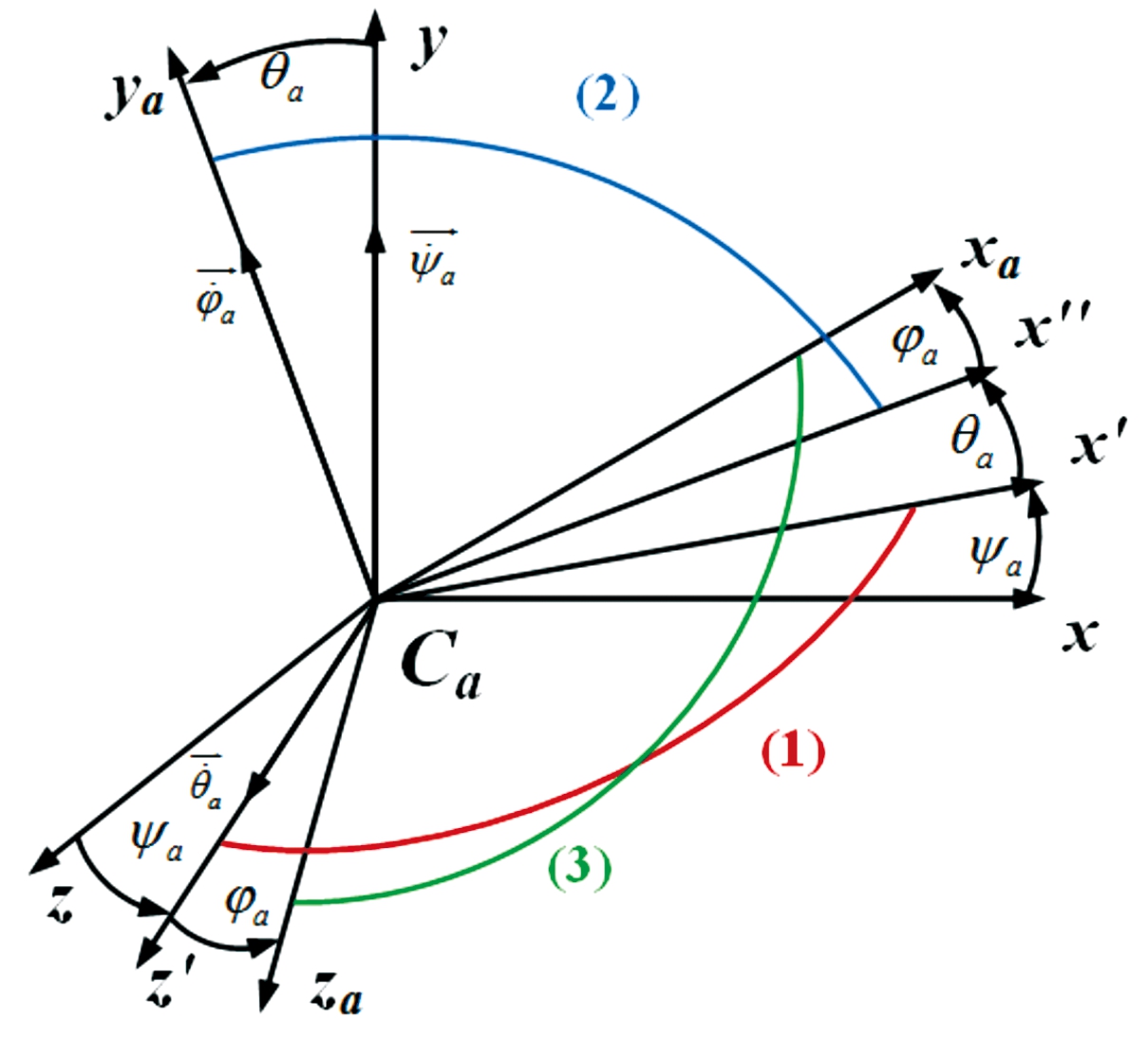
图4 导旋伞基准坐标系到固连坐标系的坐标变换
Fig.4 Transformation from reference coordinate to fixed coordinate of the parachute
各刚体的基准坐标系到各自对应的固连坐标系的转换矩阵为:
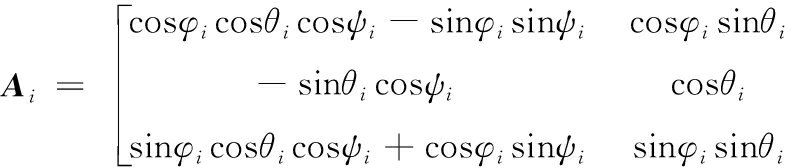
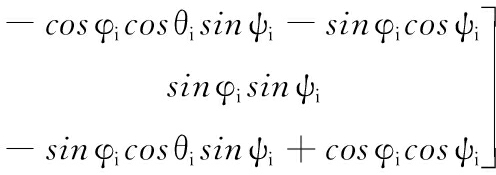
(3)
式(3)中,3个欧拉角ψi、θi、φi的单位向量在固连坐标系的3个坐标轴上的方向余弦矩阵为:
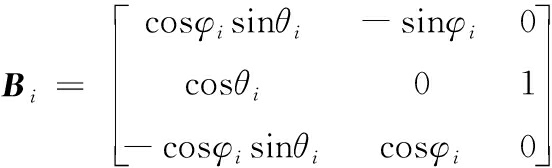
(4)
根据角速度合成定理,各个刚体的转速为:
(5)
则各刚体的转速在其固连坐标系中可以表示为:
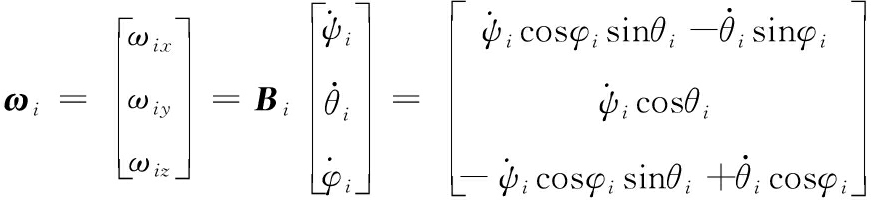
(6)
2.2.2 受力分析及广义力
分析力学中,广泛采用广义坐标和广义动量来描述系统的运动状态[22]。根据拉格朗日力学理论可知,求解广义力需求得系统所受力和力矩在其虚位移上的虚功。
1) 空气动力虚功δW1。
系统所受的空气动力包括空气阻力和升力。导旋伞和子弹所受的空气动力的表达式为:
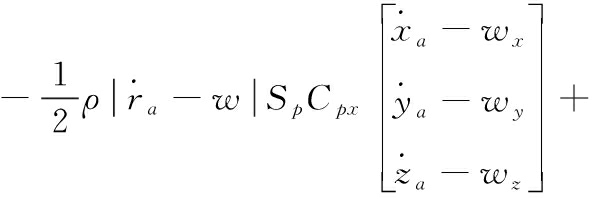
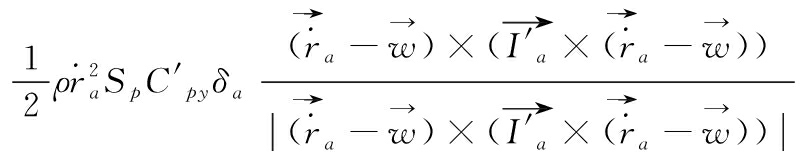
(7)
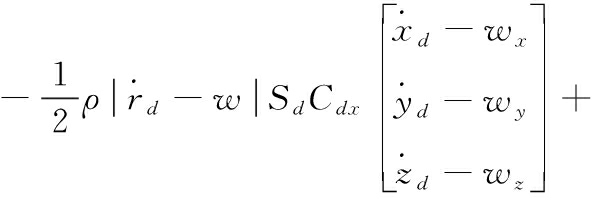
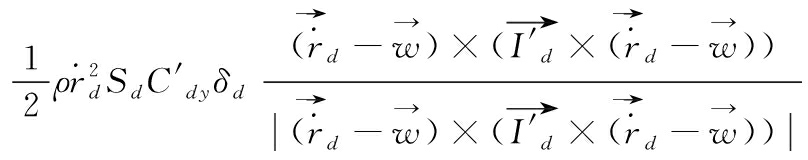
(8)
式(7)和式(8)中:
为导旋伞、子弹药的绝对速度;w为风速;
为伞轴单位坐标在导旋伞基准坐标系的投影;Sp为导旋伞的特征面积;Cpx为导旋伞的阻力系数;
为导旋伞升力系数导数; ρ为空气密度;δa为导旋伞的攻角;
为伞轴单位坐标在子弹基准坐标系的投影;Sd为子弹的特征面积;Cdx为子弹的阻力系数;
为子弹升力系数导数;δd为子弹的攻角。
导旋伞所受的力矩包括导旋力矩、极阻尼力矩、赤道阻尼力矩、静力矩,子弹所受的力矩包括极阻尼力矩和赤道阻尼力矩,它们受到的合力矩分别表示为:
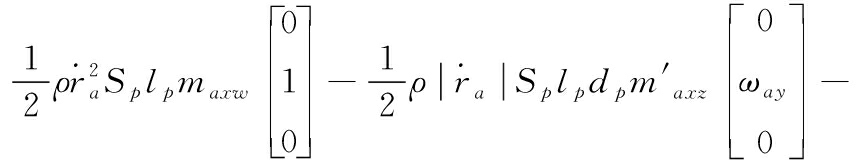
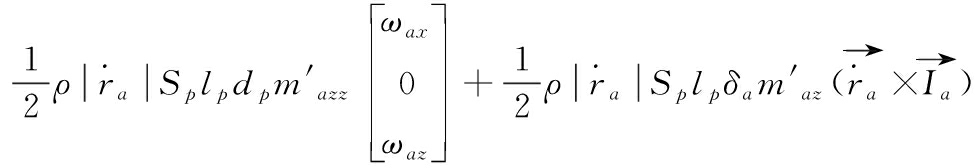
(9)
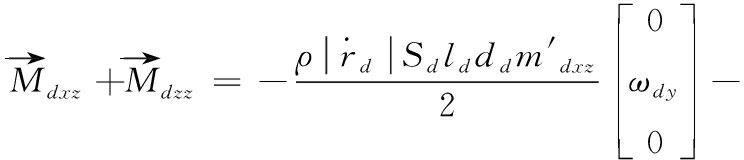
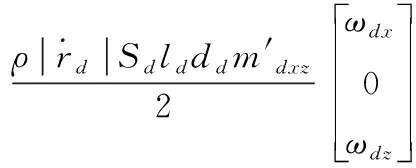
(10)
式(9)—(10)中:
为伞轴单位坐标在导旋伞固连坐标系的投影;maxw为导旋伞的导旋力矩系数;
为极阻尼力矩系数导数;
为赤道阻尼力矩系数导数;
为静力矩系数导数;lp、ld为特征长度;dp、dd为特征直径。
因此,系统的空气动力所作的虚功为:
δW1=Fa(δra)+Fd(δrd)+Ma(δpa)+Md(δpd)
(11)
2) 重力虚功δWG。
重力包括导旋伞、伞盘、摩擦盘、子弹药的总重力,重力所作的虚功为:
δWG=∑mig(δyi), (i=a,b,c,d)
(12)
3) 伞绳拉力虚功δWFT。
伞绳绕伞轴呈轴对称分布,第j根伞绳矢量在地面惯性坐标系中可以表示为:
(13)
式(13)中:Nj、Pj为伞绳分别位于伞盘和导旋伞的2个端点;j为伞绳个数,j≥4且为偶数。
将伞绳简化为只受拉力的弹簧,伞绳的原长为l0,横截面积为S0,弹性系数为
为弹性模量,阻尼系数为c,则伞绳拉力为:
(14)
则伞绳拉力所作的虚功为:
(15)
4) 摩擦力虚功δWFN。
伞盘与摩擦盘之间的相对转动产生摩擦力,则摩擦力矩虚功为:
(16)
式(16)中:MFN为摩擦力对伞轴的力矩;μ为摩擦力系数;FN为伞盘与摩擦盘间的压力;rc为摩擦盘半径。
5)广义力Q。
根据受力分析和拉格朗日力学可知,在广义坐标下的广义力为:
(17)
将式(11)、式(12)、式(15)、式(16)代入式(17),即可得到各广义坐标方向上的广义力Qr、Qp。
2.2.3 约束方程
导旋伞-子弹药系统四刚体模型中,共有2个柱铰链接,即伞盘-摩擦盘之间、摩擦盘-子弹药之间的链接。假设相邻两刚体间的铰点在运动过程中始终重合,根据各刚体间的连接关系,可得约束方程为:
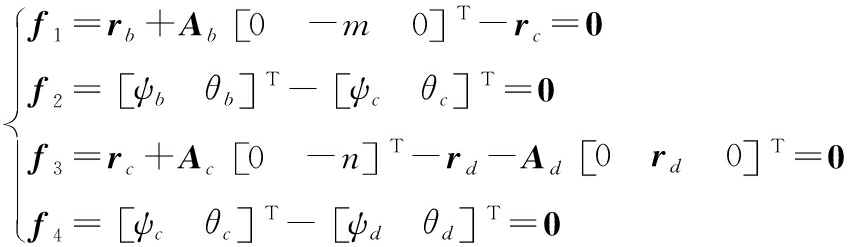
(18)
描述约束的矩阵
分别为3×12矩阵,拉格朗日乘子矩阵为λ=[λ1…λ12]。以伞盘为例,可得描述伞盘的矩阵为:
(19)
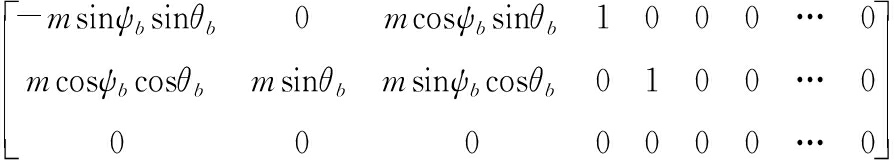
以此类推,即可得到全部约束矩阵Φr、Φp。
2.2.4 动力学方程
根据以上受力分析和系统约束方式可知,导旋伞-子弹药系统为完整约束系统,采用拉格朗日第一类方程可得系统的动力学方程为:
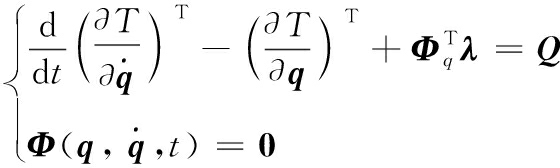
(21)
式(21)中:Q为广义力; Φq=∂Φ/∂q; λ为拉格朗日乘子矩阵;T为系统的总动能[23-24]。
对于任何刚体i的动能可以表示成平移动能和转动动能之和,即:
(22)
式(22)中:mi为刚体i的质量阵; Ji为刚体i的转动惯量矩阵。
则系统的总动能为:
T=∑Ti, (i=a,b,c,d)
(23)
将式(22)和式(23)代入式(21),整理可得系统的动力学方程的矩阵形式为:
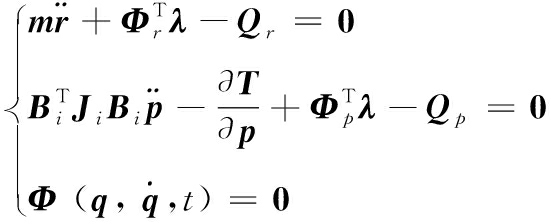
(24)
3 模型验证
为了验证基于拉格朗日力学方法建立的伞-弹动力学模型的真实有效性,采用马晓冬等[25-27]的高塔投放试验数据结果对模型进行验证分析。该团队针对涡环伞-末敏弹系统进行了详细的研究,完成了一系列的试验和仿真,并且针对该系统的试验研究发表了多篇论文。因此,该团队获得的伞塔试验数据可信度较高。
3.1 试验设备及布置
如图5所示,伞塔试验在高度为100 m的高塔上将伞-弹系统进行投放,初始落速和转速为零,通过在弹体上内置的姿态参数存储测量仪获得系统转速和扫描角的变化数据,通过外场布置的高速摄像机和标尺,测量系统的下落速度。
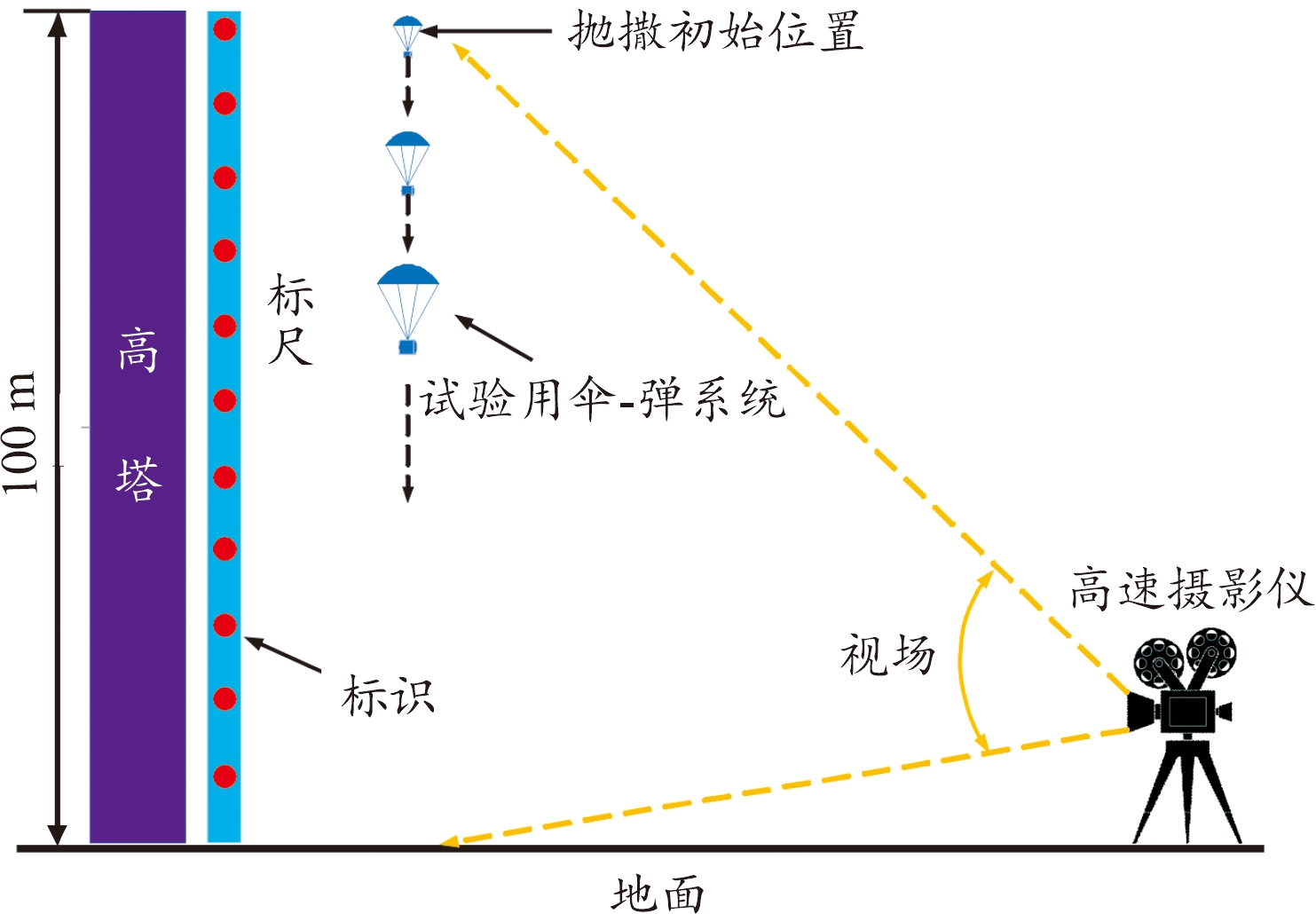
图5 高塔试验布置示意图
Fig.5 Schematic diagram of tower test layout
3.2 初始条件和主要参数
根据高塔试验中的试验模型的结构参数和气动参数,设置仿真模型的主要参数,见表1[16]。根据试验条件,取初始条件为
表1 主要参数
Table 1 Main parameter
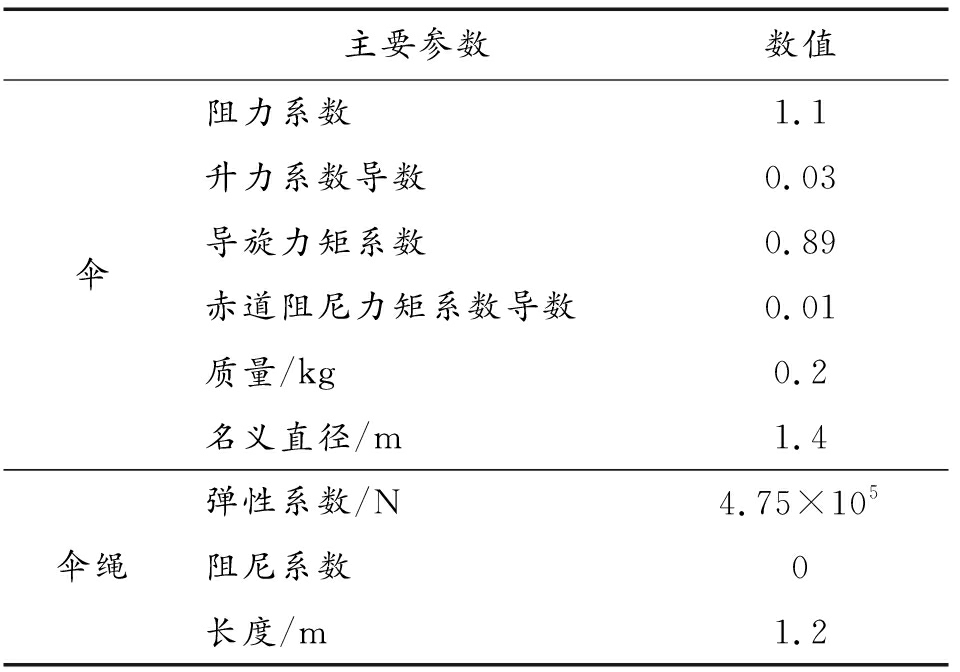
主要参数数值伞阻力系数1.1升力系数导数0.03导旋力矩系数0.89赤道阻尼力矩系数导数0.01质量/kg0.2名义直径/m1.4伞绳弹性系数/N4.75×105阻尼系数0长度/m1.2
续表(表1)
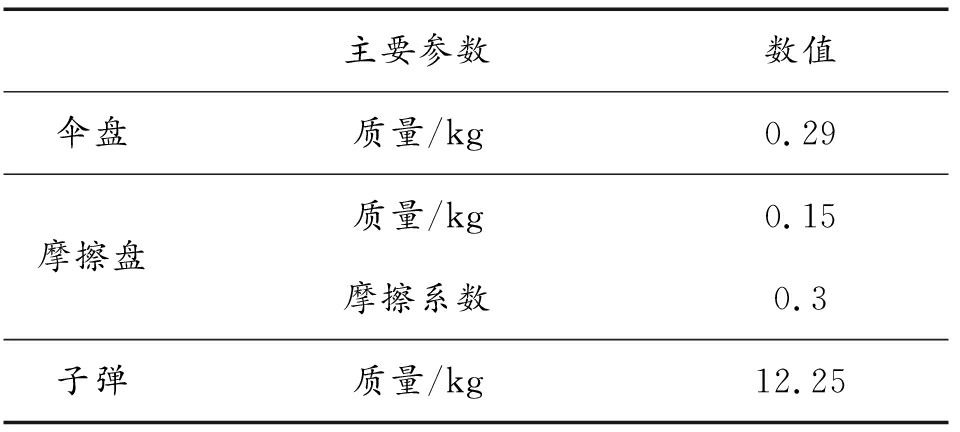
主要参数数值伞盘质量/kg0.29摩擦盘质量/kg0.15摩擦系数0.3子弹质量/kg12.25
3.3 验证分析
本文中采用基于Gear预估-校正算法的变分变步长GSTIFF积分求解器求解伞-弹系统动力学方程,计算得到伞-弹系统的运动过程的仿真结果,如图6所示。仿真与试验对比结果如表2所示。由图6可以看出,系统的下落速度在下落过程中从零逐渐增大,并在11.63 m/s的速度下达到稳定,系统转速在开始时震荡幅度比较剧烈,随着时间的推移逐渐达到稳定值3.4 r/s。
表2 试验结果与仿真结果对比
Table 2 Comparison of test results and simulation results
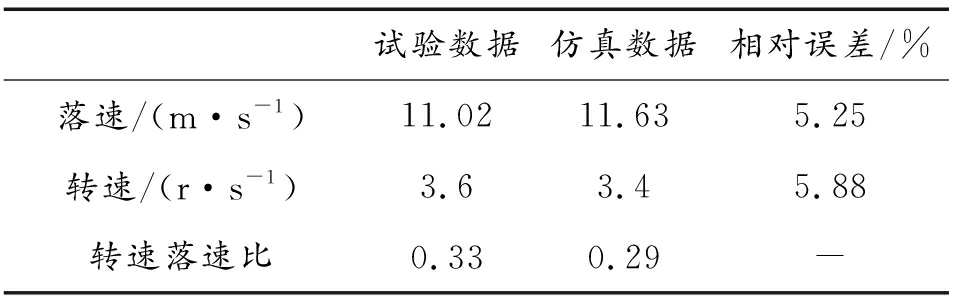
试验数据仿真数据相对误差/%落速/(m·s-1)11.0211.635.25转速/(r·s-1)3.63.45.88转速落速比0.330.29-
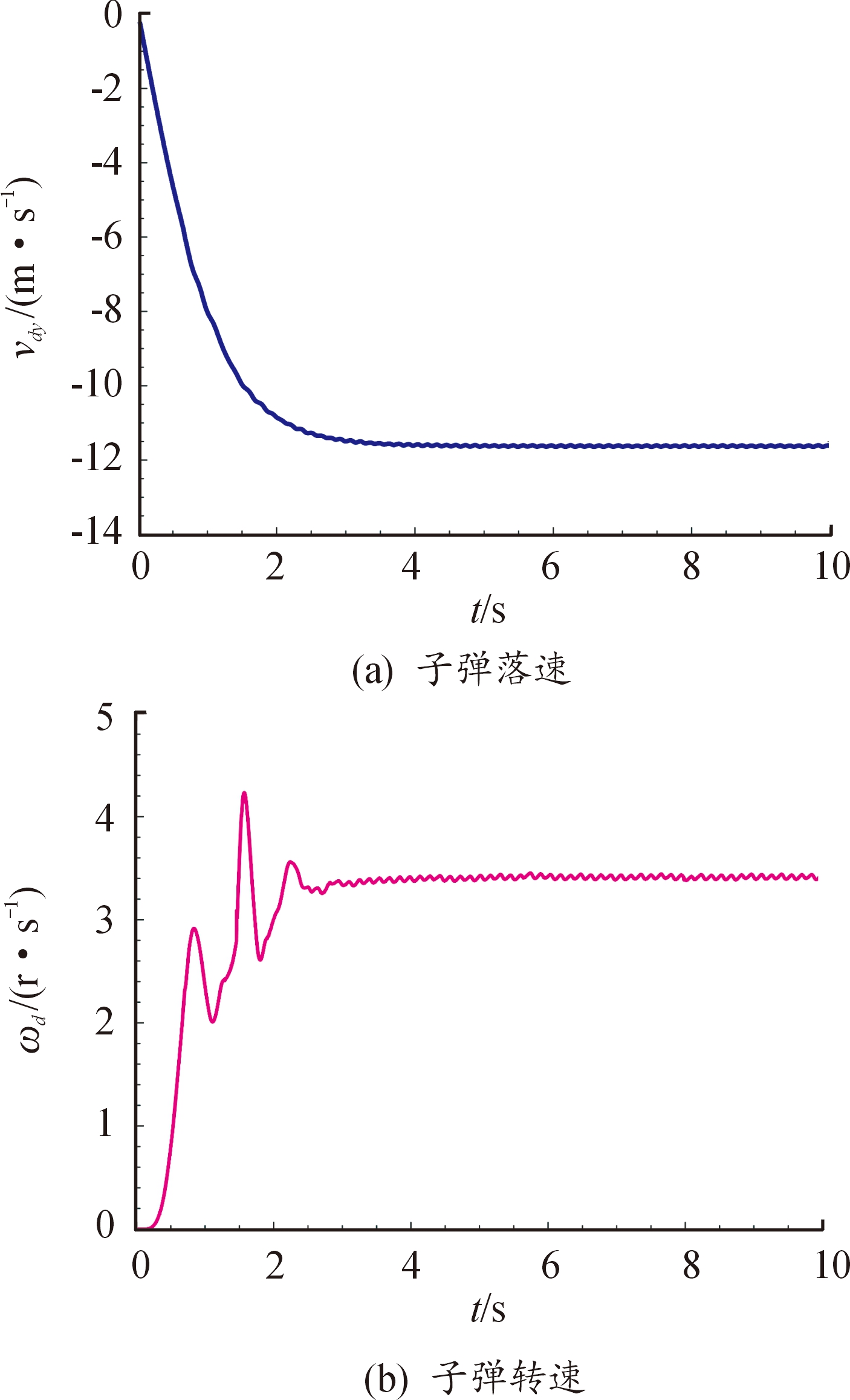
图6 仿真结果
Fig.6 Simulation results
由表2可知,系统稳定落速的仿真值比试验值稍大一些,相对误差为5.25%,稳定转速比试验值稍小一些,相对误差为5.88%。动力学模型的简化使仿真模型与真实试验模型有所差别,试验模型的加工误差以及周围环境中风的影响也是造成仿真误差的原因,但总的来看,仿真结果与试验结果的相对误差很小。因此,本文中所建立的伞-弹系统动力学模型能够真实地反应出伞-弹系统的运动状态。
4 全外弹道计算及对比分析
4.1 初始条件
根据周向敏感子弹药的工作原理可知,从上抛到下落再到开伞,一系列复杂作用过程中存在过多的冗余时间。若子弹留空时间较长,极易被敌方目标发现,很容易导致子弹药受到敌方攻击或敌方目标采取规避措施。以目前子弹药的最大打击半径(≤50 m)来看,若留空时间过长,装甲车(时速约60 km/h)会在这段时间行驶出子弹药攻击范围,导致敏感子弹药的生存能力和打击能力受到较大威胁。因此,应尽量减小子弹药的留空时间,使子弹药尽快进入攻击状态,这将有效提高系统的效能,结合该弹药系统的实际工作条件,给出优化弹道方案初始计算条件,如表3所示。子弹在实际装配过程中,往往会存在因装配误差导致的质心偏离几何对称中心的情况;在实际工作过程中,开伞一致性以及气象环境中的自然风干扰都是不可忽视的干扰因素,初始扰动参数如表4所示。
表3 初始条件
Table 3 Initial conditions
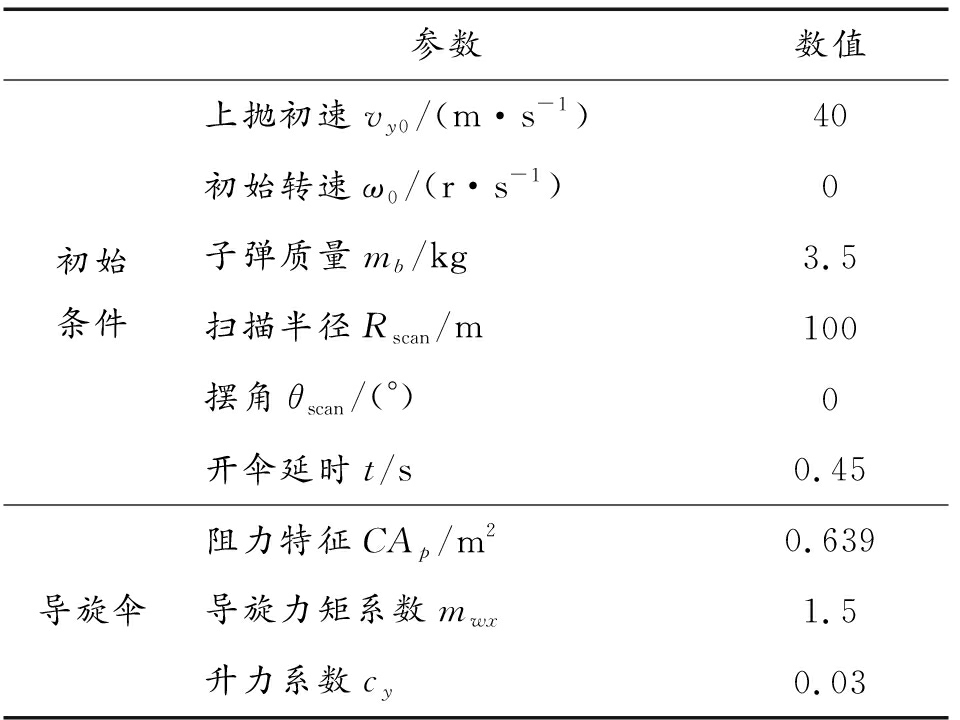
参数数值初始条件上抛初速vy0/(m·s-1)40初始转速ω0/(r·s-1)0子弹质量mb/kg3.5扫描半径Rscan/m100摆角θscan/(°)0开伞延时t/s0.45导旋伞阻力特征CAp/m20.639导旋力矩系数mwx1.5升力系数cy0.03
表4 扰动因素
Table 4 Disturbance factor
扰动因素数值质心偏移距离MED/mm5距地表10 m处风速w10/(m·s-1)5开伞时间误差Δt/s0.002
4.2 全弹道特性对比分析
为了探索扰动比较恶劣的情况下周向敏感子弹药系统能否捕获目标,分别计算了子弹药系统在理想情况以及存在扰动情况下的飞行外弹道参数,并进行了对比分析,计算结果如图7所示。
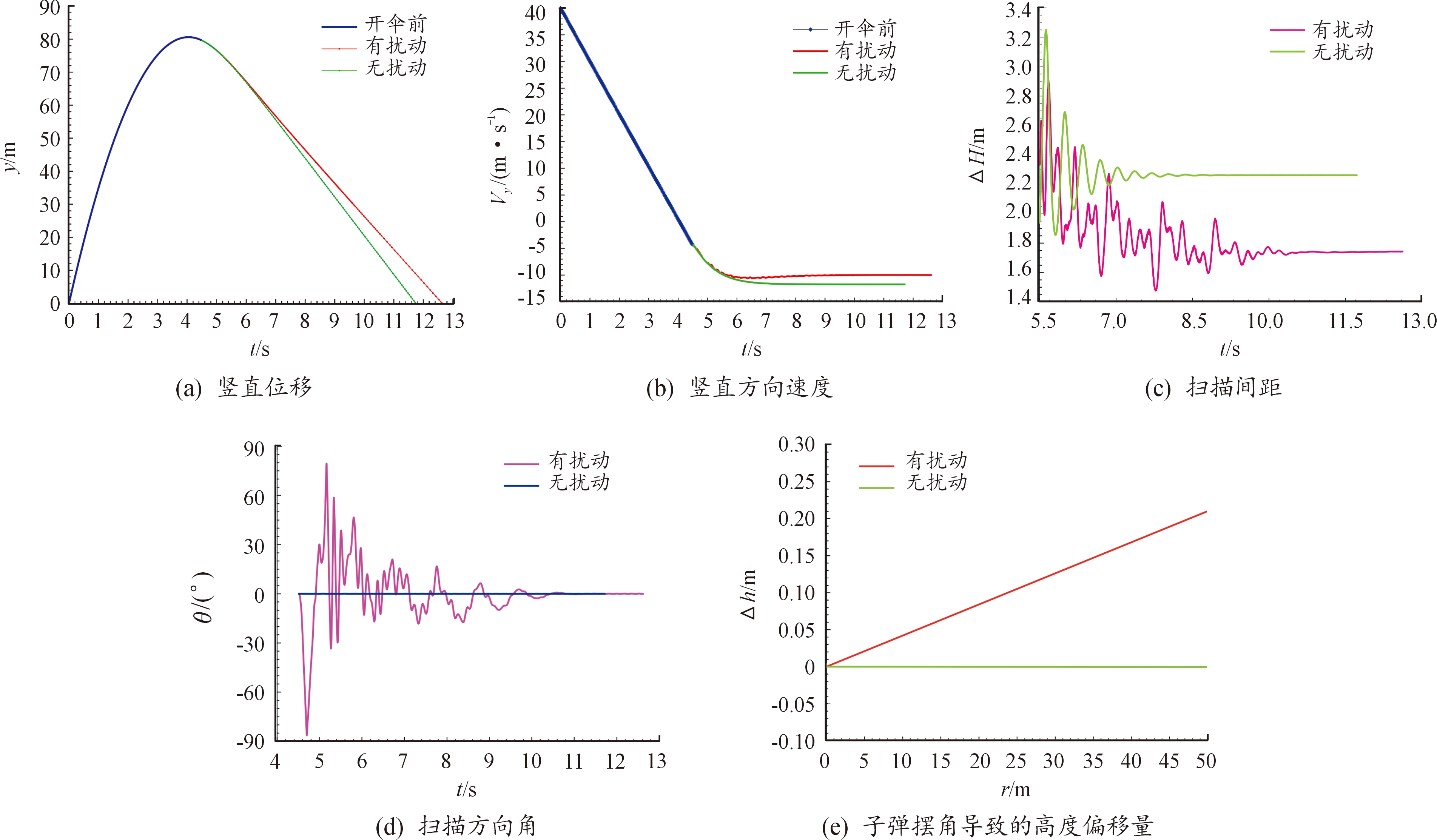
图7 外弹道参数及扫描参数的变化规律对比
Fig.7 Comparison of external ballistic parameters and scanning parameters
由计算结果可知,周向敏感子弹药上抛阶段用时4.05 s达到最高点,系统抛射最大高度为80.62 m,自由下落0.45 s后开伞。无扰动时,减速-导旋段用时4.63 s,沿竖直方向运动43.64 m,在距地面35.98 m高度开始稳态扫描,在空间形成2.26 m扫描间距的螺旋曲线;有扰动时,减速-导旋段用时6.62 s,系统沿竖直方向运动约59.98 m后,距地面19.64 m高时开始稳态扫描,在空间形成1.74 m扫描间距的螺旋曲线。与理想情况相比,有扰动时系统达到稳定的时间延长、平衡落速略微减小、稳态扫描间距减小。由子弹扰动因素导致的子弹摆角约0.24°,在扫描方向50 m(子弹威力半径)远处会产生约0.21 m的高度偏移。如果采用“一次捕获准则”,即第1次扫描到目标便开始打击目标,而有扰动存在时周向敏感子弹药的扫描间距在1.74 m左右,加上偏移高度0.21 m后为1.95 m,敏感探测器仍然可以扫描到目标的易损区域。因此,在存在扰动情况下此周向敏感子弹药弹道方案仍然具备对目标的捕获条件。
5 结论
本文基于周向敏感子弹药系统的原理组成、作用流程特点,设计了子弹药系统的弹道方案,基于牛顿力学方法以及第一类拉格朗日力学方法,分别建立了不同阶段的子弹药系统外弹道简化模型,并对比分析了有干扰与无干扰条件下周向敏感子弹药系统的外弹道特征参数以及稳态扫描参数,得到以下结论:
1) 有扰动存在时,系统在减速导旋段的扫描方向角产生大幅度的摆动,空间扫描曲线将出现疏密变化,存在漏扫目标的风险。
2) 与无扰动情况相比,稳态扫描段,导旋伞-子弹药系统扫描间距基本保持不变,但扫描方向与水平面有一定夹角,并且扫描曲线会沿着横风的方向生产偏移。
3) 与理想情况相比,有扰动时系统达到稳定的时间延长、平衡落速略微减小、稳态扫描间距减小。
4) 本文设计的弹道方案在实际有扰动的情况下仍然可以满足对目标的捕获条件,合理设计和优化弹道方案有利于提高目标捕获概率。
[1] ERICKSEN R E,GUITERAS J J,LARRIVEE J A,et al.A parachute recovery system dynamic analysis[J].Journal of Spacecraft and Rockets,1967,4(3):321-326.
[2] WHITE F M,WOLF D F.A theory of three-dimensional parachute dynamic stability[J].Journal of Aircraft,1968,5(1):86-92.
[3] DOHERR K F,HARTMUT S.9DOF-simulation of rotating parachute systems[J].Journal of Aircraft,1992,29(5):774-781.
[4] DOBROKHODOV V N,YAKIMENKO O A,JUNGE C J.Six-degree-of-freedom model of a controlled circular parachute[J].Journal of Aircraft,2003,40(3):482-493.
[5] GUGLIERI G,QUAGLIOTTI F.Validation of a simulation model for a planetary entry capsule[J].Journal of Aircraft,2003,40(1):127-136.
[6] NEUHAUS J,KENNEY P.A generic multibody parachute simulation model[C]//Proc.of theAIAA Modeling and Simulation Technologies Conference and Exhibit.2006:6622.
[7] SHEN G H,XIA Y Q,SUN H R.A 6DOF mathematical model of parachute in Mars EDL[J].Advances in Space Research,2015,55(7):1823-1831.
[8] TANG J H,QIAN L F,YIN Q,et al.Numerical study of parachute-payload land site distribution with randomize wind gust model[J].Transactions of Nanjing University of Aeronautics and Astronautics,2018,35(2):383-394.
[9] CAO Y,WEI N.Flight trajectory simulation and aerodynamic parameter identification of large-scale parachute[J].International Journal of Aerospace Engineering,2020(3):1-13.
[10]ZHU H,SUN Q,HAN J,et al.Numerical simulation and experiment for impact point prediction of parachute-warhead system[C]//Proc.of the2020 39th Chinese Control Conference (CCC),IEEE.2020:1221-1226.
[11]舒敬荣,王宝贵,韩子鹏,等.伞-弹系统三体运动分析[J].航空学报,2001,22(6):481-485.
SHUJingrong,WANG Baogui,HAN Zipeng,et al.Analysis on three body motion of parachute-projectile systems[J].Acta Aeronauticaet Astronautica Sinica,2001,22(6):481-485.
[12]唐乾刚,张青斌,张晓今,等.伞-弹系统九自由度动力学模型[J].兵工学报,2007,28(4):449-452.
TANG Qiangang,ZHANG Qingbin,ZHANG Xiaojin,et al.Nine-degree-of-freedom model of bomb-parachute system[J].Acta Armamentarii,2007,28(4):449-452.
[13]朱勇,刘莉.基于拉格朗日力学的伞-弹系统动力学模型[J].航空学报,2009,30(7):1208-1213.
ZHU Yong,LIU Li.Dynamic model of parachute-projectile systems based on lagrange mechanics[J].ActaAeronautica et AstronauticaSinica,2009,30(7):1208-1213.
[14]何民,唐硕,许志.基于凯恩方法的箭伞系统动力学建模与分析[J].飞行力学,2010,28(5):39-42.
HE Min,TANG Shuo,XU Zhi.Modeling and analysis of rocket-parachute system dynamics based on kane method[J].Flight Dynamics,2010,28(5):39-42.
[15]师娇,唐胜景,高峰,等.基于离散时间传递矩阵法的伞-弹系统动力学模型[J].宇航学报,2012,33(1):13-18.
SHI Jiao,TANG Shengjing,GAO Feng,et al.Dynamics model for parachute-submissile system based on discrete time transfer matrix method[J].Journal of Astronautics,2012,33(1):13-18.
[16]马晓冬,郭锐,刘荣忠,等.旋转伞子弹系统动力学建模与仿真[J].弹道学报,2015(3):12-17.
MA Xiaodong,GUORui,LIU Rongzhong,et al.Dynamics modeling and simulation for rotating parachute-submunition system[J].Journal of Ballistics,2015(3):12-17.
[17]马宗成,刘占辰,郑无计,等.基于拉格朗日力学的末敏弹稳态扫描阶段动力学模型[J].空军工程大学学报(自然科学版),2016,17(1):19-23.
MA Zongcheng,LIU Zhanchen,ZHENG Wuji,et al.A Dynamic Model of Rotating Parachute Systems Based on Lagrange Mechanics[J].Journal of Air Force Engineering University (Natural Science Edition),2016,17(1):19-23.
[18]杨永亮,刘荣忠,郭锐,等.旋转自稳定末敏子弹运动特性分析[J].国防科技大学学报,2018,40(1):145-150.
YANG Yongliang,LIU Rongzhong,GUO Rui,et al.Motion characteristic analysis of rotary self-stabilizing terminal sensitive submunition[J].Journal of National University of Defense Technology,2018,40(1):145-150.
[19]张俊,曹守启,吴根水,等.涡环伞降末敏子弹的稳态扫描动力学特性[J].航空动力学报,2019,34(6):1290-1296.
ZHANG Jun,CAO Shouqi,WU Genshui,et al.Dynamic characteristics of terminal-sensitive submunition with a vortex-ring parachute at steady-state scanning stage[J].Journal of Aerospace Power,2019,34(6):1290-1296.
[20]岳明凯,王程远,焦志刚,等.末敏子弹稳态扫描阶段运动特性研究[J].沈阳理工大学学报,2022,41(1):89-94.
YUE Mingkai,WANG Chengyuan,JIAO Zhigang,et al.Study on motion characteristics of terminal sensitive bullet in steady scanning stage[J].Journal of Shenyang Ligong University,2022,41(1):89-94.
[21]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.
HAN Zipeng.Exterior ballistics of projectiles and rockets[M].Beijing:Beijing Institute of Technology Press,2008.
[22]BELLOMO N,PREZIOSI L,ROMANO A.Rigid body dynamics[M].Boston:Birkhäuser Boston,2000.
[23]WHITTAKER E T.A treatise on the analytical dynamics of particles &rigid bodies[M].4th ed.Beijing:World Book Inc,2017.
[24]贾书惠.刚体动力学[M].北京:高等教育出版社,1987.
JIA Shuhui.Rigid body dynamics[M].Beijing:Higher Education Press,1987.
[25]郭锐,刘荣忠,胡志鹏,等.涡环旋转伞开伞稳定性及减速导旋运动特性研究[J].空气动力学学报,2013,31(6):733-738.
GUO Rui,LIU Rongzhong,HU Zhipeng,et al.Study on the inflated stability and motional characteristics of vortex ring parachute canopy[J].ActaAerodynamicaSinica,2013,31(6):733-738.
[26]马晓冬,郭锐,刘荣忠,等.旋转伞-末敏子弹系统动力学建模与仿真[J].弹箭与制导学报,2015,35(6):39-42,46.
MA Xiaodong,GUO Rui,LIU Rongzhong,et al.Dynamics modeling and simulation for rotating parachute-terminal-sensitive submunition systems[J].Journal of Projectiles,Rockets,Missiles and Guidance,2015,35(6):39-42,46.
[27]马晓冬,郭锐,刘荣忠,等.涡环旋转伞系统减速导旋效率研究[J].空气动力学学报,2017,35(1):57-61,70.
MA Xiaodong,GUO Rui,LIU Rongzhong,et al.Study on decelerating and spinning efficiency of vortex ring parachute system[J].ActaAerodynamicaSinica,2017,35(1):57-61,70.