0 引言
随着超空泡武器及相关理论的不断发展,水下枪发射超空泡射弹进行水下攻防作战具有较好的应用前景,相关研究[1-3]表明:超空泡射弹的水下运动稳定性对膛口初始运动参数极为敏感。因此,水下枪(炮)的膛口动态过程具有重要研究价值。
近年来,较多学者针对水下膛口动态过程进行了研究,针对水下膛口压力场的演化规律,张京辉等[4]对弹道枪水下全淹没发射不同水深时的膛口流场典型波系结构进行了研究,结果表明膛口流场典型波系结构形成的时间随水深的增大而变长。蔡涛[5]对30 mm口径火炮全淹没式发射过程进行了数值模拟,研究结果表明:弹丸出膛口前,膛口附近会产生肺状超空泡,压力波主要表现为水柱冲击波,弹丸出炮口后,主要压力波由水柱冲击波转换为弹前激波。张旋[6]对机枪水下发射枪口燃气喷射压力对膛口流场分布特性的影响进行了仿真,得到了燃气喷射压力在30~60 MPa时,燃气喷射压力越大弹丸越早脱离火药燃气的包围。
针对非对称膛口流场的演化规律,刘康等[7]研究了不同斜切角度膛口装置产生的非对称流场,发现流场中的弹体两侧存在压力差,激波压力作用在斜切角度膛口装置上可以起到抑制膛口跳动的作用。郭则庆等[8]对内埋式航炮的膛口流场进行了数值模拟实验,结果表明:在不同的来流马赫数条件下,非对称膛口流场中的两侧机翼表面压力分布规律不同,且冲击波强度与来流马赫数有关。
针对射弹与膛口流场之间的互相作用关系,Schmidt[9]通过诱发非对称膛口燃气流场,估算了由非对称气动载荷引起的弹丸线速度,计算了由于角速度和线速度引起的射弹运动状态变化,计算结果和测量值较为吻合。Dayan等[10]对非定常膛口流场进行了仿真,计算了包含射弹在内的膛口流场演化过程,对初始冲击波和马赫盘等膛口流场主要特征进行了研究,仿真计算结果与实验阴影图结果之间存在较好的一致性。
针对复杂膛口流场的仿真计算方法,Crowley等[11]研究了非结构化网格在仿真计算中的使用,并与结构化网格的计算结果进行对比。研究结果表明:与结构化网格相比,基于非结构化网格的程序计算运行时间相对较快,对于非常复杂的模型更有利于计算。
综上所述,水下非对称膛口流场与射弹的运动状态密切相关,水下发射的膛口动态过程对射弹的运动稳定性至关重要。本研究针对14.5 mm水下枪在贴壁发射时的典型非对称膛口动态过程进行二维平面仿真,以揭示不同贴壁距离条件下水下非对称膛口流场的演化过程及射弹运动规律。
1 计算模型
1.1 计算方法
数值计算采用VOF(volume of fluid)多项流模型,湍流模型采用标准k-ε模型,利用PRESTO!方法对压力项离散,采用压力隐式算子分裂算法(PISO)耦合压力和速度,动量和能量的离散采用二阶迎风格式,计算时间步长0.5 μs。
1.2 基本假设
由于水下膛口流场的演化过程十分复杂,为了能够对其进行有效的数值模拟,对计算模型进行了如下假设:
1) 不考虑火药燃烧过程产生的压力变化。
2) 将火药燃气视为可压缩理想气体,满足理想气体状态方程,忽略膛口燃气多组分化学反应的影响。
3) 弹丸在膛内沿X轴方向做正向平移运动,出膛之后不考虑重力影响,在XOY平面受环境压力作用自由运动。
4) 将水看作不可压流体,参考密度取998.2 kg/m3。
5) 膛口及射弹周围采用Schnerr-Sauer空化模型。
1.3 控制方程
按照上述计算方法和基本假设建立方程:
1) 连续性方程:
式中:下标q=1,2,3分别代表燃气相、液相和水蒸气相;ρq为对应项的密度;α1、α2、α3为对应的体积分数,且α1+α2+α3=1;vq为流体速度;Sm为单位体积内气液两相的质量流量。
2) 动量方程:
-αqdivpq+div(μ grid vq)+Sp
式中:ρ为混合物相密度;Pq为对应项的压力;Sp为汽液两相间质量输运引起的动量变化。
3) 能量方程[12]:
式中:E为平均能量;P为混合相压力;T为平均温度;keff为有效热传导率;Se为能量方程源项,即空化引起的流场能量的改变,其大小等于气液之间质量交换量与汽化潜热的乘积。
4) 理想气体气体状态方程:
pv=nRT
式中:R=8.314 J/(mol·K),为理想气体常数。
5) k-ε湍流方程:
式中:k为湍动能,ε为耗散率;i和j为自由指标,ui和uj为速度矢量,μ为黏度系数,Gk是由于平均速度引起的湍动能k的产生相;常数σk=1.0为湍动能对应的普朗特数;σε=1.3为耗散率对应的普朗特数;![]() 表示湍动黏度,常数C1ε=1.44,C2ε=1.92和Cμ=0.08为经验系数。
表示湍动黏度,常数C1ε=1.44,C2ε=1.92和Cμ=0.08为经验系数。
6) Schnerr-Sauer空化模型:
式中:Γe和Γc分别为气泡生长和溃灭时质量传递源项;αv为空泡的体积分数;c为单位体积内的气泡数;ρv和ρ1分别为汽相和液相的密度; ρ为混合相的密度;pv为蒸汽分压力;Rb为气泡的半径。
2 网格无关性及计算模型验证
2.1 物理模型
针对贴壁距离分别为d=30 mm、d=50 mm、d=70 mm、d=100 mm四种工况展开研究,以贴壁距离d=30 mm的工况为例,刚壁面到射弹表面轨迹线的距离为30 mm,射弹在膛内沿X轴正向运动,计算模型如图1,其他工况类似。
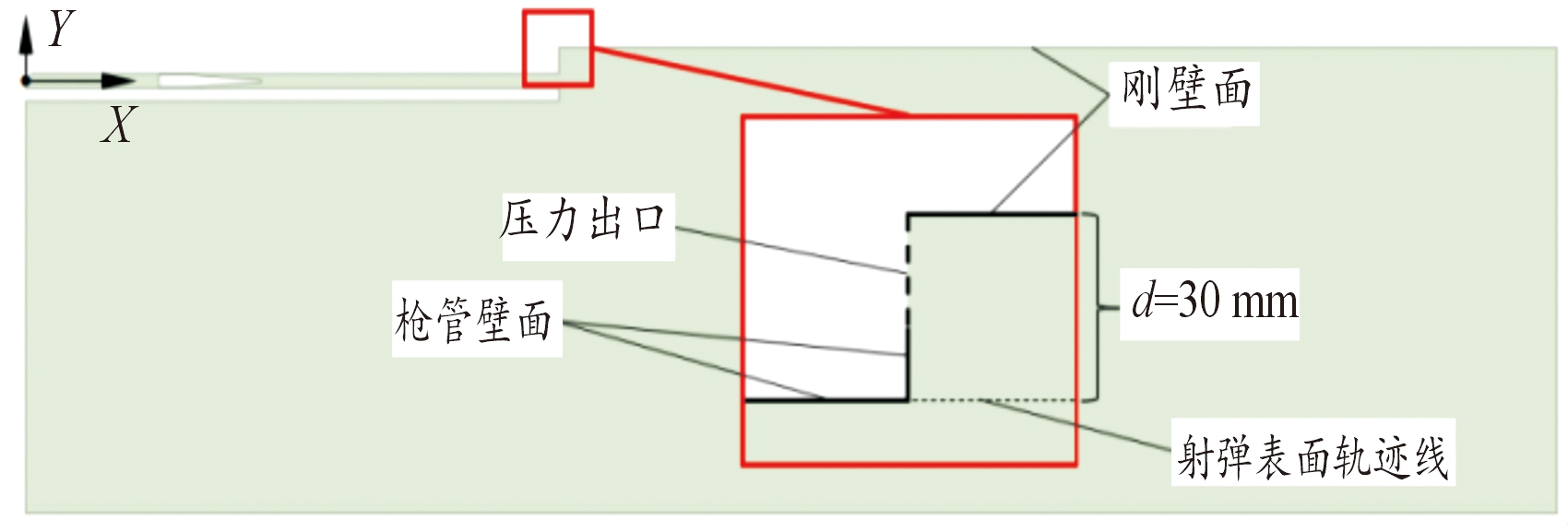
图1 贴壁30 mm模型局部放大示意图
Fig.1 Partial enlarged schematic diagram of the 30 mm model near the wall
图2为贴壁距离d=30 mm计算模型网格,计算域分为高压燃气和弹前水域2个区域,对弹丸周围网格进行加密,枪管内径14.5 mm,枪管厚度15 mm。计算域长2 300 mm,宽444.5 mm。计算域网格数量N=30万,最小尺寸为0.2 mm,采用全局三角形法进行网格划分。不同贴壁距离工况的计算域大小、形状以及网格数量略有差异,但网格质量、尺寸和划分方法与d=30 mm模型一致。

图2 贴壁30 mm模型网格示意图
Fig.2 Schematic diagram of 30 mm model grid near the wall
计算模型采用网格光顺(Smoothing)和网格重构(Remeshing)动网格技术来实现弹丸的运动,网格重新划分标准为: 0.2 mm≤l≤4 mm(l为网格长度),当射弹运动时,弹体周围网格被拉伸超过最大网格长度时,会分裂成2个网格,同理,当靠近弹头的网格长度被压缩至0.2 mm时,该网格会与相邻的网格合并。
2.2 初始条件和边界条件
模型中的枪管、弹丸边界均为刚壁面,射弹运动为沿X轴正向的刚体运动,弹前水域外边界为压力出口,弹后高压燃气区域为理想气体,初始压力值取300 MPa,弹前水域为不可压缩水介质,水深1 m,初始压力111 325 Pa,初始温度293 K。
2.3 网格无关性验证
为避免网格质量对计算结果产生较大影响,分别采用不同网格数进行试算[13],选择工况为贴壁距离d=50 mm,t=2.4 ms时刻膛口中心轴向速度分布作为网格无关性验证的特征参数。无关性验证结果如图3所示。相对于40万网格数的计算结果,30万网格数的最大相对误差仅为1.14%,而20万网格数的最大相对误差达到2.65%。综合考虑计算效率和计算精度,选择网格数为30万的网格进行仿真计算。
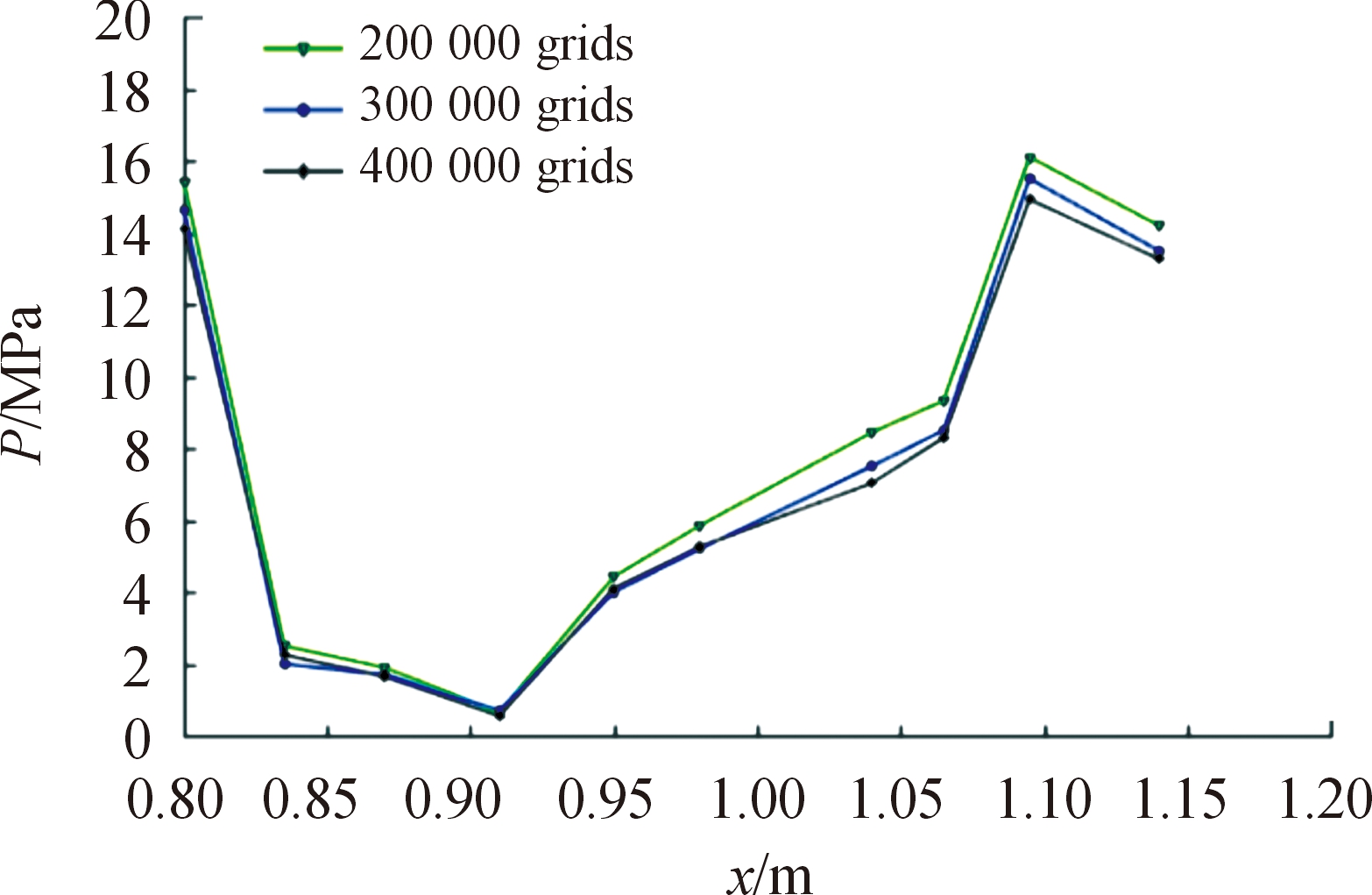
图3 不同网格数计算时弹底轴向压力分布曲线
Fig.3 Axial pressure distribution curve at the bottom of the bomb under different mesh numbers
2.4 模型验证
基于以上模型及假设,采用VOF多相流模型,标准k-ε湍流模型,利用PRESTO!方法对压力项离散,结合网格光顺(Smoothing)和网格重构(Remeshing)动网格技术对膛口流场和弹丸运动过程进行仿真计算。
为验证计算模型的合理性,对文献[14]中燃气在圆柱形充液室内喷射实验进行模拟,喷口直径为2 mm,燃气射流的初始压力为20 MPa。将试验数据同仿真计算结果进行对比,如图4所示,计算值与实验值吻合较好,最大相对误差为3.9%,初步说明了计算方法的有效性。
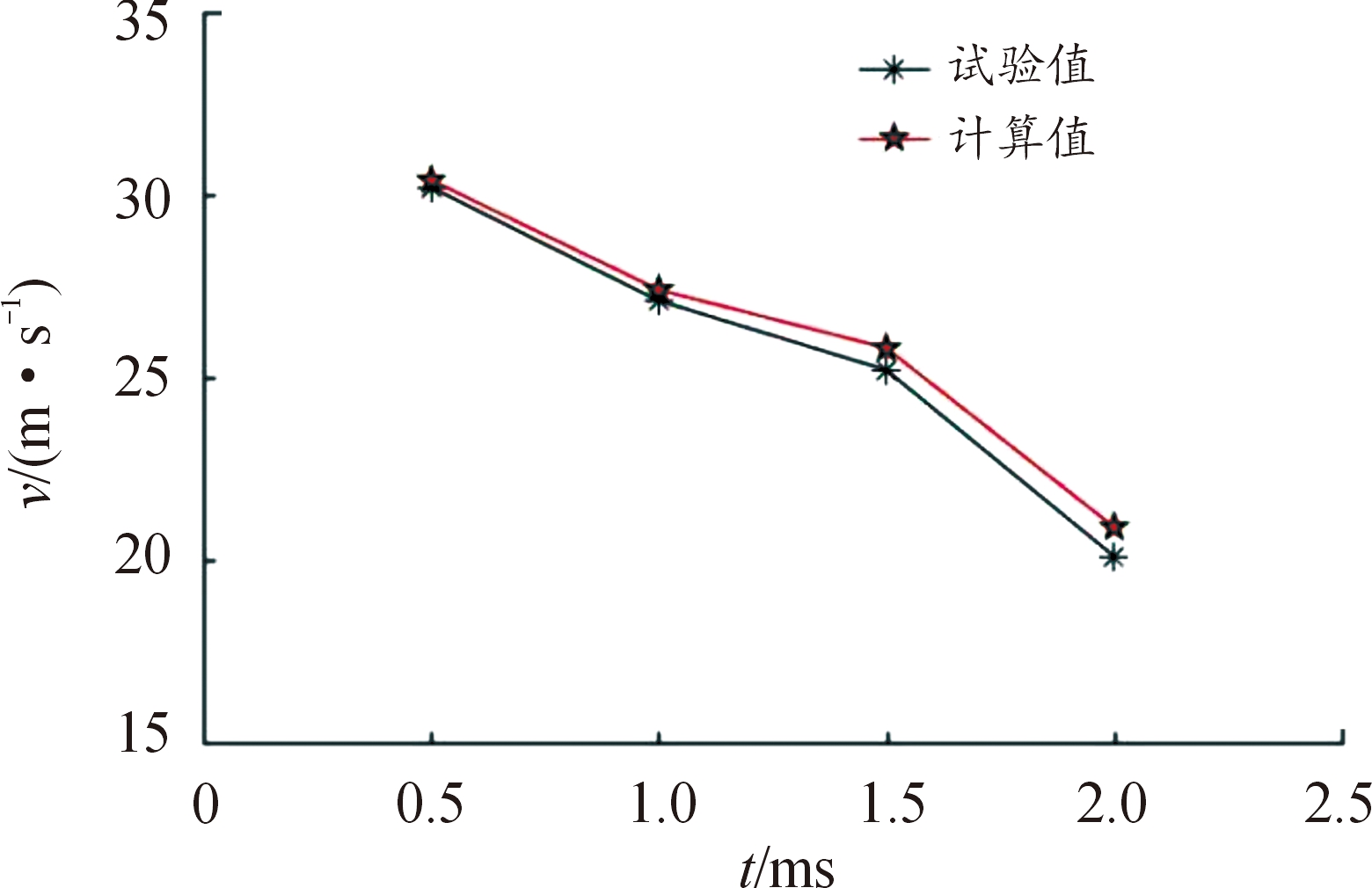
图4 燃气射流扩展速度与时间的关系曲线
Fig.4 Comparison diagram of axial displacement of jet head with time
另外,将建立模型的仿真计算结果和文献[15-16]中使用Matlab软件对各种口径的水下全淹没式发射的计算数据进行对比,如表1(口径14.5 mm为本文计算结果)。
表1 文献数据和本文计算结果对比
Table 1 Comparison of literature data and calculation results in this paper
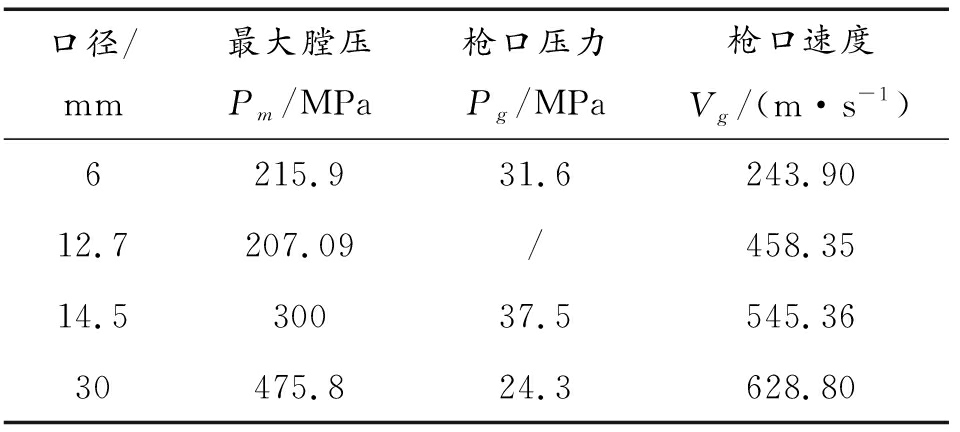
口径/mm最大膛压Pm/MPa枪口压力Pg/MPa枪口速度Vg/(m·s-1)6215.931.6243.9012.7207.09/458.3514.530037.5545.3630475.824.3628.80
结果表明:14.5 mm水下枪全淹没式发射过程的仿真计算结果和相关文献的数据较为一致,一定程度上说明了计算模型的合理性。
图5为仿真计算得到射弹空化过程局部密度云图与高速摄影捕捉的试验照片对比图。
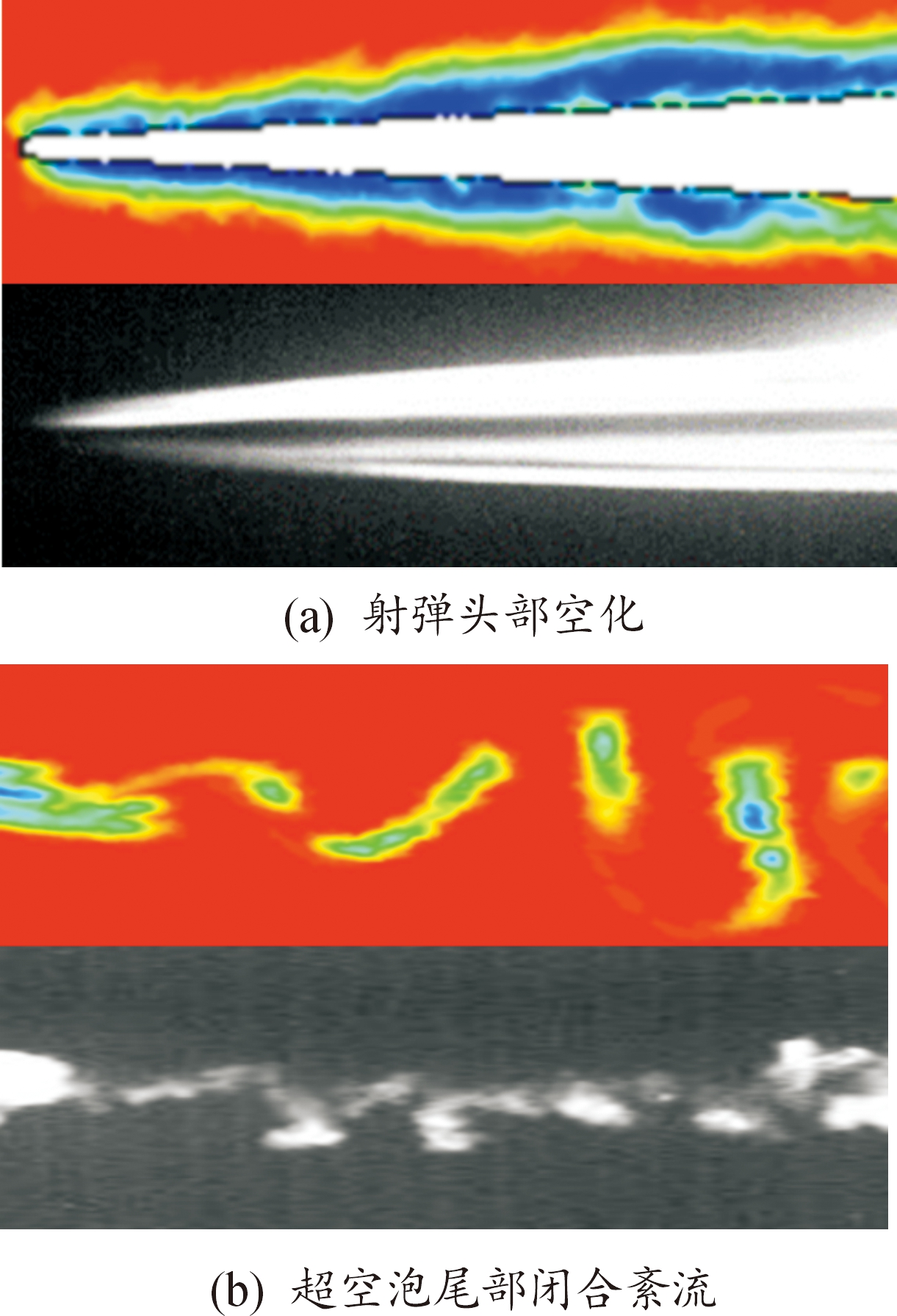
图5 仿真结果与试验照片局部对比图
Fig.5 Partial comparison of simulation results and test photos
由图5可知通过仿真得到的超空泡形态与试验照片较为吻合,进一步证明了计算模型较为合理。
3 结果分析
3.1 壁面约束对初始流场的影响
为探究水下枪在贴壁约束状态下进行全淹没式发射的膛口流场变化规律,针对14.5 mm口径弹道枪在贴壁距离分别为d=30 mm、d=50 mm、d=70 mm、d=100 mm共4中工况下的全淹没式发射膛口流场演化过程进行了仿真计算和对比分析。
由图6可以看出,射弹膛内运动时,射弹后面的燃气存在明显的速度梯度,距离弹底越近,速度越高,越靠近膛底,速度越低,体现了射弹膛内运动时的燃气扩展规律。在不同贴壁工况下,弹后高压气体推动射弹加速运动,射弹推动弹前水柱成为水射流从枪管喷出,在轴向、径向扩展形成膛口初始流场。各工况下的水柱射流在出枪口时均出现了卷吸回流现象,分析认为这是由于水射流与前方静止水域相互作用产生阻力,导致了水射流的径向扩散,另一方面,由于水射流的流速较高,膛口的水射流两侧形成了低压区,压力差导致周围水流形成回流。
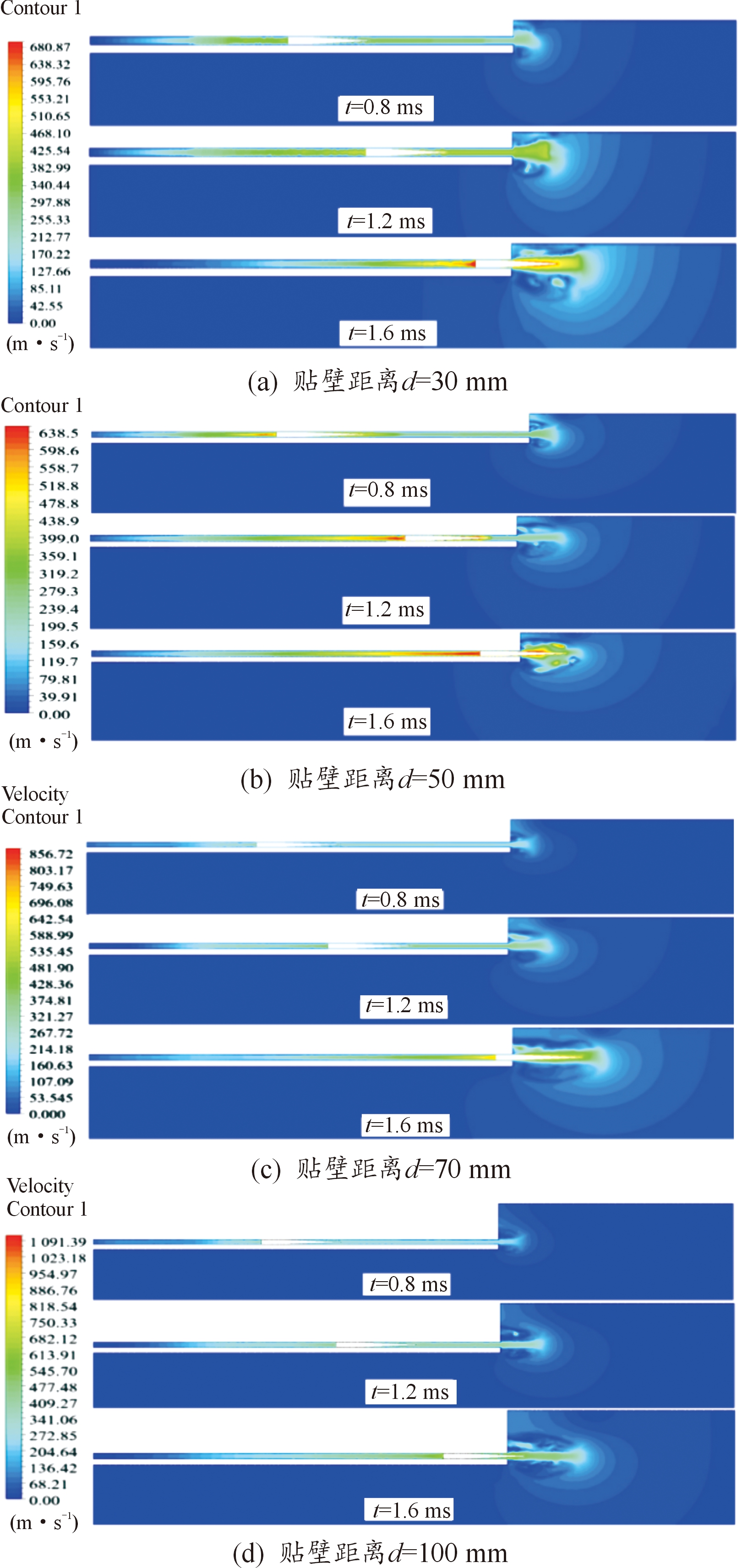
图6 各贴壁工况的不同时刻速度云图
Fig.6 Velocity contours at different times for various near-wall working conditions
在贴壁距离d=30 mm工况下,由于壁面的约束作用,水射流和壁面之间的速度梯度大,较大的剪切力使得水射流喷出枪口后整体上呈发散状态;在d=50 mm工况下,靠近刚壁面一侧的流动受到剪切力影响有所减弱,水射流出枪口后发散效果有所改善,在d=70 mm工况下,靠近刚壁面一侧水射流受剪切力的影响明显减弱,水射流出枪口后可以形成细长水柱,水射流发散情况大大改善;在d=100 mm工况下,水射流扩散几乎不受刚壁面影响,膛口初始流场形状基本对称,枪口水射流可以形成细长水柱,除射流头部以外几乎不发散。通过对比可以发现:贴壁距离越大,水射流扩散受刚壁面的约束效果越弱,弹前水射流越容易形成细长水柱,初始流场形态也越趋向于对称。
图7为t=1.3 ms时刻各种贴壁工况下的膛口初始流场相图。可以看出:在各种工况下,枪口附近都出现不同程度的空化现象,形成了文献[3]中提到的双肺状超空泡。计算结果表明:当水射流在枪口的喷射速度达到250 m/s时,膛口水射流两侧开始出现空化,随着水射流速度进一步增加,空腔不断扩展形成双肺状空化区域。由于壁面的存在,贴壁约束对空化效果产生了一定的抑制作用,当枪口贴壁越近,贴壁一侧越难形成空化,无壁面约束一侧空化效果较好。
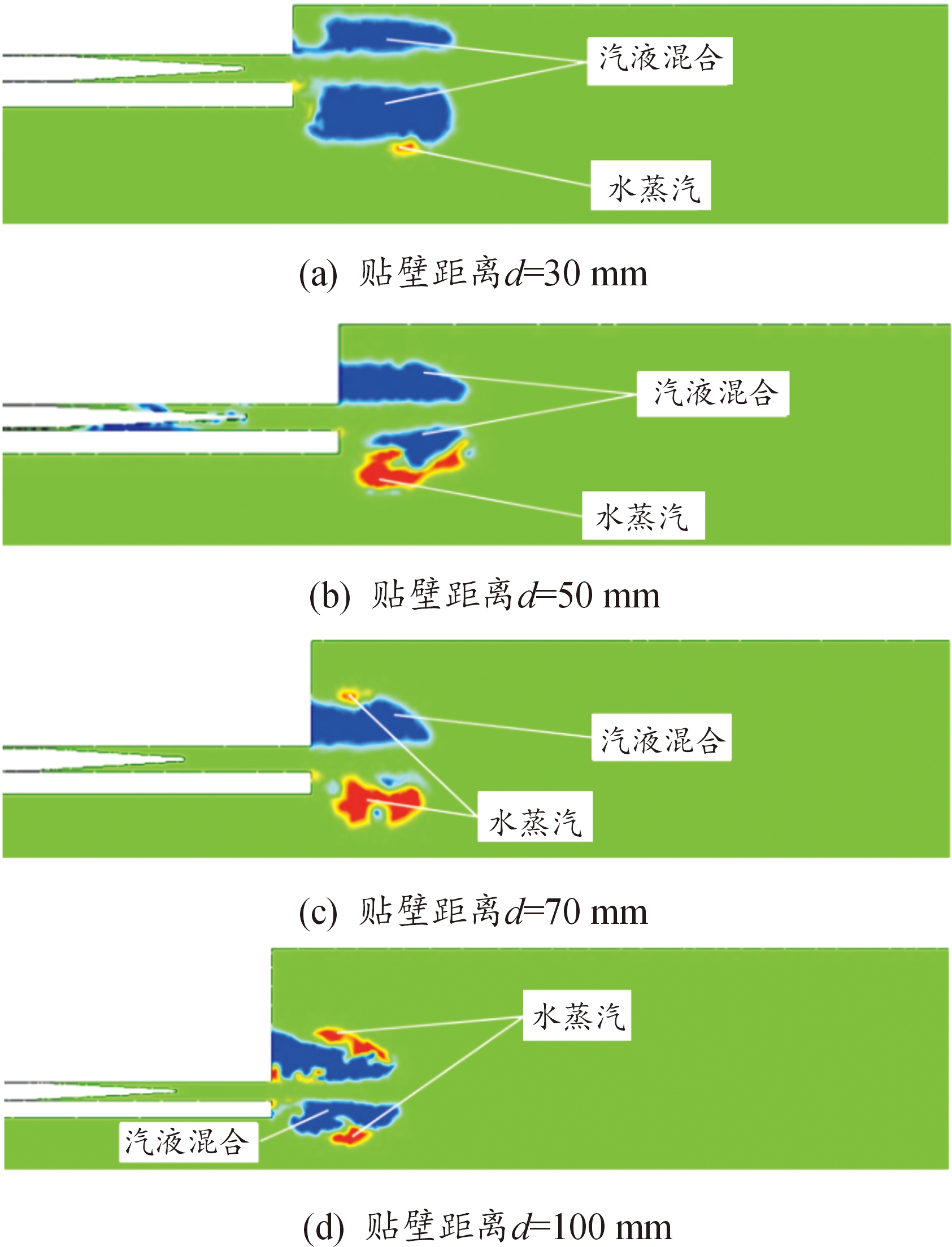
图7 不同贴壁工况的相图(t=1.3 ms)
Fig.7 Phase diagrams for different near-wall conditions(t=1.3 ms)
如图7(a)、图7(b)所示:在贴壁距离d=30 mm和d=50 mm工况下,刚壁面约束一侧无法形成完整的水蒸气相,主要是汽液混合区,且区域形态呈扁平状,初始流场不对称。当贴壁距离增大到d=70 mm时,贴壁一侧开始出现完整的水蒸气相,说明随着贴壁距离增大,壁面对膛口空化的抑制作用逐渐减弱,当贴壁距离增大到d=100 mm时,刚壁面对空化效果的抑制作用基本消失,贴壁一侧也能形成完整的水蒸汽相。
3.2 壁面约束对燃气流场的影响
针对14.5 mm水下枪全淹没式发射的弹后高压燃气扩散过程进行仿真计算。图8为贴壁100 mm工况水下全淹没式发射t=2.4 ms时的膛口流场密度云图,可见射弹已经脱离燃气包围,射弹高速运动时周围压力降低产生超空泡,超空泡尾部闭合时呈现明显的紊流特征。

图8 贴壁100 mm膛口流场密度云图
Fig.8 Density cloud map of flow field near wall 100 mm muzzle
弹后高压燃气扩展形成泰勒空腔,为研究不同贴壁工况对泰勒空腔扩展的影响,对各工况下高压燃气在X(轴向)、Y(径向)方向上的扩展距离进行计算(t=1.7~ 4.0 ms),结果如图9、图10所示。
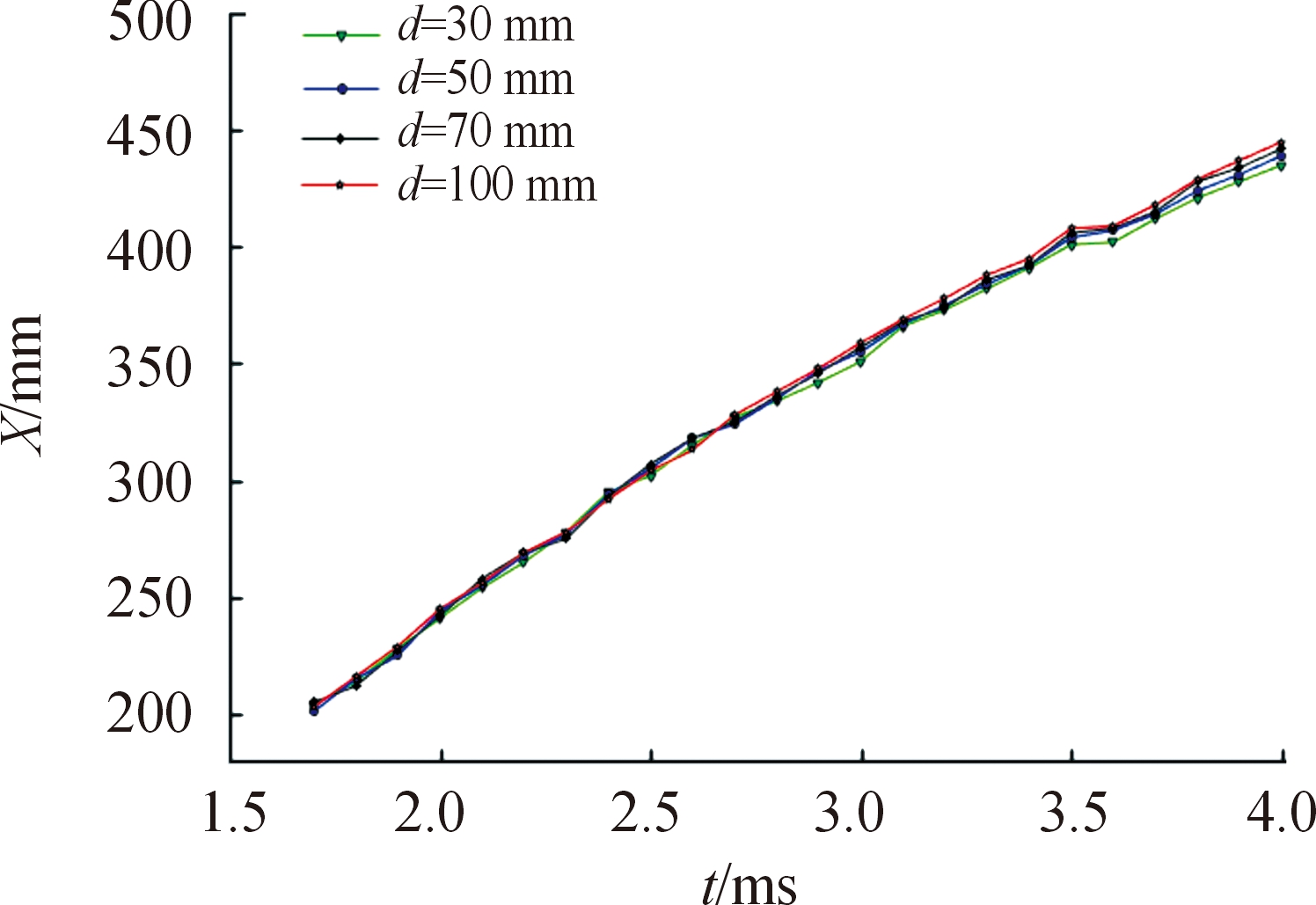
图9 泰勒空腔在X方向的边界随时间变化曲线
Fig.9 Time-dependent curve of the boundary of the Taylor cavity in the X direction
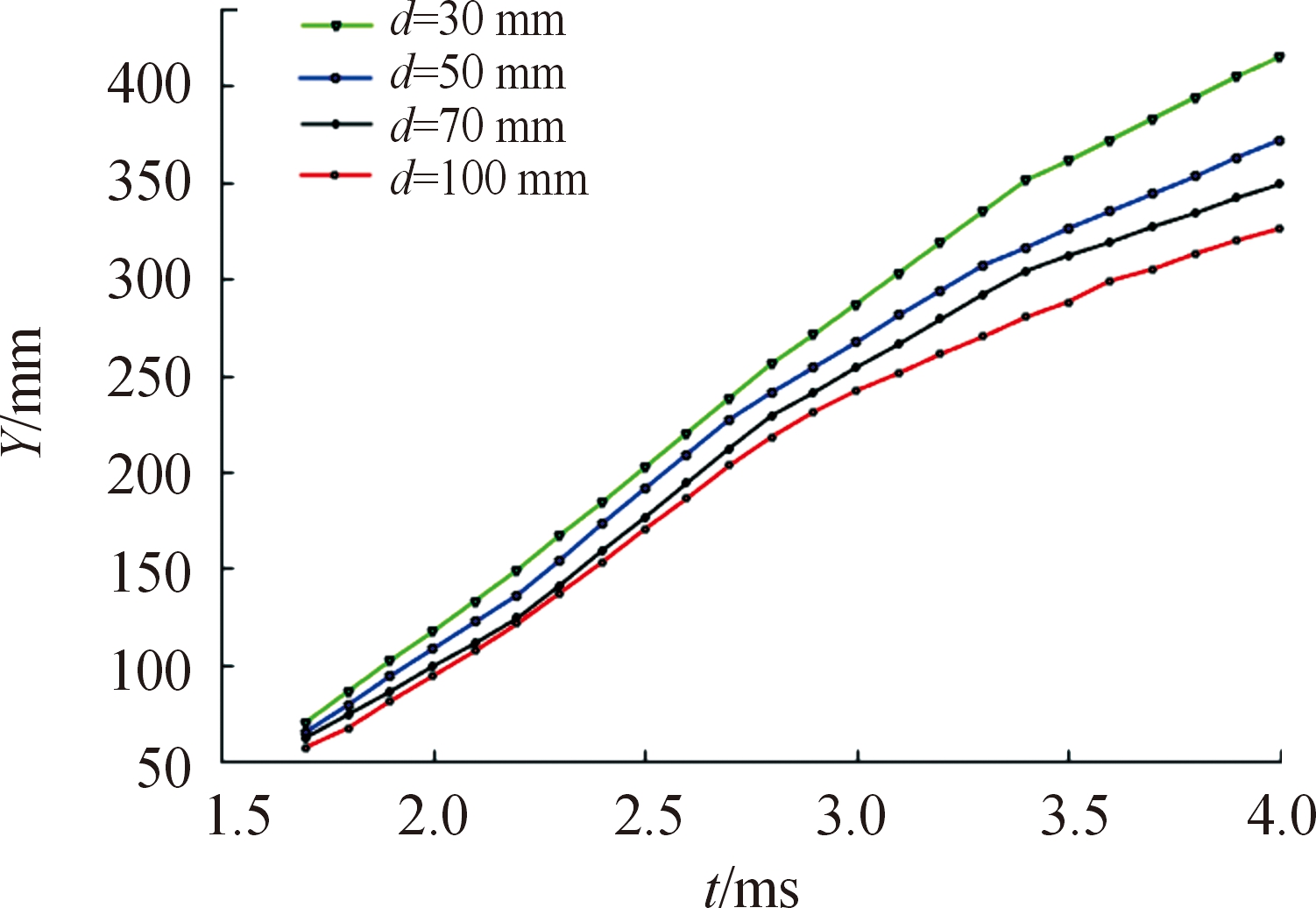
图10 泰勒空腔Y方向的边界随时间变化曲线
Fig.10 Time-dependent curve of the boundary in the Y direction of the Taylor cavity
结果表明:壁面约束对泰勒空腔边界在轴向的扩展影响微弱,而在径向扩展上影响较大;射弹在t=1.65 ms时脱离枪口,弹后气体迅速膨胀形成泰勒空腔,在1.65 ms<t<3 ms时,空腔内部压力大于外部阻力,泰勒空腔在径向的扩展速率逐渐增大,在t=3 ms时,泰勒空腔在径向的最大扩展距离为283 mm;在3 ms<t<4 ms时,空腔内部压力小于外部阻力,泰勒空腔在径向的扩展速率逐渐减小。对比各种工况发现:泰勒空腔在轴向扩展受壁面影响不大,径向扩展速率都出现先增大后减小的趋势,在同一时刻,贴壁距离越近,泰勒空腔边界在径向的位移越远。
以贴壁50 mm工况为例,对射弹出枪口后的膛口冲击波进行分析;图11为射弹出膛口过程的压力云图。
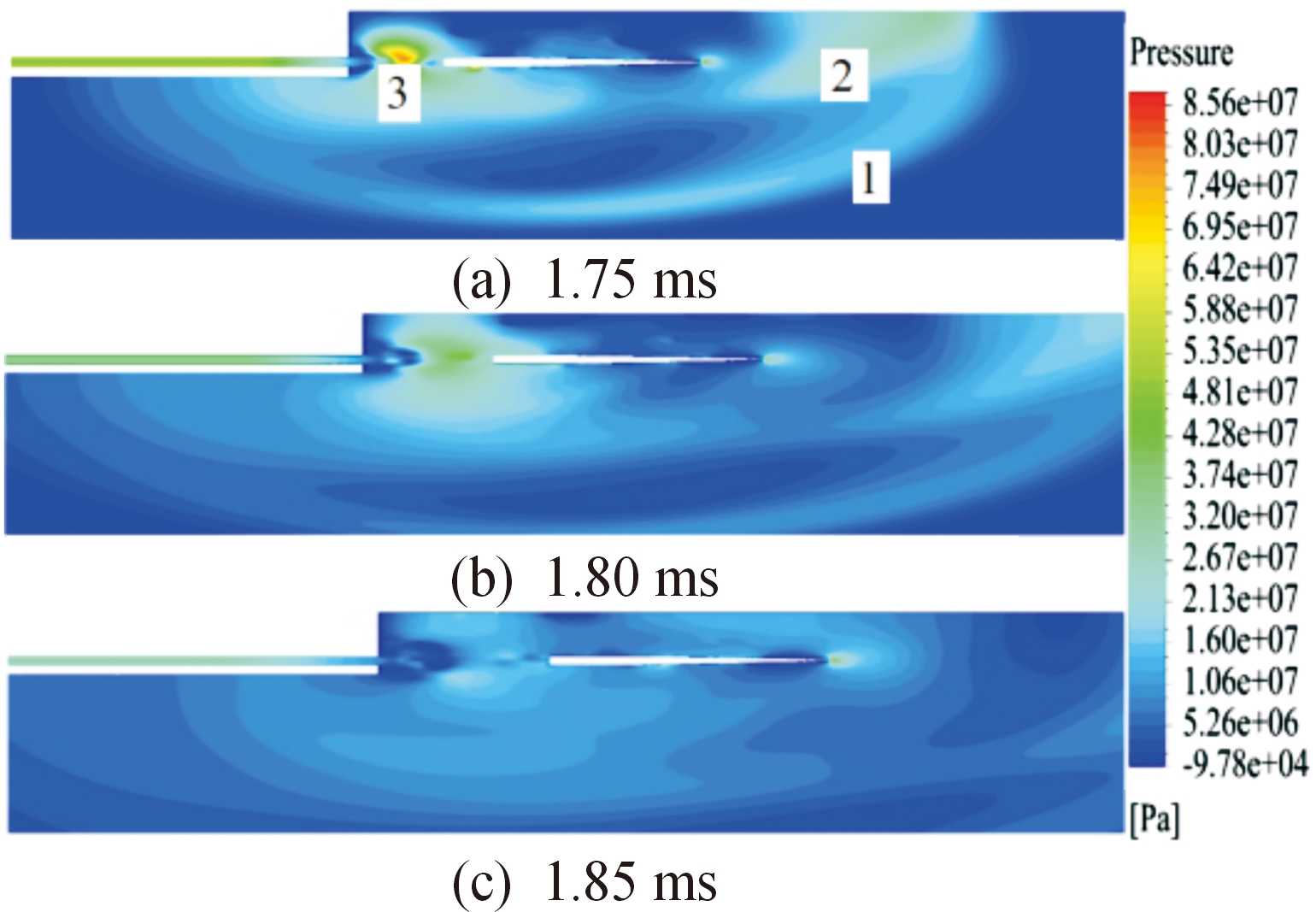
图11 贴壁50 mm工况燃气扩展压力云图
Fig.11 Gas expansion pressure cloud map near the wall at 50 mm working condition
由图11可以看出,射弹在出膛口过程中形成了多层、相交的复杂冲击波系,在刚壁面的影响下,各种激波在壁面进行反射,导致了射弹周围的环境压力的不对称。在图11(a)中指明了在贴壁工况下,射弹出膛时产生的3种主要激波:最外侧是弹顶空化器冲击水介质形成的弹前冲击波1,压力值最大为32.7 MPa;靠近弹头部的是刚壁面对弹前冲击波约束产生的反射冲击波2,在弹前冲击波1和反射冲击波2部分叠加区域,最大压力值达到41.5 MPa;靠近枪口的是弹底高压燃气扩散形成的火药燃气冲击波3,靠近膛口中心处的火药燃气冲击波与弹底和水介质相互作用,在振荡过程中产生了马赫盘,最大压力达到85.6 MPa,随着弹丸逐渐远离膛口,马赫盘处的压力峰值逐渐减小,火药燃气冲击波也呈现出下降趋势。
由于膛口冲击波在壁面处被反射,造成了射弹上下两侧不对称的压力环境,产生的压力差会对射弹运动状态产生影响[17]。为分析射弹在非对称压力场中的运动规律,对各种近壁面工况的射弹上下两侧压力分布进行监测,计算环境压力在l1、l2上的分布,图12为射弹上下两侧压力监测模型。

图12 压力监测模型
Fig.12 Pressure monitoring model
图13为近壁面d=30 mm工况,t=1.7 ms时刻,射弹上下两侧压力沿l1、l2的分布曲线。
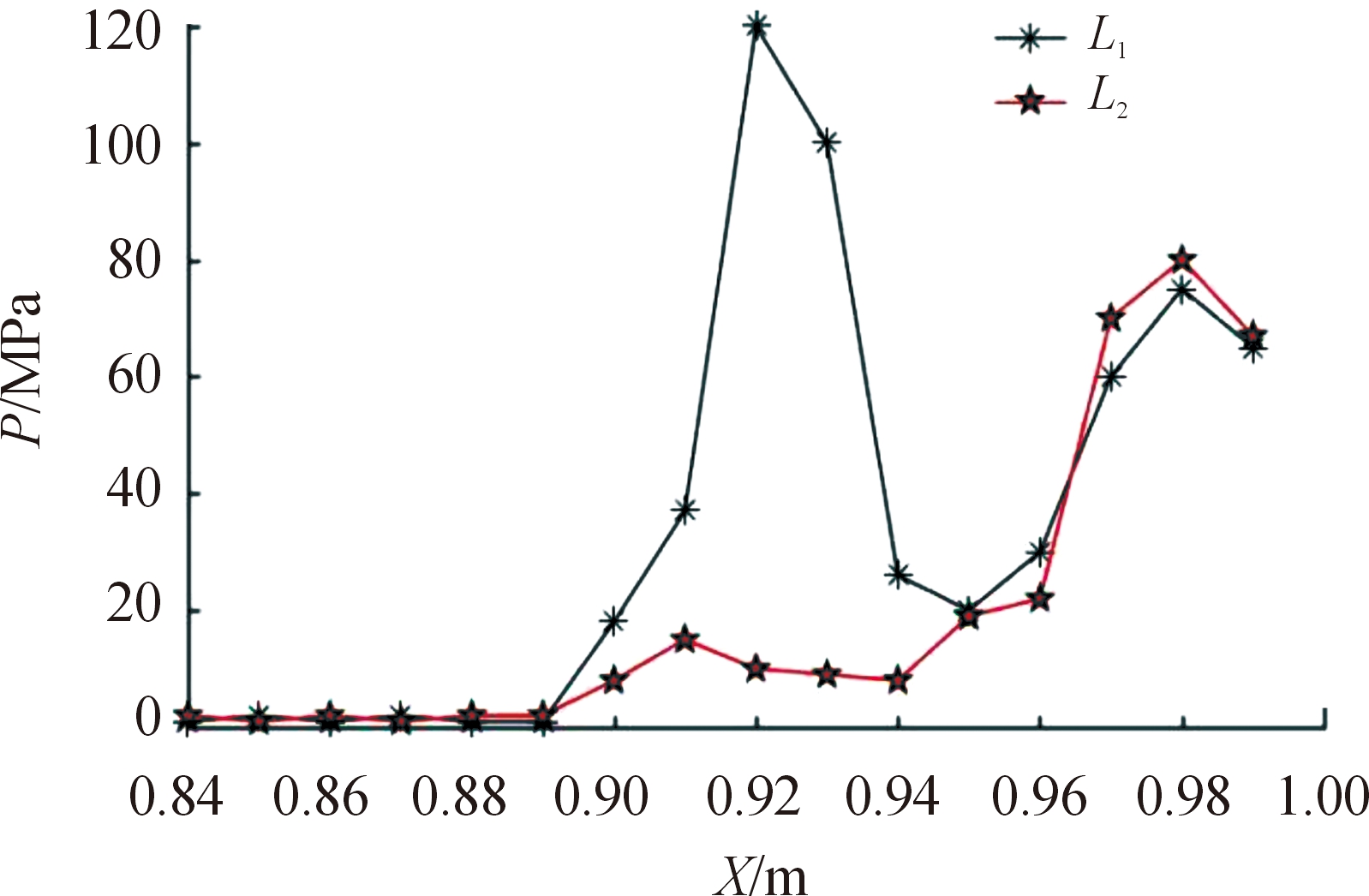
图13 射弹上下两侧压力分布图
Fig.13 Pressure distribution on the upper and lower sides of the projectile
由图13可知,刚壁面对弹前冲击波的反射使射弹两侧环境压力有较大差异,射弹头部的近壁面一侧由于受到反射冲击波的影响,其最大压力远大于无约束一侧;在t=1.7 ms时射弹两侧的最大压力差达到118.4 MPa,不同近壁面工况的射弹上下两侧最大压力差随时间变化的计算结果如图14所示(t=1.7~4.7 ms)。
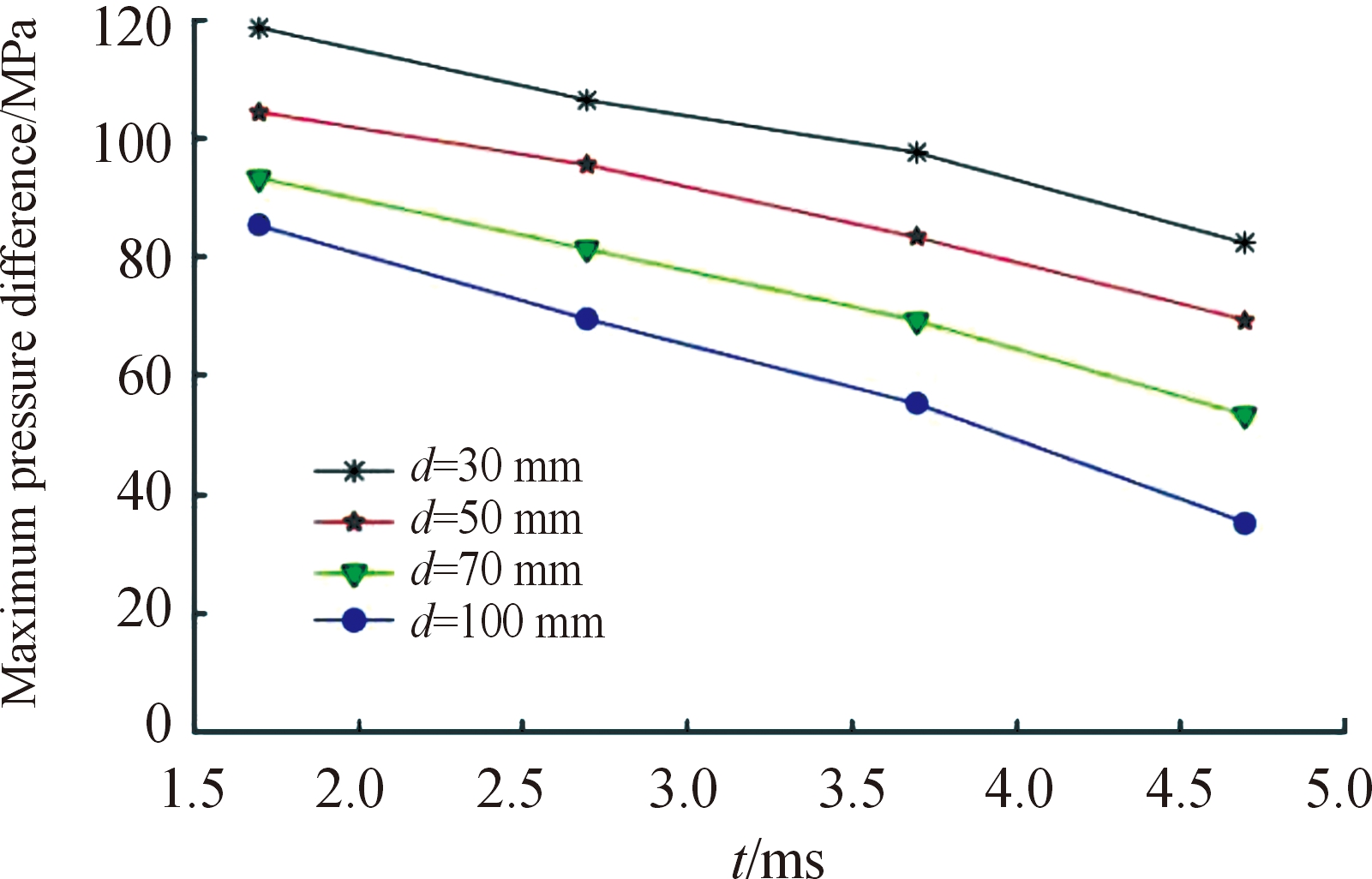
图14 射弹两侧最大压力差随时间变化图
Fig.14 Graph of pressure difference over time
由图14可知:贴壁距离越近,反射压力波在射弹上下表面造成的压力差越大。为分析压力差大小对射弹运动轨迹的影响,监测了射弹质心的坐标变化。图15为不同贴壁工况下的射弹质心纵坐标随时间变化过程(t=1.7~5.0 ms)。
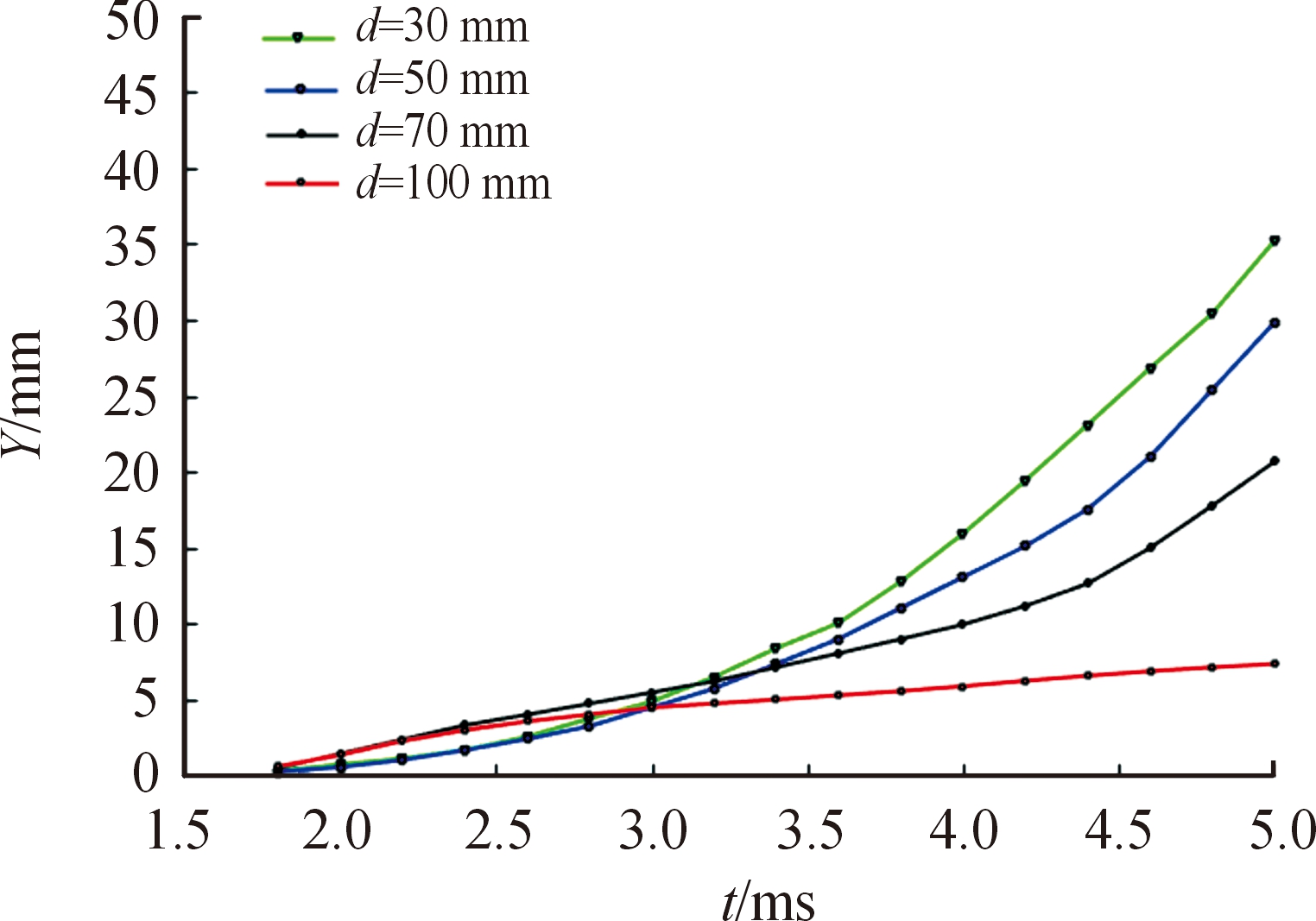
图15 不同贴壁工况射弹质心纵向位移变化曲线
Fig.15 Variation curve of longitudinal displacement of projectile under different near-wall working conditions
由图15可以看出,水下贴壁发射时,射弹质心的径向位移都偏向无壁面约束一侧,且射弹质心的径向偏移距离都随时间的延长而增大;贴壁距离越小,射弹质心的径向偏移距离越大;在d=30、50、70 mm三种工况下,射弹质心的径向偏移速率均随时间逐渐增大,表明射弹上下表面的压力差一直存在,从而造成了射弹质心的径向加速运动。同时,贴壁距离越大,射弹质心的径向位移速率越小,表明壁面对射弹质心径向运动的影响力随贴壁距离的增大逐渐减小,当贴壁距离增大到d=100 mm时,射弹质心在径向的位移变化会逐渐趋于稳定,表明壁面对射弹质心径向运动的影响基本消失。
4 结论
本文针对14.5 mm水下枪全淹没式发射时,不同贴壁距离对膛口流场演化规律以及射弹运动状态的影响进行仿真计算,主要得到以下结论:
1) 壁面对膛口初始流场有约束作用,贴壁距离越小,弹前水射流扩散受刚壁面的约束效果越强,且膛口空化效果越差;当贴壁距离增大到d=100 mm时,壁面对弹前水射流的约束基本消失。
2) 不同工况下,泰勒空腔的轴向扩展没有明显差异,泰勒空腔边界在径向的扩展速率都出现先增大后减小的趋势,空腔边界位移随贴壁距离的减小而增大,在同一时刻,贴壁距离越近,泰勒空腔边界在径向的位移越远。
3) 射弹质心的径向偏移距离随贴壁距离的减小而增大,在d=30、50、70 mm时,射弹的径向偏移速率均随时间逐渐增大,且贴壁距离越小,射弹质心的径向位移速率越大;当d=100 mm时,壁面对射弹质心径向运动的影响逐渐消失。
[1] 吕一品.超空泡航行体非线性动力学特性与运动稳定性研究[D].南京:南京理工大学,2019.
LV Yipin.Research on nonlinear dynamic characteristics and motion stability of supercavitatingvehicle[D].Nanjing:Nanjing University of Science and Technology,2019.
[2] LEE H S,KONG T Y,HONG J H.Development of a muffler for 40 mm medium caliber gun:Numerical analysis and validation[J].International Journal of Precision Engineering and Manufacturing,2018.
[3] 郑鑫.膛口流场及其对弹丸运动影响的研究[D].沈阳:沈阳理工大学,2010.
ZHENG Xin.Research on muzzle flow field and its influence on projectile movement[D].Shenyang:ShenyangLigong University,2010.
[4] 张京辉,余永刚.弹道枪不同水深下全淹没式发射膛口流场的数值分析[J].爆炸与冲击,2020,40(10):13.
ZHANG Jinghui,YU Yonggang.Numerical analysis of flow field of fully submerged firing muzzle of ballistic gun at different water depths[J].Explosion and Shock Waves,2020,40(10):13.
[5] 蔡涛.水下发射膛口多相流场分析[D].太原:中北大学,2020.
CAI Tao.Flow field analysis of underwater launch muzzle[D].Taiyuan:North University of China,2020.
[6] 张旋,余永刚,张欣尉.枪口压力对水下发射膛口流场特性的影响[J].弹道学报,2021,33(3):37-43.
ZHANG Xuan,YU Yonggang,ZHANG Xinwei.Influence of muzzle pressure on flow field characteristics of underwater launching muzzle[J].Journal of Ballistics,2021,33(3):37-43.
[7] 刘康.膛口斜切角对枪口流场影响研究[D].南京:南京理工大学,2020.
LIU Kang.Research on the influence of muzzle chamfering angle on muzzle flow field[D].Nanjing:Nanjing University of Science and Technology,2020.
[8] 郭则庆,乔海涛,姜孝海.内埋式航炮膛口流场特性数值模拟研究[J].兵工学报,2017,38(12):2373-2378.
GUO Zeqing,QIAO Haitao,JIANG Xiaohai.Numerical simulation research on flow field characteristics of buried cannon muzzle[J].ActaArmamentarii,2017,38(12):2373-2378.
[9] SCHMIDT E M.The effect of muzzle jet asymmetry on projectile motion[J].Effect of Muzzle Jet Asymmetry on Projectile Motion,1975.
[10]DAYAN Y,TOUATI D.Simulation of unsteady muzzle flow of a small-caliber gun[J].Advances In Fluid Mechanics,2006,52:165-171.
[11]CROWLEY A B,SZMELTER J.Computation of muzzle flow fileds using unstructured meshes[R].International ballistics seminar,2001.
[12]张京辉,余永刚.弹道枪水下全淹没式发射膛口流场演化特性的数值模拟研究[J].兵工学报,2020,41(3):471-480.
ZHANG Jinghui,YU Yonggang.Numerical simulation research on the evolution characteristics of the flow field of the underwater fully submerged launch muzzle of the ballistic gun[J].Acta Armamentarii,2020,41(3):471-480.
[13]张旋,代淑兰,余永刚,等.水下机枪密封式发射膛口流场特性分析[J].兵器装备工程学报,2019,40(11):60-63.
ZHANG Xuan,DAI Shulan,YU Yonggang,et al.Analysis of flow field characteristics of sealed launch muzzle of underwater machine gun[J].Journal of Ordnance Equipment Engineering,2019,40(11):60-63.
[14]莽珊珊,余永刚.高压燃气射流在整装液体中扩展过程的实验和数值模拟[J].爆炸与冲击,2011,31(3):300-305.
MANG Shanshan,YU Yonggang.Experiment and numerical simulation for high pressure combustible gas jet expansion process in a bulk-loaded liquid[J].Explosion and Shock Waves,2011,31(3):300-305.
[15]任成虎.超空泡射弹内弹道特性规律研究[D].南京:南京理工大学,2009.
REN Chenghu.Research on internal ballistic characteristics of supercavitatingprojectiles[D].Nanjing:Nanjing University of Science and Technology,2009.
[16]周永升,侯健,可学为.水下內弹道装药特性仿真分析及试验研究[J].舰船电子工程,2016,36(12):170-173.
ZHOU Yongsheng,HOU Jin,KE Xuewei.Simulation analysis and experimental research on characteristics of underwater inner ballistic charge[J].Ship Electronic Engineering,2016,36(12):170-173.
[17]KATANOD H,YAMAMOTO H,MATSUO K.Numerical simulation on supersonic flow in high-velocity oxy-fuel thermal spray gun[J].Journal of Thermal Science,15(1):65-70.