0 引言
数字孪生是以数字化方式创建物理实体或物理过程的虚拟实体,利用实时监测数据、历史运维数据以及算法模型等,模拟、验证、预测、控制物理实体全生命周期过程的技术手段[1-2]。在翼性能数字孪生是在数字空间构建一个反映发动机不同运行工况下各站位参数及整机性能参数的高精度映射模型,特别是随着在翼使用时间的累积,发动机整机性能及各部件效率逐渐退化,性能数字孪生模型需要根据在翼监测数据不断修正性能模型,以实现动态的、高精度的性能参数映射。
对于发动机性能数字孪生建模,Mitek Analytics公司通过收集机队的发动机性能数据及可靠性数据,开发了性能数字孪生(performance digital twin,PDT)模型[3]。LPTi公司利用基于物理的建模方法和实际的发动机使用数据,构建了燃气轮机数字孪生模型[4]。文献[5]采用Automation_ML对工程工具进行数字孪生建模。文献[6-7]将数字孪生概念与航空发动机可靠性相结合,探索可靠性数字孪生在航空发动机全生命周期的潜在应用。文献[8-9]利用GasTurb分别进行了CFM56-3、CFM56-5B发动机设计点性能分析并对发动机非设计点性能进行预测,文献[10]阐述了如何利用有限的数据信息构建燃气轮机的性能模型。文献[11]提出了基于多状态试验数据的发动机性能模型修正方法。
航空发动机性能模型是真实发动机物理性状的数学描述,是进行发动机故障诊断和健康状态评估以及关键件的寿命损耗评估和预测,以实现基于视情维修决策的重要基础。出于商业保密及知识产权保护的考虑,制造商(OEM)在出售发动机时并不提供性能模型,而是提供在此基础上开发的一些商业性状态监控软件或在线支持系统,如普惠的EHM,通用的GEM等。目前,航空公司对OEM提供的这些状态监控系统的深度开发和利用还不够,尚难以有效利用性能参数监控信息来定量评估各单元体健康状态及关键件的寿命损耗,因此也难以为发动机/单元体的维护与维修策略提供科学合理的决策支持。因此,借助有限的信息及发动机试车台数据来构建发动机的性能模型,以及进一步利用在翼运行监测数据不断修正性能模型,即建立在翼航空发动机性能数字孪生模型,是本论文的主要研究目标。现代涡扇发动机在线状态监测参数丰富,涵盖发动机气路主要部件及关键附件系统(滑油、燃油控制等附件系统)等,机载数据采集系统频率一般在0.25~4 Hz,整个航班采集了大量结构化的数据可供航后进一步分析,这些记录的状态数据通常称为QAR(quick access record)数据。本文提出了基于QAR数据的发动机性能模型修正方法,通过循环迭代计算的设计点性能匹配和特性图缩放和特性图参数寻优的非设计点性能匹配,借助GasTurb软件,构建了CFM756-7B发动机在翼性能数字孪生模型。
1 建模方法及步骤
1.1 数据获取及校正
在翼发动机运行中的数据由快速存取记录器(quick access recorder,QAR)记录,该记录器记录飞机不同飞行工况数据。其中可用数据有海拔(Alt)、大气温度偏差(ISA)、飞行马赫数(Mach)、燃油流量(WF)、低压转子转速(N1),高压转子转速(N2),排气温度(EGT),大气压力(P0),大气温度(T0),风扇出口总压(PT2),高压压气机出口静压(Ps3),高压压气机入口总温(T25),高压压气机出口总温(T3)和发动机进口气流流量(W2Rstd),其中W2Rstd是根据其他参数由以下公式[12]计算得到:
(1)
式中:K为常数;当气流为空气时,K=0.040 4;当气流为燃气时,K=0.039 7;A为发动机2站位截面面积;q(λ)为流量函数,可以由以下公式获得:
(2)
(3)
(4)
根据马赫数求出速度系数λ,再根据λ由式(3)得到密度比,最后通过式(4)得出流量函数q(λ)。
设计点计算时,需要将相关数据折算到标准日状态(T=288.15 K,P=101.325 kPa),流量和转速的折算公式如式(5)、式(6)所示,校正后称为折合流量和折合转速。
(5)
(6)
要建立在翼发动机性能模型需要一系列数据(运行环境数据,性能数据、工作工程参数、部件效率及损失等),仅有QAR数据并不能满足建模要求。其余数据,由于商业保密原因,无法轻易获得准确数据,需要研究者从相关论文、书籍、手册以及网络上收集、推测或假定初值。这些数据是设计点匹配的基础。
1.2 设计点性能匹配
设计点性能匹配是非设计点性能匹配的基础[10,13],只有进行设计点热力计算,确定了发动机特征尺寸后才能进行发动机非设计点热力计算,匹配发动机的非设计点性能。由于研究对象是已服役的航空发动机,发动机设计点已存在,但无法获取厂家的设计点数据。因此,从在翼发动机运行工况点选取一个高推力点(一般为起飞工况点)当作发动机的设计点[8-10],避免与理论设计点混淆,称之为循环参考点,也就是说循环参考点也是“非设计点”。
非设计点状态时,发动机各部件的工作参数均偏离设计点的工作参数,并且各部件工作状态相互制约,需要满足共同工作条件,即流量平衡、功率平衡以及转速平衡。为了达到上述平衡条件,建立航空发动机共同工作方程组,并对方程组进行求解,流程如图1所示。该共同工作方程组是非线性方程组,一般通过数值迭代方法求解。目前常用的迭代求解方法主要是 Newton-Raphson及其改进方法,以及 Newton-Broyden法[14]等。
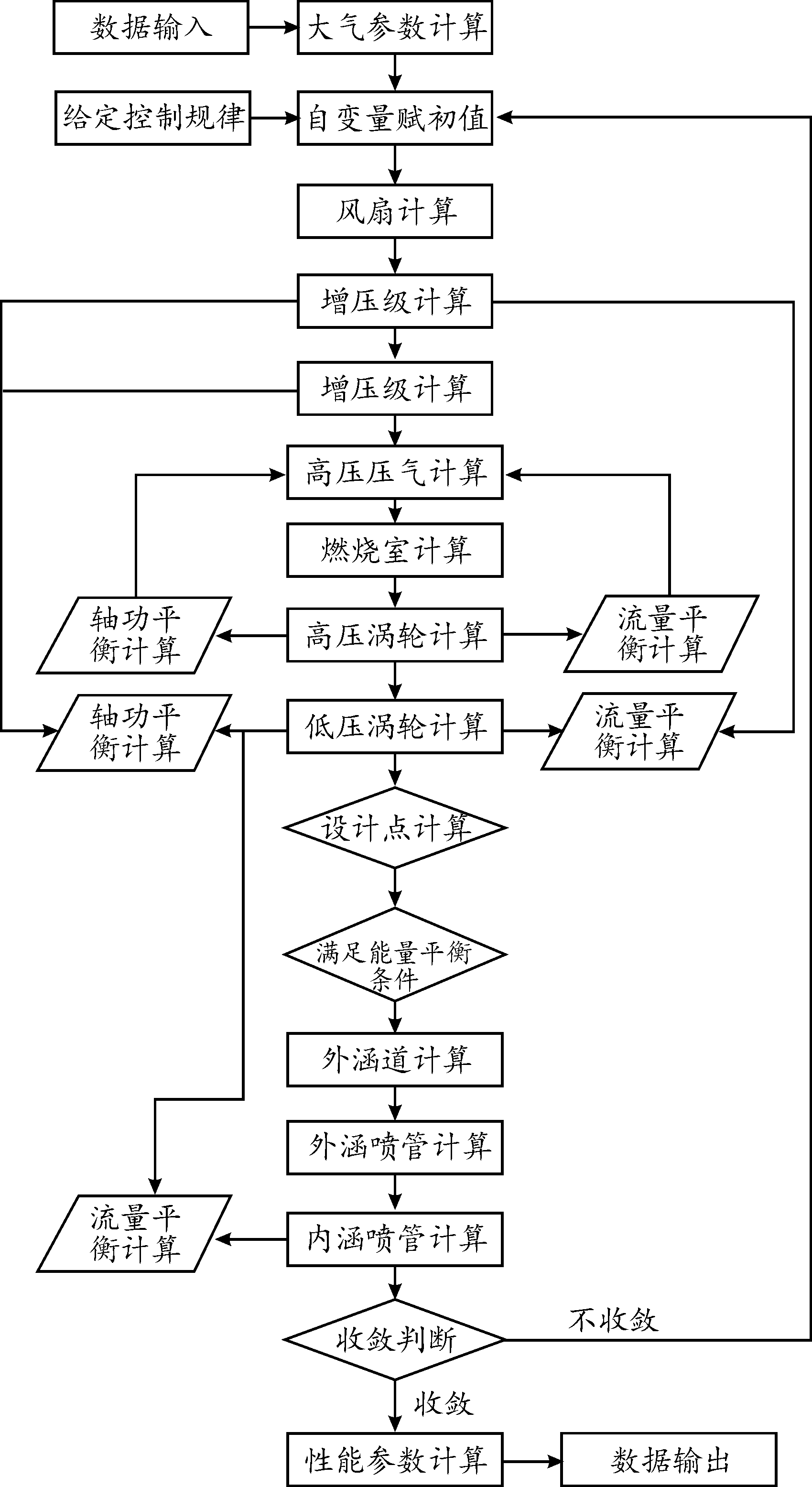
图1 设计点(循环参考点)性能匹配计算过程
Fig.1 Design point (cyclic reference point) performance matching calculation process
1.3 非设计点性能匹配
对于在翼航空发动机,运行环境和工作条件(飞行高度、马赫数、环境温度、油门杆角度等)的变化导致发动机常工作于非设计点,相应的发动机工作性能称为非设计点性能。
非设计点性能匹配和设计点性能匹配机理一致,即将发动机各部件独立出来分别进行气动热力计算,然后根据发动机工作过程中所必须遵守的气动热力学定律,把发动机的共同工作表示成一组非线性的气动力方程。两者的不同之处是设计点性能匹配需要的压比、流量、效率等数据由循环参考点数据给定。非设计点性能匹配数据通过特性图读取。因此需要合适的组件特性图来预测偏离设计点条件的部件效率。由于无法获取厂家的部件特性图,因此需要研究者通过文献查找或通过调整缩放通用特性图的方式,获得与建模对象非设计点性能匹配的特性图,本文采用基于GasTurb内置通用特性图调整缩放的方法获得压气机(LPC、IPC、HPC)和涡轮(HPT、LPT)特性图。
通常,压气机和涡轮特性图由压比、等熵效率、折合流量、折合转速4个参数表示,如图2所示。
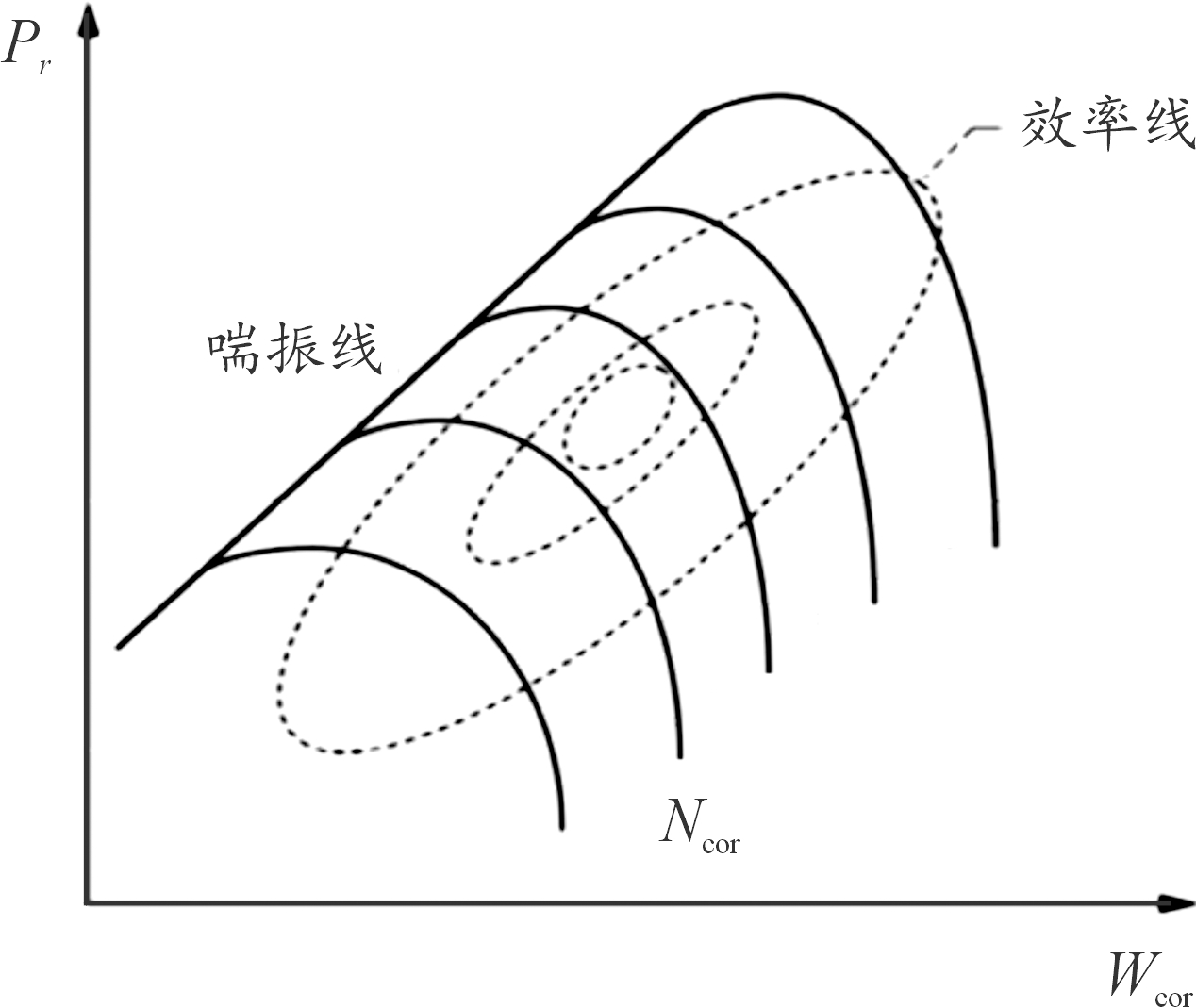
图2 通用特性图
Fig.2 General characteristic diagram
在压气机特性图中,堵塞区附近特性线斜率陡峭,易出现某一组折合转速与折合流量对应2个压比;而近喘振区附近特性图变化平缓,易出现某一组折合转速与压比对应2个折合流量[15]。为了避免上述问题,Kurzke在整个特性图中引入等β线,β取值范围在0~1,如图3所示[9]。这使得一组折合转速(Ncor)与 β 值对应唯一一组折合流量、效率与压比,即可将β 作为辅助变量用于压气机与涡轮特性图描述,特性图描述如式(7)所示。
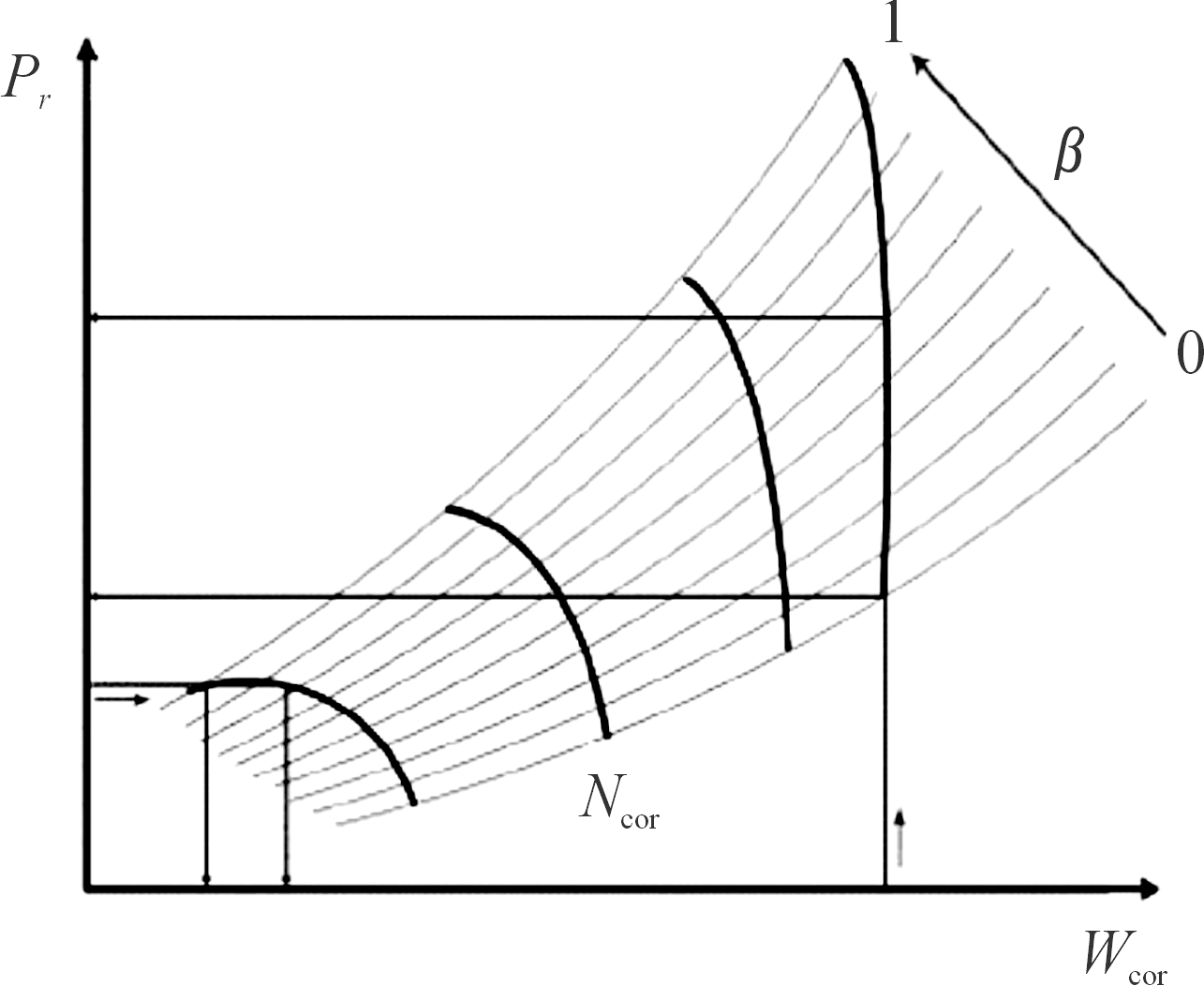
图3 β线示意图
Fig.3 β line diagram
(Wcor,η,π)= f (β,ncor)
(7)
1.3.1 调整缩放压气机特性图
压气机特性图沿一条工作线产生折合流量—效率、折合流量—折合转速2个相关性[8-10],通过调整缩放特性图匹配上述相关性,匹配成功,即得到与非设计点性能匹配的特性图。
1) 折合流量—效率匹配
由式(7)知,由β值和折合转速(Ncor)可确定部件设计点的位置(通用特性图设计点默认β=0.5,Ncor=1),通过调整β值与Ncor值获得适合的部件设计点,调整方法基于经验或试验。由于设计点性能匹配获得的整机设计点各部件参数与部件通用特性图设计点参数不一致,为了使两者保持一致,需要对特性图进行合理缩放。缩放过程中,一般需选取部件设计点为参考缩放点(reference scaling point,rsp),而将燃气轮机整机设计点各部件参数作为目标缩放点(target scaling point,tsp),利用式(8)—式(11)求出特性图的折合流量、压比、效率与折合转速修正系数速 fmass、 fpr、 fspeed:
(8)
(9)
(10)
(11)
在获得修正系数fmass、 fpr、 fspeed后,采用式(12)—式(15)分别对部件特性图的折合流量、压比、效率与折合转速进行修正。式中,下标“map,s”表示经缩放后的特性图,下标“map,o”表示未经缩放的原始特性图。
Wcor,map,s=fmass·Wcor,map,o
(12)
πmap,s=fpr·(πmap,o-1)+1
(13)
ηmap,s=feff·ηmap,o
(14)
ncor,s=fspeed·ηcor,o
(15)
综上所述,匹配部件图折合流量—效率相关性是基于经验和试验,通过更改β和值选择合适的部件设计点,并利用修正系数合理缩放得到,当再调整部件设计点无法进一步匹配效果时,考虑更换部件特性图或者修改特性图中的效率分布[8-10]。在此匹配过程中,反复将仿真结果与QAR数据进行对比,直到仿真数据与QAR数据一致为止。
2) 折合流量—折合转速匹配
当折合流量—效率相关性匹配完成后,通过在压气机特性图中重新标记(Re-Labeling)转速线匹配折合流量—折合转速相关性。
由于修改特性图效率分布和重新标记转速线的调整范围大,很难通过一次调整匹配成功,需要经过试验多次逐步缩小调整范围,根据调整实验数据,采用贝叶斯优化算法获取最优的调整参数进行调整。
3) 特性图参数试验寻优
由于需要同时调整HPC、LPC、IPC特性图的效率分布和重新标记特性图中的转速线,因此需要同时调整3张特性图的效率调整参数和转速线调整参数,分别记为δ1、δ2、δ3、δ4、δ5、δ6,称为一组特性图参数。本文先确定这6个参数的大致区间,将区间两边界值用来调整特性图,每进行一次调整获得一个试验模型,并用该模型仿真QAR工况点数据,仿真结果与QAR工况点数据进行误差对比,得出一个整体误差值,记为Δp。通过不断缩小特性图参数区间,逐步将整体误差Δp降低。但通过手动调整使整体误差接近0的方法是不现实的,因为工作量十分大。当得到多组特性图参数和对应的整体误差后,采用贝叶斯优化的方法找到整体误差接近于0时对应的特性图参数组,用该组特性图参数调整各组件特性图,便可得到误差最小的模型。具体步骤如下:
1) 设计特性图参数组
δ1、δ2、δ3、δ4、δ5,δ6分别表示HPC、LPC、IPC特性图效率分布和速度线的调整参数,每个参数根据经验和试验取调整区间两端端点值,然后随机组合得到64组特性图参数向量Y=(δ1,δ2,δ3,δ4,δ5,δ6);进一步的将调整区间逐次减半,获得多组特性图调整参数,并对特性图做相应调整。
2) 计算误差值Δp
模型仿真相对误差计算公式如下:
(16)
式中: m表示仿真参数个数; Pmodel表示模型仿真的参数矩阵; Pqar表示由QAR数据获取的对应参数矩阵。
3) 贝叶斯优化方法寻优
根据调整试验获得的特性图参数与模型整体误差Δp之间的对应关系,通过算法训练得到贝叶斯模型(δ1,δ2,δ3,δ4,δ5,δ6)=f(Δp),通过该模型反向推测模型整体误差Δp最优时的特性图参数组。
1.3.2 调整涡轮(HPT、LPT)特性图
对于双轴涡扇发动机,调整缩放HPT特性图对性能匹配效果影响非常小,因为HPT特性图运行范围非常狭窄,涡轮效率的任何变化都是由叶尖间隙效应引起,而非特性图中的设计点位置变化导致[10]。低压涡轮(LPT)性能与HPT相似。综上,对于涡扇发动机,调整HPT和LPT部件特性图设计点位置只有轻微的影响,故本文采用GasTurb内置双转子涡扇发动机特性图,并在其基础上简单调整部件特性图设计点位置。
2 建模实例与仿真分析
CFM-7B发动机为双转子、带增压级、分开排气、大涵道比涡轮风扇发动机。风扇部分是1级轴流式;低压压气机部分是4级轴流式;高压压气机部分是9级轴流式,包括1 级可调引气导向叶片和前3级可调静子叶片,第5级和第9级为引气出口,引气用途包括飞机用引气和发动机内部冷却引气,其结构及站位如图4所示。参考 Gas Turb软件说明,对应的发动机类型为:‘Geared Unmixed Flow Turbofan’,将其齿轮传动比(Gear Ratio)设定为 1,即相当于没有齿轮减速,增压级和风扇同轴同转速联动。
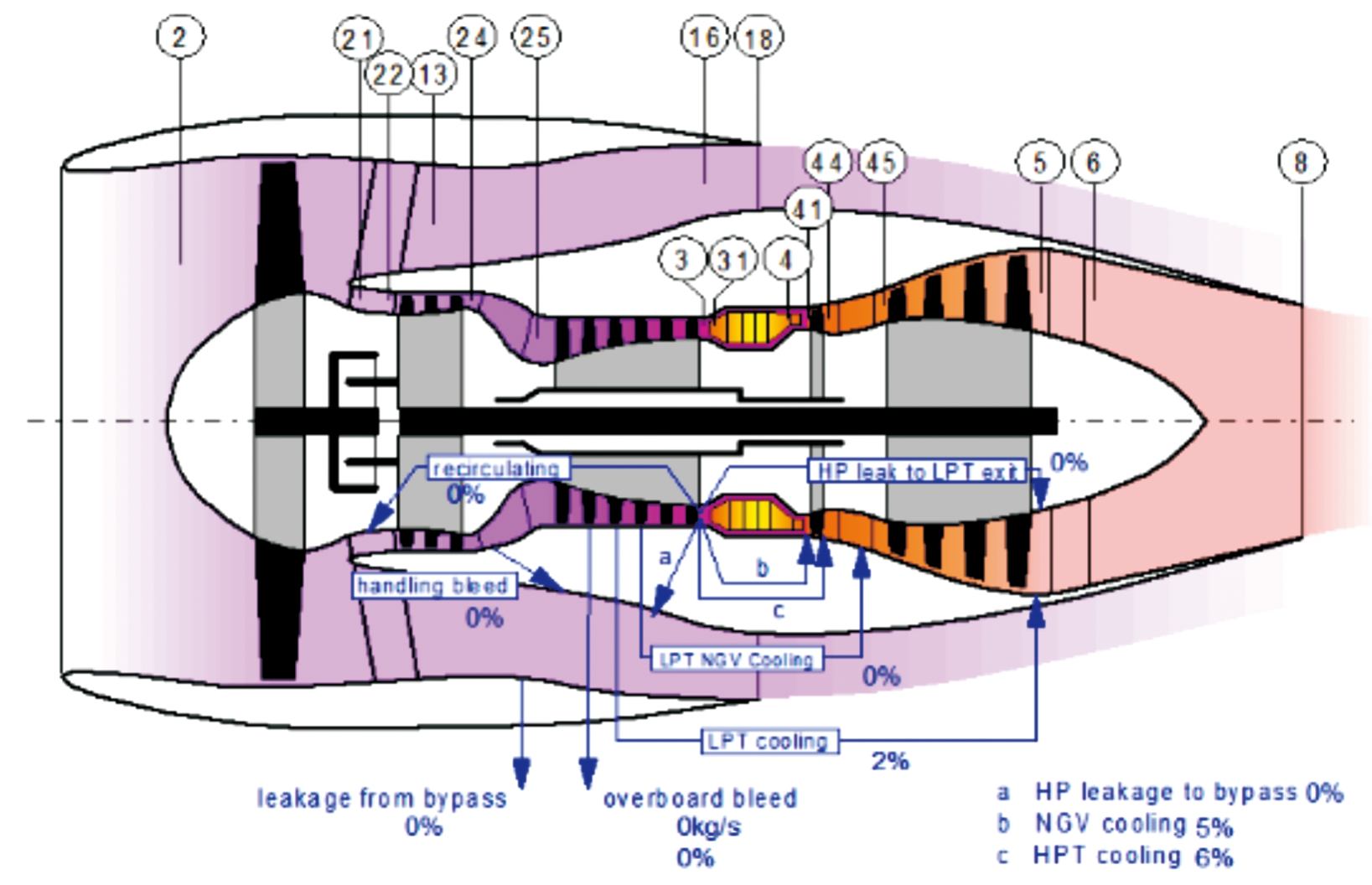
图4 CFM56-7B发动机站位示意图
Fig.4 Schematic diagram of CFM56-7B engine station
2.1 数据获取及校正
通过对QAR数据进行整理、清洗、折算、计算等工作,CFM56-7B发动机起飞等获36个工况点数据,每个工况点记录参数:Alt、ISA、Mach、WF、T3、EGT、Ps3、T25、PT2、N1、N2、W2Rstd等。通过文献[15,17-19]获得压气机压比、涡轮压比、压气机效率、涡轮效率等参数,最终获得循环参考点数据,如表1所示。
表1 CFM56-7B发动机循环参考点数据
Table 1 CFM56-7B engine cyclic reference point data

参数数值高度/m0马赫数0ISA偏差/K0高压压气机压比12设计点涵道比5.1燃烧室出口温度/K1 641燃油热值(Generic)/(MJ·kg-1)43.124发动机进口换算流量/(kg·s-1)355.17风扇效率(内)0.89风扇效率(外)0.89低压转子转速(100%)/(r·min-1)5 175增压级效率0.84高压压气机效率0.85高压转子转速(100%)/(r·min-1)14 460高压涡轮效率0.88低压涡轮效率0.86起飞燃油流量/(kg·s-1)1.24EGT/K1 073
2.2 设计点性能匹配
设计点性能匹配以循环参考点数据为输入数据,通过数值迭代方法求解航空发动机共同工作非线性方程组。求解过程中,一部分循环参考点数据为目标值,该目标值为固定值,如整机压比(P3/P2),燃烧器出口温度(T41),总质量流量(W2Rstd),推力,EGT等;一部分数据为迭代变量,计算之初为给定初始值,如组件效率,管道损失等,如表2所示。
表2 设计点迭代变量、目标值设置
Table 2 Design point iteration variables and target value settings
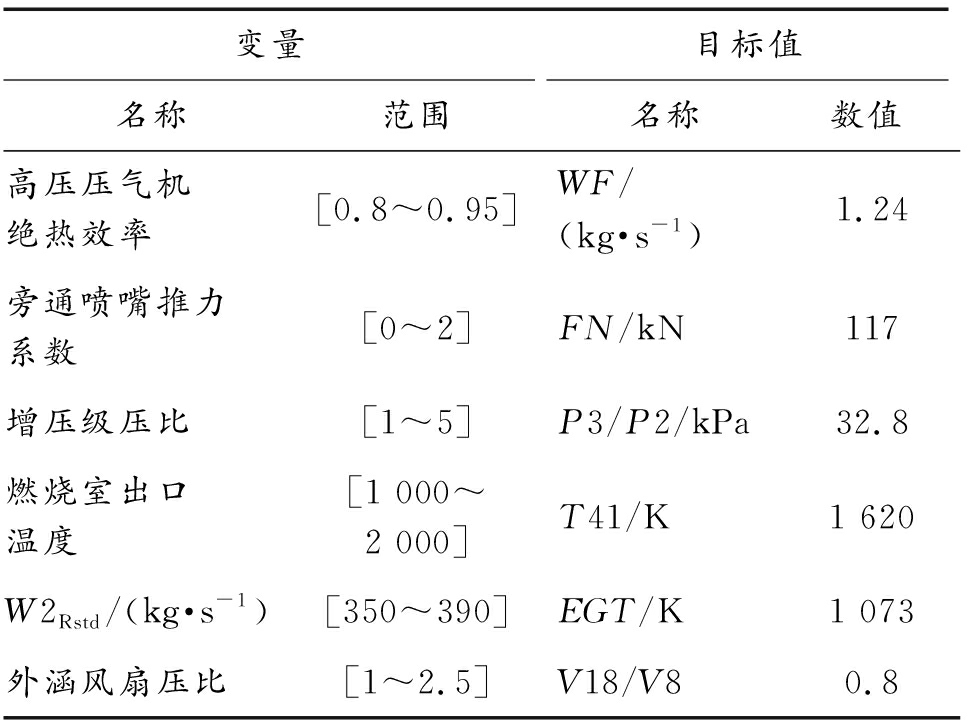
变量名称范围目标值名称数值高压压气机绝热效率[0.8~0.95]WF/(kg·s-1)1.24旁通喷嘴推力系数[0~2]FN/kN117增压级压比[1~5]P3/P2/kPa32.8燃烧室出口温度[1 000~2 000]T41/K1 620W2Rstd/(kg·s-1)[350~390]EGT/K1 073外涵风扇压比[1~2.5]V18/V80.8
设计点匹配计算结果如图5所示。发动机循环参考点推力为117 kN,燃油消耗量1.24 kg/s,EGT为1 073 K,涵道比为5.1,整机压比为32.8;匹配计算值(图中红框标注值)分别为117 kN,1.24 kg/s,1 073 K,5.1,32.8,匹配精度高。
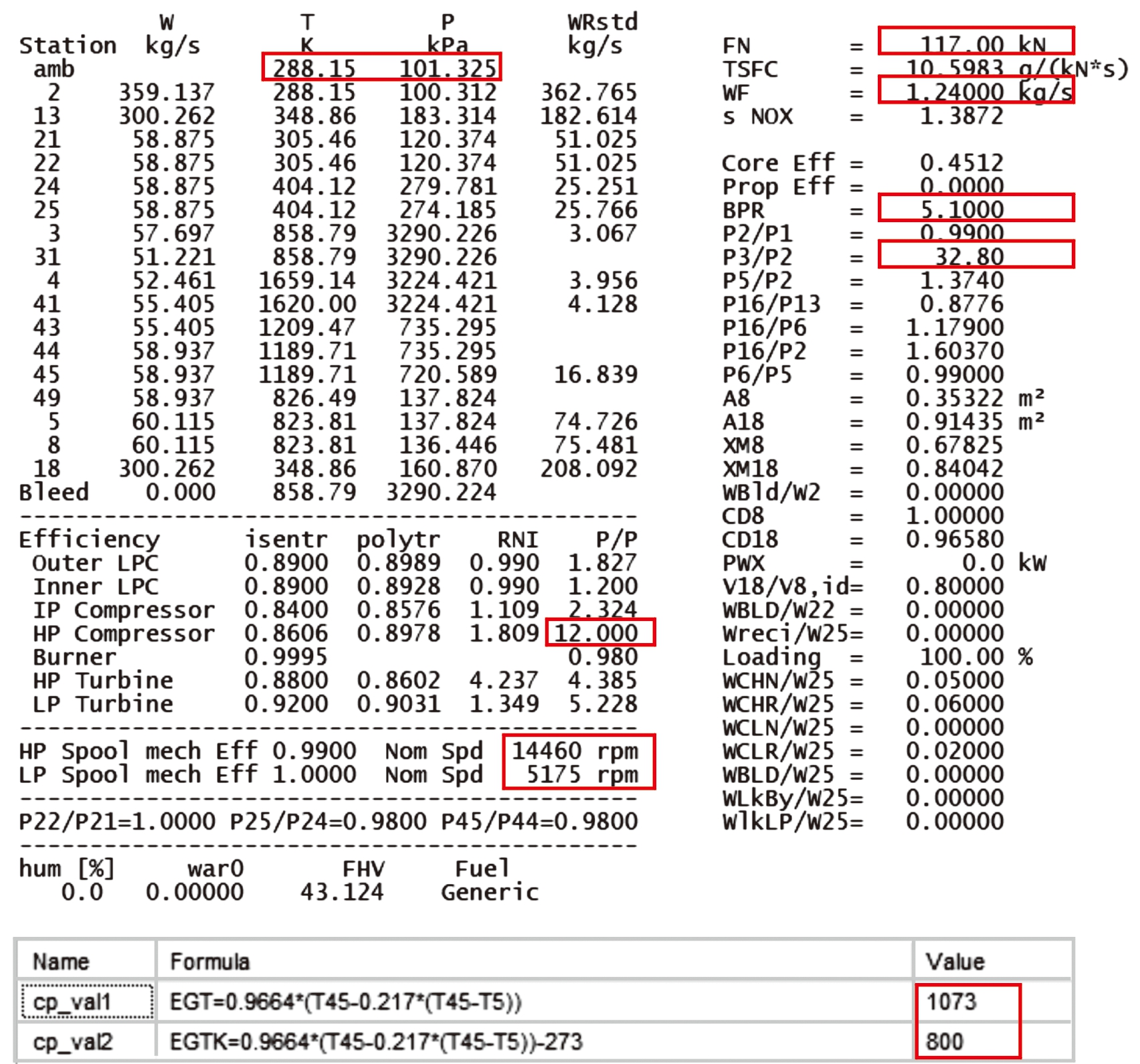
图5 设计点性能匹配结果
Fig.5 Design point performance matching results
2.3 非设计点性能匹配
非设计点性能匹配特性图选用GasTurb内置同类型发动机通用特性图,如表3所示。通过修改β值和值调整部件设计点、缩放部件特性图和修改特性图效率匹配折算流量—效率关系;通过重新标记(Re-labeling)转速线匹配折合流量—折合转速关系。由于需要多次调整试验,因此根据特性参数寻优方法获取最佳调整方案,实施步骤如下:
表3 GasTurb非设计点通用特性图选取
Table 3 Off-design point common characteristic map selection of GasTurb

部件特性图HPCHighPqPCompr1.MAPLPCSingleStgFan1.MAPIPCSubsonicCompressor1.MAPHPTSingleStgTurbine.MAPLPTMediumPqPTurbine.MAP
1) 设计特性图参数组
分别对HPC、LPC、IPC特性图的效率分布和转速线进行3组试验调整,3组调整试验区间依次减半缩小,如表4所示。每组试验得到64组(δ1,δ2,δ3,δ4,δ5,δ6)组合,3组试验共计192组组合,用每组组合参数调整模型,并用该模型仿真真实飞行工况参数。
表4 特性参数调整区间
Table 4 Characteristic parameter adjustment interval
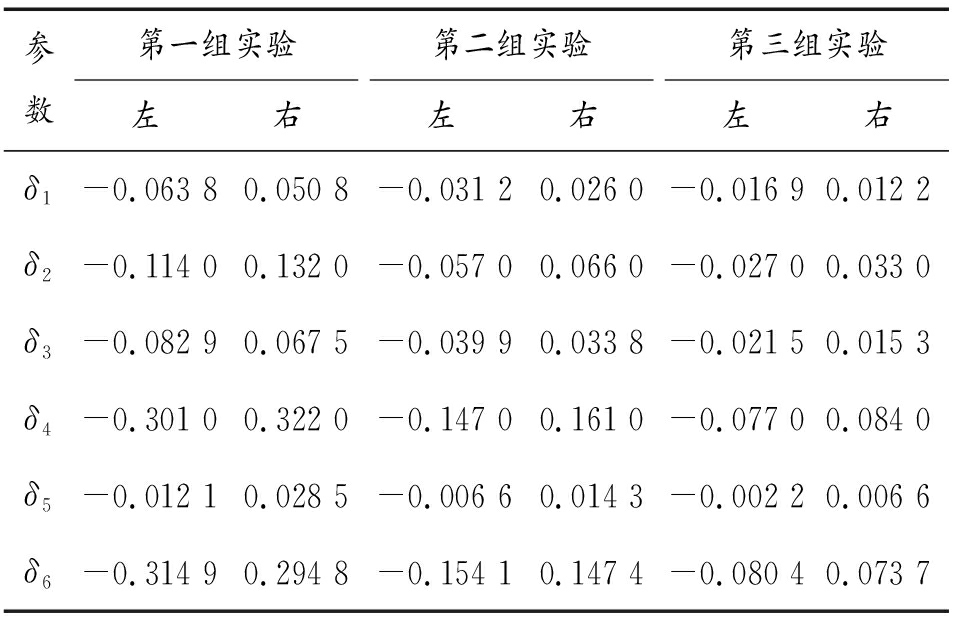
参数第一组实验左右第二组实验左右第三组实验左右δ1-0.063 80.050 8-0.031 20.026 0-0.016 90.012 2δ2-0.114 00.132 0-0.057 00.066 0-0.027 00.033 0δ3-0.082 90.067 5-0.039 90.033 8-0.021 50.015 3δ4-0.301 00.322 0-0.147 00.161 0-0.077 00.084 0δ5-0.012 10.028 5-0.006 60.014 3-0.002 20.006 6δ6-0.314 90.294 8-0.154 10.147 4-0.080 40.073 7
2) 计算误差值Δp
仿真结果涵盖了36个工况点下T3、EGT、Ps3、T25、PT2、N1、N2、T45、T5、P5等7个参数。将这些值用367的矩阵Pmodel表示如下:

提取QAR数据中36个相同工况点下的T3、EGT、Ps3、T25、PT2、N1、N2组成矩阵Pqar:

最后,由式(16)计算模型误差,调整试验结果如表5。
表5 3组调整试验结果
Table 5 Three groups of adjustment test results
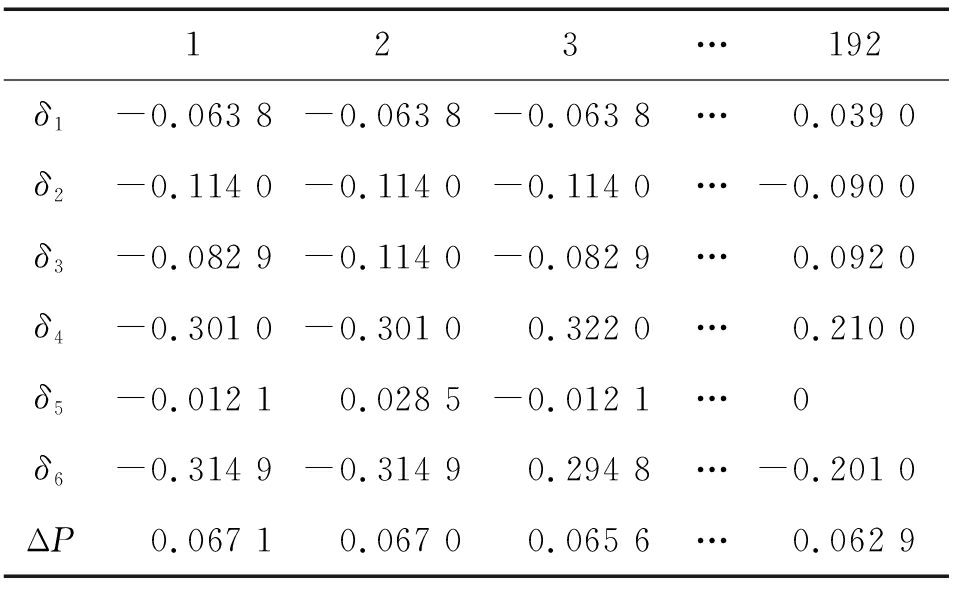
123…192δ1-0.063 8-0.063 8-0.063 8…0.039 0δ2-0.114 0-0.114 0-0.114 0…-0.090 0δ3-0.082 9-0.114 0-0.082 9…0.092 0δ4-0.301 0-0.301 00.322 0…0.210 0δ5-0.012 10.028 5-0.012 1…0δ6-0.314 9-0.314 90.294 8…-0.201 0ΔP0.067 10.067 00.065 6…0.062 9
3) 贝叶斯优化方法寻优
由表5数据训练模型(δ1,δ2,δ3,δ4,δ5,δ6)=f(Δp),通过贝叶斯优化方法获得最优特性图参数组(-0.019 4,-0.06,0.046,-0.105,-0.032 9,-0.100 5),根据该参数组调整HPC、LPC、IPC特性图,最终得到CFM56-7B总体性能模型,最优模型的整体仿真误差Δp为2.67%,该误差反映36个不同工况点全参数误差,整体精度高,适合工程应用。
2.4 实际QAR数据验证分析
由于模型对各个参数(T3、EGT、Ps3、T25、PT2、N1、N2)、各个工况点(36个QAR工况点)的仿真能力不一样,本节从模型对不同参数和对不同工况点的仿真精度2个方面对比模型仿真结果与QAR结果的差异,对模型的仿真精度进行验证和分析。
2.4.1 各参数仿真结果对比
表6为一航班覆盖的36个工况点下各参数的模型仿真结果与QAR数据相对误差。
表6 各仿真参数的相对误差
Table 6 The relative error of each simulation parameter
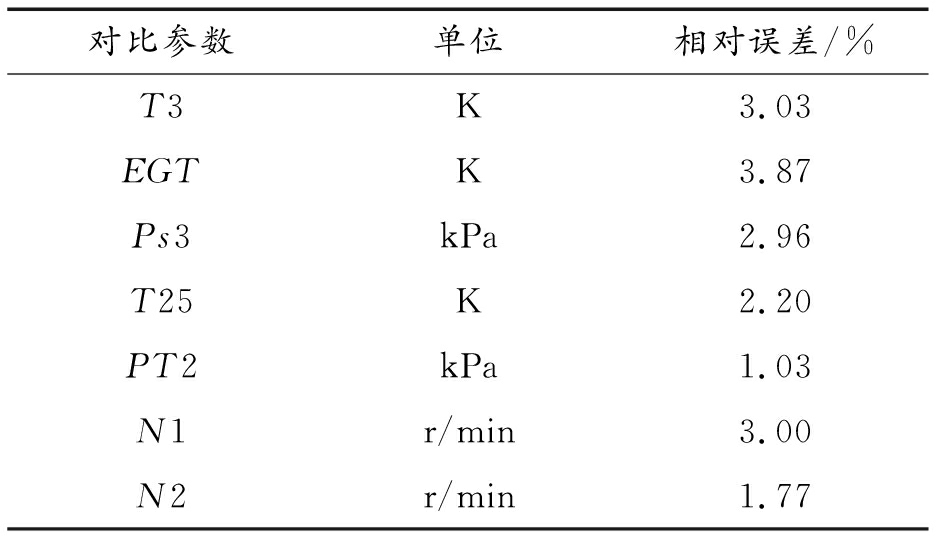
对比参数单位相对误差/%T3K3.03EGTK3.87Ps3kPa2.96T25K2.20PT2kPa1.03N1r/min3.00N2r/min1.77
由表6可知,模型对各参数的仿真精度较高,尤其是对T25、PT2、N2。各参数各个工况下的仿真结果和QAR数据对比见图6—图12,图中,X轴表示36个不同的工况。Y轴是各参数值,图中红点代表QAR数据,蓝色圆圈表示所建模型仿真的结果。
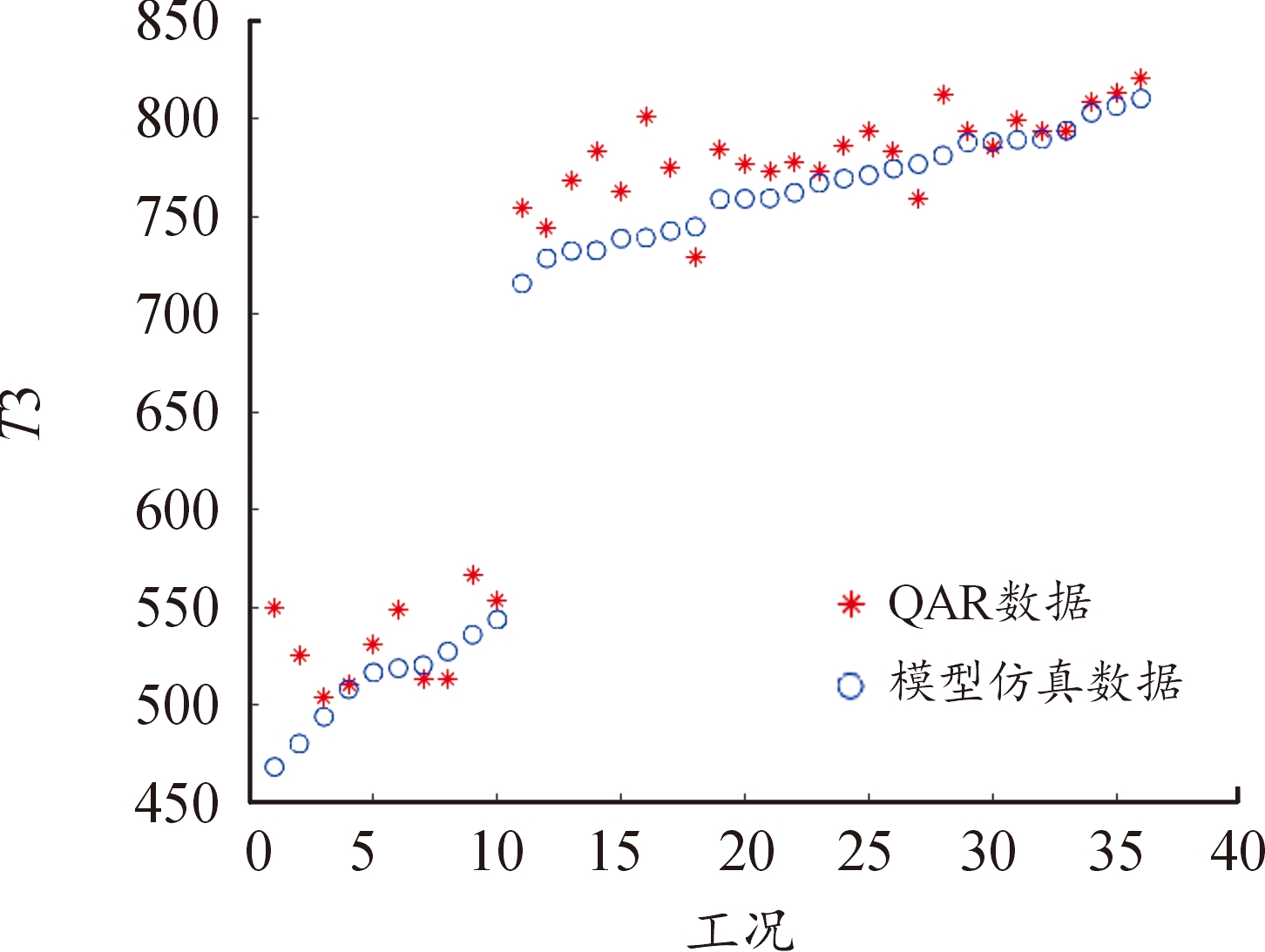
图6 T3数据对比
Fig.6 T3 data comparison
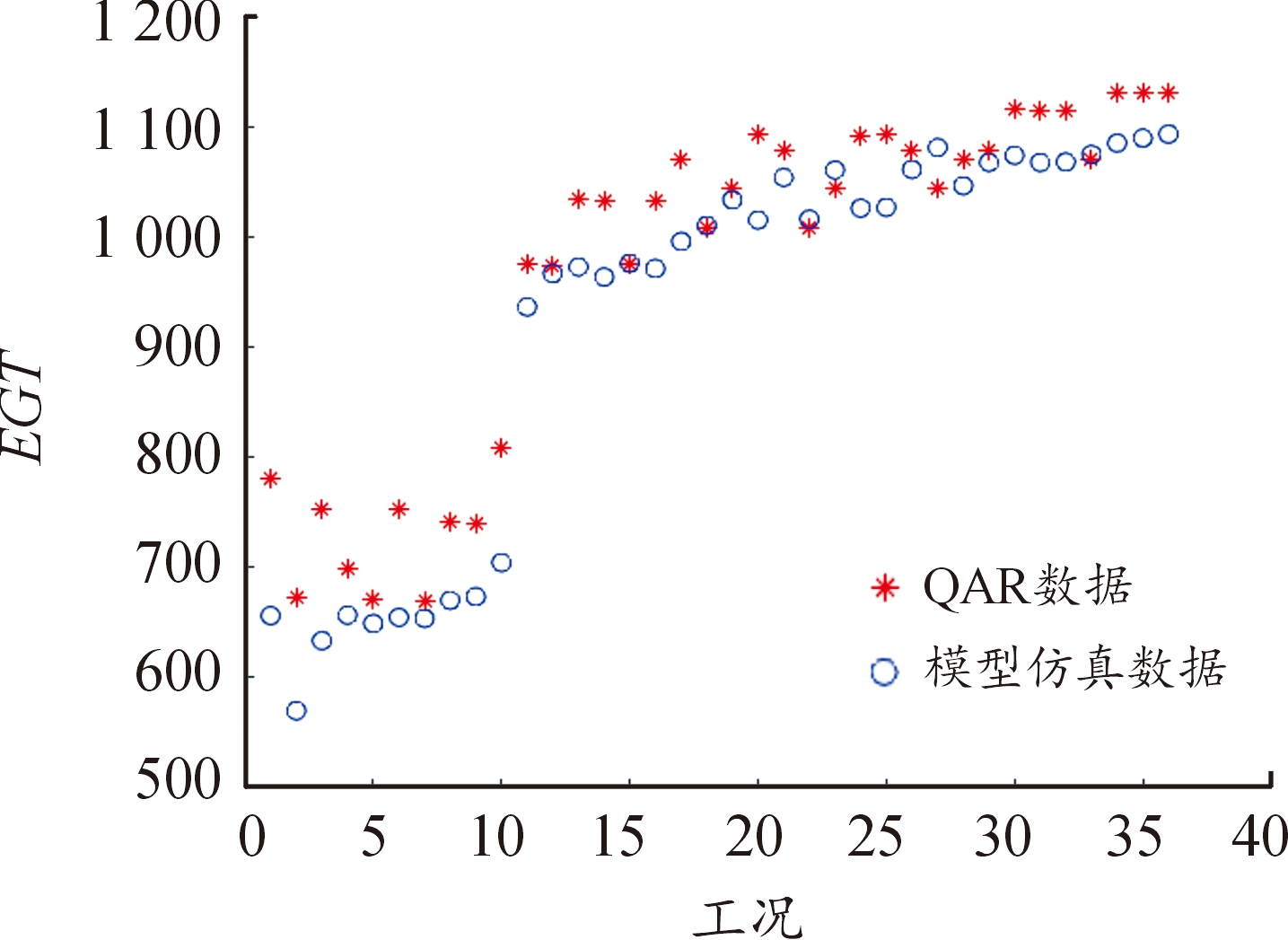
图7 EGT数据对比
Fig.7 EGT data comparison
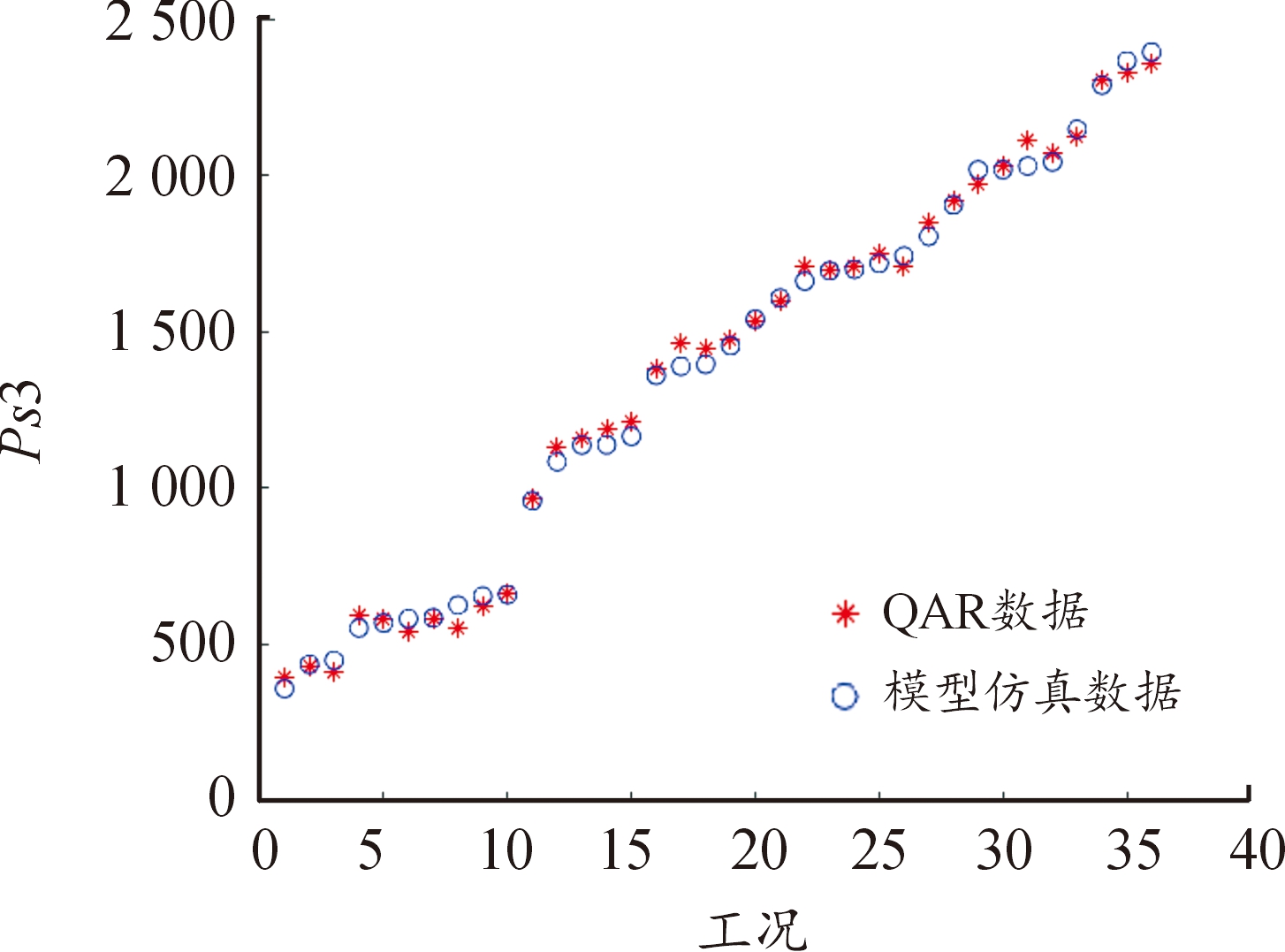
图8 Ps3数据对比
Fig.8 Ps3 data comparison
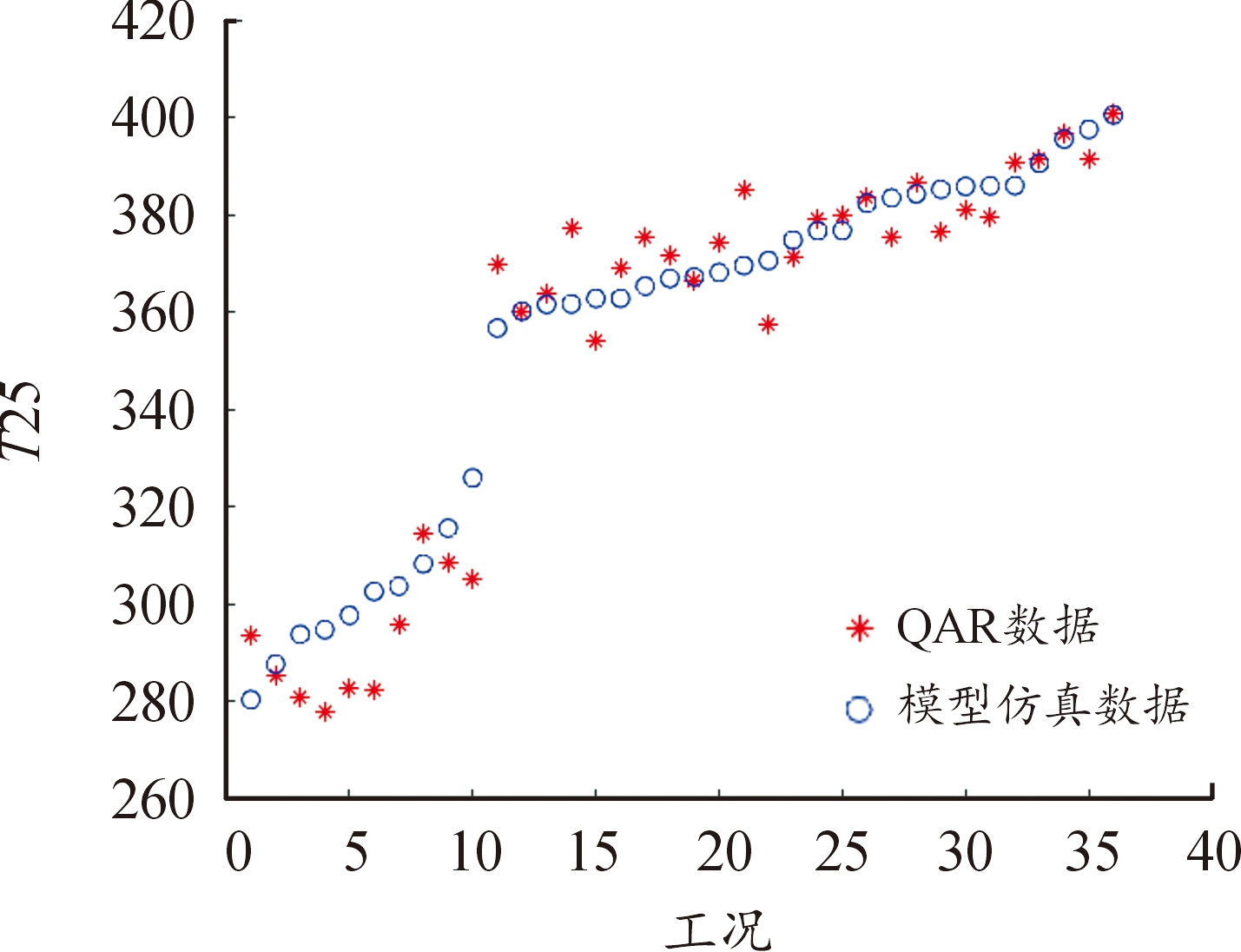
图9 T25数据对比
Fig.9 T25 data comparison
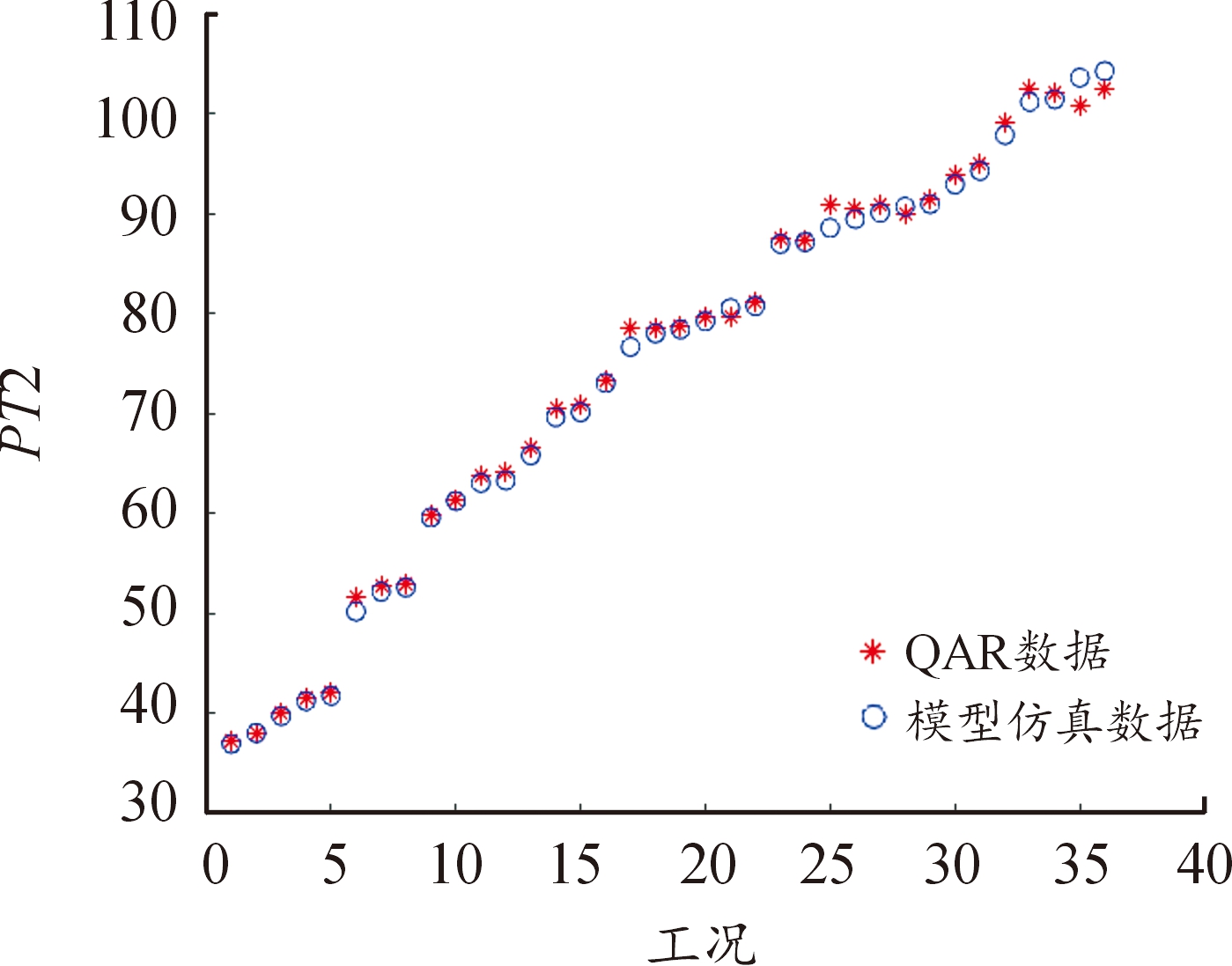
图10 PT2数据对比
Fig.10 PT2 data comparison
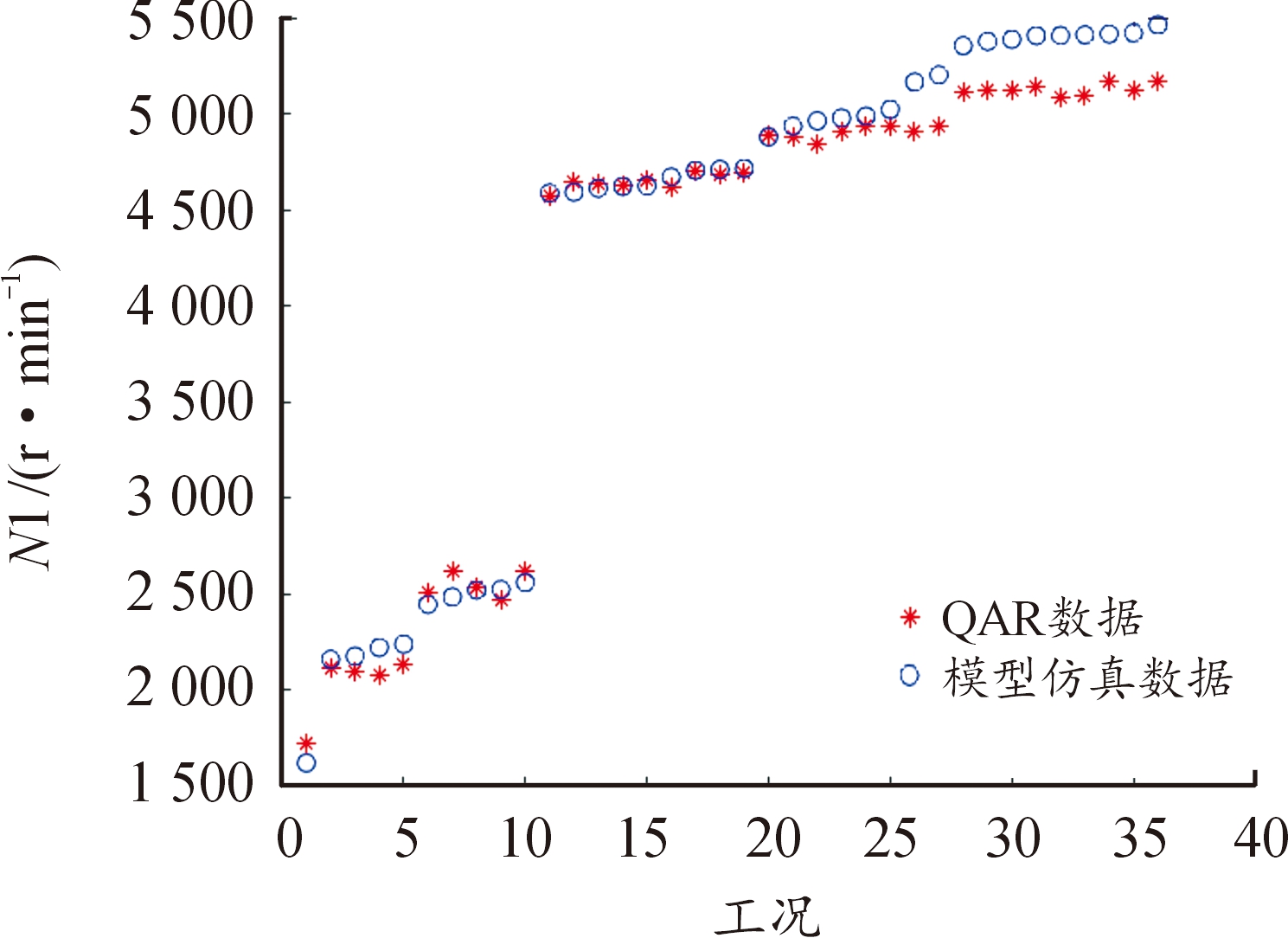
图11 N1数据对比
Fig.11 N1 data comparison
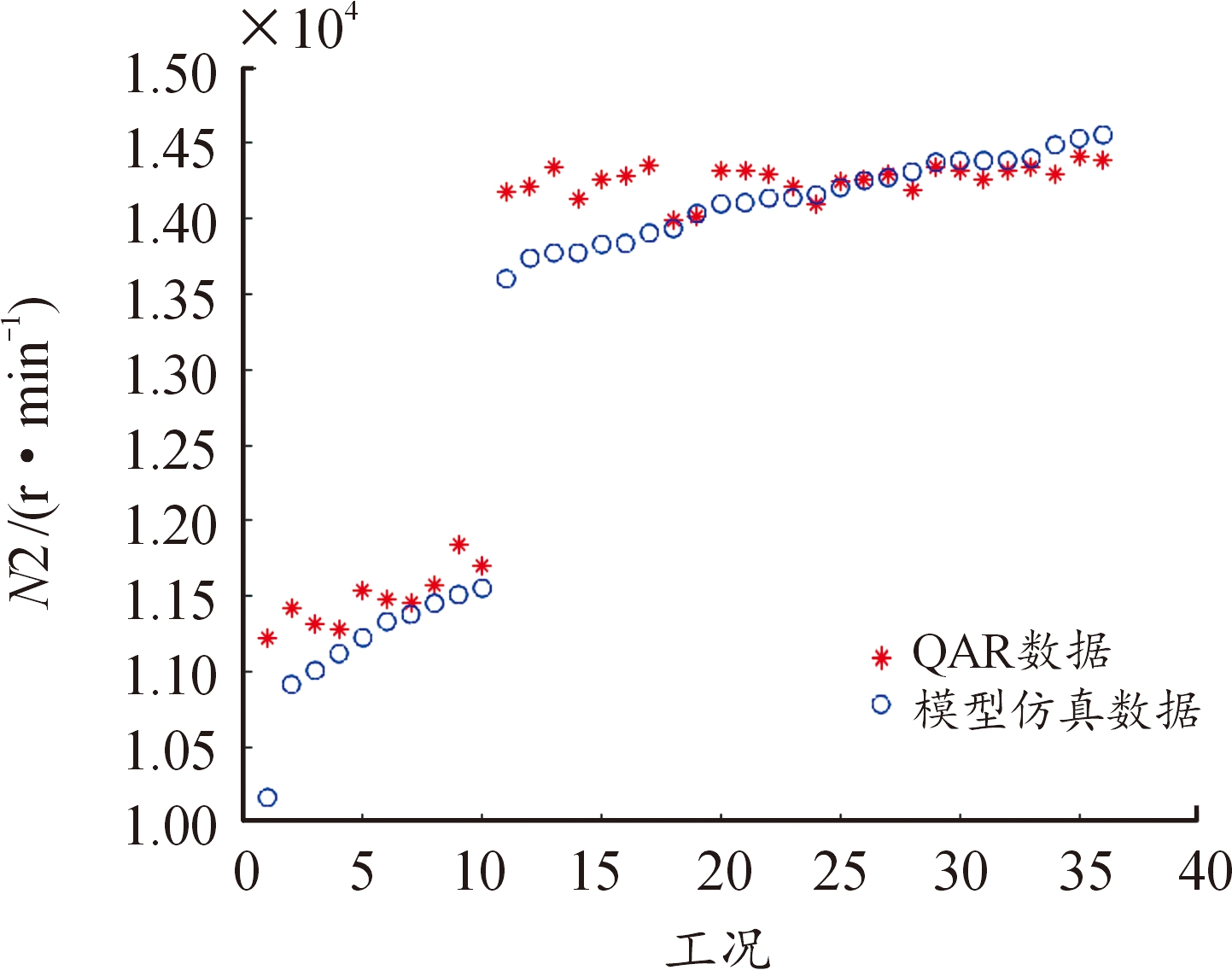
图12 N2数据对比
Fig.12 N2 data comparison
2.4.2 各工况点仿真结果对比
模型对不同工况点的仿真能力不同,所选36个工况点涵盖起飞、爬升、下降等不同飞行阶段(flight phase,FP),的整体相对误差见表7。
表7 各工况点的仿真结果相对误差
Table 7 Relative error of simulation results for each operating point
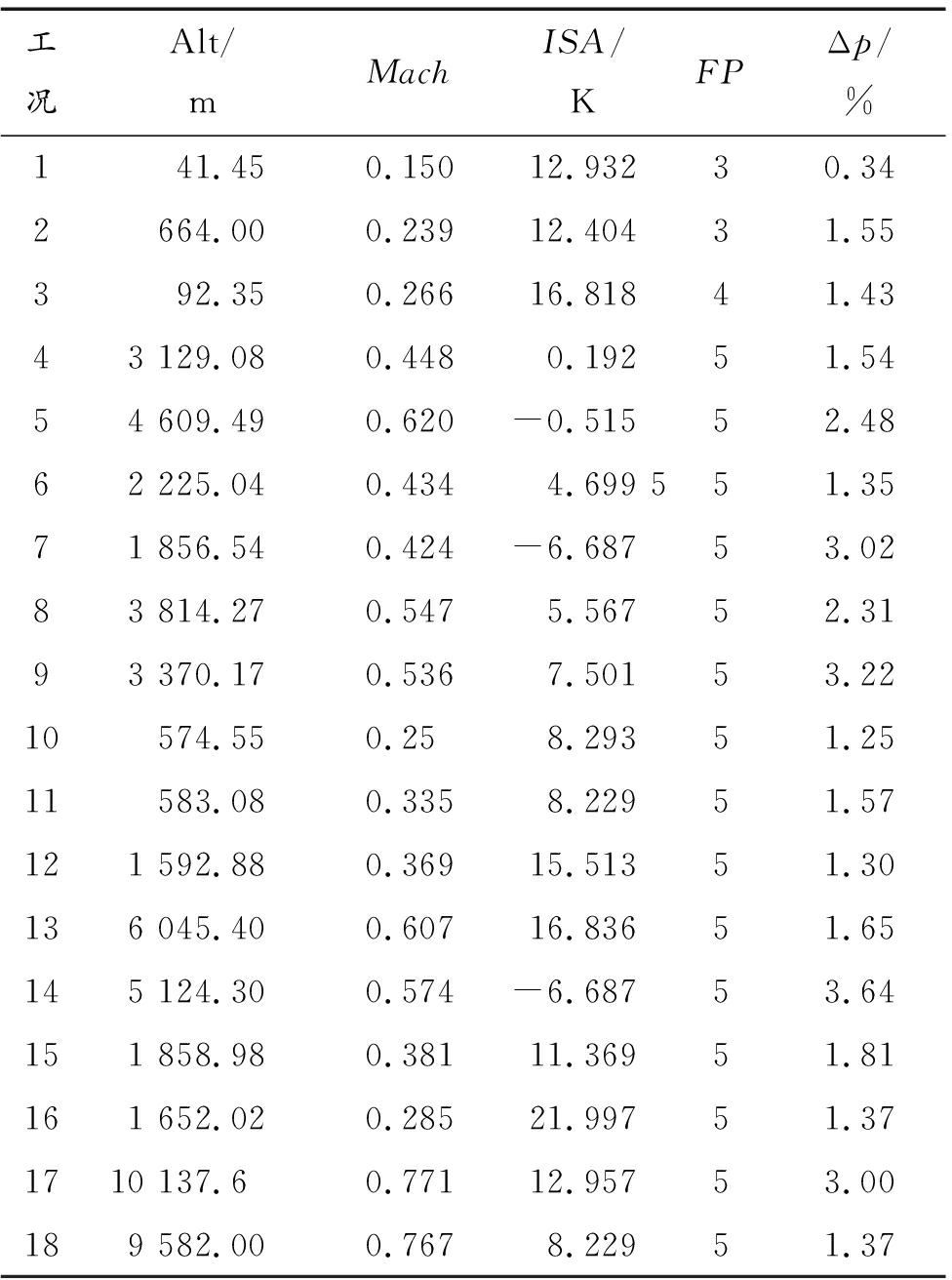
工况Alt/mMachISA/KFPΔp/%1 41.450.15012.93230.342664.000.23912.40431.55392.350.26616.81841.4343 129.080.4480.19251.5454 609.490.620-0.51552.4862 225.040.4344.699 551.3571 856.540.424-6.68753.0283 814.270.5475.56752.3193 370.170.5367.50153.2210574.550.258.29351.2511583.080.3358.22951.57121 592.880.36915.51351.30136 045.400.60716.83651.65145 124.300.574-6.68753.64151 858.980.38111.36951.81161 652.020.28521.99751.371710 137.60.77112.95753.00189 582.000.7678.22951.37
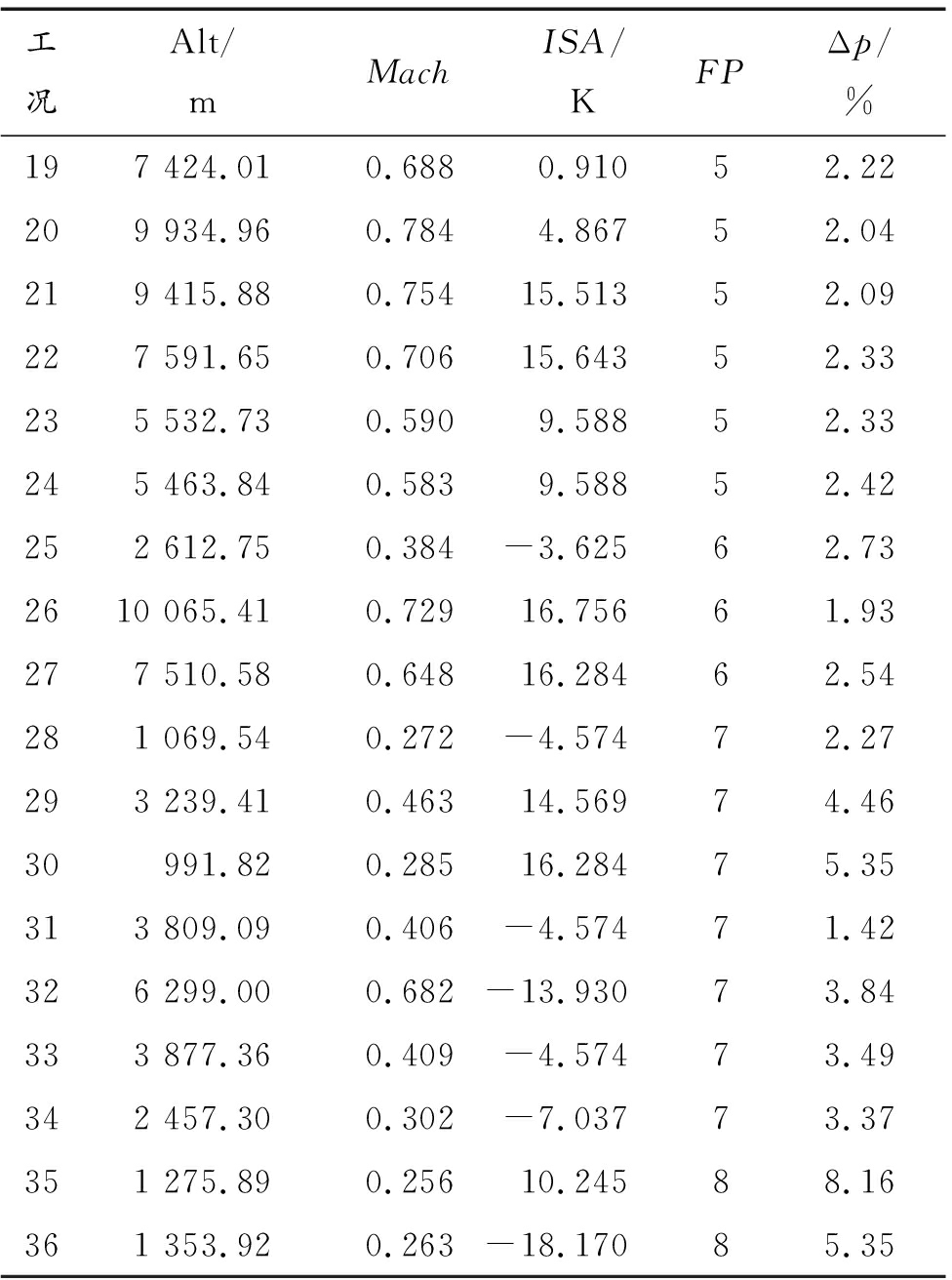
工况Alt/mMachISA/KFPΔp/%197 424.010.6880.91052.22209 934.960.7844.86752.04219 415.880.75415.51352.09227 591.650.70615.64352.33235 532.730.5909.58852.33245 463.840.5839.58852.42252 612.750.384-3.62562.732610 065.410.72916.75661.93277 510.580.64816.28462.54281 069.540.272-4.57472.27293 239.410.46314.56974.4630991.820.28516.28475.35313 809.090.406-4.57471.42326 299.000.682-13.93073.84333 877.360.409-4.57473.49342 457.300.302-7.03773.37351 275.890.25610.24588.16361 353.920.263-18.17085.35
将表7各工况点相对误差作可视化呈现后,如图 13所示。可以看出,除了小部分工况点相对误差大于4%,大部分(31/36)工况点的相对误差都在4%以下;并且其中有54.8%的工况点相对误差在2%以内,整个模型的平均误差为2.67%,限于只有36个工况点QAR数据,该误差在可接受范围之内。当QAR数据足够丰富时,该模型的精度会进一步提高。
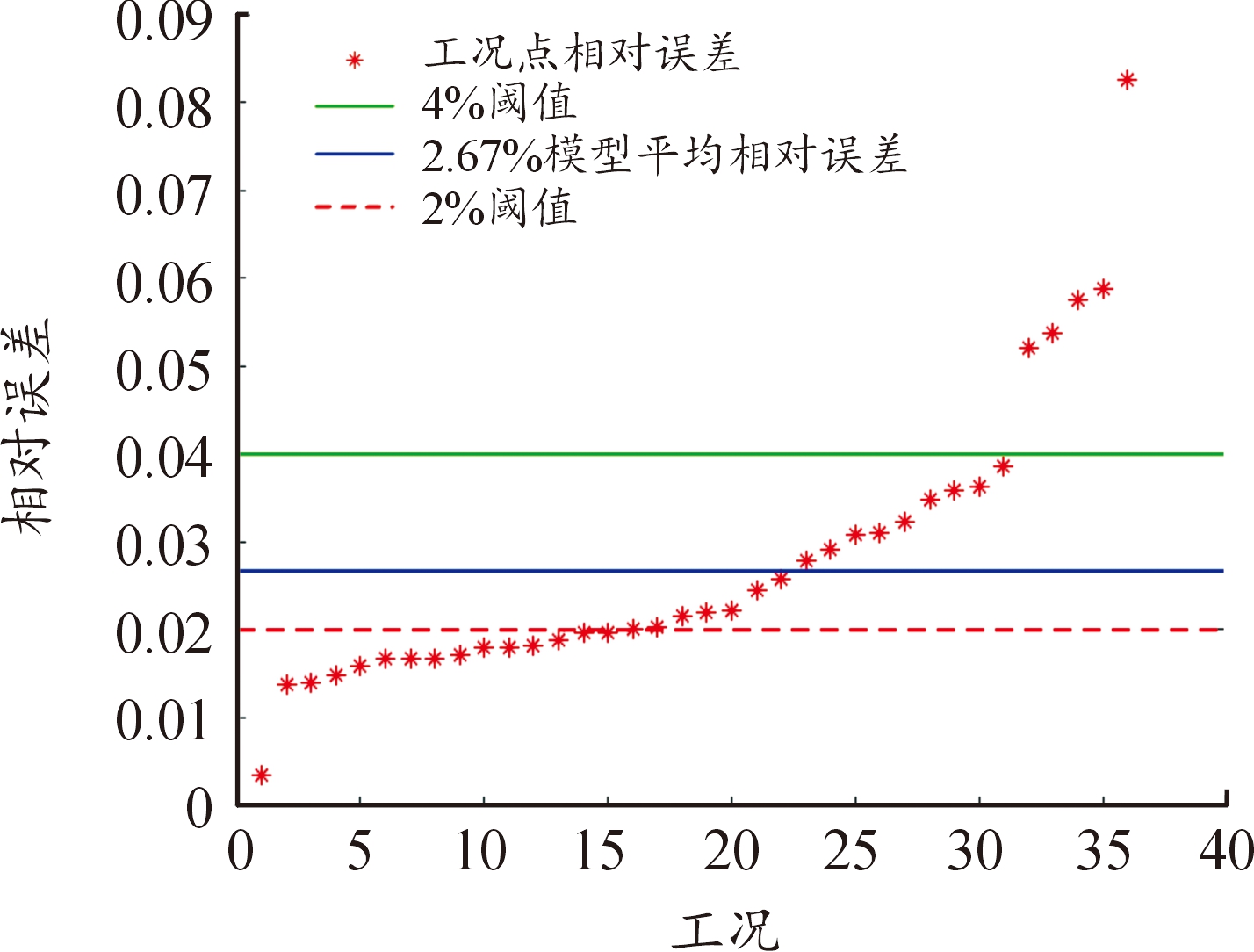
图13 各工况点的相对误差
Fig.13 The relative error of each operating point
3 结论
1) 提出基于循环迭代计算的设计点性能匹配和基于特性图缩放和特性图参数寻优的非设计点性能匹配的总体性能建模方法,利用QAR数据进行在翼发动机的总体性能匹配,为在翼发动机性能数字孪生提供了解决方案,对航空发动机性能评估、故障预测及健康管理具有支撑作用。
2) 基于GasTurb平台,利用QAR数据,构建了CFM56-7B发动机的在翼性能数字孪生模型,与QAR数据相比,模型仿真整体相对误差为2.67%;对T3、EGT、Ps3、T25、PT2、N1、N2的仿真相对误差分别为3.03%、3.87%、2.96%、2.28%、1.03%、3.04%、1.77%;对86%的工况点(起飞、爬升、巡航、下降等)的仿真相对误差小于4%,验证了该方法的有效性和实用性。
[1] 工业和信息化部.数字孪生应用白皮书[R].2020.
Ministry of Industry and Information Technology.Digital twin application white paper[R].2020.
[2] 陶飞,刘蔚然,刘检华,等.数字孪生及其应用探索[J].计算机集成制造系统,2018,24(1):1-18.
TAO Fei,LIU Weiran,LIU Jianhua,et al.Exploration of digital twin and its applications[J].Computer Integrated Manufacturing Systems,2018,24(1):1-18.
[3] National Academies of Sciences,Engineering,and Medicine.The Fourth Industrial Revolution:Proceedings of a Workshop—in Brief[J].2017.
[4] KOUL A K,SHANKAR S,WALLACE W.Predictive Maintenance-A new approach to life cycle management of turbines[J].Life Prediction Technologies Inc,2014.
[5] 陈曦,余国瑞,肖天雷,等.采用Automation ML对工程工具数字孪生建模的方法[J].信息与电脑(理论版),2019(7):23-25.
CHEN Xi,YU Guorui,XIAO Tianlei,et al.Using Automation ML for modeling of engineering tool digital twin[J].Information &Computer,2019(7):23-25.
[6] 刘魁,刘婷,魏杰,郑新前.数字孪生在航空发动机可靠性领域的应用探索[J].航空动力,2019(4):61-64.
LIU Kui,LIU Ting,WEI Jie,et al.Application exploration of digital twin in the field of reliability of aero engine[J].Aerospace Power,2019(4):61-64.
[7] 刘魁,王潘,刘婷.数字孪生在航空发动机运行维护中的应用[J].航空动力,2019(4):70-74.
LIU Kui,WANG Pan,LIU Ting.Application of digital twin in aero engine operation and maintenance[J].Aerospace Power,2019(4):70-74.
[8] MARTINS D A R.Off-design performance prediction of the CFM56-3 aircraft engine[J].Tecnico Lisboa MSc Thesis,2015.
[9] COSTA BAPTISTA F M.A 0-D off-design performance prediction model of the CFM56-5B turbofan engine[J].2017.
[10]KURZKE J.How to create a performance model of a gas turbine from a limited amount of information[C]//Turbo Expo:Power for Land,Sea,and Air.2005,46997:145-153.
[11]潘率诚,李刚团,丁朝霞,等.基于部件特性的航空发动机性能模型修正[J].燃气涡轮试验与研究,2016,29(6):26-29,33.
PAN Shuaicheng,LI Gangtuan,DING Zhaoxia,et al.Aeroengine performance model modification based on component characteristics[J].Gas Turbine Experiment and Research,2016,29(6):26-29,33.
[12]王新月.气动力学基础[M].西安:西北工业大学出版社,2006.
WANG Xinyue.FundamentalsofAerodynamics[M].Xi’an:Northwestern Polytechnical University Press,2006.
[13]廉筱纯.航空发动机原理[M].西安:西北工业大学出版社,2005:122-158.
LIAN Xiaochun.Aero-engine principle[M].Xi’an:Northwestern Polytechnical University Press,2005:122-158.
[14]叶纬,陈玉春,崔高峰,等.拟牛顿法在航空发动机特性仿真中的应用[J].计算机仿真,2007,24(10):78-81.
YE Wei,CHEN Yuchun,CUI Gaofeng,et al.Application of quasi-Newton method in aeroengine characteristic simulation[J].ComputerSimulation,2007,24(10):78-81.
[15]周桥.微小型回热循环燃气轮机性能仿真及控制规律优化研究[D].北京:中国科学院大学,2020.
ZHOU Qiao.Research on performance simulation and control lawoptimization of micro recuperated cycle gas turbine[D].Beijing:University of Chinese Academy of Sciences,2020.
[16]陈光.航空发动机结构设计分析[M].北京:北京航空航天大学出版社,2006.
CHEN Guang.Structural design and analysis of aeroengine[M].Beijing:Beihang University Press,2006.
[17]EASA.CFM56-7B series engines type-certificates[R].TCDS E.004,Brussels:EASA,2012.
[18]ICAO databank.Edb-emissions-databank v26B-New Format(web)[EB/OL]https://data.icao.Int/newDataPlus/.
[19]旷典.民航大涵道比涡扇发动机稳态模型建模及其修正技术研究[D].成都:中国民用航空飞行学院,2018.
KUANG Dian.Research on steady-state modeling and correction technology for civil aviation high-bypass ration turbofan engine[D].Chengdu:Civil Aviation Flight University of China,2018.