0 引言
混凝土作为一种常见的复合材料被广泛应用于民用和国防工程,尤其在军事防护工程中,混凝土建筑会受到各种弹体的毁伤,动能侵彻是其中一种。动能弹对混凝土的侵彻效应一直是各国研究重点。杆式穿甲弹作为典型的穿甲武器被各国军队所装备,随着发射平台技术的发展,给予杆式弹的速度逐渐提高。由于弹靶材料特性的影响,钨杆在超高速与常规速度的情况下侵彻混凝土,毁伤效应有所不同,毁伤机制也发生相应的变化,因此,研究超高速情况下钨杆侵彻混凝土是十分有必要的的。卢正操等[1]基于动态空穴膨胀模型和A-T模型,建立不同侵彻模式下计算各种参数的理论公式,对长杆弹侵彻半无限混凝土靶进行了系统的理论研究,结果表明:理论模型预测侵彻模式、侵彻深度、时程曲线和残余质量时与现有混凝土侵彻试验数据吻合得较好;周刚等[2]研究了钨合金弹体超高速侵彻混凝土靶的相关理论,开展了钨合金弹体超高速撞击混凝土靶试验,分析了成坑特性,研究了侵彻总深和残余弹体长度随撞击速度的变化规律,结果表明:超高速撞击条件下混凝土靶成坑为“弹坑+弹洞”形,成坑体积与弹体动能近似成正比,侵彻深度随弹速的提高呈现先增大后减小的现象,超高速侵深降低是弹体动能经历销蚀侵彻后“刚体侵彻阶段”减少造成的;高飞等[3]研究砂浆靶目标在动能弹超高速撞击下的破坏响应,利用2级轻气炮开展卵形头部钢杆弹以1 200~2 400 m/s速度侵彻砂浆靶试验,分析得到靶体开坑直径和开坑深度与撞击速度呈线性关系。侵深随撞击速度的增加呈现先线性增加、后逆减,在缓慢增加的趋势,分别对应刚体侵彻、半破碎侵彻和破碎侵彻。王明洋[4-5]运用内摩擦理论,结合岩石动态可压缩特性,建立了超高速动能弹对地毁伤的侵彻深、成坑和安全厚度等设计计算方法。钱秉文等[6-8]研究弹体超高速撞击混凝土靶,得到了侵深随撞击速度的增加呈先增加后减小的趋势,在某一速度侵深存在最大值。程怡豪等[9]根据试验结果在4个冲击速度区间内围绕混凝土靶的破坏特点及若干要素对靶体行为的影响规律展开论述,既低速区间内(撞击速度不超过40 m/s)简要介绍梁、柱、板壳的破坏模式,中速区间内(撞击速度为40~1 000 m/s)论述弹靶相对尺寸、粗骨料、单轴抗压强度和钢筋对混凝土厚靶侵彻效应的影响,高速区间内(撞击速度为1.0~2.0 km/s)描述半流体转变速度和成坑效应,超高速区间内(撞击速度超过2 km/s)描述密度效应占主导的流体侵彻行为。
针对上诉研究现状,本文中开展0.2~3.0 km/s超高速钨杆垂直侵彻混凝土研究,通过试验验证数值模型的合理性,通过LS-DYNA数值模拟结果分析超高速侵彻下无量纲侵深、弹体速度、质量、残余长度以及侵彻阶段分析。
1 试验验证
1.1 试验概况
图1为试验现场布置示意图,试验以125 mm火炮作为发射平台,炮口距靶板125 m,通过调节发射药量来控制弹体的着靶速度,前5 m放置章动靶纸,靶用来观察弹体着靶前飞行稳定性。靶前41 m处放置天幕测速仪,靶板为两块圆柱形混凝土靶,前靶为靶Ⅰ,后靶为靶Ⅱ,靶Ⅰ和靶Ⅱ接触放置。为了尽量避免边界效应的影响,对靶板进行钢箍加固。
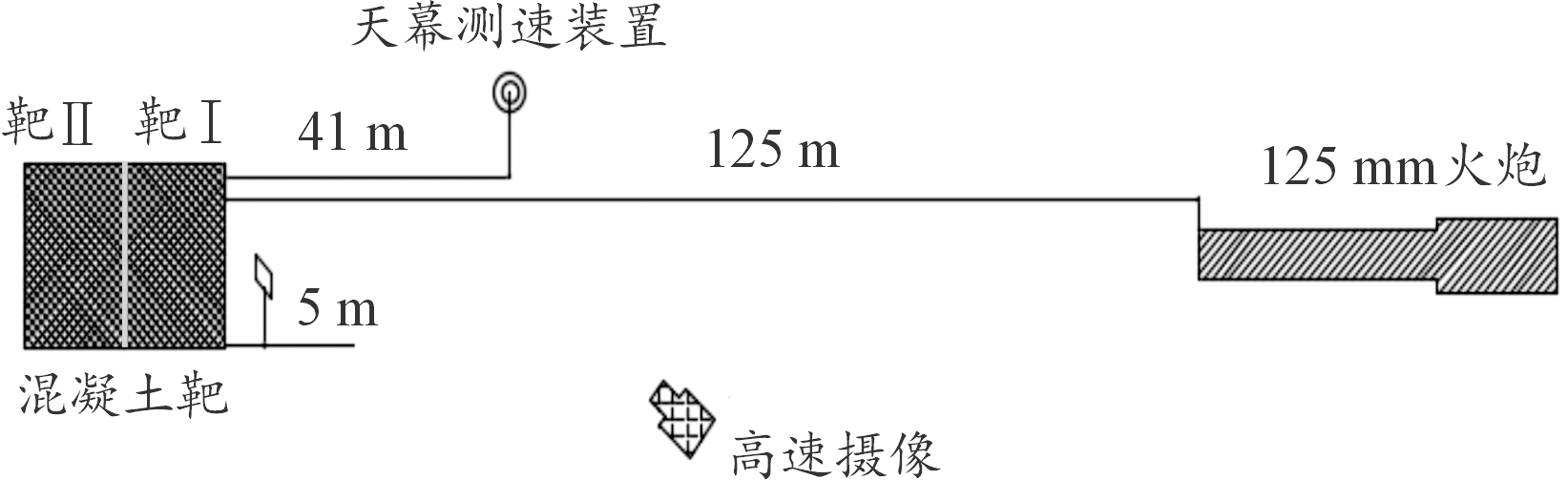
图1 试验现场布置示意图
Fig.1 Experiment site layout
1.2 数值模拟及参数
仿真模型的弹体直径24 mm,长径比为11,质量约为1.8 kg,弹体头部为尖锥型,材料为钨合金,弹体用MAT_JOHNSON_COOK本构模型和EOS_GRUEISEN状态方程描述,具体参数见表1[10]。其中Johnson-cook本构关系为:
表1 钨合金材料参数
Table 1 Tungsten material paramenters
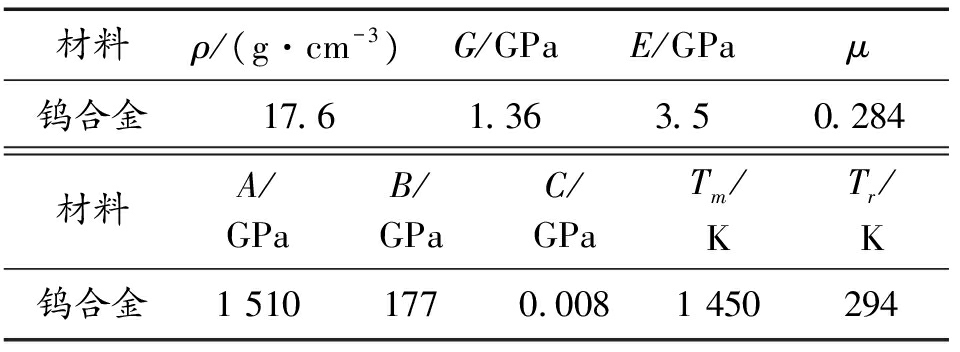
材料ρ/(g·cm-3)G/GPaE/GPaμ钨合金17.61.363.50.284材料A/GPaB/GPaC/GPaTm/KTr/K钨合金1 5101770.0081 450294
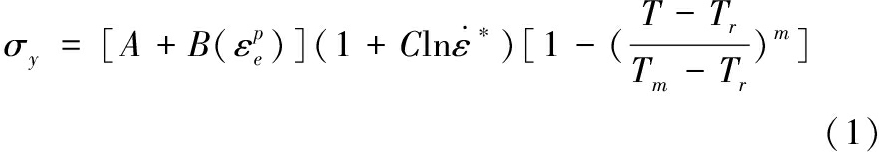
式中:σy为材料的屈服强度;A、B、C、m、n为材料常数,由试验确定;T为室温;Tr为标准温度;Tm为融化温度;![]() 为等效塑性应变;
为等效塑性应变;![]() 为无量纲等效塑性应变率。
为无量纲等效塑性应变率。
Gruneisen状态方程为:
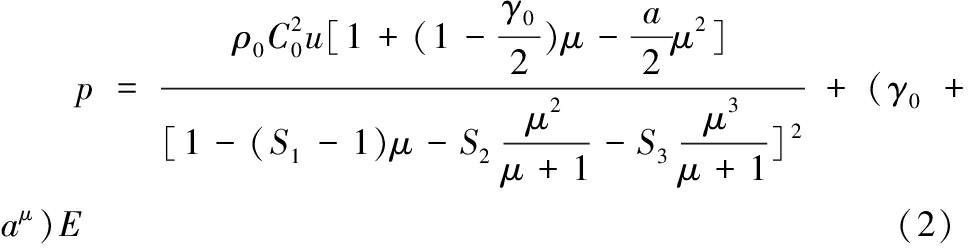
式中:p为压缩材料的压力;E为材料的内能;C0为Hugoniot关系式的截距;S1、S2、S3为Hugoniot关系式的系数; ρ0为初始密度; γ0为Gruneisen系数;a是对γ0的一维修正; μ=ρ/ρ0-1。
混凝土靶板用HJC本构模型[11],该模型是一种专门针对混凝土受冲击载荷作用而开发的动态材料模型,模型考虑了大应变、高应变率和高压情况,同时结合损伤,理论考虑了材料的拉伸断裂行为,考虑了材料压溃后的体积压缩量与压力的函数关系,并采用MAT_ADD_EROSION失效准则,主应变失效取0.4,剪应变失效取0.2[12]。靶板为2块∅1.5 m×1 m混凝土靶,具体参数见表2。其中A、B、C为混凝土材料参数,G为剪切模量, fc为单轴抗压强度,弹体与靶板均采用Lagrange算法的solid164单元。弹体头部网格尺寸0.15 mm,靶板中心网格尺寸5 mm,远离侵彻区域网格15 mm。
表2 混凝土材料参数
Table 2 Concrete material paramenters
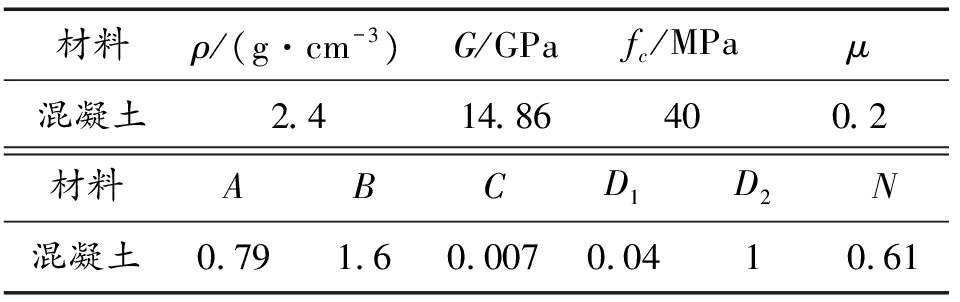
材料ρ/(g·cm-3)G/GPafc/MPaμ混凝土2.414.86400.2材料ABCD1D2N混凝土0.791.60.0070.0410.61
由于靶板及弹丸具有对称性,为节省计算时间,建立1/2模型,弹靶之间设置侵蚀接触,在对称面施加对称边界约束。有限元模型如图2所示。
图2 弹靶1/2模型
Fig.2 Projectile and target 1/2 model
1.3 试验验证及数值模拟方法
图3为章动靶纸,图4为弹体不同初速侵彻靶板的试验结果和模拟仿真结果。
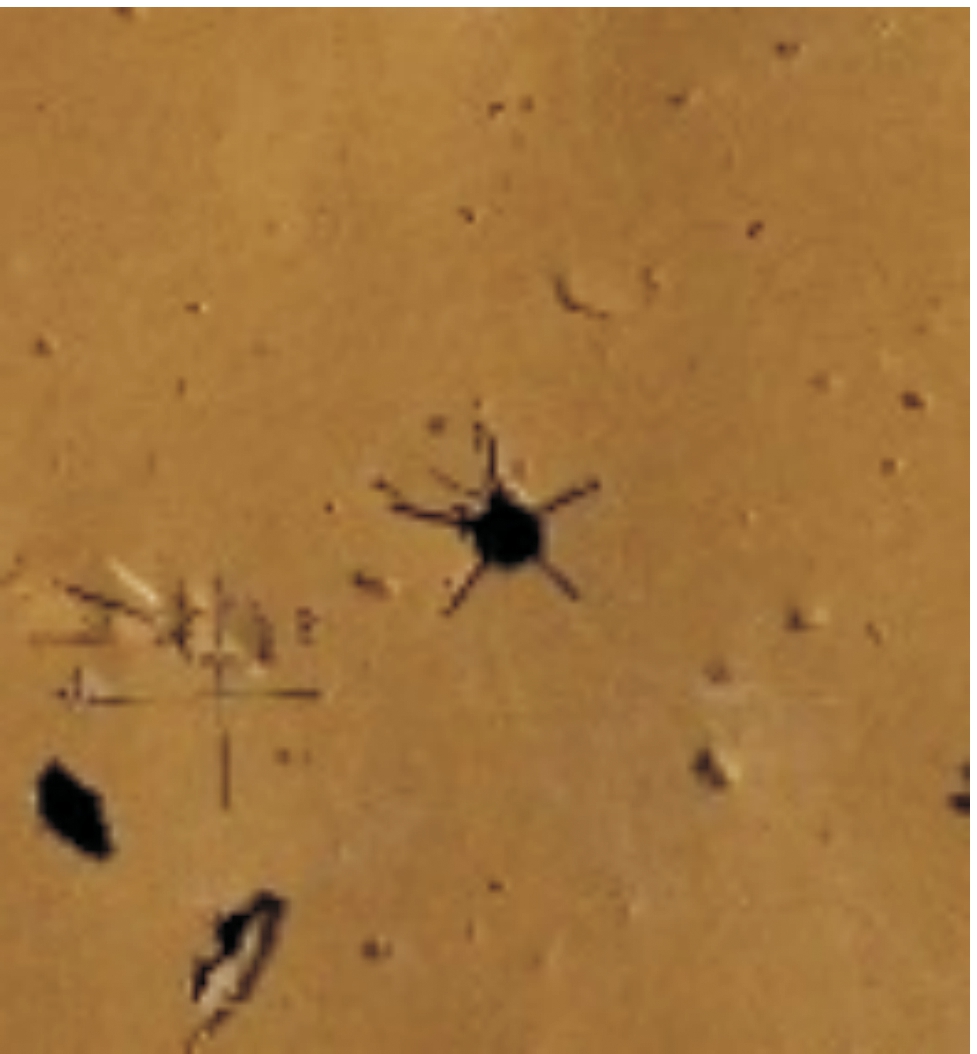
图3 章动靶纸
Fig.3 Nutation target

图4 弹体不同初速侵彻靶板的试验结果和模拟仿真结果
Fig.4 Target plate destruction at different velocity
根据章动靶纸(图3)痕迹可知,弹体着靶前飞行姿态水平,着角可以忽略,视为弹体垂直侵彻混凝土靶板。
由图4可知,由于弹体撞击和冲击波破坏,靶Ⅰ产生压缩和剪切变形,使大块混凝土破坏、碎裂,由于靶架约束,靶Ⅰ下半部分靶体处于原始位置,上半部分碎裂胀开钢箍并飞散,靶板破坏严重,弹体大部分能量由靶Ⅰ吸收,弹体进入靶Ⅱ,靶体表面形成对称的局部破坏,破坏区分为中心粉碎区、漏斗形破坏区、径向裂纹区,靶Ⅱ破坏情况如图5所示。由仿真结果可以看出,靶Ⅰ完全破坏,靶Ⅱ形成隧道,与试验结果基本一致。

图5 靶Ⅱ破环情况
Fig.5 Destruction of Target Ⅱ
由图5可知,弹体着速1 368 m/s时,靶板入孔不规则,无径向裂纹;着速提高至1 666 m/s时,靶板入孔为圆孔,表面平整无崩落,在弹体侵彻后其弹着点呈放射型裂纹,裂纹一直延伸到靶体边界;初速进一步提高至1 724 m/s时,靶板入孔明显,靶板表面大面积崩落,裂纹至靶板边缘,由此可见,随着弹体初速的增加,靶Ⅱ破坏程度逐步加深。弹体在不同初速条件下侵彻混凝土靶板侵彻深度数值模拟和试验结果对比如表3所示。
表3 侵彻深度数值模拟与试验结果对比
Table 3 Extreme penetration depth at different velocity
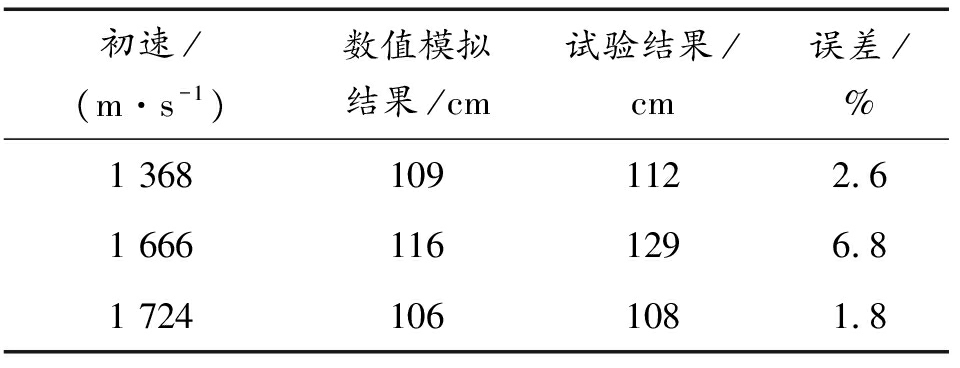
初速/(m·s-1)数值模拟结果/cm试验结果/cm误差/%1 3681091122.61 6661161296.81 7241061081.8
由表3可知,侵彻深度数值模拟和试验结果误差不大于7%。通过对比分析靶板破坏情况,极限侵彻深度,仿真数据和试验数据基本一致,说明该方法能够较好地描述超高速侵彻物理过程,可再此基础上进行侵彻机理的探究。
2 超高速侵彻阶段分析
第1节中因为试验场地和设备等因素限制,靶板为2块∅1.5 m×1 m混凝土靶。为消除靶板尺寸效应,本节数值模拟的靶板尺寸为∅1.5 m×2.5 m,弹体尺寸与第1节保持一致。
2.1 无量纲侵深
图6为无量纲侵彻深度与速度的变化关系,由图6可以看出,侵彻速度0.2~3.0 km/s区间内,无量纲侵彻深度随速度先增加后减少,在1.2 km/s附近存在侵深最大值。弹体速度小于1.2 km/s时,侵深随速度的增加而增加,弹体速度在1.2 km/s附近侵彻深度达到最大值,约80倍弹径,弹体速度大于1.2 km/s时,无量纲侵深随速度的增加而减小。因此,从侵彻深度方面讨论,超高速弹体对于中低速弹体在侵彻能力上并无优势。
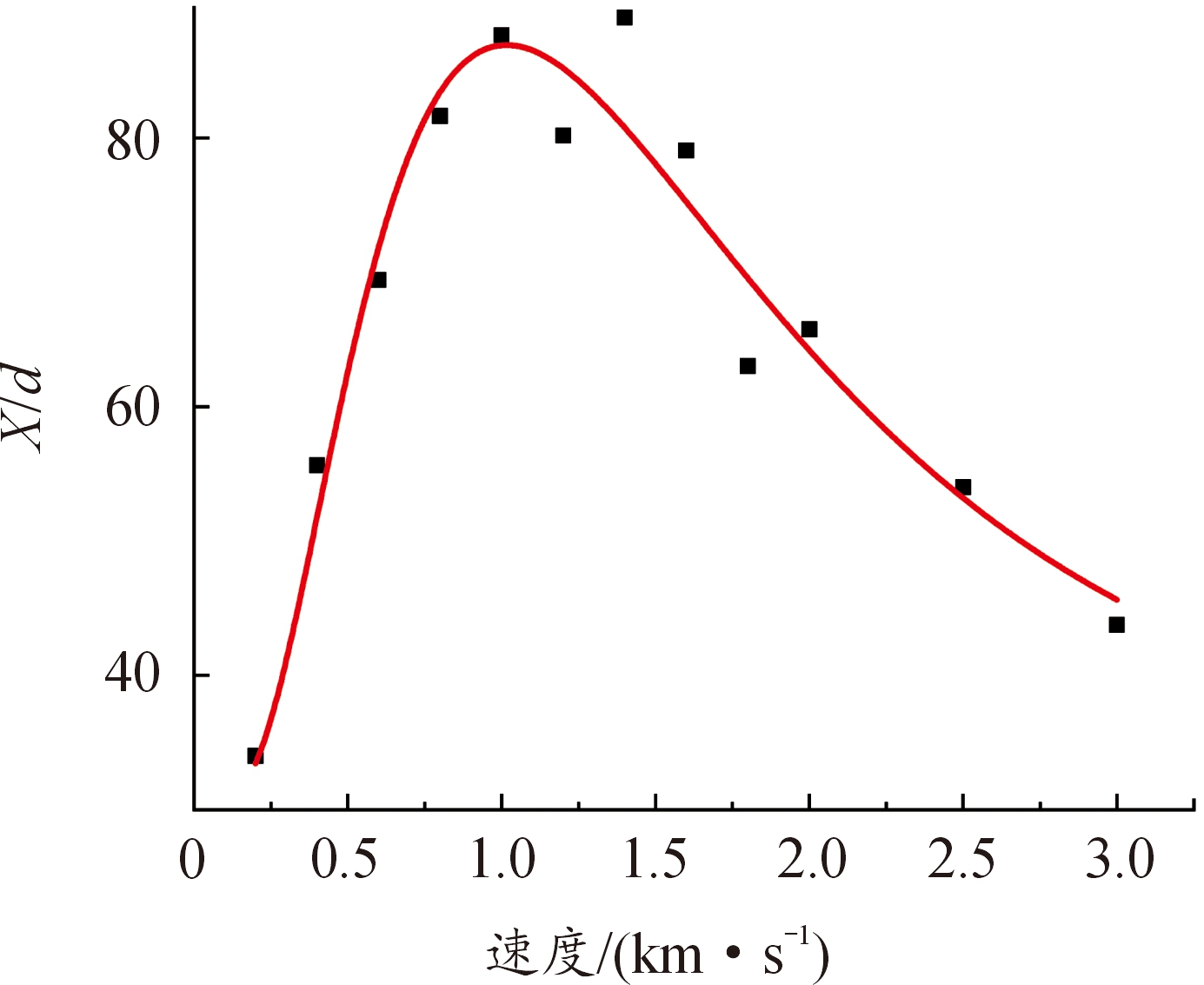
图6 无量纲侵深与速度变化关系
Fig.6 Penetration depth with velocity
2.2 弹体质量侵蚀
图7为不同速度下钨杆侵彻混凝土弹体质量时程图,由图7可知,弹体速度越大,质量侵蚀速率越大,弹体速度0.2 km/s时弹体质量基本无损失,随着速度增加弹体质量变化曲线下降段斜率逐渐增大,而3.0 km/s时弹体质量几乎损失殆尽。并且,弹体速度较低时,弹体质量下降段与平稳段分界并不明显,当弹体速度大于1.4 km/s后,质量曲线下降段与稳定段转折点清晰。
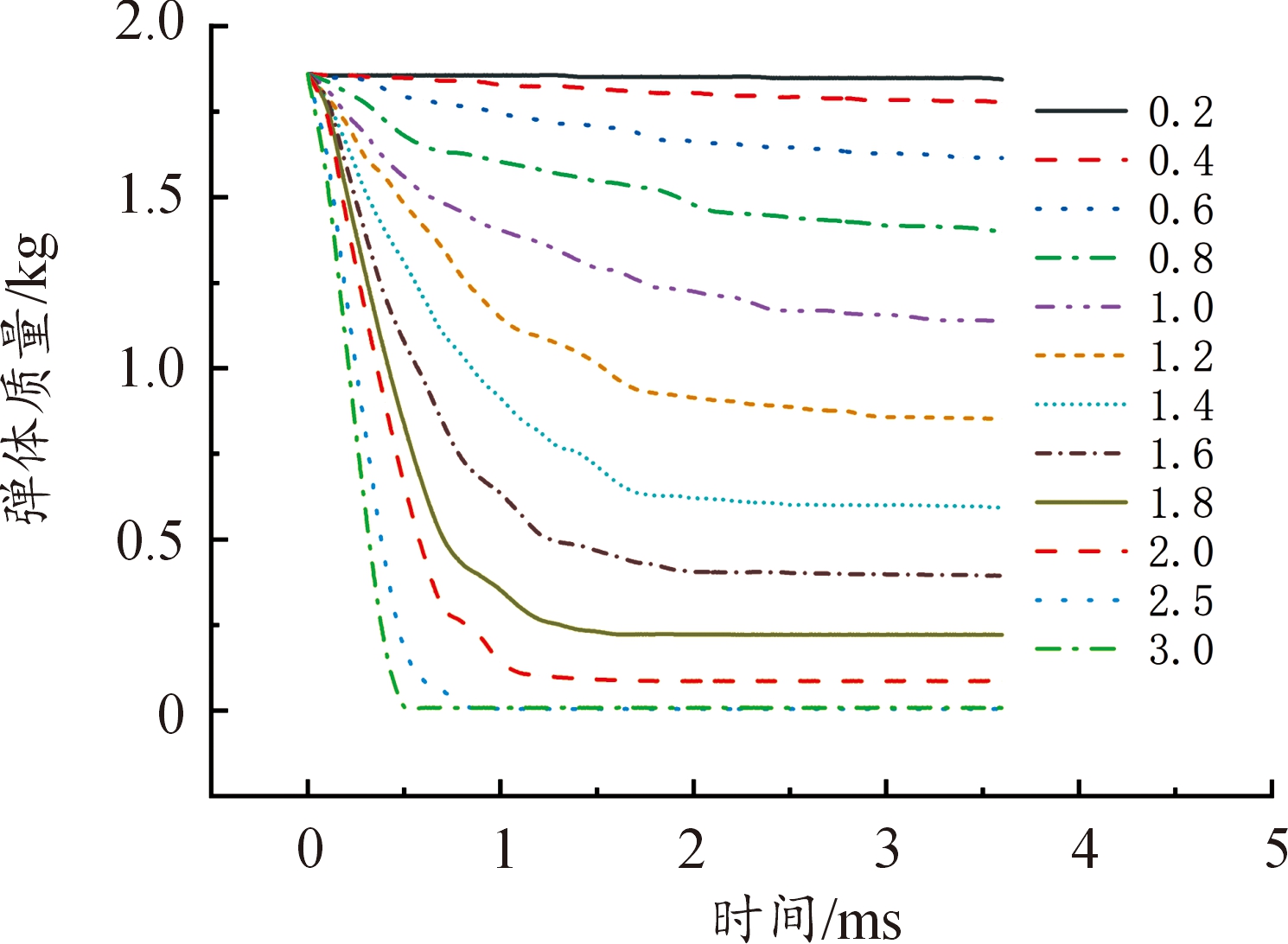
图7 弹体质量随时间变化曲线
Fig.7 Projectile mass with time
这是由于侵彻过程中,弹、靶相互作用产生高温导致弹体表面材料软化,尤其是作用剧烈的弹头部,混凝土颗粒切削软化的弹体表面材料,被切削下的弹体材料,一部分残留在混凝土中而形成弹体质量损失,另一部分与混凝土混合后随弹体侵彻结束重新覆盖于弹体表面,弹体速度越高材料软化越多,被混凝土颗粒切削下来的材料越多。另一方面,随着弹体速度的增加,侵彻机理发生改变,由刚体侵彻进入流体侵彻,此时材料的强度在侵彻过程中作用逐渐减小,材料密度起主要作用。当进入流体侵彻,弹体材料侵蚀剧烈,弹体材料侵蚀,该阶段称为“流体侵彻阶段”。当弹体速度降低到弹靶界面压力不足以侵蚀弹体时,流体侵彻阶段结束,此后弹体以刚体状态继续侵蚀,直到弹体速度降为0,该阶段称为“刚体侵彻阶段”。不同速度下弹体质量侵蚀率如表4所示。
表4 不同速度下弹体质量侵蚀率
Table 4 Mass erosion rate of the projiectie with different velocity
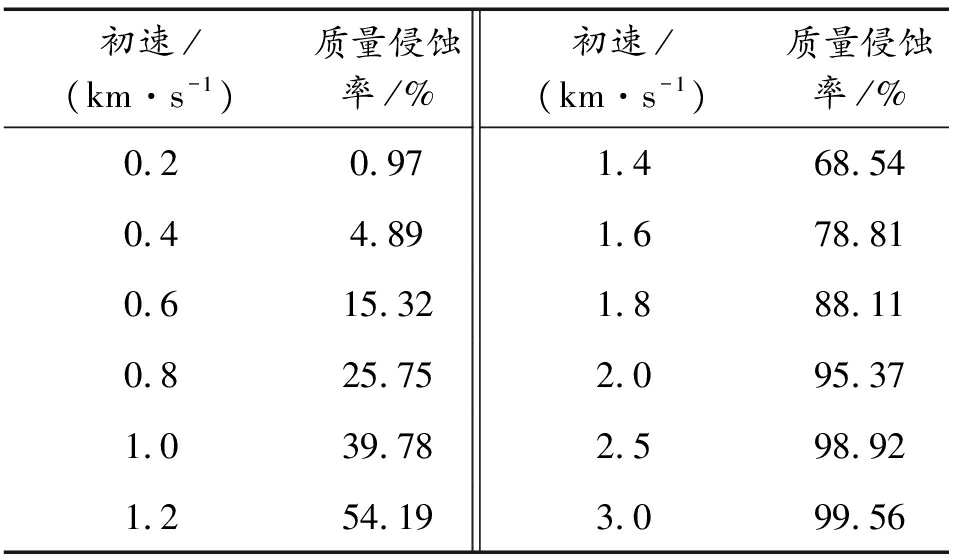
初速/(km·s-1)质量侵蚀率/%初速/(km·s-1)质量侵蚀率/%0.20.971.468.540.44.891.678.810.615.321.888.110.825.752.095.371.039.782.598.921.254.193.099.56
图8给出了弹体质量侵蚀率与初始动能的关系,由图8可知,0.5~1.6 km/s速度范围弹体质量侵蚀率与弹体初始动能呈线性关系。根据Forrest et al,1996;Frew et al,1998的试验结果Silling and Forrest(2007)指出,在侵彻速度v≤1 km/s(或v2/2≤0.5(km2/s2))时弹体质量的磨蚀与初始动能存在线性关系;侵蚀速度v≥1 km/s后,质量磨蚀维持在一常数水平。但是Forrest et al,1996;Frew et al,1998的试验弹体为不同标号的钢,而本文弹体为钨合金,因此在弹体质量的磨蚀与初始动能存在线性关系的速度区间并不一致。所以不同弹体材料侵彻混凝土,弹体质量磨蚀与初始动能线性关系的速度区间要根据弹体材料而定。
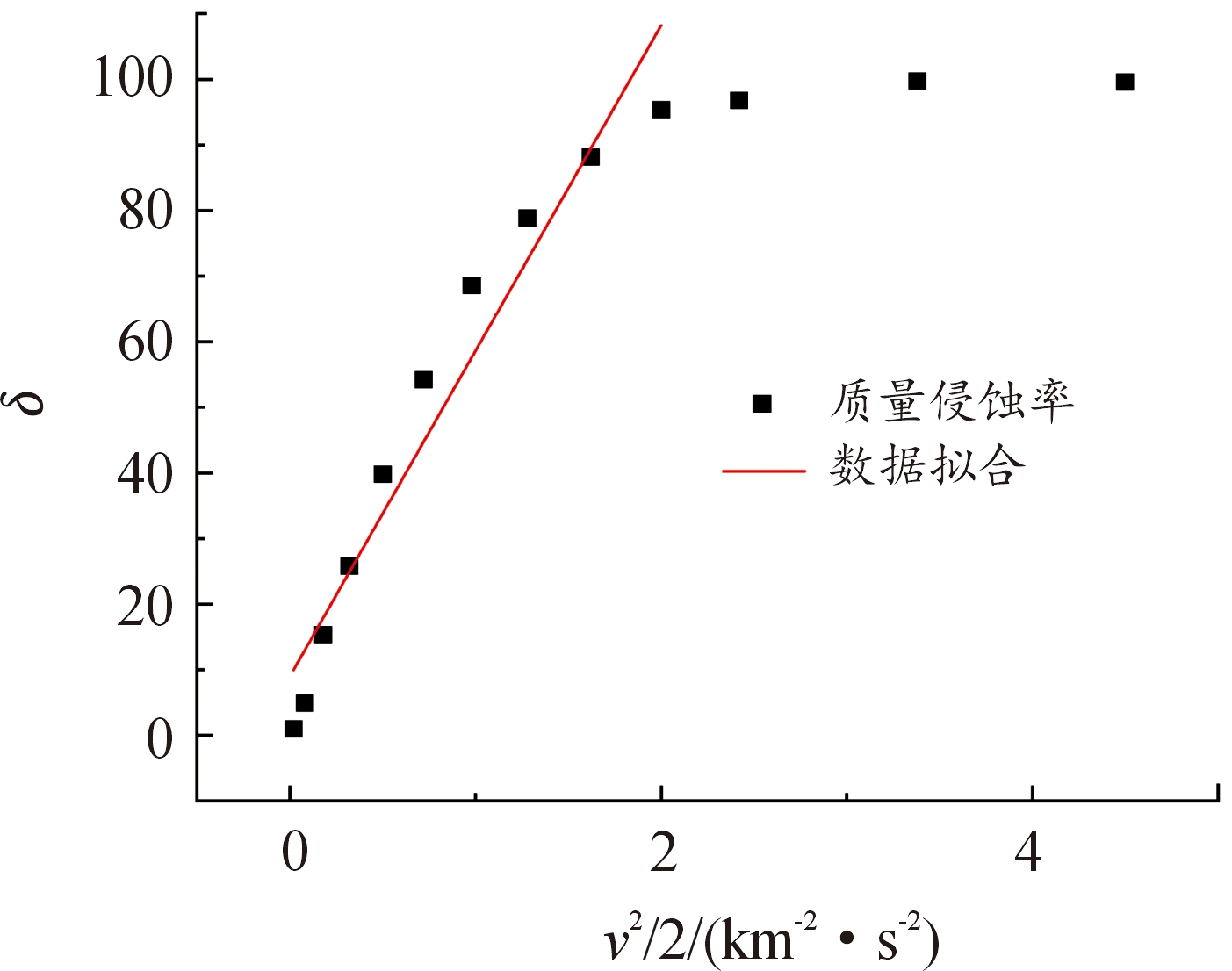
图8 弹体质量侵蚀率和初始动能呈线性关系
Fig.8 Mass erosion rate has a linear relationship with the initial kinetic energy
2.3 残余弹长
图9为残余弹长随速度变化曲线,由图9可以看出,速度0.2 km/s时残余弹长33.5 cm,与初始长度基本相同。1 km/s弹体残余长度21.1 cm,侵蚀掉原长的40.9%,随着速度的增加弹体被剧烈侵蚀,当速度3.0 km/s弹体基本被完全侵蚀。侵彻开始时刻,靶板逐渐开坑,弹体0.2~1.5 km/s速度侵彻靶板时,弹体材料并未全部侵蚀,说明弹体既经历了“流体侵彻”又经历了“刚体侵彻”。当速度大于2.0 km/s时,弹体已经被完全侵蚀,因此不包括刚体侵彻阶段。由于刚体侵彻深度在总侵彻深度中占很大比例,失去刚体侵彻阶段会使总侵深降低,当速度大于2.0 km/s时总侵彻深度随速度的增加明显降低。
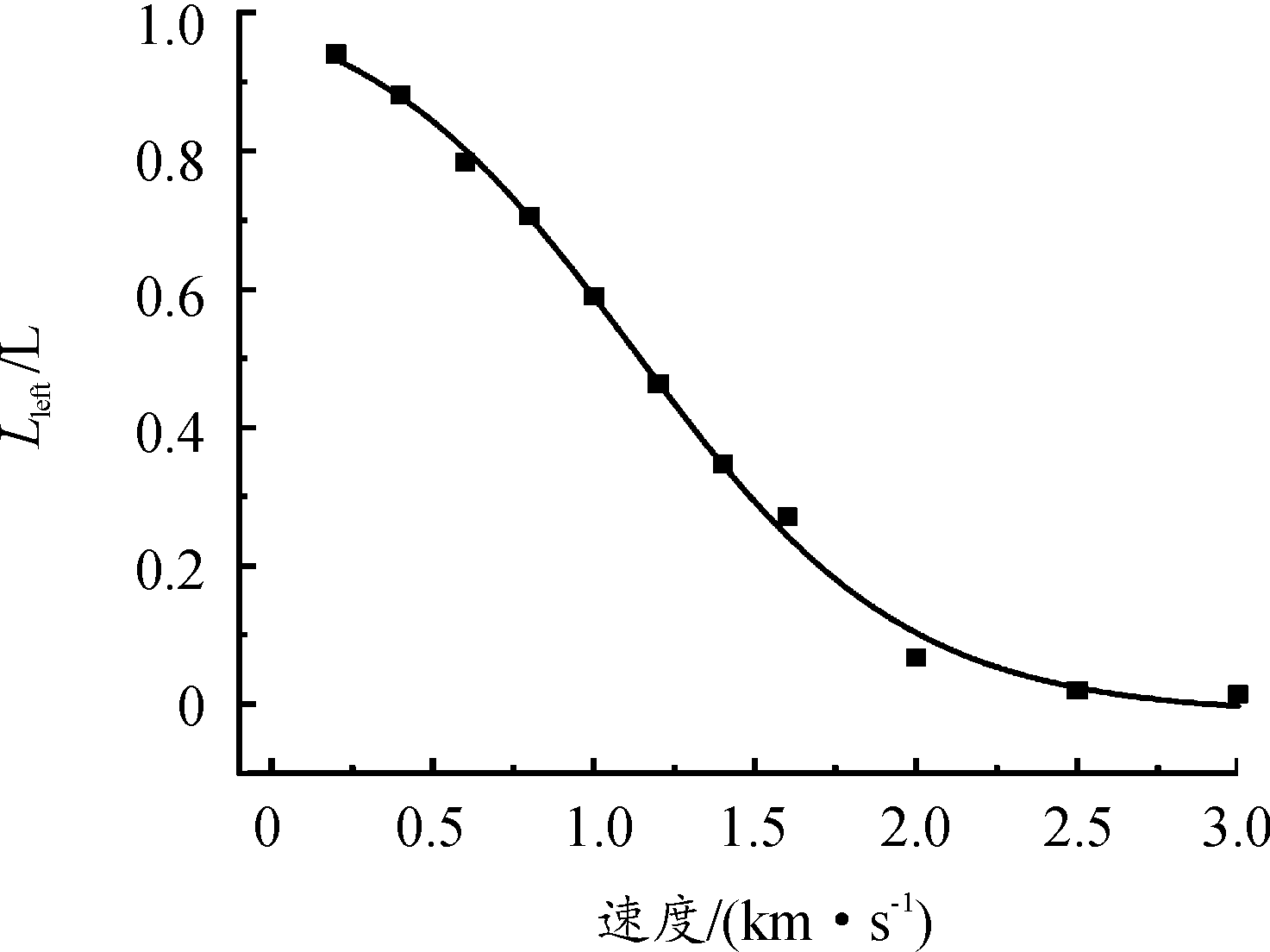
图9 残余弹长随速度变化曲线
Fig.9 Remaining length of projectile with velocity
2.4 侵彻阶段分析
根据Eichelberger[14]和orphal[15]分别提出的撞击4个阶段和第3侵彻阶段,将超高速侵彻可分为4个阶段,即:① 瞬态高压阶段;② 流体侵彻阶段;③ 刚体侵彻阶段;④ 回弹阶段。由于瞬态高压阶段和回弹阶段侵彻深度占比很小,可以忽略不计,因此本节重点关注流体侵彻阶段和刚体侵彻阶段。
弹体速度的增加会导致侵彻机制由刚体侵彻向流体侵彻转变,在某一速度下2种侵彻机制均会出现,因此研究刚体侵彻和半流体侵彻在侵彻过程中的占比,对研究超高速侵彻混凝土十分重要。
弹体尾部速度、弹体质量、侵彻深度随时间曲线如图10所示。由图10可知,弹体初速为0.6 km/s时,弹体质量和侵彻深度随时间呈连续线性变化,质量侵蚀率为15.32%,可以判断侵彻全过程基本为刚体侵彻。弹体初速增加至1.0 km/s时,弹体质量变化曲线出现了明显的转折点,侵度-时间曲线变为非线性,这是由于,侵彻开始瞬间弹体相对于靶体做减速运动,产生一个强冲击波向弹体和靶板传递,弹体承受极高的压力,此压力超过弹体材料所承受范围,导致弹体材料发生塑性变形,侵彻机制变为流体侵彻,弹体被侵蚀,质量减少,阻力变大,弹体速度逐渐下降。当弹体速度低于刚体临界速度vcri,侵彻机制转换为刚体侵彻,这个时间为1.5 ms(图9(b)),此时弹体速度为572 m/s,在流体侵彻阶段(0~1.5 ms)和刚体侵彻阶段(1.5~3.6 ms)弹体质量分别减少30.5%、12.1%,无量纲侵深分别为47.2、46.3,分别占总侵深50.4%、49.6%。这一现象在初速为1 400 m/s时更为显著,与初速1.0 km/s不同的是,初速1.4 km/s情况下,在1.8 ms时弹体质量变化曲线存在明显拐点,此时弹体速度为406 m/s。在流体侵彻阶段(0~1.8 ms)和刚体侵彻阶段(1.8~3.6 ms)内弹体质量分别减少66.2%、6.8%,侵深占比分别为70.4%、29.5%。
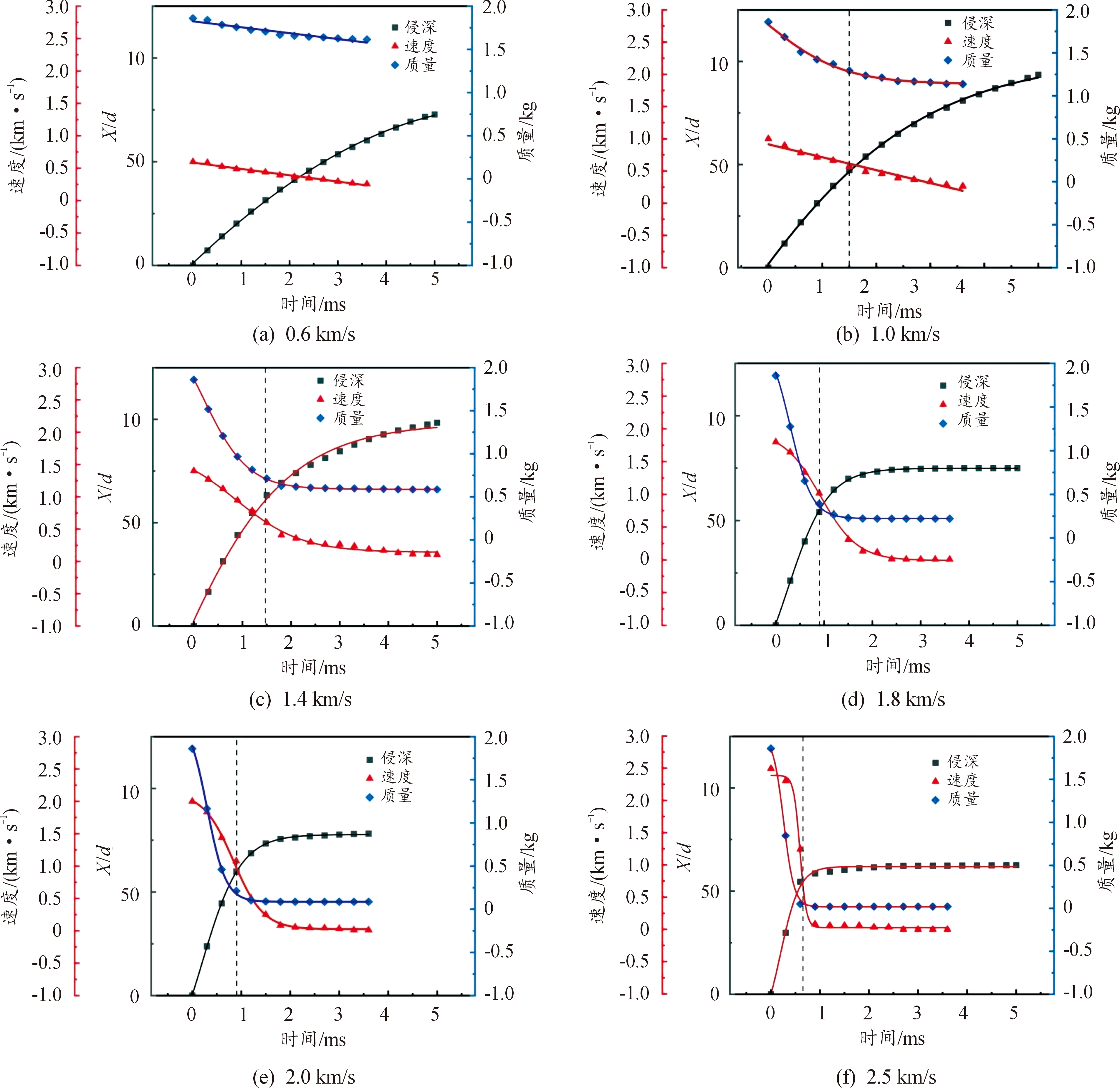
图10 弹体尾部速度、弹体质量、侵彻深度随时间曲线
Fig.10 Time histoyies of projectile velocity、mass and penetration depth
表5为不同初始速度下弹体流体/刚体侵彻深度数值模拟结果,图11为不同初速下弹体流体/刚体侵彻变化曲线。
表5 不同初速下弹体流体/刚体侵彻深度数值模拟结果
Table 5 Fluid and body penetration depth by simulation with diferent velocity
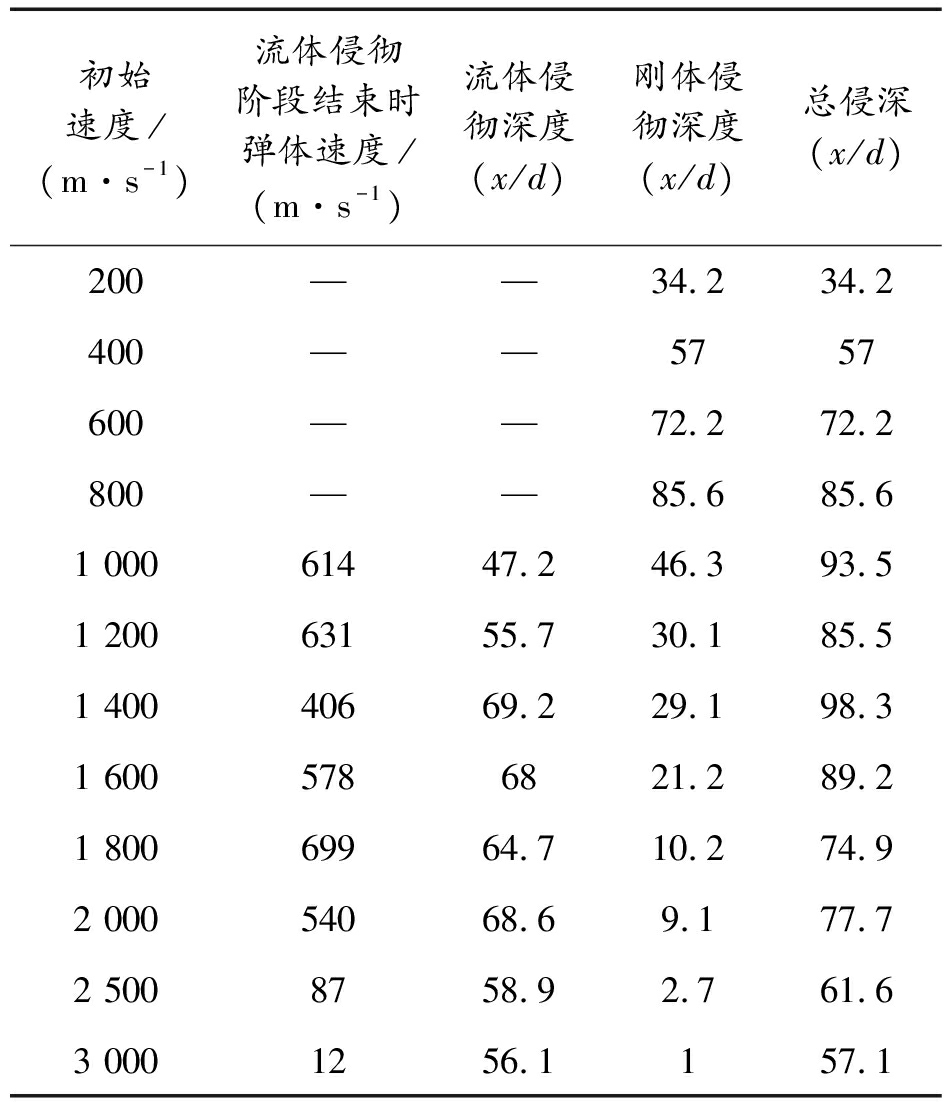
初始速度/(m·s-1)流体侵彻阶段结束时弹体速度/(m·s-1)流体侵彻深度(x/d)刚体侵彻深度(x/d)总侵深(x/d)200——34.234.2400——5757600——72.272.2800——85.685.61 00061447.246.393.51 20063155.730.185.51 40040669.229.198.31 6005786821.289.21 80069964.710.274.92 00054068.69.177.72 5008758.92.761.63 0001256.1157.1
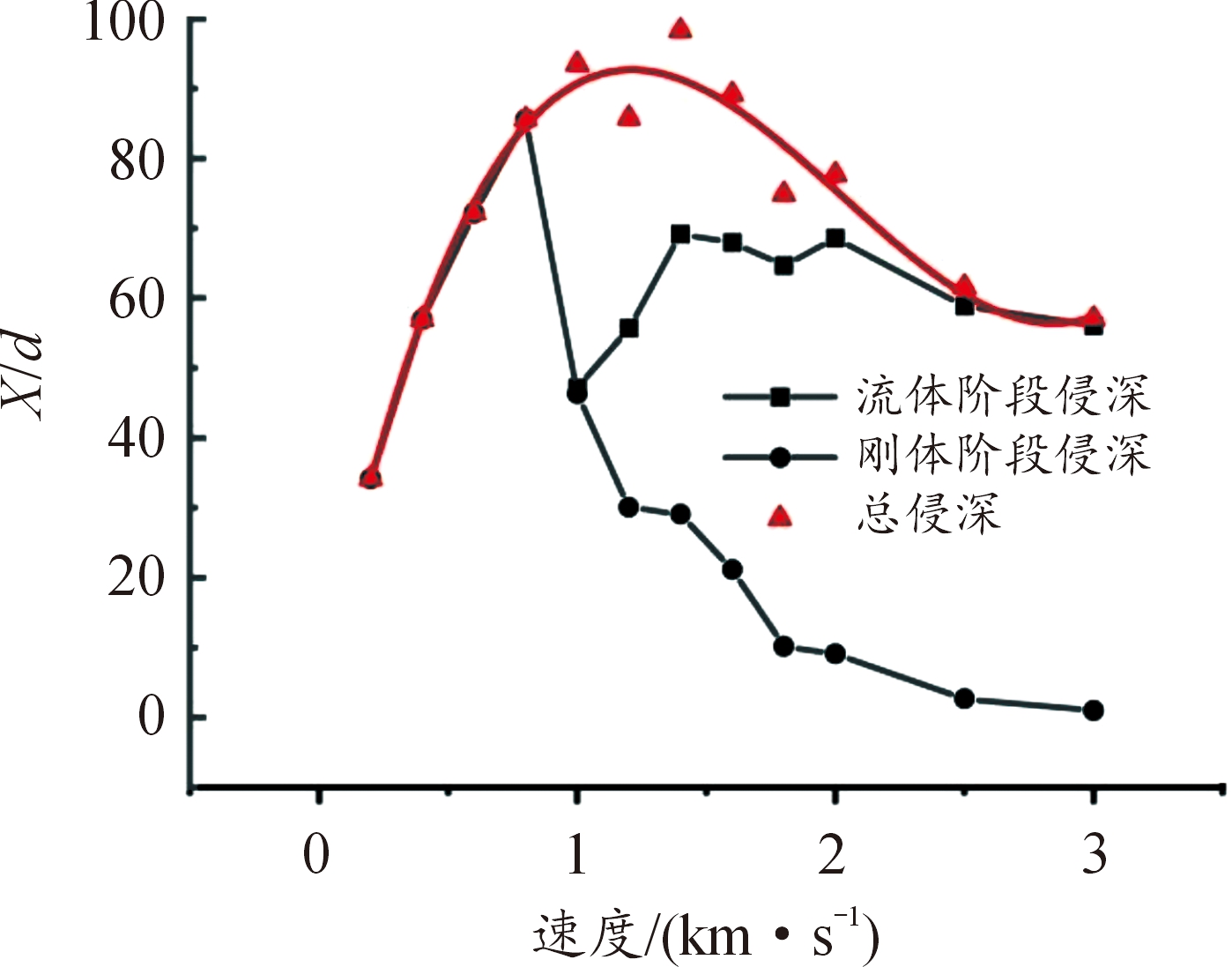
图11 不同初速下弹体流体/刚体侵彻变化曲线
Fig.11 Fluid and body penetration depth with velocity
通过表5和图11可以看出,弹体初速较低时侵彻全过程为刚体侵彻,初速达到1.0 km/s时弹体材料开始侵蚀,出现流体侵彻阶段,此时流体侵彻深度和刚体侵彻深度基本相等。随着弹体初速的增加,流体阶段侵彻深度呈现先增加后维持在一常数附近,刚体侵彻阶段侵深逐渐减小,两者叠加之后得到的总侵深呈现先增大后减小的趋势。
3 结论
本文中通过试验验证方法验证了材料本构模型的准确性,又通过数值模拟方法进一步研究了钨合金杆弹超高速侵彻混凝土靶侵彻深度随弹体初速的变化规律,得出以下结论:
1) 分析数值模拟所得数据可知,流体侵蚀阶段,弹体质量大幅度减少。0.2~1.8 km/s速度范围内,弹体质量侵蚀率与弹体初始动能呈正比例线性关系,弹体初速大于2.0 km/s质量侵蚀率高达95%。
2) 由数值模拟分析可得,侵彻深度随弹体初速增加呈现先增加后减小现象,在初速1.2 km/s附近存在侵深最大值约80倍弹径。超高速条件下侵彻深度对于中低速侵彻并无优势。
3) 弹体初速小于0.8 km/s侵彻机制为刚体侵彻,初速大于1.0 km/s时侵彻机制既包括刚体侵彻又包括流体侵彻。1.0~2.0 km/s流体侵深由47.2增加至68.6,3.0 km/s时降至56.1。在1.0~3.0 km/s刚体侵彻深度由46.3持续下降至1。流体侵深和刚体侵深的变化,导致体侵深曲线呈现先增大后减小的趋势。
[1] 卢正操,张元迪,文鹤鸣,等.长杆弹侵彻半无限混凝土靶的理论研究[J].现代应用物理,2018,9(4):17-28.
LU Zhengcao,ZHANG Yundi,WEN Heming,et al.Theoretical study on the penetration of long rods into semi-infinite concrete targets[J].Modern Applied Physics,2018,9(4):17-28.
[2] 周刚,李名锐,文鹤鸣,等.钨合金弹体对混凝土靶的超高速侵彻机理[J].爆炸与冲击,2021,41(2):93-106.
ZHOU Gang,LI Mingrui,WEN Heming,et al.Mechanism on hypervelocity penetration of a tungsten alloy projectile into a concrete target[J].Eeplosion and Shock Waves,2021,41(2):93-106.
[3] 高飞,张国凯,纪玉国,等.卵形弹体超高速侵彻砂浆靶的响应特性[J].兵工学报,2020,41(10):1979-1987.
GAO Fei,ZHANG Guokai,JI Yuguo,et al.Response characteristics of hypervelocity ogive-nose projectile into mortar target[J].Acta Armamentare,2020,41(10):1979-1987.
[4] 王明洋,李杰,李海波,等.岩石的动态压缩行为与超高速动能弹毁伤效应计算[J].爆炸与冲击,2018,38(6):1200-1217.
WANG Mingyang,LI Jie,LI Haibo,et al.Dynamic compression behavior of rock and simulation of damage effects of hypervelocity kinentic energy bomb[J].Eeplosion and Shock Waves,2018,38(6):1200-1217.
[5] 王明洋,邱艳宇,李杰,等.超高速长杆弹对岩石侵彻、地冲击效应理论与试验研究[J].岩石力学与工程学报,2018,37(3):564-572.
WANG Mingyang,QIU Yanyu,LI Jie,et al.Theoretical and experimental study on penetration in rock and ground impact effects of long rod projectiles of hyper speed[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(3):564-572.
[6] 钱秉文,周刚,李进,等.钨合金柱形弹超高速撞击水泥砂浆靶的侵彻深度研究[J].爆炸与冲击,2019,39(8):139-147.
QIAN Bingwen,ZHOU Gang,LI Jin,et al.Penetration depth of hypervelocity tungsten alloy projectile penetrating concrete target[J].Eeplosion and Shock Waves,2019,39(8):139-147.
[7] 钱秉文,周刚,李进,等.钨合金弹体超高速撞击混凝土靶成坑特性研究[J].北京理工大学学报,2018,38(10):1012-1017.
QIAN Bingwen,ZHOU Gang,LI Jin,et al.Study of the crater produced by hypervelocity tungsten alloy peojectile into concrete target[J].Transaction of Beijing Institute of Technology,2018,38(10):1012-1017.
[8] 姚志彦,李金柱,齐凯丽,等.长杆弹超高速侵彻砂浆靶临界速度的试验和计算[J].兵工学报,2022,43(7):1578-1588.
YAO Zhiyan,LI Jinzhu,QI Kaili,et al.Experimeng and calculation of critical velocity of long-rod projectile penentrating mortar target at hyperveloctiy[J].Acta Armamentare,2022,43(7):1578-1588.
[9] 程怡豪,王明洋,施存程,等.大范围着速下混凝土靶抗冲击试验研究综述[J].浙江大学学报(工学版),2015,49(4):616-625,637.
CHENG Yihao,WANG Mingyang,SHI Cuncheng,et al.Review of experiental investigation of concrete target to resist missile impact in large velocity range[J].Jouranal of Zhejing University(Engineering Science),2015,49(4):616-625,637.
[10] 王猛,杨明川,荣光,等.穿甲过程中钨合金杆式弹失效模式及数值模拟[J].稀有金属材料与工程,2015,44(9):2170-2174.
WANG Meng,YANG Mingchuan,RONG Guang,et al.Faliure model and numerical simulation of the tungsten alloy long rod when piercing into armor target[J].Ramremetal Materials and Engineering,2015,44(9):2170-2174.
[11] 刘兴锋,周兰伟,朱荣刚.侵爆战斗部对钢筋混凝土靶的侵彻能力计算方法[J].弹道学报,2021,33(4):64-70.
LIU Xingfeng,ZHOU Lanwei,ZHU Ronggang. Calculation method of capability of penetration-explosion warhead penetrating into reinforced concrete target[J].Journal of Ballistics,2021,33(4):64-70.
[12] 汪衡,汪于程,蔡金良,等.HJC模型失效参数对侵彻能力影响的数值研究[J].兵器装备工程学报,2020,41(10):150-155.
WANG Heng,WANG Yucheng,CAI Jinliang,et al.Numerical study on effect of failure parameters of HJC model on penetration effect[J].Journal of Ordnance Equipment Engineering,2020,41(10):150-155.
[13] 陈小伟.穿甲/侵彻力学的理论建模与分析(上册)[M].北京:科学出版社,2019:38-39.
CHEN Xiaowei.Modelling on the perforation and penetration Ⅰ[M].Beijing:Science Press,2019:38-39.
[14] EICHELBERGER R J.Experimetal test of the theory of penetration by metallic jets[J].Journal of Applied Physiscs.1956,17(1):63-68.
[15] ORPHAL D L.Phase three penetration[J].Intrnational Journal of Impact Engineering,1997,20(6):601-616.