0 引言
药型罩锥角、药型罩厚度、装药长径比以及装药外壳厚度等在不同程度上对射流成型及侵彻速度产生影响,具有一定规律[1]。Manfred Held[2]通过闪光X射线技术研究了药型罩锥角对射流形状及速度的影响。在一定范围内,药型罩锥角增大,射流速度逐渐减小[3]。对于一定的聚能装药结构,药型罩锥角在35°~60°之间被称为理论上的最佳角度[4-5]。T.Elshenawy等[6]认为等壁厚情况下,射流速度随着壁厚的减小而增大。Fedorov等[7]通过数值仿真提出一种可变厚度的药型罩结构,相比于等壁厚,可有效提升射流速度。对于装药外壳厚度,柴艳军等[8]认为存在一个使射流总动能达到最大值的最佳壳体厚度。对于装药长径比,李伟兵等[9]认为当装药长径比超过1.2,再增加装药长径比对聚能杆式侵彻体头部速度影响较小。段建等[10]分别研究了装药长径比、装药密度等5个因素对爆炸成型弹丸性能的影响规律。王一凡等[11]分别探究辅助装置各参数(包括水平宽度、开口直径等)对装药性能的影响。目前针对装药结构各参数对射流侵彻性能影响的研究较为全面[12-13],但对各因素影响程度大小的对比研究较少。
本文针对这一问题展开研究,基于欧拉算法,选取柱形装药结构,引入正交设计方法[14-18],探究药型罩锥角(α)、药型罩厚度(β)、装药长径比(γ)以及装药外壳厚度(d)4个因素对射流成型及侵彻性能的影响程度大小。对聚能射流成型及侵彻靶板的过程进行试验研究,与仿真结果对比,验证仿真方法的正确性。
1 计算模型及试验验证
1.1 计算模型
采用耦合欧拉-拉格朗日算法,聚能装药结构示意图如图1所示,对聚能射流的形成过程进行数值模拟。
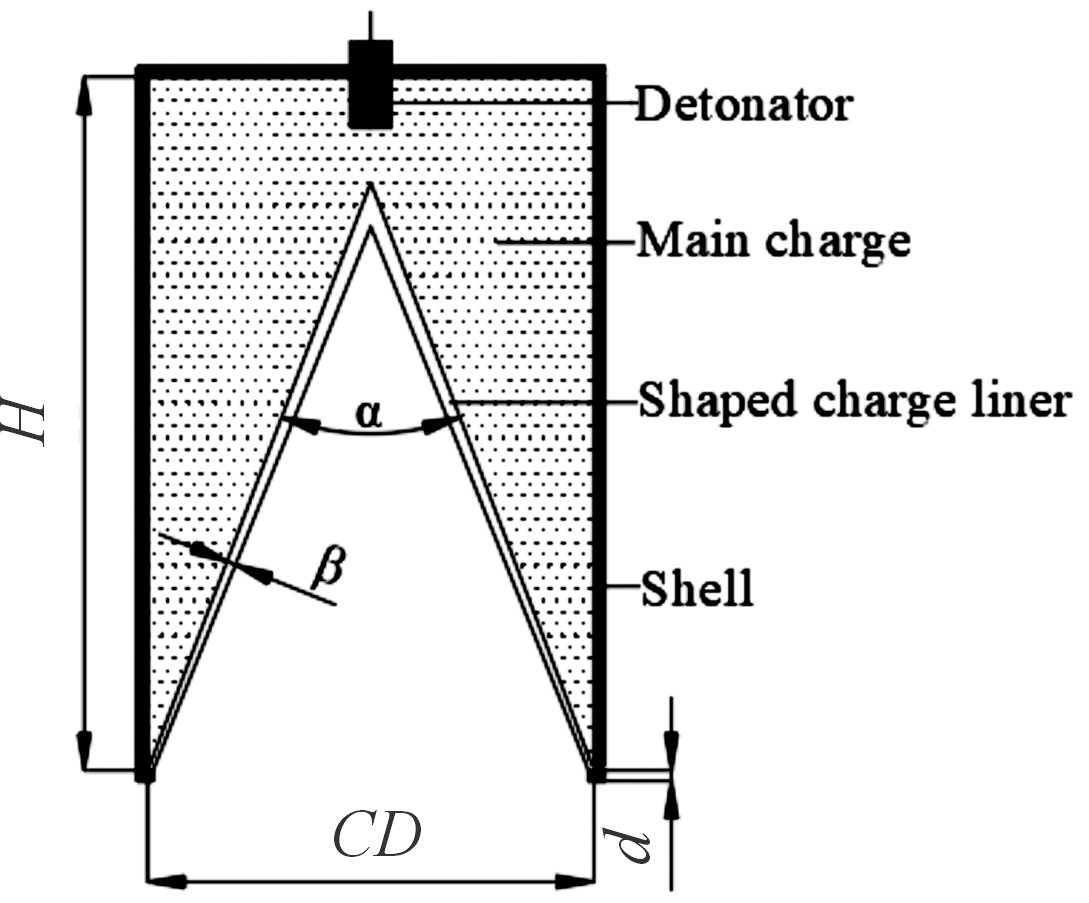
图1 聚能装药结构示意图
Fig.1 The sketch of the shaped charge structure
炸药采用EOS_JWL状态方程[19]
式中:p为爆轰压力;E为炸药比内能;ν为相对比容;参数A1、B1、R1、R2为实验数据拟合所得的与炸药状态有关的常数[20],参数A1=524.00 GPa,B1=7.68 GPa,R1=4.20,R2=1.10,ω=0.34。
药型罩材料采用Steinberg Guinan本构模型[21],剪切模量G和屈服应力Y在高应变率下的本构关系为:
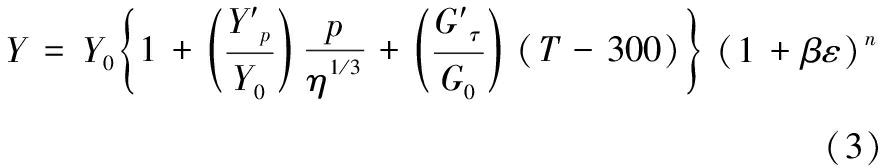
Y0[1+βε]n≤Ymax
(4)
式中:ε为有效塑性应变;T为温度;η=v0/v;Y为初始屈服应力;Ymax为最大屈服应力;β为硬化常数;n为硬化指数;![]()
靶板材料为10CrNi3MoV钢,采用如式(5)所示的Johnson-Cook本构模型:
式中:σ为Von Mises流动应力;εp为有效塑性应变;![]() 为有效塑性应变率;A=651.0 MPa为材料的屈服应力常数;B=776 MPa为材料的应变硬化系数;C=0.024为材料应变率相关系数;n=0.64为材料应变硬化指数;m=1.0、T、Tr及Tm为材料温度相关系数;Tm=1 765 K为熔点;Tr为室温。温度T=Tm,整个射流的形成与发展过程假设为绝热过程。
为有效塑性应变率;A=651.0 MPa为材料的屈服应力常数;B=776 MPa为材料的应变硬化系数;C=0.024为材料应变率相关系数;n=0.64为材料应变硬化指数;m=1.0、T、Tr及Tm为材料温度相关系数;Tm=1 765 K为熔点;Tr为室温。温度T=Tm,整个射流的形成与发展过程假设为绝热过程。
根据上述相关参数,对射流成型及侵彻靶板过程进行仿真计算。
1.2 试验验证
为验证仿真方法的正确性,开展聚能射流成型的试验及仿真计算。分别获取相同时刻试验和仿真计算中聚能射流头部的速度,对比二者相对误差。
开展聚能射流成型的仿真计算,采用图1所示装药结构。其中,炸药和药型罩材料使用1.1节中的参数模型,药型罩锥角α=40°,采用变厚度药型罩锥角,锥角顶部到底部厚度变化为β=0.025CD-0.0125CD,长径比γ=H/CD=1.55,装药外壳厚度d=4 mm,装药直径CD=88 mm。采用AUTODYN软件中的欧拉算法,流体域使用0.5 mm×0.5 mm均匀网格,起爆方式为装药底部中心点起爆方式,仿真计算过程示意图如图2所示,流体域中间隔10 mm设置观测点,用于记录射流头部速度。射流流经1.0倍炸高位置时计为0时刻,分别取0时刻,25 μs及50 μs时的射流头部速度计入表1,数值仿真结果如图3所示。
表1 射流头部速度的试验与仿真结果对比
Table 1 Comparison of experimental and simulation results of the jet head velocity
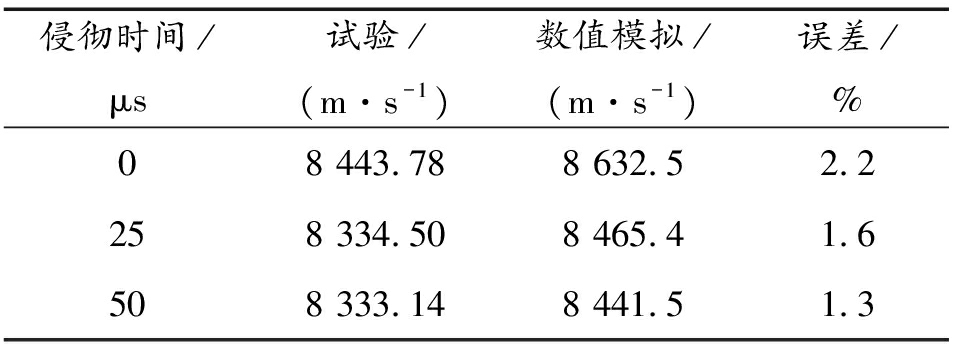
侵彻时间/μs试验/(m·s-1)数值模拟/(m·s-1)误差/%08 443.788 632.52.2258 334.508 465.41.6508 333.148 441.51.3
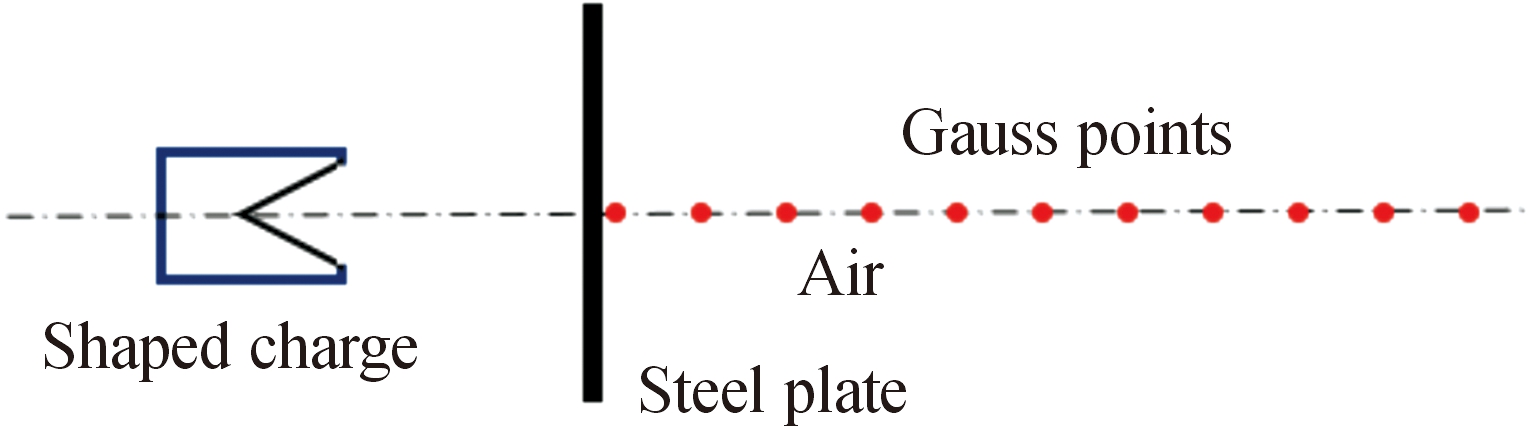
图2 仿真计算示意图
Fig.2 The schematic diagram of simulation

图3 聚能装药空射高速摄像照片及速度云图
Fig.3 High-speed photos and velocity distribution of shaped charge blasting
对聚能射流成型过程进行试验验证,试验现场采用的装药结构参数与仿真计算一致,靶板为1 000 mm×1 000 mm×12 mm的方形10CrNi3MoV钢板,用于触发装药结构引信,使之产生聚能射流,现场布置示意图如图4所示。设计固定支架用于固定钢板位置,聚能装药结构垂直入射靶板平面。现场利用1台20万帧高速摄像记录聚能装药结构侵彻靶板并形成射流的全过程,以此记录射流侵彻过程中的侵彻速度。试验后,逐帧读取高速摄像照片,每5帧保存1次,采用插值法求得射流头部速度。将聚能射流穿出靶板时刻计为0时刻,同时分别取25 μs及50 μs时的射流头部速度计入表1,高速摄像照片如图4所示。
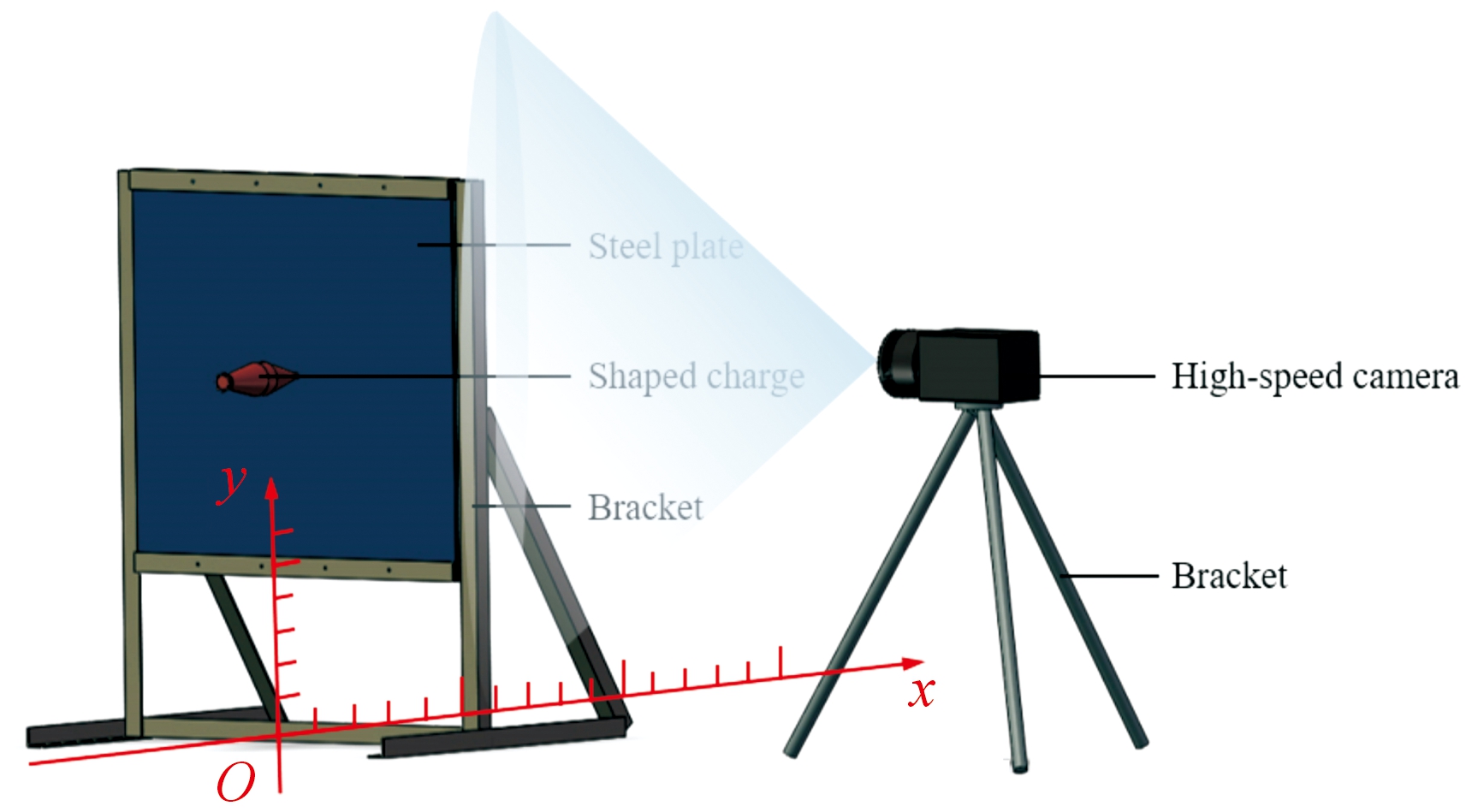
图4 试验现场布置示意图
Fig.4 Layout of test site
分别对比仿真计算及试验所得相同时刻射流头部速度,由表1中的数据可得3组数据误差分别为2.2%、1.6%、1.3%,试验与仿真结果相对误差均在10%以内,可以认为,数值与试验结果吻合性较好,验证数值仿真方法的正确性。
2 聚能装药结构的正交优化设计
2.1 优化设计因子、水平的设计
采用图1所示聚能装药结构进行正交优化设计,探究各因素对射流头部速度V以及射流有效长度L的影响。本文将高于临界破甲速度(2 000 m/s)的射流长度定义为射流的有效长度。炸高定为1.5倍装药直径(取CD=80 mm)即120 mm。CD=80 mm,炸药为JH-2,装药外壳为AL7039,起爆方式选择中心点起爆,网格大小选择0.5 mm×0.5 mm均匀网格。
正交试验设计采用柱形聚能装药形状,选取药型罩锥角A、药型罩壁厚B、聚能装药长径比C以及装药外壳厚度D作为正交设计的4个因素,各因素水平的取值如表2所示。
表2 正交设计各因素水平
Table 2 Orthogonal table
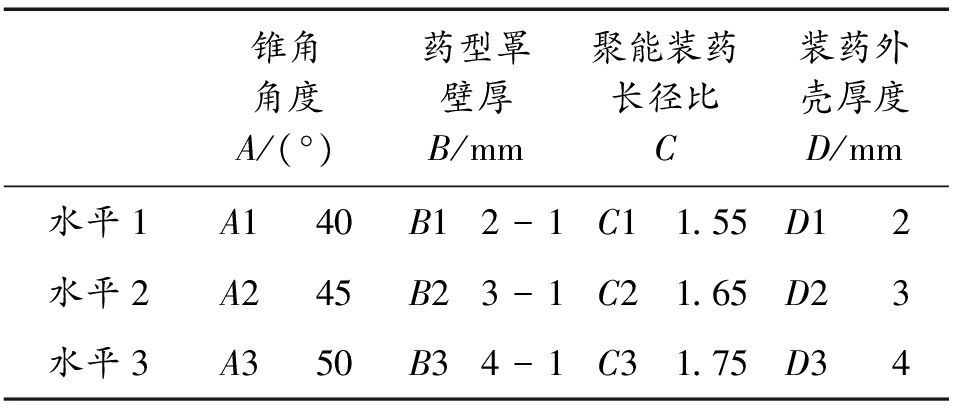
锥角角度A/(°)药型罩壁厚B/mm聚能装药长径比C装药外壳厚度D/mm水平1A140B12-1C11.55D12水平2A245B23-1C21.65D23水平3A350B34-1C31.75D34
药型罩锥角角度在35°~60°之间被称为理论上的最佳角度[4-5],因此,分别选取40°、45°以及50°三个水平;相比于等壁厚,药型罩壁厚在变厚度的情况下射流速度更高[7],为了探究变壁厚对射流侵彻性能的影响,设置由罩顶到罩底0.05CD-0.0125CD(4-1)、0.0375CD-0.0125CD(3-1)以及0.025CD-0.0125CD(2-1)三个水平;为了探究装药长径比大于1.5时,长径比对聚能射流侵彻性能的影响,分别设置1.55、1.65及1.75三个水平;对于装药外壳厚度来说,总存在一个最佳壳体厚度,使射流侵彻性能达到最佳,分别取0.025CD(2 mm)、0.0375CD(3 mm)及0.05CD(4 mm)3个水平。
若按照常规试验方案设计,需要设置34组试验,同时,各因素对侵彻性能的影响规律也很难体现,而选择正交试验设计可以有效减少试验次数,提高计算效率。选择L9(34)正交表,共包含9次试验,试验组合如表3所示。为进一步分析影响因素的重要性,对计算结果进行极差分析并列于表5。根据表5分别绘制图5、图6中不同因子水平对V、L的变化关系。
表3 正交表L9(34)
Table 3 Orthogonal design
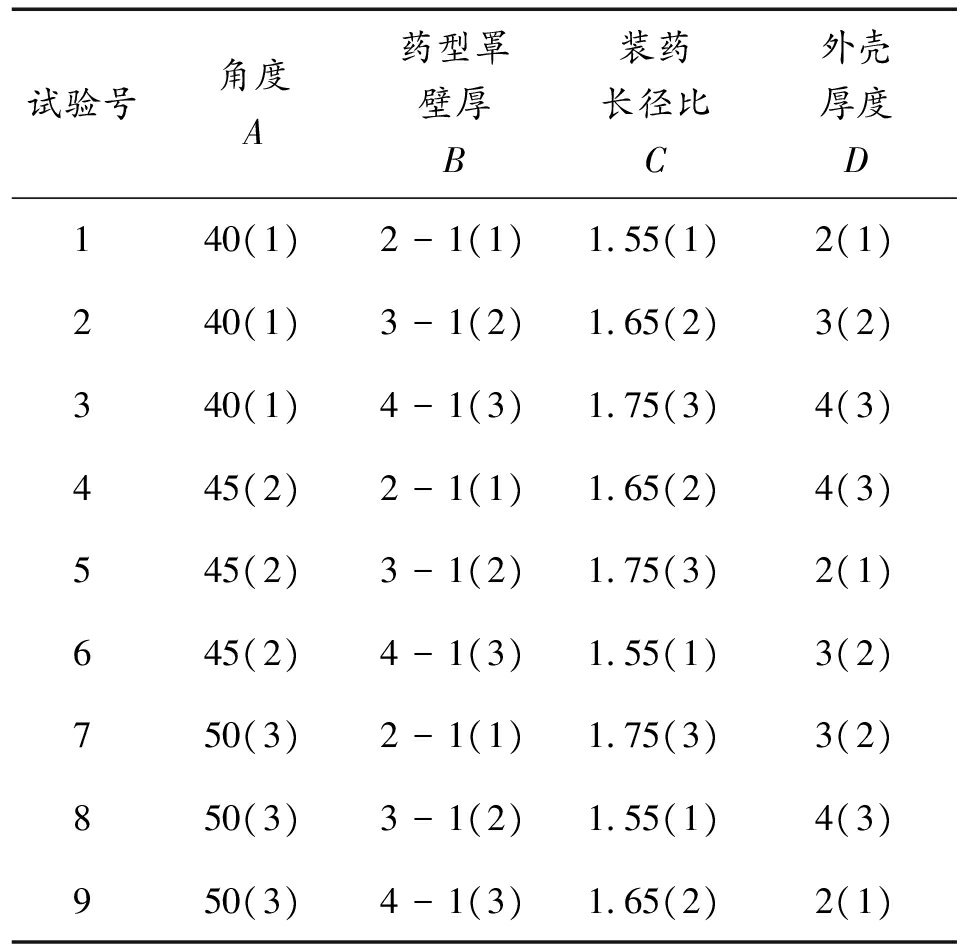
试验号角度A药型罩壁厚B装药长径比C外壳厚度D140(1)2-1(1)1.55(1)2(1)240(1)3-1(2)1.65(2)3(2)340(1)4-1(3)1.75(3)4(3)445(2)2-1(1)1.65(2)4(3)545(2)3-1(2)1.75(3)2(1)645(2)4-1(3)1.55(1)3(2)750(3)2-1(1)1.75(3)3(2)850(3)3-1(2)1.55(1)4(3)950(3)4-1(3)1.65(2)2(1)
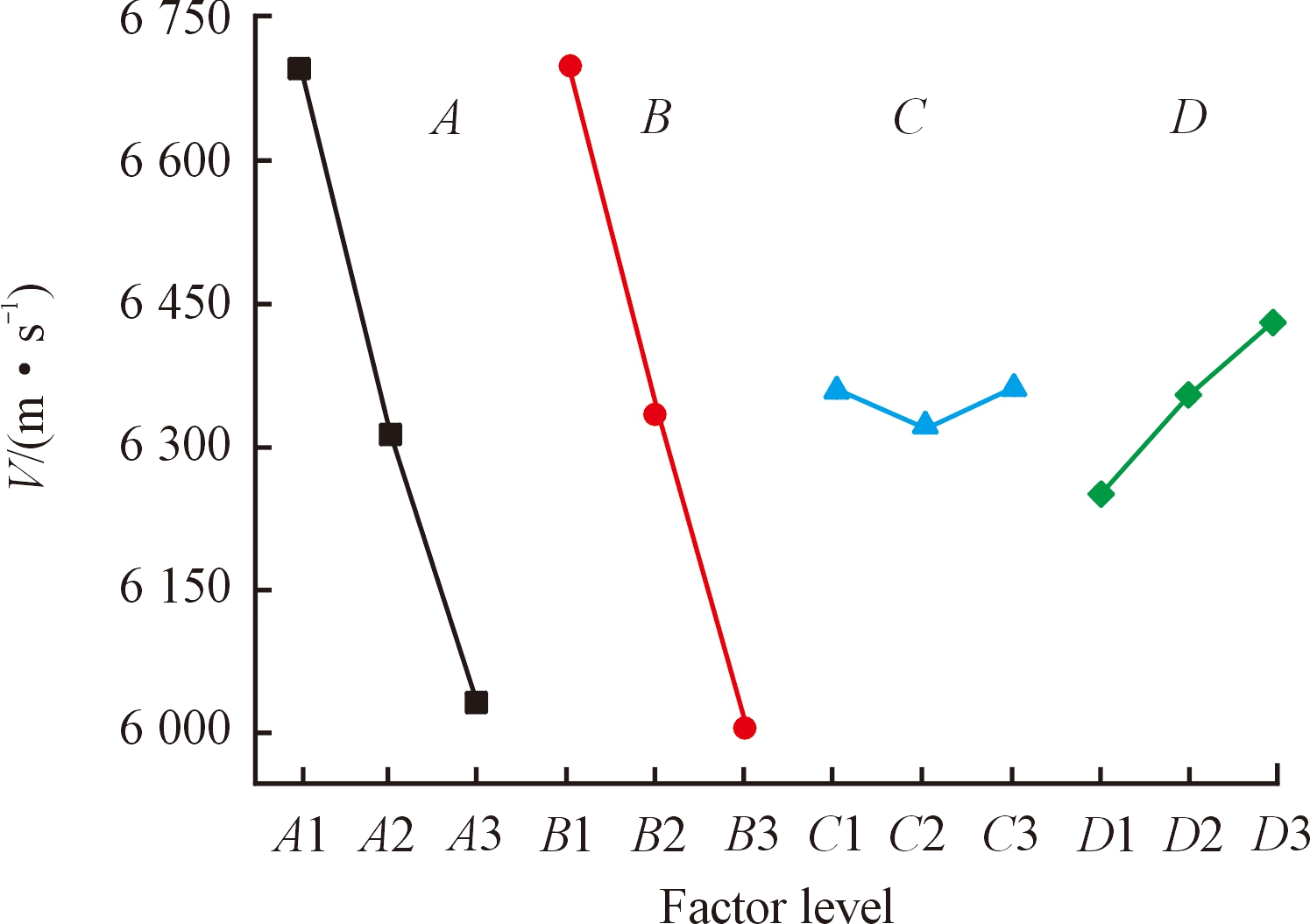
图5 不同因子水平对射流头部速度的影响
Fig.5 Effect of different factor levels on V
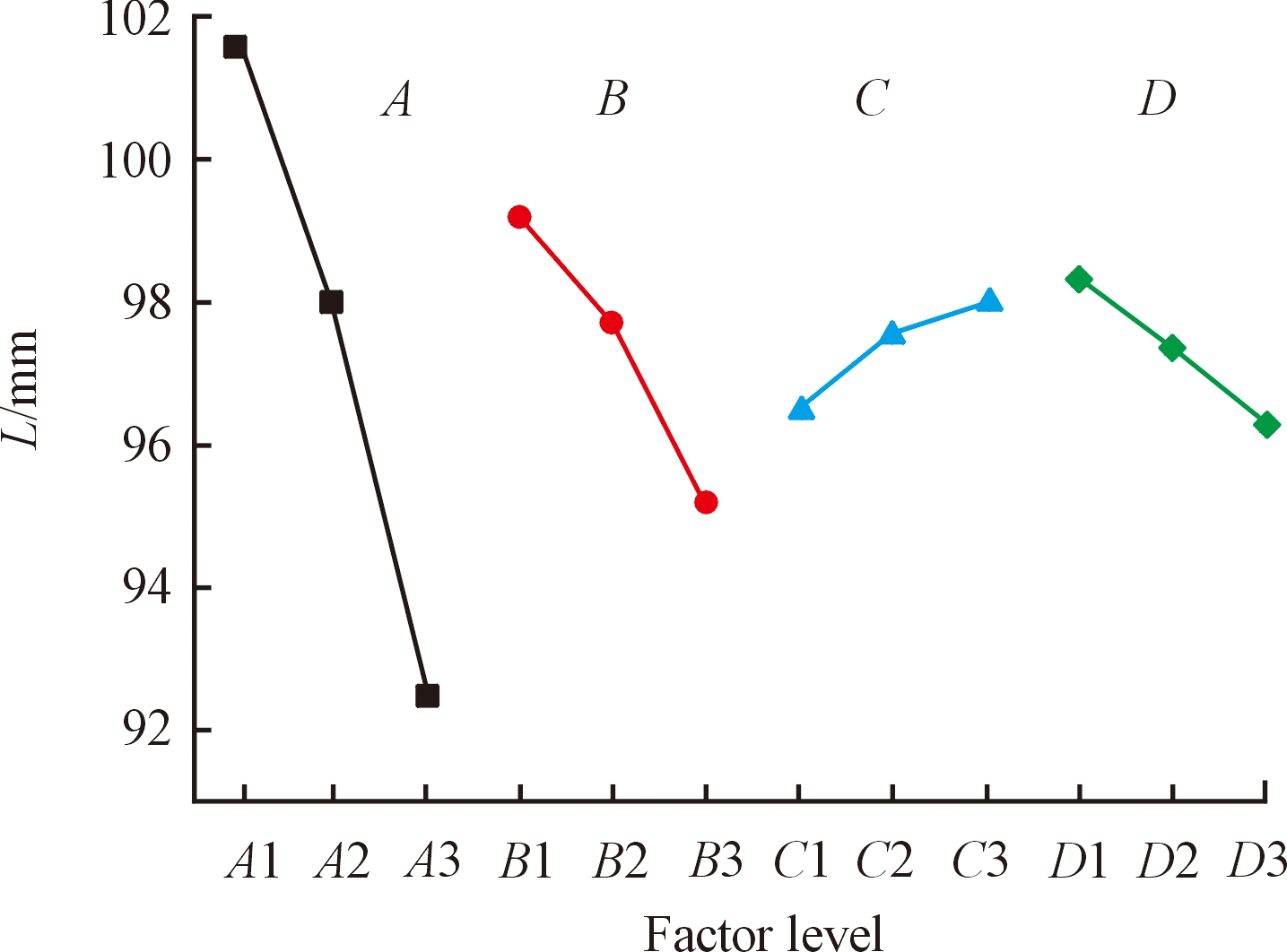
图6 不同因子水平对射流有效长度的影响
Fig.6 Effect of different factor levels on L
2.2 数值模拟结果与分析
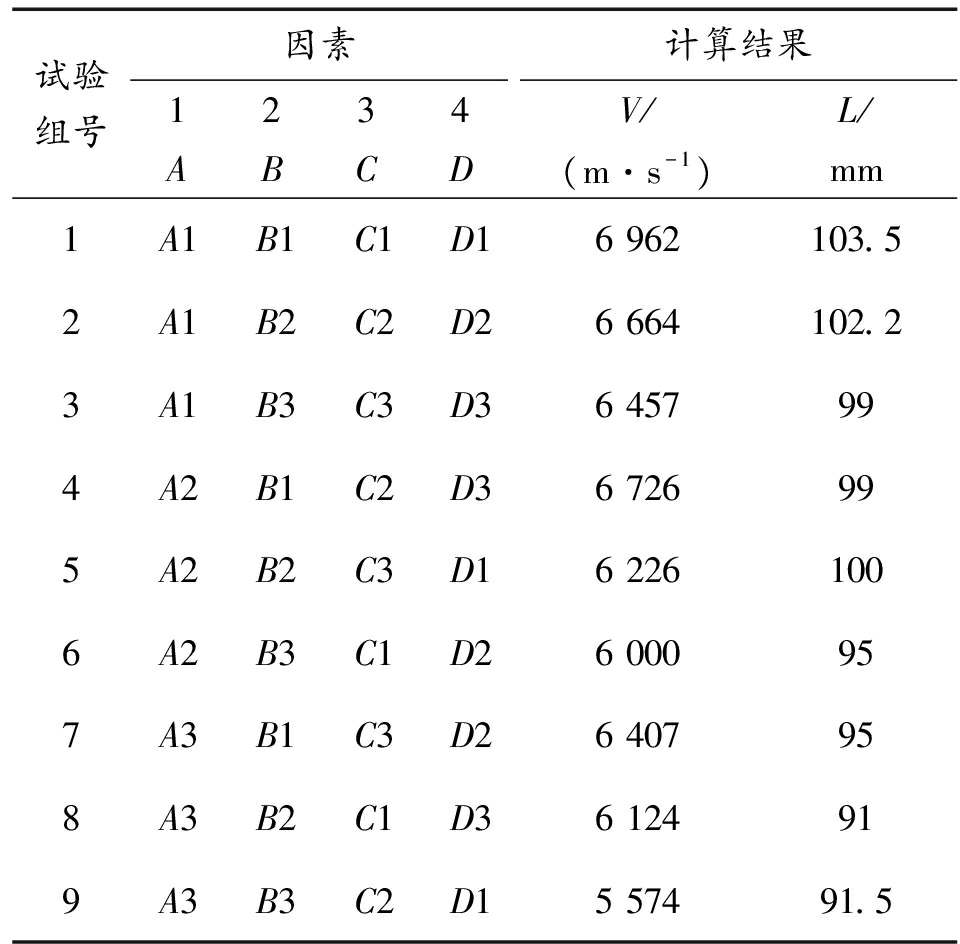
对表3中的组合进行数值计算,将计算结果列于表4所示。
表4 计算结果
Table 4 Calculated results
试验组号因素1234ABCD计算结果V/L/(m·s-1)mm1A1B1C1D16 962103.52A1B2C2D26 664102.23A1B3C3D36 457994A2B1C2D36 726995A2B2C3D16 2261006A2B3C1D26 000957A3B1C3D26 407958A3B2C1D36 124919A3B3C2D15 57491.5
由表5和图5、图6可知,当组合为A1、B1、C3、D3时,V达到最大值;当组合为A1、B1、C3、D1时,L达到最大值。由极差分析可知,4因素对V影响的主次顺序为:B、A、D、C;4因素对L影响的主次顺序为:A、B、D、C。
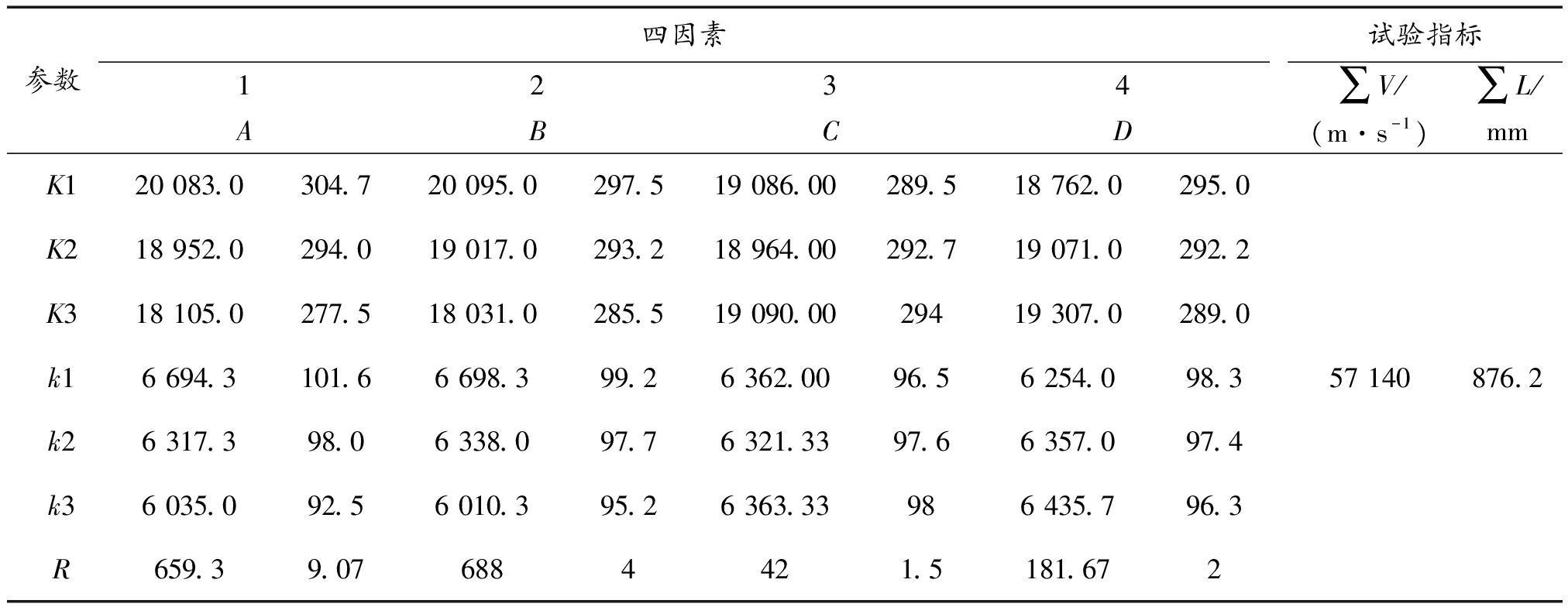
表5 极差分析表
Table 5 Extremum difference analysis
参数四因素1234ABCD试验指标∑V/∑L/(m·s-1)mmK120 083.0304.720 095.0297.519 086.00289.518 762.0295.0K218 952.0294.019 017.0293.218 964.00292.719 071.0292.2K318 105.0277.518 031.0285.519 090.0029419 307.0289.0k16 694.3101.66 698.399.26 362.0096.56 254.098.3k26 317.398.06 338.097.76 321.3397.66 357.097.4k36 035.092.56 010.395.26 363.33986 435.796.3R659.39.076884421.5181.67257 140876.2
注:Kij表示某因素某水平的总和;kij表示总和的平均值;R表示对应因素的极差R,R值越大,该因素对指标的影响越大,即该因素越重要。
为进一步分析误差影响及各因素水平有无显著差异,需要对试验指标进行方差分析。根据表4及表5中的数据,计算各因素的离差平方和S:
式中:Ki表示某因素在i水平时计算结果之和;xk为不同实验的计算结果。分别计算SA、SB、SC以及SD列于表6中。
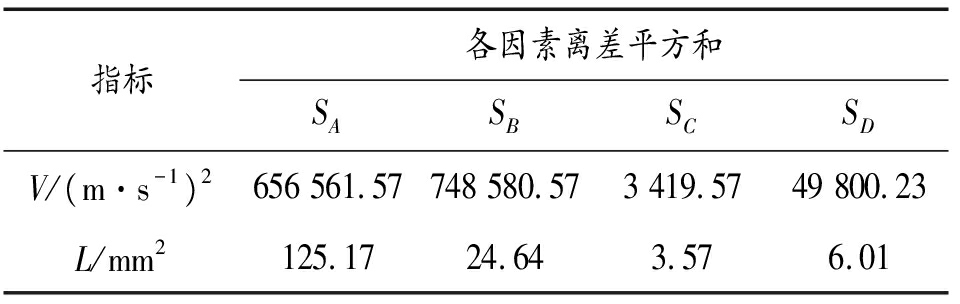
表6 各因素离差平方和
Table 6 Sum of squares of deviations of various factors
指标各因素离差平方和SASBSCSDV/(m·s-1)2656 561.57748 580.573 419.5749 800.23L/mm2125.1724.643.576.01
比较表6中射流头部速度V的各因素离差平方和,将SC作为误差来检验各因素的显著性,各因素自由度fA、fB、fC、fD=2,其中误差自由度fe=fC=2。同理,比较射流有效长度L的各因素离差平方和,将SC和SD作为误差来检验各因素的显著性,离差平方和SE=SC+SD,误差自由度fe=fC+fD=4。
式中:Sj为各因素离差平方和;fj为各因素自由度;SE为误差离差平方和;fe为误差自由度。各因素的F值列于表7。
表7 各因素F值
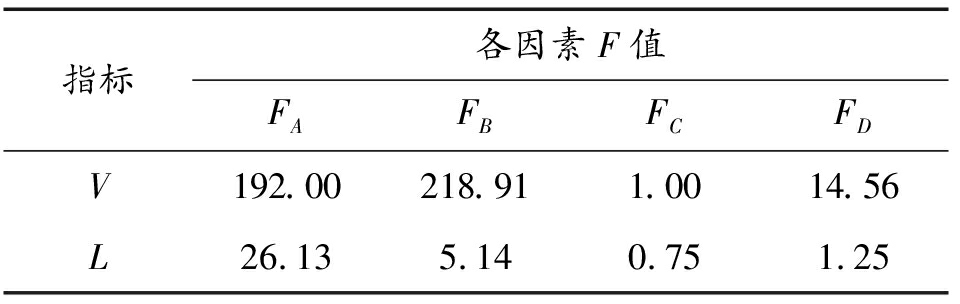
Table 7 F value of each factor
指标各因素F值FAFBFCFDV192.00218.911.0014.56L26.135.140.751.25
根据F值和因素自由度,查F分布表,α′=0.025,F0.975(2,2)=39,表7中FA、FB均大于39,认为可靠性为97.5%时,A和B这两个因素为关键因素,对V具有显著影响。当α′=0.075时, F0.925(2,2)=12.33,FD大于12.33,即认为可靠性为92.5%时,因素D对V有影响。因素C影响较小,其水平可以任意取。按照上述方法分析各因素对L的影响。当可靠性为99%时,A对L具有显著影响,为关键因素。当可靠性为90%时,B对L有影响。C和D影响较小,其水平可以任意取。
因此,对V而言,得到2组较好的水平组合为A1、B1、C1、D3和A1、B1、C3、D3为两组较好的水平组合。同理,对L而言,A1、B1、C2、D1和A1、B1、C3、D1为2组较好的水平组合。因此,共取得4组较好水平组合,分别对其进行数值模拟,结果列于表8中。
表8 仿真模拟结果
Table 8 Simulation results

试验组号因素1234ABCD计算结果V/(m·s-1)L/mm1A1B1C1D37 1481022A1B1C3D37 0961043A1B1C2D16 8701044A1B1C3D16 895105
综合考虑V与L,最优水平组合为第一组试验,即A1、B1、C1、D3。
3 结论
通过射流侵彻靶板的试验,验证仿真方法的正确性,将正交设计方法与数值模拟相结合,分析聚能装药结构参数对射流成型及侵彻性能的影响,比较其影响程度大小,最后对装药结构进行优化设计,获得了CD=80 mm,α 在40°~50°时的最佳参数组合方案:
1) 样本空间中最优水平组合为A1、B1、C1、D3即采用柱形装药形状,中心点起爆的起爆方式,β=0.025CD-0.012 5CD,α =40°,γ=H/CD=1.55,d=4 mm,相应的V=7 148 m/s,较平均射流头部速度增加12.6%,L=102 mm,较平均射流有效长度增加4.7%。
2) 综合分析(α)、药型罩厚度(β)、装药长径比(γ)以及装药外壳厚度(d)4个因素对射流侵彻性能的影响,得出:各因素对V影响的主次顺序为:β>α>d>γ;各因素对L影响的主次顺序为:α>β>d>γ。
3) 聚能装药长径比在1.55~1.75,相比于药型罩锥角角度、药型罩壁厚、装药外壳厚度,长径比对柱形中心点起爆聚能射流侵彻性能影响较小,因此在设计聚能装药结构时,可以适当减小长径比,可以有效减少装药量,减小装药体积。
[1] 纪国剑.聚能装药形成射流的仿真计算与理论研究[D].南京:南京理工大学,2004.
JI Guojian.Simulation and theoretical study on jet formation of shaped charge[D].Nanjing:Nanjing University of Science and Technology,2004.
[2] HELD M.Shaped charge optimization against ERA targets[J].Propellants Explosives Pyrotechnics,2010,30(3):216-223.
[3] 徐文龙,王成,徐斌.超聚能射流形成过程机理研究[J].兵工学报,2018,39(02):261-268.
XU Wenlong,WANG Cheng,XU Bin.Investigation of hyper shaped charge jet formation theory[J].Acta Armamentarii,2018,39(2):261-268.
[4] 王树山.终点效应学[M].北京:科学出版社,2019.
WANG Shushan.Terminal effects[M].Beijing:Science Press,2019.
[5] 焦志刚,寇东伟,杜宁.药型罩锥角对JPC与JET形成的影响[J].装备制造技术,2015(12):38-40.
JIAO Zhigang,KOU Dongwei,DU Ning.Influence on formed JPC and JET by liner angle[J].Equipment Manufacturing Technology,2015(12):38-40.
[6] ELSHENAWY T,LI Q M,et al.Breakup time of zirconium shaped charge jet[J].Propellants,Explosives,Pyrotechnics,2013,38(5):703-708.
[7] FEDOROV S V,BAYANOVA Y M,LADOV S V.Numerical analysis of the effect of the geometric parameters of a combined shaped-charge liner on the mass and velocity of explosively formed compact elements[J].Combustion Explosion &Shock Waves,2015,51(1):130-142.
[8] 柴艳军,李如江,岳继伟,等.壳体壁厚线性变化对聚能射流形成的影响[J].科技通报,2017,33(9):12-14.
CHAI Yanjun,LI Rujiang,YUE Jiwei,et al.The effect of varying linearly wall thickness cases on the formation of shaped charge jet[J].Bulletin of Science and Technology,2017,33(9):12-14.
[9] 李伟兵,王晓鸣,李文彬,等.装药长径比对聚能杆式侵彻体成型的影响[J].弹道学报,2011,23(4):61-65.
LI Weibing,WANG Xiaoming,LI Wenbin,et al.Effect of length-diameter ratio of charge on jetting projectile charge forming[J].Journal of Ballistics,2011,23(4):61-65.
[10] 段建,周刚,王可慧,等.结构参数对爆炸成型弹丸性能影响的研究[J].弹箭与制导学报,2010,30(6):103-107.
DUAN Jian,ZHOU Gang,WANG Kehui,et al.The study on influence of parameters of shaped charge on explosively formed projectile performance[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(6):103-107.
[11] 王一凡,王志军,袁毓雯,等.结构参数对新型聚能装药性能影响的数值分析[J].兵器装备工程学报,2020,41(8):7-10.
WANG Yifan,WANG Zhijun,YUAN Yuwen,et al.Numerical analysis on influence of structural parameters on shaped charge and penetration performance[J].Journal of Ordnance Equipment Engineering,2020,41(8):7-10.
[12] 张斐,张春辉,张磊,等.辅助药型罩材料对截顶药型罩形成高速射流的影响[J].兵工学报,2018,39(S1):52-56.
ZHANG Fei,ZHANG Chunhui,ZHANG Lei,et al.Effect of material of auxiliary liner on the formation of high-speed jet by truncated liner[J].Acta Armamentarii,2018,39(S1):52-56.
[13] 崔平,闫建林,施冬梅,等.聚能装药破甲效能影响因素分析及研究进展[J].爆破,2021,38(2):4-16.
CUI Ping,YAN Jianlin,SHI Dongmei,et al.Influencing factors on damage effectiveness of shaped charge and some recent progress[J].Blasting,2021,38(2):4-16.
[14] 方开泰.正交与均匀试验设计[M].北京:科学出版社,2001.
FANG Kaitai.Orthogonal experimental design[M].Beijing:Science Press,2001.
[15] 崔云航,李裕春,吴腾芳,等.线型聚能装药数值模拟与优化设计[J].爆破,2005(3):32-35.
CUI Yunhang,LI Yuchun,WU Tengfang,et al.Numerical simulation and optimization design of linear shaped charge[J].Blasting,2005(3):32-35.
[16] 崔云航,万文乾,田七,等.线型聚能装药优化设计[J].火工品,2006(4):42-46.
CUI Yunhang,WAN Wenqian,TIAN Qi,et al.Optimization design of linear shaped charge[J].Initiators &Pyrotechnics,2006(4):42-46.
[17] 张军,李裕春,黄骏逸,等.水下爆破聚能装药结构正交优化设计[J].兵器装备工程学报,2021,41(2):52-57.
ZHANG Jun,LI Yuchun,HUANG Junyi,et al.Orthogonal optimization design of shaped charge structure for underwater blasting[J].Journal of Ordnance Equipment Engineering,2021,41(2):52-57.
[18] 李磊,马宏昊,沈兆武.基于正交设计方法的双锥罩结构优化设计[J].爆炸与冲击,2013,33(6):567-573.
LI Lei,MA Honghao,SHEN Zhaowu,et al.Optimal design of biconical liner structure based on orthogonal design method[J].Explosion and Shock Waves,2013,33(6):567-573.
[19] JACOBS S J.On the equation of state for detonation products at high density[J].Symposium on Combustion,1969,12(1):501-511.
[20] DOWNAR T,STAUDENMIER J.Theory manual[J].Parcs,2004.
[21] AUTODYN 14.0.Theory manual[R].ANSYS,Inc,Pittsburgh,147-148.