0 引言
玻璃纤维增强复合材料是一种由高强玻璃纤维、环氧树脂等材料经固化反应后制备的新型材料,具有轻质、高强、防护性好、成本适中等优点,在各个领域均有着重要的应用,如交通运输、航空航天、兵器工业等[1]。许多学者对玻璃纤维增强复合材料的性能和应用进行了探讨和研究,Rendenbach等[2-3]研究了利用医用玻璃纤维增强复合材料在循环动态载荷下的的生物力学分析;郑益飞等[4]分析了工业级多壁碳纳米管融入环氧树脂后,对玻璃纤维增强复合材料的宏观力学性能影响与微观力学性能影响;Zhu等[5]研究了酸碱盐环境下玻璃纤维增强复合材料长期拉伸性能的预测,为玻璃纤维增强复合材料的应用提供理论指导;骆传龙等[6]设计实验,对2种制备方式的玻璃纤维增强复合材料的抗冲击性能进行了对比。可以看到,目前有关玻璃纤维增强复合材料力学性能的研究成果很多,但对玻璃纤维增强复合材料防弹性能的相关研究则相对较少。现有的材料防弹性能测试方法主要是依靠人工实验获取数据,再对数据进行相应的统计、处理和计算后,从力学方面、抗高速侵彻性能来分析防弹性能。但这种方法效率低、耗时长、成本高、工作量大,并且在实验的每一个环节中有着严格的要求,不能出现较大误差,否则就会影响最终的防弹性能评估结果。为此,研究引入BPNN智能算法来实现材料防弹性能的高效率、高精度预测。BPNN在各个领域也有着广泛的应用,李国庆等[7]利用框架优化的BPNN模型,实现了电力负荷的短期预测,为发电厂的布置和应对提供依据。在已有的研究中发现,BPNN存在一些缺陷,例如学习速率慢、易陷入局部寻优、网络权值和阈值需要人工设置等,影响模型的精度和速度,因此需要对其进行改进和优化[8-9]。FWA算法是一种新型群体优化算法,具有易实现、鲁棒性好、能够避免陷入局部寻优等优势。研究提出FWA算法优化BPNN,再基于FWA-BPNN(fireworks algorithm-back propagation neural network,BPNN)构建预测模型,从而对玻璃纤维增强复合材料的防弹性能进行预测,减少工作量,提高材料性能测试的效率和精度。研究的创新点主要为:针对BPNN存在的缺陷,利用FWA对其进行优化,并将改进的BPNN应用到材料的抗弹性能预测当中,提高材料防弹性能评估的效率和精度。
1 基于FWA-BPNN的防弹性能预测模型构建
1.1 玻璃纤维增强复合材料的防弹性能指标选取
利用玻璃纤维增强复合材料制作靶板,通过弹道枪、红外光幕测速系统、工业CT等设备进行弹道实验,从而测试玻璃纤维增强复合材料的防弹性能。在模拟弹飞行的过程中,应考虑到空气阻力的存在,即模拟弹从弹道枪中发射时的初始飞行速度v0会在空气中持续衰减。在飞行距离为x时,模拟弹的飞行速度衰减可由式(1)来描述:
vx=v0e-αx
(1)
式中,vx表示在飞行距离为x时模拟弹的飞行速度;α为弹速衰减系数,与模拟弹的种类有关。在忽略侵彻过程中的热能损耗的前提下,可以计算获取靶板的贯穿吸能Et,如式(2)所示。
Et=Epd+Eps
(2)
式中,Epd为模拟弹的动能损耗;Eps为模拟弹弹体发生形变所需的能量。Epd的大小与入射速度vi的大小总体呈正相关关系。璃纤维增强复合材料的抗高速侵彻破坏性能,第二个是玻璃纤维增强复合材料在高应变率下的力学性能[10-11]。为此,研究构建了玻璃纤维增强复合材料的抗高速侵彻破坏模型。首先构建物理破坏模型。在材料的入射面,材料的破坏方式主要是压缩以及剪切破坏2种形式。而在出射面,玻璃纤维增强复合材料的破坏形式主要是拉伸破坏[12-13]。因此,在与靶面垂直的方向上,靶板的破坏大致有2个阶段,在第一个阶段,为靶板的压剪耦合破坏;第二阶段,则是拉伸破坏阶段。靶板的贯穿吸能,实际上就是这2个阶段的吸能总和,如式(3)所示。
W=W1+W2
(3)
式中,W、W1、W2分别为靶板吸能、第一阶段的压剪耦合破坏吸能以及第二阶段的拉伸破坏吸能。在第一个阶段当中,压缩破坏和剪切破坏同时存在,且两者有耦合作用,靶板的破坏吸能效果与模拟弹的入射速度有着密切的联系,因此需要引入压减耦合系数对其进行修正,如式(4)所示:
ψ(vi)=k(avi+b)
(4)
式中,k、a、b均为经验常数,此时一阶段的吸能表示为式(5)。
W1=(Wc+Ws)·k(avi+b)
(5)
式中,Wc为一阶段的压缩破坏吸能;Ws为一阶段的剪切破坏吸能。在第二阶段,靶板的破坏主要是拉伸破坏,在这个过程中,靶板的破坏主要分为2个区域,分别是靶板的锥形台拉伸破坏区域,以及弹径范围内交叉梯形台拉伸破坏区域。在梯形台区域以外,均为协变拉伸破坏区域。在二阶段,靶板的拉伸破坏吸能如式(6)。
W2=ξWt
(6)
式中,Wt为交叉梯形台区域的吸能;ζ为拉伸协变系数。
将式(5)与式(6)代入式(1)中,可得到式(7)。
W=(Wc+Ws)·k(avi+b)+ξWt
(7)
在第一个阶段,模拟弹在靶板的入射点处产生一个压缩应力波,并在靶板内传播。该波在传播至靶板的背面时,发生发射作用,成为拉伸应力波。与此同时模拟弹也在侵入靶板,当模拟弹与拉伸应力波相会时,在模拟弹的前端部分,靶板受到拉伸应力作用被破坏分层,此时的拉伸应力波无法再次反射形成压缩应力波,因此靶板的后部主要受到的是模拟弹侵入运动产生的拉伸作用。而弹丸主要受到材料的压缩抗力和剪切抗力的作用。材料的压缩抗力和剪切抗力,可以根据材料的动态压缩破坏强度和动态剪切破坏强度来计算。材料的压缩抗力Fc如式(8)所示。
Fc=σdc·πr2
(8)
式中,σdc为材料的动态压缩破坏强度;r为模拟弹的半径。材料的剪切抗力Fs如式(9)。
Fs=τds·2r·Δ
(9)
式中,Δ为理想的剪切破坏厚度;τds为材料的动态剪切破坏强度。在第二个阶段,单个梯形台破坏区域,以及梯形台的吸能分析可以用图1(a)和图1(b)进行表示。
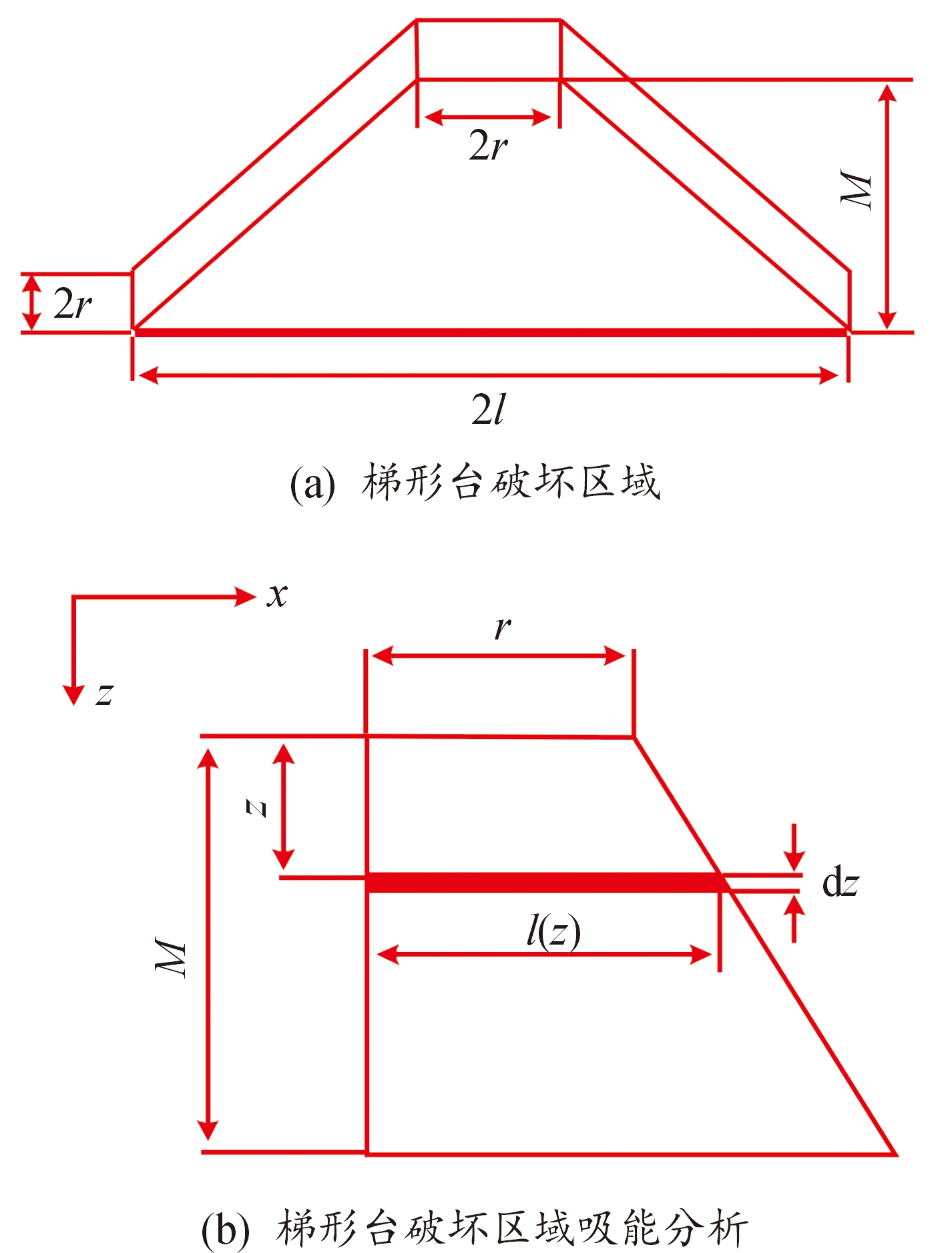
图1 梯形台破坏区域及吸能分析
Fig.1 Analysis of trapezoidal abutment failure area and energy absorption
在图1中,M表示模拟弹在靶板材料侵彻过程中第二阶段的厚度,l为材料背面拉伸破坏区域的半径,且有![]() 是靶板垂直方向的波速、CLT是靶板水平方向的波速),dz是在材料的厚度方向距离为z处取的一个微层分析单元的厚度,l(z)是该单元长度的二分之一,是z的函数;l是材料背面拉伸破坏区域的半径。对于微层分析单元,其破坏变形程度Δl与拉伸受力f可表示为式(10)和式(11):
是靶板垂直方向的波速、CLT是靶板水平方向的波速),dz是在材料的厚度方向距离为z处取的一个微层分析单元的厚度,l(z)是该单元长度的二分之一,是z的函数;l是材料背面拉伸破坏区域的半径。对于微层分析单元,其破坏变形程度Δl与拉伸受力f可表示为式(10)和式(11):
f =σdt·2r·dz
(11)
其中,εdt和σdt分别表示材料的动态拉伸破坏应变和材料的动态拉伸破坏强度。通过上述的分析研究可知,材料本身影响材料破坏吸能的关键指标指标为σdc、τds、εdt和σdt。
1.2 基于改进BPNN的防弹性能预测模型
BPNN的优势在于不需要获取或设定输入与输出之间的映射方程,只需要通过大量样本的训练和规则学习,最终达到理想精度[14-16]。BPNN的结构如图2所示。
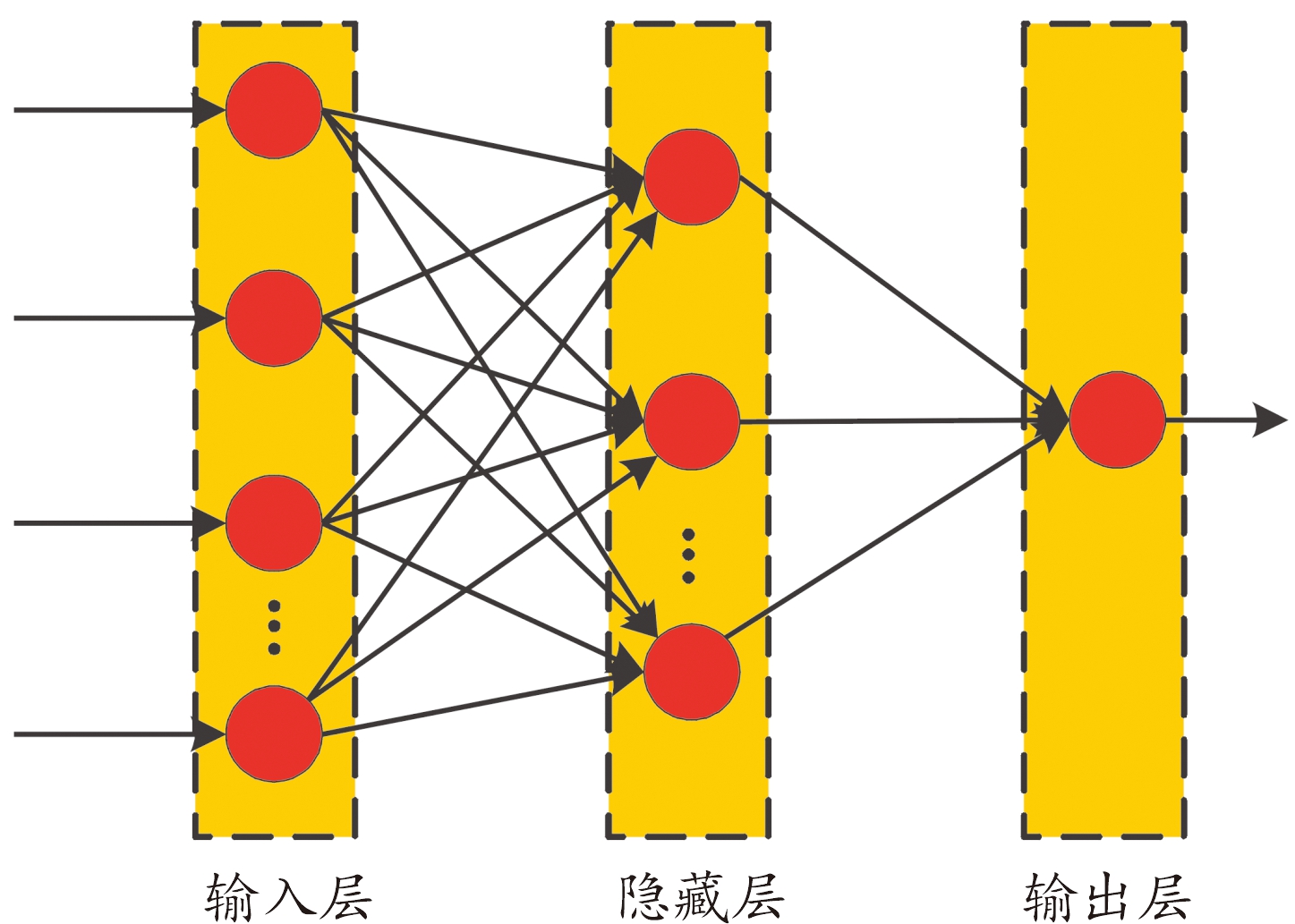
图2 BPNN的结构
Fig.2 The structure of BPNN
在对性能指标的分析内容中可知,影响材料破坏吸能,即影响材料防弹性能的指标有σdc、τds、εdt和σdt等4个指标。将这4个指标作为BPNN的输入层节点,材料的破坏吸能作为输出层节点,设置输出层层数为1,隐含层层数为1,从而评估玻璃纤维增强复合材料的防弹性能。破坏吸能的值越高,说明玻璃纤维增强复合材料的防弹性能越好。但单一的BPNN收敛速度慢,也容易在迭代过程中,输出局部最优解而非全局最优解,因此单一的BPNN在材料防弹性能的评估工作中效率和精度均不够理想。针对BPNN中存在的问题,现有的方法是采用粒子群算法(particle swarm optimization,PSO)以及遗传算法(genetic algorithm,GA)对BPNN的初始权值和阈值进行优化[17-19]。但上述2种方法也存在着较为明显的缺陷。首先是PSO-BPNN,当PSO的初始种群设置较小时,会导致寻优效果较差,BPNN的初始参数可能不是最优值;当种群设置过大时,则会导致PSO的搜索速度较慢,影响模型的效率。GA-BPNN对大样本数据的预测性能较好,但对样本规模小,且分布不均的样本模型预测能力较弱。FWA是一种模拟烟花多点爆炸的智能优化算法,具有较强的全局搜索能力和收敛性。因此研究采用FWA优化BPNN的初始参数。
FWA优化BPNN的原理为:将烟花个体的位置作为BPNN权值和阈值的一个解,FWA的最终求解结果,则是BPNN参数的最优值。FWA优化BPNN的具体步骤为:
第1步,对关键参数,即BPNN各个层的权值和阈值进行编码操作。
第2步,初始化权值和阈值,使其值均在[-1,1]内,此时每个烟花个体所处的位置标示BPNN的权值和阈值,每个烟花个体均代表BPNN中的一个神经元。
第3步是选择适应度函数。
FWA-BPNN模型的目标是通过迭代学习使输出层的结果与期望值的误差达到最小,此时BPNN的权值和阈值为最佳参数值。基于上述内容,可以得知FWA-BPNN模型的基本步骤,如图3所示。
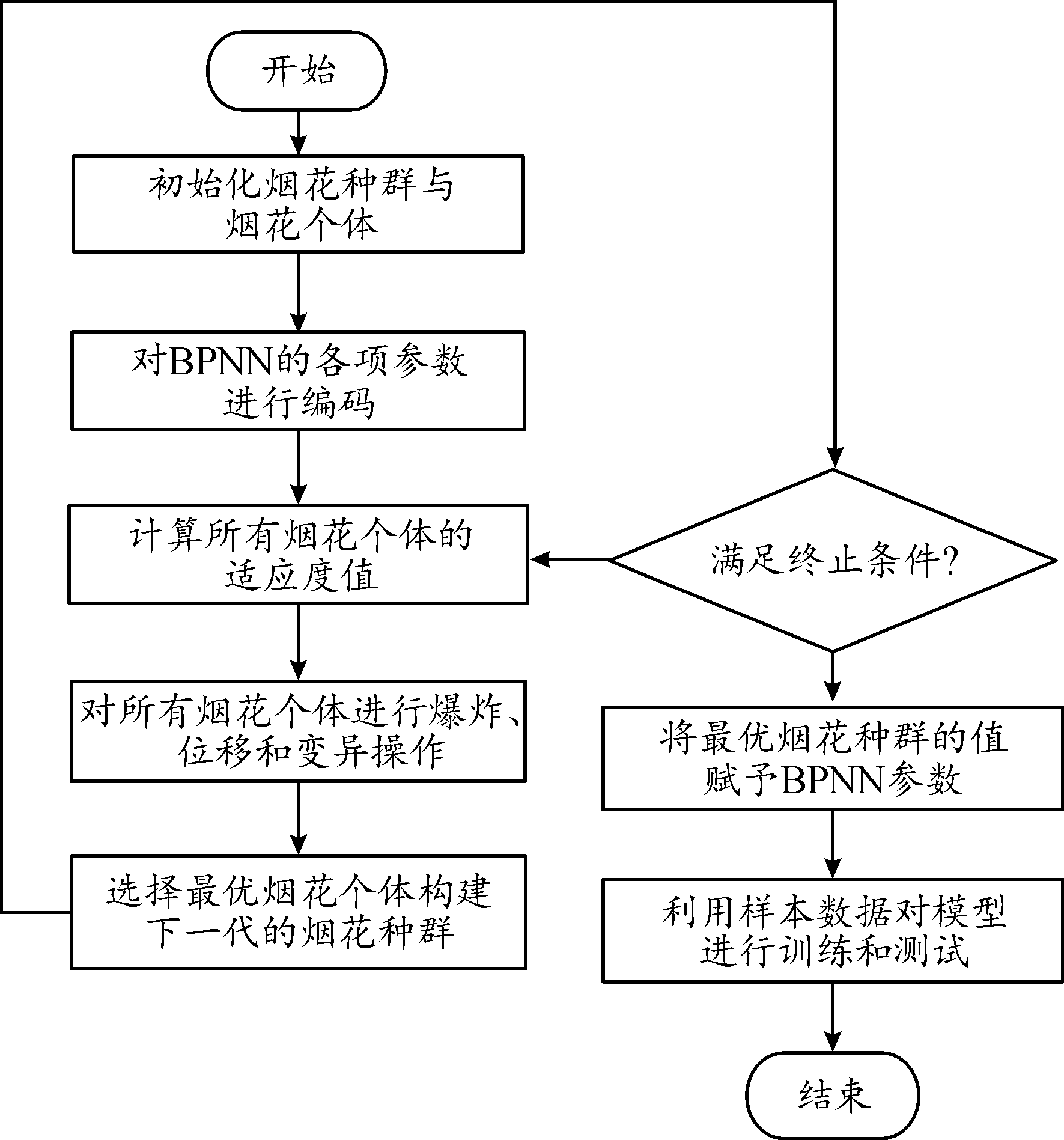
图3 FWA-BPNN模型的基本步骤
Fig.3 The basic steps of the FWA-BPNN model
研究在FWA-BPNN模型中引入平方差误差函数计算所有烟花个体的适应度值,如式(12)所示:
式中,t为期望输出值,P为BPNN的层数,S为输出单元数量,y为输出层实际输出值,其计算如式(13)所示:
式中,xj为输入值,wij为第i个神经元的第j个节点的权值,θi为第i个神经元的阈值,fi()为个体i的适应度函数。此时,烟花个体的适应度值利用式(14)进行计算:
第4步,进行烟花种群寻优。利用式(14)获取所有的烟花个体的适应度值,同时计算烟花个体的爆炸数量与爆炸半径,对所有烟花个体进行爆炸、位移以及变异操作,选择最优个体构成下一代种群。
第5步,根据个体的适应度值以及个体之间的欧式距离,判断是否满足迭代终止条件,若满足终止条件,则将得到的最优解赋予BPNN网络参数,否则继续迭代寻优。基于FWA-BPNN,构建玻璃纤维增强复合材料防弹性能预测模型,能够高效、快速地评估材料的防弹性能。为了消除量纲不同而导致模型的精度受到影响,需要对所有样本数据进行标准化处理,如式(15)所示:
式中,xk表示样本集中的第k个数据;max(X),min(X)分别表示样本集中的最大值和最小值。
2 FWA-BPNN防弹性能预测模型的性能分析
为验证FWA-BPNN防弹性能预测模型的性能,研究从各项有关玻璃纤维增强复合材料性能实验项目中的数据共5 000条,构建实验样本集。将其中的4 000条数据作为训练样本集,对FWA-BPNN防弹性能预测模型进行训练,另外1 000条数据则作为测试样本集,对模型的性能进行测试。利用MAE评估4种模型的性能,如图4所示。
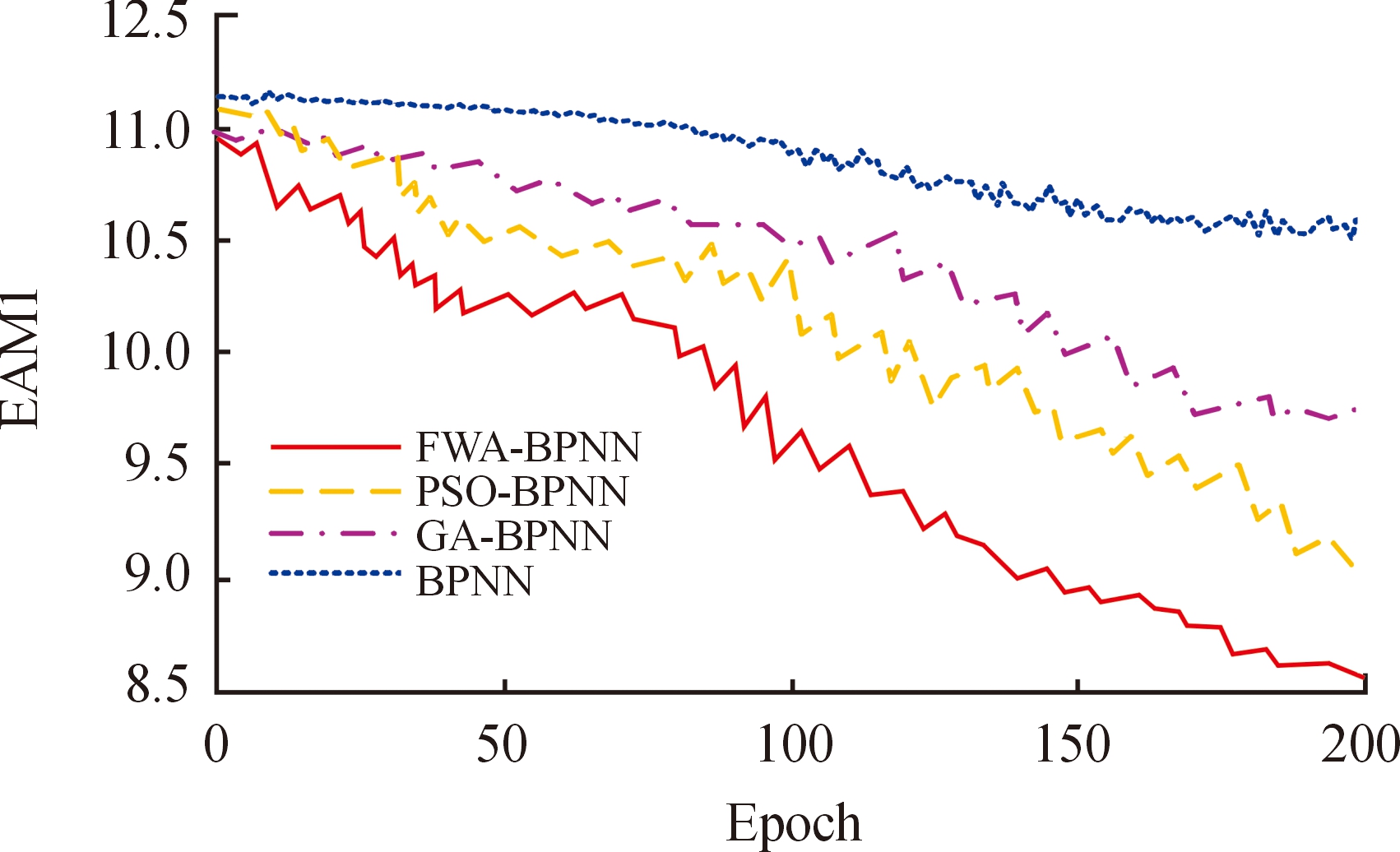
图4 4种模型的MAE值
Fig.4 MAE values of four models
在图4中能够看到,在迭代更新的过程当中,4种模型的MAE值均在减小,这表明在迭代过程中4种模型的误差值都在减小,精度在不断提升。可以清晰地看到,在迭代过程中,FWA-BPNN模型的MAE值下降得最快。在迭代至200次时,FWA-BPNN模型的MAE值下降至8.55,在4种模型中最低;而PSO-BPNN模型的MAE值在迭代至200次时为9.00,比FWA-BPNN模型高0.45;GA-BPNN模型的MAE值在迭代至200次时为9.55,比FWA-BPNN模型高1.00;BPNN模型的MAE值在迭代至200次时为10.50,比FWA-BPNN模型高1.45。采用测试数据集对4种模型的防弹性能预测精度进行验证。4种模型对玻璃纤维增强复合材料防弹性能的预测精度如图5所示。
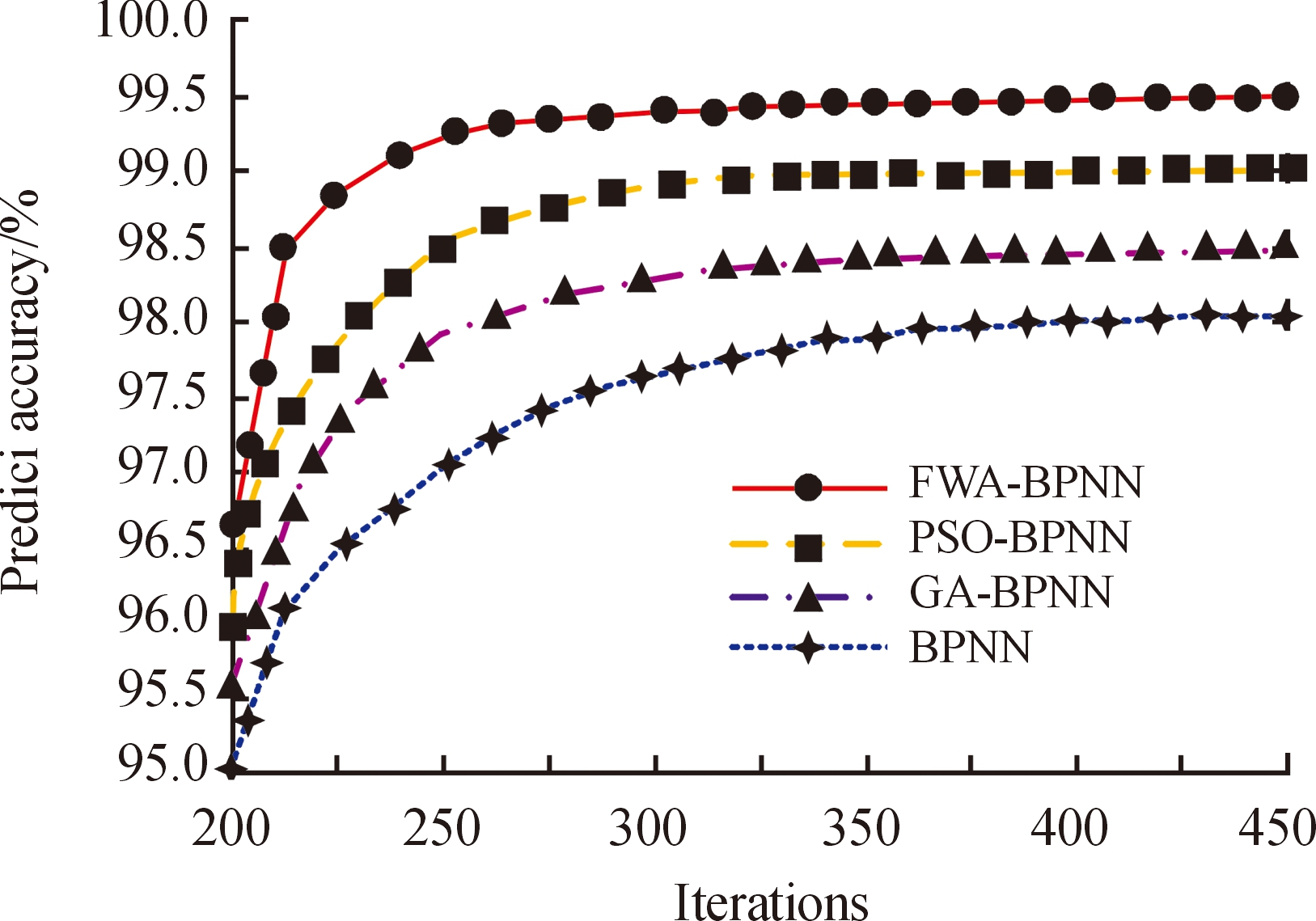
图5 4种模型对玻璃纤维增强复合材料防弹性能的预测准确率
Fig.5 Prediction accuracy of four models for bulletproof performance of glass fiber reinforced composites
在图5可以看到,在迭代更新的过程中,4种模型对玻璃纤维增强复合材料防弹性能的预测精度都在不断上涨,直到趋于稳定。在迭代次数达到400次后,4种模型对玻璃纤维增强复合材料防弹性能的预测精度均趋于稳定。其中,FWA-BPNN模型对玻璃纤维增强复合材料防弹性能的预测准确率达到99.50%;PSO-BPNN模型的预测准确率为99.00%,比FWA-BPNN模型低0.50%;GA-BPNN模型的预测准确率为98.50%,比FWA-BPNN模型低1.00%;BPNN模型的预测准确率为98.06%,比FWA-BPNN模型低1.44%。利用相同的测试数据测试4种模型,在测试过程中,记录模型的预测输出值与期望值的最大误差、最小误差以及平均误差,如表1所示。
表1 模型的预测输出值与期望值的误差
Table 1 Error between predicted output value and expected value of the model
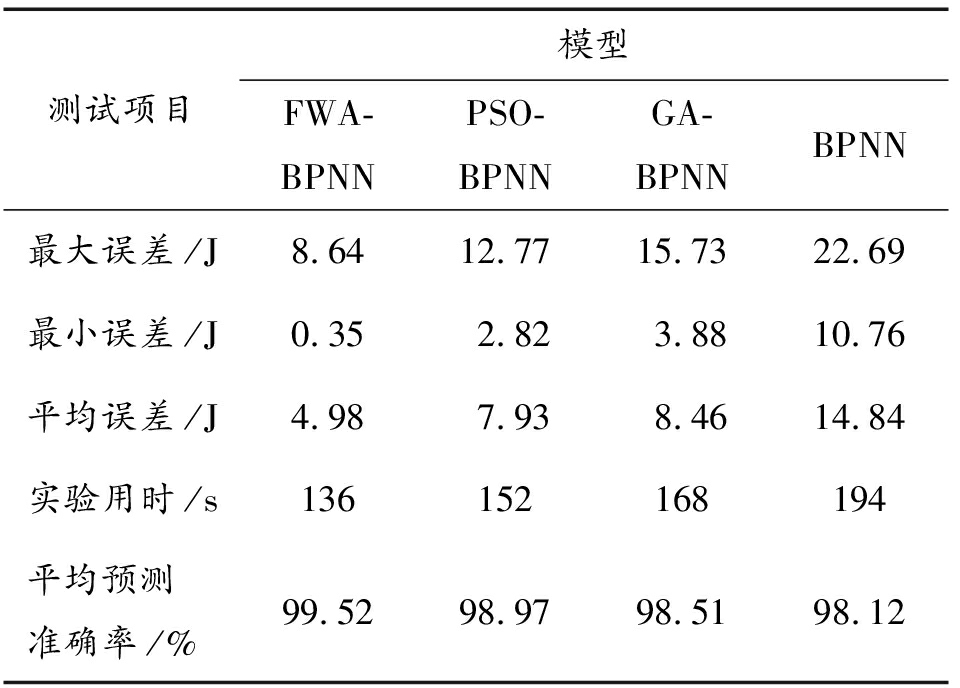
测试项目模型FWA-BPNNPSO-BPNNGA-BPNNBPNN最大误差/J8.6412.7715.7322.69最小误差/J0.352.823.8810.76平均误差/J4.987.938.4614.84实验用时/s136152168194平均预测准确率/%99.5298.9798.5198.12
在表1中,可以看到,FWA-BPNN模型的最大预测误差为8.64 J,最小预测误差为0.35 J,平均预测误差为4.98 J,均显著低于其他3种模型。PSO-BPNN的平均预测误差为2.82 J,比FWA-BPNN模型高2.47 J;GA-BPNN的平均预测误差为3.88 J,比FWA-BPNN模型高3.53 J;PSO-BPNN的平均预测误差为10.76 J,比FWA-BPNN模型高10.41 J。FWA-BPNN模型处理并预测所有样本数据的时间为136 s,显著低于其他3种模型;PSO-BPNN模型处理并预测所有样本数据的时间为152 s,比FWA-BPNN模型多16 s;GA-BPNN模型处理并预测所有样本数据的时间为168 s,比FWA-BPNN模型多32 s;BPNN模型处理并预测所有样本数据的时间为194 s,比FWA-BPNN模型多58 s。FWA-BPNN模型的平均预测准确率达到99.52%,明显高于其他3种模型。以上结果可以说明,研究提出的基于FWA-BPNN的防弹性能预测模型,能够高效率、高准确率地对玻璃纤维增强复合材料的防弹性能进行评估。
3 结论
现有的玻璃纤维增强复合材料防弹性能测试方法效率低、耗时长、成本高、工作量大。研究从材料本身的破坏吸能效果出发,选取与防弹性能直接相关的材料性能指标,并将这些指标作为FWA-BPNN模型的输入向量,实现对玻璃纤维增强复合材料防弹性能的快速评估。实验结果显示,FWA-BPNN模型在迭代至78次时适应度值达到最小;比PSO-BPNN模型少78次;比GA-BPNN模型少122次;比BPNN模型少228次。这表明FWA-BPNN模型的收敛性较强,明显优于其他3种模型。在迭代次数相同时,FWA-BPNN模型的MAE值显著低于其他3种模型,F1值显著高于其他3种模型,说明FWA-BPNN模型的精度比其他3种模型更高。在测试过程中,在迭代次数达到400次后,FWA-BPNN模型的预测准确率达到99.50%,比PSO-BPNN模型高0.50%;比GA-BPNN模型高1.00%;比BPNN模型高1.44%。FWA-BPNN模型处理并预测所有样本数据的时间为136 s,比PSO-BPNN模型少16 s;比GA-BPNN模型少168 s;比BPNN模型少58 s。综上所述,基于FWA-BPNN的防弹性能预测模型,能够高效率、高准确率地对玻璃纤维增强复合材料的防弹性能进行评估,对我国兵器防护行业的发展有一定的推动作用。研究在实验过程中,没有探讨枪支的不同对玻璃纤维增强复合材料防弹性能的影响,需要在后续研究中进一步改进优化。
[1] CHAN Y H,LEW W Z,LU E,et al.An evaluation of the biocompatibility and osseointegration of novel glass fiber reinforced composite implants:In vitro and in vivo studies-ScienceDirect[J].Dental Materials,2018,34(3):470-485.
[2] SHEKAR K C,SINGARAVEL B,PRASAD S D,et al.Effect of fiber orientation on the flexural properties of glass fiber reinforced,epoxy-matrix composite[J].Materials Science Forum,2019,969(2):502-507.
[3] RENDENBACH C,STEFFEN C,SELLENSCHLOH K,et al.Patient specific glass fiber reinforced composite versus titanium plate:a comparative biomechanical analysis under cyclic dynamic loading[J].Journal of the Mechanical Behavior of Biomedical Materials,2019,91(7):212-219.
[4] 郑益飞,申明霞,段鹏鹏,等.含MWCNTs玻璃纤维增强复合材料的力学和界面性能的研究[J].玻璃钢/复合材料,2019(12):83-88.
ZHENG Yifei,SHEN Mingxia,DUAN Pengpeng,et al.Study on mechanical and interfacial properties of glass fiber reinforced composites containing MWCNTs[J].FRP/Composite,2019(12):83-88.
[5] ZHU J,DENG Y,CHEN P,et al.Prediction of long-term tensile properties of glass fiber reinforced composites under acid-base and salt environments[J].Polymers,2022,14(15):3031-3031.
[6] 骆传龙,倪爱清,王继辉,等.玻璃纤维增强聚丙烯和环氧复合材料低速冲击损伤对比研究[J].玻璃钢/复合材料,2019(10):46-50.
LUO Chuanlong,NI Aiqing,WANG Jihui,et al.Comparative study on low velocity impact damage of glass fiber reinforced polypropylene and epoxy composites[J].FRP/Composite,2019(10):46-50.
[7] 李国庆,刘钊,金国彬,等.基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测[J].电网技术,2020(2):437-445.
LI Guoqing,LIU Zhao,JIN Guobin,et al.Ultra short term power load forecasting based on random distributed embedded framework and BP neural network[J].Power Grid Technology,2020(2):437-445.
[8] ZHANG L,LIANG F.Monitoring and analysis of athletes’ local body movement status based on BP neural network[J].Journal of Intelligent and Fuzzy Systems,2021,40(2):2325-2335.
[9] 肖良丽,纪勤敏,杜壮.玻璃纤维增强复合材料筋混杂纤维混凝土短柱轴心受压性能的研究[J].工业建筑,2022,52(2):37-41,125.
XIAO Liangli,JI Qinmin,DU Zhuang.Study on axial compression performance of hybrid fiber reinforced concrete short columns with glass fiber reinforced composite bars[J].Industrial Buildings,2022,52(2):37-41,125.
[10] 周井文,黄久超,杨叶,等.玻璃纤维增强复合材料端铣加工刀具磨损与表面质量研究[J].工具技术,2021,55(11):45-48.
ZHOU Jingwen,HUANG Jiuchao,YANG Ye,et al.Study on tool wear and surface quality in end milling of glass fiber reinforced composites[J].Tool Technology,2021,55 (11):45-48.
[11] CERITBINMEZ F,YAPICI A,KANCA E.The effect of nanoparticle additive on surface milling in glass fiber reinforced composite structures[J].Polymers and Polymer Composites,2021,29(9suppl):575-585.
[12] 白鑫,王云英,王雅娜,等.跨厚比对高强玻璃纤维增强复合材料单向板弯曲性能的影响[J].航空材料学报,2022,42(2):57-63.
BAI Xin,WANG Yunying,WANG Yana,et al.Effect of span thickness ratio on flexural properties of high-strength glass fiber reinforced composite unidirectional plates[J].Journal of Aeronautical Materials,2022,42(2):57-63.
[13] KARALIS G,TZOUNIS L,TSIRKA K,et al.Advanced glass fiber polymer composite laminate operating as a thermoelectric generator:a structural device for micropower generation and potential large-scale thermal energy harvesting[J].ACS Applied Materials &Interfaces,2021,13(20):24138-24153.
[14] 宋明,李旭阳,曹宇光,等.基于BP神经网络与小冲杆试验确定在役管道钢弹塑性性能方法研究[J].力学学报,2020,52(1):82-92.
SONG Ming,LI Xuyang,CAO Yuguang,et al.Research on the method of determining the elastoplastic properties of in-service pipeline steel based on BP neural network and small punch test[J].Journal of Mechanics,2020,52 (1):82-92.
[15] 何海婷,柳亦兵,巴黎明,等.基于BP神经网络的飞轮储能系统主动磁轴承非线性动力学模型[J].中国电机工程学报,2022,42(3):1184-1197.
HE Haiting,LIU Yibing,BA Liming,et al.Nonlinear dynamic model of active magnetic bearing in flywheel energy storage system based on BP neural network[J].Chinese Journal of Electrical Engineering,2022,42(3):1184-1197.
[16] WANG S,WU T H,SHAO T,et al.Integrated model of BP neural network and CNN algorithm for automatic wear debris classification[J].Wear,2019,426-427:1761-1770.
[17] ZHANG G,LIU H,LI P,et al.Load prediction based on hybrid model of VMD-mRMR-BPNN-LSSVM[J].Complexity,2020,2020(4):1-20.
[18] 刘致远,刘渊博,杨峰,等.Spark平台下基于优化BP神经网络模型的接触疲劳剩余寿命预测[J].重庆理工大学学报(自然科学),2021,35(10):111-119.
LIU Zhiyuan,LIU Yuanbo,YANG Feng,et al.Remaining life prediction of contact fatigue based on optimized BP neural network model on spark platform[J].Journal of Chongqing University of Technology(Natural Science),2021,35(10):111-119.
[19] ZOU X.Analysis of consumer online resale behavior measurement based on machine learning and BP neural network[J].Journal of Intelligent and Fuzzy Systems,2021,40(2):2121-2132.