0 引言
防弹玻璃是指既具有玻璃的高透光性、可视性,同时又具有一定防弹能力的透明材料。其防弹原理是玻璃将穿甲弹的冲击动能转化为玻璃的弹性势能和破碎后的表面能,从而达到防弹目的。近些年常见的防弹玻璃结构是由面板、背板以及起粘接作用的中间层组成,其防弹原理是利用硬而脆的面板受冲击后破裂来吸收一部分入射能量,继而通过中间层和背板的变形来吸收剩余能量。面板通常由无机玻璃或透明陶瓷制成,用来磨蚀和钝化弹丸,中间层由聚乙烯醇缩丁醛(PVB)或聚氨酯(PU)制成,可吸收弹丸能量,阻拦裂纹扩张,而背板由聚碳酸酯(PC)组成,聚碳酸酯具有较强的冲击强度和足够的韧性,能够降低防弹玻璃的面密度同时减少靶后破片。
针对防弹玻璃的抗侵彻性能,早期的研究通常简化为防弹玻璃受到静态力时的响应[1-2];Bless等[3]通过高速摄影观察撞击过程,发现了冲击区内损伤的快速传播与破坏波的观测结果一致,并绘制了损伤图;杨杰等[4-6]以聚乙烯醇缩丁醛(PVB)夹层防弹玻璃为主要研究对象,通过大量的试验结论分析冲击载荷下玻璃的动态力学特性,研究玻璃在冲击载荷下的破坏机理和防护机理,提出了单层透明材料难以满足防弹要求,必须采取层合的方式组成透明装甲系统来提高抗弹能力。Grujicic等[7]研究了透明装甲的结构、材料以及各层的作用,并提出了透明装甲的设计方法和材料选择方案。Anderson等[8]认为玻璃的破坏失效与弹道侵彻的时间进程相关,并量化了相关性。
本文基于12.7、14.5 mm两种口径穿燃弹,对一种抗7.62 mm穿燃弹防弹玻璃开展了抗侵彻试验,通过分析装甲与弹丸的破坏形貌,获得了该防弹玻璃的抗侵彻机理。同时采用仿真计算,研究了2种口径穿燃弹的初速、装甲倾角对装甲抗侵彻能力和后效威力的影响,包括穿燃弹极限穿透速度、剩余速度变化规律,此外本文还将计算该型防弹玻璃的防护系数。
1 试验研究
1.1 试验弹靶条件
分别开展了12.7、14.5 mm制式穿燃弹以不同初速度侵彻该型抗7.62 mm穿燃弹防弹玻璃的试验。试验靶板长宽尺寸为200 mm×200 mm,图1(b)所示结构示意图中,相邻层采用厚度为2 mm的PVB胶层粘合而成。2种口径穿燃弹实物图如图2所示,弹芯尺寸图如图3所示。
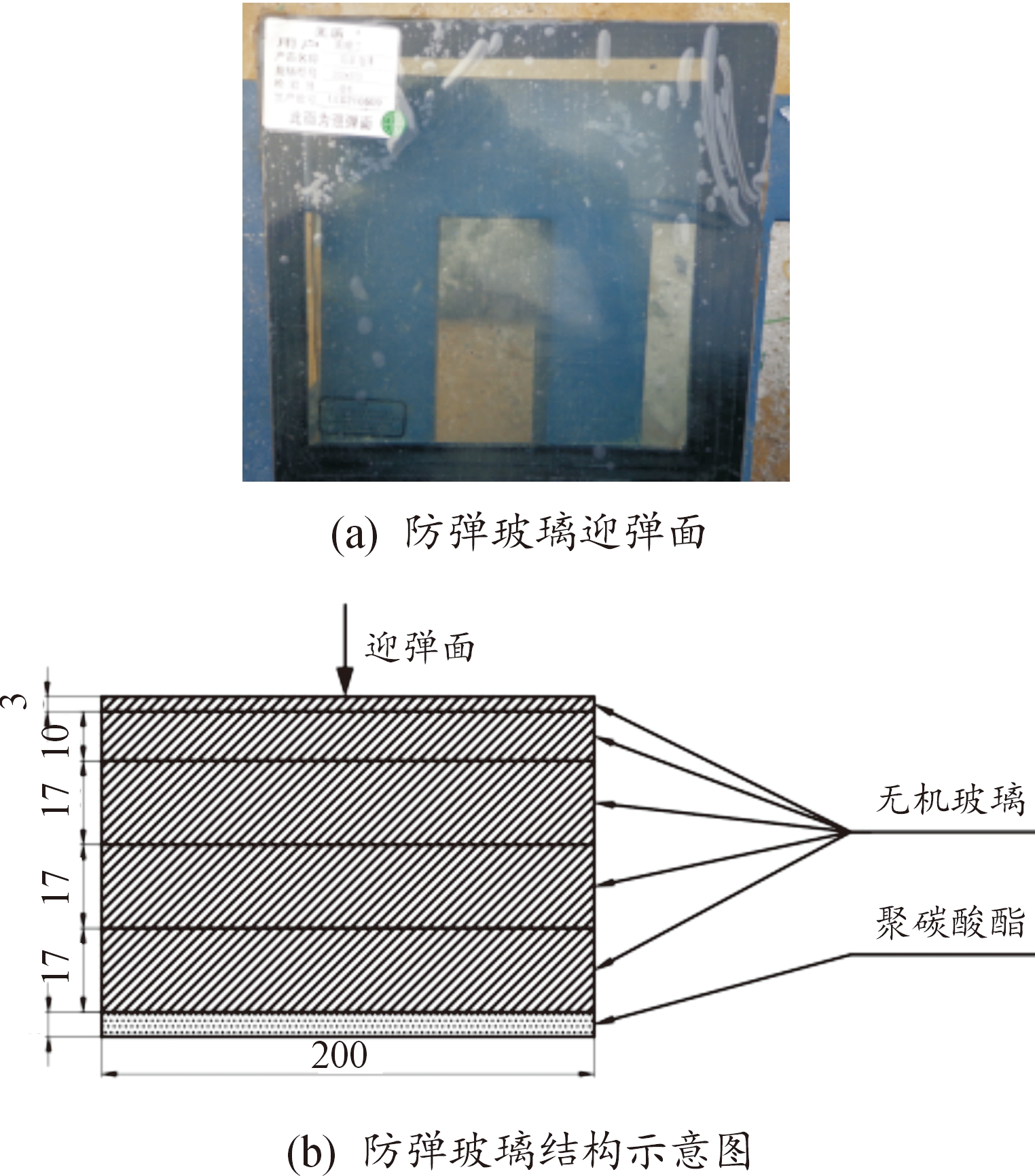
图1 防弹玻璃
Fig.1 Bullet-proof glass

图2 穿燃弹
Fig.2 Armor-piercing bullet
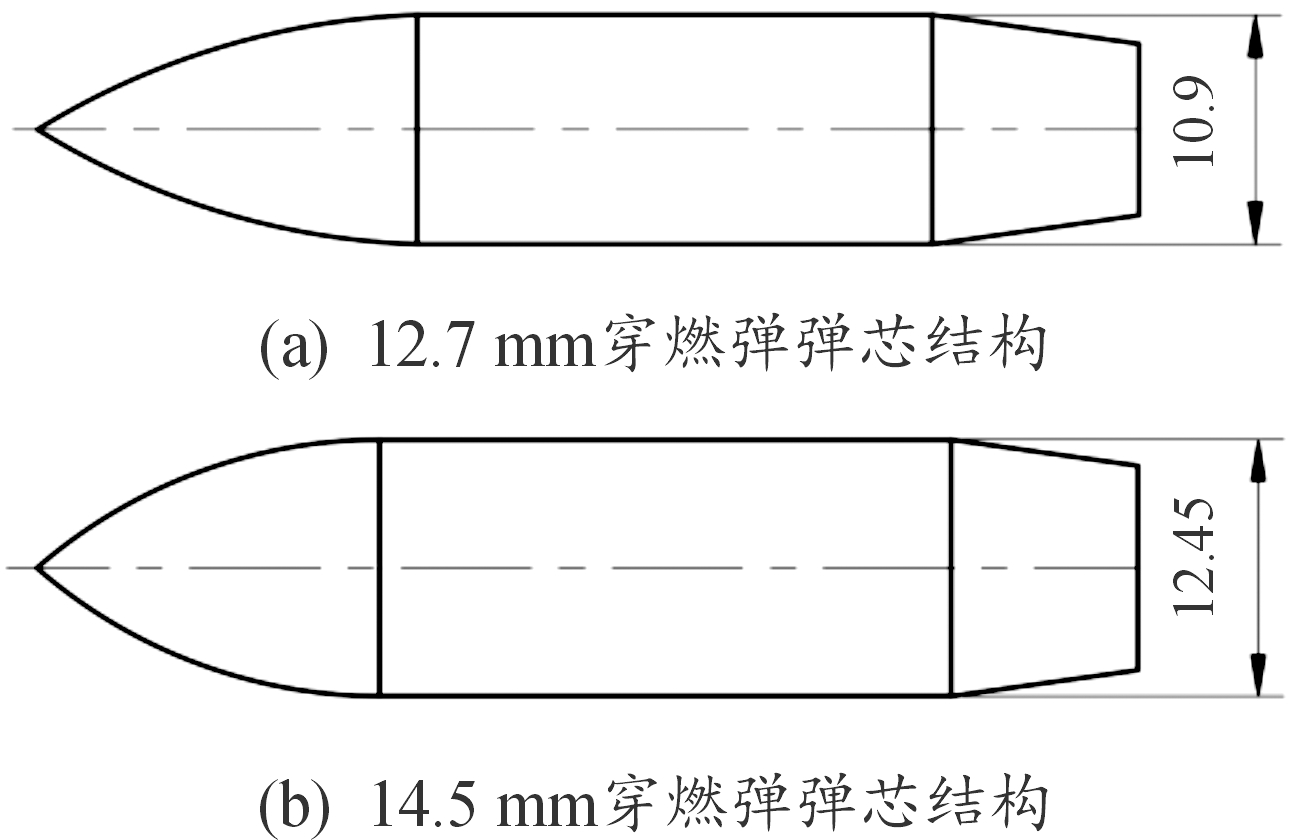
图3 2种口径穿燃弹弹芯结构
Fig.3 The core structure of two armor-piercing bullets
试验装置包括发射装置、靶架以及测速系统等,其中发射装置为12.7 mm口径弹道枪和14.5 mm口径弹道枪,试验现场布局如图4所示。

图4 试验现场布局
Fig.4 Experiment set-up
测速系统包括计时仪测速系统和高速摄影系统。计时仪测速系统采用LNG202-2型六通道电子计时仪获得弹丸初速度,测试精度可达到10-6 s;高速摄影系统通过高速摄影仪获得弹丸贯穿靶板后的剩余速度和飞行姿态。
1.2 结果与分析
通过试验得到了12.7、14.5 mm穿燃弹以不同初速正侵彻靶板后靶板与弹丸的破坏情况。
在12.7 mm穿燃弹侵彻试验中选取2个较为典型的回收靶板进行破坏形貌分析:图5(a)、(b)所示回收靶板的各玻璃层均完全破碎并产生大量裂纹,粘连大量玻璃碎片的PVB胶层仍呈分层排列,结构较为完整。迎弹面的薄层玻璃碎片粘连在PVB胶层,外翻形成规则的花瓣状翻唇。弹丸入孔呈五角星状,着靶点中心约2倍弹径区域内发生了粉碎性破坏,玻璃碎片呈细小粉末状,该区域PVB胶层被穿透并且破碎散开。透过PC背板可以看到密集的径向裂纹,裂纹原点较弹丸着靶点偏向一侧,这些连续的径向裂纹从裂纹扩展原点出发,向四周扩展到了防弹玻璃的边缘,同时穿插着大量不连续的、以径向裂纹原点为圆心的环向裂纹[9]。PC背板在弹丸的冲击作用下发生塑性变形,在背面形成鼓包,形成20 mm长的细长裂缝,弹丸出孔位置相对于着靶点发生较大偏移。

图5 12.7 mm穿燃弹侵彻试验的部分装甲形貌
Fig.5 Failure modes of some armor in the penetration test of 12.7 mm armor-piercing incendiary bullet
图5(c)、(d)所示为极限穿透速度工况下的回收靶板,相对于图5(a)所示靶板,迎弹面外翻的PVB胶层较小,弹丸入孔近似为圆形,并且孔径明显较大。透过PC背板可以看到径向裂纹的原点和环向裂纹的圆心均与着靶点重合。弹丸头部露出PC背板并出现较大偏转,出孔位置偏向一侧。
在14.5 mm穿燃弹侵彻试验中选取极限穿透速度工况的回收靶板进行破坏形貌分析:如图6所示,靶板上端各PVB胶层在弹丸的冲击作用下飞散出去,部分粘连玻璃碎片的PVB胶层散落在靶板内,下端各PVB胶层仍呈分层排列,与12.7 mm穿燃弹侵彻试验的回收靶板相比,靶板的结构完整性较差。迎弹面下端的PVB胶层外翻形成规则的花瓣状翻唇。弹丸出孔PC背板位置相对于着靶点发生较大偏移,透过PC背板可以看到玻璃裂纹明显,与12.7 mm穿燃弹侵彻试验中各工况观察到的裂纹相比,裂纹宽度更大。

图6 14.5 mm穿燃弹侵彻试验的部分装甲形貌
Fig.6 Failure modes of some armor in the penetration test of 14.5 mm armor-piercing incendiary bullet
通过高速摄像拍摄到的剩余弹体可以看出:2种口径穿燃弹贯穿靶板后,铜披已经脱落,且弹芯结构较为完整,弹芯头部几乎未发生磨蚀或破碎,如图7所示。

图7 剩余弹体形貌
Fig.7 Failure modes of residual bullet
弹丸侵彻过程中,弹道偏离角是影响装甲抗侵彻能力的重要因素。测量12.7 mm侵彻试验中各工况出孔相对靶板中心点的偏移量,如图8所示,并通过几何关系计算得到弹道偏离角。

图8 靶板出孔偏移量
Fig.8 The deviation value of the hole on the armor
忽略弹丸着靶前的攻角因素造成弹丸侵彻过程中的弹道偏离,研究弹道偏离角与弹丸初速度之间的关系。弹道偏离角随弹丸初速度变化规律如图9所示,当弹丸初速度为极限穿透速度时,此时弹道偏离角最大,随着弹丸初速度的增大,弹道偏离角减小,且加速度不断增大。
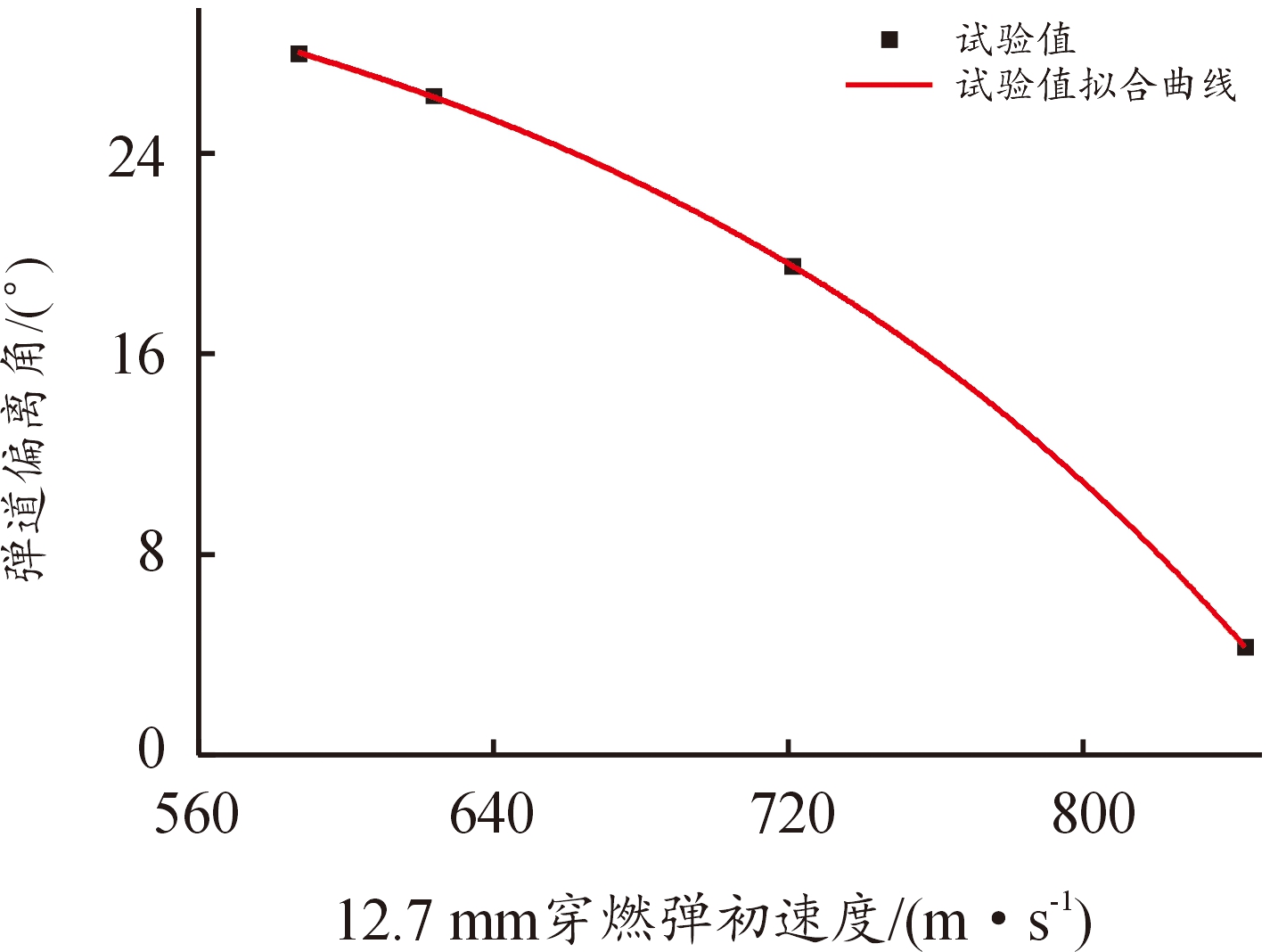
图9 弹道偏离角与弹丸初速度的关系
Fig.9 Initial velocity as a function of the trajectory deviation angle
由于该型防弹玻璃为多层复合装甲,且各层材料力学性能差异较大,弹体在侵彻过程中受到不对称侧向力作用而产生转动力矩,造成运动姿态发生改变。弹丸贯穿靶板的工况中,当弹丸的初速度过小时,受到不对称侧向作用力的作用时间较长,弹丸姿态发生明显偏转,弹道偏离角较大,而随着弹丸初速度增大,受到不对称侧向作用力的作用时间减少,弹丸侵彻过程中姿态趋于平稳,弹道偏离角较小。
测量12.7 mm侵彻试验中各工况的PC背板裂缝长度,拟合得到出孔裂缝长度随12.7 mm穿燃弹初速度的变化关系,如图10所示,出孔裂缝长度与弹丸初速度成正比增长关系。
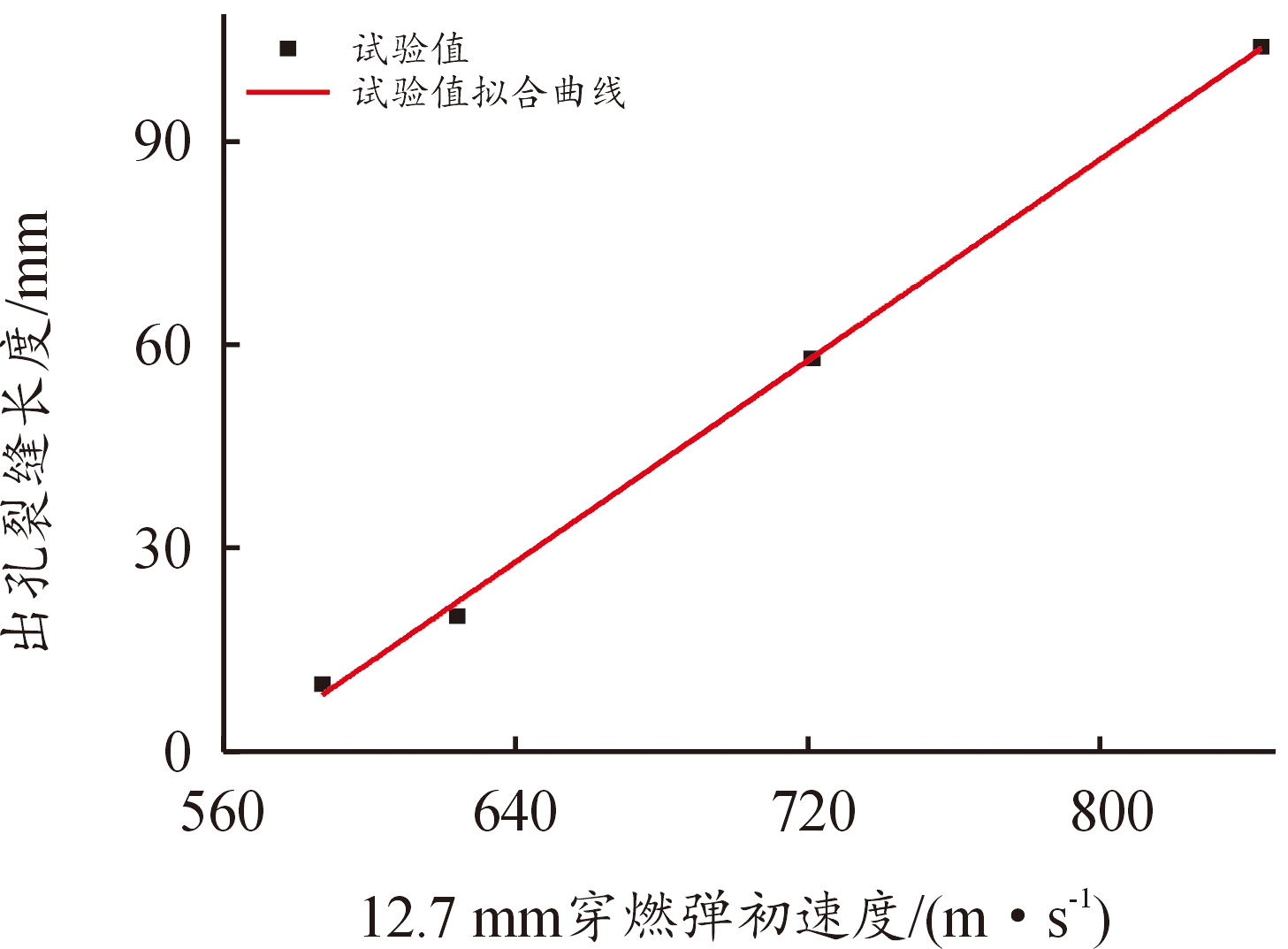
图10 出孔裂缝长度与弹丸初速度的关系
Fig.10 Initial velocity as a function of the length of hole crack
通过上述防弹玻璃破坏情况与分析,可以得出该防弹玻璃的抗侵彻机理:弹丸初速度是正侵彻工况下弹道发生偏离的主要原因:当弹丸初速度与极限穿透速度相同时,此时的弹道偏离角最大,随着弹丸初速度的增大,弹道偏离角减小。各玻璃层在受到弹丸冲击时,形成大量的径向裂纹和环向裂纹,同时在弹丸着靶点附近产生细小的玻璃碎片,吸收了大量的弹丸冲击能量作为表面能,从而有效的消耗了弹丸的能量。PVB胶层使得受到冲击完全破碎的靶板保持一个整体,极大程度地减少了飞溅物。由于PC背板具有一定的冲击强度和足够的韧性,通过鼓包的形式,吸收了弹丸的冲击能量转化为PC背板的拉伸变形能,同时较小的孔径也很大程度地减少了靶后破片。
2 仿真模型
2.1 几何模型
仿真采用的靶板结构如图1(b)所示,为了提高数值计算的效率,简化数值计算模型,忽略了聚丙烯醇缩丁醛(PVB)层,简化后模型的长宽尺寸为200 mm×200 mm,厚度为69 mm。仿真采用12.7 mm制式穿燃弹弹芯和14.5 mm制式穿燃弹弹芯,几何模型如图3所示。12.7 mm制式穿燃弹弹芯的质量为30 g,14.5 mm制式穿燃弹弹芯的质量为40.5 g,2种口径穿燃弹的弹芯材料均为T12A钢。
2.2 仿真模型
本文基于ANSYS/LS-DYNA软件建立相应的仿真模型,穿燃弹弹芯和防弹玻璃均采用八节点六面体单元,单元算法为拉格朗日算法。为减少计算量,采用1/2有限元模型,如图11所示,各层材料见图1(b),该数值计算模型网格数量共3 258 640个,网格尺寸为0.5 mm。
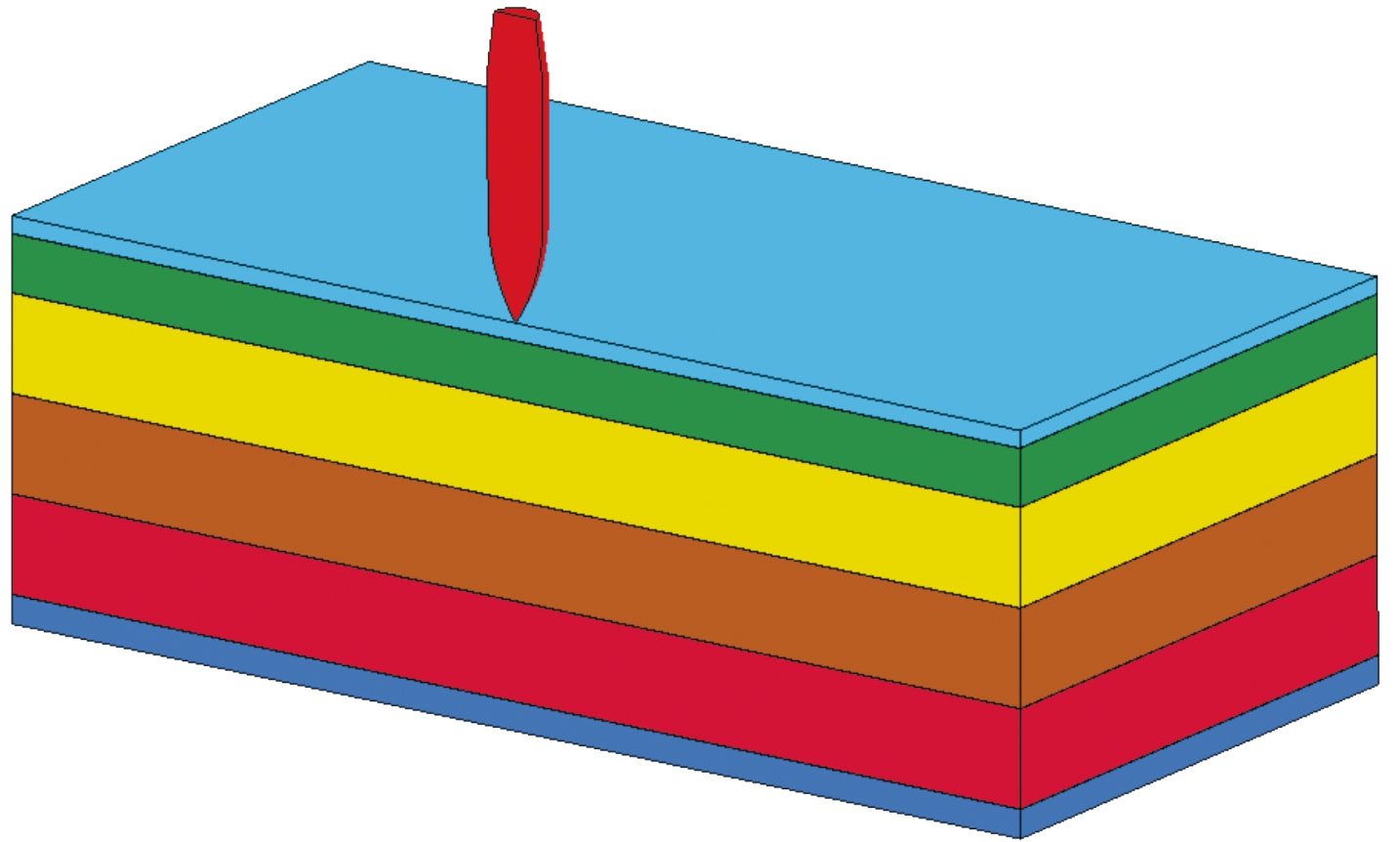
图11 防弹玻璃有限元模型
Fig.11 The finite element model of bullet-proof glass
通过关键字BOUNDARY_SPC_SET设置穿燃弹和防弹玻璃的对称面约束,穿燃弹和防弹玻璃之间通过关键字CONTACT_ERODING_SURFACE_TO_SURFACE设置侵蚀接触,2种口径穿燃弹和靶板内部分别通过关键字CONTACT_ERODING_SINGLE_SURFACE设置自接触。PVB胶层与玻璃层之间的粘合作用则是通过设置关键字CONTACT_AUTOMATIC_SURFACE_TO_SURFACE_TIEBREAK来实现,设置关键字变量OPTION、NFLS和SFLS来控制破坏粘合作用所需应力值。
穿燃弹采用高应变率下适用的JOHNSON_COOK(JC)材料模型和GRUNEISEN状态方程共同表征,玻璃材料通过JOHNSON_HOLMQUIST_CERAMICS(JH2)材料模型[12]进行表征,PC背板采用的聚碳酸酯材料,使用4号材料模型ELASTIC_PLASTIC_HYDRO进行表征,具体材料参数如表1—表3所示[13-15]。
表1 T12A的材料参数
Table 1 Material parameters of T12A
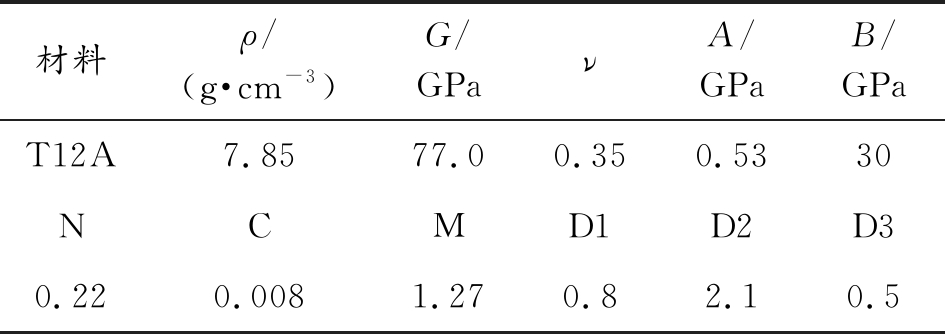
材料ρ/(g·cm-3)G/GPaνA/GPaB/GPaT12A7.8577.00.350.5330NCMD1D2D30.220.0081.270.82.10.5
表2 无机玻璃的材料参数
Table 2 Material parameters of glass
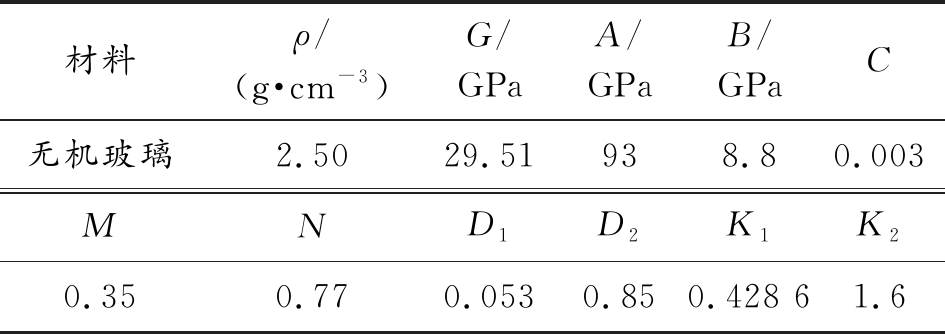
材料ρ/(g·cm-3)G/GPaA/GPaB/GPaC无机玻璃2.5029.51938.80.003MND1D2K1K20.350.770.0530.850.428 61.6
表3 聚碳酸酯的材料参数
Table 3 Material parameters of makrolon
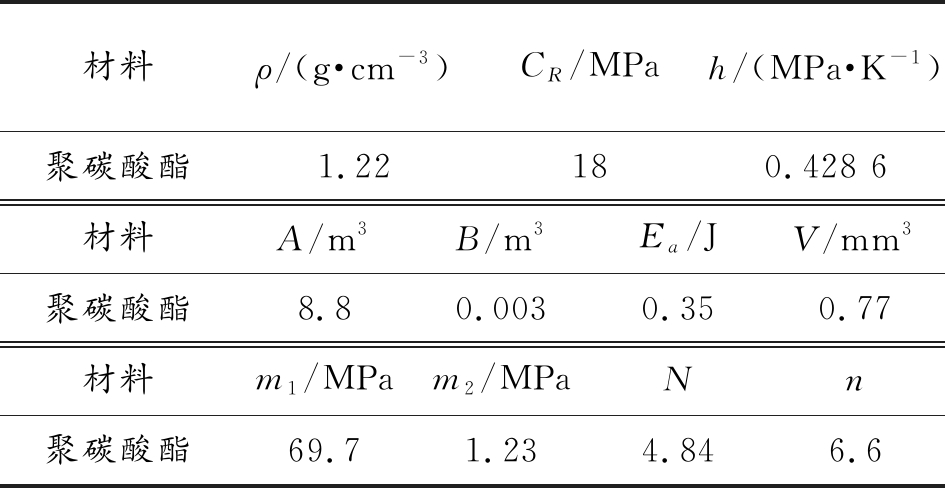
材料ρ/(g·cm-3)CR/MPah/(MPa·K-1)聚碳酸酯1.22180.428 6材料A/m3B/m3Ea/JV/mm3聚碳酸酯8.80.0030.350.77材料m1/MPam2/MPaNn聚碳酸酯69.71.234.846.6
2.3 仿真模型校验
通过试验得到了12.7 mm穿燃弹和14.5 mm穿燃弹以不同初速正侵彻防弹玻璃时,防弹玻璃的变形和破坏情况,将极限穿透速度工况的仿真结果和试验结果进行对比,如表4、表5和图12、图13所示。
表4 12.7 mm穿燃弹试验结果误差
Table 4 Comparison of 12.7 mm armor-piercing bullet experimental and simulation results
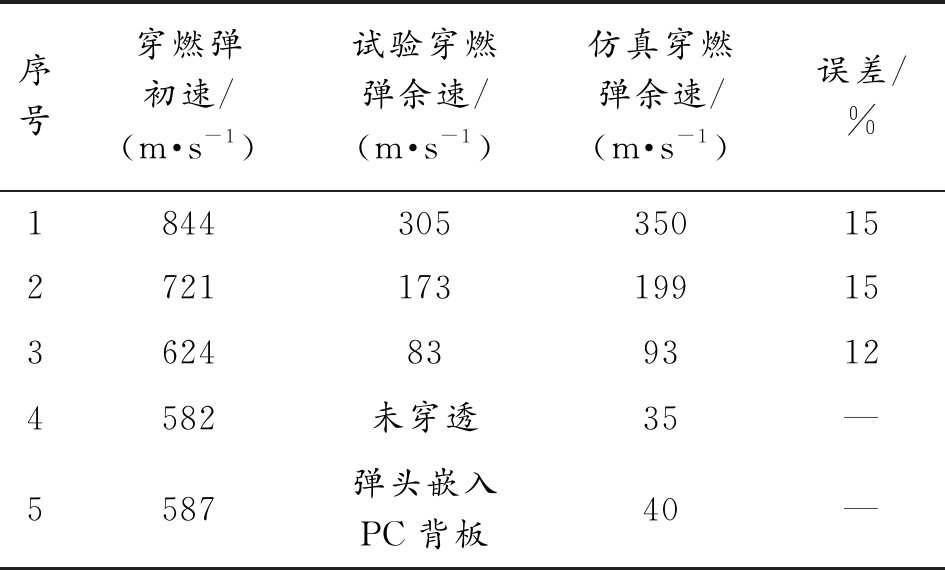
序号穿燃弹初速/(m·s-1)试验穿燃弹余速/(m·s-1)仿真穿燃弹余速/(m·s-1)误差/%18443053501527211731991536248393124582未穿透35—5587弹头嵌入PC背板40—
表5 14.5 mm穿燃弹试验结果误差
Table 5 Comparison of 14.5 mm armor-piercing bullet experimental and simulation results
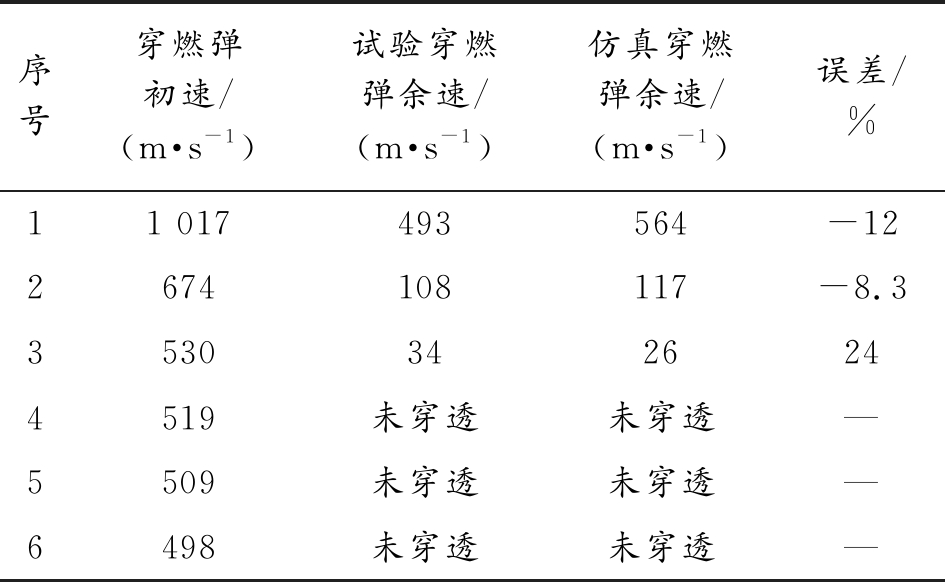
序号穿燃弹初速/(m·s-1)试验穿燃弹余速/(m·s-1)仿真穿燃弹余速/(m·s-1)误差/%11 017493564-122674108117-8.335303426244519未穿透未穿透—5509未穿透未穿透—6498未穿透未穿透—

图12 12.7 mm穿燃弹侵彻试验的装甲破环形貌对比
Fig.12 Comparison of armor damage in penetration experiment of 12.7 mm Armor-piercing bullet

图13 14.5 mm穿燃弹试验的破环形貌对比
Fig.13 Comparison of armor damage in penetration experiment of 14.5 mm Armor-piercing bullet
可以看出:仿真与试验测得的剩余速度误差较小,在合理的误差范围内,并且仿真与试验得到的靶板破坏形貌基本吻合,说明本文的仿真模型能较好地模拟12.7 mm和14.5 mm穿燃弹侵彻该型防弹玻璃的结构响应和破坏模式,后续可依据此模型进一步开展抗侵彻规律的研究。
3 仿真研究的规律分析
3.1 极限穿透速度随着角的变化规律
目前,装甲抗侵彻能力的表征主要是通过极限穿透速度大小。利用数值模拟计算得到12.7 mm穿燃弹、14.5mm穿燃弹在不同装甲倾角下侵彻防弹玻璃的极限穿透速度。图14为2种口径穿燃弹的极限穿透速度随装甲倾角的变化规律。
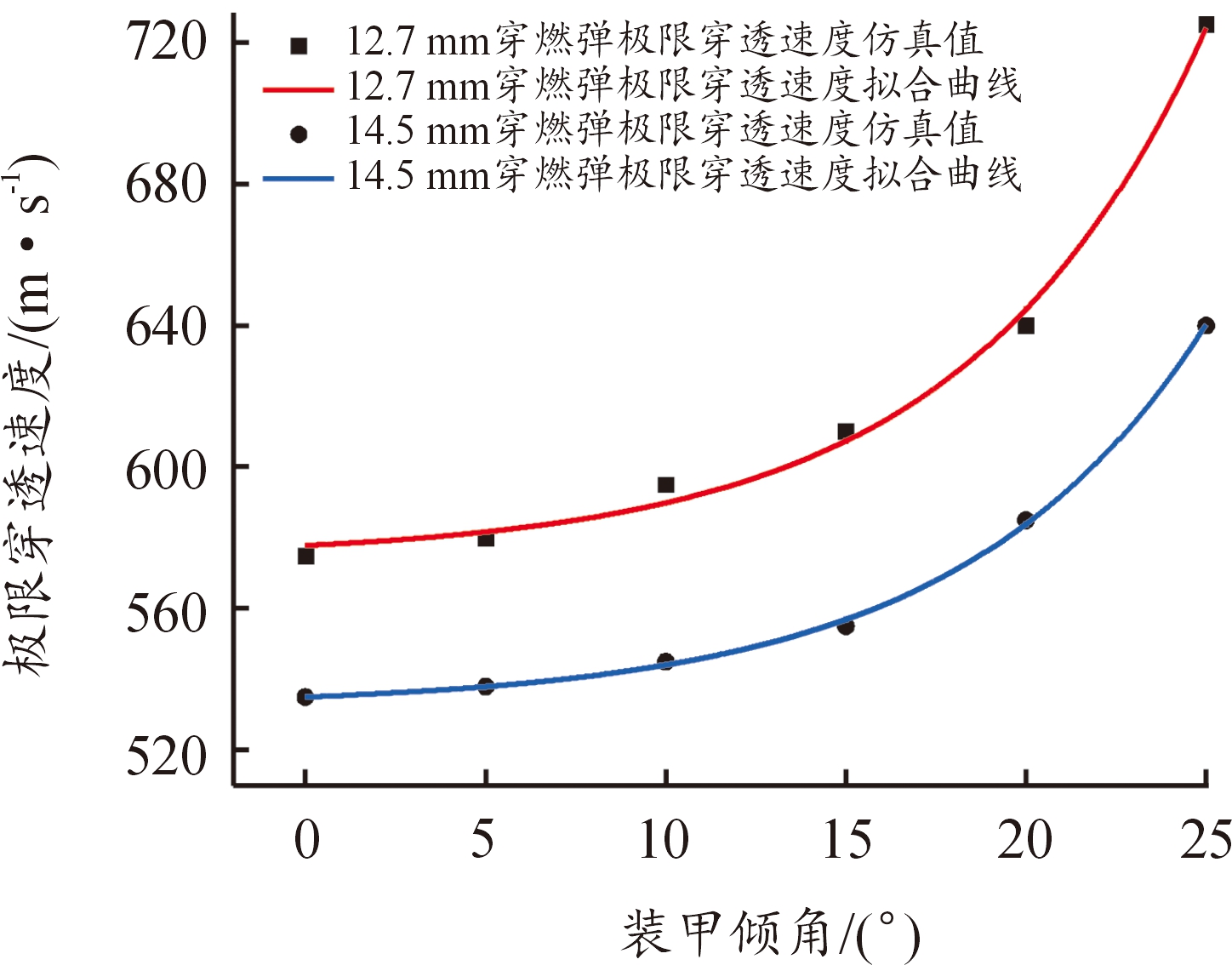
图14 极限穿透速度随装甲倾角的变化曲线
Fig.14 Initial velocity of armor-piercing bullet as a function of ballistic limit
可以看出12.7 mm穿燃弹、14.5 mm穿燃弹侵彻防弹玻璃的极限穿透速度与装甲倾角均呈指数函数关系增长,并且变化率相似。装甲倾角在0~5°时,2种口径穿燃弹的极限穿透速度均增长地非常缓慢,5~15°的装甲倾角,极限穿透速度的增长幅度较为显著,当装甲倾角增大到15~25°时,弹丸的极限穿透速度急剧增大。装甲倾角较小时,倾角带来的弹丸侵彻厚度的增加是造成弹丸极限穿透速度增大的主要原因,而较大的装甲倾角会造成弹丸的偏转角变大,进一步增加了弹丸侵彻厚度,导致弹丸的极限穿透速度急剧增大。
相对于正侵彻,12.7 mm穿燃弹侵彻倾角为25°的防弹玻璃时,极限穿透速度增大了150 m/s,14.5 mm穿燃弹的极限穿透速度增大了105 m/s。当装甲倾角增幅相同时,随着弹丸口径的增大,极限穿透速度增幅减小。
3.2 弹丸剩余速度随初速度的变化规律
12.7 mm穿燃弹和14.5 mm穿燃弹剩余速度试验值随初速度的变化规律近似线性递增,如图15所示。当2种口径穿燃弹初速度相同时,剩余速度随着穿燃弹口径的减小而减小,且随着初速度的增大,差值逐渐减小。
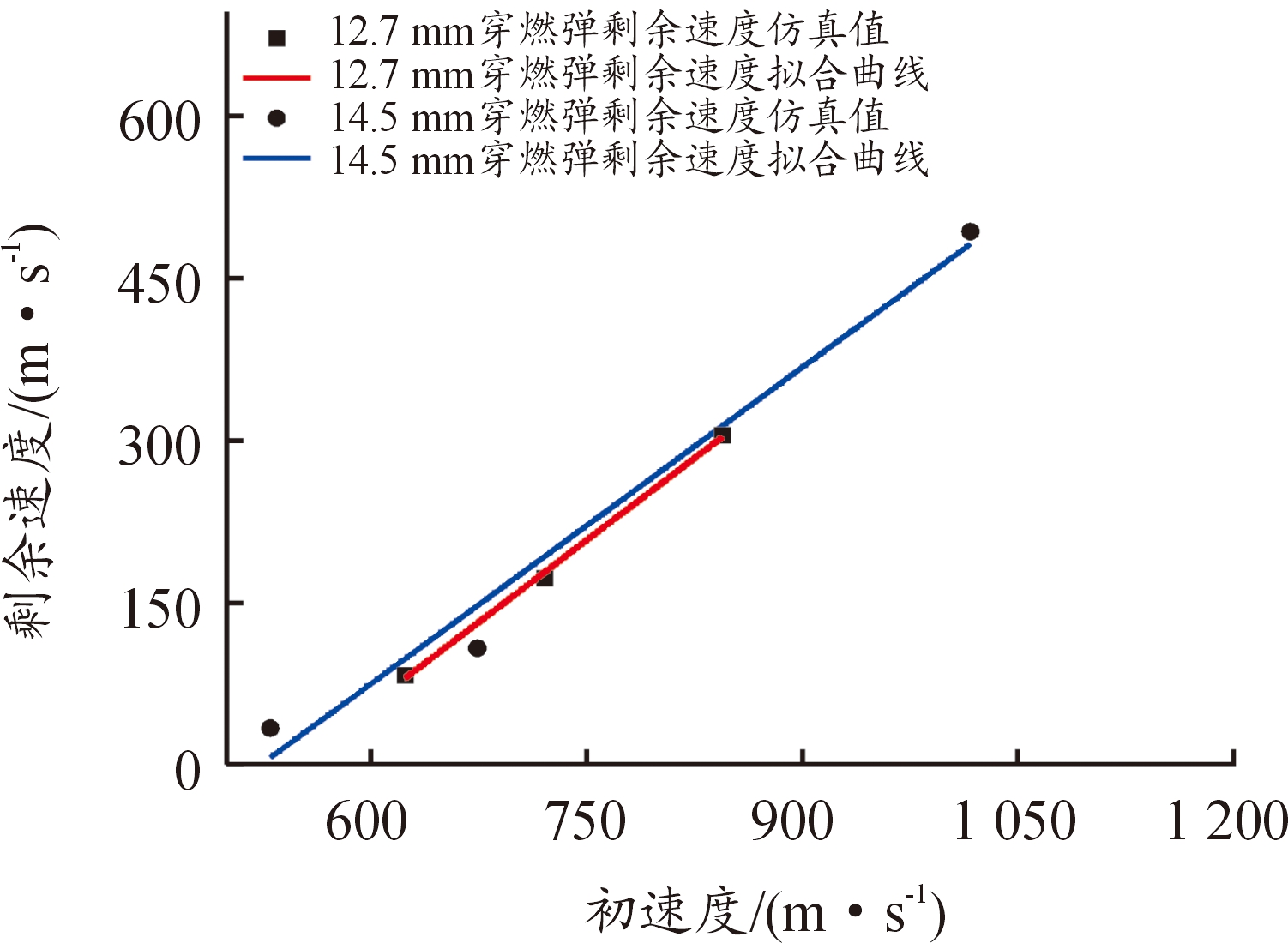
图15 剩余速度试验值随弹丸初速度的变化曲线
Fig.15 Residual velocity of experiment value as a function of the initial velocity
图16所示为2种口径穿燃弹剩余速度仿真值随初速度的变化关系,拟合得到的规律与试验所得基本吻合。初速度为700 m/s时,2种口径穿燃弹剩余速度差值约20 m/s,差值随着初速度增大而减小,剩余速度在初速度达到1 200 m/s时相等。
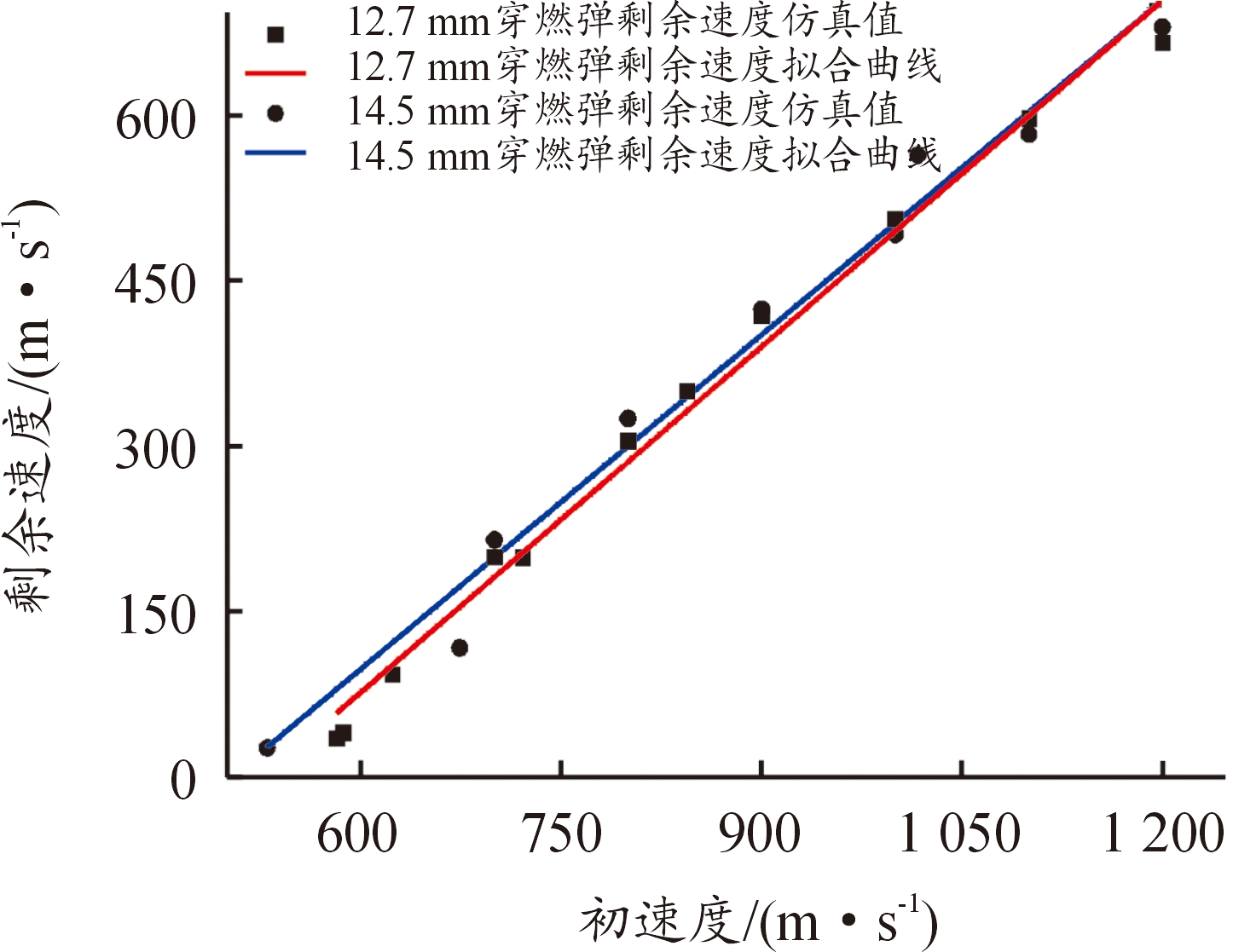
图16 剩余速度仿真值随初速度的变化曲线
Fig.16 Residual velocity of simulation value as a function of the initial velocity
4 防弹玻璃抗穿燃弹侵彻能力计算
为了对该型防弹玻璃的抗侵彻能力进行预测,利用文献[11]提供的一种多组分复合装甲混合律来初步预测该型防弹玻璃的抗侵彻能力,该公式的通式如下:
Ri=∑NiLi
(1)
式中,Ri为复合装甲抗侵彻能力(mm),Li为第i种材料的复合装甲水平等重厚度(mm),Ni为第i种材料的防护系数。
该公式中采用了复合装甲设计中常用的“水平等重厚度”概念。由于任何一种复合装甲都是层状装甲,因此在实际应用中,可以把复合装甲的每一层看做一个组分,从前至后依次进行计算。该公式适用于任何一种多种材料、多种结构组成的复合装甲。
一般计算复合装甲抗侵彻性能分为4个步骤,以穿燃弹正侵彻该型防弹玻璃(忽略PVB胶层)为例:
1) 计算各材料层的水平等重厚度Li。
![]()
(2)
式中:ρi为第i层材料的密度(×103 kg/m3);δi为第i层材料的垂直厚度(mm);αt为装甲的倾角(°)。
2) 确定各层装甲材料防护系数值Ni。
防护系数Ni是标准均质装甲钢半无限靶面密度与特种装甲材料面密度之比。
![]()
(3)
式中,Tb为标准弹种射击标准均质装甲钢半无限靶时穿入深度; ρg为钢密度7.85 g/cm3; Ti为特种装甲被同一标准弹种射击时的穿入深度。通过模拟试验方法测定12.7 mm穿燃弹模初速为500 m/s时正侵彻各装甲材料的穿深(cm),如图17所示,计算得到各层装甲材料的防护系数。
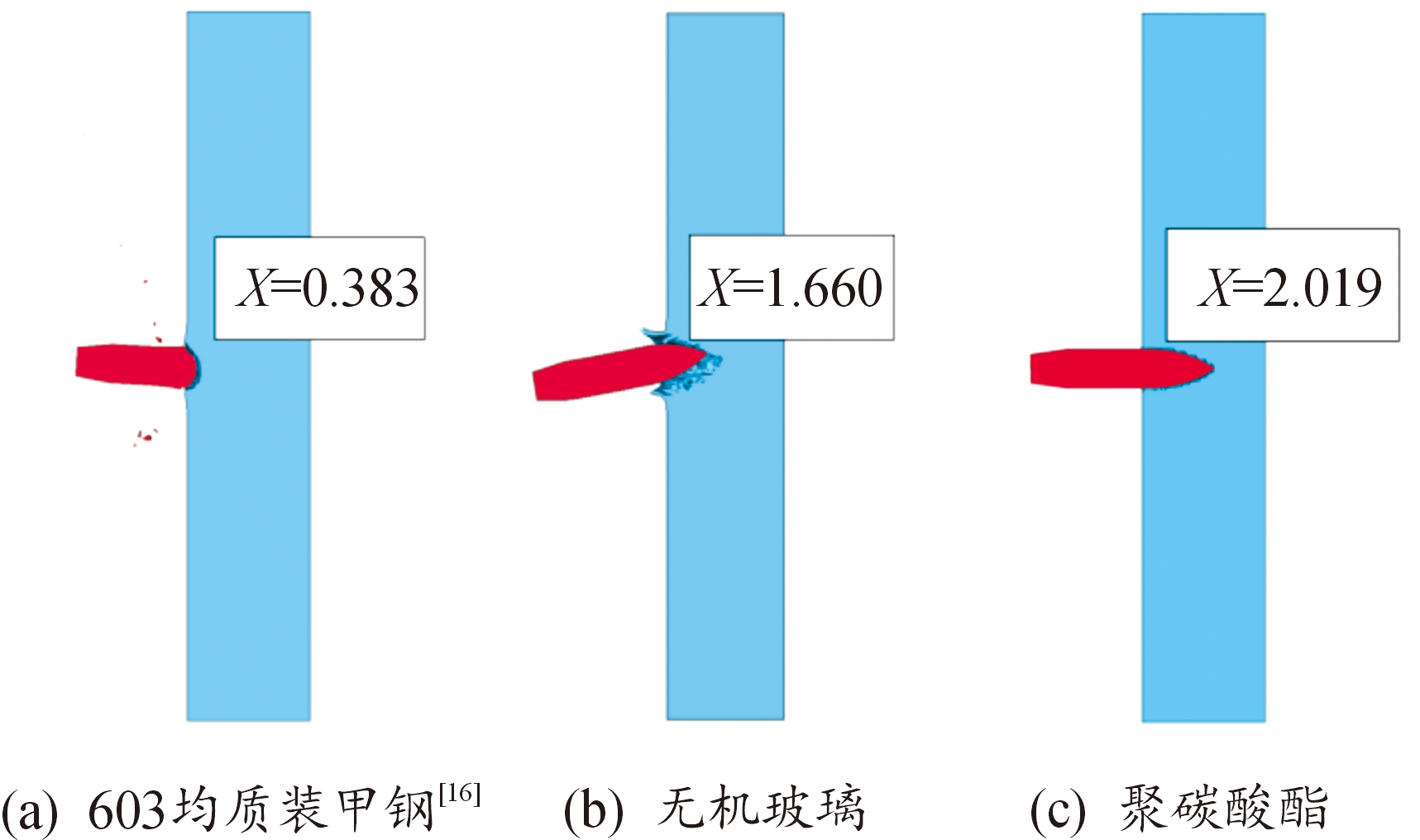
图17 各装甲材料穿入深度
Fig.17 Penetration depth of each armor material
3) 按式(4)依次计算每一层材料的抗弹能力Ri,填入表7中。
Ri=NiLi
(4)
4) 计算复合装甲总体抗弹能力。
通过式(1)将各层装甲的抗弹能力值进行累加,得到复合装甲的总体抗弹能力值,计算结果如表6所示。
表6 防弹玻璃抗弹能力计算
Table 6 Calculation of ballistic resistance of bullet-proof glass
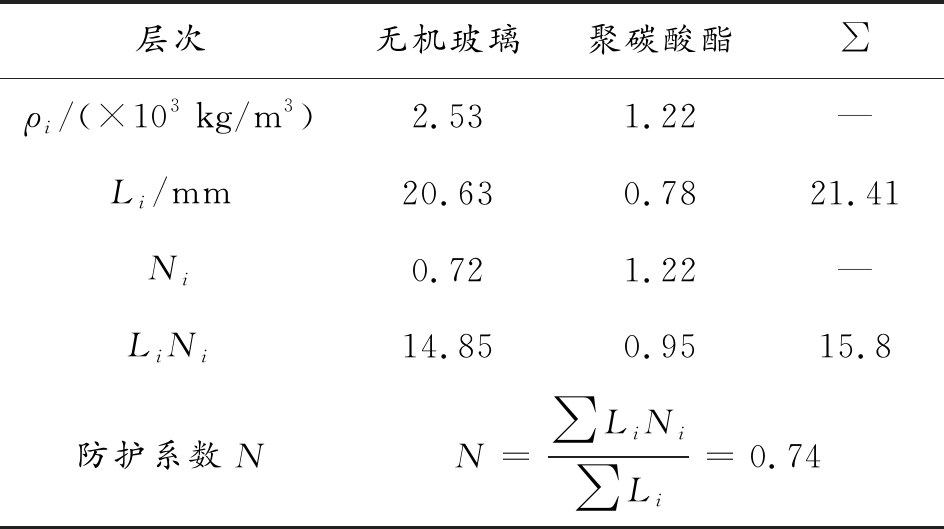
层次无机玻璃聚碳酸酯∑ρi/(×103 kg/m3)2.531.22—Li/mm20.630.7821.41Ni0.721.22—LiNi14.850.9515.8防护系数NN=∑LiNi∑Li=0.74
计算得到该型防弹玻璃的面密度为等效厚度下均质装甲钢的135.5%,防护系数为0.74,抗12.7 mm穿燃弹的能力相当于15.8 mm的603均质装甲钢。通过数值仿真计算12.7 mm穿燃弹侵彻15.8 mm的603均质装甲钢,得到极限穿透速度为559 m/s,相对试验得到的12.7 mm穿燃弹侵彻防弹玻璃的极限穿透速度误差为-4.8%,则认为防弹玻璃的防护系数是可靠的。
该混合率计算方法简便实用、适用范围广,为复合装甲研究工作提供了一种有效方法,但是该公式没有反映出装甲结构配置、材料结构交互作用等因素对抗弹能力的影响。因此给出的结果是粗略的,只能用于初步预测复合装甲的抗侵彻能力。
5 结论
基于12.7、14.5 mm两种穿燃弹,开展了该型防弹玻璃的侵彻试验研究,揭示了该防弹玻璃的抗侵彻机理。通过仿真得到了2种口径穿燃弹在不同装甲倾角下的极限穿透速度、不同初速度下的剩余速度,分析了极限穿透速度和剩余速度随穿燃弹口径的变化关系,同时对其防护能力进行工程计算,结论如下:
1) 初速度是导致弹道发生偏离的主要因素,当弹丸初速度与极限穿透速度相同时,此时的弹道偏离角最大,随着弹丸初速度的增大,弹道偏离角减小;PC背板的出孔裂缝长度与弹丸初速度成正比关系。
2) 2种口径穿燃弹侵彻防弹玻璃的极限穿透速度与装甲倾角均呈指数函数关系增长,并且变化率相似。2种口径穿燃弹的剩余速度随初速度均成正比增长关系,初速度相同时,剩余速度随着穿燃弹口径的减小而减小,且随着初速度的增大,差值逐渐减小。
3) 通过多组分复合装甲混合律计算了该防弹玻璃对12.7 mm穿燃弹的防护系数为0.74。
[1] KNEUBUEHL B P,COUPLAND R M,ROTHSCHILD M A,et al.Wound ballistics:Basics and applications[M].Berlin:Springer,2011.
[2] KNUDSEN P J T,SRENSEN O H.The initial yaw of some commonly encountered military rifle bullets[J].Int J Legal Med,1994,107(3):141-146.
[3] BLESS S J,CHEN T,RUSSELL R.Impact on glass laminates[J].23RD International Symposiu On Tarragona Ballistics,2007(4):16-20.
[4] 杨杰,邱日祥,胡志昂.防弹玻璃动态力学响应规律及抗弹性能研究[J].兵器材料科学与工程,2013,36(3):61-64.
YANG Jie,QIU Rixiang,HU Zhiang.Dynamic mechanical response and anti-bullet property of bulletproof glass[J].Ordnance Material Science and Engineering,2013,36(3):61-64.
[5] 刘正.不同聚碳酸酯层合结构对防弹玻璃性能影响的研究[J].玻璃与陶瓷,2016(2):14-19,36.
LIU Zheng.Effects of olycarbonate laminated structure on the performance of bullet proofglass[J].Glass &Enamel,2016(2):14-19,36.
[6] 陈宇宏,厉蕾.轻型防弹玻璃的结构研究[J].材料工程,2002(6):7-9.
CHEN Yuhong,LI Lei.Study on the structure of light weight bullet-proof glass[J].Journal of Materials Engineering,2002(6):7-9.
[7] GRUJICIC M,BELL W C.Design and material selection guidelines and strategies for transparent armor systems[J].Material and Design,2012,34(7):808-819.
[8] ANDERSON C E,Jr WEISS C E,CHOCRON S.Scaled impact experiments into borosilicate glass[J].26th International Symposium on Ballistics,2011(2):12-16.
[9] 濮勇,张红,谢于真,等.中高速冲击下PVB夹层玻璃开裂及碎片特性研究[J].硅酸盐通报,2019,38(11):3566-3572.
PU Yong,ZHANG Hong,XIE Yuzhen,et al.Study on crack and fragment characterristics of PVB laminated glass under medium and high speed impact[J].Bulletin of The Chinese Ceramic Society,2019,38(11):3566-3572.
[10] 葛超,董永香,陆志超,等.弹丸头部对斜侵彻弹道偏转影响研究[J].兵工学报,2015,36(2):256-262.
GE Chao,DONG Yongxiang,LU Zhichao,et al.Ballistic deflection on oblique penetration of projectiles with different noses[J],Acta Armamentaril,2015,36(2):256-262.
[11] 曹贺全,赵宝荣,徐龙堂,等.装甲防护技术[M].北京:兵器工业出版社,2012:44-47.
CAO Hequan,ZHAO Baorong,XU Longtang,et al.Armor protection technology[M].Beijing:Ordnance Industry Press,2012:44-47,205-210.
[12] GORDON R,TIM J.holmquist.Animproved computational constitutive model for brittle materials[J].American Institute of Physics,1993,309(12):982-984.
[13] 耿宝刚.钻地弹弹体材料力学性能研究[D].长沙:国防科学技术大学,2010.
GENG Baogang.Research on the mechanical properties of ground-penetrating projectile materials[D].Changsha:National University of Defense Technology,2010.
[14] 刘虎.防弹玻璃在子弹冲击下的数值模拟研究[J].导弹与航天运载技术,2017,5:99-10.
LIU Hu.Numerical simulation of sulletproof slass subjected to sullet smpact soading[J].Missles and Space Vehicles,2017(5):99-100.
[15] 曹侃.聚碳酸酯动态拉伸学行为的测试与表征[D].合肥:中国科学技术大学,2012.
CAO Kan.Exprimental investigation and modeling of dynamic tension behavior of polycarbonate[D].Hefei:Uniwersity of Science and Technology of China,2012.
[16] TIAN S Y,SONG S C.Dynamic properties test of steel 603 and 675 and establishment of cinstitutive relations[J].Journal of Ningbo University(NSEE),2003,16(4):463-471.