0 引言
近年来,随着高新技术在国防科技领域的广泛运用,导弹武器装备在现代化战争中发挥着越来越重要的作用,对于导弹武器装备的效能评估也成为作战决策和军事部署的重要依据。常用的导弹武器装备效能评估模型有:ADC法[1-2]、层次分析法[3-4]、模糊综合评价法[5]、SEA法[6-7]等。ADC法中,能力向量C是系统效能集中的体现,也是评估系统效能的关键。但在模型中,能力向量C应包含哪些能力项,ADC方法没有给出一个统一规范的标准;层次分析法往往与专家法结合起来,通过专家打分来确定指标的权重,评价结果主观性较强,这也导致评价对象的基础指标数量不能太多;模糊综合评价法并不能利用原始数据的深层信息,不能解决评价指标间相关造成的信息重复问题。而SEA法很难解决系统性能和使命性能之间的指标映射。
现如今,神经网络评估模型为解决这些问题指明了方向。针对如何利用神经网络评估模型解决这些问题,海内外学者做了大量的工作。文献[8]通过分析表现函数梯度,根据迭代梯度方向和增量因子调整修正值,克服幅度偏导造成的不利影响,从而提高训练速度;文献[9]通过遗传算法优化模型参数和结构,利用贝叶斯正则化自适应调整参数大小及数量,提高模型的泛化能力,避免出现过拟合现象;文献[10]提出采用L-M (levenberg-marquardt)方法,并结合历史数据进行多次数值拟合优化模型初始参数,减少迭代次数和模型计算量;文献[11]将鳞虾群算法运用到模型连接权值及阈值的训练中,可增强模型的搜索能力和收敛速度。文献[12]将BP神经网络算法与数据包络法相结合,虽然结果得到了优化,但是传统BP神经网络中用梯度下降法调节权值存在着收敛速度慢和易于陷入局部最优的先天缺陷。
导弹武器装备具有其特殊性:由于武器的试验成本十分昂贵,使得现有的样本规模很小。同时对评估模型的精确度有着极为苛刻的要求。而上述方法通过分析模型原理和优化参数等方式,提高了传统神经网络模型的训练速度,但是在处理小样本数据类型上结果都不甚理想。鉴于此,本文中提出一种小样本RBF神经网络模型,该模型通过充分利用历史数据和标准理论值,挖掘数据的深层信息及其相互关系,同时RBF神经网络较传统BP神经网络有更强的泛化能力,具有唯一最佳逼近的特性,能够满足导弹武器装备对评估模型精确度的苛刻要求。此外,RBF神经网络模型无局部极小问题存在,能够从根本上解决模型参数陷入局部最优的问题。同时利用Bootstrap法,合理扩充数据,满足神经网络对训练数据的要求。将此方法应用于导引头测高性能评估,能够有效地解决小样本评估问题,并有效提升导引头测高性能评估精度。
1 SAR导引头测高性能评估指标体系
SAR(Synthetic aperture radar)导引头在导弹的末制导开始工作,根据指令先后完成测高、成像、定位和制导四项任务[13],测高作为SAR导引头的第一重要作用,其测量结果对于后续的环节有着决定性的影响,对于SAR导引头整体的评估具有举足轻重的作用,故重点针对导引头测高系统建立评估体系。
导弹在末制导过程中,飞行速度特别快。同时,面临地形复杂、敌军电磁干扰等多项挑战。这些困难对SAR导引头测高性能的影响很大,现根据SAR导引头实际的工作环境采用层次分析法,建立导引头测高性能评估指标体系。如图1所示。其中8个二级指标均可由历史数据计算所得。

图1 SAR导引头测高性能评价体系
Fig.1 Seeker measurement performance evaluation system
2 传统RBF神经网络模型
径向基函数(radical basis function,RBF)是多维空间插值的传统技术,由Powell于1985年提出[15]。1988年,Broom head和Lowe根据生物神经元具有局部响应这一特点,将RBF引入神经网络设计中,提出了RBF神经网络。1989年,Jackson论证了RBF对非线性连续函数的一致逼近性能[16-17]。
RBF神经网络属于前向神经网络类型,相对于多层前馈网络(MFN),RBF网络由于具有良好的泛化能力,且网络结构简单,可以避免不必要的冗长计算[18-20]。
如图2所示,典型的RBF神经网络拓扑结构有3个层级:输入层,隐含层和输出层。隐含层的神经元激活函数由径向基函数构成,隐含层组成的数组运算单元成为隐含层节点。每个隐含层节点包含一个中心向量c,c和输入参数向量x具有相同维数,二者之间的欧氏距离定义为![]()

图2 RBF神经网络拓扑结构图
Fig.2 Topo logical structure of RBF neural network
隐含层的输出由非线性激活函数hj(t)构成:
![]()
(1)
式中:bj为一个正的标量,表示高斯基函数的宽度;m为隐含层的节点数量,网络的输出由如下加权函数实现:
![]()
(2)
式(2)中:xn为输入节点;n为输入节点个数;hm为隐藏层权值;m为隐藏层个数;ω为隐藏层到输出层的权值; f(x)为神经网络输出。
RBF神经网络算法具体步骤如下:
步骤1 基于K-均值聚类方法求取基函数中心cj(t)。
1) 网络初始化:随机选取m个训练样本作为聚类中心cj(t)。
2) 将输入的训练样本集合按最近邻规则分组:按照x(t)与中心为cj(t)之间的欧式距离将x(t)分配到输入样本的各类聚类集合中。
3) 重新调整聚类中心:计算各个聚类集合中训练样本的平均值,即新的聚类中心cj(t),如果新的聚类中心不再发生变化,则所得到的cj(t)即为RBF神经网络最终的基函数中心,否则返回2),进行下一轮的中心求解。
步骤2 求解方差
该RBF神经网络的基函数为高斯函数,方差可如下求解:
![]()
(3)
式中:cmax为所选取中心之间的最大距离。
步骤3 计算隐含层和输出层之间的权值。
隐含层至输出层之间神经元的连接权值可以用最小二乘法直接计算得到,计算公式如下:
![]()
(4)
在实际应用过程中,传统的RBF神经网络模型有2个明显缺陷,一是指标之间的相互关系十分模糊,传统的RBF神经网络同层之间没有权重,这使得传统的RBF神经网络不能够利用数据的更深层信息;二是RBF神经网络算法必须在一定数据量的支撑下才能进行有效训练,而导弹武器装备试验的成本十分高,使得现有的样本的规模很小。鉴于此,针对以上2种情况,笔者结合TOPSIS法和Bootstrap法对传统的RBF神经网络模型进行改进,从而提出了一种小样本RBF神经网络模型。
3 小样本RBF神经网络模型
3.1 TOPSIS法
3.1.1 TOPSIS法简介
逼近理想点法 (technique for order preference by similarity to ideal solution,TOPSIS) 是最著名的经典指标方法之一,最初是在1981年由Hwang和Yoon首次提出,在1992年由Chen和Hwang做了进一步的发展。
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反应各评价方案间差距。经常用于多目标多任务装备调度决策问题,是各类系统效能评估决策分析的一种常用方法,在各类系统效能评估、军事、管理等多个领域具有广泛的应用[21-23]。
3.1.2 TOPSIS法的基本原理
TOPSIS方法引入了2个基本概念:理想解和负理想解。所谓理想解是一设想的最优的解(方案),它的各个属性值都达到各备选方案中的最好的值;而负理想解是一设想的最劣的解(方案),它的各个属性值都达到各备选方案中的最坏的值。方案排序的规则是把各备选方案与理想解和负理想解做比较,若其中有一个方案最接近理想解,而同时又远离负理想解,则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择。这种方法假定了每个属性是单调递增或者递减,TOPSIS利用了欧氏距离测量方案与理想解和负理想解。然而所有评价指标中的权重多采用层次分析法来进行赋权,其最大的缺点是判断矩阵的确定过于依赖于专家,缺少对样本数据本身的深度挖掘。参考其他文献,多采用熵权法这种相对比较客观的赋权方法来进行客观赋权。然而其缺陷也想当明显。有些指标的变化很小却在系统中占据十分重要的地位,而熵权法无法解决这类问题,当然也有人提出“主观”+ “客观”的赋权方法,来弥补熵权法的缺陷,这里我提出RBF神经网络来进行赋权,能有效地避免上面的缺陷。
受到机器学习中标准化(Normalization)的启发:上一层神经元的值经过全连接层再经过激励函数传到下一层,如果输入层神经元之间的量级相差较大,会使得训练之后得到的权重变得“扭曲”,在此之上直接经过激励函数的处理会使得到的激励值分布在饱和阶段(也就是随着输入的增加,输出的值几乎不变),这导致神经网络对比较大的输入不再敏感,这非常不利于神经网络学习到规律。鉴于此,采用TOPSIS法对样本数据进行预处理来解决上述问题。经过预处理后的数据能够更好地让神经网络“消化”,加快训练速度,更好的学习到规律。
TOPSIS执行过程如下:
其基本计算流程,如图3所示。
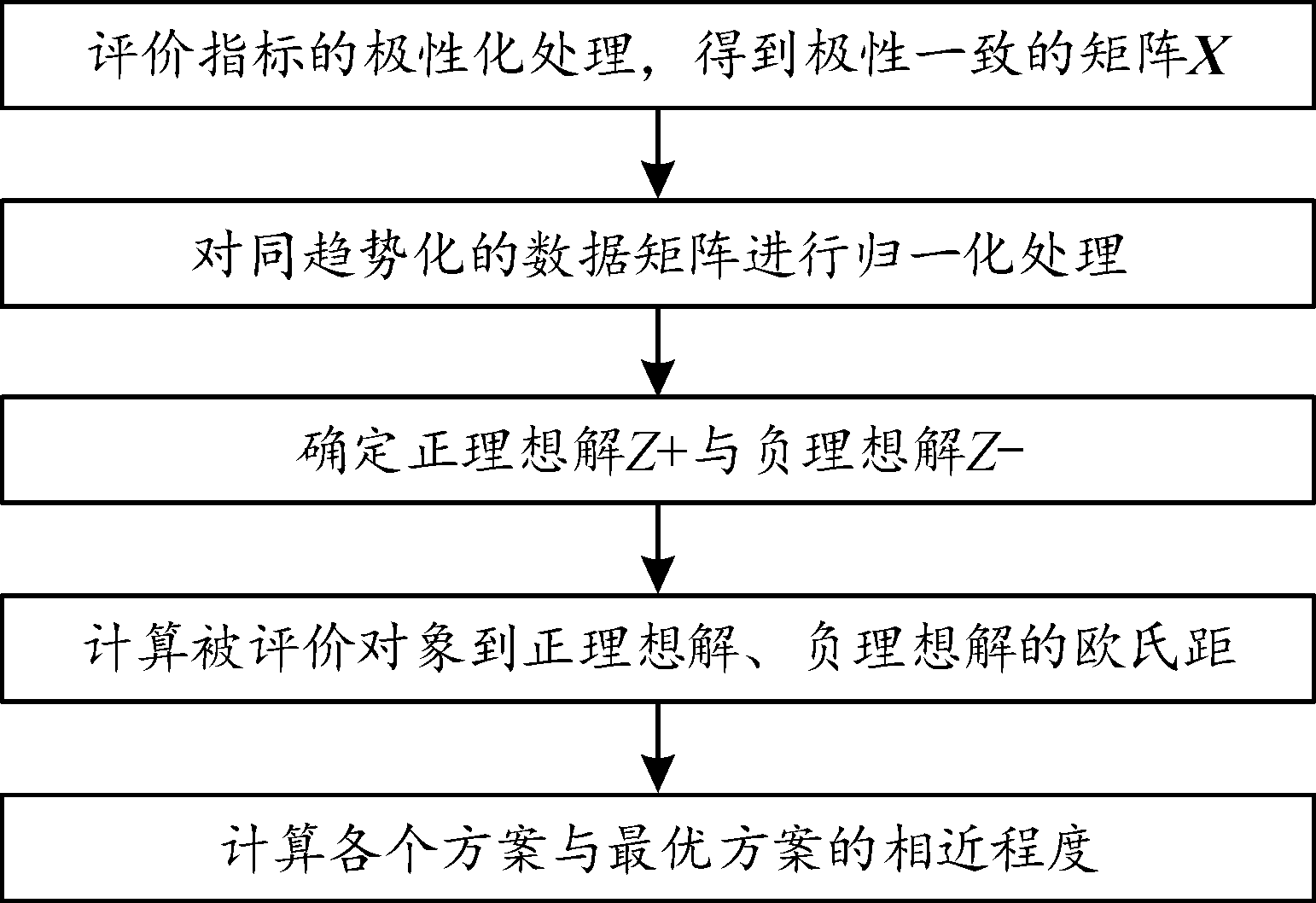
图3 TOPSIS法的基本流程图
Fig.3 Basic flow chart of TOPSIS method
3.2 Bootstrap法
3.2.1 Bootstrap法简介
导弹试验数据属于典型的小样本数据类型,而传统RBF神经网络需要大量的训练样本支撑,因此必须对导弹试验数据进行扩充。常见的处理小样本数据的方法有Bayes法,Bootstrap法和随机加权法[26],Bayes法的核心思想是将样本总体分布、实验室仿真数据等先验信息与现场实验数据相融合,由于先验信息的引入,使得结果可信度明显降低[27]。而随机加权法中对“权”的选择是无法回避的问题,到目前为止也没有较好的解决方案[28]。而Bootstrap法是一种从给定训练集中有放回的均匀抽样,也就是说,每当选中一个样本,它就可能被再次选中并被添加到训练集中。这种方法不利用任何外在信息,仅仅通过自身的再抽样完成对样本总体分布的估计。因此,Bootstrap法比Bayes法更加客观,同时又不必面临随机加权法中权重选择的问题[29]。综上所述,将Bootstrap法引入RBF神经网络对训练数据进行扩充,以解决现有数据量不足的问题。
3.2.2 Bootstrap法的主要思想
设随机子样X=(x1,x2,x3,…,xn)来自未知的总体分布F,R(X,F)为某个预先选定的随机变量,它是X和F的函数,现在要求根据观测子样X=(x1,x2,x3,…,xn)估计R(X,F)的分布特征,其基本步骤可归纳如下[29]:
1) 观测子样X=(x1,x2,x3,…,xn)的值为有限的总体样本,由它可构造子样的经验分布Fn:

(5)
式中:![]() 为x1到xn按照从小到大排序后所得的统计量。
为x1到xn按照从小到大排序后所得的统计量。
2) 从中抽取子样X=(x1,x2,x3,…,xn)称其为Bootstrap子样。
3) 用R*=R*(X*,Fn)分布取逼近R(X,F)的分布(R*的分布成为Bootstrap分布)。
获得Bootstrap分布的途径有很多,这里借助于计算机从Fn中重复抽取N个Bootstrap子样X*(1),…,X*(N),计算相应的Bootstrap统计量R*(1)=R*(X*(1),Fn),…,R(N)=R(X*(N),Fn);从而用R*(i),i=1,2,3,…,N的频率曲线作为Bootstrap分布的逼近。为了说明这种方法,以未知参数估计的误差分布计算为例进行阐明。设x1,x2,…,xn为i.i.d子样,θ=θ(F)是总体分布F的某个参数,Fn是子样(x1,x2,x3,…,xn)的经验分布函数,![]() 是θ的估计,计估计误差为
是θ的估计,计估计误差为
设![]() 是从Fn中重新抽样新得到的一个子样,记
是从Fn中重新抽样新得到的一个子样,记
式中:![]() 为
为![]() 的经验分布;
的经验分布;
Rn 为Tn的Bootstrap统计量。
利用Rn的分布去模拟Tn的分布,这是Bootstrap方法的主要思想。
3.3 算法思想
神经网络模型需要训练集和测试集,因此,将原始样本分为训练集和测试集。为解决数据信息挖掘不充分问题,通过TOPSIS法对训练集以及测试集数据进行深入挖掘,并采用Bootstrap法对经TOPSIS法处理过后的训练集进行扩充来丰富训练样本个数,接下来,利用神经网络对TOPSIS法和Bootstrap法处理后的数据进行训练,最后,对通过TOPSIS法处理后的测试集样本进行测试。
3.4 算法流程
步骤1 将原数据随机分为训练集与测试集。
步骤2 利用TOPSIS对训练集与测试集的基础指标进行处理。
步骤3 对训练集数据利用Bootstrap法进行数据扩充。
步骤4 构造RBF神经网络,采用有监督学习的方式进行训练对TOPSIS法和Bootstrap法处理后的数据进行训练,得到训练后的神经网络。
步骤5 用TOPSIS法处理后的测试集数据对训练后的神经网络模型进行验证,将得到的预测值数据与真实值数据进行对比。
步骤6 拟合优度(Goodness of Fit)是指回归方程整体的拟合程度。度量拟合优度的统计量是确定系数R2,R2最大值为1。R2的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R2的值越小,说明回归直线对观测值的拟合程度越差。依据式(6)求取确定系数。
一般来说,相对误差更能反映测量的可信程度。依据式(7)求取测高模型的相对误差(Error)。
![]()
(7)
4 仿真实验
以第1节中SAR导引头测高系统为例进行仿真实验分析,把现有12组历史样本,分为8组训练集和4组测试集,如表1所示。我们通过建立不同的RBF神经网络模型来对系统的测高性能进行评估。
表1 SAR导引头测高样本数据
Table 1 Sample of the SAR’s height measurement

编号α1/mα2/dBα3/mα4/dBα5/mα6α7α8S015545.28.61127.00.250.240.4179.55824641.07.91156.30.270.140.5878.06034040.010.01007.50.300.30.6060.00044943.27.81027.10.190.250.3973.10855842.08.41165.80.160.250.4882.23966447.77.01205.00.100.100.30100.00076245.18.61085.40.280.270.5577.89086147.29.51186.90.140.190.5084.46595943.27.91166.80.170.160.5483.640105346.58.41076.20.260.280.4876.612115945.09.11105.80.270.170.5679.850125446.28.51145.50.230.240.4582.502
4.1 仿真对象描述
导引头的测高性能的评估体系有8个基础指标,将8个基础指标作为神经网络的输入,利用有监督学习的方式训练神经网络。传统RBF神经网络作为对照组,然后将3种改进后的神经网络模型作为实验组,得到相应的预测值、决定系数和相对误差,S0是由实际命中精度与各类数据标准计算所得,并在此基础上对4种评估结果进行分析。
4.2 基于传统RBF神经网络模型的评估结果
4.2.1 实验方法
步骤1 随机选取表1中的8组数据作为训练样本,其余4组作为测试样本。
步骤2 构造RBF神经网络,采用有监督学习的方式对原始训练集数据进行训练,得到训练过后的神经网络。
步骤3 将4组测试集输入到训练完成后的RBF神经网络中,求取测试样本的评估值。
步骤4 利用式(6)求取决定系数R2,式(7)求取相对误差将结果与实际值进行对比如图4所示。

图4 传统RBF神经网络模型评估值
Fig.4 Evaluation value of traditional RBF neural network model
4.2.2 仿真结果与分析
分析图4和表2可知:传统的RBF神经网络模型对训练样本自身进行评估时,其决定系数为:0.733 71,可见回归方程的拟合效果不是很理想。4个样本点的相对误差值均大于0.01,其中样本4的相对误差更是达到了0.1。由上述仿真结果可见,模型的预测结果远远不能满足导弹武器装备的对评估模型精准度的需求。
表2 传统RBF神经网络模型评估值
Table 2 Result of the traditional RBF model

真实值预测值相对误差样本184.46576.302 70.096 6样本273.10867.643 30.074 7样本382.23981.331 10.011 0样本476.61268.594 90.104 6
4.3 基于TOPSIS改进RBF神经网络模型的评估结果
4.3.1 实验方法
步骤1 随机选取表1中的8组数据作为训练样本,其余4组作为测试样本。
步骤2 利用TOPSIS法分别对训练集数据和测试集数据的8个基础指标进行处理得到的数据如表2所示。
步骤3 用处理后的训练集数据对RBF神经网络进行有监督学习的训练,得到训练后的神经网络。
步骤4 以4组测试集为输入,利用步骤3的RBF神经网络求取测试样本的评估值,并将估计结果与真实值进行对比,如图5所示。

图5 基于TOPSIS法改进RBF神经网络模型评估值
Fig.5 Result of the RBF model processed by TOPSIS method
步骤5 利用式(6)求取决定系数R2,式(7)求取相对误差,对4个样本点的相对误差进行比较,如表3所示。
表3 经过TOPSIS法处理后的SAR导引头测高样本数据
Table 3 Sample of the SAR’s height measurement processed by TOPSIS method

编号α1/mα2/dBα3/mα4/dBα5/mα6α7α8S010.286 50.293 70.291 70.289 60.319 70.318 20.309 40.239 679.55820.239 60.266 40.268 00.297 30.287 80.343 60.180 50.339 078.06030.208 40.259 90.339 20.258 50.342 60.381 80.386 80.350 760.00040.255 20.280 70.264 60.263 70.324 30.241 80.322 30.227 973.10850.302 10.272 90.284 90.299 90.264 90.203 60.322 30.280 582.23960.333 40.310 00.237 50.310 20.228 40.127 30.128 90.175 3100.00070.323 00.293 10.291 70.279 20.246 60.356 30.348 10.321 477.89080.317 80.306 70.322 30.305 10.315 20.178 20.244 90.292 284.46590.307 30.280 70.268 00.299 90.310 60.216 40.206 30.315 683.640100.276 10.302 20.284 90.276 60.283 20.330 90.361 00.280 576.612110.307 30.292 40.308 70.284 40.264 90.343 60.219 20.327 379.850120.281 30.300 20.288 30.294 70.251 20.292 70.309 40.263 082.502
4.3.2 仿真结果与分析
分析图5和表4可知:基于TOPSIS法的RBF神经网络模型对训练样本自身进行评估时,其决定系数为:0.854 78,可见回归方程的拟合结果不甚理想。从表3可见,所有样本点的相对误差值均大于0.01,其中样本4的误差甚至达到了0.059 8。可见基于TOPSIS法的RBF神经网络模型的预测结果虽然比传统RBF神经网络有所提升,但依然不能满足导弹武器装备对评估模型的精准度要求。
表4 基于TOPSIS法的RBF神经网络模型评估值
Table 4 Result of the RBF model processed by TOPSIS method

真实值预测值相对误差样本183.64082.200 70.017 2样本277.89076.283 00.020 6样本379.85078.527 40.016 6样本478.06073.389 50.059 8
4.4 基于Bootstrap法改进RBF神经网络模型的评估结果
4.4.1 实验方法
步骤1 随机选取表1中的8组数据作为训练样本,其余4组作为测试样本。
步骤2 对训练集数据利用Bootstrap法进行扩充,得到200个新的数据集。
步骤3 用处理后的训练集数据对RBF神经网络进行有监督学习的训练,得到训练后的神经网络。
步骤4 以4组测试集为输入,利用步骤3的RBF神经网络求取测试样本的评估值,并将估计结果与真实值进行对比,如图6所示。

图6 基于Bootstrap法改进RBF神经网络模型评估值
Fig.6 Result of the RBF model processed by bootstrap method
步骤5 利用式(6)求取决定系数R2,式(7)求取相对误差将结果与实际值进行对比如图6所示。
4.4.2 仿真结果与分析
分析图6和表5可知:基于Bootstrap的RBF神经网络模型对训练样本自身进行评估时,其决定系数为:0.854 78,这表明拟合效果一般但是达不到优秀的程度。从图6可见,基于Bootstrap的RBF神经网络模型的预测值更接近于传统的RBF神经网络模型预测结果。从表5可知,虽然样本2和样本3的相对误差在0.01之内,但是样本1和样本4的相对误差依然大于0.01。可见基于Bootstrap的RBF神经网络模型虽然在一定程度上提升了预测的准确度,但评估结果依然不令人满意。
表5 基于Bootstrap法改进RBF神经网络模型评估值
Table 5 Result of the RBF model processed by bootstrap method

真实值预测值相对误差样本182.50284.032 10.018样本279.55879.992 0.005 5样本379.8580.667 40.002 6样本478.0677.894 60.013 6
4.5 基于小样本RBF神经网络模型的评估结果
4.5.1 实验方法
步骤1 随机选取表1中的8组数据作为训练样本,其余4组作为测试样本。
步骤2 对训练集数据利用Bootstrap法进行扩充得到200个Bootstrap数据集。
步骤3 利用TOPSIS法分别对200个Bootstrap训练集数据和4个原始测试集数据的8项基础指标进行处理得到204个TOPSIS_Bootstrap数据。
步骤4 把200个TOPSIS_Bootstrap训练集数据放入到RBF神经网络中,采用有监督学习的方式进行训练,得到训练过后的神经网络。
步骤5 以4组TOPSIS_Bootstrap测试集数据作为输入,利用步骤3的RBF神经网络求取测试样本的评估值,并将估计结果与真实值进行对比,如图7所示。

图7 基于TOPSIS_Bootstrap法改进后RBF神经网络模型的评估值
Fig.7 Result of the RBF model processed by Bootstrap method
步骤6 利用式(6)求取决定系数R2,式(7)求取相对误差将结果与实际值进行对比如图7所示。
4.5.2 仿真结果与分析
分析图7和表6可知:基于TOPSIS法和Bootstrap法优化后的RBF神经网络模型对训练样本自身进行评估时,其决定系数为:0.970 22。所有点的相对误差均在0.006之内,其中样本4的相对误差值更是在0.001之内。模型的预测结果比前2种RBF神经网络模型预测结果都要好很多。能够充分满足导弹武器装备的需要。
表6 基于TOPSIS_Bootstrap法改进后RBF神经网络模型的评估值
Table 6 Result of the RBF model processed by Bootstrap method

真实值预测值相对误差样本182.23981.838 20.005 9样本278.0678.168 20.001 6样本379.55880.515 90.004 8样本479.8579.720 00.000 2
4.6 结果对比
通过表7我们可以看出,由TOPSIS_Bootstrap法改进的RBF神经网络评估模型来评估的4个样本结果相对误差最小,这说明由它评估出来的结果更逼近样本的真实值。
表7 4种评估方法的结果对比
Table 7 Contrastive result of the four methods

评估模型误差1误差2误差3误差4R2传统RBF神经网络 0.096 60.074 70.011 00.104 60.733 71TOPSIS法改进RBF神经网络0.017 20.020 60.016 60.059 80.854 78Bootstrap法改进RBF神经网络0.018 50.005 50.002 60.013 60.930 47TOPSIS法Bootstrap法改进RBF神经网络0.005 90.001 60.004 80.000 20.970 22
同时,其R2值要大于前2种神经网络模型,这说明由基于TOPSIS_Bootstrap法改进后的神经网络模型得出的回归直线与真实直线之间的拟合程度更好。综上所述,本文中提出一种基于TOPSIS_Bootstrap法的小样本RBF神经网络模型有效解决了导引头测高性能评估的问题。
5 结论
本文中提出一种基于TOPSIS_Bootstrap法的小样本RBF神经网络模型,并以SAR导引头测高性能为例,对比了传统的RBF神经网络模型、基于TOPSIS法改进的RBF神经网络模型以及基于Bootstrap法改进的RBF神经网络模型,从得到的4种结果可以看出,改进后的神经网络模型的决定系数和相对误差均有着明显的改善。该模型大大削弱了导弹武器装备性能评估中的主观因素的影响,同时充分挖掘了数据的深层信息,进而扩充原有的数据,使其满足RBF神经网络对于数据量的需求,有效地解决了神经网络模型对数据量的苛刻要求。
[1] LI W,MAO N,PAN W.The effectiveness evaluation model of radar jamming system based ion WSEIAC model[C]//Proc.of the IEEE Control and Decision Conference,2008:1848-1852.
[2] LI Q Y,CHEN G.Effectiveness evaluation of missile electromagnetic launch system based on ADC model improved by EWM-FAHP-ICWGT[J].Journal of information Security and applications,2020,152(2):5-7.
[3] 王君,周林,白华珍.效能评估ADC模型中可信赖度矩阵算法探讨[J].系统工程与电子技术,2008(8)1501-1504.
WANG Jun,ZHOU Lin,BAI Huazhen.Discussion on reliability matrix algorithm in ADC model for performance evaluation[J].Systems Engineering and Electronics,2008(8)1501-1504.
[4] GUI F,XIAO M Q,MIN L,et al.Effectiveness evaluation model of fixed wing uav based on the improved adc model[J].IEEE Beijing Section、Beijing Institute of Technology (BIT),2017,5:(6)172-178.
[5] 徐沙,张洁.一种基于层次分析法的雷达抗干扰效能评估方法[J].航天电子对抗,2016,32(3):65-76.
XU Sha,ZHANG Jie.An evaluation method of radar anti-jamming effectiveness based on analytic hierarchy process[J].Aerospace Electronic Countermeasures,2016,32(03):65-76.
[6] LI W Q,PENG X D,CHEN Z S.Evaluation of cloud computing copyright protection based on AHP[J].Journal of in-formation Security and Applications,2020,5(15):465-476.
[7] LIANG D,DAI Z Y,Wang M W.Assessing customer satisfaction of O2O takeaway based on online reviews by integrating fuzzy comprehensive evaluation with AHP and probabilistic linguistic term sets[J].European of Operation Research,2020,98(32):651-669.
[8] WANG G,XIAO C L,QI Z.Development tendency analysis for the water resource carrying capacity based on system dynamics model and the improved fuzzy comprehensive evaluation method[J].The Public Access Computer Systems Review,2020,48(196):122-133.
[9] 袁德宝,张建,赵传武,等.基于改进神经网络的高程拟合[J].大地测量与地球动力学,2020,40(3):221-224.
YUAN Debao,ZHANG Jian,ZHAO Chuanwu,et al.Elevation fitting based on improved neural network[J].Journal of Geodesy and Geodynamics,2020,40(3):221-224.
[10] 崔建国,林泽力,吕瑞.基于模糊灰色聚类和赋权 法的飞机健康状态综合评估方法[J].航空学报,2014,35(3):764-772.
CUI Jianguo,LIN Zeli,LYU Rui.Comprehensive evaluation method of aircraft health status based on fuzzy grey clustering and combination weighting method[J].Acta Aeronautica et Astronautica Sinica,2014,35(3):764-772.
[11] CHEN J,WANG P C,WANG H Q.Pedestrian-induced load identification from structural responses using genetic algorithm with numerical and experimental validation[J].Winged Missiles Journal,2021,1(3):165-169.
[12] YANG R,ZHANG Y L.A method of low concentration methane measurement in tunable diode laser absorption spectroscopy and Levenberg-Marquardt algorithm[J].IEEE Journal on Selected Areas in Communication,2020,224:657-672.
[13] 王华秋,李腾辉.基于混合磷虾群智能算法的MFAC控制研究[J].重庆理工大学学报(自然科学),2020,34(9):185-191.
WANG Huaqiu,LI Tenghui.Research on MFAC control based on hybrid Krill swarm intelligent algorithm[J].Journal of Chongqing University of Technology (Natural Science),20,34(9):185-191.
[14] 何华锋,何耀民,徐永壮.基于改进型神经网络的导引头测高性能评估[J].系统工程与电子技术,2019,41(7):1544-1550.
HE Huafeng,HE Yaomin,XU Yongzhuang.Performance evaluation of seeker based on improved neural network[J].Systems Engineering and Electronics,2019,41(7):1544-1550.
[15] LI D Y,DU S Y,LIU Y X,WANG Y N,WANG M M.Reinforcement learning for angle-only intercept guidance of maneuvering targets.2020,99.
[16] YU X K,XU T H,WANG J T.Sound Velocity Profile Prediction Method Based on RBF Neural Network[J],2020,7(19):148-153.
[17] JIU M.Adaptive RBF neural network-based control of an under actuated control moment gyroscope[J].Journal of Safety and Environment,2020,6(8):1-14.
[18] WANG J W,NI Q Y,LIU G J.Image splicing detection based on convolutional neural network with weight combination[J].Strategy Journal of in-formation Security and Applications,2020,4(5):54-59.
[19] 宫园园,艾宏志.RBF神经网络的境外旅游人数预测模型研究[J].计算技术与自动化,2020,39(4):159-162.
GONG Yuan Yuan,AI Hongzhi.Research on the prediction model of overseas tourism number based on rbf neural network[J].Computing Technology and Automation,2020,39(4):159-162.
[20] SHANG S,HE K N,WANG Z B.Sea clutter suppression method of hfswr based on rbf neural network model optimized by improved gwo algorithm[J].Journal of Safety and Environment,2020,62(87):1291-1303.
[21] SONG Z Y,QIAN L Q,WU C,ZHANG Q,Unweighted TOPSIS:a new multi-criteria tool for sustainability analysis[J].Winged Missiles Journal,2020,28(1):36-48.
[22] 戴嘉琪,何华锋,贺友,等.基于过程分析的合成孔径雷达导引头试验鉴定指标体系建立[J].飞航导弹,2018(9):92-96.
DAI Jiaqi,HE Huafeng,HE You,et al.Evaluation index system of synthetic aperture radar seeker based on process analysis[J].Aerospace Missiles,2018(9):92-96.
[23] ZHOU J,XIAO H TANG F,LIU Y.Multi-objective optimization-based TOPSIS method for sustainable product design under epistemic uncertainty[J].Winged Missiles Journal,2020,48(652):76-98.
[24] WANG Y X,Enhanced cognitive workload evaluation in 3D immersive environments with TOPSIS model[J].Chinese Journal of Analyze Chemistry 2020,1(3):147-159.
[25] 张金槐.特小子样场合下,方法与仿真在飞行器试验分析中的运用[J].系统仿真学报,1996,1(8):52-60.
ZHANG Jinhuai.Application of method and simulation in aircraft test analysis under special sample situation[J].Journal of System Simulation,1996,1(8):52-60.
[26] 张湘平,张金槐,谢红卫.导弹落点散布的试验鉴定优化设计[J].宇航学报,2002(4):92-95.
ZHANG Xiangping,ZHANG Jinhuai,XIE Hongwei.Experimental identification and optimization design of missile drop dispersion[J].Journal of Astronautics,2002(4):92-95.
[27] WANG Y K,LIU Q Y,ZHAO J.A risk assessment based on Bayesian theory[J],Ship Electronic Engineering 2018,26(9):2447-2461.
[28] 吕明春,张金槐.小子样理论方法及其工程应用问题探讨[J].质量与可靠性,2009,2(5):32-34.
LYU Mingchun,ZHANG Jinhuai.Discussion on small sample theory method and its engineering application[J].Quality and Reliability,2009,2(5):32-34.
[29] 刘琦,冯静,周经伦,等.基于动态建模方法的可靠性增长试验评定[J].系统工程学报,2004,4(7):435-440.
LIU Qi,FENG Jing,ZHOU Jianglun,et al.Reliability growth test evaluation based on dynamic modeling method[J].Journal of Systems Engineering,2004,4(7):435-440.