0 引言
高马赫数飞行器因具备高机动、快速打击优势成为目前各军事大国竞相研究的热点[1-2],准平衡飞行段弹道优化是突破敌方反导拦截系统的关键。高马赫数飞行器准平衡飞行过程中不仅要考虑动压、过载、热流率等约束限制,还需要对多禁飞区(自然环境、政治军事因素形成的)进行规避[3]。现有针对禁飞区的研究成果相对较浅,主要通过弹道优化或设计横向制导逻辑规避禁飞区。
在弹道优化方面,高马赫数飞行器准平衡飞行段弹道优化问题具有较高的非线性和复杂度,经典变分法和Pontryagin极小值原理难以高效求得最优解,因此通常用直接法进行求解[4]。直接打靶法是直接法中典型的代表方法,其通过离散控制变量,将最优控制问题转化为非线性规划问题[5],具有通用性好、易实现等优点。但直接打靶法的收敛性能依赖于终端时刻和控制量初末时刻猜想值,在工程实际应用中初值难以预估,需要进行相应的改进[6]。在横向制导逻辑方面,方法主要包括触角法[7]、倾侧角符号反转法[8]、人工势场法[9]等,其通过在线设计制导策略来规避禁飞区,但并未考虑终端时刻性能指标的最优性(如最远航程等)。
遗传算法是一种模拟自然选择和生物进化过程搜索全局最优的方法[10-11],因其具有较强的鲁棒性,对初值不敏感,对于大型、复杂非线性系统的全局优化问题具有良好的性能,在弹道优化领域得到了广泛的应用。如Cai等[12]利用遗传算法优化了以航程为目标函数的预测模型的飞行路径;Dancila等[13]提出一种基于遗传算法的新型飞行轨迹优化方法,选择优化标准为总成本最小,候选轨迹定义为横向和纵向两部分;Ergezer[14]开发了一种新的多目标遗传算法来解决路径规划,优化目标为轨迹长度、完成任务所需的时间以及耗能。但需要强调的是,遗传算法中适应度函数的选取直接关系到收敛速度以及是否能寻找到最优解[15],文献[16]在适应度函数中引入自适应调节机制,设计了一种适应度函数可随种群迭代次数增加而自适应调整的自适应遗传算法,以此来增加种群多样性,进一步快速、准确的逼近全局最优解。
基于以上分析,本文中将控制量初末时刻值纳入优化设计变量,以终端约束中复合约束项(如速度和高度等)为判断条件,提出一种基于改进直接打靶法和自适应遗传算法的混合优化算法,并应用到高马赫数飞行器准平衡飞行段弹道优化问题中。通过仿真计算控制量及状态量,评估弹道性能,得出结论。
1 准平衡飞行段弹道优化问题
1.1 高马赫数飞行器运动学模型
忽略地球自转以及曲率影响,将地球假设为平面,分别在弹道坐标系和地面坐标系建立动力学方程和运动学方程,得到3自由度高马赫数飞行器质心运动方程组简化模型[17]:
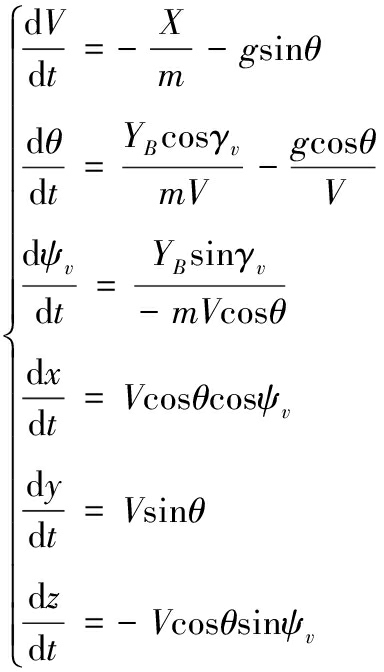
(1)
式(1)中:V(t)为飞行器速度,θ(t)和ψv(t)分别为弹道倾角和弹道偏角;y(t)为高度,x(t)和z(t)分别为纵程和横程;m(t)为飞行器质量,g为重力加速度,α(t)为攻角,γv(t)为速度倾斜角。αB为平衡攻角,βB为平衡侧滑角;YB和ZB分别为αB、βB所对应的平衡升力和平衡侧向力,X为阻力,计算表达式如下
![]()
(2)
式(2)中:Cx、Cy为阻力系数和升力系数,q=0.5*ρ*V2,其中ρ为高马赫数飞行器所处高度的空气密度,S为飞行器参考面积。
1.2 约束条件
1) 控制约束
为保证飞行器稳定飞行,控制量攻角α和速度倾斜角γv要限制在一定的范围内:
![]()
(3)
2) 过程约束
① 热流率、动压、过载约束。一般而言,高马赫飞行器在准平衡飞行过程中必须满足热流率、过载、动压等硬约束,公式表示如下
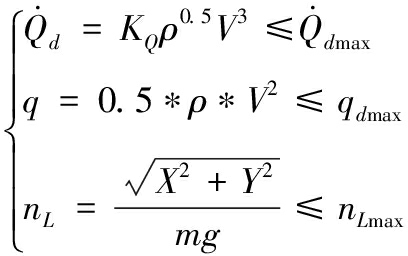
(4)
式(4)中:KQ是与飞行器相关的常值参数,可取![]() 和nLmax分别为允许的最大热流率、最大动压和最大过载。
和nLmax分别为允许的最大热流率、最大动压和最大过载。
② 禁飞区约束。禁飞区是因自然环境、政治军事因素形成的不允许飞入的区域,本文中禁飞区选取典型规则形状圆柱形,中心点为(xi,yi,zi),半径为ri,具体表达式如下
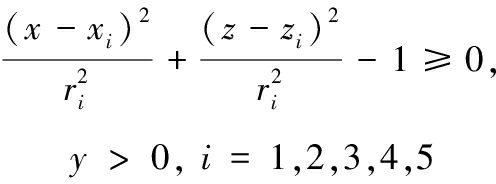
(5)
设L(x(t),t)是飞行器到禁飞区的最短距离,则禁飞区约束可表示为L(x(t),t)≥εn,其中εn为无穷小正常量[3]。
3) 终端约束。为满足中末制导交接班需求,需对准平衡飞行段终端时刻的高度、速度、弹道倾角设定约束
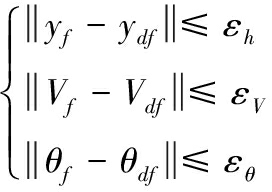
(6)
式(6)中:yf、Vf、θf分别为终端时刻的高度、速度和弹道倾角;ydf、Vdf、θdf分别为预定的终端时刻的高度、速度和弹道倾角;εh、εv、εθ分别为3个约束量的误差上界。
1.3 目标函数
一般而言,目标函数根据具体任务选定,一般可分为最大航程(最大纵程/最大横程)、飞行时间最短、终端时刻速度最大等。本文中选择最大航程(最大纵程/最大横程)为优化目标,目标函数形式如下
min J=-Ldf
(7)
式(7)中:Ldf为飞行器的航程。
1.4 问题描述
基于以上分析,高马赫数飞行器准平衡飞行段弹道优化问题可描述为:在满足质心运动方程组式(1)、控制约束式(3)、过程约束式(4)、式(5)、终端约束式(6)的条件下,寻找控制量攻角α和速度倾斜角γv最优时间序列使得目标函数式(7)最小。更一般性的最优控制问题描述如下:寻找控制变量u(t),使得Bolza型性能指标(即Mayer型和Lagrange型的组合)最小,如式(8)所示:
J=Φ[x(t0),t0,x(tf),tf]+![]() L[x(t),u(t),t]dt
L[x(t),u(t),t]dt
(8)
且满足质心运动方程组约束式(9):
![]()
(9)
边界条件约束式(10):
φ(x(t0),t0,x(tf),tf)=0
(10)
以及不等式约束(过程约束)式(11):
C(x(t),u(t),t)≤0
(11)
2 改进直接打靶法——自适应遗传算法
2.1 改进直接打靶法
直接打靶法是一种仅离散控制变量的方法,描述运动轨迹的状态变量需要根据参数化后的控制变量对运动方程组数值积分获得,对于高马赫数飞行器准平衡飞行段弹道优化问题,一般选择四阶龙格库塔法(Runge-Kutta)进行求解,以保证数值计算的精度和稳定性。需要注意的是,直接打靶法对初值要求较高,算法的精确性往往依赖于初值猜想的准确程度,可能产生局部极小的问题,为此,对直接打靶进行改进,将控制量初末时刻值一并纳入优化设计变量,以终端约束中复合约束项(如速度和高度等)为判断条件,将弹道结束时刻作为终端时刻,以此达到降低对初值敏感的目的。
1) 时间变量离散
在弹道优化问题中,一般选择单调变化物理量为参考自变量,直接打靶法中一般选择对时间进行离散,得到离散时间序列T,如式(12)所示:
t0=t1<t2<…<tk-1<tk=tf<…<tN-1<tN
(12)
本文中以终端约束中复合约束项(如速度和高度等)为判断条件,则tN可取一个较大的值,如tN=1 000 s,可令终端约束单调变化量结束时刻为tk=tf。
2) 控制变量离散
以离散节点处的控制变量为设计变量,得到离散控制序列U,如式(13)所示:
[u1,u2,…,uk-1,uk=uf,…,uN-1,uN]
(13)
时间节点之间的控制量通过插值函数ψi(t)获取,因此,连续空间的控制变量做如下近似
![]()
(14)
式(14)中:ui为网格节点处的控制变量。
3) 状态变量离散
高马赫数飞行器初始状态是已知的,即Xi,在通过优化算法得到离散控制序列U的前提下,可通过数值积分的方法,经过多次迭代积分,即可得到与时间序列对应的状态变量序列X:
[X1,X2,…,Xk-1,Xk=Xf,…,XN-1,XN]
(15)
其中,在高马赫数飞行器的弹道优化中,数值积分一般选用四阶龙格库塔法(Runge-Kutta)以保证计算精度。式(15)中:Xk=Xf为终端时刻tf对应的终端状态。
4) 最优控制问题转化
令设计变量集合如式(16)所示:
Y=[X1,u1,t1,X2,u2,t1,…,Xk-1,uk-1,tk-1,Xf,uf,tf]
(16)
式(8)所示的性能指标可以表示如下:
![]()
(17)
式(10)所示的边界条件可表示为
g1(Y)=0
(18)
式(11)所示的过程约束可表示为
g2(Y)≤0
(19)
综合式(17)—式(19),可以得到,通过改进直接打靶法弹道优化问题已经转化为经典的非线性规划问题,如式(20)所示:
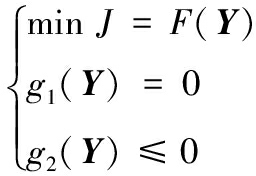
(20)
2.2 自适应遗传算法
遗传算法是一类借鉴生物界自然选择和自然遗传机制的搜索全局最优的方法,解决了众多复杂工程问题(如多目标优化等),在科学研究及工程实践中得到了广泛的应用[14,18]。遗传算法经种群初始化编码,通过选择、交叉、变异操作,实现优胜劣汰不断向最优性状进化。自适应遗传算法在遗传算法的基础上,可在适应度函数、交叉概率、变异概率等几个方面进行改进。考虑遗传算法中适应度函数的选取直接关系到收敛速度以及是否能寻找到最优解,故本文中主要针对遗传算法的适应度函数作出如下改进:① 适应度函数随着种群迭代次数的增加而自适应调整,以增加种群多样性,进一步快速、准确的逼近全局最优解。② 适应度函数进行对数变换,缩小性能指标和终端约束条件之间参数量级差距,使其更好的反应个体的优劣。③ 引入多目标分层规划方法,将多个目标按重要程度分成多个优先层次,以保证终端时刻满足终端约束的同时使性能指标最优。
具体步骤如下:
1) 种群初始化编码
自适应遗传算法首先需要进行初始化编码,将所求问题可行解表示为遗传空间的染色体或个体。本文中首先在控制约束范围内构造控制量数据集,基于改进直接打靶法按照式(12)选取若干时间点,每个节点时刻的控制量攻角和速度倾斜角构成的2个一维数组α=(α1,α2,…,αN-1,αN)、γv=(γv1,γv2,…,γvN-1,γvN)作为弹道个体的染色体,选择这种编码有几下优点:
① 控制约束式(3)可以自动满足;
② 在3自由度弹道中,当控制量攻角和速度倾斜角历程确定后可直接得到完整的弹道,若选取其他参数如弹道倾角、高度等为控制量,在迭代时都需要计算出攻角和速度倾斜角,增加了计算的时间和复杂度。
2) 插值函数
在给定的气动数据中攻角数量是有限的,需要经过插值得到更多的数据量,另外仅有节点时刻攻角值是不够的,需进行插值计算。插值的方法主要有线性插值、多项式插值、样条插值等。本文中采用三次样条插值,原因如下:
① 控制约束式(3)可以自动满足;
② 算法易实现,与线性插值相比,插值误差小于线性插值;使用样条会比使用高阶多项式更容易评估,不会受到龙格现象的影响;
③ 通过样条插值得到的攻角是一条光滑的曲线,不是线性插值的折线,利于飞行器控制系统的设计。
3) 适应度函数
适应度函数是对染色体进行评价的一种指标,也是体现自适应遗传算法“优胜劣汰”的关键之处。本文中利用Joines方法构造综合适应度函数:即基于多目标分层规划方法,将终端时刻的性能指标和终端约束加权得到适应度函数,控制约束已自动满足,其他的过程约束(动压、过载、热流率及禁飞区),可令不满足最大动压qdmax、最大过载nLmax、最大热流率![]() 和穿越禁飞区的适应度函数值设置为无穷大。Joines方法在静态罚函数的基础上进行了改进,惩罚系数随着迭代次数的增加而自适应的调整。具体形式为
和穿越禁飞区的适应度函数值设置为无穷大。Joines方法在静态罚函数的基础上进行了改进,惩罚系数随着迭代次数的增加而自适应的调整。具体形式为
![]()
(21)
式(21)中:R1=(cd)λ,fi(x)为违反第i个终端约束的惩罚函数项,pi为第i个终端约束惩罚项的权重系数,c、λ、ϑ均为常数,d为迭代次数。J为弹道优化目标函数项,q为相应的权重系数,K为常数(保证适应度为正即可)。经数值仿真验证,取c=0.5,λ=ϑ=2是比较可行的方案。另外在综合适应度函数中,终端约束项之间经过对数处理差距较小,因此主要调节下一层级性能指标权重系数q即可。
4) 选择操作
从种群中选择优胜个体,淘汰劣质个体的操作叫做选择。选择操作的目的是将优化个体直接遗传给下一代或者通过配对交叉产生新个体再遗传给下一代,通常选择轮盘赌法,设种群规模为Q,其中个体i的适应度为Fi,则第i个个体被选择的概率如式(22)所示:
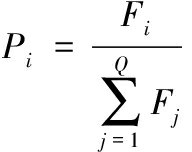
(22)
5) 交叉操作
交叉操作是体现自适应遗传算法全局搜索能力强的核心步骤,其根据交叉概率将两个染色体交叉组合,以期望父代优秀个体优秀特征遗传给子代,产生新的优秀个体。本文中选用实数交叉法,即第k个染色体ak和第l个染色体al在j位的交叉操作为
![]()
(23)
式(23)中:b为[0,1]的随机数。
6) 变异操作
变异操作的目的有2个,一是增强自适应遗传算法的局部寻优能力,二是维持种群多样性,以防止未成熟收敛现象。第i个个体的第j个基因aij变异操作为
![]()
(24)
式(24)中:amax、amin分别为基因aij的上界和下界; f(g)=r2(1-g0/Gmax)2,r2是一个随机数,g0是当前迭代次数,Gmax为最大进化次数,r是[0,1]的随机数。
2.3 混合优化算法
综前文所述,本文中提出的高马赫数飞行器准平衡飞行段弹道优化方法为混合优化算法,即改进直接打靶法-自适应遗传算法,主要包含以下步骤:
1) 利用改进直接打靶法将原弹道优化问题(原动态最优控制问题)转化为非线性规划问题;
2) 在控制约束范围内构造控制量攻角α和速度倾斜角γv数据集;
3) 将初始状态X0作为输入,将控制量初末时刻值一并纳入优化设计变量,利用自适应遗传算法优化改进直接打靶法中离散点处的控制量,并通过三次样条插值对控制量-时间历程平滑处理,以终端约束中复合约束项(如速度和高度等)为判断条件,基于四阶龙格库塔法(Runge-Kutta)进行数值积分,经过若干次迭代计算出最优控制u*,同时可以得到状态变量曲线最优轨迹X*。
算法思路框图如图1、图2所示。
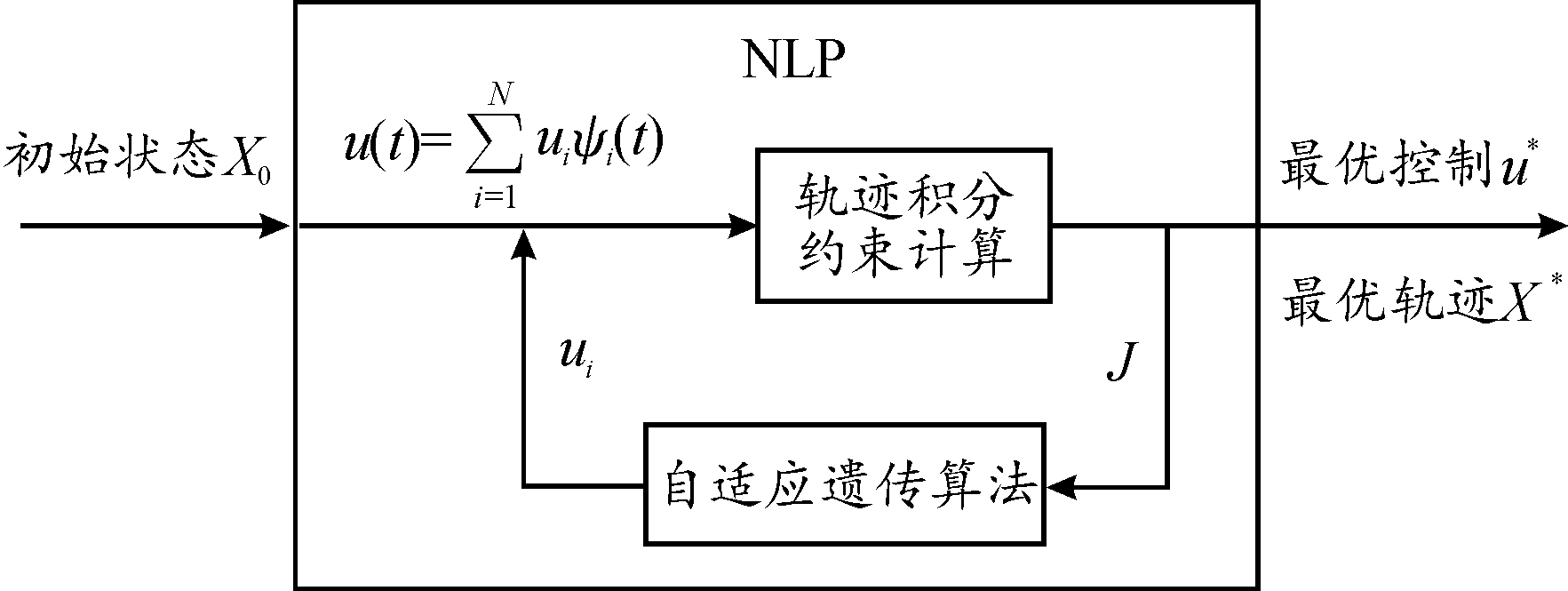
图1 改进直接打靶法求解思路
Fig.1 The solution of improved direct shooting method
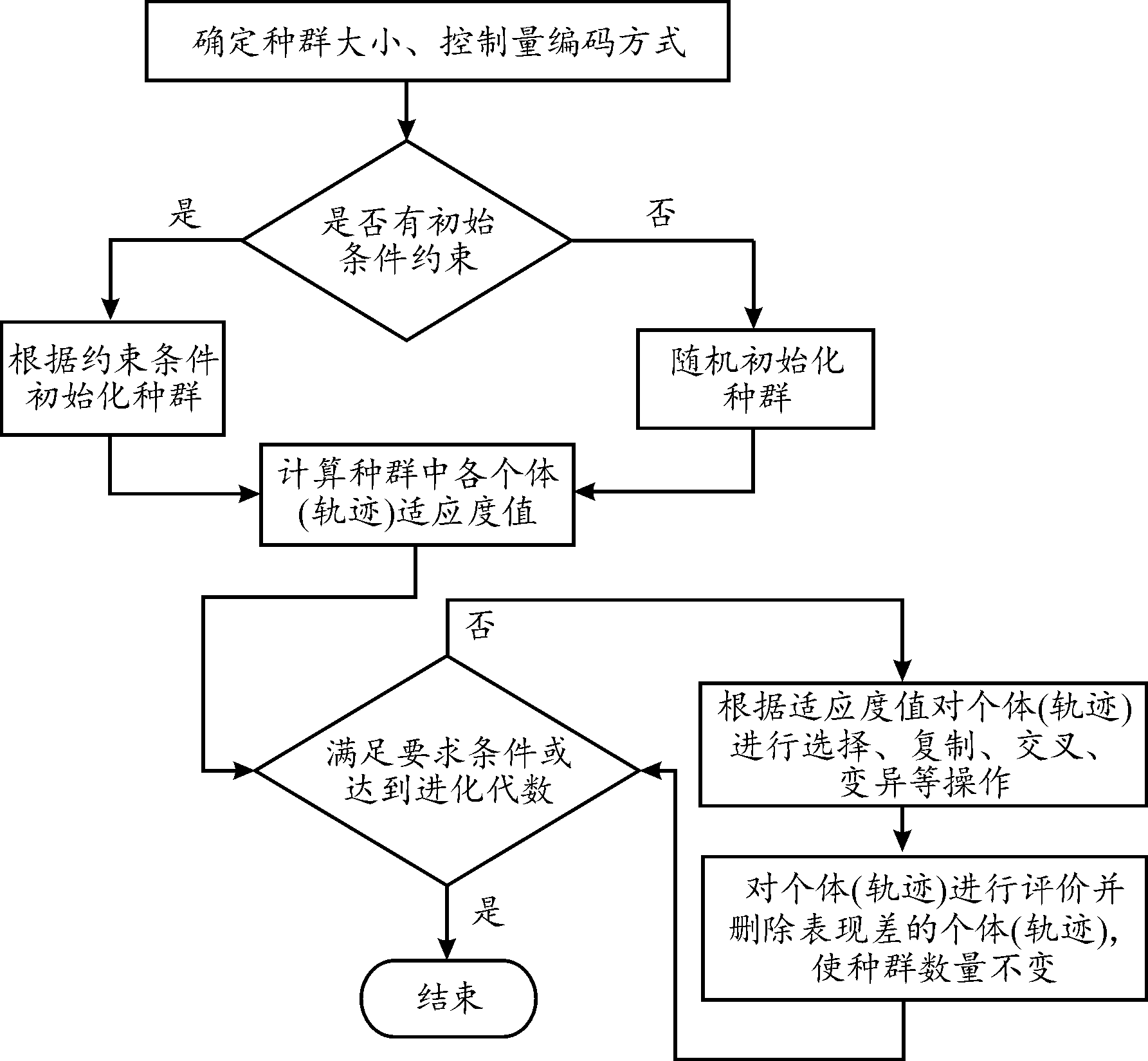
图2 自适应遗传算法流程图
Fig.2 Flow chart of adaptive genetic algorithm
3 仿真算例与分析
3.1 仿真相关参数
飞行器和地球基本参数如表1所示。控制约束如表2所示。过程约束如表3所示。边界约束(初始状态和终端状态)如表4所示。
表1 仿真基本参数
Table 1 Simulation basic parameters
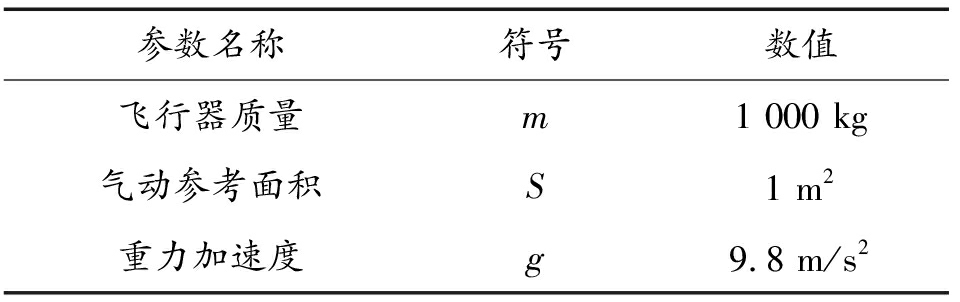
参数名称符号数值飞行器质量m1 000 kg气动参考面积S1 m2重力加速度g9.8 m/s2
表2 控制约束
Table 2 Control constraints
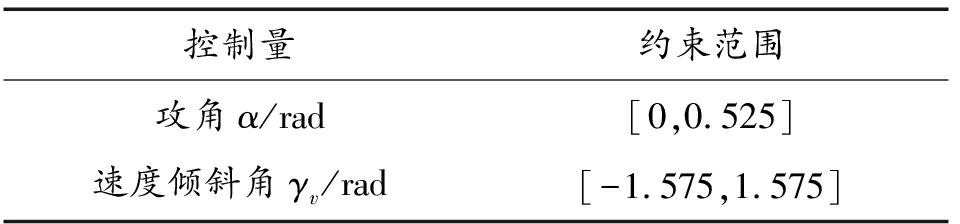
控制量约束范围攻角α/rad[0,0.525]速度倾斜角γv/rad[-1.575,1.575]
表3 过程约束
Table 3 Process constraints

最大热流率Q·dmax/(kW·m-2)最大动压qdmax/kPa最大过载nLmax/g禁飞区中心点/km半径/km60020010禁飞区1(260,0,105)100禁飞区2(100,0,200)100禁飞区3(260,0,-105)100禁飞区4(100,0,-200)100禁飞区5(500,0,0)100
表4 边界约束(初始状态和终端状态)
Table 4 Boundary constraints(initial and terminal states)

边界条件速度V/(m·s-1)弹道倾角θ/rad弹道偏角ψv/rad纵程x/km高度y/km横程z/km初始状态10 Ma000500终端状态3 Ma±40 m/s-0.052 5±0.052 527 km±1 000 m
注:初始状态高度50 km对应的速度10 Ma≈3 297.99 m/s,终端状态高度27 km对应的速度3 Ma≈899.40 m/s。
自适应遗传算法主要参数如表5所示。
表5 自适应遗传算法主要参数
Table 5 The main parameters of the adaptive genetic algorithm
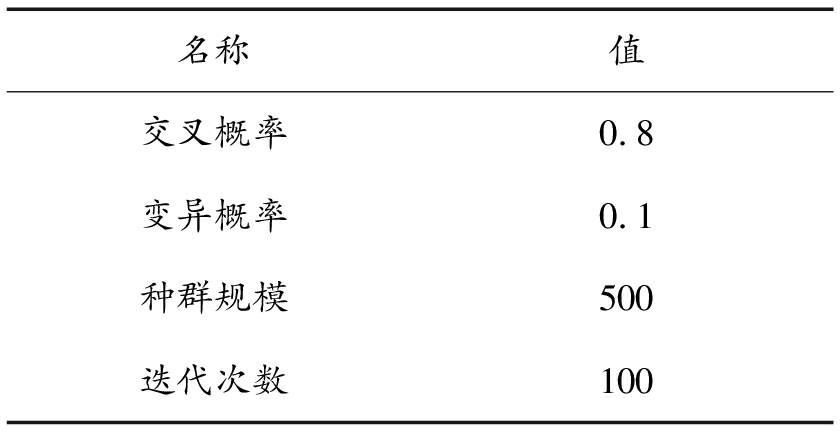
名称值交叉概率0.8变异概率0.1种群规模500迭代次数100
本文中设计的自适应遗传算法主要针对遗传算法中适应度函数进行改进,其他参数可在以下范围内进行设定:种群规模:20~100;迭代次数:100~500;交叉概率:0.4~0.99;变异概率:0.000 1~0.1[19]。为防止早熟,一般采用增大变异率或增加种群数量的方式来解决,故变异率可选范围内的最大值,种群数量可以适当的增加,迭代次数选择范围内最低值以减少计算量,交叉操作是体现自适应遗传算法全局搜索能力的核心,可取较大值,具体如表5所示。
为了验证构建的改进直接打靶法-自适应遗传算法的鲁棒性,将实际飞行过程中气动参数视为不确定性较为合理[20]。不失一般性,在原气动参数的基础上,引入正态分布白噪声,具体公式如下
![]()
(25)
式(25)中:f(xi)代表原气动系数(包含升力系数Cx和阻力系数Cy升力系数),fδ(xi)是添加了噪声后的气动系数,δ为相对误差水平,![]() 是均值为0,方差为1的正态分布随机数。
是均值为0,方差为1的正态分布随机数。
3.2 最远纵程弹道优化
在以最远纵向航程为目标的弹道优化问题中,纵向航程对应x的变化,则性能指标如式(26)所示:
J0=min(-L0)=min(-x(tf))
(26)
利用原算法(即直接打靶法-遗传算法,需要不断试测初值,另外适应度函数需进行对数变换,否则较难收敛)、构建的混合算法:改进直接打靶法-自适应遗传算法以及在此基础上引入白噪声进行仿真,结果如图3—图17所示。
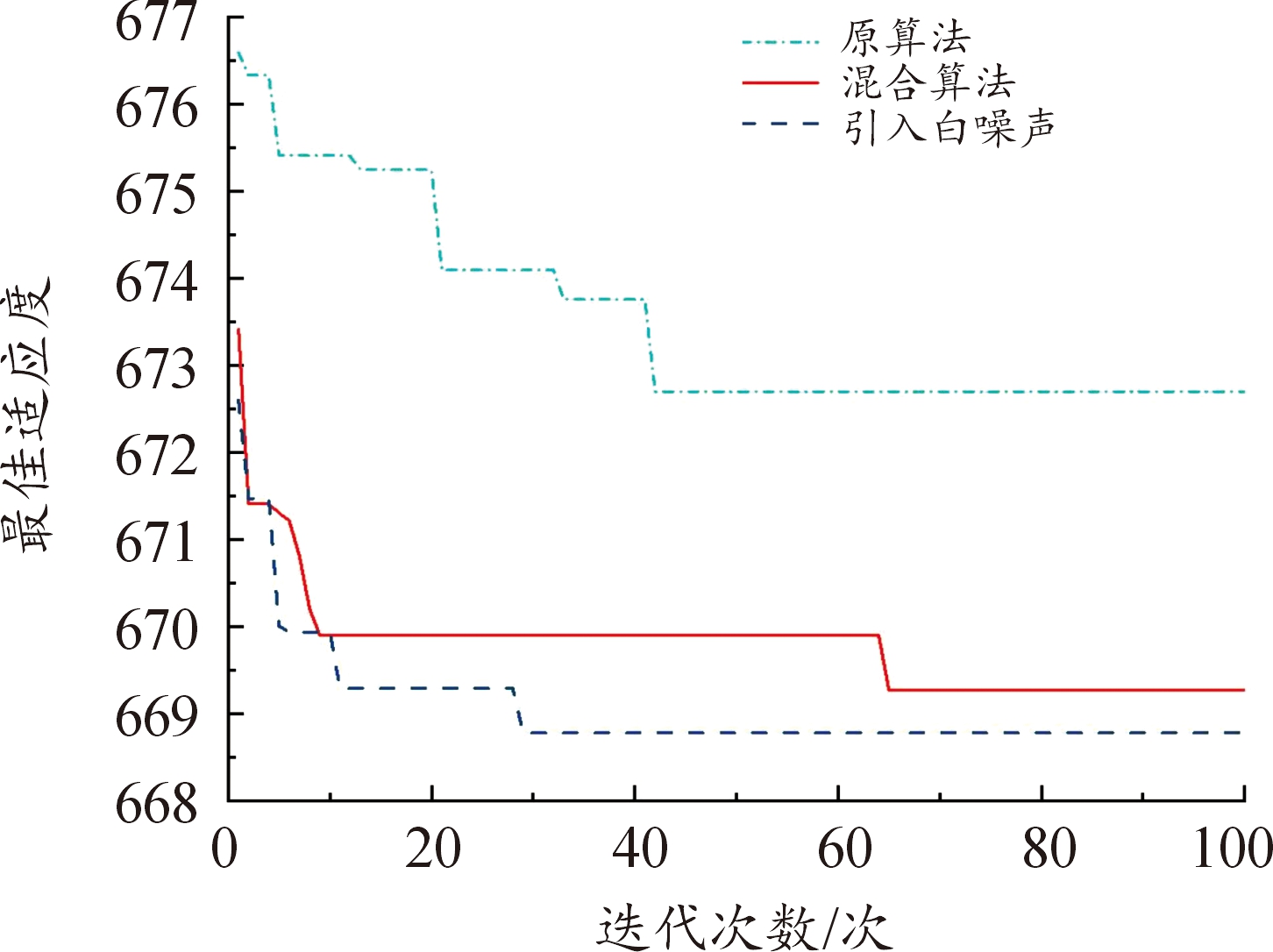
图3 最佳适应度变化曲线
Fig.3 Optimal adaptability change curve
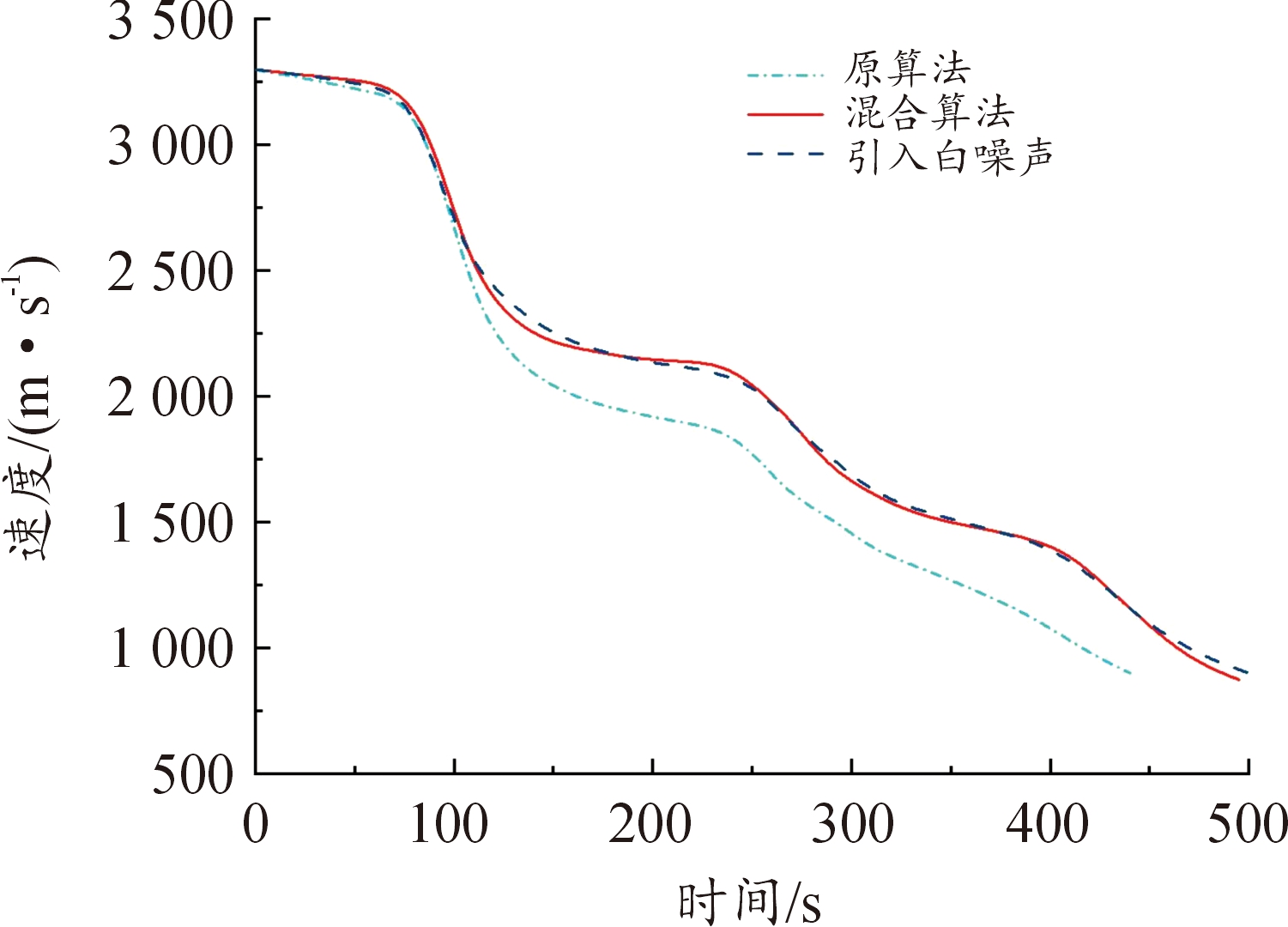
图4 速度变化曲线
Fig.4 Speed curve
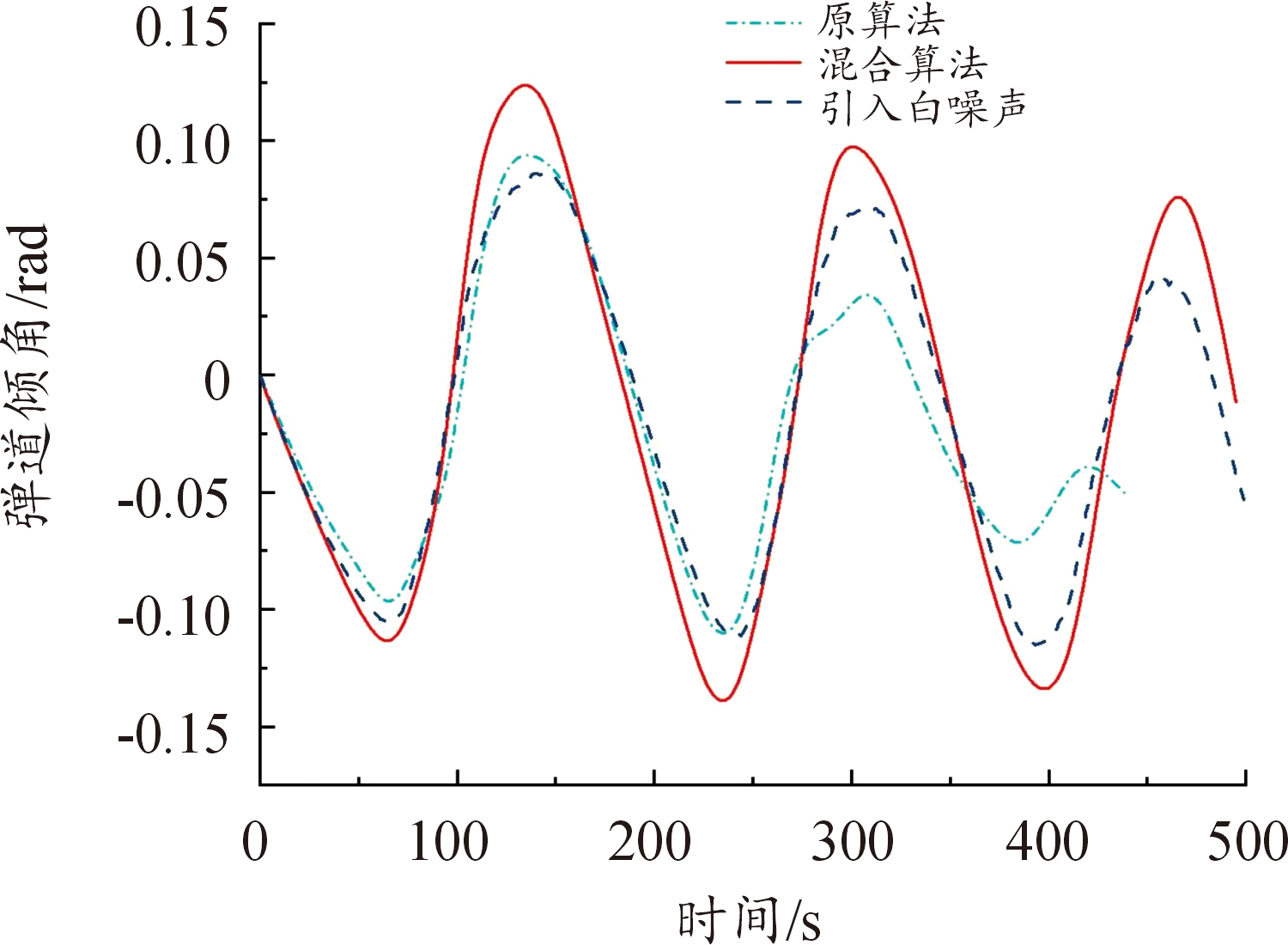
图5 弹道倾角变化曲线
Fig.5 Ballistic inclination curve

图6 弹道偏角变化曲线
Fig.6 Ballistic declination curve
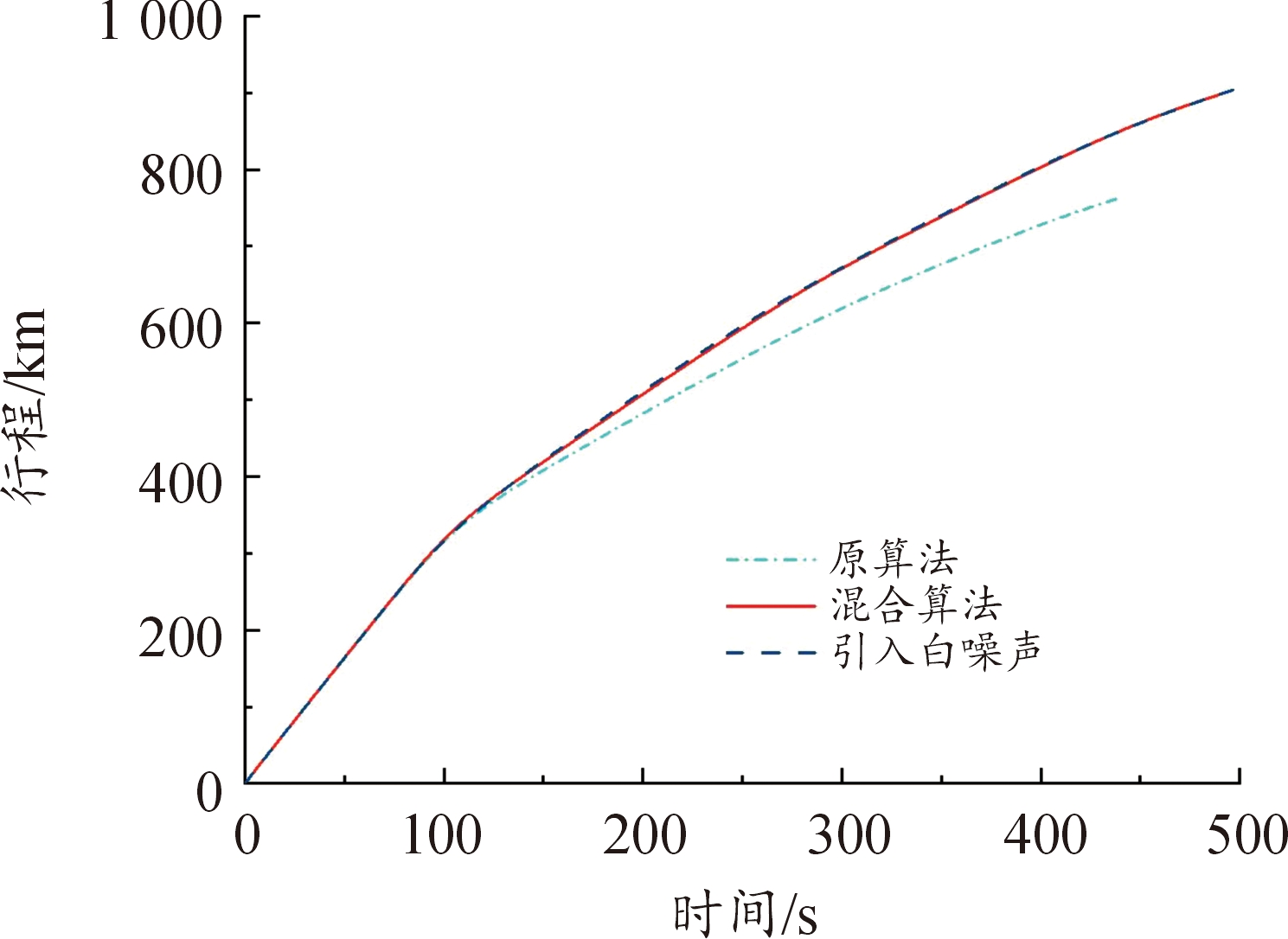
图7 纵程变化曲线
Fig.7 Longitudinal change curve
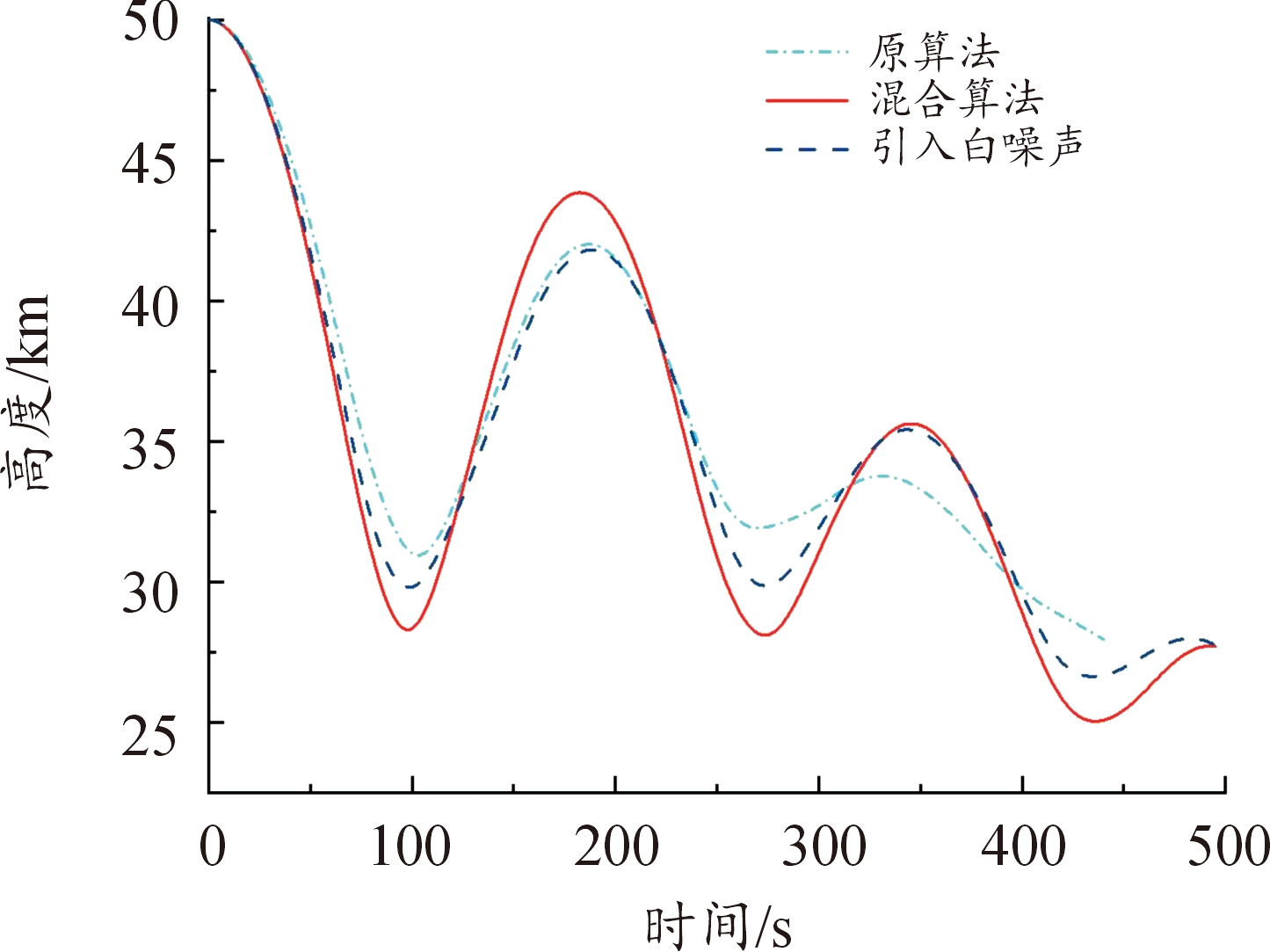
图8 高度变化曲线
Fig.8 Height change curve
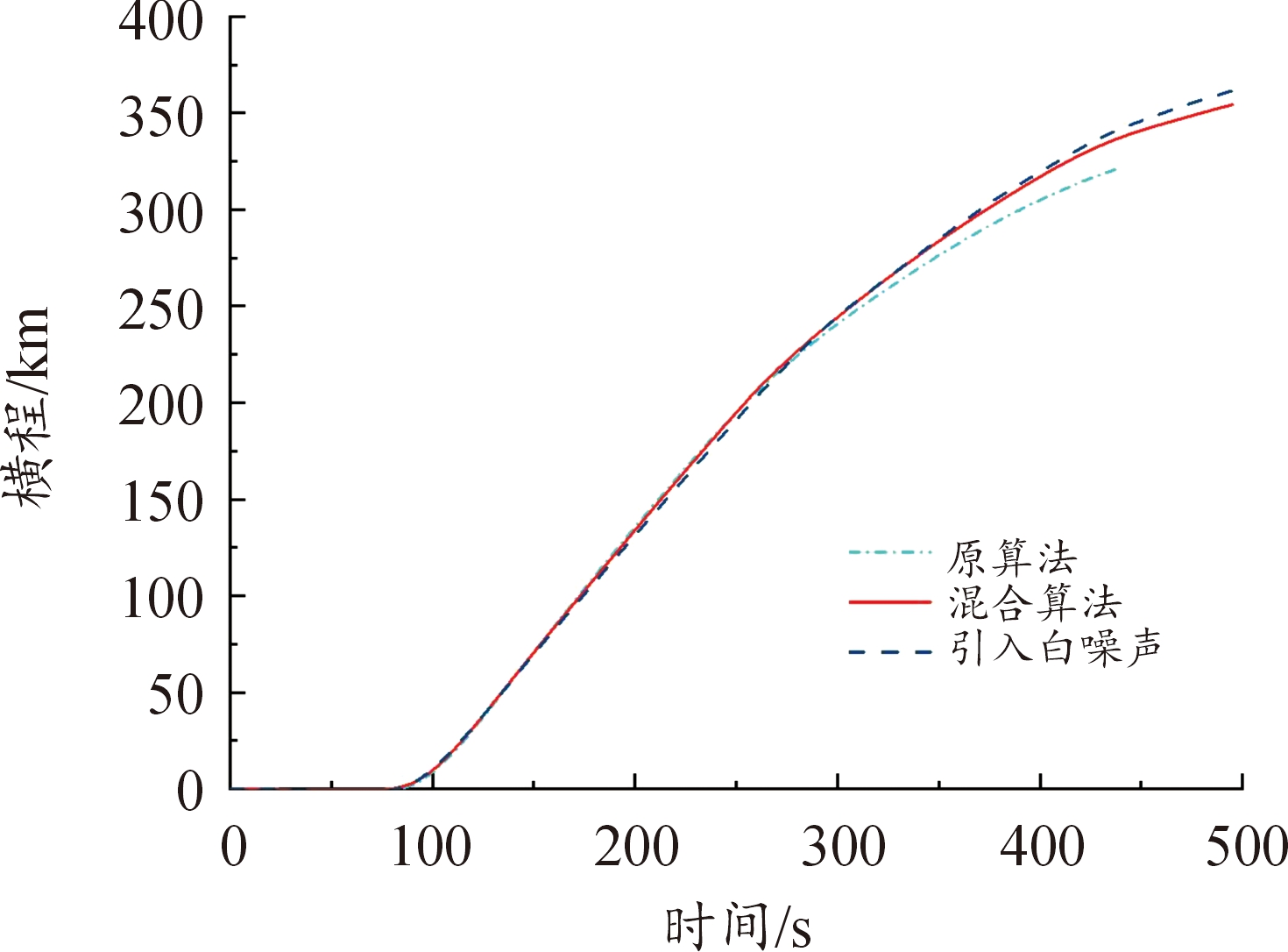
图9 横程变化曲线
Fig.9 Horizontal variation curve
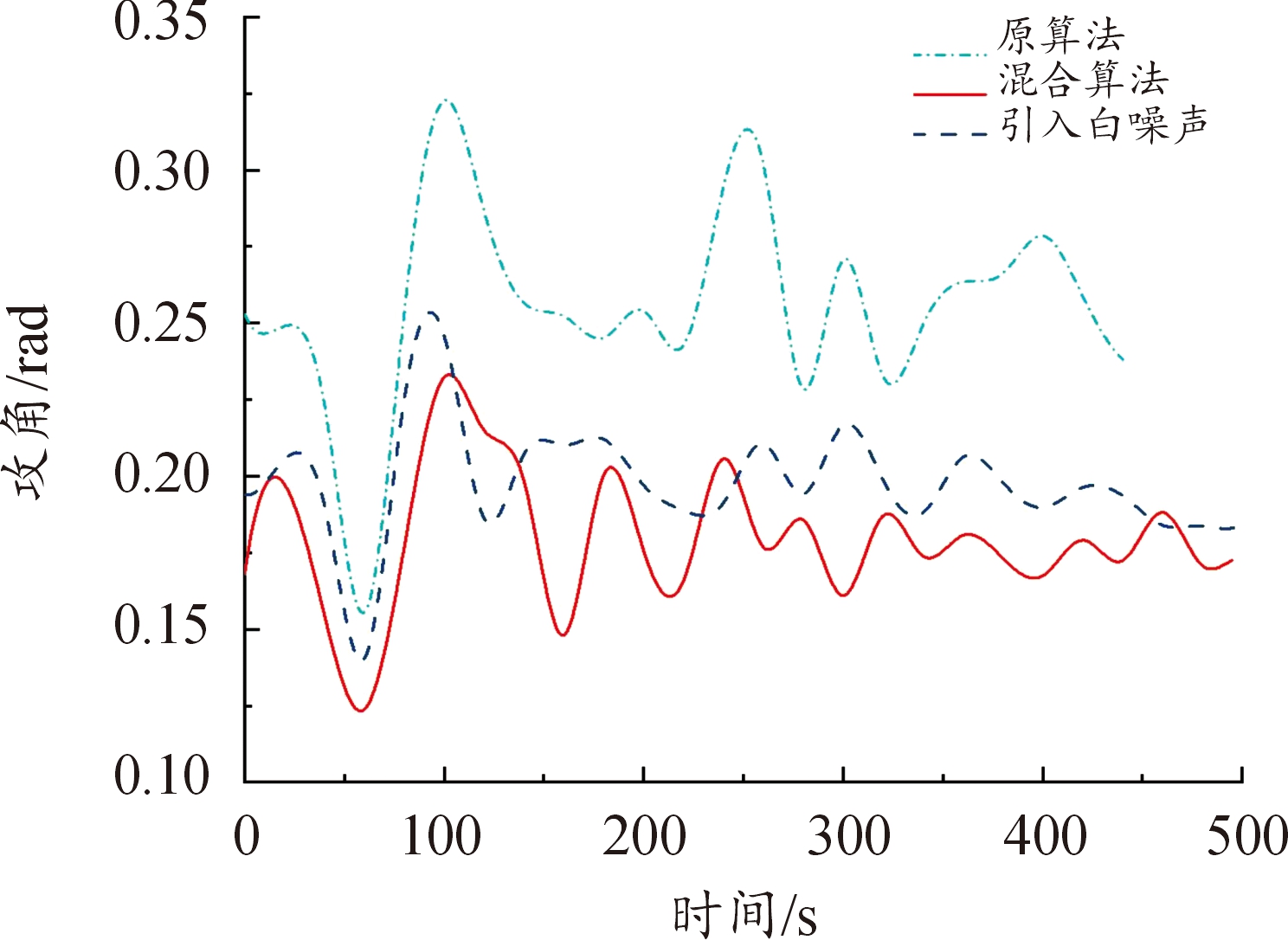
图10 攻角变化曲线
Fig.10 Angle of attack curve
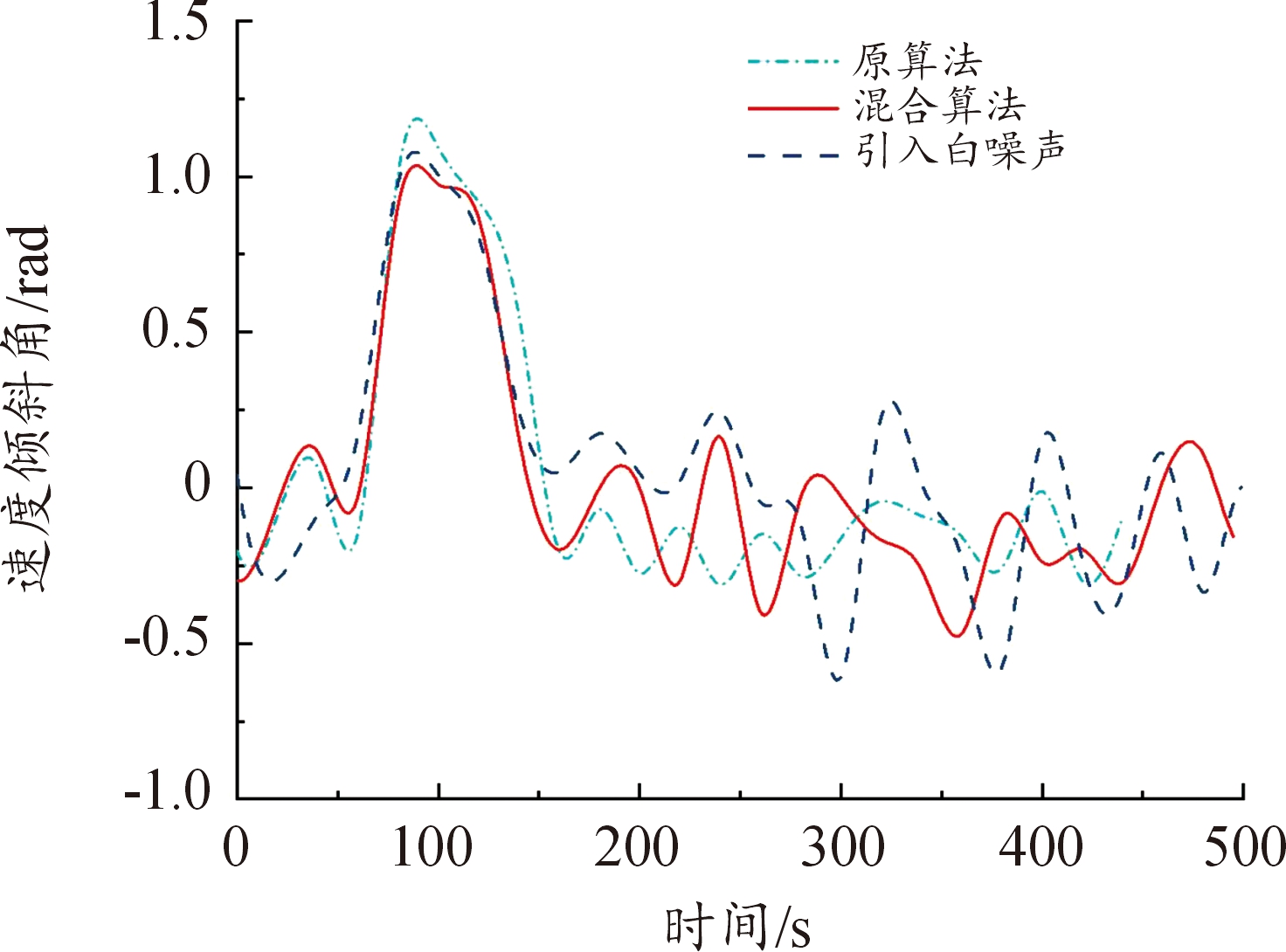
图11 速度倾斜角变化曲线
Fig.11 Velocity inclination angle variation curve
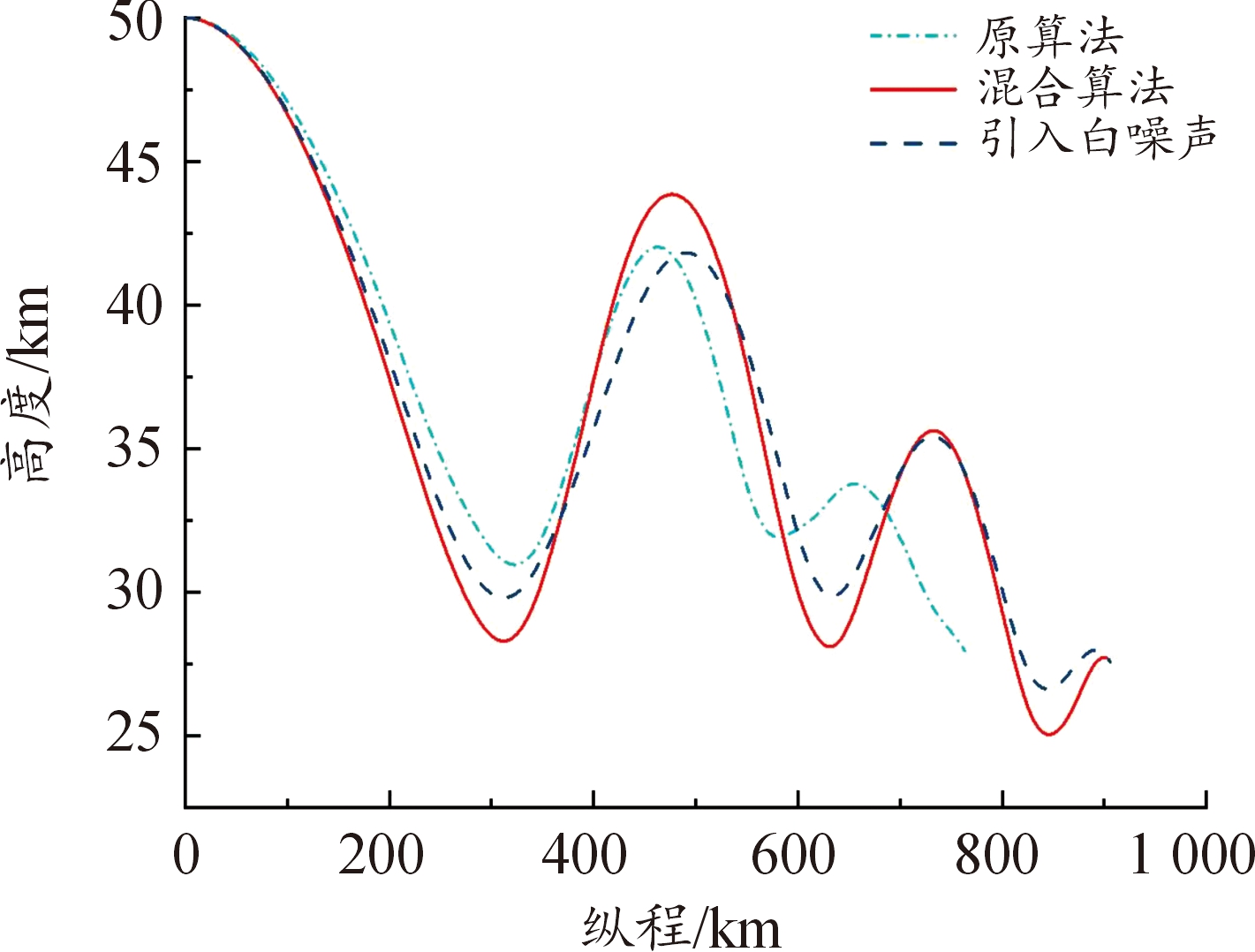
图12 高度-纵程变化曲线
Fig.12 Altitude-longitudinal change curve
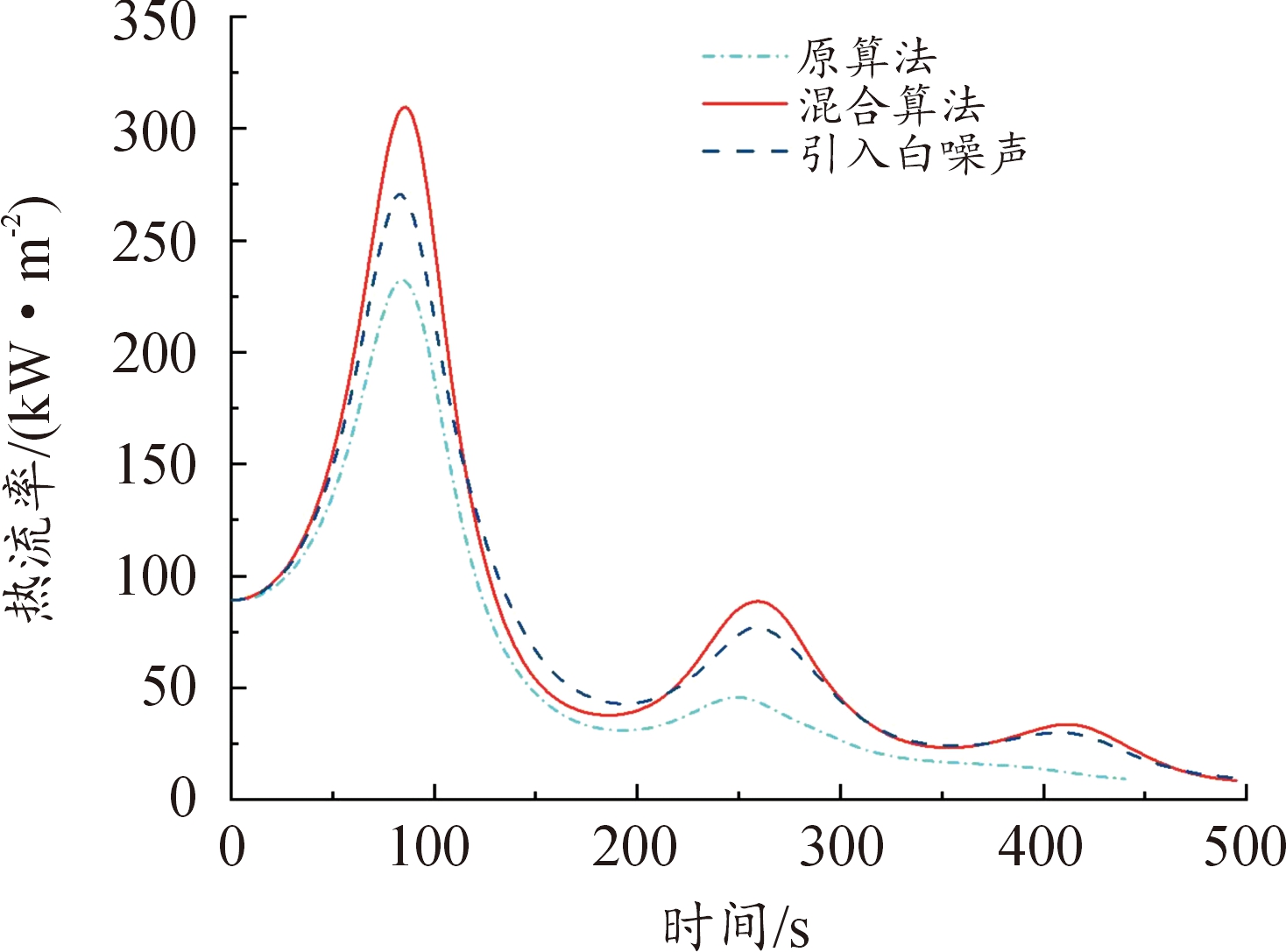
图13 热流率变化曲线
Fig.13 Heat flow rate curve change curve
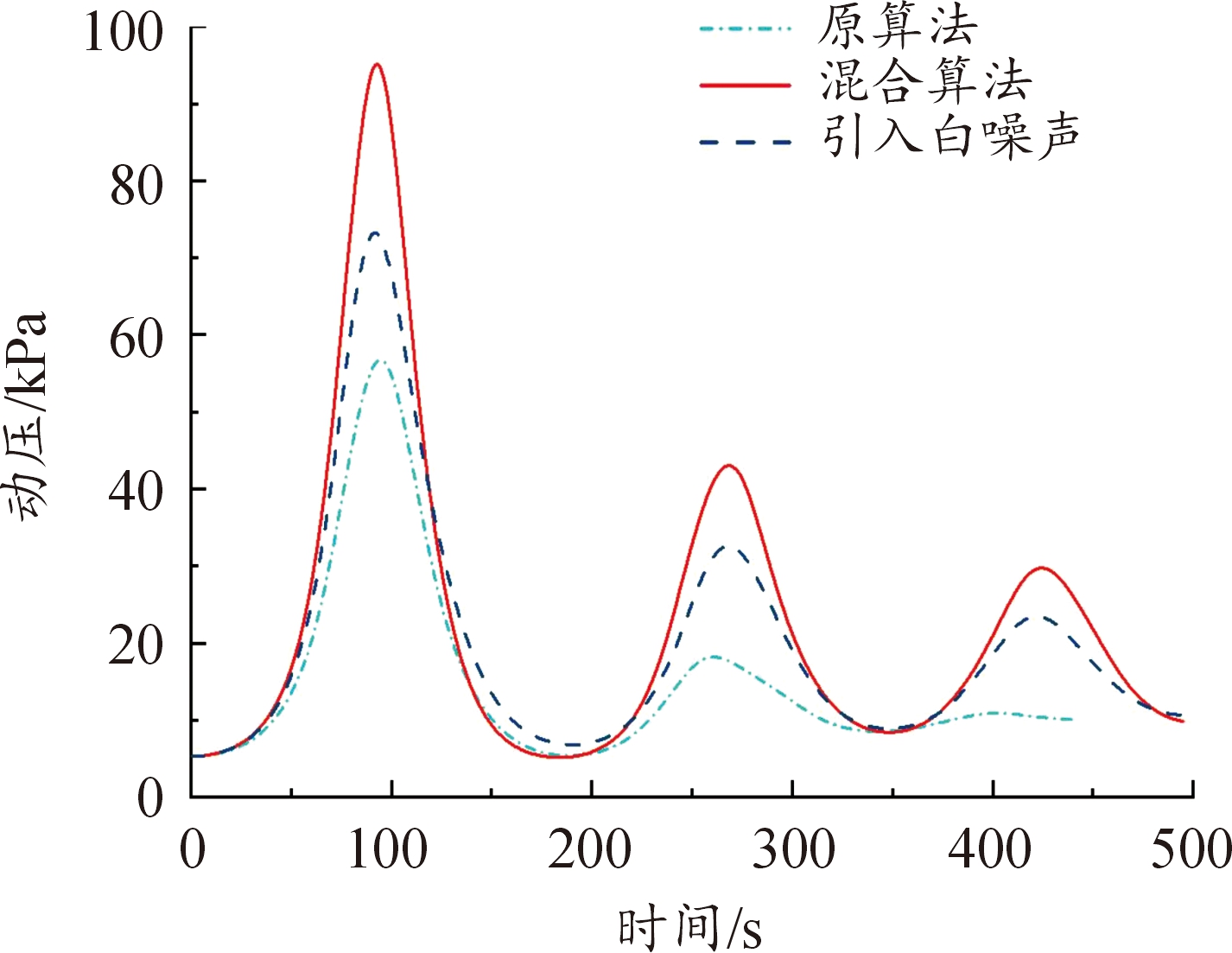
图14 动压变化曲线
Fig.14 Dynamic pressure curve
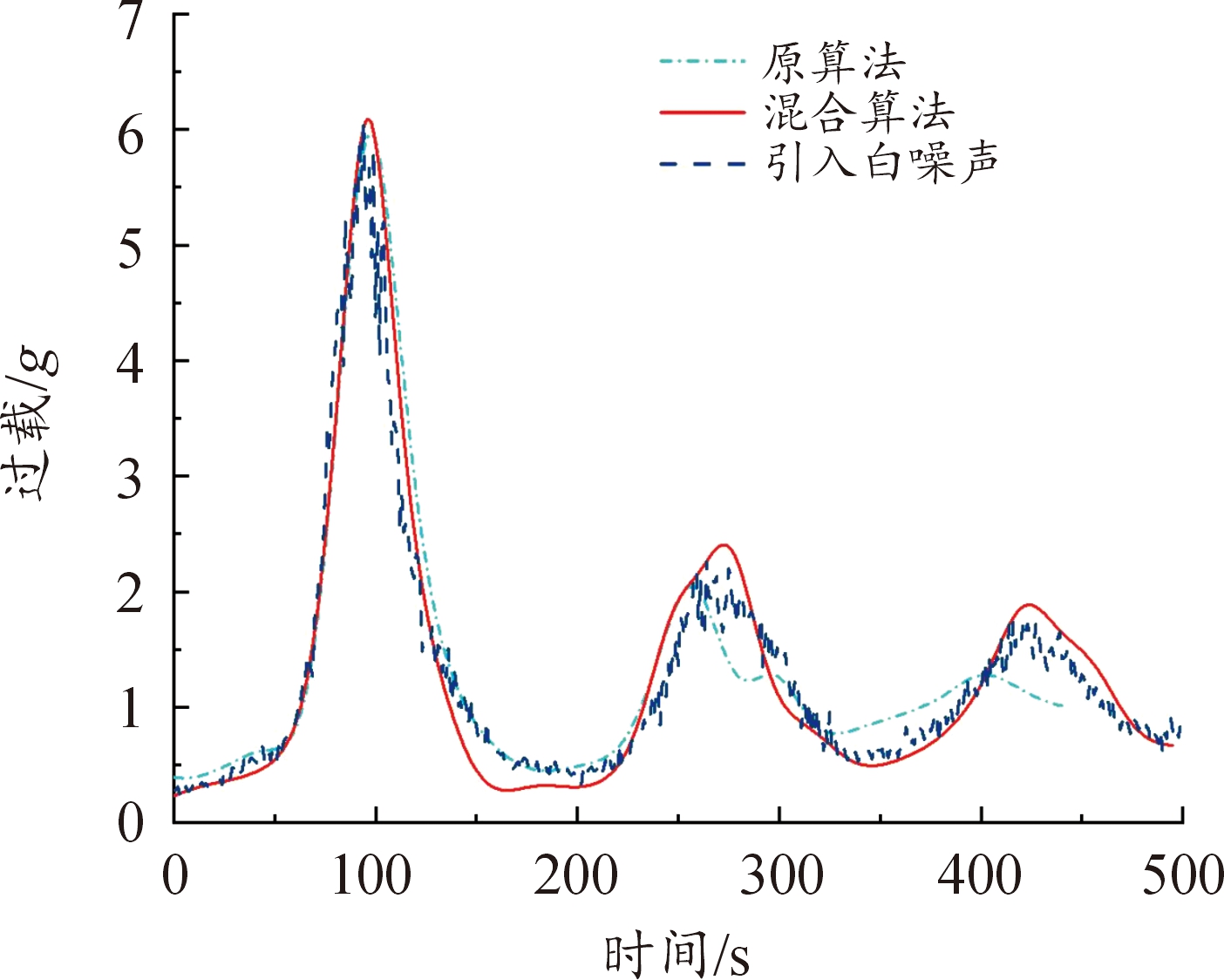
图15 过载变化曲线
Fig.15 Overload curve
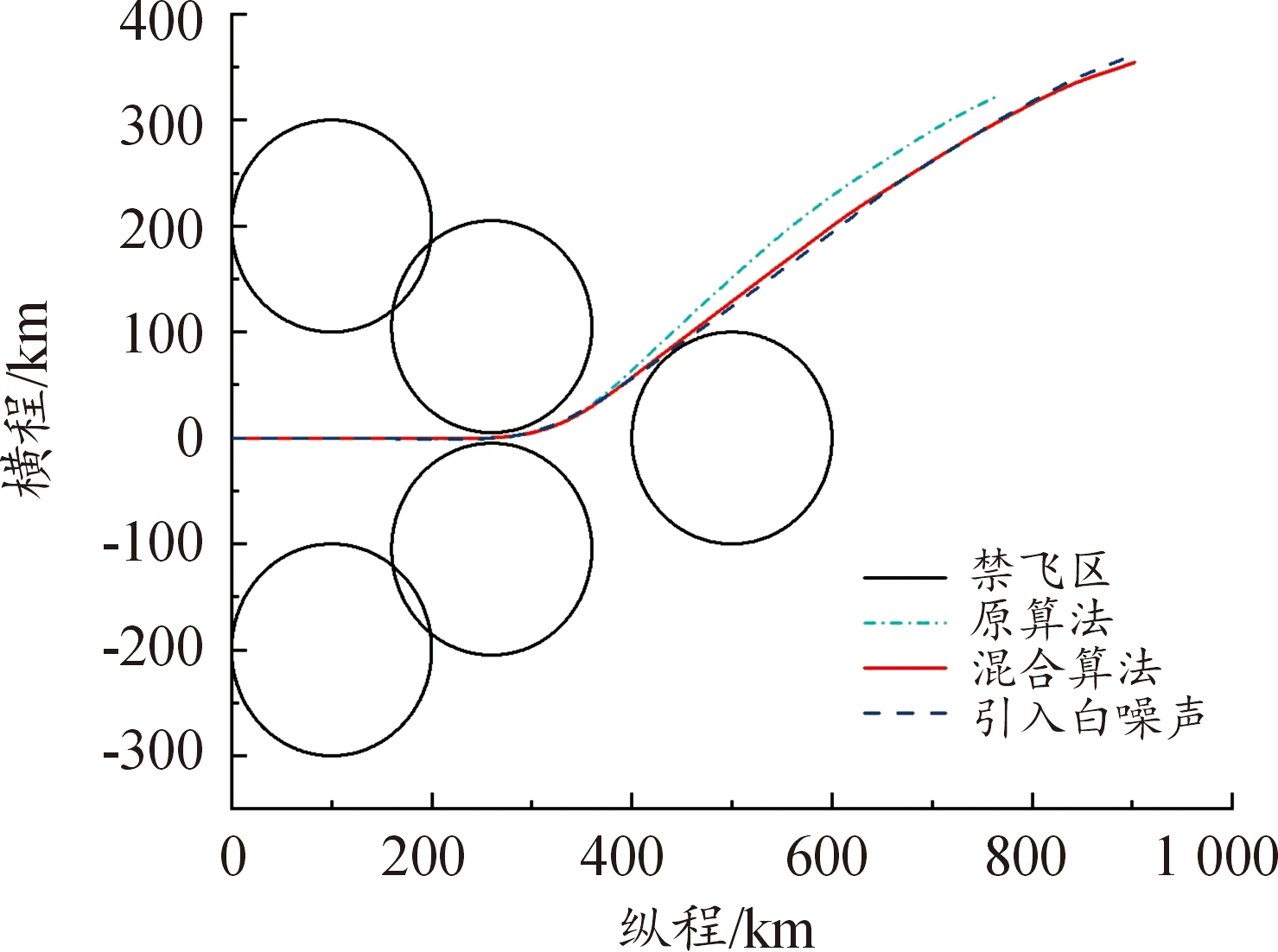
图16 规避禁飞区俯视图
Fig.16 Top view of avoiding the no-fly zone
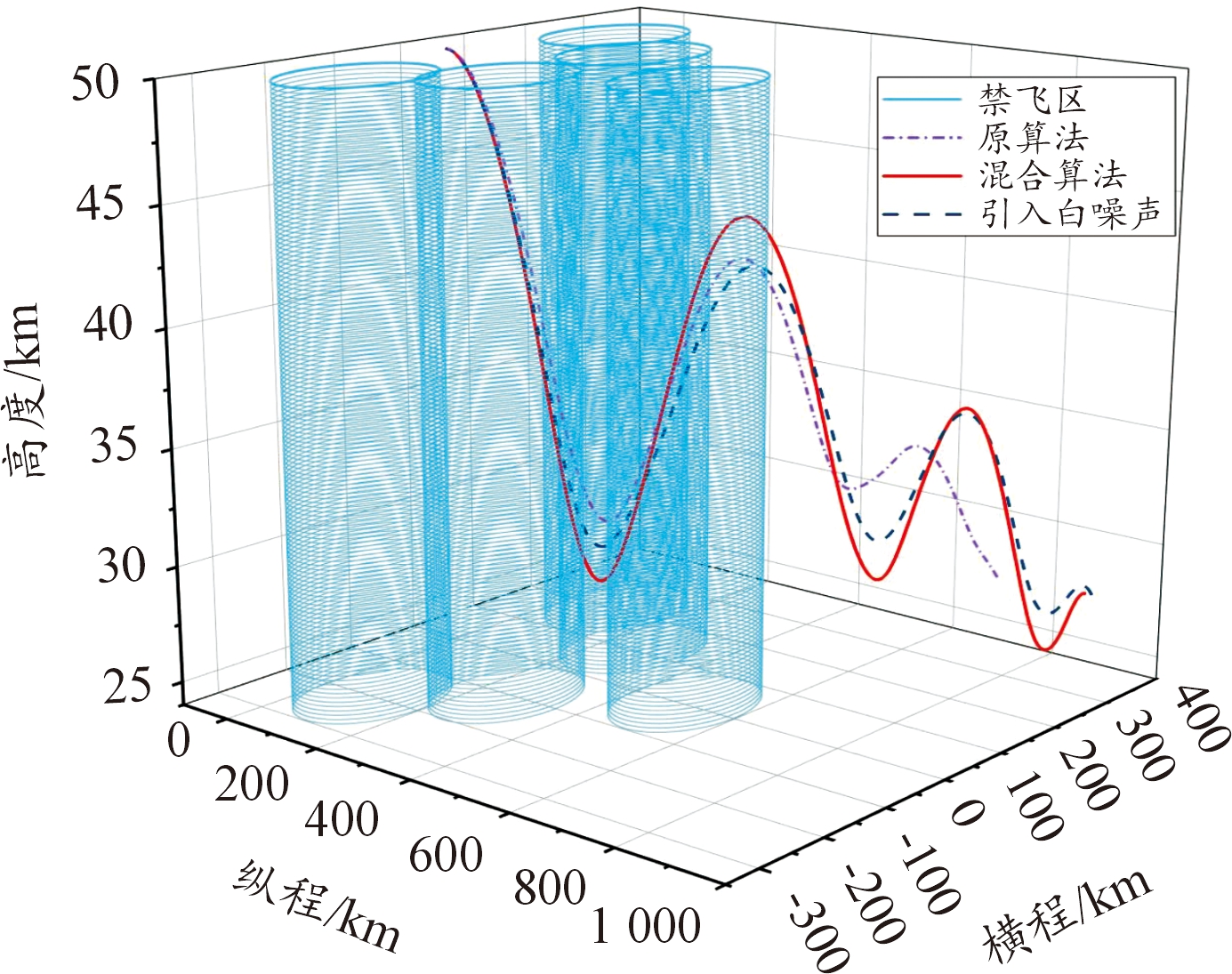
图17 规避禁飞区三维立体图
Fig.17 3D stereo map of avoiding the no-fly zon
3.3 最远横程弹道优化
在以最远横向航程为目标的弹道优化问题中,横向航程对应z的变化,则性能指标如式(27)所示:
J0=min(-L0)=min(-z(tf))
(27)
利用原算法(即直接打靶法-遗传算法,需要不断试测初值,另外适应度函数需进行对数变换,否则较难收敛)、构建的混合算法:改进直接打靶法-自适应遗传算法以及在此基础上引入白噪声进行仿真,结果如图18—图32所示。
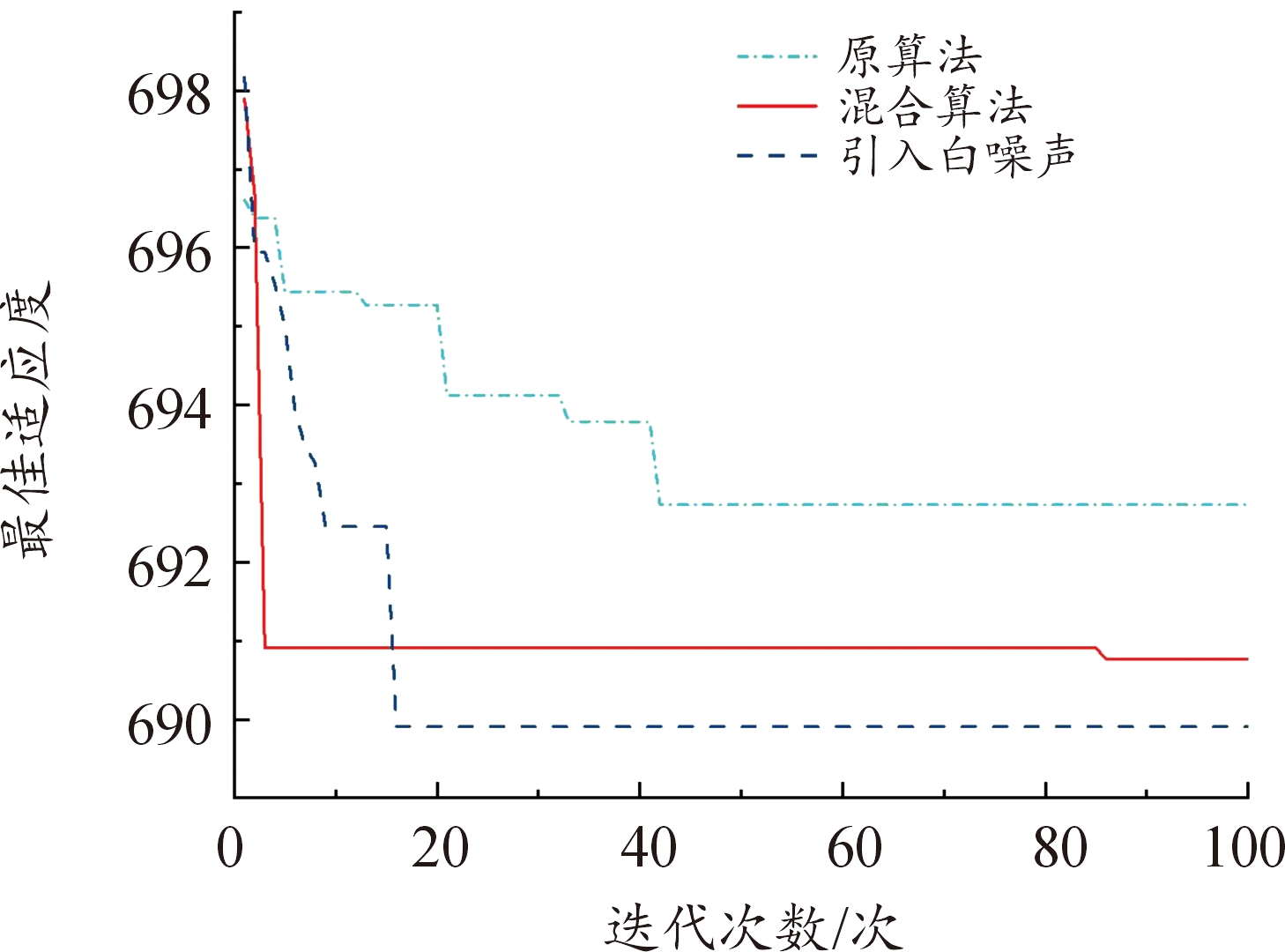
图18 最佳适应度变化曲线
Fig.18 Optimal adaptability change curve
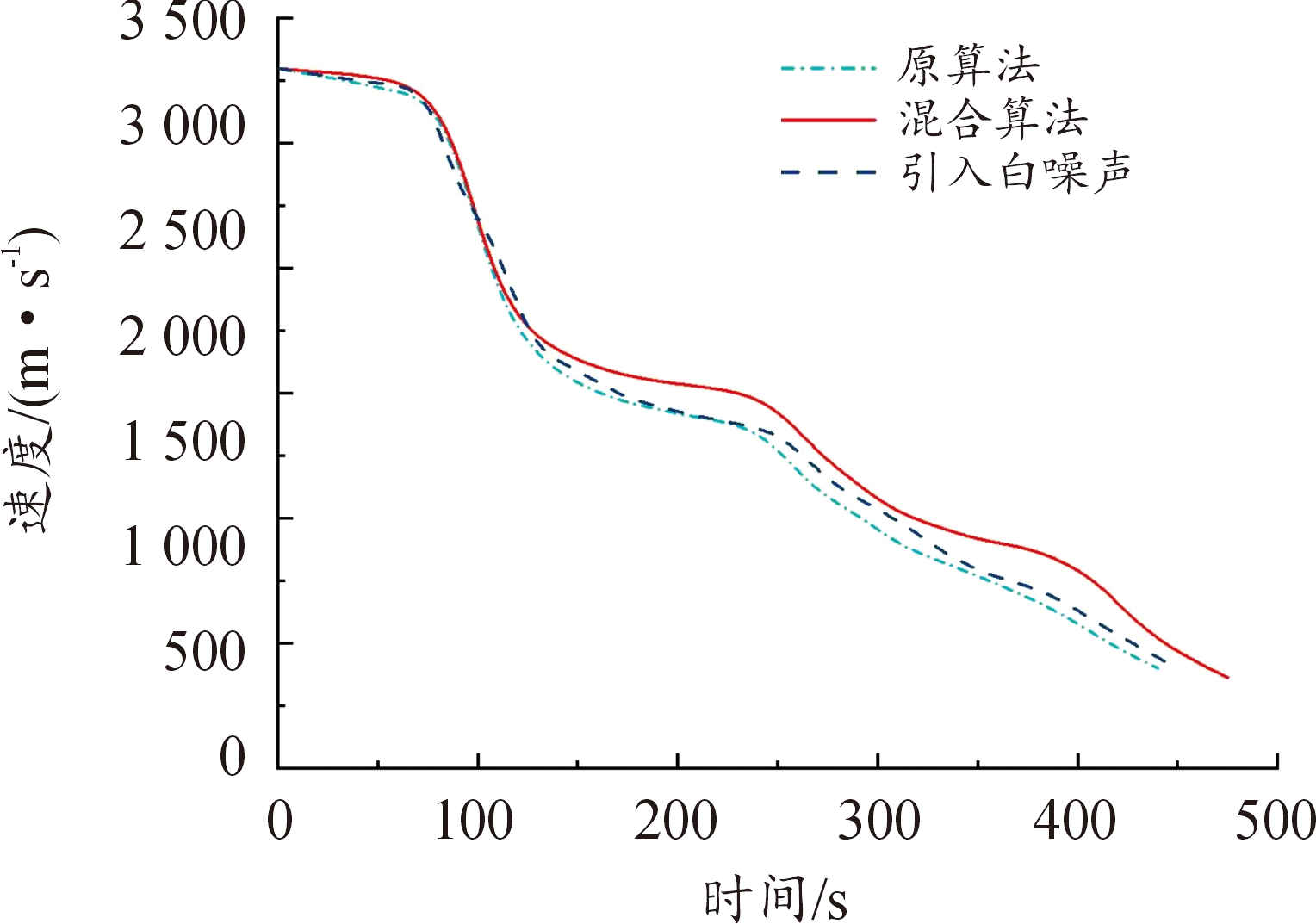
图19 速度变化曲线
Fig.19 Speed curve
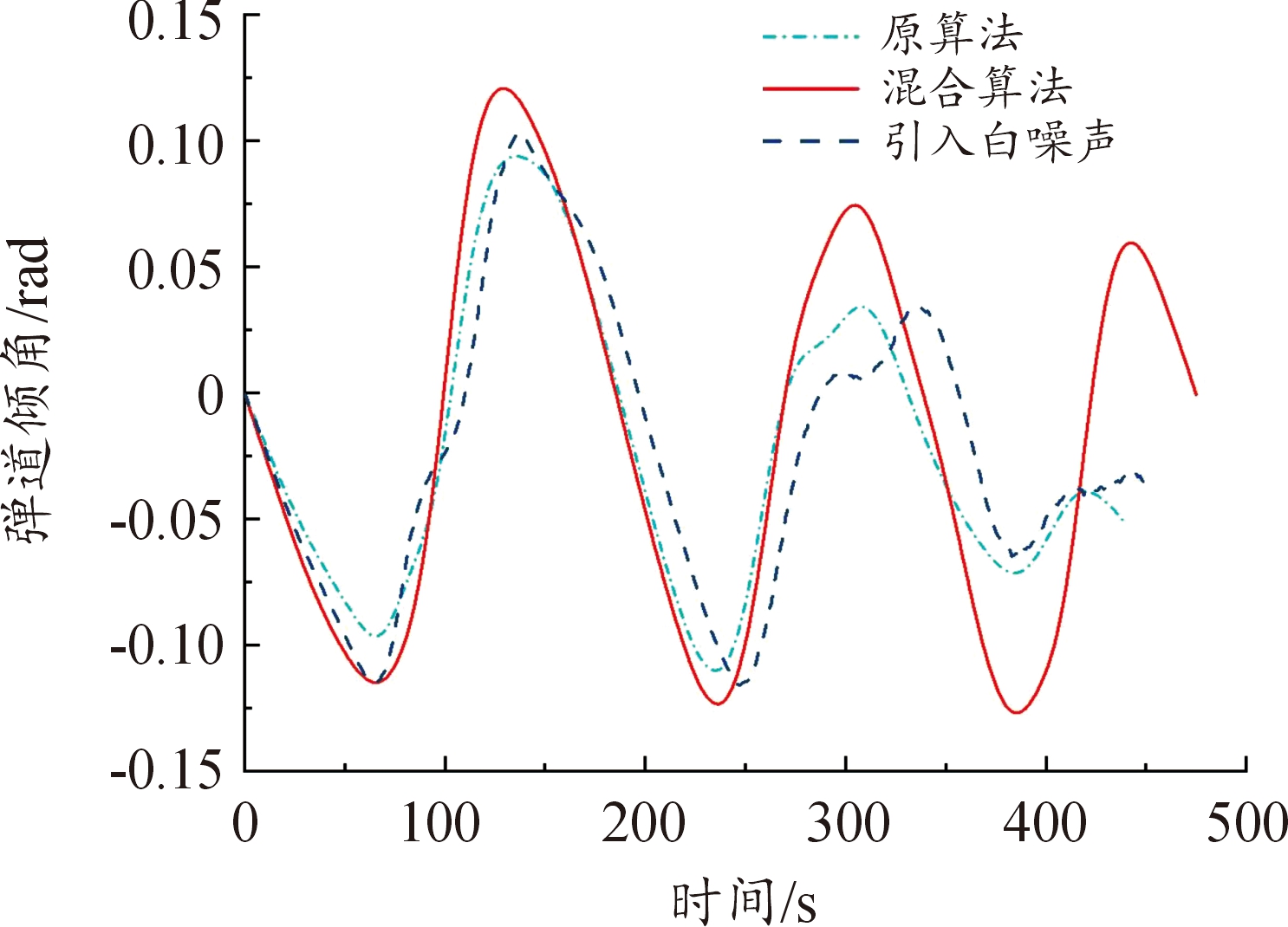
图20 弹道倾角变化曲线
Fig.20 Ballistic inclination curve
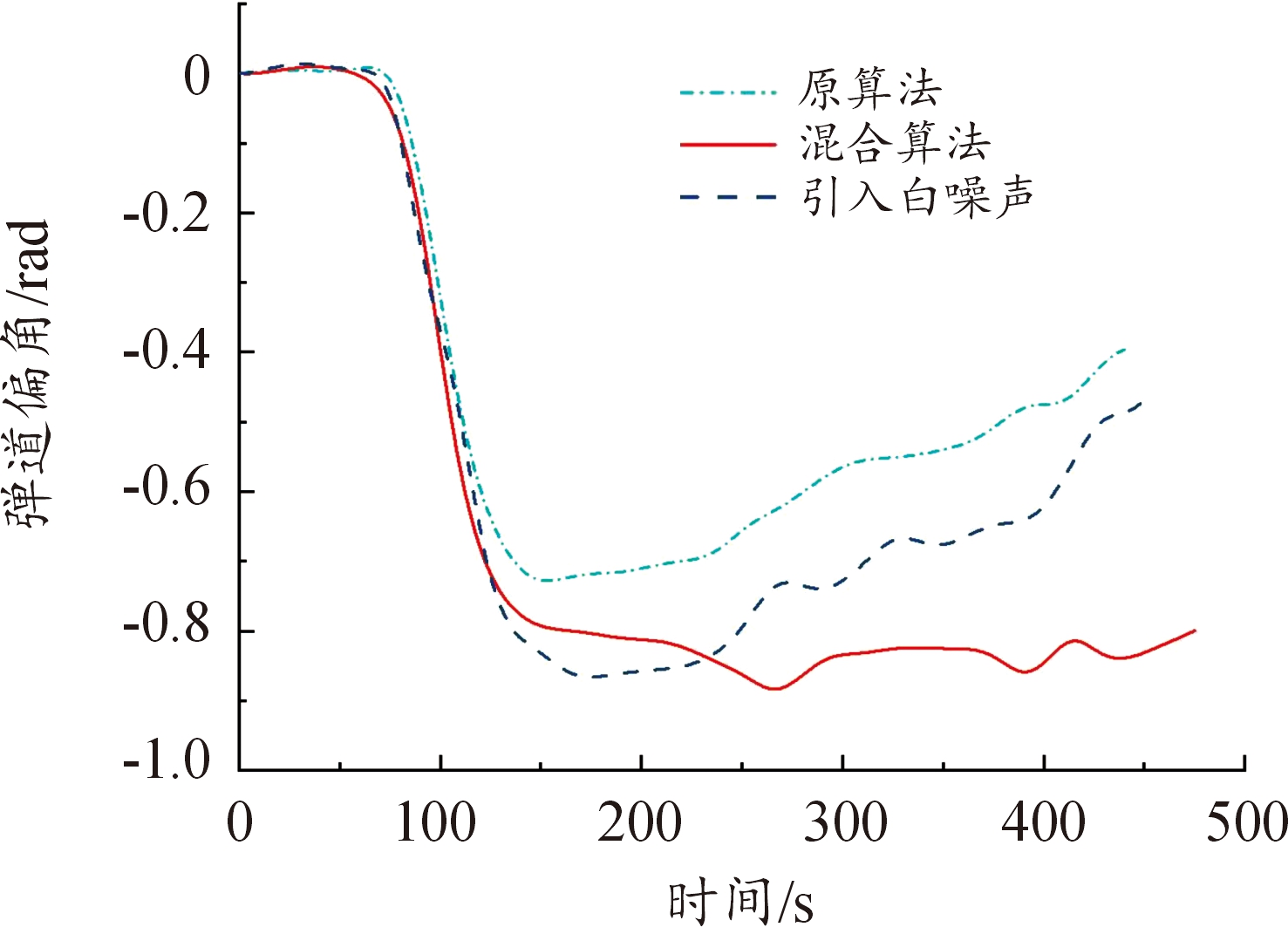
图21 弹道偏角变化曲线
Fig.21 Ballistic declination curve
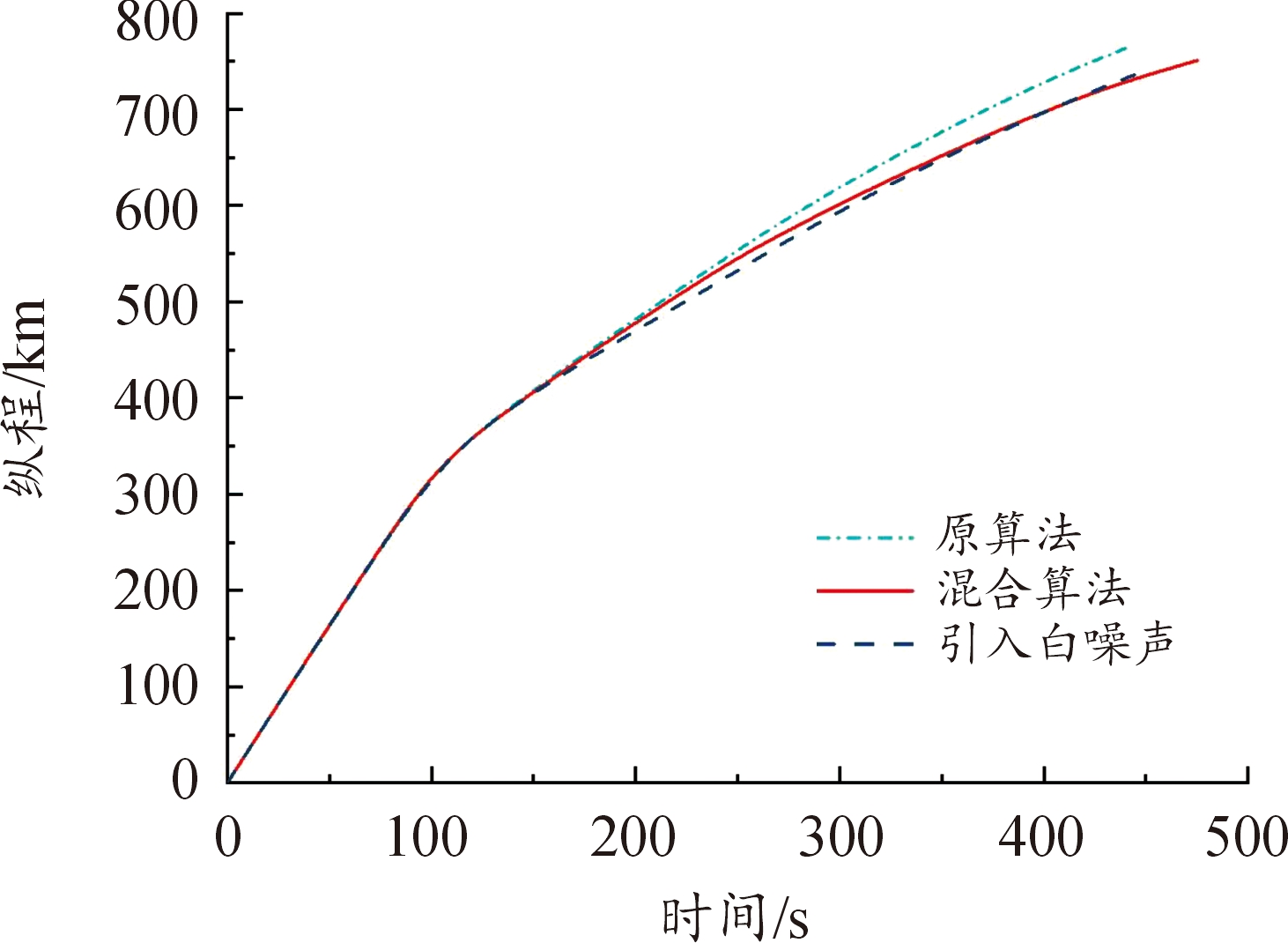
图22 纵程变化曲线
Fig.22 Longitudinal change curve
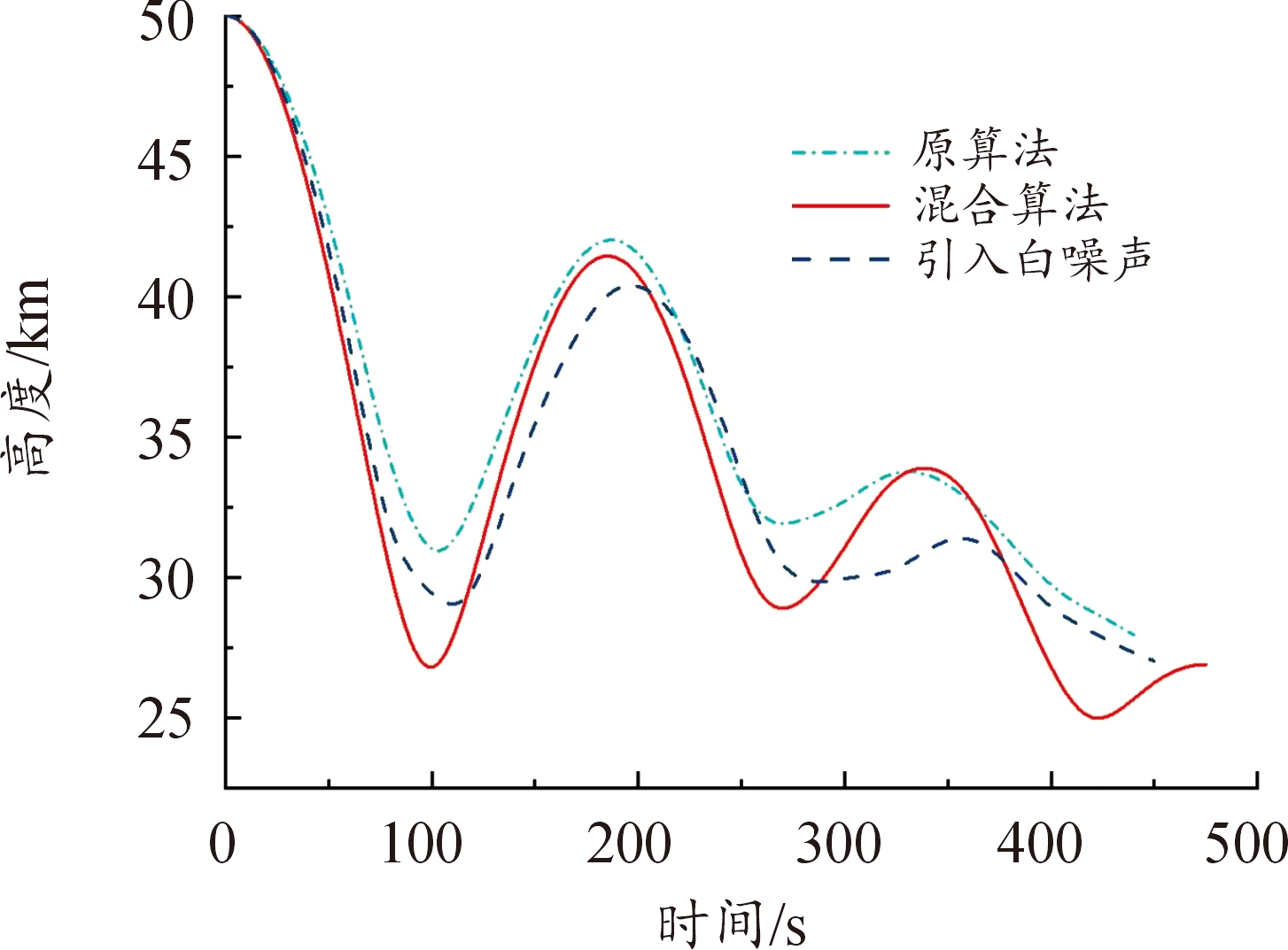
图23 高度变化曲线
Fig.23 Height change curve
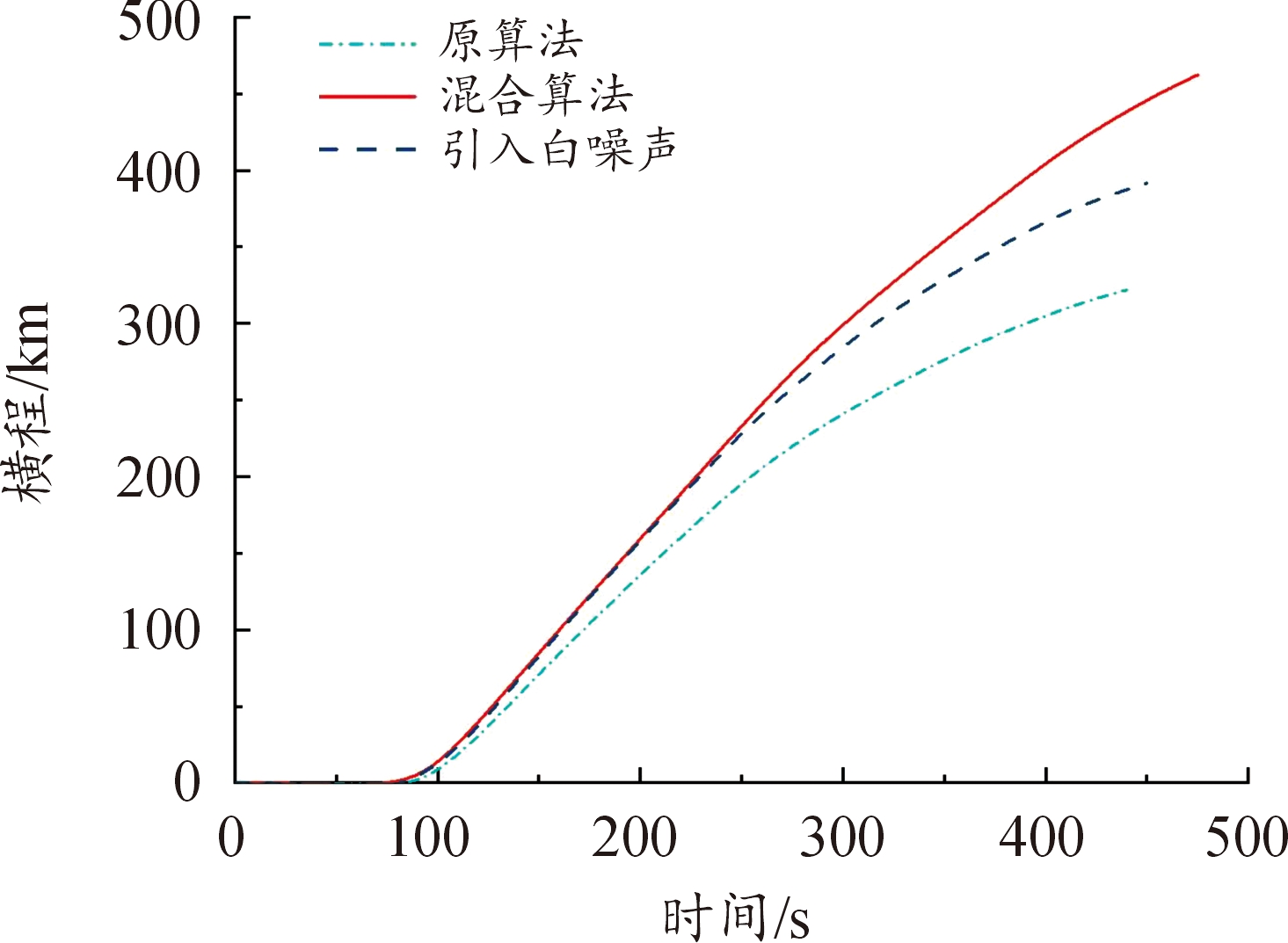
图24 横程变化曲线
Fig.24 Horizontal variation curve
图3和图18给出了种群中最佳适应度值随迭代次数变化的过程,由图可知,原遗传算法对应的适应度函数在40代左右趋于收敛,构造的自适应算法对应的最佳适应度值在初期变化较大,随着迭代次数的增加而逐渐收敛,在10代左右已经趋于平稳,后期在60~90代左右混合算法优化控制量最佳适应度函数值有些许变化,但变化较小,相较于原遗传算法收敛速度较快。这表明利用自适应遗传算法对控制变量寻优具有较好的收敛效果。
需要说明的是,原算法(直接打靶法-遗传算法)是通过大量试测初值得到的,在大部分情况下由于对初值敏感,往往得不到规避禁飞区的轨迹。而构造的混合算法将控制变量初末时刻值纳入优化设计变量,以终端约束中单调变化量(如速度)作为轨迹结束时刻的判断条件,初值不需要不断试测,效率较高。从图10—图11、图25—图26中,可以看出,构建的混合算法:改进直接打靶法-自适应遗传算法在以最远纵程/最远横程为性能指标的仿真中,控制约束在规定的范围内;图13—图15、图28—图30中,过程约束中一般约束项热流率、过载、动压也在约束范围内;图16—图17、图31—图32中,能直观看出,混合算法能够实现规避多禁飞区,满足了实际需求。
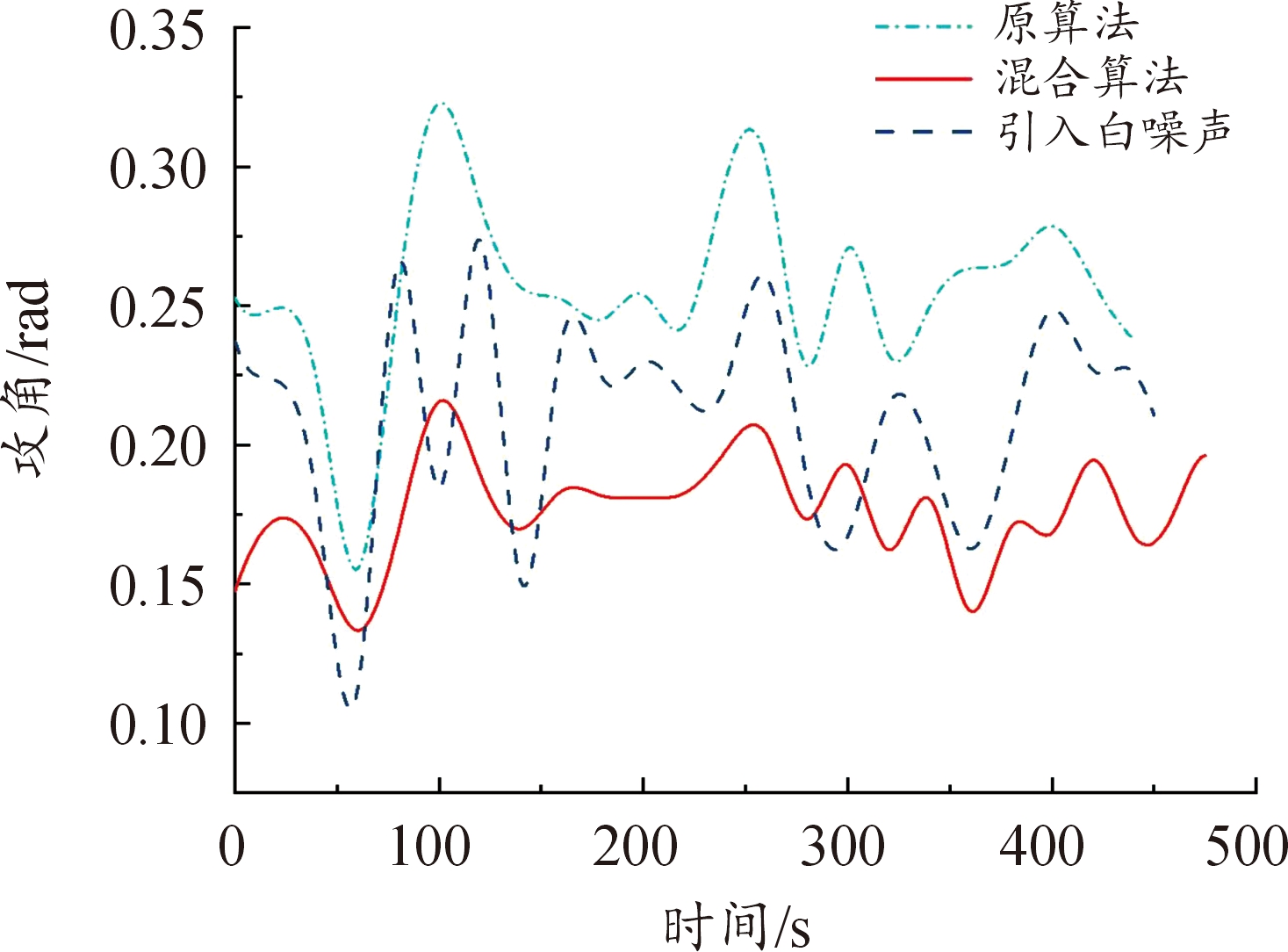
图25 攻角变化曲线
Fig.25 Angle of attack curve
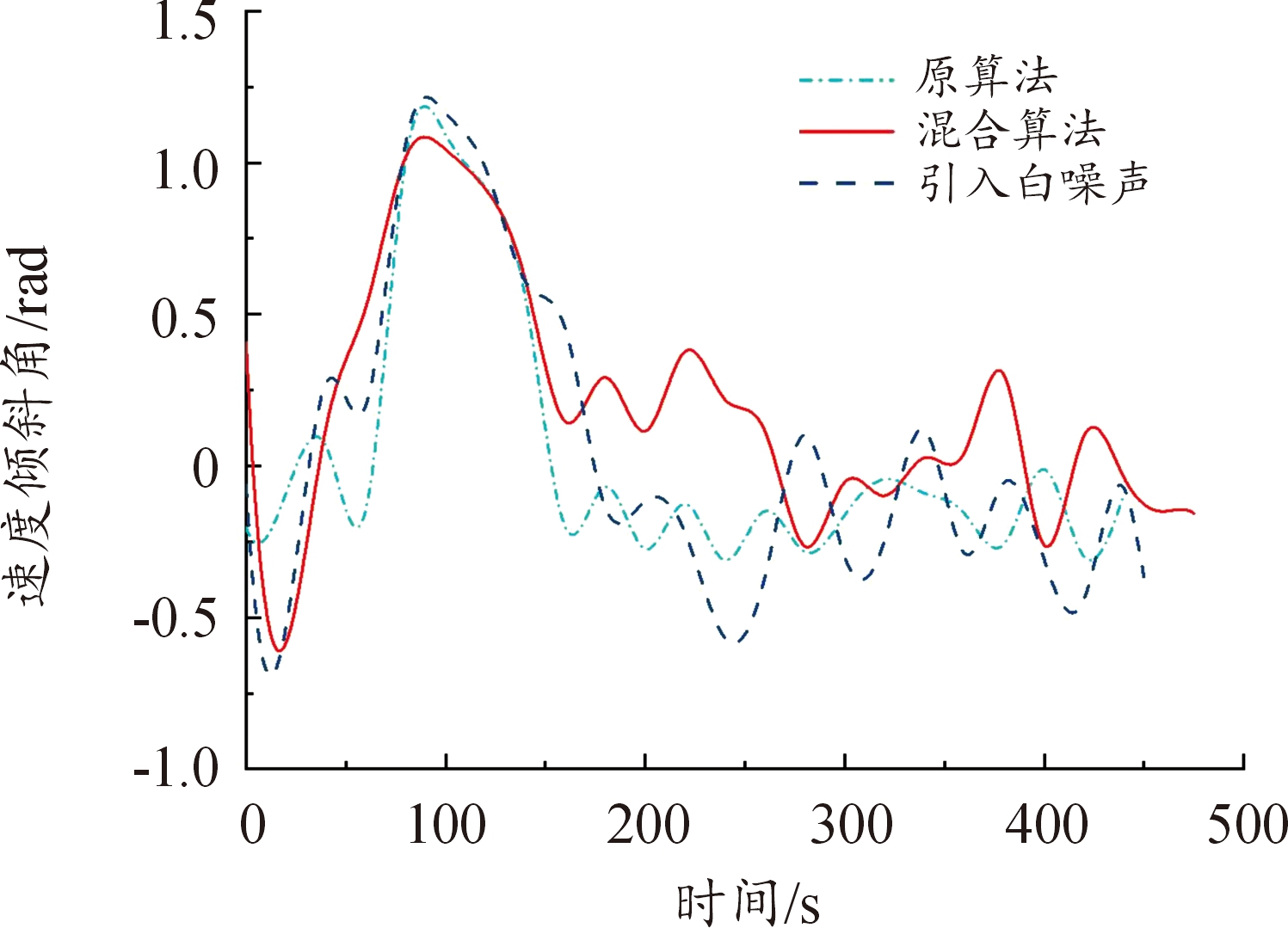
图26 速度倾斜角变化曲线
Fig.26 Velocity inclination angle variation curve
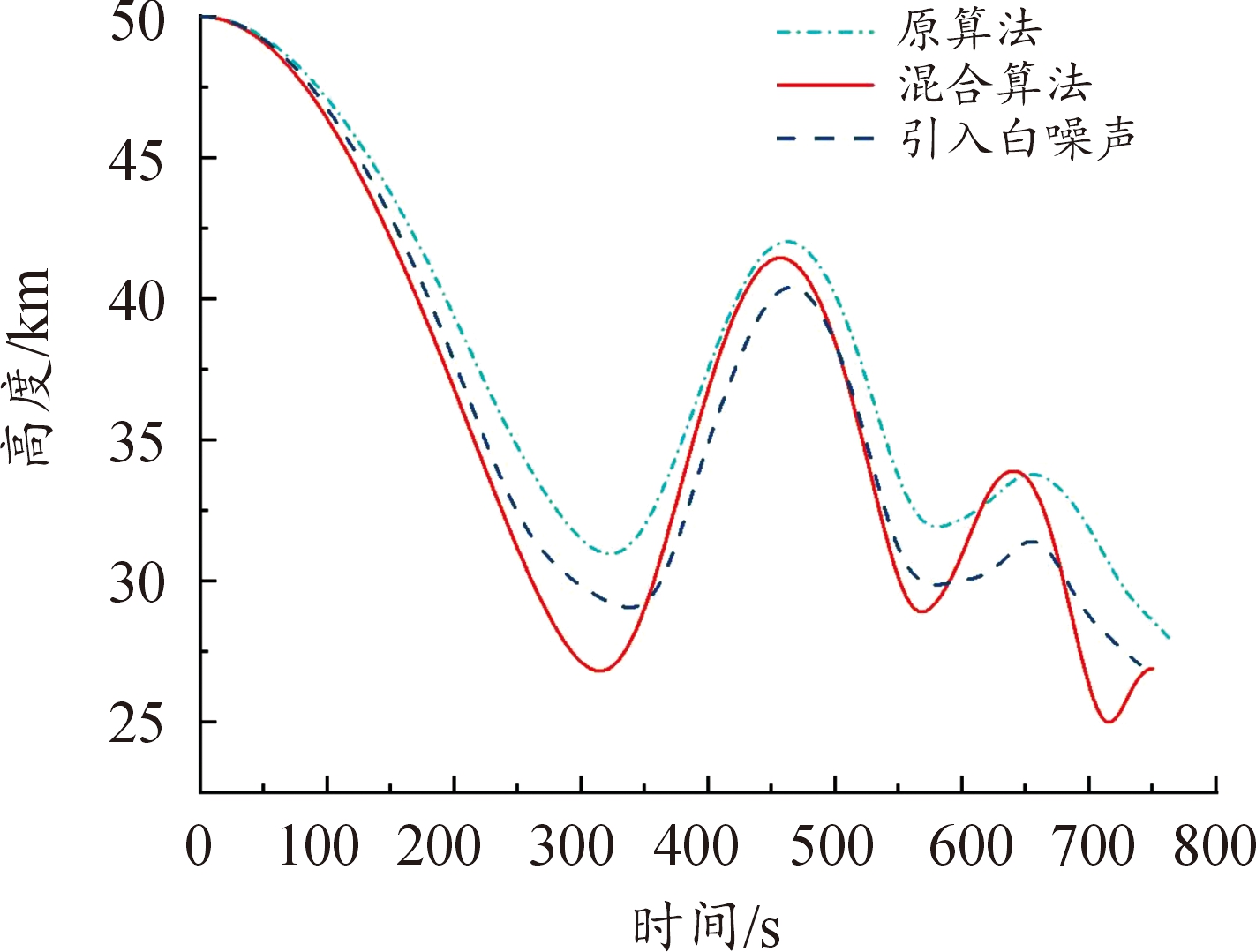
图27 高度-纵程变化曲线
Fig.27 Altitude-longitudinal change curve
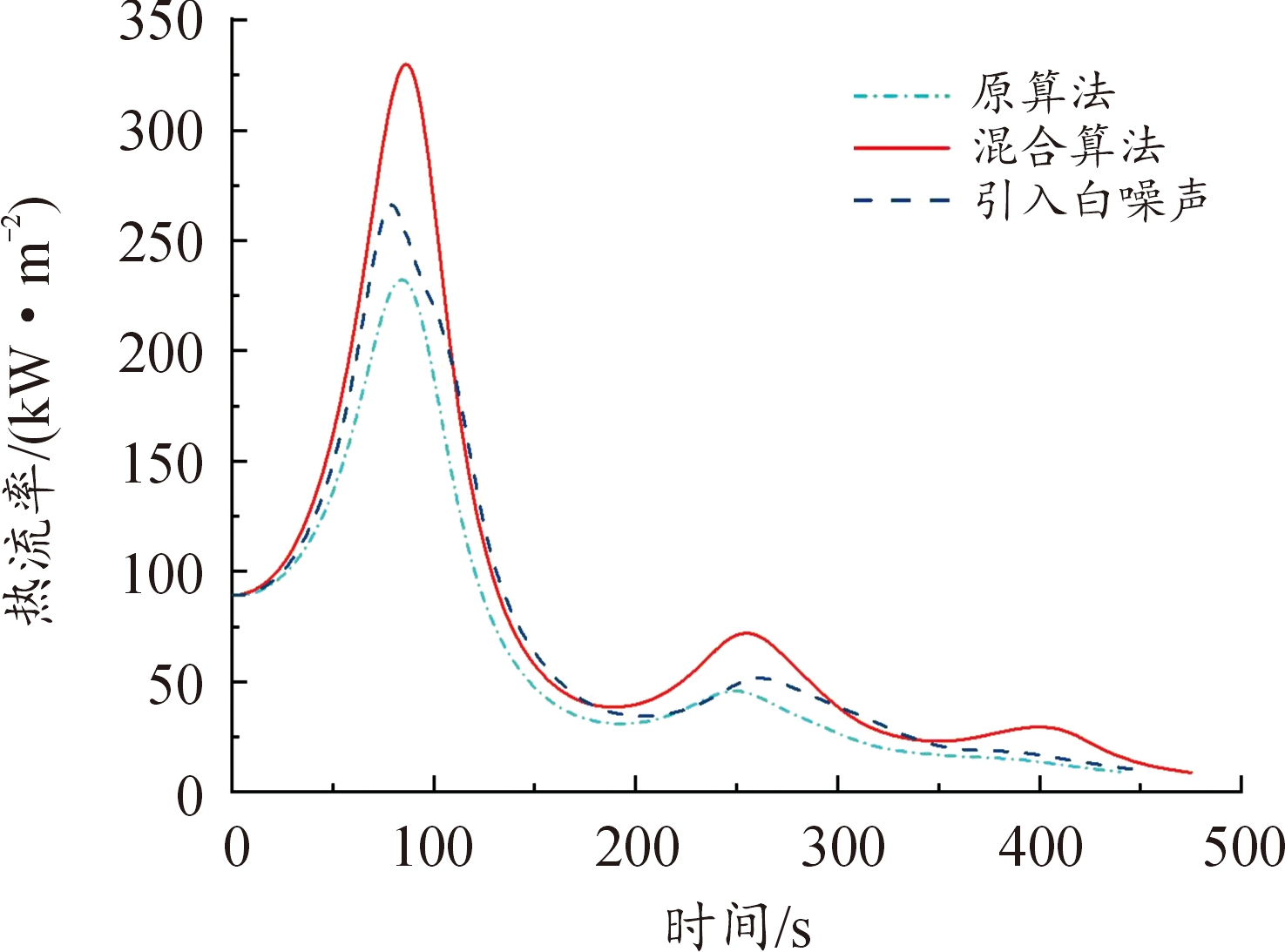
图28 热流率变化曲线
Fig.28 Heat flow rate curve change curve
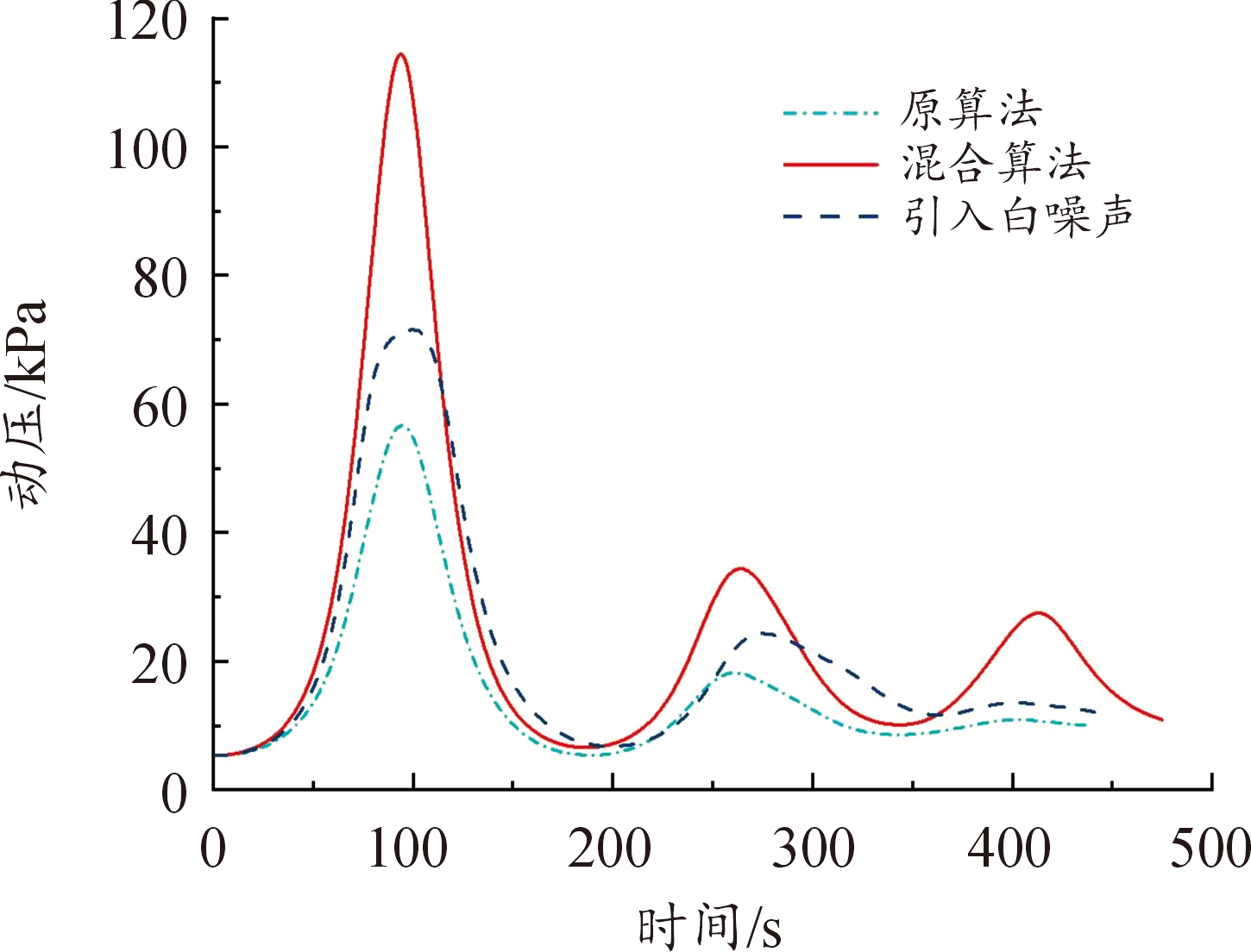
图29 动压变化曲线
Fig.29 Dynamic pressure curve

图30 过载变化曲线
Fig.30 Overload curve
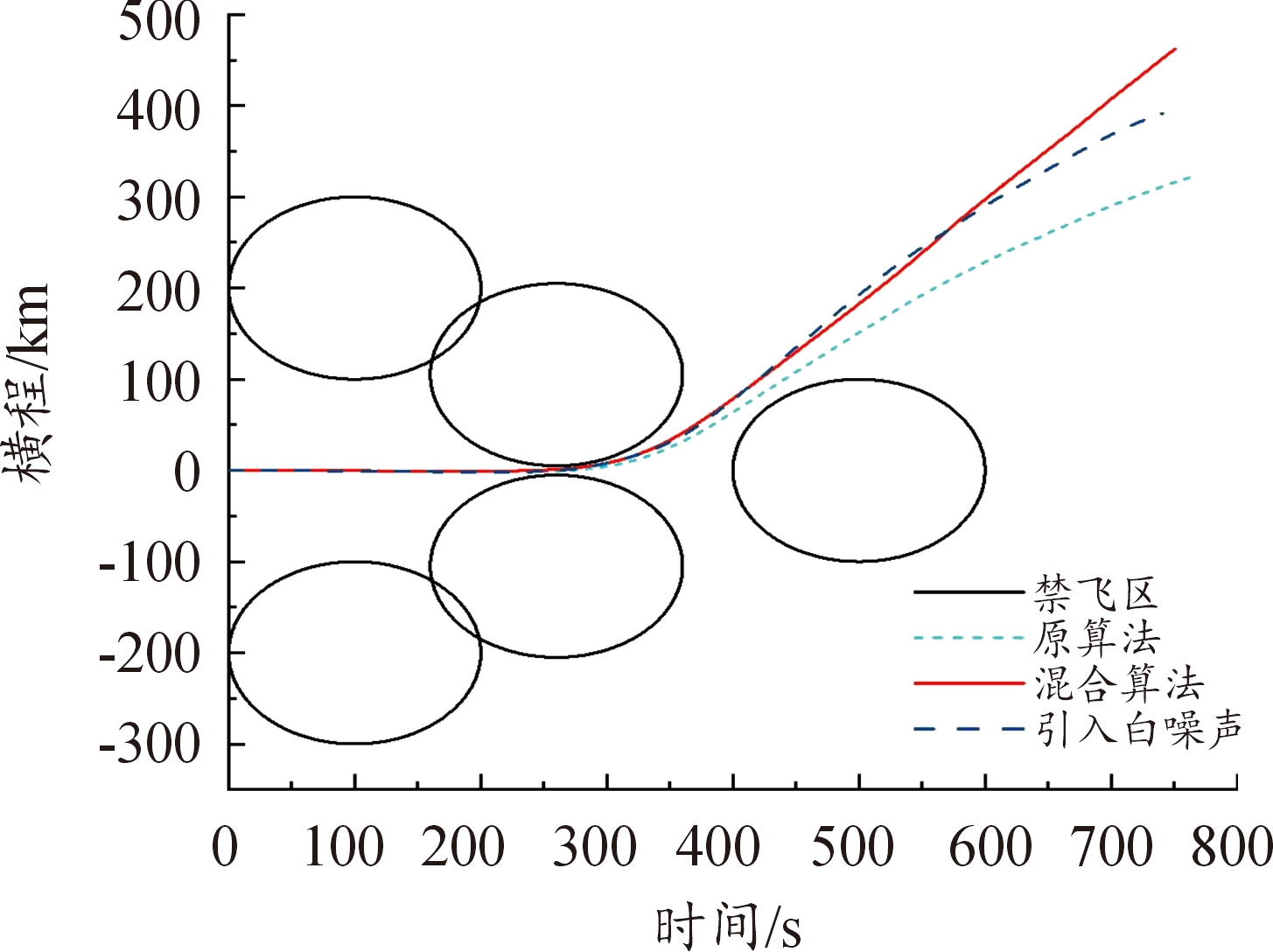
图31 规避禁飞区俯视图
Fig.31 Top view of avoiding the no-fly zone
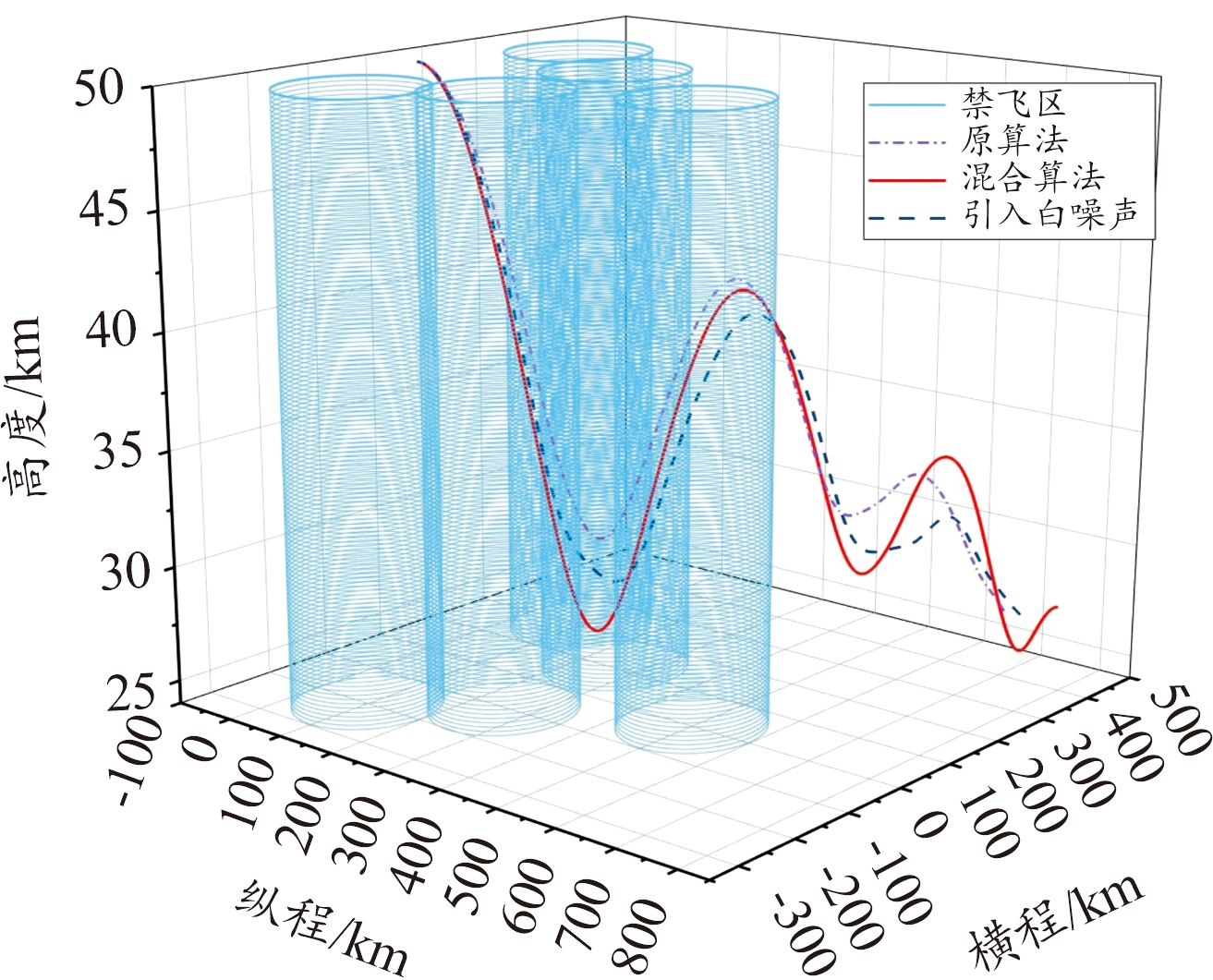
图32 规避禁飞区三维立体图
Fig.32 3D stereo map of avoiding the no-fly zone
最后,在考虑模型不确定性因素的情况下,即气动系数引入正态分布的白噪声后,最佳适应度函数曲线在20~30代左右已经趋于收敛,自适应遗传算法对控制变量寻优仍具有较好的收敛效果,相应的控制约束、过程约束(热流率、过载、动压及多禁飞区)等仍能满足相应的要求,验证了构建的混合算法具备一定的鲁棒性。
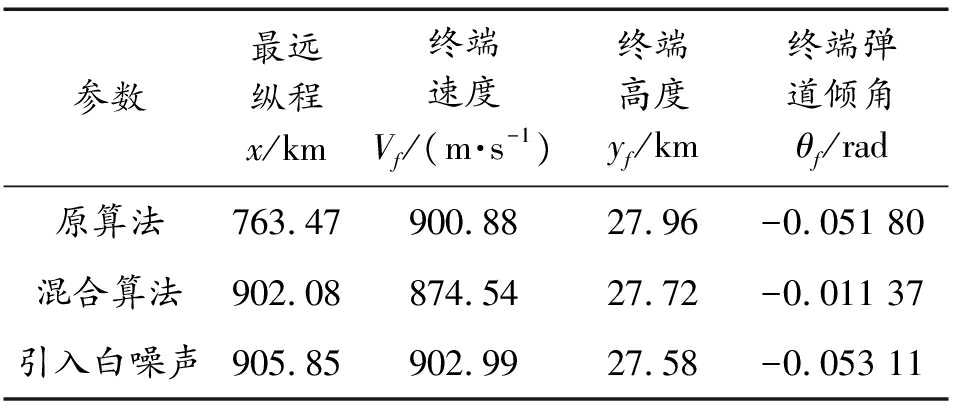
为了更直观反应构建的混合算法满足终端约束,建立如表6、表7所示。
表6 终端约束条件对应的终端状态(性能指标:最远纵程)
Table 6 Terminal state corresponding to terminal constraint(performance index:furthest longitudinal range)
参数最远纵程x/km终端速度Vf/(m·s-1)终端高度yf/km终端弹道倾角θf/rad原算法763.47900.8827.96-0.051 80混合算法902.08874.5427.72-0.011 37引入白噪声905.85902.9927.58-0.053 11
表7 终端约束条件对应的终端状态(性能指标:最远横程)
Table 7 Terminal state corresponding to terminal constraint(performance index:the furthest cross distance)
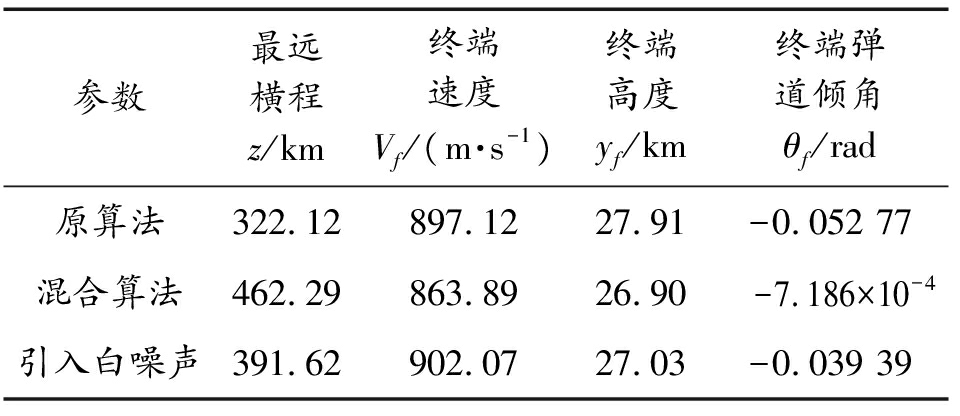
参数最远横程z/km终端速度Vf/(m·s-1)终端高度yf/km终端弹道倾角θf/rad原算法322.12897.1227.91-0.052 77混合算法462.29863.8926.90-7.186×10-4引入白噪声391.62902.0727.03-0.039 39
从图4、图5、图7、图8和图19、图20、图23、图24以及表6、表7可以看出,在以最远纵程/最远横程为性能指标的仿真中,混合算法能够满足终端约束条件,且相较于原算法性能指标最远纵程/最远横程数值更大,更接近全局最优解,验证了通过引入多目标分层规划方法以保证在终端时刻满足终端约束的同时使性能指标最优的有效性。另外,在考虑气动参数受到干扰的仿真中,终端约束仍能满足要求。
综上所述,构造的基于改进直接打靶法和自适应遗传算法得到的最优性能指标(最远纵程/最远横程)轨迹满足控制约束、过程约束(动压、过载、热流率及禁飞区)以及终端约束条件,能够规避多禁飞区,说明了构建的混合算法的有效性。其次,相较于原算法(直接打靶法-遗传算法),混合算法不需要不断试测初值,收敛速度较快,性能指标更优,能够快速、准确的逼近全局最优解。最后,在考虑模型不确定因素,即气动参数受到正态分布白噪声干扰时仍能满足要求,说明了构建的混合算法具备一定的鲁棒性。
4 结论
高马赫数飞行器准平衡飞行段弹道优化方法是高马赫数飞行器研究中主要的关键技术,考虑飞行过程中面临包含多禁飞区等复杂约束限制,提出了一种基于改进直接打靶法和自适应遗传算法的混合优化解决方案。
1) 通过对直接打靶法改进,将控制量初末时刻值一并纳入优化设计变量,以终端约束中复合约束项(如速度和高度等)为判断条件,将弹道结束时刻作为终端时刻,以此降低了对初值的敏感程度。
2) 为进一步快速、准确逼近全局最优解,对遗传算法的适应度函数进行了三点改进,构造了可随种群迭代次数增加而自适应调整的对数形式的综合适应度函数,建立了新的自适应遗传算法。
3) 基于建立的自适应遗传算法优化改进直接打靶法中离散点处的控制量,通过三次样条插值对控制量-时间历程平滑处理,并利用四阶龙格库塔法(Runge-Kutta)进行数值积分,经过若干次迭代计算出最优控制时间序列,同时得到了能够实现规避多禁飞区,满足约束条件且保证航程最远的理想轨迹。
试验表明,建立的混合优化算法不需要不断试测初值,相较于原算法(直接打靶法-遗传算法)收敛速度更快,性能指标最远纵程/最远横程数值更大,最接近全局最优解。另外,考虑实际飞行过程中模型存在的不确定性因素,在气动参数中引入了正态分布白噪声,结果表明准平衡飞行过程中各类约束条件仍能满足要求,说明了构造的混合算法具备一定的鲁棒性。在应用方面,构建的混合优化算法本质上是一种优化方法,不仅适用于高马赫数飞行器准平衡飞行段弹道优化,也适用于一般的飞行器弹道优化问题,为下一步研究不确定性量化的鲁棒弹道优化问题提供一定的参考价值。
[1] 牛青林,李强,高文强,等.类X-51A飞行器被动巡航状态红外辐射特性研究[J].兵器装备工程学报,2021,42(9):45-49.
NIU Qinglin,LI Qiang,GAO Wenqiang,et al.Study on infrared radiation characteristics of X-51A type hypersonic vehicle under cruising stste[J].Journal of Equipment Engineering,2021,42(9):45-49.
[2] 孙聪.高超声速飞行器强度技术的现状、挑战与发展趋势[J].航空学报,2022,43(6):527590-527598.
SUN Cong.Development status,challenges and trends of strength technology for hypersonic vehicles[J].Acta Aeronautica et Astronautica Sinica,2022,43(6):527590-527598.
[3] 张合新,宫梓丰,蔡光斌,等.复杂约束条件下高超声速飞行器再入轨迹优化[J].兵器装备工程学报,2019,40(1):1-6.
ZHANG Hexin,GONG Zifeng,CAI Guangbin,et al.Reentry tracking control of hypersonic vehicle with complicated constraints[J].Journal of Equipment Engineering,2019,40(1):1-6.
[4] CHENG L,SHI P,GONG S P,et al.Real-time trajectory optimization for powered planetary landings based on analytical shooting equations[J].Chinese Journal of Aeronautics,2022,35(7):91-99.
[5] MARCHETTI F,MINISCI E,RICCARDI A.Single-stage to orbit ascent trajectory optimisation with reliable evolutionary initial guess[J].Optimization and Engineering,2021(5):1-26.
[6] 赵佳钏.助推滑翔式导弹助推段轨迹优化及制导方法研究[D].哈尔滨:哈尔滨工业大学,2021.
ZHAO Jiachuan.Research on trajectory optimization and guidance method of boost-glide missile in boost phase[D].Harbin:Harbin Institute of Technology,2021.
[7] 高杨,蔡光斌,张胜修,等.多禁飞区高超声速滑翔飞行器再入机动制导[J].兵器装备工程学报,2019,40(8):32-39.
GAO Yang,CAI Guangbin,ZHANG Shengxiu,et al.Reentry maneuver guidance for hypersonic glide vehicles under multiple no-fly zones[J].Journal of Equipment Engineering,2019,40(8):32-39.
[8] HE R Z,LIU L H,TANG G J,et al.Entry trajectory generation without reversal of bank angle[J].Aerospace Science and Technology,2018,71(8):627-635.
[9] HU Y D,GAO C S,LI J L,et al.A novel adaptive lateral reentry guidance algorithm with complex distributed no-fly zones constraints[J].Chinese Journal of Aeronautics,2022,35(7):128-143.
[10] DANCILA R I,BOTEZ R M.New flight trajectory optimisation method using genetic algorithms[J].Aeronautical Journal,2021,125(1286):618-671.
[11] LIU X,JIANG D,TAO B,et al.Genetic algorithm-based trajectory optimization for digital twin robots[J].Frontiers in Bioengineering and Biotechnology,2022(9):793782.
[12] CAI F C,HUANG X.Study on trajectory optimization of hypersonic vehicle based on neural network[J].Frontiers in Energy Research,2022(10):884624-884632.
[13] DANCILA R I,BOTEZ R M.New flight trajectory optimisation method using genetic algorithms[J].Aeronautical Journal,2021,125(1286):618-671.
[14] ERGEZER H.Multi-objective trajectory planning for slung-load quadrotor system[J].IEEE Access,2021(9):1555003-1555017.
[15] 杨雄,吴东,李祥.基于卷积神经网络的遗传算法密码分析适应度函数[J].信息工程大学学报,2022,23(2):192-197.
YANG Xiong,WU Dong,LI Xiang.Fitness function based on convolutional neural network of genetic algorithm for cryptanalysis[J].Journal of Information Engineering University,2022,23(2):192-197.
[16] ZHOU J H,CHEN M,CHEN J B,et al.Optimal time-jerk trajectory planning for the landing and walking integration mechanism using adaptive genetic algorithm method[J].Review of Scientific Instruments,2020,91(4):044501-044508.
[17] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008:1-80.
QIAN Xingfang,LIN Ruixiong,ZHAO Yanan.Missile flight dynamics[M].Beijing:Beijing Institute of Technology Press,2008:1-80.
[18] CHEN G Y,LI J H.A diversity ranking based evolutionary algorithm for multi-objective and many-objective optimization[J].Swarm and Evolutionary Computation,2019,48(11):274-287.
[19] LU Z T,FENG X Y,SU Z,et al.Friction parameters dynamic change and compensation for a novel dual-drive micro-feeding system[J].Actuators,2022,11(8):236-244.
[20] 刘旭,李响,张后军,等.不确定条件下采用协方差描述函数法的再入轨迹鲁棒优化[J].宇航学报,2021,42(11):1404-1415.
LIU Xu,LI Xiang,ZHANG Houjun,et al.Robust reentry trajectory optimization under uncertainties using covariance analysis describing function technique[J].Journal of Astronautics,2021,42(11):1404-1415.