0 引言
有生目标的侵彻与创伤是国防工程和创伤医学等领域的重要研究内容。研究生物组织及其模拟物的侵彻机理一方面是国防轻武器杀伤效能优化设计的理论基础,另一方面对创伤救治工作有重要的指导意义。在弹体的侵彻模拟实验中,弹道明胶(后文简称为明胶)是一种广泛使用的标准靶标[1-3],用以替代生物组织开展侵彻创伤实验。明胶的侵彻实验能够很好地反映弹体对生物体的杀伤现象,因此,研究明胶的侵彻机理是研究有生目标侵彻创伤问题的重要方法和内容,引起了军事和医学应用领域的广泛关注[4-5],国内外不少学者都对弹体侵彻明胶的运动模型展开了研究[6-8]。
弹体侵彻明胶靶标时,弹体受到阻力的作用逐渐减速,将能量释放到靶标中;而靶标介质在弹体的作用下产生径向运动形成瞬时空腔,因此弹体侵彻明胶的过程主要包括弹体沿弹道方向的运动问题和靶标介质沿垂直于弹道方向的径向运动问题。弹体沿弹道方向运动规律由弹体受到的侵彻阻力决定,而靶标介质沿垂直于弹道方向的径向运动问题即瞬时空腔问题。由于弹体和目标介质的相互作用十分复杂,在现有的模型中,侵彻阻力模型[9-12]和瞬时空腔模型[13-14]往往是分别进行建立的,且对于瞬时空腔动态过程的建模研究非常少。关于侵彻过程中的瞬时空腔,Sellier等[13]提出弹体释放到靶标中的总能量ΔE和最大瞬时空腔体积Vm可用线性关系表示:ΔE=Vm/λ。莫根林等[14]假设瞬时空腔内壁的运动规律仅和空腔截面获得的能量有关,建立了空腔半径随时间变化的计算模型,并通过侵彻实验进行了验证。
尽管独立的阻力模型和独立的空腔模型分别能够较为准确地计算弹体侵彻深度以及瞬时空腔的大小,但关于二者的内在联系的研究还非常少。作者在前期研究[15-16]中提出,侵彻阻力模型和侵彻空腔模型之间应该有着紧密的内在联系。将文献[13]中弹体释放到靶标中的总能量和最大瞬时空腔体积之间的线性关系(ΔE=Vm/λ)中的1/λ记为Ps,则Ps等于在介质中打开单位体积空腔产生的变形能,该参数可通过空腔膨胀模型[17]进行计算,基于Ps,Liu等[18]建立了步枪弹侵彻明胶块的瞬时空腔动态模型。同时,Ps也是侵彻阻力模型中的重要参数,在研究金属、混凝土和陶瓷等材料的侵彻问题中已经得到了较为广泛的应用,可求解侵彻阻力、弹体的速度衰减规律和侵彻深度等重要参数。
利用能量转换和守恒定律建立了描述球形弹体侵彻阻力和侵彻空腔动态膨胀过程的数学模型,将弹体的运动方程和侵彻空腔的运动方程紧密结合起来。本研究分析了不同尺寸的球形弹体对明胶的侵彻实验结果,通过模型计算与实验结果的比较,获得了模型中的参数,并对模型进行了深入分析,讨论了每个参数的物理意义,为解释弹体对软组织的侵彻机理提供了参考。
1 侵彻过程建模
本研究基于以下假设建立模型:
1) 球形弹体在明胶块中的轨迹近似为直线,如图1(a)所示,侵彻空腔为轴对称空腔;
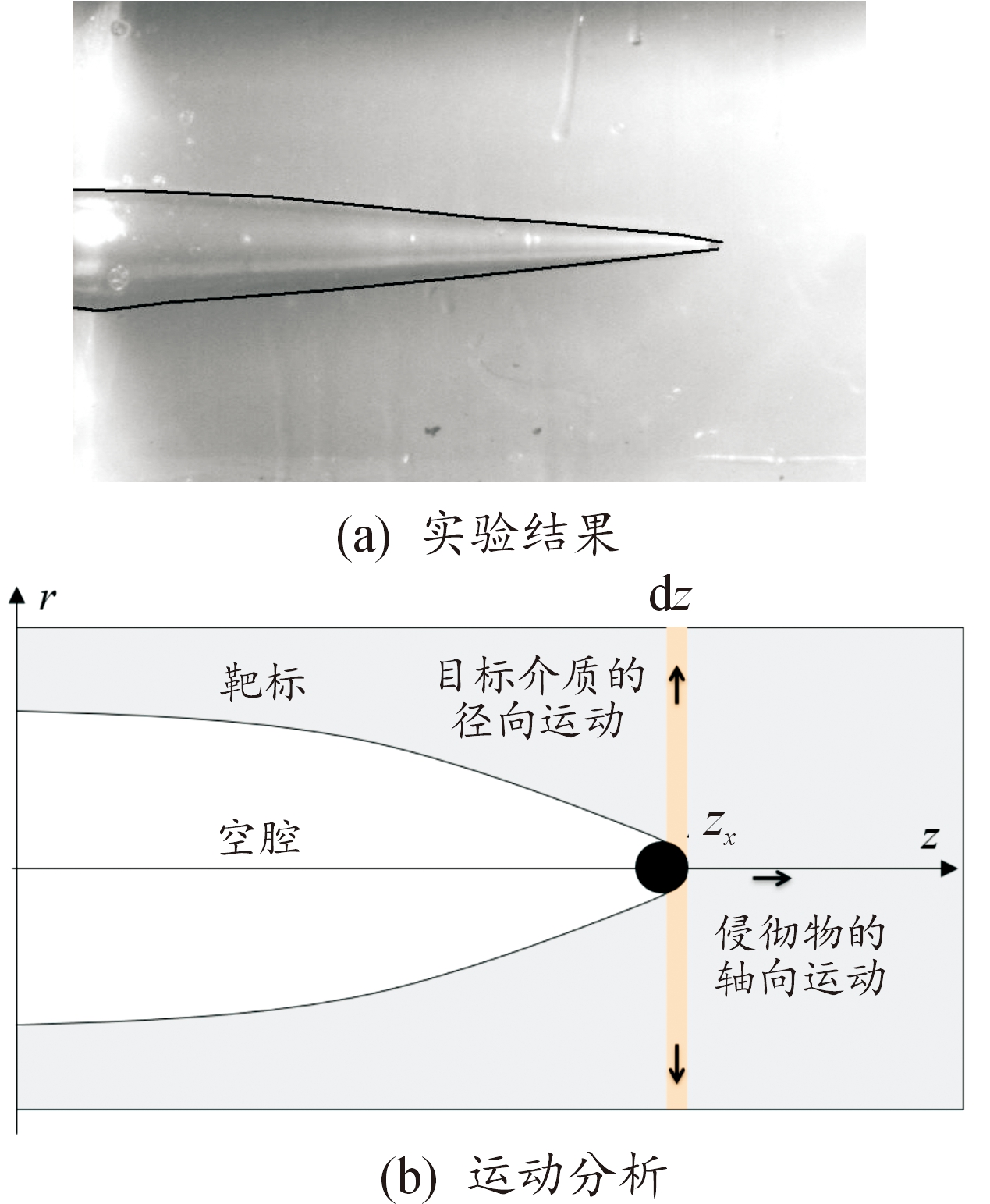
图1 球形弹体侵彻明胶的过程
Fig.1 Penetration of gelatin by spherical fragments
2) 明胶介质在弹体侵彻作用下沿径向运动形成瞬时空腔,如图1(b)所示,忽略轴向运动的影响;
3) 忽略侵彻过程中的热能;
4) 弹体为刚体。
当球形弹体侵彻明胶块时,可以从实验中看出弹体运动轨迹是近似为直线(图1(a)),假设打开的空腔为轴对称形状,则在弹道任意位置zx处(图1(b)),沿弹道方向dz厚度的靶标介质中有
dEs=dEk+dEp
(1)
式中:dEk为dz段介质中的动能;dEp为dz段介质中的变形能;dEs为弹体沿弹道前进dz长度时释放到介质中的能量。弹体在明胶中运动时,由于受到侵彻阻力的作用逐渐减速,将能量释放到靶标中,转化为靶标介质的变形能和径向运动的动能。弹体前进dz长度时释放的能量dEs为
(2)
式中:
和F分别为弹体在zx处的侵彻速度、加速度和所受的阻力;ms为弹体质量。弹体释放到介质中的能量导致介质径向膨胀,转化为介质中的变形能和动能。根据Ps的物理意义可知,dz段介质中的变形能为
dEp=Psπa2dz
(3)
式中:a为瞬时空腔的半径。假设dz段明胶介质中的空腔膨胀速度为
且不考虑材料的可压缩性,则该段介质的质量守恒方程为
(4)
式中:u为介质的径向速度,由边界条件
确定,可得式(4)微分方程的解
(5)
可计算dz段介质中的动能
(6)
式中:ρt为靶标弹性区的密度;B0=ln(R/a),积分上限R是靶标弹性变形区的边界,若材料为不可压缩,则R等于靶标的外边界尺寸,若考虑材料可压缩性,则R可能小于靶标的外边界尺寸。因此,参数B0与材料的可压缩性有关[19]。
将式(2)、式(3)和式(6)代入式(1),可得:
(7)
式(7)是基于柱形空腔膨胀理论的侵彻阻力模型。
随着空腔的膨胀,空腔半径a和膨胀速度的值随时间变化,为了方便,在式(7)中令a=as来计算侵彻阻力。as为球形弹体的半径。当a=as时,空腔膨胀速度与弹体侵彻速度用以下线性关系表达[20]
(8)
式中:β为空腔膨胀速度与弹体侵彻速度之间的比值[21]。
利用式(7)的阻力模型,可以通过求解下面的二阶微分方程获得侵彻位置z(t)和侵彻速度v(t)
(9)
当dz层的空腔膨胀到最大时,a=am,动能衰减到0,即
代入式(7)得
再次代入式(7),可得dz层的空腔动态膨胀关系
(10)
假设当弹体到达z(tx)=zx时,侵彻空腔从as开始膨胀,由初始条件,a(t=tx)=as,求解非线性一阶微分方程(10)可得到zx处的空腔半径变化规律a(t)。
综合以上推导过程可知,弹体的运动方程(9)和瞬时空腔的运动方程(10)通过一组参数紧密结合起来:Ps,B0和β。
2 侵彻实验
2.1 实验装置
图2显示了弹道实验装置的原理图,弹体是直径为3、4、4.8、6 mm的钢球(密度为7 800 kg/m3),明胶靶标(尺寸为30 cm×30 cm×30 cm)放置在距离枪口约25 m的位置,靶标的材料、制备、存储方法与文献[9]中所述一致;在弹道枪和明胶块之间距离明胶块约1 m的位置放置光电测速装置,测量弹体侵彻靶标之前的速度vs;高速摄像机(Phantom v2511)放置在垂直于弹道方向距离靶标约1.5 m的位置,用于拍摄弹体在靶标中的运动过程和明胶介质在侵彻作用下的变形过程。弹体在靶标中的位置(z,t)和侵彻轨迹中任意位置的瞬时空腔半径(a,t)可以由高速摄像从图像中直接读取,其中1像素对应约0.2 mm。
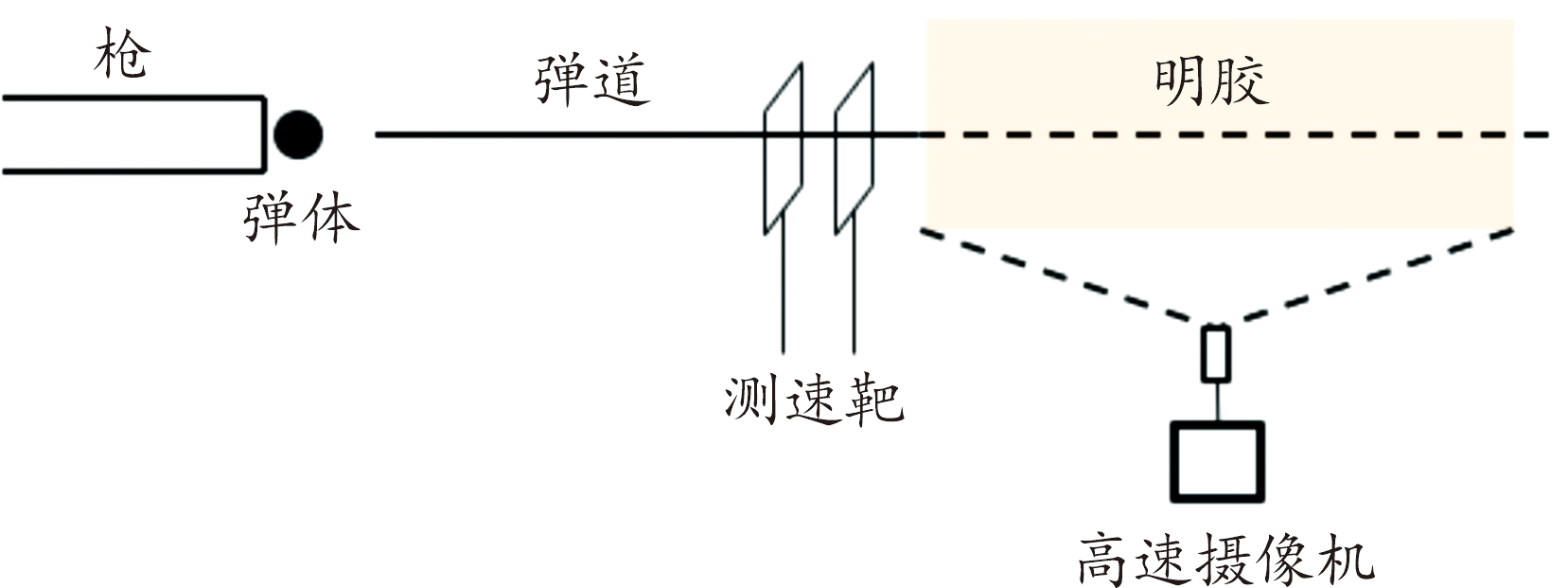
图2 侵彻实验装置原理框图
Fig.2 Schematic diagram of penetration experiment device
2.2 实验结果
典型的侵彻过程图像如图3所示。由于高速摄像机无法恰好捕捉到弹体经过靶标边界的时刻,因此选择拍摄图像里弹体首次出现在靶标中的位置作为时间零点,如图3中的白色边界线所示。表1列出了主要实验结果。3 mm球形弹体在侵彻靶标前的速度vs=700 m/s,在起始点z=0处的速度为525 m/s,侵彻过程结束后,弹体停留在明胶块中,即剩余速度vr=0 m/s。弹体释放到明胶靶标中的总动能为
J。弹体快速释放的能量导致了瞬时空腔的形成,当空腔膨胀至最大尺寸(Vm=80.5 cm3)时,目标介质中的动能可以忽略,此时,侵彻物释放的能量ΔJ完全转化为目标介质中的变形能,即Ps·Vm,因此,参数Ps可用Ps=ΔJ/Vm=3.3×105 Pa估算得到。
表1 主要实验结果
Table 1 Main experimental results
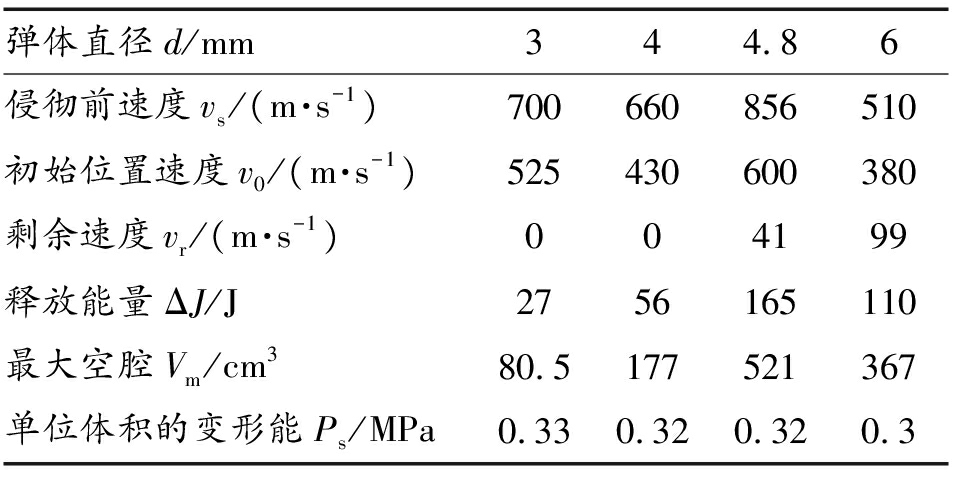
弹体直径d/mm344.86侵彻前速度vs/(m·s-1)700660856510初始位置速度v0/(m·s-1)525430600380剩余速度vr/(m·s-1)004199释放能量ΔJ/J2756165110最大空腔Vm/cm380.5177521367单位体积的变形能Ps/MPa0.330.320.320.3
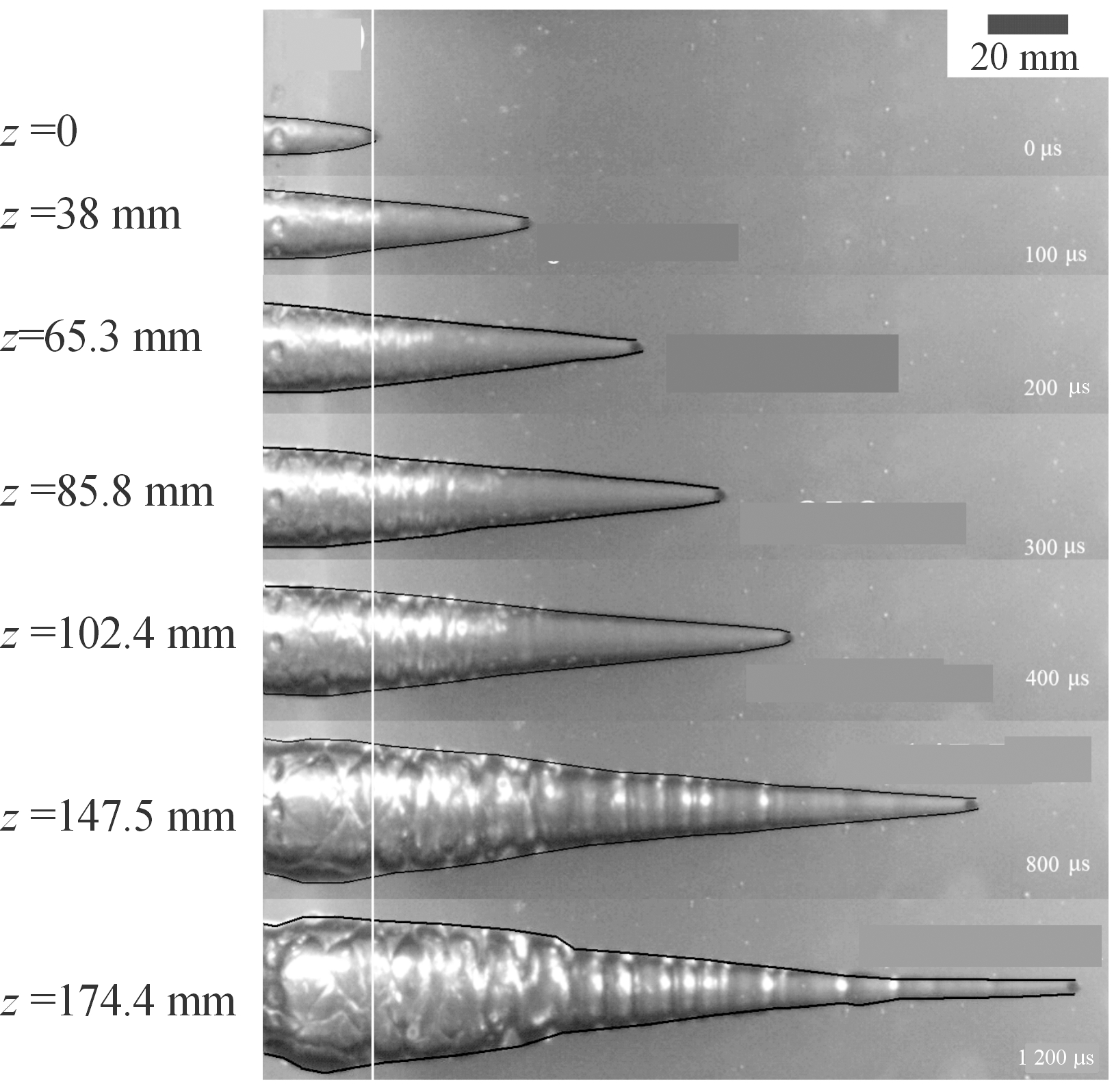
图3 典型的球形弹体侵彻明胶图像
Fig.3 Typical image of spherical projectile penetrating gelatin
直径为3、4、4.8 mm和6 mm的球形弹体的主要侵彻数据汇总在表1中。由表1中数据可知,在钢球直径不同、初始侵彻速度也不同的情况下,参数Ps的估算值变化范围较小,在0.3～0.33 MPa的范围内。
3 侵彻过程分析
3.1 模型参数
β是空腔初始膨胀速度
和弹体的侵彻速度v之间的比例系数,见式(8)。在初始条件z(0)=0、v(0)=v0下求解式(9)所示的二阶微分方程,并拟合实验数据z(t),可以计算弹道任意位置处弹体的侵彻速度v。在初始条件a(tx)=as下求解式(10)所示的微分方程,并与侵彻轨迹不同位置处的实验结果(a,t)进行拟合,可计算相应的空腔初始膨胀速度,最后,通过分析v和的关系,可得到β的值。例如,读取了图3所示的3 mm球形弹体侵彻弹道上z=0、38、65.3、85.8 mm四处的瞬时空腔半径随时间变化的数据,并利用式(10)进行曲线拟合,实验数据和拟合曲线如图4(a)所示,由拟合曲线可计算相应位置处的瞬时空腔的初始膨胀速度。采用同样的方法,读取了直径4、4.8、6 mm球形弹体的空腔数据并进行曲线拟合计算瞬时空腔的初始膨胀速度,最后获得空腔初始膨胀速度和侵彻速度v之间的关系。具体数据在表2中列出,将和v绘制在直角坐标图中并进行线性回归,可得β的平均值为0.24,如图4(b)所示。
表2 侵彻速度与空腔初始膨胀速度
Table 2 Penetration velocity and cavity expansion velocity
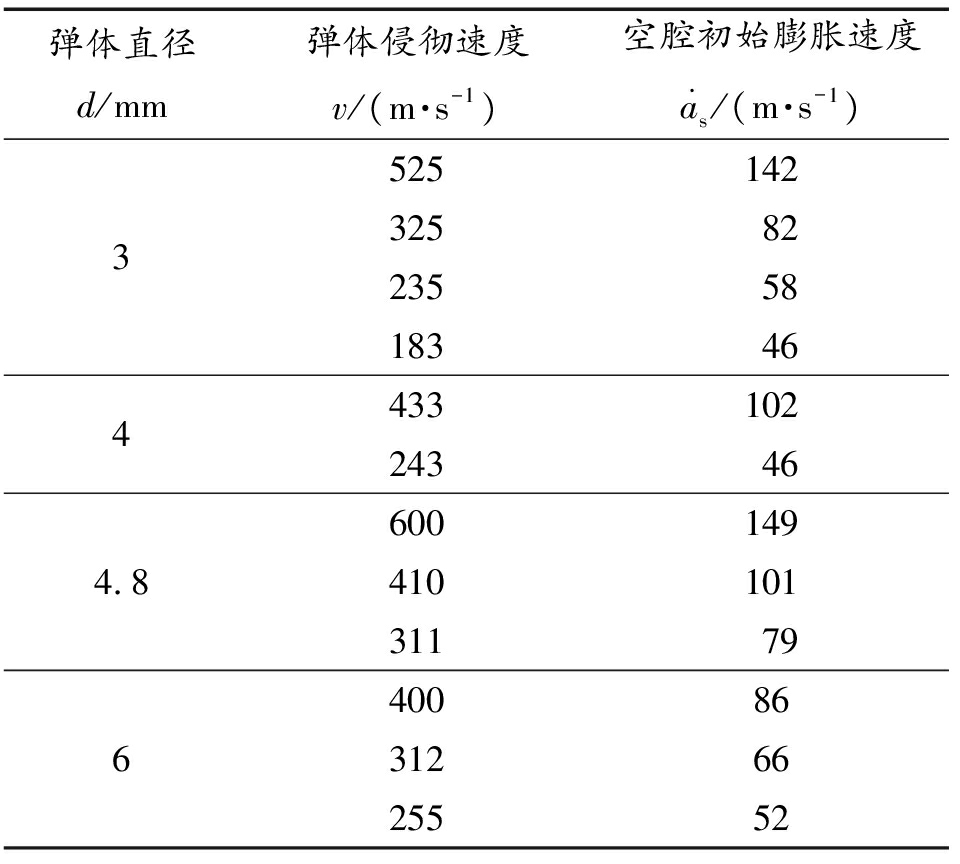
弹体直径d/mm弹体侵彻速度v/(m·s-1)空腔初始膨胀速 as/(m·s-1)35251423258223558183464433102243464.8600149410101311796400863126625552
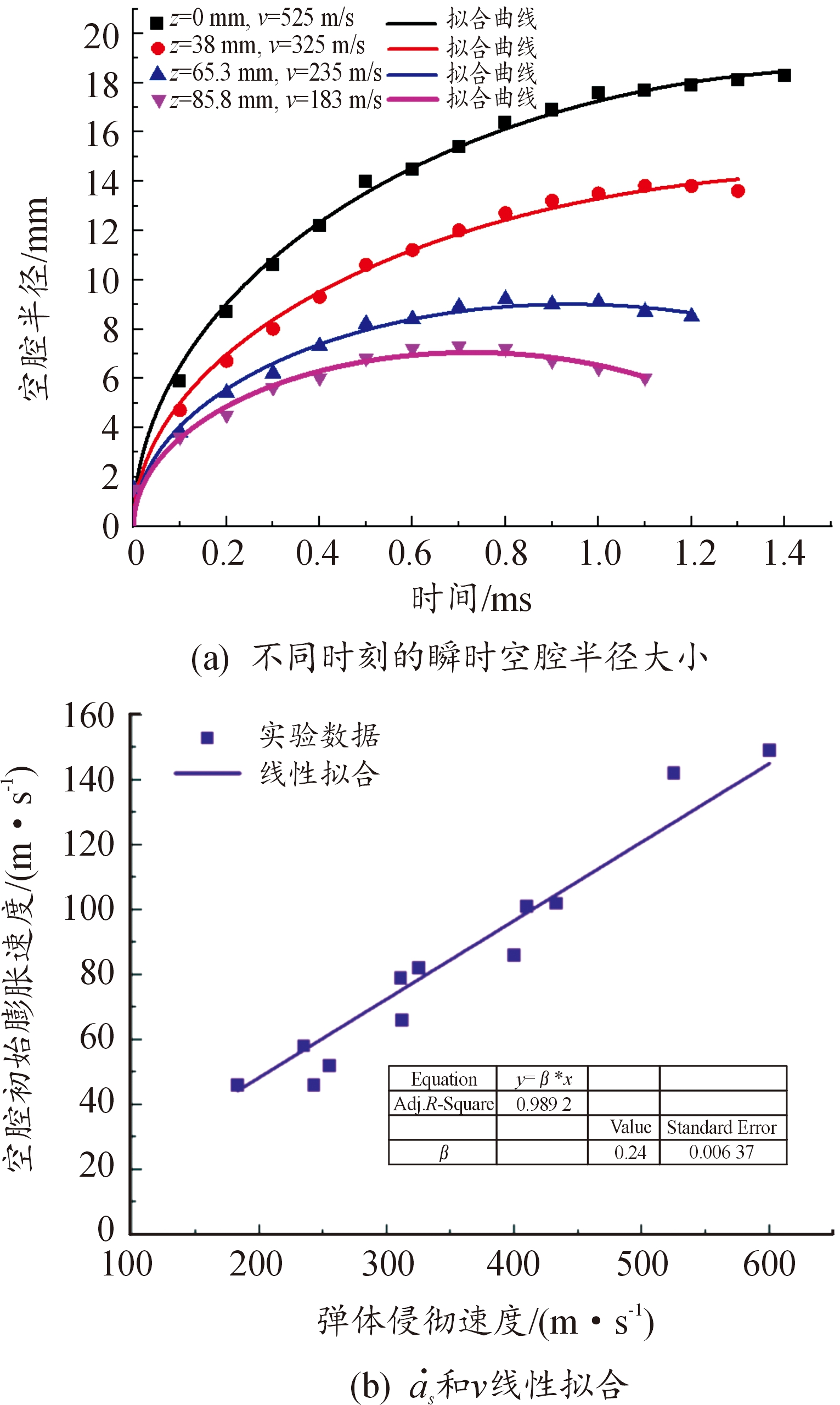
图4 侵彻空腔的膨胀速度与弹体侵彻速度的关系
Fig.4 The relationship between the expansion velocity of the penetrating cavity and the penetration velocity of the projectile
模型中的另一个参数B0,反映了靶标介质的可压缩性。低速加载条件下的力学性能实验表明,明胶是几乎不可压缩的,但是在冲击加载下明胶的可压缩性仍然缺乏充分的实验研究。由初始条件z(0)=0、v(0)=v0求解式(9)所示的二阶微分方程,拟合实验数据z(t),可以确定参数组合B0β2,结合β的值,可得到B0的值。不同直径的球形弹体侵彻数据z(t)及曲线拟合情况如图5所示。4组数据的决定系数(R2)分别为0.999 9、0.999 8、0.999 6和0.999 9,参数分析结果见表3所示,可得的平均值为3.07。
表3 参数B0的拟合结果
Table 3 Fitting results of B0
钢球直径d/mmB0β2B030.1753.0440.183.134.80.1853.2160.1682.92平均值0.177±0.0073.07±0.12
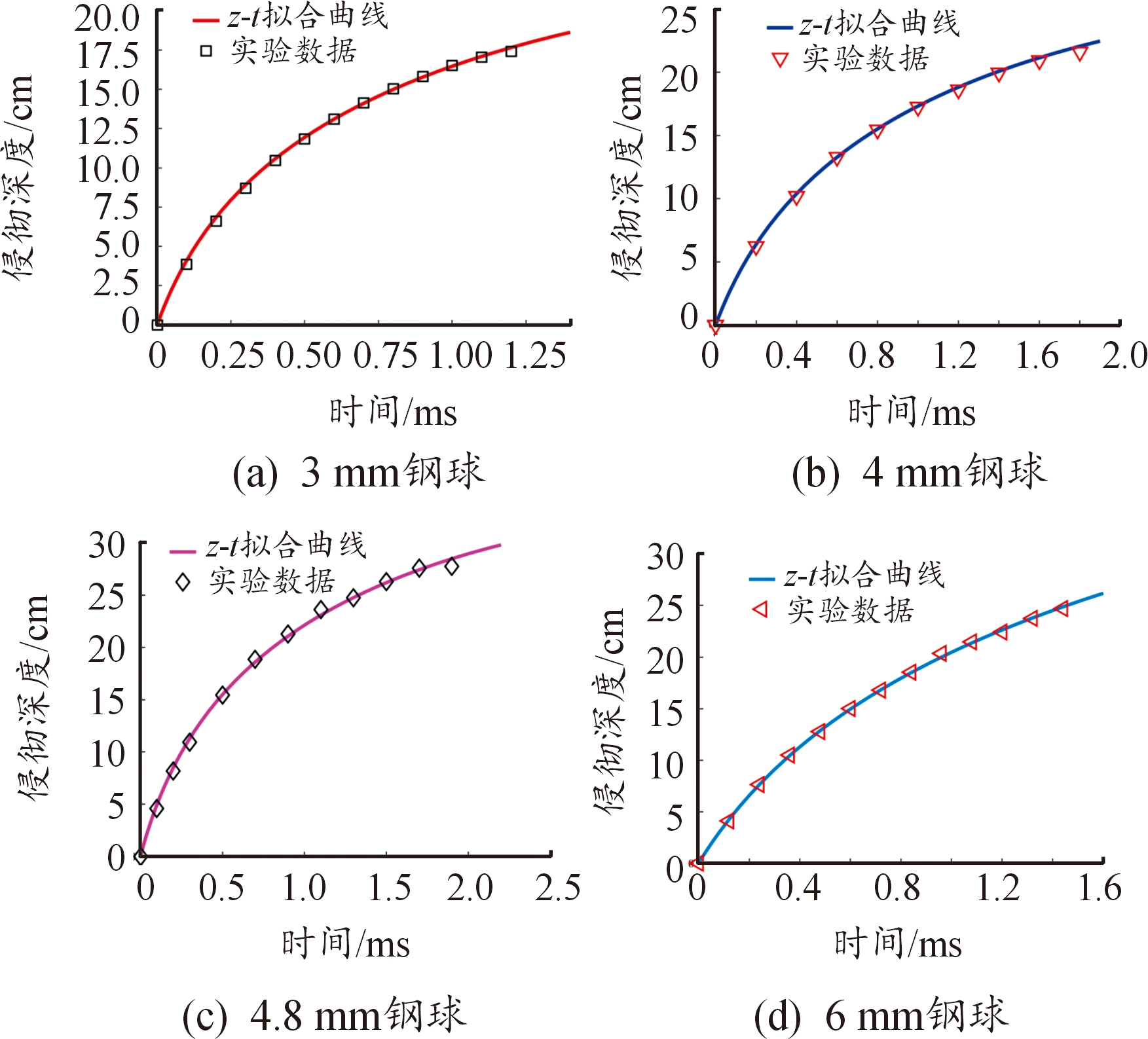
图5 弹体侵彻深度z(t)的曲线拟合情况
Fig.5 Fitting results of penetration depth z(t)
3.2 空腔膨胀过程的模型验证
根据4.1节的数据分析获得的模型参数,取平均值B0=3.07,β=0.24,求解式(9)和(10)中关于z和a的微分方程,可以计算靶标中任意时刻的瞬时空腔的轮廓和弹体侵彻深度。图6中所示为直径3 mm钢球在t=500 μs、侵彻深度为z=118 mm时产生的瞬时空腔,上图为高速摄像机拍摄的图片,下图为按相同比例绘制的模型计算结果图。
图6 侵彻实验中拍摄的瞬时轮廓和模型计算的对比
Fig.6 Comparison of temporary cavity recorded by high-speed vedio and model calculations
为了方便比较,将高速摄像机拍摄的空腔轮廓描出并配上散点,与模型计算的曲线进行对比。图7显示了直径3 mm钢球侵彻明胶过程中不同时刻的空腔轮廓与模型计算结果的比较,绘图时保证实验图像和模型图像的比例一致。在图示的4个时刻,空腔轮廓与模型计算结果的决定系数(R2)分别为0.998 2、0.992 3、0.992 1和0.989 4。
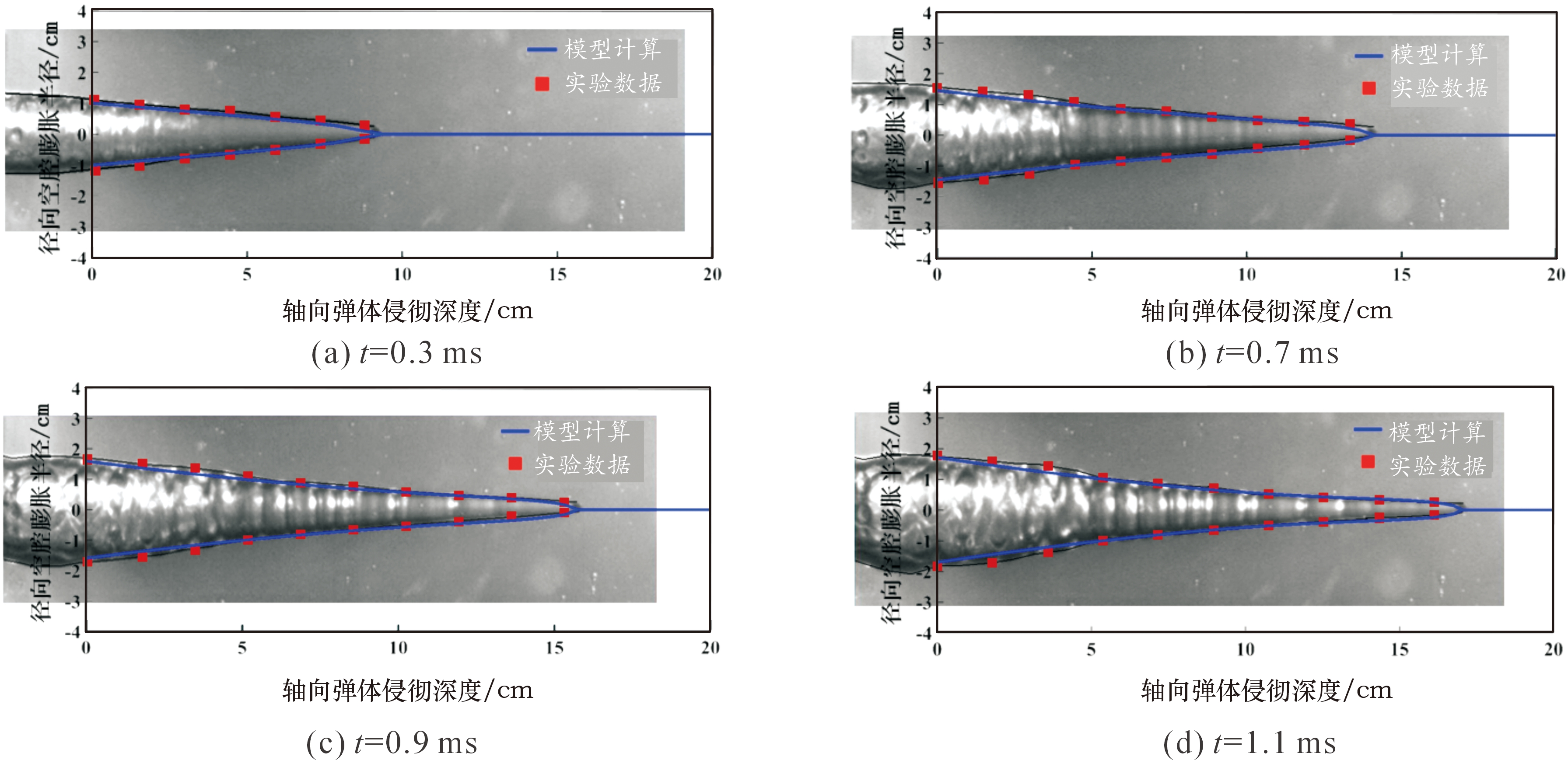
图7 直径3 mm球形弹体侵彻明胶的瞬态空腔
Fig.7 Temporary cavity of 3 mm diameter spherical projectile penetrating gelatin
图8中所示的直径4 mm钢球侵彻明胶过程中4个时间点空腔轮廓与模型计算结果的决定系数分别为0.995 8、0.985 9、0.983 3和0.991 4;图9中所示的直径4.8 mm钢球侵彻明胶过程中4个时间点的空腔轮廓与模型计算结果的决定系数分别为0.993 9、0.994 5、0.995 8和0.985 4;图10中所示的直径6 mm钢球侵彻明胶过程中4个时间点的空腔轮廓与模型计算结果的决定系数分别为0.998 3、0.995 5、0.991 5和0.991 7。
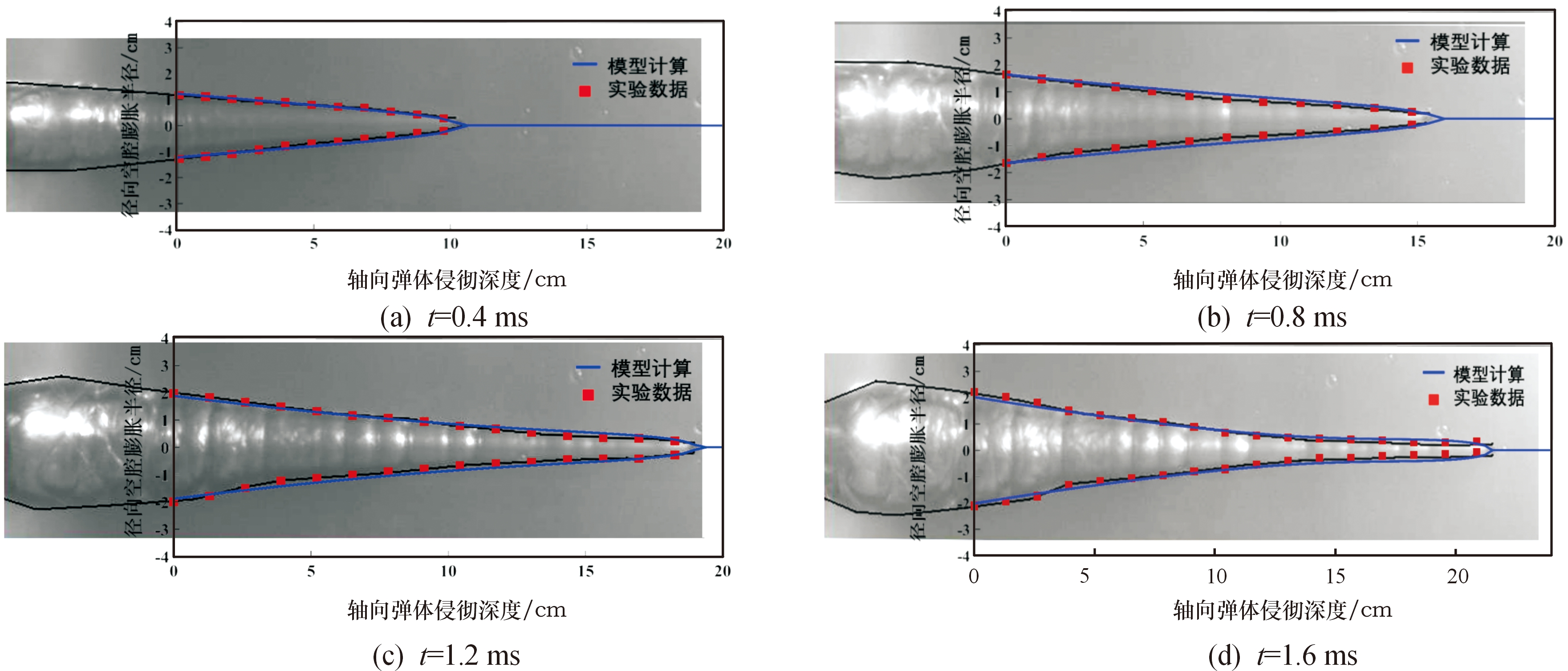
图8 直径4 mm球形弹体侵彻明胶的瞬态空腔
Fig.8 Temporary cavity of 4 mm diameter spherical projectile penetrating gelatin
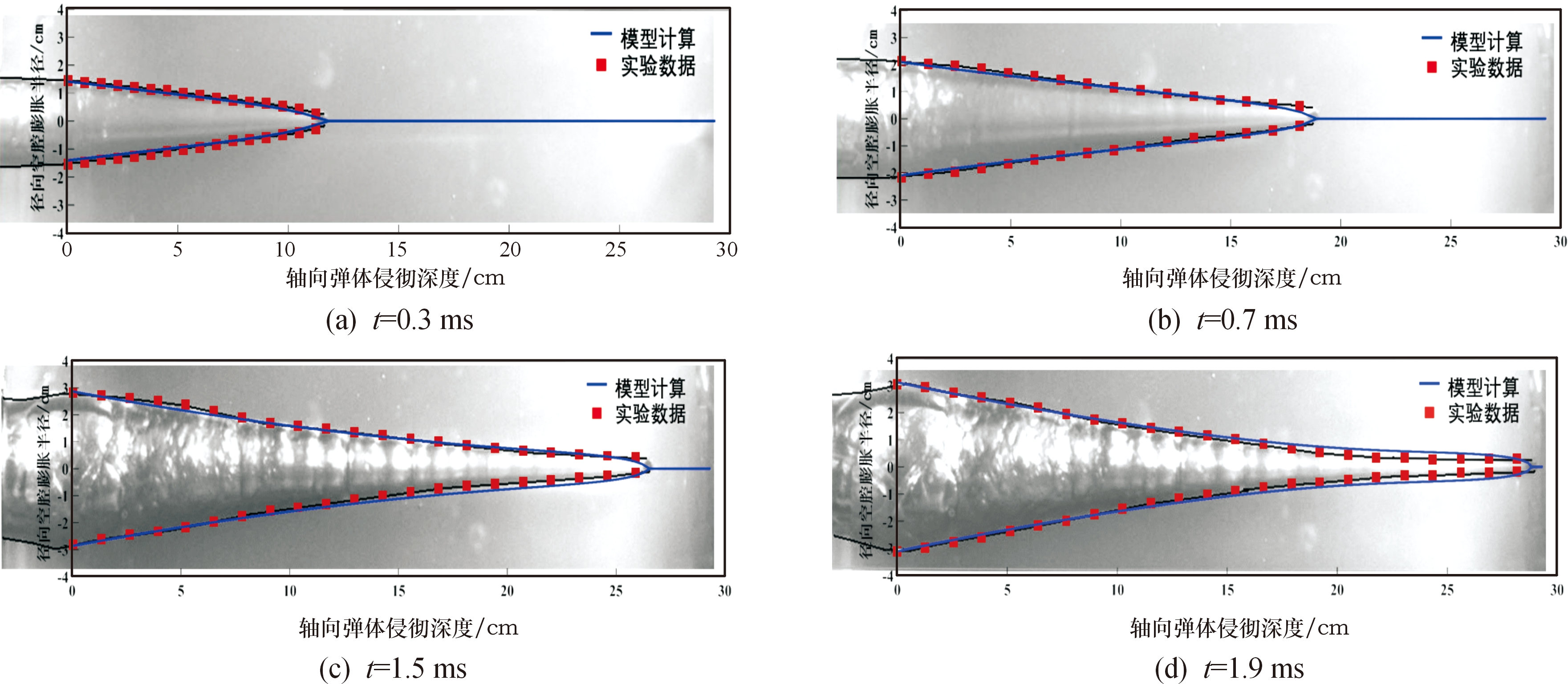
图9 直径4.8 mm球形弹体侵彻明胶的瞬态空腔
Fig.9 Temporary cavity of 4.8 mm diameter spherical projectile penetrating gelatin
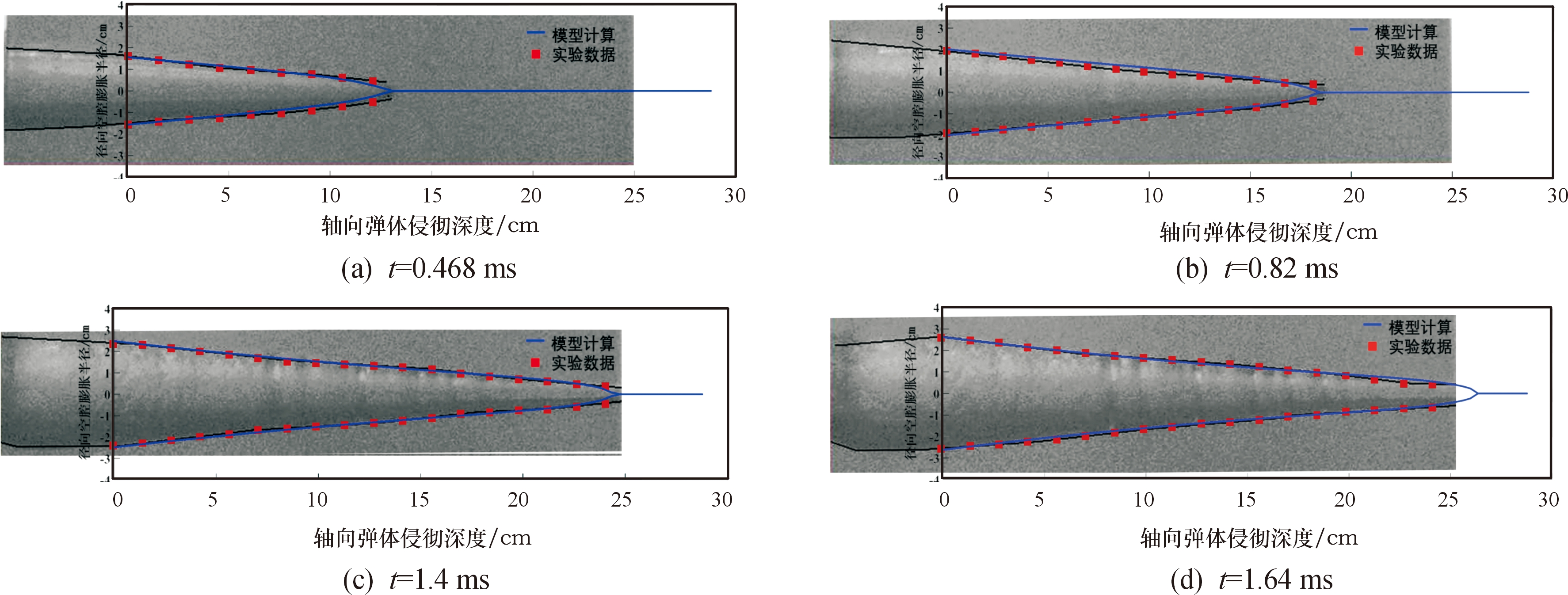
图10 直径6 mm球形弹体侵彻明胶的瞬态空腔
Fig.10 Temporary cavity of 6 mm diameter spherical projectile penetrating gelatin
从图7—图10中可以看出,从初始侵彻到空腔膨胀到最大体积,本文模型的计算结果和实验结果一致。图7—图10四图中的(a)、(b)两图为侵彻前期的空腔形状,而(c)、(d)两幅图则是侵彻后期的空腔形状,总体而言,在侵彻前期,模型的预测误差较小,而在侵彻后期,模型预测误差增大,这可能是由于相邻截面层之间的能量传递在空腔膨胀后期变得明显,而理论模型并没有考虑能量在相邻层之间的传递问题。
4 结论
主要工作是研究球形弹体在明胶中侵彻过程的建模问题。对弹体和靶标介质进行了动力学分析,提出了描述弹体和介质运动的侵彻模型。分析了球形弹体对明胶的侵彻实验结果,进行了定量研究。模型计算和实验结果之间的比较表明,由本研究所提出的预测的侵彻过程与实验中观察到的情况非常一致。主要结论如下:
1) 从能量转换和守恒的角度,可同时对弹体沿其弹道的运动(侵彻阻力)和目标介质沿垂直于弹道方向的运动(瞬时空腔)进行建模,侵彻阻力模型和瞬时空腔模型共用一组参数Ps、B0和β,可将弹体的运动与靶标介质的运动紧密结合,与以往分开建模的思路相比,更能体现侵彻过程中弹体运动和介质变形的内在联系。
2) 模型中的3个参数Ps、B0和β具有明确的物理意义,通过分析侵彻实验结果可获得参数的值或范围。当球形弹体的直径在3～6 mm、初始侵彻速度在500～900 m/s时,Ps的值为0.3～0.32 MPa,B0的值为3.07±0.124 5,β的值为0.24±0.006 37。用数值方法求解方程式(10)中模型可准确预测瞬时空腔的轮廓变化规律。
本研究中建模过程中的一个假设是沿弹道方向每个横截面内部的能量守恒,当空腔膨胀接近最后阶段时,忽略相邻横截面层之间的能量传递会增大空腔轮廓的计算误差,这一问题应在今后的工作中加以考虑。
[1] CARR D J,STEVENSON T,MAHONEY P F.The use of gelatine in wound ballistics research[J].International journal of legal medicine,2018,132(6):1659-1664.
[2] JIN Y,MAI R,WU C,et al.Comparison of ballistic impact effects between biological tissue and gelatin[J].Journal of the mechanical behavior of biomedical materials,2018,78:292-297.
[3] 张钰龙,郑宾,郭华玲,等.球形钨破片侵彻钢靶毁伤效应研究[J].兵器装备工程学报,2020,41(5):32-36.
ZHANG Yulong,ZHENG bin,GUO Hualing,et al.Study on damage effect of spherical tungsten fragments penetrating steel targets[J].Journal of Ordnance Equipment Engineering,2020,41(5):32-36.
[4] AL KHALIL M,FRISSANE H,TADDEI L,et al.SPH-based method to simulate penetrating impact mechanics into ballistic gelatin:Toward an understanding of the perforation of human tissue[J].Extreme Mechanics Letters,2019,29:100479.
[5] 樊菲,李伟兵,王晓鸣,等.爆炸成型弹丸战斗部不同侵彻着角下的毁伤能力研究[J].高压物理学报,2012,26(2):199-204.
FAN Fei,LI Weibing,WANG Xiaoming,et al.Research on the damaging ability of EFP warhead at different incidence angle[J].Chinese Journal of High Pressure Physics,2012,26(2):199-204.
[6] MO G L,LI Z X,WU Z L.A theoretical model of non-deforming bullets penetrating ballistic gelatin[J].International Journal of Impact Engineering,2018,114:105-110.
[7] 李金铭,闫文敏,董方栋,等.射击角对步枪弹侵彻玻璃靶后运动的影响规律[J].北京理工大学学报,2021,41(4):349-355.
LI Jinming,YAN Wenmin,DONG Fangdong,et al.Influence of penetration angle on rifle projectile penetrating glass target[J].Transactions of Beijing Institute of Technology,2021,41(4):349-355.
[8] 姜荃,温垚珂,张俊斌,等.步枪弹对有防护明胶靶标钝击作用传递模型研究[J].兵器装备工程学报,2021,42(4):31-36.
JIANG Quan,WEN Yaoke,ZHANG Junbin,et al.Research on transfer model of rifle projectile blunt impact on protected gelatin target[J].Journal of Ordnance Equipment Engineering,2021,42(4):31-36.
[9] LIU K,JIANG M,WU Z,et al.A mechanical model for spherical fragments penetrating gelatine[J].International Journal of Impact Engineering,2019,131:27-38.
[10] SEGLETES S B.Modeling the penetration behavior of rigid spheres into ballistic gelatin[J].Art-Tr-4393,2008.
[11] PETERS C E.A mathematical-physical model of wound ballistics[J].J Trauma (China),1990,6(Suppl 2):303-318.
[12] 刘坤,吴志林,徐万和,等.弹头侵彻明胶的运动模型[J].爆炸与冲击,2012,32(6):616-622.
LIU Kun,WU Zhilin,XU Wanhe,et al.A motion model for bullet penetrating gelatin[J].Explosion and Shock Waves,2012,32(6):616-622.
[13] SELLIER K G,KNEUBUEHL B P,RUFER R.Wound ballistics and the scientific background[M].Amsterdam:Elsevier,1994.
[14] 莫根林,吴志林,刘坤.球形破片侵彻明胶的瞬时空腔模型[J].兵工学报,2013,34(10):1324-1328.
MO Genlin,WU Zhilin,LIU Kun,et al.Temporary cavity model of spherical fragments penetrating ballistic gelatin[J].Acta Armamentarii,2013,34(10):1324-1328.
[15] LIU L,FAN Y,LI W,et al.Cavity dynamics and drag force of high-speed penetration of rigid spheres into 10wt% gelatin[J].International journal of impact engineering,2012,50:68-75.
[16] LIU L,WAN A,WANG P,et al.Modeling of penetration process of fragments in ballistic gelatin[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2022,236(7):3375-3386.
[17] LIU L,JIA Z,MA X,et al.A spherical cavity expansion model of large elastic deformation and its application to ballistic gelatin penetration problems[J].International Journal of Impact Engineering,2014,71:106-116.
[18] LIU S,XU C,WEN Y,et al.Cavity dynamics in 10 wt% gelatin penetration of rifle bullet[J].International Journal of Impact Engineering,2018,122:296-304.
[19] FORRESTAL M J,LUK V K,BRAR N S.Perforation of aluminum armor plates with conical-nose projectiles[J].Mechanics of Materials,1990,10(1/2):97-105.
[20] LIU L,FAN Y,WANG P,et al.A resistance force model for spherical projectiles penetrating ballistic gelatin based on cavity expansion theory[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2021,235(17):3135-3145.
[21] FORRESTAL M J,WARREN T L.Perforation equations for conical and ogival nose rigid projectiles into aluminum target plates[J].International Journal of Impact Engineering,2009,36(2):220-225.