0 引言
在人防工程设计过程中确定冲击荷载是进行结构安全性核算的重要一环,而确定空中点源爆炸波阵面参数是后续确定冲击波传播和结构荷载的初始计算步,其计算的精确性严重影响后续冲击波传播及工程结构爆炸荷载的核算,因此能够获取更加精确的自模拟解对工程防护结构抗力优化意义重大。空气中球面对称装药强爆炸存在移动波阵面边界,该波阵面边界和其自身控制方程相关联,该问题的求解通常称为自模拟解。Taylor[1],Von Neumann[2],Sedov[3]及国内科研人员[4]分别给出了空气中强爆炸的自模拟解。尽管形式上有所不同,但基本原理和过程是一致的。首先构建常微分形式的无量纲的冲击波压力、质点速度、密度与比例距离的关系式,该常微分的继续求解则存在多种可能的形式:精确解析解、近似解析解、数值解。其中精确解析解最终并没有给出显式的最终解[3],近似解近似过程则仍然存在误差且难以求解[1],目前通常的求解办法是采用数值解通过经典四阶Runge-Kutta方法(RK4)进行求解[5,6],该求解方法可以将波阵面参数的计算误差控制在四阶。现在数值计算软件如Autodyn中将球对称自模拟解计算结果映射到三维网格上作为冲击波初始参数并传播到结构产生后续荷载[7],这种算法对自模拟解精度提出了更高要求。本文中改进原有算法,采用误差控制的自适应步长Runge-Kutta法,以实现了对空中点源爆炸自模拟过程更精确求解。
1 空中球面对称装药强爆炸及其控制方程
本文中以空中点源爆炸波阵面参数为主要研究对象,该过程可由自模拟解求得冲击波阵面上的压力,质点速度和密度3个重要指标。空中点源爆炸的示意图如图1所示,这一过程主要基于几点假设:① 爆炸物相对于求解范围足够小(如核爆炸);② 空气为理想气体;③ 在这一过程中与外界不发生热交换。
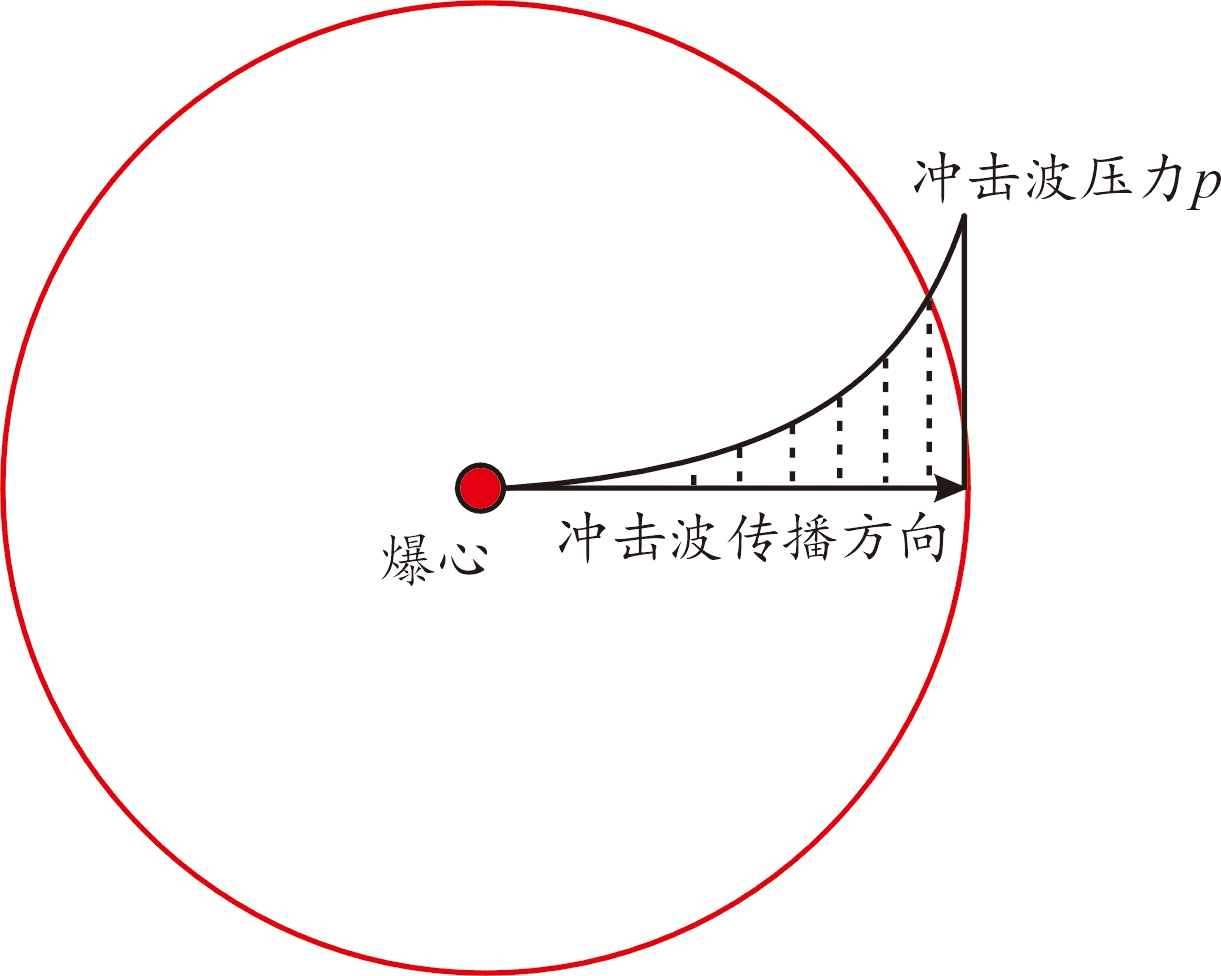
图1 空中点源爆炸示意图
Fig.1 Schematic diagram of point source explosion in the air
在以上假设条件下可建立空中点源爆炸自模拟过程的基本方程,在球对称条件下原来的三维球坐标问题则可以缩减为一维问题,另外根据自模拟过程的定义,知道所有变量均与一个变量相关,因此假定一个基本参量——波阵面半径rs,而波阵面质点速度可写为
![]()
(1)
式中:D为波阵面质点速度;rs为波阵面半径;t为时间。根据Rankine-Hugoniot条件[8-11],冲击波阵面上存在动量守恒、质量守恒和能量守恒
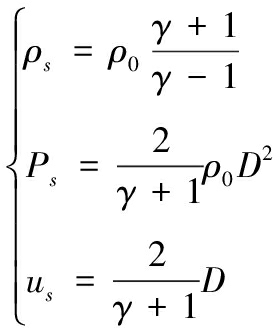
(2)
式中:ρs为波阵面上的空气密度;Ps为波阵面上的冲击波压力;us为波阵面上的质点速度;γ0空气的冲击绝热系数; ρ0为常温常压下空气密度。
球对称坐标下,理想气体的运动方程满足动量守恒、质量守恒和能量守恒方程[12]
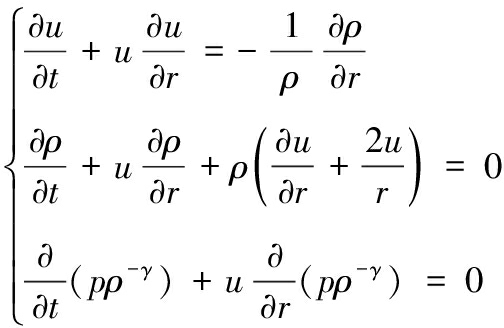
(3)
式中:u为质点密度;p为压力;ρ为密度;r为球坐标位置。式(2)、式(3)即是求解球面对称装药强爆炸自模拟解的控制方程,通过式(2)、式(3)求解对应的波阵面上质点速度、压力、密度等参数的过程即为自模拟解的求解过程。为求解这些待求未知量,需要对式(2)、式(3)进行无量纲化,并应用边界条件,然后进行差分求解。
2 控制方程的无量纲化、微分形式的自模拟解及其边界条件
根据量纲分析中的Π定理[13],比例距离和主要变量之间存在以下联系
![]()
(4)
式中:R为无量纲化的比例距离;E0为爆心的初始能量; ρ0为爆心的初始密度。能量、密度、时间表示成可量测的变量质量M,时间T以及长度L
L∝MαL2αT-2αTβMδL-3δ
(5)
式中:α、β、δ为常量。两边量纲相同,因此:
α+δ=0,2α-3δ=1,-2α+β=0
(6)
求得:
α=1/5,β=2/5,δ=-1/5
(7)
根据式(4)中的比例距离和主要变量关系以及式(5)—式(7)计算得到的量纲系数,构建得到自模拟解的独立变量无量纲的比例距离η,表示为
![]()
(8)
以无量纲的比例距离η为基本变量,根据Rankine-Hugoniot条件,待求解变量冲击波压力p、气体密度u、密度ρ,分别满足如下关系:
![]()
(9)
u=AR-3/2φ(η)
(10)
ρ=ρ0ψ(η)
(11)
将式(9)—式(11)代入式(3)进行变换(此处省略简化公式的详细步骤),得到待求解无量纲的压力f,质点速度φ及密度ψ微分形式的表达式[2,6,7]
![]()
(12)
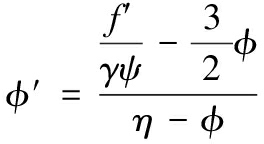
(13)
![]()
(14)
其中; γ为绝热系数,取1.4[2]。波阵面边界上存在边界条件:
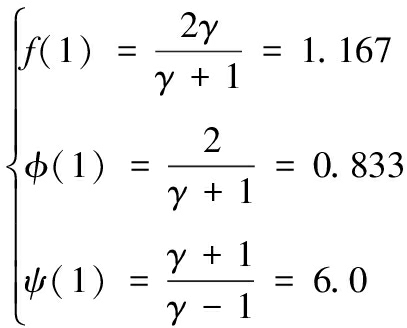
(15)
另外在球心对称点处为静止状态满足质点速度为0,因此φ(0)=0。
常微分方程组(式(12)—式(14))通常采用经典四阶Runge-Kutta方法(RK4)进行求解[5-6],该求解方法具备4阶精度。
3 自适应Runge-Kutta方法
为进一步提高计算精度,满足更高精度的工程计算要求,本研究中采用可控精度的5阶自适应Runge-Kutta方法进行求解,在满足5阶精度的情况下,可以有效减少迭代步数,同时因为误差控制的引入,可以显式的控制结果的误差,从而实现人为可控的高精度求解的要求。对于任意常微分方程存在:
g′(ξ)=G(ξ,g(ξ),g(ξ0))=g0
(16)
任意函数经泰勒展开后可表示为
![]()
(17)
式中:bi为Runge-Kutta方法中的增量步的权重系数;ki为增量步i上的导数值,Runge-Kutta方法可以给出不同的增量步数和权重值对常微分方程进行求解,其中比较典型的Runge-Kutta求解方法有前向欧拉、后向欧拉、Newmark方法以及四阶Runge-Kutta方法[14]。不同迭代方法的当前步第i步的导数ki均可表示为
![]()
(18)
其中:
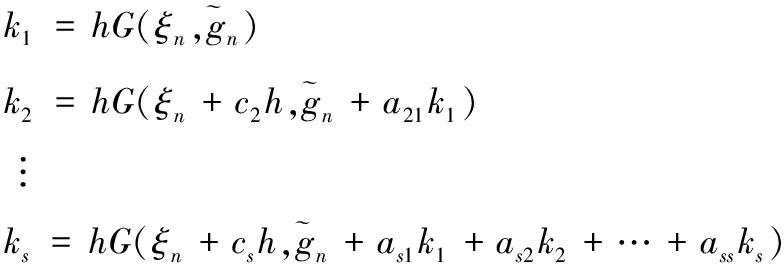
(19)
泰勒展开式误差可以用不同阶数的展开形式求差获得,因此对于自适应Runge-Kutta方法的误差通过比较2种不同阶数p、p-1得到[15]
![]()
(20)
为进一步提高原有四阶Runge-Kutta方法冲击波自模拟解的计算精度,采用四阶-五阶自适应的Runge-Kutta-Fehlberg方法(简称RKF方法)[16],p=5阶和p-1=4阶2种情况下的Butcher tableau(Runge-Kutta方法中的系数矩阵a通常通过Butcher tableau的形式给出[17]),RKF的Butcher tableau具体形式如式(22)。该方法因具有五阶精度且能够根据当前误差自动控制步长,目前在微分方程和偏微分方程的求解中得到了广泛应用[18-19]。
(21)
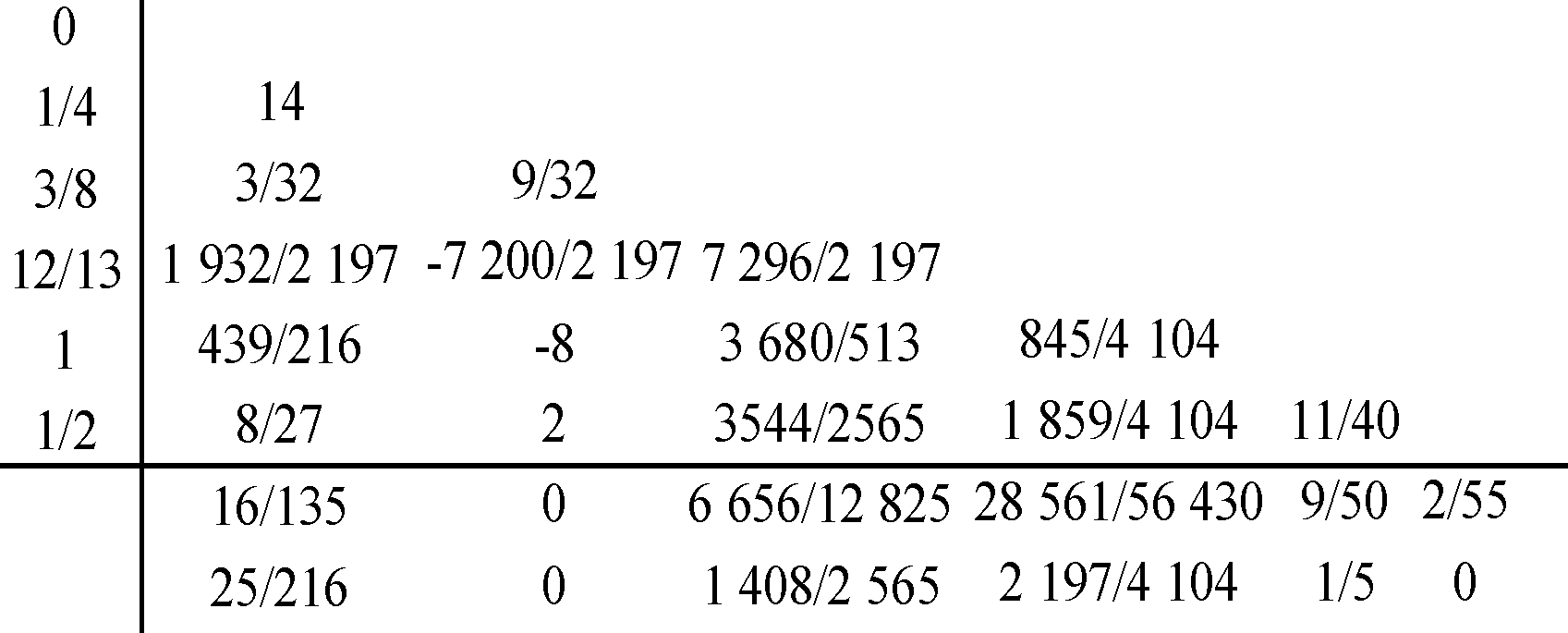
(22)
该方法的计算步长可通过如下公式获得:
![]()
(23)
RKF方法与原有的四阶Runge-Kutta方法求解自模拟解程序实现方法上的主要不同[5-6]之处在于:① Butcher tableau数据不同;② 计算完各增量点出的导数k之后,需要采用不同的权重和分别计算最终函数值,其中以五阶权重对应的结果为准;③ 计算完成进行误差的校核;④ 评估误差是否满足精度要求;⑤ 如不满足修正增量步长重新计算,如满足以当前步长作为输入值,进入下一步计算。通过Matlab程序实现了该算法,计算程序设计流程见图2所示。
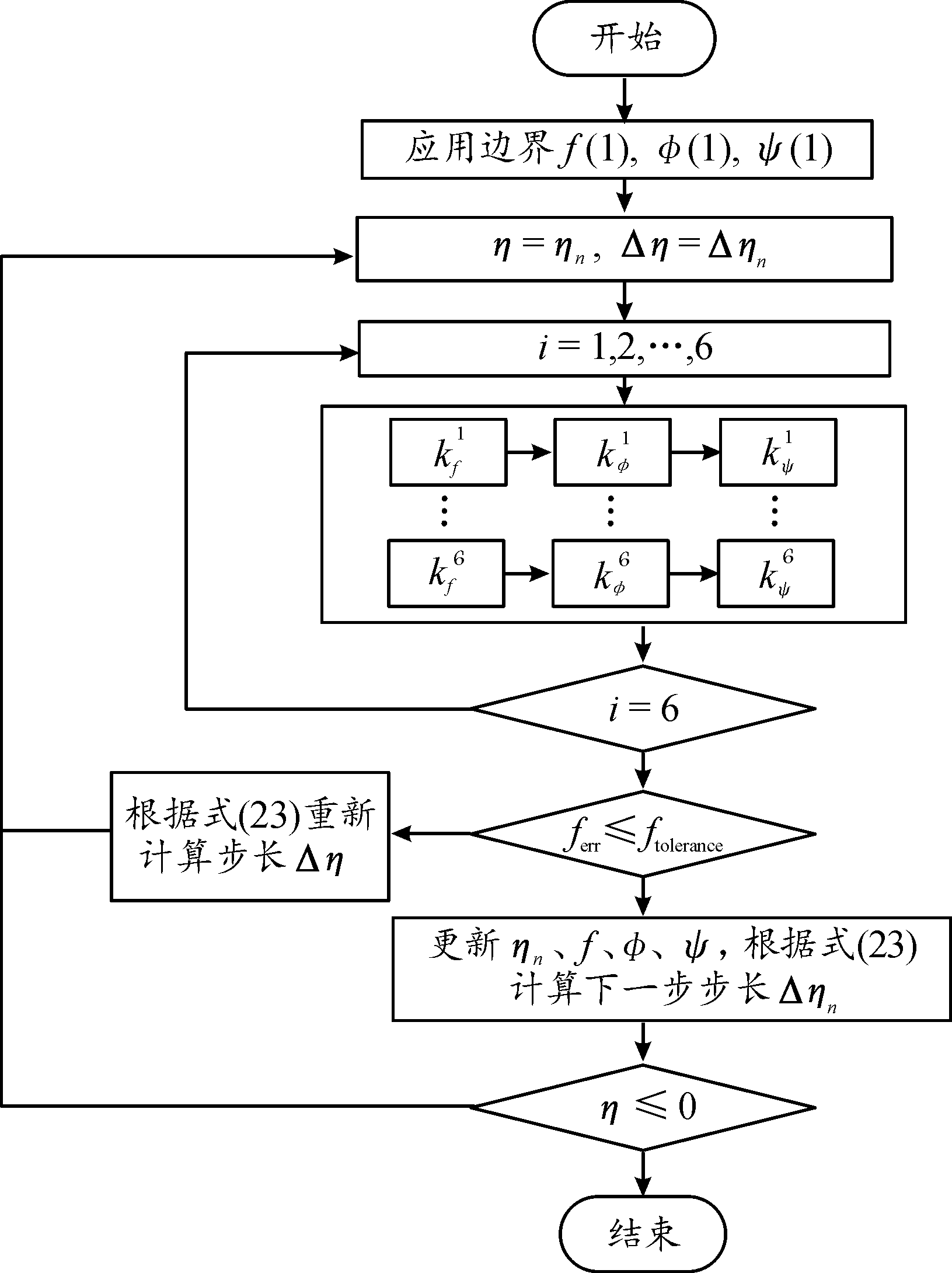
图2 RKF算法计算程序流程
Fig.2 RKF algorithm program flow
4 计算结果与分析
冲击波的自模拟问题没有显式的精确解析解,为进行对照分析,本研究中同时采用四阶Runge-Kutta方法,取极小步长Δη=0.000 1对方程进行求解,作为对照分析的基准结果。然后采用固定步长RKF算法对自模拟方程进行求解,并分析了各主要爆炸波待求参量f、φ、ψ求解误差随比例距离η变化的分布情况。最后利用自适应步长的RKF算法对自模拟方程进行求解,得到了误差控制的自模拟解。
4.1 RKF算法固定步长条件下的误差分布
分析等步长计算时的误差分布可为后续验证RKF方法是否能在误差较大区域自动缩减步长提供验证性依据。因此本文中首先采用较长的步长Δη=0.005进行等步长的RKF算法计算,分析固定步长条件下的误差分布。图3为固定步长求解结果,从其中可以看出,3个无量纲参数均从初始值η=1.0开始迭代,随着η的递减,误差逐步降低,接近数值畸点0时,误差开始陡增。从误差数值上看,无量纲压力f的误差最小,其次是无量纲密度ψ,无量纲速度φ再次之。然而数量上无量纲速度φ接近畸点是陡增至0.8,为解决该问题则需要大幅度增加计算步数。在其他数值精度均已相对可靠的情况下,因部分数值的误差需要计算系统的额外开销。因此,总结图3所示的规律可以发现,误差主要来自于自模拟过程的无量纲速度φ,为解决接近畸点处的精度问题,需要额外的计算步数。这一结果符合对算法在强非线性段加密步长的预期。
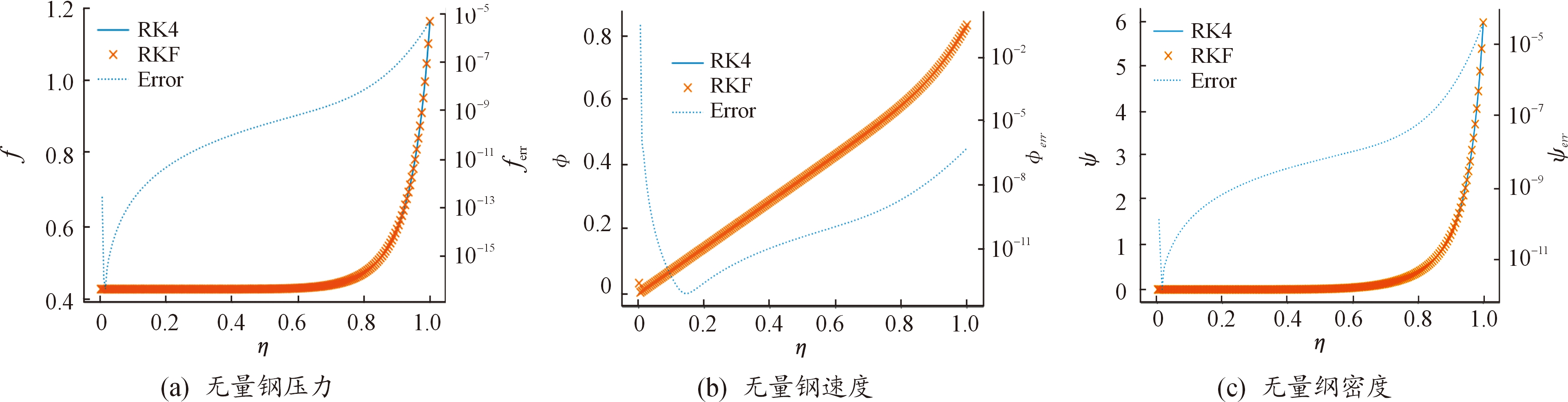
图3 固定步长求解结果
Fig.3 Fixed step solution results
4.2 自适应步长RKF算法求解精度分析
为解决4.1小节中无量纲速度φ接近畸点处误差较大的问题,通过采用自适应步长的RKF算法进行求解,理论上能够在畸点附近开始自动调节计算补充。计算中取αsafety=0.8,最大增加幅度αmax=0.4,最小缩减幅度αmin=0.125。RKF算法为五阶精度,因此计算步长是p=5。尽管RKF算法能够实现误差1.0×10-12以下的高精度计算,但是为能够在图上清楚的显示步长的变化,设置了3个较大的误差控制参数1.0×10-5、1.0×10-6、1.0×10-7,以便误差控制过程现实的更加明显,计算结果如图4所示。图3显示了两头的误差较大,而图4中两头的数据点比较密集,说明自适应步长RKF算法实现了根据误差对计算步长的自动控制。
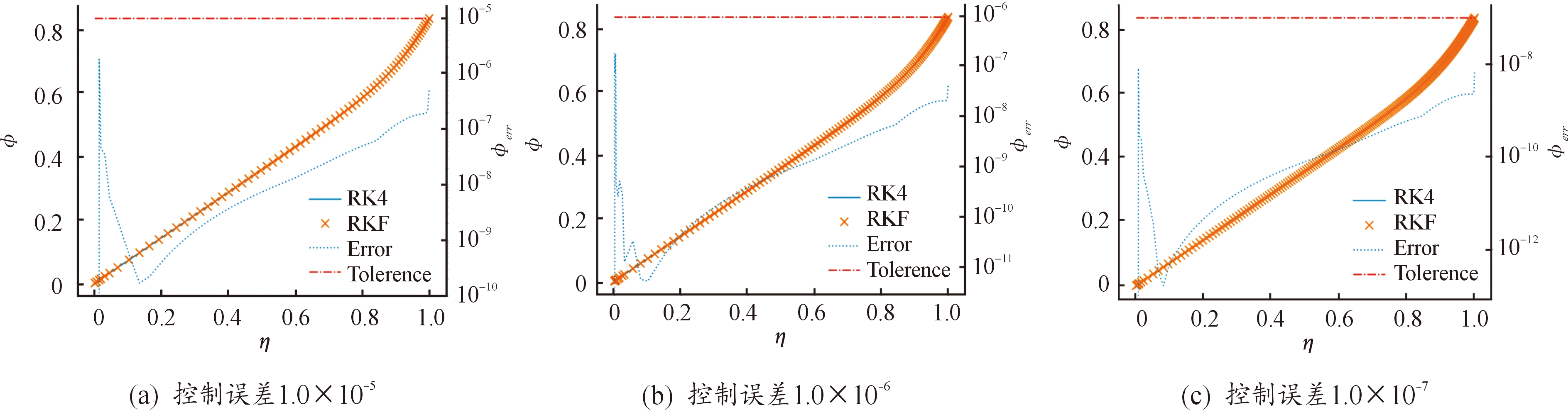
图4 自适应步长RKF算法求解结果
Fig.4 Adaptive step-size RKF algorithm solution results
4.3 不同算法的计算精度和效率分析
自适应步长RKF方法除了对误差显式控制上存在优势,在计算精度和计算效率方面是否依然存在优势还需要进一步的验证,因此本文中分别用RK4、固定步长RKF以及自动步长RKF三种方法进行了计算,其中自动步长RKF的误差控制参数同第4.2节。计算中采用的计算硬件平台为i7-7700k和64 G内存,软件平台为Windows 10 和Matlab 2019,不同算法的计算控制参数、计算时间及最大绝对误差如表1所示。
表1 不同算法的计算精度与计算时间
Table 1 Calculation accuracy and calculation efficiency of different algorithms
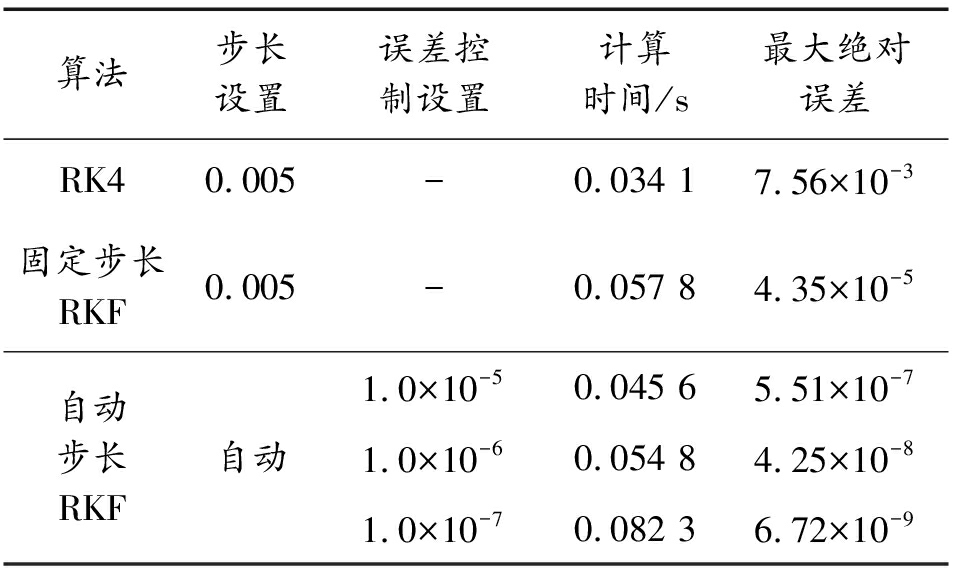
算法步长设置误差控制设置计算时间/s最大绝对误差RK40.005-0.034 17.56×10-3固定步长RKF0.005-0.057 84.35×10-5自动步长RKF自动1.0×10-50.045 65.51×10-71.0×10-60.054 84.25×10-81.0×10-70.082 36.72×10-9
从表1中可以看出RK4用时最省,为0.03 s,自动步长RKF所需时间最长为0.08 s,RKF算法在计算效率上略低于RK4算法,但是所有算法的计算时长均在0.1 s以内,因此RKF的计算效率的降低仍在可接受范围之内。对比固定步长RKF和自动步长RKF的计算效率可以发现,即使是自动步长RKF方法在最大误差小于固定步长RKF方法时,用时仍然小于固定步长RKF方法,因此自动步长RKF方法对比固定步长RKF方法计算效率上具有明显优势。分析不同计算方法的最大绝对误差,可以看出同计算步长的RKF方法的计算误差明显小于RK4方法,而自动步长RKF方法则可以很好地将误差控制在设置范围内。
5 结论
空中点源爆炸波阵面参数的误差会在累计到后续的装备毁伤计算中,因此提高其精度对提升毁伤分析的可靠性有重要意义。本研究中改进了空中点源爆炸波阵面参数的求解方法,将原常用的四阶Runge-Kutta方法改进为五阶精度的自适应步长Runge-Kutta方法,并对这2种方法的结果进行了对比。结果表明,这一改进确能将计算精度提高了一阶,且解决了原先的误差不能显式控制的问题。改进后的方法在计算效率上略有降低,但考虑到总体计算时长较短,总体效率上可以接受。冲击波阵面参数求解中引入自适应步长RKF算法可为冲击波参数的精密计算提供了理论方法和技术支持,为后续装备毁伤评估的可靠性提供有力保证。
[1] TAYLOR G I.The formation of a blast wave by a very intense explosion-Ⅱ.The atomic explosion of 1945[J].Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences,1950,201(1065):175-186.
[2] PRUNTY S.Introduction to Simple Shock Waves in Air[M].Springer,2019.
[3] SEDOV L I.Similarity and dimensional methods in mechanics[M].CRC Press,2018.
[4] 戴家谦.冲击波理论讲义[Z].1963.
DAI Jiaqian.Lecture note of shock wave[Z].1963.
[5] 周丰俊,郑磊,孙云厚,等.真实空气中TNT装药爆炸近区冲击波传播特性研究[J].中国工程科学,2017,19(6):18-26.
ZHOU Fengjun,ZHENG Lei,SUN Yunhou,et al.Research on propagation characteristic in close-in field of shock wave of tnt charge explosion[J].Strategic Study of CAE,2017,19(6):18-26.
[6] 孙云厚.真实空气中TNT装药爆炸进去强冲击波传播特征及反射规律研究[D].南京:解放军理工大学,2015.
SUN Yunhou.Study on the propagation and reflection characteristic of shock wave created by charge blasting in real air[D].Nanjing:PLA University of Science and Technology,2015.
[7] PREMARATNE P D.Nuclear subsurface explosion modeling and hydrodynamic fragmentation simulation of hazardous asteroids[Z].2014.
[8] SAAD M A.Compressible fluid flow[M].Prentice-Hall,1985.
[9] BILLINGHAM J,KING A.C.Wave Motion.Cambridge Texts in Applied Mathematics[M].Cambridge University Press,2001.
[10] EMMONS H W.Fundamentals of gas dynamics,volume 3 of Ane Books[M].Wiley,2015.
[11] LEE H S.The gas dynamics of explosions[M].UK:Cambridge University Press,2016.
[12] NEEDHAM C E.Blast Waves.Shock wave and high pressure phenomena[M].Springer Berlin Heidelberg,2010.
[13] BUCKINGHAM E.On physically similar systems; illustrations of the use of dimensional equations[J].Phys.Rev.,1914,4(10):345-376.
[14] HAIRER E,NØRSETT S P,WANNER G.Solving ordinary differential equations I.nonstiff problems[C]//Volume 29 of Springer Series in Computational Mathematics.Springer Berlin Heidelberg,1987.
[15] ELLSIEPEN P,HARTMANN S.Remarks on the interpretation of current non-linear finite element analyses as differential-algebraic equations[J].International Journal for Numerical Methods in Engineering,2001,51(6):679-707.
[16] FEHLBERG E.Klassische Runge-Kutta-Formeln vierter und niedrigerer Ordnung mit Schrittweiten-Kontrolle und ihre Anwendung auf Wärmeleitungsprobleme[J].Computing,1970,6(1):61-71.
[17] BUTCHER J C.Numerical methods for ordinary differential equations[M].Wiley,2016.
[18] FILIZ A.Numerical solution of linear volterra integro-differential equation using Runge-Kutta-Fehlberg method[J].Applied and Computational Mathematics,2014,3(1):9.
[19] SUSMITA P,SANKAR P M,PARITOSH B.Numerical solution of Lotka Volterra prey predator model by using Runge-Kutta-Fehlberg method and Laplace Adomian decomposition method[J].Alexandria Engineering Journal,2016,55(1):613-617.