0 引言
小口径火炮在短时间内形成连续弹幕,利用火力压制空中危险目标,但连续弹幕的形成需要可靠的快速供补弹系统。小口径火炮快速补弹系统(以下简称为快速补弹系统)将补给弹仓出弹口与弹鼓进弹口通过长行程软导引连接,软导引内部的闭式柔性弹链在弹仓电机与弹鼓电机同步驱动下高速运动,弹药通过闭式弹链在补给弹仓和弹鼓中完成传输,当两台电机正转时弹药从弹仓传送至弹鼓,反转时则弹药由弹鼓退回至弹仓。在快速补弹系统工作中,会出现因外界或者机械结构等因素导致的负载连续波动的情况,此情况会间接通过电机的转速以及转矩波动表现出来[1]。若双电机系统的同步性较差,电机转速或转矩的不同步使得输出转矩偏差较大,系统不能及时对此偏差进行修正,偏差的累积会使快速补弹系统造成损坏[2]。因此,针对快速补弹系统中双电机同步控制策略开展了研究。
在传统电机传动系统中,需要采用合适的控制算法,使电机的实际转速在受到一定的外部扰动后仍会快速回归到参考转速。目前使用的控制算法有传统的PID控制[3]、自适应控制[4]、模糊控制[5]、滑模控制[6]以及自抗扰控制[7]等。为了提高双电机系统抗干扰性以及同步性,国内外学者做了多方面的研究:文献[8]中提出了一种基于滑模控制的交叉耦合控制策略,提高了双电机系统在外部干扰下的同步精度。滑模控制是一种非线性控制,具有很强的鲁棒性,但其存在抖振现象,如何消除抖振是近几年研究的热点[9]。文献[10]提出了一种简单的模糊PI控制器,采用了速度误差负反馈同步驱动控制策略,通过仿真得到同步误差为0.5 r/min,但PID控制是一种线性控制器,在非线性系统中,其控制精度会有所下降[11];文献[12]提出一种基于模糊逻辑的交叉耦合控制算法,改进的交叉耦合控制通过模糊控制器动态调整耦合反馈系数,显著提高了启动阶段的同步性能,将同步误差控制在0.1 r/min附近。但其算法复杂,很难应用于实际工程中,且文中并未搭建实物测试平台,仅在软件中验证了控制策略的可行性;文献[13]针对大口径榴弹炮装填系统传统的齿隙问题,提出一种模型预测控制改善双电机系统的动态性能,并通过构成的实验台上对所提方案进行了验证。但是文中所提到的控制算法在低速情况下更为精确。文献[14]针对间接矩阵变换器馈电双电机系统开环同步问题,提出一种经济与模型预测的双电机同步控制策略,通过仿真以及试验结果证实了策略的有效性以及可行性,但文中的转速过低,当转速过高时无法确定系统的稳定性。自抗扰控制是在PID的基础上提出的一种无模型控制方法,其特点是将模型之外的参数变化以及外部干扰均视为系统之外的扰动,利用状态观测器对扰动进行实时监测,最后将监测的扰动变化量反馈到输出信号中,从而将被控对象转换为标准模型,在实际应用中具有很强的鲁棒性。
针对快速补弹系统中存在的负载扰动而使柔性弹链出现链速波动问题,开展了基于自抗扰控制的双电机同步控制策略研究。本文结构安排如下:首先对小口径火炮快速补弹系统柔性弹链动力学模型进行分析,并建立数学模型;之后对电机以及自抗扰控制系统进行数学建模,搭建基于自抗扰的控制的双电机交叉耦合同步控制系统;然后利用Simulink仿真以及实际测试验证所提算法的有效性,最后对本文的研究做出结论。
1 柔性弹链传动数学模型
弹链是由弹夹链节和链轮组成的闭合结构,多节刚性链节通过销轴级联而成,在图1中链节与链轮的啮合部分会形成一个多边形结构[15]。
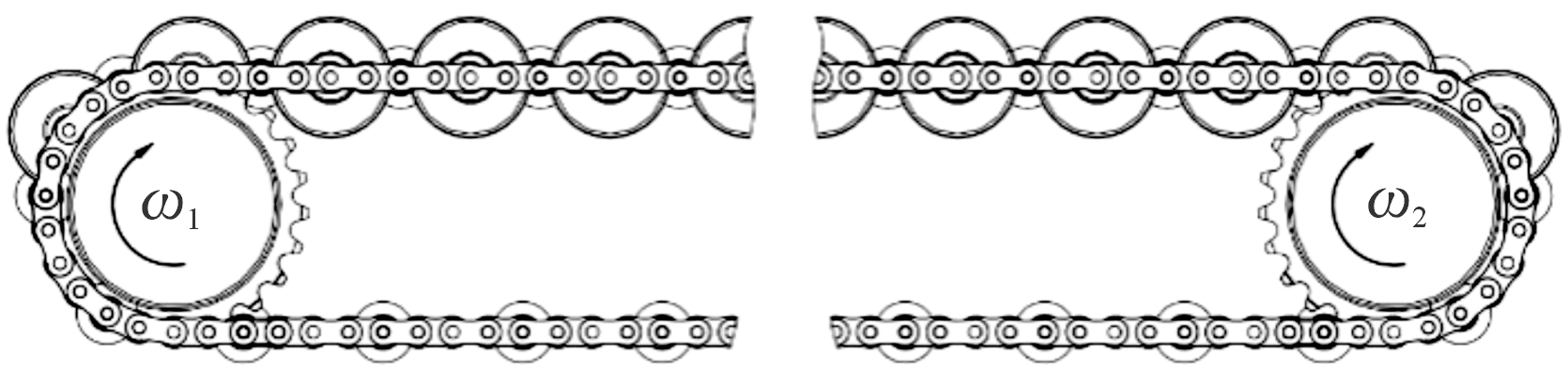
图1 弹链等效模型
Fig.1 Bullet chain equivalent model
多边形效应造成滚子和链轮在啮合点位置发生刚性碰撞,尤其在高速情况下,因碰撞产生的动载荷对于链条速度稳定性具有很大影响,严重时会使链条脱落甚至断裂[16]。当快速补弹系统存在干扰时,弹仓电机与弹鼓电机会存在一个不稳定的转速差,使得弹链产生紧边与松边。为了便于进行物理状态分析,将快速补弹系统中柔性弹链传动模型进行简化,如图2所示。
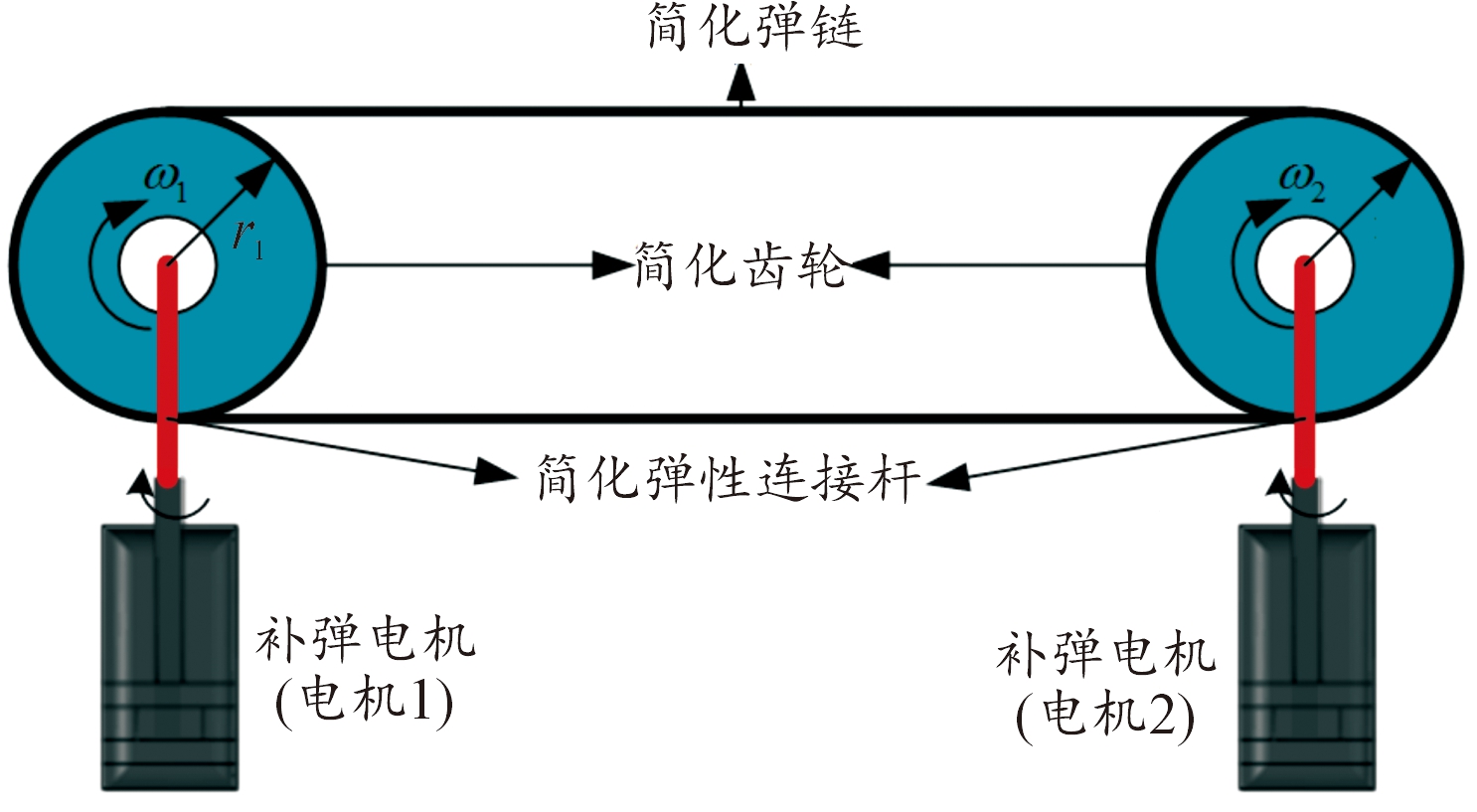
图2 弹链传动模型
Fig.2 Bullet chain drive model
图2为简化后的快速补弹系统的柔性弹链等效模型,ω1、ω2为电机1与电机2的机械角速度,r1、r2为简化齿轮的半径。在构建弹链传动简化模型时,并未将减速器考虑在内,电机与齿轮之间通过弹性连接杆连接,即电机的速度与简化齿轮速度存在一定的误差。
1.1 同步电机数学模型
在不影响模型精度的情况下,为了方便分析以及建立永磁同步电机数学模型,提出以下3点假设[17]:
1) 忽略电机铁芯的饱和。
2) 不计电机中的涡流损耗与磁滞损耗。
3) 电机中的电流为对称的三相电流。
基于上述假设,永磁同步电机在d-q轴旋转坐标系下的数学模型为
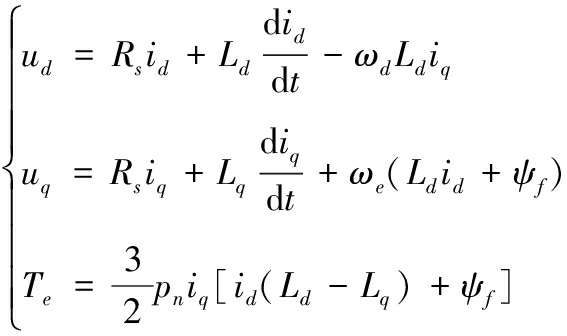
(1)
式中:ud、uq分别为定子电压的d-q轴分量;id、iq分别为定子电流的d-q轴分量;R是定子电阻;ψd、ψq分别为定子磁链的d-q轴分量;ωe为电角速度;Ld、Lq分别为d-q轴电感分量;ψf为永磁体磁链,Te为电机的电磁转矩,pn为电机的极对数。
从电机的数学表达式中可以看出,id与iq之间存在很强的耦合关系,为了更好的对电机进行控制,经常采用id=0控制来实现对id与iq进行解耦。此时电机的电磁转矩方程为
![]()
(2)
电机运动方程为
![]()
(3)
式中:J为转动惯量;TL为负载转矩;B为阻尼系数;ωr为电机的机械角速度。
1.2 双电机传动数学模型
如图2所示柔性弹链传动模型,对电机1以及电机2建立传动数学模型。由1.1所述单电机数学模型可以得出双电机传动运动方程为
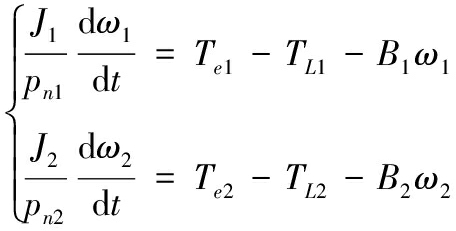
(4)
式中:ω1、ω2为电机1与电机2的机械角速度;J1、J2为电机1与电机2的转动惯量;pn1、pn2为电机1与电机2的极对数;Te1、Te2为电机1与电机2的电磁转矩;B1、B2为电机1与电机2的阻尼系数;TL1、TL2为电机1与电机2的负载转矩。其中,TL1、TL2数学表达式如下
![]()
(5)
式中:Kt1、Kt2为简化连接杆的刚度系数;c1、c2为简化连接杆的阻尼系数;θ1、θ2为电机1与电机2转动的机械角度;θt1、θt2为简化齿轮转动的机械角度。
2 基于自抗扰控制器的双电机同步控制系统设计
2.1 转速环ADRC设计
在电机控制系统中,电机转速是需要实时监控的控制量,是评价电机系统的重要指标之一。ADRC的特点是对被控对象的数学模型依赖程度不高,对系统中已知或未知的扰动有很好的抗干扰能力。以电机1为例,由式(2)以及式(3)可以得到下式
![]()
(6)
式中:iq1为电机1的q轴电流; ψf1为电机1的永磁体磁链。对(6)整理后可以得到下式
![]()
(7)
式中:b1=3pn1ψf1/2J1;a1(t)=-(TL1+B1ω1)/J1,视为系统的总扰动量。搭建ADRC速度环如图3所示。
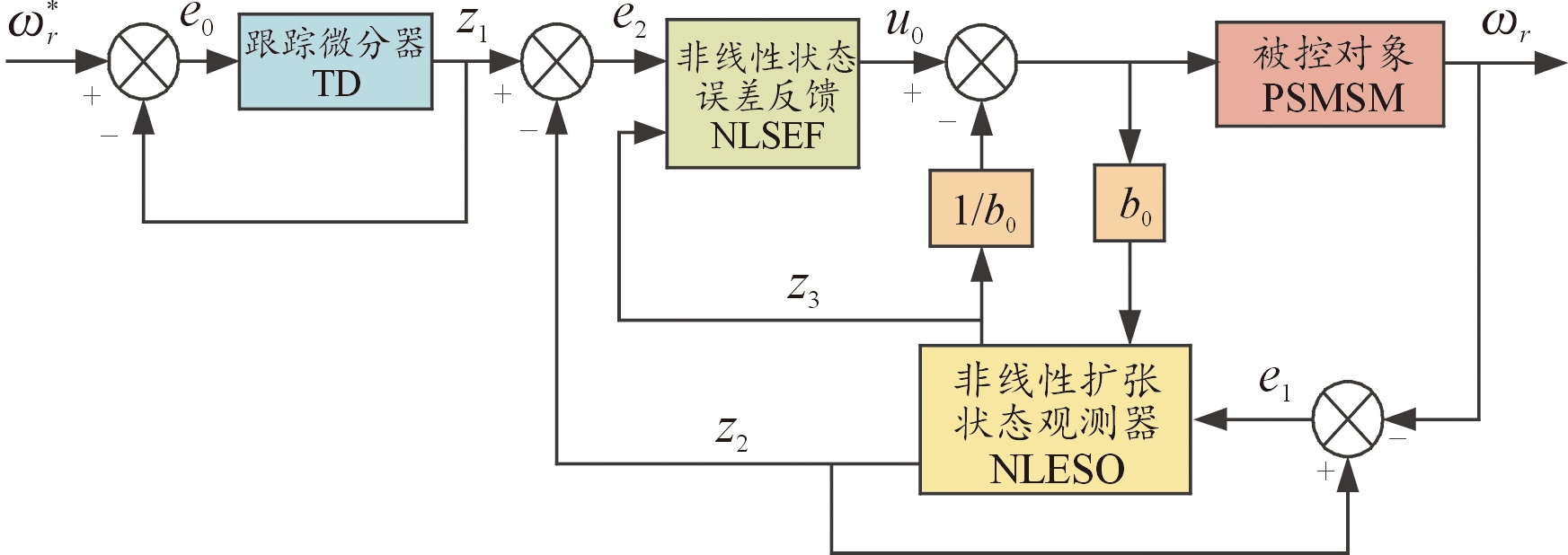
图3 速度环ADRC组成
Fig.3 Active disturbance rejection control strategy system
自抗扰控制器主要有3部分组成,分别是跟踪微分器(tracking differentiator,TD)、非线性扩张状态观测器(nonlinear extended state observer,NLESO)、非线性状态误差反馈(nonlinear state error feedback law,NLSEF)。跟踪微分器的作用是事先安排过渡过程,提取输入信号及其微分信号,解决PID超调性以及极速性之间的矛盾;非线性扩张状态观测器的作用是实时监测系统内外扰动,并用适当的方法进行补偿;非线性状态误差反馈的作用是对跟踪微分器以及非线性扩张状态观测器输出的状态变量之间的估计误差组成非线性误差反馈组合,得到误差反馈控制量,提升系统的控制性能[18]。
2.1.1 跟踪微分器设计
对永磁同步电机控制系统中输入的速度信号进行过度处理[19],得到如下表达式
![]()
(8)
式中:n*为系统的参考转速;z1为跟踪微分器输出的过渡信号; e0为误差信号;r为跟踪因子,r的值越大跟踪速度越快,但是过大会导致超调量增加;fal为最优控制函数,其定义如下[20]

(9)
式中:α为跟踪因子;δ为滤波因子,在本文中所出现的α0、α1、α2均为跟踪因子;δ0、δ1、δ2均为滤波因子,在下文中将不对以上参数进行说明。
2.1.2 非线性扩张状态观测器设计
非线性扩张状态观测器是自抗扰控制器的核心组成部分,其根本目的是估计系统内部以及外部的扰动值,并在反馈中给予补偿,利用补偿的方法消除扰动对系统的影响,从而使整个系统具有较强的抗干扰性[21]。基于PMSM速度环的非线性扩张状态观测器设计设计如下

(10)
式中:ωr为实际输出转速;z2为实际输出转速n的观测值;e1为实际输出转速n与观测值z2的误差信号;z3为系统总扰动的估计值,β1、β2为非线性扩张状态观测器输出误差校正增益,取值过大会导致扩张状态观测器的输出振荡发散,同时产生高频噪声信号;u为系统的控制量,b0为补偿因子。
2.1.3 非线性状态误差反馈设计
非线性状态误差反馈在在抗扰系统中起到数据整合的作用,其将跟踪微分器以及非线性扩张状态观测器输出的估计误差以及非线性扩张状态观测器输出的扰动补偿量整和成控制量,提升系统的稳定性[22]。基于PMSM速度环的非线性状态误差反馈设计设计如下:
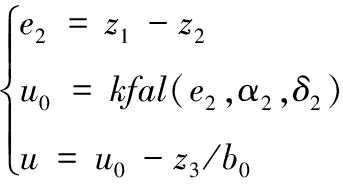
(11)
式中:u0为输出补偿量;b为补偿因子;k为调节器增益。最后得到基于速度环的永磁同步电机控制系统如图4。
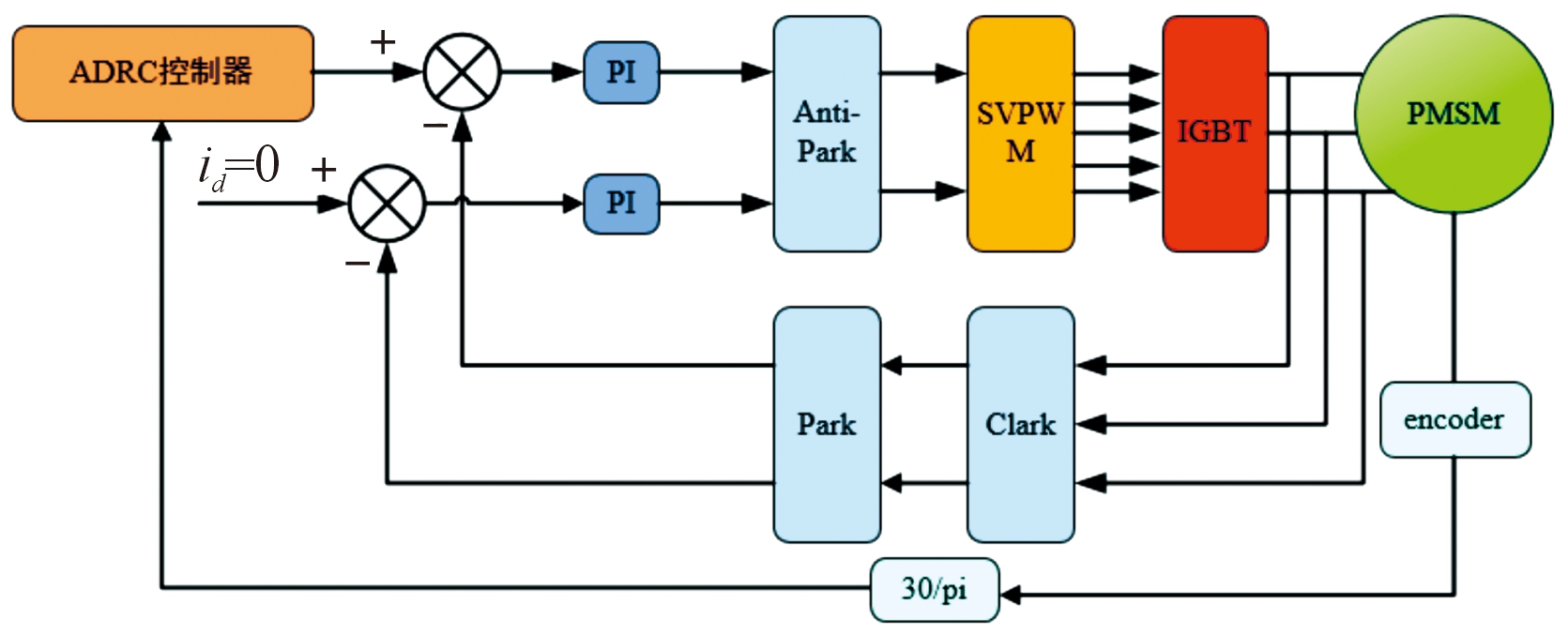
图4 永磁电机矢量控制系统框图
Fig.4 Block diagram of vector control system of PMSM
2.2 交叉耦合控制器设计
双电机同步控制器采用基于滑模变结构的交叉耦合控制策略。2个电机的输出信号经过耦合后将输出的误差信号传递给交叉耦合控制器,交叉耦合控制器将所得到的误差信号按照某种关系分别补偿到电机控制器的最输入信号之中,达到减小误差,提高精度的作用。双电机交叉耦合同步控制系统结构框图如图5所示。图中K1、K2为增益,TL1、TL2为负载转矩。
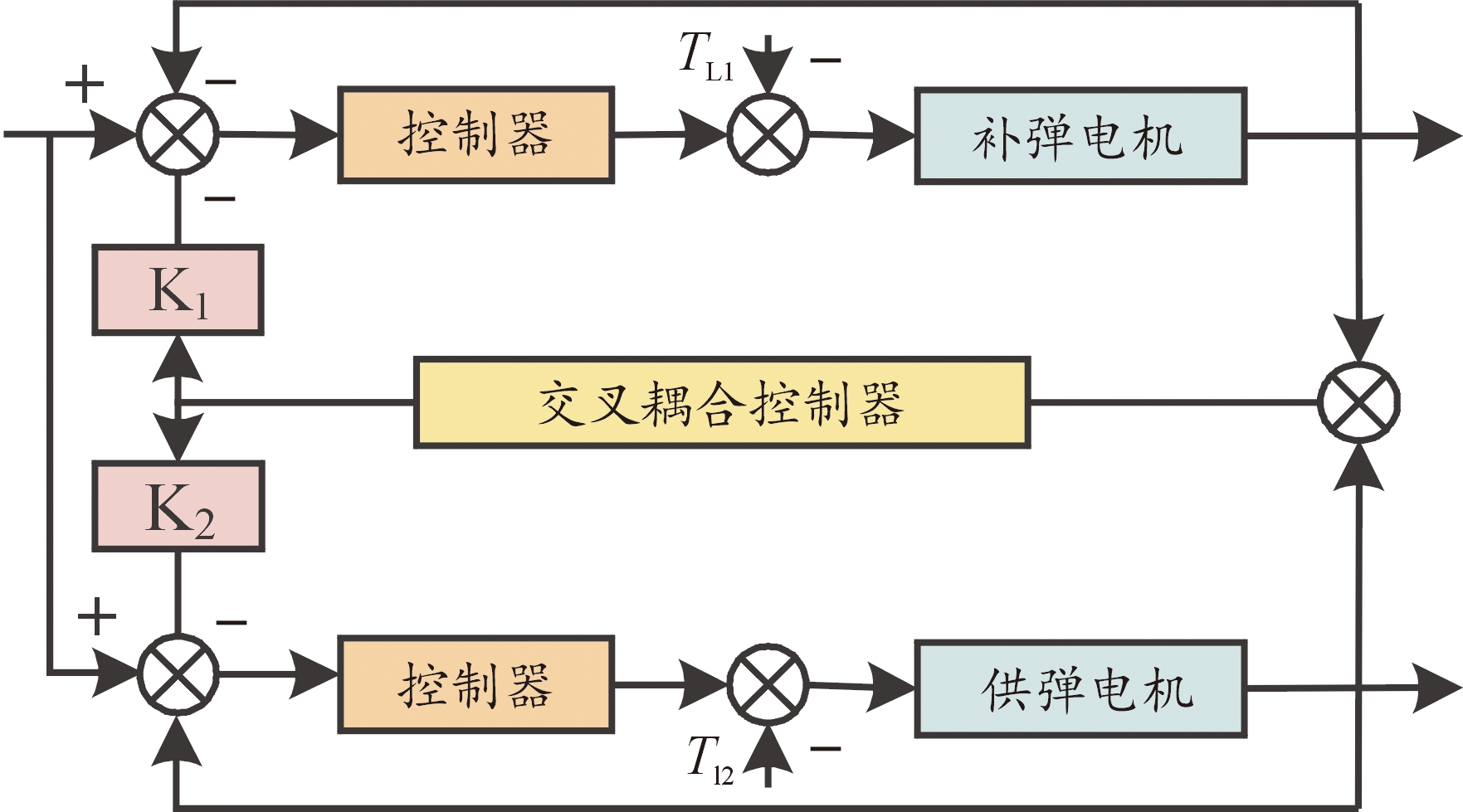
图5 交叉耦合控制系统框图
Fig.5 Block diagram of cross-coupled control system
考虑到永磁同步电机是一个二阶单输入单输出的非线性控制系统,在本文中i=1,2。则定义永磁同步电机系统状态变量为如下形式:
![]()
(12)
结合式(12)以及式(3),得到状态变量方程为
![]()
(13)
其中:b=3pnψf/2J,h=TL/J;d=B/J。永磁同步电机的全局快速终端滑模面为:
![]()
(14)
其中,α、β、p、q为滑模结构的系数,α、β>0,p、q为正奇数,为了避免奇异性的出现,一般认为,q<p<2q。
根据式(12)以及式(13)定义,假设2个电机的转速同步误差信号为
δ=ω1-ω2=x21-x11
(15)
二阶滑模控制律的滑模面定义为
![]()
(16)
将式(15)代入式(16),滑模面可以简化为下式:
![]()
(17)
由于q<p<2q,当β取值很小时,可以取滑模面方程为
τ=s2-s1
(18)
此时滑模控制率为
![]()
(19)
通过上述分析,在Matlab/Simulink建立基于ADRC的双电机同步控制系统,为了便于分析以及对比,同时在Matlab/Simulink建立基于PI的双电机同步控制系统,除了控制系统不同外,其余基本相同,图6给出了基于ADRC的双电机同步控制系统结构。

图6 基于ADRC双电机同步控制系统
Fig.6 ADRC based dual-motor synchronous control system
3 仿真分析及试验验证
3.1 仿真分析
电机参数如表1所示。在Simulink搭建ADRC控制器参数如表2所示。
表1
Table 1 Motor parameters
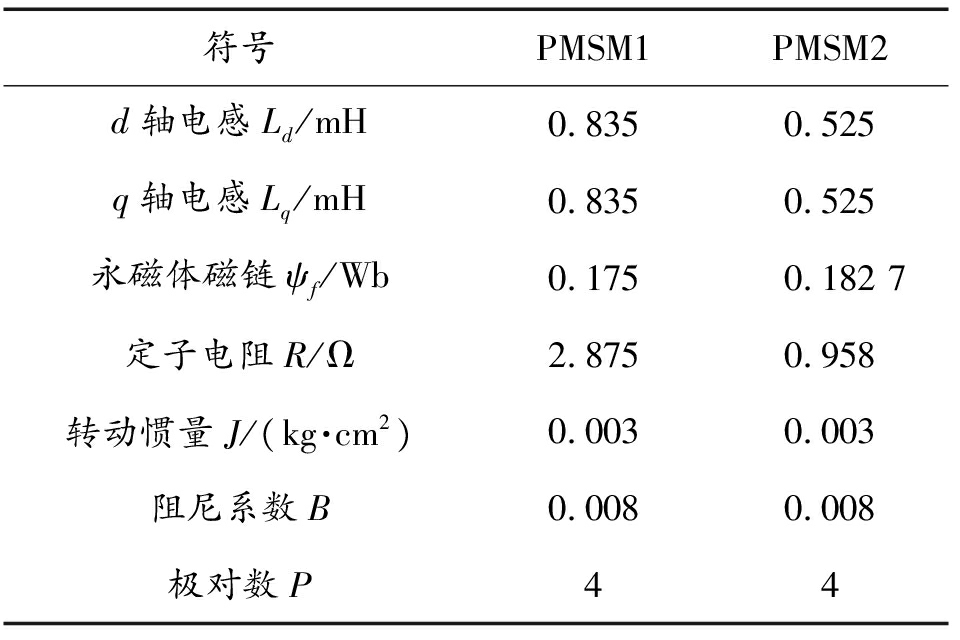
符号PMSM1PMSM2d轴电感Ld/mH0.8350.525q轴电感Lq/mH0.8350.525永磁体磁链ψf/Wb0.1750.182 7定子电阻R/Ω2.8750.958转动惯量J/(kg·cm2)0.0030.003阻尼系数B0.0080.008极对数P44
表2 ADRC控制器参数
Table 2 ADRC controller parameters
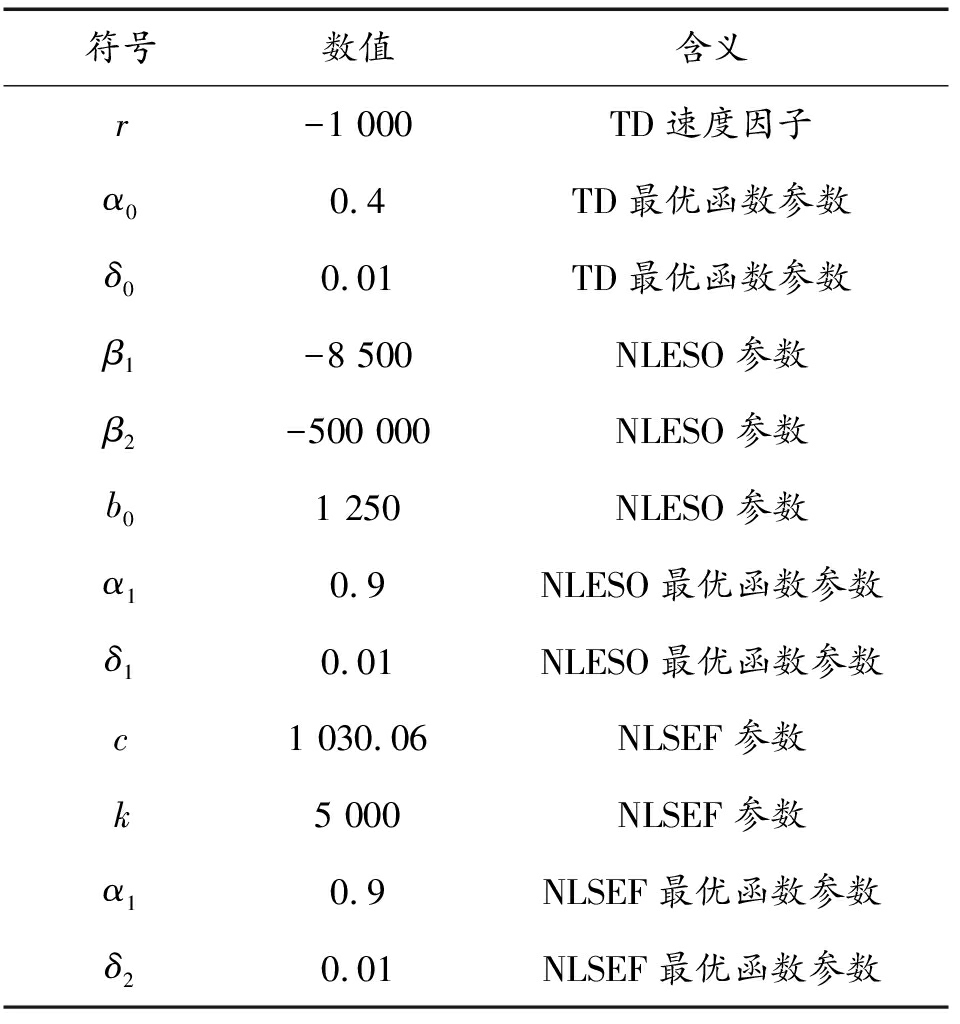
符号数值含义r-1 000TD速度因子α00.4TD最优函数参数δ00.01TD最优函数参数β1-8 500NLESO参数β2-500 000NLESO参数b01 250NLESO参数α10.9NLESO最优函数参数δ10.01NLESO最优函数参数c1 030.06NLSEF参数k5 000NLSEF参数α10.9NLSEF最优函数参数δ20.01NLSEF最优函数参数
设定双电机系统平衡后速度为1 000 r/min,并且在PMSM1与PMSM2运行一段时间后分别加入了5 N·m与-5 N·m的负载转矩。图7、图8分别表示在PI控制下以及ADRC控制下双电机同步曲线。
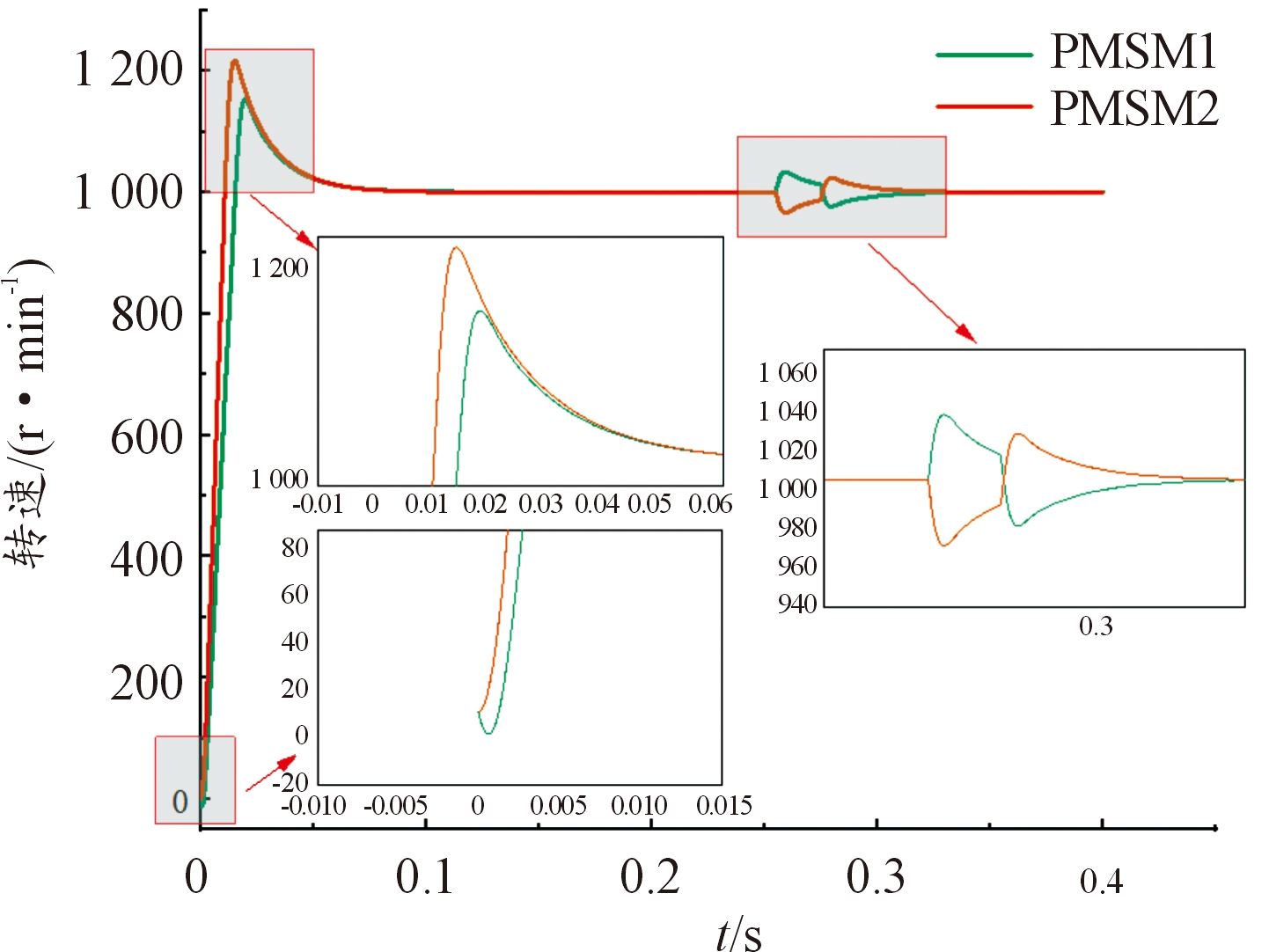
图7 PI控制策略下双电机速度曲线
Fig.7 Dual-motor speed curve under PI control strategy
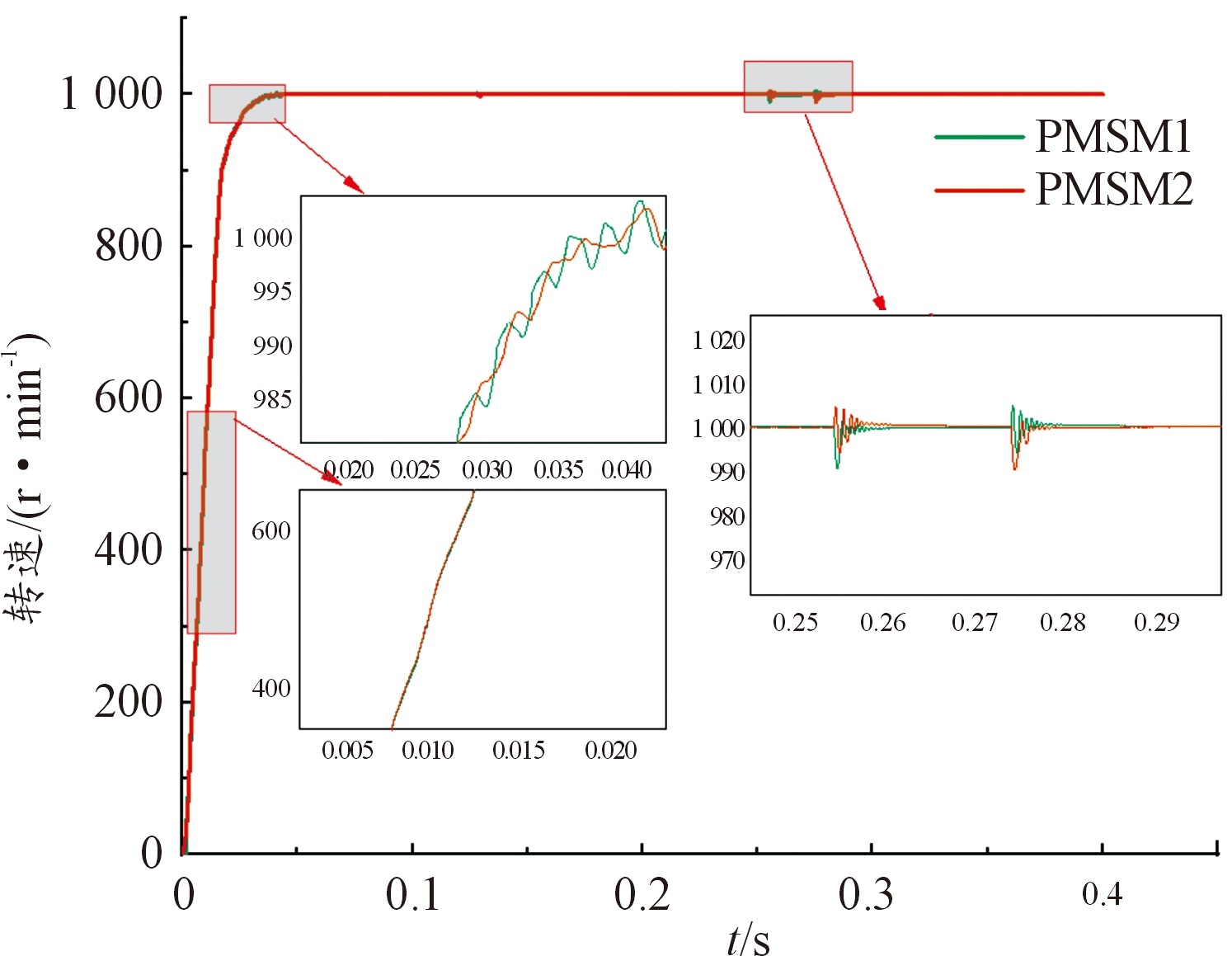
图8 ADRC策略下双电机速度曲线
Fig.8 Dual-motor speed curve under ADRC control strategy
如图9所示,采用ADRC策略的双电机最大同步误差为0.5 r/min,在7 ms时同步误差收敛到0;而采用PI控制策略的双电机最大同步误差为32 r/min,在35 ms时同步误差收敛到0。
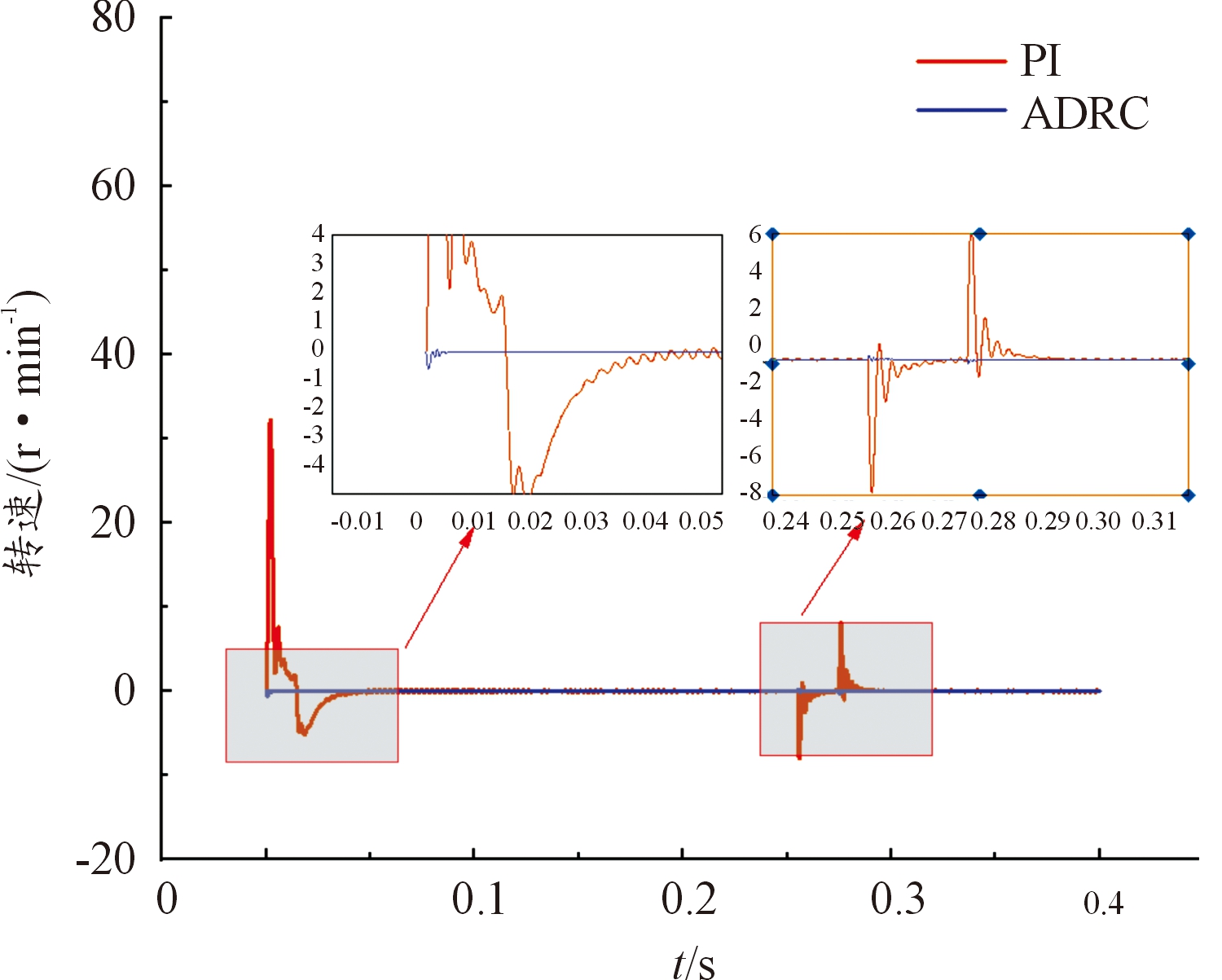
图9 速度误差曲线
Fig.9 Speed error curve
如图10为双电机在运行工作中的位置差曲线,采用ADRC策略的双电机位置差最大为0.36°,在外部负载的干扰下依然慢慢收敛于0,使用PI策略的位置差最大为1.5°,与ADRC控制策略相比,抗干扰性较差。
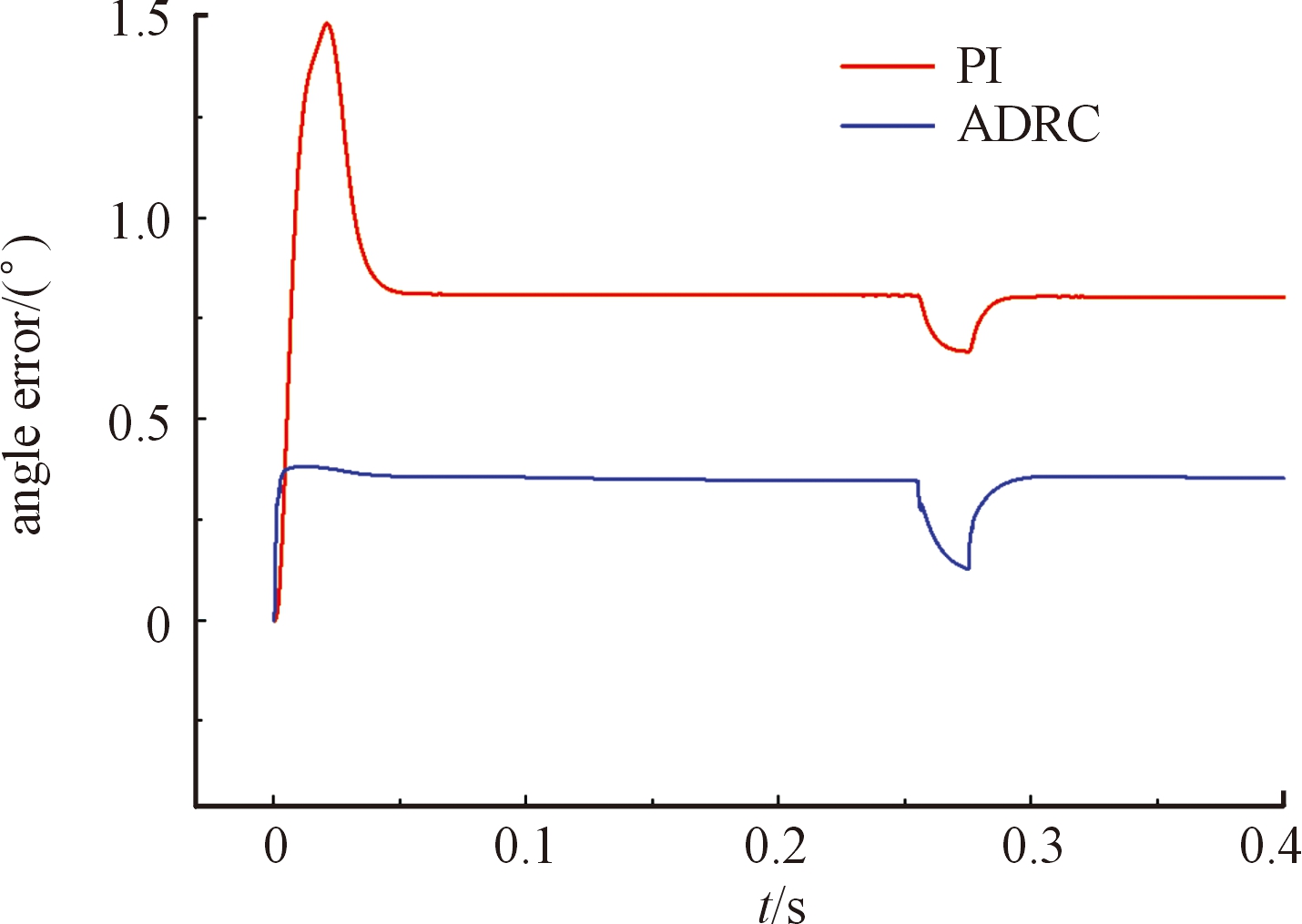
图10 位置误差曲线
Fig.10 Position error curve
综上所述,采用ADRC策略所得到的同步误差较小,转速误差最大为0.5 r/min,位置误差最大为0.36°,采用PI策略的同步效果略差一些。
3.2 试验验证及分析
为了验证本文中所提双电机同步控制算法的有效性,建立双电机同步测试平台,进行了2次实验,分别采用PI策略与ADRC策略。实验过程首先将补给弹仓中弹药输送至火炮弹鼓,然后再将弹药全部返回到补给弹仓,测试数据如图11所示。
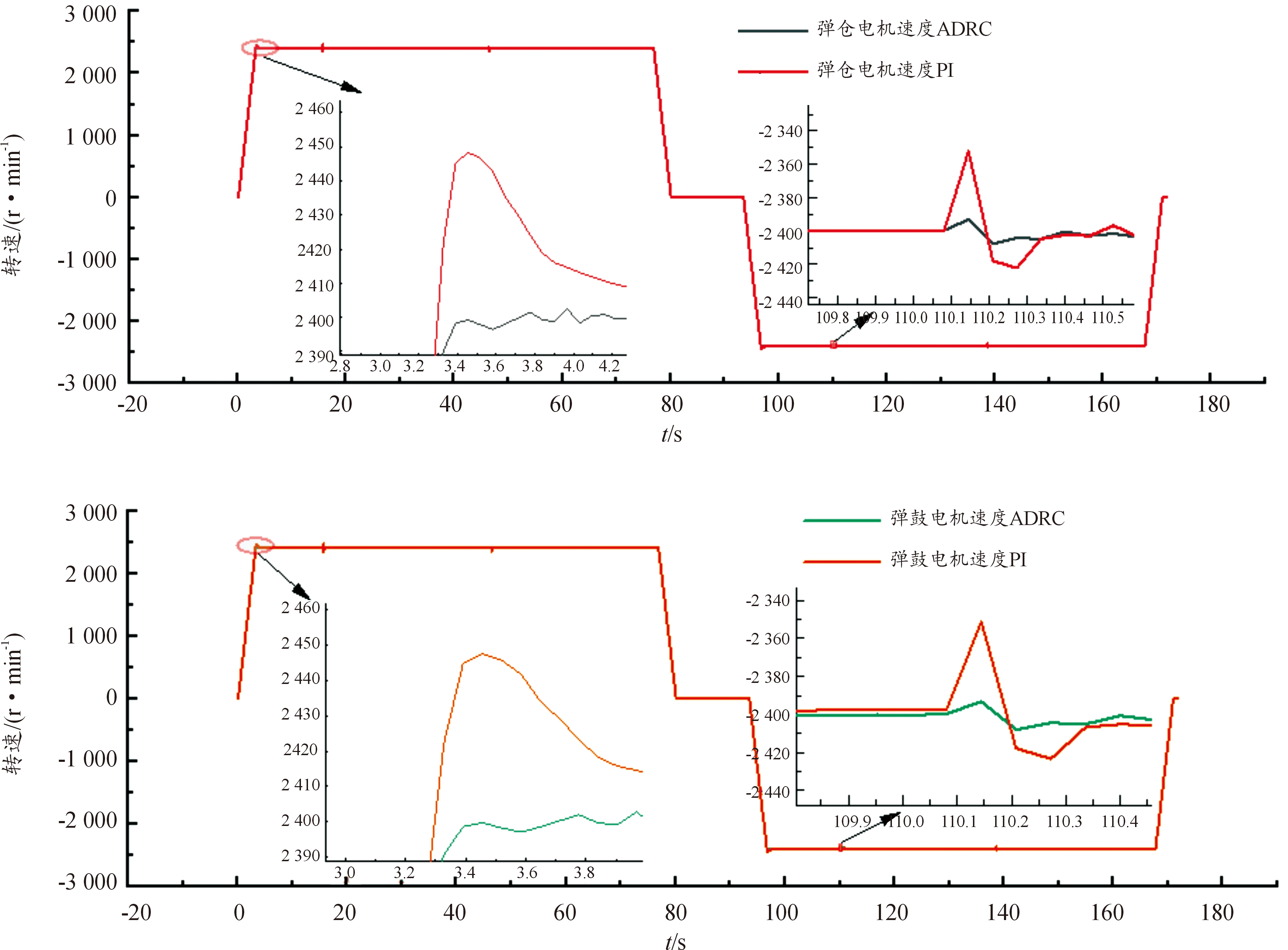
图11 不同控制策略下单电机转速曲线对比
Fig.11 Comparison of single motor speed curves under different control strategies
图11中为弹鼓电机与弹仓电机在补弹和退弹时的速度曲线,分别采用PI控制与ADRC控制,通过PI控制的弹仓电机与弹鼓电机会有一定的超调量,在短时间内会恢复至2 400 r/min。并且电机在运行中,由于负载一直处于变化之中,在运行时会存在负载波动,图11中已标出某个时间的弹仓电机与弹鼓电机的转速波动曲线,其中采用PI控制的弹仓电机与弹鼓电机转速变化较大,最大值为53 r/min;而采用ADRC控制的弹仓电机与弹鼓电机转速变化较小,最大值为10 r/min(由于采样率低,图中并不是平滑曲线)。2种控制方式下的弹仓电机与弹鼓电机同步误差如图12所示。
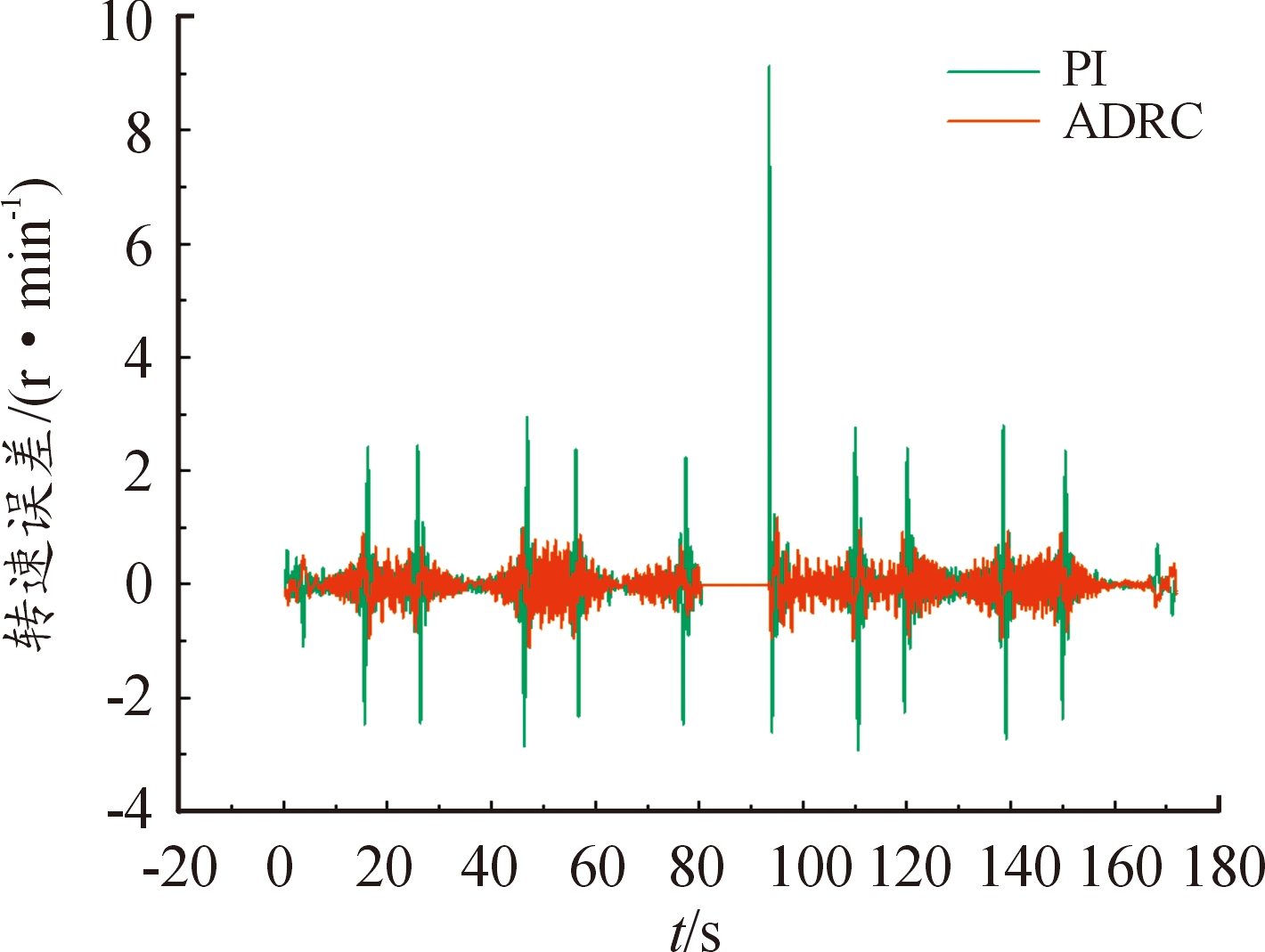
图12 实测双电机转速误差
Fig.12 Measured dual-motor speed error curve
从图12可以看出,采用PI控制的转速误差较大,最大值为9 r/min,采用ADRC控制的转速误差较小,最大值为1 r/min。
如图13所示,在补弹和退弹过程中弹鼓电机和弹仓电机的转角偏差较小,当补弹和退弹装填切换时,转角偏差量达到25°,主要是由于链式传动中松边与紧边的切换产生的。从图中可以看出,采用PI策略双电机的位置误差较大,为1.6°,采用ADRC策略的双电机位置误差为0.5°。

图13 双电机位置偏差曲线
Fig.13 Measured dual motor position error curve
结合图11—图13,采用ADRC控制的快速补弹系统,在负载发生变化时,可以及时对转速进行调整,缩小与稳定速度的误差,使系统具有较强的抗干扰性;采用ADRC与滑模相结合的同步控制方式,双电机具有较强的同步性。
4 结论
以小口径火炮快速补弹系统中电机同步性能为研究对象,建立快速补弹系统中柔性弹链传动数学模型,构建ADRC控制器以及基于滑模的交叉耦合控制器;在Simulink对双电机同步系统进行建模,对同步算法进行了分析验证,最后通过试验验证策略的可行性。得到以下结论:
1) 在补弹过程中,系统中存在的负载波动会使电机转速存在波动,采用ADRC控制策略,弹仓以及弹鼓电机的转速波动较小,具有一定的抗干扰性。
2) 将ADRC与采用滑模的交叉耦合控制器相结合,可以提高双电机系统的同步精度和抗干扰性。
3) 由于本文所涉及的补弹系统较为复杂,不能对其进行准确建模,所以未能将模型与Smulink进行联合仿真验证,在后续的研究中,将重点对此进行研究。
[1] 高骁波,杨臻,朱明一,等.小口径火炮快速补弹装置的动力学分析[J].火炮发射与控制学报,2015,36(1):44-48.
GAO Xiaobo,YANG Zhen,ZHU Mingyi,et al.Kinetic analysis of rapid ammunition replenishment device for small caliber artillery[J].Journal of Gun Launch &Control,2015,36(1):44-48.
[2] 靳威.高速柔性传输中多电机同步控制研究[D].太原:中北大学,2020.
JIN Wei.Research on multi-motor synchronous control in high-speedflexible transmission[D].Taiyuan:North University of China,2020.
[3] ZHENG W,LUO Y,CHEN Y Q,et al.A simplified fractional order PID controller's optimal tuning:A case study on a PMSM speed servo[J].Entropy,2021(2).
[4] LI Y,SUN K,TONG S.Observer-based adaptive fuzzy fault-tolerant optimal control for SISO nonlinear systems[J].IEEE transactions on cybernetics,2018,49(2):649-661.
[5] ZHENG Y,ZHAO H,ZHEN S,et al.Fuzzy-set theory based optimal robust constraint-following control for permanent magnet synchronous motor with uncertainties[J].Control Engineering Practice,2021,115.
[6] LU E,LI W,YANG X,et al.Anti-disturbance speed control of low-speed high-torque PMSM based on second-order non-singular terminal sliding mode load observer[J].ISA Transactions,2018,88:142-152.
[7] LIU W T,ZHAO T.An active disturbance rejection control for hysteresis compensation based on Neural Networks adaptive control-science direct[J].ISA Transactions,2020,109:81-88.
[8] ZHU C,TU Q,JIANG C,et al.A cross coupling control strategy for dual-motor speed synchronous system based on second order global fast terminal sliding mode control[J].IEEE Access,2020,8:217967-217976.
[9] TENG Q,JIE T,DUAN J,et al.Sliding-mode MRA observer-based model predictive current control for PMSM drive system with DC-link voltage sensorless[C]//2017 20th International Conference on Electrical Machines and Systems (ICEMS).IEEE,2017.
[10] ZHAO H,WANG C,DETAND J,et al.A simple fuzzy pi control of dual-motor driving servo system[C]//The 2016 International Conference on Advanced Materials,Structures and Mechanical Engineering(ICAMSME).2016.
[11] ZHANG D,WEI B.Convergence performance comparisons of PID,MRAC,and PID+MRAC hybrid controller[J].Frontiers of Mechanical Engineering,2016,11(2):213-217.
[12] LUO Y,LIANG D,ZHANG L,et al.Speed synchronized control of dual motors system using fuzzy logic[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia).IEEE,2020.
[13] 石欢,孙乐,李志刚,等.基于模型预测的双电机驱动系统协调控制方法[J/OL].中国电机工程学报:1-10[2022-07-14].
SHI Huan,SUN Le,LI Zhigang,et al.Coordination control of a dual-motor drive system with the model prediction[J/OL].Proceedings of the CSEE:1-10[2022-07-14].
[14] LI S,WANG Z,YAN Y,et al.Finite set model predictive control of a dual-motor torque synchronization system fed by an indirect matrix converter[J].Energies,2021,14(5):1325.
[15] 何伟栋.某链式回转弹仓设计及动力学仿真研究[D].西安:西安工业大学,2021.
HE Weidong.Design and dynamic simulation research of a china rotary magazine[D].Xi’an:Xi’an Technological University,2021.
[16] 万济民.小口径舰炮快速补弹系统输弹链动态特性研究[D].哈尔滨:哈尔滨工程大学,2017.
WAN Jimin,Research on the small-caliber naval gun rapid ammunition feedings system and dynamic characteristics of the rammer[D].Harbin:Harbin Engineering University,2017.
[17] TANG H,LI H,LIN J.Research on sensorless control method of pmsm based on a kalman filter sliding mode observer[C]//2018 10th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA).IEEE Computer Society,2018.
[18] 李杰,齐晓慧,万慧,等.自抗扰控制:研究成果总结与展望[J].控制理论与应用,2017,34(3):281-295.
LI Jie,QI Xiaohui,WAN Hui,et al.Active disturbance rejection control:theoretical results summary and future researches[J].Control Theory &Applications,2017,34(3):281-295.
[19] 周凯,孙彦成,王旭东,等.永磁同步电机的自抗扰控制调速策略[J].电机与控制学报,2018,22(2):57-63.
ZHOU Kai,SUN Yancheng,WANG Xudong,et al.Active disturbance rejection control of pmsm speed control system[J].Electric Machines and Control,2018,22(2):57-63.
[20] CHU Z,WU C,SEPEHRI N.Active disturbance rejection control applied to high-order systems with parametric uncertainties[J].International Journal of Control Automation &Systems,2019,17(6):1483-1493.
[21] FANG H Q,YUAN X J,LIU P.Active-disturbance-rejection-control and fractional-order-proportional-integral-derivative hybrid control for hydroturbine speed governor system[J].Measurement &Control,2018,51(5/6):192-201.
[22] LIU Y,WEN J,XU D,et al.The decoupled vector-control of PMSM based on nonlinear multi-input multi-output decoupling ADRC[J].Advances in Mechanical Engineering,2020,12(12).