0 引言
自适应波束形成技术作为阵列信号处理的一重要分支,旨在通过一定的优化准则,计算阵列最优加权矢量,达到有效抑制干扰、噪声来获得高处理增益并提高输出信干噪比(signal to interference and noise ratio,SINR)的效果,在通信系统、航天、医疗、雷达等领域中均有广泛应用[1-2]。典型的波束形成器,如标准Capon波束形成器,在理想情况下可达到最优性能[3],然而,实际工作场景中由于存在目标来波方向误差、阵列位置误差等,导致波束形成器输出性能下降严重。
目前,诸多学者在稳健自适应波束形成领域进行了深入研究,提出的方法主要涵盖:加载类算法[4-9]、不确定集算法[10-14]和协方差矩阵重构类算法[15-20]等。
文献[4]提出了对样本协方差矩阵的对角元素加载一个常数以提高鲁棒性的对角加载(loading sample matrix inversion,LSMI)算法,该算法普适性较强,但对最佳加载值的选取并未有确定的方法,加载值过大易降低干扰抑制能力,加载值过小对算法的改善影响较为有限。文献[8]提出了一种自适应可变对角加载技术(automatic variable loading technology,AVL-RAB)当输入信噪比(signal to noise ratio,SNR)较低时以非均匀加载矩阵为主导,当输入SNR较高时以可变对角加载矩阵为主导,提升了高SNR下输出性能,但算法抗干扰能力有所减弱。
文献[12]提出了目标导向矢量双层估计的稳健波束形成算法,首先将目标信号大致方位区间上的导向矢量构建一个线性空间,并将其用线性空间基向量组合表示,然后构建不确定集约束校正目标信号导向矢量,提高了波束形成器导向矢量失配误差下的稳健性,但在低SNR环境下,输出性能下降严重。文献[16]研究了稳健Capon波束形成(robust capon beamforming,RCB)算法,建立导向矢量不确定集约束,求解不确定集系数,当导向矢量误差较小时,算法鲁棒性较好,但当导向矢量失配时性能下降严重。文献[21]通过对目标信号导向矢量进行线性约束,提升了波束形成器的稳健性,并添加了阻塞矩阵预选环节解决了线性约束带来的自由度损失问题。
样本协方差矩阵中含有期望信号分量,会极大影响算法的性能,剔除期望信号分量时易引入其他误差,影响后续的计算过程;不确定集算法约束的大小难以确定,在各种误差存在的情况下性能波动较大。针对上述问题,本文中提出基于干扰加噪声协方差矩阵优化重构的稳健波束形成算法。首先,通过Capon功率谱得到目标导向矢量的预估值,重构干扰加噪声协方差矩阵;然后,建立干扰导向矢量不确定集约束,干扰加噪声矩阵的优化估计值;继而,根据子空间扩展知识,构造导向矢量误差不确定集约束模型,循环迭代更新目标导向矢量和干扰加噪声协方差矩阵,最终得到二者稳态估计值并计算加权矢量。
1 阵列信号模型
考虑阵元数为M的理想一维均匀线阵,假设空间中有K个入射信号,目标信号从θ0方向入射,K-1个干扰信号从θi(i=1,2,…,K-1)方向入射,假设入射信号与噪声之间相互统计独立,则阵列在t时刻的接收信号可表示为
![]()
(1)
a(θi)=[1,ej(2πd/λ)sinθi,…,ej(M-1)(2πd/λ)sinθi]H
(2)
其中:a(θi)和si(t)分别为第i个射信号的导向矢量和复包络,n(t)为噪声信号,λ为信号波长,d为阵元间距。
阵列接收信号的协方差矩阵可表示为
R=E[X(t)XH(t)]=Rs+Ri,n
(3)
![]()
(4)
![]()
(5)
其中:Rs和Ri,n分别表示目标信号自相关矩阵和干扰加噪声协方差矩阵;![]() 表示目标信号功率;
表示目标信号功率;![]() 表示第i个干扰信号功率,
表示第i个干扰信号功率,![]() 表示噪声功率,I为M维单位矩阵。
表示噪声功率,I为M维单位矩阵。
实际工作中,矩阵R一般是未知的,故采用样本协方差矩阵代替如式(6)所示:
![]()
(6)
式中:P为快拍数。
2 干扰加噪声协方差矩阵优化重构
2.1 干扰加噪声协方差矩阵预估计
假设目标大致出现的区域为Θ,在该区域内对Capon功率谱求积分,则有
![]()
(7)
将矩阵Q特征值分解,以其最显著特征值对应的特征向量作为目标导向矢量的估计值。
![]()
(8)
式中:Umax是Q特征值分解后最显著特征值对应特征向量。
从而可将期望信号的自相关矩阵估计为
![]()
(9)
式中:![]() 表示目标信号功率,则干扰加噪声协方差矩阵可估计为
表示目标信号功率,则干扰加噪声协方差矩阵可估计为
![]()
(10)
式中:σd表示对角加载量。
2.2 干扰加噪声协方差矩阵优化重构
对矩阵![]() 做特征值分解得
做特征值分解得
![]()
(11)
式中:μm代表矩阵![]() 特征值分解后的M个特征值,ui代表λn对应的特征向量,
特征值分解后的M个特征值,ui代表λn对应的特征向量,![]() 和
和![]() 分别表示干扰信号子空间的特征值矩阵和噪声子空间的特征值矩阵。
分别表示干扰信号子空间的特征值矩阵和噪声子空间的特征值矩阵。![]() 和
和![]() 分别表示干扰信号子空间和噪声子空间。
分别表示干扰信号子空间和噪声子空间。
由子空间扩展知识[22-23]可知,真实干扰导向矢量与![]() 扩展为同一子空间,且
扩展为同一子空间,且![]() 即真实干扰信号导向矢量与噪声子空间正交。基于文献[24]方法,建立干扰导向矢量约束关系如下:
即真实干扰信号导向矢量与噪声子空间正交。基于文献[24]方法,建立干扰导向矢量约束关系如下:
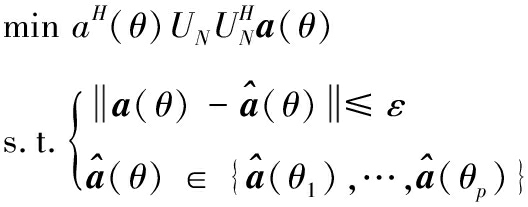
(12)
式中:ε为约束参数,![]() 为干扰导向矢量预估值,可由MUSIC算法等得出。
为干扰导向矢量预估值,可由MUSIC算法等得出。
通过拉格朗日乘数法对式(12)求解,则干扰导向矢量可表示为
![]()
(13)
式中:参数μ的值由如下计算式给出
![]()
(14)
得出干扰导向矢量的优化估计值后,继而求解干扰信号功率。
![]()
(15)
式中:Rs,i为期望信号加干扰协方差矩阵,![]() 为期望信号和干扰功率。
为期望信号和干扰功率。
设a(θl)与a(θk)为入射方向不同的信号导向矢量,在信号入射方位稀疏的条件下,不同角度的信号导向矢量相互正交[25],则当l≠k时,有aH(θl)a(θk)=0。在式(15)的左右两端分别乘aH(θl)和a(θl)得
![]()
(16)
进而可得出干扰信号功率表达式:
![]()
(17)
假设噪声扇区为Θn,则可由下式计算剩余噪声[26]
![]()
(18)
式中:N为噪声扇区中的采样点数量,a(θn)为角度θn对应的标称导向矢量。则噪声功率可估计为
![]()
(19)
则矩阵![]() 可表示为
可表示为
![]()
(20)
将式(20)代入式(17),可计算出干扰信号功率,继而可得出优化重构后的干扰加噪声协方差矩阵![]()
![]()
(21)
3 目标导向矢量估计
将第2节中优化重构后的矩阵![]() 特征值分解得
特征值分解得
![]()
(22)
基于此,为最大化阵列输出功率,并减小干扰及噪声对目标导向矢量的影响,建立约束关系如下:
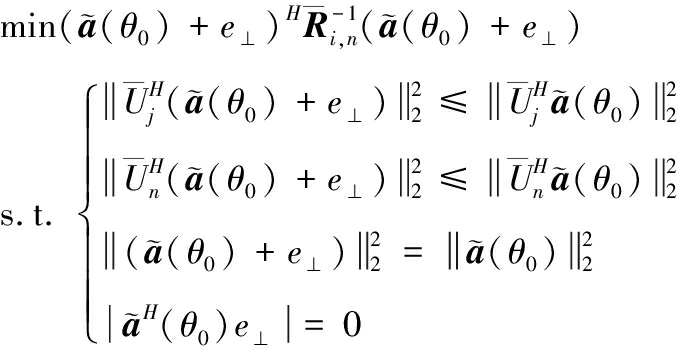
(23)
式中:e⊥表示目标导向矢量误差中与![]() 正交的分量,第1项不等式约束使
正交的分量,第1项不等式约束使![]() 比
比![]() 远离干扰信号子空间,第2项不等式约束使
远离干扰信号子空间,第2项不等式约束使![]() 比
比![]() 远离噪声子空间,第3项等式约束确保
远离噪声子空间,第3项等式约束确保![]() 与
与![]() 具有相同模长,第4项等式约束确保e⊥与
具有相同模长,第4项等式约束确保e⊥与![]() 正交。
正交。
观察约束式(23)易知,将松弛因子γ引入第三项等式约束能避免出现e⊥=0为唯一解的情况,且仅影响约束的收敛速度,不会改变式(23)的最优解[27-30]。根据式(2)可得,![]() =M,则约束模型变为
=M,则约束模型变为
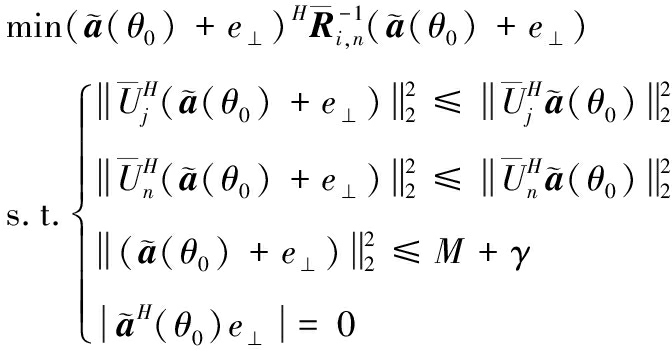
(24)
已知![]() 和Uj的条件下,可通过凸优化方法求解式(24),得出e⊥,并更新
和Uj的条件下,可通过凸优化方法求解式(24),得出e⊥,并更新![]()
4 算法求解及步骤
设参数β为收敛系数,参数itmax为最大迭代次数,设
![]()
(25)
则收敛条件可表示为
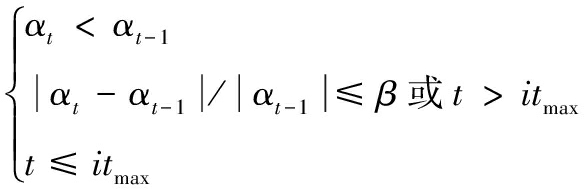
(26)
式中:t为已完成的迭代次数,当t≤itmax时,以式(26)第1、2项不等式约束为终止判决条件;而当t>itmax时,迭代终止。
将满足迭代终止判断判决条件的![]() 和
和![]() 代入下式:
代入下式:
![]()
(27)
式中:ω为加权矢量。
分析式(26)易知,β和itmax的大小会影响迭代结果的精度和迭代的次数;β过小或itmax过大会导致迭代次数增多,算法迭代时间过长;β过大或itmax过小会导致迭代精度下降。本文中算法流程如图1所示。
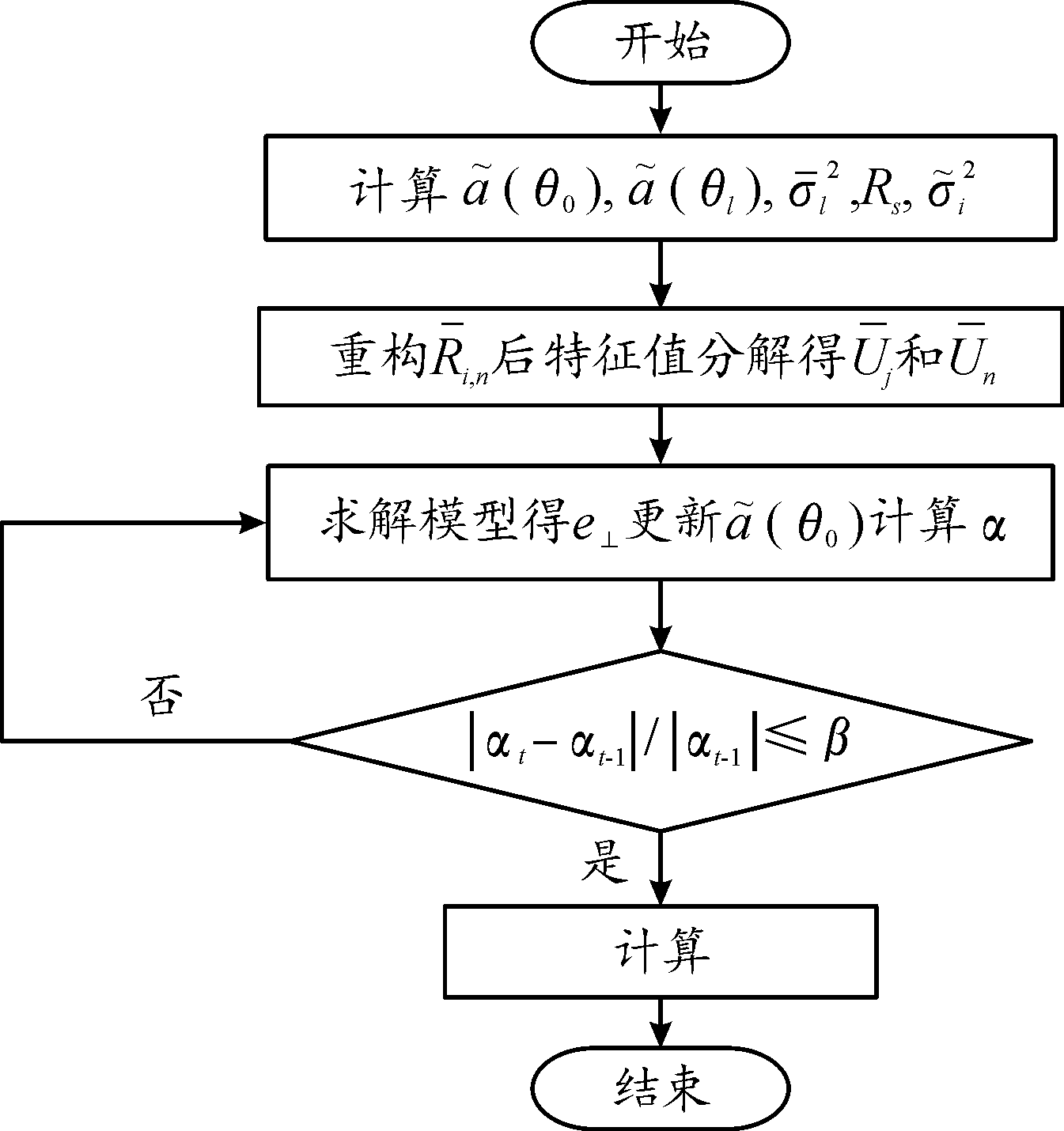
图1 算法流程图
Fig.1 Algorithm flow chart
步骤1 由式(7)—式(10)计算![]() 和
和![]()
步骤2 由式(11)—式(21),计算![]() 和
和![]() 继而得出优化后的矩阵
继而得出优化后的矩阵![]()
步骤3 将![]() 进行特征值分解,得
进行特征值分解,得![]() 和
和![]() 由式(24)得出e⊥,校正
由式(24)得出e⊥,校正![]() 为
为![]()
步骤4 由式(26)判断是否满足迭代终止条件,不满足则重复上述步骤。
步骤5 将满足迭代终止条件的![]() 和
和![]() 代入式(26)求解ω。
代入式(26)求解ω。
5 仿真实验
考虑阵元数为8的理想一维均匀线阵,阵元间距设置为0.5λ。本节中,假设目标信号实际来波方向为5,干扰信号来波方向为-10°和20°,干噪比均设为30 dB,噪声均为高斯白噪声,目标信号与干扰信号间统计无关。将本文中算法与LSMI算法、RCB算法、AVL-RAB算法分析对比,每次仿真均进行100次独立的蒙特卡洛实验。
LSMI算法加载量设为![]() 算法的导向矢量误差约束参数设为0.3M;AV-RAB算法的变换矩阵设为反单位矩阵,正交矩阵特征向量个数为2,求和区间设为[θ-5°,θ+5°],;本文中算法的求和区间同AVL-RAB算法且γ=0.1、β=10-5。
算法的导向矢量误差约束参数设为0.3M;AV-RAB算法的变换矩阵设为反单位矩阵,正交矩阵特征向量个数为2,求和区间设为[θ-5°,θ+5°],;本文中算法的求和区间同AVL-RAB算法且γ=0.1、β=10-5。
5.1 抗目标来波方向误差算法仿真及分析
本小节中,设期望信号来波方向误差服从[-3,3]区间内的随机分布,则实际信号来波方向服从[2,8]区间内的随机分布,快拍数设为200,输入SNR取[-30 dB,40 dB];分析各算法输出性能随快拍数变化趋势时,输入SNR设为1 dB。将各算法100次蒙特卡洛实验的输出SINR做统计平均,仿真结果如图2所示。
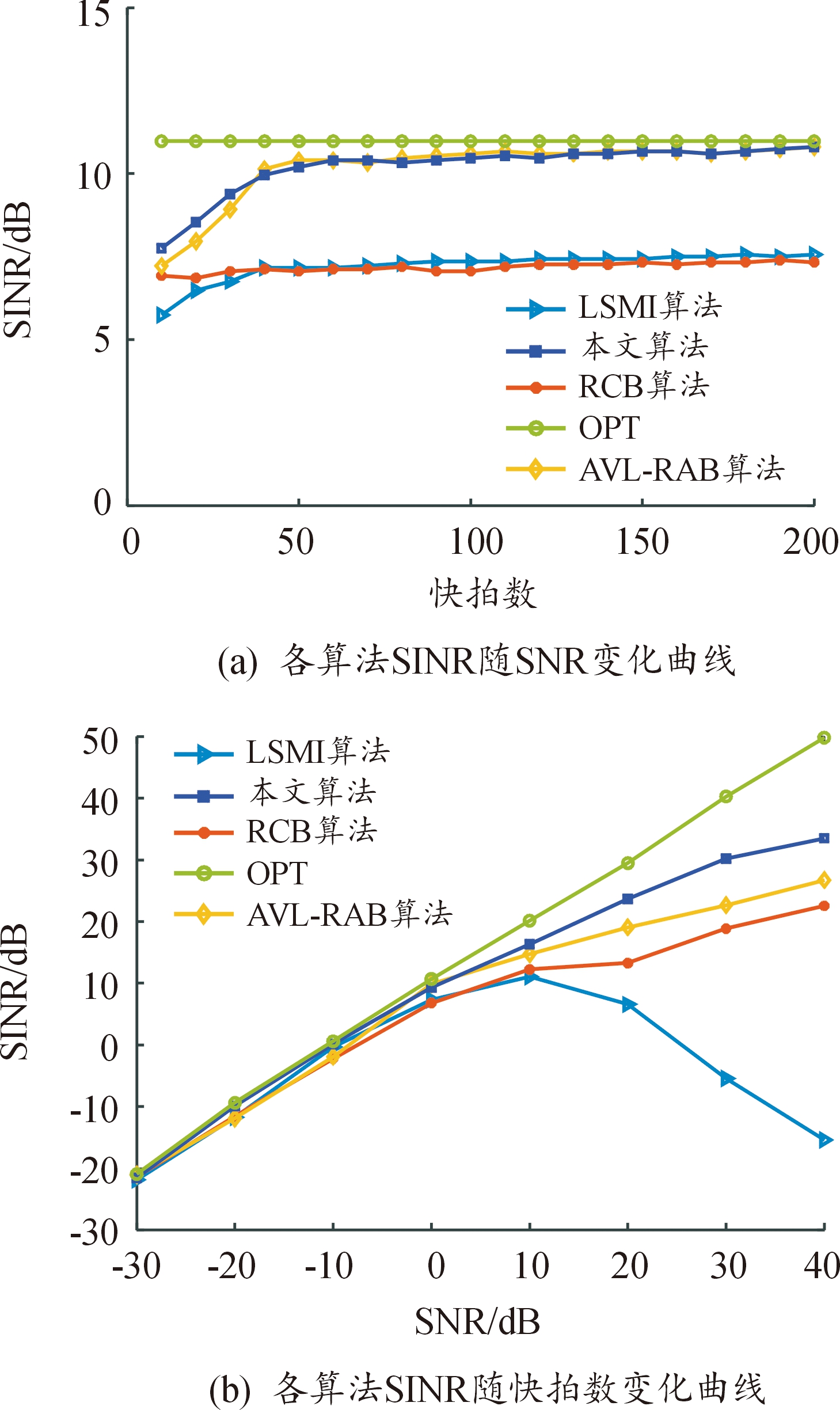
图2 目标来波方向误差下仿真对比
Fig.2 Simulation comparison under target arrival direction error
分析图2(a)可知,当目标来波方向误差存在时,LSMI算法在10 dB输出性能达到最优,随着SNR提高,算法性能下降严重;RCB算法用于求取权值的样本协方差矩阵仍包含期望信号在高SNR输入下,性能下降明显,曲线斜率变小;AVL-RAB算法采用了可变加载值加载矩阵表现整体优于RCB算法,但高SNR输入下性能仍有不足;本文中算法输出性能总体较好,尤其在高SNR输入下输出性能仍稳定提升。
分析图2(b)可知,本文中算法与AVL-RAB算法总体表现较好,尤其是在小块拍数下,快拍数大于50次后,基本达到收敛,随快拍数增大二者输出SINR提高速度变缓,且逐步接近理论最优值。
5.2 抗阵元位置误差算法仿真及分析
设每个阵元实际位置相对理想位置偏移误差在[-0.05λ,0.05λ]区间内随机分布,期望信号来波方向误差设置为3,输入信噪比取[-30 dB,40 dB],快拍数为200;仿真各算法输出性能随快拍数变化趋势时,输入SNR设为0 dB。将各算法100次蒙特卡洛实验的输出SINR做统计平均,仿真结果如图3所示。
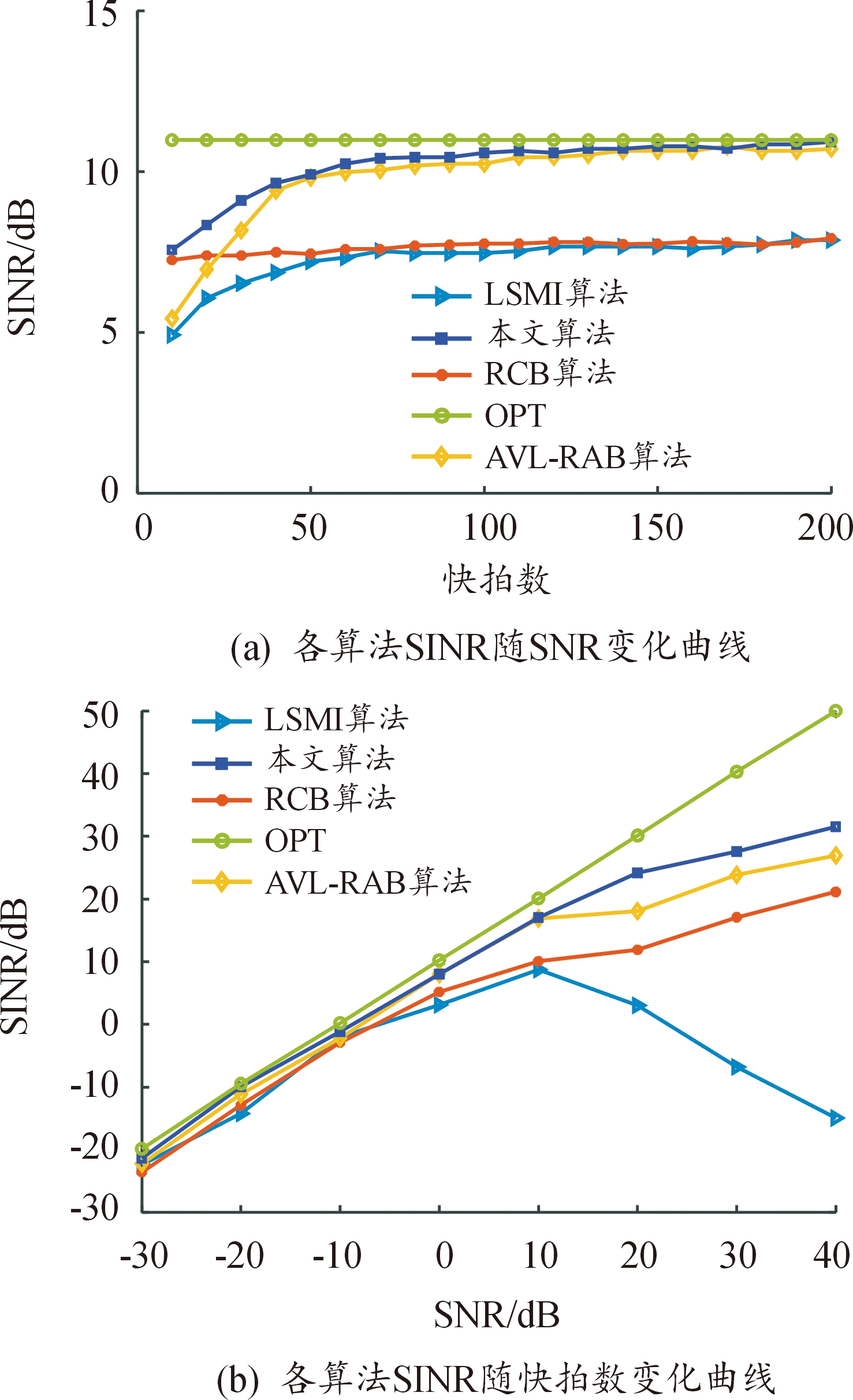
图3 阵列位置误差下仿真对比
Fig.3 Simulation comparison under array position error
分析图3(a)可知,当阵列位置误差存在时,LSMI算法性能随输入SNR提高下降严重,说明其抗阵列位置误差干扰性能较差,AVL-RAB算法输出性能总体优于RCB算法,但小块拍数下性能有所下降,是因正交矩阵特征向量计算不准确导致,本文中算法对干扰加噪声协方差矩阵进行了优化重构,表现优于其他3种算法,具备对阵列位置误差的稳健性。
分析图3(b)可知,本文中算法在小快拍数下输出性能较其他算法有明显优势,且收敛速度较快,当快拍数大于70次后接近收敛,并逐渐接近理论最优值。
5.3 抗阵列互耦误差算法仿真及分析
设互耦矩阵为C,对理想一维均匀线阵,矩阵C为Toeplitz形式,本小节中,仅考虑相邻阵元间的互耦效应,互耦系数设为0.5exp-jπ/2,其余实验条件设置如上,无特殊说明,将100次蒙特卡洛实验的输出做统计平均,仿真结果如图4所示。
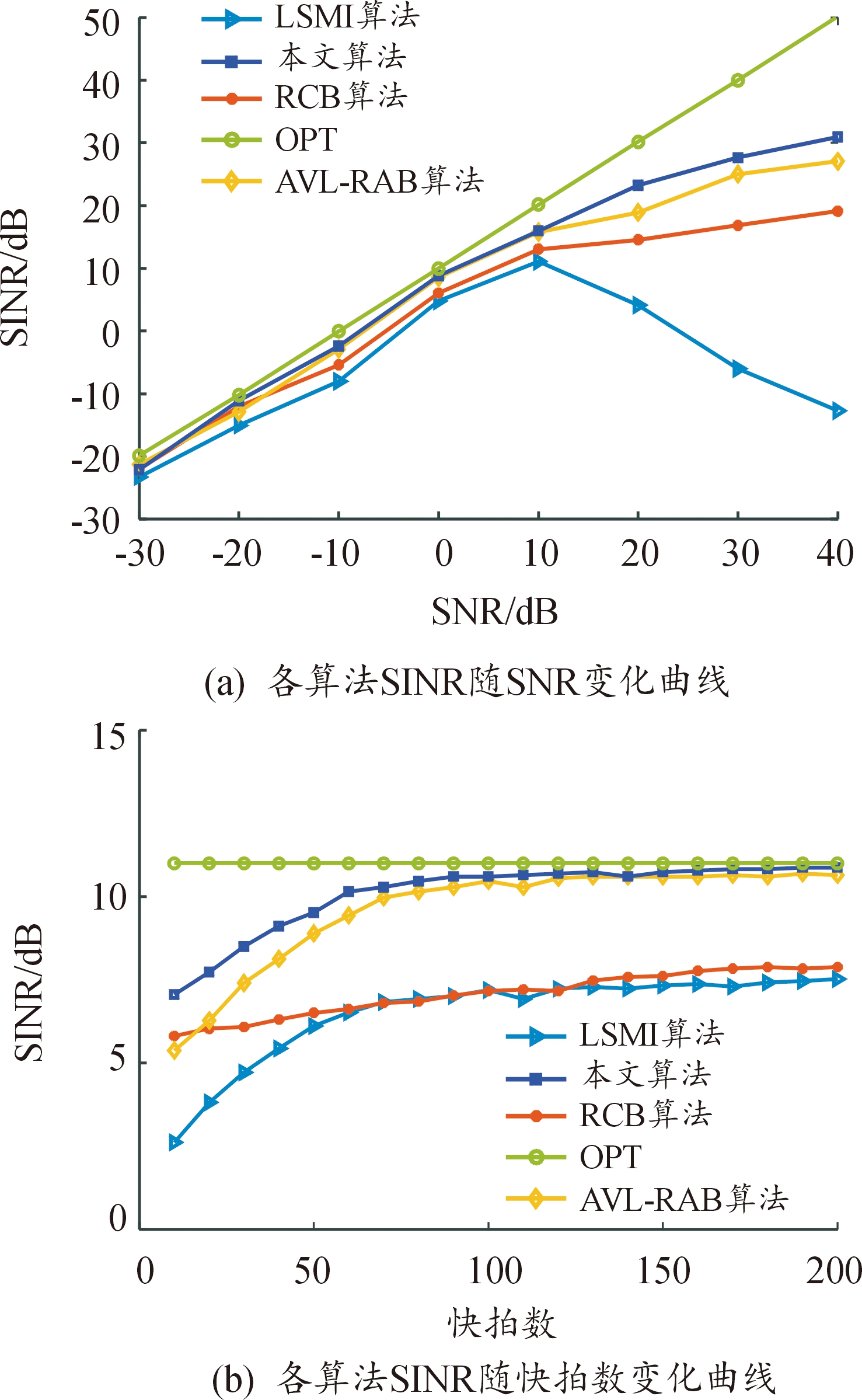
图4 阵列互耦误差下仿真对比
Fig.4 Simulation comparison under array mutual coupling error
分析图4(a)可知,当阵列互耦误差存在时,本文中算法在输入SNR大于10 dB后,输出性能较其他3种算法有明显优势,因本文中算法通过求解目标导向矢量误差约束模型,校正了目标导向矢量和干扰加噪声协方差矩阵,提高了算法抗阵列互耦误差的能力,本文中算法在高SNR输入下性能有所下降,这是因为对![]() 进行特征值分解操作时,计算结果不准确,影响了后续的求解过程。
进行特征值分解操作时,计算结果不准确,影响了后续的求解过程。
分析图4(b)可知,本文中算法输出SINR随快拍数稳健提升,且在较小快拍数条件下较其他算法仍有优势,在快拍数大于70次后基本收敛。
6 结论
本文中提出了基于干扰加噪声协方差矩阵优化重构的稳健波束形成算法。算法的基本思想是基于目标导向矢量和干扰加噪声协方差矩阵的联系,稀疏重构协方差矩阵;采用循环迭代的方法求解建立的目标导向矢量误差优化模型,得出最优加权矢量。仿真实验表明:该算法抗文中所述的3种失配误差能力较强,稳健性较好,尤其在快拍数较小或SNR较高的条件下输出性能较之其他算法明显提升。但本文中算法综合复杂度较高,降低算法的复杂度是后续研究中的重点内容。
[1] 叶中付,朱星宇.基于协方差矩阵重构的稳健自适应波束形成算法综述[J].数据采集与处理,2019,34(6):962-973.
YE Zhongfu,ZHU Xxingyu.Review for robust adaptive beamforming based on covariance matrix reconstruction[J].Journal of Data Acquisition and Processing,2019,34(6):962-973.
[2] ZHANG L,PAN C,WANG Y,et al.Robust beamforming design for intelligent reflecting surface aided cognitive radio systems with imperfect cascaded CSI[J].IEEE Transactions on Cognitive Communications and Networking,2022,8(1):186-201.
[3] CAPON J.High-resolution frequency-wavenumber spectrum analysis[J].Proceedings of the IEEE,1969,57(8):1408-1418.
[4] CARLSON B.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Transactions on Aerospace Electronic Systems,1988,24(4):397-401.
[5] MASELE M P,WU X,WANG L.A robust adaptive beamforming with diagonal loading and steering vector estimation[C]//Proc.of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology,2019:253-257.
[6] HUANG J SH,SU H T,YANG Y.Robust adaptive beamforming for MIMO radar in the presence of covariance matrix estimation error and desired signal steering vector mismatch[J].IET Radar Sonar and Navigation,2020,14(1):118-126.
[7] 毛晓军.高性能阵列天线稳健自适应波束形成技术研究[D].哈尔滨:哈尔滨工程大学,2017.
MAO Xiaojun.Study on the high performance robust adaptive beam-forming in antenna array[D].Harbin:Harbin Engineering University,2017.
[8] YANG B,LI W,LI Y,et al.Robust adaptive beamforming based on automatic variable loading in array antenna[J].Applied Computational Electromagnetics Society Journal,2021,36(7):908-913.
[9] SULEESATHIRA R.Robust null broadening beamforming based on adaptive diagonal loading for look direction mismatch[C]//Proc.of the 2021 13th International Conference on Knowledge and Smart Technology,2021:49-54.
[10] LEI Y,ZHANG H.Robust Adaptive beamforming based on norm constraint regularization correntropy for impulsive interference[C]//Proc.of the 2020 IEEE/CIC International Conference on Communications in China,2020:122-127.
[11] ZHANG X J,XIE H,FENG D ZH,et al.Fast and robust adaptive beamforming algorithms for large-scale arrays with small samples[J].Signal Processing,2021,188(2):108223-108231.
[12] 李文兴,毛晓军,翟助群.一种导向矢量双层估计的稳健波束形成算法[J].哈尔滨工程大学学报,2018,39(3):594-600.
LI Wenxing,Mao Xiaojun,ZHAI Zhuqun.A robust adaptive beamforming algorithm for double-layer estimation of steering vectors[J].Journal of Harbin Engineering University,2018,39(3):594-600.
[13] BESSON,OLIVIER.An alternative to diagonal loading for implementation of a white noise array gain constrained robust beamformer[J].Signal Processing:The Official Publication of the European Association for Signal Processing,2018,152(7):79-82.
[14] ZHANG P,YANG Z,LIAO G,et al.An RCB-like steering vector estimation method based on interference matrix reduction[J].IEEE Transactions on Aerospace and Electronic Systems,2020,57(1):636-646.
[15] LIANG J,JIANG D,HAN Y,et al.A robust beamforming algorithm based on covariance matrix reconstruction and steering vector estimation[J].Journal of Physics Conference Series,2020,16(1):062001-062008.
[16] 魏双微.基于弹性网约束的稳健变量选择[J].重庆工商大学学报(自然科学版),2022,39(2):68-74.
WEI Shuangwei.Robust variable selection based on elastic network constraint[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2022,39(2):68-74.
[17] ZHU X,X XU,YE Z.Robust adaptive beamforming via subspace for interference covariance matrix reconstruction[J].Signal Processing,2020,167(10):107289-107296.
[18] 陈明建,龙国庆,黄中瑞.基于协方差矩阵重构稳健波束形成算法[J].兵器装备工程学报,2017,38(4):1-7.
CHEN Mingjian,LONG Guoqing,HUANG Zhongrui Robust adaptive beamforming algorithm based interference-plus-noise covariance matrix reconstruction[J].Journal of Ordnance Equipment Engineering,2017,38(4):1-7.
[19] MOHAMMADZADEH S,KUKRER O.Robust adaptive beamforming for fast moving interference based on the covariance matrix reconstruction[J].Signal Processing,2019,13(4):486-493.
[20] LI Z,ZHANG Y,GE Q,et al.Middle subarray interference covariance matrix reconstruction approach for robust adaptive beamforming with mutual coupling[J].IEEE Communications Letters,2019,23(4):664-667.
[21] 吕岩,曹菲.基于线性约束最小方差的稳健波束形成算法[J].北京航空航天大学学报,2023,49(3):617-624.
LYU Yan,CAO Fei.Robust beamforming based on linear constraint minimum variance algorithm[J].Journal of Beijing University of Aeronautics and Astronautics,2023,49(3):617-624.
[22] ZHUANG J,XUE Y,KANG J,et al.Robust adaptive beamforming under data dependent constraints[J].Signal Processing,2021,188(8):108202-108209.
[23] YANG X P,LI Y Q,LIU F F,et al.Robust adaptive beamforming based on covariance matrix reconstruction with annular uncertainty set and vector space projection[J].IEEE Antennas and Wireless Propagation Letters,2020,20(2):130-134.
[24] ZHANG P.Steering vector optimization using subspace-based constraints for robust adaptive beamforming[J].Multidimensional Systems and Signal Processing,2021,32(4):1083-1102.
[25] SUN S,YE Z.Robust Adaptive beamforming based on a method for steering vector estimation and interference covariance matrix reconstruction[J].Signal Processing,2021,182(12):107939-107946.
[26] YANG H,WANG P,YE Z.Robust adaptive beamforming via covariance matrix reconstruction and interference power estimation[J].IEEE Communications Letters,2021,25(10):3394-3397.
[27] YAO D,ZHANG X,HU B,et al.Robust adaptive beamforming based on the effective steering vector estimation an covariance matrix reconstruction against sensor gain-phase errors[J].IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences,2020,1033(12):1655-1658.
[28] LIU S,ZHANG X,YAN F,et al.Fast and accurate covariance matrix reconstruction for adaptive beamforming using gauss-legendre quadrature[J].Journal of Systems Engineering and Electronics,2021,32(1):38-43.
[29] DU Y X,XU H Y,CUI W J,et al.Adaptive beamforming algorithm for coprime array based on interference and noise covariance matrix reconstruction[J].IET Radar,Sonar &Navigation,2022,16(4):668-677.
[30] MENG Z,ZHOU W D.Robust adaptive beamforming for coprime array with steering vector estimation and covariance matrix reconstruction[J].IET Communications,2020,14(16):2749-2758.