0 引言
列车车辆动力吸振器是利用质量块、弹簧以及阻尼器在列车主振系产生“反共振”现象来降低主振系振幅,并提升列车行驶安全性和舒适性的一种减振装置[1]。许多研究学者基于Voigt-DVA(voigt-dynamic vibration absorber)模型[2-3],从结构方式和实际应用中创新[4-8],并加强了DVA的减振性能,但是在实际能应用到传统DVA的工程中,DVA的过大振子重量会造成列车运输成本提高,且较大体积也会影响工程实现。
2002年,Smith提出了惯容器概念,一种能在运转过程中以较小的自身重量实现较大“虚质量”的物理元件,并设计出齿轮齿条式惯容器和滚珠丝杠式惯容器样机[9-11]。随后,Smith将惯容器与弹簧、阻尼结合应用于车辆的减振系统提升车辆的稳定性,验证了ISD(inerter spring damper)悬架的减振性能优于传统的SD(spring damper)悬架[12-13]。目前为止,由于结构的原因,滚珠丝杠式惯容器实现“虚质量”的能力大,且结构简单[14],易于运用在惯容特性需求大的工程系统中。随后,杨晓峰等[15]利用惯容器改进传统DVA的结构,解决了车辆悬架系统应用DVA的空间布置问题,实现从DVA结构转变为ISD悬架结构。葛正等[16]采用主动式惯容器对DVA进行了控制优化,提升了DVA的减振频带,提高了DVA的使用价值。综上,DVA能够实现对列车的减振作用,但DVA振子质量对实际工况会产生影响,并且惯容器与DVA的结合也具有一定减振效果。因此,从惯容器具有“虚质量”的特性入手,在性能相同的基础上通过惯容器介入列车DVA来替换振子实际质量的研究仍值得进一步探索。
本文中利用惯容器具有“虚质量”的物理特性,以DVA的减振性能为分析目标,建立了3种列车模型,并利用传统DVA参数经验公式以及智能优化算法得到DVA的结构参数,通过车体加速度均方根值对比分析了惯容器对DVA振子质量的影响。
1 系统建模
1.1 含ISD悬架的列车垂向振动模型
ISD悬架在列车中的应用已经被广为证实,其中惯容器串联阻尼器后再与弹簧并联的结构较其他结构对列车的稳定性提升明显[17],本文中将在此基础上对含有ISD悬架列车进一步研究。图1为含ISD悬架的列车垂向振动模型,该模型将列车简化为基于轮对、转向架、车体的多刚体系统,并且包含了弹簧、阻尼器并联的一系隔振结构,ISD悬架的二系隔振结构,其中ISD悬架采用惯容器bs串联阻尼器cs后再与弹簧ks并联的结构。
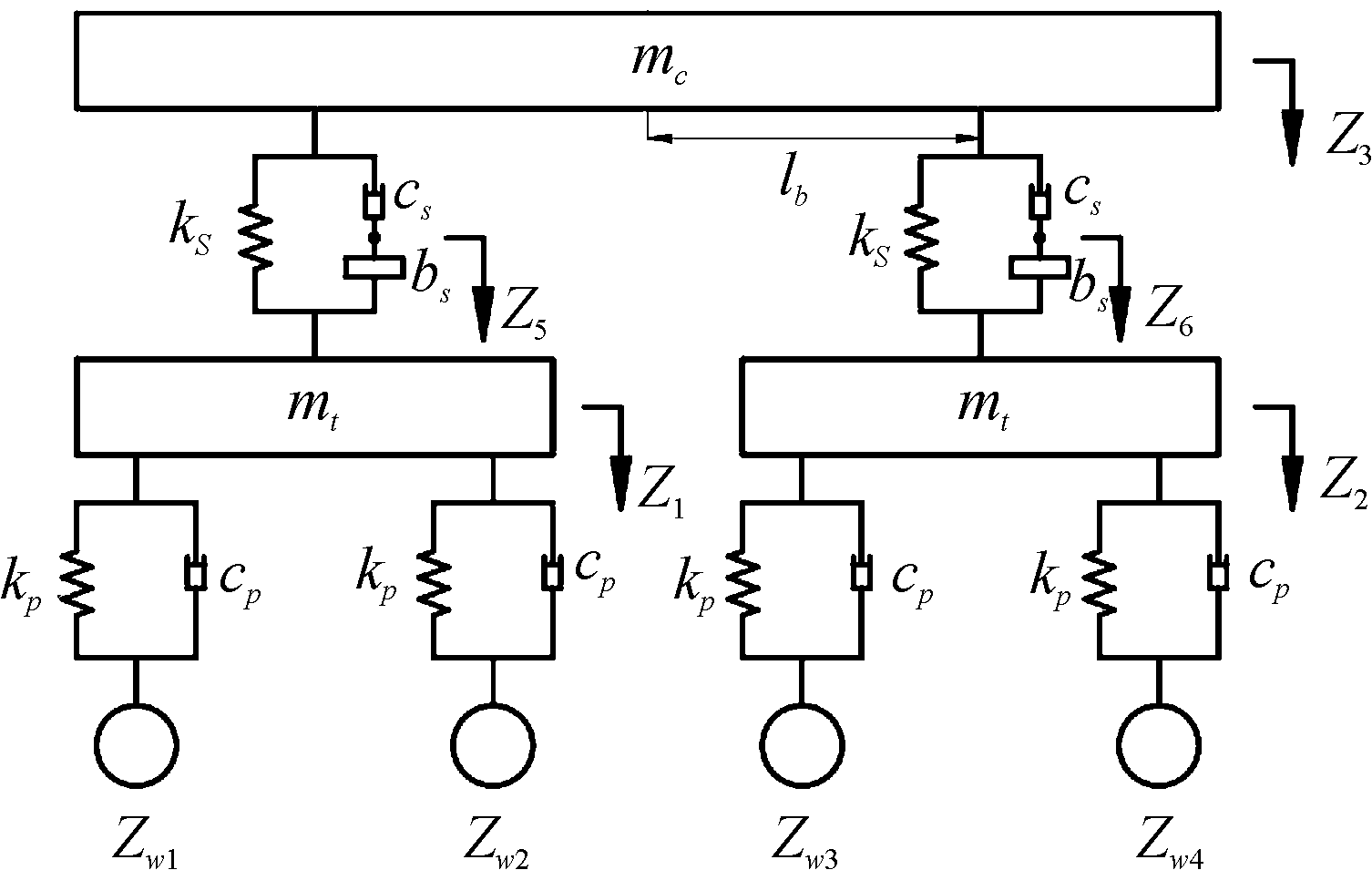
图1 含ISD悬架的列车垂向振动模型
Fig.1 Vertical vibration model of train with ISD suspension
图1中,mt为转向架质量,mc为车体质量;kp、cp分别为一系垂向刚度和垂向阻尼系数;ks、cs、bs分别为二系垂向刚度、垂向阻尼系数和惯质系数,其中惯质系数为惯容器的惯性力与其两端点间相对加速度的比值;Zi为系统的垂向位移变量;Zwi为轨道不平度。
对简化的列车模型,取向下为正方向,根据牛顿第二运动定律推导出系统动力学方程。
前转向架沉浮运动方程:
![]()
(1)
级间垂向位移Z5沉浮运动方程:
![]()
(2)
后转向架沉浮运动方程:
![]()
(3)
级间垂向位移Z6沉浮运动方程:
![]()
(4)
车体沉浮运动方程:
![]()
(5)
1.2 传统DVA的ISD悬架列车模型
在列车上安装DVA能够使得列车通过DVA自身振动给予的反方向力来实现减振效果,且可以定点安装。传统DVA选择Voigt-DVA模型[18],是由弹簧并联阻尼器后与DVA振子串联的结构,本文中选择安装于车体中间,如图2虚线框所示。
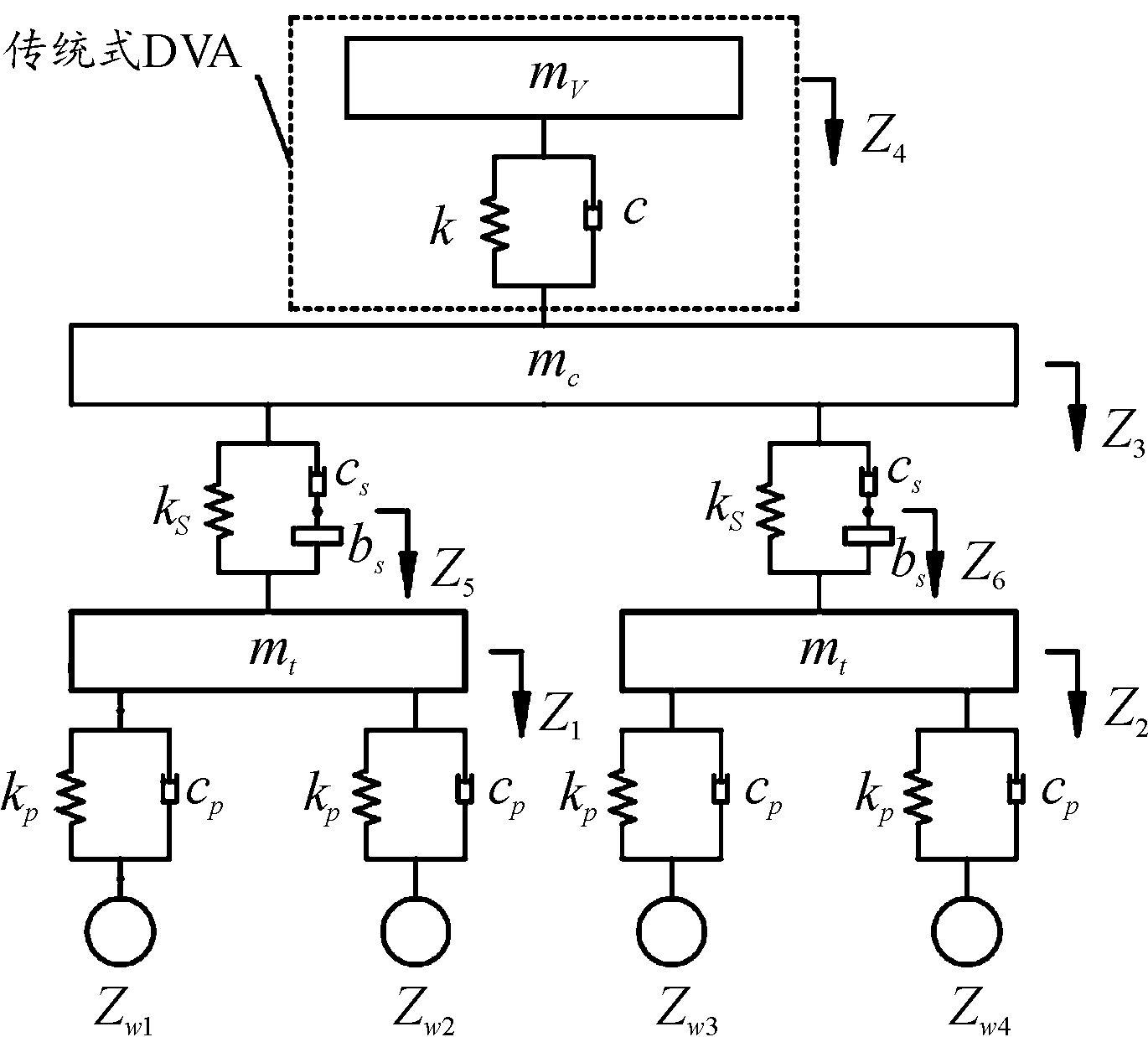
图2 传统DVA的ISD悬架列车模型
Fig.2 ISD suspension train model of traditional DVA
图2中,在含ISD悬架的列车垂向振动模型基础上,加入传统DVA,其中,k、c分别为传统DVA的弹簧刚度、阻尼系数;mV为DVA的振子质量。
安装了传统DVA后,列车系统的转向架沉浮运动方程和级间垂向位移运动方程与不安装DVA的模型方程一致,见式(1)—式(4)。根据牛顿第二运动定律推导出增加的系统动力学方程如下。
车体沉浮运动方程为
![]()
(6)
传统DVA振子沉浮运动方程为
![]()
(7)
传统DVA的最优参数采用定点理论设计,并且传统DVA的参数设计受到安装位置以及减振目标质量的影响,因此基于含ISD悬架的列车垂向振动模型,由文献[19]可得最优传统DVA最优参数公式为
![]()
(8)
![]()
(9)
![]()
(10)
式(8)—式(10)中:γo为DVA的频率比; μ为DVA振子质量与车体质量之比;ζo为DVA的阻尼比;mV为DVA振子的质量;n为正整数,对轨道列车可取值为3;v为列车行驶速度;lb为转向架定距之半;k、c分别为DVA的弹簧刚度和阻尼系数。
1.3 含惯容器式DVA的ISD悬架列车模型
1.3.1 列车模型
传统DVA振子质量一般为水泥和金属块,质量大、空间占用率多,制约着DVA的使用。因此本文中结合惯容器具有“虚质量”的物理特性,以及惯容器串联阻尼后再与弹簧并联的DVA结构,替换了传统DVA的减振结构,并提出了含惯容器式DVA的ISD悬架列车模型,如图3所示,虚线框内为含惯容器式DVA结构。
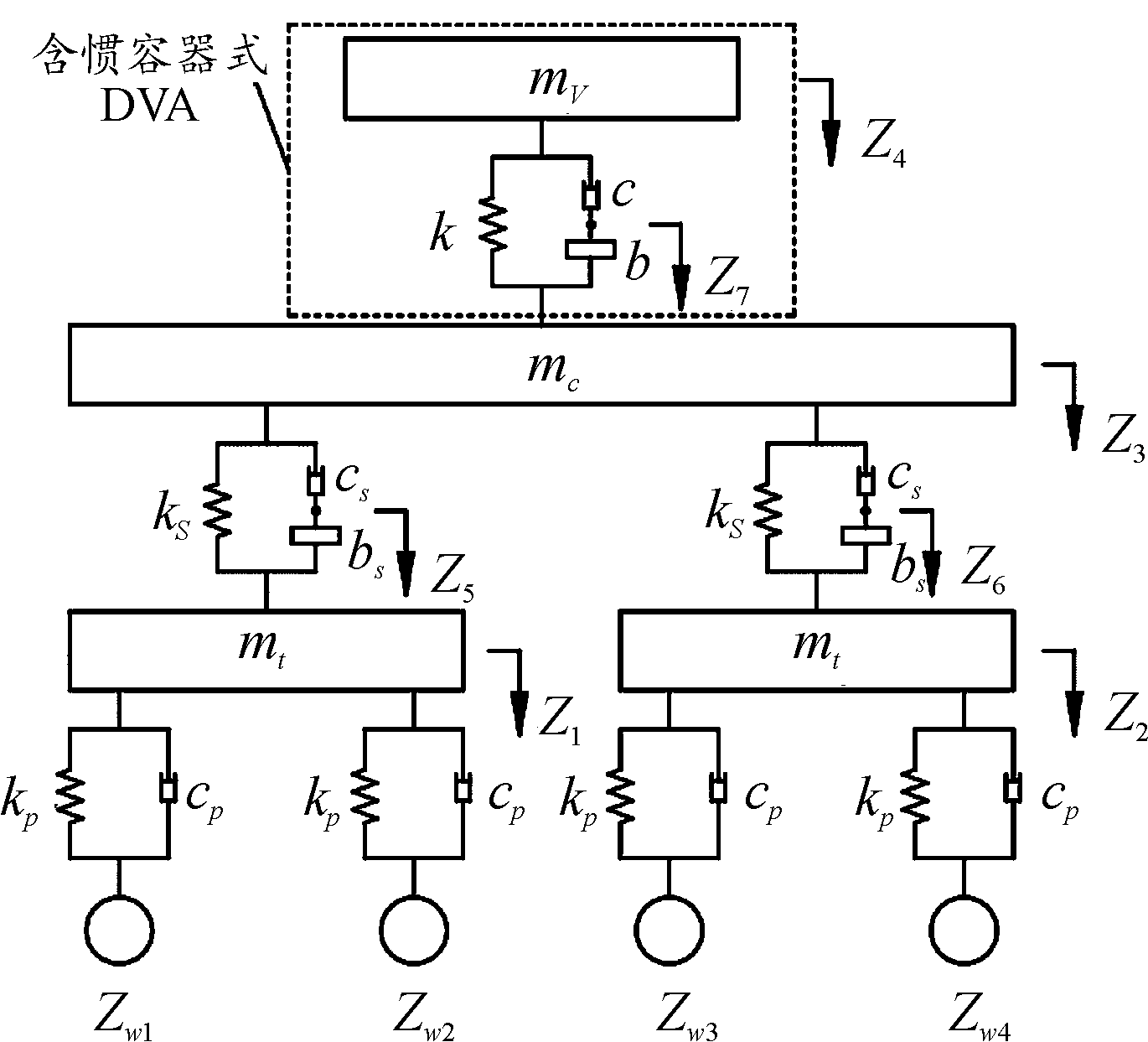
图3 含惯容器式DVA的ISD悬架列车模型
Fig.3 ISD suspension train model with inerter DVA
图3中,在含ISD悬架的列车垂向振动模型基础上,加入含惯容器式DVA,其中,k、c、b分别为含惯容器式DVA的弹簧刚度、阻尼系数和惯容器惯质系数。
安装了含惯容器式DVA后,列车系统的转向架沉浮运动方程和级间垂向位移运动方程与不安装DVA的模型方程一致,见式(1)—式(4)。根据牛顿第二运动定律推导出系统增加的动力学方程如下。
车体沉浮运动方程为
![]()
(11)
含惯容器式DVA振子沉浮运动方程为
![]()
(12)
级间垂向位移Z7沉浮运动方程为
![]()
(13)
1.3.2 含惯容器式DVA中惯容器的设计
在含惯容器式DVA结构中,需要实现振子质量被惯容器的“虚质量”代替,且惯容器本身质量对DVA整体质量影响较小,则需要采用 “虚质量”与本身质量之比较大的惯容器,因此在本文中选择滚珠丝杠式惯容器。
滚珠丝杠式惯容器主要由惯容器两端固定的外壳(左)和外壳(右)、滚珠丝杠、螺母、滚动轴承以及飞轮组成,如图4所示。
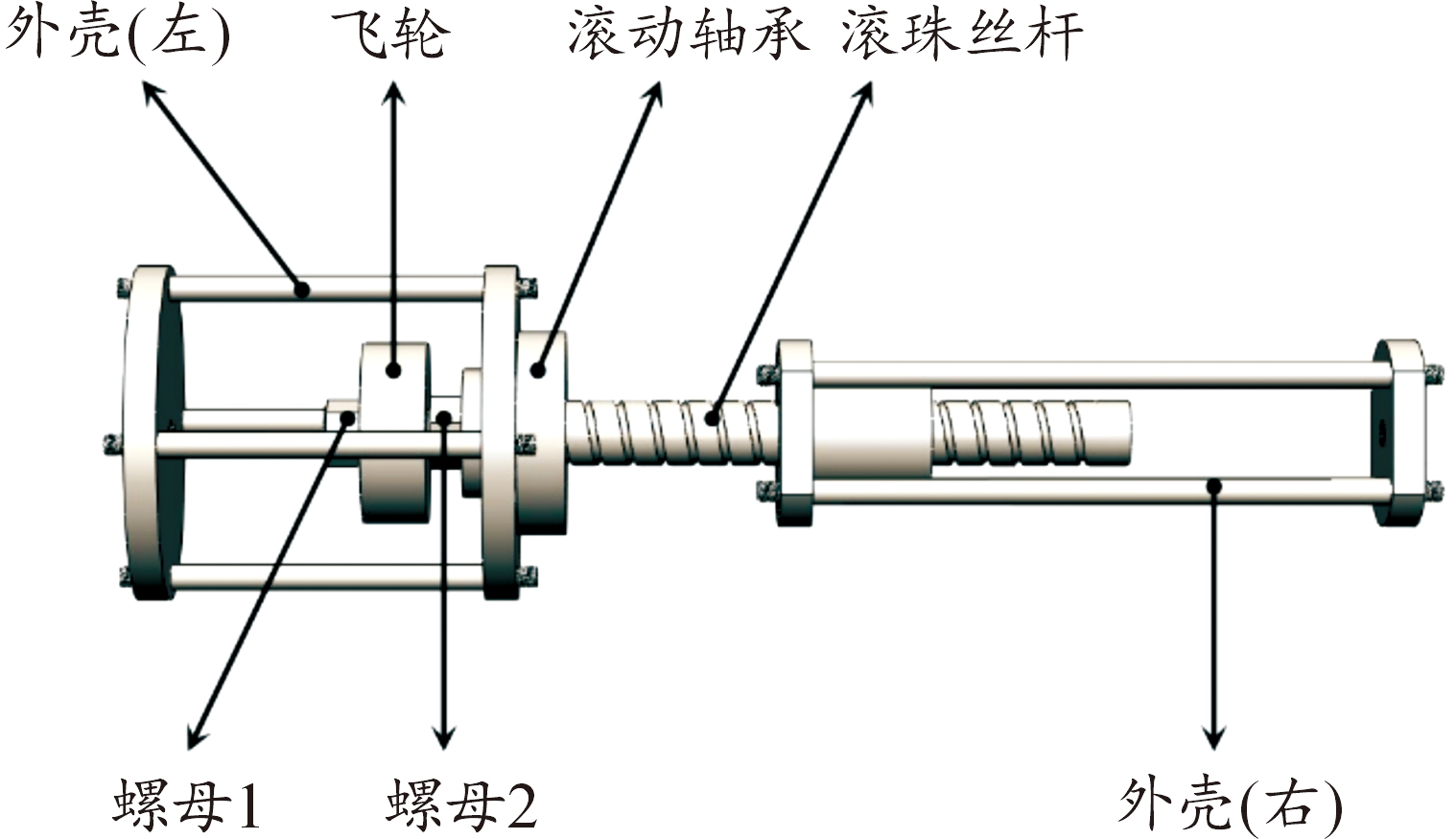
图4 滚珠丝杆式惯容器
Fig.4 Ball-screw inerter
其动力学方程为
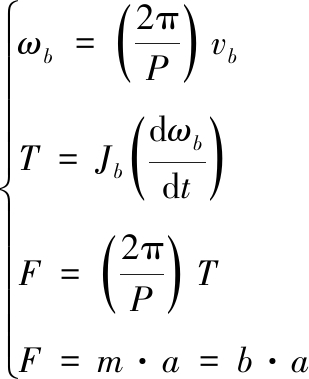
(14)
式(14)中:ωb为丝杠旋转角速度;vb为惯容器两端间的相对速度;P为滚珠丝杠副导程;T为丝杠驱动力矩;Jb为惯容器中飞轮的转动惯量;F为惯容器两端的受力;a为惯容器两端点间的相对加速度。
根据式(14)可得滚珠丝杠式惯容器的惯质系数b的计算式为
F=![]()
![]()
(15)
常见滚珠丝杠式惯容器中的飞轮为圆柱体,设飞轮质量为m,半径为r,由圆柱体转动惯量计算公式,则惯质系数还可以表示为
![]()
(16)
基于以上模型,以含ISD悬架的列车垂向振动模型为基础,分别对安装传统DVA和含惯容器DVA的模型进行定点理论计算和智能优化算法优化,最后对结果进行对比分析。
2 优化设计
2.1 优化设计流程
以含ISD悬架的列车垂向振动模型为对比分析基础,为了保证该模型的最优状态,采用智能优化算法实现参数优化,优化目标为一系kp、cp,二系ks、cs、bs。同样由于在含惯容器式DVA的ISD悬架列车模型中,不适用传统DVA设计方法,为实现优化设计,也采用智能优化算法,优化目标为DVA中的k、c、b。
粒子群优化算法(particle swarm optimization PSO)是一种模拟鸟群觅食行为的随机搜索算法,优化能力强,应用方便[20]。在粒子群算法中,粒子根据个体极值和群体极值更新自身速度和位置,在预设的迭代次数下,寻找出最优值,并且随着迭代次数的增加,适应度函数值趋于直线。流程如图5所示。
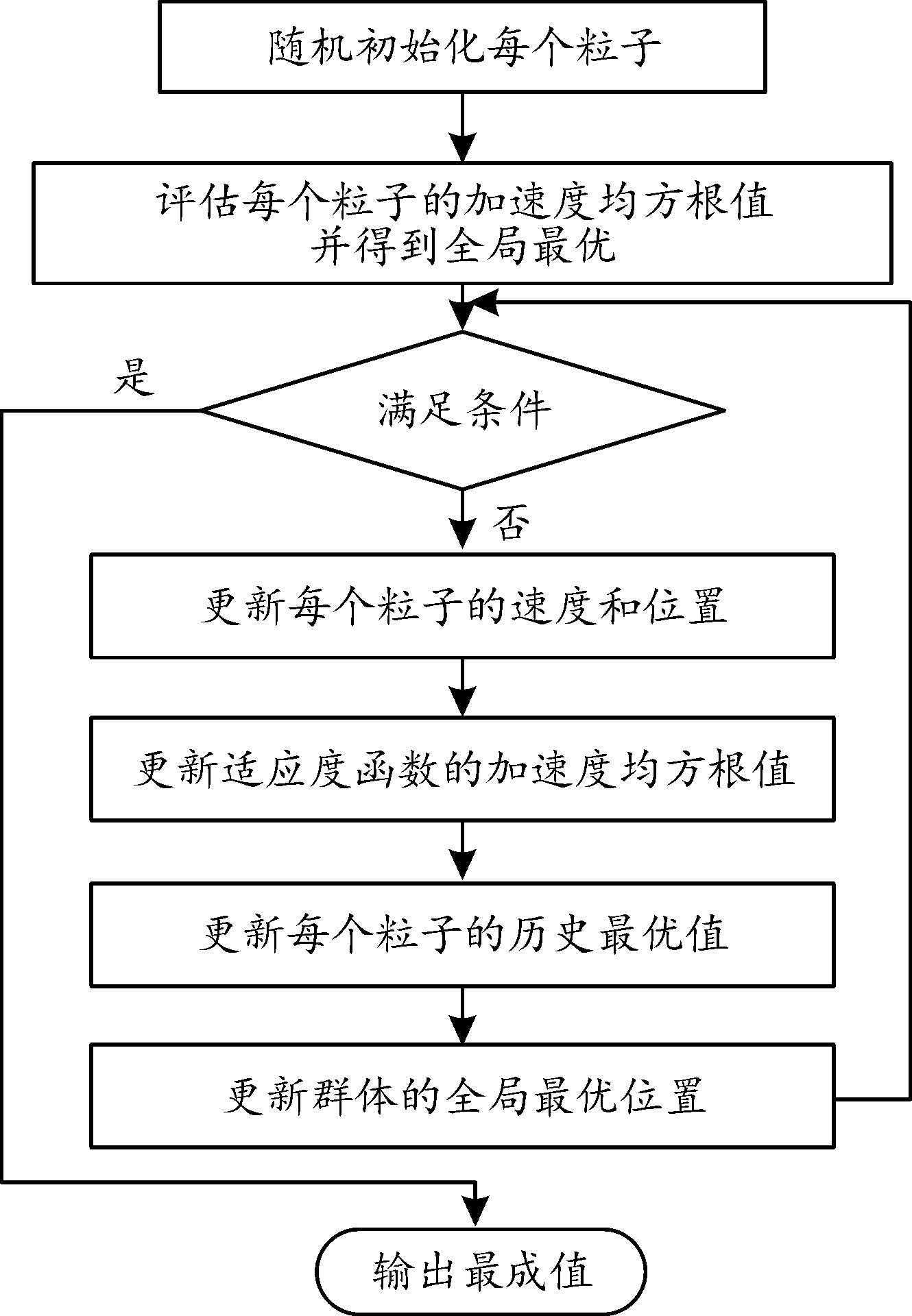
图5 粒子群优化算法流程框图
Fig.5 Flow chart of particle swarm optimization algorithm
2.2 轨道随机不平度输入模型
采用德国轨道谱高低不平度高干扰谱作为系统输入,速度为300 km/h。根据参考文献[17],得到时域计算公式为
![]()
(17)
式(17)中:![]() 为输入信号;AV为轨道粗糙度系数,m·rad;Ωc为水平截断空间频率,rad/m;Ωr为垂直截断空间频率,rad/m;V为轨道车辆的速度,m/s;ω(t)为白噪声干扰源。
为输入信号;AV为轨道粗糙度系数,m·rad;Ωc为水平截断空间频率,rad/m;Ωr为垂直截断空间频率,rad/m;V为轨道车辆的速度,m/s;ω(t)为白噪声干扰源。
利用Matlab/Simulink,考虑实际工况中前后轮对的间隔,得到德国谱位移时域信号。
2.3 优化结果
基于列车的垂向振动模型,以乘坐的舒适性作为减振系统设计重点,在简化模型中,选择车体垂向加速度的均方根值作为性能评价指标。
车体加速度均方根值越小越能提升乘坐的舒适性。因此,优化目标为
![]()
(18)
2.3.1 含ISD悬架的列车垂向振动模型参数优化
简化的列车垂向振动模型中,所需的基础参数如表1所示。
表1 列车-轨道垂向振动模型参数
Table 1 Train-track vertical vibration model parameters

参数名称参数符号取值车体质量mc/kg26 000转向架质量mt/kg2 600
利用粒子群优化算法,以含ISD悬架的列车垂向振动模型中车体加速度均方根值为目标进行参数优化,其中优化变量和算法约束条件如表2所示。
表2 悬架元件参数取值范围
Table 2 Value range of suspension component parameters

优化变量约束条件kp/(N·m-1)823 200< kp <1 528 800cp/(N·s·m-1)9 100
在300 km/h的德国轨道谱激励路面下,通过粒子群优化算法得到优化结果如表3所示。
表3 含ISD悬架的列车垂向振动模型优化结果
Table 3 Optimization results of vertical train vibration model with ISD suspension
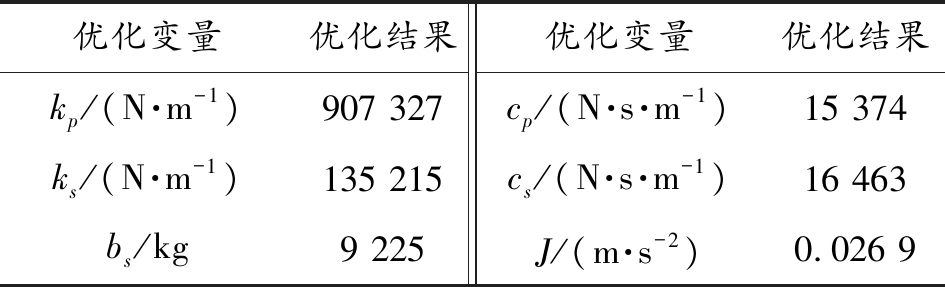
优化变量优化结果优化变量优化结果kp/(N·m-1)907 327cp/(N·s·m-1)15 374ks/(N·m-1)135 215cs/(N·s·m-1)16 463bs/kg9 225J/(m·s-2) 0.026 9
2.3.2 含惯容器式DVA的ISD悬架列车模型参数优化
由文献[21]可知,当传统DVA的振子与车体的μ为0.1时,系统能够同时满足最优同调和最优阻尼2个条件,使得系统在原来共振处的幅值大大减小,出现的2个新共振峰的峰值也很低,达到了定点理论参数优化的良好减振效果。当传统DVA的振子与车体的μ超过0.1时,会提高DVA的工程应用成本和降低DVA的减振效果。
因此在本文中,取传统DVA的振子与车体的μ等于0.1时为边界条件,在μ小于0.1时研究惯容器“虚质量”特性对DVA振子质量的替换范围,在μ等于0.1时研究含惯容器式DVA对传统DVA的减振优化。
为了在含ISD悬架的列车垂向振动模型最优参数基础上,实现惯容器“虚质量”替代DVA振子质量的目的,本文选择在含惯容器式DVA的振子质量mV从一定初始值递增到μ等于0.1的过程中,以及300 km/h的德国轨道谱激励路面下,通过粒子群优化算法得到每一次mV递增时含惯容器式DVA的元件最优参数,随后与传统DVA设计下的列车系统作对比分析。优化参数范围如表4所示。
表4 含惯容器式DVA的ISD悬架列车模型参数范围
Table 4 Parameters range of ISD suspension train model with inerter DVA

模型参数参数范围mV/kg1 000∶100∶2 600k/(N·m-1)5 000
在mV从1 000 kg开始步长为100 kg递增到2 600 kg(即μ达到0.1)的过程中,每一次mV递增时含惯容器DVA的元件最优参数如表5所示。
表5 含惯容器式DVA的ISD悬架列车模型优化结果
Table 5 ISD suspension train model optimization results with inerter DVA
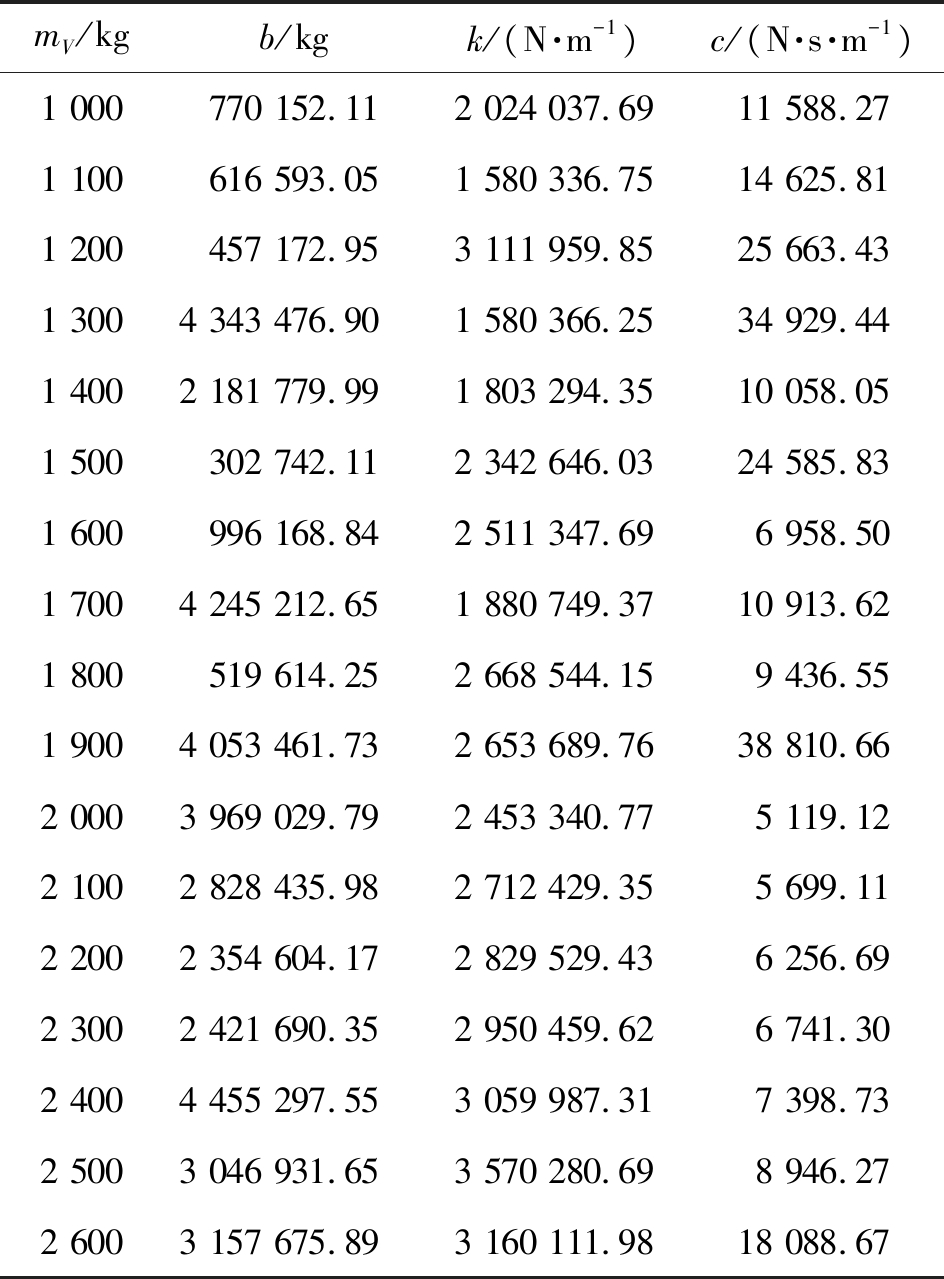
mV/kgb/kgk/(N·m-1)c/(N·s·m-1)1 000770 152.112 024 037.6911 588.271 100616 593.051 580 336.7514 625.811 200457 172.953 111 959.8525 663.431 3004 343 476.901 580 366.2534 929.441 4002 181 779.991 803 294.3510 058.051 500302 742.112 342 646.0324 585.831 600996 168.842 511 347.696 958.501 7004 245 212.651 880 749.3710 913.621 800519 614.252 668 544.159 436.551 9004 053 461.732 653 689.7638 810.662 0003 969 029.792 453 340.775 119.122 1002 828 435.982 712 429.355 699.112 2002 354 604.172 829 529.436 256.692 3002 421 690.352 950 459.626 741.302 4004 455 297.553 059 987.317 398.732 5003 046 931.653 570 280.698 946.272 6003 157 675.893 160 111.9818 088.67
在经过粒子群算法参数优化后含ISD悬架的列车垂向振动模型基础上,利用上述优化数据以及传统DVA参数设计方法,对比分析含惯容器式DVA和传统DVA在含ISD悬架的列车垂向振动模型的性能影响,并借此讨论惯容器在DVA结构中对DVA振子的质量替代范围。
3 含DVA的列车性能分析
3.1 传统DVA的ISD悬架列车模型参数
结合悬架的优化参数,根据式(8)—式(10),在μ为0.1时,可得传统DVA的ISD悬架列车模型的最优减振参数。如表6所示。
表6 传统DVA的ISD悬架列车模型参数取值
Table 6 ISD suspension train model parameter values of traditional DVA

参数名称参数符号取值传统DVA的振子质量mV/kg2 600转向架定距之半lb/m8.75传统DVA的最优刚度k/(N·m-1)17 312 175传统DVA的最优阻尼c/(N·s·m-1)78 345
3.2 车体加速度均方根值对比
经过上述分析可以得到不同模型的车体加速度结果,汇总后如图6所示。其中,以含ISD悬架和未添加DVA的列车垂向振动模型的车体加速度均方根值作为对比基础,如图6中长实线所示,值为0.026 9 m/s2。
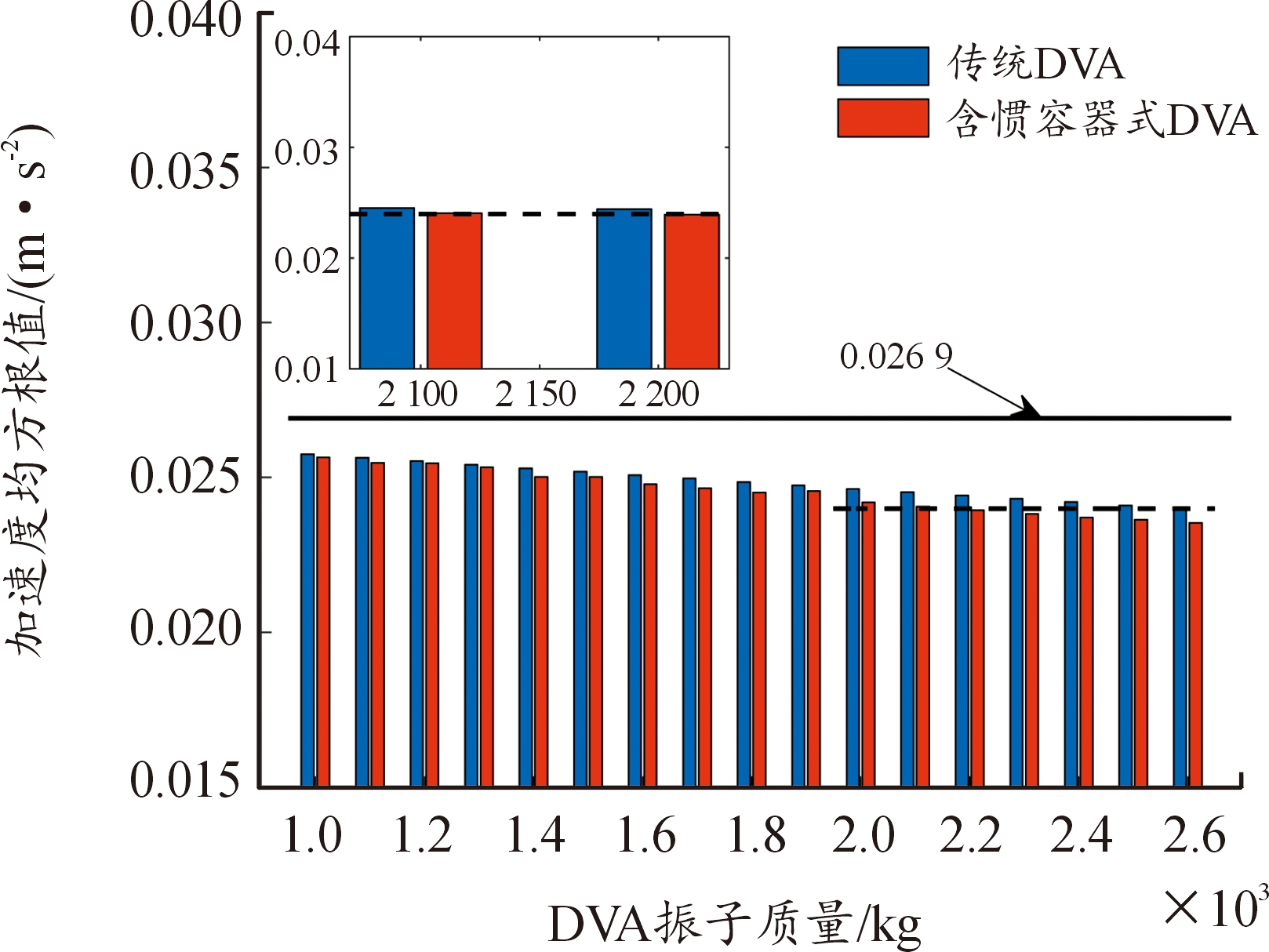
图6 惯容器对DVA的影响
Fig.6 Influence of inerter on DVA
在DVA振子质量从1 000 kg达到2 600 kg过程中,传统DVA的ISD悬架列车模型在传统DVA参数计算方法下得到传统DVA对含ISD悬架的列车垂向振动模型的减振效果,如图6中“传统DVA”所示。
在DVA振子质量从1 000 kg达到2 600 kg过程中,含惯容器式DVA的ISD悬架列车模型结合表5的优化结果,得到含惯容器式DVA对含ISD悬架的列车垂向振动模型的减振效果,如图6中“含惯容器式DVA”所示。
由图6可知,传统DVA和含惯容器式DVA对含ISD悬架的列车垂向振动模型都有性能提升。相较于没有DVA的模型,在所有振子质量取值情况下车体加速度均方根值都有所降低。同时,优化后的含惯容器式DVA较传统参数设计所得的传统DVA对车辆减振有更好的效果。
振子质量mV在2 100~2 600 kg内,含惯容器式DVA结构对传统DVA结构的性能提升如表7所示。
表7 含惯容器式DVA对传统DVA的优化
Table 7 Optimization of DVA with inerter to traditional DVA
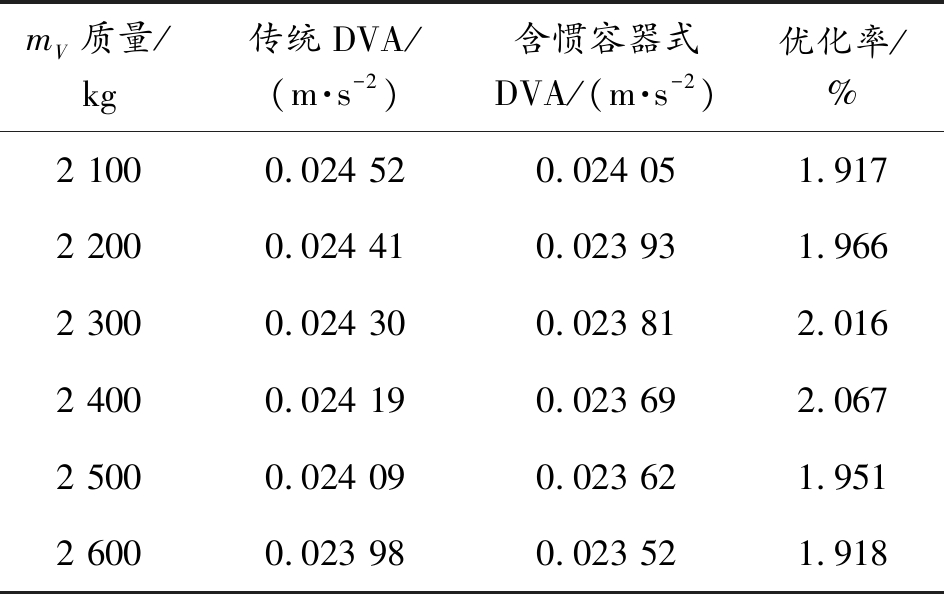
mV质量/kg传统DVA/(m·s-2)含惯容器式DVA/(m·s-2)优化率/%2 1000.024 520.024 051.9172 2000.024 410.023 931.9662 3000.024 300.023 812.0162 4000.024 190.023 692.0672 5000.024 090.023 621.9512 6000.023 980.023 521.918
振子质量mV在2 100~2 200 kg内,含惯容器式DVA结构通过粒子群优化算法达到了传统DVA结构参数经验计算方法下mV为2 600 kg时给列车带来的减振效果,如图6中局部放大图所示,其中虚线处的值为0.023 98 m/s2,且mV在2 200 kg时含惯容器式DVA结构减振效果好于mV在2 600 kg时的传统DVA结构,综上表明了惯容器 “虚质量”的物理特性是等效了接近400 kg DVA振子的质量。并且由表7可知,振子质量mV在2 100~2 600 kg的变化过程中,含惯容器式DVA比传统DVA结构对含ISD悬架的列车垂向振动模型的减振性能提升要好。
3.3 车体加速度的时域和频域效果对比
为了进一步验证惯容器质量替换的可行性,从加速度均方根值接近的不同振子取值来分析时域和频域上的车体加速度效果。取传统DVA的ISD悬架列车模型在mV为2 600 kg时和含惯容器式DVA的ISD悬架列车模型在mV为2 200 kg时车体加速度时域和频域作对比,如图7、图8所示。
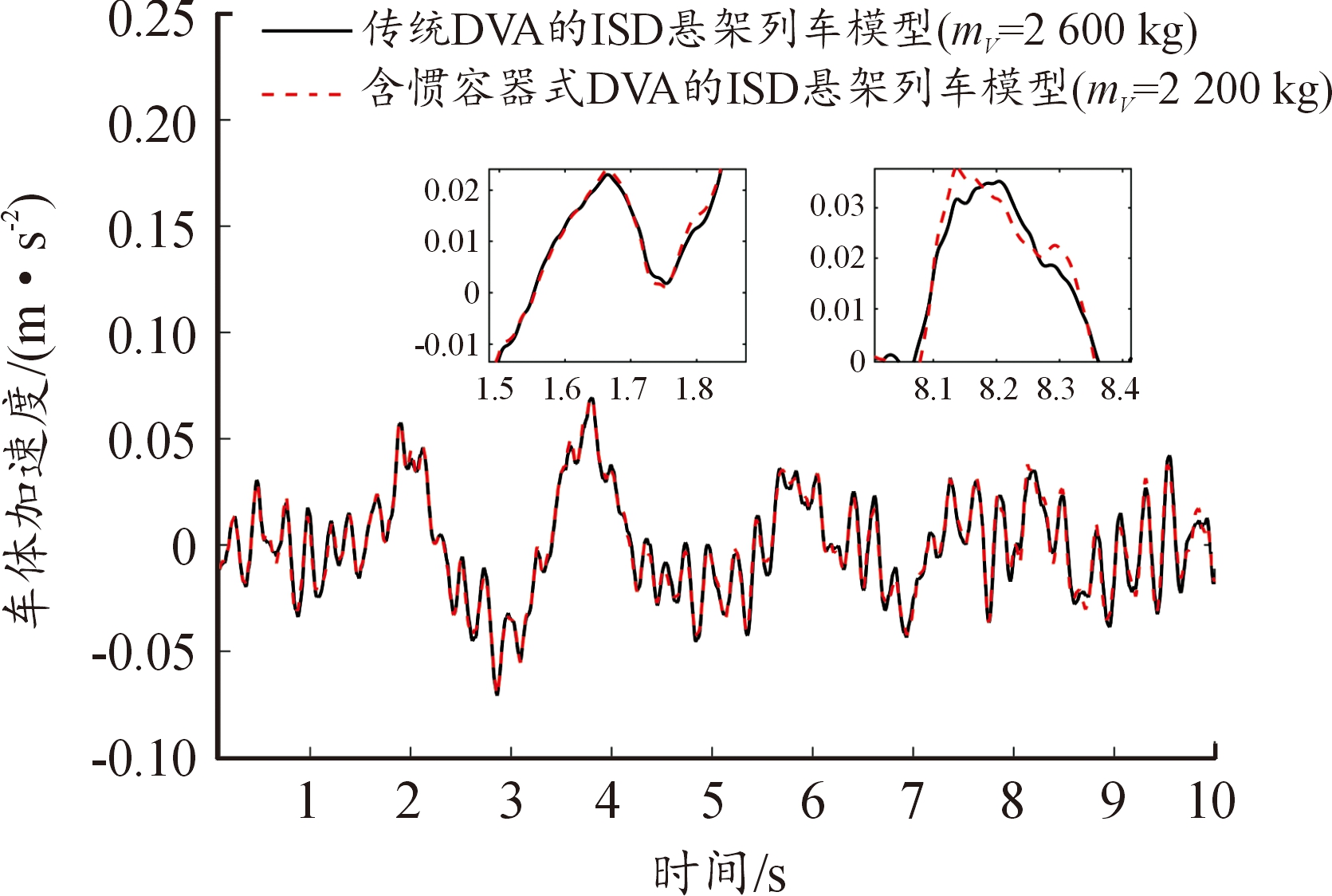
图7 车体加速度随时间变化曲线
Fig.7 Variation curve of vehicle acceleration with time
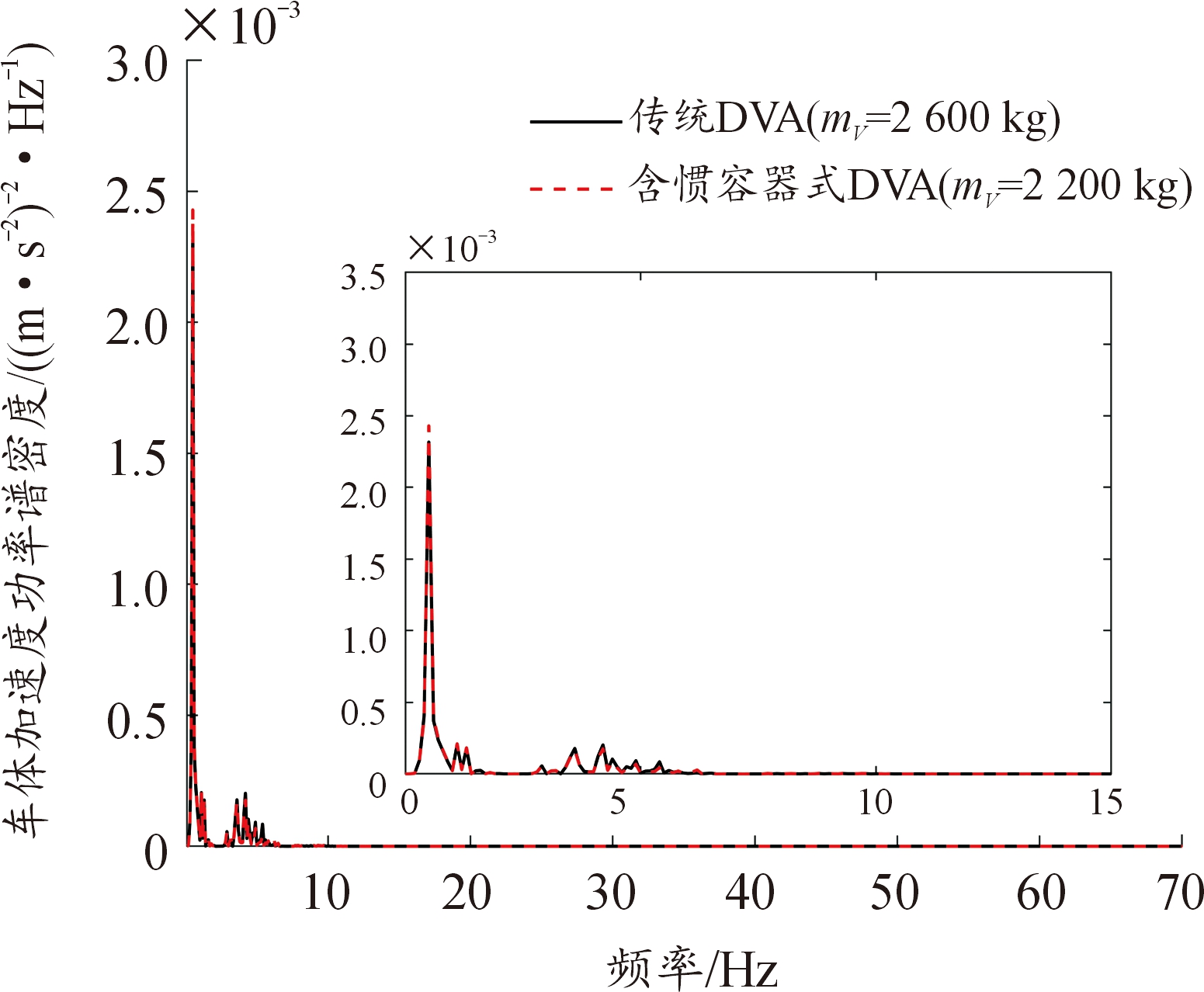
图8 车体加速度功率谱变化曲线
Fig.8 Variation curve of vehicle body acceleration power spectrum
图7为车体的加速度随时间变化的曲线,由图7可以看出,在仿真的10 s内,时域的变化基本一致;图8为车体加速度功率谱变化曲线,在仿真的70 Hz以内取0~15 Hz内对比,频域的变化也基本一致。说明了含惯容器式DVA的振子质量在2 200 kg时已经达到了传统DVA的振子质量在2 200 kg时对列车的减振效果,同时反映了惯容器能够替换DVA结构中振子的质量并且不损失结构的减振性能。
4 惯容器的实现
由表4可知,粒子群优化算法约束确定时,为实现更好的优化效果,b的优化约束范围设置较大,优化结果也表明了b的优化值需要采用 “虚质量”与本身质量之比较大的惯容器实现。
滚珠丝杠式惯容器在选择一定材料,调整r以及P的前提下,能够实现m到b较大的放大倍数。表5中能够用惯容器“虚质量”替换DVA振子质量的有效优化范围是mV从2 100~2 200 kg的中间值到2 600 kg,取该范围中惯质系数的最大值4 455 297.55kg,根据式(15)可得,滚珠丝杠式惯容器主要参数其中一种取值,如表8所示。表8的配置可以计算得到飞轮质量为91.84 kg,相较于4 455 297.55 kg的惯质系数,滚珠丝杠式惯容器实现了较小的飞轮质量得到较大 “虚质量”的物理特性。
表8 滚珠丝杠式惯容器主要参数取值
Table 8 Main parameter values of ball screw inertial container

参数名称参数符号取值飞轮材料不锈钢/(kg·m-3)7 930飞轮厚度L/m0.015飞轮半径r/m0.496滚珠丝杠导程P/m0.01飞轮质量m/kg91.84
同时由表7可知,惯容器替换传统DVA振子的质量在400~500 kg,由表8可知,根据最大惯质系数实现出来的滚珠丝杠式惯容器在91.84 kg左右,粗略计算可得实际惯容器能替换传统DVA振子的质量在300~400 kg,且逼近400 kg。
5 结论
本文中基于粒子群优化算法,对含ISD悬架的列车垂向振动模型及含惯容器式DVA结构进行了参数优化,并与传统DVA结构进行了对比分析,得到如下结论:
1) DVA的加入比没有DVA时候的车辆性能要有所提升,且含惯容器式DVA结构在振子质量相同的情况下比传统DVA结构减振效果好;
2) 在保证相同减振性能的条件下,含惯容器式DVA能够用惯容器的“虚质量”物理特性实现对DVA振子的质量替换,替换质量接近400 kg;
3) 滚珠丝杠式惯容器可根据具体的实物参数设计达到百万级的惯质系数,且自身体积质量比较小。
[1] 李琼.基于动力吸振器的城轨车辆减振降噪方法研究[D].上海:上海工程技术大学,2016.
LI Qiong.Research on vibration and noise reduction method of urban rail vehicles based on dynamic vibration absorber[D].Shanghai:Shanghai University of Engineering Science,2016.
[2] NISHIHARA O.Exact optimization of a three-element dynamic vibration absorber:minimization of the maximum amplitude magnification factor[J].Journal of Vibration &Acoustics,2019,141(1):011001.
[3] 杨晓彤,申永军,王俊锋.一种含放大机构、惯容和接地刚度的动力吸振器的参数优化[J].振动与冲击,2022,41(21):308-315.
YANG Xiaotong,SHEN Yongjun,WANG Junfeng.Parameter optimization of dynamic vibration absorber with amplifying mechanism,Inertial capacity and ground stiffness[J].Journal of Vibration and Shock,202,41(21):308-315.
[4] 宗志祥,文永蓬,尚慧琳,等.城轨车辆车体多重动力吸振器减振方法研究[J].振动与冲击,2020,39(2):154-162.
ZONG Zhixiang,WEN Yongpeng,SHANG Huilin,et al.Research on vibration reduction method of urban rail vehicle body with multiple dynamic absorber[J].Journal of Vibration and Shock,2020,39(2):154-162.
[5] 周涛,陈晓梅,张永亮,等.动力总成动力吸振器特性研究[J].内燃机,2020,204(1):34-37.
ZHOU Tao,CHEN Xiaomei,ZHANG Yongliang,et al.Research on characteristics of powertrain power absorber[J].Chinese Internal Combustion Engine,2020,204(1):34-37.
[6] 李灿,韩冬冬,陈昭.汽车半轴吸振器的减振性能研究[J].汽车零部件,2019,129(3):9-13.
LI Can,HAN Dongdong,CHEN Zhao.Research on damping performance of vibration absorber for automobile Axle[J].Automotive Parts,2019,129(3):9-13.
[7] 邹钰,文永蓬,纪忠辉,等.车轨耦合下钢轨复合吸振器的减振方法[J].振动.测试与诊断,2021,41(5):888-896.
ZOU Yu,WEN Yongpeng,JI Zhonghui,et al.Vibration reduction method of rail-rail composite vibration absorber[J].Journal of Vibration,Measurement &Diagnosis,2021,41(5):888-896.
[8] 周子博,申永军,杨绍普.含放大机构的三要素型动力吸振器H∞优化[J].振动与冲击,2022,41(5):158-165.
ZHOU Zibo,SHEN Yongjun,YANG Shaopu.H∞ optimization of a three-factor dynamic absorber with amplifying mechanism[J].Journal of Vibration and Shock,2022,41(5):158-165.
[9] JIANG J Z,SMITH M C.On the classification of series parallel electrical and mechanical networks[C]//Proceedings of the 2010 American Control Conference.IEEE,2010:1416-1421.
[10] JIANG J Z,SMITH M C.Regular positive-real functions and five-element network synthesis for electrical and mechanical networks[J].IEEE Transactions on Automatic Control,2011,56(6):1275-1290.
[11] JIANG J Z,MATAMOROS-SANCHEZ A Z,GOODALL R M,et al.Passive suspensions incorporating inerters for railway vehicle[J].Vehicle System Dynamics,2012,50(S1):263-276.
[12] SMITH M C,WANG F C.Performance benefits in passive vehicle suspensions employing inerters[C]//Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat.No.03CH37475).IEEE,2003:2258-2263.
[13] SMITH M C,WANG F C.Performance benefits in passive vehicle suspensions employing inerters[J].Vehicle system dynamics,2004,42(4):235-257.
[14] 孙晓强,陈龙,汪若尘,等.滚珠丝杠式惯容器试验及力学性能预测[J].振动与冲击,2014,33(14):61-65,83.
SUN Xiaoqiang,CHEN Long,WANG Ruochen,et al.Test and mechanical property prediction of ball screw inerter[J].Journal of Vibration and Shock,2014,33(14):6l-65,83.
[15] 杨晓峰,沈钰杰,陈龙,等.基于动力吸振理论的车辆ISD悬架设计与性能分析[J].汽车工程,2014(10):1262-1266,1277.
YANG Xiaofeng,SHEN Yujie,CHEN Long,et al Design and performance analysis of vehicle ISD suspension based on dynamic vibration absorption theory[J].Automotive Engineering,2014 (10):1262-1266,1277.
[16] 葛正,王维锐.车辆主动惯容式动力吸振悬架系统研究[J].振动与冲击,2017,36(1):167-174.
GE Zheng,WANG Weirui.Research on vehicle active inertial dynamic vibration absorbing suspension system[J].Journal of Vibration and Shock,2017,36 (1):167-174.
[17] 邱忠诚.基于惯容器的轨道高速车辆垂向减振分析与优化[D].昆明:昆明理工大学,2022.
QIU Zhongcheng.Vertical vibration reduction analysis and optimization of high-speed rail vehicles based on inertial containers[D].Kunming:Kunming University of Science and Technology,2022.
[18] 牛豆.几种动力吸振器的变形及参数优化[D].石家庄:石家庄铁道大学,2021.
NIU Dou.Deformation and parameter optimization of several dynamic vibrators[D].Shijiazhuang:Shijiazhuang Tiedao University,2021.
[19] 周劲松,张伟,孙文静,等.铁道车辆弹性车体动力吸振器减振分析[J].中国铁道科学,2009,30(3):86-90.
ZHOU Jinsong,ZHANG Wei,SUN Wenjing,et al Vibration reduction analysis of dynamic vibration absorber for elastic car body of railway vehicle[J].China Railway Science,2009,30 (3):86-90.
[20] 高星星.几种粒子群优化算法及其应用研究[D].宁夏:北方民族大学,2020.
GAO Xingxing.Research on several particle swarm optimization algorithms and their applications[D].Ningxia:Beifang University for Nationalities,2020.
[21] 高燕.动力吸振器的设计与吸振特性的研究[D].广州:华南理工大学,2019.
GAO Yan.Design of dynamic vibration absorber and research on vibration absorption characteristics[D].Guangzhou:South China University of Technology,2019.