0 引言
随着铁路客/货运量的不断增加和高铁运行速度的不断提升,钢轨的疲劳损伤现象越来越普遍[1]。因此,轮轨间的接触疲劳研究也越来越被人们重视,其中钢轨表面裂纹的扩展研究更是受到国内外学者的广泛关注[2-11]。对于钢轨表面的裂纹扩展,国内、外学者进行了大量的研究。Babnadi等[5]考虑了轨道的弹塑性材料模型研究了轨道表面裂纹的载荷、滑移、尺寸、裂纹取向及裂纹相互作用的影响。结果表明,在钢轨与车轮接触荷载相同的情况下,斜裂纹比垂直裂纹更容易扩展。昝晓东等[6]借助ANSYS模拟了二维钢轨表面裂纹的扩展,根据最大周向应力幅值判据和Paris公式确定了裂纹的扩展路径,并获得了高速度对钢轨裂纹扩展有促进作用。江晓禹等[7]考虑了应变率效应,获得了轮轨接触作用力的分布,并通过裂纹扩展方向的威尔分布得出了列车在不同速度下的裂纹转化类型。Tang等[8]采用FRANC3D和ABAQUS模拟焊接钢桥在面外载荷作用下的疲劳裂纹扩展,并对扩展过程中的应力强度因子进行计算,预测出了疲劳裂纹的扩展寿命。卢观健等[9]对经过循环碾压的钢轨的实验对钢轨损伤后的形貌进行分析,钢轨表面出现了剥离掉块的损伤形式。对于钢轨表面疲劳裂纹扩展,学者们大多是基于二维的线弹性断裂理论进行研究分析,使问题得到了简化,但对钢轨三维表面裂纹扩展过程中断裂参数的变化和三维裂纹的扩展路径研究较少,这往往会忽略实际工程中的重要三维因素,无法清晰研究微裂纹的萌生和宏观裂纹的扩展行为,局限性突出[10]。
本文中基于ABAQUS和FRANC3D对钢轨三维表面裂纹的疲劳扩展进行研究。首先,在钢轨表面预设1条三维表面直裂纹,通过施加轮轨载荷获取三维表面直裂纹危险点;然后,在危险点处基于ABAQUS和FRANC3D模拟三维表面直裂纹在轮轨载荷作用下的疲劳扩展;最后,将模拟结果与实际钢轨裂纹形貌进行对比,验证了三维表面裂纹扩展模拟的可靠性。
FRANC3D与ABAQUS两种有限元软件进行联合仿真时的工作流程如图1所示。
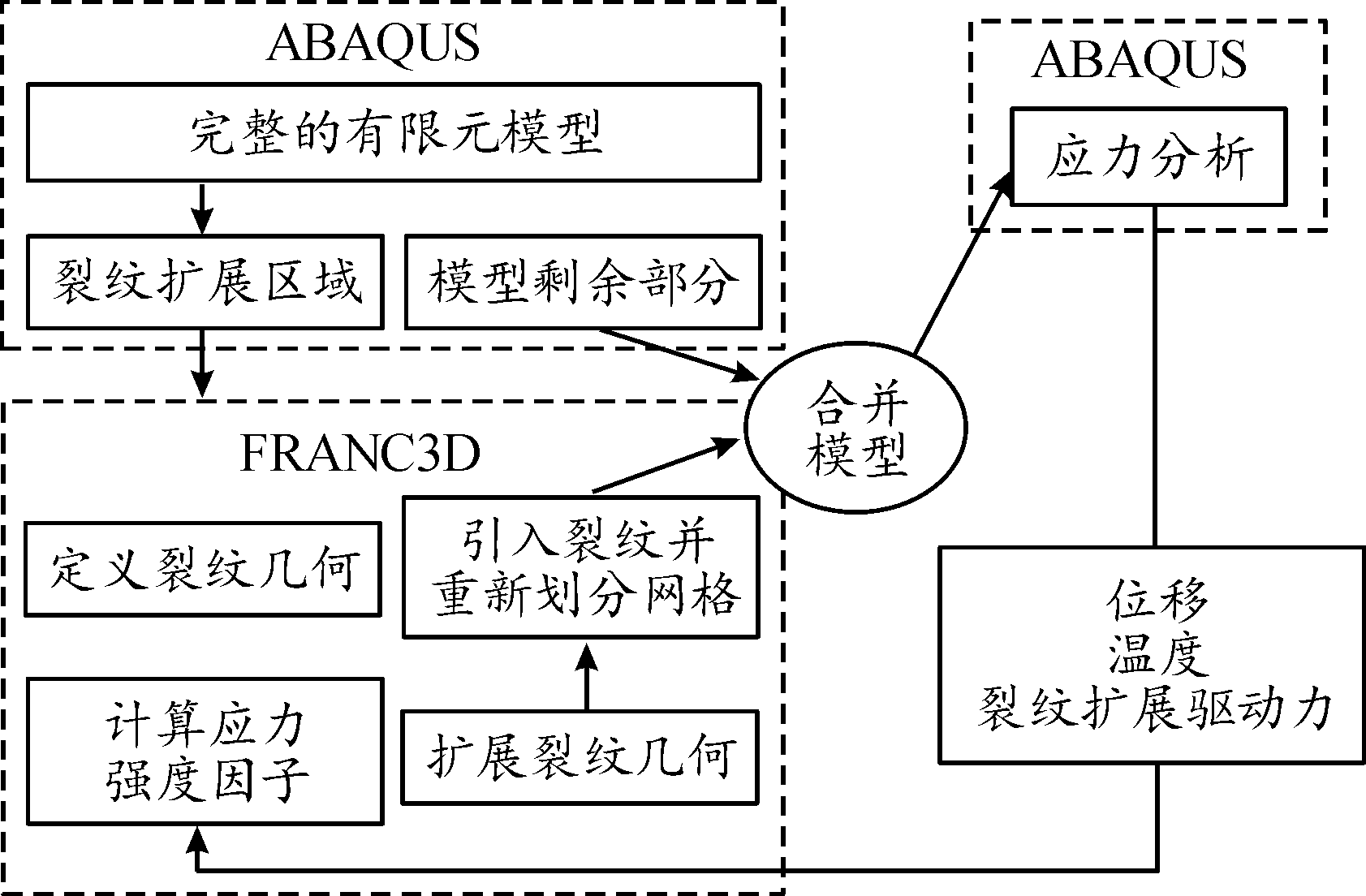
图1 ABAQUS和FRANC3D联合仿真工作流程
Fig.1 ABAQUS and FRANC3D joint simulation workflow
在ABAQUS中建立完整的有限元模型,根据插入裂纹的应力场区域,模型可分为裂纹扩展区域和模型剩余部分,并在ABAQUS中生成包含所有模型信息的inp文件,将inp文件导入到FRANC3D中,FEANC3D软件可定义裂纹的几何形状,将所定义的裂纹插入模型中,在裂纹前缘处进行网格加密,邻近裂纹尖端处使用15节点的楔形单元,这些单元将适当的单元边上的中间节点移动到靠近裂纹尖端的1/4处,裂纹尖端r1/2应力奇异。裂纹尖端楔形单元被20节点的六面体单元环包围。若模型添加简单约束载荷时可直接利用ABAQUS求解器进行求解,得到相关的断裂力学参数;若模型的边界条件较为复杂,FRANC3D可能无法识别,需将已进行网格划分的全模型inp文件导入到ABAQUS中进行边界条件的重新施加,计算得到相应的结果云图,并运行writeDtpFile.py文件后,将ABAQUS中生成的odb云图文件转换为FRANC3D需要的dtp位移文件,重新打开FRANC3D即可得到断裂力学参数。
1 理论介绍
1.1 研究模型
本文中以U71Mn钢轨60 kg/m技术参数建立三维钢轨模型。钢轨下表面进行全约束,提取轮轨间作用力施加在钢轨表面,轮轨作用力分为法向赫兹接触压力和切向摩擦力。图2为三维钢轨轮轨接触力模型。
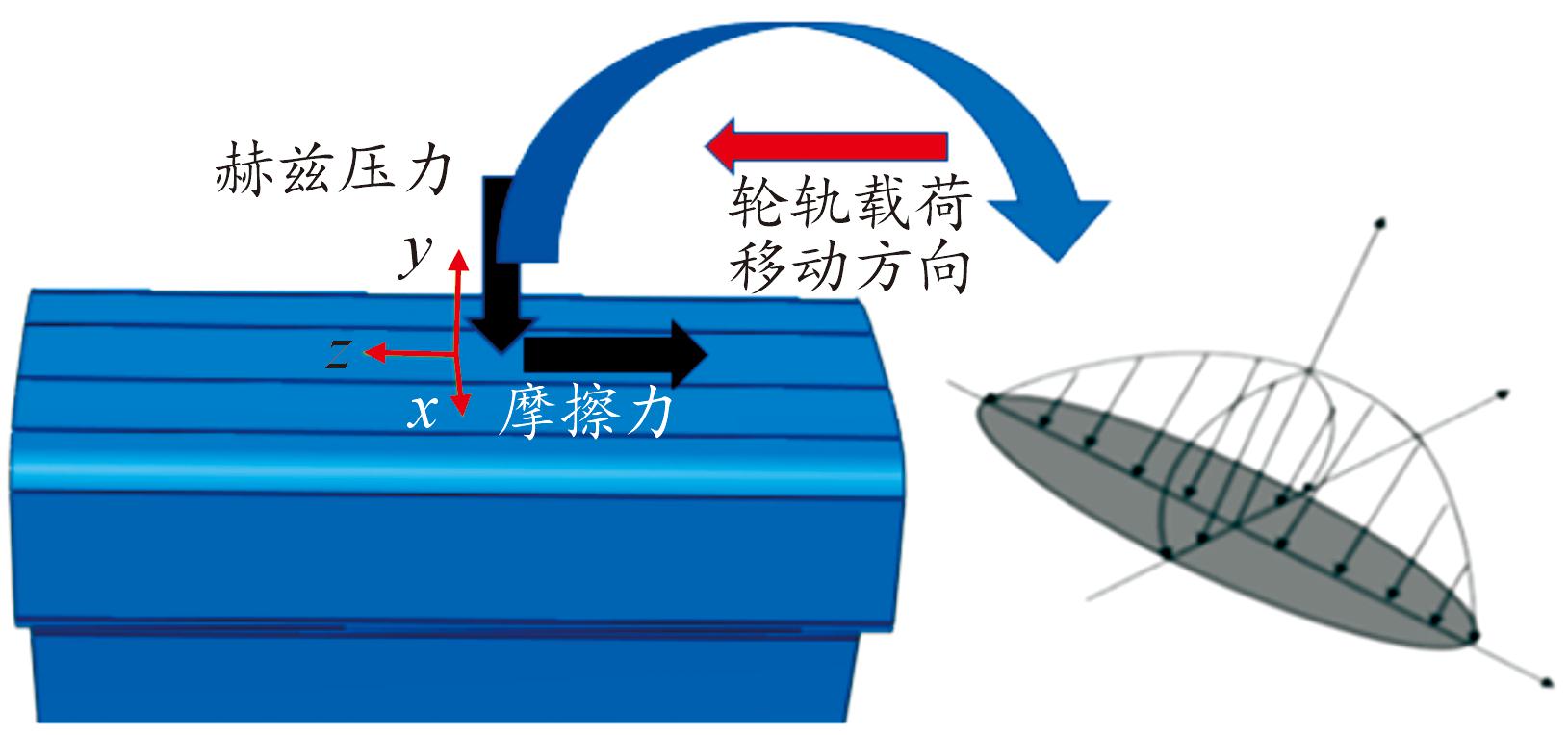
图2 三维钢轨轮轨接触力模型
Fig.2 Three-dimensional rail wheel-rail contact force model
1.2 复合型裂纹疲劳扩展速率
钢轨在车轮的往复碾压作用下,往往会由于塑性积累或钢轨表面的微缺陷而引起表面微裂纹的萌生[12],裂纹在轮轨载荷作用下不再承受单一的载荷形式,其中应力强度因子能反映出裂纹附近的应力场的强弱[12]。三维裂纹在扩展过程中的应力强度可通过M积分进行计算[13-15],当应力强度因子幅值ΔK超过疲劳裂纹扩展门槛值后,进行应力循环,钢轨表面便可能会萌生微裂纹。Paris和Erdogan提出了恒定应力比循环载荷作用下的疲劳裂纹扩展速率经验公式,即Paris公式[16]:
![]()
(1)
式(1)中: C和m是由试验测得的材料参数,U71Mn钢的材料参数可由表1得到,轮轨滚动接触裂纹在扩展过程中存在多种裂纹模式,对于三维表面裂纹的扩展,可用ΔKeff代替ΔK,等效应力强度因子Keq及幅值由式(2)和式(3)给出:
![]()
(2)
![]()
(3)
表1 U71Mn钢轨的材料参数
Table 1 U71Mn rail material parameters
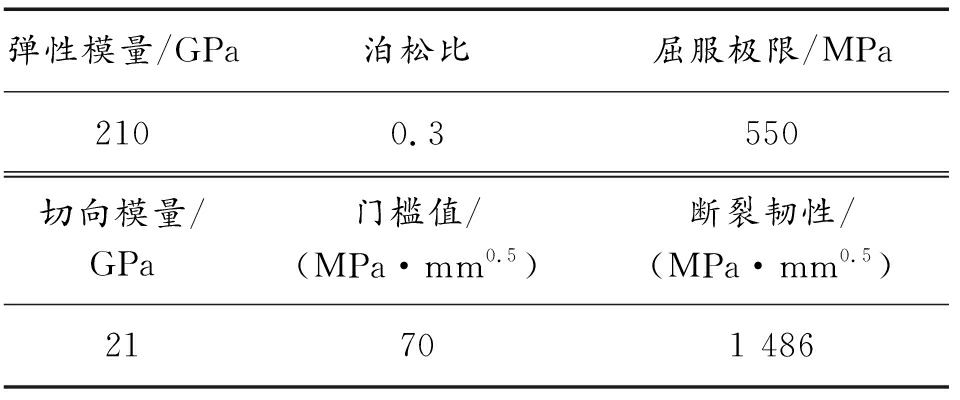
弹性模量/GPa泊松比屈服极限/MPa210 0.3550切向模量/GPa门槛值/(MPa·mm0.5)断裂韧性/(MPa·mm0.5)2170 1 486
1.3 三维疲劳裂纹扩展原理
无数个裂纹尖端点按照一定方向能形成特定形状的三维裂纹前缘,在载荷作用下三维裂纹尖端点会出现不同的应力和应变场。在线弹性条件下,应力强度因子是反映裂纹前缘附近应力场强弱的重要力学参数,当应力强度因子KI超过材料本身的断裂韧性KIC时,材料会发生脆性断裂,裂纹快速扩展。而应力强度因子KI超过材料门槛值Kth且未超过断裂韧性KIC时,材料处于疲劳阶段,裂纹可能会在循环加载若干次后,发生稳步扩展的失效现象,反之裂纹不会扩展。
三维裂纹前缘的裂纹尖端点的应力强度因子的大小会因尖端点的位置不同而变化。根据Paris公式,每个裂纹尖端点的扩展距离也是不同的,指定裂纹前缘上应力强度因子中值尖端点的扩展距离(一般取为裂纹长度的15%~20%),其他位置处节点的扩展距离可根据下式获得:
![]()
(4)
式(4)中:Δamedian,ΔKmedian分别为节点的扩展长度和等效应力强度因子幅值,ΔKi为裂纹前缘上任意节点的等效应力强度因子幅值,n缩放系数。
三维裂纹前缘的尖端点承受着复杂的疲劳循环载荷,尖端点在拉应力状态下σθθ最大时,θ作为裂纹的扩展角度,其拉应力表达式如式(5)所示。
![]()
(5)
尖端点在剪应力状态下:
![]()
(6)
最大时的值的θkink也可考虑作为裂纹扩展角度。采用最大周向应力准则[17],同时计算上述两式,选择应力最大时的角度θkink作为局部裂纹的扩展方向。
1.4 赫兹接触压力
滚动接触模型大部分是根据赫兹接触理论建立的[18-19]。本节提取车轮与钢轨接触所产生的轮轨接触压力,并施加在钢轨表面上。轮轨接触面赫兹接触应力P(x,y)可由下式表示:
![]()
(7)
最大的接触应力发生在椭圆中心:
![]()
(8)
式(8)中:P为车轮对钢轨的接触压力;a、b为椭圆接触斑的长半径和短半径;qmax为接触斑内最大的接触应力。
椭圆形接触斑长半径和短半径的表达式见式(9)和式(10):
![]()
(9)
![]()
(10)
式(10)中的A+B可由下式表示:
![]()
(11)
式(11)中:![]() 为车轮的滚动圆半径;
为车轮的滚动圆半径;![]() 为钢轨顶面横断面半径;
为钢轨顶面横断面半径;![]() 为钢轨纵向曲率半径;
为钢轨纵向曲率半径;![]() 为钢轨横断面外形半径。
为钢轨横断面外形半径。
式中G*由式(12)给出:
![]()
(12)
式(12)中: m、n为赫兹接触时计算接触应力的系数; E1、E2分别为车轮和钢轨的弹性模量; ν1、ν2分别为车轮和钢轨的泊松比,可通过查询文献[19]获得。
假设车轮和钢轨的弹性模量与泊松比均相等:E1= E2=210 GPa,v1=v2=0.3。查询文献[20], ![]() 由此可确定椭圆形接触斑的大小,即:a=6.453 mm,b=4.882 mm。轮重7.5 t 的车轮作用在钢轨上,通过赫兹接触理论计算得到的最大接触压力为1137 MPa,该结果与文献[21]描述基本一致。
由此可确定椭圆形接触斑的大小,即:a=6.453 mm,b=4.882 mm。轮重7.5 t 的车轮作用在钢轨上,通过赫兹接触理论计算得到的最大接触压力为1137 MPa,该结果与文献[21]描述基本一致。
2 有限元模拟
U71Mn钢的材料参数[22]如表1所示。钢轨模型的高度为176 mm,长度为200 mm。在模型上表面中间位置处预设“硬币型”裂纹,裂纹的半径为0.5 mm,且垂直于钢轨上表面,如图2所示。钢轨弹性平面的上表面承受轮轨载荷,为准静态分析,提取轮轨间接触应力。
移动赫兹接触压力和切向摩擦力均属于用户自定义的复杂载荷形式,需要利用ABAQUS中子程序DLOAD和UTRACLOAD进行编写添加。在ABAQUS中添加用户自定义的赫兹压力或切向摩擦力的钢轨模型导入FRANC3D中,插入裂纹并划分网格后,将处理好的模型重新导入ABAQUS中,施加边界条件和载荷条件,再利用ABAQUS的求解器进行求解。
图3为钢轨整体模型和三维表面裂纹位置。距离表面裂纹较远处,轮轨载荷对钢轨表面裂纹几乎没有影响。故选择距表面裂纹z=-20 mm移动到z=20 mm的过程,移动步长为0.4 mm,移动步数为100步。轮轨载荷每移动一步都将会使裂纹前缘的应力强度因子发生变化。图4为赫兹接触压力作用钢轨表面某位置处的位移。
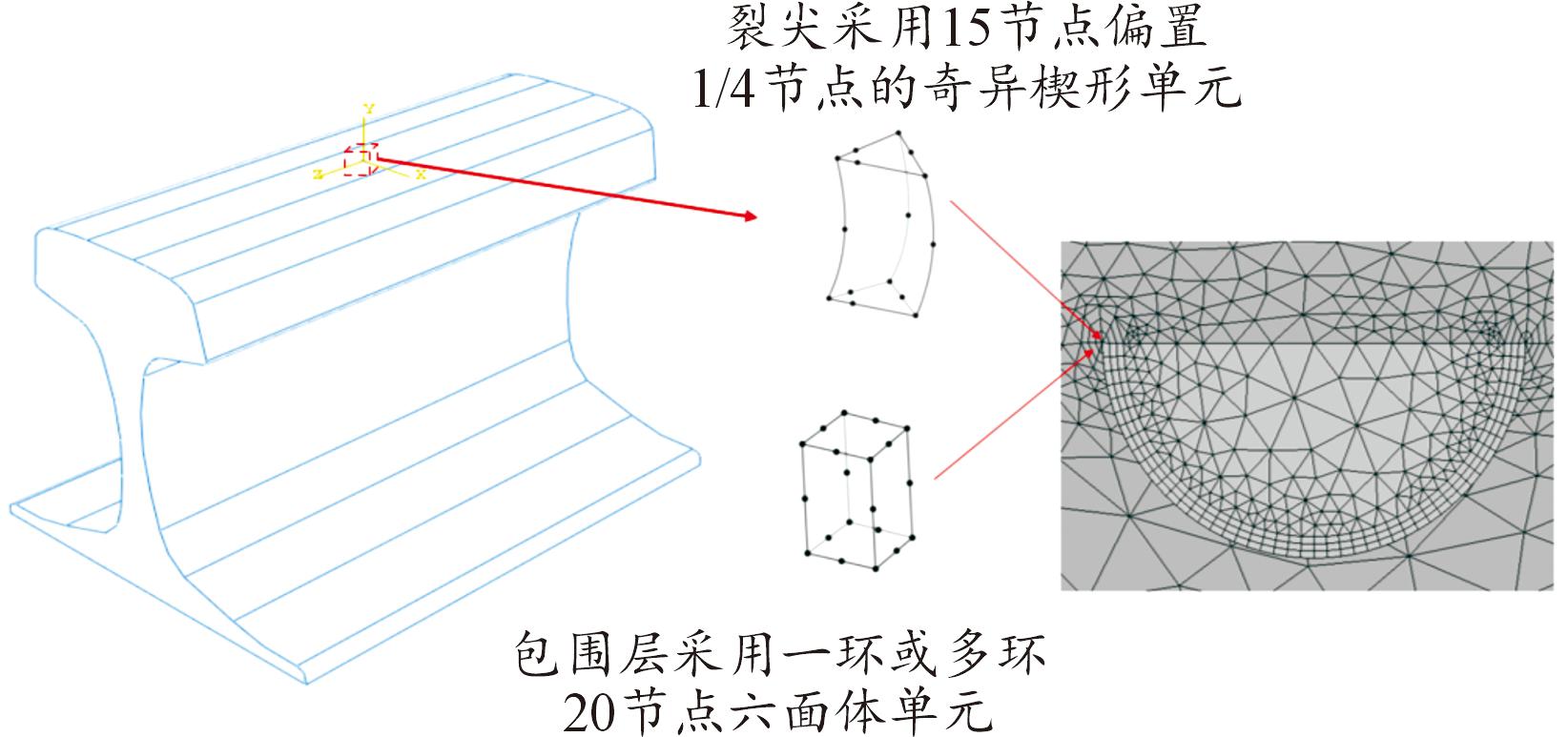
图3 钢轨整体模型和三维表面裂纹
Fig.3 Rail integral model and three-dimensional surface crack
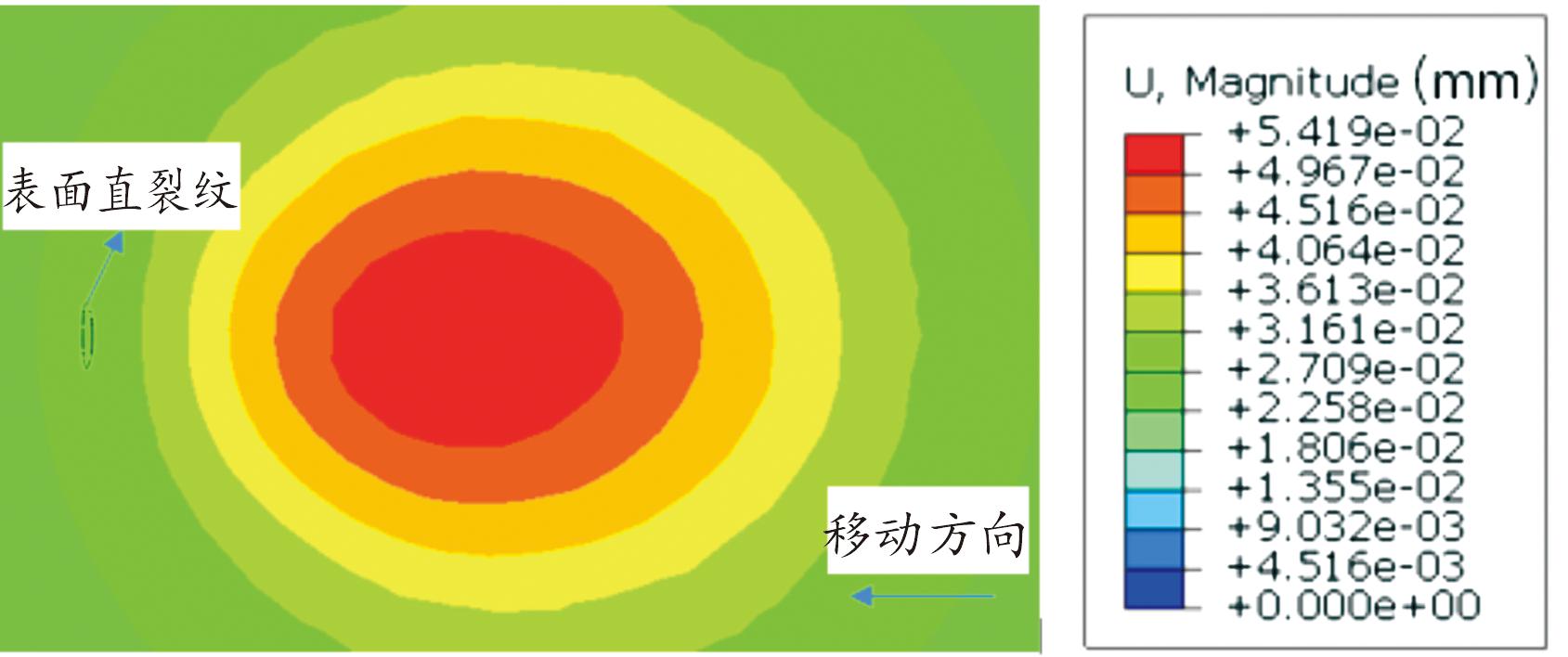
图4 赫兹接触压力作用钢轨表面某位置处的位移云图
Fig.4 Displacement contour figure of a certain position on the rail surface under Hertz contact pressure
3 结果与讨论
3.1 赫兹接触压力下钢轨表面三维裂纹扩展分析
赫兹接触压力在钢轨表面移动过程中,表面裂纹前缘会产生3种不同方向的位移分量,进而在表面裂纹前缘会产生3种基本类型的应力强度因子。在表面裂纹前缘选取可代表裂纹前缘特征的9个尖端节点,在整个表面裂纹前缘从左端点A沿曲线到右端点B的相对位置分别为0.069 5、0.169 6、0.269 7、0.369 9、0.490 0、0.630 1、0.730 3、0.830 4、0.930 5。裂纹前缘所选取的9个尖端节点的位置如图5所示。为研究钢轨表面裂纹前缘应力强度因子随车轮滚过的变化情况,仅考虑轮轨间赫兹接触压力作用时,随着赫兹接触压力位置变化,钢轨表面直裂纹前缘上3种基本类型的应力强度因子KI、KII、KIII和Keq的变化如图6所示。
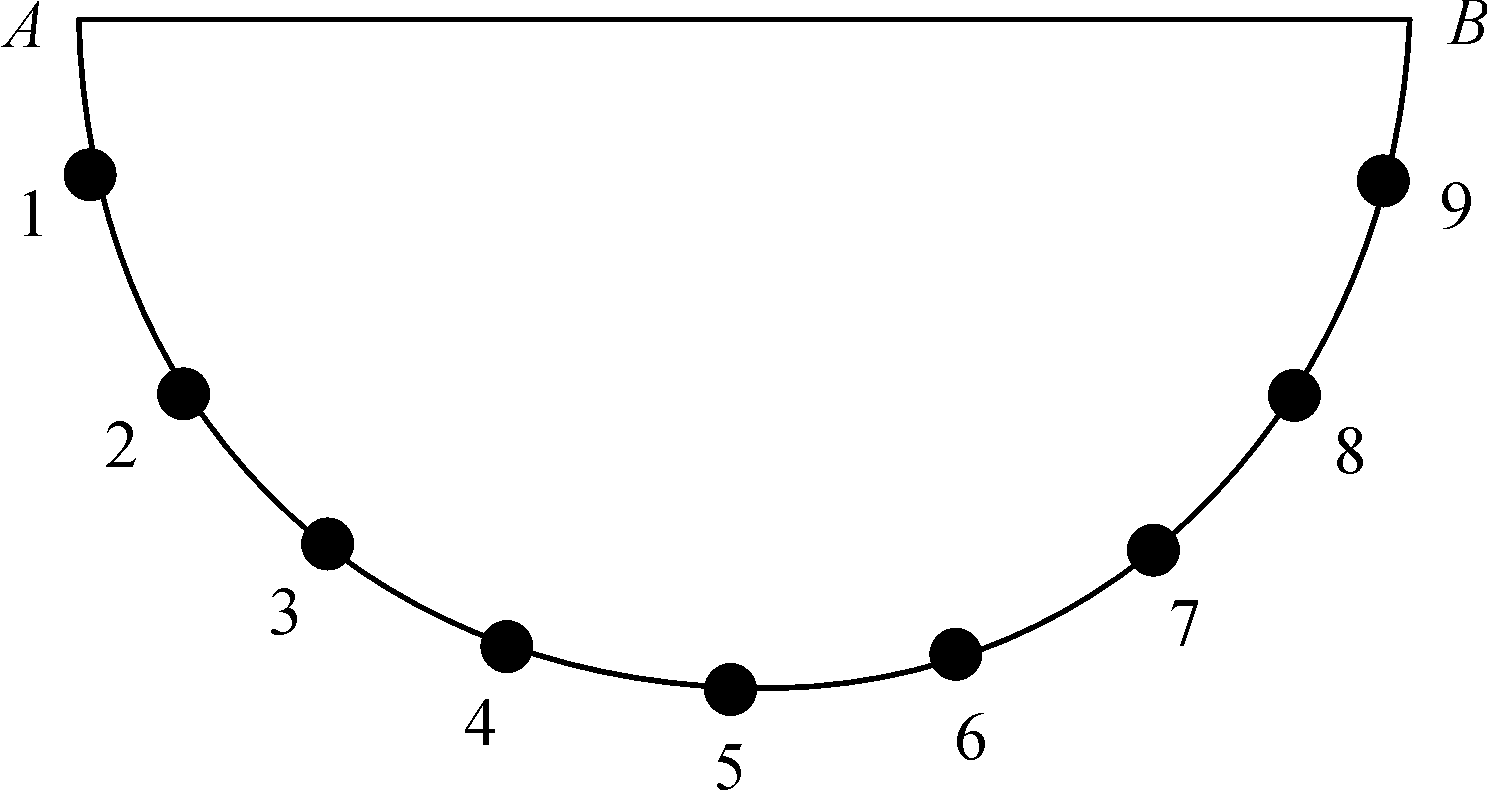
图5 选取裂纹前缘尖端节点
Fig.5 The crack front tip node is selected
从图6可以看出,当赫兹接触压力在-20 mm<z<-8 mm或8 mm<z<20 mm的范围内移动时,裂纹处于张开状态;当赫兹接触压力在-8 mm<z<8 mm的范围内移动时,裂纹处于闭合状态。此时裂纹前缘的应力强度因子KI、KII、KIII和Keq均未达到峰值。当赫兹接触压力的边缘靠近裂纹处时(2种情况:车轮从左边靠近裂纹位置,车轮滚过并离开裂纹位置),裂纹前缘的应力强度因子KI、KII、KIII和Keq均出现峰值。因此,该位置是危险位置,当赫兹接触压力作用在该位置时,裂纹更容易扩展。这是因为车轮滚过该表面裂纹一次,实际上该裂纹的应力强度因子出现了2次循环。
赫兹接触压力在靠近表面直裂纹过程中,表面裂纹前缘上越浅的节点,KI峰值越大,即节点1和9的KI最大,峰值为46.87 MPa·mm0.5。三维表面裂纹需使用等效应力强度因子Keq进行判别(参见式(2))。赫兹接触压力在z=6.67 mm处时(此时接触斑边缘靠近表面直裂纹),节点1~5皆达到了远离表面直裂纹过程中Keq最大值,分别为51.49、66.17、81.64、94.05、100.70 MPa·mm0.5。随着赫兹接触压力的继续移动,Keq呈现急剧减小后又增加的趋势。从z=8.28 mm开始,随着赫兹接触压力远离表面直裂纹,Keq表现出缓慢减小的趋势,这是因为节点距钢轨表面越远,Keq越小。随着赫兹接触压力与表面裂纹距离的增大,其对裂纹前缘应力强度因子KI、KII、KIII和Keq的影响逐渐减小,直至消失。
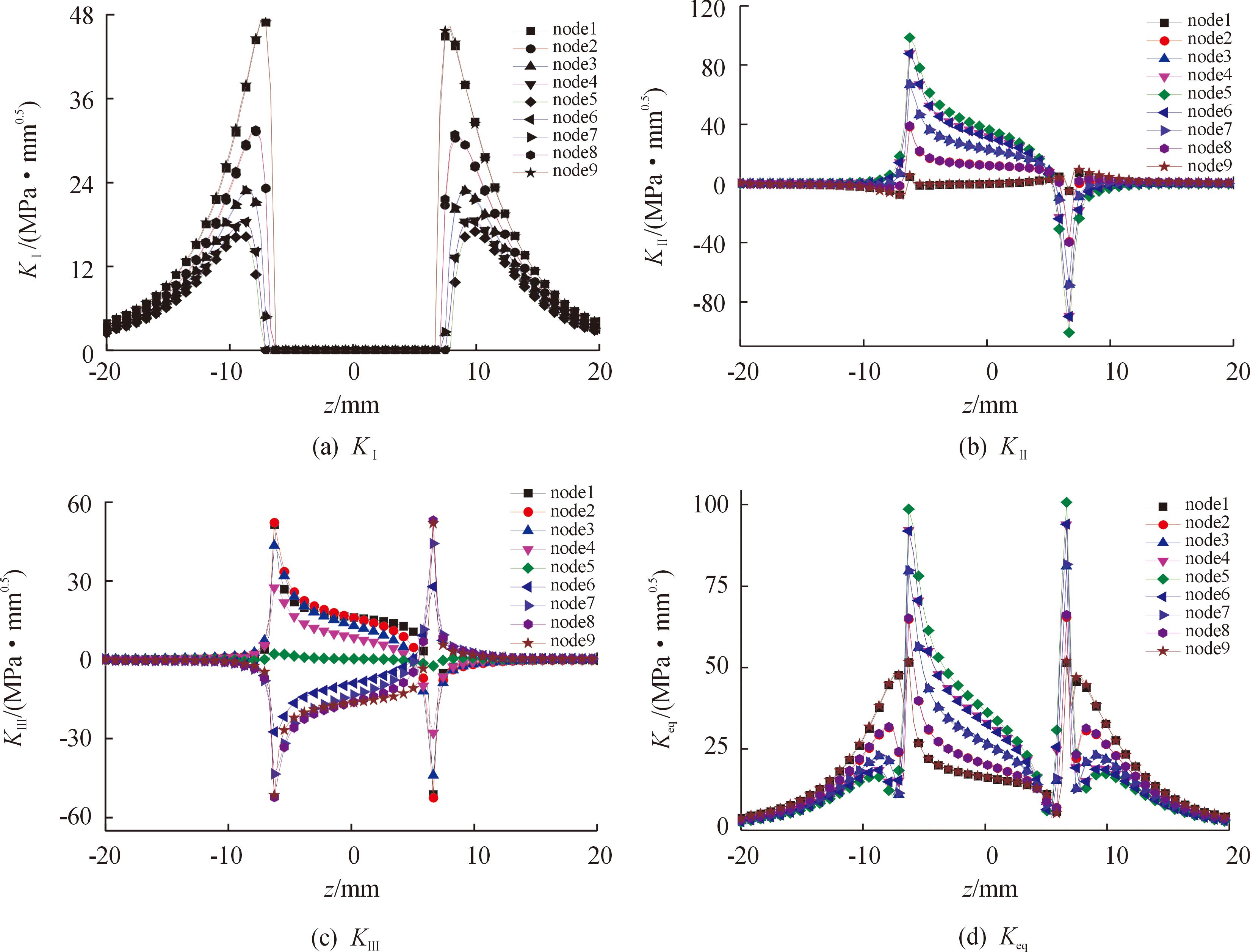
图6 移动赫兹接触压力作用下裂纹前缘的应力强度因子变化(坐标z表示赫兹接触压力中心与裂纹之间的距离)
Fig.6 Stress intensity factor variation of crack front under moving Hertz contact pressure (z represents the distance between the Hertz contact pressure center and the crack)
3.2 赫兹接触压力和摩擦力共同作用下钢轨表面的三维裂纹扩展
在赫兹接触压力的移动过程中,根据Keq的变化趋势可以看出:z=-6.3 mm是赫兹接触压力在(-20 mm,20 mm)范围内的危险位置。在危险位置处模拟真实钢轨的受力特征,车轮作用在钢轨的危险位置时,同时施加DLOAD和UTRACLOAD来模拟钢轨表面直裂纹的影响,其中钢轨表面的摩擦因数为0.3。ABAQUS可以同时调用多个子程序,需同时打开这些子程序的接口,将多个子程序放在一个后缀名为FOR的文件下[23]。
在FRANC3D中默认的裂纹每步扩展长度是Keq中值所对应节点裂纹长度的15%~20%,这使得计算出的Keq更准确,故规定每一步的扩展长度为0.075 mm[24-25]。在钢轨的危险位置处同时施加赫兹接触压力和切向滑动摩擦力,结合钢轨的材料参数、载荷条件和Paris公式,分析钢轨表面直裂纹前缘的扩展情况,如图7所示。
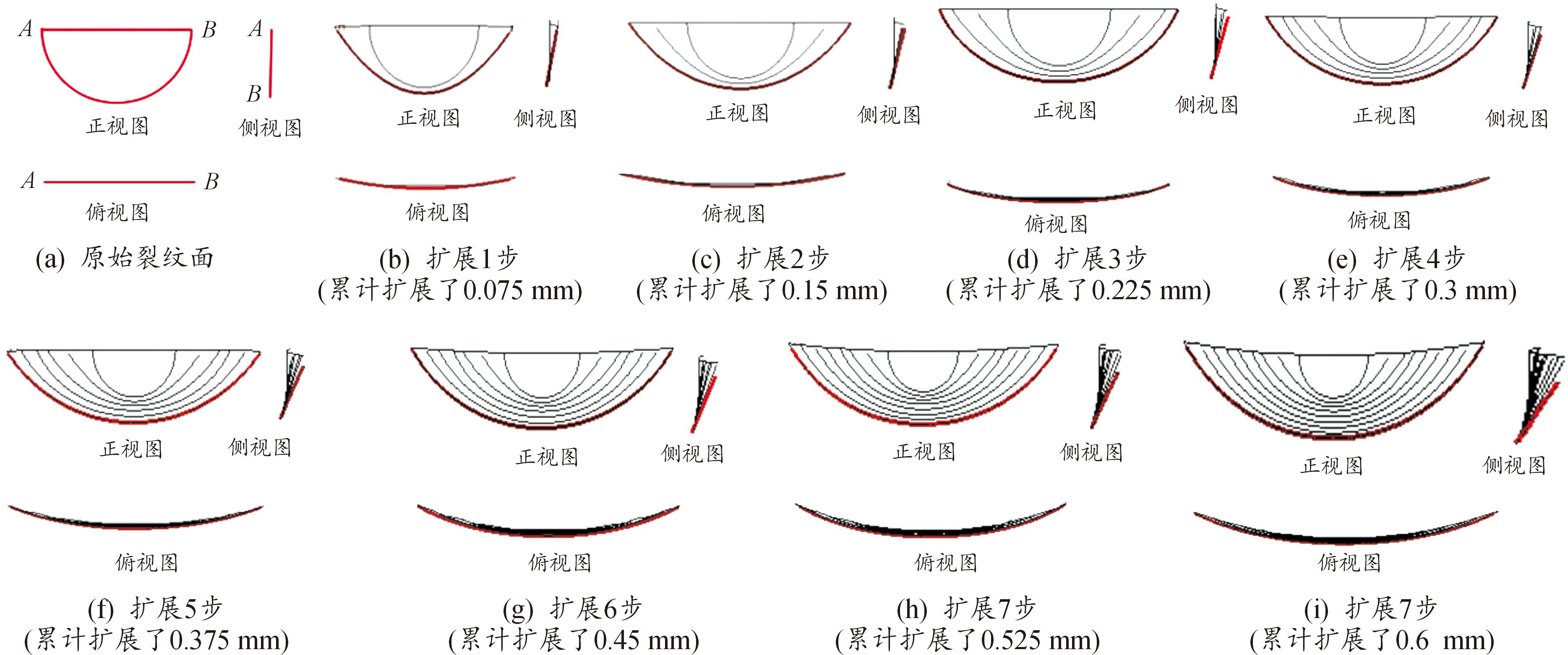
图7 表面直裂纹扩展演化
Fig.7 Evolution of surface straight crack growth
从图7的正视图可以看到,表面直裂纹从半圆硬币型裂纹扩展,由表面直裂纹前缘上Keq的变化趋势,表面直裂纹前缘上各个节点的扩展长度从靠近自由表面的裂纹两端开始向中间区域逐渐减小,每扩展1步,长半径与短半径之比都在增加,这说明随着载荷循环次数的增加,半圆形的表面裂纹面逐步向椭圆裂纹面演化,并且椭圆的离心率逐渐变大。
从图7的侧视图可以看出,表面直裂纹倾斜角度从0°开始直至扩展到第8步,每扩展1步分别对应裂纹面的倾斜角度为9°、12°、17°、19°、25°、27°、31°、35°,裂纹面向轨头内扩展,可能会导致钢轨断裂。
图8是裂纹扩展长度随循环次数的变化曲线。结合图7,可以看出:随着载荷循环次数的增加,半圆形表面裂纹的扩展深度和扩展宽度都在不断增大。
图9为循环赫兹接触压力和摩擦力的共同作用下,表面直裂纹扩展过程中,危险位置处的应力强度因子变化曲线。
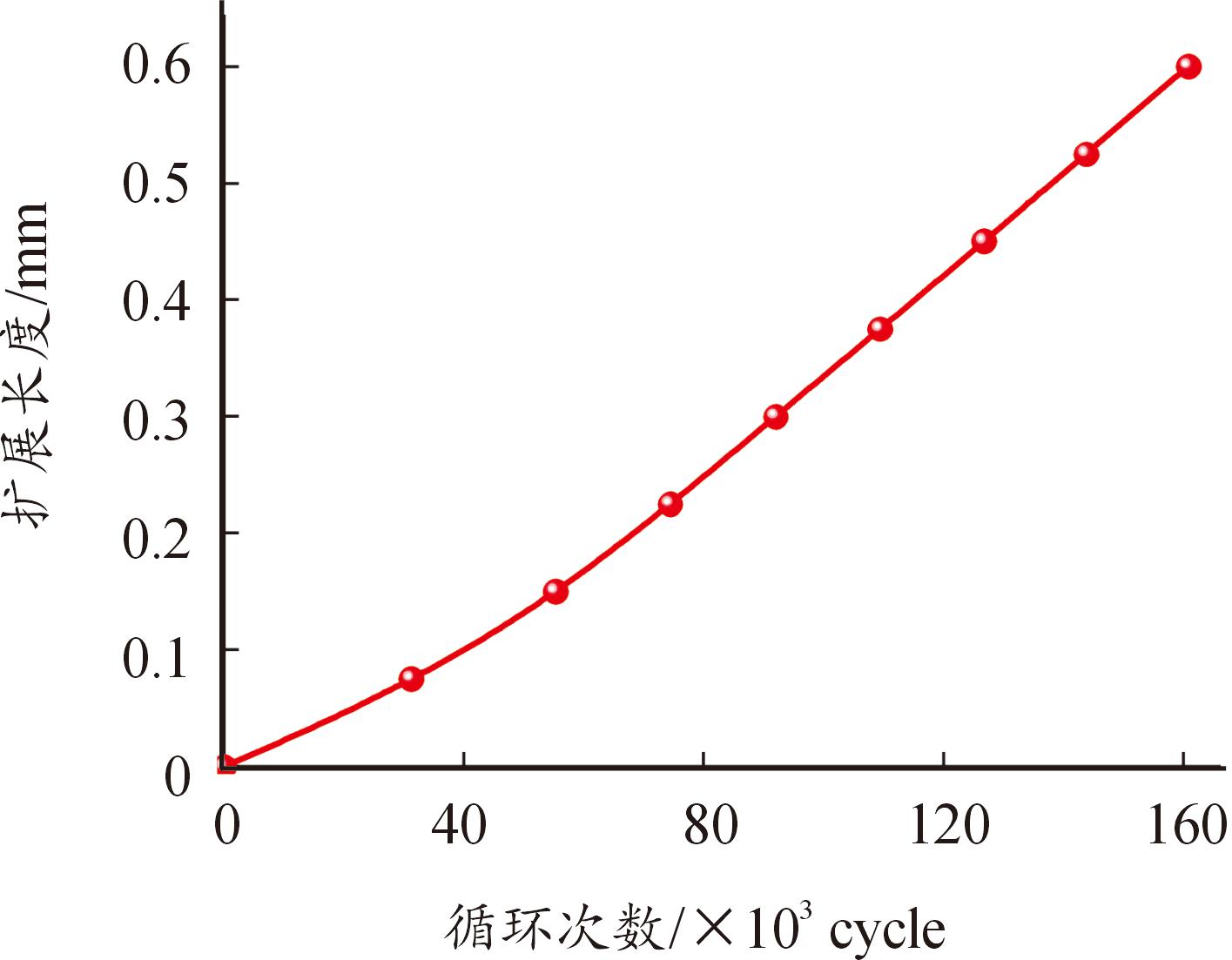
图8 裂纹扩展长度随循环次数的变化曲线
Fig.8 The variation curve of crack growth length with the number of cycles
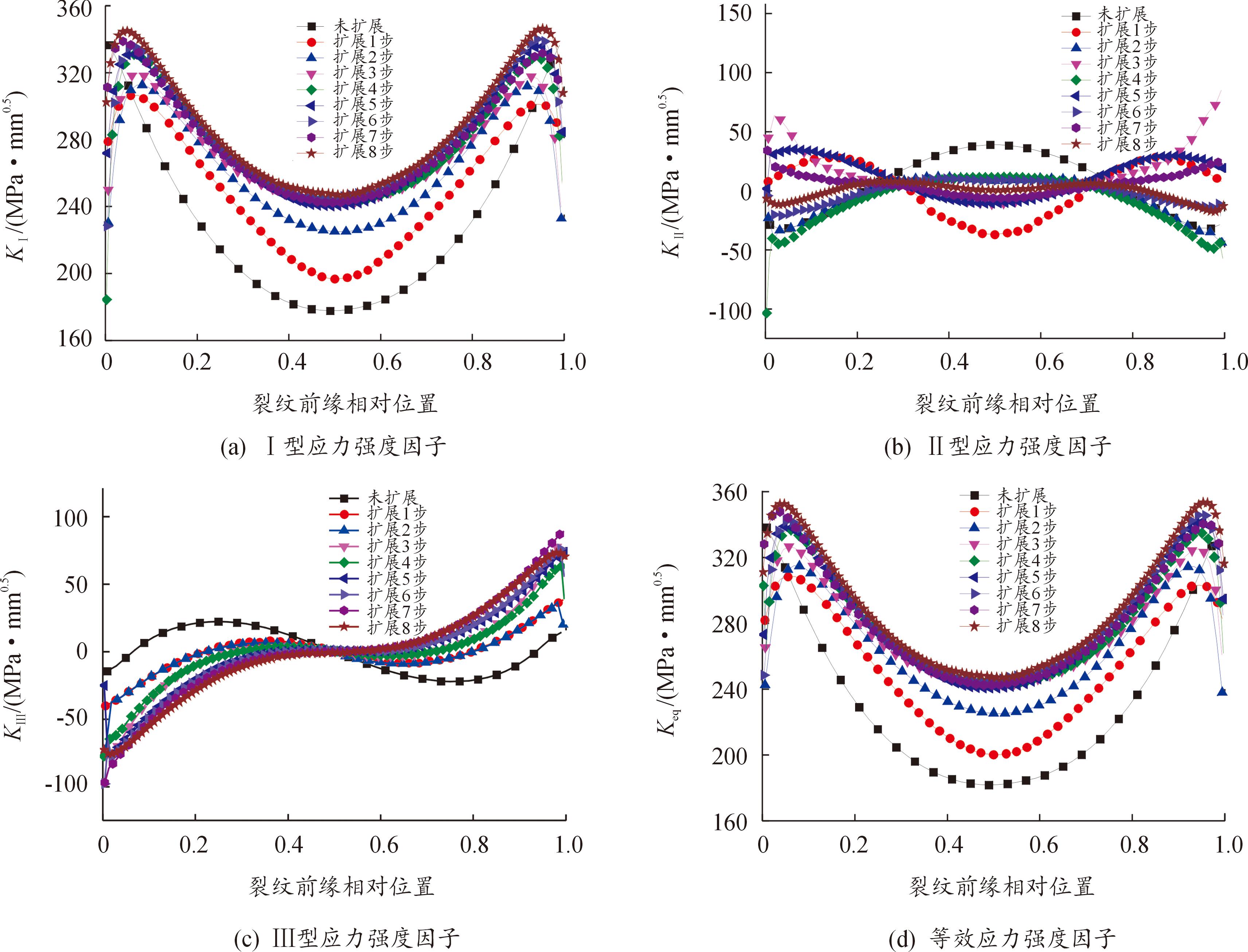
图9 扩展过程中裂纹前缘的应力强度因子的变化
Fig.9 The variation of stress intensity factor at the crack front during crack propagation
从图9(a)可以看出,随着循环次数的不断增加,KI也表现出不断增加的趋势,在裂纹扩展到第4步后,KI的增加趋势变缓,这是因为钢轨表面直裂纹从开始便已经发生了偏折扩展,裂纹前缘的方向逐步向表面直裂纹的方向过渡。从图9(b)中可以看出,表面直裂纹前缘上KII在扩展过程中表现杂乱无规律。从图9(c)可以看出扩展过程中KIII的变化趋势,KIII关于裂纹前缘相对位置0.5处对称,随着扩展步数的增加,KIII也在不断增加。图9(d)是表面裂纹扩展过程中的等效应力强度因子Keq的变化情况,由于循环剪切力载荷相对循环赫兹接触压力较大,所以三维表面裂纹的拉伸效果较强,KI的数值也较大,Keq的变化趋势以KI的大小为主导,主要表现为:随着三维表面裂纹的扩展,Keq不断增加,但增加速率逐渐减小。在FRANC3D后处理中可以得到三维表面裂纹在轮轨接触载荷作用下的扩展路径。
对图10中的三维表面直裂纹扩展8步后的角度用量角器进行了测量,裂纹偏转角度约为30°,这与实际钢轨经过轮轨载荷作用得到的表面裂纹扩展角度(31°)基本一致(列车行进方向相反),证明了三维裂纹扩展路径的可靠性。
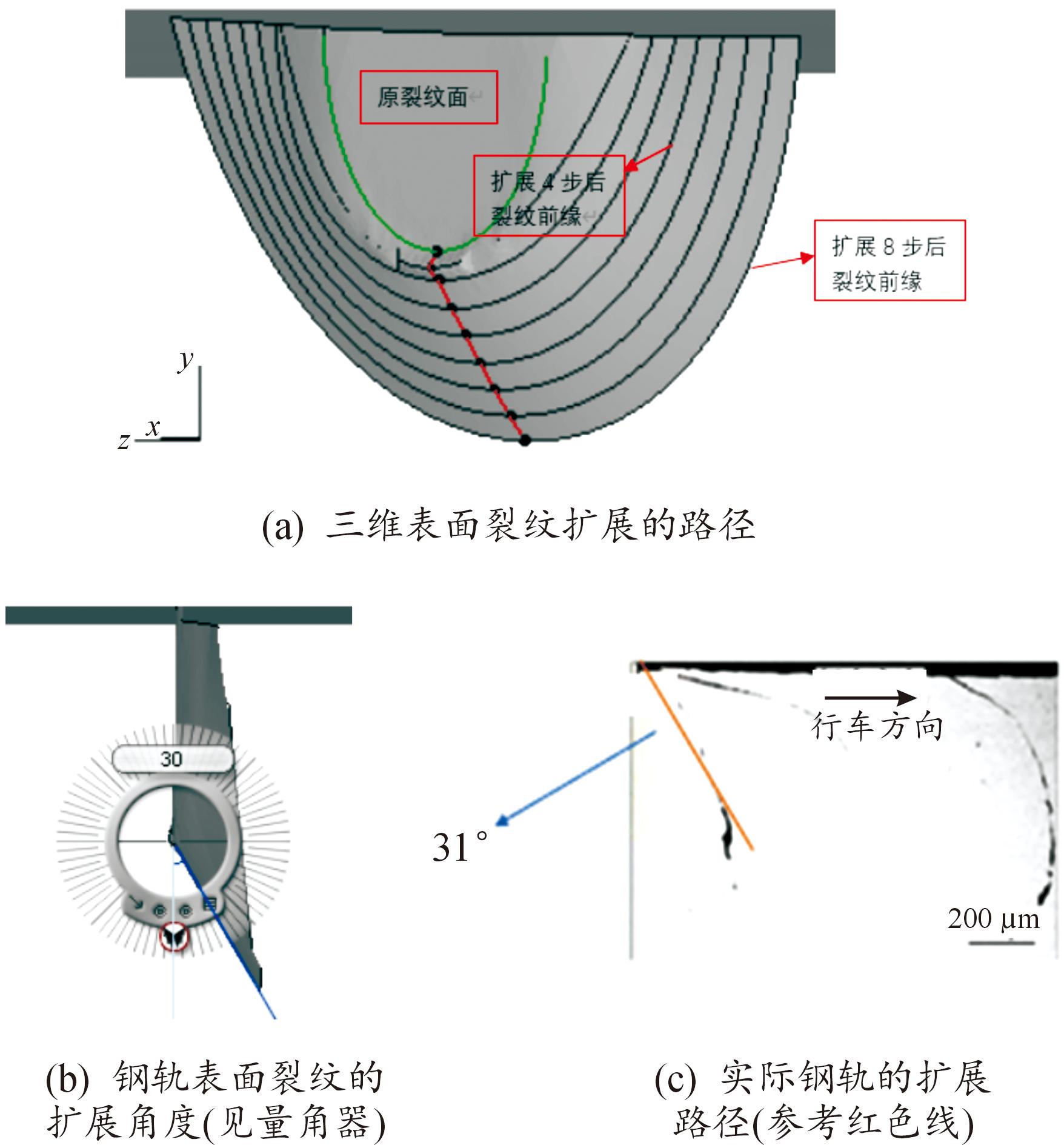
图10 钢轨表面裂纹的扩展角度
Fig.10 The propagation angle of surface cracks on steel rails
4 结论
1) 仅考虑赫兹接触压力时,车轮从较远处靠近表面直裂纹z=-7 mm处,KI逐步占据主导地位,而KII、KIII影响很小。随着车轮继续移动,KI数值骤减,KII、KIII急剧增加,此时,KII、KIII占据主导地位。在车轮覆盖表面直裂纹期间,裂纹面始终处于闭合状态,KI为零,KII、KIII缓慢减小。从z=6 mm处开始,KII、KIII开始反向增加,在z=6.7 mm的位置处,KII、KIII达到极大值,仍占据主导地位。从z=8 mm处开始,KII、KIII的影响减弱,KI占据主导地位,但随着赫兹接触压力的移动,3种类型的应力强度因子的影响逐渐消失。
2) 钢轨表面三维裂纹前缘上各点的应力强度因子分布随其距钢轨表面深度的不同存在较大的变化。通过等效应力强度因子值可以推测,该三维裂纹在车轮滚过时(未考虑切向摩擦力),裂纹前缘距钢轨表面越深时,越易发生扩展,裂纹主要向钢轨的深度方向扩展,可能使半圆形裂纹变成长轴在深度方向的椭圆形裂纹。
3) 在钢轨表面施加循环的赫兹接触压力和摩擦力时,得到了钢轨表面三维直裂纹的扩展演化形貌。随着轮轨载荷循环次数增加,扩展长度也在不断增大。该三维裂纹在车轮滚过时,当裂纹前缘距钢轨表面越近时,裂纹越易发生扩展,主要向钢轨的宽度方向扩展,使半圆形裂纹变成形状较为复杂的长轴在钢轨宽度方向的近椭圆形裂纹。
[1] 杨鸿达,张言库,李孝滔,等.钢轨表面裂纹扩展路径的数值模拟[J].四川轻化工大学学报:自然科学版,2016,29(4):12-15.
YANG Hongda,ZHANG Yanku,LI Xiaotao,et al.Numerical simulation of crack propagation path of rail surface[J].Journal of Sichuan University of Science &Engineering(Natural Science Edition),2016,29(4):12-15.
[2] KONDO K,YOROIZAKA K,SATO Y.Cause,increase,diagnosis,countermeasures and elimination of Shinkansen shelling[J].Wear,1996,191(1/2):199-203.
[3] 王强胜,李孝滔,昝晓东,等.分布位错法研究钢轨表面边缘直裂纹的力学行为[J].表面技术,2020,49(2):200-211.
WANG Qiangsheng,LI Xiaotao,ZAN Xiaodong,et al.Mechanical behavior of straight crack on the edge of rail surface by distributed dislocation method[J].Surface Technology,2020,49(2):200-211.
[4] WANG L,PYZALLA A,STADLBAUER W,et al.Microstructure features on rolling surfaces of railway rails subjected to heavy loading[J].Materials Science &Engineering A,2003,359(1):31-43.
[5] BABNADI R,HOSSEINI TEHRANI P.Numerical calculation of crack driving force using the configurational force concept for elastic-plastic rail cracks[J].Strength,Fracture and Complexity,2020,13(1):45-64.
[6] 昝晓东,李孝滔,邢帅兵,等.疲劳裂纹扩展引起的钢轨表面剥离研究[J].铁道科学与工程学报,2018,15(12):3082-3088.
ZAN Xiaodong,LI Xiaotao,XING Shuaibing,et al.Analysis of rail surface shelling resulting from fatigue crack propagation[J].Journal of Railway Science and Engineering,2018,15(12):3082-3088.
[7] 江晓禹,李孝滔,李煦,等.轮轨高速滚动接触及钢轨疲劳裂纹扩展研究[J].西南交通大学学报,2016,51(2):274-281.
JIANG Xiaoyu,LI Xiaotao,LI Xu,et al.Research on wheel/rail rolling contact at high speed and fatigue crack propagation in rail[J].Journal of Southwest Jiaotong University,2016,51(2):274-281.
[8] TANG H,CHEN S,XUE S.Numerical simulation of fatigue crack propagation in steel bridge with welded stiffeners subjected to out-of-plane loadings[C]//Proceedings of the 2019 International Conference on Modeling,Simulation,Optimization and Numerical Techniques (SMONT 2019),2019:35-61.
[9] 卢观健,杨克.钢轨伤损的形态特征及其失效机理[J].铁道学报,1996,18(3):120-124.
LU Guanjian,YANG Ke.Morphological characteristics and failure mechanism of rail damage[J].Journal of the China Railway Society,1996(3):120-124.
[10]黄如旭,杨小龙,陆波,等.三维裂纹前缘应力强度因子数值计算方法[J].舰船科学技术,2019,41(2):9-13.
HUANG Ruxu,YANG Xiaolong,LU Bo,et al.Numerical calculation method for stress intensity factor of 3-D crack front[J].Ship Science and Technology,2019,41(2):9-13.
[11]昝晓东.钢轨在滚动接触疲劳下的裂纹萌生及扩展分析[D].成都: 西南交通大学,2019:26-27.
ZAN Xiaodong.Fatigue crack initiation and propagation analysis of rail under rolling contact fatigue[D].Chengdu:Southwest Jiaotong University,2019:26-27.
[12]高翔.断裂力学分析铸造缺陷的滑轮[J].科技视界,2018(5):64-65.
GAO Xiang.Fracture mechanics analysis of casting defects pulley[J].Science &Technology Vision,2018(5):64-65.
[13]张启洞,王强胜,李文俊,等.复杂载荷作用下的三维裂纹扩展研究[J].四川轻化工大学学报(自然科学版),2020,33(6):65-70.
ZHANG Qidong,WANG Qiangsheng,LI Wenjun,et al.Study on 3-D crack propagation under complex loads[J].Journal of Sichuan University of Science &Engineering(Natural Science Edition),2020,33(6):65-70.
[14]艾书民,于明,成晓鸣,等.基于Franc3D软件的三维裂纹扩展分析与应用[J].机械强度,2018,40(1):251-254.
AI Shumin,YU Ming,CHENG Xiaoming,et al.Analysis and application of three-dimensional crack growth based on FRANC3D[J].Journal of Mechanical Strength,2018,40(1):251-254.
[15]WARZYNEK P A,CARTER B J,BANKS-SILLS L.The m-integral for computing stress intensity factors in generally anisotropic materials.2005.
[16]PARIS P C,ERDOGAN F.A critical analysis of crack propagation laws[J].Journal of Basic Engineering,1963,85(4):528-533.
[17]吕毅,许希武,郭树祥.梯度复合材料裂纹扩展路径和起裂载荷的有限元分析[J].复合材料学报,2015,32(4):1099-1106.
LYU Yi,XU Xiwu,GUO Shuxiang.Finite element analysis of crack propagation paths and crack initiation loads in graded composites[J].Acta Materiae Compositae Sinica,2015,32(4):1099-1106.
[18]曹世豪,李煦,张四放,等.Hertz理论与有限元法分析轮轨接触疲劳的差异性研究[J].机械工程学报,2015(6):126-134.
CAO Shihao,LI Xu,ZHANG Sifang,et al.Research of the differences between hertz theory and finite element method to analyze the fatigue of wheel/rail contact[J].Journal of Mechanical Engineering,2015(6):126-134.
[19]冯剑军,谭援强.基于Hertz理论圆柱和平面之间的滑动接触分析[J].摩擦学学报,2009,29(4):346-350.
FENG Jianjun,TAN Yuanqiang.Analysis of the slipping contact between a cylinder and a plane on the base of Hertz theory[J].Tribology,2009,29(4):346-350.
[20]邢帅兵.基于累积剪切塑性应变的钢轨磨耗预测[D].四川:西南交通大学,2019.
XING Shuaibing.Prediction of rall wear based on accumulated shear plastic strain[D].Sichuan:Southwest Jiaotong University,2019.
[21]曹世豪.钢轨表面疲劳裂纹的扩展与预防研究[D].成都:西南交通大学,2014.
CAO Shihao.The propagation and prevention and prevention of fatigue crack on rail surface[D]Chengdu:Sichuan:Southwest Jiaotong University,2014.
[22]昝晓东,王强胜,生月,等.考虑塑性的钢轨表面疲劳微裂纹分析[J].表面技术,2018,47(11):151-156.
ZAN Xiaodong,WANG Qiangsheng,SHENG Yue,et al.Analysis of fatigue micro-crack on rail surface under plasticity[J].Surface Technology,2018,47(11):151-156.
[23]丁海荣.直齿圆柱齿轮齿根裂纹的扩展分析和疲劳寿命预测[D].兰州:兰州理工大学,2016.
DING Hairong.Crack propagation analysis and fatigue life prediction of spur gears tooth root[D].Lanzhou:Lanzhou University of Technology,2016.
[24]安志超.腐蚀环境下三维表面裂纹扩展特征的数值研究[D].北京:北京工业大学,2018.
AN Zhichao.Numerical Study of Three-dimensional surface crack propagation in corrosion environment[D].Beijing:Beijing University of Technology,2018.
[25]熊勋,杨莹,汪舟,等.基于FRANC3D和ABAQUS联合仿真三维疲劳裂纹扩展分析及寿命预测[J].武汉理工大学学报:交通科学与工程版,2020,44(3):506-512.
XIONG Xun,YANG Ying,WANG Zhou,et al.Three-dimensional fatigue crack propagation analysis and life prediction based on co-simulation of FRANC3D and ABAQUS[J].Journal of Wuhan University of Technology(Transportation Science &Engineering),2020,44(3):506-512.