0 引言
螺旋桨飞机具有燃油消耗率低、经济性好等优点,广泛应用于运输机、巡逻机和反潜机等领域[1-3],尤其是中空长航时固定翼无人机。螺旋桨飞机不同于常规的喷气式动力飞机,其推力/拉力通常是由发动机驱动螺旋桨旋转而产生,飞机推进系统的性能不仅仅涉及螺旋桨、发动机特性,最重要的是两者的匹配性能[4]。螺旋桨动力飞机桨发匹配工作性能的好坏对飞机推进系统数学模型的准确性及飞机总体性能影响极大。因此,开展桨发匹配性能仿真研究,对螺旋桨飞机设计阶段和后期使用阶段的桨发匹配设计、性能优化,以提高螺旋桨飞机推进系统性能,具有重要现实意义。
传统的螺旋桨多是定距螺旋桨,其与发动机匹配的关键在于确定发动机的功率标定点,只能保证在设计状态具有较好的动力性能和燃油经济性,很难保证整个飞行包线的推进系统性能最佳[5-6]。而通过螺旋桨变距的方式,可有效改变螺旋桨和发动机的匹配工作状态,使得螺旋桨飞机推进系统性能的提升成为可能,并由此推动了桨发匹配设计理论的发展。1943年,美国的兰利航空实验室开展了恒速桨的全尺寸风洞试验,并开展了基于螺旋桨气动数据和活塞发动机特性的桨发匹配性设计方法研究[7-8]。目前,国内有关螺旋桨飞机桨发匹配设计研究的相关文献较少,而且主要针对涡桨动力[4,9-11],而活塞发动机又有着与涡桨发动机不同的特性[12-13]。随着中空长航时无人机的发展和应用,中小型活塞式发动机(≤300 kW)因价格低、油耗低、技术成熟、维护简单等优势,辅以恒速螺旋桨,可以实现起飞、爬升、巡航和着陆等典型剖面内的功率推力最优匹配,因此中小型航空活塞式发动机在很长时间内依然会成为该类无人机的首选动力源[14-16]。推进系统(发动机+螺旋桨)作为无人机的“核心”,其性能在很大程度上决定了飞机的总体性能,而任务剖面的功率推力最优匹配就涉及到桨发匹配设计技术。因此,开展活塞动力螺旋桨飞机桨发匹配设计技术研究,对提升活塞动力螺旋桨飞机飞行性能具有重要意义。
本文中分别对螺旋桨性能、活塞发动机性能和飞机巡航阶段飞行性能模型建模方法进行了研究,从推进系统性能最佳出发,提出了一种基于需用推力的桨发匹配设计方法和性能优化思路。在此基础上,开展了活塞动力螺旋桨飞机巡航阶段桨发匹配设计算法验证,及巡航剖面桨发匹配工作点优化设计分析。
1 螺旋桨、发动机及飞行性能模型
1.1 螺旋桨性能模型
螺旋桨性能一般用一组无因次参数表示,主要包括进距比J、功率系数CP、拉力系数CT和效率η[18]。典型螺旋桨特性曲线如图1所示。各无因次参数定义如下:
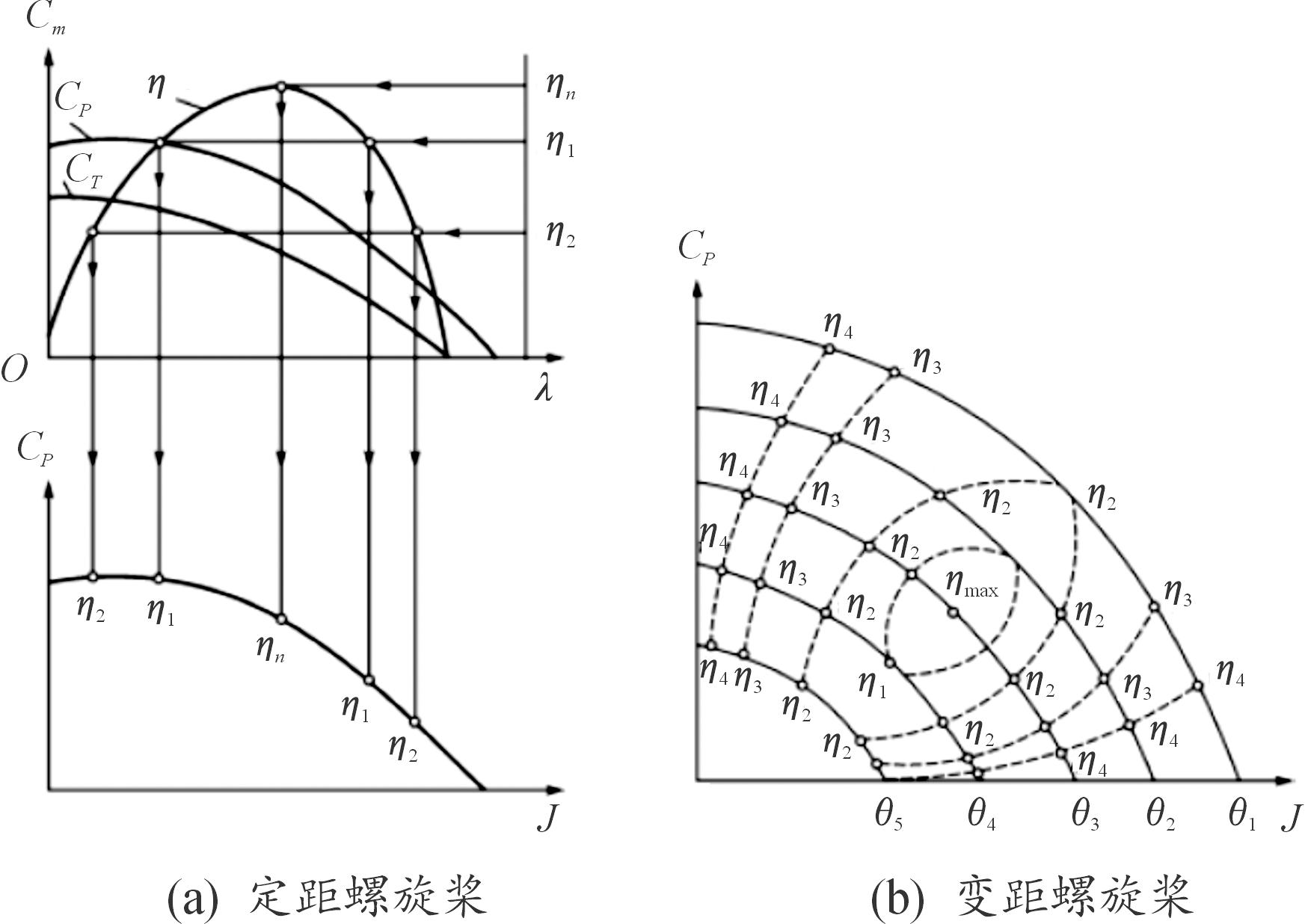
图1 典型螺旋桨特性曲线
Fig.1 Typical propeller characteristic curve
![]()
(1)
![]()
(2)
![]()
(3)
![]()
(4)
式(1)—式(3)中:V0为飞行速度;d为螺旋桨直径;ns为螺旋桨转速;P为螺旋桨功率;T为螺旋桨拉力。
螺旋桨特性可以通过试飞、数值计算或地面风洞试验方法获取[17]。本文中采取典型螺旋桨试验特性[8],螺旋桨为三叶汉密尔顿标准3155-6型,额定转速为1 340 r/min。螺旋桨特性关系曲线如图2所示。
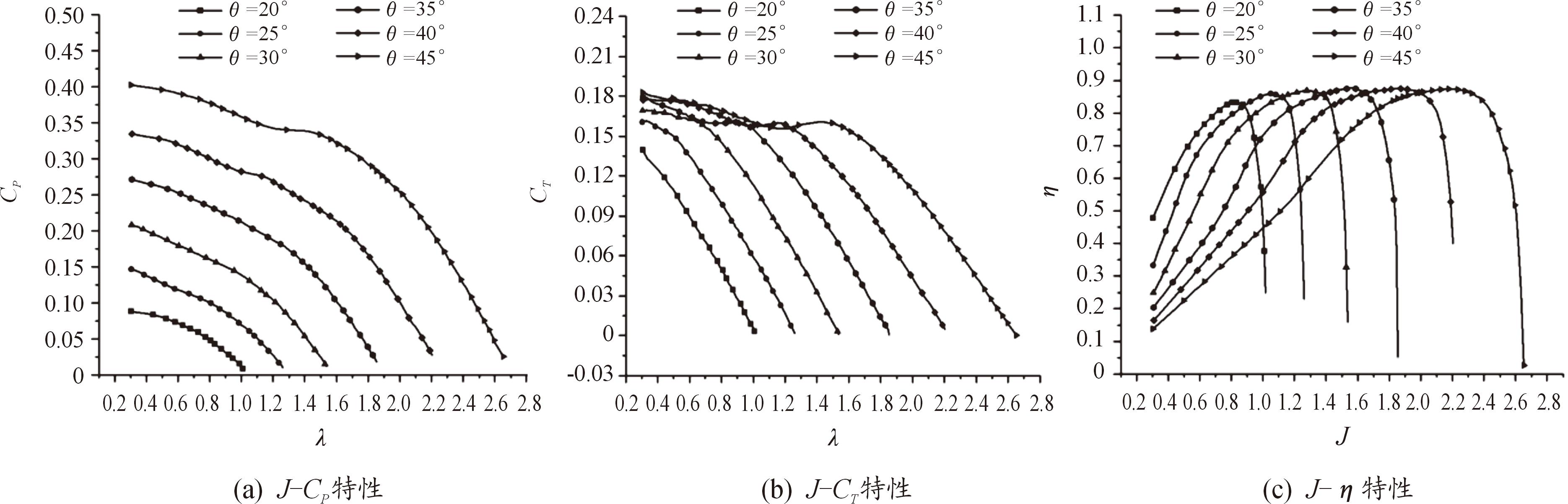
图2 某型螺旋桨特性
Fig.2 Characteristics of a certain type of propeller
1.2 活塞发动机性能模型
航空活塞发动机性能模型主要是指发动机特性曲线[12],可通过试验、仿真等方法获得。
本文中采用某型活塞发动机试验特性[8],发动机特性曲线如图3所示。该发动机额定功率为520 kW,额定转速为2 380 r/min,传动比16∶9。为便于特性表示,将发动机特性中转速和功率表示为相对活塞发动机额定状态下的百分值,且功率用扭矩表示。因此,活塞发动机特性可以表示为不同相对转速百分比nc,rel和不同相对扭矩百分比Mc,rel下发动机耗油率C曲线。
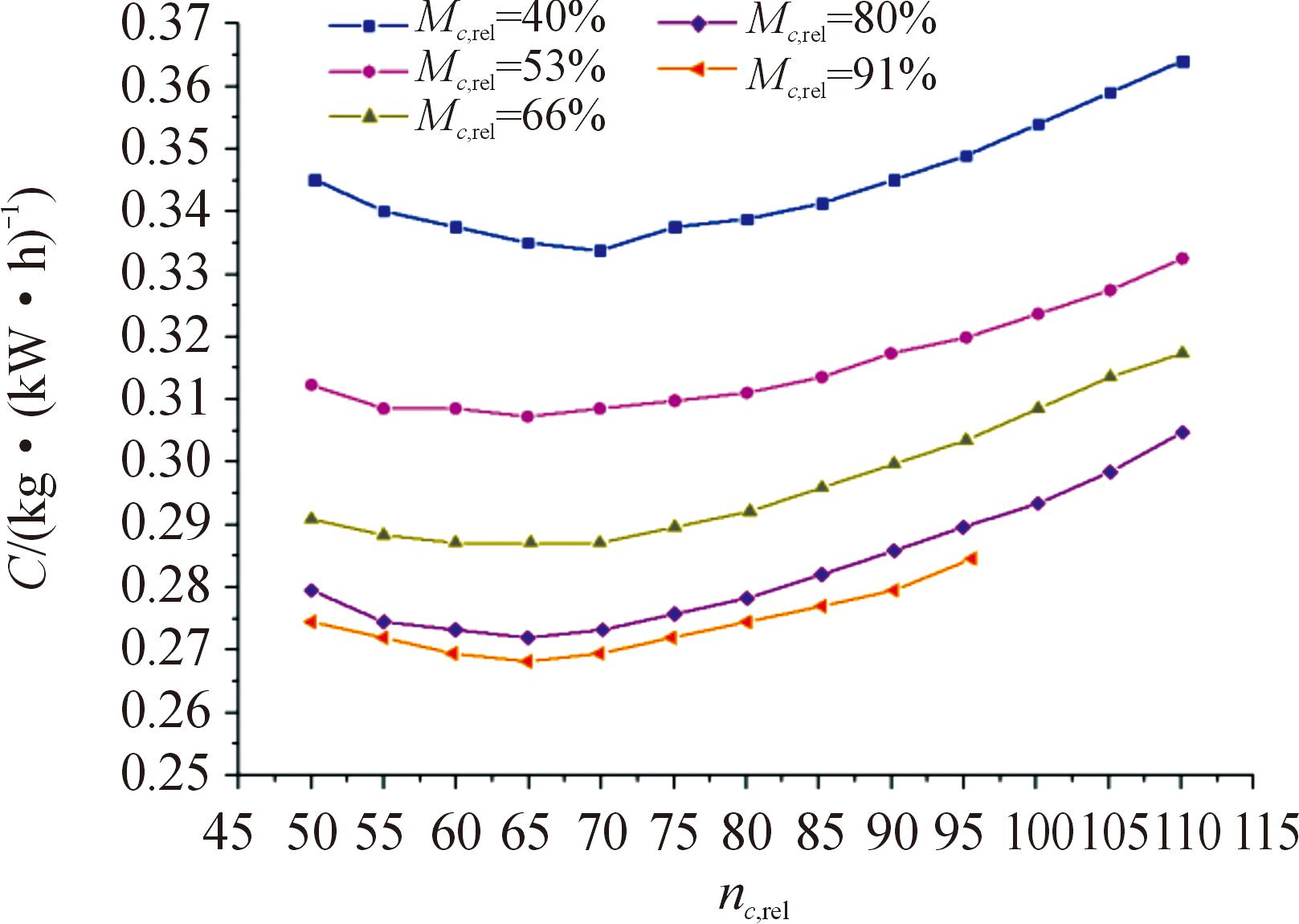
图3 某型活塞发动机特性
Fig.3 Characteristics of a certain type of piston engine
发动机功率和扭矩的关系式如下:
W=M×n/9 549
(5)
式(5)中:W为功率,kW;M为扭矩,N·m;n为转速,r/min。
1.3 飞行性能计算方法
飞机飞行性能的计算,需要建立飞机飞行动力学方程。本文中主要从飞机基本飞行性能出发计算对动力性能的需求,飞机定常飞行中受力如图4所示[18]。
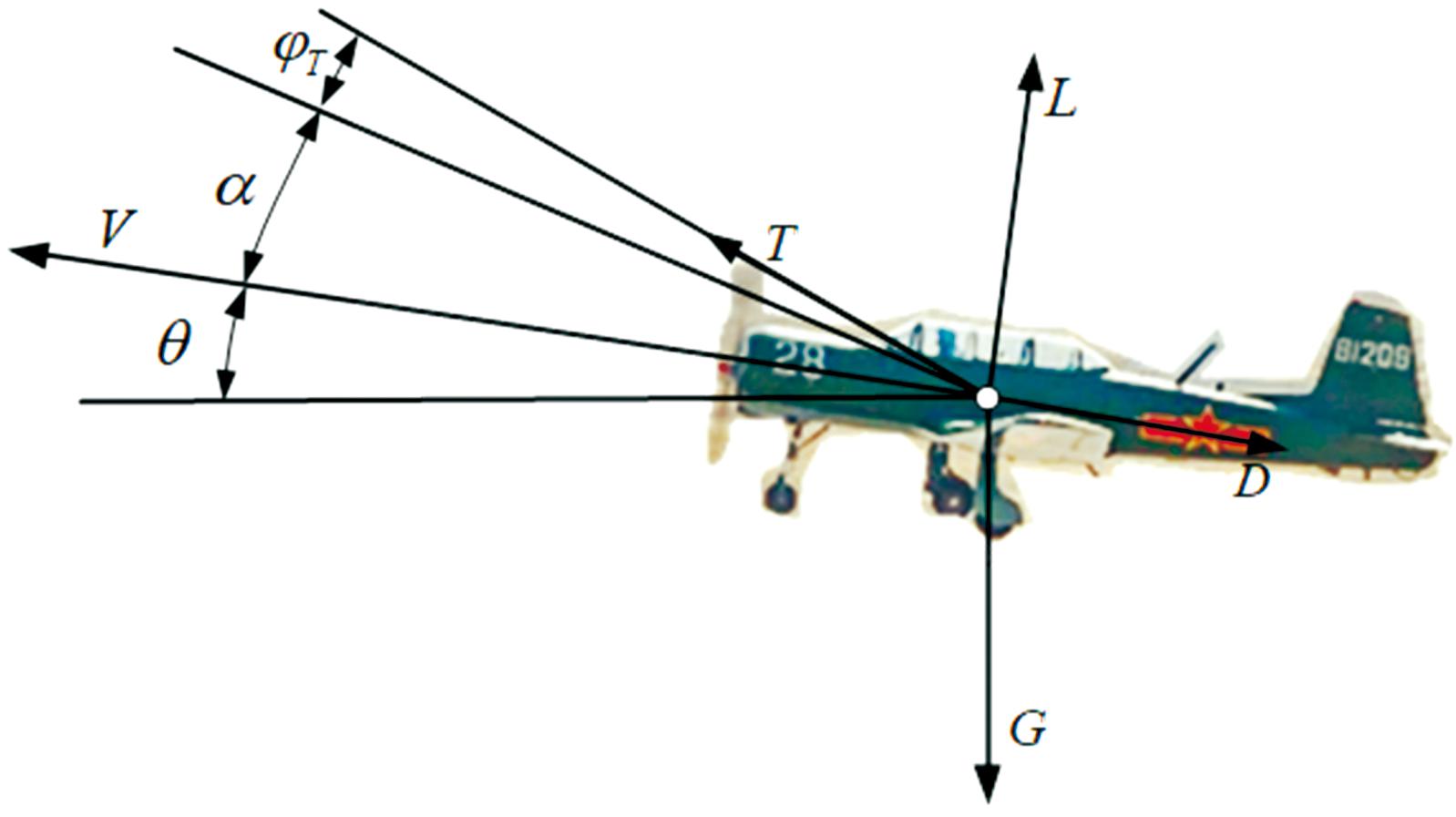
图4 定常直线飞行中飞机受力分析
Fig.4 Analysis of aircraft forces in steady straight flight
其动力学方程如下:
![]()
(6)
式(6)中: α为迎角;T为推力或拉力;L为升力;D为阻力;G为重力;θ为航迹倾斜角;V为飞行速度;φT为推力或拉力作用线与飞机迎角基准线之间的夹角。
本文中主要研究飞机水平直线巡航阶段的飞行性能,飞机作等速水平直线飞行或接近等速水平直线飞行时,θ=0,一般情况下φT≈0,则方程(6)可简化为
![]()
(7)
式(7)中:
L=ρV2CLS/2
(8)
D=ρV2CDS/2
(9)
在已知飞机质量、迎角、升力系数、阻力系数、机翼面积等参数时,可根据方程(8)计算出飞机的飞行速度,进一步计算得到拉力或推力T。
巡航阶段的航程航时计算采用布雷盖(Breguet)方程[18]进行计算,计算方程如下:
![]()
(10)
![]()
(11)
式(10)、式(11)中: S为航程;η为螺旋桨效率;C为发动机耗油率;t为航时;W1为巡航起始质量;W2为巡航结束质量。
巡航过程中,随着燃油的不断消耗,飞机重量不断减小,相应需用推力减小,发动机状态发生变化,航程、航时计算公式(10)和式(11)中相应参数值发生变化。为了提高计算精度,按照飞行重量进行分段计算航程、航时,最后将每一小段的航程、航时相加,得到整个巡航航段的航程和航时。
2 桨发匹配设计方法
2.1 桨发匹配设计思路
桨发匹配设计不能脱离飞机性能需求,单纯的进行发动机或螺旋桨工作点最优设计,其最重要的原则是满足整个推进系统,也就是发动机+螺旋桨整体性能最优,而表征发动机和螺旋桨性能的参数可以分别采用发动机耗油率和螺旋桨效率[17]。因此,桨发匹配设计需要在满足飞行器飞行性能要求下,提高匹配工作点螺旋桨效率和发动机工作效率。
根据飞机飞行性能求解过程,桨发匹配设计可分为2类[8]:
1) 已知飞机需用推力,求解发动机工作状态性能(发动机功率和耗油率等);
2) 已知发动机可用最大功率,求解螺旋桨工作状态性能(螺旋桨推力/拉力和效率等)。
由于分类1)中需要已知飞机飞行状态,因此,对应设计方法通常用于飞机巡航状态桨发匹配工作点设计及优化;而分类2)中发动机状态已知,因此,对应设计方法通常用于点性能(爬升、升限等)计算和推阻分析。
对于安装活塞动力的无人机,其飞行主要过程是巡航阶段,因此,本文中主要针对飞机巡航阶段基于需要推力,开展桨发匹配设计及优化。
图5给出了活塞动力螺旋桨飞机桨发匹配设计及优化方案。根据桨发匹配设计基本原则:在满足飞机飞行性能要求下,螺旋桨效率和发动机工作效率最优[17]。在一定的飞机飞行需用推力下,螺旋桨效率的大小用来衡量将发动机轴功率转化为螺旋桨拉力的能力,效率越大则需用的发动机轴功率就越小;发动机耗油率则用来衡量满足螺旋桨需用功率下的发动机耗油量,耗油率越小则发动机越省油。因此,发动机和螺旋桨匹配工作最优需要满足螺旋桨效率和发动机耗油率的比值η/C最大[4]。
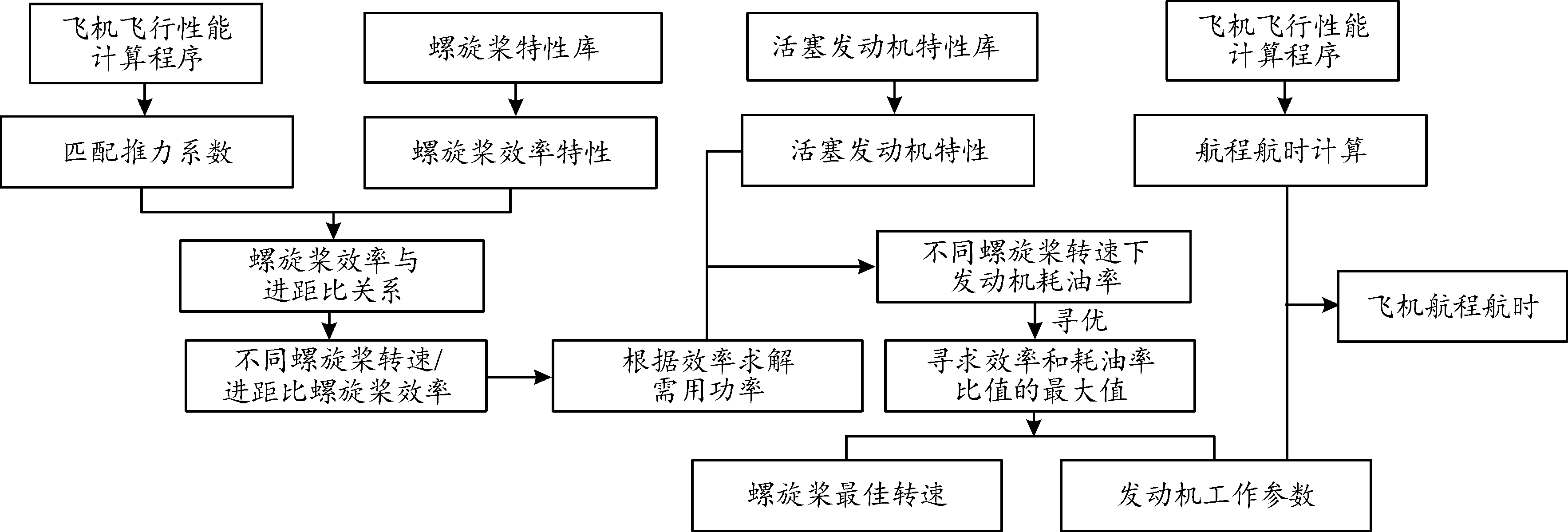
图5 桨发匹配设计及优化方案
Fig.5 Prop-engine cooperation design and optimization scheme of propeller and engine
2.2 匹配推力系数
在基于飞机巡航阶段需用推力计算时,引入无量纲参数匹配推力系数TC,该参数定义如下:
![]()
(12)
式(12)中,Te为飞机需用推力。
通过式(12)可以看出,匹配推力系数TC建立了螺旋桨拉力系数和进距比之间的关系,也就是建立了飞机需用推力与螺旋桨工作性能参数之间的关系。
巡航状态下飞机处于平飞状态,根据简单推力法[18],飞机作等速直线飞行时,升力等于重力,阻力等于推力,方向相反。因此,式(12)可整理成:
![]()
(13)
式(13)中: K为升阻比;S为机翼面积。
由式(13)可知,匹配推力系数TC的大小由机翼面积、螺旋桨直径和飞机飞行阻力系数决定。对于一架飞机,机翼面积和螺旋桨直径一定,因此,匹配推力系数仅仅与配平状态的全机阻力系数有关,而与飞机重量、飞行高度和速度等参数无关。另外,匹配推力系数建立了螺旋桨进距比和拉力系数的关系,结合螺旋桨特性,可确定螺旋桨工作点。
2.3 进距比与效率关系计算
飞机巡航状态下配平状态的全机阻力系数已知,根据式(13)可知,匹配推力系数一定,另外,根据式(12),匹配推力系数建立了螺旋桨进距比和拉力系数的关系,结合螺旋桨J-CT特性,如图6(a)所示,每条等桨距角线上的每一点对应一定匹配推力系数值。因此,巡航状态下,螺旋桨工作点在等TC线上;进一步,通过如图6(b)螺旋桨J-η特性图可确定螺旋桨效率;最终,通过匹配推力系数TC的引入,建立了等匹配推力系数下螺旋桨效率和进距比的关系。
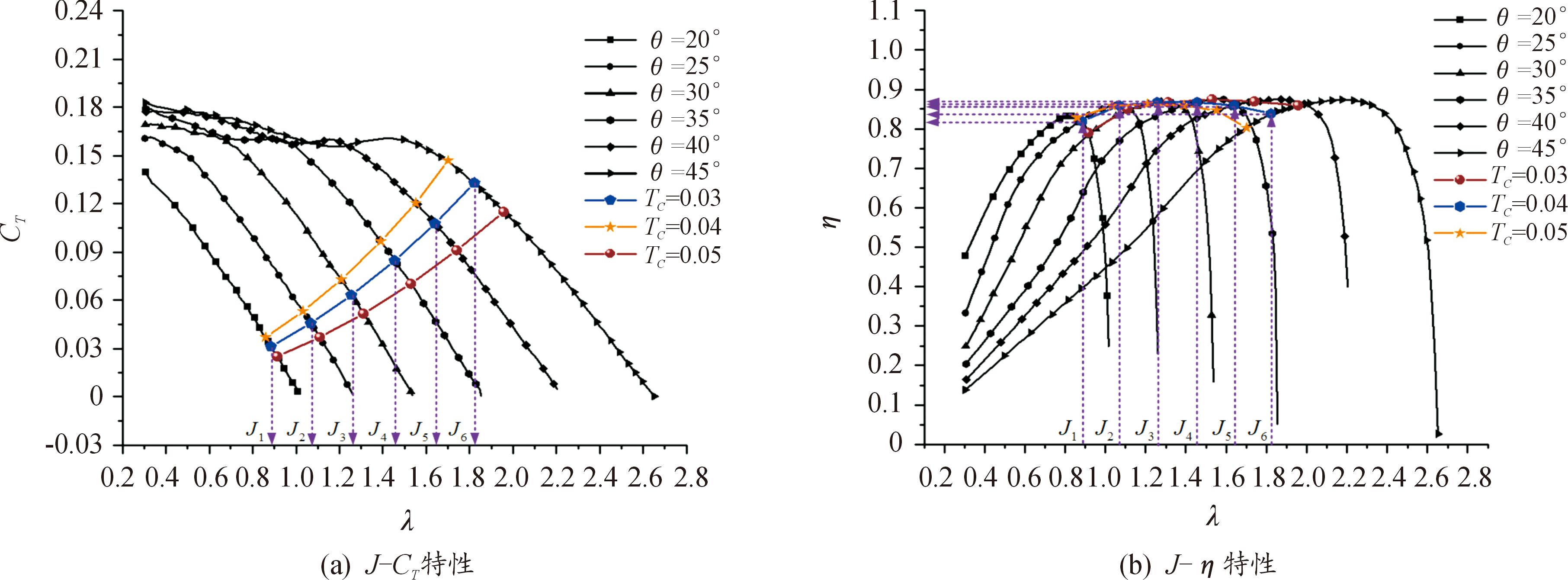
图6 等TC下螺旋桨效率与进距比关系计算过程
Fig.6 Calculation process of the relationship between propeller efficiency and pitch ratio under equivalent TC
3 桨发匹配性能计算
3.1 桨发匹配计算方法验证
基于桨发匹配设计方法,开发了计算程序,并进行了算例计算分析,算例采用公开文献[8]。
算例采用的螺旋桨和发动机特性见1.1节和1.2节。飞机安装2台某型活塞发动机,巡航阶段采用最大升阻比巡航策略,巡航高度H=3 080 m,最大配平升阻比Kmax=15.1,升力系数CL=1.283 2,阻力系数CD=0.084 98,机翼面积S=50 m2,螺旋桨直径d=3.352 8 m。根据匹配推力系数的计算公式(13)可知,巡航状态下的TC值为0.094 5,该值与公开文献计算结果相同。
采用公开文献相同的计算方法,针对巡航状态不同螺旋桨转速,计算得到发动机耗油率、螺旋效率和螺旋桨效率/耗油率比值曲线,本文中软件计算结果与公开文献结果对比曲线分别如图7、图8和图9所示。综合对比分析可知,程序的计算结果误差小于5%,说明本文中所采用的螺旋桨数据插值方法和桨发匹配设计方法的正确性。
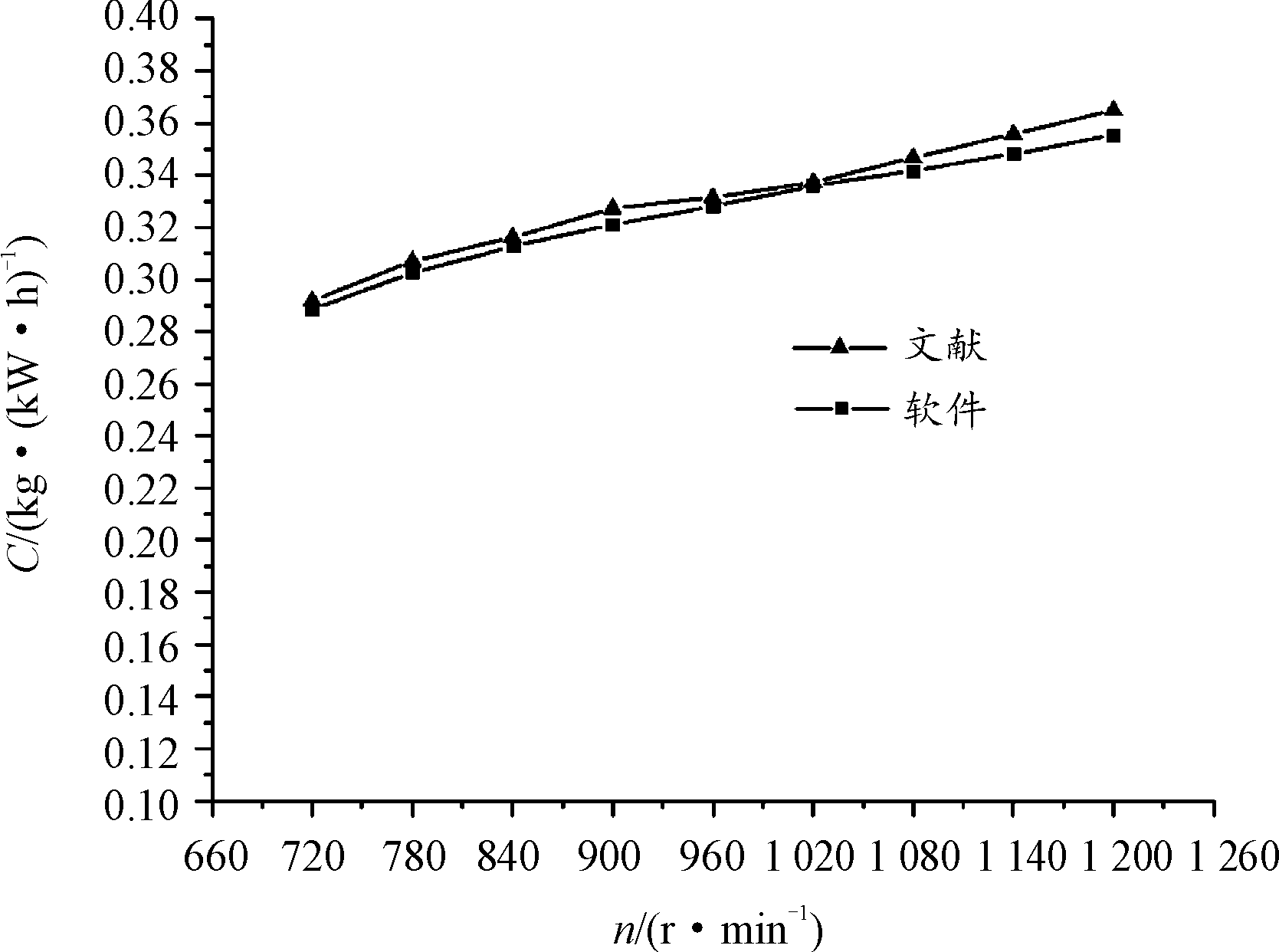
图7 发动机耗油率对比曲线
Fig.7 Comparison curve of engine specific fuel consumption rate
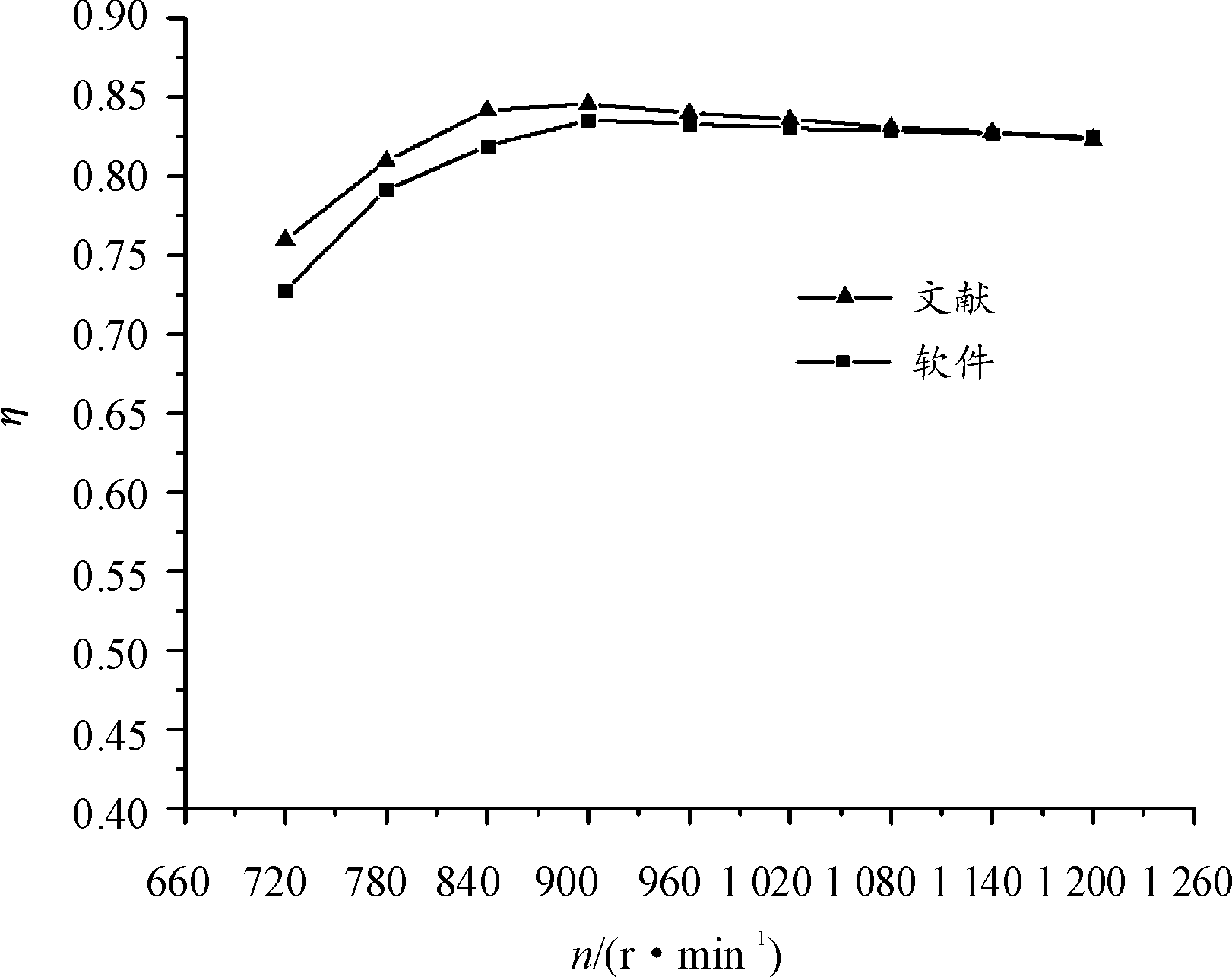
图8 螺旋桨效率对比曲线
Fig.8 Comparison curve of propeller efficiency
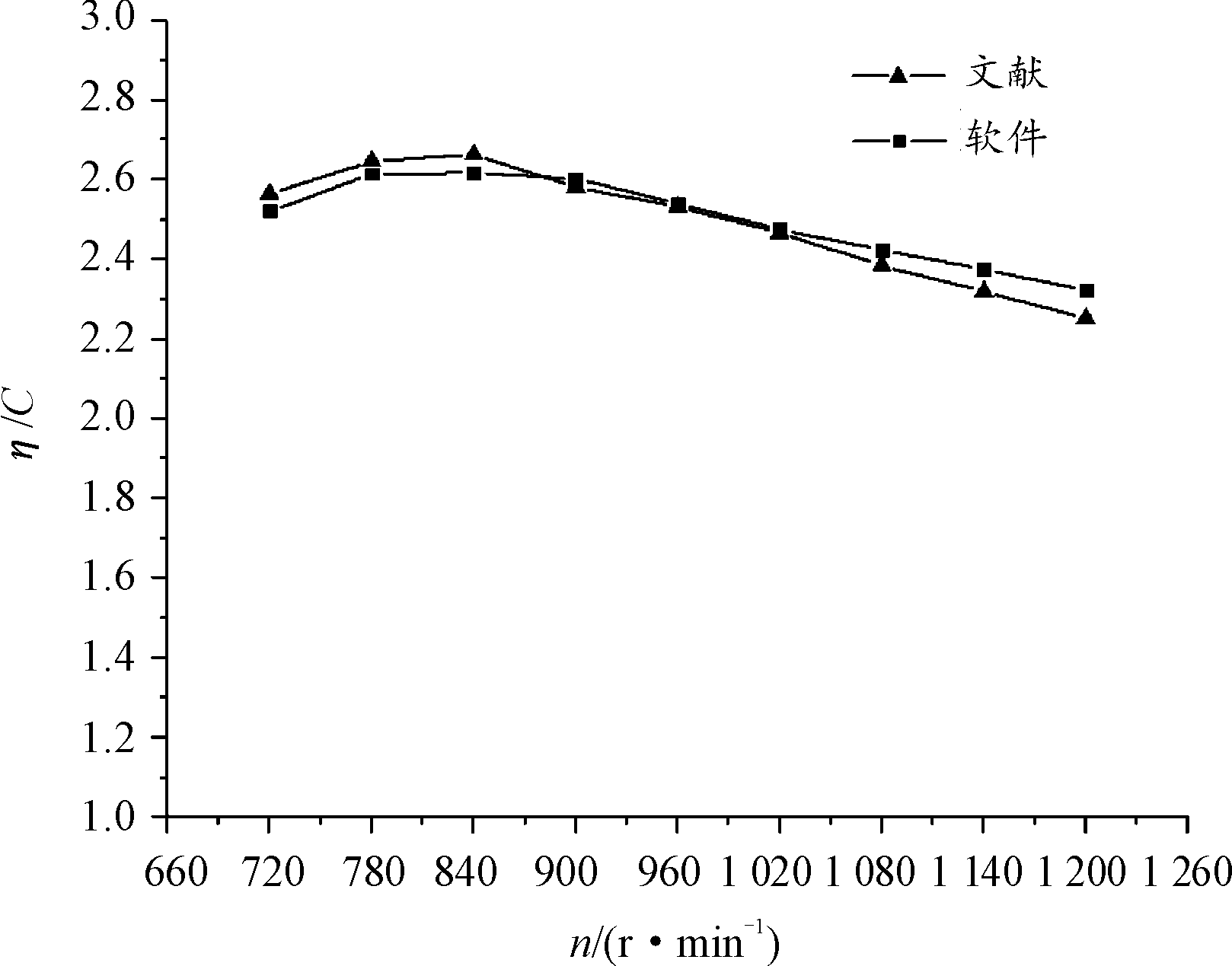
图9 螺旋桨效率/耗油率比值对比曲线
Fig.9 Comparison curve of the ratio of propeller efficiency to engine specific fuel consumption rate
由图9可知,软件计算得到螺旋桨效率/发动机耗油率比值最大值对应的螺旋桨转速为840 r/min,公开文献中对应的最大值为840 r/min,本文中仿真结果与文献值一致。
采用1.3节布雷盖(Breguet)方程进行了最优转速840 r/min下的航程计算,文献中最大航程值为3 820英里(6 148 km),本文中程序对应计算得到的航程为6 008.03 km,相对误差为-2.3%,表明本文中程序仿真结果正确性。
3.2 桨发匹配设计
针对3.1节算例,基于本文中提出的桨发匹配设计及优化方案,进一步开展了巡航阶段的桨发匹配性能优化。
巡航阶段随着燃油的消耗,飞机重量减轻,最大升阻比下,所需升力减小,飞行速度减小;同时,飞机需用推力减小,此时,如何调节螺旋桨和发动机工作状态,才能使得整个巡航阶段性能最优。
假设飞机巡航起始重量为7 600 kg,巡航结束状态重量为5 600 kg。巡航过程以每200 kg飞行重量减小作为分段,计算了飞机不同飞行重量下不同螺旋桨转速对螺旋桨和发动机性能的影响,并寻求最优匹配状态。
以飞行重量7 600 kg为例,在不同螺旋桨转速下,螺旋桨效率、发动机耗油率和两者比值变化曲线如图10所示。从图10中可知,随着螺旋桨转速的增加,螺旋桨效率先增大后减小,耗油率逐渐增大,η/C的值先增大后减小;当螺旋桨转速为820 r/min时,η/C取得最大值,即该点为螺旋桨和发动机最优匹配工作状态。
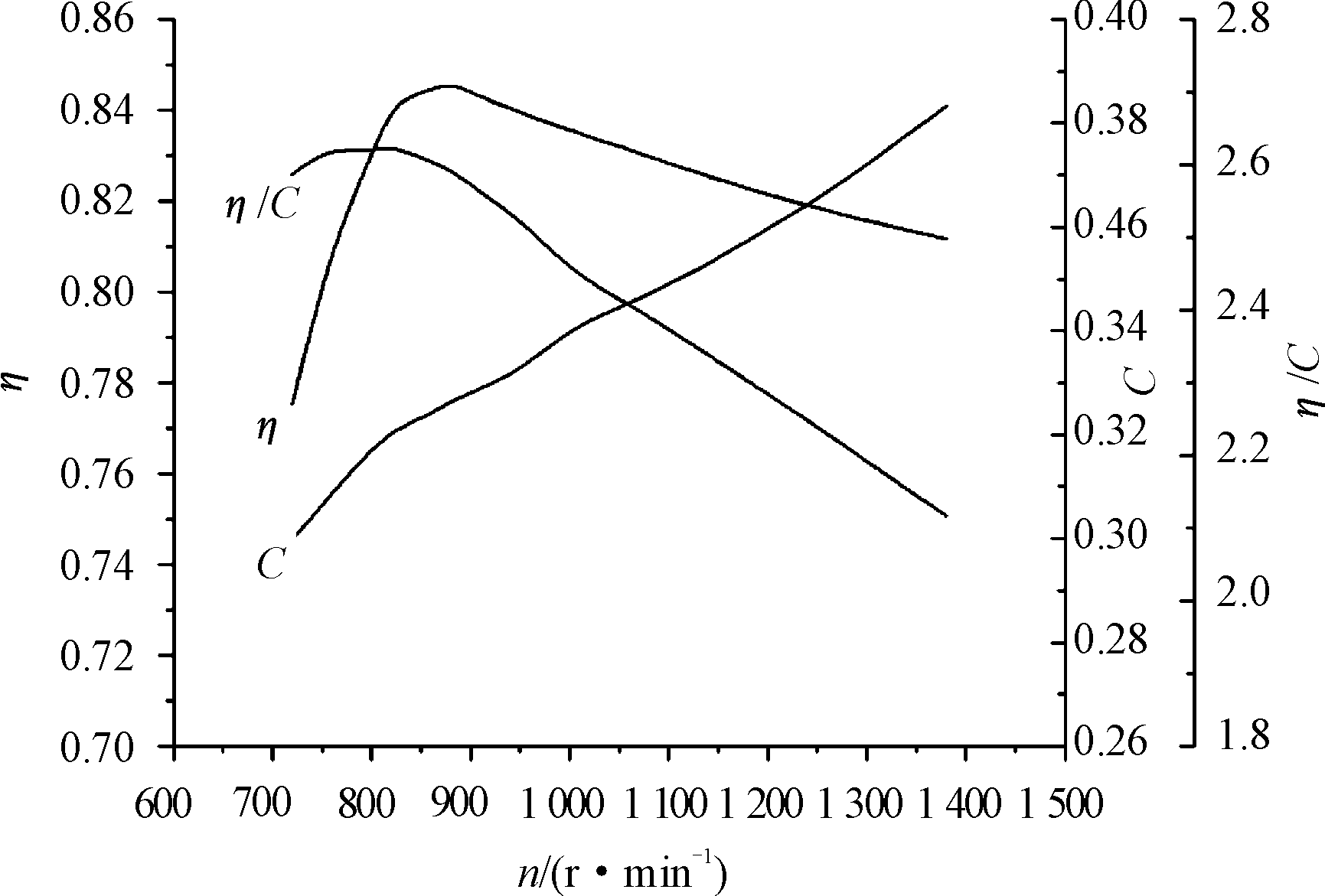
图10 效率、耗油率和两者比值随螺旋桨转速变化曲线
Fig.10 Curve of efficiency,engine specific fuel consumption rate,and their ratio changing with propeller speed
根据上述方法,分别计算不同飞行重量下的最优桨发匹配工作点。不同飞行重量下最优桨发匹配点螺旋桨转速如图11所示,分析可知,随着飞机飞行重量的减小,最优桨发匹配工作点螺旋桨转速减小,且飞行重量每减小400 kg,螺旋桨转速减小20 r/min,单调减小;呈现该规律的主要原因是由于随着飞行重量的减轻,飞行速度减小,若螺旋桨转速不变,对应的螺旋桨进距比减小,根据等TC线上最优点可知,其对应的进距比不变,因此,螺旋桨转速减小才能保证进距比不变。不同飞行重量下最优桨发匹配点所需发动机功率如图12所示,分析可知,随着飞机飞行重量的减小,所需发动机功率单调减小。
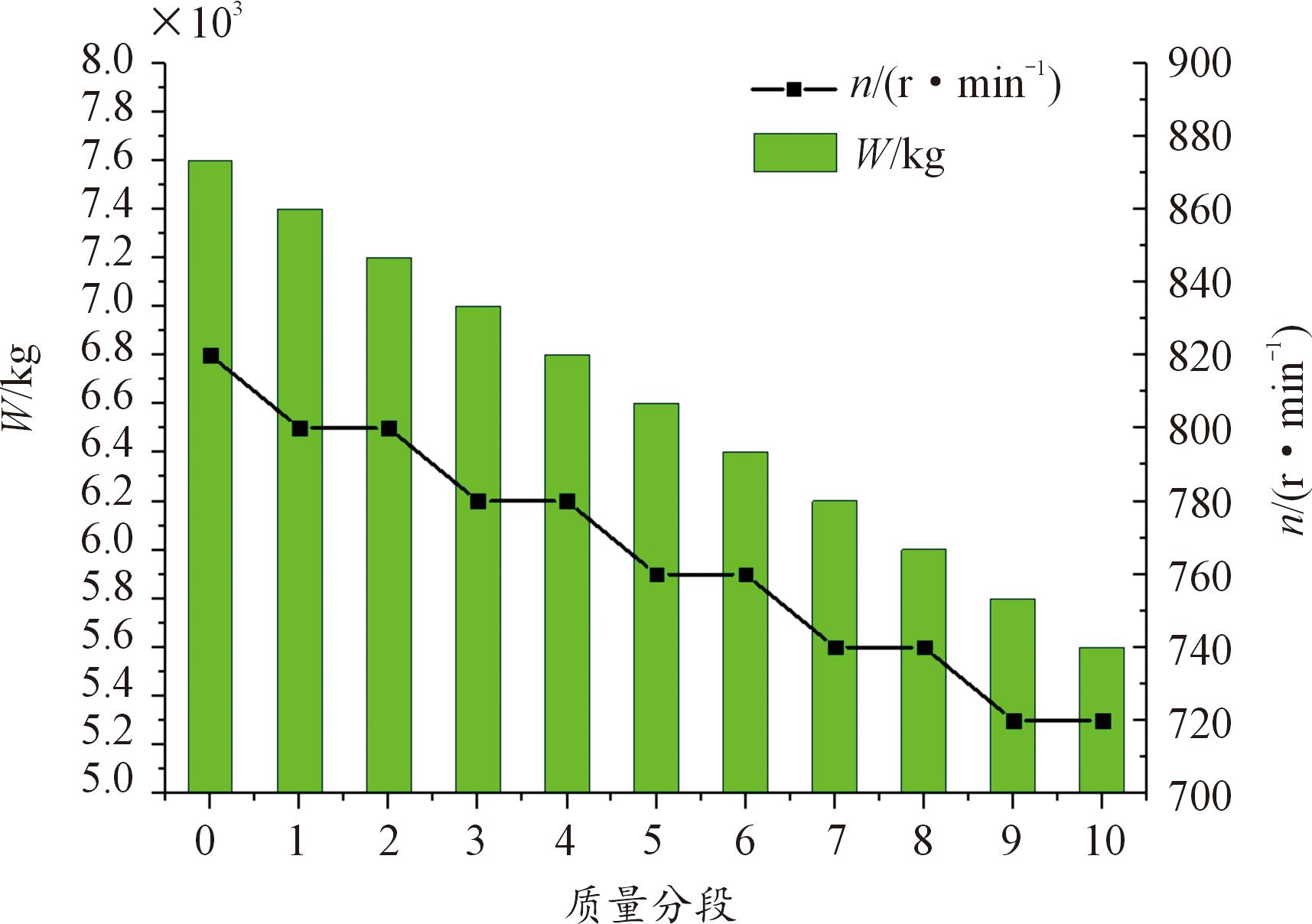
图11 螺旋桨选速
Fig.11 Propeller speed selection
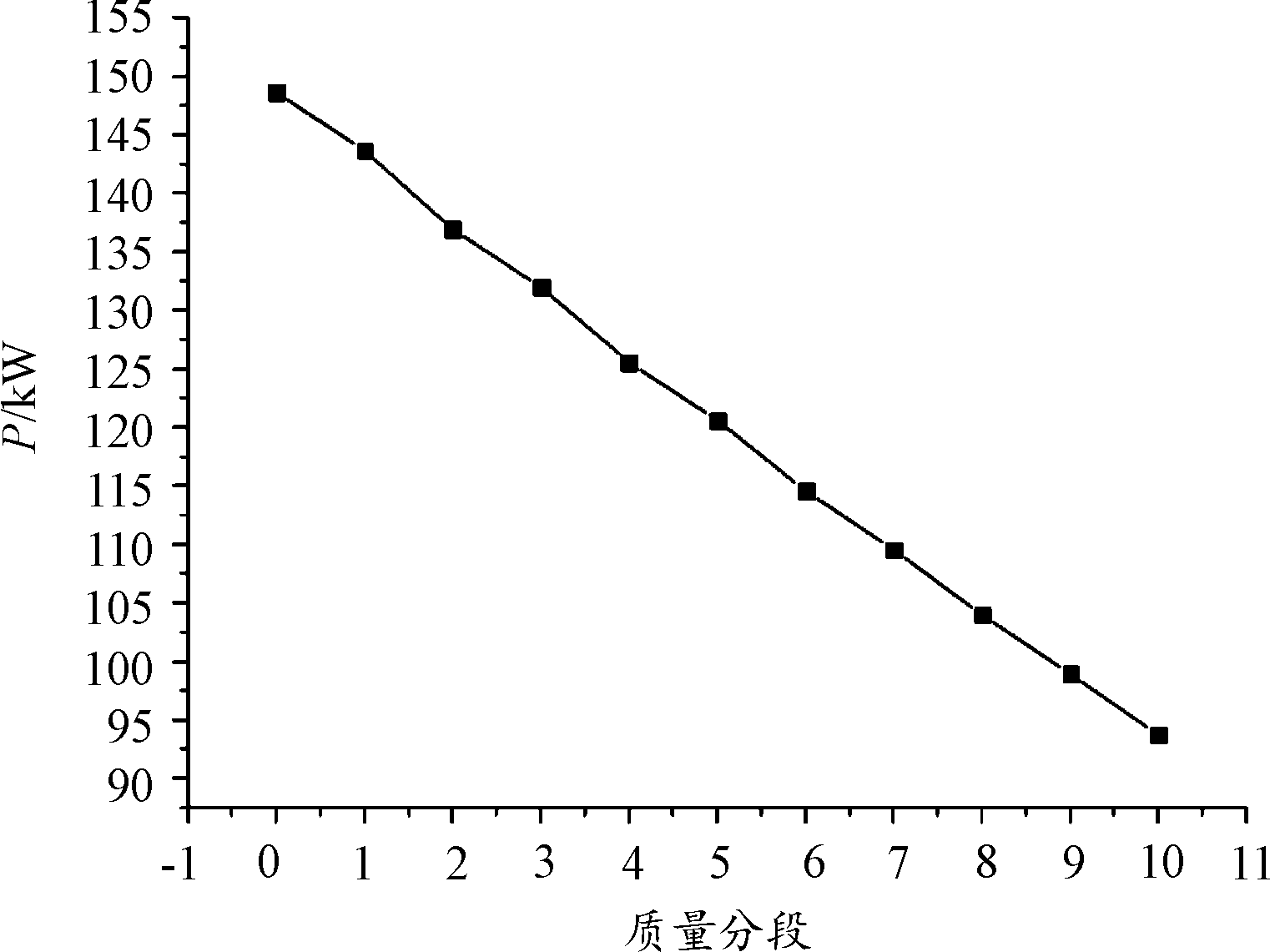
图12 不同飞行重量下最优桨发匹配点所需发动机功率
Fig.12 Engine power required for optimal propeller engine matchin point under different flight weights
根据1.3节飞行性能计算方法计算了不同飞行重量下最优桨发匹配对应飞机航程和航时,如图13所示,分析可知,随着飞机飞行重量的减轻,由于最优匹配工作点发动机所需功率减小,油耗减小,因此,相同燃油重量下飞机航程和航时有所增加。最优桨发匹配下,飞机巡航阶段的总航程为4 219 km,航时24.96 h。
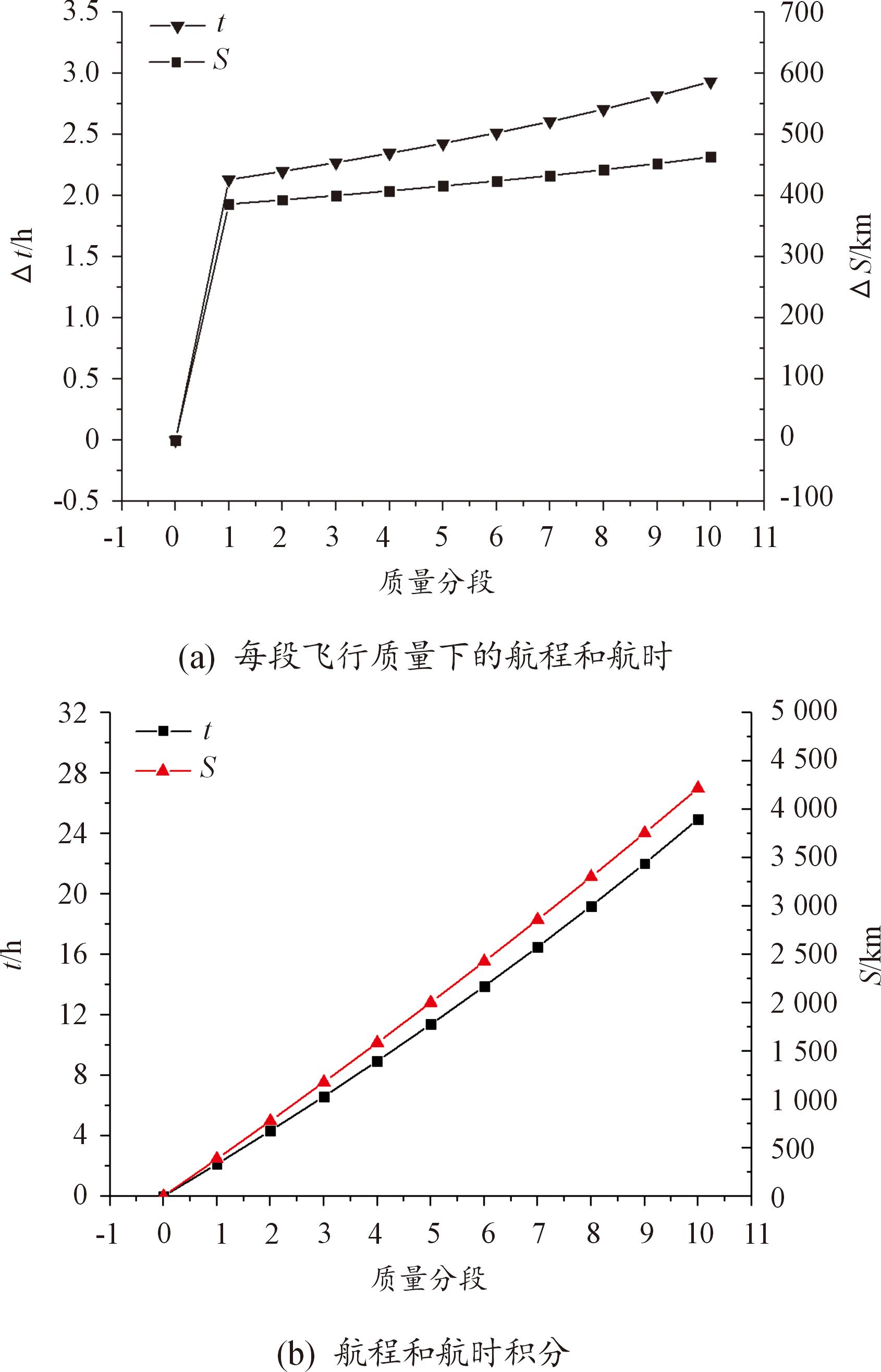
图13 巡航分段航程和航时计算结果
Fig.13 Calculation results of cruise segmented range and duration
为了对比分析采用螺旋桨最优桨发匹配转速下飞机飞行性能提升效果,计算了整个巡航过程保持不同恒定螺旋桨转速对飞机航程航时的影响。根据螺旋桨转速工作范围,选择不同的螺旋桨转速仿真计算,得到不同螺旋桨转速对巡航航程和航时的影响结果,如图14所示。
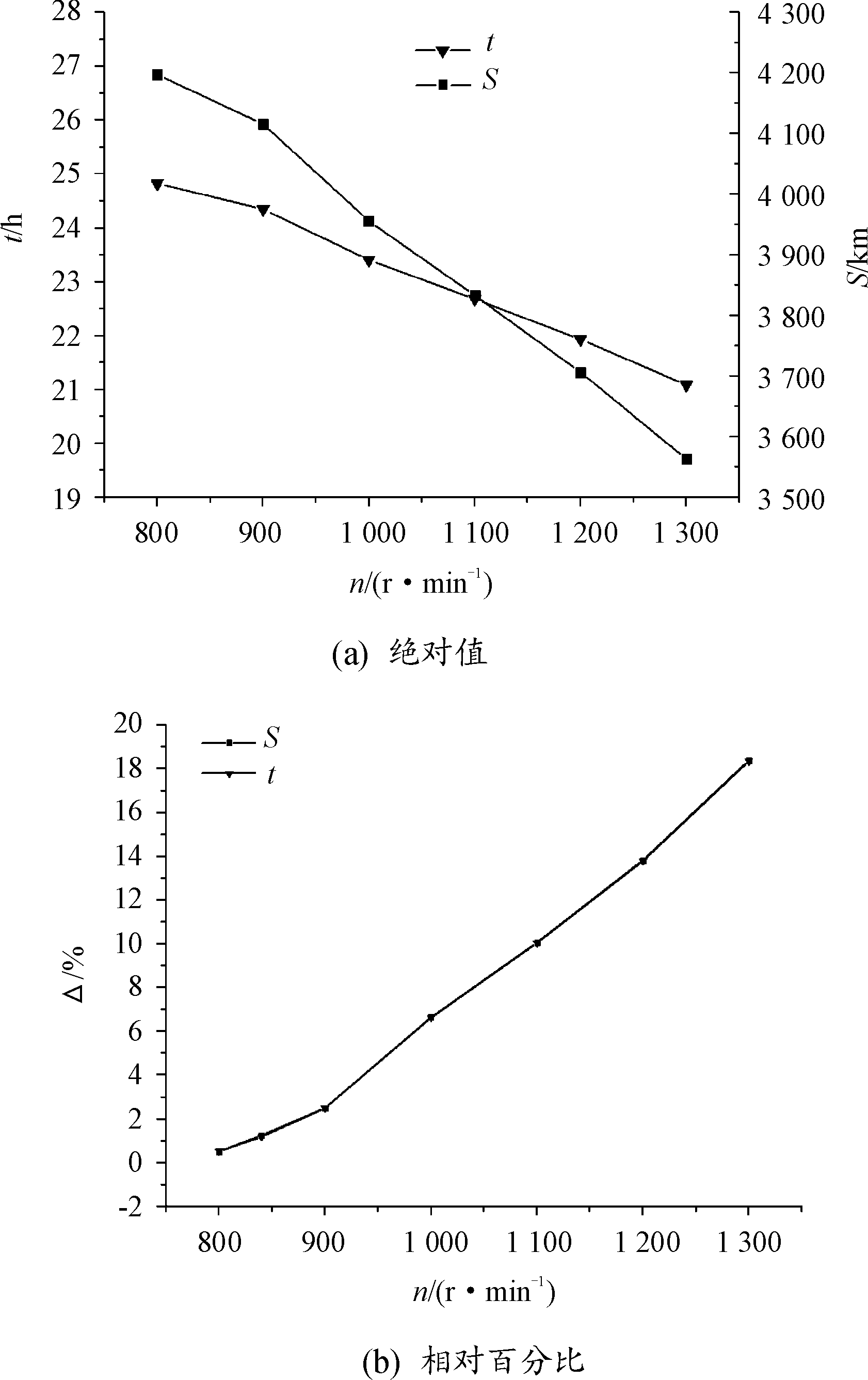
图14 不同螺旋桨转速对巡航航程和航时的影响
Fig.14 The influence of different propeller speeds on cruise range and duration
由图14可知,在螺旋工作转速范围内,当巡航阶段螺旋桨转速保持恒速,相应的飞行航程和航时均小于采用最优桨发匹配转速计算值;随着螺旋桨转速的增大,航程和航时均缩短;公开文献[8]中未优化前飞机巡航所采用螺旋桨转速为1 300 r/min,若螺旋桨按照该转速恒速工作,航程相对于本文中最优桨发匹配转速时的航程减少了656 km。因此,采取本文中提出的最优桨发匹配转速飞行策略,可使飞机巡航航程提高18.40%,航时提高18.36%。若采用公开文献[8]中优化得到的螺旋桨转速840 r/min恒速飞行,本文中优化后的飞行策略可使飞机巡航航程提高1.25%,航时提高1.19%。
综合上述分析可知,飞机在燃油量一定的情况下,巡航阶段根据不同飞行重量按照最优桨发匹配转速工作,可以有效提高飞机的航程和航时,提升飞行性能。
本文中提出的活塞动力桨发匹配设计方法,相对于传统的作图法[17]可以有效提升桨发匹配设计精度和效率。在活塞动力飞机设计阶段,可以实现桨发匹配性能快速评估,用于螺旋桨选型、桨发匹配选速等;另外,在飞机使用阶段,桨发匹配选速结果可用于指导飞机飞行过程动力系统状态控制,进一步提升飞机飞行性能。
4 结论
1) 针对活塞动力螺旋桨飞机桨发匹配性能仿真,开展了螺旋桨、活塞发动机性能和飞机飞行性能模型建模,基于飞机需用推力开展了螺旋桨巡航阶段桨发匹配设计及优化方法研究,并提出了桨发匹配设计及优化方案。
2) 基于桨发匹配设计方法,开发了计算程序,并进行了算例计算分析,对比公开文献,螺旋桨效率、发动机耗油率等计算结果误差小于5%,航程计算结果误差-2.3%,表明本文中算法的正确性。
3) 考虑巡航过程燃油消耗,飞行重量减轻对桨发匹配性能的影响,进行了巡航阶段螺旋桨转速优化,优化后的飞机巡航性能相比于采取恒定螺旋桨转速(1 300 r/min)飞行,航程提高18.40%,航时提高18.36%,收益较为显著。
4) 本文中提出的飞机巡航阶段桨发匹配选速方法,可以实现飞机设计阶段桨发匹配性能快速评估、螺旋桨选型和桨发匹配选速,以及使用阶段的桨发匹配选速,对活塞动力螺旋桨飞机桨发匹配设计及优化具有重要的工程意义。
[1] 王春晖.螺旋桨飞机舱内噪声特性分析[D].南京:南京航空航天大学,2015.WANG Chunhui.The cabin noise analysis of propeller plane[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2015.
[2] 耿欣,胡天翔,周若君,等.涡桨飞机螺旋桨气动噪声特性试验研究[J].民用飞机设计与研究,2022(1):64-69.GENG Xin,HU Tianxiang,ZHOU Ruojun,et al.Investigation on the aeroacoustic characteristics of the turboprop propeller[J].Civil Aircraft Design and Research,2022(1):64-69.
[3] 刘沛清.空气螺旋桨理论及其应用[M].北京:北京航空航天大学出版社,2006.LIU Peiqing.Theory and application of air propeller[M].Beijing:Beijing University of Aeronautics and Astronautics press,2006.
[4] 史永运,钟易成,邓君湘,等.涡轮螺旋桨动力飞机桨发匹配性能仿真研究[J].机械制造与自动化,2019,48(4):116-120.SHI Yongyun,ZHONG Yicheng,DENG Junxiang,et al.Research on prop-engine cooperation performance simulation of propeller powered aircraft[J].Mechanical Manufacturing and Automation,2019,48(4):116-120.
[5] 唐梓杰,丁水汀,杜发荣,等.航空二冲程活塞发动机与定距螺旋桨的匹配研究[J].航空动力学报:2010,25(2)379-383.TANG Zijie,DING Shuiting,DU Farong,et al.Method for match of two stroke piston engine and set propeller[J].Journal of Aerospace Power:2010,25(2)379-383.
[6] 谢辉,王力,张琳.一种适用于中小型无人机的新型螺旋桨设计[J].航空工程进展,2015,6(1):71-76.XIE Hui,WANG Li,ZHANG Lin.A new type of propeller design for the medium/small UAV[J].Advances in Aeronautical and Engineering,2015,6(1):71-76.
[7] FREEMAN H B.Comparison of full scale propeller having Raf-6 and Clarky airfoil sections[R].NACA Rept.378,1943.
[8] BIERMANN D,CONWAY R N.Propeller charts for the determination of the rotational speed for the maximum ratio of the propulsive efficiency to the specific fuel consumption[R].NACA.Report.No.749,1940.
[9] 陈怀荣,王曦.一种基于螺旋桨部件特性的螺旋桨建模方法[J].航空动力学报,2017,32(10):2526-2535.CHEN Huairong,WANG Xi.A modeling method of propeller based on the propeller component characteristic[J].Journal of Aerospace Power,2017,32(10):2526-2535.
[10] 史永运.螺旋桨动力系统桨发匹配技术研究[D].南京:南京航空航天大学,2018.SHI Yongyun.Research on prop-engine cooperation technology of propeller power system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2018.
[11] 杨彦林,王哲.某型通航飞机桨发匹配性能分析方法研究[J].科技与创新,2023(17):86-88.YANG Yanlin,WANG Zhe.Research on the performance analysis method of propeller engine matching for a certain type of navigation aircraft[J].Scienceand Technology &Innovation,2023(17):86-88.
[12] 付尧明.活塞发动机[M].2版.北京:清华大学出版社,2016.FU Yaoming.Pison engine[M].Second edition.Beijing:Tsinghua University Press,2016.
[13] 丁相玉.航空发动机原理[M].2版.北京:北京航空航天大学出版社,2018.DING Xiangyu.Aero-engine principle[M].Second edition.Beijing:Beijing University of Aeronautics and Astronautics Press,2018.
[14] 闫晓军.无人机动力[M].北京:科学出版社,2020.YAN Xiaojun.Unmanned vehicle[M].Beijing:Science Press,2020.
[15] 陈迪,田佳浩,李明新,等.中空长航时无人机动力系统发展分析[J].航空动力,2022,5:16-19.CHEN Di,TIAN Jiaohao,LI Mingxin,et al.Analysis to the development of power systems for male UAVs[J].Aerospace Power,2022,5:16-19.
[16] 孔祥恩,刘海峰.无人机用航空活塞发动机关键技术的研究进展[J].小型内燃机与车辆技术,2021,50(3):79-87.KONG Xiangen,LIU Haifeng.Research progress of key technologies of aviation piston engine for UAV[J].Small Internal Combustion Engine and Vehicle Technique,2021,50(3):79-87.
[17] 高永卫.无人机螺旋桨的空气动力学设计[M].北京:科学出版社,2022.GAO Yongwei.Aerodynamic design of unmanned aerial vehicle propellers[M].Beijing:Science Press,2022.
[18] 张锡金.飞机设计手册 第6册 气动设计[M].北京:航空工业出版社,2006.ZHANG Xijin.Aircraft design manual the sixth book aerodynamic design[M].Beijing:Aviation Industry Press,2006.