0 引言
在科技发展日新月异的今天,战争形态也悄然发生着改变,原本的密集火力压制已不再是世界各国信奉的金科玉律,而一击致命、节能环保则成为了现代弹药的发展理念[1]。现代战争对制导弹药的要求日益增强,制导弹药在未来将会按照远程化、精确化、智能化、隐形化、通用化、模块化和低成本化的趋势发展[2]。作为制导炮弹控制系统中不可或缺的关键组成部分,舵机的性能直接影响炮弹飞行过程的动态品质和打击精度,电动舵机克服了液压舵机和气动舵机结构复杂、维护不便等缺点,逐渐成为了舵机系统研究领域的重点[3-5]。
目前,电动舵机及其控制系统的发展主流是:采用永磁无刷直流电机作为伺服驱动,结合智能控制算法,实现系统的快速度、高精度与鲁棒性控制[6]。经典的PID (proportional integral derivative)算法是较早发展起来的控制策略之一,但该算法对于舵机状态的估计基于线性模型,而电动舵机是一个多变量、强耦合的复杂非线性系统,因此需要寻求有效的控制算法对内、外部非线性扰动进行抑制[7-10]。20世纪80年代以来,在仿生学进步的基础上,控制领域提出了诸多智能算法对电动舵机系统进行优化控制,如Lu等[11]在2010年提出了一种混合鲁棒H∞算法应用于飞行器的电动舵机控制系统中,实验结果表明,采用该算法不仅可以保证系统良好的动态特性,并且对于外部干扰具有较强的鲁棒性能。Li等[12]针对舵机驱动的飞机发动机推力矢量系统存在大惯量、低刚度的问题,通过鲁棒PID组成的复合控制律跟踪期望的长度,并在执行器中采用超前补偿和bang-bang控制,结果表明,所设计的推力矢量控制器能够达到满意的控制性能。Zhou等[13]提出了一种适用于导弹电动舵机的新型趋近律改进滑模控制方法,与传统方法相比有效解决了由于系统非线性因素的影响,在跟踪小角度正弦信号时存在平顶的现象,提高了电动舵机系统的控制性能。李冬辉等[14]提出了一种改进的径向基滑模控制方法,抑制了摩擦和间隙的不利影响,提高了系统的跟踪精度,削弱了小角度平顶问题,有效抑制了弹道极限环震荡现象。因此,人工智能算法显示出了优良的控制性能、稳定性与鲁棒性,并且随着计算机性能与微型控制器的飞速发展,使得将人工智能算法应用到实际开发中成为了现实。
此外,电动舵机系统中存在着诸多非线性环节,如伺服电机内部非线性、齿轮系结构中的死区齿隙和输出轴的摩擦非线性等均会影响系统的运行精度和响应速度。首先,死区齿隙具有非连续、不可微等非线性特性,且参数难以精确测量,给建立齿隙模型与补偿控制带来了较大困难,引起了国内外学者的广泛关注与深入研究。田福庆等[15]针对制导弹药电动舵机伺服控制系统中存在的齿隙、不确定参数与外部干扰,提出了一种基于反步法的全局模糊自适应控制方法,既保证了系统的跟踪速度与控制精度,对不确定参数与外部扰动也具有较强的鲁棒性。Zhang等[16]提出了一种基于模型的摩擦补偿方法,并结合基于观测器的自适应滑模控制器对电动舵机系统的速度环进行控制,利用Lyapunov稳定性理论和Barbalat引理讨论了电动舵机系统的稳定性。其次,摩擦非线性的存在会使得高精度伺服系统在稳态时出现静差或极限环振荡,在低速时出现爬行现象,这些严重影响伺服系统的动静态性能[17]。LuGre摩擦模型是Canudas[18]在1995年提出的一个较为完善的动态摩擦模型,它可以准确描述摩擦过程中复杂的动静态特性。李俊阳等[19]提出了一种带摩擦补偿的模糊自适应反步控制方法,利用Lyapunov判据证明了闭环系统的一致有界性,并通过仿真验证了所提出控制策略的有效性和鲁棒性。Wang等[20]研究了双电机伺服系统的有限时间指令反推控制问题,采用LuGre模型描述系统摩擦力,并设计模糊逻辑系统对其进行处理,证明了闭环系统的稳定性并通过实验验证了所提方案的优越性。但是上述研究仅考虑了某一特定非线性因素,未将多非线性耦合等因素对于电动舵机系统的综合影响考虑在内。
基于此,本文中研究了基于模糊自适应 (fuzzy adaptive,FA)PID算法的弹载电动舵机多非线性控制系统。首先,在舵机建模过程中引入了伺服电机、死区齿隙与LuGre摩擦等非线性因素;其次,针对舵偏角运动方向的非单一性,设计了无刷直流电机的自动换相判别模块;然后,在位置环中引入了FA-PID算法,采用模糊技术自适应优化传统PID算法;最后,通过仿真实验验证了非线性系统建模的完善性,以及采用FA-PID算法的响应快速性与鲁棒性。
1 电动舵机系统非线性建模
1.1 无刷直流电机
无刷直流电机作为电动舵机的主要伺服执行器件,其定子为Y接集中整距绕组,转子采用隐极内转子结构,在此基础上作如下假设以简化分析过程[21-22]:忽略电机铁芯饱和,不计涡流损耗和磁滞损耗;不计电枢反应,气隙磁场分布近似认为是平顶宽度为120°电角度的梯形波;忽略齿槽效应,电枢导体连续均匀分布于电枢表面;驱动系统逆变电路的功率管和续流二极管均具有理想的开关特性。无刷直流电机相电压方程的矩阵形式可表示为
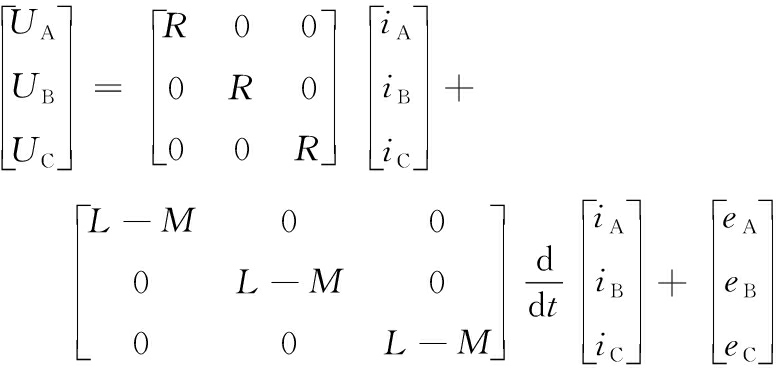
(1)
式(1)中: UA、UB、UC分别为A、B、C三相电压;R为相电阻;iA、iB、iC为三相电流;L为相绕组自感;M为相绕组互感;d/dt为微分算子;eA、eB、eC为三相感应反电动势。
电机的电磁转矩Te为
![]()
(2)
式(2)中: Ω为电机的机械角速度;Te的另一种表示形式为
Te=KT·i
(3)
式(3)中: KT为转矩系数;i为母线电流。电机的运动方程为
![]()
(4)
式(4)中: TL为负载转矩;J为转子转动惯量;Bv为粘滞摩擦系数。综上所述可以推导得出无刷直流电机的转速响应传递函数形式为
![]()
(5)
式(5)中: Ud(s)为母线电压;l为绕组等效电感;r为线电阻;ke为线反电动势系数。无刷直流电机非线性传递函数结构如图1所示,其参数如表1中所示。
表1 无刷直流电机参数
Table 1 Parameters of BLDCM
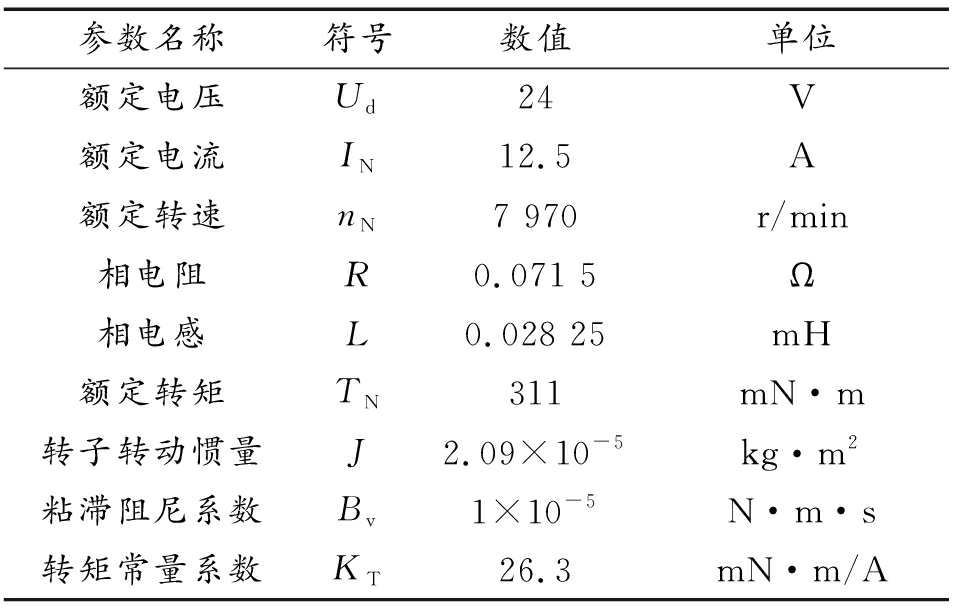
参数名称符号数值单位额定电压Ud24V额定电流IN12.5A额定转速nN7 970r/min相电阻R0.071 5Ω相电感L0.028 25mH额定转矩TN311mN·m转子转动惯量J2.09×10-5kg·m2粘滞阻尼系数Bv1×10-5N·m·s转矩常量系数KT26.3mN·m/A
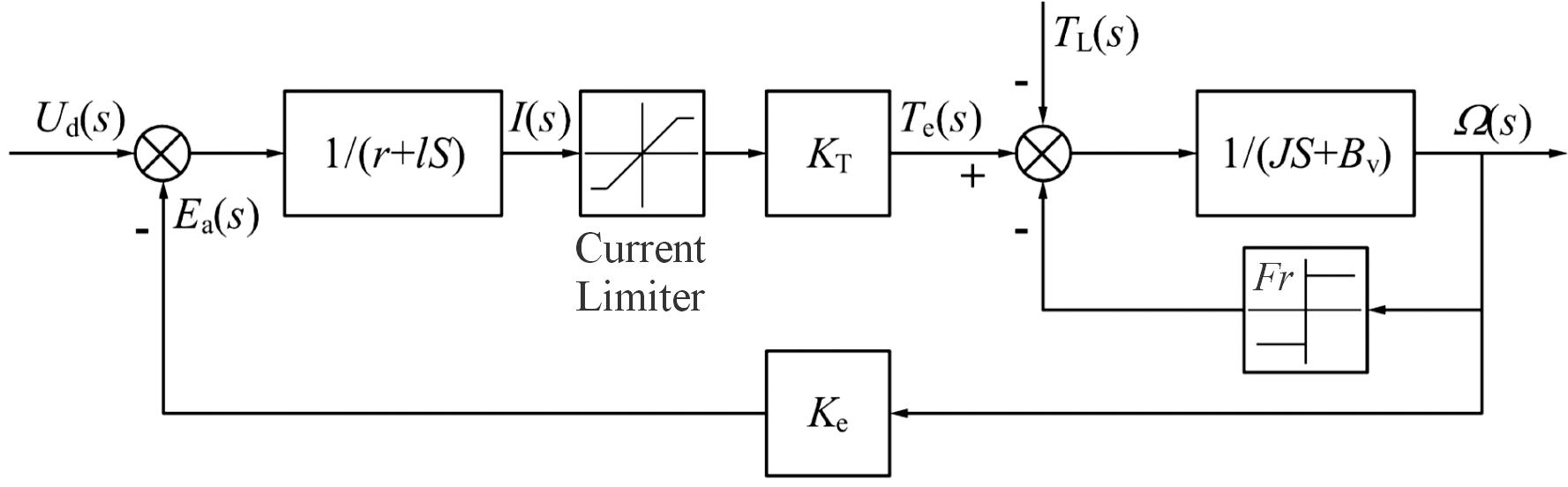
图1 无刷直流电机非线性传递函数结构
Fig.1 Nonlinear transfer function structure of BLDCM
1.2 齿轮减速传动结构
电动舵机所受外力主要由传动力矩Tk、摩擦力矩Tf、气动铰链力矩Tθ和外部干扰力矩Td组成。首先,传动力矩Tk为驱动轴与从动轴之间的传动力[23],伺服电机通过传动比为N、齿隙宽度为2j的减速齿轮驱动舵片跟踪设定转角,其数学方程为
Tk=k·f(z)
(6)
式(6)中,k为从动轴等效刚度,z=Ω-N·θl为驱动轴与从动轴间的相对转角,即实际齿隙宽度,其满足-2j≤z≤2j, θl为舵偏角位置, f(z)为齿隙死区非线性函数,即:
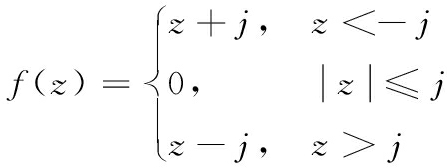
(7)
然后,本文中在摩擦力矩Tf引入了LuGre非线性摩擦模型,该模型考虑了2个接触表面之间弹性刚毛的平均偏移来表征摩擦的动态行为,可以较为准确地描述摩擦过程中复杂的动态摩擦效应[24-25],其数学模型可表示为
![]()
(8)
![]()
(9)
![]()
(10)
式(8)表示接触表面鬃毛的平均变形动力学方程,其中z为鬃毛的平均变形量,ωl为舵片的角速度,非线性函数g(ωl) >0表示不同的摩擦效应;式(9)中:FC为库伦(Coulomb)摩擦力矩,FS为最大静摩擦力矩,VS为Stribeck速度;式(10)中:σ0为鬃毛刚度系数,σ1为鬃毛阻尼系数,σ2为粘性摩擦系数。
其次,舵面受到的气动铰链力矩Tθ不仅与制导炮弹飞行时的空气动压、马赫数有关,而且与炮弹的攻角与舵面几何形状、偏转角相关,因而变化范围非常大。通常认为舵机受到的气动铰链力矩与舵面偏转角度成正比关系,为弹性负载[26],即:
Tθ=Kθ·θ
(11)
式(11)中:Tθ为舵机受到的铰链力矩;Kθ为铰链力矩系数,且Kθ=Tθmax / θmax;Tθmax为舵面受到的最大铰链力矩;θmax为最大舵偏角。电动舵机齿轮间传动效率为η,输出舵面的传递函数方程为1 / (Jss + Bs),Js为输出轴的转动惯量,Bs为输出轴的阻尼系数,电动舵机齿轮减速结构如图2所示,其主要参数如表2中所示。
表2 减速机构主要参数
Table 2 Main parameters of deceleration mechanism
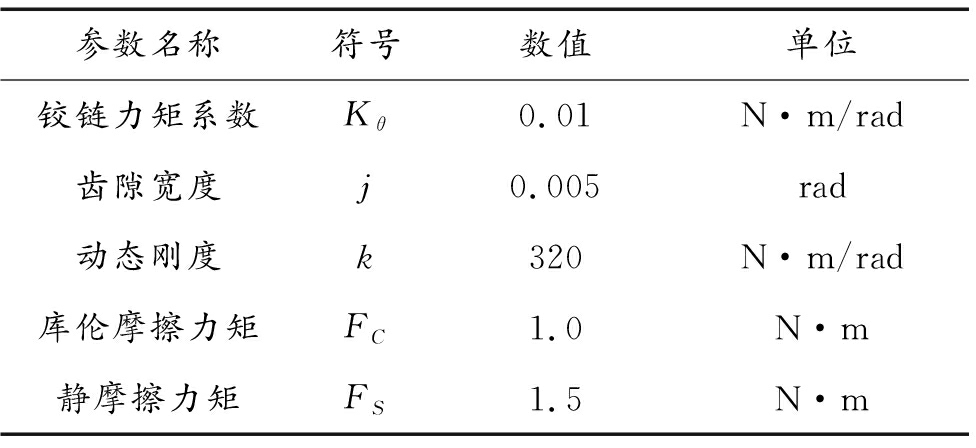
参数名称符号数值单位铰链力矩系数Kθ0.01N·m/rad齿隙宽度j0.005rad动态刚度k320N·m/rad库伦摩擦力矩FC1.0N·m静摩擦力矩FS1.5N·m
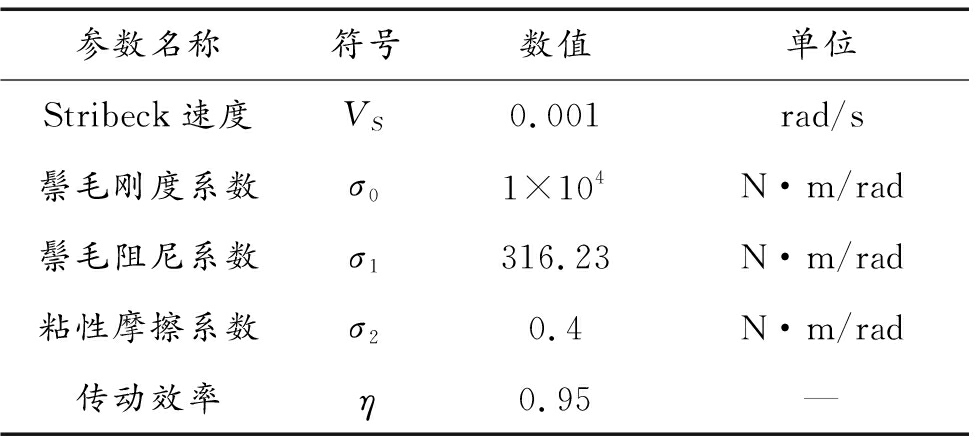
参数名称符号数值单位Stribeck速度VS0.001rad/s鬃毛刚度系数σ01×104N·m/rad鬃毛阻尼系数σ1316.23N·m/rad粘性摩擦系数σ20.4N·m/rad传动效率η0.95—
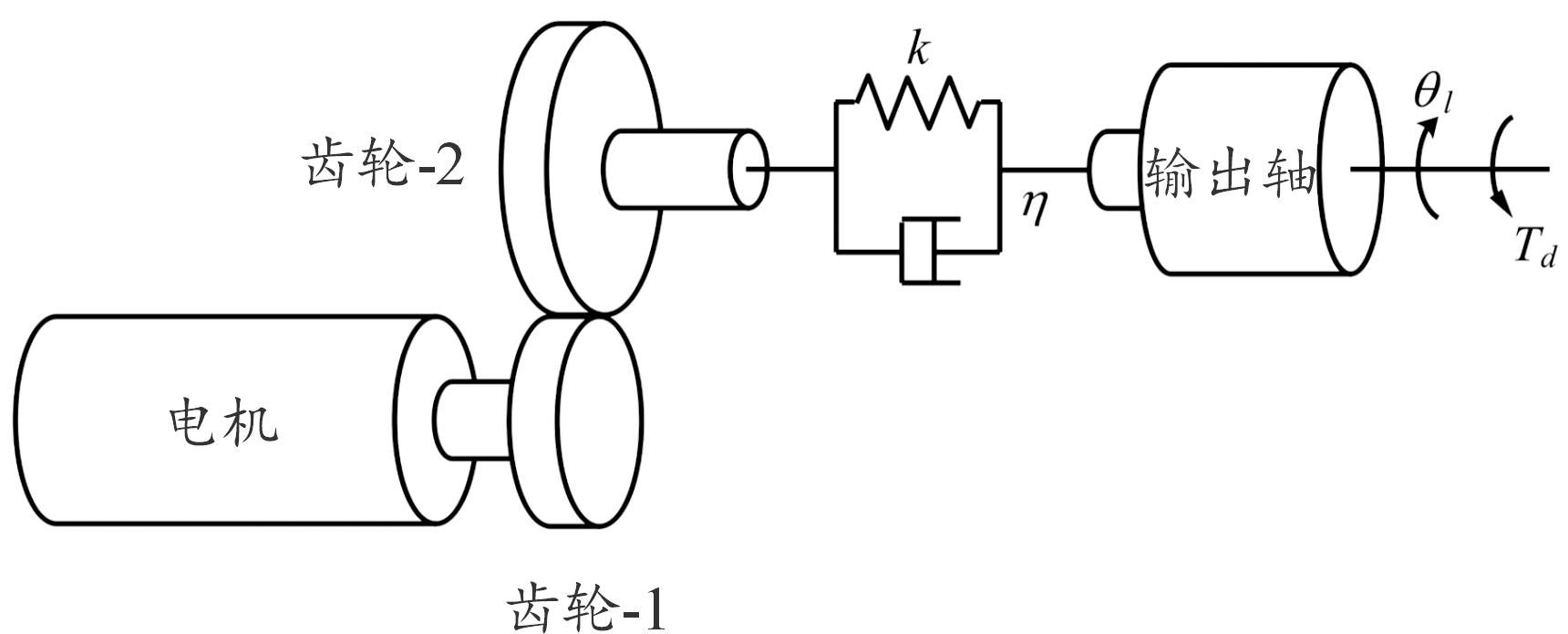
图2 电动舵机齿轮减速结构示意图
Fig.2 Gear reduction structure of EMA
此外,电动舵机通过控制无刷直流电机的正、反转实现舵面在一定范围内往返运动,在设定舵偏角位置增加的区间,电机正向旋转,提供正向转矩,电流参考值为正值;设定位置减小的区间,电机反向旋转,提供反向转矩,电流参考值为负值,因此可以通过采集电流参考值的符号来自动判别电机的转动方向。图3为弹载电动舵机非线性系统拓扑结构图。
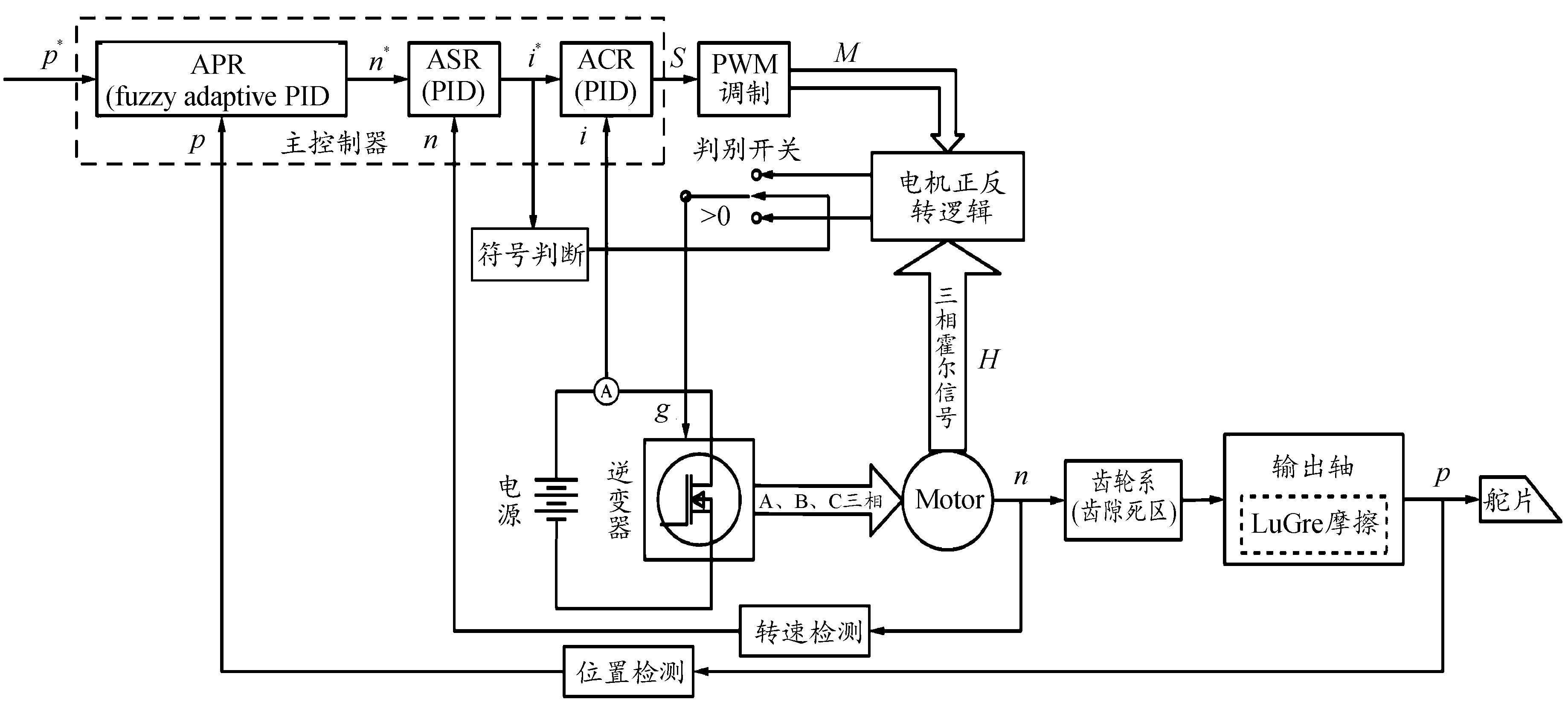
图3 弹载电动舵机非线性系统拓扑结构图
Fig.3 Topological structure of GP-EMA nonlinear system
2 FA-PID算法
美国学者L.A.Zadeh[27]于1965年首次提出了模糊集合的概念,20世纪90年代以来,模糊理论的浪潮迅速蔓延到各个领域,各式各样的模糊控制系统相继研发成功。模糊控制器通常包括输入量模糊化、数据库、规则库、推理机和输出量反模糊化5个部分。首先,设计以舵偏角位置的偏差e和偏差变化率ec作为模糊系统的输入,输出为PID算法中的参数修正值ΔKp、ΔKi、ΔKd,论域范围均设定为[-6,6],量化等级为13。
2.1 数据库
数据库中将模糊系统输入输出语言变量的模糊子集分别定义为“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”,依次用NB(Negative Big)、NM(Negative Middle)、NS(Negative Small)、ZO(Zero)、PS(Positive Small)、PM(Positive Middle)、PB(Positive Big)7个模糊语言值表示,图4为输入变量e的隶属度函数曲线,其余变量的隶属度函数与之相同,均为“三角形”函数。
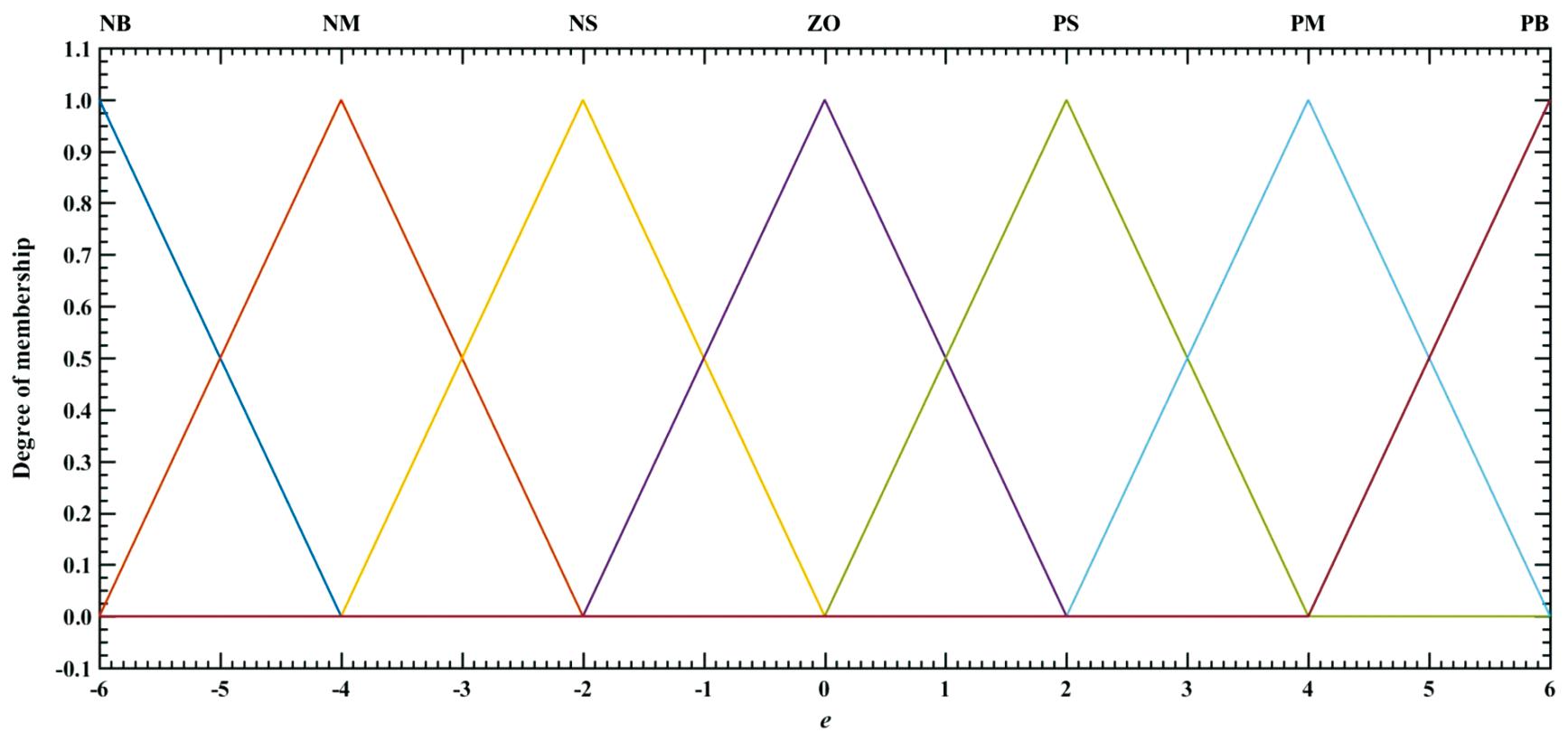
图4 输入变量e的隶属度函数曲线
Fig.4 Membership function curves of input variable e
2.2 规则库
依据控制工程知识以及专家经验建立了规则库,权值修正系数ΔKp、ΔKi与ΔKd的模糊规则空间曲面图分别如图5、图6和图7所示。
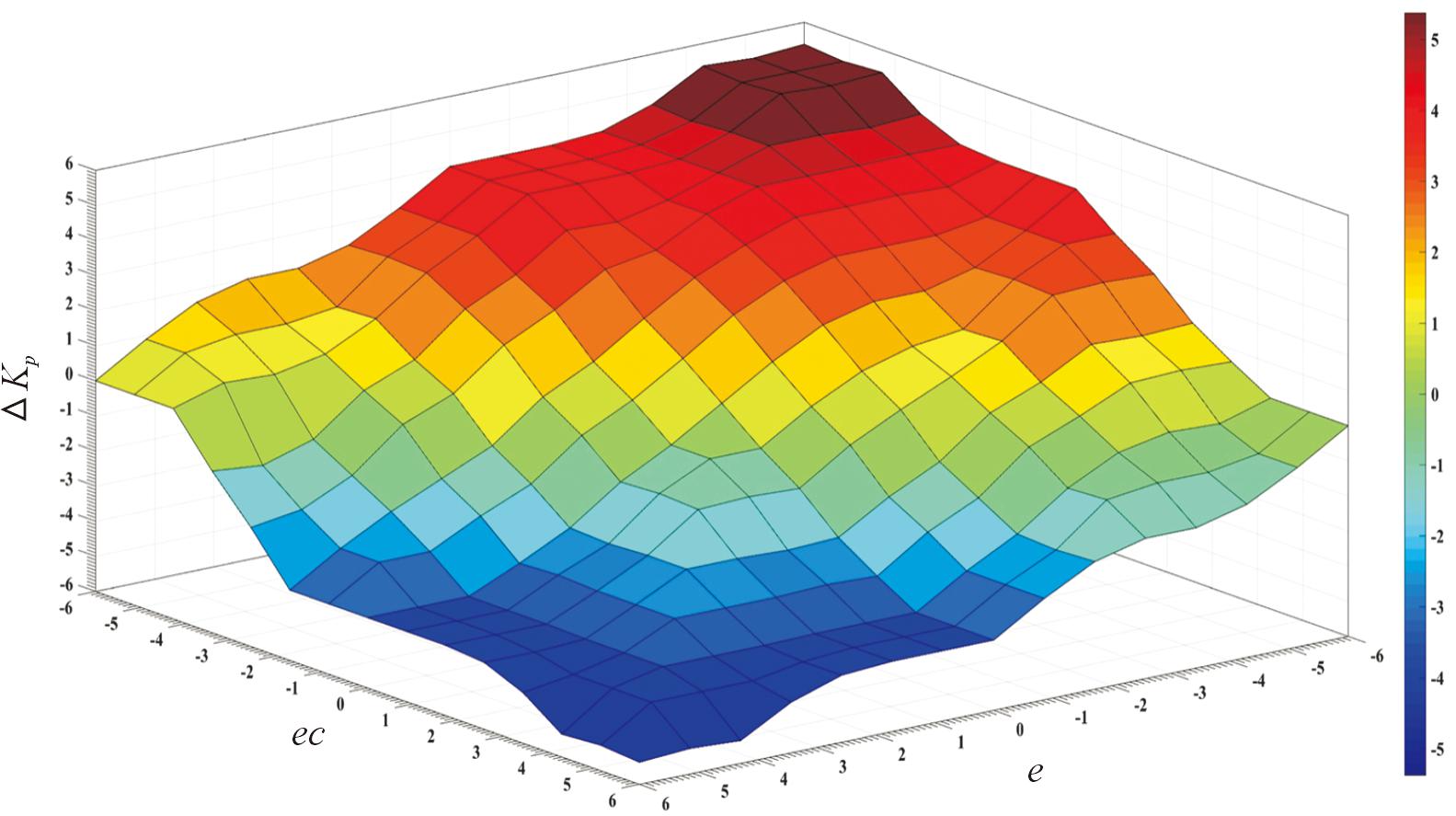
图5 ΔKp模糊规则空间曲面图
Fig.5 ΔKp fuzzy rule space surface diagram
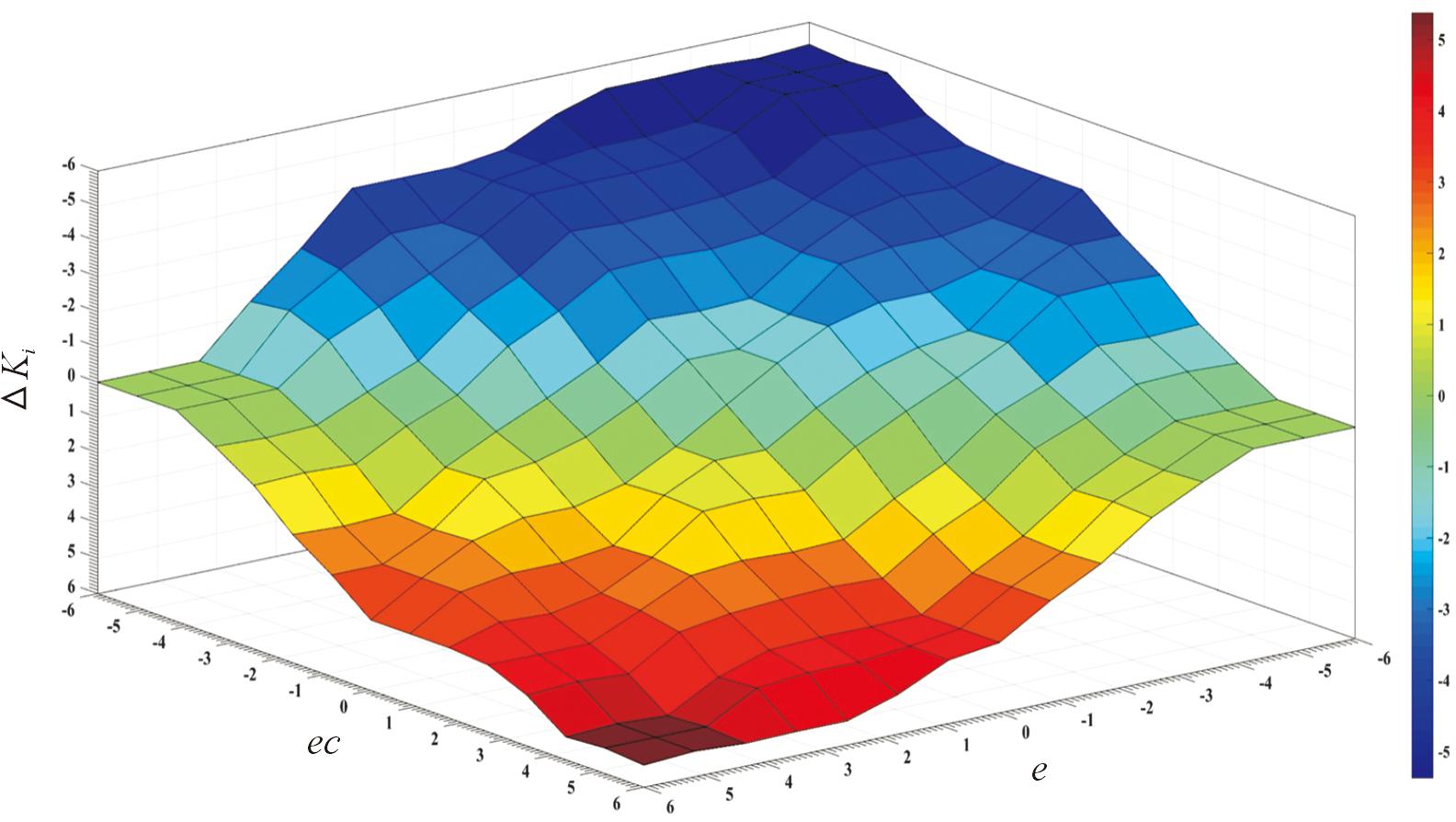
图6 ΔKi模糊规则空间曲面图
Fig.6 ΔKi fuzzy rule space surface diagram
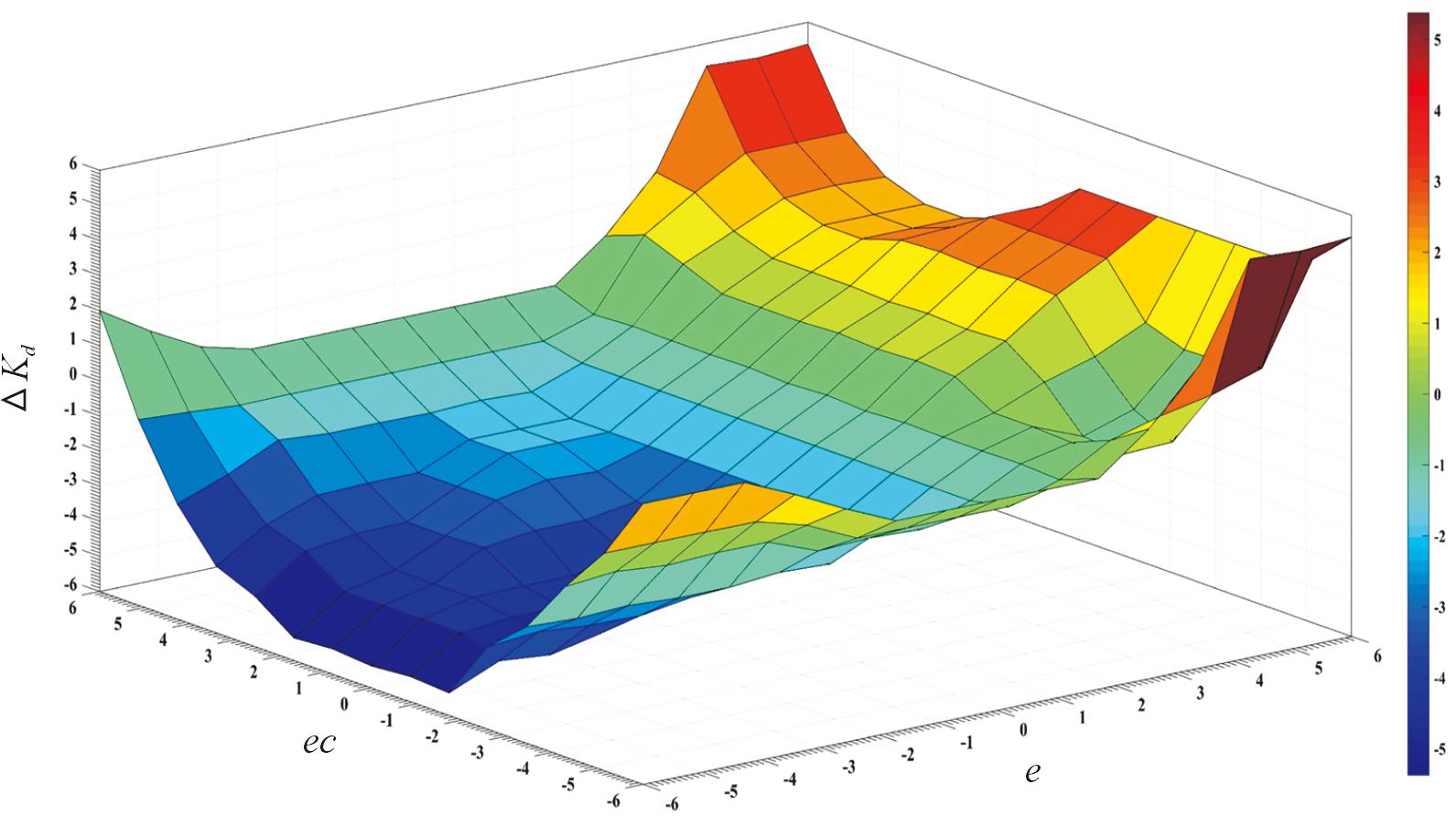
图7 ΔKd模糊规则空间曲面图
Fig.7 ΔKd fuzzy rule space surface diagram
2.3 推理机
本研究中采用Mamdani的min-max法进行系统多输入-多输出模糊关系的计算推理,其“if Ai and Bi, then Ci”的Mamdani表示方式如下:
[μAi(x)∧μBi(y)]∧μCi(z)
(12)
式(12)中: x、y、z分别为模糊论域X、Y、Z上的任意元素;μAi(x)、μBi(y)、μCi(z)分别为元素x、y、z相对于模糊集合A、B、C的隶属度函数;∧表示取小操作。推理结果可表示为
C′=(A′ and B′)∘ {[(A1and B1)→C1]∪…
∪[(Anand Bn)→Cn]}=
{(A′ and B′)∘ [(A1and B1)→C1]}∪…
∪{(A′ and B′)∘ [(Anand Bn)→Cn]}=![]()
(13)
式(13)中:“and”表示和运算;“∘ ”表示合成运算;“∪”表示取大操作。其隶属度函数为
![]()
![]()
![]()
![]()
![]()
(αAi∧μCi(z))∩(αBi∧μCi(z))=
αAi∧αBi∧μCi(z)
(14)
式(14)中:∨表示取大操作;∩表示取小操作;αAi和αBi表示模糊集合A′与A、B′与B之间交集的高度,可以看作是模糊集合A′对A、B′对B的适配程度,即隶属度。最后可以得出n条模糊运算结论如式(15)所示。
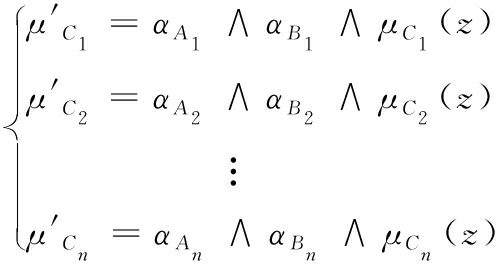
(15)
2.4 反模糊化
在推理得到的模糊集合中取一个相对最能代表该模糊集合单值的过程称为反模糊化(defuzzification),本文中采用重心法进行反模糊化运算,计算输出范围内一系列点的重心,即:
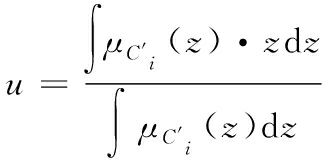
(16)
式(16)中,u表示反模糊化运算后的输出值,进而可以得出FA-PID算法的精确输出值{E,EC},即:
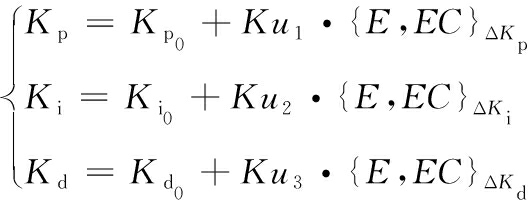
(17)
式(17)中,Kp0、Ki0和Kd0是PID算法中系数Kp、Ki和Kd的初始设定值,Ku1、Ku2和Ku3为相应的输出量化因子。
2.5 量化因子
模糊控制器除了需要具有良好的模糊规则外,合理地选择模糊控制器输入变量和输出控制量的增益系数同样非常重要。偏差e的量化因子Kc以及偏差变化率ec的量化因子Ke分别如下所示:
![]()
(18)
式(18)中:m和n分别为对应的模糊子集论域值;xc和xe分别为对应的模糊系统实际输入值。与此同时,输出量的量化因子Ku不同,加载到被控对象上的实际控制量也不同,其数值的选取同样非常重要。
3 仿真实验结果分析
3.1 电动舵机小角度位置响应分析
制导炮弹实际飞行过程中,电动舵机实时接收弹载计算机给定的舵偏角位置信号,其位置常在2°~12°、频率3~5 Hz之间运动。因此,结合制导炮弹实际飞行过程以及仿真测试环境中电动舵机系统的运行状态,本文中研究了电动舵机空载工况小角度位置下,采用FA-PID算法相比于传统PID控制的响应快速性与鲁棒性。图8为不同算法下电动舵机小角度位置响应曲线,表3为电动舵机小角度位置响应指标,可以得出采用FA-PID算法下的舵偏角位置响应延迟时间td为10.07 ms,上升时间tr为10.38 ms,峰值时间tp为18.95 ms,稳态误差仅为0.000 19°,相比于传统PID算法分别下降了约0.49%、6.91%、39.94%与94.44%,更加接近于设定参考值,且无超调现象,控制精度具有大幅度提升。
表3 电动舵机小角度位置响应指标
Table 3 Small angle position response index of EMA

算法td/mstr/mstp/msσ/%稳态误差/(°)PID10.1211.1531.55None0.003 42FA-PID10.0710.3818.95None0.000 19
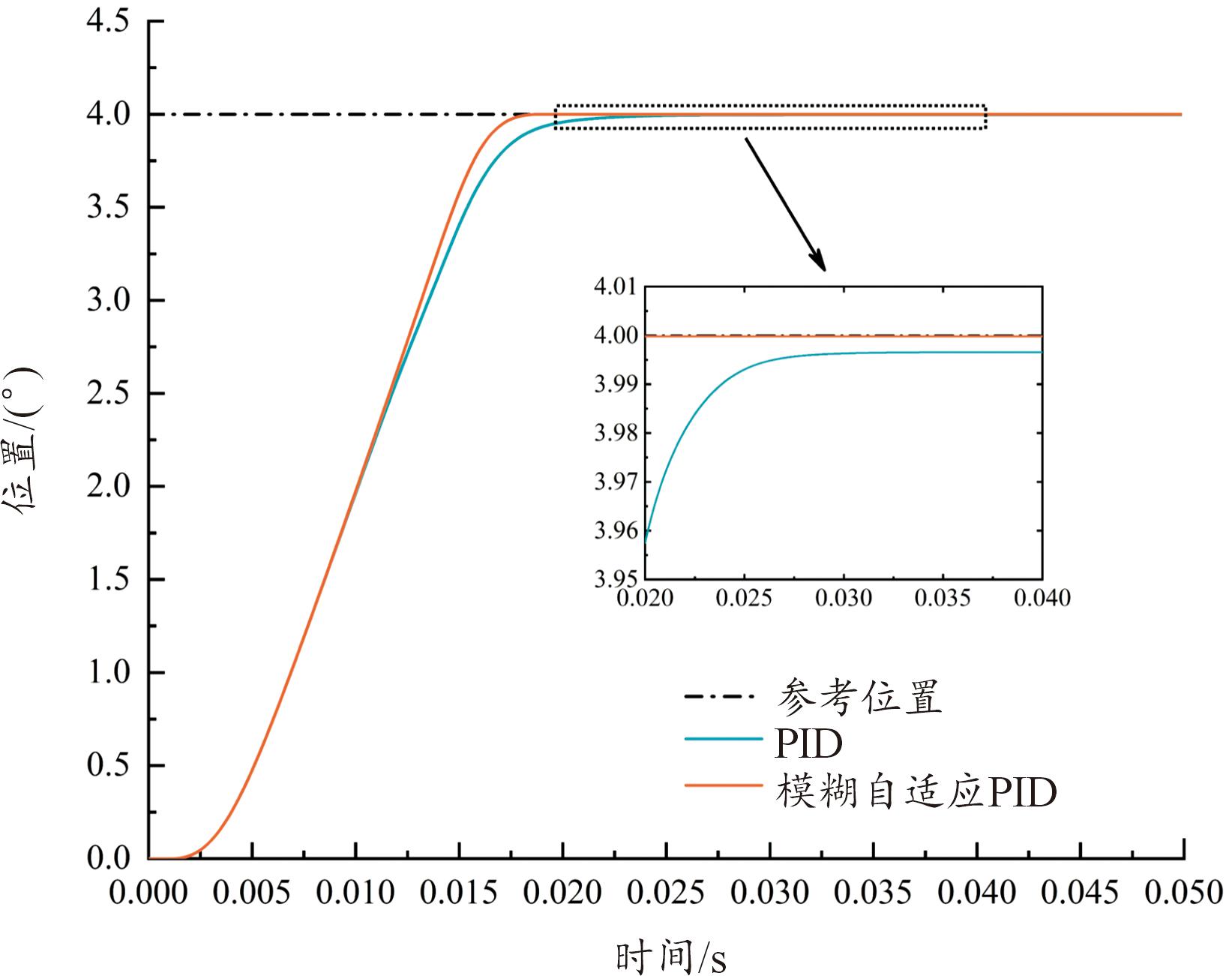
图8 电动舵机小角度位置响应曲线
Fig.8 Small angle position response curves of EMA
图9—图12分别为上述工况下所对应无刷直流电机的转速、电磁转矩、A相电流和A相反电动势曲线图,图中红色曲线表示采用FA-PID算法,蓝色曲线表示采用传统PID算法。从图9—图12中可以得出,电动舵机刚启动时转速、电磁转矩、相电流和反电动势均为零,启动瞬间电枢电流迅速增大,启动电流大有助于电机转子加速,使得电磁转矩较负载转矩大很多,转速迅速增加,转速增加使得舵偏角位置增大,随之引起反电动势增大,当电枢电流增长变缓直至达到极大值后开始减小。电流减小导致电磁转矩减小,舵偏角位置增加的加速度也变小,当舵偏角位置达到参考设定位置后,转速迅速减小,电机停止转动,系统保持稳态运行。并且从图中可以明显看出,采用FA-PID算法控制下的电机随电动舵机系统运行,相比于传统PID算法下电机转速、电磁转矩、相电流和反电动势的响应速度更快、扰动更小且运行更加平稳。
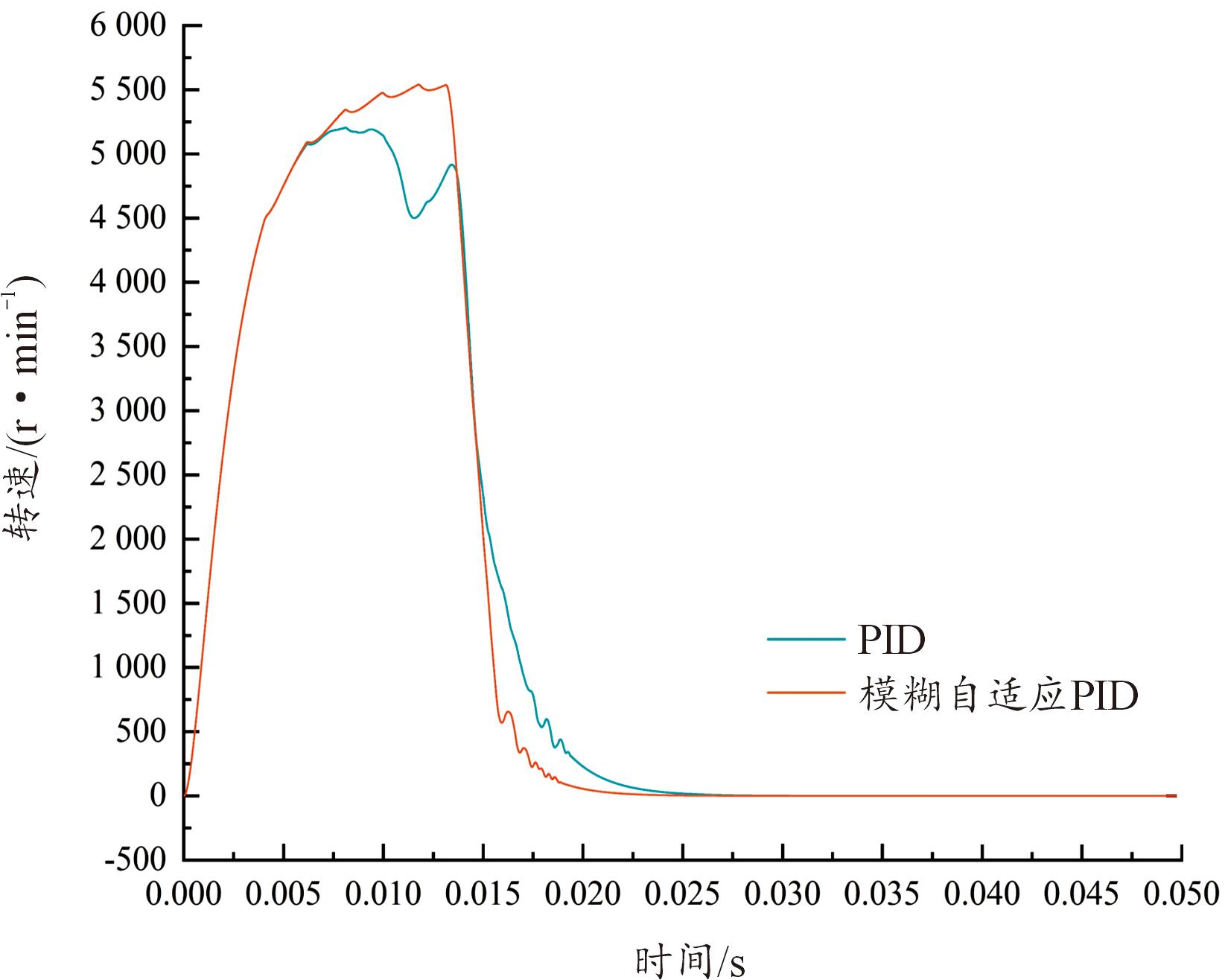
图9 电动舵机小角度位置下电机转速曲线
Fig.9 Motor speed curves under EMA samll angle position
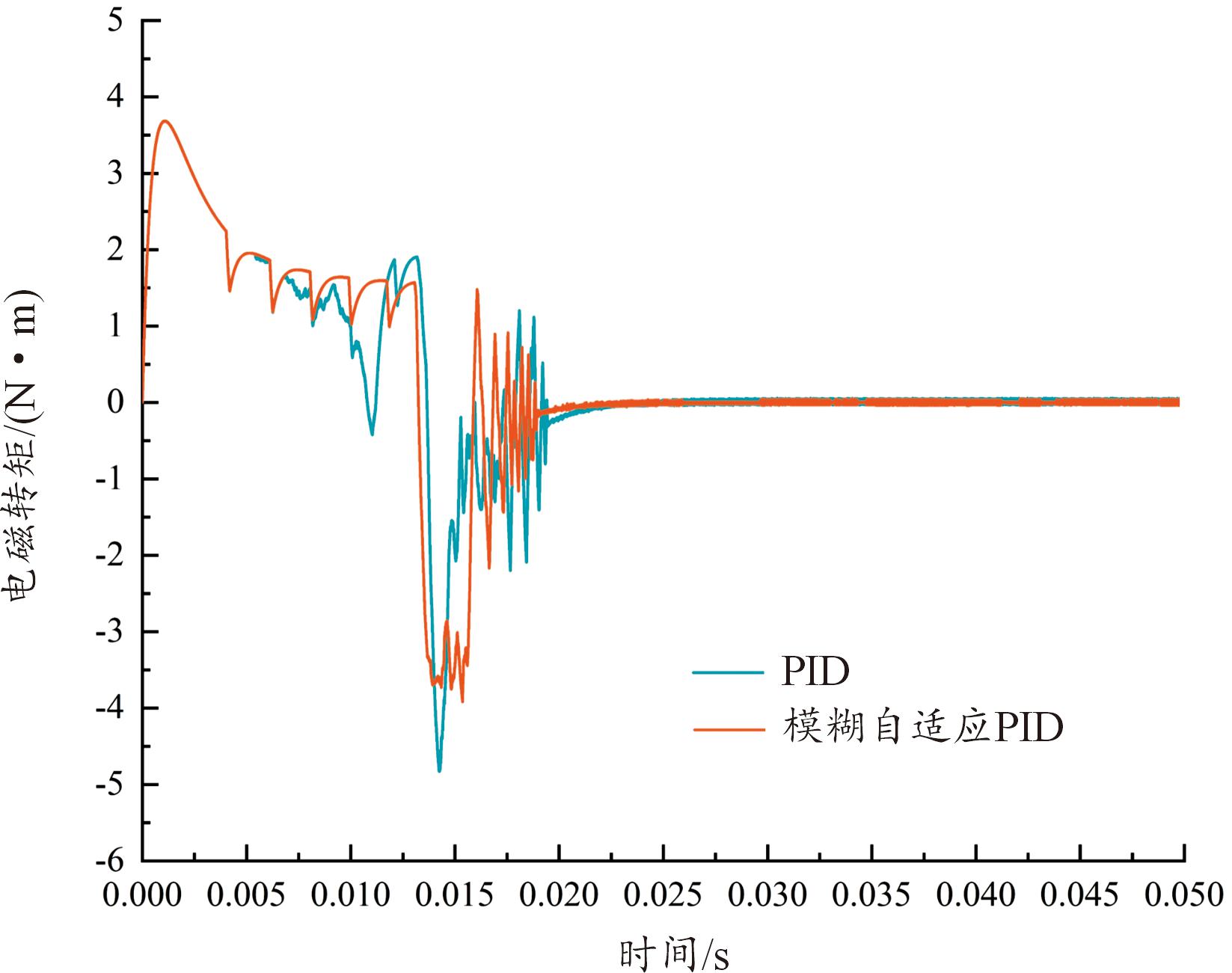
图10 电动舵机小角度位置下电磁转矩曲线
Fig.10 Electromagnetic torque curves under EMA small angle position
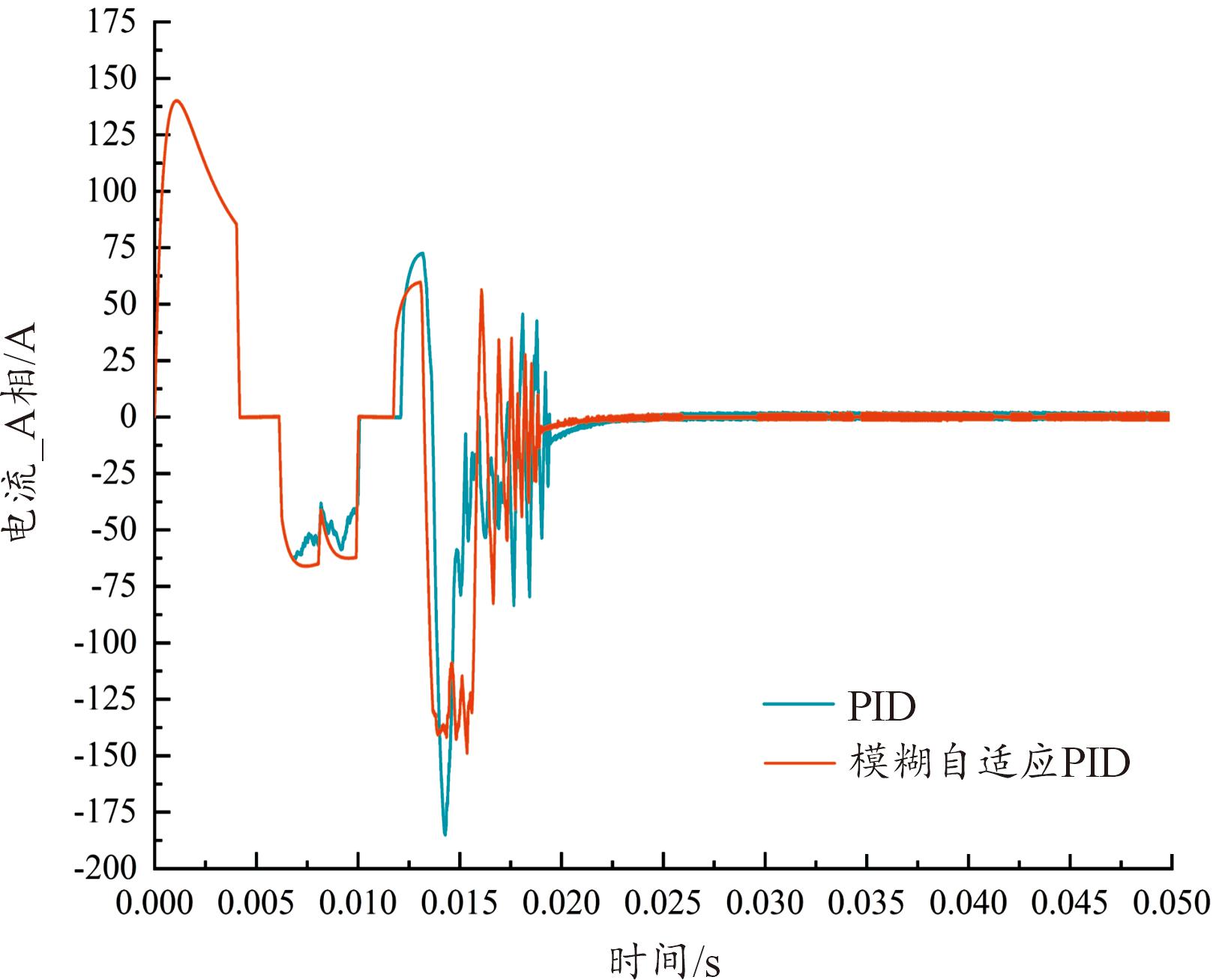
图11 电动舵机小角度位置下A相电流曲线
Fig.11 Phase-A current curves under EMA small angle position
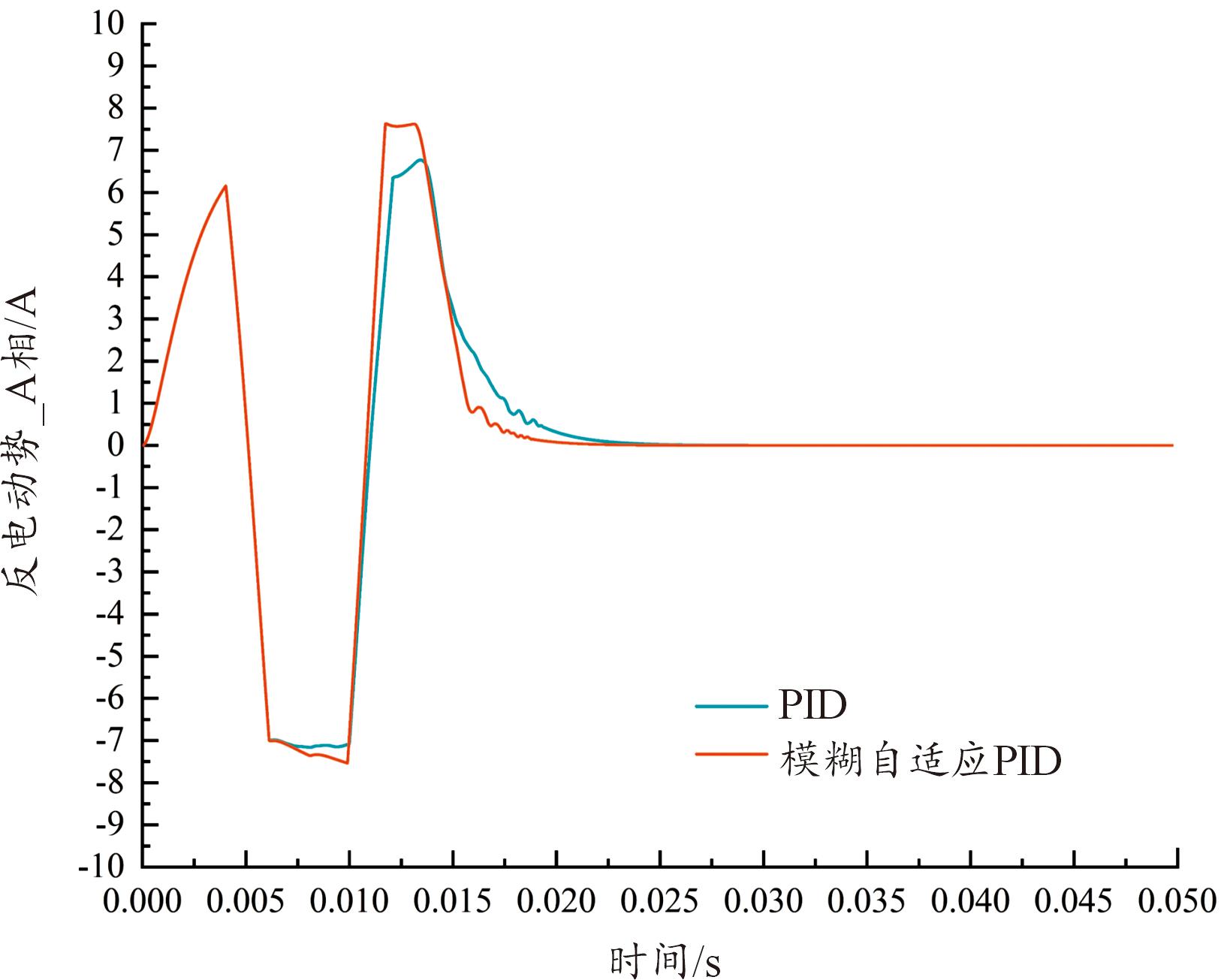
图12 电动舵机小角度位置下A相反电动势曲线
Fig.12 Phase-A electromotive force curves under EMA small angle position
3.2 电动舵机方波/正弦位置跟踪性能分析
在制导炮弹电动舵机系统的实际测试环境中,常以方波和正弦波作为设定位置信号来考核系统的各项指标以及动态性能,因此本小节分别在设定2种不同位置形式,小角度信号工况下进行舵机系统的位置跟踪响应分析研究。
图13为不同算法下设定舵偏角幅值4°、频率3 Hz的小角度方波位置响应曲线,采用参考方波信号可以得出系统的响应速度,从图13中曲线可以得出位置环采用FA-PID算法控制下的电动舵机系统具有较快的响应速度以及更小的稳态误差。图14为不同算法下设定舵偏角幅值4°、频率3 Hz的小角度正弦位置响应曲线,设定参考正弦信号方便考察系统的跟踪精度,从图中曲线可以看出采用FA-PID算法下的舵偏角位置跟踪具有较小的幅值和相位误差,更加接近于参考位置信号。
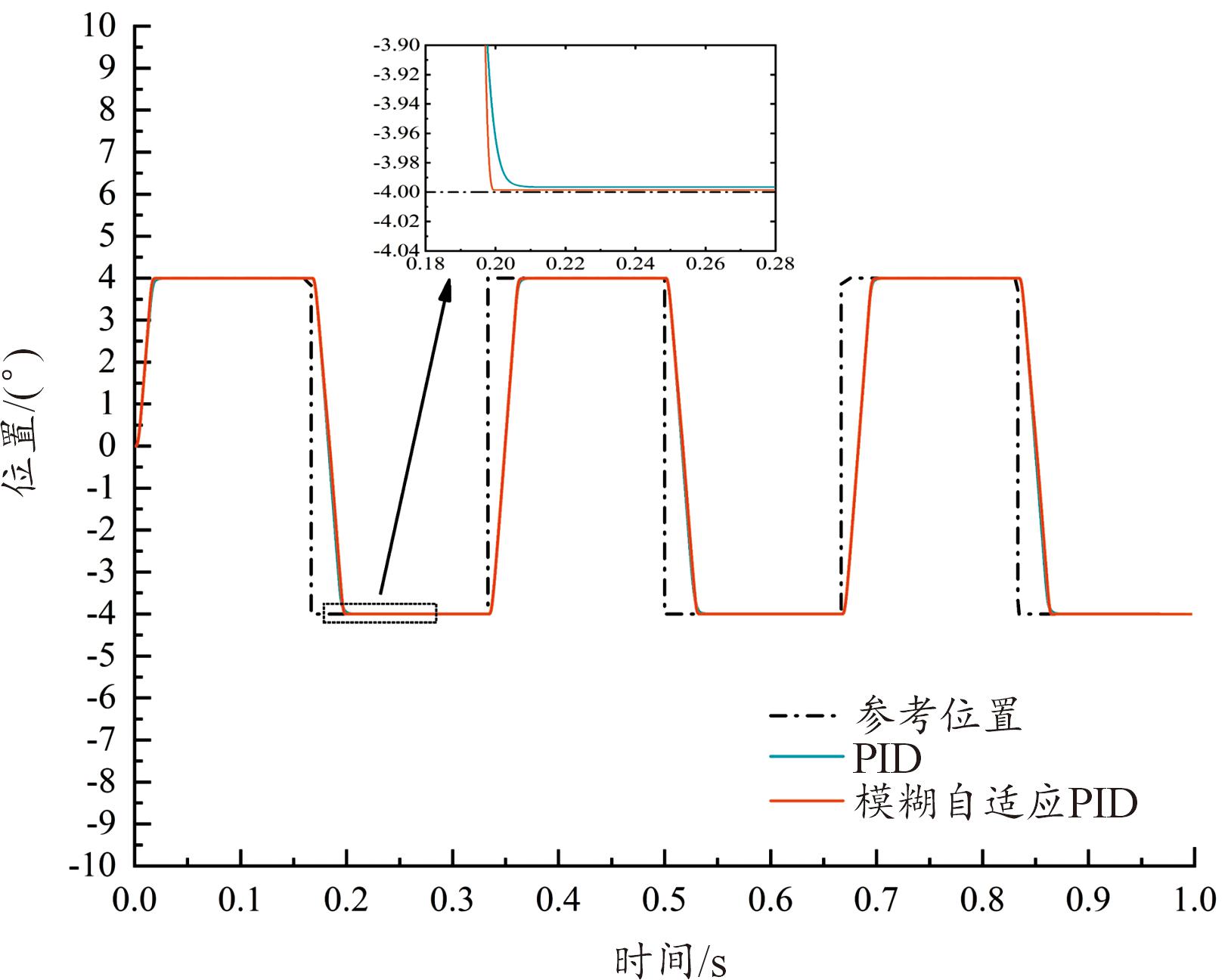
图13 不同算法下小角度方波位置响应曲线
Fig.13 Small angle square wave position response curves under different algorithms
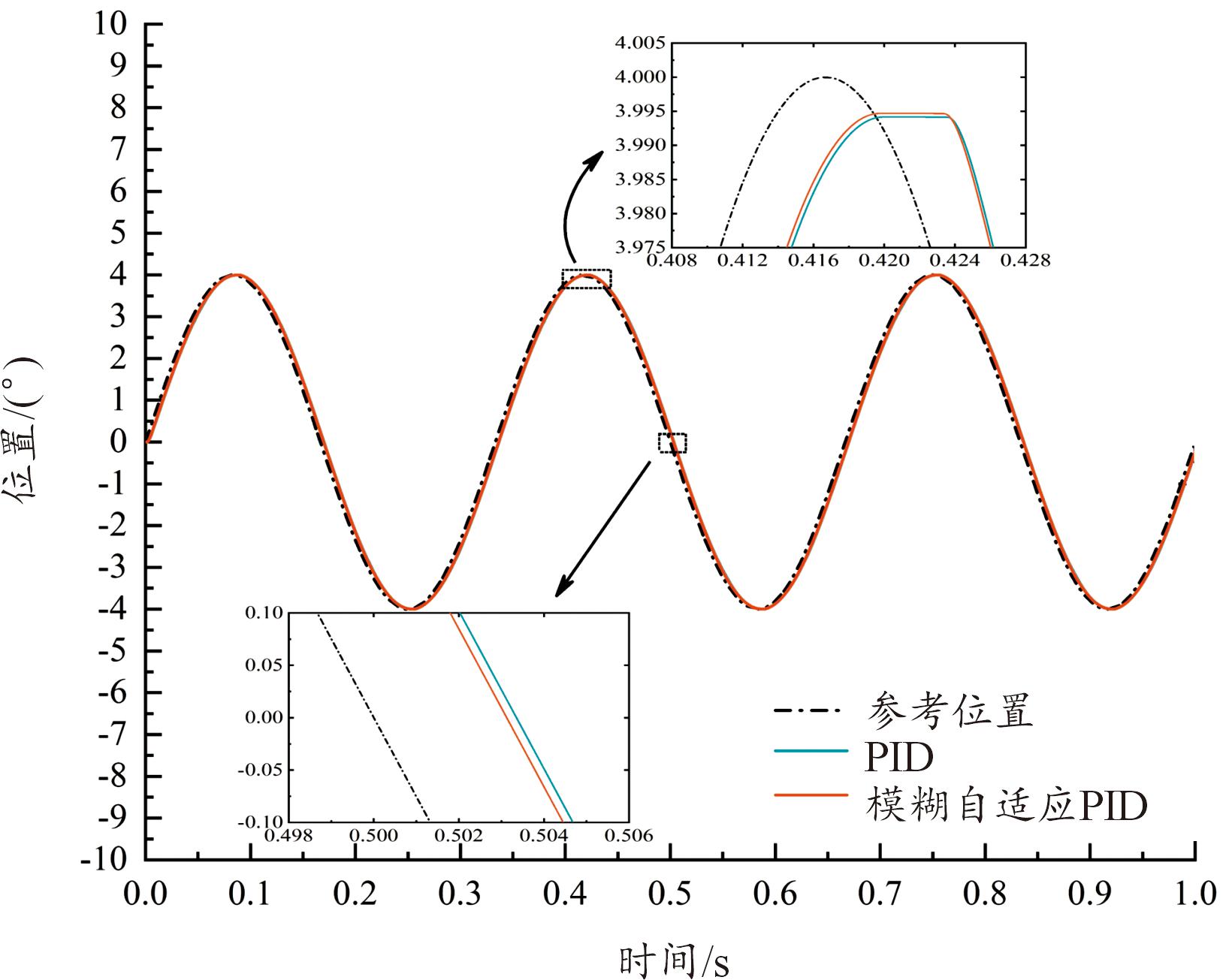
图14 不同算法下小角度正弦位置响应曲线
Fig.14 Small angle sine wave position response curves under different algorithms
4 结论
本文中针对电动舵机传统建模过程中常将各部分视为线性环节且建模不完善等问题,搭建了考虑多种非线性因素干扰下的电动舵机模型,设计了电机正反转逻辑换相判别模块,并将FA-PID算法应用于位置环控制系统中。可以得出以下结论:
1) 电动舵机位置环采用FA-PID算法相比于传统PID控制下小角度位置响应的延迟时间下降了约0.49%,上升时间下降了约6.91%,峰值时间下降了约39.94%,稳态误差下降了约94.44%,且无超调现象。
2) 电动舵机小角度位置采用FA-PID算法下的电机转速、电磁转矩、A相电流和A相反电动势具有更快的响应速度,更小的扰动且运行状态更加平稳。
3) 通过小角度方波/正弦位置信号响应跟踪情况同样可以得出FA-PID算法下的位置响应速度更快,且幅值和相位误差更小。
但与此同时,由于电动舵机系统内部存在多种非线性耦合因素的干扰,在正弦位置跟踪时易出现平顶现象,导致正弦位置跟踪不精确,因此如何抑制多种非线性复合因素的综合影响将成为下一步亟待解决的关键问题。
[1] 孟兵.弹道修正弹电动舵机的设计与控制[D].南京:南京理工大学,2014.MENG Bing.Design and control of EMA for ballistic correction projectile[D].Nanjing:Nanjing University of Science and Technology,2014.
[2] 殷希梅,张航.简谈中、小型制导弹药舵机的发展现状[J].兵工自动化,2019,38(4):71-74.YIN Ximei,ZHANG Hang.Discussion on development status of medium and small guided missile servo system[J].Ordnance Industry Automation,2019,38(4):71-74.
[3] LYSHEVSKI S E.Electromechanical flight actuators for advanced flight vehicles[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2):511-518.
[4] KIM S H,TANK M J.Modeling and experimental study on the dynamic stiffness of an electromechanical actuator[J].Journal of Spacecraft and Rockets,2016,53(4):708-719.
[5] 王一诚.弹用舵机控制技术研究[D].长沙:国防科学技术大学,2009.WANG Yicheng.The research of missile rudder control system[D].Changsha:National University of Defense Technology,2009.
[6] 崔业兵.制导火箭弹固定鸭式舵机滚转控制技术研究[D].南京:南京理工大学,2014.CUI Yebing.Research on rolling control technology of guided artillery rocket’s fixed canard rudder[D].Nanjing:Nanjing University of Science and Technology,2014.
[7] BENNETT S.Development of the PID controller[J].IEEE Control Systems,1993,13(6):58-62.
[8] 崔业兵,陈雄,蒋魏,等.自适应模糊神经控制器的电动舵机控制[J].微特电机,2013,41(12):57-60.CUI Yebing,CHEN Xiong,JIANG Wei,et al.Electromechanical actuator control with modified fuzzy neural network PID control[J].Small &Special Electrical Machine,2013,41(12):57-60.
[9] 夏长亮,李志强,王明超,等.基于RBF神经网络在线辨识的永磁无刷直流电机单神经元PID模型参考自适应控制[J].电工技术学报,2005,20(11):65-69.XIA Changliang,LI Zhiqiang,WANG Mingchao,et al.Single neuron PID model reference adaptive control for PM rushless DC motors based on RBF neural network on-line identification[J].Transactions of China Electrotechnical Society,2005,20(11):65-69.
[10] RUBAAI A,CASTRO-SITIRICHE M J,OFOLI A R.Design and implementation of parallel fuzzy PID controller for high-performance brushless motor drives:an intergrated enviroment for rapid control prototyping[J].IEEE Transactions on Industry Applications,2008,44(4):1090-1098.
[11] LU H,LI Y,TIAN S,et al.Improved hybrid robust control method for the electromechanical actuator in aircrafts[J].Chinese Journal of Mechanical Engineering,2010,23(4):443-450.
[12] LI Y,LU H,TIAN S,et al.Posture control of electromechanical actuator based thrust vector system for aircraft engine[J].IEEE Transactions on Industrial Electronics,2012,59(9):3561-3571.
[13] ZHOU M,MAO D,ZHANG M,et al.A hybrid control with PID-improved sliding mode for flat-top of missile electromechanical actuator systems[J].Sensors,2018,18:4449.
[14] 李冬辉,王立献,周满,等.基于改进径向基网络的电动舵机滑模控制[J].兵器装备工程学报,2023,44(4):217-223.LI Donghui,WANG Lixian,ZHOU Man,et al.Sliding mode control of electromechanical actuators based on an improved RBF network[J].Journal of Ordnance Equipment Engineering,2023,44(4):217-223.
[15] 田福庆,姜尚,梁伟阁.含齿隙弹载舵机的全局反步模糊自适应控制[J].自动化学报,2019,45(6):1177-1185.TIAN Fuqing,JIANG Shang,LIANG Weige.Global backstepping fuzzy adaptive control for ammunition actuator with backlash[J].Acta Automatica Sinica,2019,45(6):1177-1185.
[16] ZHANG M,ZHOU M,LIU H,et al.Friction compensation and observer-based adaptive sliding mode control of electromechanical actuator[J].Advances in Mechanical Engineering,2018,10(12):1-15.
[17] 杜仁慧,吴益飞,陈威,等.考虑LuGre摩擦的伺服系统自适应模糊控制[J].控制与决策,2013,28(8):1253-1256.DU Renhui,WU Yifei,CHEN Wei,et al.Adaptive fuzzy control for the servo system with LuGre friction[J].Control and Decision,2013,28(8):1253-1256.
[18] CANUDAS DE WIT C,OLSSON H,ASTROM K J,et al.A new model for control of systems with friction[J].IEEE Transaction on Automatic Control,1995,40(3):419-425.
[19] 李俊阳,赵琛,夏雨,等.基于改进LuGre摩擦模型的机器人关节模糊自适应反步控制[J].湖南大学学报(自然科学版),2022,49(10):147-156.LI Junyang,ZHAO Chen,XIA Yu,et al.Adaptive fuzzy backstepping control for robot joint based on modified LuGre friction model[J].Journal of Hunan Univeristy (Natural Sciences),2022,49(10):147-156.
[20] WANG B,IWASAKI M,YU J.Finite-time command-filtered backstepping control for dualvmotor servo systems with LuGre friction[J].IEEE Transactions on Industrial Informatics,2023,19(5):6376-6386.
[21] TERZIC B,JADRIC M.Design and implementation of extended kalman filter for the speed and rotor position estimation of brushless DC motor[J].IEEE Transactions on Industrial Electronics,2001,48(6):1065-1073.
[22] 谭建成,邵晓强.永磁无刷直流电机技术[M].北京:机械工业出版社,2018.TAN Jiancheng,SHAO Xiaoqiang.Permanent magnet brushless DC motor technology[M].Beijing:China Machine Press,2018.
[23] 杜仁慧,吴益飞,陈威,等.考虑齿隙伺服系统的反步自适应模糊控制[J].控制理论与应用,2013,30(2):254-260.DU Renhui,WU Yifei,CHEN Wei,et al.Adaptive backstepping fuzzy control for servo systems with backlash[J].Control Theory &Applications,2013,30(2):254-260.
[24] YUE F,LI X,CHEN C,et al.Adaptive integral backstepping sliding mode control for opto-electronic tracking system based on modified LuGre friction model[J].International Journal of Systems Science,2017,48(16):3374-3381.
[25] LIANG K,TU Q,SHEN X,et al.An improved lugre model for calculating static steering torque of rubber tracked chassis[J].Defence Technology,2022,18(5):797-810.
[26] 鲍文亮.联合直接攻击炸弹(JDAM)电动舵机控制系统的设计[D].哈尔滨:哈尔滨工业大学,2006.BAO Wenliang.Design of electromechanical actuator control system of joint direct attack munitions[D].Harbin:Harbin Institute of Technology,2006.
[27] ZADEH L A.Fuzzy sets[J].Information and Control,1965(8):338-353.